A&A 467, 21-35 (2007)
DOI: 10.1051/0004-6361:20066979
J. W. S. Blokland1 - R. Keppens1,2,3 - J. P. Goedbloed1,3
1 - FOM-Institute for Plasma Physics "Rijnhuizen'', Association Euratom-FOM, Trilateral Euregio Cluster, PO Box 1207, 3430 BE Nieuwegein, The Netherlands
2 - Centre for Plasma Astrophysics, K.U. Leuven, Belgium
3 - Astronomical Institute, Utrecht University, The Netherlands
Received 20 December 2006 / Accepted 25 February 2007
Abstract
Context. We present a detailed study of localised magnetohydrodynamical (MHD) instabilities occurring in two-dimensional magnetized accretion disks.
Aims. We model axisymmetric MHD disk tori, and solve the equations governing a two-dimensional magnetized accretion disk equilibrium and linear wave modes about this equilibrium. We show the existence of novel MHD instabilities in these two-dimensional equilibria which do not occur in an accretion disk in the cylindrical limit.
Methods. The disk equilibria are numerically computed by the FINESSE code. The stability of accretion disks is investigated analytically as well as numerically. We use the PHOENIX code to compute all the waves and instabilities accessible to the computed disk equilibrium.
Results. We concentrate on strongly magnetized disks and sub-Keplerian rotation in a large part of the disk. These disk equilibria show that the thermal pressure of the disk can only decrease outwards if there is a strong gravitational potential. Our theoretical stability analysis shows that convective continuum instabilities can only appear if the density contours coincide with the poloidal magnetic flux contours. Our numerical results confirm and complement this theoretical analysis. Furthermore, these results show that the influence of gravity can either be stabilizing or destabilizing on this new kind of MHD instability. In the likely case of a non-constant density, the height of the disk should exceed a threshold before this type of instability can play a role.
Conclusions. This localised MHD instability provides an ideal, linear route to MHD turbulence in strongly magnetized accretion disk tori.
Key words: accretion, accretion disks - instabilities - magnetohydrodynamics (MHD) - plasmas
Much research on accretion disk dynamics focuses on occuring accretion processes in an MHD framework. This is done linearly as well as non-linearly. The linear studies aim to understand the drivers of the accretion mechanism. This can be done by looking at waves and instabilities about a disk equilibrium in the cylindrical limit (see e.g. Keppens et al. 2002; Blokland et al. 2005; van der Swaluw et al. 2005, and references therein). In this limit the disk equilibrium is essentially one-dimensional and one can use a self-similar model like the one of Spruit et al. (1987). When instabilities are found, one must compute the resulting evolution non-linearly to see if these instabilities give rise to turbulence. This turbulence may be the source of an enhanced effective viscosity mechanism which causes an increased transport of angular momentum outwards, as needed for accretion (Shakura & Sunyaev 1973). Balbus & Hawley (1991) discussed that the MHD turbulence resulting from the magneto-rotational instability (Velikhov 1959 and Chandrasekhar 1960) could provide this angular momentum transport.
In the last years, global two or even three-dimensional magnetohydrodynamical (MHD) simulations of accretion disks have been performed (see for example Matsumoto & Shibata 1997 and Armitage 1998). In these simulations, the non-linear dynamics is usually interpreted as a direct consequence of the magneto-rotational instability (see for example Hawley et al. 2001) leading to angular momentum transport outwards. Another possibility for the initial and evolving dynamics is that both the convective and the magneto-rotational instability play an important role in the angular momentum transport (see for example Igumenshchev et al. 2003). In the latter case, these disks are known as convection-dominated accretion flows (CDAF). However,especially those global simulations starting from initial axisymmetric accretion tori (see for example Hawley 2000) are at best loosely connected to the linear stability studies. A detailed catalogue of the MHD spectrum of such two-dimensional disks is completely lacking. Moreover, the usual identification of the cause of the turbulent dynamics with the linear magneto-rotational or convective instability is mostly based on the extrapolation of the linear stability analysis from a one-dimensional to a two or three-dimensional accretion disk. Such extrapolating ignores the fact that if one performs a detailed MHD stability study of a two-dimensional accretion disk, one may find many new types of instability that all could lead to effective angular momentum transport. A recent example of such new, poloidal flow-driven type of instability is presented by Goedbloed et al. (2004a), where the Trans-slow Alfvén Continuum (TSAC) mode is shown to occur inside a disk with toroidal and super-slow poloidal flow in the presence of a strong gravitational potential.
This paper has two aims. The first one is to present the equations and the numerical solutions of two-dimensional MHD disk equilibria with toroidal flows, but without poloidal flows. This case is fundamentally different from the previously discussed one of combined poloidal and toroidal flows (Goedbloed et al. 2004a) because the equilibria are described by quite different flux functions. By considering an axisymmetric equilibrium, we are able to model a thick accretion disk without any further approximations. All the equilibria presented below are computed using the code FINESSE (Beliën et al. 2002). The second aim is to present a detailed stability analysis of these two-dimensional equilibria. The analysis is done theoretically as well as numerically. For the stability computations we have used the recently published spectral code PHOENIX (Blokland et al. 2006). To our knowledge, this kind of analysis for MHD disk equilibria with purely toroidal flow has never been presented in the astrophysical literature until now.
We will present a sample of disk equilibria where the disk plasma typically varies from strongly magnetized up to close to equipartition. Also, the rotational speed of the plasma varies from sub-Keplerian up to Keplerian. The theoretical part of the spectral analysis of these equilibria shows that the convective continuum instabilities may appear inside the disk. These instabilities are part of the continuous branches that exist in the MHD spectrum of the linear eigenmodes of the disk tori and are localised on magnetic flux surfaces. We derive a stability criterion for this instability. This criterion looks similar to the Schwarzschild criterion. However, our criterion governs convective instabilities along the poloidal magnetic field lines while the Schwarzschild criterion applies in the direction perpendicular to the poloidal magnetic field lines. This theoretical analysis has been verified by our numerical stability calculations.
The paper is organised as follows. In Sect. 2, we present the equations which govern a two-dimensional accretion disk equilibrium. In Sect. 3, we recall the essential elements from spectral theory of MHD waves and instabilities, such as the Frieman and Rotenberg formalism (Frieman & Rotenberg 1960), straight field line coordinates and representation. In Sect. 4, these are used to derive the equations for the continuous MHD spectrum and the stability criterion for the convective instability. The numerical codes FINESSE and PHOENIX are discussed in Sect. 5. In Sect. 6, we present our numerical results on the disk equilibria and their stability analysis. Finally, in Sect. 7, we summarise and present our conclusions.
We consider an axisymmetric accretion disk. Because of this symmetry, cylindrical coordinates
![]() are used and the equilibrium quantities only depend on the poloidal coordinates R and Z. The disk equilibrium is modeled by the ideal MHD equations,
are used and the equilibrium quantities only depend on the poloidal coordinates R and Z. The disk equilibrium is modeled by the ideal MHD equations,
| |
= | (5) | |
| = | (6) |
| (8) |
Three different projections can be applied on the momentum Eq. (1). The projections are in the toroidal direction and in the poloidal plane parallel and perpendicular to the poloidal magnetic field lines. From the toroidal projection one can show that the poloidal stream function is a flux function, i.e.
![]() .
The projection parallel to the poloidal magnetic field results in two equations,
.
The projection parallel to the poloidal magnetic field results in two equations,
![\begin{displaymath}R^{2}{\vec{\nabla}}\cdot\left( \frac{1}{R^{2}} {\vec{\nabla}}...
...ambda_{S} - \frac{\Phi}{T_{S}} \right) \right]^{-1} \right\}
\end{displaymath}](/articles/aa/full/2007/19/aa6979-06/img52.gif) |
(16) |
The density can be easily derived for all three assumptions by inserting the corresponding equation for the pressure into the momentum equations parallel to the poloidal magnetic field lines (9). The resulting density is
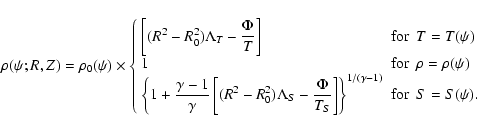 |
(17) |
For the investigation of stability properties of stationary MHD equilibria, the formalism by Frieman & Rotenberg (1960) has been used. They derived from the linearised MHD
equations, one second order differential equation for the Lagrangian displacement vector field
![]() ,
,
The analytical and numerical analysis of MHD waves and instabilities are done in "straight field line'' coordinates. To convert from cylindrical
![]() to straight field line coordinates
to straight field line coordinates
![]() one needs the metric tensor and the Jacobian associated with the non-orthogonal coordinates in which the equilibrium field lines appear straight. This is standard practice in MHD spectral studies for laboratory tokamak plasmas. The metric elements gij and the Jacobian J are
one needs the metric tensor and the Jacobian associated with the non-orthogonal coordinates in which the equilibrium field lines appear straight. This is standard practice in MHD spectral studies for laboratory tokamak plasmas. The metric elements gij and the Jacobian J are
gij = 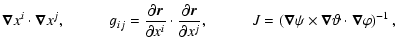 |
(24) |
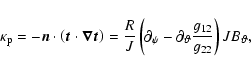 |
(26) |
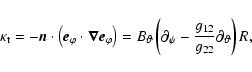 |
(27) |
On each flux surface the distinction between two wave directions can be made: one parallel and the other one perpendicular to the magnetic field. These directions correspond to the short wavelength limit of slow and Alfvén waves in cylindrical geometry. Hence, it is useful to exploit a projection based on the magnetic surfaces and field lines using the triad of unit vectors,
Using the straight field line coordinates and the projections (29) the Frieman-Rotenberg Eq. (18) can be written as
The matrices
![]() and
and
![]() enter if there is toroidal flow and/or external gravity. The expression for
these matrices are
enter if there is toroidal flow and/or external gravity. The expression for
these matrices are
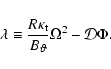 |
(40) |
Two kinds of cylindrical limits can be obtained from the spectral Eq. (33). The first one is the infinitely slender torus, meaning that the radial position of accretion disk is taken to be at infinity. In that case the matrices
![]() and
and
![]() disappear. This is due to the fact that all equilibrium quantities will be become independent of the angle
disappear. This is due to the fact that all equilibrium quantities will be become independent of the angle ![]() ,
the gravitational potential at infinity is zero, and the toroidal curvature
,
the gravitational potential at infinity is zero, and the toroidal curvature
![]() becomes zero. The flow enters only as a Doppler shift,
becomes zero. The flow enters only as a Doppler shift,
![]() ,
in the Doppler shifted eigenfrequency
,
in the Doppler shifted eigenfrequency
![]() .
.
The other limit is the cylindrical limit of a thin (
![]() )
slice of plasma at the equatorial plane of the accretion disk. In this region all equilibrium quantities only depend on the radius R, approximately. The matrices
)
slice of plasma at the equatorial plane of the accretion disk. In this region all equilibrium quantities only depend on the radius R, approximately. The matrices
![]() and
and
![]() do not disappear as in the previous limit. Also the toroidal curvature
do not disappear as in the previous limit. Also the toroidal curvature
![]() is non-zero but instead the poloidal curvature
is non-zero but instead the poloidal curvature
![]() .
In this case the spectral Eq. (33) reduces to the matrix equation for a one-dimensional accretion disk presented by Keppens et al. (2002).
.
In this case the spectral Eq. (33) reduces to the matrix equation for a one-dimensional accretion disk presented by Keppens et al. (2002).
Inserting the expression (41) into the second and third row of the spectral Eq. (33) results in an eigenvalue problem which is independent of the normal derivative. Hence, the reduced problem becomes non-singular. Exploiting this property, we can write the projected displacement field components Y and Z as follows:
| (42) |
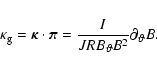 |
(48) |
![\begin{displaymath}N_{{\rm m,pol}}^{2} = \frac{\mu}{B^{2}}\left[ \frac{1}{J\rho}...
...frac{\rho}{\gamma p + B^{2}} {\vec{\nabla}}p \right) \right].
\end{displaymath}](/articles/aa/full/2007/19/aa6979-06/img146.gif) |
(49) |
The non-singular eigenvalue problem (43) is solved for poloidally periodic boundary conditionsfor the eigenfunctions ![]() ,
,
![]() .
Solving this problem for a given toroidal mode number n on each flux surface separately results in a set of discrete eigenvalues. All these discrete sets together map out the continuous spectra. In the MHD formulation with the primitive variables
.
Solving this problem for a given toroidal mode number n on each flux surface separately results in a set of discrete eigenvalues. All these discrete sets together map out the continuous spectra. In the MHD formulation with the primitive variables ![]() ,
,
![]() ,
p,
,
p, ![]() ,
an additional entropy continuum
,
an additional entropy continuum ![]() is found. This Eulerian entropy continuum does not couple to any of the other continua or stable and unstable modes (Goedbloed et al. 2004b).
is found. This Eulerian entropy continuum does not couple to any of the other continua or stable and unstable modes (Goedbloed et al. 2004b).
In this subsection a stability criterium for the continua will be derived. For this derivation we need to construct a Hilbert space with appropriate inner product. The parallel gradient operator
![]() is a Hermitian operator under the inner product
is a Hermitian operator under the inner product
| |
= | ![$\displaystyle \frac{\mu}{B^{2}}\left[ \frac{1}{J\rho}\partial_{\vartheta}\rho - \frac{\rho\mu}{\gamma p} \right]$](/articles/aa/full/2007/19/aa6979-06/img165.gif) |
|
| = | ![$\displaystyle \left[ \frac{{{\vec{B}}}_{\vartheta}\cdot{\vec{\nabla}}p}{\rho B}...
...eft( {\vec{\nabla}}\rho - \frac{\rho}{\gamma p} {\vec{\nabla}}p \right) \right]$](/articles/aa/full/2007/19/aa6979-06/img166.gif) |
||
| = | ![$\displaystyle -\left[ \frac{{{\vec{B}}}_{\vartheta}\cdot{\vec{\nabla}}p}{\rho B...
...]
\left[ \frac{{{\vec{B}}}_{\vartheta}\cdot{\vec{\nabla}}S}{\gamma BS} \right].$](/articles/aa/full/2007/19/aa6979-06/img167.gif) |
(56) |
For the stability analysis of axisymmetric accretion tori two numerical codes, the equilibrium code FINESSE (Beliën et al. 2002) and the spectral code PHOENIX (Blokland et al. 2006), have been used. In the next two subsections their algorithmic details will be briefly discussed.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{6979-01.ps} \end{figure}](/articles/aa/full/2007/19/aa6979-06/Timg177.gif) |
Figure 1: An example of the geometry of an accretion disk with a circular cross-section. Here, R0 and a are the major radius of the geometric axis and the radius of the last closed flux surface, respectively. |
| Open with DEXTER | |
The FINESSE code developed by Beliën et al. (2002) can compute a stationary axisymmetric, gravitating MHD equilibrium described by the extended Grad-Shafranov Eqs. (12), (14),
or (2) for a given poloidal cross-section and inverse aspect ratio
![]() .
Here, a and R0 are the minor radius of the last closed flux surface and the major radius of the geometric axis,
respectively. Figure 1 shows an example of the geometry of an accretion disk with a circular cross-section as seen in a poloidal plane with the central gravitational object at the origin. The extended
Grad-Shafranov equation has been discretized using a finite element method in combination with the standard
Galerkin method. The elements used are isoparametric bicubic Hermite ones. These bicubic elements ensure that the
computed solution has the desired high accuracy (fourth order) needed for the stability analysis. FINESSE solves the
elliptic PDE problem using the Picard iteration scheme. The imposed boundary conditions assume that the fixed
boundary represents the last closed flux surface. The same FINESSE code can actually handle the more general case
of stationary MHD equilibrium with non-vanishing poloidal flows as well, but here we restrict our discussion to
equilibria with purely toroidal flows.
.
Here, a and R0 are the minor radius of the last closed flux surface and the major radius of the geometric axis,
respectively. Figure 1 shows an example of the geometry of an accretion disk with a circular cross-section as seen in a poloidal plane with the central gravitational object at the origin. The extended
Grad-Shafranov equation has been discretized using a finite element method in combination with the standard
Galerkin method. The elements used are isoparametric bicubic Hermite ones. These bicubic elements ensure that the
computed solution has the desired high accuracy (fourth order) needed for the stability analysis. FINESSE solves the
elliptic PDE problem using the Picard iteration scheme. The imposed boundary conditions assume that the fixed
boundary represents the last closed flux surface. The same FINESSE code can actually handle the more general case
of stationary MHD equilibrium with non-vanishing poloidal flows as well, but here we restrict our discussion to
equilibria with purely toroidal flows.
The continuous spectrum is computed by a less expensive method introduced by Poedts & Schwarz (1993). In this method,
on each individual flux surface the cubic Hermite and the quadratic elements are replaced by
![]() and
and
![]() ,
respectively. Due to this replacement, the singular behaviour of the continuous spectrum has been
approximated by the perturbed quantities. This singular behaviour has been described by Goedbloed (1975)
and Pao (1975) for static, axisymmetric and toroidal plasma. Recently, the analogous treatment has been used
by Goedbloed et al. (2004a) for plasmas with toroidal and poloidal flows and gravity. The resulting eigenvalue
problem is then a small algebraic problem of a size set by the range in poloidal mode numbers m on each flux surface,
and is then solved using a direct QR method and a scan over all flux surfaces. This yields detailed information on all
MHD continua.
,
respectively. Due to this replacement, the singular behaviour of the continuous spectrum has been
approximated by the perturbed quantities. This singular behaviour has been described by Goedbloed (1975)
and Pao (1975) for static, axisymmetric and toroidal plasma. Recently, the analogous treatment has been used
by Goedbloed et al. (2004a) for plasmas with toroidal and poloidal flows and gravity. The resulting eigenvalue
problem is then a small algebraic problem of a size set by the range in poloidal mode numbers m on each flux surface,
and is then solved using a direct QR method and a scan over all flux surfaces. This yields detailed information on all
MHD continua.
We present our numerical results on disk equilibria and stability using the codes described in the previous section.
For the equilibrium computations the ratio of the specific heats
![]() and the gravitational potential is an
external Newtonian one, i.e.
and the gravitational potential is an
external Newtonian one, i.e.
![]() ,
where G and M* are the gravitational
constant and the mass of the central object, respectively. Furthermore, we assume that the density is a flux function
for all equilibrium computations. From our theoretical analysis above, this is the relevant case which may give rise to
damped stable and overstable continuum mode pairs due to the presence of toroidal flow and gravity.
,
where G and M* are the gravitational
constant and the mass of the central object, respectively. Furthermore, we assume that the density is a flux function
for all equilibrium computations. From our theoretical analysis above, this is the relevant case which may give rise to
damped stable and overstable continuum mode pairs due to the presence of toroidal flow and gravity.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{6979-02.ps} \end{figure}](/articles/aa/full/2007/19/aa6979-06/Timg183.gif) |
Figure 2:
The two-dimensional pressure (gray-scale) and plasma beta
|
| Open with DEXTER | |
As the first case, we take an accretion disk with constant density as also presented by Blokland et al. (2006). The equilibrium is described by the following flux functions:
![\begin{figure}
\par\includegraphics[width=6cm,clip]{6979-03a.ps}\includegraphics...
...=6cm,clip]{6979-03b.ps}\includegraphics[width=6cm,clip]{6979-03c.ps}\end{figure}](/articles/aa/full/2007/19/aa6979-06/Timg189.gif) |
Figure 3:
a) Real, and b) imaginary parts of the sub-spectrum of the MHD continua as functions of the radial flux coordinate
|
| Open with DEXTER | |
The computation of the continuous spectrum of this equilibrium is done for toroidal mode number n=-1 and poloidal mode numbers m=[-3,5]. Figure 3 shows the sub-spectrum of the MHD continua. The plots clearly indicate the existence of stable and overstable modes in the MHD continua. The plots (a) and (b) show the real and
imaginary part of the eigenfrequencies ![]() that belong to the continuous spectrum as a function of the radial flux coordinate
that belong to the continuous spectrum as a function of the radial flux coordinate
![]() .
The frequencies of the continua in the complex plane are shown in the plot (c). It should be noted that it is difficult to label the different branches of the MHD continua by a "dominant'' poloidal
mode number m. This could be done by making use of analytical expressions for an infinitely slender torus (
.
The frequencies of the continua in the complex plane are shown in the plot (c). It should be noted that it is difficult to label the different branches of the MHD continua by a "dominant'' poloidal
mode number m. This could be done by making use of analytical expressions for an infinitely slender torus (
![]() ), but then the gravity of the central object would be neglected. In our case, these expressions can hardly be used to identify the different branches of the MHD continua, because gravity plays a dominant role in the equilibrium as well as in the spectral analysis. Notice that in plot (a) two branches merge at
), but then the gravity of the central object would be neglected. In our case, these expressions can hardly be used to identify the different branches of the MHD continua, because gravity plays a dominant role in the equilibrium as well as in the spectral analysis. Notice that in plot (a) two branches merge at
![]() ,
while at the same location the imaginary part of the eigenfrequency starts to become non-zero. Intricate mode couplings thus give rise to the emergence of pairs of overstable and damped stable modes.
,
while at the same location the imaginary part of the eigenfrequency starts to become non-zero. Intricate mode couplings thus give rise to the emergence of pairs of overstable and damped stable modes.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6979-04.ps} \end{figure}](/articles/aa/full/2007/19/aa6979-06/Timg192.gif) |
Figure 4:
The growth rate of the most unstable continuum mode as a function of the value of gravitational potential on the magnetic axis
|
| Open with DEXTER | |
![\begin{figure}
\par\begin{tabular}{ll}
\includegraphics[width=5.5cm,clip]{6979-...
...
\includegraphics[width=5.5cm,clip]{6979-05c.ps} &
\end{tabular} \end{figure}](/articles/aa/full/2007/19/aa6979-06/Timg193.gif) |
Figure 5: The Brunt-Väisälä frequency projected on a flux surface for the points a), b), and c) shown in Fig. 4 shown as a contour plot in a poloidal cross-section. |
| Open with DEXTER | |
Next, we investigate the influence of the external gravitational potential on the overstable modes presented in the previous figure. This is done by varying the mass of the central object GM*. The result is shown in Fig. 4, where the most overstable mode of the MHD continua is plotted as function of
the gravitational potential on the magnetic axis
![]() .
Notice that each point in this plot corresponds to a different equilibrium calculated with FINESSE. PHOENIX is used to analyse the stability of the computed equilibrium. The gravitational potential is stabilizing from 0 to -0.01 and destabilizing from -0.01 to lower values. The zero value corresponds to a toroidally rotating, non-gravitating "tokamak'' plasma. Its instability is in agreement with the results by van der Holst et al. (2000a). Figure 5 shows the projected Brunt-Väisälä frequency for the points (a), (b), and (c) indicated in Fig. 4. Plot (a) shows that the minimum value of this frequency is reached inside the plasma, while plot (c) shows that this value is reached at the edge of the accretion disk. Point (b) is the transition from the minimum value inside to the edge of the disk as seen in plot (b).
.
Notice that each point in this plot corresponds to a different equilibrium calculated with FINESSE. PHOENIX is used to analyse the stability of the computed equilibrium. The gravitational potential is stabilizing from 0 to -0.01 and destabilizing from -0.01 to lower values. The zero value corresponds to a toroidally rotating, non-gravitating "tokamak'' plasma. Its instability is in agreement with the results by van der Holst et al. (2000a). Figure 5 shows the projected Brunt-Väisälä frequency for the points (a), (b), and (c) indicated in Fig. 4. Plot (a) shows that the minimum value of this frequency is reached inside the plasma, while plot (c) shows that this value is reached at the edge of the accretion disk. Point (b) is the transition from the minimum value inside to the edge of the disk as seen in plot (b).
To model a more realistic accretion disk equilibrium, we allow a density gradient across the poloidal magnetic
surfaces. All other flux functions are kept as in the previous case, i.e.
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{6979-06.ps} \end{figure}](/articles/aa/full/2007/19/aa6979-06/Timg201.gif) |
Figure 6:
The pressure (gray-scale) and plasma beta
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{6979-07a.ps}\includegraphics[width=6cm,clip]{6979-07b.ps}\end{figure}](/articles/aa/full/2007/19/aa6979-06/Timg202.gif) |
Figure 7:
For the accretion disk equilibrium shown in Fig. 6, a) the real parts of the sub-spectrum of MHD continua as function of the radial flux coordinate
|
| Open with DEXTER | |
For this case, the continuous spectrum has been computed for toroidal mode number n=1 and poloidal mode
numbers m=[-3,5]. The results are shown in Fig. 7, which contains two plots.
In the left one, the real part of the eigenvalues is plotted against the "radial'' coordinate
![]() ,
while the right one shows the eigenvalues in the complex plane. For this case, there are neither purely exponential
unstable or overstable modes. Due to the presence of toroidal flow, gravity and a non-constant density, it is
possible to create new or wider gaps between the different MHD continuum branches, with avoided crossings as a result
of poloidal mode couplings. This has been shown by van der Holst et al. (2000b) for tokamak equilibria with toroidal flow. In these gaps, there may exist global modes similar to the Toroidal Flow-induced Alfvén
Eigenmode (TFAE) for tokamaks found by van der Holst et al. (2000a) or to the Stratification-induced
Alfvén Eigenmode (SAE) for coronal flux tubes found by Beliën et al. (1996). We will investigate this
possibility for novel global modes in accretion disk context in future work.
,
while the right one shows the eigenvalues in the complex plane. For this case, there are neither purely exponential
unstable or overstable modes. Due to the presence of toroidal flow, gravity and a non-constant density, it is
possible to create new or wider gaps between the different MHD continuum branches, with avoided crossings as a result
of poloidal mode couplings. This has been shown by van der Holst et al. (2000b) for tokamak equilibria with toroidal flow. In these gaps, there may exist global modes similar to the Toroidal Flow-induced Alfvén
Eigenmode (TFAE) for tokamaks found by van der Holst et al. (2000a) or to the Stratification-induced
Alfvén Eigenmode (SAE) for coronal flux tubes found by Beliën et al. (1996). We will investigate this
possibility for novel global modes in accretion disk context in future work.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{6979-08.ps} \end{figure}](/articles/aa/full/2007/19/aa6979-06/Timg203.gif) |
Figure 8:
The pressure (gray-scale) and plasma beta
|
| Open with DEXTER | |
Next, we increase the inverse aspect ratio ![]() from 0.1 to 0.5, while keeping all other quantities the same.
Again, the poloidal cross-section is chosen circular. The resulting pressure profile is presented in
Fig. 8. Here, The pressure decreases monotonically outward, similar to the equilibrium
with constant density. Again, the term
from 0.1 to 0.5, while keeping all other quantities the same.
Again, the poloidal cross-section is chosen circular. The resulting pressure profile is presented in
Fig. 8. Here, The pressure decreases monotonically outward, similar to the equilibrium
with constant density. Again, the term
![]() dominates in the pressure Eq. (13).
The inverse aspect ratio is now not small so that both the gravitational potential and the density determines the
shape of the pressure profile. Also in this case, the temperature decreases in the outward direction. The plasma
beta
dominates in the pressure Eq. (13).
The inverse aspect ratio is now not small so that both the gravitational potential and the density determines the
shape of the pressure profile. Also in this case, the temperature decreases in the outward direction. The plasma
beta ![]() of this accretion disk ranges from 0.237 up to 0.970 and reaches its maximum within the disk. The
deviation from a Keplerian disk is expressed by the ratio
of this accretion disk ranges from 0.237 up to 0.970 and reaches its maximum within the disk. The
deviation from a Keplerian disk is expressed by the ratio
![]() .
Thus the
disk completely rotates sub-Keplerian.
.
Thus the
disk completely rotates sub-Keplerian.
![\begin{figure}
\par\begin{tabular}{l}
\includegraphics[height=0.2\textheight,cl...
...ludegraphics[height=0.2\textheight,clip]{6979-09c.ps} \end{tabular} \end{figure}](/articles/aa/full/2007/19/aa6979-06/Timg208.gif) |
Figure 9:
For the thick disk equilibrium shown in Fig. 8, a) the real and b) imaginary parts of the sub-spectrum of the MHD continua as a function of the radial flux coordinate
|
| Open with DEXTER | |
For this equilibrium, the continuous MHD spectrum is computed, again for toroidal mode number n=-1 and poloidal
mode numbers m=[-3,5]. A part of the spectra is plotted in Fig. 9. Plot (a) shows
the real part of the continuous MHD spectrum, while plot (c) shows the imaginary part as a function of the radial
flux coordinate
![]() .
Plot (c) contains the eigenfrequencies plotted in the complex plane.
This shows the existence of overstable modes in a thick accretion disk due to the presence of toroidal flow and
gravity. If one carefully examines the plot (a) one sees that one of the continuum branches splits in two
at
.
Plot (c) contains the eigenfrequencies plotted in the complex plane.
This shows the existence of overstable modes in a thick accretion disk due to the presence of toroidal flow and
gravity. If one carefully examines the plot (a) one sees that one of the continuum branches splits in two
at
![]() ,
where the imaginary part becomes zero and at
,
where the imaginary part becomes zero and at
![]() that these two continuum branches
merge again, whereas the imaginary part becomes non-zero.
that these two continuum branches
merge again, whereas the imaginary part becomes non-zero.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{6979-10.ps} \end{figure}](/articles/aa/full/2007/19/aa6979-06/Timg214.gif) |
Figure 10:
Growth rate of the most overstable continuum mode as a function of the inverse aspect
ratio
|
| Open with DEXTER | |
The stability of the disk equilibria have been analysed theoretically as well as numerically. From theory,
a stability criterion has been derived which closely resembles the Schwarzschild criterion. It is shown that
in a disk where the density is a flux function, the MHD continua can turn overstable due to the presence of
toroidal rotation and gravity. This instability is not possible for disks where the temperature or the entropy is a
flux function. The numerical results support our theoretical conclusion. The effect of the gravity on the overstable
modes can either be stabilizing or destabilizing. In the case of non-constant density the inverse aspect
ratio ![]() has been varied. This study shows that the continua turn overstable if the inverse aspect ratio is
larger than a certain critical value, approximately 0.24. These localised instabilities will lead to small-scale,
turbulent dynamics when the equilibria are used in initial conditions for non-linear simulations. This dynamics
is unrelated the usual magneto-rotational instability. Indeed, these instabilities, as well as the poloidal flow
driven unstable continuum modes investigated by Goedbloed et al. (2004a), provide a new route to MHD turbulence
in accretion disks. Furthermore, due to the presence of gravity, it is possible to widen or create new gaps in the
MHD continua. It is possible to show this theoretically by expanding the eigenfunctions in poloidal harmonics.
In these gaps new types of global ideal MHD eigenmodes can exist. The investigation of these global eigenmodes is
left for future work.
has been varied. This study shows that the continua turn overstable if the inverse aspect ratio is
larger than a certain critical value, approximately 0.24. These localised instabilities will lead to small-scale,
turbulent dynamics when the equilibria are used in initial conditions for non-linear simulations. This dynamics
is unrelated the usual magneto-rotational instability. Indeed, these instabilities, as well as the poloidal flow
driven unstable continuum modes investigated by Goedbloed et al. (2004a), provide a new route to MHD turbulence
in accretion disks. Furthermore, due to the presence of gravity, it is possible to widen or create new gaps in the
MHD continua. It is possible to show this theoretically by expanding the eigenfunctions in poloidal harmonics.
In these gaps new types of global ideal MHD eigenmodes can exist. The investigation of these global eigenmodes is
left for future work.
Acknowledgements
This work was carried out within the framework of the European Fusion Programme, supported by the European Communities under contract of the Association EURATOM/FOM. Views and opinions expressed herein do not necessarily reflect those of the European Commission. This work is part of the research programme of the "Stichting voor Fundamenteel Onderzoek der Materie (FOM)'', which is financially supported by the "Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO)''.