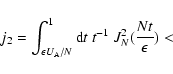A&A 467, 15-20 (2007)
DOI: 10.1051/0004-6361:20066932
M. Vukcevic1,2 - R. Schlickeiser1
1 - Institut für Theoretische Physik, Lehrstuhl IV:
Weltraum- und Astrophysik, Ruhr-Universität Bochum, 44780 Bochum, Germany
2 - Department of Physics, University of Montenegro, Podgorica, Montenegro
Received 14 December 2006 / Accepted 22 February 2007
Abstract
Context. The mean free path and anisotropy of galactic cosmic rays is calculated in weak plasma wave turbulence that is isotropically distributed with respect to the ordered uniform magnetic field.
Aims. The modifications on the value of the Hillas energy, above which cosmic rays are not confined to the Galaxy, are calculated. The original determination of the Hillas limit has been based on the case of slab turbulence where only parallel propagating plasma waves are allowed.
Methods. We use quasilinear cosmic ray Fokker-Planck coefficients to calculate the mean free path and the anisotropy in isotropic plasma wave turbulence.
Results. In isotropic plasma wave turbulence the Hillas limit is enhanced by about four orders of magnitude to
![]()
![]()
![]() PeV resulting from the dominating influence of transit-time damping interactions of cosmic rays with obliquely propagating magnetosonic waves.
PeV resulting from the dominating influence of transit-time damping interactions of cosmic rays with obliquely propagating magnetosonic waves.
Conclusions. Below the energy ![]() the cosmic ray mean free path and the anisotropy exhibit the well known E1/3 energy dependence. At energies higher than
the cosmic ray mean free path and the anisotropy exhibit the well known E1/3 energy dependence. At energies higher than ![]() both transport parameters steepen to a E3-dependence. This implies that cosmic rays even with ultrahigh energies of several hundreds of EeV can be rapidly pitch-angle scattered by interstellar plasma turbulence, and are thus confined to the Galaxy.
both transport parameters steepen to a E3-dependence. This implies that cosmic rays even with ultrahigh energies of several hundreds of EeV can be rapidly pitch-angle scattered by interstellar plasma turbulence, and are thus confined to the Galaxy.
Key words: ISM: cosmic rays - ISM: magnetic fields - plasmas - scattering
To unravel the nature of cosmic sources that accelerate cosmic rays to ultrahigh
energies has been identified as one of the eleven
fundamental science questions for the new century (Turner et al. 2002). Cosmic rays with energies up to at least 1014 eV are likely accelerated at the shock fronts associated with supernova remnants
(for review see Blandford & Eichler 1987). Radio emissions and X-rays give conclusive
evidence that electrons are accelerated there to near-light speed (Koyama et al. 1995, 1997; Tanimori et al. 2001; Allen et al. 1997; Slane et al. 1999;
Borkowski et al. 2001). The HESS observations of supernova remnants up to ![]() 100 TeV
provide direct evidence of very high energy particle acceleration in the shocks
(Aharonian et al. 2004,2005), while the
leptonic or hadronic nature of these gamma-rays is currently being disputed (e.g. Enomoto et al. 2002; Reimer & Pohl 2002). The supernova remnant origin would be consistent
with the observed GeV excess of diffuse galactic gamma radiation from the inner Galaxy
(Büsching et al. 2001), although the GeV excess has been found to be present in all directions including galactic latitudes where no supernova remnants are present and the outer Galaxy (Strong et al. 2004).
This indicates that the origin of the GeV excess is more complex and is not straightforwardly
connected with supernova remnants in the inner Galaxy.
100 TeV
provide direct evidence of very high energy particle acceleration in the shocks
(Aharonian et al. 2004,2005), while the
leptonic or hadronic nature of these gamma-rays is currently being disputed (e.g. Enomoto et al. 2002; Reimer & Pohl 2002). The supernova remnant origin would be consistent
with the observed GeV excess of diffuse galactic gamma radiation from the inner Galaxy
(Büsching et al. 2001), although the GeV excess has been found to be present in all directions including galactic latitudes where no supernova remnants are present and the outer Galaxy (Strong et al. 2004).
This indicates that the origin of the GeV excess is more complex and is not straightforwardly
connected with supernova remnants in the inner Galaxy.
More puzzling are the much higher energy cosmic rays
with energies as large as 1020.5 eV. It has been argued (Lucek & Bell 2000; Bell & Lucek 2001; Hillas 2006) that, due to the amplification of the magnetic field in the shock, the acceleration of cosmic rays in
young supernova remnants is possible up to ![]() 1018 eV. This implies that such particles may
have a Galactic origin. For ultrahigh-energy (
1018-1020.5 eV) cosmic rays an extragalatic origin is favored by many researchers.
Extragalactic ultrahigh-energy cosmic rays (UHECRs) coming
from cosmological distances
1018 eV. This implies that such particles may
have a Galactic origin. For ultrahigh-energy (
1018-1020.5 eV) cosmic rays an extragalatic origin is favored by many researchers.
Extragalactic ultrahigh-energy cosmic rays (UHECRs) coming
from cosmological distances ![]() 50 Mpc should interact with the universal
cosmic microwave background radiation (CMBR) and produce pions. For an extragalactic origin
of UHECRs the detection or non-direction of the Greisen-Kuzmin-Zatsepin cutoff resulting
from the photopion attenuation in the CMBR will have far-reaching consequences not only for
astrophysics but also for fundamental particle physics as e.g. the breakup of Lorentz symmetry (Coleman & Glashow 1997) or the non-commutative quantum picture of
spacetime (Amelio-Camelia et al. 1998).
50 Mpc should interact with the universal
cosmic microwave background radiation (CMBR) and produce pions. For an extragalactic origin
of UHECRs the detection or non-direction of the Greisen-Kuzmin-Zatsepin cutoff resulting
from the photopion attenuation in the CMBR will have far-reaching consequences not only for
astrophysics but also for fundamental particle physics as e.g. the breakup of Lorentz symmetry (Coleman & Glashow 1997) or the non-commutative quantum picture of
spacetime (Amelio-Camelia et al. 1998).
Radio synchrotron radiation intensity and polarisation surveys
of our own and external galaxies (for review see Sofue et al. 1986) have revealed that
the interstellar medium is transversed by large-scale ordered
magnetic fields with superposed plasma wave turbulence. The Galactic magnetic field
has a regular and a random component of about equal strength. The turbulent field has a broad spectrum of scales with the largest one being 10-100 pc (e.g. Beck 2007, and references therein). This could be compared with the gyroradius of ![]() 1 pc for 1015 eV particles, or
1 pc for 1015 eV particles, or ![]() 1 kpc for 1018 eV particles. The conventional size of the Galactic halo derived from abundances of radioactive isotopes in
cosmic rays is about 4-6 kpc (Ptuskin & Soutoul 1998; Strong & Moskalenko 1998;
Webber & Soutoul 1998). The turbulent magnetic field may thus present a mechanism for isotropization of Galactic cosmic rays up to
1017-1018 eV (see, e.g., Candia et al.
2003).
1 kpc for 1018 eV particles. The conventional size of the Galactic halo derived from abundances of radioactive isotopes in
cosmic rays is about 4-6 kpc (Ptuskin & Soutoul 1998; Strong & Moskalenko 1998;
Webber & Soutoul 1998). The turbulent magnetic field may thus present a mechanism for isotropization of Galactic cosmic rays up to
1017-1018 eV (see, e.g., Candia et al.
2003).
According to the current understanding (reviewed in Schlickeiser 2002) the relativistic
charged particles (hereafter referred to
as cosmic ray particles) in these space plasmas are confined and accelerated by
resonant interactions in these weakly random electromagnetic fields.
In the presence of low-frequency magnetohydrodynamic plasma waves, whose
magnetic field component is much larger than their electric field
component, the particle's phase space distribution function
adjusts rapidly to a quasi-equilibrium through pitch-angle diffusion, which
is close to the isotropic distribution. The isotropic part
of the phase space distribution function F(z,p,t) obeys the diffusion-convection-equation
![\begin{displaymath}{\partial F\over \partial t}-\; S_0=
{\partial \over \partial...
...ial F\over \partial z}\Bigr]
-\; V{\partial F\over \partial z}
\end{displaymath}](/articles/aa/full/2007/19/aa6932-06/img10.gif)
For many years the theoretical development of the resonant wave-particle
interactions has mainly concentrated on the special case that the plasma waves
propagate only parallel or antiparallel to the ordered magnetic field - the socalled slab turbulence. In this case only cosmic ray particles with gyroradii ![]() smaller than the
longest parallel wavelength
smaller than the
longest parallel wavelength
![]() of the plasma waves
can resonantly interact. Obviously this condition is
equivalent to a limit on the maximum particle rigidity R:
of the plasma waves
can resonantly interact. Obviously this condition is
equivalent to a limit on the maximum particle rigidity R:
It is the purpose of this work to investigate
how the Hillas limit (6) is affected if we discard
the assumption of purely slab plasma waves, i.e. if we allow for oblique
propagation angles ![]() of the plasma waves with respect to the ordered magnetic
field component. There is ample observational evidence that obliquely propagating
magnetohydrodynamic plasma waves exist in the interstellar medium (Armstrong et al. 1995;
Lithwick & Goldreich 2001; Cho et al. 2002).
In particular, we will consider the alternative extreme limit
that the plasma waves propagation angles are isotropically distributed
around the magnetic field direction. It has been emphasised before by
Schlickeiser & Miller (1998) referred to as SM) that oblique propagation
angles of fast magnetosonic waves leads to an order of magnitude quicker
stochastic acceleration rate as compared to the slab case, since the
compressional component of the obliquely propagating fast
mode waves allows the effect of transit-time damping acceleration of
cosmic ray particles. Here we will demonstrate that the obliqueness of
fast mode and shear Alfven wave propagation
also modifies the resulting parallel spatial diffusion coefficient
and the Hillas limit.
of the plasma waves with respect to the ordered magnetic
field component. There is ample observational evidence that obliquely propagating
magnetohydrodynamic plasma waves exist in the interstellar medium (Armstrong et al. 1995;
Lithwick & Goldreich 2001; Cho et al. 2002).
In particular, we will consider the alternative extreme limit
that the plasma waves propagation angles are isotropically distributed
around the magnetic field direction. It has been emphasised before by
Schlickeiser & Miller (1998) referred to as SM) that oblique propagation
angles of fast magnetosonic waves leads to an order of magnitude quicker
stochastic acceleration rate as compared to the slab case, since the
compressional component of the obliquely propagating fast
mode waves allows the effect of transit-time damping acceleration of
cosmic ray particles. Here we will demonstrate that the obliqueness of
fast mode and shear Alfven wave propagation
also modifies the resulting parallel spatial diffusion coefficient
and the Hillas limit.
Most cosmic plasmas have a small value of the plasma beta
![]() ,
which is defined by the ratio of the ion sound
,
which is defined by the ratio of the ion sound ![]() to Alfven
speed
to Alfven
speed ![]() ,
and thus indicates the ratio of thermal to magnetic pressure. For
low-beta plasmas the two relevant magnetohydrodynamic wave modes are the
,
and thus indicates the ratio of thermal to magnetic pressure. For
low-beta plasmas the two relevant magnetohydrodynamic wave modes are the
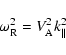 |
(7) |
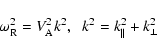 |
(8) |
Schlickeiser & Miller (1998) investigated the quasilinear interactions
of charged particles with these two plasma waves. In case of negligible
wave damping the interactions are of resonant nature: a cosmic ray
particle of given velocity v, pitch angle cosine ![]() and
gyrofrequency
and
gyrofrequency
![]() interacts with waves
whose wavenumber and real frequencies obey the condition
interacts with waves
whose wavenumber and real frequencies obey the condition
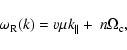 |
(9) |
For shear Alfven waves only interactions with ![]() are possible.
These are referred to as gyroresonances because inserting the
dispersion relation (7) in the resonance condition (9) yields for the
resonance parallel wavenumber
are possible.
These are referred to as gyroresonances because inserting the
dispersion relation (7) in the resonance condition (9) yields for the
resonance parallel wavenumber
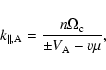 |
(10) |
In contrast, for fast magnetosonic waves the n=0 resonance is possible
for oblique propagation due its compressive magnetic field component.
The n=0 interactions are referred to as transit-time damping,
hereafter TTD. Inserting the dispersion relation (8) into the resonance
condition (9) in the case n=0 yields
| (11) |
| (12) |
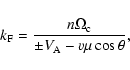 |
(13) |
The simple considerations of the last two subsections allow us the following immediate conclusions:
truecm
(1) With TTD-interactions alone, it would not be possible
to scatter particles with
![]() ,
i.e., particles with pitch
angles near 90
,
i.e., particles with pitch
angles near 90![]() .
Obviously, these particles have basically no
parallel velocity and cannot catch up with fast mode waves that
propagate with the small but finite speeds
.
Obviously, these particles have basically no
parallel velocity and cannot catch up with fast mode waves that
propagate with the small but finite speeds ![]()
![]() .
In particular this
implies that with TTD alone it is not possible to establish an isotropic
cosmic ray distribution function. Gyroresonances are needed to
provide the crucial finite scattering at small values of
.
In particular this
implies that with TTD alone it is not possible to establish an isotropic
cosmic ray distribution function. Gyroresonances are needed to
provide the crucial finite scattering at small values of ![]() .
.
truecm
(2) Conditions (11) and (12) reveal that TTD is
no gyroradius effect. It involves fast mode waves at all wavenumbers
provided the cosmic ray particles are super-Alfvenic and have large
enough values of ![]() as required by Eq. (12). Because gyroresonances
occur at single resonant wavenumbers only, see Eqs. (10) and (13), their
contribution to the value of the Fokker-Planck coefficients in the
interval
as required by Eq. (12). Because gyroresonances
occur at single resonant wavenumbers only, see Eqs. (10) and (13), their
contribution to the value of the Fokker-Planck coefficients in the
interval
![]() is much smaller than the contribution from
TTD. Therefore for comparable intensities of fast mode and shear Alfven waves, TTD will provide the overwhelming contribution to all
Fokker-Planck coefficients
is much smaller than the contribution from
TTD. Therefore for comparable intensities of fast mode and shear Alfven waves, TTD will provide the overwhelming contribution to all
Fokker-Planck coefficients
![]() ,
,
![]() and Dpp in
the interval
and Dpp in
the interval
![]() .
At small values of
.
At small values of
![]() only
gyroresonances contribute to the values of the Fokker-Planck
coefficients involving according to Eqs. (10) and (13) wavenumbers at
only
gyroresonances contribute to the values of the Fokker-Planck
coefficients involving according to Eqs. (10) and (13) wavenumbers at
![]() .
.
truecm
(3)
The momentum diffusion coefficient (4)
![\begin{displaymath}%
A_M={1\over 2}\int_{-1}^1{\rm d}\mu ~
[D_{pp}(\mu )-{D^2_{\mu p}(\mu )\over D_{\mu \mu }(\mu )}]
=A_T+A_2
\end{displaymath}](/articles/aa/full/2007/19/aa6932-06/img56.gif) |
(14) |
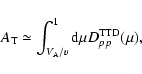 |
(15) |
![\begin{displaymath}%
A_2={1\over 2}\int_{-1}^1{\rm d}\mu ~
\left[D^{\rm A}_{pp}(...
..._{\mu p}(\mu )]^2\over D^{\rm A}_{\mu \mu }(\mu )}\right]\cdot
\end{displaymath}](/articles/aa/full/2007/19/aa6932-06/img58.gif) |
(16) |
(4)
On the other hand, the spatial diffusion coefficient (2)
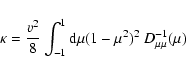 |
(17) |
(5)
According to Eq. (90) of Schlickeiser (1989) the streaming cosmic ray anisotropy due to spatial gradients in the cosmic ray density is given by
Throughout this work we consider isotropic linearly polarised
magnetohydrodynamic turbulence so that the components of
the magnetic turbulence tensor for plasma mode j is
According to Eq. (30) of SM the Fokker-Planck coefficients
![]() and
and
![]() with
with
![]() for fast mode waves are
the sum of contributions from transit-time damping (T) and
gyroresonant interactions (G):
for fast mode waves are
the sum of contributions from transit-time damping (T) and
gyroresonant interactions (G):
The gyroresonant contribution from fast mode waves is
At ![]() the contribution from shear Alfven waves to the
pitch-angle Fokker-Planck coefficient is according to Eq. (23)
the contribution from shear Alfven waves to the
pitch-angle Fokker-Planck coefficient is according to Eq. (23)
For values
![]() we obtain approximately
we obtain approximately

For values of
![]() we obtain Eq. (43)
for values of
we obtain Eq. (43)
for values of ![]() ,
where
,
where
![]() is the
largest integer smaller than
is the
largest integer smaller than
![]() ,
while
for smaller n
,
while
for smaller n
Neglecting
![]() we obtain for the cosmic ray mean free path (32)
we obtain for the cosmic ray mean free path (32)
Expresing
![]() in terms of the longest wavelength of
isotropic fast mode waves
in terms of the longest wavelength of
isotropic fast mode waves
![]() pc yields
pc yields
Only, at ultrahigh Lorentzfactors
![]() or energies
or energies
![]() the mean free path (49) approaches the much steeper dependence
the mean free path (49) approaches the much steeper dependence
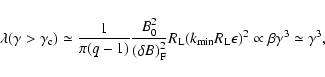 |
(53) |
Because of the direct proportionality between mean free path and anisotropy, the cosmic ray anisotropy (33) shows the same behaviour as a function of energy:
We have investigated the implications of isotropically distributed interstellar magnetohydrodynamic
plasma waves on the scattering mean free path and the spatial anisotropy of high-energy cosmic rays.
We demonstrate a drastic modification of the energy dependence of both cosmic ray transport parameters
compared to previous calculations that have assumed that the plasma waves
propagate only parallel or antiparallel to the ordered magnetic field (slab turbulence). In case of slab turbulence cosmic rays with Larmor radius ![]() resonantly interact with plasma waves with wave vectors
at
resonantly interact with plasma waves with wave vectors
at
![]() .
If the slab wave turbulence power spectrum vanishes for wavenumbers less than
.
If the slab wave turbulence power spectrum vanishes for wavenumbers less than
![]() ,
as a consequence then cosmic rays with Larmor radii larger than
,
as a consequence then cosmic rays with Larmor radii larger than
![]() cannot be scattered in pitch-angle, causing the socalled Hillas limit for the maximum energy
cannot be scattered in pitch-angle, causing the socalled Hillas limit for the maximum energy
![]() of cosmic rays being confined in the Galaxy. At about these energies this would imply a drastic increase in the spatial anisotropy of cosmic rays that has not been
detected by KASKADE and other air shower experiments.
of cosmic rays being confined in the Galaxy. At about these energies this would imply a drastic increase in the spatial anisotropy of cosmic rays that has not been
detected by KASKADE and other air shower experiments.
In case of isotropically distributed interstellar magnetohydrodynamic waves we demonstrated that
the Hillas energy ![]() is modified to a limiting total energy that is about 4 orders of magnitude larger
is modified to a limiting total energy that is about 4 orders of magnitude larger
![]()
![]()
![]() PeV, where A denotes the mass number and
PeV, where A denotes the mass number and
![]() the maximum wavenumber of isotropic plasma waves.
Below this energy the cosmic ray mean free path and the anisotropy exhibit the well known E2-qenergy dependence, where q=5/3 denotes the spectral index of the Kolmogorov spectrum. At energies higher than
the maximum wavenumber of isotropic plasma waves.
Below this energy the cosmic ray mean free path and the anisotropy exhibit the well known E2-qenergy dependence, where q=5/3 denotes the spectral index of the Kolmogorov spectrum. At energies higher than ![]() both transport parameters steepen to a E3-dependence. This implies that cosmic rays even with ultrahigh energies of several tens of EeV can be rapidly pitch-angle scattered by interstellar plasma turbulence, and are
thus confined to the Galaxy.
both transport parameters steepen to a E3-dependence. This implies that cosmic rays even with ultrahigh energies of several tens of EeV can be rapidly pitch-angle scattered by interstellar plasma turbulence, and are
thus confined to the Galaxy.
The physical reason for the four orders of magnitude higher value of the limiting energy is the occurrence of dominating transit-time damping interactions of cosmic rays with magnetosonic plasma waves due to their compressive
magnetic field component along the ordered magnetic field. This n=0 resonance is not a gyroresonance implying
that cosmic rays interact with plasma waves at all wavenumbers provided that the cosmic ray parallel speed (transit speed)
equals the parallel phase speed of magnetosonic waves. Only at small values of the cosmic ray pitch-angle
cosine
![]() ,
where the cosmic ray particles spiral at nearly ninety degrees with very small parallel speeds less than
the minimum magnetosonic phase speed
,
where the cosmic ray particles spiral at nearly ninety degrees with very small parallel speeds less than
the minimum magnetosonic phase speed ![]() ,
gyroresonant interactions are necessary to scatter csomic rays. However, the gyroresonance condition of cosmic rays at
,
gyroresonant interactions are necessary to scatter csomic rays. However, the gyroresonance condition of cosmic rays at ![]() reads
reads
![]() instead of the slab condition
instead of the slab condition
![]() causing the limiting energy enhancement from
causing the limiting energy enhancement from ![]() to
to ![]() by the large factor
by the large factor
![]() .
.
Acknowledgements
Partial support by the Deutsche Forschungsgemeinschaft through Sonderforschungsbereich 591 is acknowledged.
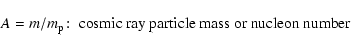
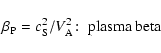
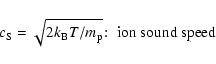
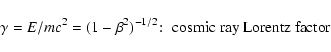


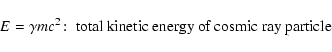
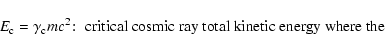
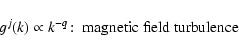


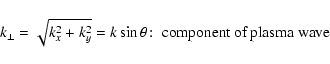

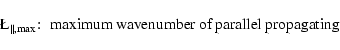



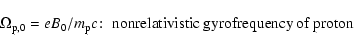

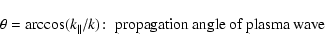
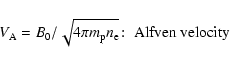
The task is to calculate the integral (42)
![\begin{displaymath}U_{\rm A}=\max \left(0, \left[R_{\rm L}^2k_{\rm min}^2-{n^2\over \epsilon ^2}\right]^{1/2}\right),
\end{displaymath}](/articles/aa/full/2007/19/aa6932-06/img251.gif)
With the identity
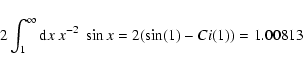
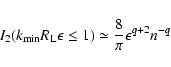
In this case
![]() for
for ![]() ,
and
,
and
![]() for
for ![]() ,
where
,
where
| (67) |
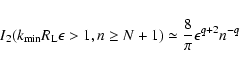
![\begin{displaymath}V[\alpha ,n\le N-1]\simeq {1\over \pi }\left({\epsilon \over ...
...\int_{\epsilon U_{\rm A}/n}^\infty
{\rm d}t~ t^{-2-2\alpha }~
\end{displaymath}](/articles/aa/full/2007/19/aa6932-06/img288.gif)
![\begin{displaymath}\times
\left[1+(-1)^n\sin \left({2nt\over \epsilon }\right)\right]\simeq
{1\over \pi (1+2\alpha )}U_{\rm A}^{-(2\alpha +1)}
\end{displaymath}](/articles/aa/full/2007/19/aa6932-06/img289.gif)
![\begin{displaymath}V[\alpha ,n=N]\simeq \left({\epsilon \over N}\right)^{2\alpha...
...\rm d}t~ t^{-1}~ J_N^2\left({Nt\over \epsilon }\right) \right.
\end{displaymath}](/articles/aa/full/2007/19/aa6932-06/img292.gif)
![\begin{displaymath}\left. +\;\int_1^\infty
{\rm d}t~ t^{-1-2\alpha }~ J_N^2\left...
...right)\right]\simeq
\left({\epsilon \over N}\right)^{2\alpha }
\end{displaymath}](/articles/aa/full/2007/19/aa6932-06/img293.gif)
where we approximate