A&A 467, 187-206 (2007)
DOI: 10.1051/0004-6361:20065918
M. Röllig1,4 - N. P. Abel2 - T. Bell3,17 - F. Bensch1 - J. Black15 - G. J. Ferland2 - B. Jonkheid5 - I. Kamp6 - M. J. Kaufman7 - J. Le Bourlot8 - F. Le Petit8,15 - R. Meijerink5 - O. Morata16 - V. Ossenkopf4,10 - E. Roueff8 - G. Shaw2 - M. Spaans9 - A. Sternberg11 - J. Stutzki4 - W.-F. Thi12 - E. F. van Dishoeck5 - P. A. M. van Hoof13 - S. Viti3 - M. G. Wolfire14
1 - Argelander-Institut für Astronomie![]() , Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
2 - University of Kentucky, Department of Physics and Astronomy, Lexington, KY 40506, USA
3 - Department of Physics & Astronomy, University College London, Gower Street, London WC1E 6BT, UK
4 - I. Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937 Köln,
Germany
5 - Leiden Observatory, PO Box 9513, 2300 RA Leiden, The Netherlands
6 - Space Telescope Science Division of ESA, Space Telescope Science Institute, Baltimore, MD 21218, USA
7 - Department of Physics, San Jose State University, 1 Washington Square, San Jose, CA 95192, USA
8 - LUTH UMR 8102, CNRS and Observatoire de Paris, Place J. Janssen, 92195 Meudon Cedex, France
9 - Kapteyn Astronomical Institute, PO Box 800, 9700 AV Groningen, The Netherlands
10 - SRON National Institute for Space Research, Postbus 800, 9700 AV Groningen, The Netherlands
11 - School of Physics and Astronomy, Tel Aviv University, Ramat Aviv 69978, Israel
12 - Institute for Astronomy, The University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
13 - Royal Observatory of Belgium, Av. Circulaire, 3 - Ringlaan 3, 1180 Brussel, Belgium
14 - Astronomy Department, University of Maryland, College Park, MD 20742-2421, USA
15 - Onsala Space Observatory, 439 92 Onsala, Sweden
16 - LAEFF, Villafranca del Castillo, Apdo. 50727, 28080 Madrid, Spain
17 - California Institute of Technology, 1200 E. California Blvd, Pasadena CA 91125, USA
Received 27 June 2006 / Accepted 2 February 2007
Abstract
Aims. We present a comparison between independent computer codes, modeling the physics and chemistry of interstellar photon dominated regions (PDRs). Our goal was to understand the mutual differences in the PDR codes and their effects on the physical and chemical structure of the model clouds, and to converge the output of different codes to a common solution.
Methods. A number of benchmark models have been created, covering low and high gas densities
n=103,105.5 cm-3 and far ultraviolet intensities
![]() in units of the Draine field (FUV:
in units of the Draine field (FUV:
![]() eV). The benchmark models were computed in two ways: one set assuming constant temperatures, thus testing the consistency of the chemical network and photo-processes, and a second set determining the temperature self consistently by solving the thermal balance, thus testing the modeling of the heating and cooling mechanisms accounting for the detailed energy balance throughout the clouds.
eV). The benchmark models were computed in two ways: one set assuming constant temperatures, thus testing the consistency of the chemical network and photo-processes, and a second set determining the temperature self consistently by solving the thermal balance, thus testing the modeling of the heating and cooling mechanisms accounting for the detailed energy balance throughout the clouds.
Results. We investigated the impact of PDR geometry and agreed on the comparison of results from spherical and plane-parallel PDR models. We identified a number of key processes governing the chemical network which have been treated differently in the various codes such as the effect of PAHs on the electron density or the temperature dependence of the dissociation of CO by cosmic ray induced secondary photons, and defined a proper common treatment. We established a comprehensive set of reference models for ongoing and future PDR model bench-marking and were able to increase the agreement in model predictions for all benchmark models significantly. Nevertheless, the remaining spread in the computed observables such as the atomic fine-structure line intensities serves as a warning that there is still a considerable uncertainty when interpreting astronomical data with our models.
Key words: ISM: abundances - astrochemistry - ISM: clouds - ISM: general - radiative transfer - methods: numerical
It is not the purpose of the benchmarking to present a preferred solution or a preferred code. PDRs are found in a large variety of objects and under very different conditions. To this end, it was neither possible nor desirable to develop a generic PDR code, able to model every possible PDR. Furthermore, the benchmarking is not meant to model any "real'' astronomical object. The main purpose of this study is technical not physical. This is also reflected in the choice of the adopted incomplete chemical reaction network (see Sect. 4).
In Sect. 2 we briefly introduce the physics involved in PDRs, in Sect. 3 we introduce some key features in PDR modeling. Section 4 describes the setup of the benchmark calculations and Sect. 5 presents the results for a selection of benchmark calculations and gives a short review over the participating codes. In Sect. 6 we discuss the results and summarize the lessons learned from the benchmark effort. A tabular overview of the individual code characteristics is given in the Appendix.
The history of PDR modeling dates back to the early 1970's (Jura 1974; Glassgold & Langer 1975; Black & Dalgarno 1977; Hollenbach et al. 1971) with steady state models for the transitions from H to H2 and from C+ to CO. In the following years a number of models, addressing the chemical and thermal structure of clouds subject to an incident flux of FUV photons have been developed (Le Bourlot et al. 1993; Störzer et al. 1996; van Dishoeck & Black 1988; Hollenbach et al. 1991; Tielens & Hollenbach 1985; Sternberg & Dalgarno 1989; de Jong et al. 1980). Additionally, a number of models, focusing on certain aspects of PDR physics and chemistry were developed, e.g. models accounting for time-dependent chemical networks, models of clumped media, and turbulent PDR models (Spaans 1996; Röllig et al. 2002; de Boisanger et al. 1992; Lee et al. 1996; Nejad & Wagenblast 1999; Bertoldi & Draine 1996; Hill & Hollenbach 1978; Bell et al. 2005; Wagenblast & Hartquist 1988; Hegmann & Kegel 1996). Standard PDR models generally do not account for dynamical properties of gas but there are some studies that consider the advection problem rather than the steady state approach (e.g. Störzer & Hollenbach 1998). For a more detailed review see Hollenbach & Tielens (1999).
In order to numerically model a PDR it is necessary to compute all local properties of a cloud such as the relative abundances of the gas constituents together with their level populations, temperature of gas and dust, gas pressure, composition of dust/PAHs, and many more. This local treatment is complicated by the radiation field which couples remote parts of the cloud. The local mean radiation field, which is responsible for photochemical reactions, gas/dust heating, and excitation of molecules depends on the position in the cloud and the (wavelength dependent) absorption along the lines of sight toward this position. This non-local coupling makes numerical PDR calculations a CPU time consuming task.
PDR modelers and observers approach the PDRs from opposite sides: PDR models start by calculating the local properties of the clouds such as the local CO density and the corresponding gas temperature and use these local properties to infer the expected global properties of the cloud like total emergent emissivities or fluxes and column densities. The observer on the other hand starts by observing global features of a source and tries to infer the local properties from that. The connection between local and global properties is complex and not necessarily unambiguous. Large variations e.g. in the CO density at the surface of the cloud may hardly affect the overall CO column density due to the dominance of the central part of the cloud with a high density. If one is interested in the total column density it does not matter whether different codes produce a different surface CO density. For the interpretation of high-J CO emission lines, however, different CO densities in the outer cloud layers make a huge difference since high temperatures are required to produce high-J CO fluxes. Thus, if different PDR model codes deviate in their predicted cloud structures, this may affect the interpretation of observations and may prevent inference of the "true'' structure behind the observed data. To this end it is very important to understand the origin of present differences in PDR model calculations. Otherwise it is impossible to rule out alternative interpretations. The ideal situation, from the modelers point of view, would be a complete knowledge of the true local structure of a real cloud and their global observable properties. This would easily allow us to calibrate PDR models. Since this case is unobtainable, we take one step back and apply a different approach: If all PDR model codes use exactly the same input and the same model assumptions they should produce the same predictions.
Because of the close interaction between chemical and thermal balance and radiative transfer, PDR codes typically iterate through the following computation steps: 1) solve the local chemical balance to determine local densities; 2) solve the local energy balance to estimate the local physical properties like temperatures, pressures, and level populations; 3) solve the radiative transfer; 4) for finite models it is necessary to successively iterate steps 1)-3). Each step requires a variety of assumptions and simplifications. Each of these aspects can be investigated to great detail and complexity (see for example van Zadelhoff et al. (2002) for a discussion of NLTE radiative transfer methods), but the explicit aim of the PDR comparison workshop was to understand the interaction of all computation steps mentioned above. Even so it was necessary to considerably reduce the model complexity in order to disentangle cause and effect.
Several aspects of PDR modeling have shown the need for detailed discussion, easily resulting in misleading conclusions if not treated properly.
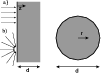 |
Figure 1: Common geometrical setups of a model PDR. The surface of any plane-parallel or spherical cloud is illuminated either a) uni-directional or b) isotropically. |
Two common geometrical setups of model PDRs are shown in Fig. 1. Most PDR models feature a plane-parallel geometry, illuminated either from one side or from both sides. This geometry naturally suggests a directed illumination, perpendicular to the cloud surface. This simplifies the radiative transfer problem significantly, since it is sufficient to account for just one line of sight, if we ignore scattering out of the line of sight (Flannery et al. 1980). Since most plane-parallel PDR models are infinite perpendicular to the cloud depth z it is also straightforward to account for an isotropic FUV irradiation within the pure 1-D formalism. For a spherical geometry one can exploit the model symmetry only for a FUV field isotropically impinging onto the cloud. In finite plane-parallel and spherical models iterations over the depth/radial structure are mandatory because radiation is coming from multiple directions, passing through cloud elements for which the physical and chemical structure and hence opacities have not been calculated in the same iteration step. To account for this "backside'' illumination it is essential to iterate on the radiation field.
The most important quantity describing the radiation field in PDR models is the local mean intensity (or alternatively the energy density) as given by:
The choice between directed and isotropic FUV fields directly influences the attenuation due to dust. In the
uni-directional case the FUV intensity along the line of sight is attenuated according to
![]() ,
where
,
where ![]() is the
optical depth of the dust at frequency
is the
optical depth of the dust at frequency ![]() .
For pure absorption the radiative
transfer equation becomes:
.
For pure absorption the radiative
transfer equation becomes:
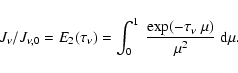 |
(3) |
The attenuation of FUV radiation is additionally complicated if we account for dust scattering.
For a full treatment by Legendre polynomials see Flannery et al. (1980).
In case of small scattering angles
![]() the scattering can be approximated by an effective
forward attenuation
the scattering can be approximated by an effective
forward attenuation
![]() ,
where
,
where ![]() is the scattering albedo. Thus, more material is needed to obtain the same attenuation as in the case without scattering. Hence a proper
scaling of
is the scattering albedo. Thus, more material is needed to obtain the same attenuation as in the case without scattering. Hence a proper
scaling of ![]() is necessary. In case of clumped gas this becomes even more complex. The
presence of stochastic density fluctuations leads to a substantial reduction of the
effective optical depth as demonstrated by Hegmann & Kegel (2003). All this has to
be considered when calculating the photodissociation and
photoionization rates, when the attenutation with depth is represented by
simple exponential forms,
is necessary. In case of clumped gas this becomes even more complex. The
presence of stochastic density fluctuations leads to a substantial reduction of the
effective optical depth as demonstrated by Hegmann & Kegel (2003). All this has to
be considered when calculating the photodissociation and
photoionization rates, when the attenutation with depth is represented by
simple exponential forms,
![]() (e.g. Roberge et al. 1991; van Dishoeck 1988), where the factor ki accounts for the
wavelength dependence of the photoprocess i
(e.g. Roberge et al. 1991; van Dishoeck 1988), where the factor ki accounts for the
wavelength dependence of the photoprocess i![]() .
.
PDR chemistry has been addressed in detail by many authors (Teyssier et al. 2004; Fuente et al. 2005,1993; Jansen et al. 1995; Sternberg & Dalgarno 1995; Le Bourlot et al. 1993; Lee et al. 1996; Meijerink & Spaans 2005; van Dishoeck & Black 1988; Hollenbach et al. 1991; Tielens & Hollenbach 1985; Walmsley et al. 1999; Bakes & Tielens 1998; Savage & Ziurys 2004). These authors discuss numerous aspects of PDR chemistry in great detail and give a comprehensive overview of the field. Here we repeat some crucial points in the chemistry of PDRs in order to motivate the benchmark standardization and to prepare the discussion of the benchmark result.
In PDRs photoprocesses are very important due to the high FUV intensity, as
well as reactions with abundant hydrogen atoms. The formation and destruction
of H2, heavily influenced by the FUV field, is of major importance for
the chemistry in PDRs. H2 forms on grain surfaces, a
process which crucially depends on the temperatures of the gas and
the grains (Hollenbach & Salpeter 1971; Cazaux & Tielens 2004), which themselves depend on the
local cooling and heating, governed by the FUV. The photo-dissociation
of H2 is a line absorption process and, thus is subject to effective
shielding (van Dishoeck & Black 1988). This leads to a sharp transition from atomic
to molecular hydrogen once the H2 absorption lines are optically
thick. The photo-dissociation of CO is also a line absorption process,
additionally complicated by the fact that the broad H2 absorption
lines overlap with CO absorption lines. Similar to H2 this leads
to a transition from atomic carbon to CO. For
![]() carbon
is predominantly present in ionized form. For an assumed FUV field of
carbon
is predominantly present in ionized form. For an assumed FUV field of
![]() ,
CO is formed at about
,
CO is formed at about
![]() .
This results
in the typical PDR stratification of H/ H2 and C+/ C/ CO. The
depth of this transition zone depends on the physical parameters but also on the contents of the
chemical network: for example the inclusion of PAHs into the chemical balance calculations shifts the C+ to C transition to smaller
.
This results
in the typical PDR stratification of H/ H2 and C+/ C/ CO. The
depth of this transition zone depends on the physical parameters but also on the contents of the
chemical network: for example the inclusion of PAHs into the chemical balance calculations shifts the C+ to C transition to smaller
![]() (e.g. Lepp & Dalgarno 1988; Bakes & Tielens 1998).
(e.g. Lepp & Dalgarno 1988; Bakes & Tielens 1998).
The solution of the chemical network itself covers the destruction and formation reactions of all chemical species considered. For each included
species i this results in a balance equation of the form:
They showed that bistability may occur
in gas-phase models (neglecting dust chemistry) of interstellar dark clouds
in a narrow parameter range of approximately
103 cm
![]() cm-3 with
the cosmic-ray ionization rate of molecular hydrogen
cm-3 with
the cosmic-ray ionization rate of molecular hydrogen
![]() s-1. Within this range
the model results may depend very sensitively on variations of input parameters
such as
s-1. Within this range
the model results may depend very sensitively on variations of input parameters
such as
![]() or the H3+ dissociative recombination rate. To
demonstrate this we show the influence of varying ionization rates in Fig. 4. The
left panel gives abundance profiles for benchmark model F1 (n=103 cm-3,
or the H3+ dissociative recombination rate. To
demonstrate this we show the influence of varying ionization rates in Fig. 4. The
left panel gives abundance profiles for benchmark model F1 (n=103 cm-3, ![]() )
the right
panel shows a similar model but with higher density (n=104 cm-3). The higher density was
chosen to make sure that we are outside the bistability regime. The solid lines in both panels are for a cosmic ray helium ionization rate of
)
the right
panel shows a similar model but with higher density (n=104 cm-3). The higher density was
chosen to make sure that we are outside the bistability regime. The solid lines in both panels are for a cosmic ray helium ionization rate of
![]() s-1, the dashed lines denote an ionization rate increased by a factor four. Different colors denote different chemical species.
The most prominent differences are highlighted with colored arrows. The factor
four in
s-1, the dashed lines denote an ionization rate increased by a factor four. Different colors denote different chemical species.
The most prominent differences are highlighted with colored arrows. The factor
four in
![]() results in differences in density up to three orders of magnitude
in the lower density case! A detailed analysis shows that the strong abundance transitions
occur for
results in differences in density up to three orders of magnitude
in the lower density case! A detailed analysis shows that the strong abundance transitions
occur for
![]() s-1. This highly
non-linear behavior disappears if we leave the critical parameter range as demonstrates in the
right panel of Fig. 4. Boger & Sternberg (2006) emphasize that this effect is a property of the gas phase
chemical network, and is damped if gas-grain processes such as grain assisted recombination of
the atomic ions are introduced (see also Shalabiea & Greenberg 1995). They conclude that
the bistability phenomenon probably does not occur in realistic dusty interstellar clouds while
Le Bourlot (2006) argues that what matters for bistability is not the number of neutralisation
channels but the degree of ionisation and that bistability may occur in interstellar clouds.
They suggest this could be one of the possible reasons of the non detection of O2 by
the ODIN satellite (Viti et al. 2001). Yet, another possible explanation for the absence of O2 is
freeze-out onto dust. However it is clear that bistability is a real property of interstellar gas-phase networks and not just a numerical artifact. Furthermore it is important to emphasize that standard PDR models may react very sensitively on the variation of input parameters (e.g.
s-1. This highly
non-linear behavior disappears if we leave the critical parameter range as demonstrates in the
right panel of Fig. 4. Boger & Sternberg (2006) emphasize that this effect is a property of the gas phase
chemical network, and is damped if gas-grain processes such as grain assisted recombination of
the atomic ions are introduced (see also Shalabiea & Greenberg 1995). They conclude that
the bistability phenomenon probably does not occur in realistic dusty interstellar clouds while
Le Bourlot (2006) argues that what matters for bistability is not the number of neutralisation
channels but the degree of ionisation and that bistability may occur in interstellar clouds.
They suggest this could be one of the possible reasons of the non detection of O2 by
the ODIN satellite (Viti et al. 2001). Yet, another possible explanation for the absence of O2 is
freeze-out onto dust. However it is clear that bistability is a real property of interstellar gas-phase networks and not just a numerical artifact. Furthermore it is important to emphasize that standard PDR models may react very sensitively on the variation of input parameters (e.g.
![]() ,
the H2 formation rate, the PAH content of the model cloud, etc.) and one has to be careful in the interpretation of surprising model signatures.
,
the H2 formation rate, the PAH content of the model cloud, etc.) and one has to be careful in the interpretation of surprising model signatures.
The numerical stability and the speed of convergence may vary significantly over different chemical networks. Three
major questions have to be addressed:
Regarding question 2 a secure brute force approach would be the inclusion of all known reactions involving all chosen species, under the questionable assumption that we actually know all important reactions and their rate coefficients. This assumption is obviously invalid for grain surface reactions and gas-grain interactions such as freeze-out and desorption. It is important not to create artificial bottlenecks in the reaction scheme by omitting important channels. The choice of reaction rate coefficients depends on factors like availability, accuracy, etc. A number of comprehensive databases of rate coefficients is available today, e.g. NSM/OHIO (Wakelam et al. 2005b,2004), UMIST (Millar, Farquhar, & Willacy 1997; Le Teuff et al. 2000), and Meudon (Le Bourlot et al. 1993), which collect the results from many different references, both theoretical and experimental.
An example for the importance of explicitly agreeing on the
details of the computation of the reaction rate is the reaction:
Another example is the formation of C in the dark cloud part of a PDR, i.e.
at values of
![]() .
A possible formation
channel for atomic carbon is the dissociation of CO by secondary UV
photons, induced by cosmic
rays (Le Teuff et al. 2000). In the outer parts of the PDR the impinging FUV field dominates the dissociation of CO,
but for high
.
A possible formation
channel for atomic carbon is the dissociation of CO by secondary UV
photons, induced by cosmic
rays (Le Teuff et al. 2000). In the outer parts of the PDR the impinging FUV field dominates the dissociation of CO,
but for high ![]() the FUV field is effectively shielded and CR induced UV photons become
important. For CO, this process depends on the level population of CO, and therefore is
temperature dependent (Gredel et al. 1987), however this temperature dependence is
often ignored. The reaction rate given by Gredel et al. (1987) has to be corrected by
a factor of
the FUV field is effectively shielded and CR induced UV photons become
important. For CO, this process depends on the level population of CO, and therefore is
temperature dependent (Gredel et al. 1987), however this temperature dependence is
often ignored. The reaction rate given by Gredel et al. (1987) has to be corrected by
a factor of
![]() effectively reducing the dissociation rate for temperatures below 300 K (Le Teuff et al. 2000). In Fig. 6 we plot the density profile of atomic carbon for an
isothermal benchmark model with temperature T=50 K. The solid
line represents the model result for an uncorrected
photo-rate using the average reaction rate for T=300 K, compared to the
results using the rate corrected for T=50 K by
(50/300)1.17, given by the dashed curve.
effectively reducing the dissociation rate for temperatures below 300 K (Le Teuff et al. 2000). In Fig. 6 we plot the density profile of atomic carbon for an
isothermal benchmark model with temperature T=50 K. The solid
line represents the model result for an uncorrected
photo-rate using the average reaction rate for T=300 K, compared to the
results using the rate corrected for T=50 K by
(50/300)1.17, given by the dashed curve.
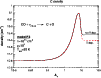 |
Figure 6:
The density profile of atomic carbon for the benchmark model F2 (low density, high FUV,
|
| Heating | Cooling |
| photoelectric heating (dust & PAH) | [CII] 158 |
| collisional de-excitation of vib. excited H2 | [OI] 63, 145 |
| H2 dissociation | [CI] 370, 610 |
| H2 formation | [SiII] 35 |
| CR ionization | CO, H2O, OH, H2 |
| gas-grain collisions | Ly |
| dissipation of turbulence | gas-grain collisions |
The properties of big grains have been reviewed recently by Draine (2003, and references therein). The first indirect evidence for the presence of VSGs in the ISM was presented by Andriesse (1978) in the case of the M17 PDR. The dust grains themselves consist of amorphous silicates and carbonaceous material and may be covered with ice mantles in the denser and colder parts of the ISM. For details of the composition of grains and their extinction due to scattering and absorption see Li & Draine (2002) and references therein.
The influence and proper treatment of electron densities together with grain ionization and recombination is still to be analyzed. Not only the charge of dust and PAHs but also the scattering properties are still in discussion (Weingartner & Draine 2001). This heavily influences the model output, e.g. the inclusion of back-scattering significantly increases the total H2 photo-dissociation rate at the surface of the model cloud compared to calculations with pure forward scattering.
The radiative transfer (RT) can be split into two distinct wavelength regimes: FUV and IR/FIR. These may also be labeled as "input'' and "output''. FUV radiation due to ambient UV field and/or young massive stars in the neighborhood impinges on the PDR. The FUV photons are absorbed on their way deeper into the cloud, giving rise to the well known stratified chemical structure of PDRs. In general, reemission processes can be neglected in the FUV, considerably simplifying the radiative transfer problem. Traveling in only one direction, from the edge to the inside, the local mean FUV intensity can usually be calculated in a few iteration steps. In contrast to the FUV, the local FIR intensity is a function of the temperature and level populations at all positions due to absorption and reemission of FIR photons. Thus a computation needs to iterate over all spatial grid points. A common simplifying approximation is the spatial decoupling via the escape probability approximation. This allows to substitute the intensity dependence by a dependence on the relevant optical depths, ignoring the spatial variation of the source function. The calculation of emission line cooling then becomes primarily a problem of calculating the local excitation state of the particular cooling species. An overview of NLTE radiative transfer methods is given by van Zadelhoff et al. (2002).
A total number of 11 model codes participated in the PDR model comparison study during
and after the workshop in Leiden. Table 2 gives an overview
of these codes.
| Model Name | Authors |
| Cloudy | G. J. Ferland, P. van Hoof, N. P. Abel, G. Shaw (Ferland et al. 1998; Shaw et al. 2005; Abel et al. 2005) |
| COSTAR | I. Kamp, F. Bertoldi, G.-J. van Zadelhoff (Kamp & Bertoldi 2000; Kamp & van Zadelhoff 2001) |
| HTBKW | D. Hollenbach, A. G. G. M. Tielens, M. G. Burton, M. J. Kaufman, M. G. Wolfire |
| (Kaufman et al. 1999; Tielens & Hollenbach 1985; Wolfire et al. 2003) | |
| KOSMA- |
H. Störzer, J. Stutzki, A. Sternberg (Störzer et al. 1996), B. Köster, M. Zielinsky, U. Leuenhagen |
| Bensch et al. (2003), Röllig et al. (2006) | |
| Lee96mod | H.-H. Lee, E. Herbst, G. Pineau des Forêts, E. Roueff, J. Le Bourlot, O. Morata (Lee et al. 1996) |
| Leiden | J. Black, E. van Dishoeck, D. Jansen and B. Jonkheid |
| (Jansen et al. 1995; Black & van Dishoeck 1987; van Dishoeck & Black 1988) | |
| Meijerink | R. Meijerink, M. Spaans (Meijerink & Spaans 2005) |
| Meudon | J. Le Bourlot, E. Roueff, F. Le Petit (Le Bourlot et al. 1993; Le Petit et al. 2005,2002) |
| Sternberg | A. Sternberg, A. Dalgarno (Boger & Sternberg 2005; Sternberg & Dalgarno 1989,1995) |
| UCL_PDR | S. Viti, W.-F. Thi, T. Bell (Taylor et al. 1993; Papadopoulos et al. 2002; Bell et al. 2005) |
| F1 | F2 |
| T=50 K | T=50 K |
| n=103 cm-3, |
n=103 cm-3, |
| F3 | F4 |
| T=50 K | T=50 K |
|
n=105.5 cm-3, |
n=105.5 cm-3, |
| V1 | V2 |
| T= variable | T= variable |
| n=103 cm-3, |
n=103 cm-3, |
| V3 | V4 |
| T= variable | T= variable |
|
n=105.5 cm-3, |
n=105.5 cm-3, |
| Chemical species in the models |
| H, H+, H2, H2+, H3+ |
| O, O+, OH+, OH, O2, O2+, H2O, H2O+, H3O+ |
| C, C+, CH, CH+, CH2, CH2+, CH3, |
| CH3+, CH4, CH4+, CH5+, CO, CO+,HCO+ |
| He, He+, e- |
The chemical reaction rates are taken from the UMIST99 database (Le Teuff et al. 2000) together with some corrections suggested by A. Sternberg. The complete reaction rate file is available online (http://www.ph1.uni-koeln.de/pdr-comparison). To reduce the overall modeling complexity, PAHs were neglected in the chemical network and were only considered for the photoelectric heating (photoelectric heating efficiency as given by Bakes & Tielens 1994) in models V1-V4. Codes which calculate time-dependent chemistry used a suitably long time-scale in order to reach steady state (e.g. UCL_PDR used 100 Myr).
All model clouds are plane-parallel, semi-infinite clouds of constant total hydrogen
density
![]() .
Spherical codes approximated this by assuming a very large radius for the cloud.
.
Spherical codes approximated this by assuming a very large radius for the cloud.
| Model Parameters | ||
|
|
0.1 | Elemental He abundance |
|
|
Elemental O abundance | |
|
|
Elemental C abundance | |
|
|
|
CR ionization rate |
|
|
Visual extinction | |
|
|
3.02 Av | FUV dust attenuation |
| 1 km s-1 | Doppler width | |
|
|
|
H2 dissociation rate |
| R |
|
H2 formation rate |
|
|
50 K | Gas temperature (for F1-F4) |
|
|
20 K | Dust temperature (for F1-F4) |
| n | 103, 105.5 cm-3 | Total density |
| 10,105 | FUV intensity w.r.t. | |
| Draine (1978) field | ||
| (i.e.
|
||
In the following section we give a short overview of the up to date results of the
PDR model comparison. The names of the model codes are printed in typewriter font
(e.g. COSTAR). We will refer to the two stages of the benchmarking
results by pre- and post-benchmark, denoting the model results at the beginning
of the comparison and at its end respectively. All pre- and post-benchmark
results are posted at http://www.ph1.uni-koeln.de/pdr-comparison. One model from the
initial 12 participating model was left out in the post-benchmark plots because the authors could
not attend the workshop.
In addition, the KOSMA-![]() models (Röllig et al. 2006) and the models
by Bensch, which participated in the comparison as seperate codes, have
been merged to a single set (labeled KOSMA-
models (Röllig et al. 2006) and the models
by Bensch, which participated in the comparison as seperate codes, have
been merged to a single set (labeled KOSMA-![]() )
as
they are variants on of the same basic model which do not differ
for the given benchmarking parameter set, and consequently
give identical results. To demonstrate
the impact of the benchmark effort on the results of the participating PDR codes we plot the
well known C/C+ /CO transition for a typical PDR environment before and after the
changes identified as necessary during the
benchmark in Fig. 7. The photo-dissociation of carbon monoxide
is thought to be well understood for almost 20 years (van Dishoeck & Black 1988). Nevertheless we see a significant scatter for the densities of C+, C, and CO in the top plot of Fig. 7.
The scatter in the pre-benchmark rates is significant. Most deviations
could be assigned to either bugs in the pre-benchmark codes, misunderstandings, or to incorrect
geometrical factors (e.g.
)
as
they are variants on of the same basic model which do not differ
for the given benchmarking parameter set, and consequently
give identical results. To demonstrate
the impact of the benchmark effort on the results of the participating PDR codes we plot the
well known C/C+ /CO transition for a typical PDR environment before and after the
changes identified as necessary during the
benchmark in Fig. 7. The photo-dissociation of carbon monoxide
is thought to be well understood for almost 20 years (van Dishoeck & Black 1988). Nevertheless we see a significant scatter for the densities of C+, C, and CO in the top plot of Fig. 7.
The scatter in the pre-benchmark rates is significant. Most deviations
could be assigned to either bugs in the pre-benchmark codes, misunderstandings, or to incorrect
geometrical factors (e.g. ![]() vs.
vs. ![]() ). This emphasizes the importance of this comparative study to establish a uniform understanding about how to calculate even these basic figures. Despite the considerable current interest because of, e.g. SPITZER results, we do not give the post-benchmark predictions for the H2 mid-IR and near IR lines (or the corresponding Boltzmann diagram). Only a small fraction of the participating codes is able to compute the detailed H2 population and emission, and the focus of this analysis is the comparison between the benchmark codes.
). This emphasizes the importance of this comparative study to establish a uniform understanding about how to calculate even these basic figures. Despite the considerable current interest because of, e.g. SPITZER results, we do not give the post-benchmark predictions for the H2 mid-IR and near IR lines (or the corresponding Boltzmann diagram). Only a small fraction of the participating codes is able to compute the detailed H2 population and emission, and the focus of this analysis is the comparison between the benchmark codes.
![\begin{figure}
\par\includegraphics[width=17 cm,clip]{5918fig8.eps}\end{figure}](/articles/aa/full/2007/19/aa5918-06/Timg94.gif) |
Figure 8:
Model F1 (n=103 cm-3, |
In the post-benchmark results, the Leiden and UCL_PDR models show a slightly different behavior. The predicted peak depth of C is somewhat smaller than for the other codes. The peak C density of UCL_PDR is roughly 50% higher than in the other codes. A comparison with the photo-ionization of C shown in Fig. 8 confirms that a slightly stronger shielding for the ionization of C is the reason for the different behavior of C and C+. The dark cloud densities for C+, C, and CO agree very well, except for a somewhat smaller C+ density in the Lee96mod results.
In Fig. 8 we plot the post-benchmark photo-rates
for dissociation of H2 (left column) and CO (middle column)
and for the ionization of C (right column), computed for model F1. Even
for this simple model there are some significant differences
between the models in the various rates. In the pre-benchmark results, several codes
calculated different photo-rates at the edge of the
model cloud, i.e. for very low values of
![]() .
Some codes calculated surface
photo-dissociation rates between 4-
.
Some codes calculated surface
photo-dissociation rates between 4-
![]() s-1 compared to the expected value of
s-1 compared to the expected value of
![]() s-1. Most of these deviations were
due to exposure to the full
s-1. Most of these deviations were
due to exposure to the full ![]() steradians FUV field instead the correct
steradians FUV field instead the correct ![]() ,
but also due to
different effects, like the FUV photon back-scattering in the Meudon results.
The pre-benchmark rates of KOSMA-
,
but also due to
different effects, like the FUV photon back-scattering in the Meudon results.
The pre-benchmark rates of KOSMA-![]() were shifted toward slightly
lower values of
were shifted toward slightly
lower values of ![]() because of an incorrect scaling between
because of an incorrect scaling between ![]() and
and
![]() and an incorrect calculation of the angular averaged photo-rate (the model features a spherical geometry with isotropic FUV illumination). The post-benchmark results (Fig. 8) show that most deviations have been corrected. The remaining offset
for the Meudon result is due to the consideration of backscattered FUV photons, increasing the local mean FUV intensity. The pre- to post-benchmark changes for the photo-rates of CO and C are even more convincing (see online archive). The post-benchmark results are in
very good agreement except for some minor difference, e.g. UCL_PDR's
photo-ionization rate of C showing some deviation from the main field.
and an incorrect calculation of the angular averaged photo-rate (the model features a spherical geometry with isotropic FUV illumination). The post-benchmark results (Fig. 8) show that most deviations have been corrected. The remaining offset
for the Meudon result is due to the consideration of backscattered FUV photons, increasing the local mean FUV intensity. The pre- to post-benchmark changes for the photo-rates of CO and C are even more convincing (see online archive). The post-benchmark results are in
very good agreement except for some minor difference, e.g. UCL_PDR's
photo-ionization rate of C showing some deviation from the main field.
![\begin{figure}
\par\includegraphics[width=14cm]{5918fi10.eps}\end{figure}](/articles/aa/full/2007/19/aa5918-06/Timg99.gif) |
Figure 10:
Model F4 (
n=105.5 cm-3, |
The depth-dependence of the H2 photo-dissociation rate is reflected in the
structure of the H-H2 transition zone. Figure 9
shows the densities of atomic and molecular hydrogen after the benchmark. The vertical lines
denote the minimum and maximum transition depths before (dashed) and after the benchmark (solid). In the pre-benchmark results
the predicted transition depth ranges from 0.08
![]() to 0.29
to 0.29
![]() .
In the post-benchmark results
this scatter is reduced by more than a factor of 3.
Sternberg gives a slightly smaller H density in the dark cloud part.
In this code, cosmic ray (CR) destruction
and grain surface formation are the only reactions considered in the calculation of the H2 density. The other codes use additional reactions. The reactions:
.
In the post-benchmark results
this scatter is reduced by more than a factor of 3.
Sternberg gives a slightly smaller H density in the dark cloud part.
In this code, cosmic ray (CR) destruction
and grain surface formation are the only reactions considered in the calculation of the H2 density. The other codes use additional reactions. The reactions:
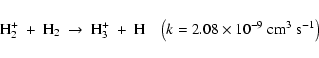
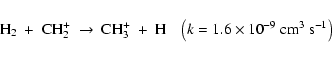
The model F1 may represent a typical translucent cloud PDR, e.g., the line of sight toward HD 147889 in Ophiuchus (Liseau et al. 1999). The low density and FUV intensity conditions emphasize some effects that would be hard to notice otherwise. This includes purely numerical issues like gridding and interpolation/extrapolation of shielding rates. These differences explain why the various codes still show some post-benchmark scatter. We relate differences in the predicted abundances to the corresponding rates for ionization and dissociation.
Since most of the codes use the same
chemical network and apply the same temperature, the major source for remaining deviations should be
related to the FUV radiative transfer. To study this we present some results of benchmark model
F4 featuring a density
n=105.5 cm-3 and a FUV intensity ![]() ,
in order to enhance
any RT related differences and discuss them in more detail.
,
in order to enhance
any RT related differences and discuss them in more detail.
The photo-rates for CO and C are in very good accord, but we notice a
considerable spread in the shielding behavior of the hydrogen photo-rate. This spread is due to
the particular implementation of H2 shielding native to every code, by either using tabulated shielding functions or explicitly calculating the total cross section at each wavelength.
The different photo-rates directly cause a different H-H2 transition profile, shown in the top panel of Fig. 11. The low molecular hydrogen
densities in the Meudon and Cloudy models are again due to the higher H2 photo-dissociation rate. Sternberg's slightly lower H2 abundance at the edge of the cloud is consistent with the marginally higher,
unshielded H2 photo-dissociation rate, seen in the top
plot in Fig. 10. The Meijerink code shows
the earliest drop in the photo-rate, reflected by the corresponding increase in the H2 density. The
qualitatively different H2 profile in KOSMA-![]() is most likely due
to the spherical geometry in the code.
Again Sternberg produces slightly smaller H densities for high values of
is most likely due
to the spherical geometry in the code.
Again Sternberg produces slightly smaller H densities for high values of
![]() .
Since
Sternberg does not consider additional reactions for the H/H2 balance its H density profile is
the only one not showing the slight kink at
.
Since
Sternberg does not consider additional reactions for the H/H2 balance its H density profile is
the only one not showing the slight kink at
![]() .
These
deviations do not significantly change the total column density of hydrogen. Hence the impact on
any comparison with observational findings is small. Nevertheless one would expect that under
the standardized benchmark conditions all codes produce very similar results, yet we note a considerable spread
in hydrogen abundances for
.
These
deviations do not significantly change the total column density of hydrogen. Hence the impact on
any comparison with observational findings is small. Nevertheless one would expect that under
the standardized benchmark conditions all codes produce very similar results, yet we note a considerable spread
in hydrogen abundances for
![]() .
This again emphasizes how
complex and difficult the numerical modeling of PDRs is. The bottom panel in Fig. 11 shows
the density profiles of C+, C, and CO. Here, the different codes are in good agreement. The largest spread
is visible for the C density between
.
This again emphasizes how
complex and difficult the numerical modeling of PDRs is. The bottom panel in Fig. 11 shows
the density profiles of C+, C, and CO. Here, the different codes are in good agreement. The largest spread
is visible for the C density between
![]() ...6. The results for C+ and CO differ less.
Lee96mod's results for C+ and C show a small offset for
...6. The results for C+ and CO differ less.
Lee96mod's results for C+ and C show a small offset for
![]() .
They produce
slightly higher C abundances and lower C+ abundances in the dark cloud part. The different codes agree very well in the predicted depth where most carbon is locked up in CO
(
.
They produce
slightly higher C abundances and lower C+ abundances in the dark cloud part. The different codes agree very well in the predicted depth where most carbon is locked up in CO
(
![]() ). This range improved considerably compared to the pre-benchmark predictions of
). This range improved considerably compared to the pre-benchmark predictions of
![]() .
.
The results from models F1-F4 clearly demonstrate the importance of the PDR code benchmarking effort. The pre-benchmark results show a significant code-dependent scatter. Although many of these deviations have been removed during the benchmark activity, we did not achieve identical results with different codes. Many uncertainties remained even in the isothermal case, raising the need for a deeper follow up study.
In Fig. 12 we show the gas temperature over
![]() .
The general temperature profile is reproduced by all codes. Even so we note
considerable differences between different codes.
The derived temperatures at the surface
vary between 1600 and 2500 K. For low values of
.
The general temperature profile is reproduced by all codes. Even so we note
considerable differences between different codes.
The derived temperatures at the surface
vary between 1600 and 2500 K. For low values of
![]() the heating is dominated
by PE heating due to the high FUV irradiation, and the main cooling is provided by [OI]
and [CII] emission. It is interesting, that the dominant cooling line
is the [OI] 63
the heating is dominated
by PE heating due to the high FUV irradiation, and the main cooling is provided by [OI]
and [CII] emission. It is interesting, that the dominant cooling line
is the [OI] 63
![]() line (cf. Fig. 16, left plot),
although its critical density is two orders of magnitude higher
than the local density (
line (cf. Fig. 16, left plot),
although its critical density is two orders of magnitude higher
than the local density (
![]() cm-3). The highest surface temperature is calculated by Leiden, while Meudon computes the lowest temperature. The bulk of models gives surface temperatures near 1900 K. All models qualitatively reproduce the temperature behavior at higher values of
cm-3). The highest surface temperature is calculated by Leiden, while Meudon computes the lowest temperature. The bulk of models gives surface temperatures near 1900 K. All models qualitatively reproduce the temperature behavior at higher values of
![]() and show a minimum temperature of 10 K between
and show a minimum temperature of 10 K between
![]() ,
followed by a subsequent rise in temperature.
The only relevant heating contribution at
,
followed by a subsequent rise in temperature.
The only relevant heating contribution at
![]() comes from cosmic ray heating, which
hardly depends on
comes from cosmic ray heating, which
hardly depends on
![]() .
At
.
At
![]() ,
the dominant cooling is by [CI] fine structure emission. This is a very efficient cooling process and the temperature reaches its minimum. At
,
the dominant cooling is by [CI] fine structure emission. This is a very efficient cooling process and the temperature reaches its minimum. At
![]() the atomic carbon density rapidly drops and CO cooling starts to exceed the fine structure cooling (cf. abundance profiles in Fig. 14). However, cooling by CO
line emission is much less efficient, especially
at these low total densities, and thus the temperature increases again.
the atomic carbon density rapidly drops and CO cooling starts to exceed the fine structure cooling (cf. abundance profiles in Fig. 14). However, cooling by CO
line emission is much less efficient, especially
at these low total densities, and thus the temperature increases again.
For the bulk of the cloud the heating contribution by H2 vibrational deexcitation is
negligible compared to photoelectric heating. Only Meijerink and Leiden predict
comparable contributions from both processes. Unfortunately, the
exact treatment of this process was not standardized and depends very much on the
detailed implementation (e.g. the two-level approximation from Burton et al. (1990) or Röllig et al. (2006)
vs. the solution of the full H2 problem like in Meudon, Cloudy, and Sternberg).
Generally the heating by H2 vibrational deexcitation depends on the local density and the
local mean FUV intensity, and should
thus decrease at large values of
![]() and dominate the heating for denser clouds.
and dominate the heating for denser clouds.
At
![]() we note a flattening of the temperature curve in many models, followed by a steeper decline somewhat deeper inside the cloud.
This is not the case for HTBKW, KOSMA-
we note a flattening of the temperature curve in many models, followed by a steeper decline somewhat deeper inside the cloud.
This is not the case for HTBKW, KOSMA-![]() ,
and Sternberg. The reason for this difference is the [OI] 63
,
and Sternberg. The reason for this difference is the [OI] 63
![]() cooling, showing a steeper decline for the three codes
(Fig. 16, left plot). For very large depths, KOSMA-
cooling, showing a steeper decline for the three codes
(Fig. 16, left plot). For very large depths, KOSMA-![]() produces slightly higher gas temperatures. This is due to the larger dust temperature and the strongest H2 vibrational deexcitation heating at
produces slightly higher gas temperatures. This is due to the larger dust temperature and the strongest H2 vibrational deexcitation heating at
![]() .
.
 |
Figure 12:
Model V2 (n=103 cm-3, |
The photoionization rate of C is given in the top right plot in Fig. 13. All models are in good agreement at the surface of the cloud. Meudon and UCL_PDR
drop slightly earlier than the bulk of the results. This is also reflected in their C density profiles
in Fig. 14 (top right) which incline slightly earlier. Deep inside the cloud Sternberg
and HTBKW show a steeper decline compared to the other codes.
The agreement for the
C+ profile is also very good. At
![]() the densities drop by a factor of 10 and
remain constant until they drop at
the densities drop by a factor of 10 and
remain constant until they drop at
![]() .
This plateau is caused by the increase
in C density, compensating the FUV attenuating. Leiden's
results show some deviations for
.
This plateau is caused by the increase
in C density, compensating the FUV attenuating. Leiden's
results show some deviations for
![]() .
Their C density remains higher throughout the
center, causing a slightly different carbon and
oxygen chemistry at
.
Their C density remains higher throughout the
center, causing a slightly different carbon and
oxygen chemistry at
![]() .
The calculated O and
O2 densities are given in Fig. 14 (bottom, right).
The dark cloud densities are in very good agreement among the models, with some deviations in the Leiden
values. The O2 profiles show some variations between
.
The calculated O and
O2 densities are given in Fig. 14 (bottom, right).
The dark cloud densities are in very good agreement among the models, with some deviations in the Leiden
values. The O2 profiles show some variations between
![]() and 10 but these are minor deviations especially taking the fact that the densities
vary over 14 orders of magnitude from the outside to the center of the cloud! The differences in O2are also reflected in the CO plot (Fig. 14, bottom left). All codes produce very similar
density profiles and dark cloud values. Leiden gives a smaller CO density beyond
and 10 but these are minor deviations especially taking the fact that the densities
vary over 14 orders of magnitude from the outside to the center of the cloud! The differences in O2are also reflected in the CO plot (Fig. 14, bottom left). All codes produce very similar
density profiles and dark cloud values. Leiden gives a smaller CO density beyond
![]() .
.
In Fig. 15 we plot the total surface brightnesses of the main
fine-structure cooling lines for the V2 model: [CII] 158 ![]() m, [OI] 63, and 146
m, [OI] 63, and 146 ![]() m, and [CI] 610 and 370
m, and [CI] 610 and 370 ![]() m.
For the spherical PDR models, the surface brightness averaged over
the projected area of the clump is shown.
The surface brightness of these fine-structure lines is
smaller by typically a few 10%, if calculated along
a pencil-beam toward the clump center as they are enhanced in the outer
cloud layers. Compared with the pre-benchmark results,
the spread in
m.
For the spherical PDR models, the surface brightness averaged over
the projected area of the clump is shown.
The surface brightness of these fine-structure lines is
smaller by typically a few 10%, if calculated along
a pencil-beam toward the clump center as they are enhanced in the outer
cloud layers. Compared with the pre-benchmark results,
the spread in ![]() has been decreased significantly from almost 3 orders of magnitude to a factor of 3-5 for [CII] and [OI]. To explain the differences in Fig. 15 we plot
in Fig. 16 the radial profiles of the local emissivities of
[OI] 63
has been decreased significantly from almost 3 orders of magnitude to a factor of 3-5 for [CII] and [OI]. To explain the differences in Fig. 15 we plot
in Fig. 16 the radial profiles of the local emissivities of
[OI] 63
![]() and [CI] 310
and [CI] 310
![]() .
Leiden gives the highest
[OI] brightnesses and also computes higher local [OI] 63
.
Leiden gives the highest
[OI] brightnesses and also computes higher local [OI] 63 ![]() m emissivities for small values of
m emissivities for small values of
![]() ,
shown in Fig. 16. COSTAR, with very
similar results for the density profile and comparable gas temperatures, gives much smaller emissivities. The reason for these deviations is still unclear.
The model dependent spread in surface brightnesses is largest for the [CI] lines. HTBKW computes
10 times higher line intensities for the [CI] 370
,
shown in Fig. 16. COSTAR, with very
similar results for the density profile and comparable gas temperatures, gives much smaller emissivities. The reason for these deviations is still unclear.
The model dependent spread in surface brightnesses is largest for the [CI] lines. HTBKW computes
10 times higher line intensities for the [CI] 370 ![]() m transition than Sternberg.
This can be explained as follows. Both codes show almost identical
column densities and abundance profiles of C0, yet the local emissivities are very different between
m transition than Sternberg.
This can be explained as follows. Both codes show almost identical
column densities and abundance profiles of C0, yet the local emissivities are very different between
![]() (Fig. 16). Sternberg, together with some other codes, compute a local minimum for the cooling at
(Fig. 16). Sternberg, together with some other codes, compute a local minimum for the cooling at
![]() ,
while the HTBKW, Cloudy, Meijerink, and Meudon models
peak at the same depth. This can be explained as a pure temperature effect, since the codes
showing a [CI] peak compute a
significantly higher temperature at
,
while the HTBKW, Cloudy, Meijerink, and Meudon models
peak at the same depth. This can be explained as a pure temperature effect, since the codes
showing a [CI] peak compute a
significantly higher temperature at
![]() :
T(HTBKW) = 83 K,
T(Sternberg) = 10 K. These different temperatures at the C0 abundance peak strongly influences the resulting [CI] surface brightnesses. Overall, the
model-dependent surface temperatures still vary significantly. This is due to the additional nonlinearity of the radiative transfer problem, which, under certain circumstances, amplifies even small abundance/temperature differences.
:
T(HTBKW) = 83 K,
T(Sternberg) = 10 K. These different temperatures at the C0 abundance peak strongly influences the resulting [CI] surface brightnesses. Overall, the
model-dependent surface temperatures still vary significantly. This is due to the additional nonlinearity of the radiative transfer problem, which, under certain circumstances, amplifies even small abundance/temperature differences.
Every participating code has its own strengths. The Meudon code and Cloudy are certainly the most complex codes in the benchmark, accounting for most physical effects by explicit calculations, starting from the detailed micro-physical processes, making the least use of fitting formulae.
Cloudy was originally developed to simulate extreme environments near accreting black holes (Ferland & Rees 1988). although it has been applied to HII regions, planetary nebulae, and the ISM. Ferland et al. (1994) describe an early PDR calculation. Its capabilities have been greatly extended over the past several years (van Hoof et al. 2004; Shaw et al. 2005; Abel et al. 2005). Due to the complexity of the code, it was initially not possible to turn off all implemented physical processes as required for the benchmark, but during this study they were able to adopt all benchmark requirements thus removing all major deviations.
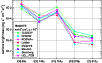 |
Figure 15:
Model V2 (n=103 cm-3, |
The codes HTBKW, Leiden, Sternberg and KOSMA-![]() are
based on PDR models that began
their development 20 years ago
and have been supported and improved since then. One of the main
differences between them is the model geometry and illumination. Plane-parallel geometry
and uni-directional illumination
is assumed in HTBKW, Leiden and Sternberg and spherical geometry with an isotropically
impinging FUV field in KOSMA-
are
based on PDR models that began
their development 20 years ago
and have been supported and improved since then. One of the main
differences between them is the model geometry and illumination. Plane-parallel geometry
and uni-directional illumination
is assumed in HTBKW, Leiden and Sternberg and spherical geometry with an isotropically
impinging FUV field in KOSMA-![]() .
The chemistry adopted generally in HTBKW is
the smallest (46 species) compared with Sternberg (78) and Leiden/KOSMA-
.
The chemistry adopted generally in HTBKW is
the smallest (46 species) compared with Sternberg (78) and Leiden/KOSMA-![]() (variable). Leiden, Sternberg and KOSMA-
(variable). Leiden, Sternberg and KOSMA-![]() explicitly solve the H2 problem (full ro-vib level population) and determine
the corresponding shielding by integrating all absorption coefficients
while HTBKW uses shielding
functions and a single-line approximation for H2. Cloudy is also capable of explicitly
calculating a fully (v,J) resolved H2 model, but this capability was switched
off in the final model. Instead they used a 3-level approximation there. Leiden
and Meudon are the only codes in the benchmark
explicitly calculating the CO shielding, all other codes use shielding factors. HTBKW is
additionally accounting for X ray and PAH heating
and computes a large number of observational line intensities, while Leiden focuses on the
line emission from the
main PDR coolants C+, C, O, and CO. However it is possible to couple their PDR output with a more
sophisticated radiative transfer code such as RATRAN (Hogerheijde & van der Tak 2000) to calculate emission
lines. This is also done
by KOSMA-
explicitly solve the H2 problem (full ro-vib level population) and determine
the corresponding shielding by integrating all absorption coefficients
while HTBKW uses shielding
functions and a single-line approximation for H2. Cloudy is also capable of explicitly
calculating a fully (v,J) resolved H2 model, but this capability was switched
off in the final model. Instead they used a 3-level approximation there. Leiden
and Meudon are the only codes in the benchmark
explicitly calculating the CO shielding, all other codes use shielding factors. HTBKW is
additionally accounting for X ray and PAH heating
and computes a large number of observational line intensities, while Leiden focuses on the
line emission from the
main PDR coolants C+, C, O, and CO. However it is possible to couple their PDR output with a more
sophisticated radiative transfer code such as RATRAN (Hogerheijde & van der Tak 2000) to calculate emission
lines. This is also done
by KOSMA-![]() ,
using ONION (Gierens et al. 1992) or SimLine (Ossenkopf et al. 2001). COSTAR was developed
in order to model circumstellar disks, featuring any given disk density profile in radial direction
and scale height in vertical direction. It uses uni-directional FUV illumination and can treat a surrounding
isotropic interstellar FUV field in addition to the uni-directional stellar field. It
computes a relatively small chemical network (48 species) but also accounts for
freeze-out onto grains and desorption effects. It relies on shielding functions for H2 and CO and does not calculate observational line intensities up to now. Nevertheless most of the COSTAR results are in good agreement with the other code results for most of the benchmark models, demonstrating that it correctly accounts for the
important PDR physics and chemistry. UCL_PDR is a plane-parallel model focused
on time-dependent chemistries with freeze-out and desorption. Its main features
are a fully time-dependent treatment - including time-varying density and
radiation profiles - and its speed, which makes it suitable for
parameter search studies where a large number of models need to be
run. It can also be coupled with the SMMOL radiative transfer code
(Rawlings & Yates 2001) for a detailed treatment
of the PDR emission properties.
Lee96mod was developed from the time-dependent chemical model by Lee, Herbst, and collaborators. It is strongly geared toward complex chemical calculations and only accounts for constant temperatures, neglecting
local cooling and heating. Meijerink is a relatively
young model with special emphasis on XDRs (X-ray dominated regions) which
quickly evolved in the course of this study and we refer
to Meijerink & Spaans (2005) for a detailed review of the current status. In the Appendix we
give a tabular overview of all main model characteristics.
,
using ONION (Gierens et al. 1992) or SimLine (Ossenkopf et al. 2001). COSTAR was developed
in order to model circumstellar disks, featuring any given disk density profile in radial direction
and scale height in vertical direction. It uses uni-directional FUV illumination and can treat a surrounding
isotropic interstellar FUV field in addition to the uni-directional stellar field. It
computes a relatively small chemical network (48 species) but also accounts for
freeze-out onto grains and desorption effects. It relies on shielding functions for H2 and CO and does not calculate observational line intensities up to now. Nevertheless most of the COSTAR results are in good agreement with the other code results for most of the benchmark models, demonstrating that it correctly accounts for the
important PDR physics and chemistry. UCL_PDR is a plane-parallel model focused
on time-dependent chemistries with freeze-out and desorption. Its main features
are a fully time-dependent treatment - including time-varying density and
radiation profiles - and its speed, which makes it suitable for
parameter search studies where a large number of models need to be
run. It can also be coupled with the SMMOL radiative transfer code
(Rawlings & Yates 2001) for a detailed treatment
of the PDR emission properties.
Lee96mod was developed from the time-dependent chemical model by Lee, Herbst, and collaborators. It is strongly geared toward complex chemical calculations and only accounts for constant temperatures, neglecting
local cooling and heating. Meijerink is a relatively
young model with special emphasis on XDRs (X-ray dominated regions) which
quickly evolved in the course of this study and we refer
to Meijerink & Spaans (2005) for a detailed review of the current status. In the Appendix we
give a tabular overview of all main model characteristics.
![\begin{figure}
\par\includegraphics[width=15cm]{5918fi16.eps} \end{figure}](/articles/aa/full/2007/19/aa5918-06/Timg130.gif) |
Figure 16:
Model V2 (n=103 cm-3, |
Due to their complex nature it is not always straightforward to compare results from different PDR models with each other. Given the large number of input paramters, it is usually possible to derive more than one set of physical parameters by comparing observations with model predictions, especially when one is chiefly interested in mean densities and temperatures. Our goal was to understand the mutual differences in the different model results and to work toward a better understanding of the key processes involved in PDR modeling. The comparison has revealed the importance of an accurate treatment of various processes, which require further studies.
The workshop and the following benchmarking activities were a success regardless of many open issues. The major results of this study are:
Future work should focus on the energy balance problem, clearly evident from the sometimes significant scatter in the results for the non-isothermal models V1-V4. The heating by photoelectric emission is closely related to the electron density and to the detailed description of grain charges, grain surface recombinations and photoelectric yield. The high temperature regime also requires an enlarged set of cooling processes. Another important consideration to be adressed, especially when it comes to comparisons with observations is the model density structure, i.e. clumping or gradients. As a consequence we plan to continue our benchmark effort in the future. This should include a calibration on real observational findings as well.
Acknowledgements
We thank the Lorentz Center, Leiden, for hosting the workshop and for the perfect organization, supplying a very productive environment. The workshop and this work was partly funded by the Deutsche Forschungs Gesellschaft DFG via Grant SFB494 and by a Spinoza grant from the Netherlands Organization for Scientific Research (NWO). We also would like to thank the referee and the editor for making helpful suggestions which helped to improve the manuscript.
|
|
|
|
|
|
|
|
|
|
|
|
||
| GEOMETRY | ||||||||||||
| spherical | x | x | ||||||||||
| plane-parallel, finite | x | x | x | x | ||||||||
| plane-parallel, semi-infinite | x | x | x | x | x | x | x | x | x | |||
| circumstellar disc | x | x | x | |||||||||
| ensemble of clouds | x | |||||||||||
| DENSITY | ||||||||||||
| homogeneous | x | x | x | x | x | x | x | x | x | x | x | |
| density-law | x | x | x | x | x | x | x | x | x | |||
| time dependent | x | x | ||||||||||
| velocity field | x | x | ||||||||||
| v = const | x | x | ||||||||||
| v= v(r,...) | x | |||||||||||
| RADIATION | ||||||||||||
| isotropic radiation field | x | x | ||||||||||
| uni-directional radiation field | x | x | x | x | x | x | x | x | x | x | ||
| combination of isotropic+illuminating star | x | |||||||||||
| Habing field | x | x | x | x | x | |||||||
| Draine field | x | x | x | x | x | x | x | |||||
| optional star | x | x | x | |||||||||
| detailed SED | x | x | ||||||||||
| other | x | x | x | x | ||||||||
| external radiation source | x | x | x | x | x | x | x | x | x | x | x | |
| internal radiation source | ||||||||||||
| CHEMISTRY | ||||||||||||
| stationary chemistry | x | x | x | x | x | x | x | x | ||||
| time-dependent chemistry | x | x | x | x | ||||||||
| advection flow | x | |||||||||||
| UMIST95 | x | x | x | x | x | x | x | |||||
| UMIST99 | x | x | x | x | x | x | ||||||
| NSM | x | x | x | |||||||||
| other database | x | x | x | x | x | x | ||||||
| fixed number of species | x | x | x | x | x | x | x | |||||
| variable number of species | x | x | x | x | ||||||||
| number of species | 96 | 48 | 128 | 46 | 577 | 419 | 78 | |||||
| PAH's included | x | x | x | x | x | x | ||||||
| freeze-out on grains included | x | x | x | x | x | |||||||
| H2 formation on grains | x | x | x | x | x | x | x | x | x | x | x | |
| formation of other molecules on grains | x | x | x | |||||||||
| desorption mechanisms included | x | x | x | |||||||||
| thermal desorption | x | x | x | |||||||||
| photoevaporation | x | |||||||||||
| CR spot heating | x | x | x | |||||||||
| grain-grain collisions | x | |||||||||||
| metallicity included | x | x | x | x | x | x | x | x | x | |||
| ISOTOPOMERS | ||||||||||||
| 13C | x | x | x | x | x | |||||||
| 17O | ||||||||||||
| 18O | x | x | x | |||||||||
| D | x | x | x | x | ||||||||
| THERMAL BALANCE | ||||||||||||
| fixed temperature | x | x | x | x | x | x | x | x | x | |||
| temperature determined from energy balance | x | x | x | x | x | x | x | x | x | x | ||
| COOLING | ||||||||||||
| gas-grain cooling | x | x | x | x | x | x | x | x | x | x | ||
| radiative recombination | x | x | x | x | ||||||||
| chemical balance | x | |||||||||||
| [OI] lines | x | x | x | x | x | x | x | x | x | x | ||
| 12CO rotational lines | x | x | x | x | x | x | x | x | x | |||
| 13CO rotational lines | x | x | x | x | x | |||||||
| [CII] line | x | x | x | x | x | x | x | x | x | x | ||
| [CI] lines | x | x | x | x | x | x | x | x | x | x | ||
| [SiII] lines | x | x | x | x | x | x | ||||||
| OH rotational lines | x | x | x | x | x | |||||||
| H2O rotational lines | x | x | x | x | x | |||||||
| H2 rotational lines | x | x | x | x | x | |||||||
| HD rotational lines | x | x | ||||||||||
| [OI] 6300 |
x | x | x | x | x | x | x | |||||
| CH rotational lines | x | x | ||||||||||
| Ly |
x | x | x | x | x | |||||||
| Fe(24 |
x | x | x | x | ||||||||
| H2 (rot-vib) | x | x | x | x | x | |||||||
| HEATING | ||||||||||||
| H2 vibrational deexcitation | x | x | x | x | x | x | x | x | x | x | ||
| single line approx. | x | x | x | x | x | x | x | |||||
| only n-levels, but no J | x | x | ||||||||||
| full rot-vib treatment | x | x | x | |||||||||
| H2 dissociation | x | x | x | x | x | x | x | x | x | x | ||
| H2 formation | x | x | x | x | x | x | x | x | x | |||
| CR heating | x | x | x | x | x | x | x | x | x | x | ||
| PE heating | x | x | x | x | x | x | x | x | x | x | ||
| XR heating | x | x | x | x | ||||||||
| PAH heating | x | x | x | x | x | x | x | |||||
| photoionization | x | x | x | x | x | x | ||||||
| carbon ionization heating | x | x | x | x | x | x | x | |||||
| other species (Si, etc.) | x | x | ||||||||||
| gas-grain collisions | x | x | x | x | x | x | x | |||||
| turbulence heating | x | x | x | |||||||||
| chemical balance | x | x | x | |||||||||
| UV TRANSFER | ||||||||||||
| solved self-consistently | x | x | x | x | x | x | x | x | x | |||
| simple exponential attenuation | x | x | x | x | x | x | x | x | x | x | x | |
| bi-exponential attenuation | x | x | ||||||||||
| full RT in lines | x | x | ||||||||||
| DUST | ||||||||||||
| treatment of rad. transfer | x | x | x | x | x | x | x | |||||
| grain size distribution | x | x | x | x | ||||||||
| extinction/scattering law | x | x | x | x | x | x | x | x | x | x | ||
| albedo | x | x | x | x | x | |||||||
| scattering law | x | x | x | |||||||||
| H2 SHIELDING | ||||||||||||
| shielding factors | x | x | x | x | x | x | x | |||||
| single line | x | x | x | |||||||||
| detailed solution | x | x | x | x | ||||||||
| CO SHIELDING | ||||||||||||
| shielding factors | x | x | x | x | x | x | x | x | x | x | ||
| single line | x | x | x | |||||||||
| detailed solution | x | x | ||||||||||
| isotope selective photodissociation | x | x | x | x | ||||||||
| UV PROFILE FUNCTION | ||||||||||||
| Gaussian | x | x | ||||||||||
| Voigt | x | x | x | x | x | |||||||
| Box | ||||||||||||
| other | ||||||||||||
| RADIATIVE TRANSFER IN COOLING LINES | ||||||||||||
| escape probability | x | x | x | x | x | x | x | x | x | x | ||
| other | ||||||||||||
| IR pumping | x | x | x | x | x | |||||||
| OBSERVATIONAL LINES | ||||||||||||
| self-consistent treatment with cooling | x | x | ||||||||||
| escape probability | x | x | x | x | x | x | x | |||||
| other | x | x | ||||||||||
| H2 | x | x | x | x | ||||||||
| HD | x | x | x | |||||||||
| 12CO | x | x | x | x | x | x | x | |||||
| 13CO | x | x | x | x | ||||||||
| C18O | x | x | ||||||||||
| 13C18O | x | x | ||||||||||
| [OI] | x | x | x | x | x | x | x | x | x | |||
| [CII] | x | x | x | x | x | x | x | x | x | |||
| [CI] | x | x | x | x | x | x | x | x | x | |||
| Si+ | x | x | x | x | ||||||||
| CS | x | x | ||||||||||
| H2O | x | |||||||||||
| H218O | ||||||||||||
| HCO+ | x | x | x | x | ||||||||
| OH | x | |||||||||||
| [SiI] | x | x | x | |||||||||
| [SI],[SII] | x | x | x | x | ||||||||
| [FeI], [FeII] | x | x | x | |||||||||
| COMPUTED LINE PROPERTIES | ||||||||||||
| resolved line profile | x | x | x | x | ||||||||
| continuum rad./rad transfer in UV | x | x | ||||||||||
| line center intensities | x | x | x | x | ||||||||
| line integrated intensities | x | x | x | x | x | x | x | |||||
| optical depths | x | x | x | x | x | x | x | |||||
| Gaussian line profile | x | x | x | x | x | x | ||||||
| box line profile | ||||||||||||
| turbulence included | x | x | x | x | ||||||||
| COLLISIONS | ||||||||||||
| H-H | x | x | x | |||||||||
| H2-H | x | x | x | x | x | x | x | |||||
| H2 - H+ | x | x | x | |||||||||
| H2 - e | x | x | x | x | ||||||||
| H2 - H2 | x | x | x | x | x | x | ||||||
| CO-H | x | x | x | x | x | x | x | |||||
| CO-H2 | x | x | x | x | x | x | x | x | ||||
| CO-e | x | x | x | x | x | |||||||
| CO - He | x | x | x | |||||||||
| C-H | x | x | x | x | x | x | x | x | x | |||
| C-H2 | x | x | x | x | x | x | x | x | ||||
| C-e | x | x | x | x | ||||||||
| C - He | x | x | x | |||||||||
| C - H2O | ||||||||||||
| C+ - H | x | x | x | x | x | x | x | |||||
| C+ - H2 | x | x | x | x | x | x | x | x | ||||
| C+ - e | x | x | x | x | x | x | x | |||||
| O - H | x | x | x | x | x | x | x | x | x | |||
| O - H2 | x | x | x | x | x | x | x | x | x | |||
| O - H+ | x | x | x | x | ||||||||
| O - e | x | x | x | x | x | |||||||
| O - He | x | x | x | |||||||||
| OH - H | ||||||||||||
| OH - He | ||||||||||||
| OH - H2 | x | x | ||||||||||
| H- - H | x | |||||||||||
| H2O - e | ||||||||||||
| H2O - H | x | |||||||||||
| H2O - H2 | x | x | ||||||||||
| H2O - O | ||||||||||||
| dust - H/H2 | x | x | ||||||||||
| dust-any | x | |||||||||||
| Si+ - H | x | x | x | |||||||||
| HD - H | x | |||||||||||
| HD - H2 | x | |||||||||||
| PAH-any | x | x | ||||||||||
| OUTPUT | ||||||||||||
| abundance profile over (AV/depth) | x | x | x | x | x | x | x | x | x | x | x | |
| column density over (AV/depth) | x | x | x | x | x | x | x | |||||
| temperature profile over (AV/depth) | x | x | x | x | x | x | x | x | x | x | ||
| emitted intensities | x | x | x | x | x | x | x | x | ||||
| opacities at line center | x | x | x | x | x | x | ||||||
| heating and cooling rates over (AV/depth) | x | x | x | x | x | x | x | |||||
| chemical rates over (AV/depth) | x | x | x | x | x | x | ||||||
| excitation diagram of H2 | x | x | x | x | ||||||||