A&A 466, 931-941 (2007)
DOI: 10.1051/0004-6361:20066687

Observational templates of star cluster disruption

The stellar group NGC 1901 in front of the Large Magellanic Cloud[*],[*]

G. Carraro1,2 - R. de la Fuente Marcos3 - S. Villanova1 - C. Moni Bidin2 - C. de la Fuente Marcos3 - H. Baumgardt4 - G. Solivella5


1 - Dipartimento di Astronomia, Università di Padova, Vicolo Osservatorio 2, 35122 Padova, Italy
2 - Departamento de Astronomía, Universidad de Chile, Casilla 36-D, Santiago, Chile
3 - Suffolk University Madrid Campus, C/ Viña 3, 28003 Madrid, Spain
4 - AIfA, University of Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
5 - Facultad de Ciencias Astronómicas y Geofísicas de la UNLP, IALP-CONICET, Paseo del Bosque s/n, La Plata, Argentina

Received 3 November 2006 / Accepted 23 January 2007

Abstract
Context. Observations indicate that present-day star formation in the Milky Way disk takes place in stellar ensembles or clusters rather than in isolation. Bound, long-lived stellar groups are known as open clusters. They gradually lose stars and are severely disrupted in their final evolutionary stages, leaving an open cluster remnant made up of a few stars.
Aims. In this paper, we study in detail the stellar content and kinematics of the poorly populated star cluster NGC 1901. This object appears projected against the Large Magellanic Cloud. The aim of the present work is to derive the current evolutionary status, binary fraction, age, and mass of this stellar group. These are fundamental quantities to compare with those from N-body models in order to study the most general topic of star cluster evolution and dissolution.
Methods. The analysis is performed using wide-field photometry in the UBVI pass-band, proper motions from the UCAC.2 catalog, and 3 epochs of high-resolution spectroscopy, as well as results from extensive N-body calculations.
Results. The star group NGC 1901 is found to be an ensemble of solar metallicity stars, $400\pm100$ Myr old, with a core radius of 0.23 pc, a tidal radius of 1.0 pc, and a location at $400\pm50$ pc from the Sun. Out of 13 confirmed members, only 5 single stars have been found. Its estimated present-day binary fraction is at least 62%. The calculated heliocentric space motion of the cluster is not compatible with possible membership in the Hyades stream.
Conclusions. Our results show that NGC 1901 is a clear prototype of an open cluster remnant characterized by a high value of the binary fraction and a significant depletion of low-mass stars. In light of numerical simulations, this is compatible with NGC 1901 being what remains of a larger system initially made of 500-750 stars.

Key words: Galaxy: open clusters and associations: individual: NGC 1901 - Galaxy: evolution

1 Introduction

Observations strongly suggest that present-day star formation in the Milky Way disk takes place in stellar clumps rather than in isolation. These stellar aggregates form from of giant molecular clouds and, in principle, they can be born bound or unbound. Unbound, short-lived (<50 Myr) stellar ensembles are called associations; bound, long-lived stellar groups are known as open clusters. On the other hand, simulations show that open clusters can also be formed from the remains of rich stellar associations (Kroupa et al. 2001).

As most of the field stars were formed in the so-called clustered mode (i.e., in clusters or associations), not in the dispersed mode (i.e., in isolation), it is natural to identify these stellar clumps as the de facto units of star formation in the Galactic disk (Clarke et al. 2000). The idea of open clusters being fundamental units of star formation is, however, controversial (Meyer et al. 2000), as it has been argued that bound open clusters cannot contribute significantly to the field star population because they are rare and long-lived (e.g. Roberts 1957). In contrast, most young embedded clusters are thought to evolve into unbound stellar associations, which produce the majority of stars that populate the Galactic disk (Lada & Lada 1991).

N-body simulations show that the dynamical evolution of open star clusters is mainly the result of encounters among cluster members, of stellar evolution, of encounters with giant molecular clouds, and also the effect of the Galactic tidal field. They gradually lose stars as they evolve, and they are disrupted in their final evolutionary stages, leaving a cluster remnant (OCR, e.g. de la Fuente Marcos 1998) made up of a few stars. For a given Galactocentric distance, the distinctive features of these ghostly objects depend upon the original membership of the cluster, the fraction of primordial binaries (PBs), and the initial mass function. The outcome of these numerical simulations shows a relatively high (about 20%) percentage of binaries in OCRs of models without PBs and up to 80% for models with a significant fraction of PBs (30%). The effects of preferential evaporation of low-mass stars in simulated OCRs are also quite strong, with a significant depletion of the primordial low-mass stellar (or substellar) population compared to the group of more massive stars. The different evolutionary status characteristic of classical open clusters and their remnants can be traced in both their stellar composition and structural parameters, particularly the degree of core-halo differentiation, which is higher in evolved objects. Simulations can also provide information on the correlation between cluster lifetimes and their primordial properties, like membership. By averaging cluster lifetimes for entire sets of numerical models (de la Fuente Marcos & de la Fuente Marcos 2004) as a function of N, the following power law is obtained: $\tau = 0.011 \ N^{0.68}$ (in Gyr) with a correlation coefficient of r = 0.995 and associated errors in $\tau$ of $\sim$10%. This slope is very similar to the slopes found by Baumgardt (2001) and Baumgardt & Makino (2003), although the details of the simulations are rather different.

Although the dynamical evolution of open star clusters has been well-studied and our degree of understanding of the various evolutionary stages turning cluster members into field population is satisfactory, the topic of the detection of open cluster remnants is still controversial, not only because their intrinsic observational properties make them difficult to identify, but also because there are no reliable classification criteria. In fact, the main question still is, in general, when does a star cluster become a cluster remnant? A first attempt to provide an answer to this important question can be found in Bica et al. (2001). In their work, they assume that a cluster becomes significantly depopulated and shows signs of being a remnant after losing 2/3 of its initial population, and they suggest the acronym POCR (possible open cluster remnant) for a number of candidates. The application of this criterion to simulated clusters is quite straightforward, but it is difficult to use with real clusters mainly because star counts are incomplete, and there is no observational method providing a reliable estimate of the initial population for a given cluster.

Unfortunately, simulations and observational results both suggest that membership is not the best criteria to determine if a dynamically evolved open cluster is an OCR. In order to detect an OCR, a certain contrast of the candidate object against the stellar background is required. To be identified initially as stellar overdensity, a cluster must have a stellar density (or, more properly, a surface luminosity) higher than the local Galactic value. Simulations suggest that, for poorly populated open clusters and before losing 2/3 of their initial population, the stellar density has become lower than the surrounding field and the resulting object can no longer be considered a remnant but instead as some type of stellar stream (proper motions of the member stars remain similar although no overdensity can be recorded). For the Solar Neighborhood, the stellar density of the system should be greater than 0.044 $M_{\odot}$ pc-3. Moreover, the density of a star cluster in the Solar Neighborhood must be higher than about 0.08 $M_{\odot}$ pc-3 in order to be stable against tidal disruption. Taking these constraints into consideration, the smallest OCRs from poorly populated clusters ( $N \leq 100$) should contain more than 40% of their initial population in order to have a higher stellar density than the surrounding field. This value is close to the one quoted in Bica et al. (2001), but the situation appears to change dramatically for richer clusters. OCRs from clusters having N in the range 200-500 should retain 10-20% of their initial members. For N in the range 750-1000, they should keep about 7% of their initial population. Densely populated clusters ( N = 10 000) generate OCRs containing about 0.1% of their initial population, but with stellar density in the range 0.3-15 $M_{\odot}$ pc-3. The OCRs from rich clusters are very different from those resulting from the evolution of small clusters. The surviving stellar system is the outcome of a long-term battle for dynamical stability and, typically, only highly stable hierarchical multiple systems are present there. They are the result of Gyrs of dynamical evolution.

Observationally, Bica et al. (2001) selected 35 groups that stand up against the mean Galactic stellar fields, and are located relatively high onto the Galactic plane. Regrettably, close scrutiny of the kinematics in some of them (Villanova et al. 2004a; Carraro et al. 2005; Carraro 2006) has shown that the contrast criterion is necessary but not sufficient for detecting a remnant. In fact, when dealing with the remnant of a physical group, one expects that the remains exhibit all the features of a physical group. Following Platais et al. (1998), we define a physical group (at odds with a random sample of field stars) as an ensemble of stars that (1) occupy a limited volume of space, (2) individually share a common space velocity, and (3) individually share the same age and chemical composition, producing distinctive features in the H-R diagram.

In an attempt to provide tight observational constraints for numerical models, we have studied the star group NGC 1901 in detail, which appears to be a promising open-cluster remnant candidate. In this paper, we present new CCD UBVI photometry and 3 epoch spectroscopy, which we combine with proper motions from the UCAC2 catalog (Zacharias et al. 2004), with the aim of clarifying the nature and dynamical status of this cluster. In Sect. 2 we provide a historical overview of the various analyzes previously carried out for this object. Observations, data reduction, and overall results are presented in Sect. 3. In Sect. 4 we analyze proper motions and in Sect. 5 we discuss cluster members. In Sect. 6 we derive cluster fundamental parameters. Section 7 is devoted to identifying possible fainter members. The current dynamical status is analyzed in Sect. 8 and the connection with the Hyades stream is considered in Sect. 9. In Sect. 10 we draw some conclusions and suggest further lines of research.

2 Historical overview

The star group NGC 1901 was discovered in 1836 by Herschel but first noticed as a possible physical group by Bok & Bok (1960) while re-defining the van Wijk (1952) photometric sequence in front of the Large Magellanic Cloud (LMC). Bok & Bok (1960) emphasize that the region of the van Wijk sequence possibly represents a loose association of stars projected against the Large Cloud, since the LMC is not very dense in this direction ( $\alpha=05^{\rm h}18^{\rm m}11^{\rm s}$, $\delta=-68^{\circ} 27^{\prime}$, $l=279\hbox{$.\!\!^\circ$ }03$, $b=-33\hbox{$.\!\!^\circ$ }60$).

The photoelectric BV photometry collected by Sanduleak & Philip (1968, hereinafter SP68) let us indeed to find out for the first time that the stars in the association compose a sequence in the color magnitude diagram (CMD), compatible with a group of stars at 330 pc from the Sun. This result was noticed to be reinforced by the preliminary objective-prism radial velocities taken a few years before by Fehrenbach (1965), which showed how a few stars did have radial velocities lower than the expected value (higher than 275 km s-1) for objects belonging to the LMC. For some of these stars, SP68 provided proper motions from a variety of sources, showing that a substantial fraction of them share a common motion.

A more detailed proper motion analysis was performed the same year by Murray et al. (1969), which confirmed the reality of the group but put it 480 pc from the Sun, and called attention to a possible dynamical relation with the Hyades, due to the very similar space motion components of the two groups. This argument has been thoroughly investigated by Eggen (1996), who found that the two systems are part of the Hyades stream. He found two separate kinematic groups that he called superclusters within the Hyades stream: the Hyades and the NGC 1901 superclusters. Using the UVW system defined in Sect. 9 the heliocentric space motion of the Hyades group is (U, V, W) = (-40.4, -16.0, -3.0) km s-1 and the equivalent result for the NGC 1901 group is (U, V, W) = (-26.4, -10.4, -1.5) km s-1. Although these results strongly suggest that two different kinematic structures are being observed, no discussion of errors or dispersions is given in Eggen's paper. Using samples observed by the Hipparcos satellite, Dehnen (1998) confirms the presence of two distinct moving groups in the area. The Hyades group was characterized by (U, V, W) = (-40, -20, 0) km s-1, and he found (U, V, W) = (-25, -10, -15) km s-1 for the NGC 1901 group. Chereul et al. (1999) give (U, V, W) = (-32.9, -14.5, -5.6) km s-1 with velocity dispersions ($\sigma_U$, $\sigma _V$, $\sigma_W$) = (6.6, 6.8, 6.5) km s-1 for the Hyades group, although they find three different groups within the supercluster. The NGC 1901 group is found at (U, V, W) = (-26.1, -7.6, -0.7) km s-1 with velocity dispersions ($\sigma_U$, $\sigma _V$, $\sigma_W$) = (2.1, 3.7, 3.2) km s-1. Again, both kinematic structures appear well-separated.

Finally, a new investigation has been recently published by Pavani et al. (2001, hereinafter P01). They extended the photometry in a small area down to V = 16. However, the poor quality of the photometry and the lack of any new kinematic information prevented them from adding new pieces of information.

3 Observational material: photometry

The U,B,V, and I images centred on NGC 1901 were obtained at the Cerro Tololo Inter-American Observatory 1.0 m telescope, which is operated by the SMARTS[*] consortium. The telescope is equipped with a new 4k $\times$ 4k CCD camera having a pixel scale of 0 $.\!\!^{\prime\prime}$289/pixel, which allows one to cover a field of $20^{\prime} \times 20^{\prime}$. Observations were carried out on November 29, 2005. Three Landolt (1992) areas (TPhoenix, Rubin 149, and PG 0231+006) were also observed to tie the instrumental magnitudes to the standard system. The night was photometric with an average seeing of 1.1 arcsec. Data were reduced using IRAF[*] packages CCDRED, DAOPHOT, and PHOTCAL. Photometry was done employing the point spread function (PSF) method (Stetson 1987). The covered area is shown in Fig. 1, while Table 1 contains the observational log-book.

The calibration equations read:


                                                             u = U + u1 + u2 (U-B) + u3 X         (a)
                                                             b = B + b1 + b2 (B-V) + b3 X         (b)
                                                             v = V + v1bv + v2bv (B-V) + v3 X         (c)
                                                             v = V + v1vi + v2vi (V-I) + v3 X         (d)
                                                             i = I + i1 + i2 (V-I) + i3 X ,         (e)


where UBVI are standard magnitudes, ubvi are the instrumental ones, X is the airmass and the derived coefficients are presented at the bottom of Table 1. As for V magnitudes, when B magnitude was available, we used expression (c) to compute them, elsewhere expression (d) was used. The standard stars in these fields provide a wide color coverage, with $-1.217\leq (U-B) \leq 2.233$, $-0.298\leq (U-B) \leq 1.999$, and $-0.361\leq (V-I) \leq 2.268$. Aperture correction was estimated in a sample of bright stars andthen applied to all the stars. It amounted at 0.315, 0.300, 0.280 and 0.280 mag for the U, B, V, and I filters, respectively.


  \begin{figure} \par\includegraphics[angle=-90,width=8.2cm,clip]{AA6687fig1.eps} \end{figure} Figure 1: DSS image of the area covered by the present study. North is up, east to the left, and the image is 20 arcmin on a side.
Open with DEXTER

We now compare our photometry with previous investigations. We restrict this comparison to the photoelectric photometry of SP68 and the modern CCD study by P01. We have 12 stars in common with SP68, and the comparison (our magnitudes and colors minus SP68 ones) reads:

\begin{displaymath}\Delta (B - V) = 0.024 \pm 0.044 \end{displaymath} (1)


\begin{displaymath}\Delta V = 0.012 \pm 0.056 , \end{displaymath} (2)

In general, this comparison is very good and it is shown in Fig. 2.

Now we turn to the only previous CCD investigation by P01. We have 30 stars in common and the comparison (out magnitudes and colros minus P01 ones) reads:

\begin{displaymath}\Delta (B - V) = 1.972 \pm 4.075 \end{displaymath} (3)


\begin{displaymath}\Delta V = -0.267 \pm 0.619, \end{displaymath} (4)

Only a sub-sample of these 30 stars is shown in Fig. 3.

Clearly some errors occurred in P01 photometry, which compares well with SP68 and the present study down to $V \sim 11.5$, but then starts deviating increasingly compared to the present study. We notice that P01 failed to compare their photometry with two more stars they have in common with SP68 (GSC091200626 and GSC092100834). While the present study also compares very well with SP68 for these two stars, P01 shows significant deviations (up to 0.5 mag in V) for them. The comparison with P01 is shown in Fig. 3. Another strange point is that P01 assign two entries to TYC-2883 and GCS 0916200883 (actually the same star, HD 269310), but provide for it two very discrepant values for the magnitude and color and different suggestions about the membership.


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{AA6687fig2.eps} \end{figure} Figure 2: Comparison with SP68 photoelectric photometry. We show here our magnitudes and colors minus SP68 ones.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{AA6687fig3.eps} \end{figure} Figure 3: Comparison with P01 CCD photometry. We show here our magnitudes and colors minus P01 ones. In this figure the two most deviating stars are not shown.
Open with DEXTER

The CMD of all the stars measured in the field of NGC 1901 (see Fig. 1) is shown in Fig. 4. The present photometry goes 7 mag deeper than P01 and provides a wider wavelength baseline (from U to I). The CMD in Fig. 4 is in the V vs. B - V plane, to compare with previous studies. The objective is to extend the NGC 1901 sequence as deep as possible. The main problem is, of course, the strong contamination from LMC stars. The LMC is dramatically visible in this CMD, with its young-star main sequence (MS), intermediate-age population red clump, asymptotic giant branch (AGB), and the older stars red giant branch (RGB).


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{AA6687fig4.eps} \end{figure} Figure 4: BV CMD for all the stars detected in the present study having $\sigma _B$ and $\sigma _V$ smaller than 0.1 mag.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.3cm,clip]{AA6687fig5.eps} \end{figure} Figure 5: Proper motion analysis. Upper panel: stars having $12 \leq K \leq 14$. Middle panel: stars having $10 \leq K \leq 12$. Lower panel: stars brighter than K = 10.0.
Open with DEXTER

4 Proper motions

We extracted the proper motion components in a 20-squared arcmin field around NGC 1901 from the UCAC2 catalog (Zacharias et al. 2004) and constructed 3 vector-point diagrams as a function of K magnitude (UCAC2 is in fact cross-correlated with 2MASS). The results are shown in Fig. 5, where the lower panel is restricted to stars having $K \leq 10$, the middle panel to stars in the range $10 \leq K \leq 12$, and the upper panel to stars in the range $12 \leq K \leq 14$. The contamination from background stars is very high in the upper and middle panels. For this reason, we consider only the stars brighter than K = 10 (lower panel) to get an estimate of the cluster mean tangential motion and derive a first list of member candidates. In this way we extracted 35 stars from the catalog, from which we derived:

\begin{displaymath}\mu_{\alpha} = 1.7 \pm 1.3~\rm [ms/yr] \end{displaymath} (5)


\begin{displaymath}\mu_{\delta} = 12.3 \pm 2.9~\rm [mas/yr]. \end{displaymath} (6)

Clearly, stars in the lower panel seem to visually clump around these values. Starting from here, we are going to consider as probable members those stars having proper motion components compatible within 2$\sigma$ of these values.

5 Observational material: spectroscopy

To obtain more solid information about the membership and dynamical status of NGC 1901, we carried out a multi-epoch spectroscopic campaign. With the aim of measuring radial velocity and detecting unresolved binaries, spectroscopy was obtained during three different runs in 2002, 2003, and 2005.

5.1 La Silla data

The first epoch of radial velocity observations has already been described in Villanova (2003) and Villanova et al. (2004b) and were carried out on the night of 2002 December 10 at the La Silla Observatory (ESO, Chile) under photometric conditions and a typical seeing of 1 arcsec. The EMMI spectrograph on the NTT 3.5-m telescope was used with a 1.0'' slit to provide a spectral resolution of R = 33 000 in the wavelength range 3800-8600 Å on the two $2048\times4096$ CCDs of the mosaic detector. For the wavelength calibration, a single spectrum of a thorium-argon lamp was secured at the end of the night because of the stability of the instrument. The typical signal-to-noise of the spectra range from 70 to 170.

5.2 CASLEO data

This observational dataset consists of 4 high-resolution spectra for radial velocities determination and 2 low-resolution spectra for MK classification. The 4 high-resolution spectra were obtained in 2003 December 11-15, with the Echelle REOSC Cassegrain spectrograph attached to the 2.15 m reflector at the Complejo Astronomico El Leoncito (CASLEO[*]), using a TEK $1024\times1024$ pixel CCD as detector. The spectra cover an approximate wavelength range of 3600 to 6000 $\AA$, at a reciprocal dispersion of $\sim$0.15 $\AA$ per pixel at 4000 $\AA$. Comparison arc images were observed at the same telescope position as the stellar images immediately before and after the stellar exposures. Spectra were all reduced using available IRAF routines. The radial velocities were determined on spectra normalized to the continuum, by fitting Gaussian profiles to the observed line using IRAF routines and measuring the position of the line or the two components present in the echelle spectra. The 2 low-resolution spectra observed from CASLEO, in 2004 December 8, with the same REOSC spectrograph as echelle, but in its simple dispersion mode, provides a sampling of 1.64 $\AA$ per pixel on the TEK $1024\times1024$, covering a wavelength range from 3900 to 5500 $\AA$, over the classical range for MK classification. All spectra were reduced using standard IRAF routines.

5.3 Las Campanas data

The third-epoch radial-velocity observations were carried out on the nights of 2005 October 18-22 at the du Pont 2.5-m telescope at Las Campanas Observatory under variable photometric conditions and a typical seeing around $1{-}2^{\prime\prime}$. The echelle spectrograph was used with a 0.7'' slit to provide a spectral resolution of R = 64 000 in the wavelength range 3600-10 400 Å on the $2048\times2048$ CCD. Images were reduced using IRAF, including bias subtraction, flat-field correction, extraction of spectral orders, wavelength calibration, sky subtraction, and spectral rectification. The single orders were merged into a single spectrum. The typical signal-to-noise of the spectra ranges from 50 to 80.

The radial velocities of the target stars in the La Silla and Las Campanas runs were measured using the IRAF fxcor task, which cross-correlates the object spectrum with the template. The peak of the cross-correlation was fitted with a Gaussian curve after rejecting the spectral regions contaminated by telluric lines ( $\lambda > 6850~ \AA$). As templates we calculated a set of spectra covering the full $T_{\rm eff}$ range (4500-9000 K) of our stars using SPECTRUM, the Local Thermodynamical Equilibrium (LTE) spectral synthesis program freely distributed by Richard O'Gray[*].

The obtained radial velocities for the three epochs are reported in Table 2, together with their errors, and plotted in Fig. 6.

Table 2: Basic data of suspected NGC 1901 members (M in the last column, or not: NM).

6 Cluster members

In this section we make use of the stellar radial velocities, proper motions, and positions in the various photometric diagrams to filter out interlopers and pick up cluster members. We consider here at first only those stars that have radial velocity, proper motion and multicolor photometry. With these stars we try to define the cluster MS, in order to be able to detect fainter photometric members later on along the extension of this MS. In the following we discuss the group membership on a star-by-star basis.


HD 35294. This is a giant star of G2IV spectral type. Its radial velocity suggests that it is a single star and a member of NGC 1901. Fehrenbach & Duflot (1974) found similar values for the radial velocity of this star, confirming its single nature. Proper motions are also compatible with membership.


HD 35183. This is clearly a binary star, but proper motions do suggest membership.


HD 35293. This is another clear binary star, and proper motions again suggest membership.


HD 35462. Proper motions suggest that it is a member, but radial velocities seem to contradict this hypothesis. However, if we combine our radial velocity measurements with older data (11 km s-1, Barbier-Brossat et al. 1994), it emerges that this is a binary star, therefore reinforcing the idea that it is a member of the group.



  \begin{figure} \par\includegraphics[width=8.1cm,clip]{AA6687fig6.eps} \end{figure} Figure 6: Radial velocity distribution. Open circles indicate RVs from the Las Campanas run, filled squares indicate RVs from the La Silla run, and filled triangles the Casleo run.
Open with DEXTER

HD 269338. This star is a binary, and proper motions and radial velocity are consistent with it being a cluster member.


HD 269319. This star is also a binary, and proper motions and radial velocity are consistent with it being a cluster member.


HD 269312.Proper motions and radial velocity suggest this is a cluster member. This star has recently been studied by Cherix et al. (2006), who finds that it is a $\delta$ Scuti variable candidate.


HD 269310. This star is a binary, and proper motion and radial velocity identify it as a cluster member. Binarity is confirmed by Barbier-Brossat et al. (1994), who report values of -16 and 10 km s-1 for this star.


HD 269301. This star is a binary, and proper motion and radial velocity indicate that it is a cluster member.


HD 269315. We propose this star is not a member. Radial velocity is significantly higher than the cluster average, and proper motions also deviate from the mean tangential motion.


HD 269324. Both radial velocity and proper motion indicate that this star is a member of NGC 1901.


HD 269334. As in the previous case, both radial velocity and proper motion suggest that this star is a member of NGC 1901.


GSC 0916200464. The high radial velocity, blue color, and proper motion readily indicate that this is a LMC star.


GSC 0916200834. This star is a clear member considering its proper motion and radial velocity.


GSC 0916200682. P01 propose that this is a member. However its proper motion indicates it is an interloper, and the radial velocity confirms this conclusion.


GSC 0916201005. Murray et al. (1969) have already suggested that this is not a member, although P01 propose it as a photometric member. Our radial velocity and UCAC 2 proper motions confirm the Murray et al. results.


GSC 0916200626. This star was found to be a proper motion non-member by Murray et al. (1969), but P01 include it in the the list among the members. According to the UCAC2 proper motions, this is a likely member. Radial velocity is compatible with membership, although it may be a binary.


MACS 0517684015. Both the radial velocity and proper motion of this binary demonstrate that it is an interloper.


UCAC2-139. The high radial velocity of this star suggests that it is an LMC probable member.


GSC 0916200216. This is a single star for which both the radial velocity and the proper motion indicate it is an interloper.


Table 3: NGC 1901 abundance analysis with NLTE correction applied when necessary.

7 NGC 1901 metal content

A chemical composition study of the cluster was performed by analyzing the spectrum of the star HD 35294, which we have shown to be a member. As the coldest stellar member, it was the ideal target for this purpose. We used the equivalent-widths method and measured the equivalent widths of the spectral lines for the most important elements (O, Na, Mg, Si, Ca, Ti, Cr, Fe, Ni, Ba) using the standard IRAF routine splot. Repeated measurements show a typical error of about 5 m$\AA$ for the weakest lines. The LTE abundance program MOOG (freely distributed by C. Sneden, University of Texas, Austin) was used to determine the metal abundances. Model atmospheres were interpolated from the models on Kurucz (1992) grids by using the values of $T_{\rm eff}$ and log (g) determined as explained below. Initial estimates of the atmospheric parameters ( $T_{\rm eff}$, log (g), and $v_{\rm t}$) were obtained according to the spectral type of the star (G2IV). Then, during the abundance analysis, $T_{\rm eff}$ and $v_{\rm t}$ were adjusted to remove trends in abundances vs. excitation potential, and equivalent width for FeI lines in order to obtain better estimates.

Besides, log (g) was adjusted in order to have the same abundance from FeI and FeII lines (ionization equilibrium). The final atmospheric parameters for HD 35294 are $T_{\rm eff}=5350\pm50$ K, $\log~(g)=3.2\pm0.1$, and $v_{\rm t}=1.08\pm0.05$ km s-1. The measured iron abundance is $\rm {[Fe/H]} = -0.08\pm0.02$. Results for all the elements are reported in Table 3. The O content was determined using both the forbidden line at 6300 $\AA$ and the permitted triplet at 7774 $\AA$. Because of blending with other spectral lines, abundance from the forbidden line was obtained by comparing the observed spectrum with synthetic ones calculated for different O contents (see Fig. 7 and Table 3). Na, Mg, and O are known to be affected by NLTE effects. For this reason we applied an abundance correction as prescribed by Gratton et al. (1999). Using these corrections, the O abundance obtained from the forbidden line (not affected by NLTE) agrees very well with the one obtained from the O triplet (affected by NLTE). The chemical composition shows a solar-scaled mixture excepted for Ba, which is super-solar at about 0.35 dex. Also Na and Mg, using the NLTE corrections, are solar-scaled as expected for a star cluster of this metallicity.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{AA6687fig7.eps} \end{figure} Figure 7: Oxygen synthesis around the 6300 Å region. The oxygen abundance covers the range -0.2 dex (upper dashed line at 6300 Å) to +0.1 dex (lower dashed line at 6300 Å).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{AA6687fig8.eps} \end{figure} Figure 8: Color magnitude diagram for cluster members. Circles indicate binaries, while triangles indicate single stars.
Open with DEXTER

Table 4: NGC 1901 additional probable members (PM in the last coulumn, or not : PNM.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{AA6687fig9.eps} \end{figure} Figure 9: Color magnitudes and two-color diagrams: looking for the fundamental parameters of NGC 1901. The upper panel shows the TCD, while the three bottom panels show the CMDs for different color combinations. The solid line in all the panels is the same isochrone shifted to fit the stars distribution, while the dashed line is the Schmidt-Kaler (1982) empirical ZAMS.
Open with DEXTER

8 NGC 1901 reddening, distance, and age

The CMD for the stars considered members of NGC 1901 is shown in Fig. 9 for various color combinations. In Fig. 9 the two-color diagram is also shown. In this figure we superpose an isochrone of 400 Myr, for the exact metallicity, as derived in Sect. 7 for the star HD 35294. The value $\rm [Fe/H] = -0.08$ translates into Z = 0.016 (Carraro et al. 1999). In the upper panel however, we simply superpose an empirical zero age main sequence (ZAMS) from Schmidt-Kaler (1982), shifted by $E(B - V) = 0.04 \pm0.01$ ( E(U - B) = 0.029). The same E(B - V) and E(U - B) are then used in the lower left and middle panels, respectively. Here, the isochrone is superposed, together with the ZAMS, both shifted by ( $V - M_V ) = 8.2 \pm0.1$. In the right panel, the isochrone and ZAMS are shifted by the same (V - MV) and by E(V - I) = 0.05. The fit is very good in all the diagrams, and from this we derive a distance of $400\pm50$ pc for NGC 1901. The reddening values we derived in different color indexes is compatible with a normal extinction law (Straizys 1992) toward the cluster. Starting from this point, we calculated the XYZ coordinates of NGC 1901 assuming 8.5 kpc for the distance of the Sun to the Galactic center. We find that $X = 8.55\pm0.050$, $Y = 0.30\pm0.05$, and $Z =-0.220 \pm0.05$ kpc.

9 Searching for fainter members

We used the results of the previous section to search for possible fainter members for which no radial velocity information is available (see Table 4). This is illustrated in Fig. 10, where the V vs. V - I CMD is shown. Here, only the stars with errors in V and (V - I) lower than 0.1 are plotted. Basically, we search for faint members moving along the ZAMS, which is displaced by the same reddening and apparent distance modulus as above. We already have detected all the cluster members brighter than V = 14. Our objective is to look for stars close to the ZAMS (probable photometric members) that have also proper motion components compatible with the bulk of the cluster members. This strategy works down to V = 16, which is the limit of the UCAC2 catalog. In the magnitude range $14 \leq V \leq 16$ we found only 3 more cluster possible members, namely $\char93 $ 34, 38, 93 (our numbering), but only one has compatible proper motion components. Although close to the ZAMS, some other stars ($\char93 $65, 70, 354 and 362) do possess incompatible proper motions, too. Below V $\approx$ 16, the contamination of the RGB/AGB stars of the LMC makes it impossible to search for cluster members in NGC 1901. It is possible, however, that below the LMC RGB some M dwarfs members of NGC 1901 can be present ( $V \approx 18$), simply looking at their position in the CMD. However, the lack of any kinematic information prevent us from assessing their membership in a reliable manner.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{AA6687fig10.eps} \end{figure} Figure 10: Color magnitude diagram: searching for NGC 1901 faint members. The dashed line is a ZAMS shifted by the distance modulus and reddening derived in Sect 8.
Open with DEXTER

10 NGC 1901 mass function and dynamical status

Table 2 suggests that NGC 1901 currently has 13 members with V < 13. If we study the radial distribution of these likely members, we obtain Fig. 11. The star density for a given value of the radius in pixels is calculated counting all the sources (members) enclosed by a circle of radius r and dividing by the area ($\pi \ r^2$) to obtain the surface density in stars/pixel2. The final step in the reductions is to calculate the statistical mean error of the star density. If n stars are expected in an area A, samplings of independent areas of this size will give a Poisson distribution with the mean error $\sqrt{n}$ (King et al. 1968).

Figure 11 suggests that the effective radius of the cluster (including half the members) is about 650 pixels or 3.1 arcmin. For the adopted value of the distance, this translates into an effective radius of 0.4 pc. The tidal radius is defined as the distance from the cluster center for which the relative acceleration becomes zero, and it corresponds to the maximum distance that a star can reach without escaping from the cluster (e.g. Binney & Tremaine 1987). At the tidal radius, the density distribution falls to zero. Following this criterion and from Fig. 11, the tidal radius can be estimated to be rt = 1.0 pc (for a radius in pixels of 1800). The concentration parameter

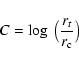\begin{displaymath}C = \log~ \bigl(\frac{r_t}{r_{\rm c}}\bigr) \end{displaymath} (7)

is a value commonly used to measure how centrally concentrated a cluster is. The core radius, $r_{\rm c}$, is a well-defined parameter of a King model (King 1962, 1966), but it is not clear from a theoretical point of view how it should be defined in situations, like the present one, in which a King model cannot be fit. On the other hand, the core radius as defined observationally is the radius at which the density distribution has fallen to just half the central density (for details see, e.g., Casertano & Hut 1985). In our case, it gives a value of 416 pixels or 0.23 pc. Therefore, the concentration parameter is rather low, about 0.64, which suggests a relaxed system with a rather small halo.


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{AA6687fig11.eps} \end{figure} Figure 11: Star counts of assumed NGC 1901 members as a function of radius.
Open with DEXTER

The current binary fraction of NGC 1901 is rather high, 8 binaries out of 13 confirmed members. This translates into a binary fraction close to $62\%$. In their classical paper about multiplicity in the Solar Neighborhood Duquennoy & Mayor (1991) conclude that two thirds of the studied systems were multiples. This figure is very close to the value found in the cluster studied here. OCRs are expected to contain a higher-than-average fraction of multiple systems. Our results for NGC 1901 are not fully conclusive in this respect, as they vare also compatible with the characteristic value of the multiple fraction for the local field population. If our estimate for the present-day binary fraction of this object is correct and we assume that it is a bona fide OCR, then simulations suggest that the primordial binary fraction for NGC 1901 was somewhat low, likely under 20$\%$. On the other hand, our result can also be interpreted as evidence of actual incompleteness. It may be possible that a certain number of binaries remain hidden between the stellar contamination induced by the LMC and beyond V = 13. If true, this may contribute to underestimating the actual binary fraction. Figure 10 appears to show a group of objects at $V \sim 21$ that may be cluster members.

The current mass function of NGC 1901 appears to be quite unusual. If we assume that Fig. 10 can be considered as representative of the CMD for this object, it is clear that the number of K and M stars is rather low. Although it could be the result of incompleteness, our analysis suggests that the scarcity of low-mass cluster members could be real, the result of dynamical evolution or preferential evaporation of low-mass stars.

The initial mass function (hereafter IMF) or frequency distribution of stellar masses at birth (for a recent review on this subject see, e.g., Chabrier 2003, also Scalo 1986) is a fundamental parameter for studying the mass spectrum of open clusters. Salpeter (1955) used the observed luminosity function for the Solar Neighborhood and theoretical evolution times to derive an IMF that may be approximated by a power-law:

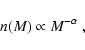\begin{displaymath}n(M) \propto M^{-\alpha} ~, \end{displaymath} (8)

where n(M) is the number of stars per unit mass interval. The value of $\alpha$ is 2.35 for masses between 0.4 and 10.0 $M_{\odot}$. For the particular case of open star clusters, Taff (1974) found different slopes in the range 2.50-2.74 depending on the concentration of stars at the center of the cluster, the contrast of the cluster with the surrounding stellar field - Shapley's (1933) and Trumpler's (1930) classifications - and the abundance of stars and range of brightness. The IMF in Taff's work can be described by $\alpha = 2.50$ for clusters with $N \leq 100$ and $\alpha = 2.65$ for clusters with N > 100. Note, however, that the canonical IMF parametrization constitutes of a two-part power-law IMF in the stellar regime (e.g. Pflamm-Altenburg & Kroupa 2006):

 \begin{displaymath}n(M) = k \ \left\{ \begin{array}{lcl} (M/M_{0})^{-\alpha_{1}... ...lpha_{2}} & & M_{1} \leq M < M_{\max}~, \end{array} \right. \end{displaymath} (9)

where $M_{0}, M_{1}, M_{\max}$ are equal to 0.08, 0.5, 150.0 $M_{\odot}$, respectively, and $\alpha_{1}$, $\alpha_{2}$ are 1.3, 2.3, respectively.


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{AA6687fig12.eps} \end{figure} Figure 12: Observed present-day mass function for NGC 1901 main sequence stars and various IMF fits. See the text for details.
Open with DEXTER

Table 5: Space motions of suspected single NGC 1901 members.

The present-day mass function (hereafter PDMF) for main sequence stars in NGC 1901 after Table 2 is displayed in Fig. 12. It shows clear signs of incompleteness for spectral types later than A9. This could be a dynamical effect, the result of an increased escape rate for low-mass stars. It is well-known that the dynamics of small and intermediate-size clusters is dominated by relatively few heavy members. In the following we use the heaviest main-sequence members of the cluster to estimate the IMF of NGC 1901. In these calculations, we assume implicitly that the dynamical evolution of the cluster has not changed the population of A stars significantly and that the actual number of these stars has remained relatively unchanged since the cluster was formed. If we use the mass intervals [1.6, 2.0] and [2.0, 3.0] $M_{\odot}$ (spectral types A9 to A5 and A4 to A0, respectively) to fit a simple power-law IMF, we obtain

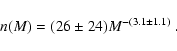\begin{displaymath}n(M) = (26 \pm 24) M^{-(3.1\pm1.1)} ~. \end{displaymath} (10)

The result is displayed in Fig. 12. This IMF produces an initial cluster with a total mass of 10 600 $M_{\odot}$ and almost 30 000 members. This result clearly overestimates the initial number of low-mass stars in the cluster. On the other hand, if we fit the data to a Salpeter IMF, we obtain

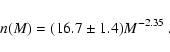\begin{displaymath}n(M) = (16.7 \pm 1.4) M^{-2.35} ~. \end{displaymath} (11)

This IMF (see Fig. 12) produces a cluster with an initial mass of 1100 $M_{\odot}$ and about 2750 members. This is also likely to be an overestimate. Our best result is obtained for a canonical two-part power-law IMF:

 \begin{displaymath}n(M) = \left\{ \begin{array}{lcl} (33\pm4) \ M^{-1.3} & & 0.... ...3\pm1.4) \ M^{-2.3} & & 0.5 \leq m < 9. \end{array} \right. \end{displaymath} (12)

The result is displayed in Fig. 12. For this IMF, the initial total mass of the cluster is 328 $M_{\odot}$ with about 820 initial members (estimated errors of 10%). This is fully consistent with results for the lifetime of 750-1000 members simulated clusters (e.g. de la Fuente Marcos 1997).

The current integrated visual magnitude of the cluster can be estimated using the expression

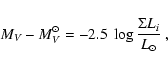\begin{displaymath}M_{V} - M_{V}^{\odot} = -2.5 \ \log \frac{\Sigma L_{i}}{L_{\odot}} ~, \end{displaymath} (13)

where MV is the integrated, absolute, visual magnitude of the cluster, $M_{V}^{\odot}$ is the solar equivalent, $L = \Sigma L_{i}$ is the total luminosity of the cluster, and $L_{\odot}$ is the solar luminosity. This visual magnitude of NGC 1901, including all the members in Table 2, is -0.4, far from the value of the Hyades, -2.7, as expected. On the other hand, if we use our best result for the IMF, the initial integrated magnitude could have been as high as -1.4.

11 NGC 1901 motion

We derive here the NGC 1901 kinematics by considering the 6 bona fide single star members. We obtain

\begin{displaymath}RV = 0.50\pm0.48 \rm ~[km~s^{-1}] . \end{displaymath}

This is derived averaging two epochs RVs, when available, and then deriving the weighted mean of the five stars.

\begin{displaymath}\mu_{\alpha} \times \cos \delta= 1.8\pm1.5 \rm ~[mas/yr] \end{displaymath}


\begin{displaymath}\mu_{\delta} = 10.7\pm1.7 \rm ~[mas/yr]. \end{displaymath}

These values show a very good match with Baumgardt et al. (2000).

To calculate the Galactic space velocity of this object and its uncertainty, we averaged the heliocentric Galactic velocity components for the five suspected single stars that have been considered as likely members in Sect. 6, namely stars 2, 13, 14, 20, and 27. These calculations were carried out as described in Johnson & Soderblom (1987) for equinox 2000. Our results refers to a right-handed coordinate system so that the velocity components are positive in the directions of the Galactic center, U, Galactic rotation, V, and the North Galactic Pole, W. We use the value of the parallax associated to the value of the distance determined in Sect. 8 and its error. Results are displayed in Table 5. They are based on relative proper motions, not absolute ones.

From these values, we derive the Heliocentric reference frame velocity UVW, which turns out to be $U = -19.0\pm1.2$ km s-1, $V = -1.6\pm0.8$ km s-1 and $W = -2.7\pm0.7$ km s-1. This yields a total velocity of $V_{\rm T} = 19.3$ km s-1. The standard deviations are $\sigma_U$ = 6.7 km s-1, $\sigma_V = 2.9$ km s-1 and $\sigma_W = 1.5$ km s-1. If only four stars are considered (star 27 could be a long-period binary), our results are $U = -19.0\pm1.5$ km s-1 ( $\sigma_U = 8.9$ km s-1), $V = -1.9\pm0.9$ km s-1 ( $\sigma_V = 1.8$ km s-1), and $W = -2.9\pm0.8$ km s-1 ( $\sigma_U = 1.6$ km s-1), then $V_{\rm T} = 19.3$ km s-1. These values are not in reasonable agreement with Eggen (1996), Dehnen (1998), and Chereul et al. (1999). One could argue that using relative proper motions may be a major factor in accounting for this lack of agreement. SIMBAD lists proper motions from the Tycho Reference Catalogue (Hog et al. 1998) for seven members (HD 35294, HD 35293, HD 35462, HD 269338, HD 269319, HD 269310, and HD 269301). The values provided by this catalog agree very well with the ones used in this paper; therefore, the observed discrepancies have not been originated by the proper motions used. On the other hand, HD 35183 has parallax and proper motions in the Hipparcos Catalogue (Perryman et al. 1997). Using the values provided by this catalog ( $d = 820 \pm584$ pc, $\mu_{\alpha} = 1.07 \pm1.03$ mas/yr, $\mu_ {\delta} = 10.97 \pm0.94$ mas/yr) and our average value for the radial velocity, we obtain $U = -43\pm33$ km s-1, $V = -3\pm3$ km s-1 and $W = -6\pm7$ km s-1 for this star. This yields a total velocity $V_{\rm T} = 43.5$ km s-1. These numbers are much closer to the values usually quoted in the literature for the Hyades stream (see Sect. 2), but they are the result of using a value of the distance that is twice the one found in our study, even though they are still significantly different. We certainly believe that the value of the distance is the main source of discrepancies in this case. In any case, NGC 1901 is older than the Sirius supercluster (300 Myr) but younger than the Hyades supercluster (600 Myr).

12 Conclusions

We have presented a detailed photometric and spectroscopic study of the stellar group NGC 1901 with the aim of providing an observational template of a star-cluster remnant to serve as an example for theoretical investigations of star cluster evolution and dissolution.

The data we have acquired allow us to derive the following conclusions:

$\bullet$ we identified 13 photometric, spectroscopic, and astrometric members;
$\bullet$ these stars identify a stellar group at 400 pc from the Sun and 400 million years old;
$\bullet$ within the errors of our spectroscopic campaign, out of 13 stars, 8 turn out to be binaries, which implies a binary fraction close to $62\%$; we suggest that this is only a lower limit.
$\bullet$ we find a prominent lack of M dwarfs and interpret this fact as evidence that the group has lost most of its low-mass members;
$\bullet$ we cannot confirm the possible kinematic association of NGC 1901 to the Stream I discussed in Eggen (1996);
$\bullet$ in light of numerical simulations (de la Fuente Marcos 1998), this is compatible with NGC 1901 being what remains of a larger system initially made up of 500-750 stars.
Finally, we would like to emphasize that future studies should be focused on constraining the binary fraction of this stellar group better. Probably a few more epochs should be sufficient to clarify the nature of all the doubtful cases.

Acknowledgements
The work of G.C. has been supported by Fundacion Andes. In preparation of this paper, we made use of the NASA Astrophysics Data System and the ASTRO-PH e-print server. This work made extensive use of the SIMBAD database, operated at the CDS, Strasbourg, France.

References

 

  
Online Material

Table 1: Journal of photometric observations of NGC 1901 and standard star fields, together with calibration coefficients (2005, November 29).


Copyright ESO 2007