A&A 466, 805-812 (2007)
DOI: 10.1051/0004-6361:20066471
Y. Chen1,2 - T. H. Reiprich3 - H. Böhringer2 - Y. Ikebe4 - Y.-Y. Zhang2
1 - Key Laboratory of Particle Astrophysics,
Institute of High Energy Physics,
Chinese Academy of Sciences,
Beijing 100049, PR China
2 -
Max-Planck-Institut für Extraterrestrische Physik, 85748 Garching,
Germany
3 -
Argelander-Institut für Astronomie, Universität Bonn,
Auf dem Hügel 71, 53121 Bonn, Germany
4 -
National Museum of Emerging Science and Innovation, Tokyo, 135-0064, Japan
Received 29 September 2006 / Accepted 17 December 2006
Abstract
We present a statistical study of the occurrence and effects of the
cooling cores in the clusters of
galaxies in a flux-limited sample, HIFLUGCS, based on
ROSAT and ASCA observations.
About 49% of the clusters in this sample have a significant,
classically-calculated cooling-flow, mass-deposition rate. The upper
envelope of the derived mass-deposition rate is roughly proportional
to the cluster mass, and the fraction of cooling core clusters is
found to decrease with it.
The cooling core clusters are found to
have smaller core radii than non-cooling core clusters, while some
non-cooling core clusters have high ![]() values (>0.8).
In the relation of the X-ray luminosity vs.
the temperature and the mass, the cooling core
clusters show a significantly higher normalization. A systematic
correlation analysis, also involving relations of the
gas mass and the total infrared
luminosity, indicates that this bias is shown to be
mostly due to an enhanced X-ray luminosity
for cooling core clusters, while the other parameters, like temperature, mass,
and gas mass may be less affected by the occurrence of a cooling core.
These results may be explained by at least some of the
non-cooling core clusters being in dynamically young states compared with
cooling core clusters, and they may turn into cooling core
clusters in a later evolutionary stage.
values (>0.8).
In the relation of the X-ray luminosity vs.
the temperature and the mass, the cooling core
clusters show a significantly higher normalization. A systematic
correlation analysis, also involving relations of the
gas mass and the total infrared
luminosity, indicates that this bias is shown to be
mostly due to an enhanced X-ray luminosity
for cooling core clusters, while the other parameters, like temperature, mass,
and gas mass may be less affected by the occurrence of a cooling core.
These results may be explained by at least some of the
non-cooling core clusters being in dynamically young states compared with
cooling core clusters, and they may turn into cooling core
clusters in a later evolutionary stage.
Key words: galaxies: clusters: general - galaxies: intergalactic medium - X-ray: galaxies: clusters
Clusters with dense gaseous cores, which have central cooling times significantly lower than a Hubble time, have formerly been termed cooling flow clusters, and it was believed that the intracluster medium (ICM) in these regions cools and condenses, as it is difficult to avoid cooling in the absence of a very fine-tuned heating mechanism (Fabian 1994). A different point of view not requiring a cooling flow has also been put forward based on ASCA spectroscopic results (e.g., Ikebe et al. 1999; Makishima et al. 2001, and references therein). With XMM-Newton observations, it was found that the spectral features predicted by the classical cooling flow model are not observed in the X-ray spectra of cooling flow regions (e.g. Peterson et al. 2001, 2003). While a slight temperature decrease by factors up to 2-3 towards the center in cooling cores is observed, the expected features for further cooling are absent. With high-resolution Chandra observations, a possible fine-tuned heat source has been found in the interaction of central AGN with the cluster ICM, which is now taken as the most probable reason for the prevention of massive cooling flows (e.g. David et al. 2001; Böhringer et al. 2002; Fabian et al. 2003; McNamara et al. 2005). Therefore we follow the now widely-used convention to call the clusters in our sample cooling core clusters (CCC) and non-cooling core clusters (NCCC).
An influence of the CCC or NCCC nature of the clusters on the scaling relations of global properties has previously been realized, e.g., in the luminosity temperature relation (e.g. Fabian et al. 1994; Markevitch 1998; McCarthy et al. 2004) and other parameters (O'Hara et al. 2006). Here we extend the studies of the influence of CCCs on the scaling relation to the largest X-ray flux limited sample of galaxy cluster with detailed X-ray data that allow a mass determination, the HIFLUGCS (the HIghest X-ray FLUx Galaxy Cluster Sample; Reiprich 2001; Reiprich & Böhringer 2002). This cluster sample is selected only by X-ray flux, irrespective of the cluster morphology, and we do not know of any signature of incompleteness in the sample. Therefore it should provide a representative mix of cluster morphologies for a given X-ray luminosity, providing the correct statistics be applied to the typical cosmological X-ray survey cluster samples.
In particular we study the segregation of CC and NCC clusters in the
![]() ,
,
![]() ,
M-T, and the
,
M-T, and the
![]() relations. A major goal in this study
is to better understand the scatter in these relations, which has to be folded into
the test of large-scale structure measures and cosmological models
(e.g., Ikebe et al. 2002; Stanek et al. 2006). It is especially interesting in the context of the
relations. A major goal in this study
is to better understand the scatter in these relations, which has to be folded into
the test of large-scale structure measures and cosmological models
(e.g., Ikebe et al. 2002; Stanek et al. 2006). It is especially interesting in the context of the
![]() relation given by Reiprich & Böhringer (2002) where the observed scatter is very
large and partly due to the large uncertainties in mass determination. Therefore it
was very difficult to separate the intrinsic scatter from the scatter introduced
by the formal and systematic measurement errors. It is the intrinsic scatter,
however, that is important
for the application. A difference in the relation amplitude between CCCs and NCCCs
could in principle provide a lower limit to the intrinsic scatter in the
relation given by Reiprich & Böhringer (2002) where the observed scatter is very
large and partly due to the large uncertainties in mass determination. Therefore it
was very difficult to separate the intrinsic scatter from the scatter introduced
by the formal and systematic measurement errors. It is the intrinsic scatter,
however, that is important
for the application. A difference in the relation amplitude between CCCs and NCCCs
could in principle provide a lower limit to the intrinsic scatter in the
![]() relation of
Reiprich & Böhringer (2002), if the systematic uncertainties are well controlled,
and thus help to understand the origin
of the scatter better. This is interesting because the best-fit cosmological
parameter values from the WMAP 3rd year data (Spergel et al. 2006)
applied to compare the predicted and observationally derived HIFLUGCS
cluster mass function provide an indication that the
intrinsic scatter is probably smaller than the systematic measurement
errors that go into the derived mass and X-ray luminosity relation
(Reiprich 2006).
Our study has a lot in common with the work of O'Hara et al. (2006),
but was started independently a few years ago, so we discuss the correspondence
of the two studies throughout the paper.
relation of
Reiprich & Böhringer (2002), if the systematic uncertainties are well controlled,
and thus help to understand the origin
of the scatter better. This is interesting because the best-fit cosmological
parameter values from the WMAP 3rd year data (Spergel et al. 2006)
applied to compare the predicted and observationally derived HIFLUGCS
cluster mass function provide an indication that the
intrinsic scatter is probably smaller than the systematic measurement
errors that go into the derived mass and X-ray luminosity relation
(Reiprich 2006).
Our study has a lot in common with the work of O'Hara et al. (2006),
but was started independently a few years ago, so we discuss the correspondence
of the two studies throughout the paper.
The paper is organized as follows. In Sect. 2 we briefly introduce the sample. In Sect. 3,
we present the method of data reduction. We compare the properties of the CCC and NCCC in
Sect. 4 and discuss the implications of the results. Section 5 provides a summary.
In the following we adopt a cosmological model with H0=50 km s-1 Mpc-1,
![]() and
and
![]() ,
a choice which was mostly made for easier
comparison with previous results.
,
a choice which was mostly made for easier
comparison with previous results.
The X-ray surface brightness profiles are derived from ROSAT PSPC observations, 36 of them are from RASS observations (allowing for a large enough field-of-view for the prominent nearby clusters), and 70 from pointing observations (Reiprich & Böhringer 2002). The large FOV of the ROSAT PSPC allows us to cover most of the clusters out to r500, the radius at which the mean density of the cluster is 500 times that of a critical density universe. In addition, it is worth noting that this flux limited sample has the largest sky area so far.
The basic properties of the clusters in the HIFLUGCS sample from
Reiprich & Böhringer (2002)
are given in Tables 1 and 2. Note that ![]() ,
the emission-measure weighted temperature,
is used in the calculation of some quantities, such as
,
the emission-measure weighted temperature,
is used in the calculation of some quantities, such as
![]() ,
,
![]() ,
and
,
and ![]() in the next section.
In Fig. 1 we show the distribution of the masses and cooling flow mass deposition rates
determined as described in the following sections. The NCC clusters with no significant
mass-deposition rates and with very small or no cooling radii are shown with their mass
distribution at the bottom of the plot. A striking feature of the plot is the ridge of
cooling core clusters with formal mass deposition rates that increase almost linearly
with cluster mass. This leads us to define the class of pronounced cooling core clusters
by a lower limit to the ratio of the formal mass deposition rate to the cluster mass, M500.
The ratio value chosen for
in the next section.
In Fig. 1 we show the distribution of the masses and cooling flow mass deposition rates
determined as described in the following sections. The NCC clusters with no significant
mass-deposition rates and with very small or no cooling radii are shown with their mass
distribution at the bottom of the plot. A striking feature of the plot is the ridge of
cooling core clusters with formal mass deposition rates that increase almost linearly
with cluster mass. This leads us to define the class of pronounced cooling core clusters
by a lower limit to the ratio of the formal mass deposition rate to the cluster mass, M500.
The ratio value chosen for
![]() of 10-13 yr-1 is indicated in
Fig. 1. A further limit in the mass deposition rate at 0.01
of 10-13 yr-1 is indicated in
Fig. 1. A further limit in the mass deposition rate at 0.01 ![]() yr-1 is used
to separate small-to-moderate cooling cores from NCCC. The total sample thus splits up into 36
pronounced CCCs, 16 small-to-moderate CCCs, and 54 NCCCs. We make use of this
classification below.
yr-1 is used
to separate small-to-moderate cooling cores from NCCC. The total sample thus splits up into 36
pronounced CCCs, 16 small-to-moderate CCCs, and 54 NCCCs. We make use of this
classification below.
![\begin{figure}
\par\includegraphics[width=7.5cm,height=5.2cm,clip]{6471fg01.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg27.gif) |
Figure 1:
Formally-deduced mass-deposition rates in the frame of
the classical cooling flow model as a function of the total
cluster mass, M500. There is a pronounced ridge line of
stronger cooling core clusters with a formal mass deposition rate
almost proportional to the cluster mass. The clusters with
insignificant mass deposition rates below a value of 0.01 |
| Open with DEXTER | |
To determine the X-ray surface brightness distribution we produced images in the 0.5 to 2 keV band (PSPC PI channel 52 to 201) and the corresponding vignetting-corrected exposure maps. The contaminating point sources and obvious substructure were excised. A center position was obtained from an iterative determination of the "center-of-mass'' of the photon distribution in a 7.5 arcmin radius aperture. The surface brightness profile was then constructed by azimuthal averaging in concentric bins. This procedure is the same as used in Reiprich & Böhringer (2002).
We fit the surface brightness profile with a single ![]() model (Cavaliere & Fusco-Femiano 1976)
model (Cavaliere & Fusco-Femiano 1976)
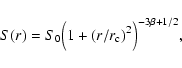 |
(1) |
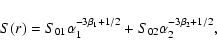 |
(2) |
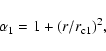 |
(3) |
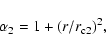 |
(4) |
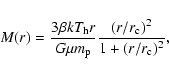 |
(5) |
 |
(6) |
| n02=n012+n022. | (7) |
The cooling time of the gas is calculated by
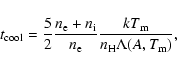 |
(8) |
Following the previously most frequently-used convention, we define the
cooling radius as the radius where the gas cooling time is equal to the
age of the cluster assumed to be close to the Hubble time (
![]() Gyr). The physical meaning of the cooling radius within the classical
cooling flow model is that, within the cooling radius, the gas will lose all
of its energy by X-ray emission and is replaced by ambient hot gas from larger
radii in a steady state inflow. We can therefore calculate the energy loss
rate from the integral of the X-ray emission inside the cooling radius
and the mass inflow rate from the enthalpy influx necessary to compensate
for this energy loss. We then account for the energy gain as the inflowing
gas moves down the gravitational potential gradient. Thus,
the total mass deposition rate within the shell i can be determined by
Gyr). The physical meaning of the cooling radius within the classical
cooling flow model is that, within the cooling radius, the gas will lose all
of its energy by X-ray emission and is replaced by ambient hot gas from larger
radii in a steady state inflow. We can therefore calculate the energy loss
rate from the integral of the X-ray emission inside the cooling radius
and the mass inflow rate from the enthalpy influx necessary to compensate
for this energy loss. We then account for the energy gain as the inflowing
gas moves down the gravitational potential gradient. Thus,
the total mass deposition rate within the shell i can be determined by
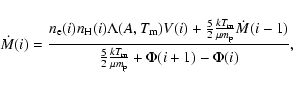 |
(9) |
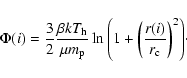 |
(10) |
In the following we investigate the relations between several
observables and the cluster mass. For all the relations we use
the BCES-Bisector fit of Akritas & Bershady (1996). The fits are
performed with the logarithmic values of the parameters and quoted
in the form
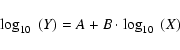
![\begin{figure}
\par\includegraphics[width=7.5cm,height=5.2cm,clip]{6471fg02.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg60.gif) |
Figure 2: The numbers of CCCs (solid lines) and NCCCs (dashed lines) versus the mass of the clusters M500. Note that the fraction of NCCCs increases with M500. |
| Open with DEXTER | |
In Fig. 2 we show the number of CCCs (here including the strong CCC and moderate CCC) and NCCCs in the sample as a function of the cluster mass. The fraction of NCCCs clearly increases with M500. This is also seen in the smaller flux-limited sample used by O'Hara et al. (2006). At the low M500end, this may partly be due to some small mass non-cooling core groups possibly having low luminosities and not reaching the flux limit of HIFLUGCS. In general, however, the main reasons may be that the fraction of dynamically young clusters increases with cluster mass and that these clusters do not generally feature cooling cores. In addition the ICM is hotter in more massive clusters making the radiative heat loss relatively slower. This is an important statistical property of the cluster sample to keep in mind, since any segregation of CCCs and NCCCs in the parameter relations can then also introduce a mass-dependent effect in the relations of the combined sample.
Figure 3 shows the distribution of the values for the core radius,
![]() ,
and slope parameter
,
and slope parameter ![]() from the fit of the
from the fit of the
![]() -model to the X-ray surface-brightness profiles of the
clusters in the sample. As in previous work (e.g. Jones &
Forman 1984; White et al. 2000; Ota & Mitsuda 2004), the
CC clusters segregate very distinctly at lower values of the
core radius than the NCC clusters. Furthermore, we find that the
high the relative
-model to the X-ray surface-brightness profiles of the
clusters in the sample. As in previous work (e.g. Jones &
Forman 1984; White et al. 2000; Ota & Mitsuda 2004), the
CC clusters segregate very distinctly at lower values of the
core radius than the NCC clusters. Furthermore, we find that the
high the relative
![]() ,
the low the
,
the low the ![]() .
In
addition, it was found that some NCCCs have high
.
In
addition, it was found that some NCCCs have high ![]() values
with
values
with
![]() ,
while such high values are not found among the
CCCs. There are 2 reasons for this behavior. For similar gravitational
potential shapes in CCCs and NCCCs, the CC clusters with central
temperature drop, and a corresponding central ICM density increase
in pressure equilibrium feature X-ray surface brightness cusps
that are fit by smaller core radii (Jones & Forman 1984). In
addition, NCCCs are often dynamically young, featuring substructure,
elongations, or disturbed core regions which result in inflated
core radii, that in turn lead to steeper outer surface brightness
slopes.
,
while such high values are not found among the
CCCs. There are 2 reasons for this behavior. For similar gravitational
potential shapes in CCCs and NCCCs, the CC clusters with central
temperature drop, and a corresponding central ICM density increase
in pressure equilibrium feature X-ray surface brightness cusps
that are fit by smaller core radii (Jones & Forman 1984). In
addition, NCCCs are often dynamically young, featuring substructure,
elongations, or disturbed core regions which result in inflated
core radii, that in turn lead to steeper outer surface brightness
slopes.
![\begin{figure}
\par\includegraphics[width=7.5cm,height=5.2cm,clip]{6471fg03.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg63.gif) |
Figure 3:
The |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,height=5.2cm,clip]{6471fg04.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg65.gif) |
Figure 4:
The |
| Open with DEXTER | |
In Fig. 4 we explore the relation of the core radius, ![]() ,
with the cluster
mass, M500. Assuming that clusters have a strictly self-similar shape, we expect
that any characteristic radius scales as
,
with the cluster
mass, M500. Assuming that clusters have a strictly self-similar shape, we expect
that any characteristic radius scales as
![]() .
The results of
the power-law scaling relation fits to the data are given in Table 6 and shown
in Fig. 4. For both subsamples, CCCs and NCCCs, the observed slope is steeper
than this simple expectation; that is, the core radius increases with mass faster
than expected. The explanation for this behavior is probably not trivial.
For the NCCCs, the reason might again be that the fraction of dynamically young
clusters with inflated core radii may be larger for higher cluster masses.
For the CCCs, it might be the
increasing dominance of the central cluster galaxy with decreasing cluster mass
that makes the core region relatively more compact for less massive systems.
.
The results of
the power-law scaling relation fits to the data are given in Table 6 and shown
in Fig. 4. For both subsamples, CCCs and NCCCs, the observed slope is steeper
than this simple expectation; that is, the core radius increases with mass faster
than expected. The explanation for this behavior is probably not trivial.
For the NCCCs, the reason might again be that the fraction of dynamically young
clusters with inflated core radii may be larger for higher cluster masses.
For the CCCs, it might be the
increasing dominance of the central cluster galaxy with decreasing cluster mass
that makes the core region relatively more compact for less massive systems.
It is interesting to note that the relation fitted to the complete sample is steeper than each of the separately fitted relations. This is exactly the effect mentioned above. It is the result of an offset in the relation of the two subsamples (significantly smaller core radii for the CCCs) and, in addition, of a biased distribution of the clusters in the two subsamples with more CCCs at the low-mass end and more NCCCs at the high-mass end. Among all the plots we show in this paper, this is the relation where this effect is most pronounced.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6471fg05.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg67.gif) |
Figure 5:
The M500- |
| Open with DEXTER | |
Figure 5 shows the relation of the globally measured X-ray temperature
of the hot component, ![]() (excluding non-ASCA derived
(excluding non-ASCA derived ![]() ),
and the
cluster mass, M500. The self-similar model prediction is a slope with a
value of 1.5, consistent with the value we obtain for the total sample with
measured
),
and the
cluster mass, M500. The self-similar model prediction is a slope with a
value of 1.5, consistent with the value we obtain for the total sample with
measured ![]() and
consistent with the discussion in Finoguenov et al. (2001).
The results of power-law fits to all the relations discussed in this section
are summarized in Table 7. Moreover, the slopes and the normalizations of the
and
consistent with the discussion in Finoguenov et al. (2001).
The results of power-law fits to all the relations discussed in this section
are summarized in Table 7. Moreover, the slopes and the normalizations of the
![]() relation for the CCCs and NCCCs are consistent within errors. Thus there is no
significant influence of cooling cores on this relation. Note, however, that
the two cluster parameters compared in this relation,
relation for the CCCs and NCCCs are consistent within errors. Thus there is no
significant influence of cooling cores on this relation. Note, however, that
the two cluster parameters compared in this relation, ![]() and M500, are
not independently obtained, but M500 is directly dependent on the
temperature measurements. If
and M500, are
not independently obtained, but M500 is directly dependent on the
temperature measurements. If ![]() has an offset
has an offset
![]() ,
M500will change to
,
M500will change to
![]() .
Note that
this slope is the same as the self-similar model prediction.
Thus the cooling cores' influence on temperature determination will appear
in the cluster mass such
that the overall effect may remain undetected (see also discussion below).
.
Note that
this slope is the same as the self-similar model prediction.
Thus the cooling cores' influence on temperature determination will appear
in the cluster mass such
that the overall effect may remain undetected (see also discussion below).
Among the relations listed in Table 7, in conjunction with the
![]() relation,
together with the
relation,
together with the
![]() relation (Fig. 11),
has the smallest scatter.
This could be due in part to the correlation of the mass and temperature parameter.
We use the
relation (Fig. 11),
has the smallest scatter.
This could be due in part to the correlation of the mass and temperature parameter.
We use the
![]() relation to show below (Sect. 4.5)
that this is not a strong effect and thus not the main reason
for the different
relation to show below (Sect. 4.5)
that this is not a strong effect and thus not the main reason
for the different ![]() normalization. Instead, the tight relation shows
that mass and temperature
are linked in a more fundamental way by simple self-similar gravitational
processes than by the other relations.
normalization. Instead, the tight relation shows
that mass and temperature
are linked in a more fundamental way by simple self-similar gravitational
processes than by the other relations.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6471fg06.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg73.gif) |
Figure 6:
The |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6471fg07.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg74.gif) |
Figure 7:
The |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6471fg08.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg75.gif) |
Figure 8:
The |
| Open with DEXTER | |
The
![]() and
and
![]() relations for the cluster sample with
measured
relations for the cluster sample with
measured ![]() and
and ![]() derived from ASCA are
shown in Figs. 6 and 7. The values of
derived from ASCA are
shown in Figs. 6 and 7. The values of ![]() are the
X-ray luminosities in (0.1-2.4 keV) derived from Ikebe et al. (2002).
Since for some clusters
are the
X-ray luminosities in (0.1-2.4 keV) derived from Ikebe et al. (2002).
Since for some clusters ![]() is measured with the central region
excluded (cooling flow correction),
here we only use
is measured with the central region
excluded (cooling flow correction),
here we only use ![]() without any cooling flow correction.
For
without any cooling flow correction.
For ![]() derived from Fukazawa et al. (1998), which includes cooling flow
correction, we use the central
derived from Fukazawa et al. (1998), which includes cooling flow
correction, we use the central ![]() (
(
![]() )
instead
(Fukazawa et al. 2000).
The resulting slopes of
)
instead
(Fukazawa et al. 2000).
The resulting slopes of
![]() relations are
relations are
![]() and
and
![]() for
for ![]() and
and ![]() ,
respectively.
They are much higher than the 1.5 predicted by a self-similar model
for the
,
respectively.
They are much higher than the 1.5 predicted by a self-similar model
for the
![]() relation (note
relation (note ![]() is in the ROSAT band, not bolometric).
This is consistent with the results in Reiprich & Böhringer (2002).
Note that the slope of
is in the ROSAT band, not bolometric).
This is consistent with the results in Reiprich & Böhringer (2002).
Note that the slope of
![]() is shallower than that of
is shallower than that of
![]() .
This may be due to
.
This may be due to ![]() having an offset to the low
temperature direction compared to
having an offset to the low
temperature direction compared to ![]() and fewer low
and fewer low ![]() clusters
being included in the
clusters
being included in the ![]() relation.
Remarkable is the clearly higher normalization of the relation for CCCs
compared to NCCCs, with offsets of factors of 2.05 and 1.84 for the relation with
relation.
Remarkable is the clearly higher normalization of the relation for CCCs
compared to NCCCs, with offsets of factors of 2.05 and 1.84 for the relation with
![]() and
and ![]() ,
respectively. The normalization difference is slightly
small using
,
respectively. The normalization difference is slightly
small using ![]() in the scaling relation and the scatter is also slightly reduced, since
in the scaling relation and the scatter is also slightly reduced, since
![]() most probably provides a better measure of the global gravitational
potential depth and better mass proxy, as this temperature is not as
downward-biased
by the central cooling core region as
most probably provides a better measure of the global gravitational
potential depth and better mass proxy, as this temperature is not as
downward-biased
by the central cooling core region as ![]() .
But the difference between
the two relations is not very large. This is already an indication that biased
temperature measurements for CCCs are not the major reason for the different
normalizations
of the relations for CCCs and NCCCs. Here the effect of the different mass
coverage of CCCs and NCCCs on the slope of the combined relation (which should
make the relation shallower) is not as strong as in Fig. 4.
The combined relation is
slightly shallower than the NCCC and CCC relations.
.
But the difference between
the two relations is not very large. This is already an indication that biased
temperature measurements for CCCs are not the major reason for the different
normalizations
of the relations for CCCs and NCCCs. Here the effect of the different mass
coverage of CCCs and NCCCs on the slope of the combined relation (which should
make the relation shallower) is not as strong as in Fig. 4.
The combined relation is
slightly shallower than the NCCC and CCC relations.
The
![]() relation is the most important relation for the application
to cosmological cluster surveys. The previously determined relation
for this sample (Reiprich & Böhringer 2002) was used to get cluster mass
estimates, for example, for the cosmological studies (Schuecker et al. 2001b, 2003;
Stanek et al. 2006). The resulting slope of
relation is the most important relation for the application
to cosmological cluster surveys. The previously determined relation
for this sample (Reiprich & Böhringer 2002) was used to get cluster mass
estimates, for example, for the cosmological studies (Schuecker et al. 2001b, 2003;
Stanek et al. 2006). The resulting slope of
![]() relation is again higher
than 1.0, which is predicted by a self-similar model, as shown in Fig. 8.
relation is again higher
than 1.0, which is predicted by a self-similar model, as shown in Fig. 8.
Like in the X-ray luminosity temperature relation, we see a substantial difference in the normalization of this relation for the CCCs and NCCCs by about a factor of 2.4. The offset between the different cluster subsamples shows that the scatter in the overall sample is partly produced by the different types of clusters, and knowing more about the clusters helps reduce this scatter as discussed below.
One important question concerns the origin of this large difference. There are, in principle, two effects caused by cool cores that add to the observed result: cluster temperatures and the cluster masses derived from temperature estimates will be biased low and luminosities will be biased high due to the enhanced emission of dense cores and more compact clusters. In turn, if the core radii of the NCCCs are inflated, the cluster masses will be biased high for the NCCCs.
To distinguish these different possibilities, we need mass estimators independent
of the temperature and independent of the core radii. In the next section
we apply these new parameters.
Figure 8 also shows that the fraction of CCCs at the high ![]() end
do not constitute a small fraction of all clusters unlike
that at the high M500 end.
This is due to CCCs usually having higher
end
do not constitute a small fraction of all clusters unlike
that at the high M500 end.
This is due to CCCs usually having higher ![]() for
the clusters with the same M500.
The CCC fraction is about 60% (11 CCCs) for the
most luminous 18 clusters (with
for
the clusters with the same M500.
The CCC fraction is about 60% (11 CCCs) for the
most luminous 18 clusters (with
![]() erg/s
and z <0.17 in the
erg/s
and z <0.17 in the ![]() CDM cosmology) in this sample.
This fraction is consistent with the distant cluster
samples with similar
CDM cosmology) in this sample.
This fraction is consistent with the distant cluster
samples with similar ![]() ,
e.g., 7 CCCs out of 12 clusters at
,
e.g., 7 CCCs out of 12 clusters at
![]() (Zhang et al. 2006b) and 6 CCCs out of 13 clusters at
(Zhang et al. 2006b) and 6 CCCs out of 13 clusters at
![]() (Zhang et al. 2006a), where
we use the same criterion of CCCs as in the HIFLUCS.
This result shows that the fraction of CCCs in luminous cluster samples
does not show a large evolutionary effect up to
(Zhang et al. 2006a), where
we use the same criterion of CCCs as in the HIFLUCS.
This result shows that the fraction of CCCs in luminous cluster samples
does not show a large evolutionary effect up to
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6471fg09.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg85.gif) |
Figure 9:
The
|
| Open with DEXTER | |
Assuming that the cluster gas mass fraction is approximately constant with cluster
mass (e.g. Allen et al. 2004; Ettori et al. 2003), we can also use the cluster
gas mass to estimate the cluster's total mass. The determination of the
cluster gas mass depends only on the X-ray surface-brightness distribution,
not on the temperature. However, the way we determine
![]() ,
based on the fiducial outer radius of r500,
introduces a weak temperature dependence, since
in our approach we used the temperature-dependent gravitational mass
to estimate r500. This dependence is roughly proportional to
T1/2 and thus much weaker than proportional
and much weaker than the dependence of
,
based on the fiducial outer radius of r500,
introduces a weak temperature dependence, since
in our approach we used the temperature-dependent gravitational mass
to estimate r500. This dependence is roughly proportional to
T1/2 and thus much weaker than proportional
and much weaker than the dependence of
![]() .
Thus if there is any strong bias in the temperature determination due to
cooling flows, we should still see this effect in a correlation analysis based on
gas mass, but it will just be weakened approximately by a factor of two.
For example, if the temperature of a cluster, T, is biased to 2T,
the measured
.
Thus if there is any strong bias in the temperature determination due to
cooling flows, we should still see this effect in a correlation analysis based on
gas mass, but it will just be weakened approximately by a factor of two.
For example, if the temperature of a cluster, T, is biased to 2T,
the measured
![]() will change to 1.4
will change to 1.4
![]() .
However, if this
cluster remains on the line with a slope 2.0 (see Table 7), it needs
.
However, if this
cluster remains on the line with a slope 2.0 (see Table 7), it needs
![]() to change to 4
to change to 4
![]() .
From this example, one can
see that
.
From this example, one can
see that
![]() is insensitive to T in the relation
is insensitive to T in the relation
![]() .
Another mass estimator is the total luminosity of the cluster
galaxies in the NIR (K-band), which is obtained from the
Two Micron All Sky Survey (2MASS) (Lin et al. 2004).
.
Another mass estimator is the total luminosity of the cluster
galaxies in the NIR (K-band), which is obtained from the
Two Micron All Sky Survey (2MASS) (Lin et al. 2004).
The
![]() -
-![]() relation in Fig. 9 shows no strong bias of CCCs versus NCCCs.
The normalization difference is less than 10% so well within the
relation in Fig. 9 shows no strong bias of CCCs versus NCCCs.
The normalization difference is less than 10% so well within the
![]() error
of the fits. The comparison of the two mass estimators
error
of the fits. The comparison of the two mass estimators
![]() and
and
![]() in Fig. 10 shows a
comparatively small difference between the CCCs and NCCCs with a factor smaller than
about 1.25, where the CCCs have on average a little higher
in Fig. 10 shows a
comparatively small difference between the CCCs and NCCCs with a factor smaller than
about 1.25, where the CCCs have on average a little higher
![]() .
Therefore we do not see a strong bias in either of the two mass estimators,
although a weak bias cannot be ruled out, especially in the gas mass.
.
Therefore we do not see a strong bias in either of the two mass estimators,
although a weak bias cannot be ruled out, especially in the gas mass.
Similarly, in Figs. 11 and 12 where we show the
![]() and
and
![]() relations, we do not see a strong temperature bias for CCCs
versus NCCCs. Similar to Figs. 6 and 7, the slope of
relations, we do not see a strong temperature bias for CCCs
versus NCCCs. Similar to Figs. 6 and 7, the slope of
![]() is shallower than that of
is shallower than that of
![]() ,
but it only has a slight
difference for the clusters with
,
but it only has a slight
difference for the clusters with
![]() keV. Note that
clusters with
keV. Note that
clusters with
![]() keV in Fig. 11 are not plotted in Fig. 12.
In addition, the difference in the normalization of this relation
for the CCCs and NCCCs is very small and
within the measurement errors, with a factor 1.10 and 1.00 for
keV in Fig. 11 are not plotted in Fig. 12.
In addition, the difference in the normalization of this relation
for the CCCs and NCCCs is very small and
within the measurement errors, with a factor 1.10 and 1.00 for ![]() and
and ![]() ,
respectively.
Therefore we conclude from the results in this section that the segregation
of CCCs and NCCCs in the
,
respectively.
Therefore we conclude from the results in this section that the segregation
of CCCs and NCCCs in the
![]() and
and
![]() relations is mainly an
X-ray luminosity effect and, to a lesser extent,
an effect of a biased temperature estimate.
A similar conclusion has been reached by O'Hara et al. (2006).
relations is mainly an
X-ray luminosity effect and, to a lesser extent,
an effect of a biased temperature estimate.
A similar conclusion has been reached by O'Hara et al. (2006).
We found no difference of the total gas mass fraction,
![]() ,
between CCCs and NCCCs
as shown in Fig. 13. This reconfirms the weak influence of cooling cores
on the mass and gas mass estimates.
,
between CCCs and NCCCs
as shown in Fig. 13. This reconfirms the weak influence of cooling cores
on the mass and gas mass estimates.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6471fg10.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg92.gif) |
Figure 10:
The
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6471fg11.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg93.gif) |
Figure 11:
The
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6471fg12.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg94.gif) |
Figure 12:
The
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6471fg13.ps}\end{figure}](/articles/aa/full/2007/18/aa6471-06/Timg95.gif) |
Figure 13:
The
|
| Open with DEXTER | |
In this paper we have used an isothermal model to determine the X-ray mass, because to date only global temperature estimates mainly from ASCA are available for such a large sample. For the central region in cooling core clusters, this is obviously not correct. But we expect that the total gravitational mass is correct at large radii, which is confirmed by our mass determination for the cluster PKS 0745-191 and Abell 1650 based on XMM-Newton observations (Chen et al. 2003; Jia et al. 2006) in which the resultant total masses are found to be consistent with this work.
In summary we find from the analysis presented in this paper that:
Acknowledgements
Y. Chen was supported by the exchange program between the Max-Planck Society and the Chinese Academy of Sciences. He thanks MPE for its very gracious hospitality. This research is partially supported by the Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry. T.H.R. acknowledges support by the Deutsche Forschungsgemeinschaft through Emmy Noether Research grant RE 1462.
Table 1: Cluster properties.
Table 2: Cluster properties of the extended cluster sample.
Table 3:
Fit parameters with a double ![]() model.
model.
Table 4: Cluster properties for the scaling relations.
Table 5: Cluster properties for the scaling relations of the extended cluster sample.
Table 6:
Fits to relations of ![]() and M500.
and M500.
Table 7: Summary of the fits to the scaling relations.