A&A 466, 1159-1177 (2007)
DOI: 10.1051/0004-6361:20066046
Collisional and dynamical evolution
of the main belt and NEA population
G. C. de Elía -
A. Brunini
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata,
Paseo del Bosque S/N (1900), La Plata, Argentina
IALP-CONICET
Received 14 July 2006 / Accepted 15 January 2007
Abstract
Aims. In this paper, we analyze the collisional evolution of the Main Belt and NEA population taking into account the major dynamical features present in both populations.
Methods. To do this, we divide the asteroid belt into three semimajor axis zones, whose boundaries are given by the  secular resonance, and the 3:1, 5:2 and 2:1 mean motion resonances with Jupiter, treating them as strong sources of dynamical removal. We also consider the action of the Yarkovsky effect and diffusive resonances as mechanisms of mass depletion. This treatment allows us to calculate the direct collisional injection into the powerful resonances, to study the collisional exchange of mass between the different regions of the Main Belt and to analyze the provenance of the NEA objects.
secular resonance, and the 3:1, 5:2 and 2:1 mean motion resonances with Jupiter, treating them as strong sources of dynamical removal. We also consider the action of the Yarkovsky effect and diffusive resonances as mechanisms of mass depletion. This treatment allows us to calculate the direct collisional injection into the powerful resonances, to study the collisional exchange of mass between the different regions of the Main Belt and to analyze the provenance of the NEA objects.
Results. Our model is in agreement with the major observational constraints associated with the Main Belt and NEA populations, such as their size distributions, the collisional history of Vesta, the number of large asteroid families and the cosmic-ray exposure (CRE) ages of meteorites. We find that none of the dynamical and collisional mechanisms included in our treatment are able to mix material between the three studied main belt regions, since more than 99% of the final mass of every ring of our model of the Main Belt is represented by primordial material. In addition, our results supports that the Yarkovsky effect is the most important process that removes material from the asteroid Main Belt, rather than collisional injection into the major resonances. With regards to the provenance of the NEAs, our work shows that  94
94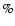 of the NEA population comes from the region inside the 5:2 mean motion resonance.
of the NEA population comes from the region inside the 5:2 mean motion resonance.
Key words: minor planets, asteroids - methods: N-body simulations - methods: numerical - solar system: formation
The Main Belt of asteroids is a vast region located between Mars and Jupiter,
roughly from 2 to 3.4 AU from the Sun. The near-Earth asteroids (NEAs) represent
another important population. NEAs have perihelion distances 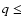 1.3 AU
and aphelion distances
1.3 AU
and aphelion distances 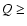 0.983 AU (Rabinowitz et al. 1994).
They are customary divided into three subcategories including the Atens
(a < 1 AU,
0.983 AU (Rabinowitz et al. 1994).
They are customary divided into three subcategories including the Atens
(a < 1 AU, 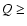 0.983 AU) and Apollos (
0.983 AU) and Apollos (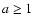 AU,
AU,
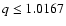 AU),
which are on Earth-crossing orbits, and the Amors (1.0167 AU
AU),
which are on Earth-crossing orbits, and the Amors (1.0167 AU
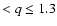 AU), which are on nearly-Earth-crossing orbits. Figure 1 shows the distribution
of Main Belt asteroids and NEAs with respect to semimajor axis, eccentricity and inclination.
AU), which are on nearly-Earth-crossing orbits. Figure 1 shows the distribution
of Main Belt asteroids and NEAs with respect to semimajor axis, eccentricity and inclination.
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{6046fi1.eps} \end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg23.gif) |
Figure 1:
The distribution of Main Belt asteroids, Mars-crossers and NEAs with respect
to semimajor axis, eccentricity and inclination. The Main Belt asteroids are plotted as
small dots while the Mars-crossers are represented as larger black points. The solid curves
delimit the NEA region. The Atens, Apollos and Amors are shown as triangles, circles and
squares, respectively. In fact, while the dashed vertical line determines the boundary between the Aten and Apollo regions, the dashed curve represents the separation between the Apollo and Amor populations. The 3:1, 5:2 and 2:1 mean motion resonances with Jupiter are labeled in both figures. On the other hand, the  secular resonance is just shown on the top panel since its position depends on the orbital inclination and only weakly on the eccentricity.
(Data obtained from http://ssd.jpl.nasa.gov/dat/ELEMENTS.NUMBR.) secular resonance is just shown on the top panel since its position depends on the orbital inclination and only weakly on the eccentricity.
(Data obtained from http://ssd.jpl.nasa.gov/dat/ELEMENTS.NUMBR.) |
| Open with DEXTER |
The Main Belt asteroids and NEAs do not represent independent populations; on the contrary, they
are intimately connected by evolutionary processes and dynamical transport mechanisms associated
to orbital resonances. While the existence of resonances in the Main Belt has been known since many years, most works aimed at studying the collisional evolution of the small bodies in such region has not accounted for them. Since the work of Williams (1969) and further studies developed by Wetherill (1979) and Wisdom (1983, 1985a, 1985b),
it is widely accepted that the resonant regions present in the asteroid Main Belt are effective escape routes from there. In fact, detailed numerical simulations performed by Gladman et al. (1997)
have shown that those objects falling into some resonance inside 2.5 AU could become NEAs and then
meteorites in only a few million of years, being the most common end state of these objects an impact onto the Sun. They have also shown that those bodies reaching one of the resonant regions outside 2.5 AU become Jupiter-crossers and are subsequently removed from the Solar System by close encounters with Jupiter. The
intense collisional activity present in the asteroid Main Belt continuously breaks up large asteroids, injecting a large quantity of material into the resonant regions, a mechanism that represents a source of mass depletion in the Main Belt.
In the early 2000s, Penco et al. (2002) included the so-called Yarkovsky effect into numerical models of the asteroid collisional evolution. The Yarkovsky effect, a radiation force, modifies the orbital parameters of asteroids giving rise to a mechanism that can deliver them into resonances and thus remove them
from the Main Belt. Besides, this effect is size dependent and owing to that, its action coupled with the presence of resonant regions not only can be another important source of steady mass depletion in the Main Belt, but can also affect their size distribution. There are strong evidences
associated with the size distribution of the NEA population which might suggest that Yarkovsky effect is the most important process that drives asteroids into resonances and primarily into the NEA source resonances, rather than direct collisional injection (Morbidelli et al. 2002; Morbidelli & Vokrouhlický 2003).
The arguments presented so far allow us to infer that the size distribution of NEAs is fundamentally determined by the Main Belt population from which they come and the collisional anddynamical mechanisms which are responsible for their transport. Thus, a complete model of the asteroid Main Belt and NEAs must follow the simultaneous evolution of both populations. Besides, a suitable code must be able to include collisional and dynamical processes, since without dynamical mechanisms acting, the NEA population would never be generated and,
without collisional evolution, there would be no fresh collisional fragments and the bodies removed from the Main Belt could not be continuously replenished.
Recently, Bottke et al. (2005a), O'Brien & Greenberg (2005) and
Bottke et al. (2005b)
developed works aimed at analyzing the evolution of the Main Belt and NEA populations.
Bottke et al. (2005a) developed a collisional evolution model aimed at studying
the Main Belt comminution from the end of accretion among D < 1000 km bodies to the present day.
These authors find that the Main Belt size distribution is predominately a fossil produced in the
first years of collisional evolution, when the Main Belt population was once far more massive than
the current population. The work presented by Bottke et al. (2005a) has allowed to analyze some questions
related to the shape of the initial Main Belt size distribution, stability of Main Belt and NEA populations, the collisional history of Vesta, asteroid disruption frequency, asteroid spin rates and the estimated size of the primordial Main Belt.
On the other hand, the study developed by O'Brien & Greenberg (2005) models the evolution of the Main Belt asteroids, the near-Earth asteroids (NEAs) and the trans-Neptunian objects (TNOs). In particular,
these authors perform a self-consistent numerical code for modeling the simultaneous evolution of
the Main Belt and NEA populations, considering collisional processes and dynamical mechanisms such
as the Yarkovsky effect and orbital resonances. This numerical algorithm is able to satisfy the
major observational constraints associated with these small-body populations, such as their size
distributions, the collisional history of Vesta, the number of large asteroid families and the
cosmic-ray exposure (CRE) ages of meteorites.
Later, Bottke et al. (2005b) performed a study aimed at
linking the collisional history of the asteroid Main Belt to its dynamical excitation and depletion. This work combines dynamical results from Petit et al. (2001) with the collisional evolution code created by Bottke et al. (2005a). The results are consistent with the Main Belt's size-frequency distribution,
the number of currently observable asteroid families produced by collisional disruption events involving parent bodies larger than 100 km, the collisional history of Vesta and the lunar and terrestrial impactor flux over the
last 3 Gyr. Moreover, this model allows also to study the NEA population, which is used to explore some questions about the small craters formed on Mercury, the Moon and Mars.
Here, we present a new multi-population code for collisional evolution that takes into account the main dynamical features present in the asteroid Main Belt and NEA region. Among the works of
Bottke et al. (2005a), O'Brien & Greenberg (2005) and Bottke et al. (2005b), the second one is the most similar to that shown in this paper,
though there are some relevant differences in the populations of the model, collisional
input parameters and in the treatment of the dynamical evolution.
In fact, the most notable difference between those papers and our work is that our model proposes to divide the asteroid belt into three
semimajor axis zones whose boundaries are given by the  ,
3:1, 5:2 and 2:1 powerful resonances, which has
allowed us to develop a more rigorous study of the Main Belt and NEA populations. We believe our model improves
those presented by Bottke et al. (2005a), O'Brien & Greenberg (2005) and
Bottke et al. (2005b), allowing us to
analyze some questions related with the mixing of material in the asteroid belt, the provenance of the NEA objects
and the collisional injection into the powerful resonances.
,
3:1, 5:2 and 2:1 powerful resonances, which has
allowed us to develop a more rigorous study of the Main Belt and NEA populations. We believe our model improves
those presented by Bottke et al. (2005a), O'Brien & Greenberg (2005) and
Bottke et al. (2005b), allowing us to
analyze some questions related with the mixing of material in the asteroid belt, the provenance of the NEA objects
and the collisional injection into the powerful resonances.
In Sect. 2 the collisional model is described, while the most important dynamical
mechanisms taken into account in our algorithm are presented in Sect. 3. In Sect. 4 we describe the full numerical model, while Sect. 5 shows the most important results derived from the collisional and dynamical evolution of the asteroid Main Belt and NEA population. Conclusions are given in the last section.
In this section, we present the main features of our algorithm aimed at describing the outcome of a collision between two bodies.
As it is usual, a catastrophic collision is defined as the one where the largest piece resulting from it contains 50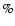 or less of the initial target mass, whereas the rest of the collisions are considered cratering events.
or less of the initial target mass, whereas the rest of the collisions are considered cratering events.
The impact velocity V and the shattering impact specific energy 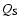 are two fundamental quantities determining, for a given body, if the collision must be studied in the catastrophic regime or in the cratering regime.
are two fundamental quantities determining, for a given body, if the collision must be studied in the catastrophic regime or in the cratering regime. 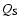 is the amount of energy per unit target mass needed to catastrophically fragment
a body, such that the largest resulting fragment has half the mass of the original target, regardless of reaccumulation of fragments.
While early works of Dohnanyi (1969), Williams & Wetherill (1994) and Tanaka et al. (1996) assumed that all asteroids had the same impact strength per unit mass (namely,
is the amount of energy per unit target mass needed to catastrophically fragment
a body, such that the largest resulting fragment has half the mass of the original target, regardless of reaccumulation of fragments.
While early works of Dohnanyi (1969), Williams & Wetherill (1994) and Tanaka et al. (1996) assumed that all asteroids had the same impact strength per unit mass (namely, 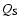 would be a constant), since more recent numerical models as well as laboratory studies it is now accepted
that
would be a constant), since more recent numerical models as well as laboratory studies it is now accepted
that 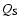 is size-dependent. Farinella et al. (1982), Housen & Holsapple (1990), Ryan (1992), Holsapple (1993), Housen & Holsapple (1999) and Benz & Asphaug
(1999) have shown that for small bodies, with diameters
is size-dependent. Farinella et al. (1982), Housen & Holsapple (1990), Ryan (1992), Holsapple (1993), Housen & Holsapple (1999) and Benz & Asphaug
(1999) have shown that for small bodies, with diameters 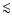 1 km, the material properties control the impact strength in such a way that it decreases with increasing size. On another hand, Davis et al. (1985), Housen & Holsapple (1990), Love & Ahrens (1996), Melosh & Ryan (1997), and Benz & Asphaug (1999) showed that for large asteroids, with diameters
1 km, the material properties control the impact strength in such a way that it decreases with increasing size. On another hand, Davis et al. (1985), Housen & Holsapple (1990), Love & Ahrens (1996), Melosh & Ryan (1997), and Benz & Asphaug (1999) showed that for large asteroids, with diameters 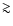 1 km, gravity dominates the impact strength which increases with increasing size. Some authors (Durda et al. 1998) have used
1 km, gravity dominates the impact strength which increases with increasing size. Some authors (Durda et al. 1998) have used 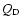 (the amount of energy per unit mass needed to fragment a body and disperse
half of its mass) rather than
(the amount of energy per unit mass needed to fragment a body and disperse
half of its mass) rather than 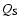 ,
as primary input parameter in their collisional evolution models. For small bodies, the gravitational binding energy is negligible and owing to that
,
as primary input parameter in their collisional evolution models. For small bodies, the gravitational binding energy is negligible and owing to that 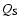 and
and 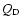 have the same
value. For larger bodies,
have the same
value. For larger bodies, 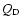 must be larger than
must be larger than 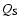 ,
since gravity is important and can therefore impede
the dispersal of fragments. In Sect. 4.3, we will discuss some aspects of
,
since gravity is important and can therefore impede
the dispersal of fragments. In Sect. 4.3, we will discuss some aspects of 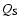 and
and 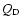 ,
specifying the most convenient input parameters for our collisional evolution model.
,
specifying the most convenient input parameters for our collisional evolution model.
On the other hand, the relative kinetic energy in a collision between two bodies of masses M1 and M2 is given by
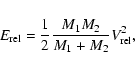 |
(1) |
where
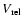 is the relative impact velocity.
is the relative impact velocity.
According to these definitions and assuming that the energy is equi-partitioned between the two colliding bodies (Hartmann 1988), for body i fragmentation occurs if
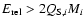 (Greenberg et al. 1978; Petit & Farinella 1993), while below this threshold, cratering happens. Thus,
if two objects collide, the last relation allows us to determine if both of them will be catastrophically fragmented,
if one will be cratered and the other will be catastrophically fragmented or if both will be cratered after the collision.
(Greenberg et al. 1978; Petit & Farinella 1993), while below this threshold, cratering happens. Thus,
if two objects collide, the last relation allows us to determine if both of them will be catastrophically fragmented,
if one will be cratered and the other will be catastrophically fragmented or if both will be cratered after the collision.
In the next subsections, we will describe our treatment of a collision in the catastrophic regime as well as in the cratering regime. Besides, for any of the three mentioned outcomes, we also study the escape and reaccumulation
processes of the resulting fragments, carrying out a previous determination of the escape velocity.
In order to model the distribution of the fragments resulting from a catastrophic fragmentation
event, we develop a model based on Petit & Farinella's (1993) algorithm.
These authors use a single-slope power law to
describe the fragment distribution from a catastrophic event. O'Brien & Greenberg's (2005) collisional algorithm is also based on Petit & Farinella's (1993)
method but introduces a two-slope power law to model the distribution
of fragments resulting from a catastrophic fragmentation, which is a more realistic description according to laboratory experiments and
hydrocode models. But, O'Brien & Greenberg (2005) show that using a two-slope
power law rather than a less realistic single-slope power law obtains
a worse fit in the simulations, which probably indicates a limitation
of the collisional model rather than suggesting that asteroids are
catastrophically fragmented following a single-slope power law. From
these results, we decide to use a single-slope power law to describe
the distribution of fragments resulting from a catastrophic event.
If a body of mass Mi is catastrophically fragmented, the mass of the largest resulting
fragment will be given by
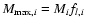 ,
where fl,i is
,
where fl,i is
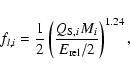 |
(2) |
according to the experimental results obtained by Fujiwara et al. (1977).
We define
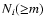 as the number of fragments of body i with a mass larger
than m.
as the number of fragments of body i with a mass larger
than m.
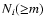 has a discontinuity at
has a discontinuity at
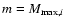 since there is just
one fragment of mass
since there is just
one fragment of mass
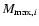 resulting from the catastrophic fragmentation of body i.
So, if
resulting from the catastrophic fragmentation of body i.
So, if 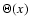 is the Heaviside step function (namely,
is the Heaviside step function (namely, 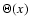 = 0 for x < 0
and
= 0 for x < 0
and 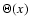 = 1 for
= 1 for 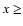 0),
0),
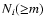 can be written as
can be written as
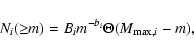 |
(3) |
where bi is the characteristic exponent. Besides, as
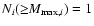 ,
so
from the last equation, we find
,
so
from the last equation, we find
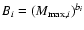 .
In order to calculate the characteristic exponent bi, we derive the cumulative mass
distribution
.
In order to calculate the characteristic exponent bi, we derive the cumulative mass
distribution
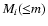 which represents the total mass of fragments of body i with a mass smaller than m. In fact,
which represents the total mass of fragments of body i with a mass smaller than m. In fact,
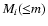 can be calculated as
can be calculated as
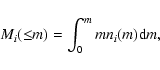 |
(4) |
where
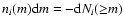 defines the differential fragment
size distribution. According to Eq. (3),
defines the differential fragment
size distribution. According to Eq. (3),
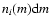 will be given by
will be given by
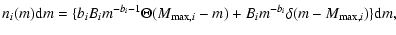 |
|
|
(5) |
where
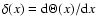 is the Dirac delta function. Then, inserting it
in Eq. (4) and using that
is the Dirac delta function. Then, inserting it
in Eq. (4) and using that
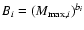 ,
so
,
so
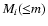 will be written as
will be written as
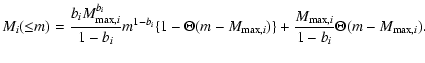 |
|
|
(6) |
From this equation, it is possible to derive a relation between fl,i, given by Eq. (2), and the characteristic exponent bi. Actually, the mass conservation implies
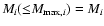 ;
then, from Eq. (6), we derive the condition
;
then, from Eq. (6), we derive the condition
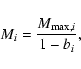 |
(7) |
and, since
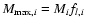 ,
so
,
so
Thus, if fl,i is calculated by Eq. (2), bi can be derived from the last equation.
With this, every parameter present in Eq. (3) is determined and so, such law can be used
in order to calculate the distribution of the fragments resulting from a catastrophic event.
Below the catastrophic fragmentation threshold
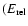 <
<
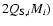 ,
a crater is formed. Again, we use Petit
& Farinella's (1993) algorithm in order to calculate the distribution of fragments resulting
from a cratering event. Imposing continuity for
,
a crater is formed. Again, we use Petit
& Farinella's (1993) algorithm in order to calculate the distribution of fragments resulting
from a cratering event. Imposing continuity for
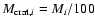 ,
the mass
,
the mass
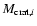 excavated from the crater can be calculated from
the following relations
excavated from the crater can be calculated from
the following relations
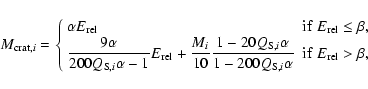 |
(9) |
where
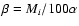 .
The parameter
.
The parameter 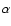 ,
known as crater excavation coefficient, depends on the material properties and ranges from about 4
,
known as crater excavation coefficient, depends on the material properties and ranges from about 4  10-4 to 10-5 s2 m-2 for soft and hard materials respectively (Stoeffler et al. 1975; Dobrovolskis & Burns 1984). As Eq. (9) indicates, the model proposed by Petit & Farinella (1993) assumes a linear dependence of
10-4 to 10-5 s2 m-2 for soft and hard materials respectively (Stoeffler et al. 1975; Dobrovolskis & Burns 1984). As Eq. (9) indicates, the model proposed by Petit & Farinella (1993) assumes a linear dependence of
 on
on
 in such a way that
for craters smaller than
in such a way that
for craters smaller than  of the target mass,
of the target mass,
 is proportional to
is proportional to
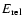 while for larger craters, the coefficients of the linear relation
are chosen such that the largest possible crater has a mass of 1/10 that of the target, which is in agreement with the studies
developed by Nolan et al. (1996).
while for larger craters, the coefficients of the linear relation
are chosen such that the largest possible crater has a mass of 1/10 that of the target, which is in agreement with the studies
developed by Nolan et al. (1996).
For cratering impacts, the surviving cratered body has a mass
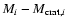 .
As in the case of a catastrophic fragmentation event,
we also assume a single-slope power law for the fragment size distribution resulting from a cratering impact. It is important to take into account that the derived expressions to treat a catastrophic impact
can be used in order to study a cratering event, replacing the target mass Mi by
.
As in the case of a catastrophic fragmentation event,
we also assume a single-slope power law for the fragment size distribution resulting from a cratering impact. It is important to take into account that the derived expressions to treat a catastrophic impact
can be used in order to study a cratering event, replacing the target mass Mi by
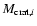 .
Thus, the mass of the largest fragment ejected from the crater will be
.
Thus, the mass of the largest fragment ejected from the crater will be
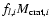 ,
where
fl,i = 0.2 since according to
Melosh (1989),
bi = 0.8 for any cratering event.
,
where
fl,i = 0.2 since according to
Melosh (1989),
bi = 0.8 for any cratering event.
After calculating the distribution of fragments associated with every one of bodies that participate in a collision, it is necessary to
determine the final fate of the fragments ejected from each one of them. If the fragment relative velocity is larger than the escape velocity
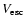 from
the two colliding bodies, it will escape, while those slower than
from
the two colliding bodies, it will escape, while those slower than
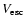 will be reaccumulated on the largest remnant. The following points must be considered:
will be reaccumulated on the largest remnant. The following points must be considered:
- To adopt a Fragment Velocity Distribution.
- To determine the Escape Velocity of the Fragments.
According to Campo Bagatin et al. (1994b), it is possible to adopt two different models in order to study the escape of fragments and reaccumulation:
- 1.
- A "Cumulative Model'', in which there is no relation between mass
and velocity of fragments. This model just assumes that the fraction of
the fragment mass ejected from body i with speeds larger than a value V is given by
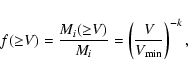 |
(10) |
where
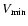 is a lower cutoff for the velocity of fragments. Gault et al. (1963) observed such a relationship, with a value of k of about 9/4.
is a lower cutoff for the velocity of fragments. Gault et al. (1963) observed such a relationship, with a value of k of about 9/4.
- 2.
- As Petit & Farinella (1993) proposed, a "Mass-Velocity
Model''. According to experimental results (Nakamura & Fujiwara 1991;
Nakamura et al. 1992; Giblin et al. 1994; Giblin 1998), this model assumes that there is a correlation between the ejection velocity and the
mass of the fragments. One can express the mass-velocity distribution as
where Ci is a constant coefficient and ri is a given exponent.
It is possible to find a relationship between the cumulative velocity
distribution exponent k and the exponent ri in the
mass-velocity model. For this, from Eq. (11), we write m(V) as
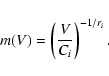 |
(12) |
Inserting it in the cumulative mass distribution given by Eq. (6)
and considering masses smaller than
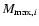 ,
we have that
,
we have that
Equations (10) and (13) allow us to see that
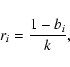 |
(14) |
where bi is obtained from Eq. (8) for a catastrophic collision or it is equal to 0.8 for a cratering event.
Here, we follow the method of Petit & Farinella (1993) to calculate the velocity distribution of fragments.
The mass-velocity distribution can be written as
| V |
= |
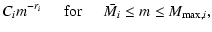 |
|
| V |
= |
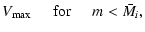 |
(15) |
where, imposing continuity,
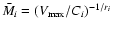 .
.
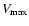 is assumed to be the maximum value for the velocity of the fragments. The inclusion of this high velocity
cutoff is motivated by a physical reason: a fragment can not be ejected with a velocity larger
than the sound speed in the material, which is assumed to be of 3000 m s-1
(O'Brien & Greenberg 2005). While this value would seem to be too large
(Vokrouhlický et al. 2006), in Sect. 5.4, we will discuss the dependence of our
simulations on this input parameter.
On the other hand, the constant coefficient Ci can be calculated from an energy
conservation equation. Assuming that the relative kinetic energy
is assumed to be the maximum value for the velocity of the fragments. The inclusion of this high velocity
cutoff is motivated by a physical reason: a fragment can not be ejected with a velocity larger
than the sound speed in the material, which is assumed to be of 3000 m s-1
(O'Brien & Greenberg 2005). While this value would seem to be too large
(Vokrouhlický et al. 2006), in Sect. 5.4, we will discuss the dependence of our
simulations on this input parameter.
On the other hand, the constant coefficient Ci can be calculated from an energy
conservation equation. Assuming that the relative kinetic energy
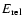 of the collision is partitioned equally between the target
and the projectile, so body i will receive an energy
of the collision is partitioned equally between the target
and the projectile, so body i will receive an energy
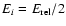 at impact. From this, we define
at impact. From this, we define
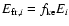 as
the kinetic energy of the fragments resulting from such body.
as
the kinetic energy of the fragments resulting from such body.
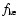 is an inelasticity parameter determining which fraction of the energy
received by a body is partitioned into kinetic energy of the fragments.
In Sect. 4.3, we will discuss some aspects of this parameter.
On the other hand, while
is an inelasticity parameter determining which fraction of the energy
received by a body is partitioned into kinetic energy of the fragments.
In Sect. 4.3, we will discuss some aspects of this parameter.
On the other hand, while
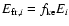 ,
it can be also written following
the mass-velocity model proposed. In fact,
,
it can be also written following
the mass-velocity model proposed. In fact,
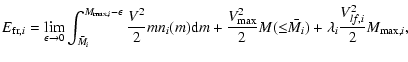 |
|
|
(16) |
where
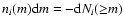 is given by Eq. (5), and the last term
is the kinetic energy of the largest fragment resulting from body i in a collision. The experimental studies
performed by Fujiwara & Tsukamoto (1980) and Nakamura & Fujiwara (1991), indicate that the largest fragment resulting from a catastrophic fragmentation event has a negligible kinetic energy
in the reference frame of the center of mass. On the other hand, in a cratering event, the largest
fragment of mass
is given by Eq. (5), and the last term
is the kinetic energy of the largest fragment resulting from body i in a collision. The experimental studies
performed by Fujiwara & Tsukamoto (1980) and Nakamura & Fujiwara (1991), indicate that the largest fragment resulting from a catastrophic fragmentation event has a negligible kinetic energy
in the reference frame of the center of mass. On the other hand, in a cratering event, the largest
fragment of mass
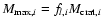 (with
fl,i=0.2) has a velocity Vlf,i given by
(with
fl,i=0.2) has a velocity Vlf,i given by
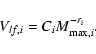 |
(17) |
So, in order to take into account this difference, we insert the corresponding term in the energy
conservation equation multiplied by a factor
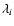 ,
where
,
where
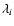 will be 0 for a catastrophic event and 1 for a cratering event.
will be 0 for a catastrophic event and 1 for a cratering event.
Equation (16) is an integral of m. Since the integrand is written in terms of
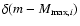 by Eq. (5),
if one wants to solve this integral over the range (
by Eq. (5),
if one wants to solve this integral over the range (
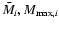 ), it is necessary to introduce epsilon and take the limit for epsilon to zero. Once V is written in terms of m (Eq. (15)), such integral can be evaluated. Thus
), it is necessary to introduce epsilon and take the limit for epsilon to zero. Once V is written in terms of m (Eq. (15)), such integral can be evaluated. Thus
From this, the constant coefficient Ci is given by the solution of
the equation
|
aCiki + b - Ci2 = 0,
|
(19) |
where a and b are given by
| a |
= |
}\Bigg]$](/articles/aa/full/2007/18/aa6046-06/img86.gif) |
|
| b |
= |
![$\displaystyle 2M_{{\rm max},i}^{2r_{i}-1}\Bigg[\frac{1-b_{i}-2r_{i}}{(1-2r_{i}-b_{i})\lambda
_{i}+b_{i}}\Bigg]E_{{\rm fr},i},$](/articles/aa/full/2007/18/aa6046-06/img87.gif) |
(20) |
and
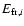 is assumed to be
is assumed to be
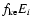 .
.
Once the fragment velocity distribution has been found for each of the bodies that participate in a collision, it is necessary to calculate the effective escape velocity
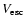 from the gravitational field of the two colliding bodies. For this, we use
the method developed by Petit & Farinella (1993) with the corrections made by O'Brien & Greenberg (2005). Thus, we calculate the escape velocity
from the gravitational field of the two colliding bodies. For this, we use
the method developed by Petit & Farinella (1993) with the corrections made by O'Brien & Greenberg (2005). Thus, we calculate the escape velocity
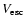 using the energy balance equation, which can be written as
using the energy balance equation, which can be written as
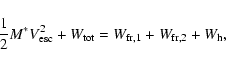 |
(21) |
where M* =
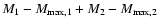 if both bodies are catastrophically fragmented, M* =
if both bodies are catastrophically fragmented, M* =
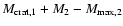 if body 1 is cratered and body 2 is catastrophically fragmented and M* =
if body 1 is cratered and body 2 is catastrophically fragmented and M* =
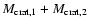 if both bodies are cratered.
The term
if both bodies are cratered.
The term
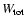 is the total gravitational potential energy of the two colliding bodies just before fragmentation event, which is given by
is the total gravitational potential energy of the two colliding bodies just before fragmentation event, which is given by
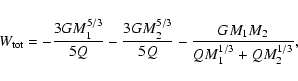 |
(22) |
where the parameter Q is
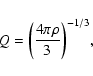 |
(23) |
and 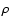 is the density of the objects. On the other hand,
the terms
is the density of the objects. On the other hand,
the terms
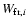 represent the gravitational potential energy of the fragments of body i resulting from the collision.
If body i is catastrophically fragmented,
represent the gravitational potential energy of the fragments of body i resulting from the collision.
If body i is catastrophically fragmented,
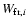 will be given by
will be given by
while if body i is cratered,
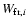 will adopt the following expression
will adopt the following expression
The term  is an estimate of the gravitational potential energy of the fragments when these are separated by a distance of
the order of the Hill's radius of the total colliding mass in the gravitational field of the central mass
is an estimate of the gravitational potential energy of the fragments when these are separated by a distance of
the order of the Hill's radius of the total colliding mass in the gravitational field of the central mass 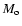 and orbital distance
and orbital distance 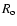 .
If both bodies are catastrophically fragmented,
.
If both bodies are catastrophically fragmented,  is given by
is given by
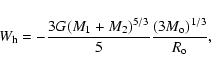 |
(26) |
where 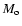 is the mass of the Sun and
is the mass of the Sun and 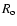 is the orbital radius where the collision occurs. On the other hand, according to O'Brien & Greenberg (2005),
if body 1 is cratered and body 2 is catastrophically fragmented, the term
is the orbital radius where the collision occurs. On the other hand, according to O'Brien & Greenberg (2005),
if body 1 is cratered and body 2 is catastrophically fragmented, the term  must be written as
must be written as
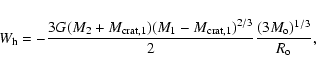 |
(27) |
while if both bodies are cratered, the term  has the form
has the form
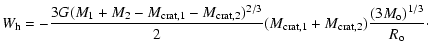 |
|
|
(28) |
Once the different W terms are calculated, it is possible to find the escape velocity
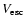 from the corresponding energy
balance equation. From this, in Sect. 4.5 we describe the treatment proposed in our algorithm in order to study the escape and reaccumulation processes of the ejected fragments.
from the corresponding energy
balance equation. From this, in Sect. 4.5 we describe the treatment proposed in our algorithm in order to study the escape and reaccumulation processes of the ejected fragments.
Table 1:
Summary of the dynamical properties of the bodies injected into the  ,
3:1 and 5:2 powerful resonances studied by different authors. The median lifetimes ( Half-Life) of bodies initially in each of those resonances and the median times required to cross the orbit of the Earth (
,
3:1 and 5:2 powerful resonances studied by different authors. The median lifetimes ( Half-Life) of bodies initially in each of those resonances and the median times required to cross the orbit of the Earth (
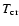 Earth) have been derived by Gladman et al. (1997).
Bottke et al. (2002) determined the median times spent in the NEA region (
Earth) have been derived by Gladman et al. (1997).
Bottke et al. (2002) determined the median times spent in the NEA region (
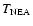 )
for bodies coming from the different resonant regions. On the other hand, the typical end states were
analyzed by Gladman et al. (1997) who followed the orbital histories of more than one
hundred particles injected into each resonance for up to
)
for bodies coming from the different resonant regions. On the other hand, the typical end states were
analyzed by Gladman et al. (1997) who followed the orbital histories of more than one
hundred particles injected into each resonance for up to  100 Myr. Finally, the mean collision probabilities with Earth (
100 Myr. Finally, the mean collision probabilities with Earth (
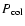 Earth), integrated over the lifetime in the Earth-crossing
region, were derived by Morbidelli & Gladman (1998).
Earth), integrated over the lifetime in the Earth-crossing
region, were derived by Morbidelli & Gladman (1998).
The population of Main Belt asteroids is determined fundamentally by collisional processes. But, as we have already said, collisions are not the only process that can play an important role in the quantitative determination of the Main Belt size distribution.
In fact, there are several dynamical mechanisms which can have a relevant influence on the evolution of these small bodies. The orbital
resonances between asteroids and the planets as well as the Yarkovsky effect play a dominant
role in removing material from the Main Belt. Besides, these dynamical mechanisms lead to a connection between the Main Belt and NEA population. These arguments lead us to think that any model trying to analyze the evolution of the small bodies in the
Inner Solar System must include such dynamical mechanisms. The purpose of this section is to give a brief description about the most
important properties of the orbital resonances in the Main Belt and the Yarkovsky effect.
It is now widely accepted that the orbital resonances in the asteroid Main Belt provide effective
"escape routes'' from there. Morbidelli et al. (2002) suggest to distinguish
between "powerful resonances'' and "diffusive resonances''.
The powerful resonances are characterized by the existence of associated well-defined gaps in
the Main Belt asteroid distribution. The  secular resonance which determines the inner
edge of the asteroid belt, and the mean motion resonances with Jupiter 3:1, 5:2 and 2:1 at 2.5,
2.8 and 3.27 AU from the Sun respectively, represent the most important resonances of this class
(see Fig. 1). Gladman et al. (1997) studied a large number of test bodies in
these resonant regions and found that the
secular resonance which determines the inner
edge of the asteroid belt, and the mean motion resonances with Jupiter 3:1, 5:2 and 2:1 at 2.5,
2.8 and 3.27 AU from the Sun respectively, represent the most important resonances of this class
(see Fig. 1). Gladman et al. (1997) studied a large number of test bodies in
these resonant regions and found that the  secular resonance and 3:1 mean motion
resonance with Jupiter are important sources of NEAs, while the rest of the major resonances are
not very effective in producing NEAs, although they can produce changes of the orbital elements of
objects entering into them, delivering such objects to cross Jupiter's orbit. In fact, the results
obtained by Gladman et al. (1997) indicate that while the majority of the powerful
resonances are important sources of mass depletion in the Main Belt, only
secular resonance and 3:1 mean motion
resonance with Jupiter are important sources of NEAs, while the rest of the major resonances are
not very effective in producing NEAs, although they can produce changes of the orbital elements of
objects entering into them, delivering such objects to cross Jupiter's orbit. In fact, the results
obtained by Gladman et al. (1997) indicate that while the majority of the powerful
resonances are important sources of mass depletion in the Main Belt, only  and 3:1 resonances are efficient NEA sources. Some of the most important numerical results derived by
Gladman et al. (1997), Morbidelli & Gladman (1998) and Bottke et al.
(2002) concerning the
and 3:1 resonances are efficient NEA sources. Some of the most important numerical results derived by
Gladman et al. (1997), Morbidelli & Gladman (1998) and Bottke et al.
(2002) concerning the  ,
3:1 and 5:2 resonances,
are summarized in Table 1.
,
3:1 and 5:2 resonances,
are summarized in Table 1.
On the other hand, the dynamical structure of the 2:1 resonance is somewhat complicated.
The numerical simulations developed by Gladman et al. (1997) suggest that the median
lifetime of bodies initially in the 2:1 resonance is larger than 100 Myr.
But, the work of Broz et al. (2005), which reexamines the origin, evolution and
survivability of objects in the 2:1 population, suggests that the Yarkovsky effect (see next section) continuously
resupplies bodies to this resonance and keeps the unstable population in an approximately steady
state, obtaining lifetimes ranging from a few million years to  100 Myr
with a median lifetime of around 10 Myr. Thus, the 2:1 resonance is capable of perturbing the
asteroid motion on timescales comparable to those of the other powerful resonances
(see Table 1).
100 Myr
with a median lifetime of around 10 Myr. Thus, the 2:1 resonance is capable of perturbing the
asteroid motion on timescales comparable to those of the other powerful resonances
(see Table 1).
On the contrary, the diffusive resonances have no associated deep gaps in the Main Belt asteroid
distribution. There are hundreds of these weak resonances that densely cross the Main Belt.
They are represented by:
- high order mean motion resonances with Jupiter,
- three-body resonances with Jupiter and Saturn (Murray et al. 1998;
Nesvorný & Morbidelli 1998, 1999), and
- mean motion resonances with Mars (Morbidelli & Nesvorný 1999).
The existence of these diffusive resonances leads many Main Belt asteroids to present a chaotic
behavior (Nesvorný et al. 2002), even though the effect of this chaoticity results
to be very weak. These thin resonances can produce slow changes of the orbital
parameters of objects, leading them to evolve into planet-crossing orbits. Particularly in the
inner ring of the asteroid belt, the diffusive resonances can explain the existence of one distinctive population of small bodies known as the Mars-crosser population (see Fig. 1). According to Migliorini et al. (1998), Mars-crossers are defined as those bodies with q > 1.3 AU and a combination of (a,e,i) values such that they cross the orbit of Mars during a secular oscillation cycle of their eccentricity. While the main population of
Mars-crossers, called Intermediate Source Mars-Crossers (IMC), is situated below the  resonance, there are other small groups with high inclination. Michel et al. (2000) developed numerical simulations of the dynamical evolution of objects on Mars-crossing orbits.
These works show that asteroids belonging to IMC group can become NEAs over a time scale of
several tens of millions of years. Later on, Bottke et al. (2002) integrated thousands
of test particles from different NEA source regions in order to compute the orbital and absolute
magnitude distribution of this population. The quantitative result of this work determines that
IMC population must be considered as an important source of NEAs, together with the
resonance, there are other small groups with high inclination. Michel et al. (2000) developed numerical simulations of the dynamical evolution of objects on Mars-crossing orbits.
These works show that asteroids belonging to IMC group can become NEAs over a time scale of
several tens of millions of years. Later on, Bottke et al. (2002) integrated thousands
of test particles from different NEA source regions in order to compute the orbital and absolute
magnitude distribution of this population. The quantitative result of this work determines that
IMC population must be considered as an important source of NEAs, together with the  and 3:1 resonances.
and 3:1 resonances.
In Table 2, we have summarized some of the most important dynamical results derived by
Bottke et al. (2002) with regards to the different NEA source regions studied by them.
It is possible to argue that the  secular resonance, the intermediate-source Mars-crossing
(IMC) population and the 3:1 mean motion resonances with Jupiter are the primary NEA sources, while
the Outer Main Belt (OB) and the Jupiter-family comets (JFC) are only secondary sources.
secular resonance, the intermediate-source Mars-crossing
(IMC) population and the 3:1 mean motion resonances with Jupiter are the primary NEA sources, while
the Outer Main Belt (OB) and the Jupiter-family comets (JFC) are only secondary sources.
Table 2:
Some of the most important dynamical results derived by Bottke et al. (2002) for bodies coming from the different NEA source regions. The sources studied by these authors were the  and 3:1 resonances, the intermediate source Mars-crossing (IMC) population (namely,
Mars-crossers below the
and 3:1 resonances, the intermediate source Mars-crossing (IMC) population (namely,
Mars-crossers below the  ), the Outer Main Belt (OB) and the Jupiter-family comets.
), the Outer Main Belt (OB) and the Jupiter-family comets.
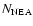 (H< 18)
represents the steady-state number of NEAs with an H magnitude smaller than 18, which is roughly
1 km in size. On the other hand,
(H< 18)
represents the steady-state number of NEAs with an H magnitude smaller than 18, which is roughly
1 km in size. On the other hand, 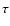 (Myr-1) gives the number of bodies injected into the NEA region
per million years while
(Myr-1) gives the number of bodies injected into the NEA region
per million years while
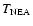 (Myr) is the mean dynamical lifetime spent in the NEA region.
(Myr) is the mean dynamical lifetime spent in the NEA region.
The Yarkovsky effect is the result of a radiation mechanism which can cause relevant changes
in the orbital parameters of the Solar System rotating bodies because of the asymmetry between
the direction of absorption of sunlight and the direction of re-emission of thermal radiation.
There are two variants of this mechanism for a rotating body moving around the Sun:
- the diurnal effect due to the rotation motion around its axis,
- the seasonal effect due to the orbital motion.
The magnitude of both effects depends on the obliquity. While the diurnal effect vanishes at
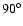 obliquity, the seasonal one vanishes at zero obliquity. Besides, the diurnal effect
reaches its maximum value at zero obliquity while the seasonal one is maximum at
obliquity, the seasonal one vanishes at zero obliquity. Besides, the diurnal effect
reaches its maximum value at zero obliquity while the seasonal one is maximum at
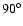 obliquity. It is important to take into account that the seasonal effect always produces a semimajor axis decrease, while the diurnal can cause an increase when the rotation is prograde or a decrease
when the rotation is retrograde.
obliquity. It is important to take into account that the seasonal effect always produces a semimajor axis decrease, while the diurnal can cause an increase when the rotation is prograde or a decrease
when the rotation is retrograde.
On the other hand, the Yarkovsky effect is size dependent. Actually, this mechanism affects the
orbital parameters of small asteroids, under the kilometer size range, while large asteroids are
mostly unaffected. Because of this dependence with the size, the Yarkovsky effect can potentially
affect the Main Belt size distribution. Besides, it is important to take into account that since this mechanism is the result of a radiation force, its efficiency drops with increasing semimajor axis from the Sun.
Several interesting works were developed in the last decade in order to study this radiation
mechanism. Farinella et al. (1998) derived a unified model of the Yarkovsky effect in
both the diurnal effect and also for the seasonal one, obtaining explicit expressions for the
semimajor axis drift rates. Penco et al. (2002) included the Yarkovsky effect into the
numerical models of the collisional evolution of the asteroid Main Belt.
Later, Morbidelli & Vokrouhlický (2003) developed simulations in order to study
the role of the Yarkovsky effect in the origin of near-Earth asteroids. This work argues that the
Yarkovsky effect is the major mechanism by which asteroids are continuously supplied to powerful
and diffusive resonances and the NEA population is maintained in steady state. These conclusions
lead us to think that this radiation mechanism together with the resonant escape routes can be an important source of steady mass depletion in the Main Belt.
There are several mechanisms that can modify the effectiveness of the Yarkovsky effect. In fact,
the Yarkovsky-O'Keefe-Radzievskii-Paddack effect, or YORP effect, and the collisional
re-orientations of the spin axes of the asteroids can produce changes of the obliquity states of
such objects, leading them to random walk in semimajor axis rather than a continuous drift.
Moreover, the detailed numerical simulations performed by
Morbidelli & Vokrouhlický (2003) show the importance
of the YORP effect for understanding why the NEA magnitude distribution is only moderately steeper
than the Main Belt magnitude distribution.
In order to quantify the removal rate of bodies due to the action of these radiation forces and
orbital resonances, Sect. 4.4 shows a simplified mathematical description of these mechanisms.
Later, Sect. 4.5 describes how these dynamical processes can be included in our numerical
algorithm.
In this section we present the full model we use to study the simultaneous evolution of the asteroid Main Belt and NEA population.
As we have already said, the most important resonances of the powerful class are the
 secular resonance and the mean motion resonances with Jupiter 3:1, 5:2 and 2:1 at about 2.5, 2.8 and 3.27 AU from the Sun, respectively.
Taking into account that less than 1 percent of the Main Belt population is located between 3.27 and 3.4 AU, we have decided to assume that 2:1 resonance marks the outer edge of the
asteroid belt. In order to study the flux of asteroids into these resonances as a result of
the collisional injection and the Yarkovsky effect, and analyze the mixing of material between
the different regions of the asteroid belt, our model divides the Main Belt into three semimajor
axis zones:
secular resonance and the mean motion resonances with Jupiter 3:1, 5:2 and 2:1 at about 2.5, 2.8 and 3.27 AU from the Sun, respectively.
Taking into account that less than 1 percent of the Main Belt population is located between 3.27 and 3.4 AU, we have decided to assume that 2:1 resonance marks the outer edge of the
asteroid belt. In order to study the flux of asteroids into these resonances as a result of
the collisional injection and the Yarkovsky effect, and analyze the mixing of material between
the different regions of the asteroid belt, our model divides the Main Belt into three semimajor
axis zones:
- the Inner Ring (IR), between the
 and 3:1 resonances, from about 2 to 2.5 AU,
and 3:1 resonances, from about 2 to 2.5 AU,
- the Middle Ring (MR), between the 3:1 and 5:2 resonances, from about 2.5 to 2.823 AU, and
- the Outer Ring (OR), between the 5:2 and 2:1 resonances, from about 2.823 to 3.27 AU.
The width of every ring is determined by the resonance borders. The boundaries of the 3:1 and 5:2 resonances depend on the orbital eccentricity while the semimajor axis of the center of the  secular resonance depends on the orbital inclination, but only weakly on the eccentricity (Morbidelli & Henrard 1991).
To define the boundaries of the
secular resonance depends on the orbital inclination, but only weakly on the eccentricity (Morbidelli & Henrard 1991).
To define the boundaries of the  and 3:1 resonances, we
follow Morbidelli & Vokrouhlický (2003).
They have shown that the boundaries can be approximated by
and 3:1 resonances, we
follow Morbidelli & Vokrouhlický (2003).
They have shown that the boundaries can be approximated by
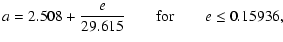 |
|
|
|
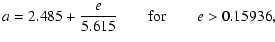 |
|
|
(29) |
for the right side of the 3:1 resonance,
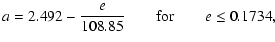 |
|
|
|
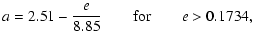 |
|
|
(30) |
for the left side of the 3:1 resonance, and
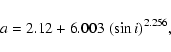 |
(31) |
for the right side of the  resonance. In order to take into account the diffusive neighborhood of these resonances to
correctly evaluate the effective flux of asteroids into them, Morbidelli &
Vokrouhlický (2003) shifted the boundaries of the 3:1 resonance by 0.015 AU away from the borders given by Eqs. (29) and (30), while they also drifted the
resonance. In order to take into account the diffusive neighborhood of these resonances to
correctly evaluate the effective flux of asteroids into them, Morbidelli &
Vokrouhlický (2003) shifted the boundaries of the 3:1 resonance by 0.015 AU away from the borders given by Eqs. (29) and (30), while they also drifted the
 resonance boundary, given by Eq. (31), outward by 0.09 AU.
resonance boundary, given by Eq. (31), outward by 0.09 AU.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{6046fi2.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg117.gif) |
Figure 2:
a) The distribution of the asteroids with respect to proper semimajor axis and eccentricity, in the vicinity of the 5:2 mean motion resonance with Jupiter. The right and left boundaries of this resonance approximated by Eqs. (32) and (33) respectively, are represented by thesolid curves. The shifted boundaries defined in order to evaluate the effective flux of asteroids into this resonant region are labeled bythe dashed curves. b) The number of asteroids as a function of distance from the left border of the 5:2 resonance. The curve shows that the density of objects grows until  0.017 AU from the resonance, remaining more or less constant over the next 0.03 AU. 0.017 AU from the resonance, remaining more or less constant over the next 0.03 AU. |
| Open with DEXTER |
To define the effective boundaries of the 5:2 resonance, we performed a similar analysis.
Using the catalog of the synthetic proper elements (Knezevic & Milani 2003),
it is possible to see a well-defined gap associated with the 5:2 resonance, which is illustrated
in Fig. 2a. The boundaries of this resonance can be approximated as
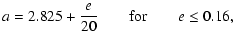 |
|
|
|
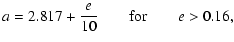 |
|
|
(32) |
for the right side, and
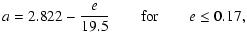 |
|
|
|
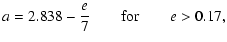 |
|
|
(33) |
for the left side. We must extend the boundaries of the 5:2 resonance because of the chaotic diffusion in the vicinity of its borders. We observed that the density of asteroids grows until  0.015-0.017 AU from the resonance and then is more or less constant over the next 0.03 AU (see Fig. 2b). In order to measure the effective flux of asteroids falling into the 5:2 resonance, we shift the boundaries of this region 0.017 AU
away from the borders given by the Eqs. (32) and (33).
0.015-0.017 AU from the resonance and then is more or less constant over the next 0.03 AU (see Fig. 2b). In order to measure the effective flux of asteroids falling into the 5:2 resonance, we shift the boundaries of this region 0.017 AU
away from the borders given by the Eqs. (32) and (33).
In the following, these shifted boundaries will be the boundaries of the  ,
3:1 and
5:2 resonances with which we are going to develop our work.
,
3:1 and
5:2 resonances with which we are going to develop our work.
Mean values for the impact velocity
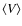 and the intrinsic collision probability
and the intrinsic collision probability
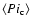 ,
are fundamental quantities for any collisional evolution study. We calculate
,
are fundamental quantities for any collisional evolution study. We calculate
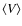 and
and
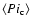 for collisions between asteroids of the Main Belt in every ring and between rings as well as for collisions between NEAs and between NEAs and Main Belt objects in every ring. For this, we use the numerical approach
developed by Marzari et al. (1996), based in the numerical integration of 3000 real asteroids from the three populations, subject to the perturbations of Jupiter and Saturn.
The timespan of the numerical integration was of 104 yr, and the integration was performed with
the simplectic code EVORB (Fernández et al. 2002). The results are shown in
Table 3.
for collisions between asteroids of the Main Belt in every ring and between rings as well as for collisions between NEAs and between NEAs and Main Belt objects in every ring. For this, we use the numerical approach
developed by Marzari et al. (1996), based in the numerical integration of 3000 real asteroids from the three populations, subject to the perturbations of Jupiter and Saturn.
The timespan of the numerical integration was of 104 yr, and the integration was performed with
the simplectic code EVORB (Fernández et al. 2002). The results are shown in
Table 3.
Table 3:
Mean values for the intrinsic collision probability
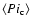 and the impact velocity
and the impact velocity
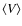 for the different populations of our model.
for the different populations of our model.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6046fi3.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg124.gif) |
Figure 3:
a) Asteroid strength laws 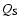 .
The solid curve denotes the .
The solid curve denotes the 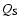 law used in our work. The dashed lines represent the estimates proposed by different authors.
b) Asteroid strength laws law used in our work. The dashed lines represent the estimates proposed by different authors.
b) Asteroid strength laws 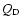 .
The solid curves denote the .
The solid curves denote the 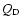 laws generated from our laws generated from our 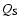 law and the different functions law and the different functions
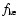 used in the populations of the model. The dashed lines represent the estimates proposed by different authors. used in the populations of the model. The dashed lines represent the estimates proposed by different authors. |
| Open with DEXTER |
O'Brien & Greenberg (2005) showed that the general shape of the final evolved
asteroid population is determined primarily by 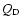 ,
but variations in
,
but variations in 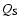 and
and
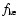 can affect such final population even if
can affect such final population even if 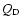 is held the same.
According to these arguments we choose
is held the same.
According to these arguments we choose 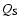 and
and
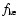 as input parameters of
our collisional model.
as input parameters of
our collisional model.
The 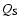 law chosen from this study is shown in Fig. 3a, which can be calculated
from an expression of the form
law chosen from this study is shown in Fig. 3a, which can be calculated
from an expression of the form
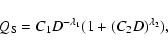 |
(34) |
where C1, C2,
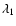 ,
and
,
and
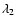 are constant coefficients whose values
are 2.85, 1.8, 0.695 and 2.22, respectively. As the reader can see in Fig. 3a, this
are constant coefficients whose values
are 2.85, 1.8, 0.695 and 2.22, respectively. As the reader can see in Fig. 3a, this
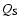 law is in a good agreement with the estimates of the impact strength of
asteroids proposed by different authors (Farinella et al. 1982; Davis et al. 1985; Housen & Holsapple 1990; Housen 1991; Holsapple 1994; Ryan & Melosh 1998; Benz & Asphaug 1999).
law is in a good agreement with the estimates of the impact strength of
asteroids proposed by different authors (Farinella et al. 1982; Davis et al. 1985; Housen & Holsapple 1990; Housen 1991; Holsapple 1994; Ryan & Melosh 1998; Benz & Asphaug 1999).
On the other hand,
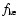 is a poorly known parameter in
collisional processes. But, many authors suggest that it may vary with size, with impact
speed and probably with the material properties. Since the impact velocity varies for the
different populations of our model (see Table 3) and the
heliocentric distribution of taxonomic classes (Mothé-Diniz et al. 2003)
indicates differences in the asteroid composition of the Main Belt,
we have decided that
is a poorly known parameter in
collisional processes. But, many authors suggest that it may vary with size, with impact
speed and probably with the material properties. Since the impact velocity varies for the
different populations of our model (see Table 3) and the
heliocentric distribution of taxonomic classes (Mothé-Diniz et al. 2003)
indicates differences in the asteroid composition of the Main Belt,
we have decided that
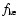 varies for the different populations.
Thus, according to that made by O'Brien & Greenberg (2005), we express
the parameter
varies for the different populations.
Thus, according to that made by O'Brien & Greenberg (2005), we express
the parameter
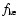 as
as
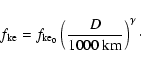 |
(35) |
Table 4 shows the values of
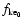 and
and 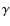 for the
different populations of our model. Such values are according to that
discussed by O'Brien & Greenberg (2005), who indicate that
for the
different populations of our model. Such values are according to that
discussed by O'Brien & Greenberg (2005), who indicate that 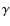 is on the order of 0.5 (always between 0 and 1) and
is on the order of 0.5 (always between 0 and 1) and
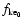 ,
the value at 1000 km, is
,
the value at 1000 km, is  0.05-0.3, which is consistent with estimates
of
0.05-0.3, which is consistent with estimates
of
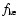 in large impacts (Davis et al. 1989).
It is important to take into account
that the combination of
in large impacts (Davis et al. 1989).
It is important to take into account
that the combination of 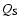 and
and
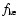 yields a given
yields a given 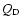 .
The
.
The
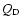 laws generated from our
laws generated from our 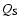 law and the different functions
law and the different functions
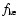 are shown in Fig. 3b. Such
are shown in Fig. 3b. Such 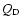 laws are in a good agreement
with those formulated by different authors (Farinella et al. 1982;
Davis et al. 1985; Housen & Holsapple 1990; Holsapple 1994; Love
& Ahrens 1996; Melosh & Ryan 1997; Durda et al. 1998; Ryan
& Melosh 1998; Benz & Asphaug 1999), and are according to the
laboratory impact experiments which obtain values near 1500 J kg-1for target diameters of
laws are in a good agreement
with those formulated by different authors (Farinella et al. 1982;
Davis et al. 1985; Housen & Holsapple 1990; Holsapple 1994; Love
& Ahrens 1996; Melosh & Ryan 1997; Durda et al. 1998; Ryan
& Melosh 1998; Benz & Asphaug 1999), and are according to the
laboratory impact experiments which obtain values near 1500 J kg-1for target diameters of  8 cm.
8 cm.
Table 4:
Values for
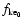 and
and 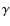 for the different populations of our model.
for the different populations of our model.
In order to calculate the removal rate of bodies from each of the three rings of the asteroid Main Belt due to the action of the Yarkovsky effect and orbital resonances, we use the expressions derived by O'Brien
& Greenberg (2005), which are based on the analytical model outlined by Farinella
et al. (1998).
Here, we give a brief mathematical description of this effect, separately considering the treatments developed for the diurnal and seasonal variants of this radiation mechanism (Sect. 3.2).
The diurnal variant is the simplest case of the Yarkovsky effect.
This variant is due to the fact that a rotating body absorbing radiation from
the Sun rotates before that energy is re-emitted as thermal infrared radiation,
leading to a longitudinal asymmetry between the direction of absorption of
sunlight and the direction of re-emission. The discussion presented in
Farinella et al. (1998) suggests that the diurnal Yarkovsky effect is effective
for all bodies larger than about 3 microns while, for smaller bodies, its
effectiveness does not become important since the heating on one side of the
object begins to affect the other side.
![\begin{figure}
\par\includegraphics[width=16.45cm,clip]{6046fi4.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg130.gif) |
Figure 4:
Our estimates of the diurnal a), seasonal b) and effective c) Yarkovsky semimajor axis drift rates 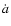 and the asteroid removal rates d) as a function of the diameter for bodies belonging to the Inner, Middle and Outer Rings of the asteroid Main Belt.
and the asteroid removal rates d) as a function of the diameter for bodies belonging to the Inner, Middle and Outer Rings of the asteroid Main Belt. |
| Open with DEXTER |
Following Farinella et al. (1998), if 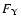 is the along-track component
of the Yarkovsky force per unit mass of the body, the semimajor axis change is given by
is the along-track component
of the Yarkovsky force per unit mass of the body, the semimajor axis change is given by
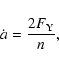 |
(36) |
where
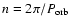 is the orbital mean motion and, according to Burns et al. (1979),
is the orbital mean motion and, according to Burns et al. (1979), 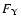 can be expressed by the formula
can be expressed by the formula
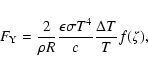 |
(37) |
where 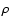 is the density of the body (assumed to be 3500 kg m-3, which is the density for basalt), R is its radius,
is the density of the body (assumed to be 3500 kg m-3, which is the density for basalt), R is its radius, 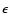 is the surface infrared emissivity (assumed to be 1),
is the surface infrared emissivity (assumed to be 1), 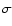 is the Stefan-Boltzmann constant, c is the speed of light, T is the effective temperature of the body,
is the Stefan-Boltzmann constant, c is the speed of light, T is the effective temperature of the body, 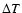 is the effective temperature difference and
is the effective temperature difference and 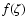 is the obliquity function. The effective temperature of the body can be calculated equating the incoming solar flux to the radiated flux from the asteroid. From this,
is the obliquity function. The effective temperature of the body can be calculated equating the incoming solar flux to the radiated flux from the asteroid. From this,
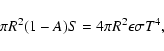 |
(38) |
where A is the albedo (assumed to be zero) and S is the solar flux in the position of the body.
S depends on the semimajor axis and can be expressed by the formula
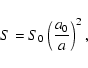 |
(39) |
where S0 = 1370 W m-2 is the solar constant and a0 and a are the semimajor axes of the Earth and the body under consideration, respectively. Finally, the average temperature gives
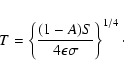 |
(40) |
The effective temperature difference 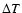 and the obliquity function
and the obliquity function 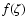 adopt
different expressions in the diurnal and seasonal variants of this mechanism. From
Peterson (1976), for the diurnal effect we have
adopt
different expressions in the diurnal and seasonal variants of this mechanism. From
Peterson (1976), for the diurnal effect we have
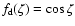 and
and
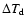 can be calculated by the formula
can be calculated by the formula
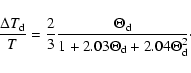 |
(41) |
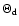 is a thermal parameter defined by Farinella et al. (1998) and represents the ratio of the thermal emission timescale to the rotation timescale. This parameter is given by
is a thermal parameter defined by Farinella et al. (1998) and represents the ratio of the thermal emission timescale to the rotation timescale. This parameter is given by
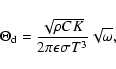 |
(42) |
where K is the thermal conductivity, 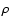 is the density, C is the specific heat (assumed
to be 680 J kg-1 K-1, which is the value corresponding to basalt and regolith) and
is the density, C is the specific heat (assumed
to be 680 J kg-1 K-1, which is the value corresponding to basalt and regolith) and
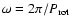 is the rotation frequency. According to O'Brien & Greenberg
(2005), we use
is the rotation frequency. According to O'Brien & Greenberg
(2005), we use
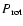 = 6 h for bodies larger than 0.15 km and
= 6 h for bodies larger than 0.15 km and
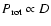 (Farinella et al. 1998) for smaller bodies. In same way, we model the density
(Farinella et al. 1998) for smaller bodies. In same way, we model the density 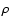 and the thermal
conductivity K for bodies smaller than 0.15 km using basalt parameters (
and the thermal
conductivity K for bodies smaller than 0.15 km using basalt parameters (
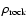 =
3500 kg m-3 and
=
3500 kg m-3 and
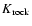 = 2.65 W m-1 K-1) while for larger bodies, we use regolith parameters
(
= 2.65 W m-1 K-1) while for larger bodies, we use regolith parameters
(
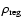 = 1500 kg m-3 and
= 1500 kg m-3 and
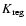 = 0.0015 W m-1 K-1), with a smooth variation between them around 0.15 km (O'Brien & Greenberg 2005).
Figure 4a shows the semimajor axis mobility due to the diurnal Yarkovsky effect as a function of the diameter for bodies belonging to the Inner, Middle and Outer Rings of the asteroid Main Belt. The obliquity is assumed to be 0
= 0.0015 W m-1 K-1), with a smooth variation between them around 0.15 km (O'Brien & Greenberg 2005).
Figure 4a shows the semimajor axis mobility due to the diurnal Yarkovsky effect as a function of the diameter for bodies belonging to the Inner, Middle and Outer Rings of the asteroid Main Belt. The obliquity is assumed to be 0 in order to consider its maximum effect (Sect. 3.2).
in order to consider its maximum effect (Sect. 3.2).
On the other hand, the seasonal Yarkovsky effect is due to the fact that a body absorbing radiation
from the Sun moves in its orbit before that energy is re-emitted as thermal infrared radiation,
leading to a latitudinal asymmetry between the direction of absorption of sunlight and the direction
of re-emission. The mathematical description of the seasonal Yarkovsky effect is somewhat more complicated. However, from O'Brien & Greenberg (2005), we approximate the seasonal effect considering it like a diurnal one with frequency n (orbital mean motion) rather than w (rotation frequency), assuming
that for this variant
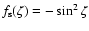 ,
and knowing that the seasonal asymmetry must be taken
into account for only a fraction of the orbit. Thus, the effective temperature difference
,
and knowing that the seasonal asymmetry must be taken
into account for only a fraction of the orbit. Thus, the effective temperature difference
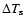 can be calculated by the expression
can be calculated by the expression
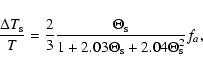 |
(43) |
where the thermal parameter
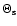 is given by
is given by
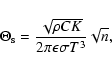 |
(44) |
and the factor fa (assumed to be 2/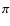 )
takes into account the partial
asymmetry. The work developed by Farinella et al. (1998) indicates that the peak seasonal Yarkovsky effect occurs
at diameters of about 20 m. To calculate the seasonal force for smaller bodies, it is necessary a mathematical description somewhat more complicated. According to O'Brien & Greenberg (2005), we model the seasonal
Yarkovsky effect for bodies smaller than 20 m in diameter assuming that
)
takes into account the partial
asymmetry. The work developed by Farinella et al. (1998) indicates that the peak seasonal Yarkovsky effect occurs
at diameters of about 20 m. To calculate the seasonal force for smaller bodies, it is necessary a mathematical description somewhat more complicated. According to O'Brien & Greenberg (2005), we model the seasonal
Yarkovsky effect for bodies smaller than 20 m in diameter assuming that
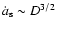 ,
which is in agreement with that made by Farinella et al. (1998). Figure 4b shows the semimajor axis mobility due
to the seasonal Yarkovsky effect as a function of the diameter for bodies belonging to the Inner, Middle and Outer Rings of the asteroid Main Belt. The obliquity is assumed to be 90
,
which is in agreement with that made by Farinella et al. (1998). Figure 4b shows the semimajor axis mobility due
to the seasonal Yarkovsky effect as a function of the diameter for bodies belonging to the Inner, Middle and Outer Rings of the asteroid Main Belt. The obliquity is assumed to be 90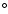 in order to consider its maximum effect (Sect. 3.2).
in order to consider its maximum effect (Sect. 3.2).
The effective Yarkovsky semimajor axis drift rate for each of the three rings of the Main Belt is a combination for the seasonal and diurnal effects. Taking into account that the mean absolute values of the obliquity
functions
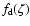 and
and
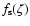 are 1/2 and 2/3, respectively,
so the maximum and minimum absolute values of effective
are 1/2 and 2/3, respectively,
so the maximum and minimum absolute values of effective 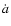 are given by
are given by
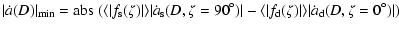 |
|
|
|
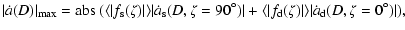 |
|
|
(45) |
and then, the average absolute value of effective 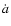 will be
will be
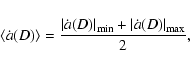 |
(46) |
(O'Brien & Greenberg 2005). Figure 4c shows the effective Yarkovsky semimajor axis drift rates 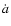 as a function of the diameter for bodies belonging to the Inner, Middle and Outer Rings of
the asteroid Main Belt, which are consistent with that obtained by O'Brien & Greenberg (2005) for the entire Main Belt.
as a function of the diameter for bodies belonging to the Inner, Middle and Outer Rings of
the asteroid Main Belt, which are consistent with that obtained by O'Brien & Greenberg (2005) for the entire Main Belt.
Once
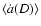 has been determined,
the fraction of bodies of diameter D removed per unit time can be calculated from the expression
has been determined,
the fraction of bodies of diameter D removed per unit time can be calculated from the expression
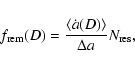 |
(47) |
where
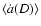 is the effective Yarkovsky semimajor axis drift rate,
is the effective Yarkovsky semimajor axis drift rate, 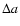 is the effective width of
the considered region and
is the effective width of
the considered region and
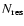 is the number of resonances that can remove bodies of a given diameter D from such region. The fraction of bodies removed per unit time is not linearly proportional to
is the number of resonances that can remove bodies of a given diameter D from such region. The fraction of bodies removed per unit time is not linearly proportional to
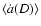 since
since
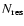 depends on the diameter D.
In fact, small bodies (D
depends on the diameter D.
In fact, small bodies (D 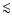 0.1 km) have high Yarkovsky drift
rates and owing to that they can jump weak resonances, being only removed by powerful resonances.
Following O'Brien & Greenberg (2005), we assume that the weak resonances start to be effective for bodies around 0.1 km while all of them become fully effective for bodies 10 km in diameter or larger. Thus, we assume that
0.1 km) have high Yarkovsky drift
rates and owing to that they can jump weak resonances, being only removed by powerful resonances.
Following O'Brien & Greenberg (2005), we assume that the weak resonances start to be effective for bodies around 0.1 km while all of them become fully effective for bodies 10 km in diameter or larger. Thus, we assume that
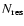 will be equal to the number of powerful resonances in the considered region at
will be equal to the number of powerful resonances in the considered region at
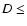 0.1 km while
0.1 km while
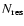 will be equal to the number of powerful
resonances plus the approximate number of diffusive resonances at
will be equal to the number of powerful
resonances plus the approximate number of diffusive resonances at 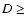 10 km, considering
a linear variation between them for intermediate diameters.
To evaluate the number of strong resonances in
each ring, we take into account the possible escape routes from such regions.
10 km, considering
a linear variation between them for intermediate diameters.
To evaluate the number of strong resonances in
each ring, we take into account the possible escape routes from such regions.
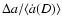 represents an estimate of the median lifetime of a body of diameter D in a region with an effective width
represents an estimate of the median lifetime of a body of diameter D in a region with an effective width 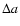 ,
where the escape routes
are located at the borders. Since the Inner and Middle Rings of the asteroid belt are divided by the
,
where the escape routes
are located at the borders. Since the Inner and Middle Rings of the asteroid belt are divided by the
 ,
3:1 and 5:2 powerful resonances and besides, we consider that there are no other strong resonances inside such regions, the number of powerful resonances is assumed to be 1 for the Inner and Middle Rings. For the Outer Ring,
whose boundaries are given by the 5:2 and 2:1 powerful resonances, we also consider the existence of the 7:3 strong resonance at
,
3:1 and 5:2 powerful resonances and besides, we consider that there are no other strong resonances inside such regions, the number of powerful resonances is assumed to be 1 for the Inner and Middle Rings. For the Outer Ring,
whose boundaries are given by the 5:2 and 2:1 powerful resonances, we also consider the existence of the 7:3 strong resonance at  2.96 AU, and owing to that the number of powerful resonances is assumed to be 2 for the
Outer Ring. On the other hand, we consider 16, 12 and 18 diffusive resonances for the Inner, Middle and Outer Rings of the asteroid belt, respectively. It is important to take into account that our model of the Yarkovsky effect
and the number of the orbital resonances associated with each ring of the Main Belt must be consistent with the results obtained by Morbidelli & Nesvorný (1999) and Bottke et al. (2002) with regard
to the dynamical removal rate for multi-kilometer bodies. In fact, while Morbidelli & Nesvorný
(1999) estimate the escape of about 4 bodies larger than 5 km per million years from the Inner Belt, Bottke et al. (2002) indicate that 790
2.96 AU, and owing to that the number of powerful resonances is assumed to be 2 for the
Outer Ring. On the other hand, we consider 16, 12 and 18 diffusive resonances for the Inner, Middle and Outer Rings of the asteroid belt, respectively. It is important to take into account that our model of the Yarkovsky effect
and the number of the orbital resonances associated with each ring of the Main Belt must be consistent with the results obtained by Morbidelli & Nesvorný (1999) and Bottke et al. (2002) with regard
to the dynamical removal rate for multi-kilometer bodies. In fact, while Morbidelli & Nesvorný
(1999) estimate the escape of about 4 bodies larger than 5 km per million years from the Inner Belt, Bottke et al. (2002) indicate that 790 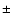 200 bodies larger than 1 km are removed
from the entire Main Belt per million years. The Yarkovsky asteroid removal rates obtained from this analysis for each of the three rings of the asteroid Main Belt are shown in Fig. 4d.
200 bodies larger than 1 km are removed
from the entire Main Belt per million years. The Yarkovsky asteroid removal rates obtained from this analysis for each of the three rings of the asteroid Main Belt are shown in Fig. 4d.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6046fi5.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg173.gif) |
Figure 5:
Asteroid removal rates used in our simulation, compared to the estimates shown in Fig. 4d. |
| Open with DEXTER |
But, as O'Brien & Greenberg (2005), we do not take into account the YORP effect nor collisional re-orientations of the spin axes and owing to that, it is likely that the real removal rates of asteroids from the different regions of the Main Belt differ somewhat from our estimates, but they probably show
similar trends and are of the same order of magnitude. So, since the asteroid removal rates obtained from our analysis are only an estimate, we decide to slightly vary them in order to obtain better fits to the observed populations of the model and results consistent with those found by Morbidelli & Nesvorný (1999) and Bottke et al. (2002) with regard to the dynamical removal rate for multi-kilometer bodies. Figure 5 shows the asteroid removal rates used in our algorithm.
In order to simulate the collisional and dynamical evolution of the asteroid Main Belt and NEA
size distributions, our numerical code evolves in time the number of bodies associated with
each of the three rings of the asteroid belt and NEA population. The populations of objects reside
in a set of 130 discrete logarithmic size bins, whose central values range from D1 = 10-10 km to D130 = 886.7 km in diameter in such a way that from one bin to the next, the mass of the bodies changes by a factor of 2 and the diameter changes by a factor of 21/3. We adopt a density of 2.7 g cm-3.
While the NEA population always starts with zero bodies, the total mass of the objects associated
with each of the three rings of the asteroid Main Belt is calculated from the model of planetary
nebulae mass distribution proposed by Weidenschilling (1977).
We adopt a surface density 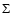 of the nebular disk of the form
of the nebular disk of the form
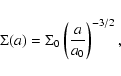 |
(48) |
where
 is the value associated to an arbitrary radius a0. Thus, the differential mass
is the value associated to an arbitrary radius a0. Thus, the differential mass
 contained in a belt of radius a and width
contained in a belt of radius a and width  will be given by
will be given by
and from this, the mass of the entire Main Belt will be written as
In the same way, the masses associated with each of the three rings of the asteroid Main Belt will be given by
Proposing a given mass for the initial Main Belt, it is possible to obtain the constant M0from Eq. (50) and then to determine the corresponding masses for the Inner, Middle and Outer Rings, given by Eqs. (51). While we tested different initial masses, the results shown here are those obtained considering an initial belt with  7 times the current belt mass, namely, 0.00315 Earth masses.
7 times the current belt mass, namely, 0.00315 Earth masses.
Once the masses associated with the Inner, Middle and Outer Rings of the asteroid Main Belt are determined, the
next step is to construct the starting populations for each of these rings, which are defined as follow:
- Inner Ring (2 < a < 2.5 AU): for
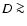 150 km, we assume that
the number of objects is equal to the observed number of asteroids in this region of the Main Belt. For 80
150 km, we assume that
the number of objects is equal to the observed number of asteroids in this region of the Main Belt. For 80 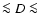 150 km, we use an incremental power-law index of
150 km, we use an incremental power-law index of  -1.6, while for
-1.6, while for 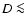 80 km, the initial incremental population follows a slope of
80 km, the initial incremental population follows a slope of
 -3.1 (see Fig. 6a).
-3.1 (see Fig. 6a).
- Middle Ring (2.5 < a < 2.823 AU): for
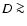 250 km, we assume
that the number of objects is equal to the observed number of asteroids in this region of the Main Belt. For 100
250 km, we assume
that the number of objects is equal to the observed number of asteroids in this region of the Main Belt. For 100 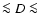 250 km, we use an incremental power-law index of
250 km, we use an incremental power-law index of  -2.2, while for
-2.2, while for 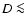 100 km, the initial incremental population follows a slope of
100 km, the initial incremental population follows a slope of
 -2.9 (see Fig. 6b).
-2.9 (see Fig. 6b).
- Outer Ring (2.823 < a < 3.27 AU): for
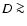 350 km, we assume
that the number of objects is equal to the observed number of asteroids in this region of the Main Belt. For 120
350 km, we assume
that the number of objects is equal to the observed number of asteroids in this region of the Main Belt. For 120 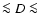 350 km, we use an incremental power-law index of
350 km, we use an incremental power-law index of  -3.3, while for
-3.3, while for 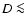 120 km, the initial incremental population follows a slope
of
120 km, the initial incremental population follows a slope
of  -2.9 (see Fig. 6c).
-2.9 (see Fig. 6c).
We construct these initial populations following the idea proposed by
Bottke et al. (2005a) for the entire Main Belt. In fact, these
authors use approximately the same number of objects as the observed Main Belt asteroids
for D> D1 = 200 km, while for
D2 < D < D1 = 200 km, where D2 ranges around 100 km,
the population follows an incremental power-law index with a value close to
the observed slope of asteroids in this size range (see Fig. 6).
Here, we assume values for D1 and D2
of 150 and 80 km, 250 and 100 km, and 350 and 120 km for the Inner,
Middle and Outer Rings, respectively.
Then, for D < D2, we assign a given incremental
power-law index for every of the three rings of the Main Belt in order to
reproduce their associated masses.
From the combination of these three populations, the initial population associated with the entire Main Belt is
determined. In fact, for 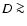 350 km, the resulting initial population of the entire asteroid belt shows the same number of objects as the observed number of asteroids of the Main Belt. Moreover, for 200
350 km, the resulting initial population of the entire asteroid belt shows the same number of objects as the observed number of asteroids of the Main Belt. Moreover, for 200 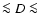 350 km, the resulting population follows an incremental power-law index of
350 km, the resulting population follows an incremental power-law index of  -5, while for
-5, while for 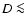 200 km, we assume a slope of
200 km, we assume a slope of
 -2.9 (see Fig. 6d).
These initial populations are consistent with the work of Bottke et al. (2005a)
which indicates that it is not possible to reproduce the various waves of the asteroid Main Belt population assuming an unique power law at the beginning.
On the other hand, the numerical simulations performed by Petit et al. (1999) and Petit et al. (2001) suggest that the asteroid Main Belt may have originally contained hundreds of times more mass that it currently has.
Moreover, these authors indicate that the gravitational perturbations from Jupiter and primordial planetary embryos reduced very fast the mass of the initial belt, reaching its actual value over time scales of a few Myr. To take into account this result and following O'Brien & Greenberg (2005), the initial populations
associated with each of the three rings of the asteroid belt are initially multiplied by a given factor and their evolution followed for 5 Myr. Then, the residual populations are reduced by the same factor and finally
their evolution is analyzed for the rest of the 4.5 Gyr. In our simulation, the used factor is assumed to be 55. This leads to an initial population of
-2.9 (see Fig. 6d).
These initial populations are consistent with the work of Bottke et al. (2005a)
which indicates that it is not possible to reproduce the various waves of the asteroid Main Belt population assuming an unique power law at the beginning.
On the other hand, the numerical simulations performed by Petit et al. (1999) and Petit et al. (2001) suggest that the asteroid Main Belt may have originally contained hundreds of times more mass that it currently has.
Moreover, these authors indicate that the gravitational perturbations from Jupiter and primordial planetary embryos reduced very fast the mass of the initial belt, reaching its actual value over time scales of a few Myr. To take into account this result and following O'Brien & Greenberg (2005), the initial populations
associated with each of the three rings of the asteroid belt are initially multiplied by a given factor and their evolution followed for 5 Myr. Then, the residual populations are reduced by the same factor and finally
their evolution is analyzed for the rest of the 4.5 Gyr. In our simulation, the used factor is assumed to be 55. This leads to an initial population of  385 times the current belt mass for
the entire Main Belt, which is consistent with the results obtained by
Petit et al. (1999) and Petit et al. (2001)
for the early asteroid belt.
385 times the current belt mass for
the entire Main Belt, which is consistent with the results obtained by
Petit et al. (1999) and Petit et al. (2001)
for the early asteroid belt.
Following Campo Bagatin et al. (1994a) and Campo Bagatin (1998), a collisional
system with a low-mass cutoff leads to waves in the size distribution of the bodies. In order
to avoid this effect, we do not evolve in time the 60 first size bins, whose central values
range from 10-10 to 10-4 km. For NEA population and each ring of the asteroid belt,
this part of the population is only used as a tail of projectiles for calculating impact rates
with larger bodies and its size distribution is determined each timestep by extrapolating the
slope of the distribution of the ten next size bins.
In each timestep, a characteristic orbit is generated at random for each of the three rings
of the asteroid Main Belt and NEA population for all the sizes. For the asteroid belt rings, we assign eccentricities e between 0 and 0.3, inclinations i between 0 and 20 and semimajor axes a in such a way that 2
and semimajor axes a in such a way that 2  a
a  2.5 for the Inner Ring, 2.5
2.5 for the Inner Ring, 2.5  a
a 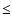 2.823 for the Middle Ring and 2.823
2.823 for the Middle Ring and 2.823 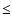 a
a 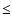 3.27 for the Outer Ring. In each case, the
combination of (a, i) values must be below the location of the
3.27 for the Outer Ring. In each case, the
combination of (a, i) values must be below the location of the  resonance, while the
combination of (a, e) values must fall outside of the gaps associated with the 3:1 and 5:2 resonances, where the boundaries of such regions were already discussed in Sect. 4.1. For the
NEA population, we use orbital parameters 0
resonance, while the
combination of (a, e) values must fall outside of the gaps associated with the 3:1 and 5:2 resonances, where the boundaries of such regions were already discussed in Sect. 4.1. For the
NEA population, we use orbital parameters 0 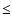 a
a 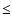 3.4, 0
3.4, 0 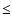 e
e 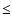 0.7 and 0
0.7 and 0 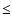 i
i  40
40 which are combined in such a way that the perihelion distance q
and the aphelion distance Q are always smaller than 1.3 AU and larger than 0.983 AU, respectively, according to the definition of NEAs. Finally, given the longitude of ascending node
which are combined in such a way that the perihelion distance q
and the aphelion distance Q are always smaller than 1.3 AU and larger than 0.983 AU, respectively, according to the definition of NEAs. Finally, given the longitude of ascending node  ,
the
argument of pericentre
,
the
argument of pericentre  and the mean anomaly M between 0 and 360
and the mean anomaly M between 0 and 360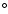 ,
an orbit can
be assigned and from this, a position-velocity pair can be derived for all bodies of each population. In Sect. 5.1, we will discuss some aspects related to this treatment.
,
an orbit can
be assigned and from this, a position-velocity pair can be derived for all bodies of each population. In Sect. 5.1, we will discuss some aspects related to this treatment.
Once a typical orbit has been computed for each of the four populations of our model, the next step
is to carry out the collisional treatment (including the analysis of the reaccumulation process)
from the algorithm outlined in Sect. 2. In order to determine the final fate of the fragments
escaping from the gravitational field of the system, it is necessary to calculate which are their
orbital elements once they are ejected with a relative velocity with respect to the parent body.
Immediately before the collision,
the barycentric position and velocity of the fragments are assumed to be those associated with their parent body. After the collision, the relative velocity of the fragments with respect to the parent
body (Eq. (15)) is assumed to be equally partitioned between the three components.
Once the barycentric position
and velocity of the fragments after the collision have been obtained, it is possible to calculate
their orbital elements and the final fate of them. For this, we use the following criterion:
- 1.
- The fragments are placed in the NEA population, if any of the following
conditions is fulfilled:
- -
- the aphelion distance
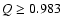 AU and the perihelion distance
AU and the perihelion distance
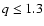 AU,
AU,
- -
- the semimajor axis a < 2 AU,
- -
- the combination of (a,i) values falls above the location of the
 secular resonance,
secular resonance,
- -
- the combination of (a,e) values falls into the gap associated with the 3:1 mean motion resonance,
- -
- the combination of (a,e) values falls into the gap associated with the 5:2 mean motion resonance.
- 2.
- The fragments are placed in the Inner Ring of the Main Belt if
- -
- 2
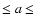 2.5 AU and the combinations of (a,e) values and (a,i) values fall outside of the gap associated with the 3:1 resonance and below the location of the
2.5 AU and the combinations of (a,e) values and (a,i) values fall outside of the gap associated with the 3:1 resonance and below the location of the  resonance, respectively.
resonance, respectively.
- 3.
- The fragments are placed in the Middle Ring of the Main Belt if
- -
- 2.5
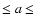 2.823 AU and the combinations of (a,e) values and (a,i) values fall outside of the gaps associated with the 3:1 and 5:2 resonances and below the location of the
2.823 AU and the combinations of (a,e) values and (a,i) values fall outside of the gaps associated with the 3:1 and 5:2 resonances and below the location of the  resonance, respectively.
resonance, respectively.
- 4.
- The fragments are placed in the Outer Ring of the Main Belt if
- -
- 2.823
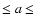 3.27 AU and the combinations of (a,e) values and (a,i) values fall outside of the gap associated with the 5:2 resonance and below the location of the
3.27 AU and the combinations of (a,e) values and (a,i) values fall outside of the gap associated with the 5:2 resonance and below the location of the  resonance, respectively.
resonance, respectively.
- 5.
- Finally, the fragments are assumed to be ejected from the Solar System on hyperbolic or parabolic orbits, no longer participating in the collisional evolution, if the eccentricity
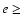 1 or a > 3.27 AU.
1 or a > 3.27 AU.
Once the collisional treatment has been developed and all the collisional information has been kept, the removal rate of bodies due to the action of the Yarkovsky effect and orbital resonances must be included in our analysis. According to the dynamical results derived by Bottke et al. (2002) with regard
to the different NEA source regions (Sect. 3.1), our algorithm assumes that the objects removed from the Inner, Middle and Outer Rings of the asteroid Main Belt are delivered to the NEA population.
On the other hand, in order to take into account the mean time spent in the NEA region by bodies coming from the different source regions, it is necessary to include a rate of dynamical removal of objects from the NEA population.
In a steady state, the rate of injection of bodies from a given source into the NEA population matches the rate of dynamical elimination of those bodies from such population. Thus, for any source
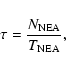 |
(52) |
(Bottke et al. 2002), where 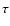 gives the number of objects injected into the NEA region per unit time,
gives the number of objects injected into the NEA region per unit time,
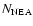 represents the steady-state number of NEAs and
represents the steady-state number of NEAs and
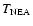 is the median time spent in that population. These values are shown in Table 2. Following O'Brien & Greenberg (2005), the mean dynamical lifetime of all
bodies in the NEA population coming from the different source regions studied by Bottke et al. (2002) is given by
is the median time spent in that population. These values are shown in Table 2. Following O'Brien & Greenberg (2005), the mean dynamical lifetime of all
bodies in the NEA population coming from the different source regions studied by Bottke et al. (2002) is given by
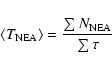 |
(53) |
where the summation extends to all the sources shown in Table 2, except the JFCs. Using the values given there, a
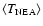 of 1.14 Myr is obtained. But, the numerical simulations performed
by Migliorini et al. (1998) suggest that the multi-kilometer NEAs may have the Mars-crosser population as primary source. Thus, our model treats the dynamical removal of objects from the NEA population using a dynamical
lifetime
of 1.14 Myr is obtained. But, the numerical simulations performed
by Migliorini et al. (1998) suggest that the multi-kilometer NEAs may have the Mars-crosser population as primary source. Thus, our model treats the dynamical removal of objects from the NEA population using a dynamical
lifetime
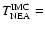 3.75 Myr associated with the Mars-crosser population for bodies with an H magnitude smaller than 12 (namely, diameters larger than
3.75 Myr associated with the Mars-crosser population for bodies with an H magnitude smaller than 12 (namely, diameters larger than  15 km) while
15 km) while
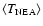 is used for bodies with larger H magnitudes.
is used for bodies with larger H magnitudes.
To study the evolution in time of the populations, the timestep 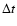 is calculated in such a way that the change
of the number of objects in any size bin is always smaller than a given amount, which is generally chosen as 1
is calculated in such a way that the change
of the number of objects in any size bin is always smaller than a given amount, which is generally chosen as 1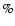 of the original number of bodies.
of the original number of bodies.
In order to test the proposed model, here we compare our results to the most important observational constraints on the collisional and dynamical history of the asteroid Main Belt and NEA population.
Thus, in Sect. 5.1, we compare our estimates of the Main Belt and NEA size distributions to observational data.
Then, in Sect. 5.2, we discuss the relation between our estimate of the mean collisional lifetimes of bodies and the meteorite cosmic-ray exposure ages. In Sect. 5.3, we analyze our results in regard to the collisional history
of Asteroid (4) Vesta. Then, we compare in Sect. 5.4 the results of our simulations with the number of asteroid families observed in the Main Belt. In Sect. 5.5, we analyze how the collisional process might contribute to the mixing of primordial material in the asteroid Main Belt. Finally, in Sect. 5.6, we study the provenance of the NEA objects.
The population of Main Belt asteroids is assumed to be reasonably complete to  30 km in diameter. Some years ago, several observational studies such as Spacewatch (Jedicke & Metcalfe 1998), the Sloan Digital Sky Survey (SDSS) (Ivezic et al. 2001) and the Subaru Sub-km Main Belt Asteroid
Survey (SMBAS) (Yoshida et al. 2003) were developed, which have allowed us to extend
the Main Belt size distribution estimate down to a diameter of about 500 m. As the reader can see in Fig. 7a, the estimated values of the asteroid Main Belt size distribution obtained from our simulations are in agreement with the observational data.
30 km in diameter. Some years ago, several observational studies such as Spacewatch (Jedicke & Metcalfe 1998), the Sloan Digital Sky Survey (SDSS) (Ivezic et al. 2001) and the Subaru Sub-km Main Belt Asteroid
Survey (SMBAS) (Yoshida et al. 2003) were developed, which have allowed us to extend
the Main Belt size distribution estimate down to a diameter of about 500 m. As the reader can see in Fig. 7a, the estimated values of the asteroid Main Belt size distribution obtained from our simulations are in agreement with the observational data.
Figure 7b shows our estimate of the NEA size distribution, which is described in terms of the absolute magnitude H. Following Bowell et al. (1989), it is possible to derive the diameter of a body with a given H-magnitude from the expression
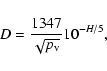 |
(54) |
where  is the visual geometric albedo which is assumed to be 0.11. The population of NEAs is believed to be observationally complete up to about H = 15, which corresponds to a diameter of
is the visual geometric albedo which is assumed to be 0.11. The population of NEAs is believed to be observationally complete up to about H = 15, which corresponds to a diameter of  4 km. Several observational surveys have been developed in order to extend the NEA H-magnitude distribution up to larger H values. In fact, Rabinowitz et al. (2000) used data obtained from Spacewatch and JPL's Near Earth Asteroid
Tracking (NEAT) program for deriving an estimate of the NEA population down to a H magnitude of
4 km. Several observational surveys have been developed in order to extend the NEA H-magnitude distribution up to larger H values. In fact, Rabinowitz et al. (2000) used data obtained from Spacewatch and JPL's Near Earth Asteroid
Tracking (NEAT) program for deriving an estimate of the NEA population down to a H magnitude of  30, while Stuart (2001) and Harris (2002) used the data from the LINEAR Survey in order to extend the NEA H-magnitude distribution down to H magnitudes of 22.5 and 25.5, respectively. From Fig. 7b, it is possible to see that the NEA population resulting from our simulation fits to the observed data. One important result
derived from our analysis is that the NEA H-magnitude distribution is determined primarily by the dynamical removal of asteroids from the Main Belt due to the action of the Yarkovsky effect and orbital resonances while the collisional processes do not play an important role.
30, while Stuart (2001) and Harris (2002) used the data from the LINEAR Survey in order to extend the NEA H-magnitude distribution down to H magnitudes of 22.5 and 25.5, respectively. From Fig. 7b, it is possible to see that the NEA population resulting from our simulation fits to the observed data. One important result
derived from our analysis is that the NEA H-magnitude distribution is determined primarily by the dynamical removal of asteroids from the Main Belt due to the action of the Yarkovsky effect and orbital resonances while the collisional processes do not play an important role.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{6046fi7.eps} \end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg206.gif) |
Figure 7:
Our estimates of the asteroid Main Belt size distribution a)
and NEA H-magnitude distribution b). Observed data are given for comparison. |
| Open with DEXTER |
As we have already said in Sect. 4.5 and following O'Brien & Greenberg (2005), we include a brief period of primordial evolution at the beginning the simulation in order to reproduce the results of Petit et al. (1999) and Petit et al. (2001) concerning the mass loss
from a massive early asteroid belt. In this phase, the initial populations associated with each of the three rings of the asteroid belt are multiplied by a factor of 55 and their evolution followed for 5 Myr. During this period, the intense collisional activity removes  74
74 of the initial mass of the Main Belt, leading to a residual initial population for the entire asteroid belt of
of the initial mass of the Main Belt, leading to a residual initial population for the entire asteroid belt of  100 times its current value. Then, the residual
initial populations associated with each of the three rings of the Main Belt are reduced by that factor of 55, which simulates the removal of about 98
100 times its current value. Then, the residual
initial populations associated with each of the three rings of the Main Belt are reduced by that factor of 55, which simulates the removal of about 98 of the masses of everyone of them. Finally, the evolution of a Main Belt initial population of
of the masses of everyone of them. Finally, the evolution of a Main Belt initial population of
 1.8 times its current value is analyzed for the rest of the 4.5 Gyr.
During this time, the collisional and dynamical mechanisms remove
1.8 times its current value is analyzed for the rest of the 4.5 Gyr.
During this time, the collisional and dynamical mechanisms remove  25
25 and
and
 17
17 of the initial mass of the Main Belt, respectively, leading to a final population for the entire asteroid belt of approximately
its current value. On the other hand, our simulations suggest that the asteroid Main Belt population acquire a smooth wave structure similar to that observed in
the current asteroid belt during the first 5 Myr of evolution (see Fig. 8). These results are consistent with those obtained by Bottke et al. (2005a), who indicate that the Main Belt size distribution is predominately a fossil.
of the initial mass of the Main Belt, respectively, leading to a final population for the entire asteroid belt of approximately
its current value. On the other hand, our simulations suggest that the asteroid Main Belt population acquire a smooth wave structure similar to that observed in
the current asteroid belt during the first 5 Myr of evolution (see Fig. 8). These results are consistent with those obtained by Bottke et al. (2005a), who indicate that the Main Belt size distribution is predominately a fossil.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6046fi8.eps} \end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg207.gif) |
Figure 8:
Our estimate of the asteroid Main Belt Size Distribution after 5 Myr. A smooth wave
structure is formed during the first 5 Myr of evolution. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{6046fi9.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg208.gif) |
Figure 9:
a) Number of bodies of diameter 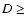 1 km removed per unit time from the entire Main Belt over the history of the Solar System. Here, we include the asteroid removal due to the Yarkovsky effect, collisional injection into the
1 km removed per unit time from the entire Main Belt over the history of the Solar System. Here, we include the asteroid removal due to the Yarkovsky effect, collisional injection into the  ,
3:1 and 5:2 resonances and collisional ejection outside 3.27 AU. A mean removal rate of 1070 asteroids larger than 1 km per Myr from the entire Main Belt is obtained, which is in
agreement with the results derived by Bottke et al. (2002). b) Number of bodies of
diameter ,
3:1 and 5:2 resonances and collisional ejection outside 3.27 AU. A mean removal rate of 1070 asteroids larger than 1 km per Myr from the entire Main Belt is obtained, which is in
agreement with the results derived by Bottke et al. (2002). b) Number of bodies of
diameter 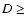 5 km removed per unit time from the Inner Ring of the Main Belt over the history of the Solar System. Here, we just include the asteroid removal due to the action of the Yarkovsky effect since the collisional injection rate into the powerful resonances and the collisional ejection of material outside 3.27 AU are negligible. A mean removal rate of 3 asteroids larger than 5 km per Myr from the Inner Ring is obtained over the last 3 Gyr, which is in agreement with the analysis developed by Morbidelli & Nesvorný (1999).
5 km removed per unit time from the Inner Ring of the Main Belt over the history of the Solar System. Here, we just include the asteroid removal due to the action of the Yarkovsky effect since the collisional injection rate into the powerful resonances and the collisional ejection of material outside 3.27 AU are negligible. A mean removal rate of 3 asteroids larger than 5 km per Myr from the Inner Ring is obtained over the last 3 Gyr, which is in agreement with the analysis developed by Morbidelli & Nesvorný (1999). |
| Open with DEXTER |
Figure 9 shows the kilometer-scale asteroid removal rates from the entire Main Belt and the Inner Ring, taking into account the action of the Yarkovsky effect, the collisional injection of material into the  ,
3:1 and
5:2 resonances and the collisional ejection outside 3.27 AU. Our results indicate that 1070 asteroids larger than 1 km are removed per Myr from the entire Main Belt, which is consistent with the analysis developed by Bottke et al. (2002). Besides, our study determines the escape of 3 asteroids larger than 5 km per Myr from the Inner
Ring of the asteroid belt over the last 3 Gyr, which is in agreement with the work performed by Morbidelli & Nesvorný (1999). Figure 9 allows us to infer that the Yarkovsky effect is the most important
process that removes material from the asteroid Main Belt, rather than collisional injection into the major resonances, which is consistent with the works of Morbidelli et al. (2002) and Morbidelli & Vokrouhlický (2003). In fact, while 891 asteroids larger than 1 km are removed per Myr due
to the action of the Yarkovsky effect, the collisional processes inject a total of about 25, 38 and 68 asteroids larger 1 km per Myr into the
,
3:1 and
5:2 resonances and the collisional ejection outside 3.27 AU. Our results indicate that 1070 asteroids larger than 1 km are removed per Myr from the entire Main Belt, which is consistent with the analysis developed by Bottke et al. (2002). Besides, our study determines the escape of 3 asteroids larger than 5 km per Myr from the Inner
Ring of the asteroid belt over the last 3 Gyr, which is in agreement with the work performed by Morbidelli & Nesvorný (1999). Figure 9 allows us to infer that the Yarkovsky effect is the most important
process that removes material from the asteroid Main Belt, rather than collisional injection into the major resonances, which is consistent with the works of Morbidelli et al. (2002) and Morbidelli & Vokrouhlický (2003). In fact, while 891 asteroids larger than 1 km are removed per Myr due
to the action of the Yarkovsky effect, the collisional processes inject a total of about 25, 38 and 68 asteroids larger 1 km per Myr into the  ,
3:1 and 5:2 resonances, respectively. These removal rates have been obtained following the dynamical treatment proposed in Sect. 4.5. From this, in each timestep only one characteristic
orbit is considered in each zone for all the sizes. To test this assumption we also performed
some simulations where, in each
timestep, different orbits were generated at random for each group of bodies
(of a given diameter D) in each zone. While the CPU time was much longer, the results did
not show relevant changes.
,
3:1 and 5:2 resonances, respectively. These removal rates have been obtained following the dynamical treatment proposed in Sect. 4.5. From this, in each timestep only one characteristic
orbit is considered in each zone for all the sizes. To test this assumption we also performed
some simulations where, in each
timestep, different orbits were generated at random for each group of bodies
(of a given diameter D) in each zone. While the CPU time was much longer, the results did
not show relevant changes.
The cosmic-ray exposure (CRE) ages of meteorites represent the time interval that a body was exposed to cosmic rays in space as a meter-sized object or near the surface of a larger body. Thus, CRE ages allow us to determine the time in space between the meteoroid's liberation from its parent body and its arrival at the Earth.
According to Marti & Graf (1992) and Morbidelli & Gladman (1998), CRE ages for the different types of ordinary chondrites, which represent the most common class of meteorites, range from a few million years to about 100 Myr with a mean age of approximately 10-20 Myr. Figure 10 shows the mean collisional lifetimes obtained from our simulations. For meter-sized objects belonging to
the Inner, Middle and Outer Rings of the asteroid Main Belt, we estimate mean collisional lifetimes of about 3.2, 4.3 and 6.8 Myr, respectively, which are within of factor 2-3 of the mean CRE ages of stony meteorites. Moreover, our results are consistent with those derived by
O'Brien & Greenberg (2005) who obtained a lifetime of about 8 Myr for meter-sized objects.
Asteroid (4) Vesta, with a diameter of approximately 500 km, orbits the Sun at a distance of about 2.362 AU. This object represents one of the most peculiar cases of the Solar System since it is the only known differentiated
asteroid with an intact basaltic crust (Keil 2002). We find that 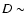 500 km
asteroids in the Inner Ring of the Main Belt have a mean collisional lifetime of
500 km
asteroids in the Inner Ring of the Main Belt have a mean collisional lifetime of  17.7 Gyr (Fig. 10), which allows us to infer that an object like Vesta has
17.7 Gyr (Fig. 10), which allows us to infer that an object like Vesta has  75
75 probability of surviving over Solar System history without receiving a catastrophic impact, which is in agreement with the preservation of the intact basaltic
crust of this asteroid.
probability of surviving over Solar System history without receiving a catastrophic impact, which is in agreement with the preservation of the intact basaltic
crust of this asteroid.
On the other hand, Hubble Space Telescope (HST) observations of Vesta have revealed the existence of a singular crater with a diameter of about 450 km on its surface. According to studies developed by Thomas et al. (1997), the diameter of the impactor that created such crater was
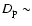 35 km. Bottke et al. (2005b) used the fact that Vesta does not have two such craters as a very specific constraint of the collisional history of this asteroid. Estimating the approximated number of projectiles N with diameters
35 km. Bottke et al. (2005b) used the fact that Vesta does not have two such craters as a very specific constraint of the collisional history of this asteroid. Estimating the approximated number of projectiles N with diameters 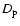 of
of  35 km and taking into
account that the average interval between such impacts on Vesta can be calculated by
35 km and taking into
account that the average interval between such impacts on Vesta can be calculated by
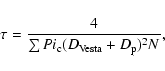 |
(55) |
where the summation extends to all the populations of the model
and
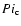 is the correspondent intrinsic collision probability,
it is possible to determine the mean
number of collisions between
is the correspondent intrinsic collision probability,
it is possible to determine the mean
number of collisions between
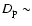 35 km objects and Vesta over the age of the Solar System. In fact, our simulations indicate that the mean number of bodies of
35 km objects and Vesta over the age of the Solar System. In fact, our simulations indicate that the mean number of bodies of  35 km in diameter
impacting Vesta over 4.5 Gyr is
35 km in diameter
impacting Vesta over 4.5 Gyr is  0.5. As Bottke et al. (2005b), this
result suggests that the odds are slightly against asteroid (4) Vesta having an unique crater of size comparable to its total size, but very much against this particular object having two such singular craters.
0.5. As Bottke et al. (2005b), this
result suggests that the odds are slightly against asteroid (4) Vesta having an unique crater of size comparable to its total size, but very much against this particular object having two such singular craters.
![\begin{figure}
\par\includegraphics[width=7.95cm,clip]{6046fi10.eps} \end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg214.gif) |
Figure 10:
Mean collisional lifetimes of bodies belonging to the Inner,
Middle and Outer Rings of the asteroid Main Belt, estimated from
our simulations. Meter-scale objects have mean collisional lifetimes
between 3.2 and 6.8 Myr, which are consistent with CRE ages of meteorites. |
| Open with DEXTER |
The existence of asteroid families represents a clear consequence of the collisional activity in the Main Belt. According to the works developed by Zappalà et al. (1995), there are a total of about 60 statistically significant asteroid clusters in proper element space, and it is possible to identify approximately 25 reliable families.
Our simulations predict the formation of 8 asteroid
families from parent bodies larger than 200 km in diameter, which is consistent with that discussed by Davis et al. (1985) who suggested the existence of 8 actual families formed
from the breakup of parent bodies larger than 200 km.
Moreover, it is important to take into account that the 8 asteroid families generated in the model
form after the brief of primordial evolution which is included to model the existence of a massive early asteroid belt.
On the other hand, the studies of asteroid families developed by Vokrouhlický et al. (2006) have shown that the typical dispersal velocity for  5 km fragments
is of order of a few tens of meters per second. Following O'Brien & Greenberg (2005)
we assume a maximum value for the velocity of fragments of 3000 m s-1,
which is of order of the sound velocity in the material (see Sect. 2.4). While this value
would seem to be too large, our studies indicate that
5 km fragments
is of order of a few tens of meters per second. Following O'Brien & Greenberg (2005)
we assume a maximum value for the velocity of fragments of 3000 m s-1,
which is of order of the sound velocity in the material (see Sect. 2.4). While this value
would seem to be too large, our studies indicate that  90
90 of
the fragments of 5 km in diameter are ejected with velocities smaller
than 80 m s -1 (see Fig. 11), which is in agreement with that discussed by Vokrouhlický et al. (2006).
of
the fragments of 5 km in diameter are ejected with velocities smaller
than 80 m s -1 (see Fig. 11), which is in agreement with that discussed by Vokrouhlický et al. (2006).
![\begin{figure}
\par\includegraphics[width=7.85cm,clip]{6046fi11.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg215.gif) |
Figure 11:
Cumulative fraction of  5 km fragments as a function of
velocity. Our study indicates that 5 km fragments as a function of
velocity. Our study indicates that  90 percent of the fragments
of 5 km in diameter are ejected with velocities smaller than 80 m s-1, which is in agreement with Vokrouhlický et al. (2006). 90 percent of the fragments
of 5 km in diameter are ejected with velocities smaller than 80 m s-1, which is in agreement with Vokrouhlický et al. (2006). |
| Open with DEXTER |
Since some decades, the distribution of taxonomic classes in the Main Belt of asteroids has been thoroughly studied by many authors. For a long time, the work performed by Gradie & Tedesco (1982) has been
widely accepted as the major reference concerning the distribution and mixing of taxonomic
classes. These authors studied a total of 656 objects with diameters larger than 50 km concluding that S-type asteroids represent the most abundant class in an inner zone between 2.1 and 2.5 AU, C-type asteroids dominate
a central zone between 2.5 and 3.2 AU while D/P types are the dominant classes in an outer zone after 3.2 AU. In addition, Gradie & Tedesco (1982) showed the existence of some C and D asteroids in the inner zone and some S types
in the outer zone. However, Mothé-Diniz et al. (2003) developed an analysis aimed at refining the heliocentric distribution of taxonomic types in the asteroid Main Belt. Using a total of 2026 objects with diameters larger than 13 km, they found important differences with Gradie & Tedesco (1982) and other previous works.
In fact, Mothé-Diniz et al. (2003) concluded that S-type asteroids represent a significant fraction of the asteroid Main Belt population beyond 3 AU. Besides, they showed relevant discrepancies in the distribution of taxonomic classes
considering different ranges of eccentricities and inclinations.
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{6046fi12.eps} \end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg216.gif) |
Figure 12:
Mass fraction of the Inner, Middle and Outer Rings
distributed in the entire Main Belt due to the action of collisional processes after 4.5 Gyr. Our results indicate that each ring conserves more than 99 percent of its primordial mass which allows us to infer that the mixing of taxonomic classes observed in the asteroid belt can not be explained only by the collisional exchange of material. |
| Open with DEXTER |
Knowing the existence of this distribution of taxonomies, the goal of this analysis is to determine
if such distribution of classes is a characteristic feature of the Main Belt formation process or could have changed over the evolution of the Solar System.
Figure 12 shows that, after 4.5 Gyr of evolution, more than 99 percent of the final mass of every ring is represented by primordial material. From this, we conclude that the distribution and
mixing of taxonomic classes observed in the asteroid Main Belt can not be explained
by the collisional exchange of mass and owing to that such distribution of taxonomies should be a primordial feature. In this study, the transport of material between the different regions of the Main Belt due to the action of the Yarkovsky effect has not been taken
into account. In order to justify this assumption, we must analyze
our model of the Yarkovsky effect together with the dynamical properties of the  ,
3:1 and 5:2 powerful resonances, which determine the boundaries of
the rings of the Main Belt. Figure 4 shows that the semimajor-axis
drift rate
,
3:1 and 5:2 powerful resonances, which determine the boundaries of
the rings of the Main Belt. Figure 4 shows that the semimajor-axis
drift rate 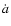 of bodies
of bodies  10-4 km is always smaller than 0.005 AU Myr-1
for any ring of the asteroid belt. In addition, as Table 1
indicates, the median lifetime of bodies initially in the
10-4 km is always smaller than 0.005 AU Myr-1
for any ring of the asteroid belt. In addition, as Table 1
indicates, the median lifetime of bodies initially in the  and 3:1 resonances
is
and 3:1 resonances
is  2 Myr while, for the 5:2 resonance, the median
lifetime is
2 Myr while, for the 5:2 resonance, the median
lifetime is  0.5 Myr. Assuming that these powerful resonances have a characteristic width of some hundreds of an AU, the time required to cross
these regions is always larger than the median lifetimes. Thus, we consider that
the Yarkovsky effect does not play an important role in mixing material between the
different zones of the Main Belt.
0.5 Myr. Assuming that these powerful resonances have a characteristic width of some hundreds of an AU, the time required to cross
these regions is always larger than the median lifetimes. Thus, we consider that
the Yarkovsky effect does not play an important role in mixing material between the
different zones of the Main Belt.
Here, we study statistically what percentage of mass of the NEA population comes from the
different regions of the Main Belt. In every timestep, we compute the injection rates from every
ring of the asteroid belt into the NEA population and the rates of dynamical elimination of those
bodies from such population. To calculate the influx rates, we take into account the action of the
Yarkovsky effect and the collisional injection into the  ,
3:1 and 5:2 resonances. To
compute the object removal rates from the NEA population, we need to determine a mean dynamical
lifetime for bodies in this population. Following Bottke et al. (2002), we obtain a mean dynamical lifetime of 3.73 Myr in the NEA region for objects coming from the Inner and Middle Rings of the asteroid belt, averaging the values associated to the
,
3:1 and 5:2 resonances. To
compute the object removal rates from the NEA population, we need to determine a mean dynamical
lifetime for bodies in this population. Following Bottke et al. (2002), we obtain a mean dynamical lifetime of 3.73 Myr in the NEA region for objects coming from the Inner and Middle Rings of the asteroid belt, averaging the values associated to the  secular resonance, the
intermediate-source Mars-crossing (IMC) population, and the 3:1 mean motion resonance. On the other
hand, a mean dynamical lifetime of 0.14 Myr is used for bodies coming from the Outer Ring of the Main Belt (Bottke et al. 2002, Table 2). Our analysis shows that
secular resonance, the
intermediate-source Mars-crossing (IMC) population, and the 3:1 mean motion resonance. On the other
hand, a mean dynamical lifetime of 0.14 Myr is used for bodies coming from the Outer Ring of the Main Belt (Bottke et al. 2002, Table 2). Our analysis shows that  94
94 of the NEA population comes from the Inner and Middle Rings of the asteroid belt and
of the NEA population comes from the Inner and Middle Rings of the asteroid belt and  6
6 comes from the Outer Ring,
which is in agreement with Bottke et al. (2002) who found that
comes from the Outer Ring,
which is in agreement with Bottke et al. (2002) who found that  85
85 of the NEA population comes from the inner and central Main Belt (namely, a < 2.8 AU),
of the NEA population comes from the inner and central Main Belt (namely, a < 2.8 AU),  8
8 comes from the outer Main Belt and
comes from the outer Main Belt and  6
6 comes from the Jupiter-family comet population.
comes from the Jupiter-family comet population.
We have presented a new multi-population code for collisional
evolution that takes into account the main dynamical features present
in the asteroid Main Belt and NEA region. The proposed collisional
model is based on Petit & Farinella's (1993) method that includes
some corrections made by O'Brien & Greenberg (2005). This algorithm allows us to
describe the escape and reaccumulation processes of the fragments
resulting from catastrophic fragmentation events and cratering
impacts. The dynamical mechanisms taken into account in our code
include mean motion and secular resonances, and the
Yarkovsky effect, which represent a source of mass depletion in the
asteroid belt and lead to a connection between the Main Belt and NEA populations.
While the previous works model the entire Main Belt, we study the
collisional and dynamical evolution of the Main Belt and NEA populations, dividing the asteroid belt into three semimajor axis zones whose boundaries are given by the  ,
3:1, 5:2 and 2:1 resonances. This treatment allows us to calculate the direct
collisional injection into these powerful resonances, to study the
collisional exchange of mass between the different regions of the Main
Belt and to analyze the provenance of the NEA objects. Our
results are consistent with the predictions made by Morbidelli et al.
(2002) and
Morbidelli & Vokrouhlický (2003), who proposed that the Yarkovsky
effect is the most important process that removes material from the
asteroid Main Belt, rather than collisional injection into the major
resonances (Sect. 5.1). Besides, we conclude that the distribution
and mixing of taxonomic classes observed in the asteroid belt
(Mothé-Diniz et al. 2003) can not be explained by the collisional
exchange of mass since more than 99 percent of the final mass of every
of the three rings of our model of the Main Belt is represented by
primordial material (Sect. 5.5). With regard to the provenance of the NEAs, our
work shows that
,
3:1, 5:2 and 2:1 resonances. This treatment allows us to calculate the direct
collisional injection into these powerful resonances, to study the
collisional exchange of mass between the different regions of the Main
Belt and to analyze the provenance of the NEA objects. Our
results are consistent with the predictions made by Morbidelli et al.
(2002) and
Morbidelli & Vokrouhlický (2003), who proposed that the Yarkovsky
effect is the most important process that removes material from the
asteroid Main Belt, rather than collisional injection into the major
resonances (Sect. 5.1). Besides, we conclude that the distribution
and mixing of taxonomic classes observed in the asteroid belt
(Mothé-Diniz et al. 2003) can not be explained by the collisional
exchange of mass since more than 99 percent of the final mass of every
of the three rings of our model of the Main Belt is represented by
primordial material (Sect. 5.5). With regard to the provenance of the NEAs, our
work shows that  94
94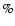 of the NEA population comes from the
Inner and Middle Rings of the asteroid belt and
of the NEA population comes from the
Inner and Middle Rings of the asteroid belt and  6
6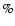 comes
from the Outer Ring (Sect. 5.6), which is in agreement with Bottke et al. (2002).
comes
from the Outer Ring (Sect. 5.6), which is in agreement with Bottke et al. (2002).
Our numerical algorithm have proved to satisfy the major observational
constraints associated with the Main Belt and NEA populations, such as
their size distributions, the collisional history of Vesta, the number
of large asteroid families and the cosmic-ray exposure (CRE) ages of
meteorites (Sect. 5). Besides, our model allows us to reproduce the
dynamical results derived by Morbidelli & Nesvorný (1999) and
Bottke et al. (2002) with regard to the removal rate for
multi-kilometer bodies from the Main Belt (Sect. 5.1).
Finally, this new multi-population code can be adapted in order to
study the collisional and dynamical evolution of any small body
population.
Acknowledgements
This work was partially financed by ANPCyT by grant PICT 03-11044.
We also acknowledge to Ricardo Gil Hutton for valuable discussions
during this work.
- Benz, W., &
Asphaug, E. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef] (In the text)
- Bottke, W. F.,
Morbidelli, A., Jedicke, R., et al. 2002, Icarus, 156, 399 [NASA ADS] [CrossRef] (In the text)
- Bottke, W. F.,
Durda, D. D., Nesvorný, D., et al. 2005a, Icarus, 175,
111 [NASA ADS] [CrossRef] (In the text)
- Bottke, W. F.,
Durda, D. D., Nesvorný, D., et al. 2005b, Icarus, 179, 63 [NASA ADS] [CrossRef] (In the text)
- Bowell, E., Hapke,
B., Domingue, D., et al. 1989, in Asteroids II, ed. R. P. Binzel,
T. Gehrels, & M. S. Matthews (Tucson, USA: University of
Arizona Press), 524
(In the text)
- Broz, M.,
Vokrouhlický, D., Roig, F., et al. 2005, MNRAS, 359, 1437 [NASA ADS] (In the text)
- Burns, J. A., Lamy,
P. L., & Soter, S. 1979, Icarus, 40, 1 [NASA ADS] [CrossRef] (In the text)
- Campo Bagatin, A. 1998,
Ph.D. Thesis, University of Valencia, Spain
(In the text)
- Campo Bagatin, A.,
Cellino, A., Davis, D. R., Farinella, P., & Paolicchi, P.
1994a, Planet. Space Sci., 42, 1079 [NASA ADS] [CrossRef] (In the text)
- Campo Bagatin, A.,
Farinella, P., & Petit, J. 1994b, Planet. Space Sci., 42,
1099 [NASA ADS] [CrossRef] (In the text)
- Davis, D. R.,
Chapman, C. R., Weidenschilling, S. J., & Greenberg, R. 1985,
Icarus, 62, 30 [NASA ADS] [CrossRef] (In the text)
- Davis, D. R.,
Weidenschilling, S. J., Farinella, P., Paolicchi, P., & Binzel,
R. P. 1989, in Asteroids II, ed. R. P. Binzel, T. Gehrels, & M.
S. Matthews (Tucson, USA: University of Arizona Press), 805
(In the text)
-
Dobrovolskis, A. R., & Burns, J. A. 1984, Icarus, 57, 464 [NASA ADS] [CrossRef] (In the text)
- Dohnanyi, J. W.
1969, J. Geophys. Res., 74, 2531 [NASA ADS] (In the text)
- Durda, D. D.,
Greenberg, R., & Jedicke, R. 1998, Icarus, 135, 431 [NASA ADS] [CrossRef] (In the text)
- Farinella,
P., Paolicchi, P., & Zappalà, V. 1982, Icarus, 52,
409 [NASA ADS] [CrossRef] (In the text)
- Farinella,
P., Vokrouhlický, D., & Hartmann, W. K. 1998, Icarus, 132,
378 [NASA ADS] [CrossRef] (In the text)
-
Fernández, J. A., Gallardo, T., & Brunini, A. 2002,
Icarus, 159, 358 [NASA ADS] [CrossRef] (In the text)
- Fujiwara, A.,
& Tsukamoto, A. 1980, Icarus, 44, 142 [NASA ADS] [CrossRef] (In the text)
- Fujiwara, A.,
Kamimoto, G., & Tsukamoto, A. 1977, Icarus, 31, 277 [NASA ADS] [CrossRef] (In the text)
- Gault, D. E.,
Shoemaker, E. M., & Moore, H. J. 1963, NASA Tech. Note
D-1767
(In the text)
- Giblin, I. 1998,
Planet. Space Sci., 46, 921 [NASA ADS] [CrossRef] (In the text)
- Giblin, I.,
Martelli, G., Smith, P. N., et al. 1994, Icarus, 110, 203 [NASA ADS] [CrossRef] (In the text)
- Gladman, B. J.,
Migliorini, F., Morbidelli, A., et al. 1997, Science, 277, 197 [NASA ADS] [CrossRef] (In the text)
- Gradie, J., &
Tedesco, E. 1982, Science, 216, 1405 [NASA ADS] [CrossRef] (In the text)
- Greenberg,
R., Hartmann, W. K., Chapman, C. R., & Wacker, J. F. 1978,
Icarus, 35, 1 [NASA ADS] [CrossRef] (In the text)
- Harris, A. W. 2002,
BAAS, 34, 835 [NASA ADS] (In the text)
- Hartmann, W. K.
1988, Lunar and Planetary Sci. XIX, 451
(In the text)
- Holsapple, K.
A. 1993, Annu. Rev. Earth Planet. Sci., 22, 333 [NASA ADS] (In the text)
- Holsapple, K.
A. 1994, Planet. Space Sci., 42, 1067 [NASA ADS] [CrossRef] (In the text)
- Housen, K. R. 1991,
Icarus, 94, 180 [NASA ADS] [CrossRef] (In the text)
- Housen, K. R.,
& Holsapple, K. A. 1990, Icarus, 84, 226 [NASA ADS] [CrossRef] (In the text)
- Housen, K. R.,
& Holsapple, K. A. 1999, Icarus, 142, 21 [NASA ADS] [CrossRef] (In the text)
- Ivezic, Z.,
Tabachnik, S., Rafikov, R., et al., and the SDSS Collaboration
2001, AJ, 122, 2749 [NASA ADS] [CrossRef] (In the text)
- Jedicke, R.,
& Metcalfe, T. S. 1998, Icarus, 131, 245 [NASA ADS] [CrossRef] (In the text)
- Keil, K. 2002, in
Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R.
P. Binzel (Tucson, USA: University of Arizona Press), 573
(In the text)
- Knezevic, Z.,
& Milani, A. 2003, A&A, 403, 1165 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Love, S. G., &
Ahrens, T. J. 1996, Icarus, 124, 141 [NASA ADS] [CrossRef] (In the text)
- Marti, K., &
Graf, T. 1992, Annu. Rev. Earth Planet. Sci., 20, 221 [NASA ADS] (In the text)
- Marzari, F.,
Scholl, H., & Farinella, P. 1996, Icarus, 119, 192 [NASA ADS] [CrossRef] (In the text)
- Melosh, H. J. 1989
(New York: Oxford University Press)
(In the text)
- Melosh, H. J.,
& Ryan, E. V. 1997, Icarus, 129, 562 [NASA ADS] [CrossRef] (In the text)
- Michel, P.,
Migliorini, F., Morbidelli, A., & Zappalà, V. 2000,
Icarus, 145, 332 [NASA ADS] [CrossRef] (In the text)
- Migliorini,
F., Michel, P., Morbidelli, A., Nesvorný, D., &
Zappalà, V. 1998, Science, 281, 2022 [NASA ADS] [CrossRef] (In the text)
- Morbidelli,
A., & Gladman, B. 1998, Meteoritics and Planetary Science, 33,
999 [NASA ADS] (In the text)
- Morbidelli,
A., & Henrard, J. 1991, Celest. Mechanics Dynamical Astron.,
51, 131 [NASA ADS] (In the text)
- Morbidelli,
A., & Nesvorný, D. 1999, Icarus, 139, 295 [NASA ADS] [CrossRef] (In the text)
- Morbidelli,
A., & Vokrouhlický, D. 2003, Icarus, 163, 120 [NASA ADS] [CrossRef] (In the text)
- Morbidelli,
A., Bottke, W. F., Froeschlé, Ch., & Michel, P. 2002, in
Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R.
P. Binzel (Tucson, USA: University of Arizona Press), 409
(In the text)
- Mothé-Diniz, T.,
Carvano, J. M., & Lazzaro, D. 2003, Icarus, 162, 10 [NASA ADS] [CrossRef] (In the text)
- Murray, N., Holman,
M., & Potter, M. 1998, AJ, 116, 2583 [NASA ADS] [CrossRef] (In the text)
- Nakamura, A.,
& Fujiwara, A. 1991, Icarus, 92, 132 [NASA ADS] [CrossRef] (In the text)
- Nakamura, A.,
Suguiyama, K., & Fujiwara, A. 1992, Icarus, 100, 127 [NASA ADS] [CrossRef] (In the text)
- Nesvorný,
D., & Morbidelli, A. 1998, AJ, 116, 3029 [NASA ADS] [CrossRef] (In the text)
- Nesvorný,
D., & Morbidelli, A. 1999, Celest. Mechanics Dynamical Astron.,
71, 243 [NASA ADS] (In the text)
- Nesvorný,
D., Ferraz-Mello, S., Holman, M., & Morbidelli, A. 2002, in
Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R.
P. Binzel (Tucson, USA: University of Arizona Press), 379
(In the text)
- Nolan, M. C.,
Asphaug, E., Melosh, H. J., & Greenberg, R. 1996, Icarus, 124,
359 [NASA ADS] [CrossRef] (In the text)
- O'Brien, D. P.,
& Greenberg, R. 2005, Icarus, 178, 179 [NASA ADS] [CrossRef] (In the text)
- Penco, U., Dell'Oro,
A., La Spina, A., et al. 2002, ACM Meeting, Berlin, Proc., ESA
SP-500, Noordwijk, NL, 363
(In the text)
- Peterson, C.
1976, Icarus, 29, 91 [NASA ADS] [CrossRef] (In the text)
- Petit, J., &
Farinella, P. 1993, Celest. Mechanics Dynamical Astron., 57, 1 [NASA ADS] (In the text)
- Petit, J.,
Morbidelli, A., & Valsecchi, G. B. 1999, Icarus, 141, 367 [NASA ADS] [CrossRef] (In the text)
- Petit, J.,
Morbidelli, A., & Chambers, J. 2001, Icarus, 153, 338 [NASA ADS] [CrossRef] (In the text)
- Rabinowitz, D. L.,
Bowell, E., Shoemaker, E. M., & Muinonen, K. 1994, Hazards Due
to Comets and Asteroids, 285
(In the text)
- Rabinowitz, D. L.,
Helin, E., Lawrence, K., & Pravdo, S. 2000, Nature, 403,
165 [NASA ADS] [CrossRef] (In the text)
- Ryan, E. V. 1992, Ph.D.
Thesis (Tucson, USA: University of Arizona)
(In the text)
- Ryan, E. V., &
Melosh, H. J. 1998, Icarus, 133, 1 [NASA ADS] [CrossRef] (In the text)
- Stoeffler,
D., Gault, D. E., Wedekind, J., & Polkowski, G. 1975, J.
Geophys. Res., 80, 4062 [NASA ADS] (In the text)
- Stuart, J. S. 2001,
Science, 294, 1691 [NASA ADS] [CrossRef] (In the text)
- Tanaka, H., Inaba,
S., & Nakazawa, K. 1996, Icarus, 123, 450 [NASA ADS] [CrossRef] (In the text)
- Thomas, P. C.,
Binzel, R. P., Gaffey, M. J., et al. 1997, Science, 277, 1492 [NASA ADS] [CrossRef] (In the text)
- Vokrouhlický, D.,
Broz, M., Bottke, W. F., Nesvorný, D., & Morbidelli, A.
2006, Icarus, 182, 118 [NASA ADS] [CrossRef] (In the text)
- Weidenschilling, S. J.
1977, Ap&SS, 51, 152 [NASA ADS] (In the text)
- Wetherill, G.
W. 1979, Icarus, 37, 96 [NASA ADS] [CrossRef] (In the text)
- Williams, D.
R., & Wetherill, G. W. 1994, Icarus, 107, 117 [NASA ADS] [CrossRef] (In the text)
- Williams, J. G.
1969, Ph.D. Thesis, University of California, Los Angeles, USA
(In the text)
- Wisdom, J. 1983,
Icarus, 56, 51 [NASA ADS] [CrossRef] (In the text)
- Wisdom, J. 1985a,
Icarus, 63, 272 [NASA ADS] [CrossRef] (In the text)
- Wisdom, J. 1985b,
Nature, 315, 731 [NASA ADS] [CrossRef] (In the text)
- Yoshida, F.,
Nakamura, T., Watanabe, J., et al. 2003, PASJ, 55, 701 [NASA ADS] (In the text)
- Zappalà, V.,
Bendjoya, P., Cellino, A., Farinella, P., & Froeschlé, Ch.
1995, Icarus, 116, 291 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{6046fi1.eps} \end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg23.gif)
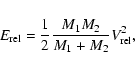
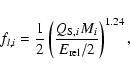
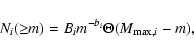
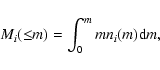
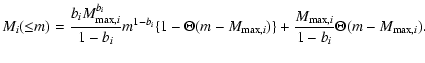
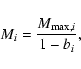
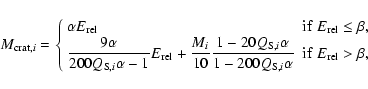
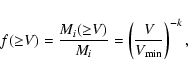
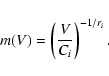
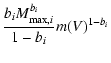
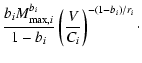
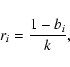
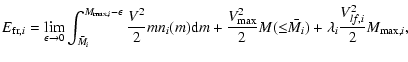
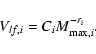
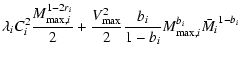
![$\displaystyle + \frac{C_{i}^{2}}{2}
\frac{b_{i}M_{{\rm max},i}^{b_{i}}}{1-b_{i}-2r_{i}}[M_{{\rm max},i}^{1-b_{i}-2r_{i}}
-\bar{M_{i}}^{1-b_{i}-2r_{i}}]$](/articles/aa/full/2007/18/aa6046-06/img83.gif)
![$\displaystyle C_{i}^{k_{i}}b_{i}
\frac{M_{{\rm max},i}^{b_{i}}V_{{\rm max}}^{2-k_{i}}}{2}\bigg[\frac{1}{1-b_{i}} -
\frac{1}{1-b_{i}-2r_{i}} \bigg]$](/articles/aa/full/2007/18/aa6046-06/img84.gif)
![$\displaystyle + C_{i}^{2}\frac{M_{{\rm max},i}^{1-2r_{i}}}{2}\bigg[\lambda_{i}
+ \frac{b_{i}}{1-b_{i}-2r_{i}} \bigg]\cdot$](/articles/aa/full/2007/18/aa6046-06/img85.gif)
}\Bigg]$](/articles/aa/full/2007/18/aa6046-06/img86.gif)
![$\displaystyle 2M_{{\rm max},i}^{2r_{i}-1}\Bigg[\frac{1-b_{i}-2r_{i}}{(1-2r_{i}-b_{i})\lambda
_{i}+b_{i}}\Bigg]E_{{\rm fr},i},$](/articles/aa/full/2007/18/aa6046-06/img87.gif)
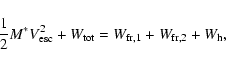
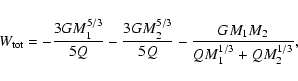
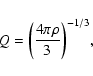
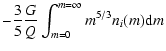
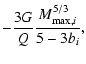
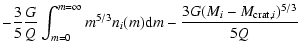
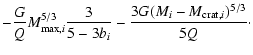
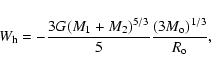
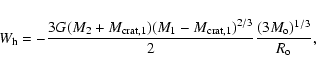
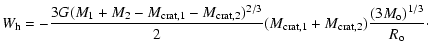
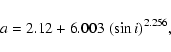
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{6046fi2.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg117.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6046fi3.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg124.gif)
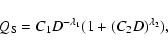
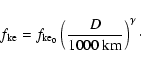
![\begin{figure}
\par\includegraphics[width=16.45cm,clip]{6046fi4.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg130.gif)
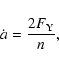
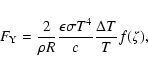
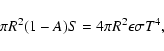
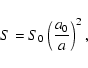
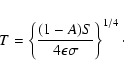
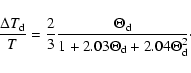
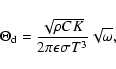
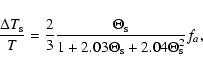
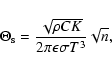
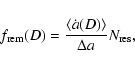
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6046fi5.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg173.gif)
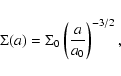
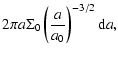
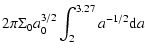
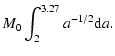
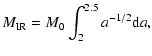
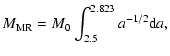
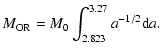
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{6046fi6.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg188.gif)
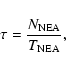
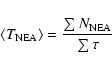
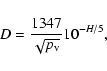
![\begin{figure}
\par\includegraphics[width=9cm,clip]{6046fi7.eps} \end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg206.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{6046fi8.eps} \end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg207.gif)
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{6046fi9.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg208.gif)
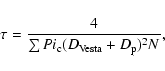
![\begin{figure}
\par\includegraphics[width=7.95cm,clip]{6046fi10.eps} \end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg214.gif)
![\begin{figure}
\par\includegraphics[width=7.85cm,clip]{6046fi11.eps}\end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg215.gif)
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{6046fi12.eps} \end{figure}](/articles/aa/full/2007/18/aa6046-06/Timg216.gif)