A&A 466, 1197-1204 (2007)
DOI: 10.1051/0004-6361:20064981
J. Woodall1 - M. Agúndez2 - A. J. Markwick-Kemper1,3 - T. J. Millar1,4
1 - Jodrell Bank Centre for Astrophysics, School of Physics and
Astronomy, University of Manchester, Sackville Street Building, Manchester
M60 1QD, UK
2 - Departamento de Astrofisica Molecular e Infrarroja, Instituto de
Estructura de la Materia, CSIC, Serrano 121 28006 Madrid, Spain
3 - Department of Astronomy, University of Virginia, PO Box 3818,
Charlottesville, VA 22903, USA
4 - Astrophysics Research Centre, School of
Mathematics and Physics, Queen's University Belfast, Belfast BT7 1NN, UK
Received 7 February 2006 / Accepted 30 January 2007
Abstract
Aims. We present a new version of the UMIST Database for Astrochemistry, the fourth such version to be released to the public. The current version contains some 4573 binary gas-phase reactions, an increase of 10% from the previous (1999) version, among 420 species, of which 23 are new to the database.
Methods. Major updates have been made to ion-neutral reactions, neutral-neutral reactions, particularly at low temperature, and dissociative recombination reactions. We have included for the first time the interstellar chemistry of fluorine. In addition to the usual database, we have also released a reaction set in which the effects of dipole-enhanced ion-neutral rate coefficients are included.
Results. These two reactions sets have been used in a dark cloud model and the results of these models are presented and discussed briefly. The database and associated software are available on the World Wide Web at www.udfa.net.
Key words: molecular data - molecular processes - ISM: molecules - astrochemistry
The use of astrochemical models to interpret observations of interstellar and circumstellar molecular line observations is widespread; recent years have seen the application of such models to protoplanetary disks (Aikawa & Herbst 1999; Aikawa et al. 2002; Markwick et al. 2002; Ilgner et al. 2004; Semenov et al. 2005), protoplanetary nebulae (Cernicharo 2004; Woods et al. 2005), hot molecular cores (Viti et al. 2004; Nomura & Millar 2004; Wakelam et al. 2004), the early universe (Flower & Pineau des Forêts 2003; Lepp 2003) as well as the more traditional applications to diffuse and dark interstellar clouds (Stantcheva & Herbst 2004; Lee et al. 2004), interstellar shocks (Bergin et al. 1999; Flower et al. 2003), YSOs (Rodgers & Charnley 2003; Doty et al. 2004; Stäuber et al. 2005), and circumstellar envelopes (Brown & Millar 2003; Willacy 2004). Many of these papers consider grain chemistry either implicitly or explicitly and several have been aimed at exploring deuterium fractionation (Roberts et al. 2003, 2004) and, in particular, the possible role that grains may play in the creation of the high fractionation ratios observed in many multi-deuterated species.
The role of surface chemistry in the synthesis of interstellar molecules is a matter of much debate presently and, given the difficulties in finding an appropriate numerical description of the surface kinetics, most arguments to support the influence of grain reactions start from the failure of gas-phase chemistry to reproduce abundances of particular molecules or classes of molecule. In this regard it is therefore important to have as complete a system of gas-phase reactions as possible to describe molecular synthesis.
In this paper we discuss the latest release of the UMIST Database for Astrochemistry which has undergone a detailed re-examination over the past two years. Although the number of reactions has increased by only 10% we have critically re-assessed the rate coefficients of all reactions and have incorporated the latest laboratory data. Indeed in this release, there is experimental data available on just over one-third of all reactions, an increase of about 6%. In the following section we present our conventions, Sect. 3 discusses the updates we have made to the data while in Sect. 4 we present the results of a dark cloud model.
He, C, N, O, F, Na, Mg, Si, P, S, Cl, and Fe, are listed in order of mass in Table 1.
The permanent electric dipole moments of the neutral molecules are listed in Table 2.
Table 3, available in full only in electronic form, contains all of the reactions and their associated rate coefficients.
Table 3: List of the first ten reactions in the database. The full database is available in electronic form at www.udfa.net.
Our reaction format is:
I, type, R1, R2, R3, P1, P2, P3, P4, ![]() ,
,
![]() ,
,
![]() ,
source,
,
source, ![]() ,
,
![]() ,
accuracy, reference code
where I is the reaction number; type the reaction type (see Table 7); R1, R2 and R3 are reactants (to allow for the
inclusion of three-body reactions); P1, P2, P3, P4 are products;
,
accuracy, reference code
where I is the reaction number; type the reaction type (see Table 7); R1, R2 and R3 are reactants (to allow for the
inclusion of three-body reactions); P1, P2, P3, P4 are products; ![]() (
(![]() )
is the lower (upper) temperature limit at which the rate coefficient
holds; source indicates
the source of the data ("M'' measured, "E'' estimated, "C'' calculated, and "L''
literature search, with the latter most often used to note rate coefficients
which are derived using several experimental values). The accuracy is
described by a letter - A, B, C, D, E - where the errors are <25%, <50%, within a factor of 2, within an order of magnitude, and highly
uncertain, respectively. Thenumerical values of the reference code is taken
from the Anicich (2004) database for ion-neutral reactions, while the other
codes are listed in Table 4.
)
is the lower (upper) temperature limit at which the rate coefficient
holds; source indicates
the source of the data ("M'' measured, "E'' estimated, "C'' calculated, and "L''
literature search, with the latter most often used to note rate coefficients
which are derived using several experimental values). The accuracy is
described by a letter - A, B, C, D, E - where the errors are <25%, <50%, within a factor of 2, within an order of magnitude, and highly
uncertain, respectively. Thenumerical values of the reference code is taken
from the Anicich (2004) database for ion-neutral reactions, while the other
codes are listed in Table 4.
As before, some reactions are duplicated when their
temperature dependence cannot be approximated by one Arrhenius-type
formula. Examples include the important reaction,
![]() which is best fit by a formula which includes a (negative)
activation energy barrier above the experimental lower limit of 158 K and, at
low temperatures, a formula which has no activation energy barrier and, at
most, only a weak temperature dependence (Smith et al. 2004;
Sims 2006; Carty et al. 2006). This reaction is
also an example of one which has a negative activation energy, usually the
result of fitting a rate coefficient over a particular temperature
range. Indiscriminate use of such rate coefficients at low temperatures,
indeed outside their range of validity, can lead to serious errors in any
model calculation. For those reactions for which more than one temperature range
is included, we have been careful to ensure that the temperature ranges do not
overlap. A more pressing concern is how to evaluate a rate coefficient outside
of its given temperature range. In general, we recommend that one uses the
entry in the database closest to the temperature of interest. In most cases,
this will give a reasonable value for the rate coefficient.
However, care needs to be taken when the rate coefficient has a negative
activation energy; in such cases one should check to see whether the rate
coefficient remains physical. For example, the reaction between C2H and
C2H2 has a rate coefficient best fit with a negative activation energy
of 25 K over the range 143-3000 K. At 10 K, it is probably still reasonable
to use this fit to determine the rate coefficient. On the other hand, the
reaction between O and NO2, which has a negative activation energy of
120 K over the range 200-2500 K, has an unreasonably large
rate coefficient at 10 K. In our experience, the rate coefficients of the
following
reactions should be set to zero in a model at 10 K: reaction numbers 6, 93,
140, 171, 266, 282, 312, 316, 351, 353, 377, 419, 431, 443, 446, 448, 488,
493, 501-2, 520, 533, 540, 660, 666-7, 949, 1684, 1731, 2939, 2946,
3533-4, 3536-7, 3552-3, 3555-6, 3558-9, 3581-6,
4007-8, 4013-4, 4016, 4079, 4109, 4112, 4115, 4138, and 4558. Some of
these are duplicated reactions.
which is best fit by a formula which includes a (negative)
activation energy barrier above the experimental lower limit of 158 K and, at
low temperatures, a formula which has no activation energy barrier and, at
most, only a weak temperature dependence (Smith et al. 2004;
Sims 2006; Carty et al. 2006). This reaction is
also an example of one which has a negative activation energy, usually the
result of fitting a rate coefficient over a particular temperature
range. Indiscriminate use of such rate coefficients at low temperatures,
indeed outside their range of validity, can lead to serious errors in any
model calculation. For those reactions for which more than one temperature range
is included, we have been careful to ensure that the temperature ranges do not
overlap. A more pressing concern is how to evaluate a rate coefficient outside
of its given temperature range. In general, we recommend that one uses the
entry in the database closest to the temperature of interest. In most cases,
this will give a reasonable value for the rate coefficient.
However, care needs to be taken when the rate coefficient has a negative
activation energy; in such cases one should check to see whether the rate
coefficient remains physical. For example, the reaction between C2H and
C2H2 has a rate coefficient best fit with a negative activation energy
of 25 K over the range 143-3000 K. At 10 K, it is probably still reasonable
to use this fit to determine the rate coefficient. On the other hand, the
reaction between O and NO2, which has a negative activation energy of
120 K over the range 200-2500 K, has an unreasonably large
rate coefficient at 10 K. In our experience, the rate coefficients of the
following
reactions should be set to zero in a model at 10 K: reaction numbers 6, 93,
140, 171, 266, 282, 312, 316, 351, 353, 377, 419, 431, 443, 446, 448, 488,
493, 501-2, 520, 533, 540, 660, 666-7, 949, 1684, 1731, 2939, 2946,
3533-4, 3536-7, 3552-3, 3555-6, 3558-9, 3581-6,
4007-8, 4013-4, 4016, 4079, 4109, 4112, 4115, 4138, and 4558. Some of
these are duplicated reactions.
In addition, we also make available a second reaction file, called Rate06-dipole, which includes the enhancement of ion-neutral rate coefficients for cases in which the neutral has a large, permanent electric dipole moment. Such enhancements, due to "dipole locking'' effects (Troe 1987; Herbst & Leung 1986b), result in rate coefficients which have a T-1/2 dependence at low temperatures. In our reaction file we include this power-law behaviour in all reactions for which (i) the neutral has a dipole moment in excess of 0.9 Debye; (ii) the reaction does not already have a temperature dependence; and (iii) the reaction does not have a measured rate coefficient at low temperatures. In general, the use of the dipole-enhanced rate file is to be preferred at the low temperatures of dark interstellar clouds. In particular, the rate coefficients are more accurate for exothermic proton-transfer reactions and many other ion-neutral reactions which proceed with unit efficiency. It is less clear that rate coefficients are enhanced when the reaction is slow at room temperature. One of the main advantages in using the dipole-enhanced rate coefficients is that they give a much better fit to the observations of protonated ions detected in the cold interstellar clouds, e.g. HCS+, HCNH+, HC3NH+, and are, as a result, to be preferred for calculations at 10 K. We discuss the influence of such coefficients on calculated abundances in Sect. 4.
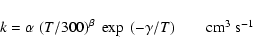 |
(1) |
For direct cosmic-ray ionisation (R2 = CRP):
| (2) |
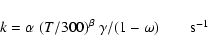 |
(3) |
For interstellar photoreactions (R2 = PHOTON), the rate is
derived as:
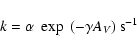 |
(4) |
Table 5: New species and alterations to chemical formulae. For the latter, we specify the old representation followed by the new.
Including 32 ternary reactions, the database has increased in size from 4113 in RATE99 to 4605 entries in RATE06, covering 4564 distinct chemical reactions as opposed to 4082 in RATE99. Table 5 lists newly included species and changes to nomenclature from those adopted in RATE99. There are 577 reactions new to RATE06, and of the reactions common to both versions of the database, around 450 of them have had their rate coefficient updated. Of these, the 156 cosmic-ray photon reaction rates were updated as described below, and for the remainder, the changes are either due to new data being available, or a reappraisal of the existing data. The reaction rate coefficients changing the most are largely neutral-neutral reactions whose low temperature behaviour has been reexamined in the literature, such as reactions between atomic oxygen and polyynes - rate coefficients for these reactions have typically increased from 10-25 in RATE99 to 10-11 in RATE06. There are only 10 reactions whose 10 K rate coefficient has increased by more than a factor of 100. There are 7 reactions whose 10 K rate coefficient has decreased by more than a factor of 100. These reactions and their data are shown in Table 6. On the database web site www.udfa.net, the changes to each rate coefficient between RATE95, RATE99 and RATE06 can be examined in more detail on a reaction by reaction basis.Table 6: The reactions whose 10 K rate coefficient has changed the most between the current and previous releases of the database. In most cases this is due to new data for the reaction being available. The reference codes follow our usual convention.
The table of reactions is ordered in broad categories as listed in Table 7. Within each category, ordering is done by mass such that species R1 is the lightest of the collision partners, and, for a given R1, R2 is listed in order of increasing mass. Figure 1 shows the changes in the source of the data and accuracy of the rate coefficients between RATE99 and RATE06. As expected, the fraction of measured reactions and the accuracy of the data has improved with time. In addition to the one-third or so reactions which have measured rate coefficients, many of the photorates are, of course, based on experimental cross-sections. We describe each category in turn, noting important changes to the data where appropriate.
| |
Figure 1: The rate coefficient data in RATE06 (dark) is more accurate, and based on more laboratory measurements than RATE99 (light). The panels show a comparison of the numbers of reactions versus their data source ( left) and quoted accuracy ( right), between the two releases. |
| Open with DEXTER | |
Table 7: The types of chemical reactions present and their count in the database, together with the number for which experimental data is available. The first column gives the abbreviation used for the types.
Since the time of our last release we have increased the number of neutral-neutral reactions by just over 100, removing around 10 reactions in the process, mostly because they are endothermic or because new laboratory measurements have indicated different products or negligible rate coefficients. Our new reactions are the result of an extensive search of the NIST Chemistry Webbook (http://webbook.nist.gov/chemistry) as well as more recent literature (the NIST Webbook has not included new data since around 2001) for reactions likely to be of interest in interstellar, circumstellar and shock chemistry. Many of the rate coefficients have been taken from the series of papers on evaluated neutral-neutral rate coefficients published by the IUPAC Subcommittee on Gas Kinetic Data Evaluation for Atmospheric Chemistry (much of its data is available on the web site http://www.iupac-kinetic.ch.cam.ac.uk), while we have made extensive use of the paper by Smith et al. (2004) which discusses the low-temperature behaviour of neutral-neutral reactions.
Almost 2950 reactions in the database fall into the category of binary reactions between a cation and a neutral species, with around 550 of these involving charge exchange rather than bond breaking. We have reviewed these reactions thoroughly, mostly using the recent - and final - release of the Anicich (2004) database which includes "all'' ion-neutral reactions measured from 1936 to the end of 2003. Around 1160 of the ion-neutral reactions listed in our database have measured rate coefficients, mostly at room temperature. Again, where low-temperature information is available - and more is available for this category than for neutral-neutral reactions - we have included this in the database. For exothermic reactions involving species with small electric dipole moments, we expect that the rate coefficients will be temperature-independent. For reactions involving species with a large electric dipole moment, we expect a dependence on the order of T-1/2 and we adopt this in our "dipole-enhanced'' rate file, see Sect. 2.
This category of reaction now involves some 500 product channels of which close to 100 have been measured. This is an area which is significantly different from previous releases due to the large amount of high-quality data which have resulted from storage ring measurements, many of which involve recombination at low collisional energies. The ability of these experiments to determine product channels has given rise to some unexpected results which are challenging traditional models of gas-phase interstellar chemistry. They include the fact that the dissociative recombination of N2H+ breaks the N-N bond in two-thirds of the collisions (Geppert et al. 2004), and that of CH3OH2+ produces methanol, CH3OH, in only 3-4% of recombinations (Geppert et al. 2006).
The database includes 91 radiative associations of which 17 have rate
coefficients determined with the aid of experimental data, often three-body
data.
New information on low-temperature radiative association processes has become
available due to the development of ion-trap systems which allow reactants to
thermalise at low temperature. Of particular importance here is the
association of CH3+ and water to form protonated methanol, CH3OH2+,
for which Herbst (1985) calculated a rate coefficient of
![]() (T/300 K)-1.7 cm3 s-1, based on experimental three-body
measurements. More recently, Luca et al. (2002) have reported a direct
measurement of the rate coefficient below 80 K and find it to be
(T/300 K)-1.7 cm3 s-1, based on experimental three-body
measurements. More recently, Luca et al. (2002) have reported a direct
measurement of the rate coefficient below 80 K and find it to be
![]() cm3 s-1, independent of temperature. This low value, some
1000 times smaller than the Herbst value at 10 K, makes it difficult to form
CH3OH at interstellar temperatures. In spite of the fact that this result has not,
as yet, been confirmed by the publication of a refereed article, we adopt it in the new
version of database, and the model results presented in
Sect. 4 use it.
cm3 s-1, independent of temperature. This low value, some
1000 times smaller than the Herbst value at 10 K, makes it difficult to form
CH3OH at interstellar temperatures. In spite of the fact that this result has not,
as yet, been confirmed by the publication of a refereed article, we adopt it in the new
version of database, and the model results presented in
Sect. 4 use it.
Some additional photoprocesses have been incorporated in to the database and a total of 216 product channels are now included. In part, these are due to the inclusion of photodissociation of the larger, organic molecules (Herbst & Leung 1986). Additional data for a few species have been provided by van Dishoeck (private communication).
Doty noticed that the probabilities, Pi, adopted in RATE99 and in the OSU databases are too large by a factor of two, reproducing as they do the original Pi listed by Sternberg et al. (1987). Thus, the probabilities in the older implementations at UMIST and OSU should be reduced by a factor of two. This error occurred because in these databases the cosmic-ray ionisation rate is per H2 molecule - as opposed to per H-atom in Sternberg et al. (1987) - while the dust extinction, implicit in the determination of the probabilities, is proportional to the total density, i.e. 2n(H2), in dense clouds. The probabilities of the 156 cosmic-ray photo-induced reactions listed here have been corrected for this error.
| |
Figure 2: The time evolution of the major sulphur-bearing species with RATE99 ( left) and with RATE06 ( right). |
| Open with DEXTER | |
Table 8: Initial elemental abundances relative to total hydrogen nuclei.
Table 9 shows steady state output for both the standard database and the dipole-enhanced database, while Figs. 3 and 4 show the time-dependent evolution of the major oxygen and sulfur-bearing species both with and without the inclusion of dipole-enhanced rate coefficients. Because of the relatively low level of ionisation in dark clouds, radicals are most rapidly destroyed by fast neutral-neutral reactions if available, whereas stable neutrals are destroyed through reaction with cations such as H3+, He+ and HCO+. As can be seen from the table and figures, the inclusion of dipole-enhanced rate coefficients reduces the abundances of the relevant neutrals, e.g. H2O, HNC, HCN, SO2 and H2S, by factors of 3-5 whereas radicals such as OH and NO are relatively unaffected. CH3CN and the cyanopolyynes, HC2n+1N, are among the most affected species because of their limited chemistry; they decrease by an order of magnitude when dipole-enhanced rate coefficients are used.
| |
Figure 3: The time evolution of the major oxygen-bearing species without ( left) and with ( right) dipole-enhanced rate coefficients in Rate06. |
| Open with DEXTER | |
| |
Figure 4: The time evolution of the major sulfur-bearing species without ( left) and with ( right) dipole-enhanced rate coefficients in Rate06. |
| Open with DEXTER | |
| |
Figure 5: The time evolution of the major sulphur-bearing species with ( left) the rate coefficient for the O + OH reaction taken from Smith et al. (2004) and with ( right) the value taken from Carty et al. (2006). Both model calculations use dipole-enhanced rate coefficients. |
| Open with DEXTER | |
The low temperature dependence of the rate coefficient for the O + OH reaction
plays a critical role in determining the abundances of many species in which
OH plays a synthetic role. As an example of the effect of the sensitivity of
calculated abundances to this rate coefficient, we plot in Fig. 5
the time-dependent abundances of several sulphur-bearing species for two cases.
One in which we use a
rate coefficient of
![]() (T/300 K)-0.25 cm3 s-1 (Smith
et al. 2004) -
(T/300 K)-0.25 cm3 s-1 (Smith
et al. 2004) -
![]() cm3 s-1 at 10 K - the other with a rate
coefficient of
cm3 s-1 at 10 K - the other with a rate
coefficient of
![]() cm3 s-1 measured by Carty et al. (2006) over the range 39-142 K and
adopted here for 10 K. The lower rate coefficient in the latter case leads to a
larger fractional abundance of OH and hence to significantly larger fractional
abundances of SO and SO2. In the non-dipole enhanced calculation, the use of
the Carty et al. (2006) rate coefficient leads to
abundances of SO and SO2 comparable to S (Fig. 4).
cm3 s-1 measured by Carty et al. (2006) over the range 39-142 K and
adopted here for 10 K. The lower rate coefficient in the latter case leads to a
larger fractional abundance of OH and hence to significantly larger fractional
abundances of SO and SO2. In the non-dipole enhanced calculation, the use of
the Carty et al. (2006) rate coefficient leads to
abundances of SO and SO2 comparable to S (Fig. 4).
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=-90,clip]{4981f6.ps}}\end{figure}](/articles/aa/full/2007/18/aa4981-06/Timg53.gif) |
Figure 6: The time evolution of the methanol abundance for various choices of key rate coefficients. The curves calculated using the latest RATE06 rate coefficients are labelled "RATE06'' and "RATE06-dipole'' for the non-dipole and dipole versions respectively. The curve labelled "RATE99'' uses the rate coefficients for the radiative association of CH3+ and H2O and the dissociative recombination of CH3OH2+ from that database. |
| Open with DEXTER | |
Finally, we plot the methanol abundance as a function of time for several choices of rate coefficients in Fig 6. The curve labelled "RATE99'' uses the data from RATE99, in particular it assumes that 50% of the dissociative recombinations of protonated methanol lead to methanol, and that the rate coefficient for the radiative association of CH3+ and H2O is that determined by Herbst (1985); in contrast, the curve labelled "RATE06'' uses the latest experimental data for the branching ratios of the dissociative recombination of protonated methanol from Geppert et al. (2006), and the low experimental rate for the radiative association of CH3+ and H2O as measured by Luca et al. (2002). The "RATE99'' curve gives values of the methanol abundance close to those observed in dark clouds, but the abundance falls by over an order of magnitude when the new experimental dissociative recombination rate coefficients are introduced. The inclusion of dipole-enhanced rate coefficients (curve "RATE06-dipole'') also has an effect since the water, which has a large dipole moment, has a lower abundance in such a case. For the most extreme case, the methanol fractional abundance is never above 10-10 and at steady-state is about 1000 times less than that predicted by RATE99. This is the most significant astrochemical difference between RATE99 and RATE06.
Acknowledgements
Several individuals, including S. Doty, A. Sternberg and E. F. van Dishoeck, made useful comments on earlier versions of the database. We are grateful to PPARC for supporting the work of J.W. and T.J.M. through the UMIST Rolling Grant and to the EU through contract number MRTN-CT-2004-512302. M.A. acknowledges the Spanish MEC for support under project AYA 2003-02785-E and grant AP2003-4619.
Table 1: List of species contained in the database ordered by mass.
Table 2: Permanent electric dipole moments in Debye of the neutral molecules. References are given for those cases in which the values of the dipole moments have been updated since RATE99.
Table 4: List of the database reaction reference codes and their correspondance with the bibliographical references. NOTE: Any digit-only code found in the database is the same code as that used for referencing reactions in Anicich (2004).
Table 9: Steady state fractional abundances with respect to H2. "Rate06'' refers to the standard database while "Dipole'' refers to the database with dipole-enhanced rate coefficients.