A&A 466, 649-659 (2007)
DOI: 10.1051/0004-6361:20066965
S. Kraus1 - Y. Y. Balega2 - J.-P. Berger3 - K.-H. Hofmann1 - R. Millan-Gabet4 - J. D. Monnier5 - K. Ohnaka1 - E. Pedretti5 - Th. Preibisch1 - D. Schertl1 - F. P. Schloerb6 - W. A. Traub7 - G. Weigelt1
1 -
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69,
53121 Bonn, Germany
2 -
Special Astrophysical Observatory, Russian Academy of Sciences, Nizhnij
Arkhyz, Zelenchuk region, Karachai-Cherkesia 357147, Russia
3 -
Laboratoire d'Astrophysique de Grenoble, UMR 5571 Université Joseph
Fourier/CNRS, BP 53, 38041 Grenoble Cedex 9, France
4 -
Michelson Science Center, California Institute of Technology, Pasadena, CA
91125, USA
5 -
Astronomy Department, University of Michigan, 500 Church Street, Ann Arbor,
MI 48104, USA
6 -
Department of Astronomy, University of Massachusetts, LGRT-B 619E, 710 North
Pleasant Street, Amherst, MA 01003, USA
7 -
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA
02183, USA
Received 19 December 2006 / Accepted 7 February 2007
Abstract
Context. Located in the Orion Trapezium cluster, ![]() Ori C is one of the youngest and nearest high-mass stars (O5-O7) known. Besides its unique properties as a magnetic rotator, the system is also known to be a close binary.
Ori C is one of the youngest and nearest high-mass stars (O5-O7) known. Besides its unique properties as a magnetic rotator, the system is also known to be a close binary.
Aims. By tracing its orbital motion, we aim to determine the orbit and dynamical mass of the system, yielding a characterization of the individual components and, ultimately, also new constraints for stellar evolution models in the high-mass regime. Furthermore, a dynamical parallax can be derived from the orbit, providing an independent estimate for the distance of the Trapezium cluster.
Methods. Using new multi-epoch visual and near-infrared bispectrum speckle interferometric observations obtained at the BTA 6 m telescope, and IOTA near-infrared long-baseline interferometry, we traced the orbital motion of the ![]() Ori C components over the interval 1997.8 to 2005.9, covering a significant arc of the orbit. Besides fitting the relative position and the flux ratio, we applied aperture synthesis techniques to our IOTA data to reconstruct a model-independent image of the
Ori C components over the interval 1997.8 to 2005.9, covering a significant arc of the orbit. Besides fitting the relative position and the flux ratio, we applied aperture synthesis techniques to our IOTA data to reconstruct a model-independent image of the ![]() Ori C binary system.
Ori C binary system.
Results. The orbital solutions suggest a highly eccentricity (
![]() )
and short-period (
)
and short-period (
![]() yrs) orbit. As the current astrometric data only allows rather weak constraints on the total dynamical mass, we present the two best-fit orbits. Of these two, the one implying a system mass of
yrs) orbit. As the current astrometric data only allows rather weak constraints on the total dynamical mass, we present the two best-fit orbits. Of these two, the one implying a system mass of
![]() and a distance of 434 pc to the Trapezium cluster can be favored. When also taking the measured flux ratio and the derived location in the HR-diagram into account, we find good agreement for all observables, assuming a spectral type of O5.5 for
and a distance of 434 pc to the Trapezium cluster can be favored. When also taking the measured flux ratio and the derived location in the HR-diagram into account, we find good agreement for all observables, assuming a spectral type of O5.5 for ![]() Ori C1 (
Ori C1 (
![]() ,
,
![]() K) and O9.5 for C2 (
K) and O9.5 for C2 (
![]() ,
,
![]() K). Using IOTA, we also obtained first interferometric observations on
K). Using IOTA, we also obtained first interferometric observations on ![]() Ori D, finding some evidence for a resolved structure, maybe by a faint, close companion.
Ori D, finding some evidence for a resolved structure, maybe by a faint, close companion.
Conclusions. We find indications that the companion C2 is massive itself, which makes it likely that its contribution to the intense UV radiation field of the Trapezium cluster is non-negligible. Furthermore, the high eccentricity of the preliminary orbit solution predicts a very small physical separation during periastron passage (![]() AU, next passage around 2007.5), suggesting strong wind-wind interaction between the two O stars.
AU, next passage around 2007.5), suggesting strong wind-wind interaction between the two O stars.
Key words:
stars: pre-main sequence -
stars: fundamental parameters -
stars: binaries: close
- techniques: interferometric
- stars: individual:
![]() Orionis C,
Orionis C,
![]() Orionis D
Orionis D
Stellar mass is the most fundamental parameter, determining, together with the chemical composition and the angular momentum, the entire evolution of a given star. Stellar evolutionary models connect these fundamental parameters with more easily accessible, but also highly uncertain observables such as the luminosity and the stellar temperature. Particularly towards the pre-main-sequence (PMS) phase and towards the extreme stellar masses (i.e. the low- and high-mass domain), the existing stellar evolutionary models are still highly uncertain and require further empirical verification through direct and unbiased mass estimates, such as those provided by the dynamical masses accessible in binary systems. Recently, several studies were able to provide dynamical masses for low-mass PMS stars (e.g. Boden et al. 2005; Tamazian et al. 2002; Schaefer et al. 2003), while direct mass measurements for young O-type stars are still lacking.
Furthermore, in contrast to the birth of low-mass stars, the formation
mechanism of high-mass stars is still poorly understood. In particular, the
remarkably high binary frequency measured for young high-mass stars might
indicate that the way high-mass stars are born differs significantly from the
mass accretion scenario via circumstellar disks, which is well-established for
low- and intermediate-mass stars. For instance, studies conducted at the
nearest high-mass star-forming region, the Orion Nebular Cluster (ONC,
at a distance of
![]() pc, Jeffries 2007), revealed 1.1 companions per
primary (for high-mass stars
pc, Jeffries 2007), revealed 1.1 companions per
primary (for high-mass stars
![]() , Preibisch et al. 1999), which is
significantly higher than the mean number of companions for intermediate
and low-mass stars.
, Preibisch et al. 1999), which is
significantly higher than the mean number of companions for intermediate
and low-mass stars.
In the very center of the ONC, four OB stars form the Orion Trapezium; three
of which (![]() Ori A, B, C) are known to be multiple (Weigelt et al. 1999; Schertl et al. 2003).
Ori A, B, C) are known to be multiple (Weigelt et al. 1999; Schertl et al. 2003).
![]() Ori D (alias HD 37023, HR 1896, Parenago 1889) has no confirmed companion,
although a preliminary analysis of the radial velocity by Vitrichenko (2002a)
suggests that it might be a spectroscopic binary with a period of
Ori D (alias HD 37023, HR 1896, Parenago 1889) has no confirmed companion,
although a preliminary analysis of the radial velocity by Vitrichenko (2002a)
suggests that it might be a spectroscopic binary with a period of ![]() or
40 days.
or
40 days.
A particularly intruiging young (<1 Myr, Hillenbrand 1997) high-mass star in
the Trapezium cluster is ![]() Ori C (alias 41 Ori C, HD 37022, HR 1895,
Parenago 1891).
Ori C (alias 41 Ori C, HD 37022, HR 1895,
Parenago 1891). ![]() Ori C is the brightest source within the ONC and also the
main source of the UV radiation ionizing the proplyds and the M42
H II region. A close (33 mas) companion with a near-infrared flux ratio of
Ori C is the brightest source within the ONC and also the
main source of the UV radiation ionizing the proplyds and the M42
H II region. A close (33 mas) companion with a near-infrared flux ratio of
![]() between the primary (
between the primary (![]() Ori C1) and the secondary (
Ori C1) and the secondary (![]() Ori C2)
was discovered in 1997 using bispectrum speckle interferometry
(Weigelt et al. 1999). Donati et al. (2002) estimated the mass of
Ori C2)
was discovered in 1997 using bispectrum speckle interferometry
(Weigelt et al. 1999). Donati et al. (2002) estimated the mass of
![]() Ori C to be
Ori C to be
![]() ,
making it the most massive star in the
cluster. The same authors give an effective temperature of
,
making it the most massive star in the
cluster. The same authors give an effective temperature of
![]() K and a stellar radius of
K and a stellar radius of
![]() .
Simón-Díaz et al. (2006) estimated the mass independently using evolutionary tracks
and by performing a quantitative analysis of
.
Simón-Díaz et al. (2006) estimated the mass independently using evolutionary tracks
and by performing a quantitative analysis of ![]() Ori C spectra and obtained
Ori C spectra and obtained
![]() and
and
![]() ,
respectively.
Long series of optical and UV spectroscopic observations revealed that the
intensity and also some line profiles vary in a strictly periodic way. With
,
respectively.
Long series of optical and UV spectroscopic observations revealed that the
intensity and also some line profiles vary in a strictly periodic way. With
![]() days, the shortest period was reported by Stahl et al. (1993).
Several authors interpret this periodicity, which in the meantime was also
detected in X-ray (Gagne et al. 1997), within an oblique magnetic rotator model,
identifying 15.422 d with the rotation period of the star. Stahl et al. (1996)
detected a steady increase in radial velocity, confirmed by Donati et al.
in 2002, which suggests a spectroscopic binary with an orbital period of at
least 8 years. Vitrichenko (2002b) searched for long-term periodicity in the radial
velocity and reported two additional periods of 66 days and 120 years, which
he interpreted as the presence of, in total, three components in the system.
days, the shortest period was reported by Stahl et al. (1993).
Several authors interpret this periodicity, which in the meantime was also
detected in X-ray (Gagne et al. 1997), within an oblique magnetic rotator model,
identifying 15.422 d with the rotation period of the star. Stahl et al. (1996)
detected a steady increase in radial velocity, confirmed by Donati et al.
in 2002, which suggests a spectroscopic binary with an orbital period of at
least 8 years. Vitrichenko (2002b) searched for long-term periodicity in the radial
velocity and reported two additional periods of 66 days and 120 years, which
he interpreted as the presence of, in total, three components in the system.
Given the unknown orbit of the speckle companion, it still must be
determined which one of these periods corresponds to the orbital motion of C2.
Since the discovery of C2 in 1997, three measurements performed with bispectrum speckle
interferometry showed that the companion indeed undertakes orbital motion
(Schertl et al. 2003), reaching the largest separation of the two components in autumn
1999 with ![]() mas. In order to follow the orbital motion, we
monitored the system using infrared and visual bispectrum speckle
interferometry and in 2005, for the first time, also using infrared
long-baseline interferometry.
mas. In order to follow the orbital motion, we
monitored the system using infrared and visual bispectrum speckle
interferometry and in 2005, for the first time, also using infrared
long-baseline interferometry.
An interesting aspect of the dynamical history of the ONC was presented
by Tan (2004). He proposed that the Becklin-Neugebauer (BN) object, which
is located 45
![]() northwest of the Trapezium stars, might be a
runaway B star ejected from the
northwest of the Trapezium stars, might be a
runaway B star ejected from the ![]() Ori C multiple system approximately
4000 yr ago. This scenario is based on proper motion measurements, which
show that BN and
Ori C multiple system approximately
4000 yr ago. This scenario is based on proper motion measurements, which
show that BN and ![]() Ori C recoil roughly in opposite directions, and by the
detection of X-ray emission potentially tracing a wind bow
shock
Ori C recoil roughly in opposite directions, and by the
detection of X-ray emission potentially tracing a wind bow
shock![]() .
Three-body interaction is a crucial part of this interpretation, and C2 is
currently the only candidate which could have been involved. Therefore, a
high-precision orbit measurement of C2 might offer the unique possibility to
recover the dynamical details of this recent stellar ejection.
However, another study (Rodríguez et al. 2005) also aimed to identify the multiple
system from which BN was ejected and identified Source I as the likely
progenitor system. Later, Gómez et al. (2005) added further evidence to this
interpretation by identifying Source n as a potential third
member of the decayed system.
.
Three-body interaction is a crucial part of this interpretation, and C2 is
currently the only candidate which could have been involved. Therefore, a
high-precision orbit measurement of C2 might offer the unique possibility to
recover the dynamical details of this recent stellar ejection.
However, another study (Rodríguez et al. 2005) also aimed to identify the multiple
system from which BN was ejected and identified Source I as the likely
progenitor system. Later, Gómez et al. (2005) added further evidence to this
interpretation by identifying Source n as a potential third
member of the decayed system.
Table 1: Observation Log.
Speckle interferometric methods are powerful techniques for overcoming the atmospheric
perturbations and for reaching the diffraction-limited resolution of ground-based
telescopes, both at near-infrared and visual wavelengths.
Since the discovery of ![]() Ori C2 in 1997, we have monitored the system
with the Big Telescope Alt-azimuthal (BTA) 6.0 m telescope of the
Special Astrophysical Observatory located on Mt. Pastukhov in Russia.
For the speckle observations at visual wavelengths, a
Ori C2 in 1997, we have monitored the system
with the Big Telescope Alt-azimuthal (BTA) 6.0 m telescope of the
Special Astrophysical Observatory located on Mt. Pastukhov in Russia.
For the speckle observations at visual wavelengths, a
![]() pixel
CCD with a multialkali S25 intensifier photocathode was used.
The near-infrared speckle observations were carried out using one
pixel
CCD with a multialkali S25 intensifier photocathode was used.
The near-infrared speckle observations were carried out using one
![]() pixel quadrant of the Rockwell HAWAII array in our speckle
camera, with pixel sizes of 13.4 mas (J-band), 20.2 mas (H-band), and
27 mas (K-band) on the sky.
pixel quadrant of the Rockwell HAWAII array in our speckle
camera, with pixel sizes of 13.4 mas (J-band), 20.2 mas (H-band), and
27 mas (K-band) on the sky.
For the speckle observations at infrared wavelengths, we recorded
interferograms of ![]() Ori C and of the nearby unresolved star
Ori C and of the nearby unresolved star ![]() Ori D in order
to compensate for the atmospheric speckle transfer function. The number of
interferograms and the detector integration times (DITs) are listed in
Table 1.
Ori D in order
to compensate for the atmospheric speckle transfer function. The number of
interferograms and the detector integration times (DITs) are listed in
Table 1.
The modulus of the Fourier transform of the object (visibility) was obtained with the speckle interferometry method (Labeyrie 1970). For image reconstruction we used the bispectrum speckle interferometry method (Weigelt 1977; Weigelt & Wirnitzer 1983; Lohmann et al. 1983; Hofmann & Weigelt 1986).
The Infrared Optical Telescope Array (IOTA) is a three-telescope, long-baseline interferometer located at the Fred Lawrence Whipple Observatory on Mount Hopkins, Arizona, operating at visual and near-infrared wavelengths (Traub et al. 2003). Its three 45 cm primary Cassegrain telescopes can be mounted on stations along an L-shaped track, reaching 15 m towards a southeastern and 35 m towards a northeastern direction. After passing a tip-tilt system, which compensates the atmospherically induced motion of the image, and path-compensating delay lines, the three beams are fed into fibers and coupled pairwise onto the IONIC3 integrated optics beam combiner (Berger et al. 2003). The interferograms are recorded by temporal modulation around zero optical path delay (OPD). During data acquisition, a fringe tracker software (Pedretti et al. 2005) continuously compensates potential OPD drifts. This allows us to measure the three interferograms nearly simultaneously within the atmospheric coherence time, preserving the valuable closure phase (CP) information.
Table 2: IOTA calibrator stars information.
For our IOTA observations, we used four different array configurations (see
Table 1), obtaining the uv-coverage shown in
Fig. 1. ![]() Ori D was observed on two different array
configurations, as shown in Fig. 2.
During each night, we systematically alternated between the target star and
calibrators in order to determine the transfer function of the instrument.
For more details about the calibrator stars and the number of recorded
Michelson interferograms, refer to Table 2.
Ori D was observed on two different array
configurations, as shown in Fig. 2.
During each night, we systematically alternated between the target star and
calibrators in order to determine the transfer function of the instrument.
For more details about the calibrator stars and the number of recorded
Michelson interferograms, refer to Table 2.
![\begin{figure}
\par\includegraphics[width=8.6cm]{6965fig1.eps} \end{figure}](/articles/aa/full/2007/17/aa6965-06/Timg42.gif) |
Figure 1:
uv-plane coverage obtained on
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm]{6965fig2.eps} \end{figure}](/articles/aa/full/2007/17/aa6965-06/Timg43.gif) |
Figure 2:
uv-plane coverage obtained on
|
| Open with DEXTER | |
In order to extract visibilities and CPs from the recorded IOTA
interferograms, we used the IDRS![]() data reduction
software. Basic principles of the algorithms implemented in this software
package were already presented in Kraus et al. (2005), although several details have
been refined to obtain optimal results for fainter sources as well, such as
those observed in this study.
data reduction
software. Basic principles of the algorithms implemented in this software
package were already presented in Kraus et al. (2005), although several details have
been refined to obtain optimal results for fainter sources as well, such as
those observed in this study.
To estimate the fringe amplitude (visibility squared, V2), we compute the continuous wavelet transform (CWT), which decomposes the signal into the OPD-scale domain, providing scale (frequency) resolution while preserving the information about the fringe OPD. The turbulent Earth atmosphere introduces fast-changing OPD variations between the combined telescopes (also known as atmospheric piston), degenerating the recorded interferograms. By measuring the extension of the fringe packet in the CWT along both the scale and the OPD axis, we identify the scans which are most affected by this effect and reject them from further processing. For the remaining scans, we apply a method similar to the procedure presented by Kervella et al. (2004). First, the fringe peak is localized in the CWT. In order to minimize noise contributions, a small window around the fringe peak position is cut out. Then we integrate along the OPD axis, yielding a power spectrum. After recentering the fringe peak position for each scan (to compensate frequency changes induced by atmospheric piston), we average the power spectra for all scans within a dataset. In the resulting averaged power spectrum, we fit and remove the background contributions and integrate over the fringe power to obtain an estimate for V2.
Another refinement in our software concerns the CP estimation. We found that the best signal-to-noise ratio (SNR) can be achieved by averaging the bispectra from all scans. The bispectrum is given by the triple product of the Fourier transform of the scans at the three baselines (Hofmann & Weigelt 1993). Then, we use the triple amplitude to select the bispectrum elements with the highest SNR and average the triple phases of these elements in the complex plane to obtain the average closure phase.
![\begin{figure}
\par\begin{tabular}{c}
\hspace*{1.5mm} $\begin{array}{ccc}
\hsp...
...degraphics[width=7.3cm]{6965f3f.ps} \end{array}$ \end{tabular}
\par\end{figure}](/articles/aa/full/2007/17/aa6965-06/Timg44.gif) |
Figure 3:
Left, Middle: bispectrum speckle J and V'-band images
reconstructed from BTA-data. Right: aperture synthesis image of
|
| Open with DEXTER | |
Interpreting optical long-baseline interferometric data often requires a priori knowledge about the expected source brightness distribution. This knowledge is used to choose an astrophysically motivated model whose parameters are fitted to the measured interferometric observables (as applied in Sect. 4).
However, the measurement of CPs allows a much more intuitive approach; namely, the direct reconstruction of an aperture synthesis image. Due to the rather small number of telescopes combined in the current generation of optical interferometric arrays, direct image reconstruction is limited to objects with a rather simple source geometry; in particular, multiple systems (for images reconstructed from IOTA data, see Monnier et al. 2004; Kraus et al. 2005).
Using our software based on the Building Block Mapping
algorithm (Hofmann & Weigelt 1993), we reconstructed an aperture synthesis image of
the ![]() Ori C system from the data collected during our IOTA run.
Starting from an initial single delta-function, this algorithm builds up the
image iteratively by adding components in order to minimize the least-square
distance between the measured bispectrum and the bispectrum of the
reconstructed image.
Ori C system from the data collected during our IOTA run.
Starting from an initial single delta-function, this algorithm builds up the
image iteratively by adding components in order to minimize the least-square
distance between the measured bispectrum and the bispectrum of the
reconstructed image.
The resulting image is shown in Fig. 3 and provides a model-independent representation of our data. By combining the data collected during six nights, we make the reasonable assumption that the orbital motion over this interval is negligible.
The clean beam, which we used for convolution to obtain the final image, is rather elliptical (see inset in Fig. 3), representing the asymmetries in the uv-coverage.
![\begin{figure}
\par\includegraphics[width=16.6cm]{6965fig4.eps} \end{figure}](/articles/aa/full/2007/17/aa6965-06/Timg45.gif) |
Figure 4:
Visibilities and closure phases derived from the recorded IOTA
interferograms for |
| Open with DEXTER | |
Table 3:
Relative astrometry and photometry for the ![]() Ori C binary system.
Ori C binary system.
Although the aperture synthesis image presented in the last section might also
be used to extract parameters like binary separation, orientation, and
intensity ratio of the components (
![]() ,
,
![]() mas,
mas,
![]()
![]() ), more precise values, including error estimates, can be obtained by
fitting the measured visibilities and CPs to an analytical binary model.
), more precise values, including error estimates, can be obtained by
fitting the measured visibilities and CPs to an analytical binary model.
The applied model is based on Eqs. (7)-(12) presented in Kraus et al. (2005) and uses the least-square Levenberg-Marquardt method to determine the best-fit binary separation vector and intensity ratio. In order to avoid potential local minima, we vary the initial values for the least-square fit on a grid, searching for the global minimum.
Since the apparent stellar diameter of ![]() Ori C is expected to be
only
Ori C is expected to be
only ![]() mas at the distance of Orion, for our fits we assume that both
stellar components appear practically unresolved to the IOTA baselines.
Furthermore, we assume that the relative position of the components did not
change significantly over the 6 nights of observation.
mas at the distance of Orion, for our fits we assume that both
stellar components appear practically unresolved to the IOTA baselines.
Furthermore, we assume that the relative position of the components did not
change significantly over the 6 nights of observation.
Figure 4 shows the measured IOTA visibilities and CPs and
the observables corresponding to our best-fit binary model
(
![]() ,
,
![]() ).
The separation
).
The separation ![]() ,
PA
,
PA ![]() ,
and intensity ratio of this binary model
are given in Table 3, together with the positions derived from
the speckle observations.
To illustrate more clearly that the measured IOTA visibilities resemble a
binary signature, in Fig. 5 we show a projection of the
sampled two-dimensional Fourier plane along the binary vector, revealing the
cosine modulation corresponding to the Fourier transform of a binary
brightness distribution.
,
and intensity ratio of this binary model
are given in Table 3, together with the positions derived from
the speckle observations.
To illustrate more clearly that the measured IOTA visibilities resemble a
binary signature, in Fig. 5 we show a projection of the
sampled two-dimensional Fourier plane along the binary vector, revealing the
cosine modulation corresponding to the Fourier transform of a binary
brightness distribution.
![\begin{figure}
\par\includegraphics[width=8.5cm]{6965fig5.eps} \end{figure}](/articles/aa/full/2007/17/aa6965-06/Timg86.gif) |
Figure 5:
Projection of the sampled Fourier plane along the fitted binary PA
of
|
| Open with DEXTER | |
For the speckle data (providing a complete Fourier sampling up to the spatial frequency corresponding to the diameter of the telescope primary mirror), we determine the binary parameters by fitting a two-dimensional cosine function directly to the 2D speckle interferogram power spectrum.
![\begin{figure}
\par\includegraphics[width=8.5cm]{6965fig6.eps} \end{figure}](/articles/aa/full/2007/17/aa6965-06/Timg87.gif) |
Figure 6:
Visibilities and closure phases derived from the recorded IOTA
interferograms for |
| Open with DEXTER | |
Besides the main target of our observational programme, ![]() Ori C, during the two
nights with the best seeing conditions, we also recorded four datasets on
Ori C, during the two
nights with the best seeing conditions, we also recorded four datasets on
![]() Ori D. Despite lower flux (
Ori D. Despite lower flux (![]() Ori D: H=5.9,
Ori D: H=5.9, ![]() Ori C: H=4.6), the
quality of the derived visibilities and CPs seems reliable,
although slightly larger errors must be assumed.
Ori C: H=4.6), the
quality of the derived visibilities and CPs seems reliable,
although slightly larger errors must be assumed. ![]() Ori D appears resolved in our
measurements with a significant non-zero CPs signal (
Ori D appears resolved in our
measurements with a significant non-zero CPs signal (![]()
![]() )
on the
A35-B15-C0 baseline. This CP indicates deviations from point-symmetry, as
expected for a binary star.
We applied the binary model fit described in Sect. 4.1 and
found the binary system with an intensity ratio of 0.14,
)
on the
A35-B15-C0 baseline. This CP indicates deviations from point-symmetry, as
expected for a binary star.
We applied the binary model fit described in Sect. 4.1 and
found the binary system with an intensity ratio of 0.14,
![]() mas, and
mas, and ![]()
![]() (Fig. 6) to be the
best-fit model (
(Fig. 6) to be the
best-fit model (
![]() ).
).
However, considering the uv-coverage of the existing dataset, this solution is likely not unique, and it can not be ruled out that other geometries, such as for inclined circumstellar disk geometries with pronounced emission from the rim at the dust sublimation radius (see e.g. Monnier et al. 2006), might also produce the asymmetry required to fit the data.
![\begin{figure}
\par\includegraphics[width=8.5cm]{6965fig7.eps} \end{figure}](/articles/aa/full/2007/17/aa6965-06/Timg92.gif) |
Figure 7:
Top: two best-fit apparent orbits of the |
| Open with DEXTER | |
Table 4:
Preliminary orbital solutions, dynamical parallaxes, and system
masses for ![]() Ori C.
Ori C.
Our multi-epoch position measurements of the ![]() Ori C system can be used to
derive a preliminary dynamical orbit. To find orbital solutions, we used the
method described by Docobo (1985). This method generates a class of Keplerian
orbits passing through three base points. From this class of possible
solutions, those orbits are selected which best agree with the measured
positions, where we use the error bars of the individual measurements as
weight.
In order to avoid over-weighting the orbit points which were
sampled with several measurements at similar epochs (two measurements in
1999.7-1999.8 and three measurements in 2003.8-2003.9), we treated each of
these clusters as single measurements.
Ori C system can be used to
derive a preliminary dynamical orbit. To find orbital solutions, we used the
method described by Docobo (1985). This method generates a class of Keplerian
orbits passing through three base points. From this class of possible
solutions, those orbits are selected which best agree with the measured
positions, where we use the error bars of the individual measurements as
weight.
In order to avoid over-weighting the orbit points which were
sampled with several measurements at similar epochs (two measurements in
1999.7-1999.8 and three measurements in 2003.8-2003.9), we treated each of
these clusters as single measurements.
In Table 4 we give the orbital elements corresponding
to the two best orbital solutions found.
As the
![]() values of the two presented orbits are
practically identical, the existing astrometric data does not allow us
to distinguish between these solutions. These orbits and the corresponding
O-C vectors are shown in Fig. 7 (see Table 3
for a list of the O-C values). As the ephemerids in
Table 5 and also the position predictions (dots) in
Fig. 7 show, future high-accuracy long-baseline
interferometric measurements are needed to distinguish between these
orbital solutions.
values of the two presented orbits are
practically identical, the existing astrometric data does not allow us
to distinguish between these solutions. These orbits and the corresponding
O-C vectors are shown in Fig. 7 (see Table 3
for a list of the O-C values). As the ephemerids in
Table 5 and also the position predictions (dots) in
Fig. 7 show, future high-accuracy long-baseline
interferometric measurements are needed to distinguish between these
orbital solutions.
Potentially, additional constraints on the ![]() Ori C binary orbit could be
provided by radial velocity measurements, such as those published by
Vitrichenko (2002b) and in the references therein.
However, the complexity of the
Ori C binary orbit could be
provided by radial velocity measurements, such as those published by
Vitrichenko (2002b) and in the references therein.
However, the complexity of the ![]() Ori C spectrum - including the line
variability corresponding to the magnetically confined wind-shock region
expected towards
Ori C spectrum - including the line
variability corresponding to the magnetically confined wind-shock region
expected towards ![]() Ori C - makes both the measurement and the interpretation
of radial velocities for
Ori C - makes both the measurement and the interpretation
of radial velocities for ![]() Ori C very challenging. Since it is
unclear whether these velocities really correspond to the orbital
motion of the binary system or perhaps to variations in the stellar wind from
Ori C very challenging. Since it is
unclear whether these velocities really correspond to the orbital
motion of the binary system or perhaps to variations in the stellar wind from
![]() Ori C, we did not include these velocity measurements as a tough constraint in
the final orbital fit, but show them together with the radial velocities
corresponding to our best-fit orbit solutions in Fig. 7.
Ori C, we did not include these velocity measurements as a tough constraint in
the final orbital fit, but show them together with the radial velocities
corresponding to our best-fit orbit solutions in Fig. 7.
Table 5:
Ephemerides for the ![]() Ori C orbital solutions presented in
Table 4.
Ori C orbital solutions presented in
Table 4.
Both orbital solutions suggest that during periastron passage, the
physical separation between C1 and C2 decreases to ![]() AU,
corresponding to just
AU,
corresponding to just ![]() stellar radii.
Besides the strong dynamical friction at work during such a close passage,
strong wind-wind interaction can also be expected.
stellar radii.
Besides the strong dynamical friction at work during such a close passage,
strong wind-wind interaction can also be expected.
It is worth mentioning that besides the presented best-fit orbital solutions, a
large number of solutions with longer orbital periods exist, which are also
fairly consistent with the astrometric measurements. However, since these orbits
have slightly higher
![]() values than the solutions presented
above and also correspond to physically unreasonable masses (
values than the solutions presented
above and also correspond to physically unreasonable masses (
![]() or
or
![]() ,
assuming d=440 pc),
we rejected these formal solutions.
,
assuming d=440 pc),
we rejected these formal solutions.
Kepler's third law relates the major axis a and the orbital period P with
the product of the system mass and the cube of the parallax;
i.e.
![]() (where a and
(where a and ![]() are
given in mas, P in years, and M in solar masses).
are
given in mas, P in years, and M in solar masses).
In order to separate the system mass and the parallax
in absence of spectroscopic orbital elements, the method by Baize & Romani (1946) can be
applied. This method assumes that the component masses follow a
mass-luminosity relation (MLR), which, together with a bolometric
correction and extinction-corrected magnitudes, allows one to solve for the
system mass
![]() and the dynamical parallax
and the dynamical parallax
![]() .
When using the MLR by Demircan & Kahraman (1991), the bolometric
correction for O5.5 and O9.5 stars by Martins et al. (2005), and the extinction
corrected magnitudes given in Table 6, we derive the dynamical
masses and parallaxes given in Table 4.
When comparing the distances corresponding to the
dynamical parallaxes derived for Orbit #1 (
.
When using the MLR by Demircan & Kahraman (1991), the bolometric
correction for O5.5 and O9.5 stars by Martins et al. (2005), and the extinction
corrected magnitudes given in Table 6, we derive the dynamical
masses and parallaxes given in Table 4.
When comparing the distances corresponding to the
dynamical parallaxes derived for Orbit #1 (
![]() pc) and Orbit #2 (
pc) and Orbit #2 (
![]() pc) with distance estimates from
the literature (e.g.
pc) with distance estimates from
the literature (e.g.
![]() pc from Jeffries 2007; see also
references herein), orbit solution #1 appears much more likely.
The dynamical system mass corresponding to Orbit #1 is
pc from Jeffries 2007; see also
references herein), orbit solution #1 appears much more likely.
The dynamical system mass corresponding to Orbit #1 is
![]() ,
which must be scaled by a factor
,
which must be scaled by a factor
![]() when
distances other than
when
distances other than
![]() pc are assumed.
pc are assumed.
Table 6:
Derived dereddened magnitudes and colors for the ![]() Ori C
components. For the photometry of the total system, we used data
from Hillenbrand et al. (1998, J=4.63, H=4.48, K=4.41) and Hillenbrand (1997,
V=5.12). An extinction of AV=1.74 (Hillenbrand 1997) was
assumed (using the reddening law by Mathis 1990 and, similar to
Mathis & Wallenhorst 1981, a high RV=5.0).
Ori C
components. For the photometry of the total system, we used data
from Hillenbrand et al. (1998, J=4.63, H=4.48, K=4.41) and Hillenbrand (1997,
V=5.12). An extinction of AV=1.74 (Hillenbrand 1997) was
assumed (using the reddening law by Mathis 1990 and, similar to
Mathis & Wallenhorst 1981, a high RV=5.0).
Several studies have already reported the detection of periodicity in the
amplitude, width, or velocity of spectral lines around ![]() Ori C. This makes
it interesting to compare whether one of those periods can be attributed to
the presence of companion C2:
Ori C. This makes
it interesting to compare whether one of those periods can be attributed to
the presence of companion C2:
Most studies which can be found in literature
attributed the whole stellar flux of ![]() Ori C to a single component and
determined a wide range of spectral types including O5.5 (Gagné et al. 2005), O6
(Simón-Díaz et al. 2006; Levato & Abt 1976), O7 (van Altena et al. 1988), to O9 (Trumpler 1931). In order to
resolve this uncertainty, it might be of importance to take the
presence of
Ori C to a single component and
determined a wide range of spectral types including O5.5 (Gagné et al. 2005), O6
(Simón-Díaz et al. 2006; Levato & Abt 1976), O7 (van Altena et al. 1988), to O9 (Trumpler 1931). In order to
resolve this uncertainty, it might be of importance to take the
presence of ![]() Ori C2 into account.
Besides the constraints on the dynamical masses derived in
Sect. 5.1, additional information about the spectral
types of
Ori C2 into account.
Besides the constraints on the dynamical masses derived in
Sect. 5.1, additional information about the spectral
types of ![]() Ori C1 and C2 can be derived from the flux ratio of the components
in the recorded bands.
Ori C1 and C2 can be derived from the flux ratio of the components
in the recorded bands.
In contrast to our earlier studies (Weigelt et al. 1999; Schertl et al. 2003), we can now
also include the V-band flux ratio measurement to constrain the spectral
types of the individual components. The V-band is of particular interest,
as a relative increase of the flux ratio
![]() from the visual to
the near-infrared would indicate the presence of circumstellar material,
either as near-infrared excess emission or intrinsic extinction towards C2
(assuming similar effective temperatures for both components).
Our speckle measurements indicate that
from the visual to
the near-infrared would indicate the presence of circumstellar material,
either as near-infrared excess emission or intrinsic extinction towards C2
(assuming similar effective temperatures for both components).
Our speckle measurements indicate that
![]() stays rather constant
from the visual to the near-infrared. Therefore, in the following we assume
that the major contribution of
stays rather constant
from the visual to the near-infrared. Therefore, in the following we assume
that the major contribution of ![]() Ori C2 to the measured flux is photospheric.
Ori C2 to the measured flux is photospheric.
In Fig. 8 we show the measured
![]() as a
function of wavelength and compare it to model curves corresponding to
various spectral-type combinations for C1 and C2. To compute the model flux
ratios, we simulate the stellar photospheric emission as black-body emission
as a
function of wavelength and compare it to model curves corresponding to
various spectral-type combinations for C1 and C2. To compute the model flux
ratios, we simulate the stellar photospheric emission as black-body emission
![]() with effective temperatures
with effective temperatures
![]() and stellar radii R,
as predicted by stellar evolutionary models (Martins et al. 2005; Claret 2004):
and stellar radii R,
as predicted by stellar evolutionary models (Martins et al. 2005; Claret 2004):
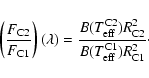 |
(1) |
![\begin{figure}
\par\includegraphics[width=8.5cm]{6965fig8.eps} \end{figure}](/articles/aa/full/2007/17/aa6965-06/Timg130.gif) |
Figure 8:
Measured intensity ratio of the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{6965fig9.eps} \end{figure}](/articles/aa/full/2007/17/aa6965-06/Timg133.gif) |
Figure 9:
HR-diagram with PMS evolutionary tracks (Z=0.02; thin solid lines
with the corresponding masses labeled aside). For masses
|
| Open with DEXTER | |
Using a value for AV from literature, the flux ratios can also be used to
estimate the photometry of the individual components
(Table 6). Then, the spectral type of C1 and C2 can be
determined by comparing the location of the stars in the HR-diagram with
stellar evolution models. For this, we adopt the procedure from Schertl et al. (2003)
and convert the derived photometry into locations in the HR-diagram using the
colors and bolometric
corrections from Kenyon & Hartmann (1995, and references therein) and Martins & Plez (2006). Assuming coevality for
both stars, the spectral type of the individual components can be constrained
by finding the location where the curves for the various spectral bands and
the isochrone intersect.
As can be seen in Fig. 9, the allowed locations for C1 intersect
the Zero-Age Main Sequence![]() (ZAMS)
around
(ZAMS)
around
![]() K,
K,
![]() (corresponding to O5) and
around
(corresponding to O5) and
around
![]() K,
K,
![]() (corresponding to O9) for C2.
(corresponding to O9) for C2.
We conclude that the spectral type combination, which simultaneously provides
good agreement to the measured flux ratios, the HR-diagram, and the
dynamical masses derived in Sect. 5.1, is given by the
following stellar parameters (using the evolutionary models from Martins et al. 2005):
Although the ![]() Ori D binary parameters presented in
Sect. 4.2 must be considered preliminary, it might be
interesting to determine the spectral type of the putative components.
We apply the procedure discussed in Sect. 5.4 to
determine the photometry of the components from the measured intensity ratio
(photometry for the unresolved system from Hillenbrand et al. 1998: H=5.84) and
derive
HD1=5.98 and
HD2=8.12, respectively.
Ori D binary parameters presented in
Sect. 4.2 must be considered preliminary, it might be
interesting to determine the spectral type of the putative components.
We apply the procedure discussed in Sect. 5.4 to
determine the photometry of the components from the measured intensity ratio
(photometry for the unresolved system from Hillenbrand et al. 1998: H=5.84) and
derive
HD1=5.98 and
HD2=8.12, respectively.
Searching again for the intersection between the allowed locations in the
HR-diagram with the isochrones applicable to the ONC (Fig. 9),
the best agreement for D1 can be found with
![]() K,
K,
![]() (corresponding to O9.5).
Accordingly, D2 might be either a B4 or B5 type star which has just reached
the ZAMS (
(corresponding to O9.5).
Accordingly, D2 might be either a B4 or B5 type star which has just reached
the ZAMS (
![]() K,
K,
![]() )
or a pre-main-sequence K0 type star (
)
or a pre-main-sequence K0 type star (
![]() K,
K,
![]() ).
).
Vitrichenko (2002a) examined radial velocity variations of ![]() Ori D and presented
preliminary spectroscopic orbital elements for a companion with a 20.2 d
period (or twice that period, P=40.5 d).
Assuming
Ori D and presented
preliminary spectroscopic orbital elements for a companion with a 20.2 d
period (or twice that period, P=40.5 d).
Assuming
![]() as the system mass, these periods correspond to a major axis
of 0.05 or 0.08 AU (
as the system mass, these periods correspond to a major axis
of 0.05 or 0.08 AU (![]() or 0.2 mas). Since this is far below the
18 mas suggested by our binary model fit, we do not associate our potential
companion with the proposed spectroscopic companion.
or 0.2 mas). Since this is far below the
18 mas suggested by our binary model fit, we do not associate our potential
companion with the proposed spectroscopic companion.
The multiplicity rate in a young stellar population such as the Trapezium
cluster is an important quantity which might allow us to draw conclusions
not only about the dynamical history of the ONC, but also
about the mechanisms controlling the star formation process.
The detection of a new companion around ![]() Ori D further increases
the multiplicity rate for high-mass stars in the ONC. For instance,
considering the sample of 13 Orion O- and B-type stars studied by
Preibisch et al. (1999) now yields 10 visual and 5 spectroscopic detected companions
(including one quintuple system, namely
Ori D further increases
the multiplicity rate for high-mass stars in the ONC. For instance,
considering the sample of 13 Orion O- and B-type stars studied by
Preibisch et al. (1999) now yields 10 visual and 5 spectroscopic detected companions
(including one quintuple system, namely ![]() Ori B). This corresponds to an
average observed companion star frequency (CSF) of 1.15 companions per
primary. Despite the fact that this value only represents a strict lower
limit due to observational incompleteness, it is already higher than
the incompleteness-corrected CSF determined by Duquennoy & Mayor (1991) for a
distance-limited sample of solar-type field stars (0.5 companions per
primary). Köhler et al. (2006) have reported that the CSF for low- and
intermediate-mass stars in the ONC is about a factor of 2.3 lower than the
CSF in the Duquennoy & Mayor sample, making the differences in the CSF
between the low-, intermediate-, and high-mass star population in the ONC
highly significant. Several studies (e.g. Bonnell & Bate 2005; Bally & Zinnecker 2005; Preibisch et al. 1999) have already interpreted this as evidence that different formation mechanisms
(e.g. stellar coalescence vs. accretion) might be at work in different
mass regimes.
Ori B). This corresponds to an
average observed companion star frequency (CSF) of 1.15 companions per
primary. Despite the fact that this value only represents a strict lower
limit due to observational incompleteness, it is already higher than
the incompleteness-corrected CSF determined by Duquennoy & Mayor (1991) for a
distance-limited sample of solar-type field stars (0.5 companions per
primary). Köhler et al. (2006) have reported that the CSF for low- and
intermediate-mass stars in the ONC is about a factor of 2.3 lower than the
CSF in the Duquennoy & Mayor sample, making the differences in the CSF
between the low-, intermediate-, and high-mass star population in the ONC
highly significant. Several studies (e.g. Bonnell & Bate 2005; Bally & Zinnecker 2005; Preibisch et al. 1999) have already interpreted this as evidence that different formation mechanisms
(e.g. stellar coalescence vs. accretion) might be at work in different
mass regimes.
We have presented new bispectrum speckle interferometric and infrared
long-baseline interferometric observations of the Orion Trapezium stars
![]() Ori C and D. This data was used to reconstruct diffraction-limited NIR and
visual speckle images of the
Ori C and D. This data was used to reconstruct diffraction-limited NIR and
visual speckle images of the ![]() Ori C binary system and, to our knowledge, the
first model-independent, long-baseline aperture-synthesis image of a young star
at infrared wavelengths.
Ori C binary system and, to our knowledge, the
first model-independent, long-baseline aperture-synthesis image of a young star
at infrared wavelengths.
For ![]() Ori D, we find some indications that the system was resolved by the
IOTA interferometer. Although the non-zero closure phase signal suggests
asymmetries in the brightness distribution (maybe indicative of a close
companion star), further observations are required to confirm this finding.
Ori D, we find some indications that the system was resolved by the
IOTA interferometer. Although the non-zero closure phase signal suggests
asymmetries in the brightness distribution (maybe indicative of a close
companion star), further observations are required to confirm this finding.
From our multi-epoch observations on ![]() Ori C (covering the interval 1997.8 to
2005.8), we derived the relative position of the companions using
model-fitting techniques, clearly tracing orbital motion. We presented two
preliminary orbital solutions, of which one can be favoured due to
theoretical arguments.
This solution implies a period of 10.98 yrs, a semi-major axis of 41.3 mas,
a total system mass of
Ori C (covering the interval 1997.8 to
2005.8), we derived the relative position of the companions using
model-fitting techniques, clearly tracing orbital motion. We presented two
preliminary orbital solutions, of which one can be favoured due to
theoretical arguments.
This solution implies a period of 10.98 yrs, a semi-major axis of 41.3 mas,
a total system mass of
![]() ,
and a distance of 434 pc. Furthermore,
we find strong indications that
,
and a distance of 434 pc. Furthermore,
we find strong indications that ![]() Ori C2 will undergo periastron passage in
mid 2007. As the binary separation at periastron is expected to be
Ori C2 will undergo periastron passage in
mid 2007. As the binary separation at periastron is expected to be
![]() mas, further long-baseline interferometric observations on
mas, further long-baseline interferometric observations on ![]() Ori C are
urgently needed to refine the orbital elements, the stellar masses, and
orbital parallaxes. Through comparison with stellar evolutionary
models and modeling of the measured intensity ratio, we find evidence that the
companion
Ori C are
urgently needed to refine the orbital elements, the stellar masses, and
orbital parallaxes. Through comparison with stellar evolutionary
models and modeling of the measured intensity ratio, we find evidence that the
companion ![]() Ori C2 is more massive (
Ori C2 is more massive (
![]() )
than previously thought; likely of late O (O9/9.5) or early B-type
(B0). The contribution of the companion to the total flux of
)
than previously thought; likely of late O (O9/9.5) or early B-type
(B0). The contribution of the companion to the total flux of ![]() Ori C and the
interaction between both stars
might be of special importance for a deeper understanding of this intriguing
object.
Therefore, we strongly encourage observers to acquire high dispersion
spectra of the system in order to trace the expected radial velocity
variations and the wind-wind interaction of the system.
Ori C and the
interaction between both stars
might be of special importance for a deeper understanding of this intriguing
object.
Therefore, we strongly encourage observers to acquire high dispersion
spectra of the system in order to trace the expected radial velocity
variations and the wind-wind interaction of the system.
Acknowledgements
We appreciate support by the IOTA technical staff, especially M. Lacasse and P. Schuller. We would like to thank the anonymous referee for helpful comments which improved the paper. SK was supported for this research through a fellowship from the International Max Planck Research School (IMPRS) for Radio and Infrared Astronomy at the University of Bonn.