A&A 466, 413-420 (2007)
DOI: 10.1051/0004-6361:20066899
Closed-form expressions for particle relative velocities induced by turbulence
(Research Note)
C. W. Ormel1
-
J. N. Cuzzi2
1 - Kapteyn Astronomical Institute, University of Groningen, PO box 800, 9700 AV Groningen, The Netherlands
2 -
Ames Research Center, NASA, Mail Stop 245-3, Moffett Field, CA 94035, USA
Received 8 December 2006 / Accepted 1 February 2007
Abstract
In this note we present complete, closed-form expressions for random relative velocities between colliding particles of arbitrary size in nebula turbulence. These results are exact for very small particles (those with stopping times much shorter than the large eddy overturn time) and are also surprisingly accurate in complete generality (that is, also apply for particles with stopping times comparable to, or much longer than, the large eddy overturn time). We note that some previous studies may have adopted previous simple expressions, which we find to be in error regarding the size dependence in the large particle regime.
Key words: turbulence - dust, extinction - planetary systems: protoplanetary disks
Gas in astrophysical environments is often in a turbulent state of motion,
constantly affected by temporally and spatially varying accelerations from
eddies having a variety of scales. A particle, due to its inertia, does not
instantaneously follow the gas motions but requires a certain time in order to
align with the gas motion. The particle's interaction with the gas is captured in the definition of the stopping time of the particle (sometimes also referred to as friction time),
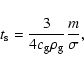 |
(1) |
where 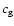 and
and
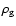 are, respectively, the sound speed and the volume mass density of the gas, and m and
are, respectively, the sound speed and the volume mass density of the gas, and m and 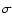 the mass and projected surface area of the particle. Due to this inertial lag, a particle develops a relative
velocity with respect to the gas. In addition, these lags also cause particles to acquire relative velocities among themselves.
the mass and projected surface area of the particle. Due to this inertial lag, a particle develops a relative
velocity with respect to the gas. In addition, these lags also cause particles to acquire relative velocities among themselves.
While the general problem of calculating these relative velocities has received
considerable attention in the basic fluid dynamics community (see Cuzzi & Hogan 2003, for references; henceforth CH03), the formalism most frequently used in the astrophysics community
was developed by Völk et al. (1980) and Markiewicz et al. (1991, henceforth MMV). In these works the final results are given in terms of integrals that were not solved analytically. Some workers have used simple fits to these numerical results in their models of dust coagulation; however, simple closed-form expressions for
particle-particle relative velocities would help streamline these models (e.g. Ormel et al. 2007; Nomura & Nakagawa 2006; Dullemond & Dominik 2005; Suttner & Yorke 2001).
Recently, CH03 obtained closed-form expressions from
the MMV model for particle velocities in inertial space 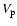 ,
for particle-gas relative velocities
,
for particle-gas relative velocities
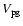 ,
and for relative velocities between two identical particles
,
and for relative velocities between two identical particles
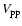 ,
but did not extend their results to the general case of two particles of different stopping times. Moreover,
CH03 stressed the validity of their analytical results for particles with stopping times much shorter than the large eddy turnover time. In this note we generalize the
approach and results of CH03 to obtain closed-form
expressions for relative velocities between particles of arbitrary, and unequal, size.
In Sect. 2 we define important quantities and review previous work. In
Sect. 3 we
present two independent approaches for obtaining the desired closed-form solutions.
In Sect. 4 we give our conclusions and a summary.
,
but did not extend their results to the general case of two particles of different stopping times. Moreover,
CH03 stressed the validity of their analytical results for particles with stopping times much shorter than the large eddy turnover time. In this note we generalize the
approach and results of CH03 to obtain closed-form
expressions for relative velocities between particles of arbitrary, and unequal, size.
In Sect. 2 we define important quantities and review previous work. In
Sect. 3 we
present two independent approaches for obtaining the desired closed-form solutions.
In Sect. 4 we give our conclusions and a summary.
2 Definitions and previous work
Nebula gas turbulence is generally described as being composed of eddies having a
range of spatial scales 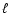 and spatial frequencies
and spatial frequencies
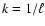 ,
with an energy
spectrum
,
with an energy
spectrum
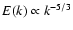 and total energy
and total energy
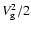 per unit mass providing
the normalization condition
per unit mass providing
the normalization condition
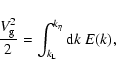 |
(2) |
from which
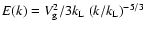 .
The largest, or integral scale, eddies have spatial scale
.
The largest, or integral scale, eddies have spatial scale
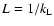 ,
and the smallest, or
Kolmogorov scale, eddies have spatial scale
,
and the smallest, or
Kolmogorov scale, eddies have spatial scale
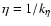 .
The form of E(k)
given above is the inertial range expression most often assumed, with E(k)=0 for
.
The form of E(k)
given above is the inertial range expression most often assumed, with E(k)=0 for
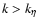 or
or
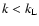 .
Völk et al. (1980) used a spectrum
P(k)=2 E(k)
and stipulated no smallest scale
.
Völk et al. (1980) used a spectrum
P(k)=2 E(k)
and stipulated no smallest scale 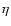 for the turbulence, but Weidenschilling (1984)
and MMV noted that a finite value for
for the turbulence, but Weidenschilling (1984)
and MMV noted that a finite value for 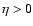 had profound effects on the
particle velocities, especially the relative velocities
had profound effects on the
particle velocities, especially the relative velocities
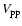 for small particles. Each eddy
wavenumber k has a characteristic velocity
for small particles. Each eddy
wavenumber k has a characteristic velocity
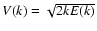 and overturn time
and overturn time
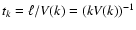 .
Our standard definition of the particle Stokes number is
.
Our standard definition of the particle Stokes number is
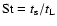 ,
where
,
where 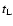 is the overturn time of the largest eddy, generally
taken to be the local orbit period. The local turbulent intensity is described by its Reynolds number, Re, defined as the ratio between the turbulent and the molecular kinematic viscosities,
is the overturn time of the largest eddy, generally
taken to be the local orbit period. The local turbulent intensity is described by its Reynolds number, Re, defined as the ratio between the turbulent and the molecular kinematic viscosities,
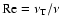 .
The values for
.
The values for 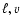 and t at the integral scale then follow from Re, e.g.,
and t at the integral scale then follow from Re, e.g.,
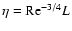 and
and
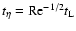 .
These expressions bring Re into the final expressions for particle velocities as a limit on certain integrals (cf.
CH03 for more detail). In the notation of astrophysical "
.
These expressions bring Re into the final expressions for particle velocities as a limit on certain integrals (cf.
CH03 for more detail). In the notation of astrophysical "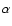 -models'',
-models'',
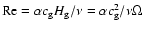 where
where 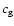 ,
,
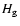 ,
and
,
and 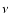 are the sound speed, vertical scale height, and kinematic viscosity of the nebula gas and
are the sound speed, vertical scale height, and kinematic viscosity of the nebula gas and 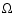 is the orbital frequency.
is the orbital frequency.
Völk et al. (1980) introduced the concept of "eddy
classes''. Class I eddies vary slowly enough that a particle, upon entering a
class I eddy, will forget its initial motion and align itself to the gas
motions of the eddy before the eddy decays or the particle leaves the eddy.
Class II eddies, on the other hand, have fluctuation times shorter than the
particle's stopping time 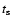 ,
and fluctuate too rapidly to provide more than
a small perturbation on the
particle. The timescale on which an eddy decays is
given by tk, while the
eddy-crossing timescale is
,
and fluctuate too rapidly to provide more than
a small perturbation on the
particle. The timescale on which an eddy decays is
given by tk, while the
eddy-crossing timescale is
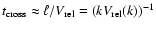 ,
with
,
with
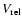 the relative velocity between
a grain and an eddy. For an eddy
to be of class I both tk and
the relative velocity between
a grain and an eddy. For an eddy
to be of class I both tk and
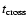 must be larger than the
particle's stopping time. The boundary between these classes occurs at k=k* (or at
tk = t*) which can be defined as
(Völk et al. 1980, MMV):
must be larger than the
particle's stopping time. The boundary between these classes occurs at k=k* (or at
tk = t*) which can be defined as
(Völk et al. 1980, MMV):
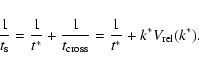 |
(3) |
It is important to realize that k* (or t*) is a function of stopping time 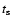 ,
that is, the boundary separating the two classes is different for each particle.
The different treatment for the two eddy classes k<k* and k>k* forms the
core of the derivation of the turbulence-induced particle velocities.
,
that is, the boundary separating the two classes is different for each particle.
The different treatment for the two eddy classes k<k* and k>k* forms the
core of the derivation of the turbulence-induced particle velocities.
All turbulent velocities in this note are statistical, root-mean-square, averaged quantities. The average inertial space particle velocity 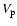 is given by
Eq. (6) of MMV.
is given by
Eq. (6) of MMV.
![$\displaystyle
V_{\rm p}^2 = \int_{k_{\rm L}}^{{\rm max}(k^*,k_{\rm L})} {\rm ...
..._{\eta}} {\rm d}k\ 2E(k) \left( 1-K \right)
\left[ g(\chi) + K h(\chi) \right],$](/articles/aa/full/2007/17/aa6899-06/img57.gif) |
|
|
(4) |
in which
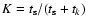 .
The K2 term in the first integral results from the more recently preferred "n=1'' gas velocity autocorrelation function (MMV and CH03). The functions
.
The K2 term in the first integral results from the more recently preferred "n=1'' gas velocity autocorrelation function (MMV and CH03). The functions
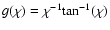 and
and
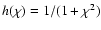 with
with
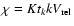 were first obtained by Völk et al. (1980).
were first obtained by Völk et al. (1980).
CH03 noted that, for very small particles with
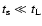 or
or
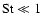 ,
the second integral becomes negligible, leaving only the first integral which is analytically solvable and for which the upper limit can be extended to
,
the second integral becomes negligible, leaving only the first integral which is analytically solvable and for which the upper limit can be extended to 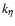 with negligible error.
Here, to generalize the approach of CH03 to particles of arbitrary size, we approximate
with negligible error.
Here, to generalize the approach of CH03 to particles of arbitrary size, we approximate
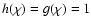 for all particle sizes (see CH03 Sect. 2.2.3 for supporting logic). Numerical calculations of
for all particle sizes (see CH03 Sect. 2.2.3 for supporting logic). Numerical calculations of 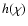 and
and 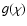 validate this approximation to order unity (see Appendix A), and we gain further confidence in it from a posteriori comparison with exact numerical model results. The general expression for
validate this approximation to order unity (see Appendix A), and we gain further confidence in it from a posteriori comparison with exact numerical model results. The general expression for
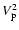 is then the same as in the
is then the same as in the
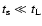 regime, and the same analytical result is obtained,
i.e. CH03,
regime, and the same analytical result is obtained,
i.e. CH03,
CH03 did not give this explicit result for 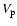 ,
but merely noted that it was
straightforward to derive it from their Eq. (19) for
,
but merely noted that it was
straightforward to derive it from their Eq. (19) for
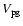 and the general
relationship
and the general
relationship
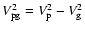 ;
however we will use it explicitly here.
;
however we will use it explicitly here.
Comparison of the predictions of this simple expression with detailed numerical
results (MMV, CH03) show that it is indeed a good approximation for arbitrary 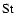 .
A more accurate approximation to Eq. (4), in which the g and h functions are approximated as power-laws in k*/k, is outlined in Appendix A. Unless
.
A more accurate approximation to Eq. (4), in which the g and h functions are approximated as power-laws in k*/k, is outlined in Appendix A. Unless
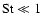 ,
we can neglect
the Reynolds number term in Eq. (6) and obtain
,
we can neglect
the Reynolds number term in Eq. (6) and obtain
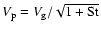 ,
a well known result (Völk et al. 1980; Cuzzi et al. 1993; Schräpler & Henning 2004) which describes the diffusivity of large particles in turbulence.
,
a well known result (Völk et al. 1980; Cuzzi et al. 1993; Schräpler & Henning 2004) which describes the diffusivity of large particles in turbulence.
3 Results
3.1 k-space approach
MMV (their Eq. (7)) expressed the relative velocities
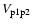 between particles of different stopping times t1 and t2 as
between particles of different stopping times t1 and t2 as
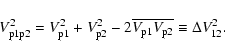 |
(7) |
Having already derived
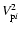 (i=1,2) above, we can determine
(i=1,2) above, we can determine
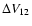 by evaluating the cross term
by evaluating the cross term
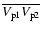 ;
this paper presents analytical solutions of this problem obtained in two separate ways. In this subsection we retain the wavenumber dependence; in the next subsection we transform to time variables. In Eq. (8) of MMV the cross term is given as a sum over the two particle sizes involved, which we separate here, writing
;
this paper presents analytical solutions of this problem obtained in two separate ways. In this subsection we retain the wavenumber dependence; in the next subsection we transform to time variables. In Eq. (8) of MMV the cross term is given as a sum over the two particle sizes involved, which we separate here, writing
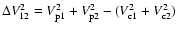 ,
where
,
where
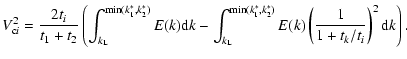 |
|
|
(8) |
Changing variable to
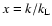 ,
substituting for E(k), and converting stopping time ti to Stokes number
,
substituting for E(k), and converting stopping time ti to Stokes number
 :
:
![\begin{displaymath}V_{{\rm c}i}^2 = \frac{2V_{\rm g}^2 t_i}{3(t_1+t_2)} \left[ \...
...m St}_i^2 {\rm d}x}{x^{5/3}({\rm St}_i + x^{-2/3})^2} \right],
\end{displaymath}](/articles/aa/full/2007/17/aa6899-06/img82.gif) |
(9) |
where we have taken, without loss of generality,
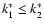 .
The first integral is trivial and the second integral can be solved exactly as in Eqs. (17)-(19) of CH03. In evaluating the specific value of the integrals above, we need a closed form for the upper limit
.
The first integral is trivial and the second integral can be solved exactly as in Eqs. (17)-(19) of CH03. In evaluating the specific value of the integrals above, we need a closed form for the upper limit
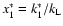 .
A simple prescription is readily found by inspection of Fig. 3 of CH03:
.
A simple prescription is readily found by inspection of Fig. 3 of CH03:
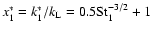 .
That is, the boundary eddy for particles with stopping time t1 is that for which
.
That is, the boundary eddy for particles with stopping time t1 is that for which
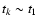 until
until
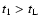 ,
beyond which it remains constant. This is merely a convenient mathematical shorthand to keep everything in closed form. Then, repeating the analytical solution of CH03 (Eqs. (17)-(19)) we obtain
,
beyond which it remains constant. This is merely a convenient mathematical shorthand to keep everything in closed form. Then, repeating the analytical solution of CH03 (Eqs. (17)-(19)) we obtain
![\begin{displaymath}V_{{\rm c}i}^2 = V_{\rm g}^2 \frac{t_i}{(t_1+t_2)} \left[ \le...
...\rm St}_i}{1 + {\rm St}_i {x_1^*}^{2/3} } \right) \right]\cdot
\end{displaymath}](/articles/aa/full/2007/17/aa6899-06/img87.gif) |
(10) |
This solution for the cross term is easily combined with Eq. (6) to obtain expressions for particle-particle relative velocities
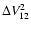 .
Further manipulation of these expressions may be possible, but the important point here is that
.
Further manipulation of these expressions may be possible, but the important point here is that
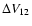 can be expressed in closed form as function of
can be expressed in closed form as function of
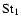 ,
,
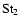 ,
,
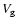 ,
and Re. With a few minutes of algebra, simpler expressions can be found in the limiting regimes of interest (
,
and Re. With a few minutes of algebra, simpler expressions can be found in the limiting regimes of interest (
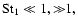 etc.) which agree well with those which we present in the next section, for analytical solutions obtained in the time domain instead of the wavenumber domain, and where an analytical solution for the boundary k*(t*) is used rather than the form for x1* adopted above. It should be recalled that, for very small particles
etc.) which agree well with those which we present in the next section, for analytical solutions obtained in the time domain instead of the wavenumber domain, and where an analytical solution for the boundary k*(t*) is used rather than the form for x1* adopted above. It should be recalled that, for very small particles
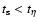 ,
x1* has an upper limit of
,
x1* has an upper limit of
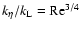 (see, e.g. CH03 Fig. 3).
(see, e.g. CH03 Fig. 3).
The integrals expressing
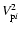 and
and
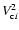 are transformed into a simpler
form by changing variables from k to tk. Since
are transformed into a simpler
form by changing variables from k to tk. Since
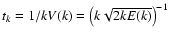 and
E(k) = A k-5/3 for a Kolmogorov
power spectrum (where A is the normalization factor), we obtain that
and
E(k) = A k-5/3 for a Kolmogorov
power spectrum (where A is the normalization factor), we obtain that
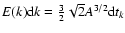 .
Now,
.
Now,
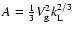 from
the normalization of the turbulent spectrum (Eq. (2)),
from
the normalization of the turbulent spectrum (Eq. (2)),
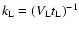 with
with 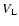 the velocity of the largest eddy, and
the velocity of the largest eddy, and
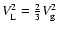 also by normalizing the power spectrum (see CH03).
We then end up with
also by normalizing the power spectrum (see CH03).
We then end up with
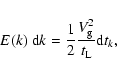 |
(11) |
which can be substituted into all the integrals, putting them into a simpler form.
For instance, Eq. (5) becomes for particle i
![\begin{displaymath}V_{{\rm p}i}^2 = \frac{V_{\rm g}^2}{t_{\rm L}} \int_{t_\eta}^...
..._k +
\frac{t_i^2}{t_i + t_k} \right]^{t_{\rm L}}_{t_\eta}\cdot
\end{displaymath}](/articles/aa/full/2007/17/aa6899-06/img102.gif) |
(12) |
Similarly, the cross term becomes
With
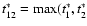 )
and
)
and
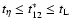 since t* refers to an eddy's turn-over time. We now solve for
since t* refers to an eddy's turn-over time. We now solve for
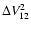 by splitting
the integral in Eq. (12) at t*12 and subtract the corresponding
by splitting
the integral in Eq. (12) at t*12 and subtract the corresponding
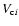 terms from Eq. (14) to get
terms from Eq. (14) to get
![$\displaystyle \Delta V_{12}^2 = \frac{V_{\rm g}^2}{t_{\rm L}} \left( \left[ t_k...
...t_1^2}{t_1 + t_k} \right]^{t_{\rm L}}_{t_{12}^*} + (1\leftrightarrow2)
\right),$](/articles/aa/full/2007/17/aa6899-06/img109.gif) |
|
|
(15) |
where the
 symbol indicates interchange between particles 1 and 2. With further manipulation and cancellation
of terms, the previous expression simplifies slightly to
symbol indicates interchange between particles 1 and 2. With further manipulation and cancellation
of terms, the previous expression simplifies slightly to
This is perhaps the most concise way to write the expressions for
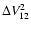 .
The first term we call
.
The first term we call
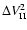 since this term involves class
II (fast) eddies. If
since this term involves class
II (fast) eddies. If
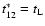 (heavy particles) all eddies are fast and only this term
remains. Conversely, if
(heavy particles) all eddies are fast and only this term
remains. Conversely, if
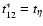 (small particles) the contribution from
(small particles) the contribution from
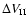 vanishes and the second term,
vanishes and the second term,
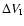 ,
determines relative velocities. In
the intermediate regime,
,
determines relative velocities. In
the intermediate regime,
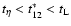 ,
both terms contribute. Written
in terms of the Stokes numbers these terms becomes
,
both terms contribute. Written
in terms of the Stokes numbers these terms becomes
Note again that since
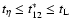 we also have that
we also have that
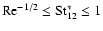 .
Below, we will first solve
for
.
Below, we will first solve
for
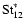 ,
and then consider solutions for
,
and then consider solutions for
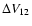 in various
limiting cases of the particle stopping times.
in various
limiting cases of the particle stopping times.
3.2.1 Solving for t*
The relative velocity between a particle with stopping time 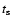 and an eddy k, is given by Völk et al. (1980), Eq. (15):
and an eddy k, is given by Völk et al. (1980), Eq. (15):
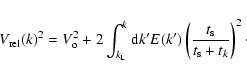 |
(19) |
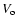 is any systematic velocity component not driven by turbulence - such as due to pressure-gradient driven azimuthal headwind, the ensuing radial drift, or vertical settling under solar gravity. We can integrate this equation in the same fashion as Eq. (14) and arrive at
is any systematic velocity component not driven by turbulence - such as due to pressure-gradient driven azimuthal headwind, the ensuing radial drift, or vertical settling under solar gravity. We can integrate this equation in the same fashion as Eq. (14) and arrive at
in which
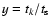 .
Also, using the definition for tk (see text above Eq. (11)), k* can be expressed as
.
Also, using the definition for tk (see text above Eq. (11)), k* can be expressed as
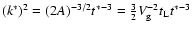 .
Inserting the expressions for k* and
.
Inserting the expressions for k* and
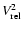 into Eq. (3), assuming that
into Eq. (3), assuming that
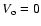 for simplicity (see however Sect. 3.3), we obtain:
for simplicity (see however Sect. 3.3), we obtain:
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{6899fig1}
\end{figure}](/articles/aa/full/2007/17/aa6899-06/Timg140.gif) |
Figure 1:
The function
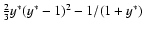 .
If .
If
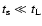 and
and
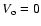 (no systematic velocity drifts; see Sect. 3.3) this equation is equal to zero
and we find a solution
(no systematic velocity drifts; see Sect. 3.3) this equation is equal to zero
and we find a solution
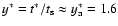 .
On the other hand, for .
On the other hand, for
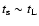 ,
the RHS of Eq. (24) is ,
the RHS of Eq. (24) is 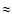 -0.5 and -0.5 and
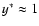 . . |
| Open with DEXTER |
where we have defined
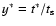 and
and
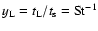 .
The LHS of Eq. (24) is plotted in Fig. 1. If
.
The LHS of Eq. (24) is plotted in Fig. 1. If
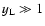 for small particles, the RHS of Eq. (24) is negligible and the numerical solution
for y* becomes
for small particles, the RHS of Eq. (24) is negligible and the numerical solution
for y* becomes
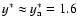 ,
or
,
or
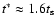 .
On the other hand, when
.
On the other hand, when 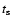 nears
nears 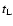 ,
the
,
the
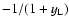 term causes the RHS of Eq. (24) to drop to -0.5,
and
term causes the RHS of Eq. (24) to drop to -0.5,
and
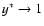 .
For
.
For
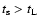 we always have that
we always have that
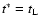 ;
i.e., for such a particle all eddies
are of class 2. In Fig. 2 we compare the exact solution (dashed line)
for t* with the
;
i.e., for such a particle all eddies
are of class 2. In Fig. 2 we compare the exact solution (dashed line)
for t* with the
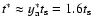 approximation (solid line; in both cases
approximation (solid line; in both cases
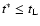 is simply enforced), and the empirical function
is simply enforced), and the empirical function
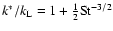 (dotted line; see Sect. 3.1).
(dotted line; see Sect. 3.1).
The exact solution for
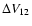 (Eq. (16)) is given in Fig. 3 both for
(Eq. (16)) is given in Fig. 3 both for
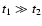 (solid curve) and for particles of equal
stopping times (dashed curve). A Reynolds number of
(solid curve) and for particles of equal
stopping times (dashed curve). A Reynolds number of
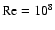 has been adopted.
has been adopted.
3.3 The role of V :
eddy-crossing effects
:
eddy-crossing effects
Systematic velocities 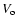 due to vertical settling, and pressure-gradient headwinds and drifts, will occur (e.g. Nakagawa et al. (1986)). Because particles drift through eddies, their transit time is affected (because
due to vertical settling, and pressure-gradient headwinds and drifts, will occur (e.g. Nakagawa et al. (1986)). Because particles drift through eddies, their transit time is affected (because
 is larger) and the boundary between class I and II eddies shifts. Cuzzi et al. (1993) include this effect, due to vertical settling, in their model of particle diffusion (their Eq. (43)). The model presented here offers a generalized way of treating this effect, which we will only sketch here.
is larger) and the boundary between class I and II eddies shifts. Cuzzi et al. (1993) include this effect, due to vertical settling, in their model of particle diffusion (their Eq. (43)). The model presented here offers a generalized way of treating this effect, which we will only sketch here.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6899fig2}
\end{figure}](/articles/aa/full/2007/17/aa6899-06/Timg157.gif) |
Figure 2:
Three different assumptions for t* (or the related k*) are shown here. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6899fig3}
\end{figure}](/articles/aa/full/2007/17/aa6899-06/Timg158.gif) |
Figure 3:
Exact solution to Eq. (16) for
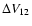 in
the case of identical particles (dashed line) and
in
the case of identical particles (dashed line) and
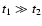 (solid line) for a Reynold number
of 108.
The dotted curves are approximations to Eq. (16) given by Eqs. (27)-(29).
(solid line) for a Reynold number
of 108.
The dotted curves are approximations to Eq. (16) given by Eqs. (27)-(29). |
| Open with DEXTER |
Repeating the procedure outlined in Sect. 3.2.1 but retaining the V0 term in
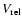 (Eq. (20)), we end up with Eq. (24) including a correction term
(Eq. (20)), we end up with Eq. (24) including a correction term
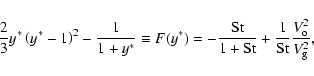 |
(22) |
where we have substituted
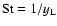 .
The correction term can be roughly constrained using an estimate of the systematic drift velocity
.
The correction term can be roughly constrained using an estimate of the systematic drift velocity
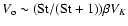 ,
where
,
where 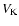 is the Keplerian velocity
at distance a from the Sun,
is the Keplerian velocity
at distance a from the Sun, 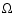 is the orbit frequency, and
is the orbit frequency, and
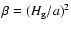 is a radial pressure gradient parameter; also we take
is a radial pressure gradient parameter; also we take
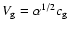 (see,
e.g., Nakagawa et al. 1986 or Cuzzi & Weidenschilling 2006). Then
(see,
e.g., Nakagawa et al. 1986 or Cuzzi & Weidenschilling 2006). Then
and Eq. (22) becomes,
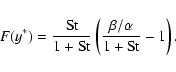 |
(24) |
Normally
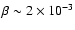 is assumed (Cuzzi et al. 1993; Nakagawa et al. 1986), but its real value, and that of
is assumed (Cuzzi et al. 1993; Nakagawa et al. 1986), but its real value, and that of 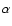 ,
are not well known. Equation (24) shows that for a given value of
,
are not well known. Equation (24) shows that for a given value of 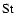 ,
F(y*) increases with increasing
,
F(y*) increases with increasing
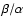 .
Consequently,
.
Consequently,
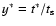 is also higher (see Fig. 1). The boundary between the class I and II eddies therefore shifts to higher values of t*, that is, there are less class I eddies for high
is also higher (see Fig. 1). The boundary between the class I and II eddies therefore shifts to higher values of t*, that is, there are less class I eddies for high
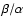 and the
and the
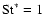 upper limit (when
upper limit (when
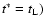 is reached at lower Stokes numbers. Inserting the definition of F(y*) (LHS of Eq. (22)) into Eq. (24) with
is reached at lower Stokes numbers. Inserting the definition of F(y*) (LHS of Eq. (22)) into Eq. (24) with
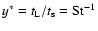 and solving for
and solving for 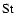 ,
we find that the Stokes number at which
,
we find that the Stokes number at which
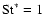 occurs at
occurs at
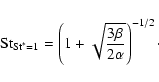 |
(25) |
For example, for
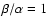 ,
,
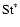 reaches its upper limit at
reaches its upper limit at
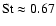 .
.
In the small particle regime (
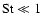 ), however, the exact value of
), however, the exact value of
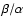 is unimportant since F(y*) is always close to zero, and the
is unimportant since F(y*) is always close to zero, and the
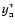 approximation is justified. It is only for
approximation is justified. It is only for
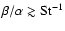 that the RHS of
Eq. (24) starts to becomes significant and
that the RHS of
Eq. (24) starts to becomes significant and
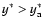 .
This is the weakly-turbulent or non-turbulent regime where class II eddies dominate even for small particles. In practise, however, it means that eddy crossing effects are important only if turbulence is very weak and we will not treat them
further in this paper.
.
This is the weakly-turbulent or non-turbulent regime where class II eddies dominate even for small particles. In practise, however, it means that eddy crossing effects are important only if turbulence is very weak and we will not treat them
further in this paper.
As intuition-building examples we obtain simple, closed-form expressions for
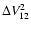 in various limiting
regimes from the t-space solutions; similar results are easily obtained from the k-space
solutions (Sect. 3.1). Without loss of generality we take particle 1 to have the largest
stopping time, i.e.,
in various limiting
regimes from the t-space solutions; similar results are easily obtained from the k-space
solutions (Sect. 3.1). Without loss of generality we take particle 1 to have the largest
stopping time, i.e.,
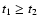 and
t12*=t1*. Moreover, we assume that
and
t12*=t1*. Moreover, we assume that
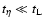 ;
i.e., that
;
i.e., that
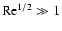 and there is an extended inertial
range of eddies. Recall again that
and there is an extended inertial
range of eddies. Recall again that
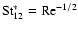 for
for
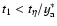 ,
and that
,
and that
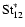 will not exceed 1.
will not exceed 1.
In this limit all eddies are of class I and
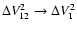 .
For each particle, the second term on the RHS of Eq. (17) is negligible; thus
.
For each particle, the second term on the RHS of Eq. (17) is negligible; thus
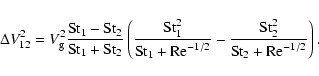 |
(26) |
In the very small particle regime (
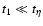 ),
),
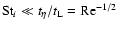 and
and
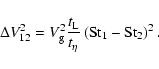 |
(27) |
Since
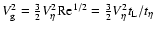 ,
this
expression transforms directly to
,
this
expression transforms directly to
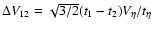 ,
in
good agreement with the heuristic, although physically motivated, expression
,
in
good agreement with the heuristic, although physically motivated, expression
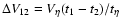 of Weidenschilling (1984).
of Weidenschilling (1984).
If t1 (the stopping time of the larger particle) approaches the Kolmogorov
scale, two changes
occur. First, the
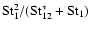 term
in Eq. (17) now becomes linear with
term
in Eq. (17) now becomes linear with
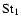 ,
since
,
since
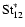 grows proportional to
grows proportional to
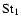 (the second term is
still negligible throughout most of this regime). Relative velocities therefore
increase as the square-root of stopping time. Second, class II eddies also
contribute to
(the second term is
still negligible throughout most of this regime). Relative velocities therefore
increase as the square-root of stopping time. Second, class II eddies also
contribute to
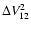 (Eq. (18)). This contribution scales
also with
(Eq. (18)). This contribution scales
also with
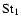 ,
but is significantly larger and does not
disappear when t1 = t2. From a physical point of view, class II eddies act
as small, random kicks to the particle trajectory, while two
particles captured by a class I eddy are subject to the same,
systematic, change in motion. Class II eddies are therefore much more effective
in generating velocity differences for similar-sized particles.
,
but is significantly larger and does not
disappear when t1 = t2. From a physical point of view, class II eddies act
as small, random kicks to the particle trajectory, while two
particles captured by a class I eddy are subject to the same,
systematic, change in motion. Class II eddies are therefore much more effective
in generating velocity differences for similar-sized particles.
In the "fully intermediate regime'', i.e.,
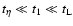 ,
we can also
ignore the
,
we can also
ignore the
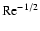 terms in Eq. (18). In addition, the
terms in Eq. (18). In addition, the
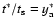 approximation holds. Upon writing
approximation holds. Upon writing
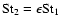 ,
Eqs. (17), (18) become linear with
,
Eqs. (17), (18) become linear with
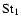 and we can write
and we can write
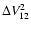 as (see Appendix B)
as (see Appendix B)
![\begin{displaymath}\Delta V_{12}^2 = V_{\rm g}^2 \left[ 2y_{\rm a} - (1+\epsilon...
...ac{\epsilon^3}{y_{\rm a}+\epsilon} \right) \right]
{\rm St}_1,
\end{displaymath}](/articles/aa/full/2007/17/aa6899-06/img200.gif) |
(28) |
where
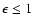 is the ratio between the stopping times and
is the ratio between the stopping times and
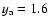 .
For
.
For
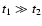 we then find that
we then find that
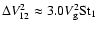 ,
while for equal
particles the numerical factor goes down to 2.0. Written in terms of stopping
times the relative velocities become,
,
while for equal
particles the numerical factor goes down to 2.0. Written in terms of stopping
times the relative velocities become,
![$\Delta V_{12} = [1.7\div2.1] V_{\rm L}
\sqrt{t_1/t_{\rm L}}$](/articles/aa/full/2007/17/aa6899-06/img204.gif) .
This also compares well with Weidenschilling (1984) fits
for this regime (who gives pre-factors of 2.1 and 3.0, respectively). Note,
however, that our full expressions for
.
This also compares well with Weidenschilling (1984) fits
for this regime (who gives pre-factors of 2.1 and 3.0, respectively). Note,
however, that our full expressions for
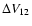 (Eqs. (16)-(18)) also capture the behavior near the
(Eqs. (16)-(18)) also capture the behavior near the  and
and
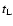 "turning points'' (see Fig. 3).
"turning points'' (see Fig. 3).
![\begin{figure}
\par\includegraphics[width=12.6cm,clip]{6899fig4}
\end{figure}](/articles/aa/full/2007/17/aa6899-06/Timg206.gif) |
Figure 4:
Contour plots of particle-particle, turbulence induced, relative velocities
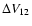 normalized to
normalized to 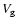 .
A) Numerical results of Markiewicz et al. (1991), without inner scale ( .
A) Numerical results of Markiewicz et al. (1991), without inner scale (
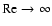 ). B) Analogous result from our closed-form expressions with the fixed ). B) Analogous result from our closed-form expressions with the fixed
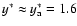 approximation
(Sect. 3.2.1). C) Like B, but with an exact solution for y* and with
approximation
(Sect. 3.2.1). C) Like B, but with an exact solution for y* and with
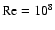 .
D) Using the CH03 formula for k*, .
D) Using the CH03 formula for k*,
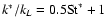 ,
and also with ,
and also with
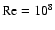 .
Contours are drawn twice per logarithmic decade (at .
Contours are drawn twice per logarithmic decade (at
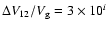 and at 10i) with an additional contour at 0.8 and 1.15.
and at 10i) with an additional contour at 0.8 and 1.15. |
| Open with DEXTER |
If
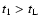 ,
,
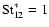 and there is no contribution from class
I eddies (Eq. (17)). Also, we can neglect the
and there is no contribution from class
I eddies (Eq. (17)). Also, we can neglect the
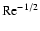 terms in
Eq. (18) and the relative velocity simply becomes
terms in
Eq. (18) and the relative velocity simply becomes
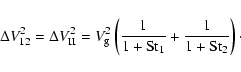 |
(29) |
This result can, of course, directly be obtained from the
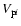 terms
(Eq. (12)) since the cross-term vanishes in this regime. For small
terms
(Eq. (12)) since the cross-term vanishes in this regime. For small
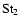 relative velocities are still
relative velocities are still 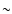
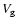 ;
however, if both
Stokes numbers are large, the relative velocity decreases roughly with
the square root of the smallest particle stopping time. Note that the linear fit of
Weidenschilling (1984) in this regime (his Eq. (15)) is inappropriate
(see, however, Völk et al. 1980, Weidenschilling 1988, Weidenschilling & Cuzzi 1993, Cuzzi et al. 1993, in which a square-root fall off is advocated).
Since an explicit, closed-form solution to the Völk et al. (1980) and MMV expressions for
;
however, if both
Stokes numbers are large, the relative velocity decreases roughly with
the square root of the smallest particle stopping time. Note that the linear fit of
Weidenschilling (1984) in this regime (his Eq. (15)) is inappropriate
(see, however, Völk et al. 1980, Weidenschilling 1988, Weidenschilling & Cuzzi 1993, Cuzzi et al. 1993, in which a square-root fall off is advocated).
Since an explicit, closed-form solution to the Völk et al. (1980) and MMV expressions for
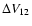 has not previously been
available, many dust coagulation models (e.g., Ormel et al. 2007; Dullemond & Dominik 2005; Suttner & Yorke 2001) have relied on the
Weidenschilling (1984) fits to calculate relative velocities.
Turbulent motions and relative velocities for particles in the
has not previously been
available, many dust coagulation models (e.g., Ormel et al. 2007; Dullemond & Dominik 2005; Suttner & Yorke 2001) have relied on the
Weidenschilling (1984) fits to calculate relative velocities.
Turbulent motions and relative velocities for particles in the
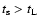 regime have therefore been underestimated in these calculations.
However, concerning these works, we also think no major conclusions have been affected, since the error is introduced only for large dust particles, that is, if the system is already well evolved.
regime have therefore been underestimated in these calculations.
However, concerning these works, we also think no major conclusions have been affected, since the error is introduced only for large dust particles, that is, if the system is already well evolved.
3.5 Contour plots
Following Völk et al. (1980) and MMV we also
present our results as contour plots. Figure 4A shows, for comparison, the results of MMV, obtained by numerical evaluation of the integrals involved without an inner turbulent scale (
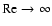 ). The next three panels of Fig. 4 show the result using our closed-form expressions derived from Eq. (16). In panel B, the
). The next three panels of Fig. 4 show the result using our closed-form expressions derived from Eq. (16). In panel B, the
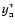 approximation has been used and, like Fig. 2 of MMV (panel A), the inner scale of the turbulence is extended to infinity so that Eqs. (28), (29) apply.
Somewhat systematically higher values for
approximation has been used and, like Fig. 2 of MMV (panel A), the inner scale of the turbulence is extended to infinity so that Eqs. (28), (29) apply.
Somewhat systematically higher values for
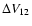 when compared to MMV can be explained by the CH03 approximation for
when compared to MMV can be explained by the CH03 approximation for 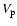 (see Eq. (6)) but these discrepancies are less than
(see Eq. (6)) but these discrepancies are less than  10%.
In panels C and D we show the contour plots corresponding to the other formulations for k* (see Fig. 2), i.e., the exact solution for y* (panel C) and the CH03 empirical approximation (panel D).
The differences between these three methods for determining k* differ around the
10%.
In panels C and D we show the contour plots corresponding to the other formulations for k* (see Fig. 2), i.e., the exact solution for y* (panel C) and the CH03 empirical approximation (panel D).
The differences between these three methods for determining k* differ around the
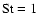 point (see Fig. 2) and are reflected in the contour plots. For
point (see Fig. 2) and are reflected in the contour plots. For
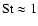 ,
panel C compares best to the numerical result of MMV, but no significant errors are made when using the
,
panel C compares best to the numerical result of MMV, but no significant errors are made when using the
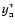 approximation or the CH03 formula for k*.
approximation or the CH03 formula for k*.
In panels C and D of Fig. 4, a Reynolds number of
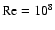 has been adopted. For
has been adopted. For
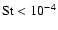 ,
therefore, velocities are greatly suppressed since only class I eddies remain to generate relative velocities and relative velocities disappear completely for equal friction times. Also, the contours are much closer spaced since in this limit the velocity
,
therefore, velocities are greatly suppressed since only class I eddies remain to generate relative velocities and relative velocities disappear completely for equal friction times. Also, the contours are much closer spaced since in this limit the velocity
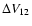 is proportional to
is proportional to 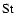 (see Eq. (26)).
(see Eq. (26)).
4 Conclusions
We have extended and, essentially, completed the work of Cuzzi & Hogan (2003),
who derived explicit, closed-form expressions for particle velocities in
turbulence based on the physics originally developed by
Völk et al. (1980) and Markiewicz et al. (1991). Within the
framework of this physics, the only approximations used here are in Eq. (6)
for the particle velocities (where a posteriori comparisons with exact numerical solutions indicate the approximation is well justified) and in Eqs. (20) et seq where the
systematic velocity 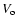 is neglected to simplify calculating the boundary between eddy
classes (generalizing this step should be straightforward, however). The full analytic
expression for
is neglected to simplify calculating the boundary between eddy
classes (generalizing this step should be straightforward, however). The full analytic
expression for
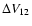 is given by Eq. (16) (or by the sum of
Eqs. (17), (18)), but more simple, explicit expressions apply in restricted
regimes (provided
is given by Eq. (16) (or by the sum of
Eqs. (17), (18)), but more simple, explicit expressions apply in restricted
regimes (provided
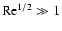 ):
):
- Equation (27), in the very small particle limit
(
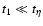 );
);
- Equation (28), in the "fully intermediate''
regime, i.e., for
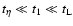 ;
;
- Equation (29), for
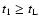 .
.
Near the
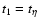 and
and
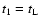 turning points the behavior is more complex (see Fig. 3) and for accurate analytical approximations
one has to revert to the full expressions for
turning points the behavior is more complex (see Fig. 3) and for accurate analytical approximations
one has to revert to the full expressions for 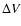 given by
Eqs. (16)-(18).
given by
Eqs. (16)-(18).
Acknowledgements
The authors thank Robert Hogan for computational assistance in creating Fig. A.1 and the referee, H. Völk, for positive feedback. C.W.O. acknowledges support from the Netherlands Organisation for Scientific Research (NWO) that made this work possible. J.N.C.'s contributions were
supported by a grant from NASA's Planetary Geology and Geophysics Program.
Appendix A: more accurate closed-form solution for
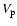 and all related velocities, using power-law approximations to the functions g and h
and all related velocities, using power-law approximations to the functions g and h
In Sect. 2 the very simple approximation
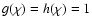 was introduced for all stokes numbers
was introduced for all stokes numbers 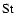 and eddy scales k. It proves to be quite adequate for most purposes; however, as noted in Sect. 3.5, small inaccuracies remain at the 10% level because the approximation overestimates the contributions of fast eddies to
and eddy scales k. It proves to be quite adequate for most purposes; however, as noted in Sect. 3.5, small inaccuracies remain at the 10% level because the approximation overestimates the contributions of fast eddies to
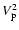 and other velocity components. Figure A.1 shows the detailed behavior of the functions g
and h for
and other velocity components. Figure A.1 shows the detailed behavior of the functions g
and h for
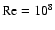 for Stokes numbers of
for Stokes numbers of
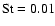 ,
0.1, and 1.0. The inflection point for all three values of
,
0.1, and 1.0. The inflection point for all three values of 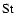 is at k=k* (recall that
is at k=k* (recall that
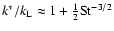 ). For k > k*, the functions are well approximated by power-laws of -1/3 and -3/4, respectively, i.e.,
g(k)=(k/k*)-1/3 and
h(k)=(k/k*)-3/4. The success of the approximation of Sect. 2 is due to the fact that the power in the weighting function k E(k) (dotted line; we multiply with k since we compare logarithmically) decreases rapidly with increasing k; thus by the time the assumption
g(k)=h(k)=1 becomes really bad, the relative contribution of successive terms has become small. For small
). For k > k*, the functions are well approximated by power-laws of -1/3 and -3/4, respectively, i.e.,
g(k)=(k/k*)-1/3 and
h(k)=(k/k*)-3/4. The success of the approximation of Sect. 2 is due to the fact that the power in the weighting function k E(k) (dotted line; we multiply with k since we compare logarithmically) decreases rapidly with increasing k; thus by the time the assumption
g(k)=h(k)=1 becomes really bad, the relative contribution of successive terms has become small. For small 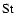 ,
the weighted contribution of eddy power has already become very small even before
,
the weighted contribution of eddy power has already become very small even before
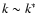 (the logic of CH03). For
(the logic of CH03). For
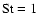 or larger, the weighting function has dropped by nearly an order of magnitude by the time h(k) (the faster-decreasing function) has dropped to 0.3 (dashed-dotted line), and this seems to account for the success of our simple assumption.
or larger, the weighting function has dropped by nearly an order of magnitude by the time h(k) (the faster-decreasing function) has dropped to 0.3 (dashed-dotted line), and this seems to account for the success of our simple assumption.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6899figA}
\end{figure}](/articles/aa/full/2007/17/aa6899-06/Timg223.gif) |
Figure A.1:
The functions g (solid lines) and h (dashed lines) plotted for three different Stokes numbers at a Reynolds number of 108. After k>k* the functions show power-law behavior. The power spectrum (weighted by k) is plotted by the dotted line. |
This behavior can be understood from the definition of
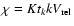 .
For
.
For 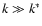 ,
,
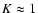 and
and
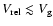 are both constant. Then, because
are both constant. Then, because
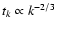 ,
,
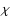 scales as
scales as
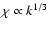 and becomes large at large k. Since
and becomes large at large k. Since
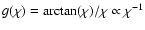 for large
for large 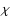 ,
we get that
,
we get that
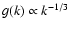 .
Similarly,
.
Similarly,
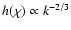 ,
which is a bit shallower than the -3/4 exponent observed over most regions of interest (Fig. A.1). While the -2/3 exponent is reached at large k, the -3/4 exponent seems more appropriate at intermediate k. Yet, in our subsequent analysis, we will use the large-k limit for this exponent (-2/3) because it simplifies the math. Thus, we approximate the g and h behavior as follows: unity for k<k*, and power laws in k/k* with exponents of -1/3 and -2/3 for k>k*. Then Eq. (4) becomes
,
which is a bit shallower than the -3/4 exponent observed over most regions of interest (Fig. A.1). While the -2/3 exponent is reached at large k, the -3/4 exponent seems more appropriate at intermediate k. Yet, in our subsequent analysis, we will use the large-k limit for this exponent (-2/3) because it simplifies the math. Thus, we approximate the g and h behavior as follows: unity for k<k*, and power laws in k/k* with exponents of -1/3 and -2/3 for k>k*. Then Eq. (4) becomes
![$\displaystyle V_{\rm p}^2 = \int_{k_{\rm L}}^{k^*} {\rm d}k\ 2E(k) \left( 1 - K...
...left(\frac{k}{k^*}\right)^{-1/3} + K \left(\frac{k}{k^*}\right)^{-2/3} \right].$](/articles/aa/full/2007/17/aa6899-06/img233.gif) |
|
|
(A.1) |
Where we have that
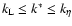 ,
such that in the case of very small or very large particles one of the integrals vanishes (Sect. 3.2.1). Since the approximation g=h=1 still holds for k<k* (or for t>t*) the velocities resulting due to class 1 eddies (Eq. (17)) are not affected; the new approximation only affects Eq. (18). By writing
,
such that in the case of very small or very large particles one of the integrals vanishes (Sect. 3.2.1). Since the approximation g=h=1 still holds for k<k* (or for t>t*) the velocities resulting due to class 1 eddies (Eq. (17)) are not affected; the new approximation only affects Eq. (18). By writing
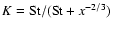 ,
,
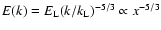 with
with
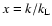 the solution to Eq. (A.1) involves integrals of the form
the solution to Eq. (A.1) involves integrals of the form
![\begin{displaymath}\int {\rm d}x\ x^{-5/3+p} \left( \frac{{\rm St}}{{\rm St} +x^{-2/3}} \right)^{n=[1,~2]}
\end{displaymath}](/articles/aa/full/2007/17/aa6899-06/img237.gif) |
(A.2) |
with n=2 for the K2 term and p=-1/3 or -2/3. These integrals can be solved analytically. Going to "t-space'', however, gives somewhat cleaner solutions and we will from here on follow that approach and show how it affects relative velocities, i.e.,
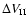 .
After the change of variables (
tk/t* = (k/k*)-2/3) the second term of Eq. (A.1) becomes
.
After the change of variables (
tk/t* = (k/k*)-2/3) the second term of Eq. (A.1) becomes
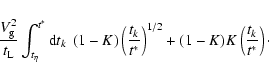 |
(A.3) |
We now introduce the dimensionless variable
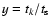 (cf. Eq. (20)). Then
tk/t* = y/y* with
(cf. Eq. (20)). Then
tk/t* = y/y* with
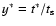 .
Also K=1/(1+y) and
1-K=y/(1+y) and
Eq. (A.3) becomes
.
Also K=1/(1+y) and
1-K=y/(1+y) and
Eq. (A.3) becomes
| |
|
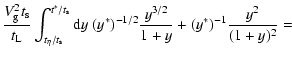 |
(A.4) |
| |
|
![$\displaystyle \frac{V_{\rm g}^2 t_{\rm s}}{t_{\rm L}} \left\{ (y^*)^{-1/2} \Big...
...(y^*)^{-1} \Big[ I_{\rm g}(y) \Big]^{t^*/t_{\rm s}}_{t_\eta/t_{\rm s}} \right\}$](/articles/aa/full/2007/17/aa6899-06/img240.gif) |
(A.5) |
in which the functions
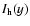 and
and
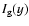 are defined as
are defined as
The expressions for
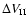 now consist of several contributions. First,
now consist of several contributions. First,
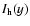 and
and
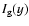 are evaluated at both the upper (y*) and lower (
are evaluated at both the upper (y*) and lower (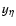 )
limits. This must be done for both particles 1 and 2,
because the
)
limits. This must be done for both particles 1 and 2,
because the
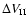 term (Eq. (18)) has separate contributions from each
particle. For the particle of highest friction time (say this is t1) the power-law approximation for g and h holds over the range
term (Eq. (18)) has separate contributions from each
particle. For the particle of highest friction time (say this is t1) the power-law approximation for g and h holds over the range
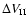 is calculated, i.e.,
is calculated, i.e.,
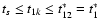 .
However, for the second particle the power-law approximation only holds for
.
However, for the second particle the power-law approximation only holds for
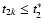 ,
while for the remaining range over which the integral in
,
while for the remaining range over which the integral in
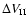 is evaluated, i.e.,
is evaluated, i.e.,
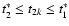 ,
the g=h=1 approximation applies.
,
the g=h=1 approximation applies.
This gives us several terms that contribute to
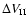 .
Collecting these terms, the new expression for
.
Collecting these terms, the new expression for
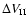 becomes
becomes
Although still fully analytical, this more accurate expression for
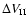 is also more complicated and we did not present it in the main body of the paper.
Equation (A.8) is useful, however, for readers whose applications demand this higher level of accuracy.
is also more complicated and we did not present it in the main body of the paper.
Equation (A.8) is useful, however, for readers whose applications demand this higher level of accuracy.
Appendix B: Derivation of Eq. (28)
We consider the limiting case of
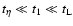 .
The
.
The
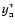 approximation for
approximation for
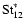 then holds, i.e.,
then holds, i.e.,
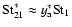 with
with
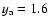 .
We will now argue that we can neglect the
.
We will now argue that we can neglect the
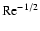 terms in Eq. (18). For particle 1 this is obvious since
terms in Eq. (18). For particle 1 this is obvious since
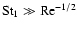 .
The last term (where
.
The last term (where
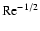 is in the denominator) then becomes simply
is in the denominator) then becomes simply
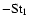 .
However, for the interchange term a similar approximation
.
However, for the interchange term a similar approximation
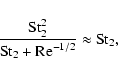 |
(B.1) |
is not that obvious since we have not put a constraint on
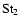 .
For example, if
.
For example, if
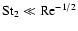 the
the
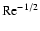 term dominates the denominator. However, in that case this term and its approximation are small anyway compared to
term dominates the denominator. However, in that case this term and its approximation are small anyway compared to
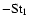 ,
such that by making the approximation in Eq. (B.1) our final result is notaffected. Similarly, if
,
such that by making the approximation in Eq. (B.1) our final result is notaffected. Similarly, if
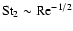 ,
Eq. (B.1) (which goes to
,
Eq. (B.1) (which goes to 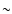
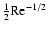 )
or its approximation (
)
or its approximation (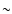
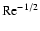 )
are insignificant since
)
are insignificant since
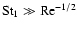 .
Only if
.
Only if
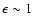 ,
i.e.,
,
i.e.,
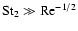 ,
does the
,
does the
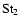 term
matter, but then the approximation in
Eq. (B.1) is well justified.
All terms in Eq. (18) are then linear in Stokes and we can reduce it to
term
matter, but then the approximation in
Eq. (B.1) is well justified.
All terms in Eq. (18) are then linear in Stokes and we can reduce it to
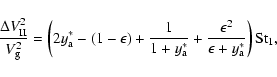 |
(B.2) |
with
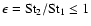 .
Similarly, Eq. (17) becomes
.
Similarly, Eq. (17) becomes
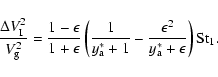 |
(B.3) |
Combining these expressions and collecting the
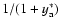 and
and
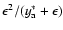 terms then gives Eq. (28).
terms then gives Eq. (28).
- Cuzzi, J. N.,
& Hogan, R. C. 2003, Icarus, 164, 127 [NASA ADS] [CrossRef] (In the text)
- Cuzzi, J. N.,
Dobrovolskis, A. R., & Champney, J. M. 1993, Icarus,
106, 102 [NASA ADS] [CrossRef]
- Cuzzi, J. N.,
& Weidenschilling, S. J. 2006, Particle-Gas Dynamics and
Primary Accretion, Meteorites and the Early Solar System II,
353
(In the text)
- Dullemond,
C. P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences]
- Markiewicz,
W. J., Mizuno, H., & Völk, H. J. 1991, A&A,
242, 286 [NASA ADS] (In the text)
- Nakagawa, Y., Sekiya,
M., & Hayashi, C. 1986, Icarus, 67, 375 [NASA ADS] [CrossRef] (In the text)
- Nomura, H., &
Nakagawa, Y. 2006, ApJ, 640, 1099 [NASA ADS] [CrossRef]
- Ormel, C. W.,
Spaans, M., & Tielens, A. G. G. M. 2007,
A&A, 461, 215 [NASA ADS] [CrossRef] [EDP Sciences]
- Schräpler, R.,
& Henning, T. 2004, ApJ, 614, 960 [NASA ADS] [CrossRef]
- Suttner, G., &
Yorke, H. W. 2001, ApJ, 551, 461 [NASA ADS]
- Völk,
H. J., Morfill, G. E., Roeser, S., & Jones,
F. C. 1980, A&A, 85, 316 [NASA ADS] (In the text)
- Weidenschilling,
S. J. 1984, Icarus, 60, 553 [NASA ADS] [CrossRef] (In the text)
- Weidenschilling,
S. J. 1988, Formation processes and time scales for meteorite
parent bodies, Meteorites and the Early Solar System, 348
(In the text)
- Weidenschilling,
S. J., & Cuzzi, J. N. 1993, in Protostars and Planets
III, ed. E. H. Levy, & J. I. Lunine, 1031
(In the text)
Copyright ESO 2007
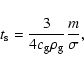
![]() ,
for particle-gas relative velocities
,
for particle-gas relative velocities
![]() ,
and for relative velocities between two identical particles
,
and for relative velocities between two identical particles
![]() ,
but did not extend their results to the general case of two particles of different stopping times. Moreover,
CH03 stressed the validity of their analytical results for particles with stopping times much shorter than the large eddy turnover time. In this note we generalize the
approach and results of CH03 to obtain closed-form
expressions for relative velocities between particles of arbitrary, and unequal, size.
In Sect. 2 we define important quantities and review previous work. In
Sect. 3 we
present two independent approaches for obtaining the desired closed-form solutions.
In Sect. 4 we give our conclusions and a summary.
,
but did not extend their results to the general case of two particles of different stopping times. Moreover,
CH03 stressed the validity of their analytical results for particles with stopping times much shorter than the large eddy turnover time. In this note we generalize the
approach and results of CH03 to obtain closed-form
expressions for relative velocities between particles of arbitrary, and unequal, size.
In Sect. 2 we define important quantities and review previous work. In
Sect. 3 we
present two independent approaches for obtaining the desired closed-form solutions.
In Sect. 4 we give our conclusions and a summary.
![]() and spatial frequencies
and spatial frequencies
![]() ,
with an energy
spectrum
,
with an energy
spectrum
![]() and total energy
and total energy
![]() per unit mass providing
the normalization condition
per unit mass providing
the normalization condition
![]() ,
and fluctuate too rapidly to provide more than
a small perturbation on the
particle. The timescale on which an eddy decays is
given by tk, while the
eddy-crossing timescale is
,
and fluctuate too rapidly to provide more than
a small perturbation on the
particle. The timescale on which an eddy decays is
given by tk, while the
eddy-crossing timescale is
![]() ,
with
,
with
![]() the relative velocity between
a grain and an eddy. For an eddy
to be of class I both tk and
the relative velocity between
a grain and an eddy. For an eddy
to be of class I both tk and
![]() must be larger than the
particle's stopping time. The boundary between these classes occurs at k=k* (or at
tk = t*) which can be defined as
(Völk et al. 1980, MMV):
must be larger than the
particle's stopping time. The boundary between these classes occurs at k=k* (or at
tk = t*) which can be defined as
(Völk et al. 1980, MMV):
![]() is given by
Eq. (6) of MMV.
is given by
Eq. (6) of MMV.
![]() or
or
![]() ,
the second integral becomes negligible, leaving only the first integral which is analytically solvable and for which the upper limit can be extended to
,
the second integral becomes negligible, leaving only the first integral which is analytically solvable and for which the upper limit can be extended to ![]() with negligible error.
Here, to generalize the approach of CH03 to particles of arbitrary size, we approximate
with negligible error.
Here, to generalize the approach of CH03 to particles of arbitrary size, we approximate
![]() for all particle sizes (see CH03 Sect. 2.2.3 for supporting logic). Numerical calculations of
for all particle sizes (see CH03 Sect. 2.2.3 for supporting logic). Numerical calculations of ![]() and
and ![]() validate this approximation to order unity (see Appendix A), and we gain further confidence in it from a posteriori comparison with exact numerical model results. The general expression for
validate this approximation to order unity (see Appendix A), and we gain further confidence in it from a posteriori comparison with exact numerical model results. The general expression for
![]() is then the same as in the
is then the same as in the
![]() regime, and the same analytical result is obtained,
i.e. CH03,
regime, and the same analytical result is obtained,
i.e. CH03,
![]() .
A more accurate approximation to Eq. (4), in which the g and h functions are approximated as power-laws in k*/k, is outlined in Appendix A. Unless
.
A more accurate approximation to Eq. (4), in which the g and h functions are approximated as power-laws in k*/k, is outlined in Appendix A. Unless
![]() ,
we can neglect
the Reynolds number term in Eq. (6) and obtain
,
we can neglect
the Reynolds number term in Eq. (6) and obtain
![]() ,
a well known result (Völk et al. 1980; Cuzzi et al. 1993; Schräpler & Henning 2004) which describes the diffusivity of large particles in turbulence.
,
a well known result (Völk et al. 1980; Cuzzi et al. 1993; Schräpler & Henning 2004) which describes the diffusivity of large particles in turbulence.
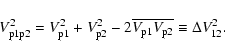
![\begin{displaymath}V_{{\rm c}i}^2 = \frac{2V_{\rm g}^2 t_i}{3(t_1+t_2)} \left[ \...
...m St}_i^2 {\rm d}x}{x^{5/3}({\rm St}_i + x^{-2/3})^2} \right],
\end{displaymath}](/articles/aa/full/2007/17/aa6899-06/img82.gif)
![\begin{displaymath}V_{{\rm c}i}^2 = V_{\rm g}^2 \frac{t_i}{(t_1+t_2)} \left[ \le...
...\rm St}_i}{1 + {\rm St}_i {x_1^*}^{2/3} } \right) \right]\cdot
\end{displaymath}](/articles/aa/full/2007/17/aa6899-06/img87.gif)
![$\displaystyle \Delta V_{12}^2 = \frac{V_{\rm g}^2}{t_{\rm L}} \left( \left[ t_k...
...t_1^2}{t_1 + t_k} \right]^{t_{\rm L}}_{t_{12}^*} + (1\leftrightarrow2)
\right),$](/articles/aa/full/2007/17/aa6899-06/img109.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{6899fig1}
\end{figure}](/articles/aa/full/2007/17/aa6899-06/Timg140.gif)
![]() (Eq. (16)) is given in Fig. 3 both for
(Eq. (16)) is given in Fig. 3 both for
![]() (solid curve) and for particles of equal
stopping times (dashed curve). A Reynolds number of
(solid curve) and for particles of equal
stopping times (dashed curve). A Reynolds number of
![]() has been adopted.
has been adopted.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6899fig2}
\end{figure}](/articles/aa/full/2007/17/aa6899-06/Timg157.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6899fig3}
\end{figure}](/articles/aa/full/2007/17/aa6899-06/Timg158.gif)
![]() (Eq. (20)), we end up with Eq. (24) including a correction term
(Eq. (20)), we end up with Eq. (24) including a correction term
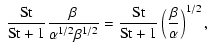
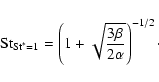
![]() ), however, the exact value of
), however, the exact value of
![]() is unimportant since F(y*) is always close to zero, and the
is unimportant since F(y*) is always close to zero, and the
![]() approximation is justified. It is only for
approximation is justified. It is only for
![]() that the RHS of
Eq. (24) starts to becomes significant and
that the RHS of
Eq. (24) starts to becomes significant and
![]() .
This is the weakly-turbulent or non-turbulent regime where class II eddies dominate even for small particles. In practise, however, it means that eddy crossing effects are important only if turbulence is very weak and we will not treat them
further in this paper.
.
This is the weakly-turbulent or non-turbulent regime where class II eddies dominate even for small particles. In practise, however, it means that eddy crossing effects are important only if turbulence is very weak and we will not treat them
further in this paper.
![]() in various limiting
regimes from the t-space solutions; similar results are easily obtained from the k-space
solutions (Sect. 3.1). Without loss of generality we take particle 1 to have the largest
stopping time, i.e.,
in various limiting
regimes from the t-space solutions; similar results are easily obtained from the k-space
solutions (Sect. 3.1). Without loss of generality we take particle 1 to have the largest
stopping time, i.e.,
![]() and
t12*=t1*. Moreover, we assume that
and
t12*=t1*. Moreover, we assume that
![]() ;
i.e., that
;
i.e., that
![]() and there is an extended inertial
range of eddies. Recall again that
and there is an extended inertial
range of eddies. Recall again that
![]() for
for
![]() ,
and that
,
and that
![]() will not exceed 1.
will not exceed 1.
![]() ,
we can also
ignore the
,
we can also
ignore the
![]() terms in Eq. (18). In addition, the
terms in Eq. (18). In addition, the
![]() approximation holds. Upon writing
approximation holds. Upon writing
![]() ,
Eqs. (17), (18) become linear with
,
Eqs. (17), (18) become linear with
![]() and we can write
and we can write
![]() as (see Appendix B)
as (see Appendix B)
![\begin{figure}
\par\includegraphics[width=12.6cm,clip]{6899fig4}
\end{figure}](/articles/aa/full/2007/17/aa6899-06/Timg206.gif)
![]() ,
,
![]() and there is no contribution from class
I eddies (Eq. (17)). Also, we can neglect the
and there is no contribution from class
I eddies (Eq. (17)). Also, we can neglect the
![]() terms in
Eq. (18) and the relative velocity simply becomes
terms in
Eq. (18) and the relative velocity simply becomes
![]() has been adopted. For
has been adopted. For
![]() ,
therefore, velocities are greatly suppressed since only class I eddies remain to generate relative velocities and relative velocities disappear completely for equal friction times. Also, the contours are much closer spaced since in this limit the velocity
,
therefore, velocities are greatly suppressed since only class I eddies remain to generate relative velocities and relative velocities disappear completely for equal friction times. Also, the contours are much closer spaced since in this limit the velocity
![]() is proportional to
is proportional to ![]() (see Eq. (26)).
(see Eq. (26)).
![]() was introduced for all stokes numbers
was introduced for all stokes numbers ![]() and eddy scales k. It proves to be quite adequate for most purposes; however, as noted in Sect. 3.5, small inaccuracies remain at the 10% level because the approximation overestimates the contributions of fast eddies to
and eddy scales k. It proves to be quite adequate for most purposes; however, as noted in Sect. 3.5, small inaccuracies remain at the 10% level because the approximation overestimates the contributions of fast eddies to
![]() and other velocity components. Figure A.1 shows the detailed behavior of the functions g
and h for
and other velocity components. Figure A.1 shows the detailed behavior of the functions g
and h for
![]() for Stokes numbers of
for Stokes numbers of
![]() ,
0.1, and 1.0. The inflection point for all three values of
,
0.1, and 1.0. The inflection point for all three values of ![]() is at k=k* (recall that
is at k=k* (recall that
![]() ). For k > k*, the functions are well approximated by power-laws of -1/3 and -3/4, respectively, i.e.,
g(k)=(k/k*)-1/3 and
h(k)=(k/k*)-3/4. The success of the approximation of Sect. 2 is due to the fact that the power in the weighting function k E(k) (dotted line; we multiply with k since we compare logarithmically) decreases rapidly with increasing k; thus by the time the assumption
g(k)=h(k)=1 becomes really bad, the relative contribution of successive terms has become small. For small
). For k > k*, the functions are well approximated by power-laws of -1/3 and -3/4, respectively, i.e.,
g(k)=(k/k*)-1/3 and
h(k)=(k/k*)-3/4. The success of the approximation of Sect. 2 is due to the fact that the power in the weighting function k E(k) (dotted line; we multiply with k since we compare logarithmically) decreases rapidly with increasing k; thus by the time the assumption
g(k)=h(k)=1 becomes really bad, the relative contribution of successive terms has become small. For small ![]() ,
the weighted contribution of eddy power has already become very small even before
,
the weighted contribution of eddy power has already become very small even before
![]() (the logic of CH03). For
(the logic of CH03). For
![]() or larger, the weighting function has dropped by nearly an order of magnitude by the time h(k) (the faster-decreasing function) has dropped to 0.3 (dashed-dotted line), and this seems to account for the success of our simple assumption.
or larger, the weighting function has dropped by nearly an order of magnitude by the time h(k) (the faster-decreasing function) has dropped to 0.3 (dashed-dotted line), and this seems to account for the success of our simple assumption.
![]() .
For
.
For ![]() ,
,
![]() and
and
![]() are both constant. Then, because
are both constant. Then, because
![]() ,
,
![]() scales as
scales as
![]() and becomes large at large k. Since
and becomes large at large k. Since
![]() for large
for large ![]() ,
we get that
,
we get that
![]() .
Similarly,
.
Similarly,
![]() ,
which is a bit shallower than the -3/4 exponent observed over most regions of interest (Fig. A.1). While the -2/3 exponent is reached at large k, the -3/4 exponent seems more appropriate at intermediate k. Yet, in our subsequent analysis, we will use the large-k limit for this exponent (-2/3) because it simplifies the math. Thus, we approximate the g and h behavior as follows: unity for k<k*, and power laws in k/k* with exponents of -1/3 and -2/3 for k>k*. Then Eq. (4) becomes
,
which is a bit shallower than the -3/4 exponent observed over most regions of interest (Fig. A.1). While the -2/3 exponent is reached at large k, the -3/4 exponent seems more appropriate at intermediate k. Yet, in our subsequent analysis, we will use the large-k limit for this exponent (-2/3) because it simplifies the math. Thus, we approximate the g and h behavior as follows: unity for k<k*, and power laws in k/k* with exponents of -1/3 and -2/3 for k>k*. Then Eq. (4) becomes
![\begin{displaymath}\int {\rm d}x\ x^{-5/3+p} \left( \frac{{\rm St}}{{\rm St} +x^{-2/3}} \right)^{n=[1,~2]}
\end{displaymath}](/articles/aa/full/2007/17/aa6899-06/img237.gif)
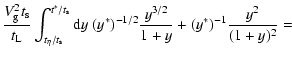
![$\displaystyle \frac{V_{\rm g}^2 t_{\rm s}}{t_{\rm L}} \left\{ (y^*)^{-1/2} \Big...
...(y^*)^{-1} \Big[ I_{\rm g}(y) \Big]^{t^*/t_{\rm s}}_{t_\eta/t_{\rm s}} \right\}$](/articles/aa/full/2007/17/aa6899-06/img240.gif)
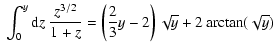
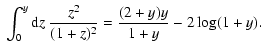
![]() .
Collecting these terms, the new expression for
.
Collecting these terms, the new expression for
![]() becomes
becomes