A&A 466, 521-529 (2007)
DOI: 10.1051/0004-6361:20066723
A. Tramacere1 - F. Massaro2 - A. Cavaliere2
1 - Dipartimento di Fisica, Università di Roma La Sapienza,
Piazzale A. Moro 2, 00185 Roma, Italy
2 - Dipartimento di Fisica, Università di Roma Tor Vergata,
via della Ricerca scientifica 1, 00133 Roma, Italy
Received 9 November 2006 / Accepted 31 January 2007
Abstract
Context. BL Lac objects undergo strong flux variations involving considerable changes in their spectral shapes. We specifically investigate the X-ray spectral evolution of Mrk 421 over a time span of about nine years.
Aims. We aim at statistically describing and physically understanding the large spectral changes in X rays observed in Mrk 421 over this time span.
Methods. We perform a homogeneous spectral analysis of a wide data set including archived observations with ASCA, BeppoSAX, RXTE, as well as published and unpublished XMM-Newton data. The presence of uncertainties is taken into account in our correlation analysis. The significance of the correlations found and possible spurious effects are studied with Monte Carlo simulations.
Results. We find that the Mrk 421 spectral energy distribution (SED) has a lower peak at energies that vary in the range, 0.1-10 keV while its X-ray spectrum is definitely curved. Parameterizing the X-ray spectra with a log-parabolic model, we find a positive correlation between the position and the height of the SED peak. In addition, we find a negative trend of the spectral curvature parameter vs. the SED peak energy.
Conclusions. We show that these relations between the spectral parameters are consistent with statistical or stochastic acceleration of the emitting particles, and provide insight into the physical processes occurring in BL Lac nuclei.
Key words: galaxies: active - galaxies: BL Lacertae objects: individual: Mrk 421 - radiation mechanisms: non-thermal - X-rays: galaxies
In the popular unification scenario of the Active Galactic Nuclei (AGNs) BL Lac objects are understood as sources in which a relativistic jet is produced by the central engine and points close to our line of sight, see Antonucci (1993) and Urry & Padovani (1995).
These objects are marked by featureless spectra and a high flux from the radio to the
![]() -ray band, endowed with strong variability and with high polarisation observed in
the optical band.
In fact, the emission from BL Lacs constitutes one of the best examples of direct
non-thermal radiation from particles not in thermal equilibrium with photons nor among
themselves. So these sources are keenly interesting to investigate particles acceleration mechanisms
in AGNs.
-ray band, endowed with strong variability and with high polarisation observed in
the optical band.
In fact, the emission from BL Lacs constitutes one of the best examples of direct
non-thermal radiation from particles not in thermal equilibrium with photons nor among
themselves. So these sources are keenly interesting to investigate particles acceleration mechanisms
in AGNs.
On a close look, their Spectral Energy Distribution (SED) appears as double-peaked. The
lower energy component is widely interpreted as synchrotron emission from highly relativistic
electrons with Lorentz factors ![]() in excess of 102; often it peaks at frequencies
in the IR to the X-ray band. The actual position of this peak
has been suggested by Padovani & Giommi (1995) as a marker for a classification; they define LBL (Low energy peaked BL Lac) objects with the first bump
in the IR-to-optical band, as opposed to the HBL (High energy peaked BL Lac) that peak
in the UV-X-ray band.
According to the Synchrotron Self Compton (SSC) emission mechanism,
the high frequency bump is to be attributed to inverse
Compton scattering of synchrotron photons by the same population of
relativistic electrons that produce the synchrotron emission (Jones et al. 1974; Ghisellini & Maraschi 1989). Both emissions are produced in a relativistic outflow
with a bulk Lorentz factor
in excess of 102; often it peaks at frequencies
in the IR to the X-ray band. The actual position of this peak
has been suggested by Padovani & Giommi (1995) as a marker for a classification; they define LBL (Low energy peaked BL Lac) objects with the first bump
in the IR-to-optical band, as opposed to the HBL (High energy peaked BL Lac) that peak
in the UV-X-ray band.
According to the Synchrotron Self Compton (SSC) emission mechanism,
the high frequency bump is to be attributed to inverse
Compton scattering of synchrotron photons by the same population of
relativistic electrons that produce the synchrotron emission (Jones et al. 1974; Ghisellini & Maraschi 1989). Both emissions are produced in a relativistic outflow
with a bulk Lorentz factor
![]() ;
when observed at an angle
;
when observed at an angle ![]() they
are subjected to the effects of a beaming factor
they
are subjected to the effects of a beaming factor
![]() .
.
With its redshift z = 0.031, Mrk 421 is among the closest and best studied HBL.
In fact, it is one of the brightest BL Lac objects in the UV and in the X-ray bands,
observed in ![]() rays by EGRET (Lin et al. 1992); it was also the first extragalactic
source detected at TeV energies in the range 0.5-1.5 TeV by the Whipple telescopes (Punch
et al. 1992; Petry et al. 1996).
rays by EGRET (Lin et al. 1992); it was also the first extragalactic
source detected at TeV energies in the range 0.5-1.5 TeV by the Whipple telescopes (Punch
et al. 1992; Petry et al. 1996).
The source is classified as HBL because its synchrotron emission peak ranges from a fraction of a keV to several keVs. In fact, its flux changes go along with strong spectral variations (Fossati et al. 2000a). The spectral shape generally exhibits a marked curvature, well described by a log-parabolic model (Landau et al. 1986).
We present here a new study of the time-variable properties of its SED based on the full collection of XMM-Newton data taken with EPIC CCD cameras, sensitive in the energy range 0.3-10 keV; we also use previous X-ray observations with ASCA, BeppoSAX, RXTE, EUVE to cover an overall time span of nine years. In particular, XMM-Newton observed Mrk 421 many times, and a large amount of data has been collected. Some of these observations have been recently analysed by other authors, but a full report of all observations between May 2000 and November 2005 had not been published yet. We perform a new analysis of all XMM-Newton observations of Mrk 421, particularly relevant as its synchrotron emission peaks in the XMM-Newton energy range.
Specifically, extending the previous work of Tanihata et al. (2004), we study correlations between the position and the height of SED peak, and interpret them in terms of signatures of the synchrotron emission. We also investigate a new correlation of the SED peak with the spectral curvature, and discuss its implications as to the electron acceleration mechanisms.
This paper is organized as follows. Section 2 describes the data set and our procedure to reduce the XMM-Newton data. Section 3 reports our data analysis, including temporal and spectral investigations. The statistical analysis and the comparison with numerical simulations and theoretical interpretations are discussed in Sects. 4 and 5. Our conclusions are given and discussed in Sect. 6.
Table 1: XMM-Newton Log of observations of Mrk 421.
Mrk 421 was observed by XMM-Newton between 25/05/00 and 9/11/05, on more than twenty occasions, by means of all EPIC CCD cameras: the EPIC-PN (Struder et al. 2001), and EPIC-MOS (Turner et al. 2001), operating in different modes and with different filters as described in Table 1. These data were reduced as follows. Extractions of all light curves, source and background spectra were done using the XMM-Newton Science Analysis System (SAS) v6.5.0. The Calibration Index File (CIF) and the summary file of the Observation Data File (ODF) were generated using Updated Calibration File (CCF) following the "User's Guide to the XMM-Newton Science Analysis Syste'' (Issue 3.1) (Loiseau et al. 2004) and "The XMM-Newton ABC Guide'' (vers. 2.01) (Snowden et al. 2004). Event files were producted by XMM-Newton EMCHAIN pipeline. The standard reduction of the events list for MOS data, was performed involving subtraction of hot and dead pixels, removal of events due to the electronic noise and correction of event energies for charge transfer losses.
To provide the most conservative screening criteria MOS data files were also filtered to
include all single to quadruple events (PATTERN ![]() 12) with pulse high rate in the
range of 500 to 12 000 eV and with expression FLAG = 0. Lightcurves for every
dataset were extracted and all high-background time intervals,
were filtered out by excluding time interval contaminated by solar flare signal.
To perform this selection, the count rate in the 10-15 keV band for the entire MOS detectors were determined. We first discarded only time intervals with a count rate that exceeds 0.35 counts per
second as indicated in the "User's Guide to the XMM-Newton Science Analysis System'' (Issue 3.1) (Loiseau et al. 2004). However applying this criterion, we noticed that a low background state, placed between two high neighboring peaks due to a solar flare,
can even include a residual contamination to the source signal which modifies the spectral
distribution. We adopted a more conservative selection for good
time intervals, because we preferred to have a high quality signal,
excluding time ranges that appeared contaminated by solar flares.
Then we selected good time intervals by direct inspection far from solar flare peaks and
without count rate variations on time scales shorter than 500 s.
The TABGTIGEN task of XMM-Newton Science Analysis System (SAS) was used to build
good time intervals.
12) with pulse high rate in the
range of 500 to 12 000 eV and with expression FLAG = 0. Lightcurves for every
dataset were extracted and all high-background time intervals,
were filtered out by excluding time interval contaminated by solar flare signal.
To perform this selection, the count rate in the 10-15 keV band for the entire MOS detectors were determined. We first discarded only time intervals with a count rate that exceeds 0.35 counts per
second as indicated in the "User's Guide to the XMM-Newton Science Analysis System'' (Issue 3.1) (Loiseau et al. 2004). However applying this criterion, we noticed that a low background state, placed between two high neighboring peaks due to a solar flare,
can even include a residual contamination to the source signal which modifies the spectral
distribution. We adopted a more conservative selection for good
time intervals, because we preferred to have a high quality signal,
excluding time ranges that appeared contaminated by solar flares.
Then we selected good time intervals by direct inspection far from solar flare peaks and
without count rate variations on time scales shorter than 500 s.
The TABGTIGEN task of XMM-Newton Science Analysis System (SAS) was used to build
good time intervals.
Photons were extracted from an annular region using different apertures to minimize pile-up, which affects MOS data. The mean value of external radius for the annular region is 40''. To filter out pixels affected by significant pile-up, the internal region was selected by using EPATPLOT task in XMM-Newton Science Analysis System (SAS) for each observation.
In FULL WINDOW images, the background spectrum was extracted from a circular region of the size comparable to the source region, in a place where visible sources were not present (typically off axis). For other observations, in PARTIAL WINDOW images, no regions sufficiently far from the
source for the background extraction were found.
In these cases we used background from blank-field event files (www.sr.bham.ac.uk).
Anyway we estimated that the average X-rays background flux was
always at ![]() 1% level of source flux, resulting in a negligible
contamination in the spectral parameter determination.
The Photon Redistribution Matrix and the Ancillary Region
File were created for each observation, by using RMFGEN and ARFGEN tasks of SAS.
A more restricted energy range (0.5-10 keV) was used to account
for possible residual calibration uncertainties.
To insure the validity of Gaussian statistics, data were grouped by combining
instrumental channels so that each new bin comprises 40 counts or more.
1% level of source flux, resulting in a negligible
contamination in the spectral parameter determination.
The Photon Redistribution Matrix and the Ancillary Region
File were created for each observation, by using RMFGEN and ARFGEN tasks of SAS.
A more restricted energy range (0.5-10 keV) was used to account
for possible residual calibration uncertainties.
To insure the validity of Gaussian statistics, data were grouped by combining
instrumental channels so that each new bin comprises 40 counts or more.
![\begin{figure}
\par\includegraphics[height=7.9cm,width=6.5cm,angle=-90,clip]{672...
...cludegraphics[height=7.9cm,width=6.5cm,angle=-90,clip]{6723fig1b.ps}\end{figure}](/articles/aa/full/2007/17/aa6723-06/Timg12.gif) |
Figure 1:
XMM-Newton EPIC-MOS spectrum from the observation of Mkn 421 performed on 08/05/01.
Left: the systematic deviations on both sides of the residuals from a best fit PL
with Galactic
|
| Open with DEXTER | |
To study the spectral behaviour of Mrk 421 over a wide time interval we also used other X-ray observations performed with ASCA, RXTE, EUVE and BeppoSAX, with references given below. All these observations were analysed in terms of the same spectral model as the XMM-Newton ones homogeneous (described in Sect. 3), so we have obtained a sample of spectral parameters that covers about 9 years of Mrk 421 observations in X rays.
Mrk 421 was pointed continuously by ASCA for 7 days between 23 April of 1998 and 30 April 1998, with all its detectors on: two SISs (Stage Imaging Spectrometers) and two GISs (Gas Imaging Spectrometers). To extend the ASCA data base to higher energy, these observations were coordinated with RXTE, specifically with the PCA (Proportional Counter Array; 2-60 keV) and the HEXTE (High Energy X-ray Timing Experiment; 15-200 keV) instruments on board RXTE. We refer to Tanihata et al. (2001) for the ASCA data reduction and spectral analysis, and to Tanihata et al. (2004) for the the combination of RXTE with ASCA.
BeppoSAX observed Mrk 421 on 7 occasions during 1997, in which all instruments on board were operating: LECS (Low Energy Concentrator Spectrometer; 0.1-10 keV), MECS (Medium Energy Concentrator Spectrometer; 1.3-10 keV) and the PDS (Phoswich Detector System; 13-300 keV). Spectral analyses of these observations are reported in Massaro et al. (2004) and references therein. Concerning 1998 BeppoSAX observations of Mrk 421, started 3 days before the ASCA pointing, Tanihata et al. (2004) reported the spectral analysis of data obtained by the LECS and the MECS (see also: Maraschi et al. 1999; Fossati et al. 2000a,b; Massaro et al. 2004). In May 1999 Mrk 421 was pointed for about 4 days; two long uninterrupted observations were performed from 26 April and 3 May, 2000, followed by another observation from 9 May 2000 and 12 May 2000. In all observations of 1999 and 2000, Mrk 421 showed a strong variability on time scales of days. Data reduction and spectral analysis of these BeppoSAX observations are described in the references above.
Our XMM-Newton spectral analysis was performed with the XSPEC software
package, version 11.3 (Arnaud 1996).
Before evaluating any spectral curvature in the 0.5-10 keV range, it is important
to reliably assess the absorption at low energies due to interstellar gas.
In the optical, high resolution images of the host, early-type galaxy of Mrk 421 do not
show in the brightness profile any evidence of large amounts of absorbing material (Urry
et al. 2000). In X-rays, it has been shown by Fossati et al. (2000b) and confirmed by Tanihata et al. (2004) and Massaro et al. (2004) that describing the spectral shape in
terms of absorption not only would require a column density much higher than the Galactic
value
![]()
![]() 1020 cm-2 (Lockman & Savage 1995), but also would yield in any case unacceptable fits with very high
1020 cm-2 (Lockman & Savage 1995), but also would yield in any case unacceptable fits with very high ![]() .
These findings motivate us to
consider intrinsically curved spectra with the column density fixed at the Galactic value,
in agreement with the above analyses of Mrk 421.
.
These findings motivate us to
consider intrinsically curved spectra with the column density fixed at the Galactic value,
in agreement with the above analyses of Mrk 421.
In fact, we tried a number of different spectral models:
single (PL) and broken (BPL) power-laws; a power-law with an exponential cutoff at high
energy (PLC); and a logarithmic parabola (LP) in the form
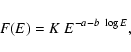 |
(1) |
![\begin{figure}
\par\includegraphics[height=6.6cm,width=5.35cm,angle=-90,clip]{67...
...ludegraphics[height=6.7cm,width=5.35cm,angle=-90,clip]{6723fig2b.ps}\end{figure}](/articles/aa/full/2007/17/aa6723-06/Timg17.gif) |
Figure 2: (Left panel): XMM-Newton light curve in the energy range 0.5-10 keV. (Right panel): XMM-Newton light curve in the energy range 4-10 keV, where count rate variations are evident between the two selected time regions. |
| Open with DEXTER | |
We find that the PL model is not adequate to describe the spectral shape, consistent with
other X-ray analyses reported above. In our observations we mostly obtained unacceptable
values for ![]() (higher than 1.5); in the few cases where the
(higher than 1.5); in the few cases where the ![]() is
acceptable, the residuals show systematic deviations clearly indicating
the presence of a curvature, see Fig. 1.
PLC and BPL models give better spectral descriptions, but they also have drawbacks.
The PLC model often estimates the cut-off energy at much higher than 10 keV, indicating
that in the instrumental range there is a mild curvature rather than a sharp exponential
cutoff. The BPL model gives systematic excess at high energies.
The LP model describes the spectral shape more satisfactorily than all the
above ones, giving systematically lower
is
acceptable, the residuals show systematic deviations clearly indicating
the presence of a curvature, see Fig. 1.
PLC and BPL models give better spectral descriptions, but they also have drawbacks.
The PLC model often estimates the cut-off energy at much higher than 10 keV, indicating
that in the instrumental range there is a mild curvature rather than a sharp exponential
cutoff. The BPL model gives systematic excess at high energies.
The LP model describes the spectral shape more satisfactorily than all the
above ones, giving systematically lower ![]() values and fewer residuals.
values and fewer residuals.
The main goal of our analysis is the search of possible
correlations between the spectral curvature (b), the SED peak energy (![]() ), and the
corresponding SED peak value (
), and the
corresponding SED peak value (![]() ).
To estimate the correlation between the parameters of the spectral energy distribution
S(E)=E2F(E) we often use in place of Eq. (1) the equivalent functional form (LPS),
see Sect. 3 in Massaro et al. (2004) and Tanihata et al. (2004)
).
To estimate the correlation between the parameters of the spectral energy distribution
S(E)=E2F(E) we often use in place of Eq. (1) the equivalent functional form (LPS),
see Sect. 3 in Massaro et al. (2004) and Tanihata et al. (2004)
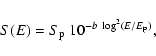 |
(2) |
We shall see that the estimates of the curvature parameter b are sensitive to changes of the source state during a pointing; so a time averaged spectrum may have a different curvature from the time resolved ones. To avoid any such bias, we segmented our data at times when significant (3 sigma) count rate variations occur, subject to the constraint of having in each time resolved spectrum more than 120 spectral bins after rebinning as indicated in Sect. 2. The duration of our time segments was shorter than a few 104 s.
An example of this effect is apparent from the two light curves plotted in Fig. 2 in the energy range 0.5-10 keV (left panel) and 4-10 keV (right panel) of the same observation on 13/11/00. The significant decrease in the count rate of the higher-energy curve is only barely detecable in the total light curve. Then the spectral analysis of the two time regions (A and B, see Fig. 2) shows a spectral dynamics not apparent when the whole data set is considered.
The spectral best fit values for all XMM-Newton observations are reported in Table 2. All statistical errors refer to the 68% confidence level (one Gaussian standard deviation).
Table 2: Spectral parameters of the LP model of time resolve spectra for the 0.5-10 XMM-Newton EPIC-MOS observations of Mrk 421.
Our results generally agree with those from observations with BeppoSAX, ASCA and Swift (see the references above and Tramacere et al. 2006 for the Swift analysis). In particular, we find values of SED peak energy and of the curvature parameter consistent with their values, but we find differences with other XMM-Newton analyses. Specifically, Sembay et al. (2002) analysed XMM-Newton observations during 2000, 2001 and 2002, but they used an energy range restricted to 2-10 keV and did not search for any curved shape. Ravasio et al. (2004), who studied EPIC-PN observations performed on 04/11/02, 14/11/02 and 01/12/02, didn't found a significant improvement using the log-parabolic model respect to the power-law one. The difference between their and our analysis is likely due to our more conservative criterion to subtract solar flares in the data reduction.
![\begin{figure}
\par\includegraphics[angle=-90,width=12.7cm,clip]{6723fig3.ps}\end{figure}](/articles/aa/full/2007/17/aa6723-06/Timg23.gif) |
Figure 3:
The scatter plot of the peak energy |
| Open with DEXTER | |
Table 3:
Statistical parameters for the correlation between ![]() and
and ![]() .
.
Correlations between ![]() and
and ![]() provide interesting indications concerning
the driver of the spectral changes in X-rays, in terms of the synchrotron emission
mechanism from one dominant homogeneous component. In this
framework (Rybicki & Lightman 1979) the dependence of
provide interesting indications concerning
the driver of the spectral changes in X-rays, in terms of the synchrotron emission
mechanism from one dominant homogeneous component. In this
framework (Rybicki & Lightman 1979) the dependence of ![]() on
on ![]() is in the form of a power-law:
is in the form of a power-law:
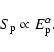 |
(3) |
On a heuristic stand, inspection of Fig. 3 indicates that the two last cases are unlikely; next we proceed to a formal statistical analysis.
We investigate whether and how ![]() and
and ![]() correlate.
The analysis is performed on two data sets: the XMM set and the FULL set.
The former corresponds to the results of the spectral analysis in Sect. 3, while the
latter is obtained on adding the results from previous analyses as reported in Sect. 3.
correlate.
The analysis is performed on two data sets: the XMM set and the FULL set.
The former corresponds to the results of the spectral analysis in Sect. 3, while the
latter is obtained on adding the results from previous analyses as reported in Sect. 3.
We test for correlations between the spectral parameters on using both a linear correlation coefficient (
![]() )
and a logarithmic one (
)
and a logarithmic one (
![]() ), and fit the data with a linear and log-linear model following the statistical methods described in D'Agostini (2005) (see also Appendix A).
), and fit the data with a linear and log-linear model following the statistical methods described in D'Agostini (2005) (see also Appendix A).
Results from our correlation study are given in Table 3.
The correlation coefficient
![]() is significant, specifically with a chance probability value close to zero. The data in the XMM set may be described by a power-law function as in Eq. (3);
the value of
is significant, specifically with a chance probability value close to zero. The data in the XMM set may be described by a power-law function as in Eq. (3);
the value of ![]() so obtained is
so obtained is ![]() = 1.4
= 1.4 ![]() 0.3. On fitting the FULL set we find the power-law index
0.3. On fitting the FULL set we find the power-law index
![]()
![]() 0.1, consistent with the
above value. Even if we took the range of
0.1, consistent with the
above value. Even if we took the range of ![]() between 0.5-1.0 keV where the
run of the FULL data apparently steepens, the values of the best fit would yield
between 0.5-1.0 keV where the
run of the FULL data apparently steepens, the values of the best fit would yield
![]()
![]() 0.1, quite far from 4. This analysis confirms that the cases
0.1, quite far from 4. This analysis confirms that the cases
![]() and
and ![]() are those most relevant as dominant mechanisms.
are those most relevant as dominant mechanisms.
A closer analysis and an interpretation of these results are given in the next subsection.
A sensitive point in our statistical analysis and its interpretation is the presence of "hidden'' parameters contributing to variability and/or to correlations. On the basis of the formalism that for reader's convenience we recall in Appendix A, in the following we discuss in details the possibility that a correlation may be introduced by a parameter that is not directly determined from the data (whence the name "hidden'').
This issue arises when one estimates two parameters, say x and y, statistically independent but depending physically on a third parameter, k say, that is not directly observed ("hidden''); in other words, we observe x=x(x', k) and y=y(y', k). Again, a correlation will arise between x and y due to their dependence on k, and this may add to any physical correlation between x' and y'.
A case in point is provided by the beaming effects.
In BL Lacs beaming is a key property; though only rarely measured directly, this
can introduce dependence between the observed quantities ![]() and
and ![]() .
It is convenient to distinguish the variables
.
It is convenient to distinguish the variables
![]() ,
,
![]() in the beam reference frame from the observed ones expressed as
in the beam reference frame from the observed ones expressed as
| (4) |
Clearly, the actual contribution depends on the probability density functions (PDF) of
![]() ,
,
![]() and
and ![]() .
To study this, we have generated with a Monte Carlo code a sample of uncorrelated pairs of variables (x',y'). We then have transformed them
according to Eq. (4), that is, with
.
To study this, we have generated with a Monte Carlo code a sample of uncorrelated pairs of variables (x',y'). We then have transformed them
according to Eq. (4), that is, with
![]() and
and
![]() ,
choosing
,
choosing
![]() as a typical value for Mrk 421.
The x' variables were generated so that the x variables have the same PDF as
as a typical value for Mrk 421.
The x' variables were generated so that the x variables have the same PDF as ![]() ;
on the other hand, the y' variables were generated from a normal distribution with mean
value
;
on the other hand, the y' variables were generated from a normal distribution with mean
value ![]() and
and
![]() .
We impose that the y variables have the same dispersion as
.
We impose that the y variables have the same dispersion as ![]() in the FULL data; this dispersion depends not only on
in the FULL data; this dispersion depends not only on ![]() but also on the distribution of
but also on the distribution of ![]() ,
so we have to derive a constraint on the value of
,
so we have to derive a constraint on the value of
![]() .
In fact, the standard deviation of the observed values of
.
In fact, the standard deviation of the observed values of ![]() is about 120 (erg
is about 120 (erg
![]()
![]() )
to be compared with the average
value of about 290 (Fig. 3); assuming, as an extreme case, that the dispersion
)
to be compared with the average
value of about 290 (Fig. 3); assuming, as an extreme case, that the dispersion
![]() of
of ![]() is generated only by the variance
is generated only by the variance
![]() ,
and applying standard propagation, we obtain
,
and applying standard propagation, we obtain
![]() .
.
We now generate ![]() from a normal distribution with
from a normal distribution with
![]() and
and
![]() = 0.75, and find a correlation coefficient
= 0.75, and find a correlation coefficient
![]() between the
logarithms of x and y. On decreasing the variance of y' and increasing that of
between the
logarithms of x and y. On decreasing the variance of y' and increasing that of ![]() ,
the correlation increases but only slightly; for example, if we take
,
the correlation increases but only slightly; for example, if we take
![]() and increase
the value of
and increase
the value of
![]() to 0.95, we obtain
to 0.95, we obtain
![]() .
.
In summary, the beaming factor can affect the observed correlation coefficient, but only
up to values
![]() which are significantly below the observed value 0.67.
We conclude that beaming alone is responsible neither for the values of
which are significantly below the observed value 0.67.
We conclude that beaming alone is responsible neither for the values of
![]() nor for the correlation observed.
We stress that the value
nor for the correlation observed.
We stress that the value
![]() ,
bounded by the dispersion
of the full data, is remarkably low when compared to the average typical value of
,
bounded by the dispersion
of the full data, is remarkably low when compared to the average typical value of
![]() ,
and implies the beaming factor to have been closely constant for
Mrk 421 during our observational span of about 9 yr.
,
and implies the beaming factor to have been closely constant for
Mrk 421 during our observational span of about 9 yr.
It follows that both the variations of ![]() corresponding to the estimated values of
corresponding to the estimated values of ![]() and their scatter must be importantly contributed by a physical
process in the beam rest frame, such as variations of magnetic fields or scaling up or
down of all the electron energies.
and their scatter must be importantly contributed by a physical
process in the beam rest frame, such as variations of magnetic fields or scaling up or
down of all the electron energies.
In fact, a second effect coming from a "hidden'' parameter with its fluctuations is to
produce scatter of the data. As explained in Appendix A, it is
possible to account for this effect by adding an "extravariance'' in the
likelihood function.
In the case of the XMM data set, the extravariance accounting for their scatter
is estimated at
![]()
![]() 0.05, and for the corresponding value of the slope we
obtain
0.05, and for the corresponding value of the slope we
obtain
![]()
![]() 0.1, whilst for the FULL data set we obtain
0.1, whilst for the FULL data set we obtain
![]()
![]() 0.02 and
0.02 and
![]()
![]() 0.05 (see Table 3).
The derived values of the
0.05 (see Table 3).
The derived values of the ![]() index are considerably affected by the
extravariance; in fact, the extravariance term in the log-likelihood function dominates
the term from measurement uncertainties, to the point of providing power-law indices
close to those obtained simply from fitting the data with no weights for their
precision.
index are considerably affected by the
extravariance; in fact, the extravariance term in the log-likelihood function dominates
the term from measurement uncertainties, to the point of providing power-law indices
close to those obtained simply from fitting the data with no weights for their
precision.
Such different values of ![]() and
and
![]() (Table 3) lead us to test an actual change in the power-law index in Eq. (3) at about 1 keV.
To do this, we split the FULL set into two sets, one with
(Table 3) lead us to test an actual change in the power-law index in Eq. (3) at about 1 keV.
To do this, we split the FULL set into two sets, one with
![]() keV and the other
with
keV and the other
with
![]() keV; results of fits are reported in the last two lines of Table 3.
The values of
keV; results of fits are reported in the last two lines of Table 3.
The values of ![]() found for the two data sets differ significantly, being
found for the two data sets differ significantly, being
![]()
![]() 0.1 and
0.1 and
![]()
![]() 0.1, for
0.1, for
![]() keV and
keV and
![]() keV, respectively. This could be interpreted as a change of
keV, respectively. This could be interpreted as a change of ![]() with the state of the source, and we estimate the associated likelihood by means of a Monte Carlo simulation.
We generate a set of values for
with the state of the source, and we estimate the associated likelihood by means of a Monte Carlo simulation.
We generate a set of values for ![]() ,
,
![]() as follows:
as follows:
Finally, we perform a study of correlation between b and ![]() ,
aimed at pinpointing
possible signatures of the electron acceleration processes in the spectral
evolution of a homogeneous dominant component.
The same data set and statistical tools of the previous section are used.
,
aimed at pinpointing
possible signatures of the electron acceleration processes in the spectral
evolution of a homogeneous dominant component.
The same data set and statistical tools of the previous section are used.
Such a correlation had never been tested previously.
An analysis of XMM set shows that the correlation coefficients are
negative and low, that is,
![]() and
and
![]() (defined in Sect. 4).
The former corresponds to a low chance occurrence (0.05), but this is significantly high (0.24) for
(defined in Sect. 4).
The former corresponds to a low chance occurrence (0.05), but this is significantly high (0.24) for
![]() .
By direct inspection we see that there are three points (enclosed by the dashed ellipse in Fig. 4) corresponding to the same XMM pointing on 01/11/00, that maximally
deviate from the average sample behaviour.
On excising this observation and reanalysing the remaining data (denoted by XMM * in Table 5) we obtain the substantially higher correlation coefficients
.
By direct inspection we see that there are three points (enclosed by the dashed ellipse in Fig. 4) corresponding to the same XMM pointing on 01/11/00, that maximally
deviate from the average sample behaviour.
On excising this observation and reanalysing the remaining data (denoted by XMM * in Table 5) we obtain the substantially higher correlation coefficients
![]() and
and
![]() ,
corresponding to the high significance, given in Table 4.
,
corresponding to the high significance, given in Table 4.
To see whether the 01/11/00 observation constitutes a unique event, we analysed the FULL
data set with and without (denoted by FULL *) this pointing; Table 4 shows that the values
of
![]() and
and
![]() for FULL and FULL * are close, indicating that the observation
excised has not materially changed the overall statistical behaviour.
for FULL and FULL * are close, indicating that the observation
excised has not materially changed the overall statistical behaviour.
These values are sufficiently high to warrant a brief discussion of the importance of the correlation found, along two ways. This pointing may constitute just a rare source state in our sample. On the other hand, this may not constitute a singular event, considering that
all XMM and FULL data (Fig. 4) appear to outline an upper limit to the curvature observed at any values of ![]() .
For example, for
.
For example, for ![]() around 1 keV, we never observe curvatures higher than about
around 1 keV, we never observe curvatures higher than about
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=11.3cm,clip]{6723fig4.ps}\end{figure}](/articles/aa/full/2007/17/aa6723-06/Timg96.gif) |
Figure 4:
The scatter plot of the peak energy |
| Open with DEXTER | |
Table 4:
Statistical parameters for the correlation between ![]() and b.
and b.
The inverse correlation between b and ![]() may be interpreted in the framework of
acceleration processes of the emitting electrons.
may be interpreted in the framework of
acceleration processes of the emitting electrons.
A first interpretation of the correlation between b and ![]() is in the
framework of statistical acceleration (Massaro et al. 2006, and references therein). In
this scenario the probability for a particle to be further accelerated decreases at high
energies, being inversely proportional to the energy itself. For example, this may occur
when the particles are confined by a magnetic field, and the confinement efficiency
decreases as the gyration radius increases.
is in the
framework of statistical acceleration (Massaro et al. 2006, and references therein). In
this scenario the probability for a particle to be further accelerated decreases at high
energies, being inversely proportional to the energy itself. For example, this may occur
when the particles are confined by a magnetic field, and the confinement efficiency
decreases as the gyration radius increases.
In such cases the electron energy distribution is curved into a log-parabolic shape, and
its curvature r is related to the fractional acceleration gain ![]() as given by
Massaro et al. (2006):
as given by
Massaro et al. (2006):
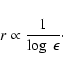 |
(5) |
| (6) |
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{6723fig5a.ps}\hspace*{4mm}
\includegraphics[width=6.2cm,clip]{6723fig5b.ps} \end{figure}](/articles/aa/full/2007/17/aa6723-06/Timg112.gif) |
Figure 5:
Histograms of |
| Open with DEXTER | |
On the other hand, a connection of log-parabolic spectra with acceleration may be also
understood in the framework provided by the Fokker-Planck equation (Kardashev 1962)
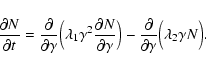 |
(7) |
![\begin{displaymath}%
N(\gamma,t) \propto \rm\gamma^{-1}~exp\Big[\frac{-(\Lambda_1 +
\Lambda_2-ln(\gamma/\gamma_0))^2}{4\Lambda_1}\Big],
\end{displaymath}](/articles/aa/full/2007/17/aa6723-06/img117.gif) |
(8) |
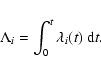
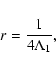 |
(9) |
On the other hand, the peak energy of
![]() is given by
is given by
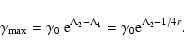 |
(10) |
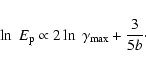 |
(11) |
In this framework the inverse correlation constitutes the signature of a stochastic
acceleration process that broadens
![]() as to decrease its curvature while
as to decrease its curvature while ![]() is driven to higher values.
is driven to higher values.
Using a large set of X-ray observations of Mrk 421,
we have presented and discussed the results concerning the spectral variations. We have
shown that correlations exist between the peak values ![]() of its SED and the peak positions
of its SED and the peak positions ![]() ,
and between the spectral curvature b and
,
and between the spectral curvature b and ![]() .
.
The former may be interpreted in the framework of synchrotron emission. The values of the
power-law slopes obtained from our fits in Sect. 4 are bounded by
![]()
![]() 0.1. As such, they rule out the case
0.1. As such, they rule out the case
![]() applying if the beaming factor
applying if the beaming factor ![]() were the dominant driver of the spectral evolution; they are instead
compatible with a combined effect of variations of B (corresponding to
were the dominant driver of the spectral evolution; they are instead
compatible with a combined effect of variations of B (corresponding to
![]() )
and of a rescaling of
)
and of a rescaling of ![]() (
(
![]() ).
).
In parallel, a secondary role for ![]() is confirmed by the bound r < 0.3 it can
contribute to the observed
is confirmed by the bound r < 0.3 it can
contribute to the observed
![]() correlation coefficient value
correlation coefficient value
![]() .
On the other hand, we have set an upper limit to the beaming variance; from the
analysis in Sect. 4.2 we have found a low fractional variation
.
On the other hand, we have set an upper limit to the beaming variance; from the
analysis in Sect. 4.2 we have found a low fractional variation
![]() even on considering conservative values
even on considering conservative values
![]() .
The remarkable implication is that the beaming factor of Mrk 421
remained closely constant during a time span of about 9 years.
.
The remarkable implication is that the beaming factor of Mrk 421
remained closely constant during a time span of about 9 years.
This limit is relevant in the framework of the internal shock scenario.
This assumes that shells ejected from the central engine with slightly different
relativistic velocities and slightly differing angles collide in the jet at sub-parsec
scales and produce flares. The temporal behaviour and the radiative efficiency of this
process depend on the collision frequency and on the collision energetics, respectively;
two versions are found in the literature.
Guetta et al. (2004) assume that shells are ejected at a frequency
close to 10-4 Hz, with ![]() values distributed around the average value of about 15after a random (uniform) distribution with a considerable dispersion, about 3.
The dispersion is considerably larger than the values obtained from our
analysis. On the other hand, Tanihata et al. (2003) assume values of
values distributed around the average value of about 15after a random (uniform) distribution with a considerable dispersion, about 3.
The dispersion is considerably larger than the values obtained from our
analysis. On the other hand, Tanihata et al. (2003) assume values of ![]() following a normal distribution with
following a normal distribution with
![]() and ejection intervals
around 600 s; whence they obtain a good reproduction of the temporal behaviour, but also a very low radiative efficiency. The upper limit derived from our analysis, much lower than the value assumed by Guetta et al. (2004), emphasizes the efficiency problem reported by
Tanihata et al. (2003).
and ejection intervals
around 600 s; whence they obtain a good reproduction of the temporal behaviour, but also a very low radiative efficiency. The upper limit derived from our analysis, much lower than the value assumed by Guetta et al. (2004), emphasizes the efficiency problem reported by
Tanihata et al. (2003).
The correlation we have observed in Mrk 421 between b and ![]() is interesting in the
framework of the electron acceleration mechanisms. In Mrk 421
we systematically observed a decrease of the curvature b as the peak energy
is interesting in the
framework of the electron acceleration mechanisms. In Mrk 421
we systematically observed a decrease of the curvature b as the peak energy ![]() increased. To understand this behaviour we have used in Sect. 5 a Fokker-Planck
description of a dominant electron energy distribution. The solution of this
equation for an initial mono-energetic injection predicts (see Eqs. (8)-(11))
that with ongoing stochastic acceleration the curvature should decrease while
the peak energy moves to higher energies.
A more detailed understanding of this dynamics requires a full computation including
radiative cooling and fixing the relative weights of the systematic vs.
the stochastic acceleration component; this will be studied
in a different paper (Tramacere et al. 2007, in prep.).
An alternative explanation of this correlation is discussed in Sect. 5 in terms of
statistical, energy-dependent acceleration probability. This leads again to a correlation as observed.
increased. To understand this behaviour we have used in Sect. 5 a Fokker-Planck
description of a dominant electron energy distribution. The solution of this
equation for an initial mono-energetic injection predicts (see Eqs. (8)-(11))
that with ongoing stochastic acceleration the curvature should decrease while
the peak energy moves to higher energies.
A more detailed understanding of this dynamics requires a full computation including
radiative cooling and fixing the relative weights of the systematic vs.
the stochastic acceleration component; this will be studied
in a different paper (Tramacere et al. 2007, in prep.).
An alternative explanation of this correlation is discussed in Sect. 5 in terms of
statistical, energy-dependent acceleration probability. This leads again to a correlation as observed.
We wish to stress a common point to both views, that is, the relevance of the curvature
parameter to understand the observed spectral evolution of the source. The negative
correlation between b and ![]() strongly indicates the dynamics of
strongly indicates the dynamics of ![]() to be related to stochastic or to statistical (and energy dependent) acceleration mechanisms; it would
not hold with the beaming as the main driver of spectral variations. So the results from
this second correlation are consistent with those from the first, namely, the
to be related to stochastic or to statistical (and energy dependent) acceleration mechanisms; it would
not hold with the beaming as the main driver of spectral variations. So the results from
this second correlation are consistent with those from the first, namely, the
![]() correlation.
correlation.
No significant correlation has been found between ![]() and b. This lack may arise
from the opposite signs of the correlations between
and b. This lack may arise
from the opposite signs of the correlations between
![]() and
and
![]() adding to the considerable dispersion of the data.
adding to the considerable dispersion of the data.
Finally, another view on this matter is provided by the analysis given in Sect. 5 (see
Fig. 5) concerning the PDF of the spectral parameters ![]() ,
b and
,
b and ![]() .
It is seen that
.
It is seen that ![]() and b have enough symmetry in their PDF to be reasonably
approximated by a Gaussian distribution with minor deviations in the tail (left panels).
The parameter
and b have enough symmetry in their PDF to be reasonably
approximated by a Gaussian distribution with minor deviations in the tail (left panels).
The parameter ![]() ,
on the contrary, shows a more skewed distribution (right upper
panel), that could be better approximated by a log-normal shape, i.e., by a Gaussian in
the variable
,
on the contrary, shows a more skewed distribution (right upper
panel), that could be better approximated by a log-normal shape, i.e., by a Gaussian in
the variable
![]() (right bottom panel). We note that a similar distribution has been
successfully used also to describe the statistical properties of the GRB peak energy
distribution that may depend on broadly similar physics (Ioka & Nakamura 2002).
(right bottom panel). We note that a similar distribution has been
successfully used also to describe the statistical properties of the GRB peak energy
distribution that may depend on broadly similar physics (Ioka & Nakamura 2002).
A point to stress is that the log-normal distribution constitutes the asymptotic limit
from the central limit theorem in multiplicative form; in fact, it has been shown by
Ioka & Nakamura (2002) that the limiting log-normal form is closely attained already
after 3 steps. Stochastic acceleration, for example, may be treated in terms of multiplication of a number of random fractional energy gains ![]() ,
see Eq. (5). The issue will be dealt
with in more detail in Tramacere et al. (2007, in prep.); here it provides complementary
support to our stress on the relevance of stochastic acceleration to understand the
spectral variations of Mrk 421.
,
see Eq. (5). The issue will be dealt
with in more detail in Tramacere et al. (2007, in prep.); here it provides complementary
support to our stress on the relevance of stochastic acceleration to understand the
spectral variations of Mrk 421.
Acknowledgements
We thank S. Bianchi, M. Tomei, M. Perri for their help in the use of the XMM-Newton Science Analysis System (SAS), and P. Giommi, E. Massaro, G. Tosti and A. Paggi, for useful discussions. One of us (F. Massaro) acknowledges support by a fellowship of the Italian Space Agency (ASI), in the context of the AGILE Space Mission. We thank our referee for helpful comments towards improving our presentation.
We first recall the general formalism used to evaluate correlation coefficients for data with uncertainties on both axes.
For two statistical variables defined as:
| (12) | |||
| (13) |
| (14) |
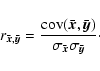 |
(15) |
| (16) |
An issue arising in the analysis of correlations (as anticipated in Sect. 4 of the main
text), is that "hidden'' parameters - adding to the "primary'' ones focused by the
analysis - can introduce a covariance term, i.e., a correlation. To evaluate its weight
we recall the general expression of the covariance term for functions of random
variables. When we have M functions
(f1,...,fM) of N random
variables x1...xN, the covariance of fk,fl is given by Barlow (1989) to read
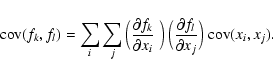 |
(17) |
We then show explicitly the formalism we actually use in fitting our data.
We follow the approach of D'Agostini (2005), who discusses a development from the
standard formalism (see Kendall & Stuart 1979) basing on Bayesian statistics.
This is an unbiased method to perform fits on data, including uncertainties on both axes
and a term of extravariance
![]() given by the fluctuations of a "hidden''
parameter. The log-likelihood function discussed by D'Agostini (2005) reads
given by the fluctuations of a "hidden''
parameter. The log-likelihood function discussed by D'Agostini (2005) reads
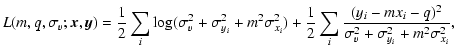 |
(18) |
| (19) |
| (20) |