A&A 466, 675-682 (2007)
DOI: 10.1051/0004-6361:20066639
M. A. Smith1,![]() - D. A. Bohlender2
- D. A. Bohlender2
1 - Department of Physics, Catholic University of America,
Washington, DC 20064, USA
2 -
National Research Council of Canada, Herzberg Institute of Astrophysics, 5071 W. Saanich Rd., Victoria, BC V9E 2E7, Canada
Received 26 October 2006 / Accepted 7 February 2007
Abstract
Recently Neiner et al. reported that the B2 IV-V star ![]() Cas
contains a weak magnetic field which varies on the same 5.37 day period found
from the modulations of its N V, C IV, and Si IV UV resonance lines.
We have studied the time variable properties of the same resonance
lines in greater detail to determine the physical characteristics
of the magnetospheric structure responsible for them.
In our formulation
this structure takes the form of an axisymmetric "disk'' similar
to those around magnetic He-strong Bp stars. This structure corotates
with the star, covering greater or lesser amounts of its
area during its transit.
Cas
contains a weak magnetic field which varies on the same 5.37 day period found
from the modulations of its N V, C IV, and Si IV UV resonance lines.
We have studied the time variable properties of the same resonance
lines in greater detail to determine the physical characteristics
of the magnetospheric structure responsible for them.
In our formulation
this structure takes the form of an axisymmetric "disk'' similar
to those around magnetic He-strong Bp stars. This structure corotates
with the star, covering greater or lesser amounts of its
area during its transit.
![]() Cas offers a special case because
we observe it from a low inclination and yet its magnetic axis is
substantially inclined to the rotation axis.
The equivalent width-phase
curves show a flat maximum for half the cycle, indicating that the
disk is extended out of the plane, extends to the star's surface in
the magnetic plane, or both. Synthetic spectra of the line profiles
during the maximum and minimum occultation phases can be
best reconciled with a disk geometry in which the resonance lines
are formed at a closed outer edge and along a thin outer layer.
We speculate that observed weak redshifted emission is formed in
"auroral caps'' located near the magnetic poles of the star.
We argue that this results from shocks of stagnated wind material
returning to the star and shocking against the outflowing wind.
Cas offers a special case because
we observe it from a low inclination and yet its magnetic axis is
substantially inclined to the rotation axis.
The equivalent width-phase
curves show a flat maximum for half the cycle, indicating that the
disk is extended out of the plane, extends to the star's surface in
the magnetic plane, or both. Synthetic spectra of the line profiles
during the maximum and minimum occultation phases can be
best reconciled with a disk geometry in which the resonance lines
are formed at a closed outer edge and along a thin outer layer.
We speculate that observed weak redshifted emission is formed in
"auroral caps'' located near the magnetic poles of the star.
We argue that this results from shocks of stagnated wind material
returning to the star and shocking against the outflowing wind.
Key words: stars: individual: ![]() Cassiopeiae -
magnetic fields - stars: circumstellar matter - stars: winds, outflows
- stars: early-type - ultraviolet: stars
Cassiopeiae -
magnetic fields - stars: circumstellar matter - stars: winds, outflows
- stars: early-type - ultraviolet: stars
Fully twenty years ago Grady et al. (1987) and Sonneborn et al. (1987)
reported that the UV resonance lines of the sharp-lined B2 IV-V star
![]() Cassiopeiae
(HD 3360; V=3.67) are variable. Interest in this star has been rekindled
recently by the report by Neiner et al. (2003; hereafter N03)
that this star has a dipolar magnetic field of
Cassiopeiae
(HD 3360; V=3.67) are variable. Interest in this star has been rekindled
recently by the report by Neiner et al. (2003; hereafter N03)
that this star has a dipolar magnetic field of
![]() G varying by
G varying by
![]() with
a period of 5.37 days. The
resonance lines of N V, C IV, and Si IV show variations with the
same period. N03 also report a nitrogen abundance enhancement
and a marginal helium overabundance ([He] =
with
a period of 5.37 days. The
resonance lines of N V, C IV, and Si IV show variations with the
same period. N03 also report a nitrogen abundance enhancement
and a marginal helium overabundance ([He] =
![]() dex).
These characteristics make
dex).
These characteristics make ![]() Cas a likely weak member of the
magnetic He-strong Bp stars.
We note for completeness that small-amplitude
nonradial pulsations are excited on this semi-evolved star's surface
(e.g., Sadsaoud et al. 1994).
Cas a likely weak member of the
magnetic He-strong Bp stars.
We note for completeness that small-amplitude
nonradial pulsations are excited on this semi-evolved star's surface
(e.g., Sadsaoud et al. 1994).
It is generally accepted that magnetic Bp stars contain fossil dipolar magnetic fields that are randomly oriented with respect to the rotational axes. Many authors (e.g., Shore 1987; Shore & Brown 1990; Babel & Montmerle 1997a,b) have attributed the time-modulated UV resonance line variations to the channeling of radiative winds from their magnetic poles to their equators. Because ionized particles cannot cross magnetic field lines, the global stellar fields play a key role in the wind outflows. Although the particles emerging from the magnetic poles can freely accelerate, wind flows are prevented from crossing transverse stellar field lines in the equatorial zones and are suppressed. Moreover, the field lines emanating from the stellar magnetic poles channel the escaping wind toward the magnetic plane. Here they collide with wind streams coming from the opposite magnetic hemisphere. This produces a shock that overionizes particles which then reionize and deexcite and emit resonance line radiation. The resonance line radiation is then scattered through the confined structure, allowing the observer to see an array of absorption and emission components as the corotating disk/shock complex corotates around the star. Many of the cooled particles settle toward the plane to form a confined "disk''. Interior to the magnetospheric structure, a sector of this disk transits in front of the star and occults part of the star's projected area and causes excess absorption in low-excitation lines of iron group ions. In Bp stars with extensive disks, the absorption from this "iron curtain'' forest is made visible by their composite effect in high resolution spectra obtained by the International Ultraviolet Explorer (IUE) (Smith & Groote 2001; hereafter SG01) and in high-level Balmer lines (Groote & Hunger 1976).
In the hydrodynamic formulation of this process by Babel
and coworkers, a shock develops where the disk particle pressure
equals the wind's energy density.
Important refinements have been added to the Babel picture
by ud-Doula and collaborators by considering the relative influences
of other forces on particles along the flow. We summarize several
effects they can have on the disk structure![]()
The ultraviolet spectra for this program included the wavelength
regions surrounding the N V, C IV, Si IV, and Al III resonance
lines and recorded on IUE echellograms with the Short Wavelength
Prime (SWP) camera. These data were obtained from the MAST
archives![]() .
We found 106 spectra, all obtained between 1979 and 1995 and all observed
through the IUE's large aperture, were suitable for analysis.
We then computed "equivalent width (EW) indices'' by ratioing the fluxes
within the line edges with fluxes of other wavelengths in the order (see SG01). Spectra for phase ranges given in Sect. 3.1 were selected,
"conditioned'', and coadded by carrying out the following
operations
.
We found 106 spectra, all obtained between 1979 and 1995 and all observed
through the IUE's large aperture, were suitable for analysis.
We then computed "equivalent width (EW) indices'' by ratioing the fluxes
within the line edges with fluxes of other wavelengths in the order (see SG01). Spectra for phase ranges given in Sect. 3.1 were selected,
"conditioned'', and coadded by carrying out the following
operations![]() (1) cross-correlating them to
remove apparent wavelength shifts, (2) forcing them to
a common continuum slope across the order, and (3) weighting the individual
spectra according to the mean fluctuation from pixels of neighboring
resolution elements. This weighting was accomplished by evaluating
the internal spectrum rms noise (assumed to be the median value of
the absolute value of the fluctuations of pixels in each
neighboring resolution element, i.e., every 3rd pixel).
The principal work in this paper concerns the analysis of pairs of
coadded resonance line spectra obtained at phases near the passage of
the South magnetic pole across the star's central meridian (following N03, taken to be
(1) cross-correlating them to
remove apparent wavelength shifts, (2) forcing them to
a common continuum slope across the order, and (3) weighting the individual
spectra according to the mean fluctuation from pixels of neighboring
resolution elements. This weighting was accomplished by evaluating
the internal spectrum rms noise (assumed to be the median value of
the absolute value of the fluctuations of pixels in each
neighboring resolution element, i.e., every 3rd pixel).
The principal work in this paper concerns the analysis of pairs of
coadded resonance line spectra obtained at phases near the passage of
the South magnetic pole across the star's central meridian (following N03, taken to be
![]() ), and approximately 0.5 cycles later,
i.e., when these lines exhibited minimum and maximum absorption,
respectively.
We quantified the variations of these line profiles in our first
figure by measuring
a dimensionless "equivalent width index'' rather than a true equivalent
width (EW) in Angstrom units. Our index is defined as the ratio of all fluxes
within a designated window across the profile to all fluxes outside them
in the echelle order containing them. Our indices are proportional to
a true equivalent width but do not rely upon inaccurate placements of
the local continua.
For the case of
), and approximately 0.5 cycles later,
i.e., when these lines exhibited minimum and maximum absorption,
respectively.
We quantified the variations of these line profiles in our first
figure by measuring
a dimensionless "equivalent width index'' rather than a true equivalent
width (EW) in Angstrom units. Our index is defined as the ratio of all fluxes
within a designated window across the profile to all fluxes outside them
in the echelle order containing them. Our indices are proportional to
a true equivalent width but do not rely upon inaccurate placements of
the local continua.
For the case of ![]() Cas,
the windows were taken to be the instrumentally broadened photospheric line
profile, or
Cas,
the windows were taken to be the instrumentally broadened photospheric line
profile, or ![]() Å for most resonance lines (
Å for most resonance lines (![]() Å for N V).
Å for N V).
In an attempt to search for variations in high-level Balmer lines
from the variable occultation of the star by the disk, we obtained 31
spectra with the 1.85 m telescope of the Dominion Astrophysical Observatory
during 2005, December 16, 2006 February 14-16 and March 8.
We used the f/5 Cassegrain spectrograph and fed the light to a CCD
detector by means of an image slicer. The resulting spectra have a
dispersion of 10 Å mm-1, a resolution of about 16 400, and
cover the wavelength region
![]() 3610-3880. These data gave a
null result, as reported below.
3610-3880. These data gave a
null result, as reported below.
To perform the analysis of the IUE spectra, we utilized a suite
of programs written by I. Hubeny and collaborators and non-LTE
solar abundance BSTAR models (Lanz & Hubeny 2006).
The first of these, synspec, is a
photospheric line synthesis program (Hubeny et al. 1994)
used for the reference photospheric profiles.
This program permits one to modify assumed
chemical abundances in the atmosphere. Indeed, the strengths of the
Fe III lines in the IUE spectrum suggested an iron
abundance of
![]() the solar value,
assuming a photospheric microturbulence
the solar value,
assuming a photospheric microturbulence
![]() km s-1. We also used synspec to convolve the
photospheric lines with functions approximating the instrumental and
rotational broadenings for the instrument and the star.
The spectroscopic resolution of IUE high-dispersion spectra
is about 13 000 and the the star's rotational broadening
(
km s-1. We also used synspec to convolve the
photospheric lines with functions approximating the instrumental and
rotational broadenings for the instrument and the star.
The spectroscopic resolution of IUE high-dispersion spectra
is about 13 000 and the the star's rotational broadening
(
![]() km s-1) are comparable.
We computed the synthetic spectra in steps of 0.01 Å.
km s-1) are comparable.
We computed the synthetic spectra in steps of 0.01 Å.
Our goal in this analysis is to assess the effects of the magnetospheric
disk on the UV resonance line spectrum as the disk moves across the
surface of ![]() Cas, alternately occulting greater or lesser areas
of the star in its circuit. To simulate the absorption and emission
signatures of the disk on the spectrum, we used the radiative transfer
program circus (Hubeny & Heap 1996; Hubeny & Lanz 1996). This
program computes strengths of absorption or emission components of lines
in a circumstellar medium from user-input quantities such as disk
temperature, column density, areal coverage factor (the portion of
the disk that passes in front of the star), and microturbulent velocity.
Circus combines this contribution with the synspec-computed
spectrum of the photosphere.
In its solution of the radiative transfer, circus calculates line
emissions and absorptions separately along a line of sight. The emission
is computed according to the assumption of LTE for an input disk
temperature
Cas, alternately occulting greater or lesser areas
of the star in its circuit. To simulate the absorption and emission
signatures of the disk on the spectrum, we used the radiative transfer
program circus (Hubeny & Heap 1996; Hubeny & Lanz 1996). This
program computes strengths of absorption or emission components of lines
in a circumstellar medium from user-input quantities such as disk
temperature, column density, areal coverage factor (the portion of
the disk that passes in front of the star), and microturbulent velocity.
Circus combines this contribution with the synspec-computed
spectrum of the photosphere.
In its solution of the radiative transfer, circus calculates line
emissions and absorptions separately along a line of sight. The emission
is computed according to the assumption of LTE for an input disk
temperature
![]() .
Because the "absorption'' of resonance lines
is actually due to scattering, it can be handled by turning off
a flag in the program that computes the emissivity coefficient in the
radiative transport equation. The result is that the background flux
of the star is affected only by the absorption coefficient.
The ability of handling the line transfer in this way permits one
to treat absorptions and emissions simultaneously or separately in
different circumstellar structures.
Circus can accommodate three separate "clouds''. In the present
analysis, we found it necessary to include two cloud structures, one
for the excess absorptions of the resonance lines and a second for
the emission components. The program allows us to input different
radial velocities and temperatures that might be useful in testing
whether different diagnostics are formed in separate regions,
allowing an assessment of whether they might arise in different volumes.
As in the work described by SG01 and Smith et al. (2006; hereafter S06),
we have assumed the clouds to be homogeneous in all properties.
However, the MHD studies described above suggest this may well be
an oversimplification.
.
Because the "absorption'' of resonance lines
is actually due to scattering, it can be handled by turning off
a flag in the program that computes the emissivity coefficient in the
radiative transport equation. The result is that the background flux
of the star is affected only by the absorption coefficient.
The ability of handling the line transfer in this way permits one
to treat absorptions and emissions simultaneously or separately in
different circumstellar structures.
Circus can accommodate three separate "clouds''. In the present
analysis, we found it necessary to include two cloud structures, one
for the excess absorptions of the resonance lines and a second for
the emission components. The program allows us to input different
radial velocities and temperatures that might be useful in testing
whether different diagnostics are formed in separate regions,
allowing an assessment of whether they might arise in different volumes.
As in the work described by SG01 and Smith et al. (2006; hereafter S06),
we have assumed the clouds to be homogeneous in all properties.
However, the MHD studies described above suggest this may well be
an oversimplification.
Among other input parameters are the disk's volume density and
microturbulent velocity ![]() .
Our results were insensitive to the values
chosen for either of them. The volume density enters only indirectly
(and insensitively) through the gas ionization equilibrium. Our trial
input density,
.
Our results were insensitive to the values
chosen for either of them. The volume density enters only indirectly
(and insensitively) through the gas ionization equilibrium. Our trial
input density, ![]() 1012 cm-3, is the order of magnitude SG01
determined for hot Bp star disks and is also the peak value determined
by the MHD simulations. Except for the absorptions of the primary
resonance lines (C IV, Si IV) the overwhelming majority of the UV metal
lines in our computations are optically thin. Since the spectral signatures
then scale as the volume of absorbers, a degeneracy arises between two
geometrical factors of the disk: its area and column length
along the observer's line of sight.
1012 cm-3, is the order of magnitude SG01
determined for hot Bp star disks and is also the peak value determined
by the MHD simulations. Except for the absorptions of the primary
resonance lines (C IV, Si IV) the overwhelming majority of the UV metal
lines in our computations are optically thin. Since the spectral signatures
then scale as the volume of absorbers, a degeneracy arises between two
geometrical factors of the disk: its area and column length
along the observer's line of sight.
The final ingredient of our models is the treatment of line of sight
velocities. Because the magnetosphere co-rotates over the star's surface,
no differential velocities exist along the line of sight to the star
during occultation. Moreover, the Doppler shift of the disk absorbers
is matched by the velocity of the star area behind them. SG01 found
that turbulent velocities in the range of 0 - 20 km s-1 can
be offset by changes in the assumed metallicity in the disk because
the lines are optically thin. These authors also found a broadening
of the Al III and N V resonance lines of about 25 km s-1 and
50 km s-1, respectively, at phases near maximum occultation. The
circus models were computed with the same underabundant iron abundance
as determined for the photosphere. We used solar abundances of
C, Si, and Al, but an overabundance [N] = 0.4 dex (N03), all
with a ![]() km s-1.
km s-1.
In our analysis we have assumed the physical parameters of
![]() Cas determined by N03. These include the redetermination of
the star's effective temperature, near 21 000 K and a
logarithmic surface gravity of about 3.8.
Therefore, we have chosen the (21 000, 4) model in the BSTAR grid as input
to our synspec computations. At the surface of the star, small
amplitude nonradial pulsations are present (N03), but we ignore them in this
discussion. Given a period of
5.37 days and the star's
Cas determined by N03. These include the redetermination of
the star's effective temperature, near 21 000 K and a
logarithmic surface gravity of about 3.8.
Therefore, we have chosen the (21 000, 4) model in the BSTAR grid as input
to our synspec computations. At the surface of the star, small
amplitude nonradial pulsations are present (N03), but we ignore them in this
discussion. Given a period of
5.37 days and the star's
![]() km s-1, the
inferred equatorial rotational velocity,
km s-1, the
inferred equatorial rotational velocity,
![]() km s-1,
is also well determined
km s-1,
is also well determined![]()
![]() Cas is a moderately rotating B star.
N03 give a rotational obliquity angle of
Cas is a moderately rotating B star.
N03 give a rotational obliquity angle of
![]() .
From i and attributes of the magnetic phase, curve N03 derive a
magnetic obliquity angle,
.
From i and attributes of the magnetic phase, curve N03 derive a
magnetic obliquity angle,
![]() .
.
The rotational phase zero ![]() is taken as the stellar
longitude containing the negative poles in the visible hemisphere.
Then the viewing angle
is taken as the stellar
longitude containing the negative poles in the visible hemisphere.
Then the viewing angle ![]() can be written as
can be written as![]()
| (1) |
The relation for the wind magnetic confinement parameter ![]() is given by uO05 as the ratio of magnetic to kinetic energies,
namely as
is given by uO05 as the ratio of magnetic to kinetic energies,
namely as![]()
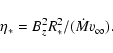 |
(2) |
N03 have determined a period of
![]() days from
the variations of the C IV, Si IV, and N V resonance lines.
To check this value, we applied the PDM period-finding algorithm
(Stellingwerf 1978) to EW indices extracted from the resonance lines
as defined above.
These extractions were done in the inner
days from
the variations of the C IV, Si IV, and N V resonance lines.
To check this value, we applied the PDM period-finding algorithm
(Stellingwerf 1978) to EW indices extracted from the resonance lines
as defined above.
These extractions were done in the inner ![]() Å
of the N V lines and inner
Å
of the N V lines and inner ![]() Å of the C IV and
Si IV lines. We ordered these values by time and and found a
value of
Å of the C IV and
Si IV lines. We ordered these values by time and and found a
value of
![]() days, thereby verifying the N03 value.
We used this period and the N03 zero point (
days, thereby verifying the N03 value.
We used this period and the N03 zero point (![]() at HJD 2 446 879.889)
to compute rotational phases. Figure 1 exhibits the
absorptions (EW index) folded around this period, but we have rescaled
them so that each exhibits the same fractional variation (this rendition
artificially increases the apparent noise in the N V curve).
Note the Fig. 1 minimum centered at phase 0.0.
Also, as previously pointed out by N03,
one may discern a hint of a secondary minimum on the broader maximum
at
at HJD 2 446 879.889)
to compute rotational phases. Figure 1 exhibits the
absorptions (EW index) folded around this period, but we have rescaled
them so that each exhibits the same fractional variation (this rendition
artificially increases the apparent noise in the N V curve).
Note the Fig. 1 minimum centered at phase 0.0.
Also, as previously pointed out by N03,
one may discern a hint of a secondary minimum on the broader maximum
at
![]() ,
but we are not convinced that it is statistically significant since
this feature does not appear in the Si IV or N V curves.
Finally, we point out that the shapes of the absorption-phase
curves are indistinguishable from one another. This is surprising
because, as noted below, the decreased absorptions they
represent occur for both optically thick and thin lines.
,
but we are not convinced that it is statistically significant since
this feature does not appear in the Si IV or N V curves.
Finally, we point out that the shapes of the absorption-phase
curves are indistinguishable from one another. This is surprising
because, as noted below, the decreased absorptions they
represent occur for both optically thick and thin lines.
![\begin{figure}
\par\includegraphics[angle=90,width=7.7cm,clip]{6639fig1.eps}
\end{figure}](/articles/aa/full/2007/17/aa6639-06/Timg49.gif) |
Figure 1:
Variation of line strength indices for the UV resonance doublets of
N V, Si IV, and C IV with phase in the spectrum of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=7.9cm,clip]{6639fig2.eps}
\end{figure}](/articles/aa/full/2007/17/aa6639-06/Timg50.gif) |
Figure 2:
Maximum (upper) and minimum absorption lines of the C IV doublet of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{6639fig3.eps}
\end{figure}](/articles/aa/full/2007/17/aa6639-06/Timg51.gif) |
Figure 3:
Maximum (upper) and minimum absorption in the N V doublet lines of
|
| Open with DEXTER | |
To reconnoiter the modulation of the line strengths with phase, we
first grouped over 20 spectra each into EW-minimum and EW-maximum phase
bins corresponding to ![]() -0.11 and 0.30-0.70, respectively,
and computed mean spectra from these groups. The results are exhibited
as thick solid lines in Figs. 2 and 3 for
the wavelength regions surrounding the C IV and N V doublets,
respectively. Minimum and maximum spectra were also computed for the
Si IV lines. The line profiles of the spectra are different in
that those for the former phases exhibit smaller absorptions and
generally steeper red wings. Part of the asymmetry in the wings is
due to the influence of the winds.
As for other Bp stars and
-0.11 and 0.30-0.70, respectively,
and computed mean spectra from these groups. The results are exhibited
as thick solid lines in Figs. 2 and 3 for
the wavelength regions surrounding the C IV and N V doublets,
respectively. Minimum and maximum spectra were also computed for the
Si IV lines. The line profiles of the spectra are different in
that those for the former phases exhibit smaller absorptions and
generally steeper red wings. Part of the asymmetry in the wings is
due to the influence of the winds.
As for other Bp stars and ![]() Ori C (Smith & Fullerton 2005), this wind is focused
by the magnetic field and streams outward preferentially at
low magnetic latitudes.
Since the wind escapes from
regions outside this disk, we do not model it in this work.
The red shoulders of the profiles at these times
are steep with respect to our computed
photospheric profiles, and we attribute this to an incipient
redshifted emission. We attribute the strengthening
of the spectra to increased blocking of the stellar flux by the intervening
disk. Our modeling of absorptions and emissions proceeded with these
assumptions, and we defer the discussion of results to the next section.
Ori C (Smith & Fullerton 2005), this wind is focused
by the magnetic field and streams outward preferentially at
low magnetic latitudes.
Since the wind escapes from
regions outside this disk, we do not model it in this work.
The red shoulders of the profiles at these times
are steep with respect to our computed
photospheric profiles, and we attribute this to an incipient
redshifted emission. We attribute the strengthening
of the spectra to increased blocking of the stellar flux by the intervening
disk. Our modeling of absorptions and emissions proceeded with these
assumptions, and we defer the discussion of results to the next section.
We have described a picture in which wind particles escaping the
magnetic poles of a Bp star shock when they impact particles near the
magnetic equator that have formerly settled to form a cooled "disk''.
The phase-dependent absorptions of key ultraviolet
lines validates this basic picture for ![]() Cas. The morphology
of the resonance lines shown is replicated within the errors by less
excited resonance lines of Al III and C II, thereby providing
evidence that the structure is a confined cool disk.
However, we were not able to estimate the disk temperature from
ratios of iron line absorptions because the available Fe II lines are
too weak to show variations. Even so, if we assume the relation for the
cool disk ionization temperature
Cas. The morphology
of the resonance lines shown is replicated within the errors by less
excited resonance lines of Al III and C II, thereby providing
evidence that the structure is a confined cool disk.
However, we were not able to estimate the disk temperature from
ratios of iron line absorptions because the available Fe II lines are
too weak to show variations. Even so, if we assume the relation for the
cool disk ionization temperature
![]()
![]() ,
as found in the Bp stars studied by SG01 and S06, we obtain a value
,
as found in the Bp stars studied by SG01 and S06, we obtain a value
![]() K. Assuming this temperature and, in the absence
of information about the extent of the coverage of the star by the
cool disk component during the occultation phase,
we find from circus modeling of the small variations of the
Al III
K. Assuming this temperature and, in the absence
of information about the extent of the coverage of the star by the
cool disk component during the occultation phase,
we find from circus modeling of the small variations of the
Al III ![]() 1855-62 and the C II
1855-62 and the C II
![]() 1335-6
multiplets that the hydrogen column densities of the
occulting disk are 1
1335-6
multiplets that the hydrogen column densities of the
occulting disk are 1
![]() cm-2, assuming
cm-2, assuming ![]() km s-1, and
km s-1, and
![]() cm-2, assuming
cm-2, assuming ![]() km s-1. We take these as convenient lower and upper estimates.
km s-1. We take these as convenient lower and upper estimates.
We note that after reducing our DAO spectra of the high-level
(H8-H13) Balmer lines and plotting the equivalent widths with phase, we
were unable to find statistically significant variations in them.
From our the measurement errors, ![]() 0.6% per line, this
undetectability translates to a column density of
0.6% per line, this
undetectability translates to a column density of ![]()
![]() cm-2, according to our circus simulations, and
assuming a
cm-2, according to our circus simulations, and
assuming a
![]() 000 K. Since this limit is a few hundred
times higher than the limits imposed by the All III and C II variations
just above, it does not add information to the disk analysis.
000 K. Since this limit is a few hundred
times higher than the limits imposed by the All III and C II variations
just above, it does not add information to the disk analysis.
The resonance line variations in the two figures bring out two
interesting characteristics. First, notice that the rms spectra in
the C IV line figure show that the profile activity is confined to
roughly ![]() 100 km s-1 from line center. However, the
wind-depressed blue wings undergo no activity through the cycle.
Similar to the resonance lines of other Bp stars, the rms
spectral amplitudes peak to the red of the line centers.
Inspection shows that this is caused primarily by steepenings of the
red shoulder of the lines in observations obtained in the EW-minimum
phases. According to the line fittings discussed below, these shoulders
cannot be fit by photospheric spectra or disk absorption spectra.
Rather, we believe these are incipient emissions corresponding to the
more pronounced emissions observed in many Bp star spectra.
Another characteristic brought out in these plots is that the doublet
ratios of these activities are 1.2 and
100 km s-1 from line center. However, the
wind-depressed blue wings undergo no activity through the cycle.
Similar to the resonance lines of other Bp stars, the rms
spectral amplitudes peak to the red of the line centers.
Inspection shows that this is caused primarily by steepenings of the
red shoulder of the lines in observations obtained in the EW-minimum
phases. According to the line fittings discussed below, these shoulders
cannot be fit by photospheric spectra or disk absorption spectra.
Rather, we believe these are incipient emissions corresponding to the
more pronounced emissions observed in many Bp star spectra.
Another characteristic brought out in these plots is that the doublet
ratios of these activities are 1.2 and
![]() for the C IV and Si IV (not shown) lines, respectively.
The ratio for the N V lines is
for the C IV and Si IV (not shown) lines, respectively.
The ratio for the N V lines is
![]() .
From these ratios we can see that the circumstellar media
in which the "disk'' component of C IV and Si IV are formed are
optically thick while the N V lines optically thin, much like their
photospheric components.
.
From these ratios we can see that the circumstellar media
in which the "disk'' component of C IV and Si IV are formed are
optically thick while the N V lines optically thin, much like their
photospheric components.
Table 1: Derived columns, areal coverages, and radial velocities (km s-1) inferred from UV resonance lines.
In our line profile fitting we found that an important diagnostic
is the line optical depths. Because the optical depths of our
models are typically within an order of magnitude of unity, we
were able to use them to estimate the optical depths of the disk
columns and ultimately
to set limits on the range of the disk temperature
![]() .
These values are represented in the table discussed below.
.
These values are represented in the table discussed below.
Our initial attempts to model the minimum and maximum EW spectra
in Figs. 2 and 3 used input circus
parameters for a single homogeneous absorbing and emitting circumstellar
"cloud''. The models assume a disk temperature
![]() ,
which for
simplicity we have assumed to be the same value. This group of models
failed to give satisfactory fits.
Although there were several problems with the fits, the most important
was the inability of the models to produce enough absorption to
fit the EW variations. This problem was accentuated by the constraint
that the change of coverage of the star must be incomplete because of the
low inclination of the star. Investigating this failure
in more detail, we found that the poor fits extended over a significant
wavelength range. For this reason, we were forced to consider circus models fit with two homogeneous clouds with different properties,
especially radial velocity. These models were successful, but only
when we increased the microturbulence
,
which for
simplicity we have assumed to be the same value. This group of models
failed to give satisfactory fits.
Although there were several problems with the fits, the most important
was the inability of the models to produce enough absorption to
fit the EW variations. This problem was accentuated by the constraint
that the change of coverage of the star must be incomplete because of the
low inclination of the star. Investigating this failure
in more detail, we found that the poor fits extended over a significant
wavelength range. For this reason, we were forced to consider circus models fit with two homogeneous clouds with different properties,
especially radial velocity. These models were successful, but only
when we increased the microturbulence ![]() to 75-90 km s-1.
We note by contrast that high cloud macroturbulences merely smear the computed
excess absorptions and emissions. They do not strengthen
them, as is required by the observations.
to 75-90 km s-1.
We note by contrast that high cloud macroturbulences merely smear the computed
excess absorptions and emissions. They do not strengthen
them, as is required by the observations.
We were not led immediately to our best fits with the two-cloud
description. Moreover, those we have selected for representation are
those obtained only for one possible disk temperature among the range
of
![]() values. One of the most important fitting
parameters, the temperature implied by fits to the
emission components,
values. One of the most important fitting
parameters, the temperature implied by fits to the
emission components,
![]() ,
is not uniquely
determined. For the C IV line fitting, the
upper limit on
,
is not uniquely
determined. For the C IV line fitting, the
upper limit on
![]() ,
26 000 K, was set by the decreased
optical depths in the line that led to different and contradictory
absorbing cloud areas or columns for the two doublet components.
The lower limit of 16 000 K was set by the appearance of nearby Fe II lines in the computed models, which are not present in the observations.
For the N V lines a low temperature limit of 26 000 K was again set
by the absence of a predicted iron line (Fe III 1243.4 Å).
The column density required for fitting
the N V lines rapidly decreases to the values found for the C IV
fittings, and we consider this the most likely result.
,
26 000 K, was set by the decreased
optical depths in the line that led to different and contradictory
absorbing cloud areas or columns for the two doublet components.
The lower limit of 16 000 K was set by the appearance of nearby Fe II lines in the computed models, which are not present in the observations.
For the N V lines a low temperature limit of 26 000 K was again set
by the absence of a predicted iron line (Fe III 1243.4 Å).
The column density required for fitting
the N V lines rapidly decreases to the values found for the C IV
fittings, and we consider this the most likely result.
Table 1 shows the results of best two-cloud models for the maximum
and minimum EW profiles of the N V, C IV and Si IV doublets, that is
for observations obtained near mid-transit (maximum occultation) phases
and those for half a cycle later, respectively. An example of a model for
the C IV and N V doublets is shown in Figs. 2 and 3
as a dashed line. Annotations give pertinent model fitting parameters.
Shadings denote the modeled incipient emissions.
In the table we give both "high'' and "low''
![]() values, as
discussed above. In each case we give modeling parameters for fits to
the maximum EW and minimum EW line in the upper and lower lines of each
double row entry. In the table we give several key fitting parameters,
including the
values, as
discussed above. In each case we give modeling parameters for fits to
the maximum EW and minimum EW line in the upper and lower lines of each
double row entry. In the table we give several key fitting parameters,
including the
![]() ,
column density, areal coverage, radial
velocity, and central optical depth of the stronger doublet member.
Errors were estimated by repeating our models with single parameters
changed by varying degrees and comparing the resulting differences
in the equivalent widths with 2
,
column density, areal coverage, radial
velocity, and central optical depth of the stronger doublet member.
Errors were estimated by repeating our models with single parameters
changed by varying degrees and comparing the resulting differences
in the equivalent widths with 2![]() changes in the line profiles
within the same wavelength window from the rms errors in the
IUE spectra. The latter was accomplishing using a Monte Carlo
approach to compute the fluctuations as described in Smith (2006).
These errors led to the following estimated 2
changes in the line profiles
within the same wavelength window from the rms errors in the
IUE spectra. The latter was accomplishing using a Monte Carlo
approach to compute the fluctuations as described in Smith (2006).
These errors led to the following estimated 2![]() errors in our
table
errors in our
table![]()
![]() km s-1 in microturbulence
km s-1 in microturbulence ![]() ,
,
![]() in fractional areal coverage for C IV and Si IV, and
in fractional areal coverage for C IV and Si IV, and
![]() in the column densities.
The errors for the latter two quantities are
in the column densities.
The errors for the latter two quantities are
![]() for the
N V doublet.
Inspection of this table brings out the following points
for the
N V doublet.
Inspection of this table brings out the following points![]()
In S06 we described a computer program written to describe the varying excess absorptions of an optically thick resonance line as a co-rotating disk shaped like a cylinder transits across the star. The line is assumed to be optically thick, the absorption of flux from the obscured region of the star is total. Then, one may express the occulted area of the star in terms of the excess absorption measured.
One can manipulate input parameters representing the dimensions of
the disk to fit observed phase absorption curves.
For the case of ![]() Cas, the curves in Fig. 1
show that the absorption curves are essentially flat out to
Cas, the curves in Fig. 1
show that the absorption curves are essentially flat out to
![]()
![]() cycles around maximum occultation phase,
cycles around maximum occultation phase,
![]() .
Unfortunately, flat absorption phase curves give information only on the
limits of ratios of dimensions
.
Unfortunately, flat absorption phase curves give information only on the
limits of ratios of dimensions![]() .
This problem is aggravated by the low S/N of IUE data, which
makes it difficult to map the progress of the disk viewed at a low i.
However, we may still investigate the general character of the disk
cylinder shape if we estimate a minimum taper in the curves (5% of
the maximum excess absorption out to
.
This problem is aggravated by the low S/N of IUE data, which
makes it difficult to map the progress of the disk viewed at a low i.
However, we may still investigate the general character of the disk
cylinder shape if we estimate a minimum taper in the curves (5% of
the maximum excess absorption out to
![]() and 0.75) that might
be hidden in the noise of the absorption curves. This taper is shown
in Fig. 1 as a dashed line.
and 0.75) that might
be hidden in the noise of the absorption curves. This taper is shown
in Fig. 1 as a dashed line.
Applying this criterion and the i and ![]() values
for
values
for ![]() Cas, we adopt an outer disk radius
Cas, we adopt an outer disk radius
![]() and we can ask, what is the interdependence between the height
(measured parallel to the rotational axis) and the thickness
of the disk in the radial direction,
and we can ask, what is the interdependence between the height
(measured parallel to the rotational axis) and the thickness
of the disk in the radial direction,
![]() ?
According to our models and our taper criterion, a disk extending in
to the star's surface along the magnetic plane can protrude no further than
3.2 R* from the central plane.
For a second case for which the disk has an inner radius of
3 R* (i.e., an evacuation of the inner 50% of the disk), our models produce
a similarly tapered phase if the disk extends
?
According to our models and our taper criterion, a disk extending in
to the star's surface along the magnetic plane can protrude no further than
3.2 R* from the central plane.
For a second case for which the disk has an inner radius of
3 R* (i.e., an evacuation of the inner 50% of the disk), our models produce
a similarly tapered phase if the disk extends ![]() 3.0 R* out
of the magnetic plane. For the cylindrical model we have
adopted there is a degeneracy between these dimensions - we have
little leverage in determining where an inner disk edge lies.
More importantly than this, the implication from the cylindrical
model representation is that the disk extends to surprisingly
large distances from the central plane. There is no indication that
disks of other Bp stars extend out of the plane to similar distances.
It seems more likely that our assumed disk geometry is in conflict
with fitting difficulties that are aggravated for star-disk systems
observed from a low inclination.
3.0 R* out
of the magnetic plane. For the cylindrical model we have
adopted there is a degeneracy between these dimensions - we have
little leverage in determining where an inner disk edge lies.
More importantly than this, the implication from the cylindrical
model representation is that the disk extends to surprisingly
large distances from the central plane. There is no indication that
disks of other Bp stars extend out of the plane to similar distances.
It seems more likely that our assumed disk geometry is in conflict
with fitting difficulties that are aggravated for star-disk systems
observed from a low inclination.
Although the concern just raised over our disk geometry arises from the
combination of high ![]() and low i for the
and low i for the ![]() Cas case, the
resonance line absorption curves of stars having high
Cas case, the
resonance line absorption curves of stars having high ![]() and i
values pose their own interpretational dilemmas. The most significant of
these is a fact noted by SG01 for those systems for which the observer's
observer's line of sight runs through the magnetic plane.
In these cases, the complete occultation of the star disk in optically
thick resonance lines presents the physical problem of how superions
responsible for the line scattering can be distributed throughout the cylinder.
How can such ions be excited in the middle of an optically thick medium?
This puzzle can be solved if, as predicted in the MHD models of
ud-Doula and coworkers, the disk is pinched off at the Alfvén
radius in the equator by the confluence of collimated wind streams.
Exterior to this point the field lines curve out and run parallel to the
magnetic equator. Then, an external observer at infinity viewing
the system in the magnetic plane sees the emission
from excited superions along this (thin) geometric boundary.
and i
values pose their own interpretational dilemmas. The most significant of
these is a fact noted by SG01 for those systems for which the observer's
observer's line of sight runs through the magnetic plane.
In these cases, the complete occultation of the star disk in optically
thick resonance lines presents the physical problem of how superions
responsible for the line scattering can be distributed throughout the cylinder.
How can such ions be excited in the middle of an optically thick medium?
This puzzle can be solved if, as predicted in the MHD models of
ud-Doula and coworkers, the disk is pinched off at the Alfvén
radius in the equator by the confluence of collimated wind streams.
Exterior to this point the field lines curve out and run parallel to the
magnetic equator. Then, an external observer at infinity viewing
the system in the magnetic plane sees the emission
from excited superions along this (thin) geometric boundary.
A third difficulty offered for the cylindrical geometry, again evident
for the ![]() Cas case, is that the absorptions should scale differently
for optically thick and thin lines as the disk moves off the limb of
the star. The excess absorptions of these two groups of lines
should scale differently - as the area and the volume of the occulting
disk, respectively. In contrast, we find that when the curves in
Fig. 1 are overplotted, their morphology is indistinguishable
for the two types of lines. This difficulty is inherent for any "solid''
disk geometry. It can be avoided if the disk opacity is confined to
a thin outer region having similar depth ranges of formation for these
lines. This circumstance is permitted if the volumes of excited ions are
confined to the outer regions of the disk.
Cas case, is that the absorptions should scale differently
for optically thick and thin lines as the disk moves off the limb of
the star. The excess absorptions of these two groups of lines
should scale differently - as the area and the volume of the occulting
disk, respectively. In contrast, we find that when the curves in
Fig. 1 are overplotted, their morphology is indistinguishable
for the two types of lines. This difficulty is inherent for any "solid''
disk geometry. It can be avoided if the disk opacity is confined to
a thin outer region having similar depth ranges of formation for these
lines. This circumstance is permitted if the volumes of excited ions are
confined to the outer regions of the disk.
![\begin{figure}
\par\includegraphics[height=17cm,width=5.5cm,angle=-90]{6639fig4.eps}
\end{figure}](/articles/aa/full/2007/17/aa6639-06/Timg84.gif) |
Figure 4:
The geometry at the times of
maximum (
|
| Open with DEXTER | |
In Fig. 4 we suggest a revised geometry in which the outer disk
edge, representing the wind-disk shock, tapers toward the equator and thus
takes the general shape of an oblate spheroid![]() .
We envisage that the excited "super-ions'' are formed in a thin outer
shell of this structure. The column and volume densities can then
be made consistent if the absorption column lengths, as
in Table 1, refer to a common shell thickness. For densities
predicted by uO02 and column lengths in Table 1, the shell thickness
to
.
We envisage that the excited "super-ions'' are formed in a thin outer
shell of this structure. The column and volume densities can then
be made consistent if the absorption column lengths, as
in Table 1, refer to a common shell thickness. For densities
predicted by uO02 and column lengths in Table 1, the shell thickness
to ![]() is then only of the order 103 km.
Since the resonance lines are formed in a skin around a cool transparent
disk, there need be no relation between their column densities and those
inferred from the Al III and C II lines.
is then only of the order 103 km.
Since the resonance lines are formed in a skin around a cool transparent
disk, there need be no relation between their column densities and those
inferred from the Al III and C II lines.
The regions where the resonance line emissions arise likewise should be reconsidered, as they cannot be understood as the result of the interaction of the wind and the edge of a dense disk. Consider first that for the Bp stars with dense, extensive disks investigated by SG01, the emissions can be present at all phases. The SG01 picture was that the resonance lines exhibit emission preferentially at those phases when the disk is viewed nearly face-on in the plane of the sky. A problem with this geometry is the positive radial velocity of the emissions. In contrast to SG01, we now believe the redshifts do not arise from the impact of the wind particles against the disk interface. Such interactions would produce emissions, but they are centered in the rest frame of the star.
A second problem is that the ratios of volumes computed from these lines' emissions and excess absorptions can be quite diverse among Bp stars. However, they should be approximately equal if the contributions in the same disk volumes arise from scatterings. These scatterings are conserved when integrated over all lines of sight.
These issues can be addressed by positing that the
absorptions and most of the emissions of UV resonance lines
are formed in different places. Our revised geometrical picture
harkens back to the results of two-dimensional
MHD models of the emission complex surrounding ![]() Ori C
discussed by uO02 and G05. Recall that these models predict that infall
condensations fall back into the outflowing wind. Indeed, the collision
of these two structures will produce redshifted emission in the external
reference frame because the center of mass is dominated by the
falling blobs. These emissions are visible mainly over a narrow range of
phases because the projected shock areas modulate with viewing angle.
For
Ori C
discussed by uO02 and G05. Recall that these models predict that infall
condensations fall back into the outflowing wind. Indeed, the collision
of these two structures will produce redshifted emission in the external
reference frame because the center of mass is dominated by the
falling blobs. These emissions are visible mainly over a narrow range of
phases because the projected shock areas modulate with viewing angle.
For ![]() Ori C the projected radial velocity in
the UV and X-ray resonance line is observed to be
Ori C the projected radial velocity in
the UV and X-ray resonance line is observed to be
![]() 100 km s-1
(Smith & Fullerton 2005, G05).
100 km s-1
(Smith & Fullerton 2005, G05).
We now ask what would be outcome of this same process if the wind were
weaker? We speculate that the answer begins with the fact
that because the lower efflux would
provide less resistance to the infall, the shock front where the pressures
equalize will lie closer to the star. This shock point will then occur
where the dense fallback blobs have accelerated to a higher velocity,
while the wind outflow, intercepting them from the opposite direction,
has only begun to accelerate. For a sufficiently weak wind (and similar
![]() )
the shock front should then describe an arc-like "auroral''
cap not far above the star's magnetic pole with a center-of-mass redshift
because of the fall back's higher velocity and density. We
expect that there are many such returning blobs at any one time, so
observations repeated at the same phase will see the same level of
emission. The projected area of the shock viewed
by the observer, and hence the recorded emission of the resonance lines,
would become maximum at
)
the shock front should then describe an arc-like "auroral''
cap not far above the star's magnetic pole with a center-of-mass redshift
because of the fall back's higher velocity and density. We
expect that there are many such returning blobs at any one time, so
observations repeated at the same phase will see the same level of
emission. The projected area of the shock viewed
by the observer, and hence the recorded emission of the resonance lines,
would become maximum at ![]() .
(The reverse would be the case
at
.
(The reverse would be the case
at
![]() when the project area of the cap would be minimal.)
Clearly, this picture begs to be confirmed by MHD simulations of
the type conducted for other Bp stars having stronger fields.
when the project area of the cap would be minimal.)
Clearly, this picture begs to be confirmed by MHD simulations of
the type conducted for other Bp stars having stronger fields.
The putative auroral shock regions are represented as shaded
regions at the "11 o'clock''
and "5 o'clock'' positions relative to the star in Fig. 4.
In this new configuration at ![]() these shocks have smaller
areas but are denser than the
the wind-shock interfaces discussed by Babel and SG01.
Note that because the emissions and absorptions are formed mainly in
two different regions of the magnetosphere, their volumes and
column densities need not be equal. In addition, one expects that the
UV line emission is formed in a separate region of the magnetosphere
from the X-ray emissions. The energies released at the auroral caps
can be expected to be moderate at most.
these shocks have smaller
areas but are denser than the
the wind-shock interfaces discussed by Babel and SG01.
Note that because the emissions and absorptions are formed mainly in
two different regions of the magnetosphere, their volumes and
column densities need not be equal. In addition, one expects that the
UV line emission is formed in a separate region of the magnetosphere
from the X-ray emissions. The energies released at the auroral caps
can be expected to be moderate at most.
This picture suggests that sometimes one might see small
amounts of blueshifted emission from the opposite hemisphere.
As shown by Fig. 4, right panel, "4-5 o'clock'' auroral cap
contribution from the aurora over the opposing figure would exhibit
a much smaller Doppler shift and projected area than the opposing cap.
We can speculate that the very high microturbulence taken for conditions
in a single structure in our previous models, are the result of a
superposition in velocity of these two shocks (each with a smaller ![]() ).
).
Our modeling of the resonance line variations of ![]() Cas shows
that the disk occults the star to some degree during the
entire rotation cycle. This attribute has not been found in
the quantitative modeling of other magnetic Bp stars whose lines we
have examined (e.g., SG01, Smith 2003; Smith & Fullerton 2005, S06).
It is probably more easily found for
Cas shows
that the disk occults the star to some degree during the
entire rotation cycle. This attribute has not been found in
the quantitative modeling of other magnetic Bp stars whose lines we
have examined (e.g., SG01, Smith 2003; Smith & Fullerton 2005, S06).
It is probably more easily found for ![]() Cas because of its
small inclination angle i. In this geometry the disk occultation
never realizes the full possible range of areal coverages (0-100%).
Cas because of its
small inclination angle i. In this geometry the disk occultation
never realizes the full possible range of areal coverages (0-100%).
As mentioned, the large areal coverage factor found for
our solutions at both
![]() and 0.50 requires
that the disk either extend nearly to the star's
surface, extend to large distances from the central magnetic plane,
or both. In Fig. 4, we noted that most or all the lines of
sight to the star intersect the disk and thus suffer flux attenuation.
and 0.50 requires
that the disk either extend nearly to the star's
surface, extend to large distances from the central magnetic plane,
or both. In Fig. 4, we noted that most or all the lines of
sight to the star intersect the disk and thus suffer flux attenuation.
Consideration of the characteristics of the emission components in
![]() Cas and the "classical'' Bp stars shows that they cannot be
easily understood with the kinematic description adopted by SG01, whether
the emission arises from a shock at the edge of a cylindical or torus
shaped disk. For example, for the Bp stars with dense or extensive
disks investigated by SG01, the emissions can be present at all phases,
and in all cases with a net redshift. We conjectured that this might
be understood by shocks created by the collisions of dense fall
back (blobs) with the outflowing wind. This releases the magnetic disk
model from other interpretational inconsistencies.
These include the frequent inequalities between the derived
volumes in which the absorptions and emission are formed. It also addresses
the high microturbulent velocities that are otherwise necessary to
fit the line profile variations.
Cas and the "classical'' Bp stars shows that they cannot be
easily understood with the kinematic description adopted by SG01, whether
the emission arises from a shock at the edge of a cylindical or torus
shaped disk. For example, for the Bp stars with dense or extensive
disks investigated by SG01, the emissions can be present at all phases,
and in all cases with a net redshift. We conjectured that this might
be understood by shocks created by the collisions of dense fall
back (blobs) with the outflowing wind. This releases the magnetic disk
model from other interpretational inconsistencies.
These include the frequent inequalities between the derived
volumes in which the absorptions and emission are formed. It also addresses
the high microturbulent velocities that are otherwise necessary to
fit the line profile variations.
The analysis of lines of a modestly inclined system like ![]() Cas
clarifies these problems and provides cause for a reconsideration
of the disk and emission region geometries. This shows that a final
picture of these complicated star-disk system requires
observations not merely over all viewing angles but of
a sample of stars with a variety of rotational and magnetic
inclination angles.
Cas
clarifies these problems and provides cause for a reconsideration
of the disk and emission region geometries. This shows that a final
picture of these complicated star-disk system requires
observations not merely over all viewing angles but of
a sample of stars with a variety of rotational and magnetic
inclination angles.
Acknowledgements
We thank the referee, Dr. Marc Gagné, for a number of comments that have added to the quality of this paper.