A&A 466, 395-398 (2007)
DOI: 10.1051/0004-6361:20067021

Ices on (90377) Sedna: confirmation and compositional constraints

J. P. Emery1,2 - C. M. Dalle Ore1,2 - D. P. Cruikshank1 - Y. R. Fernández3 - D. E. Trilling4 - J. A. Stansberry4


1 - NASA Ames Research Center, Mail Stop 245-6, Moffett Field, CA 94035, USA
2 - Carl Sagan Center, SETI Institute, 515 N Whisman Rd, Mountain View, CA 94043, USA
3 - University of Central Florida, Department of Physics, 4000 Central Florida Blvd, M.A.P. Bulding, Orlando, FL 32816-2385, USA
4 - University of Arizona, Steward Observatory, 933 N Cherry Ave., Tucson, AZ 85721, USA

Received 23 December 2006 / Accepted 25 January 2007

Abstract
We report measurements of reflectances of 90377 Sedna at $\lambda > 2.5$ $\mu $m using the Infrared Array Camera (IRAC) on the Spitzer Space Telescope. Sedna orbits well beyond even the Kuiper Belt, with a perihelion distance of 76 AU, and is therefore very faint as viewed from Earth, despite its relatively large size. Previously published near-infrared spectra show possible signatures of CH4 and N2 at $\sim$2.3 and $\sim$2.15 $\mu $m, respectively. These and other ices also exhibit much stronger absorptions at $\lambda > 2.5~\mu$m, providing the motivation for the present work. We detected flux from Sedna at 3.6 and 4.5 $\mu $m, but not at 5.8 or 8.0 $\mu $m. The measured IRAC fluxes are converted to geometric albedos and combined with previous measurements of the visible and near-infrared spectra. Strong absorption at both 3.6 and 4.5 $\mu $m (relative to the 2.0-2.5 $\mu $m region) is readily apparent, confirming the presence of ices on the surface of Sedna. Spectral modeling of the full wavelength range (0.4-4.5 $\mu $m) provides further constraints. We find that CH4 is required to fit the new data points, but that these new data points can not be adequately described with models containing CH4 and N2 as the only ices. We suggest that H2O ice is also present. Several characteristics of the spectrum of Sedna suggest an absence of atmospheric volatile transport, in contrast to the large objects Eris and 2005 FY9.

Key words: planets and satellites: individual: Sedna - Kuiper Belt - solar system: general - infrared: solar system

1 Introduction

Sedna (2003 VB12) is one of the most remote Trans-Neptunian Object in terms of both perihelion distance (76 AU) and semi-major axis (484 AU) yet discovered (Brown et al. 2004a). Its peculiar orbit places Sedna in the extended scattered disk, a group of objects whose orbits with perihelion beyond $\sim$40 AU can not be explained by interactions with giant planet resonances (Gladman et al. 2002). Several more exotic processes, including a passing star (Morbidelli & Levison 2004), formation of the Solar System in a star cluster (Brasser et al. 2006), a $\sim$1 or 2  $M_{\oplus}$ planet either just during formation or currently residing beyond Neptune (Morbidelli & Levison 2004; Gladman & Chan 2006), a wide-binary solar companion (Gomes et al. 2006), or capture of planetesimals from passing low-mass stars or brown dwarfs (Morbidelli & Levison 2004) have been suggested to explain the extended scattered disk. Some of these mechanisms predict an Oort cloud that extends from $\sim$10 000 AU all the way in to the orbit of Sedna.

Along with dynamical studies, remote determination of surface composition is crucial for understanding the origin and evolution of the outer Solar System. Sedna's large perihelion distance implies that its surface should be pristine with regard to solar heating. Irradiation from various sources over 4.5 Gyr, on the other hand, could have induced significant chemistry in an icy surface (e.g., Cooper et al. 2003). Sedna's size ( $D \sim 1300$ km, Stansberry et al. 2007; Brown et al. 2004b) suggests that this body may be differentiated and could plausably support a sub-surface liquid ocean at the present time (Hussmann et al. 2006), which also raises the possibility of current geological activity.

Barucci et al. (2005a) reported the detection of CH4 and N2 on Sedna. They obtained visible (0.4-0.9 $\mu $m) spectra that are featureless with a steep red slope (RR taxonomic class, Barucci et al. 2005b) and near-infrared (NIR; 1.1-2.5 $\mu $m) spectra that contain absorption bands at $\sim$2.15 and $\sim$2.3 $\mu $m. NIR spectra a night earlier (130 $\hbox{$^\circ$ }$ difference in longitude according to the 10.27 h rotation period of Gaudi et al. 2005) do not show the 2.3 $\mu $m feature. Trujillo et al. (2005) also did not see either feature in a K-band spectrum obtained at Gemini North, though their S/N was somewhat low and their limits on abundance of CH4 were not stringent (<$60\%$).

We have measured broad band reflected fluxes from Sedna at 3.6 and 4.5 $\mu $m. Our goal was to search for signatures of the ices reported by Barucci et al. (2005a) as well as other ices, such as H2O, and to constrain the composition and abundance of organic material that likely causes the extremely red spectral slope.

2 Observations

The data reported herein were obtained with the Infrared Array Camera (IRAC) on the Spitzer Space Telescope. Launched in August 2003, Spitzer has an aperture of 85 cm, supports three instruments (the Infrared Spectrograph and the Multiband Imaging Photometer for Spitzer along with IRAC), and surveys the infrared universe from an Earth-trailing, heliocentric orbit (Werner et al. 2004). IRAC is a broad-band imager, with a FOV of $5.8\times 5.8$ arcmin and image scale of $\sim$1.2 arcsec/pixel. The four wavelength channels are centered at roughly 3.6, 4.5, 5.8, and 8.0 $\mu $m and have widths (FWHM) of 0.68, 0.87, 1.25, and 2.52 $\mu $m, respectively (Fazio et al. 2004). It is important to keep the widths of these bands in mind, since the underlying spectra could vary significantly within each band.

IRAC uses beam splitters so that the 3.6 and 5.8-$\mu $m channels see the same FOV, while the 4.5 and 8.0-$\mu $m channels share a second FOV. Therefore, data at 3.6 $\mu $m is recorded simultaneously with that at 5.8 $\mu $m and 4.5 and 8.0-$\mu $m data are taken simultaneously. While one FOV is pointed at the target, the other covers adjacent sky. In the case of Sedna, the 4.5/8.0-$\mu $m FOV was pointed at the target first (for half of the length of time in Table 1), followed by the 3.6/5.8-$\mu $m FOV.

We observed Sedna as part of a program that includes 12 TNOs, 8 Centaurs, and 10 Trojan asteroids. The observing circumstances for Sedna are given in Table 1. The observations consisted of 16 dithered frames with 100 s exposure times each. The dithering is important to mitigate the adverse effects of bad pixels, latent images (from previous observations with bright stars in the field) and stray light from objects that may fall within certain regions just off the FOV. We observed Sedna twice, separated by 94.5 h, which allows motion that is large relative to the pixel size, but small relative to the FOV size. The paired observation provides four primary benefits: confident identification of the target by its motion, straightforward and accurate background subtraction, search for rotational variability, and increased probability of at least one good measurement (in case the object is obscured by a field star during one observation). The rotation period of Sedna was not known when we planned the observations. As it turned out, the IRAC observations we report are separated by $\sim$72 $\hbox{$^\circ$ }$ longitude (9.20 rotations).

Table 1: Observing circumstances for Sedna.

3 Data reduction

All data frames have been processed with the automated data pipeline (version 14.0) by the Spitzer Science Center (SSC). This pipeline includes steps such as dark subraction, flat fielding, and flux calibration (see data handbook at ssc.spitzer.caltech.edu/irac/dh/). The output of the SSC pipeline includes basic calibrated data (BCD), which are two-dimensional images in units of MJy/ster. Several artifacts that sometimes affect IRAC data (column pulldown, muxbleeding, array pulldown, stray light contamination) were not an issue for the Sedna data, so no corrections were needed.

We ultimately measure fluxes on each BCD frame, after a few extra processing steps described here. First, we make a background frame for each date by taking advantage of the fact that we observed essentially the same sky field on both dates, with Sedna having moved about an arcminute. We average the 16 dithered target frames from the other date (omitting outliers), after shifting them to a common pointing. This background frame is subtracted from each BCD data frame, leaving (in theory) a single positive source - Sedna - and a negative source, which is Sedna from the other date. We then apply corrections supplied by the SSC for variations in the pixel solid angle and for array location dependent photometric variations and convert the images to units of mJy/pixel.

Aperture photometry is performed for four combinations of aperture radius and background annulus: 2 pixel radius with both a 2-6 pixel and 10-20 pixel background annulus, and a 3 pixel radius with both 3-7 and 10-20 pixel annulus. These are not treated as independent measurements, but are used to assess the uncertainy associated with any single choice of parameters. Aperture corrections for these combinations are given in the IRAC data handbook for each channel. Color corrections are calculated assuming a solar spectral slope through each passband (Smith & Gottlieb 1974) and are iterated once for the measured relative 3.6/4.5-$\mu $m slope. Final fluxes reported in Table 2 are averages of all frames and aperture/annulus combinations for each channel. The listed 1$\sigma$ uncertainties take into account photon counting statistics, deviation among the 16 dithered frames, and deviation among the different aperture/annulus measurements. The uncertainty in the absolute calibration of IRAC is $\sim$2% in all channels (Reach et al. 2005).

To locate Sedna on each frame for photometry, we calculate the pixel position from the known ephemeris and the header pointing keywords. Sedna is visible in each 3.6-$\mu $m frame and in an average of the sixteen 4.5 $\mu $m frames, allowing us to verify that these locations are correct. The object is too faint for reliable centroiding, though, so we do not apply the "pixel-phase-dependent photometric correction'' described in the data handbook for the 3.6-$\mu $m channel. Sedna is not detected at 5.8 or 8.0 $\mu $m, so we report 3$\sigma$ upper limits to the flux in these channels. Unfortunately, the upper limits at 5.8 and 8.0 $\mu $m do not meaningfully constrain the albedos. The thermal flux (< $10^{-11} \mu$Jy in all four channels) from this extremely cold surface is negligible compared to the reflected flux.

Table 2: Measured fluxes and albedos

4 Analysis

In order to assess surface composition, we convert the measured fluxes into geometric albedos in each channel so they can be combined with previously published visible and NIR (0.3-2.5 $\mu $m) spectra. The geometric albedo at wavelength $\lambda$ is given by

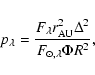\begin{displaymath}p_{\lambda}=\frac{F_{\lambda}r_{\rm AU}^{2}\Delta^2} {F_{\odot,\lambda}\Phi R^2}, \end{displaymath} (1)

where $F_\lambda$ is the measured flux, $F_{\odot,\lambda}$ is the solar flux at 1 AU, $r_{\rm AU}$ is the target's heliocentric distance in AU, $\Delta$ is the observer-target distance, $\Phi$ is a phase correction, and R is the target's radius. Rabinowitz et al. (2007) find the linear phase coefficient ($\beta$) of Sedna is $0.151\pm0.033$ in R band over the range of phase angles 0.14 to 0.65 deg. This $\beta$ results in $\Phi=0.919\pm0.017$ for the phase angles of the IRAC observations.

The radius of Sedna is somewhat uncertain. Brown et al. (2004b) constrained R to be <900 km and p v> 0.08 based on sub-mm measurements. More recently, Stansberry et al. (2007) observed Sedna's thermal emission at 70 $\mu $m with Spitzer. They conclude p v=0.20-0.02+0.60 and R=650+50-350 km. Due to Sedna's steep red spectral slope in the vis-NIR ( $V-K = 2.66\pm0.07$; Barucci et al. 2005a), the upper end of this range would imply p K>2.0, which is not very realistic. If we require p K<1.0, then p v<0.30. A more realistic estimate is then p v=0.20-0.02+0.10, giving R=650+50-120. Therefore, based on the sub-mm and thermal-IR measurements, the visible albedo of Sedna is most likely in the range 0.1-0.3.

The important factor in characterizing an absorption at $\lambda >$ 2.5 $\mu $m for Sedna is the relative albedos between IRAC and the previously published NIR data. As long as the p v used to scale the vis-NIR data is consistent with the R used to derive the IRAC albedos (p v and R are related by the visible brightness, H v), then identification of any absorption is robust. In other words, the band depth at 3.6 $\mu $m, as measured by the ratio of albedos at 2.2 and 3.6-$\mu $m, is independent of the choice of R and p v, as long as they are related by the same visible brightness. Another factor that could affect the relative 2.2 and 3.6 $\mu $m albedos is lightcurve variation. Fortunately, Sedna's visible lightcurve amplitude is very small ($\sim$0.04 mag; Gaudi et al. 2005). Furthermore, Sedna's large size suggests a nearly spherical body, so the small lightcurve amplitude is likely due to heterogeneous albedo distribution rather than shape. This is supported by apparent variations in the NIR spectrum with rotation (Barucci et al. 2005a). We adopt p v=0.15 and R=722 km (using H v=1.88; S. Tegler personal comm., http://www.physics.nau.edu/~tegler/research/survey.htm). The geometric albedos we derive for the IRAC bands are listed in Table 2 and are plotted along with the spectrum of Barucci et al. (2005a) in Fig. 1. The presence of a strong absorption in the IRAC bands is readily apparent.


  \begin{figure} \par\includegraphics[width=7.4cm,clip]{7021fig1.eps} \end{figure} Figure 1: Geometric albedos from IRAC are plotted along with the vis-NIR spectrum of Barucci et al. (2005a). The filled circles are data from 5 Feb. 2006, and the open circles are data from 9 Feb. 2006. Spectral models considering the cases of no H2O (solid gray line) and no CH4 (dashed gray line) are also plotted. The gray X symbols represent the values of the models convolved with the IRAC filter functions. These examples represent the best matches that we could find when isolating these ices. Both models shown adequately reproduce the vis-NIR region, but neither is a good fit to the IRAC data. Both models rely on organic tholins to match the steep red slope in the visible. The mixture that relies only on CH4 (solid line) is a particulate mixture of 50% CH4 (7 $\mu $m grains), 10% CH4 with embedded Titan tholin (7 $\mu $m grains), 20% Triton tholin (10 $\mu $m grains), 15% N2 (30 000 $\mu $m grains), and 5% amorphous carbon (20 $\mu $m grains). The mixture that relies only on H2O (dashed line) is a particulate mixture of 15% H2O with embedded Titan tholin (7 $\mu $m grains), 50% pyroxene (150 $\mu $m grains), 35% Titan tholin (7 $\mu $m grains).
Open with DEXTER

To investigate surface composition, we perform spectral modeling using the formulation of Shkuratov et al. (1999). Our implementation and comparisons with the other widely used formulation, that of Hapke (1993), is described by Poulet et al. (2002). Briefly, we can vary the surface materials, mixing ratios, grain sizes, and type of mixing to find the best-fit model spectrum. The three types of mixing employed are areal (checkerboard), particulate (salt-and-pepper), and intraparticle (one material embedded in a matrix of the other). The non-uniqueness of such models, particularly when applied to broad-band photometry, has been discussed and demonstrated by many authors. We are also limited in this analysis to materials for which optical constants have been measured. Nevertheless, increasing the wavelength coverage for Sedna's spectrum decreases the number of models that can successfully fit the data, thereby tightening the constraints on surface composition. This has been our motivation with the present work, to constrain the surface composition of Sedna beyond what is possible from the vis-NIR spectra alone.

Our first concern was to determine if we could use the IRAC data to test the detection of CH4 by Barucci et al. (2005a). We therefore tried to fit the full data range with mixtures that do not include CH4. Since the IRAC data clearly show an absorption at $\lambda > 2.5$-$\mu $m, it was important to consider other materials that would cause such an absorption. The most obvious material is H2O, but organics and hydrated silicates were also considered. Figure 1 shows the best model fit that we were able to find without including CH4. We were not, in any instance, able to simultaneously fit the vis-NIR spectra and the IRAC photometry with these mixtures. We next tried fitting mixtures without H2O ice, relying on CH4, tholins, and/or hydrated silicates for the $\lambda > 2.5$-$\mu $m absorption. We found that these methane mixtures could not simultaneously fit the relatively shallow absorption near 2.3-$\mu $m that Barucci et al. (2005a) ascribe to CH4 and the deep IRAC absorption. For mixtures and grain sizes that fit the IRAC bands, the 2.3 $\mu $m absorption is always far too deep, and vice versa, for mixtures that fit the vis-NIR, the IRAC absorption is not deep enough (Fig. 1).

Models that include both CH4 and H2O are able to describe the full spectral range. Our best-fit model is shown in Fig. 2. This model is a particulate mixture of five components, one of which is itself an intraparticle mixture of two materials. The mixture is composed of 50% CH4 (7 $\mu $m grains), 20% Triton tholin (10 $\mu $m grains), 10% N2 (150 000 $\mu $m grains), 5% amorphous carbon (20 $\mu $m grains), and 15% H2O with Titan tholin embedded in it (7 $\mu $m grains). The sources for optical constants are as follows: Pyroxene (100% Mg) from Dorschner et al. (1995), Titan tholin from Khare et al. (1984), Triton tholin from Khare et al. (1994), N2 (62 K) from R. Brown personal communication, and amorphous carbon from Rouleau & Martin (1991). The optical constants for H2O are spliced together from several sources: 0.3-0.88 $\mu $m (265 K) from Warren (1984), 0.88-0.96 $\mu $m (100 K) from Roush (1996), 0.96-2.7 $\mu $m (40 K) from Grundy and Schmitt (1998), and $\lambda > 2.7~\mu$m (100 K) from Bertie et al. (1960). The optical constants of CH4 are also from several sources: 0.7 to 3.2 $\mu $m (30 K) from Grundy et al. (2002), $\lambda > 3.2~\mu$m (30 K) from Hudgins et al. (1993), and $\lambda < 0.7~\mu$m extrapolated from the Grundy et al. (2002) optical constants. The tholins are necessary to provide the steep red spectral slope in the visible (Cruikshank et al. 2005). They also contribute to absorption at $\sim$3 $\mu $m, but cannot themselves account fully for the IRAC reflectances. N2 was identified by Barucci et al. (2005a) based on an absorption at 2.15 $\mu $m, but it has a much stronger feature near 4.3 $\mu $m. The 4.3 $\mu $m feature significantly decreases the albedo in the second IRAC band. Without N2, the model reflectance is too high in this band. CH4 matches absorptions at $\sim$2.3 $\mu $m and is also necessary to explain the IRAC data points, as is H2O.

  \begin{figure} \par\includegraphics[width=7.4cm,clip]{7021fig2.eps} \end{figure} Figure 2: Best-fit spectral model to the full range of the reflectance data of Sedna. Only models that contain both CH4 and H2O are able to simultaneously match the vis-NIR and the new IRAC data points. The X symbols represent the values of the model convolved with the IRAC filter functions. The mixture plotted here is described in the text.
Open with DEXTER

We therefore conclude that Sedna contains CH4, as suggested by Barucci et al. (2005a), and H2O ice, along with organics. Though not discussed by Barucci et al. (2005a), their spectrum does appear to contain a small absorption at $\sim$2 $\mu $m that is well fit by models that include H2O. The model fits that we show in Figs. 1 and 2 are admittedly very complex. We would certainly prefer to use simpler mixtures, but they simply do not fit the data. The complexity of the mixtures we are required to use is a signature of the complex surface of this fascinating body.

The IRAC albedos from 5 Feb. are $\sim$2.5$\sigma$ brigher than the albedos from 9 Feb. at 3.6 $\mu $m, and about 0.7$\sigma$ brighter at 4.5 $\mu $m. Whereas the two dates are formally consistent with each other, it is possible that we are detecting a heterogeneous surface composition, since the two IRAC dates are separated by $\sim$72 $\hbox{$^\circ$ }$ in longitude. The NIR spectra observed two nights in a row of Sedna (separated by 130 $\hbox{$^\circ$ }$ in longitude) by Barucci et al. (2005a) show apparent variability in the 2.3 $\mu $m CH4 band. Variation in CH4 on the surface would very plausably affect the IRAC data points as well, especially the 3.6-$\mu $m channel, which includes the strong C-H stretch fundamental at $\sim$3.4 $\mu $m. However, we have not specifically modeled each date separately.

5 Conclusions

Reflectance data of Sedna at 3.6 and 4.5 $\mu $m measured with the Spitzer Space Telescope exhibit strong absorption, the most likely cause of which is ices on the surface. Although it is generally very difficult to infer compositional details from such broad-band measurements, spectral modeling of the complete reflectance spectrum of Sedna from the visible to 4.5 $\mu $m suggests a compositionally complex surface containing organics, several ices, and silicates. Barucci et al. (2005a) had previously detected CH4 ice. We confirm this detection and further suggest the presence of H2O ice.

On other large, distant bodies such as Pluto and Neptune's moon Triton, the detection of N2 and CH4 ices presaged the presence of an atmosphere. The high albedos and clear methane signatures on the KBOs Eris and 2005 FY9 are also tantalizing hints that these large objects may also support thin atmospheres and volatile cycling. Although similar ices have been detected on Sedna, its surface is likely distinct from those other bodies. A comparatively low visible albedo and very strong red spectral slope indicate a much higher concentration of dark organic material. The CH4 bands at $\sim$2.3 $\mu $m on Sedna are rather weak, perhaps suggesting an absence of atmospheric volatile transport and redeposition that sets the stage for the long pathlengths necessary to explain the much deeper CH4 bands on those other large outer Solar System objects. With a perihelion of 76 AU, it is not surprising that Sedna's surface does not appear to get warm enough to mobilize volatiles. In any case, Sedna is a (so-far) unique and poorly understood object with a complex array of materials on its surface. Higher sensitivity and higher spectral resolution observations will continue to improve our understanding, and, perhaps, continue to surprise us.

Acknowledgements
This work is based [in part] on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Support for this work was provided by NASA through an award issued by JPL/Caltech.

References

 
Copyright ESO 2007