Contents

A&A 466, 63-73 (2007)
DOI: 10.1051/0004-6361:20066754

VLBI observations of seven BL Lacertae objects from RGB sample[*]

Zhongzu Wu1,2,3 - D. R. Jiang1,2 - Minfeng Gu1,2 - Yi Liu1,2


1 - Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, PR China
2 - Joint Institute for Galaxy and Cosmology (JOINGC) of SHAO and USTC
3 - Graduate School of the Chinese Academy of Sciences, Beijing 100039, PR China

Received 16 November 2006 / Accepted 27 December 2006

Abstract
We present EVN observations of seven BL Lac objects selected from the RGB sample. To investigate the intrinsic radiation property of BL Lac objects, we estimated the Doppler factor with the VLA or MERLIN core and the total 408 MHz luminosity for a sample of 170 BL Lac objects. The intrinsic (comoving) synchrotron peak frequency was then calculated by using the estimated Doppler factor. Assuming a Lorentz factor of 5, the viewing angle of jets was constrained. The high-resolution VLBI images of seven sources all show a core-jet structure. We estimated the proper motions of three sources with the VLBI archive data, and find that the apparent speed increases with the distance of components to the core for all of them. In our BL Lacs sample, the Doppler factor of LBLs is systematically larger than that of IBLs and HBLs. We find a significant anti-correlation between the total 408 MHz luminosity and the intrinsic synchrotron peak frequency. However, the scatter is much larger than for the blazar sequence. Moreover, we find a significant positive correlation between the viewing angle and the intrinsic synchrotron peak frequency. The BL Lac objects show a continuous distribution on the viewing angle. While LBLs have a smaller viewing angle than that of IBLs and HBLs, IBLs are comparable to HBLs. We conclude that the intrinsic synchrotron peak frequency is not only related to the intrinsic radio power (though with a large scatter), but also to the viewing angle for the present sample.

Key words: BL Lacertae objects: general - galaxies: active - galaxies: jets - galaxies: nuclei - radio continuum: galaxies

1 Introduction

BL Lac objects are a subclass of radio loud active galactic nuclei (AGNs) with no emission lines or less of them, but they have a strong continuum ranging from radio to $\gamma$-ray bands. Their spectral energy distribution (SED) consists of a synchrotron component at lower frequencies and an inverse Compton component at higher frequencies. Historically, BL Lac objects have been separately discovered through radio or X-ray surveys and have been divided into two classes, namely, radio-selected BL Lacs (RBLs) and X-ray selected BL Lacs (XBLs). However, this classification is based on the observing band rather than on the intrinsic physical properties. As a matter of fact, some BL Lac objects can be classified as both RBL and XBL, such as Mrk 501. Padovani & Giommi (1995) have suggested dividing RBL-like and XBL-like objects into low-energy peaked BL Lacs (LBLs) and high-energy peaked BL Lacs (HBLs) according to the location of the peak of the synchrotron emission $\nu_{\rm peak}$ (Urry & Padovani 1995). Generally, RBLs tend to be LBLs, and XBLs tend to be HBLs. The synchrotron peak frequency of RBLs is usually in the radio/IR band, while UV/X-ray band for XBLs (Giommi et al. 1995). In recent years, samples including intermediate BL Lac objects (IBLs) have been found in surveys that combine X-ray and radio observations (Perlman et al. 1998; Laurent-Muehleisen et al. 1999; Landt et al. 2001; Caccianiga et al. 1999). Their discovery has shown that BL Lac objects most likely form one class with a continuous distribution of synchrotron emission peak energies, while RBLs and XBLs represent the opposite ends of the continuum (Nieppola et al. 2006).

The so-called "blazar sequence'' was proposed to link the shape of the SED and the synchrotron peak frequency to the source luminosity for blazars, which consists of more luminous flat-spectrum radio quasars (FSRQs) and BL Lac objects (Fossati et al. 1998; Ghisellini et al. 1998). The most powerful sources have relatively small synchrotron peak frequencies, and the least powerful ones have the highest $\rm\nu_{peak}$ values. This anti-correlation can be theoretically explained by the cooling processes. In more powerful sources, the energy density is higher and the emitting particles have a higher probability of losing energy so are subjected to more cooling, resulting in a lower value for $\rm\nu_{peak}$. However, this sequence is based on the absence of high-luminosity HBLs and low-luminosity LBLs, therefore at least part of this systematic trend can result from selection effects (Antón & Browne 2005). Indeed, the evidence of low-power LBLs has been recently discovered (Padonavi et al. 2003; Caccianiga & Marchã 2004; Antón & Browne 2005), and the possible discovery of high luminosity HBLs is also reported in the Sedentary survey (Giommi et al. 2005). In addition, the high-power-high- $\rm\nu_{peak}$ FSRQs were found in the Deep X-ray Radio Blazar Survey (DXRBS), which is both X-ray and radio-selected, though they do not reach the extreme $\rm\nu_{peak}$ values of HBLs. From all these discoveries, it seems that the blazar sequence in its simplest form cannot be valid (Padovani 2006).

Instead of focusing on one or two limited surveys, Nieppola et al. (2006) have examined the properties of BL Lacs through constructing the SEDs for a large, heterogeneous sample of BL Lacs taken from the Veron-Cetty & Veron BL Lac catalogue and visible from the Metshähovi radio observatory. To our knowledge, this is the largest BL Lacs sample to revisit the blazar sequence up to now, though it is heterogeneous. The authors have found an anti-correlation between the radio power and $\rm\nu_{peak}$, with a huge scatter, reaching 5 orders of magnitude in power, and many outliers were also found, especially in the low-power-low- $\rm\nu_{peak}$ region. However, it is well known that the radio power of BL Lacs is affected by the beaming effect of radio jets, since BL Lacs are generally believed to have a relativistic jet aligned close to the line of sight (Urry & Padovani 1995). As the blazar sequence was originally proposed as the anti-correlation between the intrinsic luminosity and peak frequency, it nevertheless might be important to revisit the correlation using the intrinsic radio power. Moreover, the peak frequency $\rm\nu_{peak}\propto \it B \rm \delta \gamma_{peak}^{2}$, where B is the magnetic field, $\delta$the Doppler factor, and $\rm\gamma_{peak}$ a characteristic electron energy that is determined by a competition between accelerating and cooling processes. While blazars as a whole population suffer the Doppler boosting, the difference in Doppler factor can exist between various subsets, which implies the importance of investigating the intrinsic peak frequency after excluding the Doppler factor. As Kollgaard et al. (1996b) find, the average angles of radio jets to the line of sight is approximately $20^{\circ}$ for XBLs, but $10^{\circ}$ for RBLs. When the BL Lac objects show a continuous distribution of synchrotron emission-peak energies and most recent works focus on the correlation between the power and peak frequency, it is not clear whether they also show a continuous distribution for the angle to the line of sight, and HBLs and LBLs occupy the opposite ends of this distribution.

Apart from investigating the SED of BL Lac objects, the high-resolution radio observation is an important way to explore the radio structure of BL Lacs, from which we can obtain the physical information, such as the viewing angle, Lorentz factor and magnetic field. From the VLBI observations, the different subsets of BL Lacs can be compared based on the compact radio structure. In particular, it enables us to explore the jet orientation for BL Lac objects, because the properties of the parsec scale structure are strongly dependent on jet orientation. Kollgaard et al. (1996a) show that the jets in XBLs fade more quickly than in RBLs. The VLBI observations show that most of LBLs display the rapid superluminal apparent motions (Jorstad et al. 2001), while the TEV blazar sources (most are HBLs) display subluminal or mildly relativistic (Giroletti et al. 2004b,2006; Piner & Edwards 2004). Rector et al. (2003) have observed 15 HBLs and 3 BL Lacs from the RGB sample and find that the HBLs, like most LBLs, show parsec-scale core-jet morphologies with complex kilo-parsec scale morphologies. Moreover, the jets in HBLs are more well-aligned, suggesting that the jets of HBLs are either intrinsically straighter or are seen further off-axis than LBLs. Giroletti et al. (2004a) selected 30 low-redshift BL Lac objects and confirmed that parsec and kilo-parsec scale jets are oriented at the same P.A. in a large fraction of HBLs. The HBLs show less distortion and therefore are expected to be oriented at larger angles than the LBL sources.

Laurent-Muehleisen et al. (1999) present a sample of 127 BL Lac objects from the ROSAT ALL-Sky Survey-Green Bank catalogue (RGB), which exhibits properties intermediate between high- and low-energy-peaked BL Lac objects. In this paper, we present EVN observations of seven BL Lac objects selected from the RGB sample. Our goal is to investigate their compact radio structure. In combination with the previous observations and the archive data, we aim to explore the possible structure variation and measure the proper motion for our sources. Moreover, to explore BL Lac objects as a whole population, we investigated the distribution of the intrinsic radio power, the Doppler factor, and the viewing angle along the intrinsic synchrotron peak frequency for a sample of BL Lac objects selected from Nieppola et al. (2006).

The layout of this paper is as follows. In Sect. 2, the observations and data reduction for our seven sources are given. The compact radio structure are investigated in Sect. 3, where the proper motion are estimated for three sources as well. In Sect. 4, the intrinsic radio low-frequency luminosity, the Doppler factor, and the viewing angle are estimated for a sample of BL Lacs selected from Nieppola et al. (2006), and their distribution with the intrinsic synchrotron peak frequency is also explored. The discussions are shown in Sect. 5, while the conclusions are drawn in Sect. 6. Throughout this work, we adopt the following values for the cosmological parameters: $H_{0}=70 \rm {~km ~s^ {-1}~Mpc^{-1}}$, $\rm\Omega_{M}=0.3$, and $\rm\Omega_{\Lambda} = 0.7$, except an otherwise stated. The spectral index $\alpha$ is defined as $f_{\nu} \propto \nu^{-\alpha}$.

  
2 VLBI observations and data reduction

All seven BL Lac objects were observed with EVN at 5 GHz on 22 November 1999. The raw data were obtained with the MKIII VLBI recording system, with an effective bandwidth of 28 MHz, and correlated in Bonn at the Max-Planck-Institute. To study the structure and proper motion of these sources, we collected EVN and VLBA archive data. All seven sources are listed in Table 1: Col. (1) Source name, Col. (2) redshift, Cols. (3) the observational date and (4) the half-power beamwidth (HPBW) of the weighted beam, Col. (5) the noise of the image, Col. (6) the peak flux of the image, Col. (7) VLBI array. All the data were reduced using the NRAO Astronomical Image Processing System (AIPS) package. The system temperatures and gains were obtained from the VLBA website. After the initial reduction (including editing, amplitude calibration, instrumental phase corrections, and antenna-based fringe-fitting), we imported the calibrated data into DIFMAP package (Shepherd et al. 1994, 1995) to make images and fit the sources with a number of discrete circular Gaussian components. The fitting was done directly on the final, self-calibrated visibility data. The modelfit parameters are listed in Table 2.

  
3 Results

The VLBI images show core-jet structure for all sources we selected, and some of them are in good agreement with previous observations. The MERLIN archive images and available VLA images also show that these sources posse very straight jets. Model fitting of the radio structures in each image was performed, using the MODELFIT of Caltech DIFMAP package (uvweight = 0, -1). The modelfit parameters are presented in Table 2. To determine the uncertainty of the component position, we used the Difwrap package (Lovell 2000). The errors were estimated by perturbing the fit parameters until the resulting residual maps were unacceptable and taking the most extreme accepted points. A visual inspection was done to determine the goodness of the fit, and we used the best-fit total $\chi^2$ as the upper limit for every fit of the components.

In our seven BL Lac objects, previous VLBI observations at 6 cm are available for five of them. Combining our observations with the archive data, we got at least four-epoch observations for three sources: 1727+502, 1133+704, and 1741+196. The weighted linear fits to the component distances from the core as a function of the observing time were used to estimate the proper motion of the components. The results are given in Table 3, in which Col. (1) is the source name, (2) the components label, (3) the proper motion, and (4) the apparent speed. From Table 3, we find that all three sources have superluminal motion, and the apparent speed increases with distance from the core. For 1011+496 and 1424+240, only three-epoch data are available, therefore we do not measure their proper motion and only present their images in this work. For 4C+37.46 and 1542+614, there are no previous VLBI images and archive data available, so we present their first image.

   
3.1 Comments on individual sources

1011+496 - Snapshot VLA observations have found hints of extended structure around a bright core (Machalski & Condon 1983). This was confirmed by Kollgaard et al. (1996b), who found diffuse emission extending around $10^{\circ}$ to the north from their VLA B-configuration data. Augusto et al. (1998) have modeled this source with three components, which clearly showed that the jet of this source extends to about a few hundreds mas of the core with position angle $-99^{\circ}$. The MERLIN archive image (see Fig. 1) shows that the jet extends in nearly the same direction with our EVN and VLBA images (see Fig. 2), which show a jet in the opposite direction on the parsec scale. As the jet direction is similar in MERLIN, EVN, and VLBA images, this source is well-aligned.


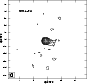  \begin{figure} \par\resizebox{3in}{!}{\includegraphics{6754fig1.eps}}\end{figure} Figure 1: The MERLIN archive image of 1011+496 at 1.6 GHz on May 6, 1999. The contour levels are -1, 1, 2, 4, 8, 16, 32, 64... times 0.001742 Jy beam-1 (3$\sigma $).


  \begin{figure} \par\includegraphics[width=12cm,clip]{6754fig2.eps}\end{figure} Figure 2: Multi-epoch EVN and VLBA images at 5 GHz. The minimum contour level is 3 times the rms noise given in Table 1. The contour levels are multiples (-1, 1, 2, 4, 8, 16, 32, 64...) of the minimum contour level and the axes are labeled in milliarcseconds. The top three panels are for 1011+496 at 1997.055, 1998.493, and 1999.893 ( from left to right); the middle for 1424+240 at 1999.696, 1999.893, and 2003.447 ( from left to right); while the bottom for 1542+614 and 4C+37.46 at 1999.893.

1133+704 - The images from three epochs (see Fig. 3) all show that the jet extends at a structural position angle of $\sim$ $110^{\circ}$, and the outer components extend to the northeast around $75^{\circ}$. These features are similar to the parsec scale jet found by Kollgaard et al. (1996a) and are well-aligned with the kilo-parsec scale halo and short inner jet presented by Giroletti et al. (2004a) and Giroletti et al. (2006). It can be seen from Fig. 3 that five components are detected in 1133+704, which is labeled as M0, M1, M2, M3, and M4, respectively. The weighted linear fits of components M1, M2, and M3 are presented in Fig. 4. As expected from the fitted line, M3 can be close to M2 at epoch 1991.433; however, it is not detected in the archive data. As M4 is only detected at two epochs, we do not perform the fit to this component. It can be seen from Table 3 that the inner components move more slowly, and the outer ones move faster.

The variability of this source has been investigated on other wavebands. Xie et al. (2004) show that the source did not show any noticeable variability, and it was quiet in the optical band during their observations. Albert et al. (2006) have detected very high-energy $\gamma$-Rays from this source, and an optical outburst in 2006 March was also observed but no evidence of flaring was detected by the University of Michigan Radio Observatory (UMRAO).


  \begin{figure} \par\includegraphics[width=16.5cm,clip]{6754fig3.eps}\end{figure} Figure 3: EVN and VLBA images of 1133+704 at 5 GHz. The epoch of observation from left to right are: epoch 1997.055, epoch 1998.493, epoch 1999.893. The axes are labeled in milliarcseconds. Contours are drawn at -1, 1, 2, 4, 8, 16,... times the noise level. Numerical parameters of the images are given in Table 1.

1424+240 - From the images of three epoch VLBI observations (Fig. 2), the component can not be well-resolved; however, the jet clearly extends to the southeast with position angle of about ${\rm PA}=150^{\circ}$. This result is similar with Fey & Charlot (2000), who modeled this source with two components at 2.3 GHz and 8.5 GHz, all with jets extending in the nearly same direction. However, this direction is a little misaligned with the VLA map found by Rector et al. (2003), which shows a compact structure consisting of a core and either a halo or roughly collinear jets extending north ${\rm PA}= -10^{\circ}$ and south ${\rm PA}= -175^{\circ}$. The MERLIN archive data (see Fig. 5) shows a very compact structure, and the jet direction is not evident.

1542+614 - There have no previous observations and archive data for this source. The redshift is unknown. We present our observations in Fig. 2. The source shows a compact core and straight jet extending to ${\rm PA} = 110^{\circ}$ on a parsec scale.

4C+37.46 - We present our image in Fig. 2, in which the source clearly shows one jet towards the northeast ${\rm PA}= 55^{\circ}$. The MERLIN archive image (see Fig. 6) also shows a jet in the same direction. The jet direction is consistent with Marecki et al. (2006), in which this source could be core-jet-lobe source, either with a steep spectrum or some diffuse structure. This source may also be a well aligned source.

1727+502 - The large amplitude variability of this source has been detected on several occasions. A violent variation of 2.1 mag in the optical band was reported by Scott et al. (1976). Fan et al. (1999) detected the variations of $\Delta{H}=0.57~\rm ~mag$ and $\Delta{K}=0.82$ mag. This source was observed by Kollgaard et al. (1996a) in 1991 at 6 cm and showed a core-jet morphology. Giroletti et al. (2004a) and Giroletti et al. (2006) show that this source displays a remarkable alignment from the parsec to the kilo-parsec scale. The multi-epoch images in Fig. 7 show a core and a jet extending to northeast with a position angle of about $-55^{\circ}$. The modelfit parameters of this source were presented in Table 2. It can be seen from Fig. 7 that six components were detected, which are labeled with C0, C1, C2, C3, C4, and C5. The weighted linear fit of components C1, C2, C3, C4, and C5 are shown in Fig. 8, and their measured proper motion and apparent speed are listed in Table 3. Interestingly, the component C5 was not detected at epoch 1991.433 (data from Kollgaard et al. 1996a) and 2002.403. From the fitted line for C5, the position of C5 at epoch 1991.433 is expected to be close to that of component C4; therefore, it is possible that these components are mixed together, causing difficulty in detection. At 2002.403, C5 very likely moved far away from the core and became very weak, so it was not detected. Due to the poor uv-coverage of our data and the fact that the beam size at this epoch is larger than other observations, we did not detect component C1 at 1999.893 (see Fig. 8). It is apparent that C3 and C4 at epoch 1998.493 was closer to the core than the expected distance from the fit. Actually, it seems that these two components move slowly (or were even stationary) before 1998.493, but move quickly afterwards, with the proper motion of C4 comparable to that of C5. However, the present data do not allow us to investigate this possibility further. From Table 3, we find that the apparent speed of components increases with the distance from the core. When looking in detail, components C4 and C5 show superluminal motion, while C1, C2 and C3 show subluminal motions. C1 is the closest component to the core, and it also shows the smallest proper motion. Actually, the error in the proper motion of C1 is larger than its proper motion. Therefore, it is possible that this component is stationary within the available observations.


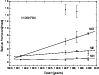  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{6754fig4.eps}}\end{figure} Figure 4: Positions of components with respect to the core at different epochs from model fitting for 1133+704. The data point at 1991.433 is taken from Kollgaard et al. (1996a). All the other epochs are those presented in this paper, and the lines represent the linear fitting of the motion for each jet component.


  \begin{figure} \par\resizebox{3in}{!}{\includegraphics{6754fig5.eps}}\end{figure} Figure 5: The MERLIN archive image of 1424+240 at 1.6 GHz observed on 1993 Apr. 1. The contour levels are -1, 1, 2, 4, 8, 16, 32, 64... times 0.001745 Jy beam-1(3$\sigma $).


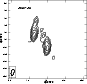  \begin{figure} \par\resizebox{3in}{!}{\includegraphics{6754fig6.eps}}\end{figure} Figure 6: The MERLIN archive image of 4C+37.46 at 5 GHz observed on 1999 May 6. The contour levels are -1, 1, 2, 4, 8, 16, 32, 64... times 0.001745 Jy beam-1 (3$\sigma $).

1741+196 - The six-epoch images of this source in Fig. 9 all show a very straight jet extending to the east with ${\rm PA}= 80^{\circ}$. This is similar to the result in Rector et al. (2003), in which one epoch VLBA map was presented, and the jet direction is nearly aligned with the VLA snapshot in Perlman et al. (1996) with $\Delta{\rm PA} = 5^{\circ}$. Five components are detected in Fig. 9, which are labeled as E0, E1, E2, E3, and E4. The weighted linear fit of E1, E2, E3, and E4 are shown in Fig. 10, and their measured proper motion and apparent speed are listed in Table 3. When we perform fits to the components, we exclude the data at epoch 2002.400, because the beam size of this epoch is much larger than others. While E4 shows a superluminal motion, E1, E2, E3 all show a rather small apparent speed. For components E2 and E3, the error in proper motion is actually larger than their proper motion. In view of this fact and the rather low value of proper motion, E2 and E3 could be stationary (within the error) in the time duration covered by the presenting available observations.

4 Properties of a sample of BL Lac objects

Nieppola et al. (2006) collected a large amount of multi-frequency data for the objects in the Mets $\ddot{\rm a}$hovi radio observatory BL Lac sample. The Mets $\ddot{\rm a}$hovi BL Lac sample includes 381 objects selected from the Veron-Cetty & Veron BL Lac Catalogue (Veron-Cetty & Veron 2000, hereafter VCV2000), and 17 objects from the literature, of which many sources are from the well-known BL Lac samples like 1Jy, S4, S5, Einstein Medium Sensitivity Survey (EMSS), Einstein Slew Survey, and DXRBS. The authors argue that this sample is supposed to have no selection criteria (other than declination) in addition to the ones in the original surveys. Based on the multi-frequency data, the SED of each source were constructed in the $\log \rm\nu-\log \nu F_{\nu}$ representation. The synchrotron component of the SED was fitted with a parabolic function

y=Ax2+Bx+C (1)

in order to determine the synchrotron peak frequency $\nu_{\rm peak}=-B/2A$. The objects were assigned an LBL/IBL/HBL classification according to $\nu_{\rm peak}$: for LBLs $\log\nu_{\rm peak}< 14.5$, for IBLs $14.5<\log~\nu_{\rm peak}<16.5$, and for HBLs $\log\nu_{\rm peak}>16.5$.

We collected the available data at 330 MHz, 360 MHz, 408 MHz, and 1.4 GHz from the Astrophysical Catalogues Support System (CATs)[*] maintained by the Special Astrophysical Observatory, Russia, and also the available VLA or MERLIN core and extended flux for their sample, resulting in a sample of 170 BL Lac objects. The redshift is known for most of the sources from NED and the literature. For the sources without redshift, we adopt the average redshift of 0.473, 0.302, 0.271 for LBLs, IBLs, and HBLs, respectively. The sample of BL Lac objects is listed in Table 4: Col. 1 the source IAU name (J2000); Col. 2 the source alias name; Col. 3 the redshift; Col. 4 the intrinsic synchrotron peak frequency (see Sect. 4.4); Col. 5 the total 408 MHz radio power; Col. 6 the 5 GHz core luminosity; Col. 7 the 5 GHz or 1.4 GHz extended flux density; Col. 8 the references; Col. 9 the Doppler factor (see Sect. 4.4); Cols. 10-12 the viewing angle estimated assuming $\Gamma= 3$, 5, and 10, respectively (see Sect. 4.5). In the following sections, we investigate the various properties, e.g. the Doppler factor, viewing angle for this sample.


  \begin{figure} \par\includegraphics[width=12cm,clip]{6754fig7.eps}\end{figure} Figure 7: EVN and VLBA images of 1727+502 at 5 GHz. The top from left to right are: epoch 1995.534, epoch 1997.055, epoch 1998.493. The bottom from left to right are: epoch 1999.893, epoch 2002.403. The axes are labeled in milliarcseconds. Contours are drawn at -1, 1, 2, 4, 8, 16,... times the noise level. Numerical parameters of the images are given in Table 1.


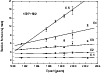  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{6754fig8.eps}}\end{figure} Figure 8: Positions of components with respect to the core at different epochs from model fitting for 1727+502. The data point at 1991.433 is taken from Kollgaard et al. (1996a). All the other epochs are those presented in this paper, and the lines represent the linear fitting of the motion for each jet component.

  
4.1 Method of estimating Doppler factor

A reliable determination of the Doppler factor, $\delta$, is a key step in studying the origins of the physical process in the compact emission regions of AGNs (Lähteenmäki & Valtaoja 1999). There are several methods available from the literature that can be used to estimate the Doppler factor. Ghisellini et al. (1993) estimated the Doppler factor for a sample of AGNs, based on the synchrotron self-Compton model. This method needs the angular size of the core from high-resolution VLBI observation and assumes that the X-ray flux originates from the self-Compton components. However, this method is limited in practice for the case of BL Lac objects. On the one hand, the detailed VLBI studies on BL Lac objects are only available for bright objects and a few other outstanding sources (Giroletti et al. 2006). On the other hand, while both the soft and the hard X-ray bands are dominated by the inverse Compton process in FSRQs, they are dominated by the synchrotron process in HBL, and the synchrotron flux dominates in the soft band and the flatter Compton component appears at higher X-ray energies in LBL (Donato et al. 2001).

In this work, we use the method suggested by Giovannini et al. (2001) and Giroletti et al. (2004a). Generally, the low-frequency radio power is a reliable indicator of the intrinsic radio power as it is only marginally affected by Doppler-boosted compact components (Bondi et al. 2001), while the relativistic boosting at the base of the jet affects the observed radio power of the core. Giovannini et al. (1988) and Giovannini et al. (2001) find a general correlation between the intrinsic core radio power and total radio power for a sample of radio galaxies

\begin{displaymath}\log P_{\rm ci5}= 0.62 \log P_{\rm t} +8.41 \end{displaymath} (2)

where $P_{\rm ci5}$ is the intrinsic core 5 GHz radio power derived assuming $\Gamma= 5$ (see Giovannini et al. 2001 for details), and Pt is the total radio power at 408 MHz. From the measured total 408 MHz radio power, we can derive the intrinsic core radio power. Thus, the Doppler factor can be derived if we know the observed radio core luminosity. As it is currently believed that most BL Lac objects are beamed FR I radio galaxies , Giroletti et al. (2004a) have applied this correlation to 30 BL Lac objects and find that the distribution of either the total radio power or the intrinsic core radio power derived from this correlation is similar with the FR I sample in Giovannini et al. (2001). This indicates that Eq. (2) is applicable to our large sample of BL Lac objects, although this relation was made from a sample of mainly radio galaxies, and only few BL Lac objects were included.


  \begin{figure} \par\includegraphics[width=12cm,clip]{6754fig9.eps}\end{figure} Figure 9: EVN and VLBA images of 1741+196 at 5 GHz. The top from left to right are: epoch 1997.055, epoch 1997.378, epoch 1998.493. The bottom from left to right are: epoch 1999.893, epoch 2002.400, epoch 2003.447. The axes are labeled in milliarcseconds. Contours are drawn at -1, 1, 2, 4, 8, 16,... times the noise level. Numerical parameters of the images are given in Table 1.


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{6754fig10.eps}}\end{figure} Figure 10: Positions of components with respect to the core at different epochs from model fitting for 1741+196. All the data points are presented in this paper, the lines represent the linear fitting of the motion for each jet component except the data point at 2002.400, as the baseline of this epoch is much shorter than the others.

  
4.2 Low-frequency radio power

The anti-correlation between the synchrotron peak frequency and the intrinsic power was first suggested by Fossati et al. (1998) and Ghisellini et al. (1998) for samples of blazars. Nieppola et al. (2006) find an anti-correlation between the luminosity at 5 GHz and 37 GHz with $\nu_{\rm peak}$ for a large sample of BL Lac objects. However, the 5 GHz and 37 GHz luminosity can be severely affected by the beaming effect from the radio jets and can't be used to indicate of the intrinsic radio power. Bondi et al. (2001) and Giroletti et al. (2004a) suggest that the low-frequency radio luminosity of BL Lac objects can indicate the intrinsic power from the radio jet. However, most of the objects in their works are HBLs and IBLs. For LBLs, especially those in the 1 Jy sample, as there is a selection criterion of the radio spectral index being less than 0.5 ( $\alpha_r\leq0.5$; $S_\nu \propto\nu^{-\alpha_r}$), the low-frequency radio emission may still be Doppler boosted (Cao et al. 2003). Indeed, Liu et al. (2006) find that the low-frequency radio emission of sources with a flat spectrum are likely to be Doppler-boosted, although only radio-loud quasars are considered in their work.

To test whether the low-frequency radio emission is Doppler-boosted, we selected 61 BL Lac objects from Nieppola et al. (2006), which have VLA observations and extended flux. These sources are listed in Table 4, including all powerful sources of the 1 Jy sample, and some other type of BL Lac objects. After extrapolating from the 1.4 GHz extended flux using $\alpha=1.0$ for 15 sources without 5 GHz extended flux, we plot the 5 GHz extended flux with the total 408 MHz flux in Fig. 11, which is directly from the available measurements, or extrapolated from 330 MHz, 360 MHz, or the total 1.4 GHz radio flux (see below). We find a generally good correlation. However, the scatter is obviously seen. This can be caused by the difference in the spectral index of two bands between sources, while both emissions are not influenced by the beaming effect. However, the possibility that the low-frequency radio emission in some sources is indeed Doppler boosted can't be excluded completely with present data. Nevertheless, we believe that the low-frequency radio emission is intrinsic, as most of the sources follow the correlation.


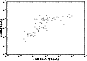  \begin{figure}\resizebox{8.8cm}{!}{\includegraphics{6754fig11.eps}}\end{figure} Figure 11: The relationship between the radio 5 GHz extended flux and the radio low-frequency 408 MHz flux.

To calculate the Doppler factor using the method in Sect. 4.2, we had to obtain the total 408 MHz luminosity. Unfortunately, not all sources in our sample had an observed 408 MHz flux. We adopted three methods of calculating 408 MHz luminosity according to the available data. For BL lac objects with the extended flux available, we estimated the 408 MHz luminosity by extrapolating from the 5 GHz or 1.4 GHz extended flux assuming a spectral index of $\alpha=1.0$. For the sources with observed low-frequency radio flux, we estimated the total 408 MHz luminosity after a K-correction using spectral index $\alpha=1.0$. For the remaining sources, neither the extended flux nor the low-frequency flux was available, so we extrapolated from the total 1.4 GHz flux density with a spectral index of $\alpha=0.207$, which is the average spectral index between 408 MHz and 1.4 GHz of the BL Lac objects in our sample. The estimated total 408 MHz radio power is listed in Col. 5 of Table 4. To compare with the FR I radio galaxies sample of Zirbel & Baum (1995), we converted the total 408 MHz radio luminosity into the same cosmological frame ( $H_{0}=50 \rm {~km ~s^ {-1}~Mpc^{-1}}$and q0=0), as used in their calculation. The distribution of this total 408 MHz radio power is shown in Fig. 12. Although our sample contains about two thirds of the BL Lac objects from the 1Jy sample, we find that the mean and median values of the 408 MHz radio power (mean  $=25.56~{\rm W~Hz}^{-1}$ and median $\rm =25.52~W~Hz^{-1}$) are consistent with those of the low-luminosity FR I radio galaxies in Zirbel & Baum (1995), which is mean  $\rm =25.50\pm0.12~W~Hz^{-1}$ and median  $\rm =25.38~W~Hz^{-1}$. This, on one hand, supports the scenario that FR I radio galaxies are the parent population of BL Lac objects; and on the other hand, it indicates that the estimated total 408 MHz radio power of our BL Lac objects is intrinsic, as it is comparable to FR I radio galaxies.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{6754fig12.eps}\end{figure} Figure 12: The distribution of 408 MHz luminosity for BL Lac objects selected from Nieppola et al. (2006).

  
4.3 Doppler factor of BL Lac objects

According to the unified schemes, classes of apparently different AGN might actually be intrinsically similar, when only viewed at different angles with respect to the line of sight. It was suggested that BL Lac objects are FR I radio sources viewed at relatively small angles to the line of sight and that the relativistic beaming has an enormous effect on the observed luminosities, so determining the Doppler factor is important in studying the properties of BL Lac objects, especially the differences between different types of BL Lac objects. To estimate the Doppler factor using the method described in Sect. 4.1, we collected 5 GHz VLA or MERLIN core flux of 170 BL Lac objects (see Table 4). The 5 GHz core luminosity was calculated with a K-correction assuming a spectral index of $\alpha=0$. The Doppler factor is then estimated by using the 5 GHz core luminosity, the estimated radio power at 408 MHz (see Sect. 4.3), and Eq. (2). In this work, we adopt $P_{\rm c,o}= P_{\rm c,i}\delta^{2+ \alpha}$ (corresponding to a continuous jet), assuming $\alpha=0$, where $P_{\rm c,o}$ is the observed 5 GHz core luminosity and $P_{\rm c,i}$ the intrinsic one calculated from Eq. (2).

The synchrotron peak frequency $\rm\nu_{peak}\propto \it B \rm \delta \gamma_{peak}^{2}$, therefore it may not be intrinsic since the Doppler factor can vary between sources in our sample. Once the Doppler factor can be estimated, it would be fundamental in calculating the intrinsic peak frequency. In this work, we calculate the intrinsic synchrotron peak frequency $\nu^{'}_{\rm peak}=\nu_{\rm peak}(1+z)/\delta$, where $\nu_{\rm peak}$ is from Nieppola et al. (2006). The factor (1+z) is included since the $\nu_{\rm peak}$ of Nieppola et al. (2006) is determined from the log $\nu-\log~\nu f_{\nu}$ panel in the observer's frame. The distribution of the Doppler factor and the intrinsic peak frequency is shown in Fig. 13. While all IBLs and HBLs have a Doppler factor below 10, LBLs have a wide spread for the Doppler factor, with most sources below 20, and it can be over 30 in a few cases. It seems that the Doppler factor systematically decreases with increasing peak frequency; however, it is similar for IBLs and HBLs. Indeed, the Spearman rank correlation analysis shows an anti-correlation between the Doppler factor and $\nu^{'}_{\rm peak}$ at $\gg$99.99 per cent significance level. This may indicate that the Doppler boosting is systematically more pronounced in LBLs than in IBLs and HBLs, although a fraction of LBLs are comparable to IBLs and HBLs.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{6754fig13.eps}\end{figure} Figure 13: The Doppler factor versus the intrinsic synchrotron peak frequency $\nu _{\rm peak}^{'}$ (see text for details).

The estimation of Doppler factor enables us to investigate the relationship between the intrinsic radio power and the intrinsic synchrotron peak frequency. The relationship between the intrinsic peak frequency and 408 MHz radio power is shown in Fig. 14. It can be seen that LBLs are statistically more powerful than other BL Lac objects. There is a significant anti-correlation between luminosity and $\nu _{\rm peak}'$ at $\gg$99.99% confidence level from the Spearman Rank Correlation analysis. Although we used the low-frequency radio emission to indicate the intrinsic radio power and correct the peak frequency for Doppler factor, our results in Fig. 14 are very similar to those of radio power at 5 GHz in Nieppola et al. (2006). Several low-luminosity LBLs are apparently seen, and they even reach lower luminosities than any of the HBLs.

We note that the 408 MHz radio power in our sample is calculated in inhomogenous ways, and the redshift of some sources is actually unknown and tentatively taken as the average value of subclasses. To verify how the correlation depends on the data, we check with a sample that has the measured 408 MHz flux and known redshift. Still, these twenty-one sources (Fig. 14) show a strong anti-correlation at about a 98 per cent confidence level. However, due to the small number of these sources, we add the sources with known redshift and 408 MHz radio power extrapolated from either 330 MHz or 360 MHz radio flux (Fig. 14), resulting in a sample of 56 sources, of which the uncertainty from extrapolation is minimized. It is clearly seen that these sources follow the general trend of whole sample. The Spearman rank correlation analysis shows a significant anti-correlation at about a 99.9 per cent confidence level. We are thus confident that the inhomogenous data derivation does not influence our results.

Despite much more scatter in our figure than in the corresponding one of Fossati et al. (1998), the anti-correlation between luminosity and $\nu _{\rm peak}'$ is still significant and possibly caused by the intrinsic physical differences (such as magnetic fields, electron energies), as suggested by Sambruna et al. (1996). As jet formation is closely connected with the central engine (Liu et al. 2006), this correlation can also be caused by the common relationship between both the radio luminosity and peak frequency and the central engine, as suggested by Wang et al. (2002) that the peak frequency is significantly correlated with the accretion rate. Although our sample is relatively large, still only a small fraction of low-luminosity LBLs are included in the sample. As a matter of fact, there is no evidence of very high-luminosity HBLs in the sample of Nieppola et al. (2006), which is our parent sample.


  \begin{figure} \par\includegraphics[width=11.3cm,clip]{6754fig14.eps}\end{figure} Figure 14: The low-frequency 408 MHz luminosity versus the intrinsic synchrotron-peak frequency $\nu _{\rm peak}'$. The open circles are the sources with the direct measurements of 408 MHz radio flux and known redshift, the open triangles are the sources calculated from either the 360 MHz, or 330 MHz radio flux with known redshift, while the solid circles are those estimated from the extended flux (at 5 GHz or 1.4 GHz), the total 1.4 GHz radio flux, or low-frequency radio flux (with unknown redshift) (see text for details).

4.4 Viewing angle

There have been several models trying to explain the differences in different types of BL Lac objects. It was originally explained as the orientation effects, with HBLs being observed at larger inclination to the jet axis (Urry & Padovani 1995). However, Sambruna et al. (1996) argue that it is difficult to model the detailed transition from an HBL to an LBL SED only in terms of orientation only and instead suggest a continuous change in the physical parameters of the jet. To study the viewing angle distribution for our sample of BL Lac objects, we estimated the viewing angle for each object assuming a Lorentz factor of $\Gamma= 5$, in combination with the estimated Doppler factor in Sect. 4.3. The difference between this angle and that of $\Gamma= 3$ and $\Gamma= 10$ are taken as the uncertainty. The distribution of the viewing angle and intrinsic synchrotron peak frequency $\nu_{\rm peak}'=\nu_{\rm peak}(1+z)/\delta$ is shown in Fig. 15, in which the errorbar are indicated with the viewing angle from $\Gamma= 3$ and $\Gamma= 10$. It can be seen that most of LBLs are in the range of angles ($0^{\circ}$, $20^{\circ}$), while most of IBLs and HBLs are in ( $15^{\circ}$, $30^{\circ}$). As an intermediate subclass between the LBLs and HBLs, the IBLs' viewing angles are larger than that of LBLs; however, it is indistinguishable from those of HBLs. Moreover, BL Lac objects, as a whole, mostly have viewing angle smaller than $30^{\circ}$. This is consistent with the unified scheme in which BL Lac objects are the aligned version of FR I radio galaxies (Urry & Padovani 1995). It clearly shows that there is a significant positive correlation between viewing angle and $\nu _{\rm peak}'$at $\gg$99.99 per cent significance level. Actually, this can be expected simply from the relationship between the Doppler factor and $\nu _{\rm peak}'$, if an uniform Lorentz factor is adopted for all sources. Therefore, it is not surprising that LBLs have smaller viewing angles compared to IBLs and HBLs, since their Doppler factor is systematically larger.

Usually, the viewing angles can be estimated by using the Doppler factor and the measurements of proper motion, however, the latter are not available for most of sources. Using the measured proper motion and the Doppler factor, we calculated the Lorentz factor for the three sources we observed. We find that the estimated Lorentz factor is generally consistent with the assumption of $\Gamma= 5$, and the range of $\Gamma$ between 3 and 10 (see Table 3). This indicates that the angle got by assuming a Lorentz factor of 5 can be reasonable for our sample. Certainly, the adoption of a Lorentz factor of 5 only makes sense for our statistical sample investigation and can't be used for an individual source. We believe that the exact value of Lorentz factor will not change our results significantly. From Fig. 15, it seems that the BL Lac objects as a single population possess a continuous range of viewing angle and a positive correlation between the viewing angle and the $\nu _{\rm peak}'$. Similar to the Doppler factor distribution, the viewing angle increases with the increasing peak frequency from LBLs to IBLs, but, it smooths out upward.

5 Discussion

In Sect. 3.1, our observations have shown that all the jets of seven BL Lac objects are very straight, and they do not exhibit large bending between the small and large scales. This result is similar with the observations of HBLs in Rector et al. (2003), in which two of our sources are included. This indicates that these sources are either intrinsically straighter or are seen further off-axis than LBL jets. In three sources with measured proper motion (Sect. 3.1), it shows that different components of the same source have different apparent speeds, and the apparent speed increases with the distance from the core. This is similar to the results in Piner et al. (2006), in which BL Lac object 0235+164 and two FSRQs were studied. This phenomena will need a change in either bulk Lorentz factor or viewing angle. However, these changes would also yield predictable changes in the brightness of components due to changing Doppler boosting, and these changes are not seen.

While recent discoveries of low-luminosity LBLs and possible high-luminosity HBLs (Padovani et al. 2003; Caccianiga & Marchã 2004; Giommi et al. 2005) seems to undermine the blazar sequence, an anti-correlation between radio power and peak frequency was found for a large sample of BL Lac objects (Nieppola et al. 2006), though with a large scatter. We improved their work by using the intrinsic low-frequency radio power and the intrinsic synchrotron peak frequency, instead. It appears that LBLs are intrinsically more powerful than other types of BL Lac objects, and the distribution of the low-frequency power of BL Lac objects as a whole is comparable to those of FR I radio galaxies. Although there is a correlation between the intrinsic low-frequency power and intrinsic peak frequency, the scatter of this relation seems large, which contrast with the much tighter relation of "blazar sequence''. More important, some LBLs have low radio power, which is difficult to explain by the radiation cooling process, which was used to explain the blazar sequence. In fact, these sources tend to weaken the blazar sequence; however, they are not enough to eliminate the correlation in this work. While the blazar sequence was suggested for a sample of blazars including FSRQs, of which the peak frequency can be lower than those of LBLs, our sample only includes BL Lac objects, although our sample is much larger. Moreover, the original peak frequency used in this work is directly adopted from Nieppola et al. (2006), which was derived by simply fitting the synchrotron component of the SED with a parabolic function. The determination of peak frequency is thus influenced by the data quality and sampling. As Nieppola et al. (2006) discuss, the peak frequencies of the most extreme objects can be exaggerated by using a simple parabolic function in the fitting procedure. Furthermore, the large scatter in Fig. 14 implies that other parameters may be at work, and the scatter can be much lower once this parameter is included. Besides the significant anti-correlation between the intrinsic low-frequency luminosity and intrinsic peak frequency, there is a positive correlation between the viewing angle and intrinsic peak frequency. LBLs apparently have smaller viewing angle, while the viewing angle of IBLs is comparable to that of HBLs. We conclude that the intrinsic synchrotron peak frequency is related not only to the intrinsic luminosity, but maybe also to the viewing angle. In fact, some HBLs like Mrk 421 and Mrk 501 are supposed to have $\delta\geq10$, which was estimated by Celotti et al. (1998) based on their TeV flux variability. However, the studies of jet morphology, core dominance, the fit to the trend of the jet brightness, and Full-Width Half-Maximum (FWHM) all show that the radio jet emission is oriented to larger angles with respect to the line of sight (Giroletti et al. 2004b; Giroletti et al. 2006).


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{6754fig15.eps}\end{figure} Figure 15: The viewing angle versus the intrinsic synchrotron peak frequency  $\nu _{\rm peak}'$. The viewing angle is estimated by assuming a Lorentz factor of 5 and using the estimated Doppler factor in Sect. 4.4. The errorbar is indicated with the viewing angle of Lorentz factors of 3 and 10.

There are only a small fraction of low-luminosity LBLs in our sample, and actually no evidence of very high-luminosity HBLs (Nieppola et al. 2006). This precludes us from draws any firm conclusion about the validity of the blazar sequence. Actually, the FSRQs with a high $\nu_{\rm peak}$ found in DXRBS do not reach the extreme $\nu_{\rm peak}$ values of HBLs. It is still unclear whether this fact indicates an intrinsic, physical limit to this parameter. An alternative scenario is one where really high-power-high- $\nu_{\rm peak}$ blazars have their thermal emission swamped by the non-thermal, featureless jet emission, which makes their redshift determination impossible. While our results seem to undermine the blazar sequence, the anti-correlation between the intrinsic emission and intrinsic peak frequency needs further investigation. It is important to compile a larger sample including various subclasses of blazars, especially blue quasars, low-luminosity LBLs, and high-luminosity HBLs and to calculate the accurate peak frequency and intrinsic luminosity. Only then, the physical mechanism of the different peak frequencies can be explored. While the peak frequency is believed to be determined by the magnetic strength and the energy distribution of relativistic electrons, the shift of the peak frequency in blazars can give us clues to this information. It might also be important to investigate the relationship between the SEDs of blazars and the central engine, such as accretion rate (Wang et al. 2002) and/or black hole mass.

6 Conclusions

In this paper, we have presented EVN and VLBA images at 5 GHz for seven BL Lac objects selected from an RGB sample (Laurent-Muehleisen et al. 1999). We collected multi-epoch data from EVN and the VLBA archive for three of them. The radio data were collected for a sample of 170 BL Lac objects selected from Nieppola et al. (2006) to study the relation of the intrinsic synchrotron peak frequency with the intrinsic low-frequency radio luminosity and the viewing angle. The main conclusions can be summarized as follows:

1.
We found that all seven sources show a core-jet structure on a pc scale, and no counter-jets were found. The jets of these sources are straight, and only small changes in the position angle are found between small and large scales. The superluminal motion is detected in all three sources with the available multi-epoch data, and the apparent speed of components are increases with the increasing distance of components to the core.

2.
Based on the method suggested in Giovannini et al. (2001) and Giroletti et al. (2004a), we calculated the Doppler factor for 170 BL Lac objects selected from Nieppola et al. (2006). Using the total 408 MHz luminosity to indicate the intrinsic radio power and correcting the synchrotron peak frequency for Doppler factor, we found a significant anti-correlation between the total 408 MHz luminosity and the intrinsic synchrotron peak frequency. However, the scatter is much larger than that of the blazar sequence. Especially, several low-power LBLs are clearly present. Our results seem to undermine the blazar sequence.

3.
The viewing angle of BL Lac objects are constrained using the estimated Doppler factor, and assuming a Lorentz factor of 5. We found a strong positive correlation between the viewing angle and the intrinsic synchrotron peak frequency. The BL Lacs show a continuous distribution of the viewing angle, and LBLs have lower values than for IBLs and HBLs. However, the IBLs are similar to HBLs for the viewing angle.
In conclusion, our results show that the intrinsic peak frequency is related not only to the intrinsic radio power (though much looser than the blazar sequence), but also to the viewing angle. A complete, large sample of BL Lacs (or blazars) is needed for future investigations.

Acknowledgements
We thank the anonymous referee for insightful comments and constructive suggestions. This work is supported by the NSFC under grants 10373019, 10333020, and 10543002. The European VLBI Network is a joint facility of European, Chinese, and other radio astronomy institutes funded by their national research councils. The National Radio Astronomy Observatory is operated by Associated Universities, Inc., under cooperative agreement with the National Science Foundation. MERLIN is a National Facility operated by the University of Manchester at Jodrell Bank Observatory on behalf of PPARC. This research made use of the NASA/ IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This work also made use of Astrophysical Catalogues Support System (CATS) maintained by the Special Astrophysical Observatory, Russia.

References

 

  
7 Online Material


   
Table 1: The VLBI observational log.
Object z Epoch HPBW Noise ($3\sigma$) Peak Array
      (mas $\times$ mas,$^\circ$) (mJy beam-1) (mJy beam-1)  
1011+496 0.2 1997.055 $2.5 \times 2.08,~ -8.36$ 0.60 116.0 1
    1998.493 $2.47 \times 1.72,~-2.76$ 0.56 103.0 1
    1999.893 $2.8 \times 1.35,~ -38.6$ 1.83 81.7 2
1133+704 0.046 1997.055 $2.77 \times 2.04,~ -32.5$ 0.30 118.0 1
    1998.493 $2.72 \times 1.7, ~87.7$ 0.39 98.7 1
    1999.893 $1.87 \times 1.32, ~-30.4$ 1.01 77.5 2
1424+240 0.16 1999.696 $2.96 \times 1.92,~ -0.412$ 0.94 125.0 1
    1999.893 $5.95 \times 1.98,~ 12.8$ 1.57 134.0 2
    2003.447 $3.02 \times 1.61,~ -8.25$ 0.60 164 1
1542+614 ... 1999.893 $2.26 \times 1.48,~ 7.24$ 0.87 93.4 2
4C+37.46 1.271 1999.893 $4.65 \times 2.17, ~15.7$ 1.38 32.2 2
1727+502 0.055 1995.534 $2.12\times 1.87, ~-34.6$ 0.37 80.1 1
    1997.055 $3.05 \times 2.43, ~3.03$ 0.35 85.7 1
    1998.493 $2.62 \times 1.52, ~-10.8$ 0.46 66.9 1
    1999.893 $4.58 \times 2.3, ~4.5$ 0.93 81.4 2
    2002.403 $2.31 \times 1.64, ~16$ 0.63 72.9 2
1741+196 0.083 1997.055 $3.75 \times 2.13, ~11.8$ 0.37 103.0 1
    1997.378 $3.07 \times 1.67, ~-5.62$ 0.42 80.1 1
    1998.493 $3.09 \times 1.58, ~-5.37$ 0.39 85.4 1
    1999.893 $5 \times 1.79, ~16.2$ 1.14 98.4 2
    2002.400 $7.68 \times 4.92, ~67.8$ 0.90 131.0 2
    2003.447 $2.98 \times 1.72, ~-6.07$ 0.41 100.0 1

1: VLBA, 2: EVN.


 

 
Table 2: Model parameters.
Source Epoch Component S (Jy) r (mas) PA (deg) a (mas)

1727+502 ......		 1995.534 C0 0.068 0.00 0.0 0.27
  1995.534 C1 0.027 $ 1.15\pm0.05$ -73.3 0.36
  1995.534 C2 0.016 $ 2.61\pm0.11$ -57.4 0.91
  1995.534 C3 0.016 $ 4.90\pm0.28$ -58.8 1.91
  1995.534 C4 0.013 $ 7.48\pm0.51$ -55.8 3.12
  1995.534 C5 0.012 $11.01\pm0.72$ -45.9 4.53
  1997.055 C0 0.065 0.00 0.0 0.00
  1997.055 C1 0.030 $ 1.20\pm0.71$ -75.4 0.60
  1997.055 C2 0.030 $ 2.73\pm0.08$ -58.8 0.97
  1997.055 C3 0.010 $ 4.99\pm0.32$ -58.8 1.84
  1997.055 C4 0.012 $ 8.06\pm0.44$ -54.4 3.62
  1997.055 C5 0.014 $13.94\pm0.41$ -46.4 5.00
  1998.493 C0 0.062 0.00 0.0 0.33
  1998.493 C1 0.023 $ 1.13\pm0.06$ -81.7 0.46
  1998.493 C2 0.022 $ 2.50\pm0.48$ -59.0 1.12
  1998.493 C3 0.028 $ 4.73\pm0.11$ -60.9 1.88
  1998.493 C4 0.012 $ 7.19\pm0.40$ -53.7 2.55
  1998.493 C5 0.015 $15.78\pm0.54$ -50.5 5.62
  1999.893 C0 0.082 0.00 0.0 0.67
  1999.893 C2 0.039 $ 2.84\pm0.26$ -57.5 1.69
  1999.893 C3 0.014 $ 6.11\pm0.76$ -53.4 1.00
  1999.893 C4 0.009 $ 9.16\pm1.35$ -50.2 4.00
  1999.893 C5 0.003 $17.76\pm1.44$ -51.4 3.32
  2002.403 C0 0.071 0.00 0.0 0.53
  2002.403 C1 0.017 $ 1.01\pm0.11$ -63.9 1.09
  2002.403 C2 0.030 $ 2.88\pm0.10$ -55.3 1.30
  2002.403 C3 0.021 $ 6.90\pm0.25$ -56.1 1.87
  2002.403 C4 0.009 $12.52\pm0.39$ -51.9 3.09
1741+196 ...... 1997.055 E0 0.070 0.00 0.0 0.00
  1997.055 E1 0.040 $ 0.74\pm0.013$ 70.2 0.65
  1997.055 E2 0.018 $ 2.86\pm0.079$ 77.9 1.60
  1997.055 E3 0.009 $ 5.96\pm0.13 $ 81.1 2.01
  1997.055 E4 0.004 $12.83\pm1.50 $ 85.2 6.41
  1997.378 E0 0.073 0.00 0.0 0.35
  1997.378 E1 0.019 $ 0.93\pm0.10 $ 70.4 0.51
  1997.378 E2 0.015 $ 2.65\pm0.079$ 79.6 1.32
  1997.378 E3 0.010 $ 5.40\pm0.22 $ 81.3 2.41
  1997.378 E4 0.004 $11.93\pm1.25 $ 84.5 5.04
  1998.493 E0 0.076 0.00 0.0 0.28
  1998.493 E1 0.022 $ 0.86\pm0.14 $ 72.0 0.69
  1998.493 E2 0.017 $ 2.65\pm0.090$ 78.0 1.41
  1998.493 E3 0.009 $ 5.95\pm0.25 $ 81.6 2.47
  1998.493 E4 0.004 $13.39\pm1.79 $ 85.4 5.55
  1999.893 E0 0.095 0.00 0.0 0.64
  1999.893 E1 0.003 $ 1.25\pm0.71$ 88.6 0.00
  1999.893 E2 0.020 $ 2.79\pm0.17$ 78.3 0.83
  1999.893 E3 0.006 $ 6.95\pm0.38$ 82.0 0.64
  1999.893 E4 0.001 $13.36\pm2.72$ 89.9 2.32
  2003.447 E0 0.092 0.00 0.0 0.31
  2003.447 E1 0.023 $ 1.09\pm0.082$ 66.1 0.64
  2003.447 E2 0.015 $ 2.80\pm0.11 $ 80.2 1.58
  2003.447 E3 0.008 $ 5.82\pm0.30 $ 84.1 2.39
  2003.447 E4 0.004 $13.83\pm1.21 $ 85.0 5.35
1133+704 ...... 1997.055 M0 0.099 0.00 0.0 0.38
  1997.055 M1 0.027 $ 0.74\pm0.13$ 111.1 0.51
  1997.055 M2 0.006 $ 2.99\pm0.50$ 99.0 2.23
  1997.055 M3 0.005 $ 6.23\pm0.88$ 76.7 4.16
  1997.055 M4 0.005 $15.61\pm1.40$ 73.1 7.15
  1998.493 M0 0.091 0.00 0.0 0.31
  1998.493 M1 0.018 $ 1.27\pm0.12$ 106.9 0.70
  1998.493 M2 0.008 $ 3.34\pm0.25$ 100.9 1.29
  1998.493 M3 0.004 $14.99\pm1.66$ 73.1 5.26
  1998.493 M4 0.003 $ 7.55\pm1.66$ 76.0 3.42
  1999.893 M0 0.080 0.00 0.0 0.35
  1999.893 M1 0.003 $0.92\pm0.42$ 119.6 0.00
  1999.893 M2 0.013 $2.71\pm0.61$ 93.0 1.03
  1999.893 M3 0.003 $8.47\pm0.26$ 78.8 0.75



 

 
Table 3: Proper motions.

Object		 Component $\mu$ ( $\rm mas~ yr^{-1}$) $\beta_{\rm app}$ $\delta$ $\theta$ (deg) $\Gamma$ $\theta_{\Gamma= 5}$ (deg)
1133+704 M1 $0.040\pm0.015$ $0.12\pm0.045$        
  M2 $0.18\pm0.032$ $0.56\pm0.10$        
  M3 $0.78\pm0.31$ $2.4\pm0.97$ 0.8 41.6 4.6 39.9
1727+502 C1 $0.0074\pm0.0085$ $0.027\pm0.031$        
  C2 $0.032\pm0.013$ $0.12\pm0.049$        
  C3 $0.16\pm0.014$ $0.58\pm0.051$        
  C4 $0.47\pm0.31$ $1.72\pm1.15$        
  C5 $1.53\pm0.26$ $5.64\pm0.96$ 1.9 18.1 9.6 23.7
1741+196 E1 $0.043\pm0.013$ $0.24\pm0.071$        
  E2 $0.0064\pm 0.019$ $0.035\pm0.11$        
  E3 $0.031\pm0.049$ $0.17 \pm 0.27$        
  E4 $0.23\pm0.21$ $1.25 \pm1.13$ 3.3 12.3 2.0 16.6



 

 
Table 4: The sample of 170 BL Lac objects selected from Nieppola et al. (2006).

IAU name		 Source z $\log \rm\nu_{peak}'$ $\log P_{\rm 408~ M}$ $\log P_{\rm core}$ $f_{\rm ext}$ Refs. $\delta$ $\theta_{3}$ $\theta_{5}$ $\theta_{10}$
0006-063 NRAO 5 0.347 12.10 26.94a 26.65 ... 1 6.0 0.0 9.4 8.8
0007+472 RX J0007.9+4711 0.302* 15.81 25.63b 25.18 ... 2 2.8 21.1 18.7 14.3
0035+598 1ES 0033+595 0.086 18.60 24.01c 24.02 4.50 3 2.3 24.7 21.1 15.9
0040+408 1ES 0037+405 0.271* 16.62 24.93c 24.42 3.07 3 1.9 28.8 23.9 17.7
0050-094 PKS 0048-097 0.537 12.94 27.29c 26.60 139.00 4 4.4 11.5 13.1 10.9
0110+418 NPM1G +41.0022 0.096 17.72 24.41d 23.58 ... 2 1.1 43.5 34.2 24.5
0112+227 S2 0109+22 0.473* 12.83 26.36b 26.60 ... 2 8.5 0.0 4.7 6.7
0115+253 RXS J0115.7+2519 0.350 13.15 25.31d 24.92 ... 2 2.6 22.5 19.7 14.9
0123+343 1ES 0120+340 0.272 17.96 24.86c 24.75 2.59 3 2.9 19.9 18.0 13.9
0124+093 MS 0122.1+0903 0.339 15.37 23.58c 23.60 0.08 5 2.0 28.4 23.6 17.5
0136+391 B3 0133+388 0.271* 16.31 25.44a 24.95 ... 2 2.4 23.7 20.5 15.5
0141-094 PKS 0139-09 0.733 12.77 27.17c 26.99 50.00 6 7.4 0.0 6.7 7.5
0148+140 1ES 0145+138 0.125 15.76 24.22e 22.88 ... 7 0.5 65.8 49.9 34.9
0153+712 8C 0149+710 0.022 14.65 23.99b 23.50 ... 2 1.3 38.2 30.4 22.0
0201+005 MS 0158.5+0019 0.299 17.62 24.46c 24.29 0.83 5 2.3 24.9 21.3 16.0
0208+353 MS 0205.7+3509 0.318 14.90 23.91c 24.10 0.20 5 2.7 21.2 18.8 14.4
0214+517 87GB 02109+5130 0.049 17.53 24.50b 23.94 ... 2 1.5 34.4 27.8 20.3
0222+430 3C 66A 0.440 15.20 27.55a 26.65 ... 8 3.9 14.3 14.6 11.8
0232+202 1ES 0229+200 0.140 19.22 24.75d 24.32 ... 7 1.9 28.7 23.8 17.7
0238+166 AO 0235+164 0.940 12.83 27.24c 27.35 31.40 9 10.8 0.0 0.0 5.3
0301+346 MS 0257.9+3429 0.245 13.10 24.49c 24.14 1.38 5 1.9 29.1 24.1 17.8
0314+247 RXS J0314.0+2445 0.054 12.71 22.95d 22.60 ... 2 1.0 46.0 36.0 25.7
0326+024 2E 0323+0214 0.147 19.61 24.16c 24.01 2.00 10 2.1 27.2 22.8 17.0
0416+010 2E 0414+0057 0.287 20.49 25.70d 24.99 ... 1 2.1 26.6 22.4 16.7
0422+198 MS 0419.3+1943 0.512 16.63 25.15c 24.73 1.14 5 2.3 24.7 21.1 15.9
0424+006 PKS 0422+004 0.310 15.01 26.33b 26.32 ... 9 6.2 0.0 8.9 8.5
0505+042 RXS J0505.5+0416 0.027 16.87 23.57d 23.17 ... 2 1.2 39.9 31.7 22.8
0507+676 1ES 0502+675 0.314 18.55 24.20c 24.90 0.40 3 5.6 3.8 10.2 9.2
0508+845 S5 0454+84 0.112 12.59 23.75c 25.19 5.10f 4,9 10.8 0.0 0.0 5.3
0509-040 4U 0506-03 0.304 17.77 25.57c 24.82 36.00f 11 1.9 28.7 23.8 17.7
0613+711 MS 0607.9+7108 0.267 14.41 24.03c 24.39 0.40 5 3.5 16.4 15.8 12.5
0625+446 87GB 06216+4441 0.473* 13.04 26.25d 26.15 ... 8 5.5 5.2 10.5 9.4
0650+250 1ES 0647+250 0.203 17.85 24.85c 24.83 4.89 3 3.2 17.9 16.7 13.1
0654+427 B3 0651+428 0.126 14.79 25.07a 24.70 ... 2 2.4 24.2 20.8 15.7
0656+426 NPM1G +42.0131 0.059 17.34 25.85c 24.30 699.00f 12 0.9 49.5 38.4 27.3
0710+591 EXO 0706.1+5913 0.125 20.83 25.03b 24.46 ... 7 1.9 29.3 24.3 17.9
0721+713 S5 0716+714 0.300 14.07 26.50c 25.85 316.00f 4 3.2 18.0 16.8 13.1
0738+177 PKS 0735+17 0.424 12.64 25.43c 27.10 12.00f 4 29.4 0.0 0.0 0.0
0744+745 MS 0737.9+7441 0.315 13.24 24.75c 24.71 1.42 5 3.1 19.1 17.5 13.6
0753+538 S4 0749+54 0.200 12.23 25.47e 26.12 ... 13 9.3 0.0 3.1 6.2
0757+099 PKS 0754+100 0.266 12.48 25.26c 26.56 6.70 9 17.7 0.0 0.0 2.0
0806+595 SBS 0802+596 0.300 16.43 25.26e 24.81 ... 2 2.4 24.3 20.9 15.7
0809+523 1ES 0806+524 0.137 16.09 24.90e 24.88 ... 3 3.3 17.4 16.4 12.9
0818+423 OJ 425 0.245 12.73 26.41a 26.17 ... 14 5.0 8.3 11.6 10.0
0823+223 4C 22.21 0.951 12.94 28.53c 26.96 602.60 4 2.7 21.4 18.9 14.5
0825+031 PKS 0823+033 0.506 11.79 25.23c 26.98 1.40 14 29.4 0.0 0.0 0.0
0831+044 PKS 0829+046 0.174 12.81 25.74b 25.95 ... 7 6.2 0.0 9.0 8.6
0831+087 1H 0827+089 0.941 13.90 26.67d 26.15 ... 11 4.0 13.3 14.0 11.4
0832+492 OJ 448 0.548 12.33 25.98c 26.36 23.40f 4 8.4 0.0 4.9 6.8
0854+441 US 1889 0.382 17.31 26.05a 25.06 ... 2 1.8 30.3 24.9 18.4
0854+201 OJ 287 0.306 12.75 25.25c 26.56 17.00f 4,9 17.9 0.0 0.0 2.0
0915+295 B2 0912+29 0.302* 15.64 26.20b 25.59 ... 2 3.0 19.7 17.9 13.8
0916+526 RXS J0916.8+5238 0.271* 17.01 25.61d 24.92 ... 2 2.1 27.0 22.7 16.9
0929+502 RXS J0929.2+5013 0.370 13.76 26.08e 26.50 ... 8 9.2 0.0 3.1 6.2
0930+498 1ES 0927+500 0.188 20.77 24.06e 24.18 ... 3 2.7 21.6 19.1 14.6
0930+350 B2 0927+35 0.302* 14.35 26.48b 25.95 ... 8 3.7 15.3 15.2 12.1
0952+656 RGB J0952+656 0.302* 14.90 25.46e 24.78 ... 2 2.0 28.0 23.3 17.3
0954+492 MS 0950.9+4929 0.380 16.73 24.20c 24.06 0.26 5 2.1 26.6 22.4 16.7
0958+655 S4 0954+65 0.368 13.06 25.66c 25.97 28.60f 4,15 6.8 0.0 7.9 8.0
1012+424 RXS J1012.7+4229 0.364 20.82 25.83a 24.98 ... 2 1.9 28.7 23.9 17.7
1015+494 GB 1011+496 0.200 16.41 25.80b 25.22 ... 16 2.6 22.5 19.7 14.9
1031+508 1ES 1028+511 0.360 18.16 25.32e 25.16 ... 3 3.4 17.0 16.2 12.7
1037+571 RXS J1037.7+5711 0.302* 14.50 25.43d 25.30 ... 2 3.7 15.2 15.1 12.1
1047+546 1ES 1044+549 0.473* 12.86 24.68d 24.32 ... 3 2.0 27.4 22.9 17.1
1053+494 MS 1050.7+4946 0.140 14.95 24.30c 24.26 3.12 5 2.5 23.3 20.2 15.3
1104+382 MRK 421 0.031 18.20 24.40a 24.14 ... 7 2.0 27.7 23.2 17.2
1109+241 1ES 1106+244 0.271* 16.70 24.96d 24.50 ... 3 2.1 27.4 22.9 17.1
1120+422 EXO 1118.0+4228 0.124 17.21 24.10d 23.83 ... 2 1.8 30.7 25.2 18.6
1136+701 MRK 180 0.046 18.73 25.16c 23.80 237.00 3 0.8 52.2 40.3 28.6
1136+676 RXS J1136.5+6737 0.134 17.18 24.17e 24.23 ... 2 2.6 22.0 19.4 14.8
1149+246 EXO 1449.9+2455 0.402 19.63 25.32d 24.79 ... 2 2.2 25.8 21.9 16.4
1150+242 B2 1147+245 0.200 13.18 25.30c 25.79 50.00f 4,15 7.1 0.0 7.3 7.7
1151+589 RXS J1151.4+5859 0.302* 16.10 25.98b 25.33 ... 2 2.6 22.6 19.7 15.0
1209+413 B3 1206+416 0.302* 13.88 25.64a 25.95 ... 8 6.7 0.0 8.0 8.1
1215+075 1ES 1212+078 0.130 15.57 24.80d 24.56 ... 7 2.5 23.6 20.4 15.4
1217+301 B2 1215+30 0.130 15.10 25.46b 25.24 ... 7 3.4 17.0 16.2 12.7
1220+345 GB2 1217+348 0.130 13.97 25.04e 25.01 ... 2 3.5 16.5 15.9 12.5
1221+301 PG 1218+304 0.182 18.80 24.86e 24.65 ... 7 2.6 22.4 19.6 14.9
1221+282 ON 231 0.102 14.16 25.12c 25.43 41.00 3 5.3 6.2 10.8 9.5
1223+806 S5 1221+80 0.473* 13.74 26.99e 26.41 ... 8 4.3 11.8 13.2 10.9
1224+246 MS 1221.8+2452 0.218 13.60 24.25c 24.38 1.05 5 3.0 19.7 17.9 13.8
1230+253 RXS J1230.2+2517 0.135 14.40 25.26b 25.18 ... 2 3.6 15.8 15.4 12.3
1231+642 MS 1229.2+6430 0.164 15.84 24.33c 24.43 2.34 5 3.0 19.7 17.9 13.8
1237+629 MS 1235.4+6315 0.297 15.61 24.38c 24.48 0.70 17 3.0 19.3 17.6 13.6
1241+066 1ES 1239+069 0.150 17.05 23.48c 23.73 0.40 3 2.5 23.6 20.4 15.4
1248+583 PG 1246+586 0.847 14.27 26.90b 27.17 ... 8 11.1 0.0 0.0 5.1
1253+530 S4 1250+53 0.302* 14.39 26.45b 25.89 ... 8 3.5 16.2 15.7 12.4
1257+242 1ES 1255+244 0.141 16.83 24.00d 23.51 ... 3 1.3 38.0 30.3 22.0
1310+325 AUCVn 0.996 12.61 26.54c 27.74 5.40 9,15 27.7 0.0 0.0 0.0
1322+081 1ES 1320+084N 0.049 12.99 22.74d 22.81 ... 3 1.4 35.6 28.6 20.8
1341+399 RXS J1341.0+3959 0.163 19.97 25.19a 24.33 ... 2 1.4 35.5 28.5 20.8
1402+159 MC 1400+162 0.244 16.29 26.54a 25.41 ... 1 1.9 29.0 24.1 17.8
1404+040 MS 1402.3+0416(went 0.344 15.74 25.76c 24.80 11.89 3 1.6 32.3 26.4 19.3
1409+596 MS 1407.9+5954 0.496 16.40 25.50c 25.02 2.75 5 2.6 22.8 19.8 15.1
1415+485 RGB J1415+485 0.500 14.13 25.73e 25.57 ... 2 4.1 13.1 14.0 11.4
1415+133 PKS 1413+135 0.247 12.39 26.66a 26.01 ... 1 3.5 16.5 15.9 12.6
1417+257 2E 1415+2557 0.237 19.00 25.29d 24.74 ... 2 2.1 26.5 22.4 16.7
1419+543 OQ 530 0.152 13.17 24.68c 25.81 22.00f 4,7 11.4 0.0 0.0 5.0
1427+238 PKS 1424+240 0.160 15.34 25.69a 25.18 ... 2 2.7 21.9 19.3 14.7
1427+541 RGB J1427+541 0.106 14.79 24.38e 23.80 ... 2 1.4 36.4 29.2 21.2
1428+426 H 1426+428 0.129 18.41 24.43e 23.93 ... 7 1.6 33.5 27.2 19.9
1439+395 PG 1437+398 0.344 16.56 25.98a 25.05 ... 2 1.9 29.4 24.3 18.0
1442+120 1ES 1440+122 0.162 16.20 24.80d 24.41 ... 3 2.1 27.3 22.9 17.0
1444+636 MS 1443.5+6349 0.298 16.94 24.31c 23.93 0.59 5 1.7 31.6 25.9 19.0
1448+361 RXS J1448.0+3608 0.271* 16.43 25.03d 24.72 ... 2 2.5 23.1 20.1 15.2
1458+373 B3 1456+375 0.333 12.86 25.91a 25.93 ... 8 5.4 5.7 10.7 9.5
1501+226 MS 1458.8+2249 0.235 14.69 24.73c 25.06 2.66 5 4.6 10.4 12.5 10.5
1509+559 SBS 1508+561 0.302* 14.83 24.83e 24.80 ... 2 3.2 18.3 17.0 13.2
1516+293 RXS J1516.7+2918 0.130 18.56 25.01a 24.13 ... 2 1.3 38.1 30.4 22.0
1517+654 1H 1515+660 0.702 17.82 25.72e 25.39 ... 2 3.3 17.4 16.4 12.9
1532+302 RXS J1532.0+3016 0.064 16.86 23.87d 23.64 ... 2 1.7 32.0 26.1 19.2
1533+342 RXS J1533.4+3416 0.810 17.89 25.78e 25.75 ... 2 4.9 8.9 11.9 10.1
1534+372 RGB J1534+372 0.143 13.97 24.02e 23.98 ... 2 2.2 25.8 21.8 16.3
1535+533 1ES 1533+535 0.890 19.55 25.96d 25.31 ... 3 2.5 22.8 19.9 15.1
1536+016 MS 1534.2+0148 0.312 18.67 25.53c 24.79 8.78 5 1.9 29.1 24.1 17.8
1540+819 1ES 1544+820 0.271* 17.53 25.42e 24.89 ... 3 2.3 24.9 21.3 16.0
1540+147 4C 14.6 0.605 14.25 27.58c 27.10 202.00 9 6.3 0.0 8.7 8.4
1542+614 RXS J1542.9+6129 0.302* 14.19 25.27e 25.36 ... 2 4.4 11.3 13.0 10.8
1554+201 MS 1552.1+2020 0.222 16.89 25.09c 24.58 6.86 5 2.1 27.3 22.9 17.0
1555+111 PG 1553+11 0.360 15.92 26.29b 26.11 ... 2 5.1 7.7 11.4 9.9
1602+308 RXS J1602.2+3050 0.302* 16.27 25.36d 24.65 ... 2 1.8 29.6 24.5 18.1
1626+352 RXS J1626.4+3513 0.497 15.05 25.39d 24.95 ... 2 2.5 23.0 20.0 15.1
1644+457 RXS J1644.2+4546 0.225 17.28 25.67a 24.89 ... 2 1.9 28.4 23.7 17.5
1652+403 RGB J1652+403 0.240 14.80 24.60d 24.19 ... 2 1.8 29.6 24.5 18.1
1653+397 MRK 501 0.034 16.17 23.79c 24.51 67.00f 4,7 4.8 9.3 12.0 10.2
1704+716 RXS J1704.8+7138 0.350 15.32 25.06e 24.72 ... 2 2.5 23.6 20.4 15.4
1719+177 PKS 1717+177 0.137 12.43 25.19a 25.42 ... 2 5.0 7.9 11.5 9.9
1724+400 B2 1722+40 1.049 12.64 27.81a 26.99 ... 8 4.7 9.7 12.2 10.3
1725+118 H 1722+119 0.018 15.75 23.06d 22.80 ... 2 1.1 41.6 32.9 23.6
1728+502 IZw187 0.055 17.16 24.20b 23.96 ... 10 1.9 28.9 24.0 17.8
1739+476 OT 465 0.473* 13.34 27.13b 26.69 ... 8 5.4 5.5 10.6 9.4
1742+597 RGBJ 1742+597 0.400 13.75 25.72e 25.49 ... 2 3.7 15.0 15.0 12.0
1743+195 NPM1G +19.0510 0.084 17.44 24.40c 24.53 11.60 3 3.2 18.2 17.0 13.2
1745+398 B3 1743+398B 0.267 17.59 26.55a 25.31 ... 2 1.7 31.6 25.9 19.0
1747+469 B3 1746+470 1.484 13.30 27.26a 27.41 ... 8 11.3 0.0 0.0 5.0
1748+700 S4 1749+70 0.770 13.80 26.63c 26.91 45.70f 4,14 9.9 0.0 0.0 5.8
1749+433 B3 1747+433 0.473* 13.08 26.62a 26.21 ... 8 4.5 11.1 12.9 10.7
1750+470 RXS J1750.0+4700 0.160 18.31 25.28a 23.78 ... 2 0.7 55.5 42.7 30.2
1751+096 PKS 1749+096 0.322 11.33 24.92c 26.99 2.00 14 37.1 0.0 0.0 0.0
1756+553 RXS J1756.2+5522 0.271* 19.74 24.72e 24.26 ... 2 1.8 29.7 24.6 18.1
1757+705 MS 1757.7+7034 0.407 13.37 24.65c 24.64 0.62 5 3.0 19.3 17.6 13.6
1800+784 S5 1803+784 0.680 13.35 27.57e 27.36 ... 4,15 8.5 0.0 4.7 6.7
1806+698 3C 371 0.051 14.42 25.87c 24.95 990.00 4,7 1.8 30.4 25.0 18.4
1808+468 RGB J1808+468 0.450 14.34 25.85e 25.33 ... 2 2.8 20.8 18.6 14.3
1811+442 RGB J1811+442 0.350 15.30 25.92e 24.26 ... 2 0.8 52.3 40.4 28.7
1813+317 B2 1811+31 0.117 15.34 25.00b 24.37 ... 2 1.7 31.1 25.5 18.8
1824+568 4C 56.27 0.664 12.56 28.02c 26.99 452.00 9 4.1 13.2 14.0 11.4
1829+540 RXS J1829.4+5402 0.302* 15.06 25.73e 24.61 ... 2 1.3 37.1 29.7 21.5
1838+480 RXS J1838.7+4802 0.300 13.24 25.05d 24.71 ... 2 2.5 23.6 20.4 15.4
1841+591 RGB J1841+591 0.530 14.94 25.68e 24.64 ... 2 1.4 35.4 28.5 20.7
1853+672 1ES 1853+671 0.212 16.25 23.81c 24.12 0.40 3 3.0 19.5 17.7 13.7
1927+612 S4 1926+61 0.473* 12.72 26.62b 26.67 ... 8 7.7 0.0 6.3 7.3
1959+651 1ES 1959+650 0.047 17.33 23.01c 24.10 1.60 3 5.2 6.9 11.1 9.7
2005+778 S5 2007+77 0.342 12.39 26.14c 26.38 28.90 9 7.7 0.0 6.2 7.3
2009+724 S5 2010+72 0.473* 12.94 27.02e 26.90 ... 8 7.5 0.0 6.7 7.5
2022+761 S5 2023+76 0.473* 13.54 26.65e 26.39 ... 13 5.4 5.7 10.7 9.5
2039+523 1ES 2037+521 0.053 15.60 22.27c 23.31 0.23 3 3.6 16.0 15.6 12.4
2134-018 PKS 2131-021 1.285 12.04 27.93c 27.87 70.80 14 11.9 0.0 0.0 4.7
2145+073 MS 2143.4+0704 0.237 13.61 25.13c 24.79 6.60 5 2.5 22.9 20.0 15.1
2152+175 PKS 2149+17 0.473* 13.00 26.03c 26.57 36.70f 4 10.4 0.0 0.0 5.5
2202+422 BL LAC 0.070 13.15 24.21c 25.73 40.00f 4,7 14.5 0.0 0.0 3.5
2250+384 B3 2247+381 0.119 15.35 24.64a 24.29 ... 2 2.0 27.6 23.1 17.2
2257+077 PKS 2254+074 0.190 13.31 24.78c 25.66 17.00f 9,10 8.9 0.0 4.0 6.4
2319+161 Q J2319+161 0.302* 15.29 25.13d 24.58 ... 2 2.0 27.9 23.3 17.3
2322+346 TEX 2320+343 0.098 16.68 24.59b 23.82 ... 2 1.2 39.4 31.3 22.6
2323+421 1ES 2321+419 0.059 13.05 23.09d 23.18 ... 11 1.7 31.5 25.8 18.9
2329+177 1ES 2326+174 0.213 17.84 24.64d 24.30 ... 3 2.0 27.4 23.0 17.1
2339+055 MS 2336.5+0517 0.740 14.89 25.74d 24.88 ... 5 1.8 30.0 24.7 18.2
2347+517 1ES 2344+514 0.044 15.86 23.30c 23.97 3.58 3 3.6 15.6 15.3 12.2
2350+196 MS 2347.4+1924 0.515 15.72 24.80d 24.29 ... 5 1.8 30.0 24.8 18.3
Notes: Col. 1: the source IAU name (J2000). Col. 2: the source alias name. Col. 3: the redshift. `*' indicate that the redshift is unknown, and taken as the average redshift of LBL/IBL/HBL subclass. Col. 4: the intrinsic synchrotron peak frequency after excluding the Doppler factor. Col. 5: the total radio power at 408 MHz (notes: `a' - from 408 MHz; `b' - from 360 MHz; `c' - from extended flux; `d' - from total 1.4 GHz; `e' - from 330 MHz). Col. 6: the 5 GHz core luminosity. Col. 7: the 5 GHz extended flux density in mJy, `f' indicates the extend flux at 1.4 GHz. Col. 8: the references for core and extended flux: (1: Liu & Zhang (2002) 2: Laurent-Muehleisen et al. (1999) 3: Perlman et al. (1996) 4: Rector & Stocke (2001) 5: Cavallotti et al. (2004) 6: Cassaro et al. (1999) 7: Giroletti et al. (2004b) 8: Taylor et al. (1996) 9: Murphy et al. (1993) 10: Laurent-Muehleisen et al. (1993) 11: Kollgaard et al. (1996b) 12: Rector et al. (2003) 13: Taylor et al. (1994) 14: Rector & Stocke (2003) 15: Cassaro et al. (2002) 16: Augusto et al. (1998) 17: Rector et al. (2000)). Col. 9: the Doppler factor. Cols. 10-12: the viewing angle of $\Gamma= 3$, 5 and 10, respectively.



Copyright ESO 2007