A&A 466, 41-61 (2007)
DOI: 10.1051/0004-6361:20065849
M. Krumpe1 - G. Lamer1 - A. D. Schwope1 - S. Wagner2 - G. Zamorani3 - M. Mignoli3 - R. Staubert4 - L. Wisotzki1 - G. Hasinger5
1 - Astrophysikalisches Institut Potsdam,
An der Sternwarte 16,
14482 Potsdam, Germany
2 -
Landessternwarte Heidelberg-Königstuhl, 69117 Heidelberg,
Germany
3 -
INAF - Osservatorio Astronomico di Bologna, Bologna, Italy
4 -
Universität Tübingen, Institut für Astronomie und
Astrophysik, 72076 Tübingen, Germany
5 -
Max-Planck-Institut für Extraterrestrische Physik,
Giessenbachstrasse, Postfach 1312, 85741 Garching, Germany
Received 16 June 2006 / Accepted 7 December 2006
Abstract
We report on a medium deep XMM-Newton survey of the Marano
Field and optical follow-up observations.
The mosaicked XMM-Newton pointings in this optical quasar survey field
cover 0.6 deg2 with a total of 120 ks good observation time.
We detected 328 X-ray sources in total. The turnover flux of our sample is
![]() erg cm-2 s-1 in
the 0.2-10 keV band.
With VLT FORS1 and FORS2 spectroscopy we classified
96 new X-ray counterparts.
erg cm-2 s-1 in
the 0.2-10 keV band.
With VLT FORS1 and FORS2 spectroscopy we classified
96 new X-ray counterparts.
The central 0.28 deg2, where detailed optical
follow-up observations were performed, contain 170
X-ray sources (detection likelihood ML>10), out of which
48 had already been detected by ROSAT.
In this region we recover 23 out of 29
optically selected quasars.
With a total of 110 classifications in our core sample we
reach a completeness of ![]() 65%.
About one-third of the XMM-Newton
sources are classified as type II AGN
with redshifts mostly below 1.0.
Furthermore, we detect five high redshift type II AGN
(
65%.
About one-third of the XMM-Newton
sources are classified as type II AGN
with redshifts mostly below 1.0.
Furthermore, we detect five high redshift type II AGN
(
![]() ).
).
We show that the true redshift distribution of type II AGN
remains uncertain, since their lack of emission lines in a wide optical
wavelength range hampers
their identification in the redshift range 1<z<2.
The optical and X-ray colours of the core sample indicate that
most of the still unidentified X-ray sources are likely to
be type II AGN. We calculate absorbing column densities
and show that the ratio
of absorbed to unabsorbed objects is significantly higher for type II AGN than for
type I AGN.
Nevertheless, we find a few unabsorbed type II AGN. The X-ray hardness
ratios of some high redshift type I AGN also give an indication of
heavy absorption. However, none of these type I objects is bright
enough for spectral extraction and detailed model fitting.
Types I and II AGN cover the same range in intrinsic X-ray luminosity,
(
![]() ), although type II AGN have a lower
median intrinsic X-ray luminosity (log
), although type II AGN have a lower
median intrinsic X-ray luminosity (log
![]() )
compared to type I AGN (log
)
compared to type I AGN (log
![]() ).
Furthermore, we classified three X-ray bright optically normal
galaxies (XBONGs) as counterparts. They show properties similar to
type II AGN, probably harbouring an active nucleus.
).
Furthermore, we classified three X-ray bright optically normal
galaxies (XBONGs) as counterparts. They show properties similar to
type II AGN, probably harbouring an active nucleus.
Key words: surveys - X-rays: galaxies - galaxies: active - galaxies: quasars: general
The Marano Field was named by an early optical quasar survey
up to a limiting magnitude of
![]() by
Marano et al. (1988). Based on different optical selection techniques
(colour-colour diagrams, grism plates, variability analysis) they
discovered 23 broad emission line quasars and defined an extensive
list of quasar candidates. Zitelli et al. (1992) completed this work by
presenting a spectroscopically complete sample of quasars with
by
Marano et al. (1988). Based on different optical selection techniques
(colour-colour diagrams, grism plates, variability analysis) they
discovered 23 broad emission line quasars and defined an extensive
list of quasar candidates. Zitelli et al. (1992) completed this work by
presenting a spectroscopically complete sample of quasars with
![]() using this list of quasar candidates.
They confirmed 54 quasars including the former 23 quasars. Between
December 1992 and July 1993, ROSAT observed the central Marano Field
(
using this list of quasar candidates.
They confirmed 54 quasars including the former 23 quasars. Between
December 1992 and July 1993, ROSAT observed the central Marano Field
(![]() 0.2 deg2) for 56 ks (Zamorani et al. 1999). The data revealed
50 X-ray sources with a limitingflux of
0.2 deg2) for 56 ks (Zamorani et al. 1999). The data revealed
50 X-ray sources with a limitingflux of
![]() erg cm-2 s-1
in the ROSAT band (0.5- 2.0 keV).
Multi-colour CCD and spectroscopic data identified 42 X-ray sources
(33 quasars, 2 galaxies, 3 clusters, and 4 stars). 66% of the
optically selected quasars within the ROSAT field-of-view were detected
as ROSAT X-ray sources. Gruppioni et al. (1999) carried out a deep radio
survey at 1.4 and 2.4 GHz and detected 68 radio sources
(
erg cm-2 s-1
in the ROSAT band (0.5- 2.0 keV).
Multi-colour CCD and spectroscopic data identified 42 X-ray sources
(33 quasars, 2 galaxies, 3 clusters, and 4 stars). 66% of the
optically selected quasars within the ROSAT field-of-view were detected
as ROSAT X-ray sources. Gruppioni et al. (1999) carried out a deep radio
survey at 1.4 and 2.4 GHz and detected 68 radio sources
(
![]() mJy). Follow-up observation provided redshifts
for 30 objects.
mJy). Follow-up observation provided redshifts
for 30 objects.
Our new XMM-Newton data comprise an area three times larger, compared to the ROSAT
survey, and are thus almost comparable in size to the optical quasar survey.
We are reaching a survey sensitivity of
![]() erg cm-2 s-1 (turnover
flux) over a contiguous area of 0.6 deg2. The
XMM-Newton survey of the Marano Field is thus
comparable with deep ROSAT surveys (e.g., the UDS, Hasinger et al. 1998)
or with medium deep CHANDRA surveys (e.g., ChaMP, ).
erg cm-2 s-1 (turnover
flux) over a contiguous area of 0.6 deg2. The
XMM-Newton survey of the Marano Field is thus
comparable with deep ROSAT surveys (e.g., the UDS, Hasinger et al. 1998)
or with medium deep CHANDRA surveys (e.g., ChaMP, ).
The paper is organised as follows. In Sect. 2 we list the
X-ray and optical data and the reduction of the data.
Section 3 describes and summarises the
spectroscopic classification of the X-ray sources.
In Sect. 4 we make use of the spectroscopic classification and
redshift determination to analyse the properties
of different object classes. In this section we concentrate
on a "core sample'' of objects in the central part of the field, where
we reached the highest degree of completeness in the spectroscopic
classification.
Section 5 addresses additional objects in the Marano Field that
are not X-ray detected. These objects were obtained as a control sample.
Section 6 dicusses the results of the different
object classes. Finally, our conclusions are outlined in
Sect. 7.
Unless mentioned otherwise, all errors refer to a ![]() confidence interval.
confidence interval.
Since the area of the optical quasar survey in the Marano Field is larger
than the XMM-Newton field of view, the X-ray observations have been
performed as a grid of
![]() overlapping pointings with a spacing
of
overlapping pointings with a spacing
of ![]() 5 arcmin in right ascension and declination.
The pointing in the north-western corner of the grid was shifted
to cover the position of a deep far-infrared survey with the ISO satellite
(Table 1 and Fig. 1).
The ISO data are not addressed in this paper.
5 arcmin in right ascension and declination.
The pointing in the north-western corner of the grid was shifted
to cover the position of a deep far-infrared survey with the ISO satellite
(Table 1 and Fig. 1).
The ISO data are not addressed in this paper.
Table 1: XMM-Newton observations of the Marano Field. filter: T.-thin, M.-medium.
Due to the overlapping pointings some deviations from the standard XMM-Newton
data analysis procedures were necessary, and are described here.
The photon event tables from the 16 grid pointings were merged into
a single event table with a common sky coordinate frame using the XMM SAS merge task. In this coordinate frame we created 240 images
(one for each pointing, energy range, and instrument). The 5 bands
used are 0.2-0.5 keV, 0.5-2.0 keV, 2.0-4.5 keV, 4.5-7.5 keV, and 7.5-12.0 keV.
Each image has
![]() pixels with four arcseconds binning.
For each of these images separate exposure maps and background
maps were created using the XMM SAS tasks eexpmap and esplinemap.
One of the pointings (ObsID 0129320801) had accidentally been scheduled
with "medium'' thickness filters, while all other pointings had been
observed with "thin'' filters. To correct for the somewhat
lower throughput of the medium filters at soft energies, we multiplied
all exposure maps of this pointing with a correction factor derived
from the energy conversion factors for the "thin'' and "medium'' filters.
These ECFs were taken from the SSC document SSC-LUX-TN-0059 v.3
(Osborne 2001).
The correction is largest in the softest band (0.2-0.5 keV), where
the effective exposure in the affected pointing is reduced by 11%.
pixels with four arcseconds binning.
For each of these images separate exposure maps and background
maps were created using the XMM SAS tasks eexpmap and esplinemap.
One of the pointings (ObsID 0129320801) had accidentally been scheduled
with "medium'' thickness filters, while all other pointings had been
observed with "thin'' filters. To correct for the somewhat
lower throughput of the medium filters at soft energies, we multiplied
all exposure maps of this pointing with a correction factor derived
from the energy conversion factors for the "thin'' and "medium'' filters.
These ECFs were taken from the SSC document SSC-LUX-TN-0059 v.3
(Osborne 2001).
The correction is largest in the softest band (0.2-0.5 keV), where
the effective exposure in the affected pointing is reduced by 11%.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5849_1.ps}\end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg41.gif) |
Figure 1:
Averaged mos1 and mos2 exposure map (0.5-2.0 keV) of the
|
| Open with DEXTER | |
We then added the images, exposure maps, and background maps of the
individual pointings, resulting in 15 images for 5 energy bands and
3 detectors. These images were used simultaneously as input for a
detection run with eboxdetect and emldetect.
The task emldetect applies a PSF-fit to each source found by
eboxdetect to determine the source parameters.
Since we use merged mosaic images of the field, each source image results from
the superposition of several pointings. In each pointing the source is detected
at a different position on the detector.
Therefore, the standard configuration of emldetect, which uses the
off-axis angle and position-angle of each source to extract the appropriate
PSF from calibration files, could not be used here. Instead emldetect
was modified to use the calibration PSF corresponding to an off-axis
angle
![]() throughout the entire field.
This PSF is circular symmetric and is a good representation of the point
sources in the merged images.
For this work no extent models were fitted to the sources, therefore
the source list produced by emldetect does not contain
any information whether a source is extended or point-like.
Generally, the X-ray data reduction and
analysis was performed with XMM SAS version 5.1 (from 18/06/2001) with
the abovementioned exception of an adapted version of emldetect.
The version of emldetect used here suffered from an error, which
resulted in the overestimation of detection likelihood values
(XMM-Newton-NEWS #29, 11-Mar.-2003). All likelihood values quoted here have
been corrected to adhere to the relation
throughout the entire field.
This PSF is circular symmetric and is a good representation of the point
sources in the merged images.
For this work no extent models were fitted to the sources, therefore
the source list produced by emldetect does not contain
any information whether a source is extended or point-like.
Generally, the X-ray data reduction and
analysis was performed with XMM SAS version 5.1 (from 18/06/2001) with
the abovementioned exception of an adapted version of emldetect.
The version of emldetect used here suffered from an error, which
resulted in the overestimation of detection likelihood values
(XMM-Newton-NEWS #29, 11-Mar.-2003). All likelihood values quoted here have
been corrected to adhere to the relation
![]() ,
where ML is the
detection likelihood and P is the probability that the detection is caused
by a random fluctuation of the background.
All count rates and derived quantities are taken from the PSF fitting of emldetect.
Using the combined expoure maps, emldetect corrects the source count rates for all
spatial variations of telescope and detector efficiency, i.e., the count rates relate
to the optical axis of each EPIC camera.
Following Cash (1979), the 68% confidence intervals for the
source positions and source fluxes were calculated
using emldetect as follows:
each parameter is varied until the statistic
,
where ML is the
detection likelihood and P is the probability that the detection is caused
by a random fluctuation of the background.
All count rates and derived quantities are taken from the PSF fitting of emldetect.
Using the combined expoure maps, emldetect corrects the source count rates for all
spatial variations of telescope and detector efficiency, i.e., the count rates relate
to the optical axis of each EPIC camera.
Following Cash (1979), the 68% confidence intervals for the
source positions and source fluxes were calculated
using emldetect as follows:
each parameter is varied until the statistic
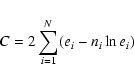
For all sources 3 hardness ratios of the form HR = (CR2 - CR1)/(CR1 + CR2) were calculated between the adjacent pn-detector energy bands 0.2-0.5 keV, 0.5-2.0 keV, 2.0-4.5 keV, and 4.5-7.5 keV. For example, HR2 was calculated between the bands 0.5-2.0 keV and 2.0-4.5 keV. The different energy responses of the mos- and pn-detectors result in different hardness ratios for the same source. If not noted otherwise the pn-values are used throughout the paper.
In total we detected 328 X-ray sources with detection likelihoods
![]() .
The X-ray fluxes are in the range
.
The X-ray fluxes are in the range
![]() erg cm-2 s-1
(0.2-10 keV).
The X-ray flux histogram (Fig. 3) shows the
X-ray detection limit of our survey. Below
erg cm-2 s-1
(0.2-10 keV).
The X-ray flux histogram (Fig. 3) shows the
X-ray detection limit of our survey. Below
![]() erg cm-2 s-1 we are unable to detect the majority of
the X-ray sources.
In the central region (Fig. 2) we found 252 X-ray sources.
The complete X-ray source list can be found in
the Online Material, Appendix A.
erg cm-2 s-1 we are unable to detect the majority of
the X-ray sources.
In the central region (Fig. 2) we found 252 X-ray sources.
The complete X-ray source list can be found in
the Online Material, Appendix A.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5849_2.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg49.gif) |
Figure 2:
PN exposure map (0.5-2.0 keV) of the
|
| Open with DEXTER | |
XMM-Newton redetected all 50 ROSAT X-ray sources (Zamorani et al. 1999).
However, two ROSAT X-ray sources have low detection likelihoods
and were thus not included in the final XMM-Newton
X-ray source list (Online Material, Appendix A).
Figure 4 compares ROSAT and EPIC X-ray fluxes in the
0.5-2.0 keV band.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5849_3.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg51.gif) |
Figure 3:
0.2-10 keV X-ray flux histogram of the 328 XMM-Newton detected
X-ray sources in the Marano Field. Up to an X-ray flux of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5849_4.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg52.gif) |
Figure 4: Comparison between the 0.5-2 keV X-ray fluxes measured by ROSAT and XMM-Newton of all 50 ROSAT X-ray sources in the Marano Field. XMM-Newton fluxes are averages of the three individual EPIC camera fluxes. The black solid line represents equal ROSAT and XMM-Newton fluxes. |
| Open with DEXTER | |
The central region of the Marano Field has been observed
in the UBVRI bands with the ESO
Wide-Field-Imager (WFI).
Here we make use of the deep (7000 s) R-band image (Mignoli & Zamorani 1998) with a
limiting magnitude
![]() (defined as turnover magnitude minus 0.5 mag, see Fig. 5).
The WFI-image covers an area of 35
(defined as turnover magnitude minus 0.5 mag, see Fig. 5).
The WFI-image covers an area of 35 ![]() 32 arcmin
well aligned with the region of the deepest XMM-Newton coverage
(Fig. 1).
32 arcmin
well aligned with the region of the deepest XMM-Newton coverage
(Fig. 1).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{5849_5.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg57.gif) |
Figure 5: Magnitude histogram of the sources detected in the WFI R-band image. Completeness in detecting objects is lost for R>23. |
| Open with DEXTER | |
The K-band data (
![]() m) were obtained at the ESO New
Technology Telescope (NTT) with the SOFI instrument.
With an area of 754 arcmin2 the K-band mosaic
covers a slightly smaller area than the WFI R-band observation and
is well aligned with the deepest XMM-Newton exposure
(Fig. 1).
The SOFI observations consist of a mosaic of 33
jittered pointings, each covering
m) were obtained at the ESO New
Technology Telescope (NTT) with the SOFI instrument.
With an area of 754 arcmin2 the K-band mosaic
covers a slightly smaller area than the WFI R-band observation and
is well aligned with the deepest XMM-Newton exposure
(Fig. 1).
The SOFI observations consist of a mosaic of 33
jittered pointings, each covering
![]() arcmin
with an exposure time of 29 min each.
The limiting magnitude is
arcmin
with an exposure time of 29 min each.
The limiting magnitude is ![]() (turnover magnitude minus 0.5 mag, see Fig. 6).
(turnover magnitude minus 0.5 mag, see Fig. 6).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5849_6.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg61.gif) |
Figure 6: Histogram of the K-band magnitudes in the NTT-SOFI images. Completeness in detecting objects is lost for K>20.5. |
| Open with DEXTER | |
Our target selection for the optical spectroscopy
was primarily based on FORS1/FORS2 R-band pre-images.
WFI R-band and SOFI K-band data were used in addition
to support the target selection on the pre-images
in case of faint counterparts.
The chosen fields represent a compromise in terms of
maximum survey area and source density because of
limited telescope time.
First priority for spectroscopic follow up was given to candidates with a
likelihood of existence ML > 10 within a 2
![]() error radius.
The total position error is
error radius.
The total position error is
![]() .
The statistical errors
.
The statistical errors
![]() of the positions were calculated
as described in Sect. 2.1.
The systematic errors are caused by uncertainties in the spacecraft attitude,
errors in the linearisation of the detector coordinates, and undersampling
of the PSF (in particular for the PN camera).
At this stage, we allowed a systematic position error of
of the positions were calculated
as described in Sect. 2.1.
The systematic errors are caused by uncertainties in the spacecraft attitude,
errors in the linearisation of the detector coordinates, and undersampling
of the PSF (in particular for the PN camera).
At this stage, we allowed a systematic position error of
![]() ,
see
Sect. 3.2 for a more accurate estimation of the systematic
position errors.
,
see
Sect. 3.2 for a more accurate estimation of the systematic
position errors.
The multi-object spectroscopy masks were designed with the software fims 2 provided by ESO. For all spectroscopic targets we used straight slitlets with a nominal length of ten arcseconds and width of one arcsecond. For extended sources or closely spaced candidate counterparts, a different slit length, 6-14 arcsec, was used. Still available mask positions were filled with candidate objects not fulfilling the main selection criteria and with additional random non-X-ray emitting galaxies.
The second run was performed with FORS2 in spectroscopic
mask mode (MXU) from November 27th-30th, 2002.
We aimed for an exposure time of 3 ![]() 1800 s per mask,
but weather and time constraints required some deviations from
this general scheme (Table 2). Grism
GRIS_150I+27 was used for all masks.
1800 s per mask,
but weather and time constraints required some deviations from
this general scheme (Table 2). Grism
GRIS_150I+27 was used for all masks.
Table 2: Details of FORS2 spectroscopic mask mode observation (see Fig. 2).
Table 3: Setups for the optical spectroscopy.
To prevent second order contamination, the first mask (mask6) in the observing sequence was observed through filter GC 375, which limited the wavelength range from 3850 to 7500 Å. A comparison with the second mask without an order separating filter showed that the contamination effect is negligible. Hence, for all following masks the filter was removed from the light path resulting in a wavelength range for central targets of the final spectra from 3500 to 10 000 Å.
The reduction of the data was accomplished by a semiautomatic pipeline coded in MIDAS. It was specially designed to reduce FORS2-MXU data with as little interaction with the user as possible. After modifications this code was also used to reduce the FORS1-MOS data. The bias correction was done in the standard manner with careful attention to possible time dependence on the bias level and dark current. An ordinary flat field correction was used to rectify the pixel-to-pixel variation.
Table 4: Origin of optical counterparts to XMM sources.
![\begin{figure}
\par\includegraphics[angle=270,width=7.9cm,clip]{5849_7.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg71.gif) |
Figure 7: Optical atmospheric absorption corrected, wavelength and flux calibrated spectrum for X-ray source 480. The black spectrum marks the object's spectrum. The green line (see the online colour version of the manuscript) shows the error spectrum. Possible emission and absorption features in the spectrum are labelled. The spectral feature at 5580 Å is spurious due to incomplete substraction of a night sky line. |
| Open with DEXTER | |
The extraction is based on an optimal extraction algorithm (Horne 1986) including a cosmic ray rejection. Extensive tests determined the optimal extraction parameters. Standard flux calibration was applied. Since FORS2-mask6 was observed with an additional filter, a different standard star was used. All spectra were corrected for atmospheric absorption using the standard ESO extinction correction function scaled to the given airmass.
The n individual spectra of a given counterpart object were combined to form one single final spectrum. The individual spectra were firstly normalised to the same mean intensity. The normalisation factor was determined from an analysis of all spectra in a given mask. The final spectrum is the uncertainty-weighted mean spectrum.
![\begin{figure}
\par\includegraphics[angle=270,width=8.3cm,clip]{5849_8.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg73.gif) |
Figure 8:
Adopted mean k correction from observed R-band to rest-frame
|
| Open with DEXTER | |
For the large majority of our spectra the signal-to-noise ratio (SNR)
is sufficient to give reliable classifications and redshifts.
Like other X-ray identification surveys, we encounter the problem of
difficult classification of the optical spectra below a certain SNR.
For spectra with a SNR = 3-5, the identification of narrow emission
lines was still possible. However, at this SNR faint broad emission
lines and normal galaxy spectra are very
difficult to identify.
Figure 7 shows a spectrum of a narrow emission line
galaxy with a SNR = 2.4 (continuum near the O II emission line), which is
close to the identification limit. Only one significant narrow emission
line at ![]() 7100 Å is found. The spectral shape makes it reasonable
to identify this line as O II emission line.
Even though this classification is likely, an unambiguous redshift
determination and classification of the type cannot be given.
Spectra with a SNR less then
7100 Å is found. The spectral shape makes it reasonable
to identify this line as O II emission line.
Even though this classification is likely, an unambiguous redshift
determination and classification of the type cannot be given.
Spectra with a SNR less then ![]() 2.5
are not identifiable.
The reliability of the redshift determination and classification of the
optical spectra is given by flags in Col. (9) Flags of Table 8.
2.5
are not identifiable.
The reliability of the redshift determination and classification of the
optical spectra is given by flags in Col. (9) Flags of Table 8.
Table 5: X-ray counterpart distribution.
Table 6: Properties of the core sample.
The complete list of X-ray classification is given in Table 8. The columns are described as follows:Table 7:
Fractions of absorbed sources
in different X-ray luminosity bins based in Fig. 19c. Only objects with
![]() are selected.
are selected.
(1) No
Classification of a counterpart object consists of the sequence number of
the X-ray source list and a suffix (A, B) to discriminate
between different candidates.
(2) RA [hh:min:s] and (3) Dec [deg:min:s]
Right ascension and declination of the optical candidate counterpart
(J2000).
(4) DistOX [arcsec]
Spatial offset between the X-ray and optical positions.
(5) K
SOFI K-band magnitude of the spectroscopically classified candidate, whenever available.
(6) R
WFI R-band magnitude of the spectroscopically classified candidate, whenever possible.
(7) Class
Spectroscopic classification of the identified object. S - star, G - normal galaxy
(no emission lines), N - narrow emission line galaxy with unresolved emission
lines (at 6000 ![]() our spectral resolution of 21
our spectral resolution of 21 ![]() corresponds to 1050 km s-1), B - broad emission line object
(all measured line widths have
corresponds to 1050 km s-1), B - broad emission line object
(all measured line widths have
![]() km s-1), and ? - undefined object.
km s-1), and ? - undefined object.
(8) z
Spectroscopic redshift of the identified object. The
redshift is taken from the literature for objects with
"1 - -'' and "0 - -'' in Col. (9) Flags.
Column (15) Rem.
states the source of redshift determination and classification.
(9) Flags
X-ray identification flag, redshift flag, and classification reliability flag.
The first number (0,1) marks whether a spectroscopically classified object was accepted
as X-ray counterpart. Objects which we consider to be the correct
identification of the X-ray source are flagged by "1'', while "0'' flags objects
not considered as the X-ray source.
The second (middle) flag states the redshift reliablility. A redshift flag
"1'' means a reliable, well-established redshift determined by several spectral
features. "0'' marks objects where the redshift determination relies on
a single but reasonable spectral feature.
The third (last) flag characterises the classification reliability. A flag
"1'' marks that the object type as given in "(7) Class'' is
well established and reliable. Flag "0'' indicates an uncertain
classification of
the object type. Either high SNR spectral features of the object do not
allow a proper classification or the optical spectra do not allow
to give a reliable classification of the object type because of a low SNR
and/or insufficient wavelength coverage of the optical spectra.
The latter is illustrated in Fig. 7. The narrow O II
line indicates a narrow emission line galaxy. However, the SNR of the
spectrum does not allow us to judge the existence of a
broad Mg II line and, hence, a classification as type I AGN.
Since C IV and C III are outside the spectrum's
wavelength range, Mg II is the only possible broad-line feature.
The most likely classification of this object is a narrow emission line
galaxy. However, the given arguments show that a classification as type I AGN
cannot be excluded. Therefore, the classification flag for this object is "0''.
Objects with "1 - -'' and "0 - -'' have only an X-ray identification flag
since their redshift and classification relies on follow-up surveys
previously done in the Marano Field (see Col. (15) Rem.).
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{5849_9.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg79.gif) |
Figure 9:
Adopted conversion term to estimate AB magnitudes
at fixed rest-frame wavelength
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{5849_10.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg80.gif) |
Figure 10:
a) Number of objects identified as X-ray
counterparts vs. difference in X-ray and optical position
scaled to a 1
|
| Open with DEXTER | |
(10) log (L
XOBS [erg s-1])
Observed rest-frame X-ray luminosity (logarithmic units) in the
0.2-10 keV energy band calculated by using Eq. (1).
The k-correction vanishes since we assume
an energy index
![]() with
with
![]() (
(![]() -photon index) based on Alexander et al. (2003) and Mainieri et al. (2002). The luminosity
distance
-photon index) based on Alexander et al. (2003) and Mainieri et al. (2002). The luminosity
distance
![]() was computed by the analytical fit for flat
cosmologies with
was computed by the analytical fit for flat
cosmologies with
![]() ,
,
![]() ,
,
![]() km s-1 Mpc-1 following Szokoly et al. (2004).
km s-1 Mpc-1 following Szokoly et al. (2004).
(11) MB
Absolute magnitudes
![]() (in the Johnson system) were estimated only
for type I AGN using the relation
(in the Johnson system) were estimated only
for type I AGN using the relation
(12)
![]()
The broad band spectral index
![]() roughly characterises
the UV-X-ray spectral energy distribution by connecting the
rest-frame points at 2500 Å and 1 keV with a simple power-law,
roughly characterises
the UV-X-ray spectral energy distribution by connecting the
rest-frame points at 2500 Å and 1 keV with a simple power-law,
![]() .
For each broad emission line AGN we estimated its flux at a fixed
rest-frame wavelength of
.
For each broad emission line AGN we estimated its flux at a fixed
rest-frame wavelength of
![]() Å, applying the relation
Å, applying the relation
(13) NH [cm-2]
X-ray absorbing hydrogen column density in units of
![]() (see Sect. 4.4).
(see Sect. 4.4).
(14) log (
LXINT [erg s-1] )
Intrinsic rest-frame X-ray luminosity (logarithmic units) in the
0.2-10 keV energy band after X-ray flux correction for the absorbing
hydrogen column density. Calculation uses Eq. (1).
(15) Rem.
Remarks for individual objects: 1 - optically selected and spectroscopically classified
quasar by Marano et al. (1988); 2 - optically selected and spectroscopically classified
quasar by Zitelli et al. (1992); 3 - ROSAT X-ray source with spectroscopic classification
and redshift determination by Zamorani et al. (1999); 4 - ROSAT X-ray source with
no or wrong identification by Zamorani et al. (1999); 5 - unclassified radio objects
within
![]() ,
Gruppioni et al. (1999);
6 - spectroscopic classification and redshift taken from
Teplitz et al. (2003); 7 - radio source, spectroscopic classification and redshift
taken from Gruppioni et al. (1999), and
C - individual comment to an object (see Sect. 3.1).
,
Gruppioni et al. (1999);
6 - spectroscopic classification and redshift taken from
Teplitz et al. (2003); 7 - radio source, spectroscopic classification and redshift
taken from Gruppioni et al. (1999), and
C - individual comment to an object (see Sect. 3.1).
9A: New redshift determined for this source, formerly known as Zamorani et al. (1999) X043-12.
15A: Object 15A is not regarded as the optical counterpart, since the
identification of the line features is uncertain and the positional
offset is rather large. A very faint object at the detection
limit lies in the X-ray error circle. A lower limit of
![]() for this source
was estimated by assuming a limiting magnitude of R=24.
for this source
was estimated by assuming a limiting magnitude of R=24.
17A: Source 17 is a likely X-ray blend with large contrast between the
two individual sources. Object 17A is a unique identification of
the brighter X-ray source, whose X-ray flux is likely to be
overestimated due to blending.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5849_11.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg104.gif) |
Figure 11:
WFI R-band magnitude vs. difference in X-ray and optical
position
scaled to a
|
| Open with DEXTER | |
20A and 20B: Zamorani et al. (1999) identified source 20 with the M star 20B. Some contribution of the M star's X-ray flux cannot be excluded, but the identification with the type II AGN (object 20A) seems more likely, since the X-ray colours indicate a relatively hard spectrum.
22A and 22B: X-ray source 22 is a probable blend. Objects 22A and 22B fall on top of the two suspected point sources. We regard both optical objects as likely counterparts of the X-ray blend and distribute the measured X-ray flux evenly between the two sources.
26A: New redshift determined for this source, formerly known as Zamorani et al. (1999) X301-29.
32A: N V strongest emission line in the spectrum (brighter than
Ly-![]() ). Narrow emission lines are present and the object is
classified as "N'' (narrow emission line galaxy). However, all
narrow emission lines have underlying broad components.
Therefore, the classification flag is set to "0''.
). Narrow emission lines are present and the object is
classified as "N'' (narrow emission line galaxy). However, all
narrow emission lines have underlying broad components.
Therefore, the classification flag is set to "0''.
35A and 35B: Two galaxies at equal redshift, the brighter galaxy 35A is regarded as the X-ray counterpart. The possibility that the X-ray source is a galaxy cluster cannot completely excluded, but an X-ray extent is not obvious. For 35A a new redshift is determined (update to Zamorani et al. 1999, X022-48).
42A: New redshift determined for this source, formerly known as Zamorani et al. (1999) X031-24.
46A: X-ray blend with major contribution from the southwestern component with type I AGN 46A as counterpart.
47A and 47B: Two narrow emission line galaxies at equal redshift. The possibility that the X-ray source is a galaxy cluster cannot completely excluded, but an X-ray extent is not obvious. 47A is assumed to be the optical counterpart.
63A: Unresolved narrow emission lines are present and the object is classified as "N'' (narrow emission line galaxy). However, the C IV emission line has an underlying broad component. Therefore, the classification flag is set to "0''.
66A: The identification is not unique, since the optical
image reveals a possible second
object inside the 1![]() -X-ray position error
circle.
-X-ray position error
circle.
133A: Narrow emission lines are present. The object is
classified as "N'' (narrow emission line galaxy). However,
Ly-![]() shows a resolved, broad base. Therefore,
the classification flag is set "0''.
shows a resolved, broad base. Therefore,
the classification flag is set "0''.
Table 8: Optical properties of candidate counterparts of Marano XMM-Newton X-ray sources. For a detailed explanation of the individual columns see Sect. 3.
151A: Probably a spurious detection of the X-ray source. The source is kept in the source list for the formal reason of having an ML = 5.2, but is not considered further.
191A: Optical spectrum in Zitelli et al. (1992) indicates a type I AGN
with typical broad emission lines. However, this object shows
the lowest X-ray-to-optical flux ratio of all AGN in our sample.
![]() suggests an X-ray faint AGN.
Since this object was not detected by ROSAT, it is unlikely
that the extreme
suggests an X-ray faint AGN.
Since this object was not detected by ROSAT, it is unlikely
that the extreme
![]() -ratio is due to a
temporary low X-ray state of the object. Furthermore, it is one of
the type I objects with intrinsic absorption
(
-ratio is due to a
temporary low X-ray state of the object. Furthermore, it is one of
the type I objects with intrinsic absorption
(
![]() cm-2).
cm-2).
217A and 217B: X-ray blend, the identification of 217A with the southeastern component seems unambiguous, the identification of 217B with the northwestern component is not unique, since a similarly bright, close-by, but still unidentified object is present at the same distance from the X-ray source.
224A and 224B: Two galaxies at equal redshift, no obvious X-ray extent.
253A and 253B: Two objects at similar redshift with
![]() difference in the
optical. The brighter object 253A is regarded as
the identification.
difference in the
optical. The brighter object 253A is regarded as
the identification.
280A: Object is classified as "B'' since C III is
well resolved with
![]() (FWHM).
Ly-
(FWHM).
Ly-![]() and C IV are narrow emision lines, but
show strong absorption with broad underlying components.
The classification flag is set "0''. Possible broad absorption line quasar.
and C IV are narrow emision lines, but
show strong absorption with broad underlying components.
The classification flag is set "0''. Possible broad absorption line quasar.
361A: Broad absorption line quasar.
382A and 496A: Physical quasar pair, separated by
![]() ,
at z =
1.904,
,
at z =
1.904,
![]() kpc. The spectra are different, i.e., the two objects are
not lensed images of the same source.
kpc. The spectra are different, i.e., the two objects are
not lensed images of the same source.
437A: Spectrum, optical, and X-ray image,
and relative soft hardness ratios point undoubtedly
to an M star as X-ray source. However, a flux ratio
![]() is unusually high for an M star as the X-ray identification.
is unusually high for an M star as the X-ray identification.
512A and 512B: Zamorani et al. (1999) identify the NELG 512B with the X-ray
source. The
![]() fainter NELG 512A lies somewhat closer
to the X-ray position. While both galaxies may contribute
to the observed X-ray flux, we assume object 512A as the
counterpart in the following.
fainter NELG 512A lies somewhat closer
to the X-ray position. While both galaxies may contribute
to the observed X-ray flux, we assume object 512A as the
counterpart in the following.
582A: Spectrum, optical, and X-ray image,
and relative soft hardness ratios point undoubtedly
to an M star as X-ray source. However, a flux ratio
![]() is unusually high for an M star as the X-ray identification.
is unusually high for an M star as the X-ray identification.
607A and 653A: Detected as a single X-ray source by ROSAT Zamorani et al. (1999)
X404-23,
X-ray source 653 is brighter and closer to X404-23
and, therefore, treated as the detected ROSAT X-ray source.
The broad spectral feature at 7100![]() in the optical
spectrum of 607A is spurious due to the zeroth order light of
the neighbouring slit.
in the optical
spectrum of 607A is spurious due to the zeroth order light of
the neighbouring slit.
615A and 615B: Both objects, the broad emission line object 615A and the narrow emission line object 615B, are possible counterparts to the X-ray source. We regard the fainter, but positionally better matching object 615A as the counterpart.
632A: Spectrum suggests a BL-Lac object, but the object is not a radio source, classification unclear.
Since type I AGN are a well-established class of X-ray emitters with relatively low surface density, false matches should not play any role for this object class. However, when investigating the classes of optically normal and narrow emission line galaxies, the problem of false matches has to be taken into account due to the high surface densities of these objects. To check the quality of our optical X-ray counterpart identification, we applied various tests.
First, the derived false match rate will depend on the assumed
position errors, which take into account the statistical
and the systematic position error (see Sect. 2.3).
The difference in X-ray and optical position scaled to a
![]() position error is shown in Fig. 10a.
When we assume systematic errors of 2 arcsec, the theoretical Gaussian
distribution (Eq. (7))
position error is shown in Fig. 10a.
When we assume systematic errors of 2 arcsec, the theoretical Gaussian
distribution (Eq. (7))
Considering
![]() ,
we calculate the false match rate
by following Sutherland & Saunders (1992) and Ciliegi et al. (2003). For every spectroscopically
classified counterpart we determine the likelihood ratio L by
,
we calculate the false match rate
by following Sutherland & Saunders (1992) and Ciliegi et al. (2003). For every spectroscopically
classified counterpart we determine the likelihood ratio L by
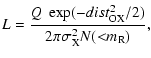 |
(8) |
The total number of false matches can then be calculated by adding up all probabilities
![]() that the counterpart is spurious. Statistically,
that the counterpart is spurious. Statistically, ![]() 25% of our narrow emission line galaxy are spurious counterparts.
However, after visually examining objects
with low probabilities
25% of our narrow emission line galaxy are spurious counterparts.
However, after visually examining objects
with low probabilities
![]() ,
we find that
in at least two cases (422A, 485A) the X-ray position given by the source detection
software is influenced by blending with another X-ray source and the counterparts
are consistent with the peak of the brighter X-ray source (see Appendix C, finding chart).
Taking this into account, we estimate that the false match rate is
,
we find that
in at least two cases (422A, 485A) the X-ray position given by the source detection
software is influenced by blending with another X-ray source and the counterparts
are consistent with the peak of the brighter X-ray source (see Appendix C, finding chart).
Taking this into account, we estimate that the false match rate is ![]() 20%
for the sample of type II AGN.
For the optically normal galaxies the false match rate calculated with the
likelihood method is
20%
for the sample of type II AGN.
For the optically normal galaxies the false match rate calculated with the
likelihood method is ![]() 2%.
2%.
As a further quality check we plot the position error vs. WFI R-band magnitude. False matches would be recognisable due to different distributions of the type I and type II counterparts in this diagram. However, Fig. 11 shows that all object classes occupy the same regions in the diagram. Hence, the diagram does not indicate any serious contamination by false matches even for faint counterparts.
Our survey suffers somewhat from incomplete optical coverage of the X-ray survey area and, hence, a low identification rate over the whole area. To reach conclusions for the survey of a certain statistical significance we constrain our survey area and sample size to the central 0.28 deg2 with a pn-exposure >6 ks and significance of detection of individual sources with ML >10. We refer to this as the "core sample''. See Fig. 2 for the definition of the core region. Note that the maximum exposure is 35.5 ks for the PN camera and 78 ks for each of the MOS cameras.
The core sample contains 170 X-ray sources (ML>10).
No optical data are available for six out of the 170 X-ray
sources which fall outside the WFI R-band image and are also not covered
by VLT pre-images. A further six X-ray sources from the core sample have no
optical detection in the WFI R-band image in a 3
![]() position
error circle (
position
error circle (
![]() ).
122 X-ray sources are new detections, while 35 are spectroscopically classified ROSAT X-ray
sources, and 13 are optically unidentified ROSAT sources. Out of the 140
spectroscopically classified objects in the Marano Field, 110 are
associated with X-ray sources of the core sample. A summary of the
properties of the core sample is given in
Table 6.
).
122 X-ray sources are new detections, while 35 are spectroscopically classified ROSAT X-ray
sources, and 13 are optically unidentified ROSAT sources. Out of the 140
spectroscopically classified objects in the Marano Field, 110 are
associated with X-ray sources of the core sample. A summary of the
properties of the core sample is given in
Table 6.
Figure 12 shows R-band magnitude
histograms of the core sample X-ray sources that were spectroscopically
classified and only optically identified, respectively.
The (
![]() ,
ML)-distribution of X-ray sources in the core region
is given in Fig. 13.
The identification ratio
of the core sample is 65%.
In the next subsections we always refer to this sample.
,
ML)-distribution of X-ray sources in the core region
is given in Fig. 13.
The identification ratio
of the core sample is 65%.
In the next subsections we always refer to this sample.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5849_12.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg216.gif) |
Figure 12:
WFI R-band magnitude histogram for the core sample in the
XMM-Newton Marano Field survey. The solid line represents the R-magnitude
distribution of the spectroscopically classified X-ray counterparts. The
dashed line shows the distribution of the optically identified but not
spectroscopically classified X-ray counterparts.
Six X-ray sources, which have no counterpart within a 3
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5849_13.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg217.gif) |
Figure 13:
Likelihood vs. 0.2-10 keV X-ray-flux of the 252 central X-ray
sources (pn-detector exposure time |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5849_14.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg220.gif) |
Figure 14:
X-ray diagnostic diagram based on hardness ratios. HR2 is
calculated by
using the 0.5-2.0 keV and 2.0-4.5 keV band, HR3 2.0-4.5 keV and 4.5-7.5 keV.
Only X-ray sources that have
|
| Open with DEXTER | |
The small number of optically normal galaxies span a large range in HR2. Two have HR2 values that belong to the softest in the whole core sample. The other two have X-ray spectra similar to those of soft type II AGN or very hard type I AGN.
In addition to the spectroscopically classified objects, we also plot unidentified objects
from the core region. Out of the 60 total unidentified X-ray
sources, only 24 meet the selection criterion of
![]() .
Based on the rather clear separation between type I and II AGN, one may assign
a likely classification to the yet unidentified sources. Among the 24
unidentified sources with reliable X-ray colours, the numbers of type I and
type II AGN candidates appear to be similar.
.
Based on the rather clear separation between type I and II AGN, one may assign
a likely classification to the yet unidentified sources. Among the 24
unidentified sources with reliable X-ray colours, the numbers of type I and
type II AGN candidates appear to be similar.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5849_15.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg221.gif) |
Figure 15:
Redshift distribution of AGN in the Marano Field. a)
Complete sample of 64 optically selected quasars
(
|
| Open with DEXTER | |
Previous extensive studies of AGN in the Marano Field
enable us to compare these samples with our XMM-Newton
detections.
The optical survey by Zitelli et al. (1992) covers ![]() 0.7
0.7
![]() .
The selected quasars, which are all of type I, show an almost flat
distribution in redshift (Fig. 15a) up to z=2.8.
The ROSAT
.
The selected quasars, which are all of type I, show an almost flat
distribution in redshift (Fig. 15a) up to z=2.8.
The ROSAT
![]() survey in the field (Zamorani et al. 1999)
recovered most of the optically selected quasars at redshifts
up to
survey in the field (Zamorani et al. 1999)
recovered most of the optically selected quasars at redshifts
up to ![]() (Fig. 15b).
The newly detected ROSAT AGN, with few exceptions, are type I AGN,
which is expected due to the limited capability of ROSAT to detect absorbed
sources.
(Fig. 15b).
The newly detected ROSAT AGN, with few exceptions, are type I AGN,
which is expected due to the limited capability of ROSAT to detect absorbed
sources.
In the
![]() core region of the XMM-survey we have detected
23 of the 29 broad emission line quasars of the optically selected sample
of Zitelli et al. (1992). The detection rate of optically selected quasars
remains constantly high over all redshifts.
However, looking at the type I AGN newly discovered with XMM-Newton
(Fig. 15c), it is apparent that the X-ray selection
tends to detect quasars at lower redshifts than the optical surveys. This is
particularly obvious from the redshift distribution of the ROSAT detected
quasars, representing the brightest X-ray sources in the field.
But the mean redshift
core region of the XMM-survey we have detected
23 of the 29 broad emission line quasars of the optically selected sample
of Zitelli et al. (1992). The detection rate of optically selected quasars
remains constantly high over all redshifts.
However, looking at the type I AGN newly discovered with XMM-Newton
(Fig. 15c), it is apparent that the X-ray selection
tends to detect quasars at lower redshifts than the optical surveys. This is
particularly obvious from the redshift distribution of the ROSAT detected
quasars, representing the brightest X-ray sources in the field.
But the mean redshift
![]() of the XMM-Newton detected type I AGN is
also lower than that of the optically selected sample
of the XMM-Newton detected type I AGN is
also lower than that of the optically selected sample
![]() ,
despite the fact
that the XMM-Newton-observations are deeper in terms of the surface density of quasars
than the optical survey.
Possible reasons for these differences are discussed in Sect. 6.
,
despite the fact
that the XMM-Newton-observations are deeper in terms of the surface density of quasars
than the optical survey.
Possible reasons for these differences are discussed in Sect. 6.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5849_16.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg227.gif) |
Figure 16: Observed X-ray luminosity (0.2-10 keV) vs. redshift. Labels: crosses - 70 type I AGN, asterisks - 30 type II AGN, and triangles - 5 galaxies. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5849_17.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg228.gif) |
Figure 17:
Observed X-ray luminosity (0.2-10 keV) vs. hardness ratio. HR2
is calculated by using 0.5-2.0 keV & 2.0-4.5 keV bands.
Only X-ray sources that have
|
| Open with DEXTER | |
The redshift distribution according to object
class of the XMM-Newton detected core sample
is given in Fig. 15d.
We find that almost half of the new XMM-Newton
sources are classified as type II AGN with redshifts mostly below 1.0.
Type I AGN extend over a wide range of redshifts
with a maximum at
![]() .
Type II AGN are comparable to type I AGN
in number density at low redshifts, but are mostly found below z=1.
Five type II quasars at z > 2.2 have been identified.
Optically normal galaxies without emission lines are found at z < 0.9.
.
Type II AGN are comparable to type I AGN
in number density at low redshifts, but are mostly found below z=1.
Five type II quasars at z > 2.2 have been identified.
Optically normal galaxies without emission lines are found at z < 0.9.
For the X-ray sources with measured redshifts X-ray luminosities can be
computed.
The coverage of the survey in redshift - X-ray luminosity space
is plotted in Fig. 16.
Szokoly (2004) showed that the different object classes
identified in X-ray surveys occupy different regions in
a diagram of hardness ratios versus observed X-ray luminosities.
In Fig. 17
we follow a scheme similar to that adopted by Szokoly (2004)
and consider objects
with an X-ray luminosity log
![]() as quasars (QSOs).
The majority of type I AGN (
as quasars (QSOs).
The majority of type I AGN (![]() 70%) are actually type I QSOs. Most of
type II AGN (
70%) are actually type I QSOs. Most of
type II AGN (![]() 71%) are low X-ray luminosity objects.
Only type II objects with redshifts
71%) are low X-ray luminosity objects.
Only type II objects with redshifts ![]() (marked in grey in
Fig. 17) have X-ray luminosities of type II QSOs.
(marked in grey in
Fig. 17) have X-ray luminosities of type II QSOs.
High-redshift type II QSOs with intrinsic absorption are found to be indistiguishable from non-absorbed type I AGN on the basis of their X-ray spectral hardness ratios, since the absorbed part of the spectrum is shifted out of the observable spectral window towards lower energies. This explains the emptiness of the upper right corner of Fig. 17 labelled "type II QSO'', a classification that applies to low redshift objects only.
Optically normal galaxies vary clearly in X-ray luminosity. The HR2-soft objects have very low X-ray luminosities. The two HR2-hard normal galaxies are found in the same region as the softest type II AGN, but are harder than type I AGN.
Szokoly (2004) use HR2=-0.2 as a threshold for the separation of
type I and type II objects. Assuming a ![]() ,
this value corresponds
to a hydrogen column density
,
this value corresponds
to a hydrogen column density
![]() /cm
-2=1022, 1023 for
z= 0.25 and 2.1, respectively. For their CHANDRA observation they computed
/cm
-2=1022, 1023 for
z= 0.25 and 2.1, respectively. For their CHANDRA observation they computed
![]() in the 0.5-10 keV band and their hardness ratio was based on the
0.5-2 keV and 2-10 keV bands. Because their definition of the X-ray bands differs from
our study, the
majority of their objects have higher hardness ratios (compared to our HR2).
Furthermore, the XMM-Newton
pn-detector, which was used for calculating the hardness ratios, has a higher
efficiency in the 0.5-2 keV band compared to the CHANDRA detector.
Therefore, we lowered the HR2 threshold from
HR2 = -0.2 in
Szokoly (2004) to
HR2 = -0.45.
Our threshold corresponds to
in the 0.5-10 keV band and their hardness ratio was based on the
0.5-2 keV and 2-10 keV bands. Because their definition of the X-ray bands differs from
our study, the
majority of their objects have higher hardness ratios (compared to our HR2).
Furthermore, the XMM-Newton
pn-detector, which was used for calculating the hardness ratios, has a higher
efficiency in the 0.5-2 keV band compared to the CHANDRA detector.
Therefore, we lowered the HR2 threshold from
HR2 = -0.2 in
Szokoly (2004) to
HR2 = -0.45.
Our threshold corresponds to
![]() /cm
/cm
![]() ,
and
,
and
![]() for
for ![]() and
z= 0.25, 1, and 2.1. This is about two times
lower than the
and
z= 0.25, 1, and 2.1. This is about two times
lower than the ![]() cutoff Szokoly (2004) are using.
cutoff Szokoly (2004) are using.
The hardness ratio diagram (Fig. 14) supports
the view that the majority of type II AGN and a small fraction of
type I AGN are obscured sources. Hence, the observed X-ray luminosity
does not represent the intrinsic object X-ray luminosity.
The significant deficit of soft photons as compared to a power-law spectrum
reflects the existence of an absorbing component that is expressed by the
hydrogen column density
![]() .
For most of the sources the number of detected counts is not sufficient
to extract a spectrum and fit a power-law model with
.
For most of the sources the number of detected counts is not sufficient
to extract a spectrum and fit a power-law model with
![]() and the photon index
and the photon index ![]() as free parameters.
We, therefore, applied a technique that uses the measured hardness ratios to calculate the
as free parameters.
We, therefore, applied a technique that uses the measured hardness ratios to calculate the
![]() value for each source with a set of fixed power-law indices.
Mainieri et al. (2002)
found a mean value of
value for each source with a set of fixed power-law indices.
Mainieri et al. (2002)
found a mean value of
![]() for 61
type I and type II AGN in the Lockman Hole. The majority of type I and II AGN
are found in the range of
for 61
type I and type II AGN in the Lockman Hole. The majority of type I and II AGN
are found in the range of
![]() .
The finding is confirmed
by Mateos (2005). They find
.
The finding is confirmed
by Mateos (2005). They find
![]() with a
with a
![]() .
Therefore, we use the observed pn-, mos1-, and mos2-hardness-ratios
(0.2-0.5 keV, 0.5-2.0 keV, 2.0-4.5 keV, and 4.5-7.5 keV) and performed three
runs to determine
.
Therefore, we use the observed pn-, mos1-, and mos2-hardness-ratios
(0.2-0.5 keV, 0.5-2.0 keV, 2.0-4.5 keV, and 4.5-7.5 keV) and performed three
runs to determine
![]() with the values
with the values
![]() ,
and 2.3
for all objects.
,
and 2.3
for all objects.
First of all, we computed a grid of model hardness ratios for
all EPIC instruments with Xspec
(using the models wabs, zwabs, and powerlaw).
As input the galactic absorption in the line of sight in the field
with
![]() cm-2, the redshift
of the object and a grid of hydrogen column densities
(
cm-2, the redshift
of the object and a grid of hydrogen column densities
(
![]() )
is used.
We then computed the
)
is used.
We then computed the ![]() values for the deviations of the
measured hardness ratios and their model values, summed over
the three instruments and the three hardness ratios HR1, HR2, and HR3.
The procedure was applied only to
those sources that had at least five out of nine hardness ratios
with
values for the deviations of the
measured hardness ratios and their model values, summed over
the three instruments and the three hardness ratios HR1, HR2, and HR3.
The procedure was applied only to
those sources that had at least five out of nine hardness ratios
with
![]() .
.
The
![]() of a source is determined by finding the minimum of
of a source is determined by finding the minimum of
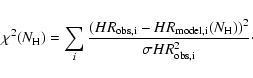
We tested our procedure by performing an individual Xspec
![]() -fit
for the brightest type II AGN, which has sufficient X-ray data quality.
The hardness ratios of 32A (z=2.727)
indicate the highest absorption among the brightest type II AGN.
A spectral fit with
wabs, zwabs, powerlaw, and
-fit
for the brightest type II AGN, which has sufficient X-ray data quality.
The hardness ratios of 32A (z=2.727)
indicate the highest absorption among the brightest type II AGN.
A spectral fit with
wabs, zwabs, powerlaw, and ![]() as a free parameter determined
as a free parameter determined
![]() and
and
![]() ).
The best fit
).
The best fit
![]() ,
for a fixed value of
,
for a fixed value of
![]() ,
with the
hardness-ratio
,
with the
hardness-ratio ![]() -minimum fit is
-minimum fit is
![]() .
A spectral fit with a fixed
.
A spectral fit with a fixed
![]() results in
results in
![]() .
The given
.
The given
![]() in Table 8 was performed with the hardness-ratio
in Table 8 was performed with the hardness-ratio
![]() -minimum fit and finds
-minimum fit and finds
![]() .
Hence, both
fit methods give comparable results, at least for high SNR sources.
.
Hence, both
fit methods give comparable results, at least for high SNR sources.
Figure 18 shows the computed hydrogen column densities
for type II AGN and optically normal galaxies.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5849_18.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg255.gif) |
Figure 18:
Calculated intrinsic hydrogen column density histogram for the
central Marano Field. The solid line shows the distribution of
type II AGN that have reasonable fits in hydrogen column density.
Objects with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5849_19.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg258.gif) |
Figure 19:
a) Histogram of the absorbed (observed)
X-ray luminosity (0.2-10 keV) for the core sample.
Dotted line - 70 type
I AGN, solid line - 30 type II AGN, and dashed line - 5 galaxies.
b) Histogram of the X-ray luminosity (0.2-10 keV) corrected
for intrinsic absorption (core sample). Same notation as in a).
c) Corrected X-ray luminosity (0.2-10 keV) vs. hydrogen
column density (core sample). Crosses - type I AGN,
asterisks - type II AGN, and triangles - galaxies.
The upper right corner is suggested as being defined as the "type II QSO region'' by
Mainieri et al. (2002). Objects with
|
| Open with DEXTER | |
The computed hydrogen column density of type II AGN object 145A is the highest
in our sample (
![]() ). Since this
corresponds to the highest value in the model grid, no reliable error estimate
can be given for this object. However, the extremely high column density for
this object is confirmed by the fact that it is one of the few sources
detected in the 4.5-7.5 keV EPIC images, but it is not visible in the
softer bands.
). Since this
corresponds to the highest value in the model grid, no reliable error estimate
can be given for this object. However, the extremely high column density for
this object is confirmed by the fact that it is one of the few sources
detected in the 4.5-7.5 keV EPIC images, but it is not visible in the
softer bands.
Based on the hydrogen column densities, we calculated the unabsorbed
(intrinsic) X-ray luminosities by computing a correction factor for the
observed X-ray flux.
Figure 19 shows the comparison of the
absorbed (a) and unabsorbed (b) X-ray luminosity distributions.
Even after correcting the X-ray luminosity, type II AGN
have lower median X-ray luminosities than type I AGN, although
type I and II AGN cover the same X-ray luminosity range.
In contrary to the almost flat distribution of type II AGN with a
median of
![]() ,
type I AGN show
a significant peak at
,
type I AGN show
a significant peak at
![]() in observed and intrinsic X-ray luminosity.
Type I AGN 5A exhibits the highest X-ray luminosity in our sample.
in observed and intrinsic X-ray luminosity.
Type I AGN 5A exhibits the highest X-ray luminosity in our sample.
The hydrogen column density as a function of the intrinsic X-ray luminosity
is shown in Fig. 19c. Mainieri et al. (2002) suggest labelling the
region defined by
![]() and
and
![]() as the "type II QSO region''. They proposed this classification
based on 61 AGN identified from XMM-Newton sources in the Lockman Hole.
Following this classification our sample includes 10 type II QSOs.
as the "type II QSO region''. They proposed this classification
based on 61 AGN identified from XMM-Newton sources in the Lockman Hole.
Following this classification our sample includes 10 type II QSOs.
In our case this region of the plot is also populated by nine type I QSOs,
which formally have intrinsic hydrogen column densities
![]() .
However, most of these
detections of intrinsic
.
However, most of these
detections of intrinsic
![]() have low significance; only
four of all type I QSOs show absorption at the
have low significance; only
four of all type I QSOs show absorption at the ![]() level
(see Table 7).
For about half of the type II AGN, significant intrinsic absorption
(
level
(see Table 7).
For about half of the type II AGN, significant intrinsic absorption
(
![]() )
was measured, and no
dependence of the absorbed fraction on luminosity is evident
(Table 7).
)
was measured, and no
dependence of the absorbed fraction on luminosity is evident
(Table 7).
The distribution of our core sample in the
![]() -plane
is illustrated in Fig. 20. In general, type I AGN show higher X-ray
fluxes and are brighter in the R-band. Type II AGN are found at lower X-ray
fluxes and have fainter R-band counterparts.
Two of the optically normal galaxies have X-ray-to-optical flux ratios similar to type I and type II AGN.
Another two are among the objects with lowest X-ray-to-optical flux ratios in the sample.
-plane
is illustrated in Fig. 20. In general, type I AGN show higher X-ray
fluxes and are brighter in the R-band. Type II AGN are found at lower X-ray
fluxes and have fainter R-band counterparts.
Two of the optically normal galaxies have X-ray-to-optical flux ratios similar to type I and type II AGN.
Another two are among the objects with lowest X-ray-to-optical flux ratios in the sample.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5849_20.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg269.gif) |
Figure 20:
Observed X-ray flux (0.2-10 keV) vs. R-band magnitude.
Dashed lines indicate
the
|
| Open with DEXTER | |
Our types I and II AGN show a large variety in X-ray flux and R-band magnitude.
They are detected at X-ray fluxes from
![]() to
to
![]() erg cm-2 s-1 and in R-band
magnitudes from
erg cm-2 s-1 and in R-band
magnitudes from ![]() down to the detection limit of
down to the detection limit of
![]() .
There is one type I AGN (191A) at an unusually low value
.
There is one type I AGN (191A) at an unusually low value
![]() ,
a factor of 100 below the mean value of type I AGN.
The highest ratio in X-ray to optical
flux is found for the type II AGN object 39A with
,
a factor of 100 below the mean value of type I AGN.
The highest ratio in X-ray to optical
flux is found for the type II AGN object 39A with
![]() .
.
Most of the stars are found at star-typical
![]() with R < 17.
Nevertheless, we also detected two M stars with
with R < 17.
Nevertheless, we also detected two M stars with
![]() and
and
![]() .
Unidentified sources with WFI R-band data are added to
Fig. 20.
We plotted unidentified objects that have no detection in the R-band
catalogue at R = 24.
.
Unidentified sources with WFI R-band data are added to
Fig. 20.
We plotted unidentified objects that have no detection in the R-band
catalogue at R = 24.
Figure 21 shows that type II AGN tend to be fainter and redder in the optical window than type I AGN. This figure shows a general trend for both type I and type II AGN to become redder for fainter R-magnitudes. The lack of faint blue objects can be explained by the K-band detection limit of K=20, where we lose completeness (see Fig. 6). However, the lack of bright red objects cannot be caused by any detection bias. The type II AGN have redder R-K colours, although with some overlap with the reddest type I AGN in the sample. These trends can be explained by an increasing contribution of the host galaxies for fainter type I AGN and type II AGN. The faint R-magnitudes and high R-K values indicate higher optical obscurations in type II AGN. This is in agreement with previous X-ray studies of these objects that revealed a significantly higher ratio of absorbed to unabsorbed objects compared to type I AGN.
In our survey type I and type II objects do not separate as clearly as seen in a similar plot in Mainieri et al. (2002). Therefore, we checked whether the reddest and faintest type I objects are reliably classified. The most extreme type I objects are 69A, 84A, and 585A. Their optical spectra clearly show broad emission lines, but their continua are redder than typical type I spectra. In addition, object 585A shows only weak emission lines.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5849_21.ps} \end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg278.gif) |
Figure 21: Colour magnitude diagram of spectroscopically classified X-ray sources. Labels: crosses - 56 type I AGN, asterisks - 20 type II AGN, and triangles - 4 galaxies. Only objects with detections in both R and K are included. The absence of blue, faint objects (below the solid line) is due only to the K-magnitude limit. |
| Open with DEXTER | |
The optically normal galaxies are brighter in R-magnitudes than the typical type II AGN,
but show similar
R-K. All classified galaxies have R<21.5.
The majority of type II AGN and galaxies have
![]() ,
consistent with the spectrum of the host galaxy being the dominating component.
A considerable fraction of type I AGN also have red R-K colours.
These are mostly low luminosity objects, where the host galaxy may also
dominate the optical continuum.
,
consistent with the spectrum of the host galaxy being the dominating component.
A considerable fraction of type I AGN also have red R-K colours.
These are mostly low luminosity objects, where the host galaxy may also
dominate the optical continuum.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5849_22.ps}
\end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg280.gif) |
Figure 22: Redshift distribution of the additional objects. Labels: solid line - 37 NELGs, and dotted line - 8 optically normal galaxies. |
| Open with DEXTER | |
Figure 22 illustrates the redshift distribution of the additional non-X-ray emitting objects in the Marano Field. Narrow emission line galaxies (NELG) outnumber normal galaxies substantially. This is due to the fact that a large fraction of the spectra without emission lines did not have sufficient SNR to determine a redshift. There is a non-X-ray emitting NELG peak at z =0.5-0.9. At z > 1.0 the detection of NELG and normal galaxies drops dramatically.
Despite the low number of objects, from Figs. 22 and 15d we can compare the redshift distributions between X-ray emitting type II AGN and non-X-ray emitting NELG. Both populations show more or less the same distribution up to z = 1.2. The two groups peak at z =0.5-0.9.
The similar redshift distributions could mean that the X-ray emitting NELGs are drawn from the same population of galaxies as the control sample. On the other hand, the similar redshift distribution could also be due to a large fraction of false matches of NELGs to our X-ray sources. A detailed discussion of the number of false matches is given in Sect. 3.2 and shows that false matches make only a minor contribution to our sample of narrow line AGN.
In Sect. 4.2 we showed that
the X-ray selected type I AGN peak at lower redshifts
than the optically selected sample.
It is interesting to see whether this difference in the redshift
distributions is due to a redshift dependence of the QSO spectral
energy distributions (SED).
As a parameter which characterises the SED,
we calculated the optical to X-ray broad band spectral index
![]() between the UV luminosity density at 2500
between the UV luminosity density at 2500 ![]() and the X-ray luminosity density at 1 keV (see Sect. 3).
and the X-ray luminosity density at 1 keV (see Sect. 3).
No significant correlation of
![]() with redshift
(Fig. 23) or X-ray luminosity can be found.
However, there is a very significant (
with redshift
(Fig. 23) or X-ray luminosity can be found.
However, there is a very significant (
![]() )
correlation of the optical luminosity and
)
correlation of the optical luminosity and
![]() (Fig. 24).
This correlation has been found in various samples observed with
EINSTEIN (Avni & Tananbaum 1986), ROSAT (e.g., Green et al 1995; Lamer et al. 1997), and CHANDRA (e.g., Steffen et al. 2006).
For a large sample of optically selected AGN, Steffen et al. (2006) computed the
bivariate linear regression coefficients of
(Fig. 24).
This correlation has been found in various samples observed with
EINSTEIN (Avni & Tananbaum 1986), ROSAT (e.g., Green et al 1995; Lamer et al. 1997), and CHANDRA (e.g., Steffen et al. 2006).
For a large sample of optically selected AGN, Steffen et al. (2006) computed the
bivariate linear regression coefficients of
![]() as a function of
as a function of
![]() and z.
They find that
and z.
They find that
![]() is correlated with
is correlated with
![]() ,
but find no significant correlation
with z (see also Avni & Tananbaum 1986 for similar results on earlier
EINSTEIN data).
,
but find no significant correlation
with z (see also Avni & Tananbaum 1986 for similar results on earlier
EINSTEIN data).
If
![]() and optical luminosity are correlated, a non-linear
relation between X-ray luminosity and optical luminosity is expected.
Therefore, we plotted the X-ray luminosities versus the optical
luminosity densities (Fig. 25) and computed the linear
regression coefficients
between
and optical luminosity are correlated, a non-linear
relation between X-ray luminosity and optical luminosity is expected.
Therefore, we plotted the X-ray luminosities versus the optical
luminosity densities (Fig. 25) and computed the linear
regression coefficients
between
![]() and
and
![]() .
Both variables
.
Both variables
![]() and
and
![]() are
measured quantities and neither of them can be regarded as the independent or
dependent variable.
We used the ordinary least-squares (OLS) bisector algorithm
as described by Isobe et al. (1990), which is symmetric regarding the choice
of independent and dependent variable.
are
measured quantities and neither of them can be regarded as the independent or
dependent variable.
We used the ordinary least-squares (OLS) bisector algorithm
as described by Isobe et al. (1990), which is symmetric regarding the choice
of independent and dependent variable.
We find a best-fit regression
![]() .
This slope is marginally (2
.
This slope is marginally (2![]() significance) flatter than the
significance) flatter than the ![]() expected for a linear
expected for a linear
![]() relation.
With the same method Steffen et al. (2006) find a slightly flatter slope
relation.
With the same method Steffen et al. (2006) find a slightly flatter slope
![]() .
.
A correlation flatter than ![]() implies that the optical luminosities in the sample are
spread over a wider range of values than the X-ray luminosities.
This might explain the above-mentioned discrepancies of the redshift distributions
of X-ray and optically selected QSOs. The low luminosity objects are more likely
to be detectable in X-rays, while the highest luminosity objects are relatively more
luminous in the optical, and therefore detectable at higher redshifts in optical surveys.
implies that the optical luminosities in the sample are
spread over a wider range of values than the X-ray luminosities.
This might explain the above-mentioned discrepancies of the redshift distributions
of X-ray and optically selected QSOs. The low luminosity objects are more likely
to be detectable in X-rays, while the highest luminosity objects are relatively more
luminous in the optical, and therefore detectable at higher redshifts in optical surveys.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5849_23.ps}\end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg288.gif) |
Figure 23:
UV to X-ray spectral index
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5849_24.ps}\par\end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg290.gif) |
Figure 24:
UV to X-ray spectral index
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5849_25.ps}\end{figure}](/articles/aa/full/2007/16/aa5849-06/Timg291.gif) |
Figure 25:
Observed 0.2-10 keV X-ray luminosity vs. optical luminosity density at
|
| Open with DEXTER | |
Type II AGN show only narrow emission lines and the optical continuum
radiation is
dominated by the host galaxy. The spectroscopical classification
of X-ray sources relies on emission lines like Ly-![]() ,
C IV, C III, Mg II, O II, and others. Analysis
of the optical spectra of type II AGN with z > 0.6 in our sample,
in Szokoly et al. (2004), and in Caccianiga et al. (2004) indicates
that almost all objects show no Mg II emission lines. Only
in a few cases
marginal Mg II emission is recognised. Effectively, no
strong spectral features are present in the wavelength range between
,
C IV, C III, Mg II, O II, and others. Analysis
of the optical spectra of type II AGN with z > 0.6 in our sample,
in Szokoly et al. (2004), and in Caccianiga et al. (2004) indicates
that almost all objects show no Mg II emission lines. Only
in a few cases
marginal Mg II emission is recognised. Effectively, no
strong spectral features are present in the wavelength range between
![]() (C III]) and
(C III]) and ![]() ([O II]).
([O II]).
Since the UV host galaxy continuum is usually very faint,
the detection of type II AGN in optical imaging is already
hampered by the lack of a strong UV continuum and emission lines, if the
imaging bandpass falls into this rest frame range.
For R-band imaging (5800-7300 ![]() )
this is the case
for the redshift range
)
this is the case
for the redshift range
![]() .
Our multi-object spectroscopy covers a useful range of
.
Our multi-object spectroscopy covers a useful range of
![]() Å.
This range is reduced, if an object is not centred on the mask,
but offset from the centre in the dispersion direction.
Hence, in many cases only one emission line would be detectable for
type II AGN in the redshift range
Å.
This range is reduced, if an object is not centred on the mask,
but offset from the centre in the dispersion direction.
Hence, in many cases only one emission line would be detectable for
type II AGN in the redshift range ![]() 1.0-2.0. With a low SNR spectrum
this would usually not be sufficient for a clear spectroscopical classification.
For a few sources, which were undetected or very faint in the R-band images, we were able to
position a MXU slit
using the K-band counterparts (e.g., 20A, 63A, and 463A).
In all of these cases a high redshift type II AGN could be identified.
1.0-2.0. With a low SNR spectrum
this would usually not be sufficient for a clear spectroscopical classification.
For a few sources, which were undetected or very faint in the R-band images, we were able to
position a MXU slit
using the K-band counterparts (e.g., 20A, 63A, and 463A).
In all of these cases a high redshift type II AGN could be identified.
Figure 14 supports the assumption that a large fraction
of unidentified sources consists of type II AGN.
Above HR2=-0.1 only type II AGN are found as counterparts for identified
X-ray sources. In this region 50% of the X-ray sources are not
classified and are expected to be type II AGN.
Furthermore, Fig. 20 gives more evidence that the unidentified
sources overlap with the type II AGN region.
A ratio
![]() is clearly a sign of AGN activity,
since normal galaxies and stars usually have
is clearly a sign of AGN activity,
since normal galaxies and stars usually have
![]() .
Both type II AGN and unidentified objects are found at AGN-typical
.
Both type II AGN and unidentified objects are found at AGN-typical
![]() ,
with low X-ray fluxes and faint optical counterparts.
,
with low X-ray fluxes and faint optical counterparts.
We conclude that the majority of the unidentified X-ray sources are likely
to consist of
type II AGN, most of them presumably with redshifts z>1.
Therefore, the intrinsic redshift distribution of the type II AGN is uncertain.
The number of unidentified sources is sufficient to fill
the observed gap between
![]() .
.
Five objects in the core sample have been spectroscopically classified
as galaxies without any emission lines.
The soft X-ray radiation of the low X-ray luminosity galaxies
(objects 120A, 241A) can be explained by a halo of
X-ray emitting hot gas around elliptical galaxies (; White & Davis 1998).
Three optically normal galaxies have X-ray-to-optical flux ratios and
X-ray luminosities typically found for AGN. Objects of this type have
been named X-ray bright optically normal galaxies (XBONGs; Comastri et al. 2002).
The objects 8A, 49A, and 204A have intermediate redshifts (0.3<z<0.9)
and fairly high X-ray luminosities (log
![]() ), rather hard
X-ray spectra, and faint optical counterparts (R>19).
The high X-ray luminosities and
), rather hard
X-ray spectra, and faint optical counterparts (R>19).
The high X-ray luminosities and
![]() indicate active nuclei.
The computed
hydrogen column densities show moderate absorption.
indicate active nuclei.
The computed
hydrogen column densities show moderate absorption.
The properties of our XBONGs are in agreement with other
studies (Silverman et al. 2005; ).
Even though different scenarios are discussed, the nature of XBONGs still remains
unclear (Brandt & Hasinger 2005).
Comastri et al. (2002) assume that the non-detection of optical emission
lines and the hard X-ray colours are due to a heavily absorbed AGN embedded
in a galaxy whose X-ray emission is due to a scattered/reprocessed
nuclear component.
The three XBONGs do not show harder HR2 values than type II AGN
and also do not have the highest column densities of the AGN sample. Hence,
a heavily absorbed AGN without scattered/reprocessed X-ray radiation is
ruled out. Scattered or reprocessed radiation is necessary to explain the
X-ray and optical observations. Following Komossa et al. (1998), the observed
X-ray luminosity of a scattered emission by a warm reflector is only a
hundredth or thousandth of the intrinsic X-ray luminosity. For our objects
with observed log
![]() ,
this would require intrinsic X-ray
luminosities of log
,
this would require intrinsic X-ray
luminosities of log
![]() ,
which would make them by far the
most luminous X-ray emitters in the sample.
,
which would make them by far the
most luminous X-ray emitters in the sample.
Another possible explanation for these objects is given by Severgnini et al. (2003).
They studied three low redshift XBONGs with log
![]() and
find
and
find ![]() values similar to our sample. In their interpretation
the faint emission lines of an obscured or unobscured AGN up to an intrinsic log
values similar to our sample. In their interpretation
the faint emission lines of an obscured or unobscured AGN up to an intrinsic log
![]() can be overwhelmed by a host galaxy with an absolute magnitude
can be overwhelmed by a host galaxy with an absolute magnitude
![]() .
However, XBONGs 8A and 49A are not consistent with the scenario mentioned by
Severgnini et al. (2003).
The AGN of 49A with an intrinsic log
.
However, XBONGs 8A and 49A are not consistent with the scenario mentioned by
Severgnini et al. (2003).
The AGN of 49A with an intrinsic log
![]() should be
optically too bright to be hidden by a galaxy of
should be
optically too bright to be hidden by a galaxy of
![]() .
Moreover, source 8A, which is also detected as a radio source (Gruppioni et al. 1999),
has an intrinsic log
.
Moreover, source 8A, which is also detected as a radio source (Gruppioni et al. 1999),
has an intrinsic log
![]() .
Therefore, it is more X-ray
luminous by almost one order of magnitude
than the examples in Severgnini et al. (2003).
The absolute magnitude of the host galaxy is
.
Therefore, it is more X-ray
luminous by almost one order of magnitude
than the examples in Severgnini et al. (2003).
The absolute magnitude of the host galaxy is
![]() ,
but an optically much brighter galaxy is needed to
hide the emission lines of such a powerful AGN.
By adding a template type I spectrum to the measured spectra
of objects 8A and 49A, we estimated that
any hidden type I AGN in these objects would have
,
but an optically much brighter galaxy is needed to
hide the emission lines of such a powerful AGN.
By adding a template type I spectrum to the measured spectra
of objects 8A and 49A, we estimated that
any hidden type I AGN in these objects would have
![]() values of
values of ![]() 0.8 or less.
0.8 or less.
Regarding the X-ray and optical colours, our XBONGs are very similar to type II AGN. Therefore, it is likely that these sources have a narrow line type II spectrum, which is intrinsically weak or dust absorbed and not detected above the continuum of the host galaxy. This result is consistent with Caccianiga et al. (2004), who state that more accurate re-observation (high resolution data and/or better spectral coverage) of hard X-ray emitting galaxies will reveal narrow emission lines and, therefore, their real AGN nature. Severgnini et al. (2003) also claim possible misclassification of type II AGN as XBONGs. However, some of these objects are still classified as XBONGs after a high resolution observation with better spectral coverage.
As for type II AGN, the observed redshift distribution of XBONGs could be due to an observational bias. XBONGs are found with brighter R-magnitudes than typical type II AGN up to z=1. But missing emission line features make them optically even more difficult to identify than type II AGN. For a reliable classification they have to be optically brighter, thus limiting their maximum redshift.
With a total of 120 ks good observation time we detect 328 X-ray
sources. Among 140 spectroscopic classifications of 187 optical
counterparts (in a 3
![]() position
error with
position
error with
![]() )
to 328 X-ray sources (not
completely covered by optical data), we find
89 broad emission line objects, 36 narrow emission line objects, 6 galaxies,
and 9 stars. In the central region of the Marano Field we reach an
identification completeness of 65%.
)
to 328 X-ray sources (not
completely covered by optical data), we find
89 broad emission line objects, 36 narrow emission line objects, 6 galaxies,
and 9 stars. In the central region of the Marano Field we reach an
identification completeness of 65%.
While the redshift distribution of the optically selected QSOs in the field
is basically flat up to ![]() ,
the distribution of the
XMM-Newton sources peaks at
,
the distribution of the
XMM-Newton sources peaks at ![]() .
Using our sample of XMM-Newton sources classified as type I AGN,
we investigate possible causes for this tendency of
deep X-ray surveys to discover faint populations at
comparably low redshifts.
We find no significant correlation of the optical to
X-ray SED slope
.
Using our sample of XMM-Newton sources classified as type I AGN,
we investigate possible causes for this tendency of
deep X-ray surveys to discover faint populations at
comparably low redshifts.
We find no significant correlation of the optical to
X-ray SED slope
![]() with redshift.
As is widely reported in the literature,
with redshift.
As is widely reported in the literature,
![]() is tightly correlated
with optical luminosity.
A different representation of this correlation is
the non-linear dependency
is tightly correlated
with optical luminosity.
A different representation of this correlation is
the non-linear dependency
![]() .
The best-fit regression
.
The best-fit regression
![]() implies that the optical luminosities in a typical sample spread over a wider
range than the X-ray luminosities.
Therefore, the less luminous objects of the population are more easily detected in
X-rays than in the optical.
On the other hand, an increase of optical luminosity is, on average, not
accompanied by a proportional increase in X-ray luminosity.
Hence, the luminous (and more distant) objects are detected more efficiently
in optical surveys.
implies that the optical luminosities in a typical sample spread over a wider
range than the X-ray luminosities.
Therefore, the less luminous objects of the population are more easily detected in
X-rays than in the optical.
On the other hand, an increase of optical luminosity is, on average, not
accompanied by a proportional increase in X-ray luminosity.
Hence, the luminous (and more distant) objects are detected more efficiently
in optical surveys.
In the core region of the field we classified 31 new type II AGN.
Most of them are found at redshifts z<1.5;
additionally we find five high redshift type II
AGN at z>2.2. Fifteen objects can be classified as type II QSOs
with intrinsic X-ray luminosities
![]() erg s-1.
erg s-1.
We show that the optical identification of type II AGN is very difficult in the redshift range z=1-2 due to the absence of suitable emission lines in the optical window. Therefore, their intrinsic redshift distribution remains unclear. We demonstrate that the use of K-band data for MXU slit positioning reveals type II AGN or XBONGs that would have likely been missed in R-band images. The X-ray selected type II AGN have a very similar redshift distribution to non-X-ray emitting narrow emission line galaxies, which have been spectroscopically classified in the same field as a control sample.
The intrinsic hydrogen column densities, as derived from X-ray hardness ratios,
show that the fraction of
absorbed X-ray sources is much higher for type II AGN than for type I.
Nevertheless, we find a few unabsorbed type II AGN and some evidence for
absorption in high redshift type I AGN.
However, due to the faintness of the sources,
the significance of absorption in the individual type I AGN is low.
Furthermore, at high redshifts statistical fluctuations in the
X-ray spectrum can lead to high values of spuriously measured
![]() values (e.g., Akylas et al. 2006).
If we only include
values (e.g., Akylas et al. 2006).
If we only include ![]() detections of intrinsic
detections of intrinsic ![]() in our analysis, only 4 absorbed type I AGN remain and no
dependency of absorbed fraction on redshift is obvious.
In the CHANDRA data from Chandra Deep Field South (CDFS),
Tozzi et al. (2003) find hints of an increase of absorbed fraction with
redshift. However, these data probably also suffer from the uncertainties
mentioned above. Using XMM data in the same field, Dwelly & Page (2006) find
little evidence that the absorption distribution is dependent on
either intrinsic X-ray luminosity or redshift.
Our type I and type II AGN cover the same range in absorption corrected
X-ray luminosity. However, the mean corrected X-ray
luminosity is smaller for type II AGN than
for type I AGN.
in our analysis, only 4 absorbed type I AGN remain and no
dependency of absorbed fraction on redshift is obvious.
In the CHANDRA data from Chandra Deep Field South (CDFS),
Tozzi et al. (2003) find hints of an increase of absorbed fraction with
redshift. However, these data probably also suffer from the uncertainties
mentioned above. Using XMM data in the same field, Dwelly & Page (2006) find
little evidence that the absorption distribution is dependent on
either intrinsic X-ray luminosity or redshift.
Our type I and type II AGN cover the same range in absorption corrected
X-ray luminosity. However, the mean corrected X-ray
luminosity is smaller for type II AGN than
for type I AGN.
Three of the XMM-Newton classifications are X-ray bright optically
normal galaxies (XBONGs), which show X-ray
luminosities typical for AGN, but no optical emission lines.
Their X-ray luminosities of log
![]() are comparable to
the mean type II AGN X-ray luminosity. They do not show harder X-ray
spectra and do not reveal higher hydrogen column densities than the average type II AGN.
We conclude that the objects are very similar to type II AGN.
However, their narrow emission lines are not detected, since they are either
intrinsically weak or obscured by dust.
are comparable to
the mean type II AGN X-ray luminosity. They do not show harder X-ray
spectra and do not reveal higher hydrogen column densities than the average type II AGN.
We conclude that the objects are very similar to type II AGN.
However, their narrow emission lines are not detected, since they are either
intrinsically weak or obscured by dust.
Acknowledgements
Mirko Krumpe is supported by the Deutsches Zentrum für Luft- und Raumfahrt (DLR) GmbH under contract No. FKZ 50 OR 0404. Georg Lamer acknowledges support by the Deutsches Zentrum für Luft- und Raumfahrt (DLR) GmbH under contract No. FKZ 50 OX 0201.
Table A.1: X-ray source list.
Table B.1: Optical properties of candidate counterparts of marginal Marano Field XMM-Newton X-ray sources. For a detailed explanation of the individual columns see Sect. 3.
137A: Broad absorption line quasar.
315A and 315B: As counterpart candidates for X-ray source 315, an M star (315A) and a NELG (315B) are found. The hardness ratios of 315 indicated an obscured X-ray object. Therefore, we regarded 315B as the identification.
Table B.2: X-ray source list for marginal X-ray sources. The explanation of the individual columns is given in Appendix A.
(2) RA [hh:min:s] and (3) Dec [degmin:s]
Right ascension and declination of the spectroscopically classified object.
(4) z
Spectroscopic redshift of the classified object.
(5) K
SOFI K-band magnitude of the spectroscopically classified object, whenever possible.
(6) R
WFI R-band magnitude of the spectroscopically classified object, whenever possible.
(7) Class
Classification of the optical identified object. S - star, G - normal galaxy
(no emission lines), and N - narrow emission line galaxy (unresolved emission
lines).
Table D.1: Optical data of additional objects.