A&A 465, 725-747 (2007)
DOI: 10.1051/0004-6361:20066832
Large-N expansions applied to gravitational clustering
P. Valageas
Service de Physique Théorique, CEA Saclay, 91191 Gif-sur-Yvette,
France
Received 28 November 2006 / Accepted 26 January 2007
Abstract
We develop a path-integral formalism to study the formation of large-scale
structures in the universe. Starting from the equations of motion of
hydrodynamics (single-stream approximation) we derive the action which
describes the statistical properties of the density and velocity fields
for Gaussian initial conditions. Then, we present large-N expansions
(associated with a generalization to N fields or with a semi-classical
expansion) of the path-integral defined by this action. This provides a
systematic expansion for two-point functions such as the response function
and the usual two-point correlation. We present the results of two such
expansions (and related variants) at one-loop order for a SCDM and
a 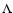 CDM cosmology.
We find that the response function exhibits fast oscillations in the non-linear
regime with an amplitude which either follows the linear prediction (for the
direct steepest-descent scheme) or decays (for the 2PI effective action
scheme). On the other hand, the correlation function agrees with the
standard one-loop result in the quasi-linear regime and remains well-behaved
in the highly non-linear regime. This suggests that these large-N expansions
could provide a good framework to study the dynamics of gravitational
clustering in the non-linear regime. Moreover, the use of various expansion
schemes allows one to estimate their range of validity without the need of
N-body simulations and could provide a better accuracy in the weakly
non-linear regime.
CDM cosmology.
We find that the response function exhibits fast oscillations in the non-linear
regime with an amplitude which either follows the linear prediction (for the
direct steepest-descent scheme) or decays (for the 2PI effective action
scheme). On the other hand, the correlation function agrees with the
standard one-loop result in the quasi-linear regime and remains well-behaved
in the highly non-linear regime. This suggests that these large-N expansions
could provide a good framework to study the dynamics of gravitational
clustering in the non-linear regime. Moreover, the use of various expansion
schemes allows one to estimate their range of validity without the need of
N-body simulations and could provide a better accuracy in the weakly
non-linear regime.
Key words: gravitation - cosmology: theory - cosmology: large-scale structure of Universe
1 Introduction
The large-scale structures we observe in the present universe (such as
galaxies and clusters of galaxies) have formed thanks to gravitational
instability (Pebbles 1980) which amplified the small density perturbations
created in the early universe (e.g. through quantum fluctuations generated
during an inflationary phase, Liddle & Lyth 1993). Moreover, the power
increases at small scales as in the CDM model (Peebles 1982) which leads to
a hierarchical scenario where small scales become non-linear first. Then,
small structures merge in the course of time to build increasingly large
objects. Therefore, at large scales or at early times one can use
a perturbative approach to describe the density field
(e.g. Bernardeau et al. 2002, for a review). This is of great
practical interest for observations such as weak-lensing surveys (e.g.
Bernardeau et al. 1997) and CMB studies (e.g. Seljak & Zaldarriaga 1996).
At smaller scales one uses N-body numerical simulations to obtain fits to
the density power-spectrum (e.g. Smith et al. 2003) which can be compared
with observations.
In the weakly non-linear regime one may apply the standard perturbative
expansion over powers of the initial density fluctuations (e.g., Fry 1984;
Goroff et al. 1986). This procedure is used within the hydrodynamical
framework where the system is described by density and velocity fields
rather than by the phase-space distribution
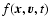 ,
that is one
starts from the Euler equation of motion rather than the Vlasov equation.
This is quite successful at tree-order where one can
obtain the leading-order contribution to all p-point correlations and
reconstruct the density probability distribution (Bernardeau 1994), assuming
Gaussian initial fluctuations as in usual inflationary scenarios
(Liddle & Lyth 1993). However, several problems show up when one tries to
compute higher-order corrections. First,ultraviolet divergences appear
for linear power-spectra
,
that is one
starts from the Euler equation of motion rather than the Vlasov equation.
This is quite successful at tree-order where one can
obtain the leading-order contribution to all p-point correlations and
reconstruct the density probability distribution (Bernardeau 1994), assuming
Gaussian initial fluctuations as in usual inflationary scenarios
(Liddle & Lyth 1993). However, several problems show up when one tries to
compute higher-order corrections. First,ultraviolet divergences appear
for linear power-spectra
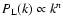 with
with 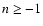 (Scoccimarro & Frieman 1996b) which would break the self-similarity seen
in numerical simulations. This may also be interpreted as a consequence of
the breakdown of the hydrodynamical description beyond shell-crossing
(Valageas 2002). However, for n<-1 the one-loop correction yields a good
agreement with numerical simulation (Scoccimarro & Frieman 1996b). Secondly,
being an expansion over powers of
(Scoccimarro & Frieman 1996b) which would break the self-similarity seen
in numerical simulations. This may also be interpreted as a consequence of
the breakdown of the hydrodynamical description beyond shell-crossing
(Valageas 2002). However, for n<-1 the one-loop correction yields a good
agreement with numerical simulation (Scoccimarro & Frieman 1996b). Secondly,
being an expansion over powers of
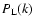 this standard perturbative approach
yields a series of terms which grow increasingly fast into the non-linear
regime at higher orders and cannot relax at small scales. This makes the
series badly behaved and it seems difficult to go deeper into the non-linear
regime in this manner.
this standard perturbative approach
yields a series of terms which grow increasingly fast into the non-linear
regime at higher orders and cannot relax at small scales. This makes the
series badly behaved and it seems difficult to go deeper into the non-linear
regime in this manner.
On the other hand, a good description of the weakly
non-linear regime becomes of great practical interest as cosmological probes
now aim to constrain cosmological parameters with an accuracy of the order
of  to keep pace with CMB observations. In particular, weak-lensing surveys
mainly probe this transition regime to non-linearity and a good accuracy
for the matter power-spectrum is required to make the most of observations and
constrain the dark energy equation of state (Munshi et al. 2007).
Another probe of the expansion history of the Universe is provided by the
measure of the baryon acoustic oscillations which also requires a good
description of weakly non-linear effects
(Seo & Eisenstein 2007; Koehler et al. 2007).
to keep pace with CMB observations. In particular, weak-lensing surveys
mainly probe this transition regime to non-linearity and a good accuracy
for the matter power-spectrum is required to make the most of observations and
constrain the dark energy equation of state (Munshi et al. 2007).
Another probe of the expansion history of the Universe is provided by the
measure of the baryon acoustic oscillations which also requires a good
description of weakly non-linear effects
(Seo & Eisenstein 2007; Koehler et al. 2007).
As a consequence, it is worth investigating other approaches which may
partly cure some of these problems and provide a better description
of the non-linear regime. For instance, McDonald (2006) proposed
a renormalization group method to improve the standard perturbative
approach. On the other hand, Crocce & Scoccimarro (2006a,b)
presented a diagrammatic technique to organize the various terms which
arise in the standard perturbative expansion and to perform some infinite
partial resummations. Besides, using the asymptotic behavior of the vertices
of the theory they managed to complete the resummation in the small-scale
limit for the response function R (also called the propagator).
In this article, we apply to the hydrodynamical framework the method
presented in Valageas (2004) for the Vlasov equation. This approach
introduces a path-integral formalism to derive the statistical properties
of the system from its action S. Then, one applies a "large-N expansion''
(which can be seen as similar to the semi-classical expansion over powers
of 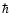 or can be derived from a generalization to N fields) to compute
the quantities of interest such as the two-point correlation.
This offers a different perspective to address the non-linear regime of
gravitational clustering which complements other approaches and may also
serve as a basis for other approximation schemes than the ones described in this
article.
For instance, previous approaches can be recovered by expanding the path-integral
obtained in this paper in different manners (e.g. the usual perturbative expansion
corresponds to the expansion over the non-Gaussian part of the action S). The two
large-N expansions discussed in this article are two other means of performing
systematic expansions to compute the required correlation functions. This also
amounts to reorganize the standard perturbative expansion by performing some partial
infinite resummations. In this fashion, one can hope to obtain new expansion schemes
which are better suited to describe the non-linear regime of gravitational
clustering.
or can be derived from a generalization to N fields) to compute
the quantities of interest such as the two-point correlation.
This offers a different perspective to address the non-linear regime of
gravitational clustering which complements other approaches and may also
serve as a basis for other approximation schemes than the ones described in this
article.
For instance, previous approaches can be recovered by expanding the path-integral
obtained in this paper in different manners (e.g. the usual perturbative expansion
corresponds to the expansion over the non-Gaussian part of the action S). The two
large-N expansions discussed in this article are two other means of performing
systematic expansions to compute the required correlation functions. This also
amounts to reorganize the standard perturbative expansion by performing some partial
infinite resummations. In this fashion, one can hope to obtain new expansion schemes
which are better suited to describe the non-linear regime of gravitational
clustering.
First, we recall in Sect. 2 the equations of motion
obtained within the hydrodynamical framework. Next, we derive the path-integral
formulation of the problem in Sect. 3 and we describe
two possible large-N expansions in Sect. 4.
Finally, we present our numerical results in
Sects. 5-7,
focusing on a critical-density universe. Since our formalism applies equally
well to any cosmology we describe our results for a  CDM universe
in Sect. 8. Finally, we conclude in Sect. 9.
CDM universe
in Sect. 8. Finally, we conclude in Sect. 9.
2 Equations of motion
2.1 Fluid approach
At scales much larger than the Jeans length both the cold dark matter and the
baryons can be described as a pressureless dust. Moreover, before orbit
crossing one can use a hydrodynamical approach (in the continuum limit where
the mass m of particles goes to zero). Then, at scales much smaller than the
horizon where the Newtonian approximation is valid, the equations of motion
read (Peebles 1980):
![\begin{displaymath}\frac{\partial\delta}{\partial\tau} + \nabla.[(1+\delta) {\vec v}] = 0,
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img53.gif) |
(1) |
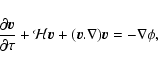 |
(2) |
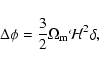 |
(3) |
where
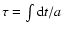 is the conformal time (and a the scale factor),
is the conformal time (and a the scale factor),
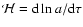 the
conformal expansion rate and
the
conformal expansion rate and
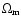 the matter density cosmological parameter.
Here
the matter density cosmological parameter.
Here 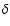 is the matter density contrast and
is the matter density contrast and 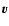 the peculiar velocity.
Since the vorticity field decays within linear theory (Peebles 1980) we take
the velocity to be a potential field so that
the peculiar velocity.
Since the vorticity field decays within linear theory (Peebles 1980) we take
the velocity to be a potential field so that 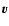 is fully specified by its
divergence
is fully specified by its
divergence
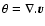 .
Then, in Fourier space
Eqs. (1)-(3) read (Goroff et al. 1986):
.
Then, in Fourier space
Eqs. (1)-(3) read (Goroff et al. 1986):
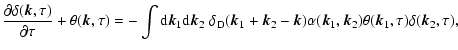 |
|
|
(4) |
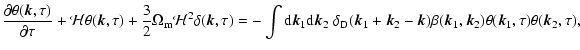 |
|
|
(5) |
where
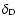 is the Dirac distribution, the coupling functions
is the Dirac distribution, the coupling functions 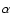 and
and 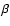 are given by:
are given by:
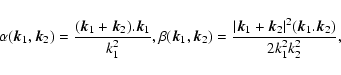 |
(6) |
and we defined the Fourier transforms as:
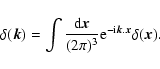 |
(7) |
As in Crocce & Scoccimarro (2006a,b) let us define the two-component vector
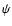 as:
as:
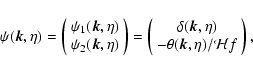 |
(8) |
where we introduced the time coordinate 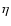 defined from the linear
growing rate D+ of the density contrast:
defined from the linear
growing rate D+ of the density contrast:
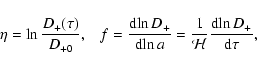 |
(9) |
with D+0 is the value of D+ today at redshift z=0 and:
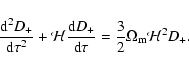 |
(10) |
Then, the equations of motion (4)-(5) can be
written as:
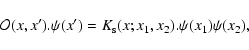 |
(11) |
where we introduced the coordinate
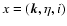 where i=1,2 is the
discrete index of the two-component vectors. In Eq. (11) and in the
following we use the convention that repeated coordinates are integrated over
as:
where i=1,2 is the
discrete index of the two-component vectors. In Eq. (11) and in the
following we use the convention that repeated coordinates are integrated over
as:
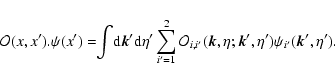 |
(12) |
The matrix 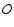 reads:
reads:
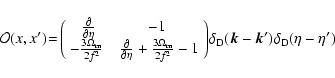 |
(13) |
whereas the symmetric vertex
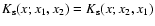 writes:
writes:
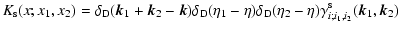 |
|
|
(14) |
with:
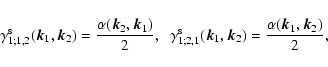 |
(15) |
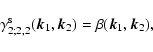 |
(16) |
and zero otherwise (Crocce & Scoccimarro 2006a).
2.2 Linear regime
At large scales or at early times where the density and velocity fluctuations
are small one can linearize the equation of motion (11) which yields
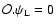 .
Then, the linear growing mode is merely:
.
Then, the linear growing mode is merely:
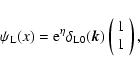 |
(17) |
where
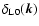 is the linear density contrast today at redshift
z=0. We shall define the initial conditions by the linear growing mode (17) (which is consistent with the fact that we only kept the curl-free
part of the peculiar velocity in
Eqs. (4), (5)). Moreover, we assume Gaussian
homogeneous and isotropic initial conditions defined by the linear
power-spectrum
is the linear density contrast today at redshift
z=0. We shall define the initial conditions by the linear growing mode (17) (which is consistent with the fact that we only kept the curl-free
part of the peculiar velocity in
Eqs. (4), (5)). Moreover, we assume Gaussian
homogeneous and isotropic initial conditions defined by the linear
power-spectrum
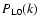 :
:
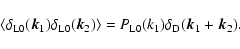 |
(18) |
It is convenient to define the power per logarithmic wavenumber
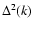 by:
by:
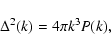 |
(19) |
whence:
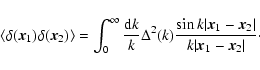 |
(20) |
Thus, for a CDM cosmology the linear power
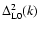 grows as k4 at small k and as
grows as k4 at small k and as 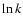 at high k.
Then, the linear two-point correlation function
at high k.
Then, the linear two-point correlation function
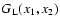 reads:
reads:
As in Valageas (2004) it is convenient to introduce the response function
R(x1,x2) (which is also called the propagator in Crocce & Scoccimarro
2006a,b) defined by the functional derivative:
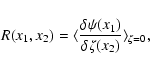 |
(22) |
where 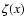 is a "noise'' added to the r.h.s. in Eq. (11).
Thus,
R(x1,x2) measures the linear response of the system to an external
source of noise. Because of causality it contains an Heaviside factor
is a "noise'' added to the r.h.s. in Eq. (11).
Thus,
R(x1,x2) measures the linear response of the system to an external
source of noise. Because of causality it contains an Heaviside factor
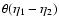 since the field
since the field 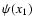 can only depend on the
values of the "noise'' at earlier times
can only depend on the
values of the "noise'' at earlier times
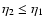 .
Moreover,
it satisfies the initial condition:
.
Moreover,
it satisfies the initial condition:
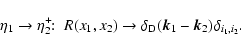 |
(23) |
In the linear regime, the response  may be obtained by first calculating
the linear solution
may be obtained by first calculating
the linear solution
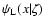 of the linearized equations of motion
of the linearized equations of motion
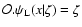 and next taking the functional derivative
(22). Alternatively, one can directly obtain the matrix
and next taking the functional derivative
(22). Alternatively, one can directly obtain the matrix 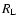 from
the initial condition (23) and the linear dynamics
from
the initial condition (23) and the linear dynamics
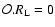 (as implied by the definition (22) and
(as implied by the definition (22) and
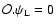 ).
For the Einstein-de-Sitter cosmology (
).
For the Einstein-de-Sitter cosmology (
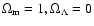 )
where the factors
)
where the factors
 are constant and equal to unity, this can be easily solved
by looking for eigenmodes or performing a Laplace transform as in
Crocce & Scoccimarro (2006a). This yields:
are constant and equal to unity, this can be easily solved
by looking for eigenmodes or performing a Laplace transform as in
Crocce & Scoccimarro (2006a). This yields:
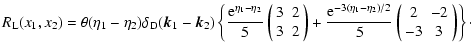 |
(24) |
For other cosmological parameters one must solve numerically the linearized
equation of motion for 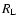 .
Note that in all cases it exhibits the factor
.
Note that in all cases it exhibits the factor
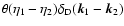 times a term which is
independent of wavenumbers
times a term which is
independent of wavenumbers
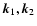 .
.
3 Path-integral formalism
As in Valageas (2004) we can apply a path-integral approach to the
hydrodynamical system (11) since we are only interested in the
statistical properties of the density and velocity fields (we do not look for
peculiar solutions of the equations of motion). Let us briefly recall how this
can be done (also Martin et al. 1973; Phythian 1977).
In order to include explicitly the initial conditions we rewrite
Eq. (11) as:
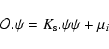 |
(25) |
with 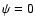 for
for
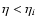 and:
and:
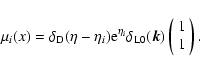 |
(26) |
Thus, the source 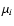 merely provides the initial conditions at time
merely provides the initial conditions at time
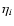 ,
obtained from the linear growing mode (17). We shall
eventually take the limit
,
obtained from the linear growing mode (17). We shall
eventually take the limit
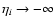 .
Next, we define the
generating functional Z[j] by:
.
Next, we define the
generating functional Z[j] by:
![\begin{displaymath}Z[j] = \langle{\rm e}^{j.\psi} \rangle= \int [{\rm d}\mu_i] \...
...m e}^{j.\psi[\mu_i]-\frac{1}{2} \mu_i . \Delta_i^{-1} . \mu_i}
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img117.gif) |
(27) |
where we took the average over the Gaussian initial conditions:
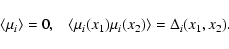 |
(28) |
All statistical properties of the field 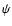 may be obtained from Z[j].
It is convenient to write Eq. (27) as:
may be obtained from Z[j].
It is convenient to write Eq. (27) as:
![$\displaystyle Z[j] =\int [{\rm d}\mu_i] [{\rm d}\psi] \; \vert\det M\vert \;
\d...
..._{\rm s}.\psi\psi)
{\rm e}^{j.\psi-\frac{1}{2} \mu_i . \Delta_i^{-1} . \mu_i} ,$](/articles/aa/full/2007/15/aa6832-06/img119.gif) |
|
|
(29) |
where the Jacobian 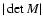 is defined by the functional derivative
is defined by the functional derivative
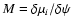 .
We can compute the latter by factorizing the
operator
.
We can compute the latter by factorizing the
operator
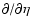 :
:
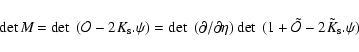 |
(30) |
with:
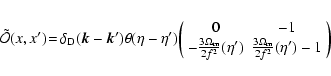 |
(31) |
(note that we separated the identity part out of
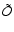 )
and:
)
and:
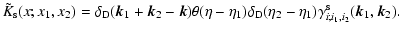 |
|
|
(32) |
Then, we have:
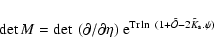 |
(33) |
and:
where we used the fact that the trace of powers 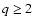 vanishes because of
the Heaviside factors
vanishes because of
the Heaviside factors
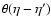 (Zinn-Justin 1989; Valageas 2004).
Next, the trace
(Zinn-Justin 1989; Valageas 2004).
Next, the trace
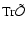 is an
irrelevant constant whereas
is an
irrelevant constant whereas
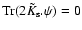 (we regularize as
usual the gravitational interaction at large distances to remove ambiguities,
e.g. perform angular integrals first, see also Valageas 2004). Therefore,
the Jacobian in the
functional integral (29) is a constant which can be absorbed into
the normalization. Then, introducing an imaginary ghost field
(we regularize as
usual the gravitational interaction at large distances to remove ambiguities,
e.g. perform angular integrals first, see also Valageas 2004). Therefore,
the Jacobian in the
functional integral (29) is a constant which can be absorbed into
the normalization. Then, introducing an imaginary ghost field 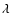 to express the Dirac as an exponential and performing the Gaussian
integration over
to express the Dirac as an exponential and performing the Gaussian
integration over 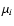 we obtain:
we obtain:
| Z[j] |
= |
![$\displaystyle \int [{\rm d}\mu_i] [{\rm d}\psi] [{\rm d}\lambda] \; {\rm e}^{j....
...\mu_i-{\cal O}.\psi+K_{\rm s}.\psi\psi) - \frac{1}{2}\mu_i.\Delta_i^{-1}.\mu_i}$](/articles/aa/full/2007/15/aa6832-06/img136.gif) |
|
| |
= |
![$\displaystyle \int [{\rm d}\psi] [{\rm d}\lambda] \; {\rm e}^{j.\psi
+ \lambda.(-{\cal O}.\psi+K_{\rm s}.\psi\psi) + \frac{1}{2}\lambda.\Delta_i.\lambda} .$](/articles/aa/full/2007/15/aa6832-06/img137.gif) |
(35) |
Thus, the statistical properties of the system (11) are described
by the action
![$S[\psi,\lambda]$](/articles/aa/full/2007/15/aa6832-06/img138.gif) defined by:
defined by:
![\begin{displaymath}S[\psi,\lambda] = \lambda.({\cal O}.\psi-K_{\rm s}.\psi\psi)
- \frac{1}{2}\lambda.\Delta_i.\lambda.
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img139.gif) |
(36) |
Moreover, we can note that adding a "noise'' 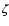 to the r.h.s. of
Eq. (11) amounts to change
to the r.h.s. of
Eq. (11) amounts to change
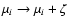 which
translates into
which
translates into
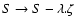 .
Therefore, functional
derivatives with respect to
.
Therefore, functional
derivatives with respect to 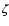 are equivalent to insertions of the ghost
field
are equivalent to insertions of the ghost
field 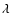 .
In particular, we have:
.
In particular, we have:
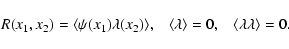 |
(37) |
4 Large-N expansions
The path-integral (35) can be computed by expanding
over powers of its non-Gaussian part (i.e. over powers of 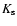 ). This
actually yields the usual perturbative expansion over powers of the
linear power-spectrum
). This
actually yields the usual perturbative expansion over powers of the
linear power-spectrum 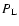 (see also Valageas 2001, 2004, for the
case of the Vlasov equation of motion).
On the other hand, the path-integral (35) may also be studied
through a large-N expansion as in Valageas (2004). Thus, one considers
the generating functional ZN[j,h] defined by:
(see also Valageas 2001, 2004, for the
case of the Vlasov equation of motion).
On the other hand, the path-integral (35) may also be studied
through a large-N expansion as in Valageas (2004). Thus, one considers
the generating functional ZN[j,h] defined by:
![\begin{displaymath}Z_N[j,h] = \int [{\rm d}\psi] [{\rm d}\lambda] \; {\rm e}^{N[j.\psi+h.\lambda-S[\psi,\lambda]]}
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img146.gif) |
(38) |
and one looks for an expansion over powers of 1/N, taking eventually N=1into the results.
As discussed in Valageas (2004) the large-N expansions may also be derived
from a generalization of the dynamics to N fields
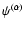 .
This yields the same results once we take care of the long-wavelength
divergences which constrain which subsets of diagrams need to be gathered.
.
This yields the same results once we take care of the long-wavelength
divergences which constrain which subsets of diagrams need to be gathered.
4.1 Steepest-descent method
A first approach to handle the large-N limit of
Eq. (38) is to use a steepest-descent method (also called a
semi-classical or loopwise expansion in the case of usual Quantum field
theory with 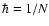 ). This yields for auxiliary correlation and response
functions G0 and R0 the equations (Valageas 2004):
). This yields for auxiliary correlation and response
functions G0 and R0 the equations (Valageas 2004):
whereas the actualcorrelation and response functions obey:
where the self-energy terms  and
and  are given at one-loop order by:
are given at one-loop order by:
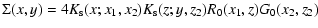 |
|
|
(45) |
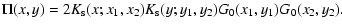 |
|
|
(46) |
Note that Eqs. (39)-(44) are exact and that the expansion over
powers of 1/N only enters the expression of the self-energy (45)-(46). Here we only kept the lowest-order terms
(see Valageas 2004) for the next-order terms). We also took the limit
 so that terms involving
so that terms involving  vanish.
From Sect. 2.2 and Eqs. (39)-(41) we find that the
auxiliary matrices G0 and R0 are actually equal to their linear
counterparts:
vanish.
From Sect. 2.2 and Eqs. (39)-(41) we find that the
auxiliary matrices G0 and R0 are actually equal to their linear
counterparts:
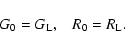 |
(47) |
4.2 2PI effective action method
As described in Valageas (2004) a second approach is to first introduce the
double Legendre transform
![$\Gamma[\psi,G]$](/articles/aa/full/2007/15/aa6832-06/img159.gif) of the functional
of the functional 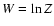 (with
respect to both the field
(with
respect to both the field 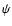 and its two-point correlation G) and next
to apply the 1/N expansion to
and its two-point correlation G) and next
to apply the 1/N expansion to 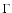 .
This "2PI effective action''method yields the
same Eqs. (42)-(44) and the self-energy shows the same
structure as (45)-(46) where G0 and R0 are replaced by G and R. Thus, the direct steepest-descent method yields a series of
linear equations which can be solved directly whereas the 2PI effective
action method gives a system of non-linear equations (through the dependence
on G and R of
.
This "2PI effective action''method yields the
same Eqs. (42)-(44) and the self-energy shows the same
structure as (45)-(46) where G0 and R0 are replaced by G and R. Thus, the direct steepest-descent method yields a series of
linear equations which can be solved directly whereas the 2PI effective
action method gives a system of non-linear equations (through the dependence
on G and R of  and
and  )
which must usually be solved numerically
by an iterative scheme. However, thanks to the Heaviside factors appearing
in the response R and the self-energy
)
which must usually be solved numerically
by an iterative scheme. However, thanks to the Heaviside factors appearing
in the response R and the self-energy  these equations can be solved
directly by integrating forward over time
these equations can be solved
directly by integrating forward over time  .
.
4.3 General properties
As discussed in Valageas (2004)
both the steepest-descent and 2PI effective action methods agree with the
standard perturbative analysis over powers of
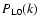 up to the order
used for the self-energy (e.g. up to order
up to the order
used for the self-energy (e.g. up to order
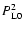 if we only consider
the one-loop terms (45)-(46)). As compared with the standard
perturbative approach, the two schemes described above also include
two different infinite partial resummations, as can be seen from
Eqs. (42)-(44) which clearly generate terms at all orders over
if we only consider
the one-loop terms (45)-(46)). As compared with the standard
perturbative approach, the two schemes described above also include
two different infinite partial resummations, as can be seen from
Eqs. (42)-(44) which clearly generate terms at all orders over
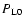 for G and R even if
for G and R even if  and
and  are only linear or
quadratic over
are only linear or
quadratic over
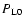 .
.
We can note that the equations we obtain for the hydrodynamical system (1)-(3) are simpler than for the collisionless
system studied in Valageas (2004) which is described by the Vlasov-Poisson
system. Indeed, here the mean
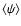 vanishes at all orders.
This can be explicitly
checked from Eqs. (1)-(3) and in the derivation
of Eqs. (39)-(46).
This is not the case for the Vlasov dynamics where Eq. (47)
does not hold.
vanishes at all orders.
This can be explicitly
checked from Eqs. (1)-(3) and in the derivation
of Eqs. (39)-(46).
This is not the case for the Vlasov dynamics where Eq. (47)
does not hold.
Using a diagrammatic technique Crocce & Scoccimarro (2006a,b) derived
Eqs. (42)-(46) in an integral form (i.e. without the
differential operator 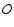 in the l.h.s.) by first integrating the equation
of motion (11). Of course, our path-integral approach can also
be applied to the integral form of Eq. (11). This amounts to
write Eq. (11) as
in the l.h.s.) by first integrating the equation
of motion (11). Of course, our path-integral approach can also
be applied to the integral form of Eq. (11). This amounts to
write Eq. (11) as
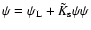 where
where
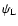 is the linear growing mode and
is the linear growing mode and
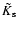 the integral form
of the vertex
the integral form
of the vertex 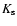 .
Then, the procedure presented in Sect. 3
can be applied to this integral form of the equation of motion, as described
for instance in Valageas (2001). In this article we preferred to keep
Eq. (11) in its differential form so that the r.h.s. does not contain
an integral over time. Then the self-energy terms
.
Then, the procedure presented in Sect. 3
can be applied to this integral form of the equation of motion, as described
for instance in Valageas (2001). In this article we preferred to keep
Eq. (11) in its differential form so that the r.h.s. does not contain
an integral over time. Then the self-energy terms
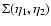 and
and
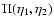 only depend on the response and correlation at the
same times
only depend on the response and correlation at the
same times
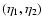 ,
see Eqs. (45), (46). By contrast,
the integrated vertex
,
see Eqs. (45), (46). By contrast,
the integrated vertex
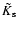 would lead to self-energies which depend
on the values of the response and correlation at all past times which would
entail less efficient numerical computations.
would lead to self-energies which depend
on the values of the response and correlation at all past times which would
entail less efficient numerical computations.
4.4 Integral expression for the two-point correlation
Thanks to statistical homogeneity and isotropy the matrices G0,G and  are symmetric and of the form:
are symmetric and of the form:
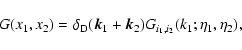 |
(48) |
with:
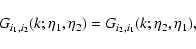 |
(49) |
whereas the matrices R0,R and  are of the form:
are of the form:
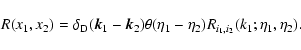 |
(50) |
Besides, from Eqs. (42)-(44) we see that the correlation Gcan also be written in terms of the response R as:
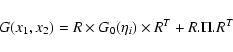 |
(51) |
where the second product is defined as in (12) whereas the
first product does not contain any integration over time:
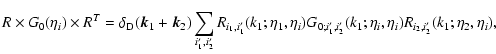 |
|
|
(52) |
and we let
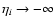 .
The physical meaning of Eq. (51) is clear. The first term in the r.h.s.
means that the fluctuations at the initial time
.
The physical meaning of Eq. (51) is clear. The first term in the r.h.s.
means that the fluctuations at the initial time 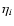 are merely
transported forward in time through the matrix R. This is the only non-zero
term in the linear regime (with
are merely
transported forward in time through the matrix R. This is the only non-zero
term in the linear regime (with
 and
and
 ). The effect of the
non-linear dynamics is to modify the transport matrix R and to add a second
term to the r.h.s. of Eq. (51).
The latter has the meaning of a source term which produces fluctuations with
two-point correlation
). The effect of the
non-linear dynamics is to modify the transport matrix R and to add a second
term to the r.h.s. of Eq. (51).
The latter has the meaning of a source term which produces fluctuations with
two-point correlation
 at the times
at the times
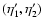 which are next transported
forward to later times
which are next transported
forward to later times
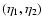 by the matrices
by the matrices
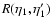 and
and
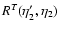 .
Thus, the "dot product'' means
that we need to integrate over all fluctuations produced at all earlier times
.
Thus, the "dot product'' means
that we need to integrate over all fluctuations produced at all earlier times
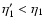 and
and
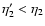 .
This interpretation considers
.
This interpretation considers  as an external source for an "effective''
linear dynamics. For the system which we study here the "source''
as an external source for an "effective''
linear dynamics. For the system which we study here the "source''
 is not external but corresponds to the non-linear interaction of the
field
is not external but corresponds to the non-linear interaction of the
field 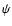 ,
as seen from the explicit expression (46). Moreover,
the linear operator which would define the transport with time also depends on G and R through
,
as seen from the explicit expression (46). Moreover,
the linear operator which would define the transport with time also depends on G and R through  ,
see Eqs. (45) and (44).
,
see Eqs. (45) and (44).
Alternatively, Crocce & Scoccimarro (2006a) pointed out that the expression (51) is somewhat similar to the result obtained within a
phenomenological halo model (Seljak 2000). Indeed, the latter model splits
the non-linear power-spectrum into two terms, one that dominates in the linear
regime (2-halo term) and the other that dominates in the highly non-linear
regime (1-halo term). They could be identified with the first and second
terms of Eq. (51). However, it is not clear whether the analogy can be
pursued much further. In particular, Eq. (51) is explicitly dynamical
(i.e. it explicitly involves integrations over past events) whereas the
halo model gives a static expression (it writes the two-point correlation
as integrals over the current halo distribution, which is the basic
time-dependent quantity).
Note that within the 2PI effective action method, even if R would be
treated independently of G the expression (51) does not give a
quadratic dependence of G on R since  depends quadratically on G.
Besides, solving Eq. (51) perturbatively over G0 at fixed R
actually generates terms at all orders q over powers G0q.
By contrast, in the steepest-descent approach where
depends quadratically on G.
Besides, solving Eq. (51) perturbatively over G0 at fixed R
actually generates terms at all orders q over powers G0q.
By contrast, in the steepest-descent approach where  only depends on G0the expression (51) is fully explicit and quadratic over both
only depends on G0the expression (51) is fully explicit and quadratic over both
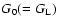 and R if the latter are treated independently. This is a
signature of the additional resummations involved in the 2PI effective action
method as compared with the direct steepest-descent approach.
and R if the latter are treated independently. This is a
signature of the additional resummations involved in the 2PI effective action
method as compared with the direct steepest-descent approach.
An advantage of Eq. (51) is that once
 and R are known, we obtain an explicit expression for G. Hence
we do not need to solve Eq. (42) (by solving
for R we have already performed the "inversion'' of
and R are known, we obtain an explicit expression for G. Hence
we do not need to solve Eq. (42) (by solving
for R we have already performed the "inversion'' of
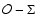 ).
A second advantage of Eq. (51) is that it provides an expression for
G which is clearly symmetric. Moreover, since we start from a two-point
correlation
).
A second advantage of Eq. (51) is that it provides an expression for
G which is clearly symmetric. Moreover, since we start from a two-point
correlation
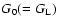 which is positive, as shown by Eq. (21),
we see from Eqs. (46) and (51) that both
which is positive, as shown by Eq. (21),
we see from Eqs. (46) and (51) that both  and G are
positive. This also holds for the 2PI effective action approach which may be
obtained by iterating the system (42)-(46) (substituting G and
R into the self-energy).
and G are
positive. This also holds for the 2PI effective action approach which may be
obtained by iterating the system (42)-(46) (substituting G and
R into the self-energy).
4.5 Integration over wavenumber for the self-energy
Using the symmetry (49) for  and the form (50) for
and the form (50) for  we see that
we see that
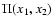 and
and
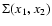 only need to be computed at
times
only need to be computed at
times
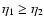 .
Besides, thanks to the various Dirac factors
the expressions (45)-(46) only involve an integral over one
wavenumber
.
Besides, thanks to the various Dirac factors
the expressions (45)-(46) only involve an integral over one
wavenumber 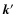 .
Thus, using the expression (14) of the kernel
.
Thus, using the expression (14) of the kernel 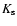 we can write from Eqs. (45), (46) the self-energy as:
we can write from Eqs. (45), (46) the self-energy as:
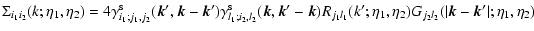 |
|
|
(53) |
and:
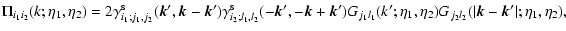 |
|
|
(54) |
where we integrate over 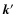 and we sum over
j1,j2,l1,l2.
In order to keep the symmetry
and we sum over
j1,j2,l1,l2.
In order to keep the symmetry
 in the numerical
integration we use symmetric elliptic coordinates:
in the numerical
integration we use symmetric elliptic coordinates:
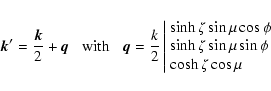 |
(55) |
where 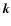 is taken along the third axis and
is taken along the third axis and
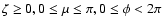 .
.
At equal times
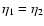 we can obtain from Eq. (53):
we can obtain from Eq. (53):
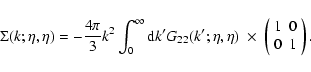 |
(56) |
The explicit expression (56) shows that within the direct
steepest-descent method we need a linear power-spectrum
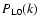 with a
logarithmic slope
with a
logarithmic slope
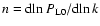 such that n>-1 at large scales
and n<-1 at small scales to obtain finite results. These constraints are
the same as those which appear in the standard perturbative approach.
The divergence at long wavelengths
eventually cancels out if we only consider the equal-time correlations of
the density field, as seen in Jain & Bertschinger (1996) (also
Vishniac 1983). As pointed out by these authors, this can be understood from
the fact that contributions to the velocity field from long-wave modes
correspond to an almost uniform translation of the fluid and therefore should
not affect the growth of density structures on small scales. However, these
infrared contributions can no longer be ignored when one studies
different-times correlations or the velocity field itself. The same problem
appears when one considers the collisionless dynamics as described by the
Vlasov equation (Valageas 2004). The small-scale divergences are more
harmful as they do not cancel in such a fashion. In fact, they may be
understood as the signature of anomalous terms (which do not scale as integer
powers of
such that n>-1 at large scales
and n<-1 at small scales to obtain finite results. These constraints are
the same as those which appear in the standard perturbative approach.
The divergence at long wavelengths
eventually cancels out if we only consider the equal-time correlations of
the density field, as seen in Jain & Bertschinger (1996) (also
Vishniac 1983). As pointed out by these authors, this can be understood from
the fact that contributions to the velocity field from long-wave modes
correspond to an almost uniform translation of the fluid and therefore should
not affect the growth of density structures on small scales. However, these
infrared contributions can no longer be ignored when one studies
different-times correlations or the velocity field itself. The same problem
appears when one considers the collisionless dynamics as described by the
Vlasov equation (Valageas 2004). The small-scale divergences are more
harmful as they do not cancel in such a fashion. In fact, they may be
understood as the signature of anomalous terms (which do not scale as integer
powers of
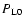 )
which cannot be recovered by
the standard perturbative scheme as discussed in Valageas (2002). It is
probably necessary to go beyond the hydrodynamical approximation (1)-(3) to cure this small-scale problem (e.g.
use the Vlasov equation which does not break down at shell-crossing).
On the other hand, note that within the 2PI effective action scheme these
constraints apply to the non-linear power G22(k) which may have
a different asymptotic behavior than the linear power-spectrum at small
scales. Therefore, the range of initial conditions where the integral in
Eq. (56) converges at high k may be different within this
scheme.
)
which cannot be recovered by
the standard perturbative scheme as discussed in Valageas (2002). It is
probably necessary to go beyond the hydrodynamical approximation (1)-(3) to cure this small-scale problem (e.g.
use the Vlasov equation which does not break down at shell-crossing).
On the other hand, note that within the 2PI effective action scheme these
constraints apply to the non-linear power G22(k) which may have
a different asymptotic behavior than the linear power-spectrum at small
scales. Therefore, the range of initial conditions where the integral in
Eq. (56) converges at high k may be different within this
scheme.
5 Direct steepest-descent method
We present in the following sections our numerical results which we compare
to fits obtained from direct numerical simulations and to the standard
perturbative analysis.
We consider an Einstein-de-Sitter cosmology with
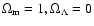 ,
a shape parameter
,
a shape parameter
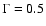 and a normalization
and a normalization
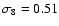 for the linear power-spectrum
for the linear power-spectrum
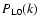 and a Hubble constant
H0=50 km s-1 Mpc-1 (i.e. the reduced Hubble parameter is h=0.5)
as in Smith et al. (2003) so as to compare our results with N-body simulations.
Since we mainly wish to investigate in this
article the properties of the large-N expansions described in
Sect. 4 we first focus on the Einstein-de-Sitter
cosmology where both
and a Hubble constant
H0=50 km s-1 Mpc-1 (i.e. the reduced Hubble parameter is h=0.5)
as in Smith et al. (2003) so as to compare our results with N-body simulations.
Since we mainly wish to investigate in this
article the properties of the large-N expansions described in
Sect. 4 we first focus on the Einstein-de-Sitter
cosmology where both 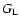 and
and 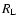 have simple analytical forms (21)-(24). We shall discuss the case of a
have simple analytical forms (21)-(24). We shall discuss the case of a 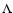 CDM cosmology
in Sect. 8 below.
CDM cosmology
in Sect. 8 below.
We first study in this section the results obtained from the direct
steepest-descent method of Sect. 4.1 which involves the
auxiliary two-point functions G0 and R0.
Since the latter are equal to their linear counterparts (47) the correlation G0 is given by Eq. (21) whereas
R0 is obtained by solving Eq. (40) forward in time, in agreement
with the discussion below Eq. (23). For the Einstein-de-Sitter
cosmology which we consider here R0 is actually given by the explicit
expression (24).
5.1 Self-energy
From G0 and R0 we need to compute the self-energy from
Eqs. (45), (46).
In fact, for the Einstein-de-Sitter cosmology the time-dependence of the
self-energy can be factorized as follows using Eqs. (21), (24).
First, the auxiliary response R0 can be written from Eq. (24) as:
![$\displaystyle R_0(x_1,x_2) = \theta(\eta_1-\eta_2) \delta_{\rm D}({\vec k}_1-{\...
...t[ {\rm e}^{\eta_1-\eta_2} R_0^+ + {\rm e}^{-3(\eta_1-\eta_2)/2}
R_0^- \right],$](/articles/aa/full/2007/15/aa6832-06/img202.gif) |
|
|
(57) |
with:
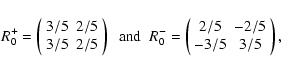 |
(58) |
where we separated the contributions from the growing mode R0+ and the
decaying mode R0-. Then, from Eq. (53) the self-energy term
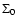 which is linear over R0 also splits into two terms as:
which is linear over R0 also splits into two terms as:
![$\displaystyle \Sigma_0(x_1,x_2) = \theta(\eta_1-\eta_2) \delta_{\rm D}({\vec k}...
...eta_1} \Sigma_0^+(k_1) + {\rm e}^{-\eta_1/2+5\eta_2/2}
\Sigma_0^-(k_1) \right],$](/articles/aa/full/2007/15/aa6832-06/img205.gif) |
|
|
(59) |
with:
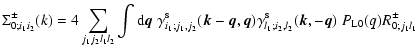 |
|
|
(60) |
where we used Eq. (21). Besides, from the expressions
(15)-(16) of the vertices
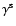 we obtain:
we obtain:
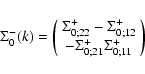 |
(61) |
which is consistent with Eq. (56).
In particular, we have:
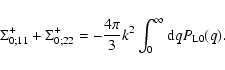 |
(62) |
Moreover, at high k we have the asymptotic behaviors:
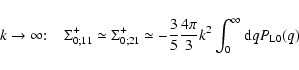 |
(63) |
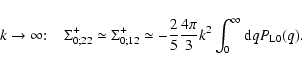 |
(64) |
Of course, we can check that this is consistent with Eq. (62).
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.4cm,clip]{6832f1.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg212.gif) |
Figure 1:
The self-energy terms
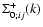 of Eq. (60)
as a function of wavenumber k. We display the four components
of Eq. (60)
as a function of wavenumber k. We display the four components
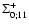 (solid line),
(solid line),
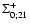 (dot-dashed line),
(dot-dashed line),
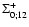 (dotted line) and
(dotted line) and
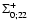 (dashed line).
They are all negative except for
(dashed line).
They are all negative except for
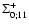 which is positive at
k < 0.2 h Mpc-1 and negative at higher k. All terms are of the same
magnitude and grow roughly as k2 in agreement with Eq. (62).
which is positive at
k < 0.2 h Mpc-1 and negative at higher k. All terms are of the same
magnitude and grow roughly as k2 in agreement with Eq. (62). |
| Open with DEXTER |
We display in Fig. 1 the self-energy term
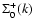 as a function of wavenumber k, from which
as a function of wavenumber k, from which 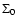 can be obtained using
Eqs. (59), (61). All components
can be obtained using
Eqs. (59), (61). All components
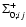 are of
the same magnitude and negative except for
are of
the same magnitude and negative except for
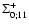 which is positive
at large scales
which is positive
at large scales
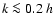 Mpc-1. All terms grow as k2 at high
wavenumbers and we recover the asymptotic behaviors (63)-(64). Note that the self-energy
decreases at large scales so that the two-point functions obtained from
Eqs. (42)-(44) will converge to the linear asymptotics
Mpc-1. All terms grow as k2 at high
wavenumbers and we recover the asymptotic behaviors (63)-(64). Note that the self-energy
decreases at large scales so that the two-point functions obtained from
Eqs. (42)-(44) will converge to the linear asymptotics
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.6cm,clip]{6832f2.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg216.gif) |
Figure 2:
The self-energy
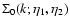 as a function of
forward time
as a function of
forward time  ,
for ,
for
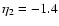 (i.e. z2=3) and wavenumbers
k=0.1,1 and
(i.e. z2=3) and wavenumbers
k=0.1,1 and
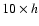 Mpc-1.
The line styles are as in Fig. 1.
The diagonal components vanish for Mpc-1.
The line styles are as in Fig. 1.
The diagonal components vanish for
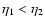 whereas the off-diagonal
components vanish for
whereas the off-diagonal
components vanish for
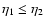 .
All terms are negative except for .
All terms are negative except for
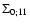 which becomes positive at
which becomes positive at
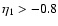 for k=0.1 h Mpc-1.
for k=0.1 h Mpc-1. |
| Open with DEXTER |
We show in Fig. 2 the evolution forward over time  of the
self-energy
of the
self-energy
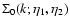 for time
for time
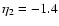 (i.e. z2=3) and wavenumbers k=0.1,1 and
(i.e. z2=3) and wavenumbers k=0.1,1 and
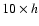 Mpc-1
(from bottom to top).
The absolute value of the self-energy is larger for higher k in agreement
with Fig. 1.
All components are negative (except for
Mpc-1
(from bottom to top).
The absolute value of the self-energy is larger for higher k in agreement
with Fig. 1.
All components are negative (except for
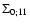 at
at
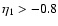 in the case k=0.1 h Mpc-1) and exhibit a smooth dependence with time
following Eq. (59) which goes to
in the case k=0.1 h Mpc-1) and exhibit a smooth dependence with time
following Eq. (59) which goes to
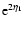 at large
at large  .
.
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.6cm,clip]{6832f3.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg218.gif) |
Figure 3:
The self-energy
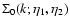 as a function of
backward time
as a function of
backward time 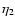 ,
for ,
for 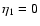 (i.e. z1=0) and wavenumbers
k=0.1,1 and
(i.e. z1=0) and wavenumbers
k=0.1,1 and
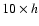 Mpc-1.
The line styles are as in Fig. 1.
All terms are negative except for Mpc-1.
The line styles are as in Fig. 1.
All terms are negative except for
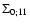 which becomes positive at
which becomes positive at
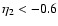 for k=0.1 h Mpc-1.
for k=0.1 h Mpc-1. |
| Open with DEXTER |
We show in Fig. 3 the evolution backward over time 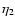 of the
self-energy
of the
self-energy
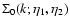 for time
for time 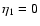 (i.e. z1=0) and wavenumbers k=0.1,1 and
(i.e. z1=0) and wavenumbers k=0.1,1 and
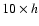 Mpc-1
(from bottom to top). The behavior agrees with
Figs. 1, 2.
Following Eq. (59)
Mpc-1
(from bottom to top). The behavior agrees with
Figs. 1, 2.
Following Eq. (59) 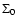 converges to a constant for
converges to a constant for
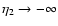 .
.
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.4cm,clip]{6832f4.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg221.gif) |
Figure 4:
The self-energy 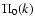 as a function of wavenumber k.
At high k all components are very close and positive.
At
as a function of wavenumber k.
At high k all components are very close and positive.
At
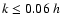 Mpc-1 the off-diagonal components become negative. Mpc-1 the off-diagonal components become negative. |
| Open with DEXTER |
Finally, using the factorized form (21) of the auxiliary two-point
correlation the self-energy 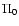 can be written as:
can be written as:
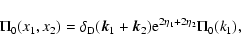 |
(65) |
with:
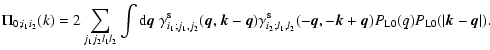 |
|
|
(66) |
In agreement with the symmetry
(49) we can check that
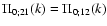 .
.
Since the time-dependence (65) is quite simple we only display
the self-energy term 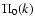 of Eq. (66) as a function of
wavenumber k in Fig. 4.
At high k all components are very close and positive.
The dependence on wavenumber k follows the smooth growth at small scales
of the logarithmic power
of Eq. (66) as a function of
wavenumber k in Fig. 4.
At high k all components are very close and positive.
The dependence on wavenumber k follows the smooth growth at small scales
of the logarithmic power
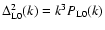 .
As for
.
As for 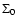 the self-energy term
the self-energy term 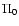 decreases very fast at low
k so that the two-point functions obtained from Eqs. (42)-(44)
will converge to the linear asymptotics at large scales.
decreases very fast at low
k so that the two-point functions obtained from Eqs. (42)-(44)
will converge to the linear asymptotics at large scales.
5.2 Response function
From the self-energy obtained in Sect. 5.1 we compute the
response function from Eq. (43). Thanks to the Heaviside
factor within the term
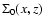 the r.h.s. only involves earlier times
hence Eq. (43) can be integrated forward over time
the r.h.s. only involves earlier times
hence Eq. (43) can be integrated forward over time  at
fixed
at
fixed 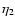 to give
to give
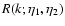 .
Note that each wavenumber k
evolves independently thanks to the Dirac factors
.
Note that each wavenumber k
evolves independently thanks to the Dirac factors
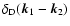 within both
within both 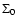 and R as in Eq. (50). Thus all processes
associated with mode-coupling between different wavenumbers
and R as in Eq. (50). Thus all processes
associated with mode-coupling between different wavenumbers 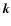 are
contained in the calculation of the self-energy
are
contained in the calculation of the self-energy 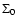 (and
(and 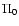 ),
as in Eqs. (60), (66).
),
as in Eqs. (60), (66).
Equation (43) also writes for
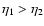 :
:
| |
|
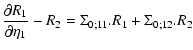 |
(67) |
| |
|
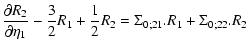 |
(68) |
where
(R1,R2)=(R11,R21) or
(R12,R22), indeed in this case
the two columns of the matrix R are not coupled. Using
Eqs. (59) and (61) the first Eq. (67) also reads:
Taking advantage of the simple dependence on time  of the r.h.s. it is
possible to eliminate the integrals over
of the r.h.s. it is
possible to eliminate the integrals over 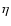 by taking two derivatives of
Eq. (69) with respect to
by taking two derivatives of
Eq. (69) with respect to  .
This yields:
.
This yields:
![$\displaystyle \frac{\partial^3 R_1}{\partial\eta_1^3} - \frac{3}{2} \frac{\part...
...} + \frac{5}{2} \Sigma_{0;11}^+ R_1 + \frac{5}{2} \Sigma_{0;12}^+ R_2 \right] .$](/articles/aa/full/2007/15/aa6832-06/img234.gif) |
|
|
(70) |
In a similar fashion, one obtains from Eq. (68):
![$\displaystyle \frac{\partial^3 R_2}{\partial\eta_1^3} - \frac{3}{2} \frac{\part...
...} + \frac{5}{2} \Sigma_{0;21}^+ R_1 + \frac{5}{2} \Sigma_{0;22}^+ R_2 \right] .$](/articles/aa/full/2007/15/aa6832-06/img235.gif) |
|
|
(71) |
These equations apply to
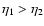 and need to be supplemented by
initial conditions obtained from Eqs. (67), (68) and
Eq. (23) which yield at point
and need to be supplemented by
initial conditions obtained from Eqs. (67), (68) and
Eq. (23) which yield at point
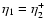 :
:
| XT |
= |
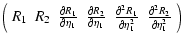 |
(72) |
| |
= |
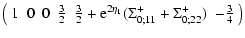 |
(73) |
for the pair
(R11,R21) and:
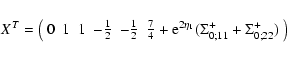 |
(74) |
for the pair
(R12,R22). One can easily check that the linear response
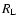 of Eq. (24) is a solution of Eqs. (70), (71)
with
of Eq. (24) is a solution of Eqs. (70), (71)
with
 .
The advantage of these differential equations over the
integro-differential Eqs. (67), (68) is that they no longer
require the computation of integrals over past values of the response R.
Therefore, one does not need to save the values of R on a grid
with a very fine mesh and one can advance over large time steps
.
The advantage of these differential equations over the
integro-differential Eqs. (67), (68) is that they no longer
require the computation of integrals over past values of the response R.
Therefore, one does not need to save the values of R on a grid
with a very fine mesh and one can advance over large time steps  .
Moreover, each time-step runs faster since one does not need to compute
lengthy integrals as in Eqs. (67), (68). We use an adaptative
Runge-Kutta algorithm to solve numerically between two grid
points the Eqs. (70), (71), written as a system of coupled
first-order linear equations over the components of the vector X of
Eq. (72).
.
Moreover, each time-step runs faster since one does not need to compute
lengthy integrals as in Eqs. (67), (68). We use an adaptative
Runge-Kutta algorithm to solve numerically between two grid
points the Eqs. (70), (71), written as a system of coupled
first-order linear equations over the components of the vector X of
Eq. (72).
![\begin{figure}
\par\includegraphics[width=8cm,height=7.4cm,clip]{6832f5.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg241.gif) |
Figure 5:
The non-linear response
 as a function of forward
time
as a function of forward
time  ,
for ,
for
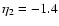 (i.e. z2=3) and wavenumbers k=1
( left panel) and
(i.e. z2=3) and wavenumbers k=1
( left panel) and
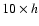 Mpc-1 ( right panel).
We also plot the linear response Mpc-1 ( right panel).
We also plot the linear response 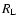 which shows a simple exponential
growth.
which shows a simple exponential
growth. |
| Open with DEXTER |
We can note that Eqs. (70), (71) are somewhat similar to
Bessel functions in terms of the scale factor
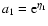 but are of
degree three rather than two. In the small-scale limit
but are of
degree three rather than two. In the small-scale limit
 we can look for an asymptotic solution of
the form:
we can look for an asymptotic solution of
the form:
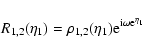 |
(75) |
where the functions
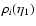 may be expanded as:
may be expanded as:
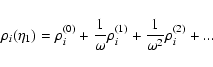 |
(76) |
and
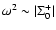 .
We obtain at order
.
We obtain at order 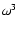 after
substituting into Eqs. (70), (71):
after
substituting into Eqs. (70), (71):
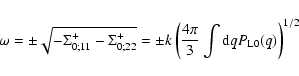 |
(77) |
where we used Eq. (62). At order 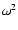 we obtain:
we obtain:
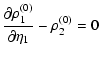 |
|
|
(78) |
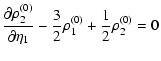 |
|
|
(79) |
where we used the asymptotic behavior (63), (64)
to simplify factors of the form
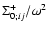 .
By comparison with Eqs. (67), (68), we see that these equations
are precisely the equations obeyed by the linear response
.
By comparison with Eqs. (67), (68), we see that these equations
are precisely the equations obeyed by the linear response
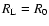 .
Moreover, the initial conditions at
.
Moreover, the initial conditions at
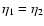 are precisely the same
if we redefine at order 0:
are precisely the same
if we redefine at order 0:
Therefore, at high k the "envelope''
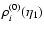 of the
non-linear response
of the
non-linear response
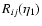 follows exactly the linear response
follows exactly the linear response 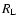 .
In addition, the response R exhibits periodic oscillations over the time
variable a1 with a frequency which increases at high wavenumbers as
.
In addition, the response R exhibits periodic oscillations over the time
variable a1 with a frequency which increases at high wavenumbers as
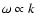 .
Therefore, at one-loop order within the direct
steepest-descent expansion the memory of initial conditions is not really
erased at small scales or late times since the amplitude of the response
R does not decay but only exhibits strong oscillations.
.
Therefore, at one-loop order within the direct
steepest-descent expansion the memory of initial conditions is not really
erased at small scales or late times since the amplitude of the response
R does not decay but only exhibits strong oscillations.
![\begin{figure}
\par\includegraphics[width=8cm,height=7.4cm,clip]{6832f6.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg261.gif) |
Figure 6:
The non-linear response
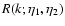 as a function of backward
time
as a function of backward
time 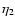 ,
for ,
for 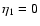 (i.e. z1=0) and wavenumbers k=1
( left panel) and
(i.e. z1=0) and wavenumbers k=1
( left panel) and
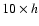 Mpc-1 ( right panel).
We also plot the linear response Mpc-1 ( right panel).
We also plot the linear response 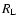 which shows a simple exponential
growth.
which shows a simple exponential
growth. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f7.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg262.gif) |
Figure 7:
The non-linear response function
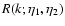 as a function
of wavenumber k, at times
as a function
of wavenumber k, at times
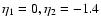 ,
i.e.
z1=0,z2=3.
The horizontal lines are the linear response ,
i.e.
z1=0,z2=3.
The horizontal lines are the linear response 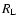 of Eq. (24) which
is independent of k.
of Eq. (24) which
is independent of k. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,height=7.3cm,clip]{6832f8.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg263.gif) |
Figure 8:
The density two-point correlation
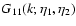 as a
function of time
as a
function of time  ,
for ,
for
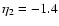 (i.e. z2=3) and wavenumbers
k=1 ( left panel) and
(i.e. z2=3) and wavenumbers
k=1 ( left panel) and
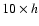 Mpc-1 ( right panel).
We plot the logarithmic power Mpc-1 ( right panel).
We plot the logarithmic power
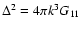 .
We display the linear power .
We display the linear power
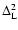 of
Eq. (21) (dashed line), the usual one-loop perturbative result
of
Eq. (21) (dashed line), the usual one-loop perturbative result
 of Eq. (81) (dotted line), the full non-linear
power
of Eq. (81) (dotted line), the full non-linear
power  from Eq. (51) (solid line) and the contribution
from Eq. (51) (solid line) and the contribution
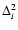 from Eq. (52) (dot-dashed line). Note that G11 whence
from Eq. (52) (dot-dashed line). Note that G11 whence
 can be negative, as shown by the oscillations displayed in the
figure.
can be negative, as shown by the oscillations displayed in the
figure. |
| Open with DEXTER |
We first display in Fig. 5 the evolution forward over time
 of the non-linear response
of the non-linear response
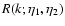 for wavenumbers k=1
(left panel) and
for wavenumbers k=1
(left panel) and
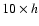 Mpc-1 (right panel). We do not show the case
k=0.1 h Mpc-1 where the response R closely follows the linear response
Mpc-1 (right panel). We do not show the case
k=0.1 h Mpc-1 where the response R closely follows the linear response
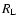 given in Eq. (24). In agreement with the analysis performed
through Eqs. (75)-(80) we find that the non-linear response
R exhibits oscillations
given in Eq. (24). In agreement with the analysis performed
through Eqs. (75)-(80) we find that the non-linear response
R exhibits oscillations 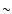
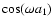 with a frequency
with a frequency 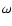 which grows at higher k and an amplitude which follows the linear response
which grows at higher k and an amplitude which follows the linear response
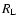 .
Moreover, all components Rij oscillate in phase.
.
Moreover, all components Rij oscillate in phase.
Next, we show in Fig. 6 the evolution backward over time 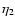 of the non-linear response R. It shows a behavior similar to the
forward evolution displayed in Fig. 5 with respect to
of the non-linear response R. It shows a behavior similar to the
forward evolution displayed in Fig. 5 with respect to  .
At large scales we recover the smooth increase (in absolute values) at early
times
.
At large scales we recover the smooth increase (in absolute values) at early
times 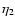 of linear theory (24) whereas at small scales we obtain
fast oscillations
of linear theory (24) whereas at small scales we obtain
fast oscillations 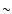
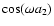 related to
Eqs. (75)-(80) with an amplitude which follows again
the linear response
related to
Eqs. (75)-(80) with an amplitude which follows again
the linear response  .
.
Finally, since at equal times the response function obeys
Eq. (23) we only display in Fig. 7 the response at
unequal times
 .
At low k we recover the linear
response
.
At low k we recover the linear
response  .
At higher k above 0.2 h Mpc-1 the non-linear response obtained
at one-loop order within this steepest-descent approach departs from the
linear prediction and shows oscillations with increasingly high frequencies
while their amplitude follows the linear response
.
At higher k above 0.2 h Mpc-1 the non-linear response obtained
at one-loop order within this steepest-descent approach departs from the
linear prediction and shows oscillations with increasingly high frequencies
while their amplitude follows the linear response 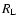 at high k.
This behavior is a result of the oscillatory behavior with time
at high k.
This behavior is a result of the oscillatory behavior with time  displayed in Fig. 5 above and analyzed in
Eqs. (75)-(80).
displayed in Fig. 5 above and analyzed in
Eqs. (75)-(80).
5.3 Two-point correlation
Finally, from Eq. (51) we compute the non-linear two-point correlation
function G obtained through the steepest-descent method at one-loop order.
We compare our results in Figs. 8-11 at redshifts
z=0,3 with a fit
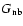 from numerical simulations (Smith et al. 2003),
the linear prediction
from numerical simulations (Smith et al. 2003),
the linear prediction 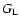 (Eq. (21)) and the usual one-loop result
(Eq. (21)) and the usual one-loop result
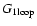 obtained from the standard perturbative expansion over powers
of the linear density field.
The standard one-loop power-spectrum can be written
(e.g., Jain & Bertschinger 1994; Scoccimarro & Frieman 1996a,b) as:
obtained from the standard perturbative expansion over powers
of the linear density field.
The standard one-loop power-spectrum can be written
(e.g., Jain & Bertschinger 1994; Scoccimarro & Frieman 1996a,b) as:
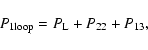 |
(81) |
where 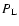 is the linear contribution and P22 and P13 are of order
is the linear contribution and P22 and P13 are of order
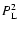 with:
with:
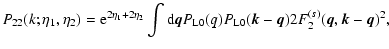 |
|
|
(82) |
and:
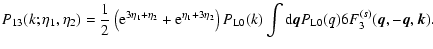 |
|
|
(83) |
The angular kernels F2(s) and F3(s) are obtained from the
couplings 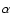 and
and 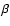 of Eq. (6). In particular
we have (Goroff et al. 1986):
of Eq. (6). In particular
we have (Goroff et al. 1986):
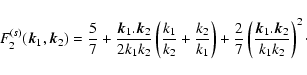 |
(84) |
On the other hand, after integration over angles
in Eq. (83) one obtains (Makino et al. 1992):
From Eqs. (82)-(85) we can see that at large wavenumbers
 the integrals over q in Eqs. (82), (85)
are dominated by the region where the slope n of the linear power-spectrum
is of order
the integrals over q in Eqs. (82), (85)
are dominated by the region where the slope n of the linear power-spectrum
is of order
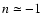 .
This yields:
.
This yields:
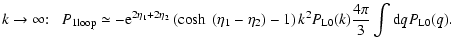 |
|
|
(86) |
Therefore, at unequal times
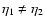 the standard one-loop
prediction becomes negative at high k and the logarithmic power (as defined
below in Eq. (87)) grows as
the standard one-loop
prediction becomes negative at high k and the logarithmic power (as defined
below in Eq. (87)) grows as
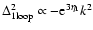 with k and
with k and  ,
in agreement with Figs. 8, 11. Note that the
leading term (86) vanishes at equal times
,
in agreement with Figs. 8, 11. Note that the
leading term (86) vanishes at equal times
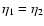 .
This is related to the cancellation of the infrared divergences which appear
for linear power-spectra
.
This is related to the cancellation of the infrared divergences which appear
for linear power-spectra
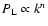 with
with 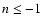 when one
considers equal-times statistics (Vishniac 1983; Jain & Bertschinger 1996).
when one
considers equal-times statistics (Vishniac 1983; Jain & Bertschinger 1996).
The dependence
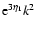 merely reflects the order
merely reflects the order
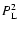 of the
perturbative expansion. In order to go deeper into the non-linear regime one
may consider higher order terms but the latter grow increasingly fast and
one would need at least partial resummations to obtain a well-behaved series
(e.g. Crocce & Scoccimarro 2006a). This is precisely what the large-N
expansions discussed in this article attempt to perform.
of the
perturbative expansion. In order to go deeper into the non-linear regime one
may consider higher order terms but the latter grow increasingly fast and
one would need at least partial resummations to obtain a well-behaved series
(e.g. Crocce & Scoccimarro 2006a). This is precisely what the large-N
expansions discussed in this article attempt to perform.
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f9.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg286.gif) |
Figure 9:
The logarithmic power
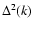 of Eq. (19) at
redshift z=0, that is for equal times
of Eq. (19) at
redshift z=0, that is for equal times
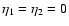 (z1=z2=0).
We display the linear power
(z1=z2=0).
We display the linear power
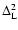 (dashed line), the usual one-loop
perturbative result
(dashed line), the usual one-loop
perturbative result
 (dotted line), the full non-linear
power
(dotted line), the full non-linear
power  from Eq. (51) (solid line) and the contribution
from Eq. (51) (solid line) and the contribution
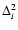 from Eq. (52) (dot-dashed line). We also show the fit
from Eq. (52) (dot-dashed line). We also show the fit
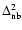 (upper solid line) from numerical simulations
(Smith et al. 2003). All quantities (including
(upper solid line) from numerical simulations
(Smith et al. 2003). All quantities (including
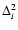 which is the
square of an oscillating function) are positive.
which is the
square of an oscillating function) are positive. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f11.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg288.gif) |
Figure 11:
The logarithmic power
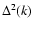 as in Fig. 9
but at unequal times
as in Fig. 9
but at unequal times
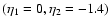 (i.e.
z1=0,z2=3).
(i.e.
z1=0,z2=3). |
| Open with DEXTER |
We first show in Fig. 8 the evolution over time  of
the density two-point correlation
of
the density two-point correlation
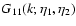 ,
which is
symmetric with respect to
,
which is
symmetric with respect to
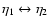 .
We actually
display the "logarithmic power''
.
We actually
display the "logarithmic power''
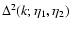 defined as
in Eq. (19) by:
defined as
in Eq. (19) by:
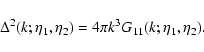 |
(87) |
At equal times
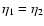 it is equal to the usual logarithmic power
and we have
it is equal to the usual logarithmic power
and we have
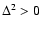 .
However, at different times
.
However, at different times
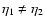 we can have G11<0 whence
we can have G11<0 whence
 .
We present the cases k=1
(left panel) and
.
We present the cases k=1
(left panel) and
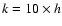 Mpc-1 (right panel) in Fig. 8
for
Mpc-1 (right panel) in Fig. 8
for
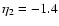 .
For clarity we only display the density-density
correlation G11. Other components Gij show a similar behavior.
.
For clarity we only display the density-density
correlation G11. Other components Gij show a similar behavior.
The oscillations show that G11 can indeed be negative at unequal times.
At these small scales the non-linear power  is already significantly
different from the linear power
is already significantly
different from the linear power
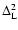 but we can check in the left panel
that
but we can check in the left panel
that  matches the usual one-loop power
matches the usual one-loop power
 of Eq. (81) at small
of Eq. (81) at small  .
As recalled in
Sect. 4.3 the one-loop large-N expansions indeed match
the usual perturbative expansion up to one-loop order (i.e.
.
As recalled in
Sect. 4.3 the one-loop large-N expansions indeed match
the usual perturbative expansion up to one-loop order (i.e.
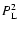 ). At later
times while
). At later
times while
 grows very fast as
grows very fast as
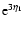 from
Eq. (83) the prediction
from
Eq. (83) the prediction  of the one-loop steepest-descent
approach remains well-behaved of order
of the one-loop steepest-descent
approach remains well-behaved of order
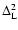 .
Thus, we can see in the right panel that at very small scales where
.
Thus, we can see in the right panel that at very small scales where
 has become exceedingly large
has become exceedingly large  remains
well-controlled. In fact, following the behavior of the response function
analyzed in Sect. 5.2 it exhibits fast oscillations with
an amplitude close to
remains
well-controlled. In fact, following the behavior of the response function
analyzed in Sect. 5.2 it exhibits fast oscillations with
an amplitude close to
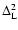 .
We also show in Fig. 8
the power
.
We also show in Fig. 8
the power
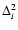 obtained from the first term alone of Eq. (51)
which is detailed in Eq. (52). This corresponds to the "non-linear
transport'' of the initial linear fluctuations without taking into
account the fluctuations
obtained from the first term alone of Eq. (51)
which is detailed in Eq. (52). This corresponds to the "non-linear
transport'' of the initial linear fluctuations without taking into
account the fluctuations  generated at all times by the non-linear
dynamics. We can see that this term is sub-dominant in the mildly non-linear
regime (left panel) but happens to be again of same order as
generated at all times by the non-linear
dynamics. We can see that this term is sub-dominant in the mildly non-linear
regime (left panel) but happens to be again of same order as  in the highly non-linear regime.
in the highly non-linear regime.
Next, we show in Fig. 9 the logarithmic power
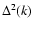 today at equal redshifts z1=z2=0 (i.e. equal times
today at equal redshifts z1=z2=0 (i.e. equal times
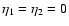 ).
In agreement with Eqs. (51), (52) and the subsequent discussion
both
).
In agreement with Eqs. (51), (52) and the subsequent discussion
both  and
and
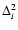 are positive (
are positive (
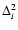 is the square of
an oscillating function).
At large scales
is the square of
an oscillating function).
At large scales  converges to the linear regime
converges to the linear regime
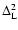 .
At smaller scales we can check again that
.
At smaller scales we can check again that  first follows the usual
one-loop power
first follows the usual
one-loop power
 and next goes back to
and next goes back to
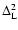 whereas
whereas
 keeps increasing very fast in magnitude.
Unfortunately,
keeps increasing very fast in magnitude.
Unfortunately,  does not agree with the fit
does not agree with the fit
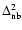 from
numerical simulations (Smith et al. 2003) on a larger range of k as compared
with
from
numerical simulations (Smith et al. 2003) on a larger range of k as compared
with
 (although the rough agreement between
(although the rough agreement between
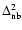 and
and
 at small scale is purely
coincidental).
On the other hand, whereas adding higher-order terms in the standard
perturbative expansion may not improve much the agreement with N-body
simulations (especially since it would lead to increasingly steep terms at
high k) the series obtained in the large-N approach is likely to be
well-behaved as various terms do not "explode'' at small scales.
However, this would require intricate calculations.
We can note that although
at small scale is purely
coincidental).
On the other hand, whereas adding higher-order terms in the standard
perturbative expansion may not improve much the agreement with N-body
simulations (especially since it would lead to increasingly steep terms at
high k) the series obtained in the large-N approach is likely to be
well-behaved as various terms do not "explode'' at small scales.
However, this would require intricate calculations.
We can note that although
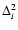 is of
order
is of
order  one cannot neglect the fluctuations
one cannot neglect the fluctuations  generated by
the non-linear dynamics and the sum yields a smooth power
generated by
the non-linear dynamics and the sum yields a smooth power  .
.
We also display in Fig. 10 the logarithmic power
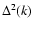 at equal redshifts z1=z2=3. We recover the same behaviors as those
obtained at redshift z=0.
at equal redshifts z1=z2=3. We recover the same behaviors as those
obtained at redshift z=0.
Finally, we show in Fig. 11 the logarithmic power
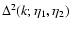 at unequal times
at unequal times
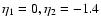 ,
that is
at redshifts
z1=0,z2=3. We find again that
,
that is
at redshifts
z1=0,z2=3. We find again that  matches the usual
one-loop power
matches the usual
one-loop power
 at large scales and follows its change
of sign at
at large scales and follows its change
of sign at
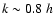 Mpc-1. Note indeed that at unequal times
Mpc-1. Note indeed that at unequal times
 need not be positive. At smaller scales, the steepest-descent
large-N result
need not be positive. At smaller scales, the steepest-descent
large-N result
 departs from the fast growing
departs from the fast growing
 and shows
a series of oscillations of moderate amplitude, which again follow
and shows
a series of oscillations of moderate amplitude, which again follow
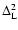 .
These features suggest that the first change of sign in
Fig. 11, which is common to both
.
These features suggest that the first change of sign in
Fig. 11, which is common to both
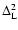 and
and
 ,
may be real and not a mere artefact of the
one-loop expansion. Note that in spite of the oscillations with time
seen in Figs. 8, 11 the large-N approach
automatically ensures that
,
may be real and not a mere artefact of the
one-loop expansion. Note that in spite of the oscillations with time
seen in Figs. 8, 11 the large-N approach
automatically ensures that
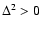 at equal times thanks to the
structure of Eq. (51). This property holds at all orders over 1/N
since Eq. (51) is independent of the expressions of the self-energies
at equal times thanks to the
structure of Eq. (51). This property holds at all orders over 1/N
since Eq. (51) is independent of the expressions of the self-energies
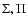 .
.
6 2PI effective action approach
We now present the results obtained at one-loop order from the 2PI
effective action approach recalled in Sect. 4.2.
Thus, we need to solve the system of coupled Eqs. (42)-(46)
where in the expression (45)-(46) of the self-energy the
auxiliary two-point functions G0 and R0 are replaced by G and R.
Thanks to causality, which leads to the Heaviside factor
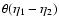 of Eq. (50) within both R and
of Eq. (50) within both R and  ,
we solve the system (42)-(46) by moving forward over time.
,
we solve the system (42)-(46) by moving forward over time.
Thus, we use a grid
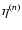 with
with
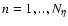 for the time variables. At the earliest time-step
for the time variables. At the earliest time-step
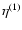 we initialize
all matrices by their linear value at
we initialize
all matrices by their linear value at
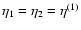 .
Next, once we have obtained all two-point functions
up to time
.
Next, once we have obtained all two-point functions
up to time
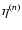 (i.e. over
(i.e. over
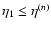 and
and
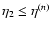 ,
initially n=1) we advance to the next time-step
,
initially n=1) we advance to the next time-step
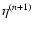 as follows. The response R at equal times
as follows. The response R at equal times
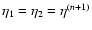 is first obtained from Eq. (23).
Next, we move backward over time
is first obtained from Eq. (23).
Next, we move backward over time
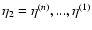 at
fixed
at
fixed
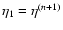 by using Eqs. (43) and (45).
That is, to compute
by using Eqs. (43) and (45).
That is, to compute
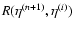 with i=n,..,1 we use for
each value of i the integro-differential Eq. (43) to move over
with i=n,..,1 we use for
each value of i the integro-differential Eq. (43) to move over
 from
from
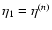 up to
up to
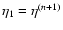 at fixed
at fixed
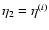 .
Thanks to the Heaviside factors the r.h.s. of
Eq. (43) only involves
.
Thanks to the Heaviside factors the r.h.s. of
Eq. (43) only involves
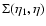 and
and
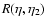 with
with
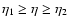 which are already known. Besides, once
which are already known. Besides, once
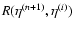 has been obtained we compute
has been obtained we compute
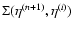 from Eq. (45) before moving downward
to step i-1. Since R and
from Eq. (45) before moving downward
to step i-1. Since R and  vanish for
vanish for
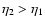 we have
actually obtained in this fashion R and
we have
actually obtained in this fashion R and  for all
for all
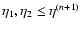 (indeed
(indeed
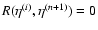 for
for 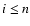 ).
).
Next, we compute  and G from Eqs. (46) and (51).
At fixed
and G from Eqs. (46) and (51).
At fixed
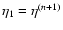 we now move forward over time
we now move forward over time
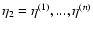 .
Indeed, the r.h.s of Eq. (51)
only involves
.
Indeed, the r.h.s of Eq. (51)
only involves
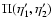 with
with
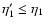 and
and
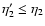 which is already known. Besides, once
which is already known. Besides, once
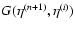 has been obtained we compute
has been obtained we compute
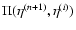 from Eq. (46) before moving forward
to step i+1 and we use the symmetry (49) to derive
from Eq. (46) before moving forward
to step i+1 and we use the symmetry (49) to derive
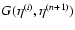 as well as
as well as
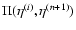 .
.
In fact, at each step i for
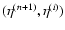 the integrals
in the r.h.s. of Eqs. (43), (51) also involve the values
the integrals
in the r.h.s. of Eqs. (43), (51) also involve the values
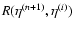 and
and
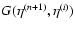 which are
being computed if we use the boundary points in the numerical computation
of the time-integrals. Rather than using open formulae for the integrals we
perform a few iterations at each time-step
which are
being computed if we use the boundary points in the numerical computation
of the time-integrals. Rather than using open formulae for the integrals we
perform a few iterations at each time-step
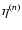 .
This procedure
converges over a few loops.
.
This procedure
converges over a few loops.
Finally, to speed-up the numerical computation we use finite elements over
Fourier space 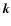 to store the structure of the self-energy terms
to store the structure of the self-energy terms  and
and  .
Thus, since all matrices only depend on the wavenumber modulus
.
Thus, since all matrices only depend on the wavenumber modulus
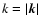 we use a grid k(n) with
n=1,...,Nk. Next, in order to
interpolate for all values of k we can write for instance any matrix such
as G(k) as:
we use a grid k(n) with
n=1,...,Nk. Next, in order to
interpolate for all values of k we can write for instance any matrix such
as G(k) as:
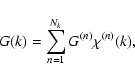 |
(88) |
with:
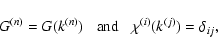 |
(89) |
where
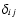 is the Kronecker symbol. The basis functions
is the Kronecker symbol. The basis functions
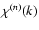 define our interpolation scheme. We could use basis functions
which all extend over the full range
define our interpolation scheme. We could use basis functions
which all extend over the full range
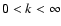 (i.e. a spectral method
built from cardinal functions) but we prefer here to use simple finite
elements with
(i.e. a spectral method
built from cardinal functions) but we prefer here to use simple finite
elements with
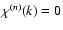 if
k<k(n-1) or
k>k(n+1).
For convenience we actually use triangular functions over the variable
if
k<k(n-1) or
k>k(n+1).
For convenience we actually use triangular functions over the variable
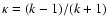 which maps
which maps
![$]0,\infty[$](/articles/aa/full/2007/15/aa6832-06/img335.gif) to ]-1,1[:
to ]-1,1[:
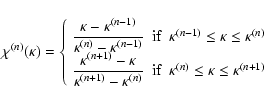 |
(90) |
which is equivalent to use linear interpolation over  for G(k).
Then, we can take advantage of the fact that the kernels
for G(k).
Then, we can take advantage of the fact that the kernels
 in Eqs. (53), (54) do not
depend on time to compute once for all the integrals over wavenumber needed
for the self-energy
in Eqs. (53), (54) do not
depend on time to compute once for all the integrals over wavenumber needed
for the self-energy  and
and  .
Thus, we define the quantities:
.
Thus, we define the quantities:
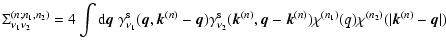 |
|
|
(91) |
and:
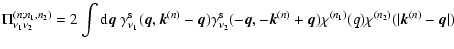 |
|
|
(92) |
where we noted
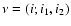 the indices of the vertices
the indices of the vertices
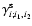 .
These quantities
.
These quantities
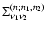 and
and
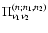 only depend on the vertices
only depend on the vertices
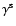 given in Eqs. (15), (16) and on the grid which we use over
wavenumbers hence they are computed at the beginning of the code within
initialization subroutines. Next, the self-energy at a given time
given in Eqs. (15), (16) and on the grid which we use over
wavenumbers hence they are computed at the beginning of the code within
initialization subroutines. Next, the self-energy at a given time
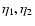 is obtained as:
is obtained as:
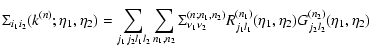 |
|
|
(93) |
with
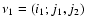 and
and
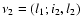 ,
and:
,
and:
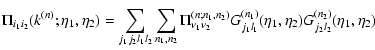 |
|
|
(94) |
with
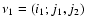 and
and
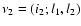 .
Therefore, using
Eqs. (93), (94) we obtain the self-energy by advancing
over times
.
Therefore, using
Eqs. (93), (94) we obtain the self-energy by advancing
over times
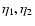 as described above without performing new
integrations over wavenumbers at each step (they are replaced by the discrete
sums over n1,n2 with weights
as described above without performing new
integrations over wavenumbers at each step (they are replaced by the discrete
sums over n1,n2 with weights
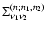 or
or
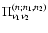 ).
).
6.1 Response R and self-energy 
![\begin{figure}
\par\includegraphics[width=8cm,height=7.2cm,clip]{6832f12.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg351.gif) |
Figure 12:
The non-linear response
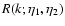 as a function of forward
time
as a function of forward
time  ,
for ,
for
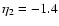 (i.e. z2=3) and wavenumbers k=1
( left panel) and
(i.e. z2=3) and wavenumbers k=1
( left panel) and
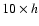 Mpc-1 ( right panel), as in
Fig. 5 but for the 2PI effective action method.
For comparison we also plot the first half-oscillation of the response
obtained in Sect. 5 from the direct
steepest-descent method (curves labeled "sd'') which was shown in
Fig. 5. Mpc-1 ( right panel), as in
Fig. 5 but for the 2PI effective action method.
For comparison we also plot the first half-oscillation of the response
obtained in Sect. 5 from the direct
steepest-descent method (curves labeled "sd'') which was shown in
Fig. 5. |
| Open with DEXTER |
We first display in Fig. 12 the evolution forward over time  of the response
of the response
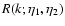 .
We can see that the non-linear response
exhibits oscillations as for the steepest-descent result of Fig. 5
but its amplitude now decays at large times
.
We can see that the non-linear response
exhibits oscillations as for the steepest-descent result of Fig. 5
but its amplitude now decays at large times  instead of following the
linear envelope. This can be understood analytically from the
following simple model. Let us consider the equation:
instead of following the
linear envelope. This can be understood analytically from the
following simple model. Let us consider the equation:
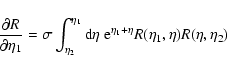 |
(95) |
for a one-component response
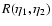 .
This is a simplified form
of the system (43), (45) where we used the linear
time-dependence (21) for G to obtain a closed equation for R.
The parameter
.
This is a simplified form
of the system (43), (45) where we used the linear
time-dependence (21) for G to obtain a closed equation for R.
The parameter
 represents the amplitude of the self-energy
represents the amplitude of the self-energy
 at the wavenumber of interest. Then, the linear regime
at the wavenumber of interest. Then, the linear regime  corresponds to
corresponds to 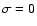 and yields the solution:
and yields the solution:
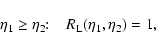 |
(96) |
where we used the initial condition
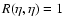 at equal times.
Next, the steepest-descent method presented in
Sects. 4.1 and 5
amounts to replace
at equal times.
Next, the steepest-descent method presented in
Sects. 4.1 and 5
amounts to replace
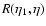 by
by
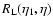 into the integral
in the r.h.s. of Eq. (95). This yields a linear equation for Rwhich can be transformed into a differential equation as in
Sect. 5.2 by taking the derivative of Eq. (95)
with respect to
into the integral
in the r.h.s. of Eq. (95). This yields a linear equation for Rwhich can be transformed into a differential equation as in
Sect. 5.2 by taking the derivative of Eq. (95)
with respect to  .
Since we only have one component one differentiation
is sufficient to remove the integral and we obtain:
.
Since we only have one component one differentiation
is sufficient to remove the integral and we obtain:
 |
(97) |
where we introduced the scale-factor
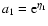 as the
new time-variable. Therefore, we obtain the solution:
as the
new time-variable. Therefore, we obtain the solution:
![\begin{displaymath}R(a_1,a_2) = \cos~[\omega(a_1-a_2)] \;\;\; \mbox{with}
\;\;\; \omega= \sqrt{-\sigma} .
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img361.gif) |
(98) |
Thus, as in Sect. 5.2 we obtain within the
steepest-descent method an oscillating response function with an amplitude
given by the linear response  and a frequency over the time-variable
a1 given by
and a frequency over the time-variable
a1 given by
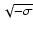 .
Finally, in the 2PI effective action
method we need to solve the non-linear Eq. (95) which also
reads:
.
Finally, in the 2PI effective action
method we need to solve the non-linear Eq. (95) which also
reads:
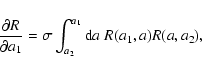 |
(99) |
where we changed variables from 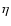 to
to
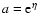 .
We can look for
a solution of Eq. (99) of the form
R(a1,a2)=R(a1-a2)so that the r.h.s. of Eq. (99) becomes a simple convolution:
.
We can look for
a solution of Eq. (99) of the form
R(a1,a2)=R(a1-a2)so that the r.h.s. of Eq. (99) becomes a simple convolution:
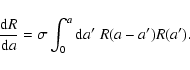 |
(100) |
Introducing the Laplace transform
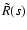 defined by:
defined by:
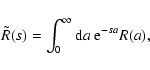 |
(101) |
and taking the Laplace transform of Eq. (100) we obtain:
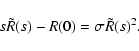 |
(102) |
Using R(0)=1 and requiring that
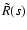 vanishes for
vanishes for
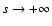 yields:
yields:
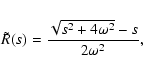 |
(103) |
where we introduced 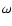 as defined in Eq. (98).
This is a well-known Laplace transform and Eq. (103) directly gives:
as defined in Eq. (98).
This is a well-known Laplace transform and Eq. (103) directly gives:
![\begin{displaymath}R(a_1,a_2)= \frac{J_1[2\omega(a_1-a_2)]}{\omega(a_1-a_2)} ,
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img371.gif) |
(104) |
where J1 is a Bessel function of the first kind.
Thus, we see that within the 2PI effective action method the response
function exhibits oscillations as in the direct steepest-descent method.
However, their amplitude is no longer given by the linear response and becomes
much smaller at late times along with a higher frequency. For the simple
model (95) the amplitude of the response function decays as
a1-3/2 instead of being constant while the frequency becomes twice
larger. This explains the qualitative behavior seen in Fig. 12.
In particular, note that in agreement with the simple model
(95)-(104) the comparison of the right panel of
Fig. 12 with Fig. 5 shows that the frequency of the
oscillations is indeed about twice larger in the non-linear regime
for the 2PI effective action result than for the steepest-descent prediction.
Of course, the result shown in Fig. 12 is more complicated than
the simple model (95) since the two-point correlation Gwhich enters  whence R also depends non-linearly on R through
Eq. (42) or the more explicit expression (51).
However, as we shall check in Sect. 7.3 the dependence
of
whence R also depends non-linearly on R through
Eq. (42) or the more explicit expression (51).
However, as we shall check in Sect. 7.3 the dependence
of  on G does not change much the behavior of the response R(see Fig. 29).
on G does not change much the behavior of the response R(see Fig. 29).
On the other hand, we can see in Fig. 12 that the first quarter
of oscillation, from 1 to 0, of the response R follows rather closely
the curves labeled "sd'' obtained from the steepest-descent method
presented in Sect. 5 which were also shown in
Fig. 5. Besides this agreement remains valid at quite large
k (right panel) where two-point functions obtained from both methods
are generically very different as shown by the figures below.
This property can be understood from Eq. (56) which shows
that the dependence on wavenumber
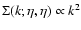 of the self-energy
of the self-energy  at equal times is identical for both approaches
(at one-loop order). Moreover, Eq. (56) shows that the
normalization is governed by the value of the two-point correlation
at equal times is identical for both approaches
(at one-loop order). Moreover, Eq. (56) shows that the
normalization is governed by the value of the two-point correlation
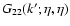 at the point where the logarithmic slope is n=-1(this integral actually corresponds to the mean square velocity
at the point where the logarithmic slope is n=-1(this integral actually corresponds to the mean square velocity
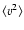 ). At redshift z=0 this wavenumber is still within the linear
regime (for the SCDM cosmology which we consider here) therefore the
self-energy
). At redshift z=0 this wavenumber is still within the linear
regime (for the SCDM cosmology which we consider here) therefore the
self-energy  at equal times
at equal times
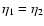 obtained within the
steepest-descent method and the 2PI effective action approach are very close
until z=0. Then, the early time-evolutions at
obtained within the
steepest-descent method and the 2PI effective action approach are very close
until z=0. Then, the early time-evolutions at
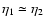 of the
response R obtained within both methods from Eq. (43) are
very close. We can see from Fig. 12 that this agreement holds
until the response R first vanishes. Beyond this point the steepest-descent
method yields increasingly large oscillations (Fig. 5) whereas
the 2PI effective action yields small oscillations which decay to
zero (Fig. 12).
of the
response R obtained within both methods from Eq. (43) are
very close. We can see from Fig. 12 that this agreement holds
until the response R first vanishes. Beyond this point the steepest-descent
method yields increasingly large oscillations (Fig. 5) whereas
the 2PI effective action yields small oscillations which decay to
zero (Fig. 12).
Next, we show in Fig. 13 the evolution backward over time 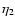 of the response R. In a manner consistent with Fig. 12 it
exhibits oscillations which are strongly damped at large time separations
|a1-a2|, whence at early times
of the response R. In a manner consistent with Fig. 12 it
exhibits oscillations which are strongly damped at large time separations
|a1-a2|, whence at early times 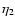 ,
while the frequency is also
larger than for the steepest-descent result shown in Fig. 6.
Again the behavior at nearly
equal times
,
while the frequency is also
larger than for the steepest-descent result shown in Fig. 6.
Again the behavior at nearly
equal times
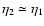 is close to the prediction of the
steepest-descent method presented in Sect. 5
until the response first vanishes. The response at unequal times
is close to the prediction of the
steepest-descent method presented in Sect. 5
until the response first vanishes. The response at unequal times
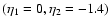 is shown as a function of wavenumber k in
Fig. 14. At large scales we recover the linear regime whereas at small
scales we obtain oscillations which show a fast decay into the non-linear
regime. This is consistent with the time-dependence displayed in
Figs. 12, 13.
is shown as a function of wavenumber k in
Fig. 14. At large scales we recover the linear regime whereas at small
scales we obtain oscillations which show a fast decay into the non-linear
regime. This is consistent with the time-dependence displayed in
Figs. 12, 13.
Therefore, in contrast with the
steepest-descent approach we find that within the 2PI effective action method
the memory of initial conditions is in some sense erased as the response
function decays for large time separation. This agrees with the intuitive
expectation that within the real collisionless gravitational dynamics
the details of the initial conditions are erased at small scales. Indeed,
after shell-crossing one can expect for instance that virialization processes
build halos which mainly depend on a few integrated quantities which
characterize the collapsed region (such as the mass, initial overdensity,
angular momentum, ...) and exhibit relaxed cores (e.g. isotropic velocity
distributions), as suggested by numerical simulations. However, we must note
that the system studied in this paper is defined from the hydrodynamical
equations of motion (1)-(3) which break
down at shell-crossing. Therefore, there is no guarantee a priori that
such small-scale relaxation processes should come out from
Eqs. (1)-(3). It appears through the
2PI effective action method presented in this paper and
Figs. 12-14 that this is actually the case. In fact,
studying the large-k behavior of the kernel 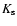 Crocce & Scoccimarro
(2006b) managed to resum all dominant diagrams in this large-k limit
and obtained a Gaussian decay
Crocce & Scoccimarro
(2006b) managed to resum all dominant diagrams in this large-k limit
and obtained a Gaussian decay
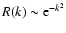 .
In our case, the
simple model (95) suggests that the one-loop 2PI effective action
method only yields a power-law decay as in Eq. (104). Since at the
one-loop order considered in this article we do not resum all diagrams it is
not really surprising that we do not recover the "exact'' Gaussian decay.
However, note that the large-N expansion does not give a mere Taylor series
expansion of such a Gaussian decay (which would blow up at large k or large
times) but already captures at a qualitative level the damping of the response
R at small scale or at large time separation thanks to the non-linearity of
the evolution equation obeyed by R.
.
In our case, the
simple model (95) suggests that the one-loop 2PI effective action
method only yields a power-law decay as in Eq. (104). Since at the
one-loop order considered in this article we do not resum all diagrams it is
not really surprising that we do not recover the "exact'' Gaussian decay.
However, note that the large-N expansion does not give a mere Taylor series
expansion of such a Gaussian decay (which would blow up at large k or large
times) but already captures at a qualitative level the damping of the response
R at small scale or at large time separation thanks to the non-linearity of
the evolution equation obeyed by R.
![\begin{figure}
\par\includegraphics[width=8cm,height=7.2cm,clip]{6832f13.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg378.gif) |
Figure 13:
The non-linear response
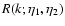 as a function of backward
time
as a function of backward
time 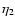 ,
for ,
for 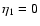 (i.e. z1=0) and wavenumbers k=1
( left panel) and
(i.e. z1=0) and wavenumbers k=1
( left panel) and
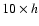 Mpc-1 ( right panel).
We also plot in the left panel the first half-oscillation of the response
obtained in Sect. 5 from the direct
steepest-descent method (curves labeled "sd'') which was shown in
Fig. 6. Mpc-1 ( right panel).
We also plot in the left panel the first half-oscillation of the response
obtained in Sect. 5 from the direct
steepest-descent method (curves labeled "sd'') which was shown in
Fig. 6. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f14.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg379.gif) |
Figure 14:
The non-linear response function
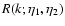 as a function
of wavenumber k, at times
as a function
of wavenumber k, at times
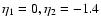 .
We also plot the first
half-oscillation of the response obtained in
Sect. 5 from the direct steepest-descent method
(curves labeled "sd'') which was shown in Fig. 7. .
We also plot the first
half-oscillation of the response obtained in
Sect. 5 from the direct steepest-descent method
(curves labeled "sd'') which was shown in Fig. 7. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6832f15.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg380.gif) |
Figure 15:
The self-energy
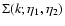 as a function of
forward time
as a function of
forward time  ,
for ,
for
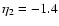 (i.e. z2=3) and wavenumbers
k=1 ( left panel) and
(i.e. z2=3) and wavenumbers
k=1 ( left panel) and
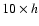 Mpc-1 ( right panel).
The curves labeled "sd'' are the prediction of the steepest-descent method
as in Fig. 2. Mpc-1 ( right panel).
The curves labeled "sd'' are the prediction of the steepest-descent method
as in Fig. 2. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6832f16.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg381.gif) |
Figure 16:
The self-energy
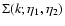 as a function of
backward time
as a function of
backward time 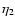 ,
for ,
for 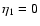 (i.e. z1=0) and wavenumbers
k=1 ( left panel) and
(i.e. z1=0) and wavenumbers
k=1 ( left panel) and
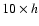 Mpc-1 ( right panel).
The curves labeled "sd'' are the prediction of the steepest-descent method
as in Fig. 3. Mpc-1 ( right panel).
The curves labeled "sd'' are the prediction of the steepest-descent method
as in Fig. 3. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f17.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg382.gif) |
Figure 17:
The self-energy 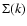 as a function of wavenumber k at
unequal redshifts
z1=0,z2=3. The curves labeled
"sd'' are the prediction of the steepest-descent method.
as a function of wavenumber k at
unequal redshifts
z1=0,z2=3. The curves labeled
"sd'' are the prediction of the steepest-descent method. |
| Open with DEXTER |
We display in Figs. 15 and 16 the evolution with times
 and
and 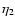 of the self-energy
of the self-energy  .
At large scales
(k<0.1 h Mpc-1) and small time separations we recover the results
obtained within the direct steepest-descent method but at smaller scales
we obtain a series of oscillations with an amplitude which decreases at
large time separations.
This follows from the behavior of the non-linear response R analyzed in
Figs. 12-14 above.
Indeed, the self-energy
.
At large scales
(k<0.1 h Mpc-1) and small time separations we recover the results
obtained within the direct steepest-descent method but at smaller scales
we obtain a series of oscillations with an amplitude which decreases at
large time separations.
This follows from the behavior of the non-linear response R analyzed in
Figs. 12-14 above.
Indeed, the self-energy  depends linearly on the response R, see
Eq. (93). Again the behavior at nearly equal times
depends linearly on the response R, see
Eq. (93). Again the behavior at nearly equal times
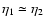 is similar for both approaches (see in particular
the left panel of Fig. 15).
The right panel of Fig. 15 shows that at high wavenumbers the
envelope of the oscillations of
is similar for both approaches (see in particular
the left panel of Fig. 15).
The right panel of Fig. 15 shows that at high wavenumbers the
envelope of the oscillations of  decays as a power-law of
decays as a power-law of
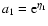 at late times. This agrees with the analysis of the simple
model (95).
In a similar fashion, Fig. 17 which displays the dependence
on wavenumber k of
at late times. This agrees with the analysis of the simple
model (95).
In a similar fashion, Fig. 17 which displays the dependence
on wavenumber k of
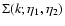 ,
at fixed times
,
at fixed times
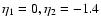 ,
matches the results obtained from the
direct steepest-descent method at low k (except for
,
matches the results obtained from the
direct steepest-descent method at low k (except for
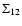 )
and
exhibits decaying oscillations at high k.
We can note in Fig. 17 that the term
)
and
exhibits decaying oscillations at high k.
We can note in Fig. 17 that the term
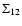 (dotted line)
does not match the steepest-descent result in the limit
(dotted line)
does not match the steepest-descent result in the limit
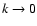 .
This is due to the behavior of the associated kernels
.
This is due to the behavior of the associated kernels
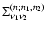 of Eq. (91). More precisely,
using Eqs. (15)-(15), Eq. (53) reads in this case:
of Eq. (91). More precisely,
using Eqs. (15)-(15), Eq. (53) reads in this case:
where we did not write the time-dependence. At large wavenumbers q the
integrand
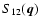 simplifies to:
simplifies to:
![\begin{displaymath}S_{12}({\vec q}) \sim \frac{({\vec k}.{\vec q})^2}{k^2q^2}
[ R_{21} G_{11} + R_{22} G_{12} - R_{11} G_{21} - R_{12} G_{22}] .
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img391.gif) |
(106) |
Therefore, in the linear regime (or for the steepest-descent self-energy
 )
where
)
where
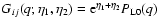 the two-point correlations Gij factorize and we have:
the two-point correlations Gij factorize and we have:
![\begin{displaymath}q \gg \! k \! : S_{0;12}({\vec q}) \sim P_{\rm L0}(q)
[R_{\rm L;21}+R_{\rm L;22}-R_{\rm L;11}-R_{\rm L;12}].
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img393.gif) |
(107) |
For a CDM-like power-spectrum
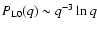 at large wavenumbers
while the linear response
at large wavenumbers
while the linear response
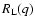 is constant with respect to q.
Hence the integration over
is constant with respect to q.
Hence the integration over 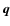 yields at first sight a logarithmic divergence
for
yields at first sight a logarithmic divergence
for
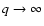 .
In fact, we can check from Eq. (24) that for
the linear response the terms in the bracket in Eq. (107) actually
cancel so that the integral is well-defined for the linear two-point functions
(the integrand decreases as 1/q4 at large q) and it is dominated by
wavenumbers
.
In fact, we can check from Eq. (24) that for
the linear response the terms in the bracket in Eq. (107) actually
cancel so that the integral is well-defined for the linear two-point functions
(the integrand decreases as 1/q4 at large q) and it is dominated by
wavenumbers 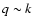 ,
in agreement with the results obtained in
Sect. 5.1. However, for the 2PI effective action method where
we must use the non-linear two-point functions in Eq. (106) this
cancellation no longer holds at weakly non-linear scales
,
in agreement with the results obtained in
Sect. 5.1. However, for the 2PI effective action method where
we must use the non-linear two-point functions in Eq. (106) this
cancellation no longer holds at weakly non-linear scales
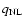 where they
depart from the linear predictions. The integral still converges because of the
decay of the non-linear response at high q but this implies that
for
where they
depart from the linear predictions. The integral still converges because of the
decay of the non-linear response at high q but this implies that
for
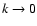 the self-energy term
the self-energy term
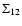 is dominated by the
contribution of wavenumbers
is dominated by the
contribution of wavenumbers
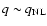 associated with the non-linear
transition and not by wavenumbers
associated with the non-linear
transition and not by wavenumbers 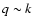 .
Therefore,
.
Therefore,
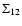 does not
converge to the steepest-descent prediction
does not
converge to the steepest-descent prediction
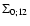 at large scales
at large scales
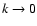 .
By contrast, for other terms the integrand behaves as:
.
By contrast, for other terms the integrand behaves as:
 |
(108) |
The additional power of 1/q ensures that the logarithmic divergence of
Eq. (107) does not appear and at large scales the self-energy
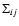 is dominated by the contribution from wavenumbers
is dominated by the contribution from wavenumbers 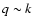 hence it matches the results obtained within the steepest-descent approach.
hence it matches the results obtained within the steepest-descent approach.
6.2 Correlation G and self-energy 
![\begin{figure}
\par\includegraphics[width=8cm,height=7.4cm,clip]{6832f18.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg404.gif) |
Figure 18:
The density two-point correlation
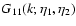 as a
function of time
as a
function of time  ,
for ,
for
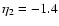 (i.e. z2=3) and wavenumbers
k=1 ( left panel) and
(i.e. z2=3) and wavenumbers
k=1 ( left panel) and
 Mpc-1 ( right panel). We plot the
logarithmic power Mpc-1 ( right panel). We plot the
logarithmic power
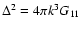 .
We display the full non-linear
power .
We display the full non-linear
power  from Eq. (51) (solid line) and the contribution
from Eq. (51) (solid line) and the contribution
 from Eq. (52) (dot-dashed line), as well as the usual
one-loop perturbative result
from Eq. (52) (dot-dashed line), as well as the usual
one-loop perturbative result
 of Eq. (81)
(dotted line) and the prediction of the steepest-descent method
("sd'', dotted line) also shown in Fig. 8.
of Eq. (81)
(dotted line) and the prediction of the steepest-descent method
("sd'', dotted line) also shown in Fig. 8. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f19.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg405.gif) |
Figure 19:
The logarithmic power
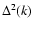 at redshift z=0, that is
at equal times z1=z2=0. We display the full non-linear power
at redshift z=0, that is
at equal times z1=z2=0. We display the full non-linear power  from Eq. (51) (solid line) and the contribution
from Eq. (51) (solid line) and the contribution
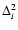 from
Eq. (52) (dot-dashed line), as well as the linear power
from
Eq. (52) (dot-dashed line), as well as the linear power
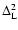 (dashed line), the usual one-loop perturbative result (dashed line), the usual one-loop perturbative result
 of Eq. (81) (dotted line), the prediction of the steepest-descent
method ("sd'', dotted line) also shown in Fig. 9 and the
fit
of Eq. (81) (dotted line), the prediction of the steepest-descent
method ("sd'', dotted line) also shown in Fig. 9 and the
fit
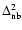 from numerical simulations (Smith et al. 2003).
All quantities (including
from numerical simulations (Smith et al. 2003).
All quantities (including
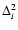 )
are positive. )
are positive. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f20.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg406.gif) |
Figure 20:
The logarithmic power
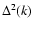 at redshift z=3, that is
at equal times z1=z2=3.
at redshift z=3, that is
at equal times z1=z2=3. |
| Open with DEXTER |
Finally, we present in this section our results for the two-point correlation
G and the self-energy  .
We first display in Fig. 18 the
evolution with time
.
We first display in Fig. 18 the
evolution with time  of the density "logarithmic power''
of the density "logarithmic power''
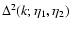 defined in Eq. (87). As shown in the left
panel at early times and large scales we recover the steepest-descent result
since we must also match the usual one-loop expansion (81).
At later times or at smaller scales we obtained oscillations which are
strongly damped at large time separations in contrast with Fig. 8.
This difference of behaviors of the correlations G between the direct
steepest-descent method and the 2PI effective action scheme follows from the
difference already seen in terms of the response R analyzed in
Sect. 6.1.
The right panel of Fig. 18 is particularly interesting as it shows
that in the highly non-linear regime the two-point correlation exhibits a peak
at equal times
defined in Eq. (87). As shown in the left
panel at early times and large scales we recover the steepest-descent result
since we must also match the usual one-loop expansion (81).
At later times or at smaller scales we obtained oscillations which are
strongly damped at large time separations in contrast with Fig. 8.
This difference of behaviors of the correlations G between the direct
steepest-descent method and the 2PI effective action scheme follows from the
difference already seen in terms of the response R analyzed in
Sect. 6.1.
The right panel of Fig. 18 is particularly interesting as it shows
that in the highly non-linear regime the two-point correlation exhibits a peak
at equal times
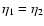 but whereas both the standard one-loop
expansion and the steepest-descent method yield large oscillations
at larger time separations the 2PI effective action approach leads to a
strong damping. Thus, this is the only method (among those presented in this
paper) which yields (at one-loop order)
a damping of correlations at small scales and large time separations which
is expected to reflect the qualitative behavior of the exact gravitational
dynamics.
but whereas both the standard one-loop
expansion and the steepest-descent method yield large oscillations
at larger time separations the 2PI effective action approach leads to a
strong damping. Thus, this is the only method (among those presented in this
paper) which yields (at one-loop order)
a damping of correlations at small scales and large time separations which
is expected to reflect the qualitative behavior of the exact gravitational
dynamics.
Next, we show in Figs. 19, 20 the logarithmic power
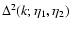 at equal redshifts z1=z2=0 and z1=z2=3as a function of wavenumber k.
We find again that our results match the steepest-descent prediction as well
as the usual one-loop power (81) at large scales.
At small scales, despite the damping at unequal times shown in
Fig. 14 for the response function and in Fig. 18 for the
correlation function we obtain a steady growth of the power
at equal redshifts z1=z2=0 and z1=z2=3as a function of wavenumber k.
We find again that our results match the steepest-descent prediction as well
as the usual one-loop power (81) at large scales.
At small scales, despite the damping at unequal times shown in
Fig. 14 for the response function and in Fig. 18 for the
correlation function we obtain a steady growth of the power
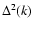 in between the linear prediction
in between the linear prediction
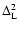 and the usual one-loop
prediction
and the usual one-loop
prediction
 .
Besides, the agreement with the results
from numerical simulations is better than for the steepest-descent prediction.
Of course, because of the damping of the response R at large time
separations analyzed above we can check that the contribution
.
Besides, the agreement with the results
from numerical simulations is better than for the steepest-descent prediction.
Of course, because of the damping of the response R at large time
separations analyzed above we can check that the contribution
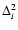 from Eq. (52) associated with the transport of the initial fluctuations
becomes negligible in the non-linear regime (contrary to what happens within
the steepest-descent approach, see Figs. 9, 10).
However, the continuous generation of fluctuations, described by the
self-energy
from Eq. (52) associated with the transport of the initial fluctuations
becomes negligible in the non-linear regime (contrary to what happens within
the steepest-descent approach, see Figs. 9, 10).
However, the continuous generation of fluctuations, described by the
self-energy  in Eq. (51) and associated with the non-linearity
of the dynamics, sustains a high level of density fluctuations
in Eq. (51) and associated with the non-linearity
of the dynamics, sustains a high level of density fluctuations
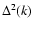 into the non-linear regime. The latter seen at equal times
into the non-linear regime. The latter seen at equal times
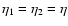 are related to the values of
are related to the values of
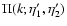 at nearly equal times
at nearly equal times
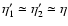 .
.
We show in Fig. 21 the logarithmic power
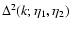 at unequal times as a function of wavenumber k.
We find again that our result matches the steepest-descent prediction as well
as the usual one-loop power (81) at large scales.
However, the correlation now quickly decays at small scales in the non-linear
regime. This follows from the damping at large time separations analyzed above
for the response function which leads to a decorrelation at small scales and
large time separations.
at unequal times as a function of wavenumber k.
We find again that our result matches the steepest-descent prediction as well
as the usual one-loop power (81) at large scales.
However, the correlation now quickly decays at small scales in the non-linear
regime. This follows from the damping at large time separations analyzed above
for the response function which leads to a decorrelation at small scales and
large time separations.
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f21.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg411.gif) |
Figure 21:
The logarithmic power
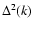 at unequal times
at unequal times
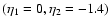 (i.e.
z1=0,z2=3).
(i.e.
z1=0,z2=3). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.5cm,clip]{6832f22.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg412.gif) |
Figure 22:
The self-energy
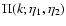 as a function of
forward time
as a function of
forward time  ,
for ,
for
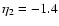 (i.e. z2=3) and wavenumbers
k=1 and
(i.e. z2=3) and wavenumbers
k=1 and
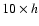 Mpc-1. Mpc-1. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f23.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg413.gif) |
Figure 23:
The self-energy 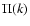 as a function of wavenumber k at equal
redshifts z1=z2=0. We also plot the prediction of the steepest-descent
method (curves labeled "sd'').
as a function of wavenumber k at equal
redshifts z1=z2=0. We also plot the prediction of the steepest-descent
method (curves labeled "sd''). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f24.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg414.gif) |
Figure 24:
The self-energy 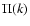 as a function of wavenumber k at unequal
redshifts
z1=0,z2=3. We also plot the prediction of the steepest-descent
method (curves labeled "sd'').
as a function of wavenumber k at unequal
redshifts
z1=0,z2=3. We also plot the prediction of the steepest-descent
method (curves labeled "sd''). |
| Open with DEXTER |
We display in Fig. 22 the self-energy  as a function
of forward time
as a function
of forward time  .
We do not show the results of the steepest-descent
method which follow a mere exponential growth from Eq. (65)
At weakly non-linear scales (
.
We do not show the results of the steepest-descent
method which follow a mere exponential growth from Eq. (65)
At weakly non-linear scales (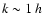 Mpc-1) we recover at early times
the exponential growth of the steepest-descent prediction whereas at late
times we obtain a fast decay. At highly non-linear scales (k=10 h Mpc-1)
we obtain a peak at equal times
Mpc-1) we recover at early times
the exponential growth of the steepest-descent prediction whereas at late
times we obtain a fast decay. At highly non-linear scales (k=10 h Mpc-1)
we obtain a peak at equal times
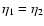 and strongly damped
oscillations at large time separations. This is clearly consistent with the
results obtained for the correlation G11 displayed in Fig. 18.
and strongly damped
oscillations at large time separations. This is clearly consistent with the
results obtained for the correlation G11 displayed in Fig. 18.
Next, we show in Fig. 23 the self-energy  at equal
redshifts z1=z2=0 as a function of wavenumber k. We again recover the
steepest-descent prediction at large scales. However, at small scales we
now obtain a steady growth whereas the steepest-descent method yields a smooth
decline. Therefore, in agreement with Figs. 19, 20
we find that the coupled system of Eqs. (46) (with G0 replaced
by G) and (51) entails at equal times a stronger growth of the
correlation G and of the self-energy
at equal
redshifts z1=z2=0 as a function of wavenumber k. We again recover the
steepest-descent prediction at large scales. However, at small scales we
now obtain a steady growth whereas the steepest-descent method yields a smooth
decline. Therefore, in agreement with Figs. 19, 20
we find that the coupled system of Eqs. (46) (with G0 replaced
by G) and (51) entails at equal times a stronger growth of the
correlation G and of the self-energy  into the non-linear regime as
compared with the non-coupled equations associated with the steepest-descent
method.
into the non-linear regime as
compared with the non-coupled equations associated with the steepest-descent
method.
Finally, we display in Fig. 24 the self-energy  at unequal
redshifts
z1=0,z2=3 as a function of wavenumber k. In agreement with
our results for other two-point functions we recover the steepest-descent
prediction at large scales and decaying oscillations at small scales.
at unequal
redshifts
z1=0,z2=3 as a function of wavenumber k. In agreement with
our results for other two-point functions we recover the steepest-descent
prediction at large scales and decaying oscillations at small scales.
7 Simplified response approximations
The results obtained in the previous sections suggest that a convenient
approximation would be to use a simple analytical form for the response
function R and to compute the correlation G and the self-energy  from Eqs. (46), (51). This avoids the computation of the
self-energy term
from Eqs. (46), (51). This avoids the computation of the
self-energy term  and the numerical integration of the
integro-differential Eq. (43) which requires rather small
time-steps. By contrast, Eq. (51) is a Volterra integral equation
of the second kind which is usually better behaved. We shall investigate
two such approximations associated with the direct steepest-descent approach
and the 2PI effective action scheme.
and the numerical integration of the
integro-differential Eq. (43) which requires rather small
time-steps. By contrast, Eq. (51) is a Volterra integral equation
of the second kind which is usually better behaved. We shall investigate
two such approximations associated with the direct steepest-descent approach
and the 2PI effective action scheme.
7.1 Simplified response for the steepest-descent scheme
Within the framework of the direct steepest-descent scheme studied in
Sect. 5 we found that the response function
exhibits in the non-linear regime a series of oscillations with an envelope
given by the linear theory prediction. Therefore, following Eq. (80)
we consider the approximate response
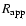 defined as:
defined as:
![\begin{displaymath}R_{\rm app}(x_1,x_2)= R_{\rm L}(x_1,x_2) \cos~[\omega(k)(a_1-a_2)] ,
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img417.gif) |
(109) |
where
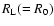 is the linear response given in Eq. (24),
is the linear response given in Eq. (24),
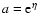 is the scale factor and
is the scale factor and 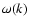 is given by Eq. (77).
is given by Eq. (77).
Here it is interesting to see how expression (109) may be interpreted.
In the linear regime the density and velocity fluctuations
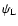 are merely
amplified by a time-dependent factor (proportional to the scale-factor) which
implies in particular that the physics is exactly local:
are merely
amplified by a time-dependent factor (proportional to the scale-factor) which
implies in particular that the physics is exactly local:
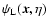 only depends on the initial conditions (and a possible
external noise) at the same location
only depends on the initial conditions (and a possible
external noise) at the same location 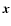 .
Thus in real space we have
.
Thus in real space we have
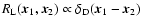 and in Fourier space,
using the factorization (50) associated with statistical homogeneity,
and in Fourier space,
using the factorization (50) associated with statistical homogeneity,
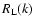 is constant with respect to k, in agreement with Eq. (24).
On the other hand, the cosine dependence of Eq. (109) yields in real
space:
is constant with respect to k, in agreement with Eq. (24).
On the other hand, the cosine dependence of Eq. (109) yields in real
space:
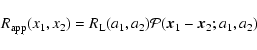 |
(110) |
where
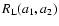 is the time-dependent factor of the linear response
(24) and we introduced the
distribution
is the time-dependent factor of the linear response
(24) and we introduced the
distribution
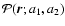 obtained from Eq. (109) as:
obtained from Eq. (109) as:
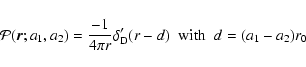 |
(111) |
where
 and:
and:
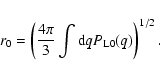 |
(112) |
Thus, Eqs. (109)-(112) may be interpreted as the displacement
of the linear fluctuations over a random distance 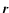 with a probability
distribution
with a probability
distribution
 (whereas the linear
regime obviously corresponds to the distribution
(whereas the linear
regime obviously corresponds to the distribution
 ).
This non-linear operation corresponds to some diffusion of the initial
conditions (over angles of the shift
).
This non-linear operation corresponds to some diffusion of the initial
conditions (over angles of the shift 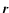 )
but
the singular distribution over the length
)
but
the singular distribution over the length
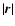 leads to the mere cosine
tail in Fourier space instead of a strong decay.
This can be contrasted to the Zeldovich approximation (Zeldovich 1970) where
the trajectory of particles with initial comoving location
leads to the mere cosine
tail in Fourier space instead of a strong decay.
This can be contrasted to the Zeldovich approximation (Zeldovich 1970) where
the trajectory of particles with initial comoving location 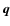 is
written as
is
written as
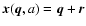 with
with
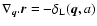 .
Thus the
displacement field is Gaussian which leads to a Gaussian decay at high k(Crocce & Scoccimarro 2006a).
However, we must emphasize that we only write Eq. (110) for comparison
but this is not necessarily the best way to understand the result of the
direct-steepest approach (at this stage expression (110) is only a
mere re-writing of Eq. (109)). In particular, there is no reason
why the non-linear response should be factorized as in Eq. (110)
as
.
Thus the
displacement field is Gaussian which leads to a Gaussian decay at high k(Crocce & Scoccimarro 2006a).
However, we must emphasize that we only write Eq. (110) for comparison
but this is not necessarily the best way to understand the result of the
direct-steepest approach (at this stage expression (110) is only a
mere re-writing of Eq. (109)). In particular, there is no reason
why the non-linear response should be factorized as in Eq. (110)
as 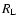 times a displacement term.
times a displacement term.
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f25.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg436.gif) |
Figure 25:
The logarithmic power
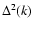 at redshift z=0.
We display the ratio
at redshift z=0.
We display the ratio
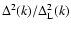 ,
where ,
where
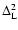 is the
linear power, for the usual one-loop perturbative result
is the
linear power, for the usual one-loop perturbative result
 (dotted line), a fit
(dotted line), a fit
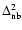 (upper solid line) from numerical simulations (Smith et al. 2003), the result
of the steepest-descent method ("sd'', dotted line) shown in
Fig. 9 and the approximate power
(upper solid line) from numerical simulations (Smith et al. 2003), the result
of the steepest-descent method ("sd'', dotted line) shown in
Fig. 9 and the approximate power
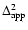 (solid line) obtained from the approximation (109).
(solid line) obtained from the approximation (109). |
| Open with DEXTER |
Next, we use the steepest-descent prescription (65)-(66)
for the self-energy  and we compute numerically the correlation Gfrom the explicit expression (51). In fact, using Eq. (65) the
integrals over time may be performed analytically which yields:
and we compute numerically the correlation Gfrom the explicit expression (51). In fact, using Eq. (65) the
integrals over time may be performed analytically which yields:
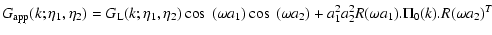 |
|
|
(113) |
with:
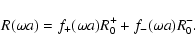 |
(114) |
The matrices  are given in Eqs. (58) and we
introduced the functions:
are given in Eqs. (58) and we
introduced the functions:
![\begin{displaymath}f_+(x)= \int_0^1 {\rm d}t \; \cos~[x(1-t)] = \frac{\sin~(x)}{x}
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img440.gif) |
(115) |
and:
![$\displaystyle f_-(x) = \int_0^1 {\rm d}t \; t^{5/2} \cos~[x(1-t)] = \frac{5}{2x...
.../2}} \left[ \cos~(x) S(\!\sqrt{2x/\pi})
- \sin~(x) C(\!\sqrt{2x/\pi}) \right] ,$](/articles/aa/full/2007/15/aa6832-06/img441.gif) |
|
|
(116) |
where C(x) and S(x) are the Fresnel integrals. At early times or large
scales the first term dominates in Eq. (113) and we recover the linear
regime
 .
At late times and small scales we must take into
account both terms and for large
.
At late times and small scales we must take into
account both terms and for large
 we obtain:
we obtain:
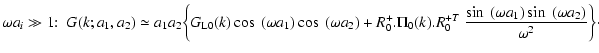 |
|
|
(117) |
Thus, we can see that at late times the non-linear correlation grows as
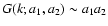 with oscillations for
with oscillations for
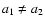 .
This
agrees with the results presented in Sect. 5.3.
.
This
agrees with the results presented in Sect. 5.3.
We show our results for the equal-time density correlation G11 (i.e. the
power
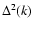 )
in Figs. 25, 26 at
redshifts z=0 and z=3. We display the ratio to the linear power
)
in Figs. 25, 26 at
redshifts z=0 and z=3. We display the ratio to the linear power
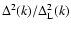 to zoom over the weakly non-linear region and
we also plot the exact one-loop steepest-descent prediction ("sd'')
shown in Fig. 9 for comparison.
Figures 25, 26 clearly show that the
exact one-loop steepest-descent prediction matches the standard one-loop
perturbative result at large scales. Moreover, Fig. 25
suggests that at z=0 the fit from numerical simulations (Smith et al. 2003)
may be off by
to zoom over the weakly non-linear region and
we also plot the exact one-loop steepest-descent prediction ("sd'')
shown in Fig. 9 for comparison.
Figures 25, 26 clearly show that the
exact one-loop steepest-descent prediction matches the standard one-loop
perturbative result at large scales. Moreover, Fig. 25
suggests that at z=0 the fit from numerical simulations (Smith et al. 2003)
may be off by 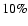 at
at
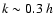 Mpc-1. The power
Mpc-1. The power
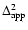 follows roughly the behavior of the "exact'' one-loop
steepest-descent prediction but it is smaller by up to
follows roughly the behavior of the "exact'' one-loop
steepest-descent prediction but it is smaller by up to 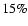 and does
not match very well the one-loop perturbative result. This failure
at intermediate scales is not really surprising since Eq. (80)
was derived in the large-k limit using the asymptotic behaviors
(63)-(64). However, as can be seen in Fig. 1
they are only reached for k>10 h Mpc-1. Therefore, the approximation (109) is not sufficient to obtain accurate results over weakly
non-linear scales. This shows that the results obtained for the two-point
correlation are rather sensitive to the approximations used for the response R. In fact, since the direct steepest-descent method is quite
simple and easy to compute the approximation (109) is not very useful
for precise quantitative predictions and it is best to use the rigorous method
presented in Sect. 5.
and does
not match very well the one-loop perturbative result. This failure
at intermediate scales is not really surprising since Eq. (80)
was derived in the large-k limit using the asymptotic behaviors
(63)-(64). However, as can be seen in Fig. 1
they are only reached for k>10 h Mpc-1. Therefore, the approximation (109) is not sufficient to obtain accurate results over weakly
non-linear scales. This shows that the results obtained for the two-point
correlation are rather sensitive to the approximations used for the response R. In fact, since the direct steepest-descent method is quite
simple and easy to compute the approximation (109) is not very useful
for precise quantitative predictions and it is best to use the rigorous method
presented in Sect. 5.
7.2 Simplified response for the 2PI effective action scheme
Within the 2PI effective action method we found in
Sect. 6
that the response function exhibits oscillations as for the steepest-descent
prediction but their amplitude decays at large times. Following the analysis
of the simple model (95) and Eq. (104) we consider the
approximate response
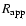 defined as:
defined as:
![\begin{displaymath}R_{\rm app}(x_1,x_2)= R_{\rm L}(x_1,x_2) \frac{J_1[2\omega(k)(a_1-a_2)]}
{\omega(k)(a_1-a_2)}\cdot
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img451.gif) |
(118) |
Of course, this expression can again be written in the form (110)
in real space, with a distribution
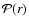 which is now given by:
which is now given by:
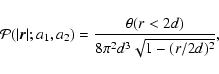 |
(119) |
where the top-hat factor
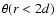 obeys
obeys 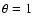 for r<2d and
for r<2d and
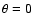 for r>2d. The decay of the response function at high k
corresponds to the smoother distribution (119) as compared with
Eq. (111), but the discontinuity at r=2d leads to a slow power-law
damping instead of an exponential decay. Again, Eq. (119) is a mere
rewriting of Eq. (118) and we do not claim here that the distribution
for r>2d. The decay of the response function at high k
corresponds to the smoother distribution (119) as compared with
Eq. (111), but the discontinuity at r=2d leads to a slow power-law
damping instead of an exponential decay. Again, Eq. (119) is a mere
rewriting of Eq. (118) and we do not claim here that the distribution
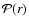 is anything more than a phenomenological tool.
is anything more than a phenomenological tool.
Then, we use Eq. (46) (with G0 replaced by G) and Eq. (51)
to compute the self-energy  and the correlation G, following the
procedure described in Sect. 6.
and the correlation G, following the
procedure described in Sect. 6.
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f27.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg456.gif) |
Figure 27:
The logarithmic power
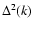 at redshift z=0.
We display the ratio
at redshift z=0.
We display the ratio
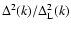 ,
where ,
where
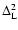 is the
linear power, for the usual one-loop perturbative result
is the
linear power, for the usual one-loop perturbative result
 (dotted line), a fit
(dotted line), a fit
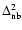 (upper solid line) from numerical simulations (Smith et al. 2003), the result
of the 2PI effective action method ("2PI'', dotted line) shown in
Fig. 19 and the approximate power
(upper solid line) from numerical simulations (Smith et al. 2003), the result
of the 2PI effective action method ("2PI'', dotted line) shown in
Fig. 19 and the approximate power
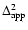 (solid line) obtained from the approximation (118).
(solid line) obtained from the approximation (118). |
| Open with DEXTER |
We show our results for the power
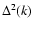 )
in
Figs. 27, 28 at redshifts z=0 and z=3.
We again display the ratio to the linear power
)
in
Figs. 27, 28 at redshifts z=0 and z=3.
We again display the ratio to the linear power
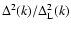 and
we also plot the exact 2PI effective action prediction ("2PI'')
shown in Fig. 19 for comparison.
Figures 27, 28 again clearly show that the
exact 2PI effective action prediction matches the standard one-loop
perturbative result at large scales. In a fashion similar to the
approximation (109) we find that the power
and
we also plot the exact 2PI effective action prediction ("2PI'')
shown in Fig. 19 for comparison.
Figures 27, 28 again clearly show that the
exact 2PI effective action prediction matches the standard one-loop
perturbative result at large scales. In a fashion similar to the
approximation (109) we find that the power
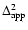 follows roughly the behavior of the exact one-loop 2PI effective action
prediction but it is smaller by up to
follows roughly the behavior of the exact one-loop 2PI effective action
prediction but it is smaller by up to 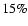 and does not match very well
the one-loop perturbative result. This shows again that the two-point
correlation is rather sensitive to the value of the response function.
and does not match very well
the one-loop perturbative result. This shows again that the two-point
correlation is rather sensitive to the value of the response function.
7.3 Mixed approaches
Finally, we consider in this section mixed approaches which use elements from
both the steepest-descent and 2PI effective action schemes.
The idea is to simplify the computation involved in the
2PI effective action method by separating the computations of the pairs
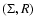 and
and 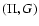 .
That is, we first compute the self-energy
.
That is, we first compute the self-energy  and the response R from the coupled Eqs. (43), (45),
where we use G0 and R in the expression (45) for
and the response R from the coupled Eqs. (43), (45),
where we use G0 and R in the expression (45) for  (the steepest-descent scheme uses G0 and R0 whereas the 2PI effective
action scheme uses G and R). Thus, the pair
(the steepest-descent scheme uses G0 and R0 whereas the 2PI effective
action scheme uses G and R). Thus, the pair
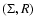 becomes
independent of
becomes
independent of 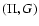 and can be computed in a first step.
Since we keep the explicit dependence on R in the self-energy
and can be computed in a first step.
Since we keep the explicit dependence on R in the self-energy  the evolution Eq. (43) for the response function is no longer
linear but quadratic, hence we expect to recover the damping discussed in
Sect. 6.1 (see the analysis of
Eq. (95)).
We display our results in Fig. 29 which shows that the non-linear
response exhibits indeed a damping close to the one obtained in
Fig. 14 for the full 2PI effective action scheme.
the evolution Eq. (43) for the response function is no longer
linear but quadratic, hence we expect to recover the damping discussed in
Sect. 6.1 (see the analysis of
Eq. (95)).
We display our results in Fig. 29 which shows that the non-linear
response exhibits indeed a damping close to the one obtained in
Fig. 14 for the full 2PI effective action scheme.
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f29.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg460.gif) |
Figure 29:
The non-linear response function
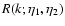 as a function
of wavenumber k, at times
as a function
of wavenumber k, at times
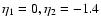 ,
for the mixed approaches
where G0 is used in the computation of ,
for the mixed approaches
where G0 is used in the computation of  . . |
| Open with DEXTER |
Next, we compute the pair  from the Eqs. (46) and (51). Here we can consider two procedures as we may use either G0 or G in the computation of
from the Eqs. (46) and (51). Here we can consider two procedures as we may use either G0 or G in the computation of  .
Clearly, these mixed schemes still agree with the usual one-loop
perturbative results. These two-step approaches are slightly faster than the
full 2PI effective action method for numerical computations. Indeed, as
explained in Sect. 6, within the 2PI effective action approach the equations obtained for two-point functions and
self-energies form a coupled system of non-linear equations. This leads to
an iterative scheme for their numerical computation (which converges within
.
Clearly, these mixed schemes still agree with the usual one-loop
perturbative results. These two-step approaches are slightly faster than the
full 2PI effective action method for numerical computations. Indeed, as
explained in Sect. 6, within the 2PI effective action approach the equations obtained for two-point functions and
self-energies form a coupled system of non-linear equations. This leads to
an iterative scheme for their numerical computation (which converges within 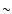 7 steps at worst for the scales we consider here). On the other hand,
at each step the computation of the correlation G takes most of the computer
time (especially at late times) because of the double integral over times
in Eq. (51) but it converges faster (at fixed R) than the response R (at fixed G). Therefore, it saves time to separate the computations
of R (many fast iteration steps) and G (few long iteration steps).
7 steps at worst for the scales we consider here). On the other hand,
at each step the computation of the correlation G takes most of the computer
time (especially at late times) because of the double integral over times
in Eq. (51) but it converges faster (at fixed R) than the response R (at fixed G). Therefore, it saves time to separate the computations
of R (many fast iteration steps) and G (few long iteration steps).
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f30.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg461.gif) |
Figure 30:
The logarithmic power
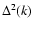 at redshift z=0, that is
at equal times z1=z2=0. We display the linear power
at redshift z=0, that is
at equal times z1=z2=0. We display the linear power
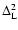 (dashed line), the usual one-loop perturbative result
(dashed line), the usual one-loop perturbative result
 (dotted line), a fit
(dotted line), a fit
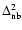 (lower solid line) from numerical
simulations (Smith et al. 2003), the mixed approach
(lower solid line) from numerical
simulations (Smith et al. 2003), the mixed approach
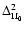 based
on
based
on 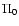 (dashed line) and the mixed approach
(dashed line) and the mixed approach
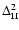 where
where
 is coupled to G (upper solid line).
is coupled to G (upper solid line). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f31.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg462.gif) |
Figure 31:
The logarithmic power
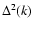 at redshift z=3, that is
at equal times z1=z2=3.
at redshift z=3, that is
at equal times z1=z2=3. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f32.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg463.gif) |
Figure 32:
The ratio
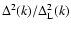 at redshift z=0 of the
logarithmic power
at redshift z=0 of the
logarithmic power  to the linear power
to the linear power
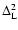 .
We display the ratio .
We display the ratio
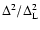 for the usual one-loop
perturbative result
for the usual one-loop
perturbative result
 (dotted line), a fit
(dotted line), a fit
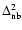 (lower solid line) from numerical simulations
(Smith et al. 2003), the mixed approach
(lower solid line) from numerical simulations
(Smith et al. 2003), the mixed approach
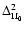 based on
based on 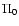 (dashed line) and the mixed approach
(dashed line) and the mixed approach
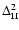 where
where  is coupled
to G (upper solid line).
is coupled
to G (upper solid line). |
| Open with DEXTER |
We display in Figs. 30-33
our results for the power
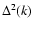 at redshifts z=0 and z=3 for
both schemes. The dashed curve
at redshifts z=0 and z=3 for
both schemes. The dashed curve
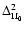 shows the power obtained
when the self-energy term
shows the power obtained
when the self-energy term 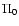 is used (as in the steepest-descent
approach) so that the correlation G is directly given by the explicit
expression (51). The solid curve
is used (as in the steepest-descent
approach) so that the correlation G is directly given by the explicit
expression (51). The solid curve
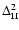 corresponds to
the case where we use the non-linear correlation G in the expression (46) of the self-energy, so that Eqs. (46) and (51)
are a coupled non-linear system which we solve iteratively (as in the
2PI effective action scheme).
We can see that both methods exhibit a similar behavior until
corresponds to
the case where we use the non-linear correlation G in the expression (46) of the self-energy, so that Eqs. (46) and (51)
are a coupled non-linear system which we solve iteratively (as in the
2PI effective action scheme).
We can see that both methods exhibit a similar behavior until
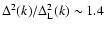 .
Farther into the non-linear regime
the "
.
Farther into the non-linear regime
the "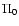 -scheme'' breaks from the non-linear growth of the power-spectrum
and shows oscillations which converge close to the linear power,
in a manner reminiscent of the steepest-descent
approximation, whereas the coupled "
-scheme'' breaks from the non-linear growth of the power-spectrum
and shows oscillations which converge close to the linear power,
in a manner reminiscent of the steepest-descent
approximation, whereas the coupled " -scheme'' follows this non-linear
growth. On the other hand, in the weakly non-linear regime displayed in
Figs. 32-33 the predicted power
-scheme'' follows this non-linear
growth. On the other hand, in the weakly non-linear regime displayed in
Figs. 32-33 the predicted power
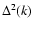 is suppressed as compared with the usual one-loop result. Depending on the
redshift this can improve or worsen the global agreement with numerical
simulations.
However, Fig. 33 suggests that when the usual one-loop
result shows a better global agreement with simulations it is a mere
coincidence as the simulation result separates last from the large-N
predictions (and the closer agreement with the usual one-loop result
at smaller scales has no theoretical basis). Nevertheless, the limited
accuracy of the numerical simulations prevents one from drawing definite
conclusions.
We can note in Fig. 30 that in the highly non-linear regime
the approximation
is suppressed as compared with the usual one-loop result. Depending on the
redshift this can improve or worsen the global agreement with numerical
simulations.
However, Fig. 33 suggests that when the usual one-loop
result shows a better global agreement with simulations it is a mere
coincidence as the simulation result separates last from the large-N
predictions (and the closer agreement with the usual one-loop result
at smaller scales has no theoretical basis). Nevertheless, the limited
accuracy of the numerical simulations prevents one from drawing definite
conclusions.
We can note in Fig. 30 that in the highly non-linear regime
the approximation
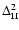 grows larger than for the full 2PI
effective action prediction displayed in Fig. 19. Indeed,
in the latter case the non-linear response is further damped by the
strong growth of the two-point correlation G (this would correspond to
a larger
grows larger than for the full 2PI
effective action prediction displayed in Fig. 19. Indeed,
in the latter case the non-linear response is further damped by the
strong growth of the two-point correlation G (this would correspond to
a larger 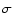 whence
whence 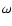 in the simple model (104)) and
this "negative feedback'' within the coupled system R,G leads to a smaller
G as compared with the approximation
in the simple model (104)) and
this "negative feedback'' within the coupled system R,G leads to a smaller
G as compared with the approximation
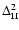 where this feedback
is neglected. In fact, at very high k (beyond the range shown in
Fig. 30) the power
where this feedback
is neglected. In fact, at very high k (beyond the range shown in
Fig. 30) the power
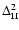 appears to diverge. It is
not clear whether this is due to the finite resolution of the numerical
computation or to a true divergence. However, for practical purposes this is
not a serious shortcoming since it occurs at small scales beyond the range of
validity of this approach (one would need to go beyond one-loop order and
probably beyond the hydrodynamical approach as shell-crossing can no longer
be neglected).
appears to diverge. It is
not clear whether this is due to the finite resolution of the numerical
computation or to a true divergence. However, for practical purposes this is
not a serious shortcoming since it occurs at small scales beyond the range of
validity of this approach (one would need to go beyond one-loop order and
probably beyond the hydrodynamical approach as shell-crossing can no longer
be neglected).
The good agreement in the weakly non-linear regime of these various schemes
enables one to evaluate their range of validity without the need to compare
their prediction with N-body simulations, which could be of great practical
interest. In fact, Fig. 32 suggests that this procedure
can provide a better accuracy than numerical simulations in this regime,
where the latter may still be off by 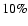 .
.
8 Application to a 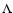 CDM universe
CDM universe
We finally describe in this section how the results obtained in the previous
sections can be applied to more general cosmologies, such as a
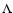 CDM universe. As seen in Sect. 2.1 our formalism applies
equally well to any cosmology. We only need to use the relevant matrix
CDM universe. As seen in Sect. 2.1 our formalism applies
equally well to any cosmology. We only need to use the relevant matrix 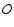 ,
that is to take into account the time dependence of the ratio
,
that is to take into account the time dependence of the ratio
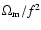 in
Eq. (13), and to recall that
in
Eq. (13), and to recall that 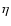 is the logarithm of the linear
growth factor, see Eq. (9). In practice, a widely used approximation
is to take
is the logarithm of the linear
growth factor, see Eq. (9). In practice, a widely used approximation
is to take
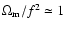 so that the results obtained for the
critical-density universe directly apply to the case
so that the results obtained for the
critical-density universe directly apply to the case
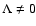 and the
only change is the time-redshift relation
and the
only change is the time-redshift relation
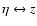 .
We shall use this simple approximation here and compare our results to
numerical simulations. Thus, we consider the cosmological parameters
.
We shall use this simple approximation here and compare our results to
numerical simulations. Thus, we consider the cosmological parameters
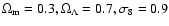 and H0=70 km s-1 Mpc-1as in Smith et al. (2003).
and H0=70 km s-1 Mpc-1as in Smith et al. (2003).
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f34.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg471.gif) |
Figure 34:
The non-linear response function
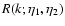 given by the
direct steepest-descent method as a function of wavenumber k for a
given by the
direct steepest-descent method as a function of wavenumber k for a
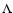 CDM universe, at redshifts
z1=0,z2=3.
The horizontal lines are the linear response CDM universe, at redshifts
z1=0,z2=3.
The horizontal lines are the linear response 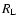 of Eq. (24) which
is independent of k.
of Eq. (24) which
is independent of k. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f35.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg472.gif) |
Figure 35:
The non-linear response function
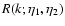 given by the
2PI effective action method as a function of wavenumber k for a
given by the
2PI effective action method as a function of wavenumber k for a
 CDM universe, at redshifts
z1=0,z2=3.
We also plot the first half-oscillation of the response obtained
from the direct steepest-descent method (curves labeled "sd'') which was
shown in Fig. 34. CDM universe, at redshifts
z1=0,z2=3.
We also plot the first half-oscillation of the response obtained
from the direct steepest-descent method (curves labeled "sd'') which was
shown in Fig. 34. |
| Open with DEXTER |
We first plot in Figs. 34, 35 the non-linear
response functions we obtain within the one-loop steepest-descent
and 2PI effective action methods. We can check that we recover the behavior
obtained for the critical-density universe displayed in
Figs. 7, 14. The steepest-descent approach yields again
oscillations in the non-linear regime with an amplitude given by the
linear response at high k whereas the 2PI effective action method
gives damped oscillations. The transition to the non-linear regime
occurs at slightly smaller wavenumber because of the larger normalization  of the linear power-spectrum.
of the linear power-spectrum.
We show in Figs. 36-39 our results
for the two-point correlation G11, that is the non-linear density
power spectrum. We again recover the behavior analyzed in previous sections
for the critical-density universe. Both large-N expansion schemes agree
with the standard one-loop expansion at large scales. At small scales the
steepest-descent result goes back to values close to the linear power
 whereas the 2PI effective action result keeps growing in a manner
similar to the usual perturbative result and numerical simulations.
The degree of agreement between the N-body simulations and either one
of the standard and 2PI results depends on redshift, that is on the slope of
the linear power-spectrum at the relevant scales.
whereas the 2PI effective action result keeps growing in a manner
similar to the usual perturbative result and numerical simulations.
The degree of agreement between the N-body simulations and either one
of the standard and 2PI results depends on redshift, that is on the slope of
the linear power-spectrum at the relevant scales.
Thus, the large-N expansions developed in this article apply in the same
manner for different cosmologies and exhibit the same properties.
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f36.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg474.gif) |
Figure 36:
The logarithmic power
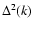 at redshift z=0 for a
at redshift z=0 for a
 CDM universe. We display the linear power CDM universe. We display the linear power
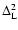 (dashed line), the usual one-loop perturbative result
(dashed line), the usual one-loop perturbative result
 (dotted line), a fit
(dotted line), a fit
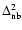 (lower solid line) from numerical
simulations (Smith et al. 2003), the steepest-descent prediction (dotted line
"sd'') and the 2PI effective action result (solid line "2PI'').
(lower solid line) from numerical
simulations (Smith et al. 2003), the steepest-descent prediction (dotted line
"sd'') and the 2PI effective action result (solid line "2PI''). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f37.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg475.gif) |
Figure 37:
The logarithmic power
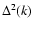 at redshift z=3 for a
at redshift z=3 for a
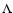 CDM universe. CDM universe. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f38.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg476.gif) |
Figure 38:
The ratio
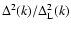 at redshift z=0 of the
logarithmic power
at redshift z=0 of the
logarithmic power  to the linear power
to the linear power
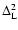 for a
for a
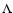 CDM universe.
We display the ratio CDM universe.
We display the ratio
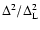 for the usual one-loop
perturbative result
for the usual one-loop
perturbative result
 (dotted line), a fit
(dotted line), a fit
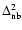 (lower solid line) from numerical simulations
(Smith et al. 2003), the steepest-descent prediction (dashed line "sd'')
and the 2PI effective action result (solid line "2PI'').
(lower solid line) from numerical simulations
(Smith et al. 2003), the steepest-descent prediction (dashed line "sd'')
and the 2PI effective action result (solid line "2PI''). |
| Open with DEXTER |
9 Conclusion
In this article we have studied the predictions at one-loop order of large-Nexpansions for the two-point correlations associated with the formation
of large-scale structures in the expanding universe. Focussing on weakly
non-linear scales we have used the hydrodynamical equations of motion
as a starting point. Then, we have recalled the path-integral formalism
which describes the statistical properties of the system, assuming Gaussian
initial conditions, and we have presented two possible large-N expansions.
Next, we have described in details the numerical predictions obtained for
a SCDM cosmology.
First, we have presented a direct steepest-descent approach where the
self-energy is expressed in terms of the linear response and correlation.
This allows simple computations as the time-dependence of the
self-energy can be factorized (for a critical density universe). Moreover,
the non-linear response R can be computed directly from this self-energy as
it is not coupled to the non-linear correlation G and it obeys a simple
linear equation. This also allows a detailed analysis of its behavior.
We have found that at one-loop order this
approach yields a non-linear response which exhibits strong oscillations
in the non-linear regime (small scales or late times) with an amplitude
which is given by the linear response. Therefore, the response does not
decay but only exhibits increasingly fast oscillations of the form
![$R_{\rm L} \cos~[(a_1-a_2)k/k_*]$](/articles/aa/full/2007/15/aa6832-06/img478.gif) .
However, once the response is integrated over
time such oscillations lead to some damping as compared with the linear
response. Then, we have computed the non-linear correlation which can be
explicitly written in terms of this non-linear response which transports
forward over time the initial density and velocity fluctuations
as well as the fluctuations generated at all previous times by non-linear
couplings. We have checked that in the quasi-linear regime the non-linear
correlation agrees with the usual one-loop prediction (obtained from the
standard perturbative expansion over powers of the initial fluctuations).
In the highly non-linear regime the correlation separates from the
steep growth displayed by the standard one-loop result and converges
back to the linear amplitude. Unfortunately, this behavior does not improve
the agreement with N-body numerical simulations. Nevertheless, it suggests
that this large-N expansion is well-behaved as the two-point functions
do not "explode'' in the highly non-linear regime. Contrary to the
standard perturbative expansion, where higher-order terms grow as increasingly
large powers of k and a(t), the higher-order terms obtained within this
method may remain of finite amplitude.
.
However, once the response is integrated over
time such oscillations lead to some damping as compared with the linear
response. Then, we have computed the non-linear correlation which can be
explicitly written in terms of this non-linear response which transports
forward over time the initial density and velocity fluctuations
as well as the fluctuations generated at all previous times by non-linear
couplings. We have checked that in the quasi-linear regime the non-linear
correlation agrees with the usual one-loop prediction (obtained from the
standard perturbative expansion over powers of the initial fluctuations).
In the highly non-linear regime the correlation separates from the
steep growth displayed by the standard one-loop result and converges
back to the linear amplitude. Unfortunately, this behavior does not improve
the agreement with N-body numerical simulations. Nevertheless, it suggests
that this large-N expansion is well-behaved as the two-point functions
do not "explode'' in the highly non-linear regime. Contrary to the
standard perturbative expansion, where higher-order terms grow as increasingly
large powers of k and a(t), the higher-order terms obtained within this
method may remain of finite amplitude.
Secondly, we have described a 2PI effective action approach where all
two-point functions are coupled. The numerical computation requires an
iterative procedure but thanks to causality the equations can be solved
by integrating forward over time with the help of a few iterations at each
time-step (keeping an implicit scheme in the non-linear integro-differential
equations). Then, we have found that the one-loop non-linear response again
exhibits fast oscillations in the non-linear regime but its amplitude now
shows a fast decay. We have explained how this damping is produced by the
non-linearity of the evolution equation obeyed by the response function.
This yields
a power-law decay such as
![$R_{\rm L} J_1[2(a_1-a_2)k/k_*]/[(a_1-a_2)k/k_*]$](/articles/aa/full/2007/15/aa6832-06/img479.gif) .
In the quasi-linear regime the non-linear correlation agrees again with the
usual one-loop prediction but in the highly non-linear regime it no longer
converges back to the linear power. It rather shows a moderate growth
intermediate between the linear prediction and the result of numerical
simulations, with an amplitude which depends on the redshift (whence on the
slope of the linear power-spectrum). Therefore, this method appears to be
superior to the direct steepest-descent approach which could not recover
any non-linear damping (at one-loop order) but it requires more complex
numerical computations.
.
In the quasi-linear regime the non-linear correlation agrees again with the
usual one-loop prediction but in the highly non-linear regime it no longer
converges back to the linear power. It rather shows a moderate growth
intermediate between the linear prediction and the result of numerical
simulations, with an amplitude which depends on the redshift (whence on the
slope of the linear power-spectrum). Therefore, this method appears to be
superior to the direct steepest-descent approach which could not recover
any non-linear damping (at one-loop order) but it requires more complex
numerical computations.
Thirdly, we have described other approximation schemes built from these
two approaches. Thus, we have found that using a simple explicit approximation
for the non-linear response within either large-N scheme gives correct
qualitative results but does not manage to reproduce accurately the
quantitative results obtained from the full large-N approaches. Next,
we have investigated the approximations obtained by separating the
computations of the response and the correlation (but keeping a non-linear
dynamics for the response). As expected we have found that this yields
a non-linear response which closely follows the damping obtained by the
full 2PI effective action approach and it gives good results (as compared
with the full large-N schemes) for the correlation.
Finally, we have shown that these results also apply to more general
cosmologies such as a 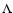 CDM universe, since our formalism extends
to any expansion history of the Universe provided we use the correct
time-redshift relation and linear growth factors.
CDM universe, since our formalism extends
to any expansion history of the Universe provided we use the correct
time-redshift relation and linear growth factors.
Thus, we have shown in this article that large-N expansions provide an
interesting systematic approach to the formation of large-scale structures
in the expanding universe. They already show at one-loop order some damping
in the non-linear regime for the response function and the amplitude of
the two-point correlation remains well-behaved. Unfortunately, for practical
purposes the accuracy provided by these large-N expansions at one-loop order
is not significantly better than the usual perturbative result for weakly
non-linear scales. Nevertheless, the improvement may become greater at higher
orders since the expansion is likely to be better behaved, but this requires
rather complex computations which are beyond the scope of this paper.
On the other hand, one of the goals of this article was to describe a different
approach to the problem of non-linear gravitational clustering than the standard
expansion schemes, namely a path-integral formalism. An important feature of
this approach is that the statistical nature of the problem is already included
in the definition of the system, that is the action
![$S[\psi,\lambda]$](/articles/aa/full/2007/15/aa6832-06/img138.gif) describes
both the equations of motion (here in the hydrodynamical limit) and the average
over Gaussian initial conditions. This also means that one directly works with
correlation functions (such as the power spectrum). By contrast, in usual
expansion schemes (or in N-body numerical simulations) one first works
with the density field associated with a specific initial condition, that is one
tries to express the non-linear density field in terms of the linear density
field (e.g. as a truncated power series) and next performs the average over the
initial condition. In principles, this formalism can present several advantages.
First, the statistical quantities such as the power-spectrum are precisely
the objects of interest for practical purposes. Secondly, they exhibit symmetries
(such as homogeneity and isotropy) which are not satisfied by peculiar realizations
of the initial conditions. Moreover, they are smooth functions (such as power laws)
rather than singular distributions. This could facilitate the numerical
computations and the building of various approximations.
describes
both the equations of motion (here in the hydrodynamical limit) and the average
over Gaussian initial conditions. This also means that one directly works with
correlation functions (such as the power spectrum). By contrast, in usual
expansion schemes (or in N-body numerical simulations) one first works
with the density field associated with a specific initial condition, that is one
tries to express the non-linear density field in terms of the linear density
field (e.g. as a truncated power series) and next performs the average over the
initial condition. In principles, this formalism can present several advantages.
First, the statistical quantities such as the power-spectrum are precisely
the objects of interest for practical purposes. Secondly, they exhibit symmetries
(such as homogeneity and isotropy) which are not satisfied by peculiar realizations
of the initial conditions. Moreover, they are smooth functions (such as power laws)
rather than singular distributions. This could facilitate the numerical
computations and the building of various approximations.
Of course, one can recover the standard perturbative results
by expanding over the cubic part of the action, as recalled in this paper and
discussed in more details in Valageas (2004). However, the advantage of this
formalism is that it may serve as a starting point to other approximation schemes
by applying the methods of statistical mechanics and field theory. Thus, we have
described in details in this paper two large-N expansion schemes. In addition
to the interesting properties of these two methods discussed above, we can note
that it is useful to have several rigorous expansion schemes which only
differ by higher-order terms than the truncation order. Indeed, since one can expect
that they should be correct up to the scale where they start to depart from one
another, this should allow one to estimate their range of validity without computing
explicitly higher-order terms or performing N-body simulations.
In fact, in the weakly non-linear regime where all expansion schemes agree this
procedure should provide a better accuracy than N-body simulations which may still be
inaccurate by up to 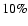 .
Farther into the non-linear regime, it seems
that the usual one-loop result and the 2PI effective action scheme
give better results than the direct steepest-descent method.
On the other hand, one can hope that other methods than these two expansion schemes
could be applied to the action
.
Farther into the non-linear regime, it seems
that the usual one-loop result and the 2PI effective action scheme
give better results than the direct steepest-descent method.
On the other hand, one can hope that other methods than these two expansion schemes
could be applied to the action
![$S[\psi,\lambda]$](/articles/aa/full/2007/15/aa6832-06/img138.gif) .
.
In regard to recent works we can
note that the Schwinger-Dyson equations obtained in Crocce & Scoccimarro (2006a)
can also be obtained from the approach described in this paper, provided we use
the equations of motion in their integral form (that is we first integrate the
time-derivative), as also described in Valageas (2001). Whereas
Crocce & Scoccimarro (2006a) used a diagrammatic technique and the resummation
of all diagrams gives back the usual Schwinger-Dyson equations the path-integral
formalism directly gives these equations by expanding the action (or its Legendre
transform) about a saddle-point. On the other hand, the diagrammatic approach
also provides a direct expression of the response function
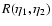 (in the
limit
(in the
limit
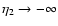 )
as a series of diagrams (which could be recovered
here by writing the self-energy
)
as a series of diagrams (which could be recovered
here by writing the self-energy  as a series of diagrams). Thus,
Crocce & Scoccimarro (2006a) managed to resum these diagrams in the high-k limit
and to obtain the asymptotic behavior of
as a series of diagrams). Thus,
Crocce & Scoccimarro (2006a) managed to resum these diagrams in the high-k limit
and to obtain the asymptotic behavior of
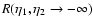 .
It is not clear yet how this result could be directly obtained from the
path-integral formalism without expanding over diagrams.
.
It is not clear yet how this result could be directly obtained from the
path-integral formalism without expanding over diagrams.
Among the points which deserve further studies,
it would be interesting to apply these approaches to
higher-order correlations beyond the two-point functions investigated here.
On the other hand, the analysis presented in this article
is based on the hydrodynamical equations of motion which break down at
small scales beyond shell-crossing. It is possible to apply these large-N
expansions to the Vlasov equation (Valageas 2004) but the numerical
computations would be significantly more complex (since one needs to add
velocities to space coordinates). Nevertheless, the results obtained within
the hydrodynamical framework (damping and well-behaved non-linear
asymptotics) can be expected to remain valid in the collisionless case and
studies such as the present one may serve as a first step towards an
application to the Vlasov dynamics. Such large-N
expansions could also be applied to simpler effective dynamics which attempt
to go beyond shell-crossing (based for instance on a Schroedinger equation,
Widrow & Kaiser 1993).
These works would be of great practical interest as several cosmological probes
(such as weak lensing surveys and measures of the baryon acoustic oscillations)
which aim to measure the recent expansion history of the Universe in order
to constrain the dark energy equation of state (as well as other cosmological
parameters) are very sensitive to the weakly non-linear scales where non-linear
effects can no longer be neglected.
-
Bernardeau, F. 1994, A&A, 291, 697 [NASA ADS] (In the text)
-
Bernardeau, F., van Waerbeke, L., & Mellier, Y. 1997, A&A,
322, 1 [NASA ADS] (In the text)
-
Bernardeau, F., Colombi, S., Gaztanaga, E., & Scoccimarro, R.
2002, Phys. Rept., 367, 1 [NASA ADS] [CrossRef] (In the text)
- Crocce, M.,
& Scoccimarro, R. 2006a, Phys. Rev. D, 73, 063519 [NASA ADS] [CrossRef] (In the text)
- Crocce, M.,
& Scoccimarro, R. 2006b, Phys. Rev. D, 73, 063520 [NASA ADS] [CrossRef] (In the text)
- Fry, J. N. 1984, ApJ,
279, 499 [NASA ADS] [CrossRef] (In the text)
- Goroff, M. H.,
Grinstein, B., Rey, S.-J., & Wise, M. B. 1986, ApJ, 311, 6 [NASA ADS] [CrossRef] (In the text)
- Jain, B., &
Bertschinger, E. 1994, ApJ, 431, 495 [NASA ADS] [CrossRef] (In the text)
- Jain, B., &
Bertschinger, E. 1996, ApJ, 456, 43 [NASA ADS] [CrossRef] (In the text)
- Koehler, R.
S., Schuecker, P., & Gebhardt, K. 2007
[arXiv:astro-ph/0609354]
(In the text)
- Liddle, A. R.,
& Lyth, D. H. 1993, Phys. Rep., 231, 1 [NASA ADS] [CrossRef] (In the text)
- Makino, N.,
Sasaki, M., & Suto, Y. 1992, Phys. Rev. D, 46, 585 [NASA ADS] [CrossRef] (In the text)
- McDonald,
P. 2006, Phys. Rev. D, 75, 043514 [NASA ADS] [CrossRef] (In the text)
- Martin, P. C.,
Siggia, E. D., & Rose, H. A. 1973, Phys. Rev. A, 8, 423 [NASA ADS] [CrossRef] (In the text)
- Munshi, D.,
Valageas, P., Van Waerbeke, L., & Heavens, A. 2007
[arXiv:astro-ph/0612667]
(In the text)
- Peebles, P.
J. E. 1980, The large scale structure of the universe (Princeton
University Press)
(In the text)
- Peebles, P.
J. E. 1982, ApJ, 263, L1 [NASA ADS] [CrossRef] (In the text)
- Phythian,
R. 1977, J. Phys. A, 10, 777 [NASA ADS] [CrossRef] (In the text)
-
Scoccimarro, R., & Frieman, J. 1996a, ApJS, 105, 37 [NASA ADS] [CrossRef] (In the text)
-
Scoccimarro, R., & Frieman, J. 1996b, ApJ, 473, 620 [NASA ADS] [CrossRef] (In the text)
- Seljak, U.
2000, MNRAS, 318, 203 [NASA ADS] (In the text)
- Seljak, U.,
& Zaldarriaga, M. 1996, ApJ, 469, 437 [NASA ADS] [CrossRef] (In the text)
- Seo, H.-J., &
Eisenstein, D. J. 2007 [arXiv:astro-ph/0701079]
(In the text)
- Smith, R. E.,
Peacock, J. A., Jenkins, A., et al. 2003, MNRAS, 341, 1311 [NASA ADS] (In the text)
- Valageas,
P. 2001, A&A, 379, 8 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Valageas,
P. 2002, A&A, 382, 477 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Valageas,
P. 2004, A&A, 421, 23 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Vishniac,
E. T. 1983, MNRAS, 203, 345 [NASA ADS] (In the text)
- Widrow, L. M.,
& Kaiser, N. 1993, ApJ, 416, L71 [NASA ADS] [CrossRef] (In the text)
-
Zeldovich, Y. B. 1970, A&A, 5, 84 [NASA ADS] (In the text)
- Zinn-Justin, J.
1989, Quantum field theory and critical phenomena (Oxford:
Clarendon Press)
(In the text)
Copyright ESO 2007
![\begin{displaymath}\frac{\partial\delta}{\partial\tau} + \nabla.[(1+\delta) {\vec v}] = 0,
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img53.gif)
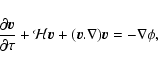
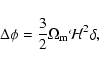
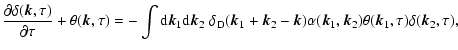
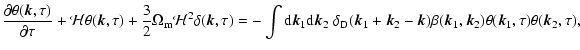
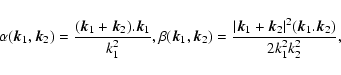
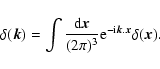
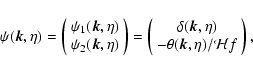
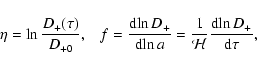
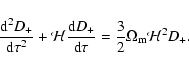
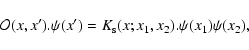
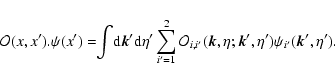
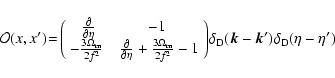
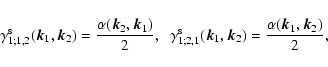
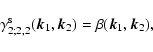
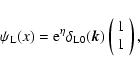
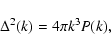
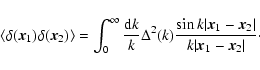
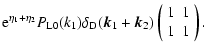
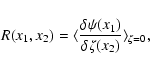
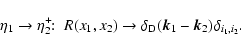
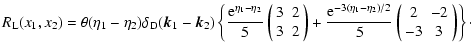
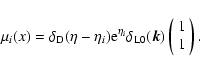
![\begin{displaymath}Z[j] = \langle{\rm e}^{j.\psi} \rangle= \int [{\rm d}\mu_i] \...
...m e}^{j.\psi[\mu_i]-\frac{1}{2} \mu_i . \Delta_i^{-1} . \mu_i}
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img117.gif)
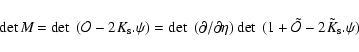
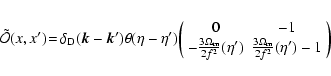
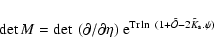
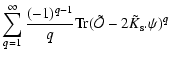
![\begin{displaymath}S[\psi,\lambda] = \lambda.({\cal O}.\psi-K_{\rm s}.\psi\psi)
- \frac{1}{2}\lambda.\Delta_i.\lambda.
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img139.gif)
![\begin{displaymath}Z_N[j,h] = \int [{\rm d}\psi] [{\rm d}\lambda] \; {\rm e}^{N[j.\psi+h.\lambda-S[\psi,\lambda]]}
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img146.gif)
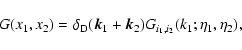
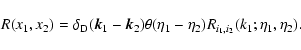
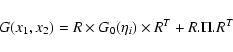
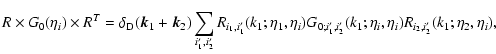
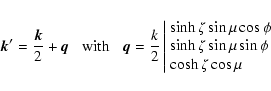
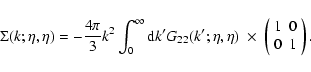
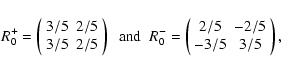
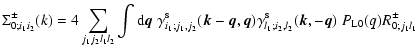
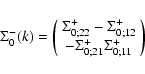
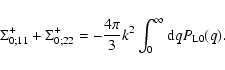
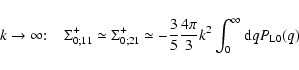
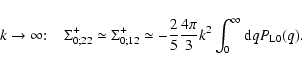
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.4cm,clip]{6832f1.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg212.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.6cm,clip]{6832f2.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg216.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.6cm,clip]{6832f3.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg218.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,height=6.4cm,clip]{6832f4.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg221.gif)
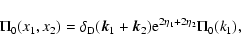
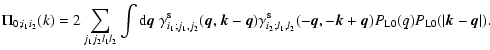
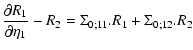
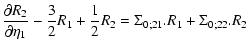
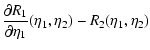
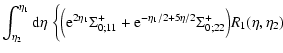
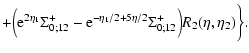
![$\displaystyle \frac{\partial^3 R_1}{\partial\eta_1^3} - \frac{3}{2} \frac{\part...
...} + \frac{5}{2} \Sigma_{0;11}^+ R_1 + \frac{5}{2} \Sigma_{0;12}^+ R_2 \right] .$](/articles/aa/full/2007/15/aa6832-06/img234.gif)
![$\displaystyle \frac{\partial^3 R_2}{\partial\eta_1^3} - \frac{3}{2} \frac{\part...
...} + \frac{5}{2} \Sigma_{0;21}^+ R_1 + \frac{5}{2} \Sigma_{0;22}^+ R_2 \right] .$](/articles/aa/full/2007/15/aa6832-06/img235.gif)
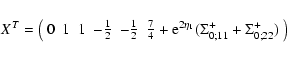
![\begin{figure}
\par\includegraphics[width=8cm,height=7.4cm,clip]{6832f5.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg241.gif)
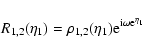
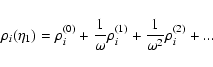
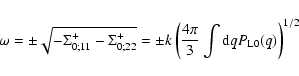
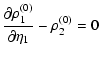
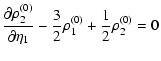
![\begin{figure}
\par\includegraphics[width=8cm,height=7.4cm,clip]{6832f6.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg261.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f7.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg262.gif)
![\begin{figure}
\par\includegraphics[width=8cm,height=7.3cm,clip]{6832f8.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg263.gif)
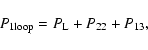
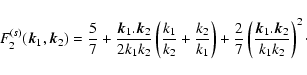
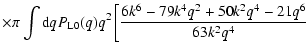
![$\displaystyle + \left. \frac{(q^2-k^2)^3(7q^2+2k^2)}{42k^3q^5}
\ln\left\vert\frac{k+q}{k-q}\right\vert \right] \cdot$](/articles/aa/full/2007/15/aa6832-06/img277.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f9.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg286.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f10.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg287.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f11.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg288.gif)
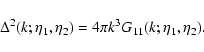
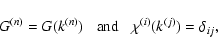
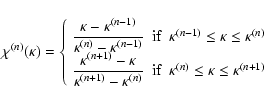
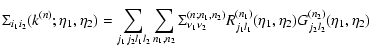
![\begin{figure}
\par\includegraphics[width=8cm,height=7.2cm,clip]{6832f12.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg351.gif)
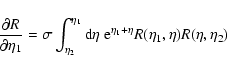

![\begin{displaymath}R(a_1,a_2) = \cos~[\omega(a_1-a_2)] \;\;\; \mbox{with}
\;\;\; \omega= \sqrt{-\sigma} .
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img361.gif)
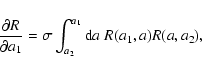
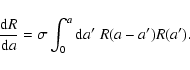
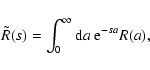
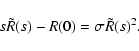
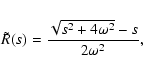
![\begin{displaymath}R(a_1,a_2)= \frac{J_1[2\omega(a_1-a_2)]}{\omega(a_1-a_2)} ,
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img371.gif)
![\begin{figure}
\par\includegraphics[width=8cm,height=7.2cm,clip]{6832f13.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg378.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f14.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg379.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6832f15.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg380.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6832f16.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg381.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f17.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg382.gif)
}{k^2 \vert{\vec k}-{\vec q}\vert^2}$](/articles/aa/full/2007/15/aa6832-06/img386.gif)
![$\displaystyle - R_{12}(q) G_{22}(\vert{\vec k}-{\vec q}\vert) \frac{[{\vec k}.({\vec k}-{\vec q})]^2 q^2}{k^2 \vert{\vec k}-{\vec q}\vert^4}$](/articles/aa/full/2007/15/aa6832-06/img387.gif)
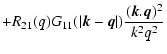
![$\displaystyle - R_{22}(q) G_{12}(\vert{\vec k}-{\vec q}\vert)
\frac{({\vec k}.{...
...\vec k}.({\vec k}-{\vec q})]}{k^2 \vert{\vec k}-{\vec q}\vert^2} \biggl \rbrace$](/articles/aa/full/2007/15/aa6832-06/img389.gif)
![\begin{displaymath}S_{12}({\vec q}) \sim \frac{({\vec k}.{\vec q})^2}{k^2q^2}
[ R_{21} G_{11} + R_{22} G_{12} - R_{11} G_{21} - R_{12} G_{22}] .
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img391.gif)

![\begin{figure}
\par\includegraphics[width=8cm,height=7.4cm,clip]{6832f18.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg404.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f19.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg405.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f20.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg406.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f21.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg411.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.5cm,clip]{6832f22.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg412.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f23.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg413.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f24.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg414.gif)
![\begin{displaymath}R_{\rm app}(x_1,x_2)= R_{\rm L}(x_1,x_2) \cos~[\omega(k)(a_1-a_2)] ,
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img417.gif)
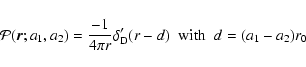
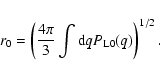
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f25.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg436.gif)
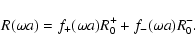
![\begin{displaymath}f_+(x)= \int_0^1 {\rm d}t \; \cos~[x(1-t)] = \frac{\sin~(x)}{x}
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img440.gif)
![$\displaystyle f_-(x) = \int_0^1 {\rm d}t \; t^{5/2} \cos~[x(1-t)] = \frac{5}{2x...
.../2}} \left[ \cos~(x) S(\!\sqrt{2x/\pi})
- \sin~(x) C(\!\sqrt{2x/\pi}) \right] ,$](/articles/aa/full/2007/15/aa6832-06/img441.gif)
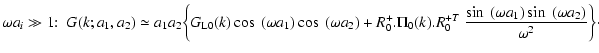
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f26.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg447.gif)
![\begin{displaymath}R_{\rm app}(x_1,x_2)= R_{\rm L}(x_1,x_2) \frac{J_1[2\omega(k)(a_1-a_2)]}
{\omega(k)(a_1-a_2)}\cdot
\end{displaymath}](/articles/aa/full/2007/15/aa6832-06/img451.gif)
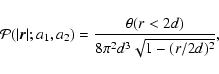
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f27.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg456.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f28.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg457.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f29.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg460.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f30.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg461.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f31.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg462.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f32.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg463.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f33.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg464.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f34.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg471.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f35.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg472.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f36.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg474.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f37.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg475.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f38.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg476.gif)
![\begin{figure}
\par\includegraphics[width=7cm,height=6.2cm,clip]{6832f39.ps}\end{figure}](/articles/aa/full/2007/15/aa6832-06/Timg477.gif)