A&A 465, 1035-1040 (2007)
DOI: 10.1051/0004-6361:20065424
S. Ko![]() omanski
omanski
Instytut Astronomiczny Uniwersytetu Wroc![]() awskiego, Kopernika 11, 51-622 Wroc
awskiego, Kopernika 11, 51-622 Wroc![]() aw, Poland
aw, Poland
Received 12 April 2006 / Accepted 20 December 2006
Abstract
Aims. We analyse three well-observed long-duration arcade flares (LDAFs) to find their general properties. Results concerning energy release in LDAFs (energy balance and diagnostic diagrams) are shown.
Methods. Yohkoh observations and Kitt Peak Vacuum Telescope magnetograms are used to determine physical parameters of flare loop-top kernels (temperature, density, altitude). Using these parameters the energy release is studied in detail.
Results. We found that: (1) the energy release in LDAFs occurs during their whole decay phase; (2) the kernel heating (![]() )
is of the order of 0.01-1 erg cm-3 s-1; (3) the kernels usually cannot be distinguished in SXT images when
)
is of the order of 0.01-1 erg cm-3 s-1; (3) the kernels usually cannot be distinguished in SXT images when ![]() is drops below a particular value. This value depends on the altitude of the kernels.
is drops below a particular value. This value depends on the altitude of the kernels.
Key words: Sun: corona - Sun: flares - Sun: X-rays, gamma rays
Long-duration arcade flares (LDAFs) are very interesting phenomena. This type of solar flare is characterized, like all long-duration events (LDE), by a slow decrease of brightness in soft X-rays (SXR) lasting for many hours. The second characteristic feature of these flares is their morphology. A typical LDAF consists of several loops which form an arcade with bright emission kernels placed at the tops of the loops (loop-top kernels). Analysis of SXR images indicates that the kernels may be connected by a magnetic tube (so-called arcade channel; see Jakimiec et al. 1997; Tomczak 1994 and Ko![]() omanski 2007 (Paper I)).
omanski 2007 (Paper I)).
LDAFs have more a complicated structure than compact flares. Nevertheless, their investigation can help us in better understanding the physics of flaring structures. Detailed analysis of satellite observations carried out by many authors has led to several important results (e.g. Sheeley et al. 1975; Kahler et al. 1977; Feldman et al. 1995; Harra-Murnion et al. 1998; Shibasaki 2002). One of the most important conclusions is that continuous energy release and plasma heating must exist during the LDAF decay phase to ensure the long duration of their loop-top kernels in spite of radiative and conductive losses (Vorpahl et al. 1977). Czaykowska et al. (1999) found that during the decay phase of LDAFs chromospheric evaporation occurs, indicating that the reconnection and heating processes must take place during that phase. In Isobe et al. (2002) LDAF of 12 May 1997 was analysed. The authors estimated the energy release rate for the decay phase of the flare a as whole, but excellent Yohkoh observations allow the investigation of heating of individual kernels. Depending on the flare model the energy release takes place inside the kernels (Jakimiec 2002a,b) or above the kernels (e.g. Kopp & Pneuman 1976; Shibata 1999; Hirose et al. 2001). In the second model the primary energy release site is difficult to observe. Thus, the detailed investigation of kernel heating allows us to study the magnetic energy release during the decay phase and helps us to understand the reconnection process. Recently in Bak-Steslicka & Jakimiec (2005) several LDEs with slow rise phase (so-called slow LDEs) were investigated. The authors estimated kernel heating rates for the rise phase.
Table 1: Analysed LDAFs - data from GOES/SEM database.
We present the analysis of three LDAFs well observed by Yohkoh. In a previous paper (Paper I) we investigated the morphological properties and physical parameters of these flares. In this paper we concentrate on the energy release during the decay phase. Methods that we used allow us to investigate the heating rates of loop-top kernels. These methods are described in Sect. 2. Results of the investigation are shown in Sect. 3. Conclusions are given in Sect. 4.
Basic information about the selected LDAFs are given in Table 1. To analyse the flares we applied observations made by Yohkoh SXT and HXT telescopes and the Kitt Peak Vacuum Telescope (KPVT). Values of parameters necessary for the energy release estimation (temperature T, density N, altitude h) were presented in Paper I. The estimation can be made in two ways. In the first method temperature-density (T-N) diagnostic diagrams are used. The second one concerns the energy balance calculation. Both methods were used to analyse the selected LDAFs. Below we describe them.
The method of investigation of flare evolution in temperature-density diagrams was worked out by Jakimiec et al. (1986, 1987, 1992) and Sylwester et al. (1993). It was shown that temporal evolution of flares does not depend much on their morphology. Thus, the diagrams allow us to qualitatively study temporal changes of the energy release in flares.
The flare evolution in T-N diagrams is described in detail in Jakimiec et al. (1992). We present here only the description of the decay phase. Figure 1 shows an example of a T-N diagram computed for two different energy release decay-times. Evolution of a flare during the decay phase depends on how fast the heating rate
![]() decreases.
decreases.
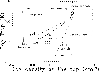 |
Figure 1:
Computed T-N diagram illustrating the dependence of the decay phase on energy release decay-time. The S-S line is defined by the relation between T and N for steady-state loops with a given length. The thermodynamic decay time
|
| Open with DEXTER | |
The inclination ![]() of the decay-phase branch is defined as:
of the decay-phase branch is defined as:
 |
Figure 2:
Schematic N-T diagram showing effect of a changing flaring loop length on the QSS evolution. Flares with a larger and constant L (L1, L2, L3) lie higher on the T-N diagram than those with a shorter L. In most cases L increases with time and simultaneously N decreases. In such case a flare evolves along the branch with an inclination smaller than 0.5. In the figure an example for which
|
| Open with DEXTER | |
The second factor affecting the QSS branch inclination has an instrumental background. It was shown in Paper I that LDAFs kernels are multithermal during the decay phase. Because the SXT temperature diagnostics is more sensitive to cooler plasma (see Jakimiec et al. 1998), the temperature changes ![]() are underestimated and hence the emission measure changes
are underestimated and hence the emission measure changes
![]() as well as the electron density changes
as well as the electron density changes ![]() are overestimated. Together this leads to a significant underestimation of the inclination
are overestimated. Together this leads to a significant underestimation of the inclination ![]() .
This effect is confirmed when one compares the temperature obtained from the Al12/Al.1 diagnostics with the temperature obtained from the Be119/Al12 diagnostics. The first diagnostics gives systematically lower temperatures and smaller inclination
.
This effect is confirmed when one compares the temperature obtained from the Al12/Al.1 diagnostics with the temperature obtained from the Be119/Al12 diagnostics. The first diagnostics gives systematically lower temperatures and smaller inclination ![]() than Be119/Al12 diagnostics (see Fig. 3), which is in agreement with the fact that the Al.1 intensities are more sensitive to cooler plasma than Be119 intensities (see Fig. 9 in Tsuneta et al. 1991).
than Be119/Al12 diagnostics (see Fig. 3), which is in agreement with the fact that the Al.1 intensities are more sensitive to cooler plasma than Be119 intensities (see Fig. 9 in Tsuneta et al. 1991).
 |
Figure 3: The temperature-density diagnostic diagram for the decay phase of the 27 April 1998 flare. The N and T values were obtained from the Be119/Al12 (squares) and Al12/Al.1 (triangles) diagnostics. |
| Open with DEXTER | |
Due to the above-mentioned factors we can expect that the observed inclination ![]() for the QSS evolution in the T-N diagram might be significantly smaller than the theoretical value of 0.5.
for the QSS evolution in the T-N diagram might be significantly smaller than the theoretical value of 0.5.
The energy balance of a loop-top kernel during the decay phase can be written as follows:
The Eq. (4) allows us to calculate upper and lower limits for the heating rate. The upper limit
![]() is calculated directly from Eq. (4). However sometimes loops connecting a kernel with the chromosphere are faint. The low intensity of these loops suggests that the energy flow might be reduced e.g. due to their filamentary structure (see Jakimiec et al. 1998). Therefore the lower limit of heating rate
is calculated directly from Eq. (4). However sometimes loops connecting a kernel with the chromosphere are faint. The low intensity of these loops suggests that the energy flow might be reduced e.g. due to their filamentary structure (see Jakimiec et al. 1998). Therefore the lower limit of heating rate
![]() is obtained under the assumption
is obtained under the assumption
![]() .
The relative error of
.
The relative error of ![]() is about 30-40 per cent.
is about 30-40 per cent.
For all analysed kernels we use values of parameters (T and N) obtained from fluxes measured in the Al.1 and Al12 filters (the ratio Al12/Al.1 will be called the Al12 diagnostics). It was shown in Paper I that the Al12 diagnostics gives lower temperatures for analysed kernels than the Be119 diagnostics (from the ratio of fluxes measured in the filters Be119 and Al12). This means that the mean temperature of kernels taken from the Al12 diagnostics is significantly underestimated. This fact affects the energy balance calculation. The Be119 diagnostics also underestimates the temperature, but not so much (the Be119 diagnostics is not very sensitive to 20 MK plasma (see Jakimiec et al. 1998)). Because of this it would be better to use the Be119 diagnostics. Unfortunately, the Be119 images are usually available only for the rise and maximum phases of flares evolution. Thus, we decided to calculate the energy balance with T and N taken from the Al12 diagnostics. This approach allows us to study the almost entire decay phase of LDAFs, but we must estimate how this diagnostics affects the values
![]() and
and
![]() :
:
![\begin{figure}
\par\includegraphics[width=17cm,clip]{5424fig4.eps}\end{figure}](/articles/aa/full/2007/15/aa5424-06/Timg48.gif) |
Figure 4: Yohkoh/SXT images in the Al12 filter for the analysed LDAFs. In each image the heliographical grid and the magnetic field configuration taken from the Kitt Peak magnetogram are overlaid (light-grey line: +5 Gs, dark-grey line: -5 Gs). |
| Open with DEXTER | |
In this subsection we give a short description of the selected flares morphology. A more comprehensive presentation was given in Paper I.
The LDAF of 7 May 1993 occurred in the NOAA AR 7500 at the N14E41. The flare began at 20:30 UT and reached its maximum (M1.6) 50 min later. The decay phase of the flare lasted about 6 h. Four loop-top kernels (A, B, C and D) were observed during the decay phase of the flare (see Fig. 4a).
The 14 May 1993 flare occurred at the N19W48, in the same active region as the 7 May 1993 flare. It began at 21:55 UT and had two maxima. The first one (M1.4) was at 22:05 UT, then the SXR flux decreased until 22:26 UT. The second, higher maximum (M4.4) was reached at 22:58 UT. After that the flare flux decreased for about 8 h. Yohkoh/SXT images show that both maxima occurred in the same flare. The flare has four loop-top kernels (A, B, C and D; see Fig. 4b). The kernels B and C were not well separated and this is why they were analysed as one structure (the kernel B+C).
The X1.0 flare of 27 April 1998 occurred in the NOAA AR 8210 at the S16E50. The flare began at 8:36 UT and was preceded by a slow increase of the soft X-ray. After the flare maximum, which was at 9:20 UT, the SXR flux very slowly decreased for about 20 h. In the SXT images we can see two kernels (A and B) during the early decay phase (see Fig. 4c). Later, after 15 UT, the kernels disappeared and we see in the images a bright structure which connected the tops of arcade loops. The structure is called "the whole arcade channel'' in Fig. 7.
The T-N diagrams for all kernels are shown in Figs. 5-7. Gaps in the decay-phase branches are caused by satellite nights. The inclination
![]() of these branches are presented in Tables A.1-A.3. The tables give also values of the term
of these branches are presented in Tables A.1-A.3. The tables give also values of the term
![]() and values of
and values of ![]() for the QSS branch corrected on a flaring loop length increase (
for the QSS branch corrected on a flaring loop length increase (
![]() ). The results of energy balance calculations for kernels are given in Tables A.4-A.6.
). The results of energy balance calculations for kernels are given in Tables A.4-A.6.
Kernels belonging to one flare might be in the different stages of evolution at a given time. For example, while the kernel A of the 7 May flare was on the decay branch, the kernel D was at its ![]() maximum. Moreover, in some cases there are significant differences in
maximum. Moreover, in some cases there are significant differences in ![]() between kernels of a given flare (see Tables A.4-A.6). These two results may suggest that reconnection is not uniform along the flaring arcade. This conclusion is supported by the morphology (see Paper I). In the case of the 14 May 1993 LDAF, kernels appeared and disappeared sequentially. It looks as if the reconnection developed progressively along the arcade.
between kernels of a given flare (see Tables A.4-A.6). These two results may suggest that reconnection is not uniform along the flaring arcade. This conclusion is supported by the morphology (see Paper I). In the case of the 14 May 1993 LDAF, kernels appeared and disappeared sequentially. It looks as if the reconnection developed progressively along the arcade.
In many cases the inclination of the decay-phase branch was not constant and might change significantly over a short time. In some cases this behavior can be explained as a result of the change in the upward motion velocity of a kernel (see kernel B+C before and after 3:00 UT, Table A.2). However in most cases this explanation is not sufficient and we can expect that "bends'' in the decay branch are due to some changes in the reconnection rate.
 |
Figure 5: T-N diagnostic diagram for the decay phase of the 7 May 1993 flare kernels. The evolution runs as the arrow indicates and then from the right to the left. |
| Open with DEXTER | |
 |
Figure 6: The same as Fig. 5 but for kernels of the 14 May 1993 flare. |
| Open with DEXTER | |
 |
Figure 7: The same as Fig. 5 but for kernels of the 27 April 1998 flare. |
| Open with DEXTER | |
The value of ![]() is smaller than 0.3 for all analysed kernels. Cases with
is smaller than 0.3 for all analysed kernels. Cases with
![]() are not rare. Such a situation may appear in the early and late decay phase as well. Comparison between the observed inclinations
are not rare. Such a situation may appear in the early and late decay phase as well. Comparison between the observed inclinations
![]() and the QSS inclination corrected on the loop length increase (
and the QSS inclination corrected on the loop length increase (
![]() )
shows that the first ones are always smaller. This indicates that the kernels were heated during the whole decay phase, which suggests continuous energy release with e-folding decay time
)
shows that the first ones are always smaller. This indicates that the kernels were heated during the whole decay phase, which suggests continuous energy release with e-folding decay time ![]() longer than thermodynamic decay time
longer than thermodynamic decay time
![]() .
This is confirmed by calculations. Estimated
.
This is confirmed by calculations. Estimated ![]() for the kernels are in the range of 3000-7000 s and are several times larger than
for the kernels are in the range of 3000-7000 s and are several times larger than
![]() .
In some cases differences between
.
In some cases differences between
![]() and
and
![]() are too large to be explained by the instrumental effect described in Sect. 2.1, especially when
are too large to be explained by the instrumental effect described in Sect. 2.1, especially when
![]() .
In the paper of Jakimiec et al. (2005) this behavior (so-called below-the-QSS evolution) is explained as being the result of specific evolution of
.
In the paper of Jakimiec et al. (2005) this behavior (so-called below-the-QSS evolution) is explained as being the result of specific evolution of ![]() .
.
The calculated energy balance for LDAFs kernels indicates that kernels were heated during their whole decay phase. Values of ![]() are small (smaller than 1 erg cm-3 s-1) but even the lower limit of the heating rate
are small (smaller than 1 erg cm-3 s-1) but even the lower limit of the heating rate
![]() is not zero. This proves that there is energy release during this phase in LDAFs. These results are similar to those obtained by Isobe et al. (2002) and Bak-Steslicka & Jakimiec (2005). Calculated heating rates decreased very slowly with time. This confirm conclusions derived from the T-N diagrams.
is not zero. This proves that there is energy release during this phase in LDAFs. These results are similar to those obtained by Isobe et al. (2002) and Bak-Steslicka & Jakimiec (2005). Calculated heating rates decreased very slowly with time. This confirm conclusions derived from the T-N diagrams.
A very interesting result of our investigation is that the kernels cannot be distinguished in SXT images when ![]() drops below a particular value. This value seems to depend on the altitude (or loop semilength; see Fig. 8). This suggests that at a given altitude above the photosphere, loop-top kernels cannot exist and flaring loops become more uniformly bright when the heating/energy release rate drops below a particular value. The higher the altitude of a kernel the lower the rate of heating necessary to support the kernel existence. This relation can be easily explained. From Tables A.4-A.6 we see that
drops below a particular value. This value seems to depend on the altitude (or loop semilength; see Fig. 8). This suggests that at a given altitude above the photosphere, loop-top kernels cannot exist and flaring loops become more uniformly bright when the heating/energy release rate drops below a particular value. The higher the altitude of a kernel the lower the rate of heating necessary to support the kernel existence. This relation can be easily explained. From Tables A.4-A.6 we see that
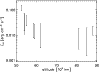 |
Figure 8:
Relation between the altitude and heating rate |
| Open with DEXTER | |
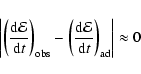 |
(5) |
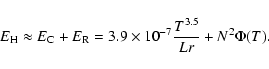 |
(6) |
Acknowledgements
I thank the Yohkoh and KPVT teams for the excellent observations and Prof. J. Jakimiec and Prof. M. Tomczak for discussions and reviewing of this manuscript.
Table A.1: Evolution during the decay phase for the 7 May 1993 flare.
Table A.2: Evolution during the decay phase for the 14 May 1993 flare.
Table A.3: Evolution during the decay phase for the 27 April 1993 flare.
Table A.4: Energy balance for the kernels of the 7 May 1993 flare.
Table A.5: Energy balance for the kernels of the 14 May 1993 flare.
Table A.6: Energy balance for the kernels of the 27 April 1998 flare.