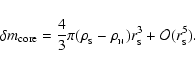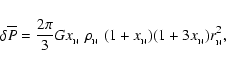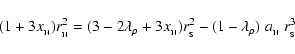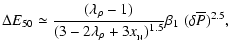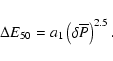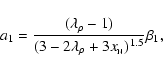A&A 465, 533-539 (2007)
DOI: 10.1051/0004-6361:20066515
Energy release associated with a first-order phase transition in a rotating
neutron star core
J. L. Zdunik1 -
M. Bejger1,2 -
P. Haensel1 -
E. Gourgoulhon2
1 - N. Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
2 - LUTH, UMR 8102 du CNRS, Observatoire de Paris, 92195 Meudon Cedex, France
Received 6 October 2006 / Accepted 2 January 2007
Abstract
Aims. We calculate energy release associated with a first order phase transition at the center of a rotating neutron star. This quantity is equal to the difference in mass-energies between the initial normal phase configuration and the final configuration containing a superdense matter core, with total baryon number and angular momentum kept constant.
Methods. The calculations of the energy release are based on precise numerical 2D calculations, in which both the polytropic equations of state (EOS) as well as realistic EOS of the normal phase are used. Presented results are obtained for a broad range of metastability of initial configuration and size of the new superdense phase core in the final configuration. When the equatorial radius of the dense core of the superdense phase is much smaller than the stellar equatorial radius, analytical expressions for the energy release are obtained.
Results. For a fixed "overpressure'',
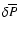 ,
defined as the relative excess of central pressure of a collapsing metastable star over the pressure of the equilibrium first-order phase transition, the energy release
,
defined as the relative excess of central pressure of a collapsing metastable star over the pressure of the equilibrium first-order phase transition, the energy release 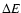 remarkably does not depend on the stellar angular momentum and coincides with that for nonrotating stars with the same
remarkably does not depend on the stellar angular momentum and coincides with that for nonrotating stars with the same
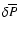 .
The energy release is proportional to
.
The energy release is proportional to
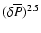 for small
for small
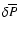 ,
when sufficiently precise brute force 2D numerical calculations are not possible. At higher
,
when sufficiently precise brute force 2D numerical calculations are not possible. At higher
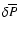 ,
results of 1D calculations of
,
results of 1D calculations of
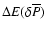 for non-rotating stars are shown to reproduce, with very high precision, the exact 2D results for rotating stars.
for non-rotating stars are shown to reproduce, with very high precision, the exact 2D results for rotating stars.
Key words: dense matter - equation of state - stars: neutron - stars: rotation
1 Introduction
One of the intriguing predictions of some theories of dense matter
in neutron-star cores is a phase
transition into an "exotic'' state (i.e., not observed in the
laboratory). Theoretical predictions include boson
condensation of pions and kaons, and deconfinement of quarks
(see, e.g., Glendenning 2000; Weber 1999).
First-order phase transitions accompanied by discontinuities in the
thermodynamical potential densities, are the most interesting
as far as the structure and dynamics of neutron stars are
concerned. In the simplest case, one
considers states consisting of one pure phase. Because of the high
degeneracy of matter constituents, effects of temperature are
neglected. In thermodynamic equilibrium, the phase transition
occurs at a well defined pressure P0, and is
accompanied by a density jump at the phase interface.
A first-order phase transition allows for a metastability of
the pure "normal'' (lower density) phase at P>P0.
Consequently, a metastable core could form during neutron-star
evolution in which central pressure increases, due to
accretion or spin-down. Then, nucleation of the exotic (higher
density) phase implies formation of a core of the exotic
phase and is accompanied by a core-quake and energy release. A theory
that enables one to calculate the changes in stellar
parameters implied by a first-order phase transition in a non-rotating neutron star was developed by Haensel et al. (1986) and Zdunik et al. (1987) (an earlier Newtonian theory was presented by Schaeffer et al. 1983, see also Diaz Alonso 1983). The energy released in a corequake was shown to depend strongly on the size of the dense phase core, the leading term
being proportional to the fifth power of this core radius.
In the present paper we calculate the energy release due to a phase transition in a rotating neutron star. Our theory is
based on 2D simulations and is much closer to reality
than the 1D theory developed in Haensel et al. (1986) and Zdunik
et al. (1987). In the real world, evolutionary processes that lead
to the increase of the central density in neutron star
(accretion, slowing-down), as well as the collapse itself, all occur
in a rotating star. Of course, the 2D calculations are
incomparably more difficult than the 1D ones. However, as we
show in the present paper, when suitably parametrized, the
energy released during a corequake
depends only on the excess of the central pressure of
the metastable configuration over P0, being to a good
approximation independent of the
angular momentum of the collapsing star.
In the present paper we restrict ourselves to the case when
the radius of the core of the new phase is much smaller than the
stellar radius, and the typical energy release will be
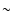 1050 erg. This is to be contrasted with a strong
phase transition, considered in relation to long gamma-ray
bursts at cosmological distances, where the core radius is
a sizable fraction of the stellar radius and energy release
1050 erg. This is to be contrasted with a strong
phase transition, considered in relation to long gamma-ray
bursts at cosmological distances, where the core radius is
a sizable fraction of the stellar radius and energy release
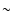 1052-1053 erg (see, e.g., Berezhiani et al. 2003).
1052-1053 erg (see, e.g., Berezhiani et al. 2003).
The paper is organized in the following way. In Sect. 2
we introduce notations and describe general properties of the first-order
phase transitions in the stellar core with particular emphasis on
the metastability and instability of neutron star cores.
Analytic considerations, concerning the response of a star to
a first-order phase transition at its center, and in particular,
the calculation within the linear response approximation
of the energy release associated with such a transition, are presented in
Sect. 4. Analytic models of the EOSs with first-order phase
transitions, allowing for very precise 2D calculations, are
considered in Sect. 3.1, where we derive generic
properties of the energy release due to a first order phase transition
at the center of a rotating star. In Sect. 3.2
we present our results obtained for a realistic EOS of normal
phase, and we confirm remarkable properties of the
energy-overpressure relation, obtained in the previous
section. In Sect. 5 we present
practical formulae suitable for the calculation of energy
release associated with a first order phase transition at the
center of a rotating neutron star. Finally, Sect. 6 contains discussion of our results and several examples of the application of our formula for the energy
release.
2 EOS with a first order phase transition
Let us consider a general case of a first-order phase transition
between the N (normal) and S (superdense) phases
of dense matter. At densities under consideration, all constituents
of matter are strongly degenerate, and the temperature dependence
of pressure and energy density can be neglected.
At a given baryon density, 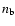 ,
the energy density of
the N-phase of matter (including rest energies of particles that
are matter constituents) is
,
the energy density of
the N-phase of matter (including rest energies of particles that
are matter constituents) is
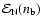 and pressure
and pressure
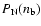 .
The baryon chemical potential = enthalpy per baryon in the
N phase is
.
The baryon chemical potential = enthalpy per baryon in the
N phase is
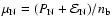 .
Similarly, one can calculate thermodynamic quantities for
the S-phase.
.
Similarly, one can calculate thermodynamic quantities for
the S-phase.
The local pressure P is a proper thermodynamic variable, continuous and monotonous in
the stellar interior. The equilibrium
state of the matter at a given P is realized at the minimum of
enthalpy per baryon. For P<P0, this minimum is realized by
the N phase, and for P>P0 - by the S one. The value of P0 is obtained from the crossing condition
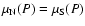 ,
which also yields the values of the
matter densities,
,
which also yields the values of the
matter densities,
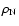 and
and
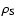 ,
and the
corresponding baryon densities,
,
and the
corresponding baryon densities, 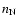 and
and 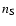 ,
at the N-S phase coexistence interface. These parameters are obtained
assuming thermodynamic equilibrium. A schematic plot of the EOS
of matter with a first order phase transition N-S, in the
vicinity of the phase transition point, is plotted in Fig. 1.
,
at the N-S phase coexistence interface. These parameters are obtained
assuming thermodynamic equilibrium. A schematic plot of the EOS
of matter with a first order phase transition N-S, in the
vicinity of the phase transition point, is plotted in Fig. 1.
The solid segment of the N-phase curve, in Fig. 1, corresponds to the stable N-phase state. For pressure above P0, the N phase becomes
metastable with respect to the conversion into the S phase.
The S phase can appear through the nucleation process - a spontaneous
formation of S-phase droplets. However, an energy barrier
resulting from the surface tension at the N-S interface delays
the nucleation for a time identified with a lifetime of the
metastable state
 .
The value of
.
The value of
 decreases sharply with P>P0, and drops to zero at some
decreases sharply with P>P0, and drops to zero at some
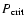 ,
where the energy barrier separating the S-state from
the N-state vanishes. For
,
where the energy barrier separating the S-state from
the N-state vanishes. For
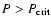 the N phase is simply
unstable and converts with no delay into the S phase.
the N phase is simply
unstable and converts with no delay into the S phase.
Consider a neutron star built of matter in the N phase.
Its central pressure 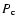 increases during spin-down or
accretion. A quasistatic compression of the N-phase core
moves matter into a metastable state with P>P0. A metastable core
of the N phase is bounded by a surface with P=P0. As soon
as the central compression timescale of
metastable core
increases during spin-down or
accretion. A quasistatic compression of the N-phase core
moves matter into a metastable state with P>P0. A metastable core
of the N phase is bounded by a surface with P=P0. As soon
as the central compression timescale of
metastable core
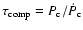 becomes equal
to
becomes equal
to
 ,
droplets of the S phase appear at the star center. This happens at central pressure
,
droplets of the S phase appear at the star center. This happens at central pressure
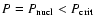 .
The S-phase droplets introduce
a pressure deficit, destabilize the metastable core and consequently, the whole
star. The S-phase core grows, and
the process of the N
.
The S-phase droplets introduce
a pressure deficit, destabilize the metastable core and consequently, the whole
star. The S-phase core grows, and
the process of the N
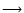 S phase transition proceeds until the
final hydrostatic equilibrium state is reached. In the final
state, a central core of the S-phase is bounded by an N-S coexistence
surface of constant pressure P0 on which the matter density undergoes a jump from
S phase transition proceeds until the
final hydrostatic equilibrium state is reached. In the final
state, a central core of the S-phase is bounded by an N-S coexistence
surface of constant pressure P0 on which the matter density undergoes a jump from
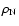 on the outer N-phase side to
on the outer N-phase side to
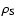 on the inner S-phase side.
on the inner S-phase side.
In the present paper we restrict ourselves to the case of the
density jump satisfying
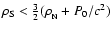 .
Therefore, stellar configurations with a core of
the S phase of arbitrarily small radius are stable (Seidov 1971;
see also Kaempfer 1981; and Zdunik et al. 1987).
The case of a strong first order phase transition with
.
Therefore, stellar configurations with a core of
the S phase of arbitrarily small radius are stable (Seidov 1971;
see also Kaempfer 1981; and Zdunik et al. 1987).
The case of a strong first order phase transition with
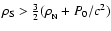 ,
when
configurations with a small S phase core are unstable
and collapse into those with a large S phase core,
will be presented in a separate paper.
,
when
configurations with a small S phase core are unstable
and collapse into those with a large S phase core,
will be presented in a separate paper.
![\begin{figure}
\par\includegraphics[width=7.25cm,clip]{6515fig1.eps}\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg51.gif) |
Figure 1:
A schematic representation, in the 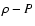 plane, of an EOS with a first order phase
transition. Solid segments: stable N and S phase
(in thermodynamic equilibrium). Dash-dot segment:
metastable N phase. The S phase nucleates at plane, of an EOS with a first order phase
transition. Solid segments: stable N and S phase
(in thermodynamic equilibrium). Dash-dot segment:
metastable N phase. The S phase nucleates at
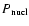 ,
which
depends on the temperature and the compression rate. At ,
which
depends on the temperature and the compression rate. At
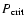 nucleation of the S phase is instantaneous, because the energy
barrier, separating the N phase from the S phase,
vanishes. nucleation of the S phase is instantaneous, because the energy
barrier, separating the N phase from the S phase,
vanishes. |
| Open with DEXTER |
The metastable stellar state of the N phase can be described by central overcompression - the fractional excess of density relative to
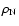 ,
,
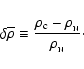 |
(1) |
Equivalently, we define a dimensionless central overpressure,
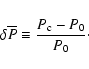 |
(2) |
Let us now consider the timescales and their interplay. First, there is a microscopic nucleation timescale
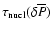 .
The time dependence
.
The time dependence
 results from a global
evolution of the neutron star and depends on the astrophysical
scenario of central compression; it will be characterized
by
results from a global
evolution of the neutron star and depends on the astrophysical
scenario of central compression; it will be characterized
by
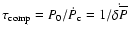 .
The time needed to compress matter in the center of the star
from P0 to
.
The time needed to compress matter in the center of the star
from P0 to 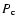 is, in a linear approximation, equal
to
is, in a linear approximation, equal
to
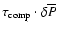 .
During this time the system remains in
a metastable state. In contrast, the functional dependence
.
During this time the system remains in
a metastable state. In contrast, the functional dependence
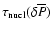 is given by the local dense matter microphysics and is a very sensitive function
of P, being very large for P close to P0 and dropping abruptly
above some pressure (see for example, Iida & Sato 1997).
As a result, the condition for the
time
is given by the local dense matter microphysics and is a very sensitive function
of P, being very large for P close to P0 and dropping abruptly
above some pressure (see for example, Iida & Sato 1997).
As a result, the condition for the
time
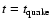 at which the metastable stellar
configuration collapses can be estimated by solving the equation:
at which the metastable stellar
configuration collapses can be estimated by solving the equation:
![\begin{displaymath}%
\tau_{\rm nucl}\left[\delta\overline{P}(t)\right]
=q\cdot\tau_{\rm comp} \cdot\delta\overline{P}
\end{displaymath}](/articles/aa/full/2007/14/aa6515-06/img59.gif) |
(3) |
where a small dimensionless coefficient q reflects the very steep character of the function
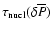 and is of the order
10-2-10-3 (details will be
presented in a forthcoming paper).
and is of the order
10-2-10-3 (details will be
presented in a forthcoming paper).
3 Calculation of the energy release
We restrict ourselves to axially symmetric, rigidly rotating neutron stars
in hydrostatic equilibrium. In what follows, by "radius'' we mean
a circumferential radius in an equatorial plane.
We assume that at a central pressure
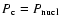 the nucleation of the S phase in an overcompressed core, of radius
the nucleation of the S phase in an overcompressed core, of radius
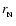 ,
of configuration
,
of configuration 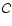 ,
initiates the
phase transition and formation of an S-phase core of radius
,
initiates the
phase transition and formation of an S-phase core of radius
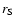 in a new configuration
in a new configuration
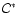 ,
as presented in Fig. 2. Transition to an S phase at the
core boundary, occurring at
,
as presented in Fig. 2. Transition to an S phase at the
core boundary, occurring at
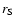 ,
is associated with a density
jump characterized by
,
is associated with a density
jump characterized by
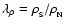 .
Because we are interested in relatively small S-phase cores, we will
approximate its EOS by a polytrope with the exponent
.
Because we are interested in relatively small S-phase cores, we will
approximate its EOS by a polytrope with the exponent
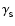 ,
equal to the adiabatic index
of the S phase at
,
equal to the adiabatic index
of the S phase at
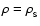 .
Of course, in reality the adiabatic index of
the S phase does depend on the density. However, for small cores the
polytropic EOS is an excellent approximation, and in the limit when
only leading terms in the
.
Of course, in reality the adiabatic index of
the S phase does depend on the density. However, for small cores the
polytropic EOS is an excellent approximation, and in the limit when
only leading terms in the
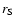 -expansion are kept, this
approximation becomes exact (Bejger et al. 2005).
-expansion are kept, this
approximation becomes exact (Bejger et al. 2005).
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{6515fig2.ps} %
\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg65.gif) |
Figure 2:
Transition from a one-phase configuration 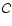 with a meta-stable core of radius
with a meta-stable core of radius
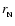 to a two-phase configuration
to a two-phase configuration
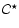 with S-phase core with a radius
with S-phase core with a radius 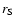 .
By "radius'' we mean an equatorial circumferential
radius. These two configurations have the same baryon number .
By "radius'' we mean an equatorial circumferential
radius. These two configurations have the same baryon number 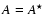 and total angular momentum and total angular momentum 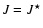 . . |
| Open with DEXTER |
Having a pair of EOSs, one with and one without a softening by phase transition, the next step is to compare the hydrostatic equilibria
of neutron stars corresponding to each of these EOSs. The
models that we calculate are rigidly rotating, axisymmetric
solutions of Einstein's equations.
The numerical computations have been performed
by means of a code built on the Lorene library
(http://www.lorene.obspm.fr), with an accuracy of 10-6 or better
measured using general relativistic virial theorems.
The neutron-star models can be labeled by the
central density
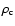 and rotational frequency
and rotational frequency
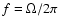 .
These parameters are natural from the point of view of numerical calculations (
.
These parameters are natural from the point of view of numerical calculations (
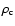 and f are input parameters in the numerical code).
But we can imagine another parametrization, more useful for other purposes.
For example, to study the stability
of rotating stars, the better choice is central density,
and f are input parameters in the numerical code).
But we can imagine another parametrization, more useful for other purposes.
For example, to study the stability
of rotating stars, the better choice is central density,
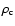 ,
and total angular momentum of the star, J.
,
and total angular momentum of the star, J.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6515fig3.eps} %
\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg68.gif) |
Figure 3:
Total baryon number A of the hydrostatic stellar
configuration versus central pressure 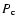 ,
at fixed stellar
angular momentum J, for the EOS depicted in Fig. 1. The solid line
denotes stable states, dash-dot line - the states that are
meta-stable with respect to the N ,
at fixed stellar
angular momentum J, for the EOS depicted in Fig. 1. The solid line
denotes stable states, dash-dot line - the states that are
meta-stable with respect to the N
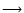 S transition.
For a central pressure S transition.
For a central pressure
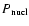 the S-phase nucleates in the super-compressed core of
configuration
the S-phase nucleates in the super-compressed core of
configuration 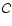 ,
and this results in a transition ,
and this results in a transition
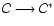 into a stable configuration with
a S-phase core and central pressure
into a stable configuration with
a S-phase core and central pressure
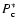 .
Both
configurations .
Both
configurations 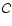 and
and
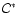 have the same baryonnumber A.
have the same baryonnumber A. |
| Open with DEXTER |
Below
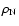 ,
the EOS for two cases (with and without phase transition)
is the same. For the problem of non-rotating stars, considered two decades ago (Haensel et al. 1986; Zdunik et al. 1987), the configuration with
,
the EOS for two cases (with and without phase transition)
is the same. For the problem of non-rotating stars, considered two decades ago (Haensel et al. 1986; Zdunik et al. 1987), the configuration with
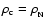 was denoted by
was denoted by
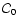 ,
and treated as a "reference configuration''.
Configurations
,
and treated as a "reference configuration''.
Configurations
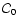 ,
,
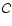 ,
and
,
and
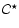 are depicted in the
are depicted in the
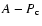 plane in Fig. 3. The radius, gravitational mass,
and the total baryon number of
plane in Fig. 3. The radius, gravitational mass,
and the total baryon number of
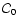 will be denoted by R0, M0, and A0.
For rotating stars we do not have one "reference configuration'' but a set of "reference
configurations'' which depend on rotation rate
will be denoted by R0, M0, and A0.
For rotating stars we do not have one "reference configuration'' but a set of "reference
configurations'' which depend on rotation rate
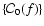 or total angular momentum
or total angular momentum
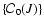 of the initial metastable configuration. As discussed in Sect. 2, there also exists a set of
configurations resulting from the
metastability of the matter in N phase. The maximum central
pressure which can be reached in the N-phase star is defined
by the value
of the initial metastable configuration. As discussed in Sect. 2, there also exists a set of
configurations resulting from the
metastability of the matter in N phase. The maximum central
pressure which can be reached in the N-phase star is defined
by the value
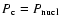 .
For
.
For
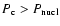 ,
the phase transition in the center of the star takes
place on a timescale much shorter than time of the stellar
evolution (accretion or spin down). Thus the "critical
line'' defined by the condition
,
the phase transition in the center of the star takes
place on a timescale much shorter than time of the stellar
evolution (accretion or spin down). Thus the "critical
line'' defined by the condition
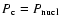 corresponds to the configurations for which nucleation in the
center triggers a collapse of the whole star and a corequake.
From the astrophysical point of view, the phase transition in the center followed by a corequake takes place at a point on a "critical line''.
Consequently, "normalization'' of results with respect to
parameters of the "reference configuration'' is more
complicated than in the case of non-rotating stars. There are many
possibilities to define the "reference configuration'' for a star
with a metastable core (
corresponds to the configurations for which nucleation in the
center triggers a collapse of the whole star and a corequake.
From the astrophysical point of view, the phase transition in the center followed by a corequake takes place at a point on a "critical line''.
Consequently, "normalization'' of results with respect to
parameters of the "reference configuration'' is more
complicated than in the case of non-rotating stars. There are many
possibilities to define the "reference configuration'' for a star
with a metastable core (
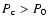 ), rotating with
frequency f and possessing a total angular momentum J and total
baryon number A. Such a "reference configuration'' should be defined as the
configuration with the central pressure equal to
), rotating with
frequency f and possessing a total angular momentum J and total
baryon number A. Such a "reference configuration'' should be defined as the
configuration with the central pressure equal to 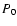 ,
as shown in Fig. 3.
However, we can choose either a reference configuration star with the
same J or the same fas that of the collapsing metastable configuration
,
as shown in Fig. 3.
However, we can choose either a reference configuration star with the
same J or the same fas that of the collapsing metastable configuration 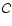 .
In fact,
to reach the metastable configuration
with
.
In fact,
to reach the metastable configuration
with
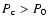 ,
we have to cross the "reference
line'' at the point defined by the evolutionary process leading to the instability.
Properties of the "critical line'' and "reference line'' in
the space of rotating configurations of slowing down or
accreting neutron stars will be analyzed in more detail in a forthcoming paper.
,
we have to cross the "reference
line'' at the point defined by the evolutionary process leading to the instability.
Properties of the "critical line'' and "reference line'' in
the space of rotating configurations of slowing down or
accreting neutron stars will be analyzed in more detail in a forthcoming paper.
We additionally assume that the transition of the star from a one-phase configuration to the
configuration with a small dense core of S phase, takes place at fixed baryon
number A (no matter ejection) and fixed total angular momentum of the star J(radiation loss of J neglected).
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{6515fig4.eps}\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg79.gif) |
Figure 4:
The energy release due to the corequake of
rotating neutron star as a function of the dimensionless
equatorial radius of the new phase core,
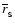 .
Different curves
correspond to the different values of total angular momentum of
rotating star, fixed along each curve, .
Different curves
correspond to the different values of total angular momentum of
rotating star, fixed along each curve,
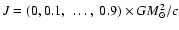 ,
from the bottom curve to the top curve. ,
from the bottom curve to the top curve. |
| Open with DEXTER |
The energy release during transition
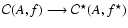 is calculated from the change of the stellar mass-energy
during this process,
is calculated from the change of the stellar mass-energy
during this process,
![\begin{displaymath}%
\Delta E=\left[M({\cal C })-M({\cal C}^\star)\right]_{A,J}c^2.
\end{displaymath}](/articles/aa/full/2007/14/aa6515-06/img81.gif) |
(4) |
3.1 Energy release for polytropic EOSs
In the present section we simplify the analysis, removing
problems connected with numerical precision. To this aim, we will use the
polytropic EOSs for the N and S phases. The polytropic EOSs
not only guarantee a high precision of numerical calculation, but also open the possibility
of the exploration of a wide region of the parameter space.
A description of the polytropic EOSs and their application to
relativistic stars with phase transitions was
presented in detail in our previous publications in this series (Bejger et al. 2005;
Zdunik et al. 2006).
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{6515fig5.eps}\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg86.gif) |
Figure 5:
The energy release due to the mini-collapse of
a rotating neutron star as a function of the overpressure
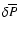 of the N phase of the matter in the center of the star, for the polytropic EOS ( of the N phase of the matter in the center of the star, for the polytropic EOS (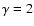 )
with
a first order phase transition located at three different points (pressures P0)
for which the mass of the reference nonrotating configuration is equal
to )
with
a first order phase transition located at three different points (pressures P0)
for which the mass of the reference nonrotating configuration is equal
to
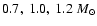 .
For each value of P0 two models of S phase EOS are
considered (one of the examples of the EOS depicted in
Fig. 7). They correspond to the S phase
described by the polytropes with .
For each value of P0 two models of S phase EOS are
considered (one of the examples of the EOS depicted in
Fig. 7). They correspond to the S phase
described by the polytropes with
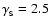 (upper curve) and
(upper curve) and
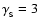 (lower curve). The points of different color correspond to the different values of total angular momentum of the rotating star,
(lower curve). The points of different color correspond to the different values of total angular momentum of the rotating star,
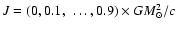 .
For a given EOS, results for all rotating configurations can be very well
approximated by a single curve, independent of J. (This figure is available in color in the electronic form.) .
For a given EOS, results for all rotating configurations can be very well
approximated by a single curve, independent of J. (This figure is available in color in the electronic form.) |
| Open with DEXTER |
In Fig. 4 we presented the energy release
as a function of
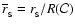 ,
for several values of the angular
momentum of the metastable configurations
,
for several values of the angular
momentum of the metastable configurations
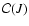 .
The reference
configuration is
.
The reference
configuration is 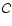 - the initial configuration of the corequake
with a metastable core in the center and central pressure
- the initial configuration of the corequake
with a metastable core in the center and central pressure
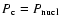 .
As we see in Fig. 4, the energy release
corresponding to a given value of
.
As we see in Fig. 4, the energy release
corresponding to a given value of
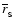 depends rather strongly on the rotation rate (here presented for the fixed values
of total angular momentum).
depends rather strongly on the rotation rate (here presented for the fixed values
of total angular momentum).
In Fig. 5 we presented the energy release
as a function of the overpressure of the metastable N phase in the center of the
metastable star
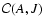 ,
,
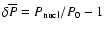 ,
for several values
of J. As we already stressed, the value of
,
for several values
of J. As we already stressed, the value of
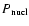 (or
(or
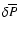 )
can be determined from microscopic considerations,
combined with physical conditions prevailing
at the star center as well as with their time evolution rate. Having determined
)
can be determined from microscopic considerations,
combined with physical conditions prevailing
at the star center as well as with their time evolution rate. Having determined
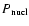 ,
we can determine the energy release,
,
we can determine the energy release, 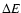 ,
due to the
corequake
,
due to the
corequake
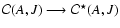 ,
where the metastable one-phase configuration, and the final two-phase
configuration, have the same values of the baryon number Aand total angular momentum J, which are conserved during the transition.
,
where the metastable one-phase configuration, and the final two-phase
configuration, have the same values of the baryon number Aand total angular momentum J, which are conserved during the transition.
As we see in Fig. 5, the energy release
in a (mini)collapse of a rotating star is independent of
the rotation rate of the collapsing configuration, and depends
exclusively on the degree of metastability of the N phase at the stellar
center (departure of matter from chemical equilibrium), measured by
the overpressure
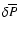 .
In particular,
to calculate the energy release associated with a corequake of a rotating neutron star, it is sufficient to know the value of
.
In particular,
to calculate the energy release associated with a corequake of a rotating neutron star, it is sufficient to know the value of 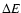 for a non-rotating star of the same central overpressure, which can be deduced from expressions derived in Zdunik et al. (1987).
for a non-rotating star of the same central overpressure, which can be deduced from expressions derived in Zdunik et al. (1987).
![\begin{figure}
\par\includegraphics[width=8.65cm,clip]{6515fig6.eps} %
\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg93.gif) |
Figure 6:
Top panel: the ratio of polar radial coordinate to
the equatorial radial coordinate radius versus frequency of rotation.
Bottom panel: the ratio of the kinetic energy, T and the absolute value
of the potential energy, W versus stellar angular momentum.
Calculations performed for stellar configurations
consisting of the N phase of dense matter, described by the polytropic
EOS. Large dots correspond to the values of the total stellar angular
momentum,
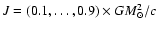 ,
which were used in Figs. 4,
5. ,
which were used in Figs. 4,
5. |
| Open with DEXTER |
The configurations
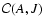 and
and
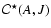 ,
considered in this
section, are really fast rotating ones, not so far from
the Keplerian limit. This is visualized in
Fig. 6, where we plotted the oblateness of the
star and the kinetic to potential energy ratio.
And still, in spite of fast rotation and large oblateness, the energy release
is the same as in a non-rotating star of the same
initial central overpressure.
,
considered in this
section, are really fast rotating ones, not so far from
the Keplerian limit. This is visualized in
Fig. 6, where we plotted the oblateness of the
star and the kinetic to potential energy ratio.
And still, in spite of fast rotation and large oblateness, the energy release
is the same as in a non-rotating star of the same
initial central overpressure.
3.2 Energy release for realistic EOS
In the present section we consider a realistic EOS of the N phase.
In order to explore how a realistic rotating neutron star will
respond to the appearance of a core of S phase core, we used
a recent SLy EOS of Douchin & Haensel (2001). The SLy EOS describes in
a unified way (i.e., starting from a single effective nuclear
Hamiltonian) both the crust and the core of a neutron star. In its
original version, the SLy EOS assumes that the neutron star core is
composed of neutrons, protons, electrons and muons. We introduced
a softening by a first order phase transition at 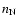 ,
as shown in Fig. 7.
,
as shown in Fig. 7.
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{6515fig7.eps}\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg100.gif) |
Figure 7:
The EOSs with first order phase transitions, used
in the present paper. Upper panel: the SLy EOS for the N phase, with a phase transition
to the dense S phase. We assume
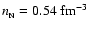 and
and
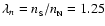 ,
which results in ,
which results in
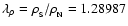 .
For a further description of the EOS, see the text. Lower panel: polytropic models of the EOS with a first order
phase transition. We assume .
For a further description of the EOS, see the text. Lower panel: polytropic models of the EOS with a first order
phase transition. We assume
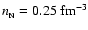 and
and
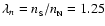 ,
which results in ,
which results in
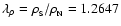 . . |
| Open with DEXTER |
We considered two EOSs of the S phase. Both were of polytropic form
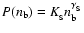 ,
with
,
with
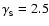 and
and
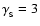 ,
respectively. We assume the values of
,
respectively. We assume the values of
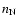 and
and
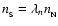 .
The values of
.
The values of
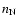 and
and 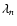 determine then P0. Equality of baryon chemical potentials
at P=P0 fixes the other constant of the S-phase EOS,
which is the value of energy per baryon (including rest
energy) at zero pressure. In this way, the values
of
determine then P0. Equality of baryon chemical potentials
at P=P0 fixes the other constant of the S-phase EOS,
which is the value of energy per baryon (including rest
energy) at zero pressure. In this way, the values
of
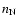 and
and 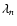 ,
together with
,
together with
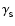 ,
fully determine the EOS of the S phase.
,
fully determine the EOS of the S phase.
In Fig. 8 we show the energy release due to the
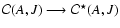 transition
versus overpressure, for two selected values of
transition
versus overpressure, for two selected values of
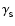 .
As in
the case of the polytropic models of the N phase, all color points
lie along the same line. For a given overpressure
.
As in
the case of the polytropic models of the N phase, all color points
lie along the same line. For a given overpressure
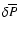 ,
the energy release does not depend on J of the collapsing metastable
configuration, confirming in this way results obtained for the polytropic
EOSs. This property is fulfilled very well for a broad range of
of stellar angular momentum,
,
the energy release does not depend on J of the collapsing metastable
configuration, confirming in this way results obtained for the polytropic
EOSs. This property is fulfilled very well for a broad range of
of stellar angular momentum,
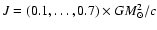 .
.
Our numerical results for different equations of state and models of phase transitions
presented in Figs. 5 and 8 show that the energy release
associated with a phase transition in the core does not depend on the stellar
rotation rate for a fixed overpressure at which the phase transition takes place.
To estimate the "accuracy'' of this conclusion we can calculate the departures of the energy
release for the rotating stars from the curve determined for nonrotating configurations.
The relative differences are of the order of 1-2% for
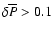 (except for
the smallest masses in Figs. 5, 8 (
(except for
the smallest masses in Figs. 5, 8 (
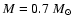 and
and
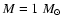 respectively) where they can be as large as 5%). For
respectively) where they can be as large as 5%). For
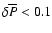 the relative differences are larger because the absolute value of
the relative differences are larger because the absolute value of 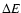 is very small and the differences are comparable to the numerical accuracy.
is very small and the differences are comparable to the numerical accuracy.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6515fig8.eps}\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg110.gif) |
Figure 8:
The energy release due to the mini-collapse of
rotating neutron star as a function of the metastability of the normal phase of the matter
in the center of the star for the SLy EOS with first order phase transition
located at two different points (pressures P0)
for which the mass of the reference nonrotating configuration is equal
to
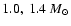 .
For each value of P0two models of the dense core EOS are presented - polytropes with .
For each value of P0two models of the dense core EOS are presented - polytropes with
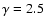 (upper curve)
and
(upper curve)
and 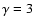 .
The points of different color correspond to the different values of
total angular momentum of rotating star. The results for all rotating configurations
can be very well approximated by one curve. (This figure is available in color in the electronic form.) .
The points of different color correspond to the different values of
total angular momentum of rotating star. The results for all rotating configurations
can be very well approximated by one curve. (This figure is available in color in the electronic form.) |
| Open with DEXTER |
4 Calculation of the energy release using linear response theory
Below
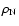 ,
the EOS for two cases (with and without phase transition)
is the same. The ambiguity of the definition of
,
the EOS for two cases (with and without phase transition)
is the same. The ambiguity of the definition of
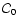 for rotating stars was discussed in Sect. 3. We can choose a reference configuration star with the same J or the same f as that of collapsing metastable one.
To reach the metastable configuration
with
for rotating stars was discussed in Sect. 3. We can choose a reference configuration star with the same J or the same f as that of collapsing metastable one.
To reach the metastable configuration
with
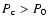 ,
we have to cross the "reference
line'' at the point defined by the evolutionary process leading to the instability.
,
we have to cross the "reference
line'' at the point defined by the evolutionary process leading to the instability.
We assume that transition of the star from a one-phase configuration to the
configuration with a small dense core built of S phase takes place at fixed baryon
number A (no matter ejection) and fixed total angular momentum of the star J(radiation loss of J neglected). Thus for a fixed baryon number A and fixed J,
we will calculate the mass-energy difference between 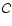 and
and
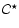 .
.
We assume that the mass of the S-phase core is much smaller
than the total stellar mass. Therefore,
from now on we will be able to restrict ourselves to a linear response of
neutron star to the appearance of the new dense S-phase core. The
calculation is based on expressing the change in the density
profile, due to the presence to a small core, as the combination
of two independent solutions of the linearly perturbed equations
of stellar structure (Haensel et al. 1986; Zdunik et al. 1987).
The presence of a denser phase in the core changes the boundary
condition at the phase transition pressure 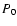 and allows us to determine the numerical coefficients in the
expression for the density profile change. The leading term in the
perturbation of the boundary condition at the edge of the new
phase results from the mass excess due to the
higher density of the new S phase as compared to the
N one in the supercompressed core.
and allows us to determine the numerical coefficients in the
expression for the density profile change. The leading term in the
perturbation of the boundary condition at the edge of the new
phase results from the mass excess due to the
higher density of the new S phase as compared to the
N one in the supercompressed core.
4.1 Non-rotating neutron stars
We use expressions obtained for static case by Haensel et al. (1986), and Zdunik et al.
(1987). For a non-rotating configuration of hydrostatic
equilibrium, the density jump
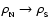 leads to the lowest-order expression for the
core-mass excess (with respect to the pure N-phase configuration),
leads to the lowest-order expression for the
core-mass excess (with respect to the pure N-phase configuration),
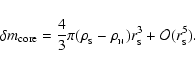 |
(5) |
The radius of the overcompressed N-phase core,
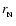 ,
is connected to the overpressure
that can be achieved by the N phase of matter by
,
is connected to the overpressure
that can be achieved by the N phase of matter by
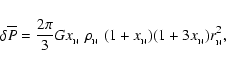 |
(6) |
where
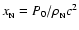 .
.
The conservation of the stellar baryon number during the
 transition implies a relation between
transition implies a relation between
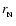 and
and
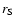 in which
neglecting terms
in which
neglecting terms
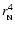 and higher, reads
and higher, reads
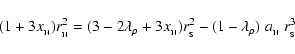 |
(7) |
where
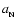 is a numerical coefficient depending on
is a numerical coefficient depending on
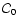 .
.
Using then Eqs. (6) and (7), the leading term for the energy release
expression 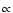
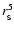 contains a prefactor
contains a prefactor
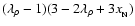 ,
while the next order term
,
while the next order term 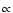
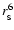 contains a prefactor
contains a prefactor
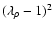 .
The
final expression for a normalized energy release reads
.
The
final expression for a normalized energy release reads
where
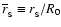 .
The coefficients
.
The coefficients 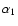 and
and 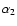 are functionals of the static reference configuration,
are functionals of the static reference configuration,
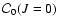 .
Expressing now
.
Expressing now
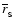 in
terms of overpressure, we obtain the energy release in terms of
the overpressure,
in
terms of overpressure, we obtain the energy release in terms of
the overpressure,
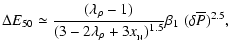 |
|
|
(9) |
where we use standard notation
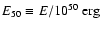 .
The coefficient
.
The coefficient 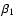 depends only
on the EOS of the N phase. More precisely, this coefficient
is a functional of the nonrotating reference configuration
depends only
on the EOS of the N phase. More precisely, this coefficient
is a functional of the nonrotating reference configuration
 and depends rather weakly on the mass M0 of the reference configuration
and depends rather weakly on the mass M0 of the reference configuration
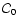 for
a rather broad range of masses, between
for
a rather broad range of masses, between
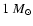 and
and
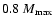 .
For EOSs considered in the present paper, numerical calculations give to a good approximation
.
For EOSs considered in the present paper, numerical calculations give to a good approximation
 .
.
4.2 Rotating neutron stars
The numerical results of Sect. 3 clearly show that for for a given central
overpressure of collapsing configuration,
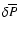 ,
the energy release does not depend on J and coincides with that of non-rotating
stars. Therefore, the formula (9) of Sect. 4.1 is valid also in the rotating case, provided
,
the energy release does not depend on J and coincides with that of non-rotating
stars. Therefore, the formula (9) of Sect. 4.1 is valid also in the rotating case, provided
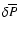 is sufficiently small.
Our calculations show that this formula is quite precise for
is sufficiently small.
Our calculations show that this formula is quite precise for
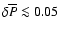 .
The prefactor in front of
.
The prefactor in front of 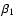 ,
involving
,
involving
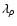 and
and
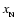 ,
is identical to those
obtained for the J=0 transition in Haensel et al. (1986) and Zdunik et al. (1987). The coefficient
,
is identical to those
obtained for the J=0 transition in Haensel et al. (1986) and Zdunik et al. (1987). The coefficient 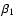 depends only on the EOS of the N phase. More precisely, this coefficient
is a functional of the nonrotating reference configuration
depends only on the EOS of the N phase. More precisely, this coefficient
is a functional of the nonrotating reference configuration
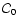 .
.
5 Numerical estimates of the energy release
For practical application, and for small overpressures,
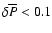 ,
it is convenient to
summarize results obtained in Sects. 3.1-3.2
in a formula
,
it is convenient to
summarize results obtained in Sects. 3.1-3.2
in a formula
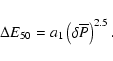 |
(10) |
The only dependence of coefficient a1 on the phase transition parameter
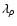 is via
prefactors,
is via
prefactors,
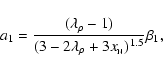 |
(11) |
which allows for a rapid re-calculation of a1 when one changes
the value of the density jump.
For the phase transition model considered in Sects. 3.2, the energy accompanying
phase transition in a metastable star with central overpressure
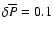 is about 2
is about 2  1050 erg, and
becomes one order of magnitude smaller for
1050 erg, and
becomes one order of magnitude smaller for
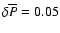 .
.
6 Discussion and conclusions
The most important result of the present paper is that the
total energy release associated with a first order phase
transition at the center of a rotating neutron star
depends only on the overpressure at the center of the
metastable configuration and is independent of the star
rotation rate. This result holds even for fast stellar rotation,
when the star shape deviates significantly from sphericity, and
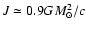 ,
and for overpressures as high as 10-20%.
This property is of great practical
importance because it implies that the calculation of the
energy release for a given overpressure, requiring very high precision
to guarantee
,
and for overpressures as high as 10-20%.
This property is of great practical
importance because it implies that the calculation of the
energy release for a given overpressure, requiring very high precision
to guarantee 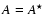 ,
can be reduced to the case of
non-rotating spherically symmetric stars.
,
can be reduced to the case of
non-rotating spherically symmetric stars.
To illustrate the practical importance of our result, let us
consider the case of overpressure
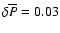 ,
when the energy release is 2
,
when the energy release is 2  1049 erg. For a
1049 erg. For a
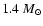 star this constitutes about 10-5 of the
stellar mass-energy. Therefore, to arrive at a meaningful result for the
energy of this magnitude, conservation of the total baryon
number has to be satisfied at the level of one part in a million, which is next to impossible for a 2D calculation with a realistic EOS. However, such a precision
can be easily reached for spherical stars, provided the EOS is
used in a thermodynamically consistent way (see, e.g., Haensel
& Proszynski 1982).
star this constitutes about 10-5 of the
stellar mass-energy. Therefore, to arrive at a meaningful result for the
energy of this magnitude, conservation of the total baryon
number has to be satisfied at the level of one part in a million, which is next to impossible for a 2D calculation with a realistic EOS. However, such a precision
can be easily reached for spherical stars, provided the EOS is
used in a thermodynamically consistent way (see, e.g., Haensel
& Proszynski 1982).
Moreover, we have shown that for overpressures smaller than 5%, the energy release is proportional to power 2.5 of the overpressure, with the coefficient
weakly dependent on the mass of collapsing configuration, for
stellar masses in the range from
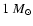 to about
to about
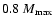 .
.
The energy release 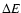 that we calculated is an absolute upper bound on the energies that can be released as a result of a phase transition at the star
center. The available channels may include, for example, stellar
pulsations, gravitational radiation, heating of stellar
interior, and X-ray emission from the neutron star surface.
Moreover, the phase transition in a rotating star
implies shrinking of stellar radius, decrease of the moment of
inertia, and spin-up of rotation. These topics will
be considered in our next paper.
that we calculated is an absolute upper bound on the energies that can be released as a result of a phase transition at the star
center. The available channels may include, for example, stellar
pulsations, gravitational radiation, heating of stellar
interior, and X-ray emission from the neutron star surface.
Moreover, the phase transition in a rotating star
implies shrinking of stellar radius, decrease of the moment of
inertia, and spin-up of rotation. These topics will
be considered in our next paper.
The present paper refers to the case of a small core of the
superdense phase. Therefore, as the energy release scales
as the fifth power of the core radius, the energy release is two-three
orders of magnitude smaller than that obtained by, e.g., Berezhiani et al.
(2003). The case of phase transitions in rotating neutron stars
leading to large cores and energy release  1052 erg is now being
studied.
1052 erg is now being
studied.
Acknowledgements
This work was partially supported by the
Polish MEiN grant no. 1P03D.008.27 and by the LEA
Astrophysics Poland-France
(Astro-PF) program. M.B. was partially supported by the Marie Curie
Intra-european Fellowship MEIF-CT-2005-023644
within the 6th European Community Framework
Programme.
- Bejger, M.,
Haensel, P., & Zdunik, J. L. 2005, MNRAS, 359, 699 (In the text)
- Berezhiani, Z.,
Bombaci, I., Drago, A., Frontera, F., & Lavagno, A. 2003, ApJ,
586, 1250 [CrossRef] (In the text)
- Diaz Alonso, J. 1983,
A&A, 125, 287
- Douchin, F., & Haensel,
P. 2001, A&A, 380, 151 [CrossRef] [EDP Sciences] (In the text)
- Glendenning, N.
K. 2000, Compact Stars. Nuclear Physics, Particle Physics, and
General Relativity (Berlin: Springer)
(In the text)
- Haensel, P.,
& Proszynski, M. 1982, ApJ, 258, 306 [CrossRef] (In the text)
- Haensel, P., Zdunik, J. L.,
& Schaeffer, R. 1986, A&A, 160, 251 (In the text)
- Iida, K.,
& Sato, K. 1997, Prog. Theor. Phys., 98, 277 [CrossRef] (In the text)
- Kaempfer,
B. 1981, Phys. Lett. B, 101, 366 (In the text)
- Schaeffer, R.,
Haensel, P., & Zdunik, J. L. 1983, A&A, 126, 121 [EDP Sciences] (In the text)
- Seidov, Z. F.
1971, Sov. Astron.- Astron. Zh., 15, 347 (In the text)
- Weber, F. 1999,
Pulsars as Astrophysical Laboratories for Nuclear and Particle
Physics (Bristol & Philadelphia: IoP Publishing)
(In the text)
- Zdunik, J. L., Haensel, P.,
& Schaeffer, R. 1987, A&A, 172, 95 (In the text)
- Zdunik, J. L., Bejger, M.,
Haensel, P., & Gourgoulhon, E. 2006, A&A, 450, 747 [CrossRef] [EDP Sciences] (In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=7.25cm,clip]{6515fig1.eps}\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg51.gif)
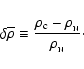
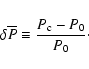
![\begin{displaymath}%
\tau_{\rm nucl}\left[\delta\overline{P}(t)\right]
=q\cdot\tau_{\rm comp} \cdot\delta\overline{P}
\end{displaymath}](/articles/aa/full/2007/14/aa6515-06/img59.gif)
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{6515fig2.ps} %
\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg65.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6515fig3.eps} %
\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg68.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{6515fig4.eps}\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg79.gif)
![\begin{displaymath}%
\Delta E=\left[M({\cal C })-M({\cal C}^\star)\right]_{A,J}c^2.
\end{displaymath}](/articles/aa/full/2007/14/aa6515-06/img81.gif)
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{6515fig5.eps}\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=8.65cm,clip]{6515fig6.eps} %
\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg93.gif)
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{6515fig7.eps}\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6515fig8.eps}\end{figure}](/articles/aa/full/2007/14/aa6515-06/Timg110.gif)