A&A 465, 641-645 (2007)
DOI: 10.1051/0004-6361:20065991
Modelling dications in the diurnal ionosphere of Venus
G. Gronoff1 -
J. Lilensten1 -
C. Simon1 -
O. Witasse2 -
R. Thissen3 -
O. Dutuit3 -
C. Alcaraz3
1 - Laboratoire de Planétologie de Grenoble, Université Joseph Fourier - CNRS, France
2 -
Research and Scientific Support Department of ESA, ESTEC, Noordwijk, The Netherlands
3 -
Laboratoire de Chimie Physique - CNRS - UMR 8000, Univ. Paris Sud, 91405 Orsay, France
Received 7 July 2006 / Accepted 9 December 2006
Abstract
Context. Previous studies have shown that doubly-charged positive ions, including molecular ions, can have detectable densities in the ionospheres of Mars, Titan, and the Earth.
Aims. In the present paper, we continue our approach by modelling the Venusian ionosphere. The neutral atmosphere of Venus has a similar composition to the ones encountered in the other terrestrial planets, with carbon dioxide (as on Mars), nitrogen (as on Earth and Titan), and atomic oxygen (as on Earth).
Methods. We computed the doubly-charged positive ion production through photoionisation (primary production) and electron impact ionisation (secondary production). We computed the densities under the photochemical equilibrium assumption.
Results. We predict a
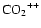 layer centred around
layer centred around
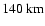 altitude with a density reaching 30 dications per
altitude with a density reaching 30 dications per
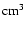 in active solar conditions and a
in active solar conditions and a
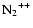 layer centred around a
layer centred around a
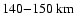 altitude with density reaching
altitude with density reaching
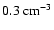 .
We find good agreement between the modelled
.
We find good agreement between the modelled
 densities and Pioneer Venus Orbiter measurements. Finally, we investigate the problem of possible detection of these ions by the European spacecraft Venus Express.
densities and Pioneer Venus Orbiter measurements. Finally, we investigate the problem of possible detection of these ions by the European spacecraft Venus Express.
Conclusions. Although molecular doubly-charged positive ion densities are low, these ions cannot be considered as negligible compared to other minor ion species. Their detection should be possible in the future through remote sensing or in-situ methods including ion mass spectrometry and UV spectroscopy.
Key words: planets and satellites: individual: Venus - atmospheric effects - Sun: UV radiation - space vehicles: instruments
The study of planetary ionospheres is among the major scientific goals
of many planetary missions. Venus Express (VEX), a European Space Agency mission, is the first dedicated mission to Venus since Magellan in the 1990s.
The VEX spacecraft entered into the Venus
orbit on 11 April 2006, and it has since then started acquiring its planetary data, thereby providing a global view of Venus' atmosphere.
The scientific goals cover the
following themes: atmosphere dynamics, structure, composition,
clouds and haze, radiative balance, surface properties, and - most important in the frame of this paper - plasma/escape
processes. The study of the ionosphere of Venus is clearly included
in the last theme, and the following experiments are expected
to contribute: VERA (Häusler et al. 2006), SPICAV (Bertaux et al. 2006), and ASPERA (Barabash et al. 2006).
A review of our current knowledge of certain key topics
associated with the aeronomy of Venus can be found in Witasse & Nagy (2006).
We report here on a study of the modelling of doubly-charged positive ions in the
diurnal ionosphere.
Plasma densities depend on production
and loss mechanisms, as well as on the dynamics.
Production can be of either a chemical or physical
origin. In the latter case we consider
two sources: photoabsorption (called primary photoproduction) and
electron impact ionisation (called secondary production).
In optically thin upper atmospheres, as in the case for Venus in the EUV range (<
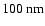 )
above
)
above
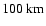 ,
the primary production is computed through a Beer-Lambert law.
The secondary production computation
requires solving a kinetic transport equation (Lilensten & Blelly 2002).
In Witasse et al. (2002,2003), this approach was adapted to Mars,
allowing the authors to predict the existence of a
,
the primary production is computed through a Beer-Lambert law.
The secondary production computation
requires solving a kinetic transport equation (Lilensten & Blelly 2002).
In Witasse et al. (2002,2003), this approach was adapted to Mars,
allowing the authors to predict the existence of a
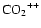 layer.
The same approach was developed by Simon et al. (2005) and Lilensten et al. (2005) for the Earth and Titan cases, respectively.
The present paper aims at presenting the calculation of the three main stable dications in the Venusian ionosphere:
layer.
The same approach was developed by Simon et al. (2005) and Lilensten et al. (2005) for the Earth and Titan cases, respectively.
The present paper aims at presenting the calculation of the three main stable dications in the Venusian ionosphere:
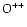 ,
,
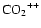 ,
and
,
and
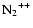 .
The
.
The
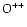 dication has already been detected and quantified in the Venusian ionosphere by Pioneer
Venus Orbiter (PVO) (Taylor et al. 1980), eventually allowing comparisons to be made with models such as the one of Fox & Victor (1981).
The
dication has already been detected and quantified in the Venusian ionosphere by Pioneer
Venus Orbiter (PVO) (Taylor et al. 1980), eventually allowing comparisons to be made with models such as the one of Fox & Victor (1981).
The
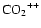 and
and
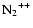 molecular ions have not yet been identified and are modelled here for the first time in the ionosphere of Venus.
molecular ions have not yet been identified and are modelled here for the first time in the ionosphere of Venus.
Several input parameters must be taken into account for modelling the contribution doubly-charged ions in terms of productions and densities: the solar flux and the neutral atmosphere.
We use the semi-empirical solar EUV/XUV model called solar 2000 (Tobiska & Eparvier 1998; Tobiska 1991,1993). Like most models currently used in planetary aeronomy (Torr & Torr 1985,1979; Richards et al. 1994), this model is based on measurements recorded onboard the Dynamics Explorer satellites (Hinteregger et al. 1973) and onboard rockets. It also takes data into account from other sources, such as the SME, OSO, and AEROS spacecrafts, as well as ground-based facilities. The UV spectrum is divided into 39 energy boxes.
The neutral atmosphere is yielded by the VTS3 model (Hedin et al. 1983), restricted to the main species (
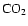 ,
,
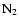 ,
,
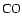 ,
,
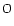 ,
,
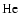 ).
This model is run for the conditions that match the orbit in terms of solar activity, location, time, and solar-zenith angle.
The
).
This model is run for the conditions that match the orbit in terms of solar activity, location, time, and solar-zenith angle.
The
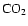 molecule is the major constituent below
molecule is the major constituent below
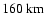 altitude,
altitude, 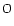 below
below
 ,
while
,
while 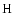 and
and 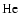 become dominant above.
The
become dominant above.
The 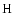 density is about
density is about
 above
above
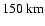 altitude
and does not affect the results below
altitude
and does not affect the results below
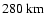 (Fox & Sung 2001).
However, as will be shown later, the evolution of hydrogen density has an influence on the
(Fox & Sung 2001).
However, as will be shown later, the evolution of hydrogen density has an influence on the
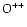 density above this altitude. In order to take its variations into account, we use the results of Hartle et al. (1996) who examined the solar cycle variations of the hydrogen in the thermosphere of Venus.
The altitude range for our computations is
density above this altitude. In order to take its variations into account, we use the results of Hartle et al. (1996) who examined the solar cycle variations of the hydrogen in the thermosphere of Venus.
The altitude range for our computations is
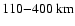 altitude.
altitude.
The dication density computed for a neutral species A is given by
where
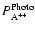 is the primary ion photoproduction and
is the primary ion photoproduction and
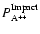 the secondary production created through electron-neutral collisions. The values of
the secondary production created through electron-neutral collisions. The values of
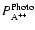 and
and
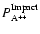 are direct outputs of the transport code (see below Lilensten & Blelly 2002; Simon et al. 2005).
In the case of
are direct outputs of the transport code (see below Lilensten & Blelly 2002; Simon et al. 2005).
In the case of
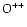 ,
there are two different ionisation processes: direct double ionisation of the atomic oxygen and single ionisation of
,
there are two different ionisation processes: direct double ionisation of the atomic oxygen and single ionisation of  .
Both are taken into account. We do not deal with the ionisation of
.
Both are taken into account. We do not deal with the ionisation of
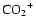 and
and
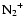 because these very minor ions in the Venusian ionosphere (Fox & Sung 2001) cannot yield a significant amount of dications. The constant
because these very minor ions in the Venusian ionosphere (Fox & Sung 2001) cannot yield a significant amount of dications. The constant 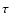 represents the natural lifetime of the molecular doubly-charged ion, and
represents the natural lifetime of the molecular doubly-charged ion, and
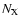 is the density of a neutral reactant X,
is the density of a neutral reactant X, 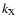 the reaction rate in
the reaction rate in
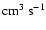 ,
and
,
and
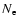 represents the electron density.
In the following,
represents the electron density.
In the following,
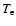 is the electronic temperature and
is the electronic temperature and
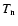 the neutral one. The processes for each species taken into account in the modelling are described below. A description of the techniques used for laboratory measurements can be found in Dutuit et al. (1996) and Franceschi et al. (2003).
the neutral one. The processes for each species taken into account in the modelling are described below. A description of the techniques used for laboratory measurements can be found in Dutuit et al. (1996) and Franceschi et al. (2003).
We consider 32 ionisation processes, summarised in Table 1.
The cross sections for the single ionisation of neutral species are explained in Witasse et al. (2002,2003), Lilensten et al. (2005), Simon et al. (2005), and references therein.
In Table 2, we give the references for the double-ionisation cross sections of the different neutral species.
The 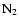 double-photoionisation cross section and its evolution with photon energy was estimated on the basis of a method proposed in Samson (1990).
Samson shows that the double-photoionisation cross section
double-photoionisation cross section and its evolution with photon energy was estimated on the basis of a method proposed in Samson (1990).
Samson shows that the double-photoionisation cross section
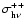 of a species A (
of a species A (
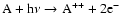 )
is proportional to the electron-impact ionisation
)
is proportional to the electron-impact ionisation
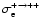 of the monocation (A
of the monocation (A
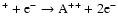 ), multiplied by the total photoabsorption
), multiplied by the total photoabsorption
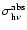 of the neutral species (
of the neutral species (
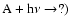 .
The proportionality constant q is estimated as
.
The proportionality constant q is estimated as
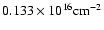 in the case of
in the case of
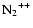 .
Thus, we have:
.
Thus, we have:
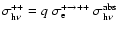 .
.
Table 1:
Summary of the ion productions taken into account here and their corresponding ionisation thresholds.
Table 2:
Sources for double-ionisation cross sections, either from theoretical estimates
or from laboratory measurements.
The Pioneer Venus Orbiter carried 17 experiments, including a neutral mass spectrometer and an ion-mass spectrometer (Russell 1992).
It allowed Hedin et al. (1983) to build a model of the Venusian thermosphere. However, although the mission lasted 14 years, no low-altitude data were being recorded during low solar activity, which put some constraints and uncertainties on the thermospheric model.
The Ion and Neutral Mass Spectrometer (INMS) allowed the detection of atomic doubly-charged ions such as
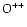 (Taylor et al. 1980). However, the spectrometer was designed to detect only specific, preselected ions excluding
(Taylor et al. 1980). However, the spectrometer was designed to detect only specific, preselected ions excluding
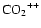 .
The sensitivity threshold of INMS was 5 particles per
.
The sensitivity threshold of INMS was 5 particles per
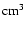 .
The
.
The
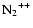 dication cannot be distinguished from
dication cannot be distinguished from 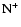 because both ions have the same
because both ions have the same
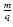 ratio (where m is the mass and q the charge).
We have selected three orbits in the PVO data base, which represent three different geophysical conditions:
ratio (where m is the mass and q the charge).
We have selected three orbits in the PVO data base, which represent three different geophysical conditions:
- Orbit 185: 1979-6-07;
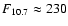 .
Solar zenith angle
.
Solar zenith angle 
 :
the usual orbit used for
:
the usual orbit used for
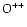 density calculations (Fox & Victor 1981). The mean latitude over the orbit
density calculations (Fox & Victor 1981). The mean latitude over the orbit 
 .
.
- Orbit 441: 1980-2-19;
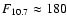 .
Solar zenith angle
.
Solar zenith angle 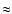
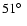 :
it is an orbit with a medium solar angle. The mean latitude over the orbit
:
it is an orbit with a medium solar angle. The mean latitude over the orbit 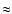
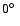 .
.
- Orbit 14: 1978-12-18;
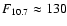 .
Solar zenith angle
.
Solar zenith angle 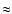
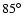 :
it is a boundary condition for both model and experimental conditions. The mean latitude over the orbit
:
it is a boundary condition for both model and experimental conditions. The mean latitude over the orbit 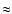
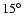 .
.
The PVO measurements used as inputs in our model are the electron density, the electron temperature, and the  density. The latter will be of utmost importance in the modelling, as the final density results are very sensitive to this parameter. As stated above, the solar flux comes from the EUV model of Tobiska (1993) and they correspond to the decimetric indexes on the day of the experiment. The ion temperature is adapted from Fox & Sung (2001).
The
density. The latter will be of utmost importance in the modelling, as the final density results are very sensitive to this parameter. As stated above, the solar flux comes from the EUV model of Tobiska (1993) and they correspond to the decimetric indexes on the day of the experiment. The ion temperature is adapted from Fox & Sung (2001).
The 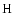 densities have been inferred from Hartle et al. (1996). For orbit 185 and 441, their values are
densities have been inferred from Hartle et al. (1996). For orbit 185 and 441, their values are
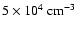 above
above
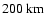 ,
corresponding to high solar activity. For orbit 14, the value is
,
corresponding to high solar activity. For orbit 14, the value is
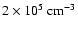 corresponding to a mean solar activity above the terminator.
corresponding to a mean solar activity above the terminator.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.9cm,clip]{5991fig1.eps}
\par\end{figure}](/articles/aa/full/2007/14/aa5991-06/Timg104.gif) |
Figure 1:
The
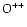 density comparison between the model and the PVO experiment.
The black points correspond to the PVO measurements.
The thick full lines shows the result of our modelling.
The thin full lines correspond to the larger divergence when varying
density comparison between the model and the PVO experiment.
The black points correspond to the PVO measurements.
The thick full lines shows the result of our modelling.
The thin full lines correspond to the larger divergence when varying 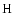 between
between
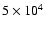 and
and
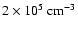 beyond
beyond
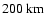 .
The dashed lines correspond to the model without .
The dashed lines correspond to the model without  photoionisation.
photoionisation.
|
| Open with DEXTER |
The results are shown in Fig. 1.
For orbit 185, the
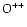 density was modelled by Fox & Victor (1981).
Using a photoionisation model, Fox computed a reaction rate constant of
density was modelled by Fox & Victor (1981).
Using a photoionisation model, Fox computed a reaction rate constant of
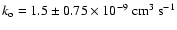 for the reaction
for the reaction
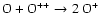 .
This model took neither the electron impact ionisation nor the electron recombination of
.
This model took neither the electron impact ionisation nor the electron recombination of
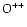 into account. More recently, the Simon et al. (2005) calculations on Earth showed a better agreement considering a constant rate of
into account. More recently, the Simon et al. (2005) calculations on Earth showed a better agreement considering a constant rate of
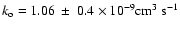 .
We considered both values here, and found much better agreement with the second one.
We did not need to adjust the other input parameters, like the input solar flux, the chemical reaction rates, the absorption and collision cross sections, and the neutral atmosphere.
.
We considered both values here, and found much better agreement with the second one.
We did not need to adjust the other input parameters, like the input solar flux, the chemical reaction rates, the absorption and collision cross sections, and the neutral atmosphere.
The agreement is already very good in orbits 185 and 441 when the  density used in the model comes from PVO measurements with
density used in the model comes from PVO measurements with
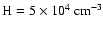 above
above
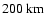 .
This
.
This 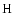 density value is compatible with the solar conditions during orbit 185 as seen from Hartle et al. (1996). When this value is enhanced to
density value is compatible with the solar conditions during orbit 185 as seen from Hartle et al. (1996). When this value is enhanced to
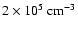 ,
the model and measurements diverge above
,
the model and measurements diverge above
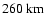 .
When neglecting the single ionisation of
.
When neglecting the single ionisation of  (Fig. 1) a worse divergence occurs above the same altitude.
(Fig. 1) a worse divergence occurs above the same altitude.
At low altitudes, the model slightly overestimates the
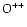 density. According to Fox & Sung (2001), the atomic
density. According to Fox & Sung (2001), the atomic 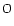 mixing ratio can be too high at high solar activity in the VTS3 model (Hedin et al. 1983), explaining this small discrepancy.
mixing ratio can be too high at high solar activity in the VTS3 model (Hedin et al. 1983), explaining this small discrepancy.
The 14th orbit constitutes a boundary condition. The latitude is about
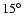 ,
while the solar zenith angle is
,
while the solar zenith angle is
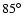 .
In that case, we are at the planet's terminator. Moreover, the solar activity is lower (
.
In that case, we are at the planet's terminator. Moreover, the solar activity is lower (
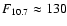 ). In these conditions, the
). In these conditions, the 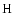 density is likely to be
density is likely to be
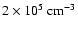 (Hartle et al. 1996). With this value, our model fits the measurements perfectly, while a lower
(Hartle et al. 1996). With this value, our model fits the measurements perfectly, while a lower 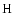 density value (
density value (
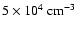 )
results in a degradation above
)
results in a degradation above
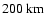 .
.
From these three cases, we have highlighted the usability range in which our model is valid.
In Fig. 2, we show the dication densities at a middle latitude in two solar conditions: strong (
F10.7 = 200) and quiet (
F10.7 = 80). We predict a
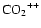 layer centred on an altitude of
layer centred on an altitude of
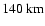 with a density reaching
with a density reaching
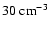 in active solar conditions and
in active solar conditions and
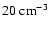 in quiet solar conditions. These values are close to the
in quiet solar conditions. These values are close to the
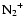 values (Fox & Sung 2001). At a low altitude (
values (Fox & Sung 2001). At a low altitude (
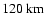 ), they are higher than the
), they are higher than the
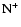 or
or
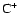 densities.
The density of the
densities.
The density of the
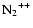 layer centred on
layer centred on
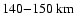 altitude can reach
altitude can reach
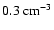 .
This makes
.
This makes
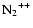 a very minor ion in the Venusian ionosphere.
a very minor ion in the Venusian ionosphere.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.9cm,clip]{5991fig2.eps}
\par\end{figure}](/articles/aa/full/2007/14/aa5991-06/Timg114.gif) |
Figure 2:
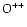 , ,
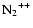 , ,
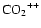 densities.
Latitude:
densities.
Latitude:
 ,
solar zenith angle: ,
solar zenith angle:
 density:
density:
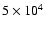 Full lines:
F10.7=200.
Dashed lines:
F10.7=80.
Full lines:
F10.7=200.
Dashed lines:
F10.7=80. |
| Open with DEXTER |
The ion mass spectrometry technique cannot be used to detect
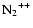 because this method performs the selection by the mass-to-charge
(m/q) ratio. Lilensten et al. (2005) have shown that
because this method performs the selection by the mass-to-charge
(m/q) ratio. Lilensten et al. (2005) have shown that
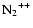 may still be detected by fluorescence in the case of Titan.
The emissive excited state
may still be detected by fluorescence in the case of Titan.
The emissive excited state
 is
is
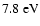 above
the ground state (Ahmad 2002; Olsson et al. 1988). Two bands
corresponding to the
above
the ground state (Ahmad 2002; Olsson et al. 1988). Two bands
corresponding to the
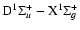 (0, 0) and (1, 1) transitions have already been observed experimentally in the
(0, 0) and (1, 1) transitions have already been observed experimentally in the
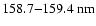 range (Cossart & Launay 1985; Olsson et al. 1988). Using the results
of Ehresmann et al. (2003), a rough approximation leads us to suppose that
nearly
range (Cossart & Launay 1985; Olsson et al. 1988). Using the results
of Ehresmann et al. (2003), a rough approximation leads us to suppose that
nearly 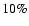 of the total of
of the total of
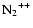 ions created by double photoionisation
at the cross-section peak near
ions created by double photoionisation
at the cross-section peak near
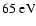 are produced in the
are produced in the
 state.
From a simple altitude integration, we would expect about 0.6 Rayleigh produced
in the fluorescence state in quiet conditions and 1.7 Rayleigh in active solar
conditions. These values are three times higher than those predicted on Titan.
state.
From a simple altitude integration, we would expect about 0.6 Rayleigh produced
in the fluorescence state in quiet conditions and 1.7 Rayleigh in active solar
conditions. These values are three times higher than those predicted on Titan.
The Venus Express SPICAV ultraviolet spectrometer has a range of
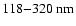 with a resolution of
with a resolution of
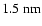 ;
therefore, the detection of such a fluorescence may be difficult but not impossible.
;
therefore, the detection of such a fluorescence may be difficult but not impossible.
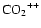
The
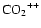 dication has no significant known fluorescence line. Therefore, the most appropriate method of detection is the ion-mass
spectrometry technique. For
dication has no significant known fluorescence line. Therefore, the most appropriate method of detection is the ion-mass
spectrometry technique. For
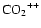 the mass-to-charge ratio equals 22. Therefore this ion is a very good
candidate for detection, since no other species in the Cytherean
atmosphere has the same ratio. The closest ratios are 16 for
the mass-to-charge ratio equals 22. Therefore this ion is a very good
candidate for detection, since no other species in the Cytherean
atmosphere has the same ratio. The closest ratios are 16 for
 and 28 for both
and 28 for both
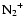 and
and
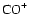 .
The only species with the same
mass-to-charge ratio is the
.
The only species with the same
mass-to-charge ratio is the
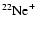 ion. However the main isotope of
ion. However the main isotope of
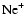 has an m/q ratio of 20, and its density in the Cytherean ionosphere is known to be extremely low, well below the density of
has an m/q ratio of 20, and its density in the Cytherean ionosphere is known to be extremely low, well below the density of
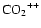 predicted here.
Thus no contamination from this component is likely to occur.
Finally, the Analyser of Space Plasma and Energetic Atoms (ASPERA-4) onboard Venus Express was not designed to detect
predicted here.
Thus no contamination from this component is likely to occur.
Finally, the Analyser of Space Plasma and Energetic Atoms (ASPERA-4) onboard Venus Express was not designed to detect
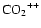 .
.
For the first time, the density of molecular dications has been
modelled in the diurnal upper atmosphere of Venus.
The
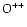 density was also computed and successfully compared to PVO measurements. These densities have been calculated
by using a kinetic code for the production rates and a simple chemical
scheme for the chemical losses. Doubly-charged ions were produced on the dayside through
primary photoionisation and secondary electron impact ionisation.
In the subsolar case, an additional source of ionisation may be solar-wind electrons and protons precipitating in the ionosphere and colliding with the thermosphere. These ions are essentially lost by dissociative recombination
with thermal electrons and by chemical reactions with the neutral atmosphere.
Consequently, a molecular dication layer can be created. The
density was also computed and successfully compared to PVO measurements. These densities have been calculated
by using a kinetic code for the production rates and a simple chemical
scheme for the chemical losses. Doubly-charged ions were produced on the dayside through
primary photoionisation and secondary electron impact ionisation.
In the subsolar case, an additional source of ionisation may be solar-wind electrons and protons precipitating in the ionosphere and colliding with the thermosphere. These ions are essentially lost by dissociative recombination
with thermal electrons and by chemical reactions with the neutral atmosphere.
Consequently, a molecular dication layer can be created. The
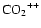 dication layer is centred on an altitude of
dication layer is centred on an altitude of
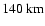 with a density reaching
with a density reaching
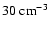 in active solar conditions.
The density of the
in active solar conditions.
The density of the
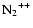 layer centred at
layer centred at
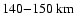 altitude can reach
altitude can reach
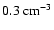 .
The
.
The
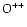 dication is most abundant at about
dication is most abundant at about
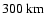 ,
with typical values of
,
with typical values of
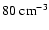 .
In the near future, we plan to extend our approach to electron precipitation from the solar-wind, a process which can play a major role in the upper atmosphere, depending on the solar activity.
The measurement of molecular doubly-charged ions is a challenge for Venus Express and any planetary orbiter. The detection of such ions is of prime interest for the community involved in aeronomy studies that seek to understand their role in planetary ionospheres.
.
In the near future, we plan to extend our approach to electron precipitation from the solar-wind, a process which can play a major role in the upper atmosphere, depending on the solar activity.
The measurement of molecular doubly-charged ions is a challenge for Venus Express and any planetary orbiter. The detection of such ions is of prime interest for the community involved in aeronomy studies that seek to understand their role in planetary ionospheres.
Acknowledgements
The authors wish to thank Mathieu Barthélemy (LPG, France) for helpful discussions and Héloise Soldi-Lose (Institut fur Chemie, Berlin, Germany) for useful advices.
- Aguilar, A.,
Covington, A. M., Hinojosa, G., et al. 2003, ApJS, 146,
467 [CrossRef]
- Ahmad, M. 2002,
Ph.D. Thesis, Université Paris VI,
- Aitken,
K. L., & Harrison, M. F. A. 1971, J. Phys. B:
At. Mol. Opt. Phys., 4, 1176
- Angel, G., &
Samson, J. 1988, J. Phys. B: At. Mol. Opt. Phys., 21, 2441 [CrossRef]
- Baluja, K.,
& Zeippen, C. 1988, J. Phys. B: At. Mol. Opt. Phys., 21,
2441 [CrossRef]
- Barabash,
S., et al. 2006, Planet. Space Sci., in press
(In the text)
- Bertaux,
J.-L., et al. 2006, Planet. Space Sci., in
press
(In the text)
- Cossart, D.,
& Launay, F. 1985, J. Mol. Spectr., 113, 159 [CrossRef]
- Dutuit, O.,
Alcaraz, C., Gerlichc, D., et al. 1996, Chem. Phys., 209,
177 [CrossRef] (In the text)
-
Ehresmann, A., Liebel, H., Schmoranzer, H., et al. 2003, J.
Phys. B: At. Mol. Opt. Phys., 36, 3669 [CrossRef] (In the text)
- Fennelly,
J. A., & Torr, D. G. 1992, At. Dat. Nucl. Dat. Tab.,
51, 321
- Fox, J. L.,
& Sung, K. Y. 2001, J. Geophys. Res., 106,
21305 [CrossRef] (In the text)
- Fox, J. L.,
& Victor, G. A. 1981, J. Geophys. Res., 86,
2438 (In the text)
-
Franceschi, P., Thissen, R., Zabka, J., et al. 2003, Int. J.
Mass Spectrom., 228, 507 (In the text)
- Halas, S., &
Adamczyk, B. 1972, Int. J. Mass Spectrom. Ion Phys, 10, 157 [CrossRef]
- Hartle,
R. E., Donahue, T. M., Grebowsky, J. M., & Mayr,
H. G. 1996, J. Geophys. Res., 101, 4525 [CrossRef] (In the text)
- Häusler,
B., Pätzold, M., Tyler, G. L., et al. 2006,
Planet. Space Sci., 54, 1315 [CrossRef] (In the text)
- Hedin,
A. E., Niemann, H. B., Kasprzak, W. T., & Seiff,
A. 1983, J. Geophys. Res., 88, 73 (In the text)
-
Hinteregger, H. E., Bedo, D. E., & Manson, J. E.
1973, Rad. Sci., 8, 349 (In the text)
- Honvault,
P., Gargaud, M., Bacchus-Montabonel, M. C., & McCarroll,
R. 1995, A&A, 302, 931 (In the text)
- Itikawa, Y.,
& Ichimura, A. 1990, J. Phys. Chem. Ref. Dat., 19, 637
- Johnsen, R.,
& Biondi, M. A. 1978, Geophys. Res. Lett., 5,
847 (In the text)
- Kimura, M., Gu,
J. P., Hirsch, G., & Buenker, R. J. 1996,
Phys. Rev. A, 53, 4164 [CrossRef] (In the text)
- Kjeldsen,
H., Kristensen, B., Brooks, R. L., et al. 2002, ApJS,
138, 219 [CrossRef]
-
Krishnakumar, E., & Srivastava, S. K. 1990, J. Phys. B:
At. Mol. Opt. Phys., 23, 1893 [CrossRef]
-
Lilensten, J., & Blelly, P. L. 2002, J. Atm. Terr. Phys.,
64, 775 (In the text)
-
Lilensten, J., Witasse, O., Simon, C., et al. 2005,
Geophys. Res. Lett., 32, 3203 [CrossRef] (In the text)
- Märk,
T. D. 1975, J. Chem. Phys., 63, 885 [CrossRef]
- Masuoka, T.
1994, Phys. Rev. A, 50, 3886 [CrossRef]
- Mathur, D.
2004, Phys. Rep., 391, 1 [CrossRef]
- Mathur, D.,
Andersen, L., Hvelplund, P., Kella, D., & Safvan, C. 1995, J.
Phys. B: At. Mol. Opt. Phys., 28, 3415 [CrossRef] (In the text)
- Nakada, M.,
& Singer, S. 1968, Geophys. J. Roy. Astr. Soc., 15, 163 (In the text)
- Olsson,
B. J., Kindvall, G., & Larsson, M. 1988,
J. Chem. Phys., 88, 7501 [CrossRef]
- Richards,
P. G., Fennelly, J. A., & Torr, D. G. 1994,
J. Geophys. Res., 99, 13283 [CrossRef]
- Russell,
C. T. 1992, Washington DC American Geophysical Union
Geophysical Monograph Series, 66, 225 (In the text)
- Samson,
J. A. 1990, , 65, 2861
(In the text)
- Seiersen,
K., Al-Khalili, A., Heber, O., et al. 2003a,
Phys. Rev. A, 68, 022708 [CrossRef] (In the text)
- Seiersen,
K., Heber, O., Jensen, M. J., Safvan, C. P., &
Andersen, L. H. 2003b, J. Chem. Phys., 119, 839 [CrossRef] (In the text)
- Simon, C.,
Lilensten, J., Dutuit, O., et al. 2005, Ann. Geoph., 23,
781 (In the text)
- Straub,
H. C., Renault, P., Lindsay, B. G., Smith, K. A.,
& Stebbings, R. F. 1996, Phys. Rev. A, 54,
2146 [CrossRef]
- Taylor,
H. A., Brinton, H. C., Bauer, S. J., et al.
1980, J. Geophys. Res., 85, 7765 (In the text)
- Tian, C., &
Vidal, C. R. 1998, J. Chem. Phys., 108, 927 [CrossRef]
- Tobiska,
W. K. 1991, J. Atm. Terr. Phys., 53, 1005 [CrossRef]
- Tobiska,
W. K. 1993, J. Geophys. Res., 98, 18879
- Tobiska,
W. K., & Eparvier, F. G. 1998, Sol. Phys., 177,
147 [CrossRef]
- Torr, D. G.,
& Torr, M. R. 1979, J. Atm. Terr. Phys., 41, 797 [CrossRef]
- Torr, M. R.,
& Torr, D. G. 1985, J. Geophys. Res., 90,
6675
- Witasse, O.,
Dutuit, O., Lilensten, J., et al. 2002,
Geophys. Res. Lett., 29, 104 [CrossRef]
- Witasse, O.,
Dutuit, O., Lilensten, J., et al. 2003,
Geophys. Res. Lett., 30, 12 [CrossRef]
- Witasse, O.,
& Nagy, A. F. 2006, Planet. Space Sci., 54,
1381 [CrossRef] (In the text)
- Yamada, I.,
Danjo, A., Hirayama, T., et al. 1988, J. Phys. Soc. Jpn.,
57(8), 2699-2704
- Ziegler,
D. L., Newman, J. H., Smith, K. A., & Stebbings,
R. F. 1982, Planet. Space Sci., 30, 451 [CrossRef]
- Zipf, E. C.
1985, Planet. Space Sci., 33, 1303 [CrossRef]
Copyright ESO 2007
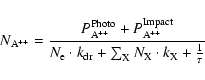
![\begin{figure}
\par\includegraphics[angle=-90,width=8.9cm,clip]{5991fig1.eps}
\par\end{figure}](/articles/aa/full/2007/14/aa5991-06/Timg104.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.9cm,clip]{5991fig2.eps}
\par\end{figure}](/articles/aa/full/2007/14/aa5991-06/Timg114.gif)