A&A 465, 263-269 (2007)
DOI: 10.1051/0004-6361:20066510
On the applicability of the level set method beyond the
flamelet regime in thermonuclear supernova simulations
W. Schmidt
Lehrstuhl für Astronomie, Institut für Theoretische Physik und Astrophysik,
Universität Würzburg, Am Hubland, 97074 Würzburg, Germany
Received 5 October 2006 / Accepted 5 January 2007
Abstract
In thermonuclear supernovae, intermediate mass elements
are mostly produced by distributed burning provided that a
deflagration to detonation transition does not set in. Apart from
the two-dimensional study by Röpke & Hillebrandt (2005, A&A, 429, L29), very little
attention has been payed so far to the correct treatment of this
burning regime in numerical simulations. In this article, the
physics of distributed burning is reviewed from the literature on
terrestrial combustion and differences which arise from the very
small Prandtl numbers encountered in degenerate matter are pointed
out. Then it is shown that the level set method continues to be
applicable beyond the flamelet regime as long as the width of the
flame brush does not become smaller than the numerical cutoff
length. Implementing this constraint with a simple parameterisation
of the effect of turbulence onto the energy generation rate, the
production of intermediate mass elements increases substantially
compared to previous simulations, in which the burning process was
stopped once the mass density dropped below
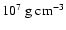 .
Although these results depend on the
chosen numerical resolution, an improvement of the constraints on the
the total mass of burning products in the pure deflagration scenario
can be achieved.
.
Although these results depend on the
chosen numerical resolution, an improvement of the constraints on the
the total mass of burning products in the pure deflagration scenario
can be achieved.
Key words: stars: supernovae: general -
hydrodynamics - turbulence - methods: numerical
In the course of the last few years, observational indications in
favour of a delayed detonation in type Ia supernovae (SNe Ia) have
mounted. For example, calculations of the X-ray spectrum of the
Tycho supernova remnant assuming various hydrodynamical models
appear to support a deflagration to detonation transition (DDT)
(Badenes et al. 2006). Furthermore, an investigation of near-infrared
emission lines of three branch-normal supernovae by
Marion et al. (2006) implies very little carbon residuals at radial
velocities less than
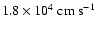 .
Even
the most advanced three-dimensional simulations of thermonuclear
supernovae assuming pure deflagrations (Schmidt & Niemeyer 2006; Röpke et al. 2006)
fail to satisfy this constraint. In models with delayed detonations
(Gamezo et al. 2005), on the other hand, the supersonic propagation of
burning fronts dispose of virtually all carbon except for the
outermost layers. Furthermore, a gravitational confined detonation was
suggested as an alternative scenario (Plewa et al. 2004).
.
Even
the most advanced three-dimensional simulations of thermonuclear
supernovae assuming pure deflagrations (Schmidt & Niemeyer 2006; Röpke et al. 2006)
fail to satisfy this constraint. In models with delayed detonations
(Gamezo et al. 2005), on the other hand, the supersonic propagation of
burning fronts dispose of virtually all carbon except for the
outermost layers. Furthermore, a gravitational confined detonation was
suggested as an alternative scenario (Plewa et al. 2004).
However, a recent numerical study by Maier & Niemeyer (2006) demonstrated
that detonation waves fail to penetrate processed material stemming
from the initial deflagration phase. Therefore, pockets of unburned
material are likely to survive even a delayed detonation. Apart from
that, Niemeyer (1999) pointed out several theoretical
arguments against DDTs. In addition, accommodating the observed
variability of SNe Ia (Stritzinger et al. 2006) within the DDT scenario
appears to be difficult, because delayed detonations tend to produce
at least a solar mass of iron group elements and explosion energies
in excess of
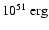 ,
which are typical values
characterising bright SNe Ia. But there are also SNe Ia of moderate
or low luminosity producing much smaller masses of iron-group
elements and less explosion energy. Apart from that,
Jha et al. (2006) inferred non-negligible amounts of carbon at low
expansion velocities from the late-time spectroscopy of the SN 2002cx, a peculiar supernova with very low luminosity. If this
result was confirmed by further observations, one might conceive of
a sub-class of SNe Ia originating either from Chandrasekhar mass
white dwarfs which are only partially burned by pure deflagrations
or from sub-Chandrasekhar mass progenitors. In this article, we
shall be concerned exclusively with the Chandrasekhar mass scenario.
,
which are typical values
characterising bright SNe Ia. But there are also SNe Ia of moderate
or low luminosity producing much smaller masses of iron-group
elements and less explosion energy. Apart from that,
Jha et al. (2006) inferred non-negligible amounts of carbon at low
expansion velocities from the late-time spectroscopy of the SN 2002cx, a peculiar supernova with very low luminosity. If this
result was confirmed by further observations, one might conceive of
a sub-class of SNe Ia originating either from Chandrasekhar mass
white dwarfs which are only partially burned by pure deflagrations
or from sub-Chandrasekhar mass progenitors. In this article, we
shall be concerned exclusively with the Chandrasekhar mass scenario.
Schmidt & Niemeyer (2006) showed that the explosion energy and mass of iron
group elements in thermonuclear supernova simulations with pure
deflagration can be varied over about an order of magnitude if
non-simultaneous point ignitions are applied. To that end, the
simple MLT model of the pre-supernova core proposed by
Wunsch & Woosley (2004) was adopted for the implementation of a stochastic
ignition procedure. In a numerical case study, models with a total
number of ignitions ranging from a few up to several hundred events
per octant were investigated. The main result is that the total mass
of iron group elements can be adjusted to any value smaller than
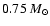 with a maximal explosion energy of roughly
with a maximal explosion energy of roughly
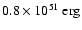 .
Therefore, these models are
feasible candidates for less energetic SNe Ia.
.
Therefore, these models are
feasible candidates for less energetic SNe Ia.
Due to the artificially chosen termination of thermonuclear burning
at mass densities below
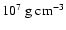 ,
however, the
prediction of the carbon and oxygen residuals in the models with
stochastic ignition by Schmidt & Niemeyer (2006) was not reliable. The
transition from the flamelet regime to the regime of distributed
burning is expected to occur at a mass density of about
,
however, the
prediction of the carbon and oxygen residuals in the models with
stochastic ignition by Schmidt & Niemeyer (2006) was not reliable. The
transition from the flamelet regime to the regime of distributed
burning is expected to occur at a mass density of about
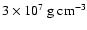 (Niemeyer & Kerstein 1997; Niemeyer & Woosley 1997). Since the
level set method - as implemented by Reinecke et al. (1999b) - was
applied for the numerical flame front propagation, the treatment of
the distributed burning regime remained unclear. As a first
approximation, distributed burning was mostly suppressed by
introducing the aforementioned density threshold. This resulted in
an overestimate of the amount of unburned material. Apart from that,
a delayed detonation might be triggered in the late burning phase
(Khokhlov et al. 1997; Niemeyer & Woosley 1997). However, the arguments put forward by
Niemeyer (1999) and the numerical results by Bell et al. (2004)
shed serious doubt on this proposition. For this reason, it appears
even more important to consider the possibility of the subsonic
distributed burning mode at lower densities.
(Niemeyer & Kerstein 1997; Niemeyer & Woosley 1997). Since the
level set method - as implemented by Reinecke et al. (1999b) - was
applied for the numerical flame front propagation, the treatment of
the distributed burning regime remained unclear. As a first
approximation, distributed burning was mostly suppressed by
introducing the aforementioned density threshold. This resulted in
an overestimate of the amount of unburned material. Apart from that,
a delayed detonation might be triggered in the late burning phase
(Khokhlov et al. 1997; Niemeyer & Woosley 1997). However, the arguments put forward by
Niemeyer (1999) and the numerical results by Bell et al. (2004)
shed serious doubt on this proposition. For this reason, it appears
even more important to consider the possibility of the subsonic
distributed burning mode at lower densities.
A first attempt to include distributed burning in deflagration
models of SNe Ia was made by Röpke & Hillebrandt (2005). They carried out
two-dimensional simulations demonstrating that the explosion energy
increases and the fraction of carbon and oxygen at low radial
velocities is reduced. However, their prescription of the turbulent
burning speed in the distributed regime suffered from a
misconception of the relevant scales. In this article, we will argue
that the existing treatment of burning fronts with the level set
method can be carried over to the distributed regime provided that
the burning time scale is smaller than the eddy turn-over time scale
associated with the numerical cutoff length. Consequently, this
constraint has to be observed in numerical simulations of
thermonuclear supernovae with the level set method.
After reviewing the physics of distributed burning in
Sect. 2, we will show in
Sect. 3 that the turbulent burning speed
continues to be determined by the magnitude of turbulent velocity
fluctuations at unresolved scales after the onset of distributed
burning. In Sect. 4, we will discuss results from
numerical simulations of thermonuclear supernovae with stochastic
ignition, where the burning process was terminated based on a
comparison of the burning and unresolved eddy turn-over time
scales. Thereby, it was possible to increase the production of
intermediate mass elements significantly compared to previous
simulations with a density threshold of
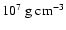 for thermonuclear burning. In particular, we found that the total
mass of intermediate mass elements appears to be independent of the
details of the ignition process, although slower ignition implies a
larger amount of fuel at the transition from the flamelet to the
distributed burning regime.
for thermonuclear burning. In particular, we found that the total
mass of intermediate mass elements appears to be independent of the
details of the ignition process, although slower ignition implies a
larger amount of fuel at the transition from the flamelet to the
distributed burning regime.
2 Distributed burning
In combustion physics, two different regimes of deflagration are
distinguished: on the one hand, the flamelet regime, in which
the microscopic flame propagation speed is solely determined by the
thermal conductivity of the fuel. In the distributed burning
regime, on the other hand, the transport of heat and mass is
influenced by turbulence even at scales comparable to the width of
the flame brush. As argued by Niemeyer & Kerstein (1997), the correct
criterion for the transition from burning in the flamelet regime to
distributed burning is that the flame width 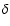 is about the
Gibson length
is about the
Gibson length
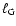 .
The Gibson length is implicitly
defined by the equality of the velocity
.
The Gibson length is implicitly
defined by the equality of the velocity 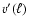 associated with
turbulent eddies of size
associated with
turbulent eddies of size 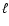 and the laminar flame speed
and the laminar flame speed
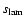 (Peters 1988):
(Peters 1988):
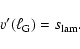 |
(1) |
In the flamelet regime, the flame front propagates sufficiently fast
through eddies smaller than the Gibson length such that turbulence
has virtually no effect on the internal structure of the reaction
zone. The width of the flame is then given by
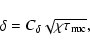 |
(2) |
where 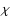 is the thermal conductivity,
is the thermal conductivity,
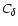 a constant
dimensionless coefficient and the thermonuclear reaction time scale
is defined by
a constant
dimensionless coefficient and the thermonuclear reaction time scale
is defined by
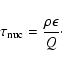 |
(3) |
Here 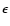 is the specific thermonuclear energy release and Qthe rate of energy generation per unit time and unit volume. The
time scale
is the specific thermonuclear energy release and Qthe rate of energy generation per unit time and unit volume. The
time scale
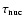 and the conductivity
and the conductivity 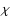 also
determine the laminar flame speed:
also
determine the laminar flame speed:
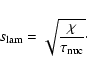 |
(4) |
Once
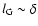 ,
however, turbulence will begin to
affect the transport of heat due to turbulent mixing of preheated
material into fuel. As a consequence of the enhanced diffusivity,
the flame front is broadened. If the turbulence intensity does not
become too high, however, only the preheat zone will be broadened
while the reaction zone is not disturbed by turbulent eddies due to
the increased viscosity near the flame. This was, for instance,
demonstrated in numerical simulations by Kim & Menon (2000b). The
effect of turbulence onto the flame can be quantified in terms of a
turbulent diffusivity
,
however, turbulence will begin to
affect the transport of heat due to turbulent mixing of preheated
material into fuel. As a consequence of the enhanced diffusivity,
the flame front is broadened. If the turbulence intensity does not
become too high, however, only the preheat zone will be broadened
while the reaction zone is not disturbed by turbulent eddies due to
the increased viscosity near the flame. This was, for instance,
demonstrated in numerical simulations by Kim & Menon (2000b). The
effect of turbulence onto the flame can be quantified in terms of a
turbulent diffusivity
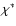 and the width
and the width
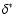 of
the broadened preheating zone. According to Damköhler's
hypothesis, the propagation speed
of
the broadened preheating zone. According to Damköhler's
hypothesis, the propagation speed
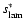 of the
broadened flame is enhanced in proportion to the square root of the
turbulent diffusivity relative to the thermal diffusivity
(Damköhler 1940):
of the
broadened flame is enhanced in proportion to the square root of the
turbulent diffusivity relative to the thermal diffusivity
(Damköhler 1940):
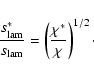 |
(5) |
This relation follows exactly if the rate of energy generation Qis unaffected by turbulence. Since the width of the reaction zone
tends to become significantly smaller than
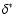 (by a
factor greater than 10), this mode of burning is called the
thin-reaction-zones regime.
(by a
factor greater than 10), this mode of burning is called the
thin-reaction-zones regime.
The conductivity 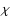 can be related to the viscosity
can be related to the viscosity 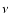 by
by
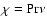 ,
where the Prandtl number is a
dimensionless characteristic number of the fuel. In stark contrast
to most terrestrial fluids which have a Prandtl number of the
roughly unity,
,
where the Prandtl number is a
dimensionless characteristic number of the fuel. In stark contrast
to most terrestrial fluids which have a Prandtl number of the
roughly unity,
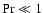 for degenerate carbon and oxygen
in white dwarfs (Nandkumar & Pethick 1984). Introducing the turbulent
viscosity
for degenerate carbon and oxygen
in white dwarfs (Nandkumar & Pethick 1984). Introducing the turbulent
viscosity
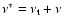 ,
the turbulent
diffusivity can be expressed as
,
the turbulent
diffusivity can be expressed as
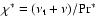 ,
where
,
where
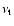 accounts for the effect of turbulent eddies in
the range of length scales from the Kolmogorov scale
accounts for the effect of turbulent eddies in
the range of length scales from the Kolmogorov scale
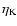 to the
to the
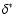 .
Thus,
Eq. (5) can be written in the form
.
Thus,
Eq. (5) can be written in the form
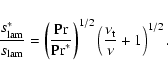 |
(6) |
Assuming that turbulence becomes asymptotically isotropic towards
scales small compared to the integral scale, we may use
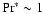 for the turbulent Prandtl number
(Yakhot & Orszag 1986) and the velocity fluctuations
for the turbulent Prandtl number
(Yakhot & Orszag 1986) and the velocity fluctuations 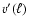 at
sufficiently small length scales
at
sufficiently small length scales 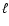 asymptotically obey the
Kolmogorov-Obukhov 1/3-law (Frisch 1995),
asymptotically obey the
Kolmogorov-Obukhov 1/3-law (Frisch 1995),
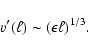 |
(7) |
Numerical evidence for asymptotic isotropy and the above power law
in simulations of Rayleigh-Taylor-unstable thermonuclear flames was reported
by Zingale et al. (2005).
The rate of energy dissipation
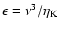 ,
where the Kolmogorov scale
,
where the Kolmogorov scale
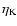 is about the size of
the smallest eddies. Thus, substitution of
is about the size of
the smallest eddies. Thus, substitution of
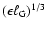 on the left hand side of
Eq. (1) yields
on the left hand side of
Eq. (1) yields
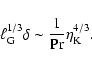 |
(8) |
Since
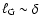 upon the onset of distributed
burning, it follows from the above relation that
upon the onset of distributed
burning, it follows from the above relation that
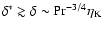 .
In thermonuclear supernovae,
.
In thermonuclear supernovae,
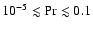 (Nandkumar & Pethick 1984). Thus, the the broadened flame is much wider
than the Kolmogorov scale.
(Nandkumar & Pethick 1984). Thus, the the broadened flame is much wider
than the Kolmogorov scale.
Assuming approximate local equilibrium of the energy flux through
the cascade of turbulent eddies from size
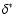 down to
the Kolmogorov scale, we have
down to
the Kolmogorov scale, we have
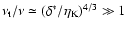 .
Equation (6) for the enhanced flame
propagation speed then implies
.
Equation (6) for the enhanced flame
propagation speed then implies
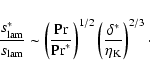 |
(9) |
Note that the asymptote
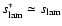 corresponds to
corresponds to
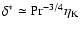 which is
consistent with the estimate in the previous paragraph. Since the
definition of the flame width (2) implies
which is
consistent with the estimate in the previous paragraph. Since the
definition of the flame width (2) implies
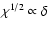 ,
it follows form
Damköhler's relation (5) that
,
it follows form
Damköhler's relation (5) that
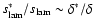 .
Combining this result with
relation (9), it is possible to
eliminate the width of the broadened flame
.
Combining this result with
relation (9), it is possible to
eliminate the width of the broadened flame
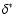 and
calculate
and
calculate
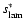 as a function of known
parameters. For a detailed specification of the coefficients and the
resulting expression for
as a function of known
parameters. For a detailed specification of the coefficients and the
resulting expression for
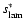 we refer to
Kim & Menon (2000a).
we refer to
Kim & Menon (2000a).
In terms of time scales, the thin-reaction-zones regime is
characterised by
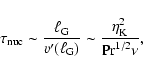 |
(10) |
where the expression on the very right follows from the
1/3-law (7) and
relation (8) with
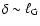 .
For constant viscosity, growing
energy flux corresponds to a decreasing Kolmogorov scale. However,
as the time scale
.
For constant viscosity, growing
energy flux corresponds to a decreasing Kolmogorov scale. However,
as the time scale
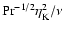 becomes much smaller than
becomes much smaller than
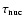 ,
turbulent eddies
will penetrate and eventually break the reaction zone. In this
broken-reaction-zones regime, turbulence entrains preheated
fuel with patches of already burned material at a time scale smaller
than the nuclear time scale (3). It appears that the
dilution of burning material within the reaction zone would imply a
modification of the rate of energy generation per unit volume. As a
simple parametrisation, we set
,
turbulent eddies
will penetrate and eventually break the reaction zone. In this
broken-reaction-zones regime, turbulence entrains preheated
fuel with patches of already burned material at a time scale smaller
than the nuclear time scale (3). It appears that the
dilution of burning material within the reaction zone would imply a
modification of the rate of energy generation per unit volume. As a
simple parametrisation, we set
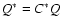 ,
where Q is
the corresponding energy generation rate if turbulence was absent.
In the case of premixed combustion, which evidently applies to
thermonuclear fusion, the entrainment of fuel with ash may inhibit
but cannot boost the burning process, i.e.
,
where Q is
the corresponding energy generation rate if turbulence was absent.
In the case of premixed combustion, which evidently applies to
thermonuclear fusion, the entrainment of fuel with ash may inhibit
but cannot boost the burning process, i.e.
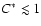 .
In
any case, the quantitative determination of
.
In
any case, the quantitative determination of 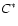 requires
three-dimensional direct numerical simulations of turbulent burning
with a detailed reaction network at different densities and varying
turbulence intensity. Numerical investigations pointing in this
direction were presented by Bell et al. (2004). In conclusion,
writing the effective reaction time scale as
requires
three-dimensional direct numerical simulations of turbulent burning
with a detailed reaction network at different densities and varying
turbulence intensity. Numerical investigations pointing in this
direction were presented by Bell et al. (2004). In conclusion,
writing the effective reaction time scale as
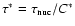 ,
we have
,
we have
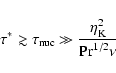 |
(11) |
in the broken-reaction-zones regime.
3 Extended level set prescription
Reinecke et al. (1999a) introduced the level set method for the
modelling of burning fronts in thermonuclear supernova simulations.
The basic idea of this approach is to represent the flames by the
zero level set of a distance function that is determined by a
partial differential equation. The intrinsic propagation speed in
the flamelet regime is the laminar burning speed
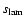 .
Because simulations of SNe Ia are essentially large eddy
simulations, however, the effective propagation speed is
asymptotically proportional to the magnitude of unresolved turbulent
velocity fluctuations, i.e.
.
Because simulations of SNe Ia are essentially large eddy
simulations, however, the effective propagation speed is
asymptotically proportional to the magnitude of unresolved turbulent
velocity fluctuations, i.e.
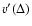 ,
where
,
where 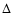 is the
resolution of the numerical grid (Niemeyer & Hillebrandt 1995). For this
reason, the effective propagation speed of the numerically computed
flame fronts is called the turbulent flame speed and denoted by
is the
resolution of the numerical grid (Niemeyer & Hillebrandt 1995). For this
reason, the effective propagation speed of the numerically computed
flame fronts is called the turbulent flame speed and denoted by
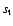 .
For the calculation of
.
For the calculation of
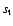 ,
we have
adopted Pocheau's model (Pocheau 1994; Schmidt et al. 2006b):
,
we have
adopted Pocheau's model (Pocheau 1994; Schmidt et al. 2006b):
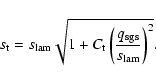 |
(12) |
For fully developed turbulence, the flame propagation speed is
asymptotically given by
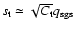 .
LES of
turbulent combustion in a box indicated that a sound burning rate
was obtained with
.
LES of
turbulent combustion in a box indicated that a sound burning rate
was obtained with
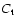 not differing too far from unity
(Schmidt et al. 2005). We adopted the value
not differing too far from unity
(Schmidt et al. 2005). We adopted the value
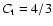 which
is consistent with Peters (1999). The subgrid scale turbulent
velocity
which
is consistent with Peters (1999). The subgrid scale turbulent
velocity
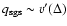 is computed by means of
the localised subgrid scale model proposed by Schmidt et al. (2006a). As
a great benefit for the application to thermonuclear supernova
simulations, this subgrid scale model does not rely on certain flow
properties such as isotropy or a particular mechanism for the
production of turbulence on large scales.
is computed by means of
the localised subgrid scale model proposed by Schmidt et al. (2006a). As
a great benefit for the application to thermonuclear supernova
simulations, this subgrid scale model does not rely on certain flow
properties such as isotropy or a particular mechanism for the
production of turbulence on large scales.
According to Kim & Menon (2000a), the above model for the turbulent
flame speed can be readily extended into the thin-reaction-zones
regime:
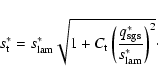 |
(13) |
Here, the laminar flame speed is substituted by the enhanced flame
propagation speed
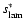 introduced in
Sect. 2. Since
introduced in
Sect. 2. Since
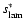 incorporates the effects of turbulence at length scales
incorporates the effects of turbulence at length scales
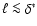 ,
the contribution of turbulent velocity
fluctuations in this range of length scales has to be subtracted
from
,
the contribution of turbulent velocity
fluctuations in this range of length scales has to be subtracted
from
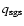 .
This results in the reduced subgrid scale
turbulence velocity
.
This results in the reduced subgrid scale
turbulence velocity
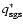 corresponding to the
range of length scales between the width of the broadened flame,
corresponding to the
range of length scales between the width of the broadened flame,
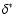 ,
and the numerical resolution. In the case of
Kolmogorov scaling (7),
,
and the numerical resolution. In the case of
Kolmogorov scaling (7),
![\begin{displaymath}\frac{q_{{\rm sgs}}^{\ast}}{q_{{\rm sgs}}}\simeq
\left[1-\left(\frac{\delta^{\ast}}{\Delta}\right)^{2/3}\right]^{1/2}\cdot
\end{displaymath}](/articles/aa/full/2007/13/aa6510-06/img77.gif) |
(14) |
The transition from the flamelet to the distributed burning regime
is expected to occur within the range of densities from 107 to
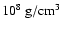 .
The calculations of Timmes & Woosley (1992)
show that
.
The calculations of Timmes & Woosley (1992)
show that 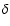 assumes values between 10-2 and a few
assumes values between 10-2 and a few 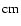 within this range of densities. The width
within this range of densities. The width
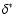 of the broadened flame cannot exceed
of the broadened flame cannot exceed 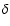 by
more than a factor
by
more than a factor 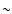 10 without turbulent eddies breaking up
the reaction zone (Kim & Menon 2000a). Thus, it appears that
10 without turbulent eddies breaking up
the reaction zone (Kim & Menon 2000a). Thus, it appears that
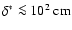 for the
thin-reaction-zones regime in thermonuclear supernovae. Even in the
most elaborate numerical simulations, on the other hand,
for the
thin-reaction-zones regime in thermonuclear supernovae. Even in the
most elaborate numerical simulations, on the other hand,
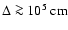 .
Thus,
.
Thus,
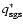 differs from
differs from
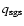 by a few percent at most and the
broadened flame may still very well be represented by a sharp
discontinuity. Moreover, the enhanced flame speed is small compared
to
by a few percent at most and the
broadened flame may still very well be represented by a sharp
discontinuity. Moreover, the enhanced flame speed is small compared
to
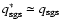 ,
because
,
because
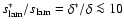 and
and
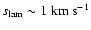 for
for
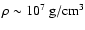 (Timmes & Woosley 1992), whereas
(Timmes & Woosley 1992), whereas
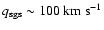 (Schmidt et al. 2006b).
Therefore, the flame speed model (12) can be
carried over unaltered to the thin-reaction-zones regime with an
accuracy better than about 10%, which is within the intrinsic
uncertainties of the model.
(Schmidt et al. 2006b).
Therefore, the flame speed model (12) can be
carried over unaltered to the thin-reaction-zones regime with an
accuracy better than about 10%, which is within the intrinsic
uncertainties of the model.
As the exploding white dwarf expands further and the density drops
below 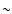
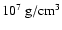 ,
the nuclear time scale rises
rapidly and, inevitably, the
condition (11) for the
broken-reaction-zone regimes will be met. The broadened flame will
then dissolve into a flame brush in which fuel and ash are mixed by
turbulent eddies. Although there is no well defined width
,
the nuclear time scale rises
rapidly and, inevitably, the
condition (11) for the
broken-reaction-zone regimes will be met. The broadened flame will
then dissolve into a flame brush in which fuel and ash are mixed by
turbulent eddies. Although there is no well defined width
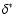 of the flame brush, we can specify a turbulent
mixing length
of the flame brush, we can specify a turbulent
mixing length
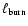 which corresponds to the
typical size of eddies with turn-over time of the order of the
effective reaction time
which corresponds to the
typical size of eddies with turn-over time of the order of the
effective reaction time
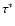 :
:
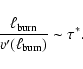 |
(15) |
The length scale
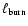 can be regarded as
generalisation of the Gibson length.
can be regarded as
generalisation of the Gibson length.
Since the width of the flame in the thin-reaction-zones regime is
very small compared to typical grid resolutions in simulations of
thermonuclear supernovae, the flame brush in the
broken-reaction-zones regime will initially not be resolved either,
i.e.
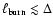 .
In terms of time scales,
.
In terms of time scales,
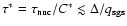 .
As long as this constraint is satisfied, it appears to be a sensible
approximation to propagate the unresolved turbulent flame brush with
the level set method. For
.
As long as this constraint is satisfied, it appears to be a sensible
approximation to propagate the unresolved turbulent flame brush with
the level set method. For
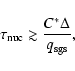 |
(16) |
on the other hand, the level set representation breaks down. Thus,
without implementing an explicit treatment of volume-burning in the
code, the burning process has to be terminated in a numerical
simulation once the above condition is met. Of course, this implies
a dependence of the termination of the burning process on the
numerical resolution. Without including volume-burning, however,
this implication is inevitable. Former numerical simulations of
thermonuclear supernovae with the level set method merely appeared
to be converged because of an artifical termination criterion that
was chosen to be independent of the resolution (see the following
section).
The extension of the level set method into the distributed burning
regime as outlined in this Section markedly differs from the flame
speed model applied by Röpke & Hillebrandt (2005), which is based on
Damköhler's hypothesis (5) and,
consequently, is restricted to the thin-reaction-zones regime.
Essentially, their model is based on the assumption
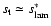 or, equivalently,
or, equivalently,
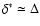 .
It should become clear from the above
discussion, however, that this assumption does not hold.
.
It should become clear from the above
discussion, however, that this assumption does not hold.
4 Numerical simulations
We investigated the effect of including burning with the extended
level set prescription in a follow-up study of Schmidt & Niemeyer (2006). To
that end, we modified the criterion for the termination of the
burning process in the code as follows. From the values of
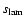 and
and 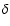 calculated by Timmes & Woosley (1992), we
obtained
calculated by Timmes & Woosley (1992), we
obtained
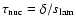 and linearly
fitted
and linearly
fitted
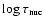 as a function of
as a function of
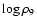 ,
where
,
where 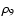 is the mass density in units of
is the mass density in units of
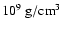 ,
for
,
for
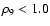 .
The power law
resulting from this fit is
.
The power law
resulting from this fit is
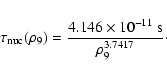 |
(17) |
The data points as well as the corresponding values of the fit
function are listed in Table 1. Evaluating
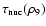 locally in each cell, it can be
checked whether the criterion 16 is fulfilled for a
certain prescribed constant
locally in each cell, it can be
checked whether the criterion 16 is fulfilled for a
certain prescribed constant
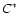 .
If the nuclear time
scale becomes larger than the threshold given by the right-hand
side, burning will be terminated. Since
.
If the nuclear time
scale becomes larger than the threshold given by the right-hand
side, burning will be terminated. Since
 and
and
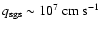 after about one second,
after about one second,
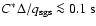 .
Thus,
the power law 17 has to be somewhat extrapolated
towards
.
Thus,
the power law 17 has to be somewhat extrapolated
towards
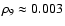 ,
which appears to be reasonable.
,
which appears to be reasonable.
To begin with, we computed a series of single-octant simulations on
grids consisting of N=1283 cells with the code described in
Schmidt et al. (2006b). Due to the hybrid geometry of these grids, with a
fine-resolved uniform inner part and exponentially growing cell size
in the outer part, in combination with the co-expanding grid technique
introduced by (Röpke 2005), it was possible to study trends even
with a relatively small number of grid cells. If we had chosen a
higher resolution, the applicability of the level set method would
have been constrained even further. This can be seen from the
criterion (16) with the scaling law
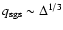 .
Since the nuclear time scale
.
Since the nuclear time scale
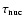 gradually increases as the explosion progresses,
lowering the cutoff length
gradually increases as the explosion progresses,
lowering the cutoff length 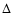 implies that the termination point
will be met earlier. On the other hand, a certain resolution is
mandatory for capturing the large-scale production of turbulence by
Rayleigh-Taylor instabilities. From the resolution study in
Schmidt et al. (2006b) and the influence of doubling the resolution of
thermonuclear supernova simulations with stochastic ignition discussed
by Schmidt & Niemeyer (2006), we conclude that 1283 cells per octant are
sufficient for arriving at a sensible estimate of the total amount of
burning products.
implies that the termination point
will be met earlier. On the other hand, a certain resolution is
mandatory for capturing the large-scale production of turbulence by
Rayleigh-Taylor instabilities. From the resolution study in
Schmidt et al. (2006b) and the influence of doubling the resolution of
thermonuclear supernova simulations with stochastic ignition discussed
by Schmidt & Niemeyer (2006), we conclude that 1283 cells per octant are
sufficient for arriving at a sensible estimate of the total amount of
burning products.
Table 1:
Power-law fit of the nuclear energy timescale
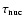 in the
range
in the
range
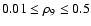 .
The numerical data are taken from
Timmes & Woosley (1992).
.
The numerical data are taken from
Timmes & Woosley (1992).
![\begin{figure}
\par\includegraphics[width=14.8cm,clip]{6510_color/6510fig1}
\end{figure}](/articles/aa/full/2007/13/aa6510-06/Timg119.gif) |
Figure 1:
Single-octant simulations with N=1283,
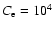 and various choices of
and various choices of 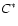 .
Plotted are the
evolution of the total energy and the integrated
mass of intermediate mass elements, respectively. Also
shown is a reference simulation, in which the burning
process was stopped at the density threshold .
Plotted are the
evolution of the total energy and the integrated
mass of intermediate mass elements, respectively. Also
shown is a reference simulation, in which the burning
process was stopped at the density threshold
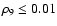 . . |
| Open with DEXTER |
Applying the stochastic ignition procedure formulated by
Schmidt & Niemeyer (2006), we selected a reference model with
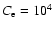 ,
where the parameter
,
where the parameter
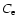 adjusts the time scale of Poisson processes generating the ignition
events in thin adjacent spherical shells. Depending on the choice of
adjusts the time scale of Poisson processes generating the ignition
events in thin adjacent spherical shells. Depending on the choice of
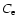 ,
the outcome of the explosion, in particular, the
release of nuclear energy and the total mass of iron group elements
is varying greatly. For
,
the outcome of the explosion, in particular, the
release of nuclear energy and the total mass of iron group elements
is varying greatly. For
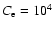 ,
the total number of
ignition events per octant is roughly 100 and the yield of nuclear
energy becomes nearly maximal (see Table 1 and Fig. 1 in
Schmidt & Niemeyer 2006). We repeated this simulation with the same
initial white dwarf model and parameter settings, except for the
termination of the burning process as explained above, using three
different values of
,
the total number of
ignition events per octant is roughly 100 and the yield of nuclear
energy becomes nearly maximal (see Table 1 and Fig. 1 in
Schmidt & Niemeyer 2006). We repeated this simulation with the same
initial white dwarf model and parameter settings, except for the
termination of the burning process as explained above, using three
different values of 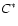 .
.
Table 2:
Total energy release and masses of burning products at
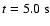 for the simulations shown in Fig. 1.
for the simulations shown in Fig. 1.
![\begin{figure}
\par\includegraphics[width=14.8cm,clip]{6510_color/6510fig2}
\end{figure}](/articles/aa/full/2007/13/aa6510-06/Timg128.gif) |
Figure 2:
Evolution of the total energy and the integrated
mass of intermediate mass elements, respectively, for
several full-star simulations with N=2563. For
each value of the exponentiation parameter
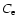 ,
which controls the number of
ignitions events, either ,
which controls the number of
ignitions events, either
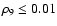 or
or
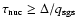 (corresponding to
(corresponding to
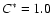 )
was
set for the termination of the burning process. )
was
set for the termination of the burning process. |
| Open with DEXTER |
The time evolution of the total amount of intermediate mass elements
(represented by 24Mg) plotted in the right panel of
Fig. 1 clearly shows the influence of the burning
termination criterion. Assuming
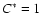 ,
the total magnesium
mass
,
the total magnesium
mass
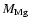 at
at
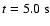 increases by
increases by 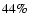 compared to the reference simulation (see Table 2, in
which burning ceases for
compared to the reference simulation (see Table 2, in
which burning ceases for
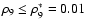 .
One
should note that this is only a lower bound, because
.
One
should note that this is only a lower bound, because
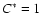 indicates that the broken-reaction-zones regime has just been
entered and volume burning at resolved scales, which cannot be
treated with the present code, would consume even more carbon and
oxygen. The mass of iron group elements (54Ni), on the other
hand, remains unaffected which, of course, reflects nickel being
produced entirely within the flamelet regime at densities
indicates that the broken-reaction-zones regime has just been
entered and volume burning at resolved scales, which cannot be
treated with the present code, would consume even more carbon and
oxygen. The mass of iron group elements (54Ni), on the other
hand, remains unaffected which, of course, reflects nickel being
produced entirely within the flamelet regime at densities
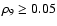 while magnesium is stemming largely from
distributed burning at lower densities. Even for
while magnesium is stemming largely from
distributed burning at lower densities. Even for
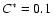 ,
meaning that the extended level set prescription breaks down well
within the broken-reaction-zones regime, the yield of intermediate
mass elements is still higher than in the case of the density
threshold
,
meaning that the extended level set prescription breaks down well
within the broken-reaction-zones regime, the yield of intermediate
mass elements is still higher than in the case of the density
threshold
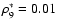 .
If
.
If
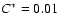 ,
on the other
hand,
,
on the other
hand,
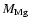 becomes slightly smaller. Since
becomes slightly smaller. Since
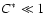 implies a greatly reduced energy generation rate, the physical
quenching of the flame brush would be nearly reached in this case
and, as a consequence, only little volume burning could possibly
follow. In this case, we can be fairly sure that the actual amount
of burning products would be more or less what is seen in the
simulation.
implies a greatly reduced energy generation rate, the physical
quenching of the flame brush would be nearly reached in this case
and, as a consequence, only little volume burning could possibly
follow. In this case, we can be fairly sure that the actual amount
of burning products would be more or less what is seen in the
simulation.
We also performed full-star simulations with N=2563, for which
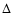 is initially the same as in the single-octant simulations.
Varying the exponentiation parameter
is initially the same as in the single-octant simulations.
Varying the exponentiation parameter
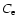 ,
the burning
process was terminated once
,
the burning
process was terminated once
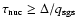 ,
i.e.
,
i.e.
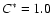 .
The results in comparison to the corresponding
simulations with the termination criterion
.
The results in comparison to the corresponding
simulations with the termination criterion
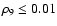 from
Schmidt & Niemeyer (2006) are plotted in Fig. 2. Because of
the substantially larger mass of unburned carbon and oxygen that
will be left over at the transition from iron group to intermediate
mass element production if
from
Schmidt & Niemeyer (2006) are plotted in Fig. 2. Because of
the substantially larger mass of unburned carbon and oxygen that
will be left over at the transition from iron group to intermediate
mass element production if 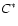 is smaller and, consequently,
the ignition proceeds slower, one would expect
is smaller and, consequently,
the ignition proceeds slower, one would expect
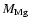 to
increase with
to
increase with
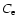 .
However, the burning statistics
listed in Table 3 clearly demonstrates that
.
However, the burning statistics
listed in Table 3 clearly demonstrates that
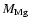 is almost constant for varying
is almost constant for varying
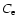 .
Hence, distributed burning appears to consume about the same amount
of fuel independent of the state of the exploding star at the end of
the flamelet regime.
.
Hence, distributed burning appears to consume about the same amount
of fuel independent of the state of the exploding star at the end of
the flamelet regime.
Table 3:
Total energy release and masses of burning products at
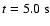 for the simulations shown in Fig. 2.
for the simulations shown in Fig. 2.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6510_color/6510fig3}\par\vspace*{2mm}
\includegraphics[width=6.9cm,clip]{6510fig4}
\end{figure}](/articles/aa/full/2007/13/aa6510-06/Timg136.gif) |
Figure 3:
Total and fractional mass densities in a central
section and the corresponding probability density functions
in radial velocity space for a full-star simulation with
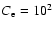 at
at
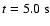 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6510_color/6510fig5}\par\vspace*{2mm}
\includegraphics[width=6.9cm,clip]{6510fig6} \end{figure}](/articles/aa/full/2007/13/aa6510-06/Timg137.gif) |
Figure 4:
Total and fractional mass densities in a central
section and the corresponding probability density functions
in radial velocity space for a full-star simulation with
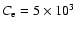 at
at
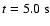 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6510_color/6510fig7}\par\vspace*{2mm}
\includegraphics[width=7.3cm,clip]{6510fig8}
\end{figure}](/articles/aa/full/2007/13/aa6510-06/Timg138.gif) |
Figure 5:
Total and fractional mass densities in a central
section and the corresponding probability density functions
in radial velocity space for a full-star simulation with
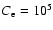 at
at
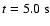 . .
|
| Open with DEXTER |
Figures 3-5 show contour plots of the
total mass density and the partial densities of C+O, Mg and Ni,
respectively, in two-dimensional central sections at time
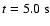 .
In comparison to Figs. 2-4 in
(Schmidt & Niemeyer 2006), which show the corresponding density contours in
the simulations with the burning process terminated if
.
In comparison to Figs. 2-4 in
(Schmidt & Niemeyer 2006), which show the corresponding density contours in
the simulations with the burning process terminated if
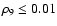 ,
one can see that the explosion ejecta are substantially
enriched in intermediate mass elements. This is also illustrated by
the plots of the fractional masses as function of radial velocity in
Figs. 3-5. Although the residuals of
unburned material at low radial velocities, which have been plaguing
the deflagration models, are still present in each case, it is
likely the a significant further reduction would result from volume
burning beyond the break-down of the level set description.
Nevertheless, a non-negligible amount of carbon and oxygen at radial
velocities larger than about
,
one can see that the explosion ejecta are substantially
enriched in intermediate mass elements. This is also illustrated by
the plots of the fractional masses as function of radial velocity in
Figs. 3-5. Although the residuals of
unburned material at low radial velocities, which have been plaguing
the deflagration models, are still present in each case, it is
likely the a significant further reduction would result from volume
burning beyond the break-down of the level set description.
Nevertheless, a non-negligible amount of carbon and oxygen at radial
velocities larger than about
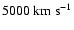 will be left over
for any conceivable choice of parameters.
will be left over
for any conceivable choice of parameters.
We have argued that the turbulent flame propagation speed in
thermonuclear supernova simulations is given by the subgrid scale
turbulent velocity even in the distributed burning regime. Moreover,
the level set representation of the flame front remains valid beyond
the flamelet regime provided that the width of the flame brush is
smaller than grid resolution. In terms of time scales, this
constraint corresponds the termination criterion (16).
Very little is known about the interaction between turbulence and the
burning process in the broken-reaction-zones regime, in which
turbulence is mixing fuel and ash faster than the nuclear reactions
are progressing. Since the break-down of the level set description
possibly occurs in this regime, we introduced the dimensionless
parameter 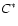 which specifies the reduction of the energy
generation rate due to turbulent entrainment of fuel and ash. The
limiting case
which specifies the reduction of the energy
generation rate due to turbulent entrainment of fuel and ash. The
limiting case
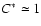 corresponds to the
thin-reaction-zones regime. In this regime, the flame is broadened due
to the enhanced diffusivity in the preheating zone while the reaction
zone is not significantly affected by turbulent eddies. As turbulence
increasingly disturbs the reaction zone,
corresponds to the
thin-reaction-zones regime. In this regime, the flame is broadened due
to the enhanced diffusivity in the preheating zone while the reaction
zone is not significantly affected by turbulent eddies. As turbulence
increasingly disturbs the reaction zone, 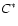 diminishes. For
diminishes. For
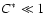 ,
burning will be quenched.
,
burning will be quenched.
Setting 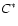 to values in the range from 0.01 to 1, we
performed several supernova simulations with burning being
terminated once (16) was fulfilled. In these
simulations, we applied the stochastic ignition procedure described
in (Schmidt & Niemeyer 2006). For
to values in the range from 0.01 to 1, we
performed several supernova simulations with burning being
terminated once (16) was fulfilled. In these
simulations, we applied the stochastic ignition procedure described
in (Schmidt & Niemeyer 2006). For
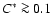 ,
a greater fraction
of intermediate mass elements was produced as in reference
simulations with termination of the burning process at the density
threshold
,
a greater fraction
of intermediate mass elements was produced as in reference
simulations with termination of the burning process at the density
threshold
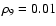 .
Remarkably, we found that
.
Remarkably, we found that
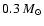 of intermediate mass elements was produced in the case
of intermediate mass elements was produced in the case
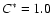 independent of the rapidity of the ignition process.
Consequently, the ignition process mainly determines the total mass of
iron group elements, whereas the production of intermediate mass
elements appears to depend solely on the progression of distributed
burning.
independent of the rapidity of the ignition process.
Consequently, the ignition process mainly determines the total mass of
iron group elements, whereas the production of intermediate mass
elements appears to depend solely on the progression of distributed
burning.
Although a substantial increase of the amount of iron group elements
might result from volume burning at resolved scales, which cannot be
treated within the present methodology, it seems unlikely that the
remaining fraction of carbon and oxygen would be consumed completely.
For this reason, if clear indications of carbon residuals at least in
certain type Ia supernovae were not found, delayed detonations would
be an unavoidable conclusion. Even in this case, however, studying the
physics of distributed burning in more detail might very well help to
clarify the physical mechanism of the putative DDT. On the other hand,
if burning was completed in the distributed mode in some SNe Ia,
small-scale numerical models of burning in the broken-reaction-zones
regime and explicit treatment of volume burning in large-scale
supernova simulations would be the prerequisites for further progress.
Acknowledgements
I thank Jens C. Niemeyer, Friedrich Röpke and Wolfgang Hillebrandt for inspiring
discussions at Schloss Ringberg.
The simulations were run on the HLRB of the Leibniz Computing Centre
in Munich. This work was supported by the Alfried Krupp Prize for
Young University Teachers of the Alfried Krupp von Bohlen und
Halbach Foundation.
- Badenes, C.,
Borkowski, K. J., Hughes, J. P., Hwang, U., & Bravo,
E. 2006, ApJ, 645, 1373 [NASA ADS] [CrossRef] (In the text)
- Bell, J. B.,
Day, M. S., Rendleman, C. A., Woosley, S. E., &
Zingale, M. 2004, ApJ, 608, 883 [NASA ADS] [CrossRef] (In the text)
- Damköhler, G. 1940,
Z. Elektrochem., 46, 601 (In the text)
- Frisch, U. 1995,
Turbulence (Cambridge University Press)
(In the text)
- Gamezo,
V. N., Khokhlov, A. M., & Oran, E. S. 2005, ApJ,
623, 337 [NASA ADS] [CrossRef] (In the text)
- Jha, S.,
Branch, D., Chornock, R., et al. 2006, AJ, 132, 189 [NASA ADS] [CrossRef] (In the text)
- Khokhlov,
A. M., Oran, E. S., & Wheeler, J. C. 1997, ApJ,
478, 678 [NASA ADS] [CrossRef]
- Kim, W., &
Menon, S. 2000a, Combust. Sci. Tech., 160, 119 (In the text)
- Kim, W., &
Menon, S. 2000b, Proc. of the Combustion Institute, 28, 203 (In the text)
- Maier, A.,
& Niemeyer, J. C. 2006, A&A, 451, 207 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Marion,
G. H., Höflich, P., Wheeler, J. C., et al.
2006, ApJ, 645, 1392 [NASA ADS] [CrossRef] (In the text)
- Nandkumar, R.,
& Pethick, C. J. 1984, MNRAS, 209, 511 [NASA ADS] (In the text)
- Niemeyer,
J. C. 1999, ApJ, 523, L57 [NASA ADS] [CrossRef] (In the text)
- Niemeyer,
J. C., & Hillebrandt, W. 1995, AJ, 452, 769 [NASA ADS] [CrossRef] (In the text)
- Niemeyer,
J. C., & Kerstein, A. R. 1997, New Astron., 2,
239 [NASA ADS]
- Niemeyer,
J. C., & Woosley, S. E. 1997, ApJ, 475, 740 [NASA ADS] [CrossRef]
- Peters, N. 1988, in
21st Int. Symp. on Combustion, Combustion Institute,
Pittsburgh, 1232
(In the text)
- Peters, N. 1999, J.
Fluid Mech., 384, 107 [NASA ADS] [CrossRef] (In the text)
- Plewa, T.,
Calder, A. C., & Lamb, D. Q. 2004, ApJ, 612, L37 [NASA ADS] [CrossRef] (In the text)
- Pocheau, A. 1994,
Phys. Rev. E, 49, 1109 [NASA ADS] [CrossRef]
- Reinecke,
M., Hillebrandt, W., & Niemeyer, J. C. 1999a, A&A,
347, 739 [NASA ADS] (In the text)
- Reinecke,
M., Hillebrandt, W., Niemeyer, J. C., Klein, R., &
Gröbl, A. 1999b, A&A, 347, 724 [NASA ADS] (In the text)
- Röpke, F. K.
2005, A&A, 432, 969 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Röpke,
F. K., & Hillebrandt, W. 2005, A&A, 429, L29 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Röpke,
F. K., Hillebrandt, W., Niemeyer, J. C., & Woosley,
S. E. 2006, A&A, 448, 1 [NASA ADS] [CrossRef] [EDP Sciences]
- Schmidt, W.,
& Niemeyer, J. C. 2006, A&A, 446, 627 [NASA ADS] [CrossRef] [EDP Sciences]
- Schmidt, W.,
Hillebrandt, W., & Niemeyer, J. C. 2005, Combust. Theory
Modelling, 9, 693 [CrossRef] (In the text)
- Schmidt, W.,
Niemeyer, J. C., & Hillebrandt 2006a, A&A, 450,
265 [NASA ADS] [CrossRef] [EDP Sciences]
- Schmidt, W.,
Niemeyer, J. C., Hillebrandt, W., & Röpke, F. K.
2006b, A&A, 450, 283 [NASA ADS] [CrossRef] [EDP Sciences]
- Stritzinger,
M., Leibundgut, B., Walch, S., & Contardo, G. 2006, A&A,
450, 241 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Timmes,
F. X., & Woosley, S. E. 1992, ApJ, 396, 649 [NASA ADS] [CrossRef] (In the text)
- Wunsch, S., &
Woosley, S. E. 2004, AJ, 616, 1102 [NASA ADS] [CrossRef] (In the text)
- Yakhot, V., &
Orszag, S. A. 1986, Phys. Rev. Lett., 57, 1722 [NASA ADS] [CrossRef] (In the text)
- Zingale, M.,
Woosley, S. E., Rendleman, C. A., Day, M. S., &
Bell, J. B. 2005, ApJ, 632, 1021 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2007
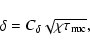
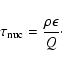
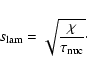
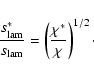
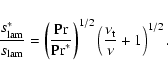
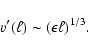
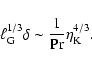
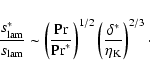
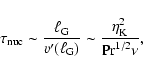
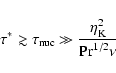
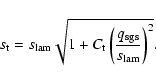
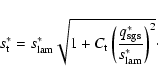
![\begin{displaymath}\frac{q_{{\rm sgs}}^{\ast}}{q_{{\rm sgs}}}\simeq
\left[1-\left(\frac{\delta^{\ast}}{\Delta}\right)^{2/3}\right]^{1/2}\cdot
\end{displaymath}](/articles/aa/full/2007/13/aa6510-06/img77.gif)
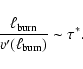
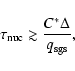
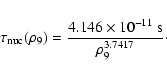
![\begin{figure}
\par\includegraphics[width=14.8cm,clip]{6510_color/6510fig1}
\end{figure}](/articles/aa/full/2007/13/aa6510-06/Timg119.gif)
![\begin{figure}
\par\includegraphics[width=14.8cm,clip]{6510_color/6510fig2}
\end{figure}](/articles/aa/full/2007/13/aa6510-06/Timg128.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6510_color/6510fig3}\par\vspace*{2mm}
\includegraphics[width=6.9cm,clip]{6510fig4}
\end{figure}](/articles/aa/full/2007/13/aa6510-06/Timg136.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6510_color/6510fig5}\par\vspace*{2mm}
\includegraphics[width=6.9cm,clip]{6510fig6} \end{figure}](/articles/aa/full/2007/13/aa6510-06/Timg137.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6510_color/6510fig7}\par\vspace*{2mm}
\includegraphics[width=7.3cm,clip]{6510fig8}
\end{figure}](/articles/aa/full/2007/13/aa6510-06/Timg138.gif)