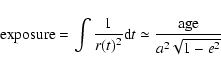
A&A 464, 1139-1146 (2007)
DOI: 10.1051/0004-6361:20066532

Towards a general model of space weathering of S-complex asteroids and ordinary chondrites

P. Paolicchi¹ - S. Marchi² - D. Nesvorný³ - S. Magrin⁴ - M. Lazzarin⁵

1 - Dipartimento di Fisica, Università di Pisa, largo Pontecorvo 3, 56127 Pisa, Italy
2 - Dipartimento di Astronomia, Università di Padova, Vicolo dell'Osservatorio 2, 35122 Padova, Italy
3 - Department of Space Studies, Southwest Research Institute, 1050 Walnut St., Boulder, CO 80302, USA
4 - Dipartimento di Astronomia, Università di Padova, Vicolo dell'Osservatorio 2, 35122 Padova, Italy
5 - Dipartimento di Astronomia, Università di Padova, Vicolo dell'Osservatorio 2, 35122 Padova, Italy

Received 10 October 2006 / Accepted 5 January 2007

Abstract
Context. The effect of the space weathering on the spectral properties of the S-complex asteroids has been widely discussed in recent times, and a systematic reddening due to the exposure to the various influxes has been found. The evolution of spectral properties is also affected by other processes, such as close encounters with planetary bodies.
Aims. In this paper we present our model of asteroidal space weathering, combining the previous analyses and using an increased dataset. We also provide a link with ordinary chondrite meteorites.
Methods. We revise also some age estimates in terms of dynamical and physical considerations.
Results. The present analysis qualitatively confirms the previous results, but a by far more refined and reliable slope-exposure relation is obtained, capable to include in a unique scenario the ordinary chondrite meteorites, NEOs, Mars Crossers and Main Belt asteroids. Moreover, we show that, on the basis of spectroscopic properties, Mars Crossers should be, on the average, significantly younger than Main Belt asteroids of the same size. Finally, we find that the solar ion flux is the most relevant source of the asteroidal space weathering.
Conclusions. The properties of ordinary chondrite meteorites, NEOs, Mars Crossers and Main Belt asteroids can be included in a unique scenario. This has unveiled the relevant processes - some newly discovered - which play an important role in determining the evolution of the spectral properties of these bodies over time.

Key words: miror planets, asteroids

1 Introduction

The action of the space environment on optical properties of asteroid surfaces has been put into evidence in several recent papers (Hiroi & Sasaki 2001; Brunetto & Strazzulla 2005; Hapke 2001; Clark et al. 2002; Chapman 2004). In particular, the analysis of the so-called space weathering has been thorough and systematic for what concerns the S-complex asteroids, for which the surface is expected to become redder and darker over time. After the work of Binzel et al. (2004) devoted to Near Earth Asteroids, a colour-age relation has been suggested in an analysis devoted to Main Belt family asteroids (Nesvorný et al. 2005; Jedicke et al. 2004). More recently, a general relation has been shown to hold for all S-complex asteroids (Marchi et al. 2006a, hereinafter referred as Paper I). It has also been shown that the most significant parameter to be correlated with the colour change (in technical terms, the observed spectral slope) is not the diameter nor the age but the "exposure'' defined as

$${\rm exposure} = \int{\frac{1}{r(t)^2}{\rm d}t} \simeq \frac{\rm age}{a^2 \sqrt{1-e^2}}$$

i.e. the age times the inverse squared mean distance from the Sun (function of the semimajor axis, a and of the eccentricity, e). The relevance of the exposure parameter entails the dominance, at least for distances smaller than about 3-4 AU, of space weathering effects connected to the Sun (such as, for instance, the ion bombardment; see Lazzarin et al. 2006).

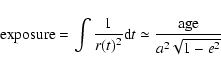
In a following paper (Marchi et al. 2006b, hereinafter referred as Paper II) a relation has been evidenced to hold for Near Earth Asteroids and Mars crossers, involving the perihelion distance and the spectral slope. The underlying idea is that a smaller perihelion distance increases the probability of having undergone a recent close encounter with one of the inner planets (Nesvorný et al. 2005). The tidal effects of a deep encounter might severely affect the surface, introducing, among the others, a sort of de-weathering, i.e. a rejuvenation of the asteroidal surface.

In the reality the weathering and the de-weathering effects act simultaneously on the asteroids (MBAs, NEAs and so on), even if the range of application of the tidal-triggered de-weathering is essentially limited to the inner bodies.

In this paper we try to combine the analyses introduced in Papers I and II. We will use an updated database, including also the new spectroscopic data obtained by S³OS² survey (about 190 objects were not present in previous works; Lazzaro et al. 2004) and 70 MCs, for a grand total of 1026 S-complex asteroids, most of which are from SMASSII. The combined analysis will require also a more detailed discussion of various dynamical and evolutionary effects.

2 Improving the analysis

A detailed study of the role of space weathering (SW hereinafter) has to deal with large samples. Studies of single asteroids, as those performed by space missions (e.g. NEAR, Galileo, etc., on Eros, Ida etc.), provide many important data. Nevertheless, the problem of the diversity and the complexity of the SW processes arose from these different studies, so that one may speak of three different "kinds'' of SW: lunar-like, Eros-like and Ida-like. As for the lunar case, weathering causes reddening and darkening; in the case of Ida, significant spectral variations are seen but no albedo variations. Finally, for Eros, large albedo variations are seen, but no apparent spectral variations.

We think that a global understanding may come only from a systematic analysis of large samples, namely through a statistical approach.

The statistical analysis of the spectroscopic properties of asteroids, aimed to improve the understanding of the space-weathering processes, faces a fundamental difficulty. On one side, one has to deal with a large number of bodies, to avoid overwhelming statistical errors and biases. On the other hand every available large observational sample is not homogeneous, including bodies of different size, structure, chemical composition, collisional and dynamical history, and present orbital properties. Thus we are forced to introduce strong simplifications, and, simultaneously, to try to understand the whole complexity of the involved physical processes.

For instance, the relation, computed in Paper I, estimated the age of a MB asteroid in terms only of its individual collisional lifetime. It is a simplification, even if reasonable, which does not take into account some additional constraints, discussed below.

2.1 The role of dynamical families

In Paper I we have estimated the age of the Main Belt asteroids in terms of their individual collisional lifetimes. The estimate may be wrong when the asteroid is member of a dynamical family. The formation of a family is assumed to outcome from a violent collisional process (e.g. Zappalà et al. 2002), usually catastrophically breaking both projectile and target involved in the impact, sometimes (for instance, in the case of Vesta family) only creating a large crater on the - massive - target body. In all cases the process converts internal parts of the parent body into surface regions of the resulting fragments. Also the - space weathered - surface of the parent body is presumably deeply shaken, and thus it may appear as rejuvenated when observed as surface of the largest remnant. However, this latter consideration is rather tentative, and the surface properties of the largest remnant may depend on the individual properties of the generating collision. In general we expect that, when the family has been created, most of the surfaces of its members are spectroscopically young: the age of the family is an upper limit to the age of its members; this value has thus to be used also to constrain the time a family asteroid has been exposed to space-weathering. In principle some bodies may be also younger, if the further collisional evolution has been intense enough.

For most of the spectroscopically studied family members, which are, usually, not too small bodies, the family age is smaller than the mean age one should obtain from the formula used in Paper I. In the present paper we have used the new estimates of family ages presented in Nesvorný et al. (2006). Whenever the age (computed according to our method) of a family asteroid exceeds the estimated age of the family we use this latter value as its true age. A further discussion will be presented below. For background asteroids we estimate the age with the same method used in Paper I.

2.2 Proper elements

We should take into account an additional, more subtle and general, effect. It is well-known that the osculating orbital elements of the asteroids are valid only for the present time: they are affected by several changes with time, due to the combined perturbations of various planets. The short periodic variations may be eliminated using the mean elements instead of the osculating ones (Knezevic et al. 2002); a further step leads to the definition of proper elements, which are not, rigorously speaking, the mean orbital elements, but which are endowed of several advantages: they are - in most cases - nearly constant in time, are fairly representative of the long term averaged elements, and have been listed in general catalogues. Thus it is reasonable to use the proper elements instead of the osculating ones. This improvement has been introduced in the present paper, for all the cases in which proper elements are available.

2.3 Resonances and chaos

It is well-known (see, for instance, Nesvorný et al. 2002a; Morbidelli et al. 2002) that the Main Belt is densely textured by resonant regions; among them the main mean motion resonances, as well-known from a long time, sculpt the overall structure of the Main Belt. In presence of a mean motion resonance, as for a first approximation, the proper semimajor axis does not change, but the other elements, and in particular the eccentricity, are rapidly varying with time, often with a marked chaotic behaviour. In general, the stability in time of proper elements may be strongly different for different asteroids, also in the same region of the Belt. The plots of Fig. have been obtained from data downloaded from the Website Astdys (Knezevic & Milani 2003, and http://hamilton.dm.unipi.it/astdys/astibo) and are similar to the figures http://hamilton.dm.unipi.it/astdys/propsynth/allae.gif and ...allai.gif, there represented . They represent the quality (reliability, stability) of synthetic proper elements in the a-i and a-e planes. In the present figures only the asteroids used in our analysis have been represented.

Figure 1: The stability of the proper elements in the MB (we plot a vs. e ( upper panel) and a vs. $\sin i$ ( lower panel)). As in the original Astdys figures the black dots are the bodies with stable proper elements; in some cases the proper element undergo some not negligible oscillations (here represented by stars; we used the rms deviation, maximum between e and i, for sake of homogeneity with the above quoted figures presented in the Astdys site). In other cases the chaotic behaviour is suggested by a Lyapounov time smaller than a given threshold ( $\tau_{\rm L} <20~000~\rm{y}$, here represented by diamonds).

Open with DEXTER

In some cases the proper elements undergo some not negligible oscillations in time; in other cases the chaotic behaviour is suggested by a Lyapounov time $\tau_{\rm L}$ smaller than a given threshold (the diamonds correspond to a $\tau_{\rm L} <20~000~\rm{y}$). Both these problems involve only a minority of the bodies (633 over 745 MBAs in our sample do not undergo either problem). In principle even significant oscillations of the proper elements may be not too interesting for our purposes (they affect the dependence on the distance from the Sun, but not too critically), while sometimes a chaotic evolution may cause even a major instability of the orbit.

In general the age of an asteroid depends on its past evolution which has carried it into the present orbit, and not on the present properties of its orbit; moreover if the orbits are chaotic it is not safe to try to reconstruct the past evolution. However, being in a unstable orbit - now - suggests that also the past evolution may have been strongly perturbed: in other terms, the probability of a past history including strong changes in the orbital parameters is larger.

Sometimes, for instance, a chaotic evolution increases the probability of close encounters with inner or outer planets. In this case the estimated asteroid age should be affected by dynamical considerations and, in general, should be smaller than that resulting from the bare collisional evolution.

In general, we can suggest that several Main Belt asteroids may be younger than we estimated with our model. Consequently, we are presumably underestimating the steepness of the slope-age relation, presented in Paper I.

It is less obvious whether similar considerations may apply also to bodies which undergo a significant oscillation of the proper elements, even if this feature also is diagnostic of a "perturbed'' dynamical evolution.

In order to clarify the above mentioned problems, in Fig. 2 (left panel) we plotted the slope (from our data) vs. the Lyapounov exponent (obtained from Astdys) for the MBAs in our sample. Since most of the Astdys estimates have been obtained with an integration time of $2\times 10^6~\rm {y}$, we decided to take into account only the cases for which the Lyapounov exponent was exceeding the value of 5 which is, according to the units (My) used in the Astdys file, equivalent to a Lyapounov time of $200~000~\rm {y}$. For smaller exponents a fully reliable computation should require a longer integration time (A. Milani, private communication).

A steady decrease of the mean slope for the shorter Lyapounov times can be found: the mean slope (computed for all 745 MBAs) is of the order of 0.5, decreasing to about 0.485 for $\tau_{\rm L} <20~000~\rm{y}$ (68 bodies) and to 0.425 for $\tau_{\rm L} < 10~000~\rm {y}$ (only 27 bodies). In general a slope-Lyapounov exponent linear correlation can be obtained. However, due also to the poor statistics, its statistical significance is not sure (the two tailed probability is of the order of $10\%$, while a $5\%$ level is required for a fully meaningful correlation).

In Fig. 2 (right panel) we plotted the slope vs. the rms deviation of proper elements (maximum between e and i). Again, a slope-rms anticorrelation comes out, but its statistical significance is even more uncertain (the two-tailed probability rises up to $31\%$).

Figure 2: The figure in the left panel represents the spectral slope of the numbered MB asteroids vs. the Lyapounov exponent (in $~\rm{My^{-1}}$, logarithmic scale) obtained by Astdys database. Note that only the cases for which the exponent is larger than 5 have been included (see text). The curve represents the best linear fit. The figure in the right panel represents the slope vs. the maximum rms deviation (in logarithmic scale), concerning proper eccentricity or inclination, obtained during the computation of synthetic proper elements. The curve represents the best linear fit.

Open with DEXTER

At the moment the statistical relevance of the above mentioned dynamical effects, at least for what concerns the age estimate, seems to be poor: the percentage of involved bodies is rather small and the correlations are shallow and statistically not significant. Maybe a future increase of the observational database and an improvement of dynamical computations will change the present conclusions.

Note also that the task of individually estimating the "dynamical age'' for all MB asteroids is extremely ambitious. Even if we assume that the presence of a chaotic orbit - now - is strictly meaningful to guess the properties of the past evolution, we have to remind that a chaotic behaviour means usually a strong evolution for what concerns the proper eccentricity, not the semimajor axis. If the resonance is not too strong, or close to other secular resonances, the main effect may be only the oscillation of the asteroid in the same macroregion of the Belt. Only in a few cases the history may be qualitatively different.

On the other hand, it is well-known (A. Milani, private communication) that several asteroids close to the secular resonance $\nu_6$ have, simultaneously, a strong dynamical instability and a small computed Lyapounov exponent. Something similar happens also for Mars Crossers (see next section), whose dynamical status is far from being too quiet: however their Lyapounov exponents are distributed in a qualitatively similar way as MBAs and the slope-Lyapounov exponent plot gives no significant correlation.

On the basis of the previous considerations we decided not to include in our model any dynamical correction to the age of MBAs.

2.4 Mars crossers; the exposure-corrected-slope perihelion relation and the age correction

The situation may be different for what concerns the sample of Mars crossers, bodies which are at the border between NEAs and MB bodies, and are thus critical to glue the properties of MB asteroids and NEOs.

The considerations presented before suggest that their age estimates, obtained neglecting the dynamical corrections, may be wrong. Even the properties of the region, in the MB, from which they may have been originated, are somehow peculiar. The relevance of the - relatively - young (Nesvorny et al. 2006) Flora cluster in the region may affect their age.

Apart the theoretical considerations, the existence of some problems concerning MCs comes out into evidence when we try to combine the results of Papers I and  II.

In Paper II we plotted the spectral slope vs. the perihelion distance, for NEO and MC bodies, finding a significant relation.

However, the spectral slope is the combined result of ageing (space-weathering) and rejuvenating processes. If a body has suffered a recent deeply close encounter with a planet, its spectral properties are dominated by rejuvenating effects; otherwise, they depend on its age. Thus, in mean, we expect that older bodies should have a redder spectrum, for a given perihelion distance, and closer bodies a flatter one, for a given age. In order to eliminate from the perihelion effect possible fake trends - as for instance those due to systematic differences in size - we introduce the exposure-corrected-slope (ECS) vs. perihelion relation (Fig. 3), where the ECS is defined as the difference between the observed slope and the correcting term due to the slope-exposure relation discussed in Paper I (for the moment we do not include the improving corrections presented above). The slope-perihelion relation continues to hold. However, the data concerning the Mars crossers seem to have been systematically over-corrected.

Figure 3: The combination of Papers I and II: the exposure-corrected slope (see text) vs. the perihelion. The symbols have a size which is proportional to the physical size of the corresponding body. Different symbols are used for S and Q types (see Paper II for a detailed discussion). The slope-perihelion relation is confirmed, but the Mars Crossers have a systematically smaller ECS in comparison to NEOs. See the text for discussion. The vertical dotted lines correspond to the semimajor axes of the planets.

Open with DEXTER

It seems reasonable to argue that this result is a direct consequence of the significant overestimate of their age. As already told, it is not easy to estimate their real age. Moreover some MCs may have already suffered a close encounter with Mars, with a consequent rejuvenation of the surface properties. In principle, every body should be analyzed independently; however this project goes beyond the scope of the present analysis.

A first order estimate of the age correction might be introduced assuming that the smaller mean spectral slope of Mars crossers compared to MBAs is fully due to their typical smaller age. The mean slope of MCs is $\simeq$0.447 $\mu$m, compared to the above quoted MBA value ($\simeq$0.503 $\mu$m).

We replot the slope-exposure relation, for MBAs only (excluding NEOs and MC bodies), but including the correction (above discussed) for proper elements and family members (Fig. 4). In the plot the "mean-MC'' (slope-exposure) is also plotted, where the age, and thus the exposure, are computed according to the usual formula. This mean value is well below the best fit line. As already told, this discrepancy may be due both to a smaller age and to some rejuvenating close encounter. However we neglect this latter term, and correct the age of all MCs by a factor $\alpha$, in order to realign the MCs to the MBAs plot. It turns out that $\alpha \simeq 0.31$. In other words, for a given size, MCs are about 70% younger then MBAs.

Figure 4: The slope-exposure relation for the MB asteroids (+) allows to obtain a linear fit. The mean slope-exposure value corresponding to Mars crossers is well below the best fit line. We adjusted the age (and thus the exposure) of Mars crossers to have their mean value consistent with the MBAs best fit line. With this correction the Mars crossers are represented in the figure. The exposure correction correspond to the distance between the two vertical lines.

Open with DEXTER

2.5 Including NEOs

We are now ready to include all S-complex asteroids (NEOs, MCs and MBAs) in a unique plot (Fig. 5). We can also try to plot a best fit curve. We replot a linear fit, as we did in Paper I. The linear fit, represented in the figure, is highly significant. However, taking into account some general physical considerations (see the Discussion) and the fit presented by Nesvorný et al. (2005) for what concerns family asteroids, we decided to look also for a logarithmic slope-exposure one.

	Figure 5: The slope-exposure plot including MBAs, MC and NEOs. A linear fit is plotted, as done in Paper I. A logarithmic plot is also represented (see the text for comparison and discussion).
Open with DEXTER

The best fit curve is represented in the figure. It corresponds to a correlation coefficient equal to 0.375. In terms of the rms deviation of the data from the fit (variance) we pass from a value ${\rm rms}=0.2211$ (linear fit) to a value ${\rm rms}=0.2051$ (logarithmic fit; note that the number of parameters is the same in the two cases). Thus, combining the physical suggestions and this - moderate - statistical improvement, we decided to go on with the logarithmic plot.

3 The slope vs. perihelion correction

3.1 Slope-perihelion, Act II

We recall the conclusions presented in Paper II. There is a significant evidence for the existence of a slope-perihelion correlation, in the range of NEOs and MCs. It should be taken into account, not to mix different effects. In order to do so, we represent the ECS vs. perihelion for all asteroids in our sample. The ECS has been computed (see above) subtracting from the actual spectral slope the mean slope obtained from the best fit curve of Fig. 5 and corresponding to the same exposure. The plot is represented in Fig. 6.

Figure 6: Using the logarithmic fit presented in the previous figure, we have corrected the observed slope. We plot the residual slope value (i.e. the difference between the real and the fit values) as function of the perihelion. The existence of a significant relation between the residual slope and the perihelion is apparent at least for semimajor axis smaller than 1 AU. The features in the region between the Earth and Mars are discussed in the text.

Open with DEXTER

As we can see, there is a systematic and significant residual deviation for perihelia smaller than - about - 1AU. The figure reproduces the slope-perihelion real relation, and should be seen as an improved version of Fig. 1, Paper II. No significant deviation is present for perihelia larger than Mars semimajor axis. The intermediate region is somehow less clear. Some effect can be found among MCs, in accordance with the suggestions given in Paper II, but there is a decrease in the outer region of NEOs. However, due to the not striking statistical evidence, we decide, at least for the moment, to neglect this effect, and to limit the slope-perihelion correction to 1.016 AU (namely the Earth's aphelion distance). The linear fit slope-perihelion for distance less than 1.016 AU:

$${\rm slope} \simeq -0.44 + 0.47\cdot q$$

(q is the perihelion distance in AU) is then used to introduce a perihelion correction to the slope exposure relation. The simplest way to do it is simply to compute the PCS (perihelion corrected slope), by subtracting the perihelion correction (if applicable) from the observed slope.

3.2 The corrected best fit

After the elimination of the perihelion correction, the observed reddening has again been fitted with a log-relation (Fig. 7). In principle, one should follow a more sophisticated path, looking for a multi-parameter slope-perihelion-exposure relation. We remark also that the problems presented above may entail a partial indetermination of the age-correction for MCs and, as a consequence, a possible overextension of the perihelion correction region from about 1 to 1.6 AU (as in Paper II). However we see that the corrected slope-exposure plot is rather similar to the uncorrected one. Thus we guess that the uncertainties involved in the modelling and in the procedure should be not significant, and adopt the resulting plot as enough accurate.

Figure 7: Slope final plot. In the right panel we represent the distribution of the slope of ordinary chondrites. Note that the slope is on the ordinate, while the number of objects is in abscissa. The mean slope for ordinary chondrites is represented by the horizontal line, which continues also in the left panel. In this latter, we represent the slope-exposure for all asteroids in our sample. The exposure is now represented in a logarithmic scale, thus the logarithmic fit is given by a line. We compare the "nominal'' fit (represented in Fig. 5) and the perihelion-corrected one (solid line). We represent also the slope-exposure relation which can be obtained from the photometric data on family asteroids presented by Nesvorny et al. (2005). See text for discussion.

Open with DEXTER

The best fit coefficients are:

$$PCS \simeq 0.07+0.17\cdot \log~({\rm exposure}).$$

The variance is slightly smaller than that obtained above ( ${\rm rms}=0.200$). The exposure range is from about 0.7 to 800 My AU^-2. At 1 AU this corresponds to an excursion from 0.7 My to 800 My; or 2.8 My to 3.2 Gy at 2 AU.

In this range of exposure, PCS vary from 0.044 $\mu$m to 0.559 $\mu$m, namely it increases by more than one order of magnitude. Notice that the reddening is very steep at the beginning, and, for instance, the 80% of the excursion is reached at about 200 My at 1 AU; or 800 My at 2 AU.

Also the albedo (see Sect. 2) is assumed to play an important role in the SW. However, no statistically significant correlation between the albedo and the exposure trend has been found (using a sample of 292 S-complex MBAs wih IRAS albedo), maybe also due to the poor statistics.

4 Discussion, open problems and conclusions

The fit obtained in the previous Section is not the only possible one, but is fully representative of the two major features of the data: the steep increase in the slopes for very short exposures, and the nearly-saturated trend for large exposures. Both features are qualitatively observed also in laboratory experiments. Indeed in laboratory experiments is not easy to obtain an unique relation capable to reproduce the reddening: the exact reddening rate depends on several parameters, as the composition, the grain size and so on. Nevertheless, the logarithmic relation is the most suitable for the purpose of a general description (R. Brunetto, private communication). On the other hand, the log-fit cannot be significant (due to its divergent behaviour at the t=0, $\rm exposure=0$ limit) to reproduce the very beginning of the slope-exposure relation, in particular for $\rm exposure \sim 0$. We may shed light on this region with the aid of ordinary chondrite meteorites (OCs). We selected from RELAB (http://www.planetary.brown.edu/relab/rel_pub/) a large sample of non-weathered OCs (about 180), which can be used as the zero-exposure point (see also Marchi et al. 2005). Their average value is 0.059 $\mu$m. It turns out that this value is very similar to the value of the log-fit at 0.7 My AU^-2. It is presumably an artifact due to the logarithmic fit, more than a threshold time limit for a significant weathering.

However, a new - somehow critical - information has to be added to the above discussion. This is provided by the laboratory experiments and by the asteroid (832) Karin.

A detailed comparison between the timescales suggested by our analysis of data with those obtained from laboratory experiments is not straightforward, due to severe scaling problems from laboratory simulations and astrophysical cases. Moreover, several processes act simultaneously in space: the analysis is by far more difficult. However, it is estimated that at 1 AU heavy solar ion irradiation attains pronounced reddening over 10⁴-10⁶ y (via target atom displacements, see Brunetto & Strazzulla 2005); a similar timescale is attained also for solar light ions (via sputtering, see Hapke 2001, and references therein). In comparison, laser irradiation (simulating micro meteoroid impacts) seems to be slower, some 10⁸ y at the same distance. The SW due to ion irradiation seems to work in the very first period of an asteroid life. More than thirty years after the pioneering papers by Hapke on the sputtering by hydrogen atoms (see, for instance, Hapke 1973), the debate about the relative importance of heavy vs. light ions, and of the related physical processes, remains open. However, it is not relevant for the purpose of the present paper.

Somehow this fast reddening is confirmed by the observations of (832) Karin, a very interesting object, whose age (5.7 My, see Nesvorný et al. 2002b) is accurately known. We can easily obtain its resulting exposure, if we assume that the surface properties have been reset at the breakup time:

$${\rm exposure} \sim 0.68~\rm {My~AU}^{-2}.$$

Recently Brunetto et al. (2006) provided the first modeling of its visual-NIR spectrum, indicating that its reddening is compatible with its estimated age on the basis of the rapid heavy ion bombardment. They also reported how the nonweathered (832) Karin should look like, and therefore can be used as zero-exposure point. Its visual slopes are 0.2987 and -0.1554 $\mu$m, respectively. So, despite of (832) Karin's young age, it seems that its surface has suffered a substantial reddening compared to its assumed original properties.

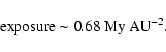
Notice also that other asteroids with low exposure and red slopes do exist (see Fig. 7), they mainly belong to the NEO population where large indetermination on the exposure may be present.

It is not obvious how to relate these results with our data. From a purely mathematical point of view, our logarithmic fit is completely consistent with a strong early reddening (in mathematical terms, even with a infinite initial reddening rate). However, if the initial reddening is relevant, two serious problems arise:

• the mean slopes of the young asteroids should exceed those of OCs by a lot, by far more than we see; in the plot a body such as (832) Karin (which is not in our sample) should be well above the mean relation, while the "original Karin'' should be in the lower slope range of OCs;
• if the reddening timescale is so short, one should obtain a complete saturation of space weathering at ages well smaller than the ages of the oldest asteroids in our sample. The curve should become flat. It is not so, and it is not an artifact of the fitting process. Also the running average curve slope-exposure shows no complete saturation at all.

The difficulty is presumably real. One might avoid it with ad hoc explanations: the reddening model used for (832) Karin may be wrong; the interpretation of experimental data may require some re-calibration; the surface of (832) Karin might be not all so young (for this hypothesis observations covering all rotational phases should be urged). However we think that these solutions are not satisfactory. On the other hand our statistical analysis seems very robust; thus we guess that other processes should be at work to slow down the SW on the asteroidal surfaces and to avoid full saturation.

The most immediate suggestion may be to invoke the regolith mixing. In analogy with what observed on the Moon, regolith evolution is a complex process, which involves gardening (stirring of grains by micrometeorites), erosion (from impacts and solar wind sputtering), maturation (exposure on the bare surface to solar winds ions and micrometeorite impacts) and comminution of coarse grains into finer grains, blanket deposition of coarse-grained layers, and other processes. As a result, the degree of maturation of the regolith varies with depth, and reaches depths by far exceeding the tens of nanometers attained in laboratory experiments (e.g. see Rao et al. 1999; Korotev et al. 1997). Therefore the observed discrepancy would be the result of the reddening and the mixing of the upper layer due to meteoritic impacts. Unfortunately, the verification or falsification of a such a possibility is presently out of reach, also due to the lacking knowledge of the meteoroid distribution in the Main Belt. We might obtain and indirect clue of the existence of a complex surface evolution from the analysis of the different degrees of space weathering measured in different places of spatially resolved asteroids. The only existing data we have involve smaller sizes, namely dust particles. However, given the involved sizes (from sub-microns to hundreds of $\mu$m) they are not expected to be relevant for the layer mixing processes. Nevertheless, the dust may play a role in the reddening of the surfaces, as suggested by laser irradiation experiments (e.g. Sasaki et al. 2001). However the extrapolation of this experiments to the reality of impact between dust particles and asteroidal surfaces is still under debate. For this, we need to know the sources of the dust. We remind that the dust is produced by several sources (cometary, asteroidal, transnettunian etc.) and the relative contribution is not yet established (see for instance Ipatov & Mather 2006; Dermott et al. 2002). Different sources have different impact velocity and size distribution, so impacts may have completely different outcome. Also the radial density distribution is not well constrained inside the Main Belt. Therefore the extrapolation of the timescale produced by Sasaki et al. (2001) ( $10^8~\rm {y}$ at 1 AU) to the Main Belt region could be completely misleading.

Here we limit to stress that if the main source for the dust is the collisions among asteroids in the Main Belt (Dermott et al. 2002), we may expect to find some correlation between the position of the main asteroidal families (which originate the dust bands, which in turn provide material for the zodiacal background) and the asteroidal spectral reddening. We find no correlation between the position of the families and the oscillations of the average corrected slope (see Fig. 8).

Figure 8: We represent the deviation of the mean slope from the fitted relation as a function of the semimajor axis in the region of Main Belt. For comparison, we represent also the location of dynamical families, with different properties (the dots correspond to strongly fractured families, for which the estimated mass of the largest fragment is less than $30\%$ of the parent body mass. The comparison shows no evident correlation between the structure of the deviation plot and the presence of families. See text for discussion.

Open with DEXTER

Moreover in this case the radial distribution of the dust within the Main Belt is expected to be very weakly related to the radial distance, in contrary of the trend we find (see Paper I). In other words, this seems to suggest that the contribution of the dust to the reddening of MBAs is negligible, a conclusion which is also supported by the time-scales considerations reported before. On the contrary, if the cometary contribution to the dust is dominant (Ipatov & Mather 2006) no firm conclusion can be drawn.

4.1 The slope-age (or exposure) relation for the families

It is also interesting to compare the slope-exposure relation limited to family asteroids, obtained according to our data, i.e. with the use of the slope computed from the spectroscopic data, to that published in Jedicke et al. (2004), Nesvorný et al. (2005), obtained with photometric data. Notice that those works used the principal component analysis (PC1 and PC2) and not the photometric slope. In order to compare their results with ours, we have converted their PC1 into slope, using the linear relation proposed by Nesvorný et al. (2006, see their Fig. 10). In addition, their definition of slope is different from ours because of the different spectral range (from 0.52 to 0.92 $\mu$m our spectral slope; from 0.36 to 0.91 $\mu$m the photometric one) and the normalization (our spectra have been normalized at 0.55 $\mu$m). Therefore the definition of our spectral slope is not the same of the photometric one and we cannot expect the same values. Finally, we estimated the exposure for each family using the family's age and the orbit of the largest members. The results are compared in Fig. 7. We show that the slope-exposure trends found in the analysis limited to MB families and the present one, more general and spanning a larger exposure range, are very similar, even if the absolute value of the estimated slope is different, due to different definitions.

4.2 Conclusions

The combination of the slope-exposure and slope-perihelion relations presented in Papers I and II has been performed, also with the use of new data and of an improved analysis of the age of MB and MC asteroids. The presented final slope-exposure relation qualitatively confirms the results, and the underlying physical ideas, discussed in the previous papers. However, the slope-exposure relation is less steep than previously discussed, and may be properly fitted with a logarithmic relation.

Moreover, we find a clear perihelion effects which is safely identified below the Earth's aphelion, but which may be extended also to Mars distance. Concerning the perihelion effect, it is probably related (as suggested in Paper II) to tidal interactions with inner planet. However we caution that another, possible important, effect, may play an important role: the slope variation due to Sun's heating (see Marchi et al. 2006c; Paolicchi et al. 2006). However, we will deal with this complex problem in a future paper.

As a side result, we have found that the Mars Crossers are presumably - in mean - younger by about a factor 3 than their MB siblings of the same size.

We compared the asteroidal data with a sample of unweathered OCs. Even with some minor open problems the existence of a unique space-weathering scenario including meteorites as well as Near Earth, Mars Crossers and Main Belt asteroids can be suggested.

However, the SW timescales that we obtain from our observational sample are systematically larger than one might expect, on the basis of laboratory experiments (and also, maybe, of (832) Karin data), even if a progressive saturation has to be taken into account. A complex asteroidal regolith evolution, as found for the Moon, might be invoked to solve the discrepancy. On the basis of a preliminary analysis, however, the role of the asteroidal dust seems to be not very important for these processes.

Finally, our slope-exposure relation can be compared with that obtained, for the family members only, with the aid of photometric data. The two trends are approximatively parallel, with a rather large shift, presumably due to different methods and definition of the slope. Thus the spectroscopic and photometric methods seems to be consistent each other - at least for S-complex asteroids (but not only; see Lazzarin et al. 2006); nevertheless we caution that the use of family asteroids may in principle be affected by large biases, causing unpredictable effects (Lazzarin et al. 2006).

Acknowledgements

We are grateful to A.Milani, Z.Knezevic and to the referee B. Hapke for useful suggestions. The authors from Italy have been supported by MIUR-PRIN funds.

References

• Binzel, R. P., Rivkin, A. S., Stuart J. S., et al. 2004 Icarus, 170, 259
• Brunetto, R., & Strazzulla, G. 2005, Icarus, 179, 265 [NASA ADS] [CrossRef]
• Brunetto, R., Vernazza, P., Marchi, S., et al. 2006, Icarus, 184, 327 [NASA ADS] [CrossRef]
• Clark, B. E., Hapke B., Pieters, C., & Britt, D. 2002, Asteroid Space Weathering and Regolith Evolution, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson, USA: University of Arizona Press), 585
• Chapman, C. R. 2004, Ann. Rev. of Earth and Planet. Sci., 32, 539 [NASA ADS]
• Dermott, S. F., Durda, D. D., Grogan, K., & Kehoe, T. J. J. 2002, Asteroidal Dust, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson, USA: University of Arizona Press), 423
• Hapke, B. 1973, Earth, Moon, and Planets, 7, 342
• Hapke, B. 2001, J Geophys. Res. 106(E5), 10039
• Hiroi, T., & Sasaki, S. 2001, M&PS, 36, 1587 [NASA ADS]
• Ipatov, S. I., & Mather, J. C., 2006, Adv. Space Res., 37, 126 [NASA ADS]
• Jedicke, R., Nesvorný, D., Whiteley, R., Ivezic, Z., & Juric, M. 2004, Nature, 429, 275 [NASA ADS] [CrossRef]
• Knezevic, Z., & Milani, A. 2003, A&A, 403, 1165 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Knezevic, Z., Lemaitre, A., & Milani, M. 2002, The determination of Asteroid proper Elements, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson, USA: University of Arizona Press), 603 (In the text)
• Korotev, R. L., Morris, R. V., Jolliff, B. L., & Schwarz, C. 1997, Geochim. Cosmochim. Acta, 61, 2989 [NASA ADS] [CrossRef]
• Lazzarin, M., Marchi, S., Moroz, L. V., et al. 2006, ApJ, 147, L179 [NASA ADS] [CrossRef] (In the text)
• Lazzaro, D., Angeli, C. A., Carvano, J. M., et al. 2004, Icarus, 172, 179 [NASA ADS] [CrossRef] (In the text)
• Marchi, S., Brunetto, R., Magrin, S., Lazzarin, M., & Gandolfi, D. 2005 A&A, 443, 769 (In the text)
• Marchi, S., Paolicchi, P., Lazzarin, M., & Magrin, S. 2006a, AJ, 131, 1138 [NASA ADS] [CrossRef] (In the text)
• Marchi, S., Magrin, S., Nesvorný, D., Paolicchi, P., & Lazzarin, M. 2006b, MNRAS, 368, L39 [NASA ADS] (In the text)
• Marchi S., Paolicchi P., Lazzarin M., & Magrin, S. 2006c, Space weathering of asteroids: similarities and discrepancies between Main Belt asteroids and NEOs, IAU XXVI Gen.Assembly, Prague, Symp. 236, Proc., in press
• Morbidelli, A., Bottke, W. F., Froeschlè, Ch., & Michel, P. 2002, Origin and Evolution of Near-Earth Objects, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson, USA: University of Arizona Press), 409
• Nesvorný, D., Ferraz-Mello, S., Holman, M., & Morbidelli, A. 2002a, Regular and Chaotic Dynamics in the Mean-Motion Resonances: Implications for the Structure and Evolution ot the Asteroid Belt, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson, USA: University of Arizona Press), 379
• Nesvorný, D., Bottke, W. F., Jr., Dones, L., & Levison, H. F. 2002b, Nature, 417, 720 [NASA ADS] [CrossRef] (In the text)
• Nesvorný, D., Jedicke, R., Whiteley, R. J., & Ivezic, Z. 2005, Icarus, 173, 132 [NASA ADS] [CrossRef]
• Nesvorný, D., Bottke, W. F., Vokrouhlický, D. , Morbidelli, A., & Jedicke, R. 2006, Asteroid families, Asteroids, Comets, Meteors, Proceedings of the 229th IAU Symp., Búzios, Brasil August 7-12, 2005, ed. Lazzaro, Ferraz-Mello & Angel (Cambridge University Press), 289 (In the text)
• Paolicchi, P. Lazzarin, M., Marchi, S., & Magrin, S. 2006, Space weathering of asteroids: similarities and discrepancies between Main Belt asteroids and NEOs, IAU XXVI Gen. Assembly, Prague, Abstract Book, 96
• Rao, M. N., Wentworth, S. J., Basu, A., Garrison, D. H., & McKay, D. S. 1999, Met. Plan. Science, 34, 853 [NASA ADS]
• Sasaki, S., Nakamura, K., Hamabe, Y., Kurahashi, E., & Hiroi, T. 2001, Nature, 410, 555 [NASA ADS] [CrossRef] (In the text)
• Zappalà, V., Cellino, A., Dell'Oro, A., & Paolicchi, P. 2002, Physical and Dynamical Properties of Asteroid Families, in Asteroids III, ed. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson, USA: University of Arizona Press), 619 (In the text)