A&A 464, 631-634 (2007)
DOI: 10.1051/0004-6361:20066564
Temperature fluctuations in H II regions: t2 for the
two-phase model
Y. Zhang1,2 -
B. Ercolano3 -
X.-W. Liu1
1 - Department of Astronomy, Peking University,
Beijing 100871, PR China
2 -
Department of Physics, University of Hong Kong, Pokfulam Road, Hong Kong, PR China
3 -
Harvard-Smithsonian Centre for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
Received 13 October 2006 / Accepted 22 November 2006
Abstract
Aims. We investigate temperature fluctuations in H II regions in terms of a two-phase model, which assumes that the nebular gas consists of a hot and a cold phase.
Methods. We derive general formulae for T([O III]), the [O III] forbidden line temperature, and T(H I), the hydrogen Balmer jump temperature, in terms of the temperatures of the hot and cold phases, 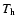 and
and 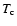 .
.
Results. For large temperature differences, the values of t2 required to account for the observed difference between T([O III]) and T(H I) are much lower than those deduced using the classical formulae that assume random and small amplitude temperature fluctuations. One should therefore be cautious when using a two-phase model to account for empirically derived t2 values. We present a correction of a recent work by Giammanco & Beckman, who use a two-phase model to estimate the ionization rate of H II regions by cosmic rays. We show that a very small amount of cold gas is sufficient to account for t2 values typically inferred for H II regions.
Key words: ISM: general - ISM: H II regions
Temperature fluctuations in H II regions are a much-discussed problem.
Peimbert (1967) investigated for the first time the effects of such
fluctuations on temperatures empirically derived from spectroscopic
observations and found that they may lead to higher electron temperatures being
derived from the collisionally excited [O III] nebular-to-auroral
forbidden-line ratio, T([O III]), than those derived from the Balmer
jump of the H I recombination spectrum, T(H I). If significant
temperature fluctuations exist in H II regions and yet are ignored in
the analysis, they may lead to underestimating ionic abundances calculated from
collisionally excited lines (CELs) (e.g. Esteban et al. 2002). The
parameter t2 (Peimbert 1967) was introduced to quantitatively characterize
temperature fluctuations. Since then the parameter has been extensively used in
nebular studies. Under the conditions that
![$[T(r)-T_0]^2/T_0^2\ll1$](/articles/aa/full/2007/11/aa6564-06/img8.gif) ,
where
T(r) is the local electron temperature and T0 is the average value weighted by
the square of density, the value of t2 can be determined either by comparing
T([O III]) and T(H I) or by comparing ionic abundances
derived from CELs and from recombination lines (RLs) (see Peimbert et al.
2004, for further details).
,
where
T(r) is the local electron temperature and T0 is the average value weighted by
the square of density, the value of t2 can be determined either by comparing
T([O III]) and T(H I) or by comparing ionic abundances
derived from CELs and from recombination lines (RLs) (see Peimbert et al.
2004, for further details).
Two-phase models, which approximate a nebula by two components of different
physical conditions, represent an over-simplified, yet frequently used method
of studying nebular physics (e.g. Viegas & Clegg 1994; Zhang et al.
2005). Using a two-phase model, Stasinska (2002) points out
that the classical picture of temperature fluctuations may be misleading under
certain conditions, and three parameters are needed to characterize temperature
inhomogeneities. One of the open questions in the study of H II regions
is that values of t2 derived from observations are consistently higher than
those predicted by photoionization models (Stasinska 2000).
Recently, Giammanco & Beckman (2005, GB05 thereafter) constructed a
two-temperature-phase model capable of explaining t2 values deduced for a
number of H II regions by means of incorporating a component of cool
ionic gas ionized by cosmic rays. However, t2 values deduced from
observations cannot be applied directly to two-phase models. This is because
empirical values of t2 deduced from observations were calculated from
formulae derived by assuming random and small-amplitude
temperature fluctuations,
assumptions that are apparently broken for a two-phase model.
The purpose of the current work is to quantitatively study the relationship
between the t2 values predicted by two-phase models and those measured by
observations. We show that, in the case of a very cold ionic gas component
embedded in a "normal'' H II region, t2 deduced from observations
using the empirical method may have significantly overestimated the real
values.
According to Peimbert (1967), for a given ionic species of number
density 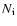 ,
the thermal structure of an H II region can be
characterized by an average temperature T0 and a mean square temperature
fluctuation parameter t2, defined as
,
the thermal structure of an H II region can be
characterized by an average temperature T0 and a mean square temperature
fluctuation parameter t2, defined as
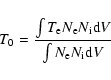 |
(1) |
and
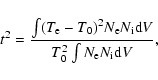 |
(2) |
respectively.
Assuming 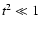 ,
T0 and t2 can be determined from measured
T([O III]) and T(H I) using relations,
,
T0 and t2 can be determined from measured
T([O III]) and T(H I) using relations,
![\begin{displaymath}
T([\hbox{O {\sc iii}}])=T_0\left[1+\frac{1}{2}\left(\frac{9.13\times10^4}{T_0}-3\right)t^2\right]
\end{displaymath}](/articles/aa/full/2007/11/aa6564-06/img13.gif) |
(3) |
and
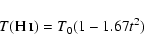 |
(4) |
(Peimbert 1967; Garnett 1992). Esteban et al. (2002)
report t2 values for a sample of H II regions. Their values are
reproduced in the first row of Table 1. Although they were obtained by
comparing ionic abundances derived from CELs and from RLs, we assume that they
are the same as would be deduced from from T([O III]) and
T(H I) using Eqs. (3) and (4). The assumption is supported by studies
of Torres-Peimbert & Peimbert (2003), who find general agreement between
t2 values inferred from the differences between T([O III]) and
T(H I) and those inferred from the apparent discrepancies between CEL
and ORL abundances. Esteban et al. (2002) did not provide values of
T0. For the purpose of comparison, we follow GB05 and assume that
T0=T([O III]), as given in the second row of Table 1.
However, as pointed out previously by Stasinska (2002), the
empirical method of estimating t2 using Eqs. (3) and (4) may be invalid
under certain conditions. In the following, we show that in the two-phase
model, values of t2 that are required to account for the measured
differences between T([O III]) and T(H I) (or differences
between ORL and CEL abundances) may be much lower than that derived from the
empirical method.
In the framework of the two-phase model, which assumes that the electron
temperature structure of an H II region consists of a hot and a
cold phase, we follow GB05 and assume equal densities of the two phases and an
ionization fraction of unity for the hot gas. Electron temperatures are
designated as 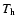 and
and 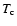 for the hot and cold phases,
respectively. The intensity of an [O III] forbidden line transition of
wavelength
for the hot and cold phases,
respectively. The intensity of an [O III] forbidden line transition of
wavelength 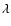 is given by
is given by
![\begin{displaymath}
I([\hbox{O {\sc iii}]})_\lambda \sim \int N({\rm O}^{2+})N_{\rm e}T_{\rm e}^{-1/2}\exp(-\Delta E/kT_{\rm e}){\rm d}V ,
\end{displaymath}](/articles/aa/full/2007/11/aa6564-06/img16.gif) |
(5) |
where 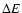 is the excitation energy of the upper level. It follows that
is the excitation energy of the upper level. It follows that
![\begin{displaymath}\frac{I([\hbox{O {\sc iii}}])_{4959,5007}}{I([\hbox{O {\sc ii...
...}^{\rm c}V^{\rm c}
T_{\rm c}^{-1/2}\exp(-62~200/T_{\rm c})} ,
\end{displaymath}](/articles/aa/full/2007/11/aa6564-06/img18.gif) |
(6) |
where C is a constant depending only on atomic data, and super- or subscript
"h'' and "c'' refer to quantities of the hot and cold phases, respectively. In
the cold phase, the ionization fraction of oxygen is expected to be lower than
that of hydrogen. As a reasonable approximation, we assume that
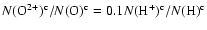 .
Our analysis is insensitive to this assumption since the cold phase
essentially contributes no [O III] forbidden line fluxes given its very
low temperature and the fact that emissivities of forbidden lines decline
exponentially with decreasing temperature (cf. Eq. (5)). We thus obtain
.
Our analysis is insensitive to this assumption since the cold phase
essentially contributes no [O III] forbidden line fluxes given its very
low temperature and the fact that emissivities of forbidden lines decline
exponentially with decreasing temperature (cf. Eq. (5)). We thus obtain
![\begin{displaymath}
T([\mbox{O {\sc iii}}])=33~000\ln^{-1}\left[\frac{T_{\rm h}^...
....1\theta x^2
T_{\rm c}^{-1/2}\exp(-62~200/T_{\rm c})}\right] ,
\end{displaymath}](/articles/aa/full/2007/11/aa6564-06/img20.gif) |
(7) |
where, using the notation of GB05, 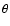 is the mass ratio of the cold to
hot gas, and x is the ionization fraction of hydrogen in the cold gas. It can be
easily seen that for
is the mass ratio of the cold to
hot gas, and x is the ionization fraction of hydrogen in the cold gas. It can be
easily seen that for
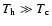 ,
,
![$T([\hbox{O {\sc iii}}]) \sim T_{\rm
h}$](/articles/aa/full/2007/11/aa6564-06/img22.gif) .
.
Similarly, from the flux of the Balmer jump,
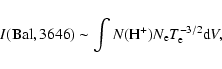 |
(8) |
and the flux of H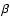 ,
,
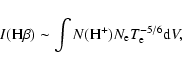 |
(9) |
we have
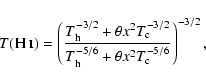 |
(10) |
or
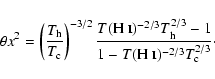 |
(11) |
Equation (10) shows that T(H I) weights towards 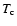 .
Following GB05, for a two-phase model, we obtain
.
Following GB05, for a two-phase model, we obtain
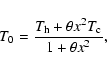 |
(12) |
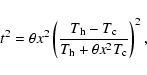 |
(13) |
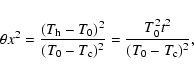 |
(14) |
and
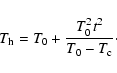 |
(15) |
Therefore, for the two-phase scenario, T0 and t2 should be determined
from Eqs. (7), (10), (12), and (13) instead
of from Eqs. (3) and (4). The latter are only valid for random
and small amplitude fluctuations.
In Fig. 1 for given values of
 and
and 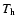 ,
we
compare t2 as a function of
,
we
compare t2 as a function of
![$T([\hbox{O {\sc iii}}])-T(\hbox{H {\sc i}})$](/articles/aa/full/2007/11/aa6564-06/img32.gif) derived from
the empirical method using Eqs. (3) and (4), and that
derived in the scenario of two-phase model using Eqs. (7), (10),
and (13). The
plots show that, depending on
derived from
the empirical method using Eqs. (3) and (4), and that
derived in the scenario of two-phase model using Eqs. (7), (10),
and (13). The
plots show that, depending on
 above a critical value of
above a critical value of
![$T([\hbox{O {\sc iii}}])-T(\hbox{H {\sc i}})$](/articles/aa/full/2007/11/aa6564-06/img32.gif) ,
the empirical method significantly
overestimates t2, particularly for the case of small
,
the empirical method significantly
overestimates t2, particularly for the case of small
 .
The
amount of deviation is insensitive to the value adopted for
.
The
amount of deviation is insensitive to the value adopted for 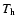 .
In
addition, we find that as the temperature difference between the two phases is
larger than a critical value (typically
.
In
addition, we find that as the temperature difference between the two phases is
larger than a critical value (typically  6000 K), empirical t2deduced from observations can no longer be used at their face values to
constrain two-phase models, a point overlooked by GB05 as discussed in the
following section.
6000 K), empirical t2deduced from observations can no longer be used at their face values to
constrain two-phase models, a point overlooked by GB05 as discussed in the
following section.
Table 1:
Estimated values of
t2, T0, and
 for
for
 ,
1000, and 4000 K for a
sample of H II regions.
,
1000, and 4000 K for a
sample of H II regions.
 and
and
 are taken from
Esteban et al. (2002). The numbers in parentheses are values
derived by GB05 and included here for comparison.
are taken from
Esteban et al. (2002). The numbers in parentheses are values
derived by GB05 and included here for comparison.
![\begin{figure}
\includegraphics[width=13.5cm,clip]{6564fig1.ps}
\end{figure}](/articles/aa/full/2007/11/aa6564-06/Timg37.gif) |
Figure 1:
t2 versus (T([O III])-T(H I)), deduced from
the empirical method (Eqs. (3) and (4), dotted lines) and for
two-phase model (Eqs. (7), (10), (12), and (13),
solid lines). Left panels:
 = 0.01; right panels: = 0.01; right panels:
 = 0.1; upper panels: = 0.1; upper panels: 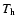 = 10 000 K; lower
panels: = 10 000 K; lower
panels: 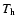 = 15 000 K. = 15 000 K. |
| Open with DEXTER |
GB05 showed that the ionization of cold neutral gas by cosmic rays may
significantly contribute to temperature fluctuations. They used a two-phase
model to explain t2 values obtained by Esteban et al. (2002) for a
number of H II regions. However, the high temperature difference between
the two phases in GB05 model (see their Table 1) suggests that t2 values
obtained by Esteban et al. cannot be applied directly to two-phase models.
Values of
 derived by GB05 need to be re-considered.
derived by GB05 need to be re-considered.
We re-estimate
 values for the sample of H II regions of
Esteban et al. (2002). Following GB05, three values of
values for the sample of H II regions of
Esteban et al. (2002). Following GB05, three values of 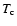 are
assumed, 100, 1000, and 4000 K. Under these conditions, temperature in the
cold gas is too low to collisionally excite the [O III] lines, and
consequently Eq. (7) can be simplified to
are
assumed, 100, 1000, and 4000 K. Under these conditions, temperature in the
cold gas is too low to collisionally excite the [O III] lines, and
consequently Eq. (7) can be simplified to
![\begin{displaymath}
T([\hbox{O {\sc iii}}])=T_{\rm h} .
\end{displaymath}](/articles/aa/full/2007/11/aa6564-06/img38.gif) |
(16) |
Substituting values of T0 and t2 given by Esteban et al.
(2002) (hereafter referred as
 and
and
 ,
in order
to distinguish them from those deduced from Eqs. (12) and (13)) into
Eqs. (3) and (4), we obtain T([O III])(
,
in order
to distinguish them from those deduced from Eqs. (12) and (13)) into
Eqs. (3) and (4), we obtain T([O III])(
 ,
,
 )
and T(H I)(
)
and T(H I)(
 ,
,
 ), which
are tabulated in Rows 3 and 4 of Table 1. Note that here we take the
same assumption by GB05 that
), which
are tabulated in Rows 3 and 4 of Table 1. Note that here we take the
same assumption by GB05 that
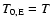 ([O III]). Then
([O III]). Then
 can be determined from Eq. (11), where
can be determined from Eq. (11), where
 ,
,
![$T_{\rm
h}=T([\hbox{O {\sc iii}}])(t^2_{\rm E},T_{0,{\rm E}})$](/articles/aa/full/2007/11/aa6564-06/img41.gif) .
Although the values of
T([O III])(
.
Although the values of
T([O III])(
 ,
,
 )
thus obtained are slightly
higher than the actual values deduced from observations (see Table 1),
the resulting
)
thus obtained are slightly
higher than the actual values deduced from observations (see Table 1),
the resulting
 are hardly affected.
are hardly affected.
In Table 1 we compare our
 values to those of GB05 (given
in parentheses); for low values of
values to those of GB05 (given
in parentheses); for low values of
 differences of up to a factor
of a hundred are found. It can easily be seen that the discrepancies increase
with decreasing temperature of the cold gas, as suggested by Fig. 1.
For
differences of up to a factor
of a hundred are found. It can easily be seen that the discrepancies increase
with decreasing temperature of the cold gas, as suggested by Fig. 1.
For
 K, our derived values of
K, our derived values of
 are very low,
suggesting that the values of t2 reported by Esteban et al. (2002)
can be explained by the existence of a very small amount of cold gas.
are very low,
suggesting that the values of t2 reported by Esteban et al. (2002)
can be explained by the existence of a very small amount of cold gas.
Table 1 also gives t2 and T0 values derived from the
Eqs. (12) and (13). As the Table shows, the real t2 values are
lower when
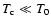 than those derived from the empirical method.
As a result, values of the cosmic ray ionization rate,
than those derived from the empirical method.
As a result, values of the cosmic ray ionization rate, 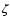 ,
derived by GB05
have been grossly overestimated (cf. their Eq. (17)). Our conclusion is
consistent with the range of values inferred for the Orion nebula from
Gamma ray observations.
,
derived by GB05
have been grossly overestimated (cf. their Eq. (17)). Our conclusion is
consistent with the range of values inferred for the Orion nebula from
Gamma ray observations.
We have studied the relationship between values of t2 predicted by a
two-phase model and those derived empirically from observations (empirical
method). Our results show that the existence of extremely cold gas within
H II regions may lead to overestimated t2 calculated from empirically
determined T([O III]) and T(H I). We stress that care should
be taken when using the two-phase model to study large temperature fluctuations
of H II regions. In this model, CELs are hardly produced by the cold
gas, which on the other hand makes a large contribution to the flux at the Balmer
jump, due to the
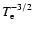 dependence of
dependence of
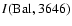 .
Accordingly, the existence of a very small amount of cold material may lead to
a large discrepancy between T([O III]) and T(H I). In other
words, in spite of its small mass, the existence of extremely cold material can
reproduce apparently large t2 (as derived from the empirical method), much
larger than the actual value (as defined by Eq. (2)).
.
Accordingly, the existence of a very small amount of cold material may lead to
a large discrepancy between T([O III]) and T(H I). In other
words, in spite of its small mass, the existence of extremely cold material can
reproduce apparently large t2 (as derived from the empirical method), much
larger than the actual value (as defined by Eq. (2)).
Finally, we revisited the GB05 study of cosmic ray ionization as a mechanism
for creating temperature fluctuations in H II regions. While this
provides a potential mechanism for creating cold ionized plasma in H II
regions, we show that the values of 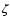 required to produce the ionization have
been overestimated in their treatment, due to the t2 discrepancy discussed
above. Based on the formulae presented here, we re-estimated their model
parameters. The corrections are apparent, particularly in cases where
temperature of the cold gas component is low, resulting in lower values of
required to produce the ionization have
been overestimated in their treatment, due to the t2 discrepancy discussed
above. Based on the formulae presented here, we re-estimated their model
parameters. The corrections are apparent, particularly in cases where
temperature of the cold gas component is low, resulting in lower values of 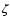 that agree better with the estimates for the Orion nebula published
in the literature.
that agree better with the estimates for the Orion nebula published
in the literature.
Acknowledgements
We thank the referee, Dr. C. Morisset, for helpful
comments that improved clarity of the paper. We would also like to thank
Dr. Morisset for computing new values of t2 and T0, based on our
estimates of
 .
Those values are now tabulated in Table 1.
Y.Z. and X.W.L. acknowledge support by NSFC grant #10325312.
.
Those values are now tabulated in Table 1.
Y.Z. and X.W.L. acknowledge support by NSFC grant #10325312.
- Esteban, C., Peimbert, M.,
Torres-Peimbert, S., & Rodríguez, M. 2002, ApJ, 581,
241 [NASA ADS] [CrossRef] (In the text)
- Garnett, D. R. 1992, AJ, 103,
1330 [NASA ADS] [CrossRef] (In the text)
- Giammanco, C., & Beckman,
J. E. 2005, A&A, 437, L11 [NASA ADS] [CrossRef] [EDP Sciences] (GB05)
(In the text)
- Peimbert, M. 1967, ApJ, 150,
825 [NASA ADS] [CrossRef] (In the text)
- Peimbert, M., Peimbert, A.,
Ruiz, M. T., & Esteban, C. 2004, ApJ, 150, 431 [NASA ADS] [CrossRef] (In the text)
- Stasinska, G. 2000, Rev. Mex.
Astron. Astrofis., 9, 158 (In the text)
- Stasinska, G. 2002, Rev. Mex.
Astron. Astrofis., 12, 62 (In the text)
- Torres-Peimbert, S., &
Peimbert, M. 2003, in Planetary Nebulae: Their Evolution and Role
in the Universe, ed. P. R. Wood & M. Dopita (San Francisco:
ASP), IAU Symp., 209, 363
(In the text)
- Viegas, S. M., & Clegg,
R. E. S. 1994, MNRAS, 271, 993 [NASA ADS] (In the text)
- Zhang, Y., Liu, X.-W., Liu,
Y., & Rubin, R. H. 2005, MNRAS, 358, 457 [NASA ADS] (In the text)
Copyright ESO 2007
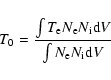
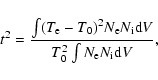
![\begin{displaymath}
T([\hbox{O {\sc iii}}])=T_0\left[1+\frac{1}{2}\left(\frac{9.13\times10^4}{T_0}-3\right)t^2\right]
\end{displaymath}](/articles/aa/full/2007/11/aa6564-06/img13.gif)
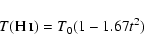
![\begin{displaymath}
I([\hbox{O {\sc iii}]})_\lambda \sim \int N({\rm O}^{2+})N_{\rm e}T_{\rm e}^{-1/2}\exp(-\Delta E/kT_{\rm e}){\rm d}V ,
\end{displaymath}](/articles/aa/full/2007/11/aa6564-06/img16.gif)
![\begin{displaymath}\frac{I([\hbox{O {\sc iii}}])_{4959,5007}}{I([\hbox{O {\sc ii...
...}^{\rm c}V^{\rm c}
T_{\rm c}^{-1/2}\exp(-62~200/T_{\rm c})} ,
\end{displaymath}](/articles/aa/full/2007/11/aa6564-06/img18.gif)
![\begin{displaymath}
T([\mbox{O {\sc iii}}])=33~000\ln^{-1}\left[\frac{T_{\rm h}^...
....1\theta x^2
T_{\rm c}^{-1/2}\exp(-62~200/T_{\rm c})}\right] ,
\end{displaymath}](/articles/aa/full/2007/11/aa6564-06/img20.gif)
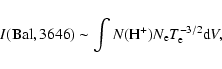
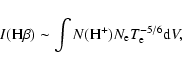
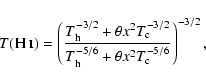
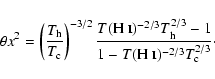
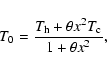
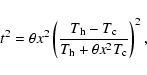
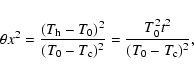
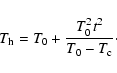
![\begin{figure}
\includegraphics[width=13.5cm,clip]{6564fig1.ps}
\end{figure}](/articles/aa/full/2007/11/aa6564-06/Timg37.gif)