A&A 464, 245-252 (2007)
DOI: 10.1051/0004-6361:20066531
Deuterium fractionation in warm dense interstellar clumps
E. Roueff1 - B. Parise2 - E. Herbst3
1 - LUTH, Observatoire de Paris, Section de Meudon, Place Jules Janssen, 92195 Meudon, France
2 -
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
3 -
Departments of Physics, Astronomy, and Chemistry, The Ohio State University, Columbus, OH 43210, USA
Received 10 October 2006 / Accepted 12 December 2006
Abstract
Aims. In a recently published 1-millimeter line survey of the Orion Bar by Leurini et al., the confirmation of dense neutral clumps was reported based mainly on an analysis of methanol spectral lines. Within these clumps, a high abundance ratio was found between the deuterated isotopologue DCN and HCN.
Methods. In this paper, we use steady-state chemical modelling to determine if the DCN/HCN abundance ratio can be understood in terms of gas-phase processes.
Results. Our results show that, at temperatures (50-75 K) and densities (
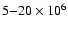 cm-3) in the vicinity of those measured, the calculated DCN/HCN abundance ratio can reach 0.01 or even higher, in good agreement with the measured range of 0.007-0.009. Moreover, the fractional abundance of HCN is also calculated to be in the vicinity of that reported. Other computed abundance ratios between deuterated and normal isotopologues are reported for the physical conditions of the clumps. The abundance ratios are analyzed as functions of temperature and density in terms of a simple formula. In general, calculated ratios can be somewhat dependent on the choice of two very different sets of elemental abundances, one of which is the "standard'' low-metal set, while the other we term the "warm-core'' set.
cm-3) in the vicinity of those measured, the calculated DCN/HCN abundance ratio can reach 0.01 or even higher, in good agreement with the measured range of 0.007-0.009. Moreover, the fractional abundance of HCN is also calculated to be in the vicinity of that reported. Other computed abundance ratios between deuterated and normal isotopologues are reported for the physical conditions of the clumps. The abundance ratios are analyzed as functions of temperature and density in terms of a simple formula. In general, calculated ratios can be somewhat dependent on the choice of two very different sets of elemental abundances, one of which is the "standard'' low-metal set, while the other we term the "warm-core'' set.
Key words: ISM: abundances - ISM: molecules - molecular processes
Deuterium fractionation is a well-known process in the dense interstellar medium in which deuterated isotopologues of interstellar molecules achieve abundances compared with normal species much higher than the deuterium-to-hydrogen elemental abundance ratio. Such fractionation can occur both in the gas phase and on the surfaces of dust particles. In the gas phase, the origin of the fractionation is mainly "thermodynamic'' rather than kinetic: ion-molecule reactions in which deuterium and hydrogen atoms from reservoirs (H2 and HD) are exchanged proceed much more rapidly in the exothermic direction at low temperatures. As an example, consider the dominant system at a typical temperature for a cold source of 10 K:
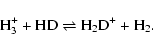 |
(1) |
The reaction that proceeds in the left-to-right direction is exothermic by 232 K
(Gerlich et al. 2002) both because of differences in zero-point vibrational energies and the non-existence of the ground rotational state of H3+ due to the Pauli Exclusion Principle. Thus, at low temperatures, the endothermic reaction occurs slowly, and the equilibrium constant becomes very large, raising the abundance ratio H2D+/H3+ to values much higher than the HD/H2 reservoir value of 3  10-5. Normally this "thermodynamic equilibrium '' value for the H2D+/H3+ ratio (
10-5. Normally this "thermodynamic equilibrium '' value for the H2D+/H3+ ratio (
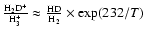 ) is not reached because the destruction of the ion H2D+ is dominated by reactions with heavy species such as CO and by recombination with electrons. At high densities and low temperatures, however, such as pertain to the centers of so-called pre-stellar cores, accretion of heavy gas-phase species onto the grains and neutralization of electrons on grains allow the H2D+/H3+ ratio to approach the high thermodynamic value, although there are complications caused by ortho-para effects
(Gerlich et al. 2002). Moreover, deuteration need not stop at the singly-deuterated isotopologue; further exothermic reactions with HD lead to both D2H+ and finally D3+ (Walmsley et al. 2004; Roberts et al. 2004,2003). At high enough depletions, calculations lead to the bold prediction that the totally deuterated ion is the most abundant of the four, although observations of the rotational spectrum of this ion are not possible because it does not possess a permanent dipole moment. The recent detection of D2H+ does offer strong support for this picture of deuterium fractionation (Vastel et al. 2004).
) is not reached because the destruction of the ion H2D+ is dominated by reactions with heavy species such as CO and by recombination with electrons. At high densities and low temperatures, however, such as pertain to the centers of so-called pre-stellar cores, accretion of heavy gas-phase species onto the grains and neutralization of electrons on grains allow the H2D+/H3+ ratio to approach the high thermodynamic value, although there are complications caused by ortho-para effects
(Gerlich et al. 2002). Moreover, deuteration need not stop at the singly-deuterated isotopologue; further exothermic reactions with HD lead to both D2H+ and finally D3+ (Walmsley et al. 2004; Roberts et al. 2004,2003). At high enough depletions, calculations lead to the bold prediction that the totally deuterated ion is the most abundant of the four, although observations of the rotational spectrum of this ion are not possible because it does not possess a permanent dipole moment. The recent detection of D2H+ does offer strong support for this picture of deuterium fractionation (Vastel et al. 2004).
The production of deuterated ions from H3+ leads to high abundances of other deuterated species through secondary ion-molecule reactions, as the deuterated ions react with a variety of neutral species. Not only singly deuterated isotopologues are produced by secondary reactions involving deuterated ions; species such as NHD2, ND3, and D2CO are observed and understood at least partially in terms of gas-phase syntheses (Osamura et al. 2005; Roberts & Millar 2000; Roueff et al. 2005; Gerin et al. 2006). Although H3+ is not the only important molecular ion to exchange deuterons with HD exothermically and rapidly, it is the most abundant under most conditions. Two other ions that react rapidly with HD - CH3+ (Asvany et al. 2004) and C2H2+ (Gerlich & Schlemmer 2002) - are also of some importance, leading to the ions CH2D+ and C2HD+ (Millar et al. 1989; Herbst et al. 1987):
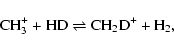 |
(2) |
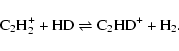 |
(3) |
The left-to-right exothermicities, 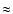 390 K (Asvany et al. 2004) and
390 K (Asvany et al. 2004) and 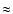 550 K (Herbst et al. 1987), respectively, are considerably larger than for the reaction involving H3+.
550 K (Herbst et al. 1987), respectively, are considerably larger than for the reaction involving H3+.
Detailed gas-phase models including deuterated species have been constructed using large networks of gas-phase reactions with both the steady-state and pseudo-time-dependent pictures (Millar et al. 1989; Roberts & Millar 2000; Turner 2001; Roberts et al. 2004; Roueff et al. 2005; Millar 2002; Gerlich et al. 2002). A rather complete discussion of the complex chemistry of deuteration at temperatures up to 40 K and densities through 105 cm-3 has been given by Turner (2001).
The calculated ratios between deuterated and normal isotopologues are often in quantitative agreement with observations, and it is typically found that there is much less time-dependence to the calculated ratios than to calculated fractional abundances, so that steady-state approximations are often useful. Some models include depletion of gas-phase species in an active sense (Roberts et al. 2002), while others even include surface fractionation processes (Aikawa et al. 2005). Fractionation on grain surfaces is thought to occur following the formation of a large atomic D/H ratio in the gas. The deuterium and hydrogen atoms, after landing on surfaces, then react with a variety of heavy species leading to both deuterated and normal isotopologues (Tielens 1983). A key series of processes leads to the deuterated isotopologues of methanol, which are produced on grain surfaces by hydrogenation and deuteration of CO (Nagaoka et al. 2005; Stantcheva & Herbst 2003; Charnley et al. 1997).
As temperature increases, the deuterium fractionation achieved by gas-phase processes generally becomes less noticeable for a variety of reasons. Most importantly, the abundance ratios between deuterated and normal ions achieved in exchange reactions are reduced as the endothermic reactions become more rapid. The extent of this reduction versus increasing temperature is a function of the exothermicity of the reaction system: since the exothermicity of exchange reactions of HD with CH3+ and C2H2+ exceeds that of HD with H3+
(Herbst et al. 1987), deuterated isotopologues of the former can cause some general deuteration at higher temperatures, although the normal ions are less abundant than H3+. Secondly, as the temperature increases, depletions of heavy species onto grains are less and less likely. Indeed, desorption becomes important and can, for a limited time, enhance deuteration in the gas phase as the results of previous fractionation on grain surfaces transfer to the gas. Such processes are thought to occur in hot cores and hot corinos, with kinetic temperatures of 100 K and larger, allowing the detection of deuterated isotopologues of methanol in the gas phase
(Parise et al. 2002,2004,2006), although eventually the deuteration must reduce to the gas-phase value appropriate to the temperature (Osamura et al. 2004).
Recently, Leurini et al. (2006) used the APEX millimeter- and submillimeter-wave telescope to study the Orion Bar, perhaps the best-known photon-dominated region (PDR), in the 1 mm region. Looking at the Orion Bar (HCN) position, they utilized methanol transitions to characterize a phase of warm (50-75 K), dense (
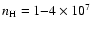 cm-3) clumps of matter originally studied by Lis & Schilke (2003). Moreover, they detected DCN in this environment, and were able to estimate a DCN/HCN abundance ratio (using the 13C isotopologue of HCN) of 0.007-0.009. Leurini et al. (2006) speculated that, unlike the case of hot cores, the abundance ratio might actually reflect steady-state gas-phase conditions and, at the rather high temperature, the fractionation might be caused by reactions involving CH2D+. As the authors state: "the Orion Bar thus appears a unique reference to test the fractionation reactions involving CH2D+''. In this paper, we report a study of the deuterium fractionation that can occur under the conditions of the warm clumps in the Orion Bar at steady-state. Our results show that the hypothesis of Leurini et al. (2006) is indeed correct, and also reveal some interesting features such as a strong direct density dependence to the fractionation, which occurs in the absence of depletion onto grains for two very different sets of elemental abundances chosen.
cm-3) clumps of matter originally studied by Lis & Schilke (2003). Moreover, they detected DCN in this environment, and were able to estimate a DCN/HCN abundance ratio (using the 13C isotopologue of HCN) of 0.007-0.009. Leurini et al. (2006) speculated that, unlike the case of hot cores, the abundance ratio might actually reflect steady-state gas-phase conditions and, at the rather high temperature, the fractionation might be caused by reactions involving CH2D+. As the authors state: "the Orion Bar thus appears a unique reference to test the fractionation reactions involving CH2D+''. In this paper, we report a study of the deuterium fractionation that can occur under the conditions of the warm clumps in the Orion Bar at steady-state. Our results show that the hypothesis of Leurini et al. (2006) is indeed correct, and also reveal some interesting features such as a strong direct density dependence to the fractionation, which occurs in the absence of depletion onto grains for two very different sets of elemental abundances chosen.
In the remainder of the paper, we first discuss the chemical model used. In Sect. 3, our results for DCN/HCN and other ratios are discussed and interpreted in terms of limited reactions, while in the last section, we discuss the results in terms of the observations of Leurini et al. (2006).
The Meudon gas-phase network (Roueff et al. 2005; Gerlich et al. 2002) has been used for this study. This network comprises 218 species including multideuterated isotopologues involving the elements C, N, O and S connected by more than 3250 gas phase chemical reactions. It should be noted that all deuterated isotopologues of Hn+, HnCO+, and HnCS+ with n up to a value of 3, CHn+ with n up to a value of 5, molecular hydrogen, water, ammonia, formaldehyde, and thioformaldehyde are included in the network. However, the chemical network does not include methanol chemistry, because it does not occur in the gas phase. No distinction is made here between para and ortho forms of the various isotopologues of the H3+ molecular ions. Neutralization of atomic ions on grain surfaces is taken into account as described in Le Bourlot et al. (1995). Neutralization of molecular ions on grain surfaces is less important because it is much slower than dissociative recombination with electrons in the gas. If we consider classical grains with radius 0.1 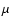 ,
the rate coefficient for ballistic accretion is typically
,
the rate coefficient for ballistic accretion is typically
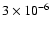 cm3 s-1 whereas the rate coefficient for dissociative recombination is typically 10-6 cm3 s-1. Assuming a number density of grains relative to H of
cm3 s-1 whereas the rate coefficient for dissociative recombination is typically 10-6 cm3 s-1. Assuming a number density of grains relative to H of
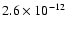 for classical grains and a fractional ionization of at least 10-9, we see that dissociative recombination dominates unless one considers very small grains to be negatively charged. Such small grains, when grouped with PAH's, are likely to have a fractional abundance of
for classical grains and a fractional ionization of at least 10-9, we see that dissociative recombination dominates unless one considers very small grains to be negatively charged. Such small grains, when grouped with PAH's, are likely to have a fractional abundance of 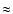 10-7. If a large percentage are negatively charged, the recombination of atomic and molecular ions may well be dominated by reactions with PAH- rather than with electrons. On the other hand, the small amount of experimental evidence on the sticking of electrons to PAH neutrals shows that the rate coefficients are far smaller than estimated by astrochemists (Moustefaoui et al. 1998). The situation is currently being studied by Wakelam & Herbst. Pending a better understanding of the abundance of PAH anions, we do not include PAH's in this analysis.
10-7. If a large percentage are negatively charged, the recombination of atomic and molecular ions may well be dominated by reactions with PAH- rather than with electrons. On the other hand, the small amount of experimental evidence on the sticking of electrons to PAH neutrals shows that the rate coefficients are far smaller than estimated by astrochemists (Moustefaoui et al. 1998). The situation is currently being studied by Wakelam & Herbst. Pending a better understanding of the abundance of PAH anions, we do not include PAH's in this analysis.
The physical conditions of the warm clumps are assumed to be homogeneous. Since the history of the physical conditions of this matter is not known, it is simplest to assume that the chemistry is at steady state. Although an early-time solution might lead to larger column densities of selected species, it is our experience that calculated ratios of deuterated to normal isotopologues are less sensitive to time dependence assuming constant physical conditions. We have performed calculations at temperatures from 10 K to 70 K and at gas densities
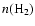 of 10
of 10
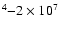 cm-3. Two sets of elemental abundances, shown in Table 1, have been utilized for the gas-phase material. To obtain the first, known as "warm-core'' abundances, we assume that some of the material comprising ice mantles in colder sources has desorbed into the gas. The second set of abundances closely resembles the well-known "low-metal'' collection, which leads to best results for dark cold clouds such as L134N (Wakelam et al. 2006). The low-metal set features moderate depletions of C, N, and O and strong depletions of S and the only metal in the network, Fe. The elemental abundance of Fe is taken as the sum of all elemental abundances of metals in order to reproduce the available electronic charges. The elemental abundance of helium, which is not condensable on the grain surfaces, is taken from Grevesse et al. (1996). Our value is 40% lower than the value used in the low-metal collection. In the warm-core set of elemental abundances, all depletions are reduced, with the increase in sulphur being the most dramatic. The element Fe is depleted by a factor of 20 less; this difference will lead to a lower fractional ionization in the low-metal case. The warm-core values have some resemblance to the abundances used for PDR environments, where the depletions are less strong. These choices are somewhat arbitrary but should mimic two possible extreme cases.
cm-3. Two sets of elemental abundances, shown in Table 1, have been utilized for the gas-phase material. To obtain the first, known as "warm-core'' abundances, we assume that some of the material comprising ice mantles in colder sources has desorbed into the gas. The second set of abundances closely resembles the well-known "low-metal'' collection, which leads to best results for dark cold clouds such as L134N (Wakelam et al. 2006). The low-metal set features moderate depletions of C, N, and O and strong depletions of S and the only metal in the network, Fe. The elemental abundance of Fe is taken as the sum of all elemental abundances of metals in order to reproduce the available electronic charges. The elemental abundance of helium, which is not condensable on the grain surfaces, is taken from Grevesse et al. (1996). Our value is 40% lower than the value used in the low-metal collection. In the warm-core set of elemental abundances, all depletions are reduced, with the increase in sulphur being the most dramatic. The element Fe is depleted by a factor of 20 less; this difference will lead to a lower fractional ionization in the low-metal case. The warm-core values have some resemblance to the abundances used for PDR environments, where the depletions are less strong. These choices are somewhat arbitrary but should mimic two possible extreme cases.
Table 1:
Elemental abundances with respect to the number of protons. Number in parenthesis refer to powers of ten.
3 Results
The results initially discussed here are in the form of figures of abundance ratios between deuterated and normal isotopologues plotted against density for temperatures of 10, 20, 30, 40, 50, 60, and 70 K.
We show in Fig. 1 the abundance ratios H2D+/H3+ and CH2D+/CH3+ with warm-core and low-metal abundances, respectively. For the case of H2D+/H3+, there is very little density dependence with either set of elemental abundances, and the temperature dependence is the standard monotonic one once the temperature gets higher than 20 K and the backwards rate coefficient (see Eq. (1)) becomes important. When the temperature reaches 60 K, the abundance ratio is just slightly larger than 0.1%. The abundance ratio is easily obtained at steady state by consideration of the exchange reaction system plus the destruction of H2D+ by electrons and heavy species such as CO (Roberts et al. 2002). The simple equation obtained is:
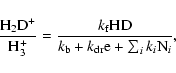 |
(4) |
where 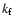 is the rate coefficient for the forward (exothermic) exchange reaction,
is the rate coefficient for the forward (exothermic) exchange reaction, 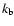 is that for the backwards (endothermic) process,
is that for the backwards (endothermic) process,
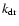 is the rate coefficient for the dissociative recombination of H2D+ with electrons (e), and ki is the rate coefficient for reaction with heavy species, designated Ni. The abundances of all species are fractional with respect to H2. The normal use of brackets for fractional abundances is omitted. Under the conditions studied here, the term in the denominator that is most important at lower temperatures is the destruction by heavy species Ni and at higher temperatures the backward exchange reaction. Note that the further reaction of H2D+ with HD to form D2H+ has been ignored because it is not important unless the Ni are depleted at low temperature. Both this reaction and the subsequent reaction of D2H+ with HD to form D3+ are in our model.
is the rate coefficient for the dissociative recombination of H2D+ with electrons (e), and ki is the rate coefficient for reaction with heavy species, designated Ni. The abundances of all species are fractional with respect to H2. The normal use of brackets for fractional abundances is omitted. Under the conditions studied here, the term in the denominator that is most important at lower temperatures is the destruction by heavy species Ni and at higher temperatures the backward exchange reaction. Note that the further reaction of H2D+ with HD to form D2H+ has been ignored because it is not important unless the Ni are depleted at low temperature. Both this reaction and the subsequent reaction of D2H+ with HD to form D3+ are in our model.
The case of CH2D+/CH3+ is a different story. The temperature dependence, which is the same for each set of elemental abundances, shows that the abundance ratio of the ions actually increases in the range 10-40 K before decreasing at higher temperatures. To understand this dependence, one can again determine the abundance ratio from an exchange reaction system and other destruction reactions of CH2D+. The equation:
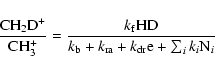 |
(5) |
contains an extra term in the denominator when compared with the expression for H2D+/H3+. This term derives from the
radiative association of CH2D+ with H2, which has the estimated rate coefficient
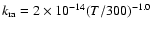 cm3 s-1 (Roberts et al. 2004).
cm3 s-1 (Roberts et al. 2004).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6531fig1.eps}
\end{figure}](/articles/aa/full/2007/10/aa6531-06/Timg20.gif) |
Figure 1:
Deuterium fractionation ratios. Left: warm-core conditions, right: low-metal conditions.The symbols for the assorted temperatures in this and subsequent figures are as follows: full squares (70 K), full circles (60 K), open circles (50 K), open squares (40 K), full diamonds (30 K), full triangles (20 K), open diamonds (10 K). |
| Open with DEXTER |
This destruction route is dominant for higher densities at temperatures up to about 40 K, but decreases by a factor of 4 from 10 K to 40 K. Around 40 K, the backwards rate coefficient, 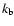 ,
becomes equal with
,
becomes equal with
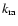 and at higher temperatures dominates. Interestingly, CH2D+ does not react rapidly with CO so that its reaction with the heavy neutrals O and O2 are the dominant ones in this class, although they are not critical in this analysis. Another factor in the temperature dependence is the rate coefficient
and at higher temperatures dominates. Interestingly, CH2D+ does not react rapidly with CO so that its reaction with the heavy neutrals O and O2 are the dominant ones in this class, although they are not critical in this analysis. Another factor in the temperature dependence is the rate coefficient 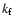 .
The measured rate coefficient at 15 K (Asvany et al. 2004) is noticeably less than that at 80 K (Smith et al. 1982), and we have used an artificial activation energy of 15 K to parameterize the two measurements. This factor also helps enlarge the direct temperature dependence seen in the 10-40 K range. Unlike the temperature dependence, the density dependence differs strongly between the two sets of abundances. The strong density dependence for the warm-core abundances is due to the greater fractional ionization at low densities, which strongly reduces the ionic abundance ratio (see Eq. (5)) and lowers the temperature dependence. At 60 K, the
CH2D+/CH3+ abundance ratio still exceeds 0.01 for all densities with the low-metal abundances and for densities above 105 cm-3 with the warm-core abundances.
.
The measured rate coefficient at 15 K (Asvany et al. 2004) is noticeably less than that at 80 K (Smith et al. 1982), and we have used an artificial activation energy of 15 K to parameterize the two measurements. This factor also helps enlarge the direct temperature dependence seen in the 10-40 K range. Unlike the temperature dependence, the density dependence differs strongly between the two sets of abundances. The strong density dependence for the warm-core abundances is due to the greater fractional ionization at low densities, which strongly reduces the ionic abundance ratio (see Eq. (5)) and lowers the temperature dependence. At 60 K, the
CH2D+/CH3+ abundance ratio still exceeds 0.01 for all densities with the low-metal abundances and for densities above 105 cm-3 with the warm-core abundances.
The case of C2HD+/C2H2+ is rather similar to that of CH2D+/CH3+ since C2HD+, like C2H2+, should undergo a radiative association reaction with H2 (Gerlich & Schlemmer 2002). The rate coefficient of this reaction is estimated to be only slightly larger than that for
CH2D+ + H2. In discussing most of the secondary species below, we ignore processes starting from C2HD+/C2H2+ based on the finding that these ions are less abundant than CH2D+ and CH3+ under the conditions considered here and that they are less closely related to the particular secondary species studied. The exception concerns the radicals C2D and C2H.
In trying to understand the calculated abundance ratios between deuterated isotopologues and normal ones other than the parents, it is important to distinguish between deuteration during the formation of a species, and deuteration during the destruction of a species. As an example of the former, consider the ion DCO+. This ion is formed at low temperatures primarily from the parent H2D+ via the reaction
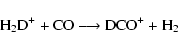 |
(6) |
while the normal isotopologue HCO+ is produced mainly via the corresponding reaction with
H3+. A similar story holds for N2D+ and N2H+. As an example of the latter, consider the species NH2D. After NH3 is formed, it undergoes destruction by ions, one of which is the reaction with H2D+ to lead to the deuterated ion NH3D+. This ion can then undergo dissociative recombination to form
NH2D + H among other products. A different mechanism can occur for radicals such as OH, in which rapid reaction with atomic deuterium leads to the deuterated isotopologue.
At steady-state, one can show that the XD/XH abundance ratio between relatively non-reactive species (non-radicals) is approximately the following:
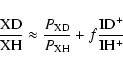 |
(7) |
where the two terms on the right refer to deuteration via formation and destruction routes respectively.
Here P stands for the production rate, which can come from any of the three parent ion pairs, and ID+ and IH+ stand for the total abundance of deuterating ions (H2D+, DCO+...) and protonating ions (H3+, HCO+...) respectively. What is omitted from this equation are destruction pathways of XH leading to XD via routes more complex than simple deuteration. The factor
f in the equation is the efficiency (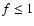 )
with which the ID+/IH+ abundance ratio is transfered to the secondary pair. It can be estimated from more detailed results by working out the steady-state kinetics of the formation of XD from XH and its destruction via all ions. The derivation leads to the formula
)
with which the ID+/IH+ abundance ratio is transfered to the secondary pair. It can be estimated from more detailed results by working out the steady-state kinetics of the formation of XD from XH and its destruction via all ions. The derivation leads to the formula
where f1 is the fraction of deuterations of XH that lead to XD and f2 is the ratio of the abundance of IH+ to the total abundance of reacting ions. In general, f should not depend significantly on n and T. Equation (7) contains the assumption that all ion-molecule rate coefficients are the same.
As an example estimation of f, assume that XH is deuterated to form XHD+ on one-half of the reactions with ID+, and the deuterated ion then dissociatively recombines with electrons to form XD + H on one-half of the reactions. The neutral XD is then destroyed by a number of ions in the model including non-protonating ions such that the effective rate of destruction is 2 times the rate of reaction with protonating ions IH+. Solving for the abundance ratio of XD to XH then yields f = 1/8. As the temperature rises, the second term lessens but deuteration can still occur during the formation of a species via processes that lead back to CH2D+ and C2HD+ or, less efficiently, through destruction of XH via these ions or secondary non-deuterating ones initiating processes that eventually produce XD.
Let us now see whether we can analyze the temperature and density dependence of selected abundance ratios of deuterated to normal isotopologues of secondary species using the simple analysis embodied in Eq. (7). For the ionic ratios DCO+/HCO+ and N2D+/N2H+, deuteration occurs during the production of these species. Figure 2 shows that the temperature dependence is essentially monotonic, following that of H2D+/H3+ since these ions are their major precursors. In addition, there is little density dependence except for DCO+/HCO+, which increases for warm-core abundances at densities higher than 106 cm-3 at the larger temperatures. This effect may derive from a secondary formation route involving CH3+ (CH2D+) and O:
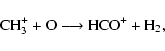 |
(9) |
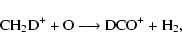 |
(10) |
since this primary abundance ratio does show a similar density dependence.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6531fig2.eps}
\end{figure}](/articles/aa/full/2007/10/aa6531-06/Timg27.gif) |
Figure 2:
Deuterium fractionation ratios. Left: warm-core conditions, right: low-metal conditions. |
| Open with DEXTER |
The species we will now consider - HCN, HNC, H2CO, and NH3 - are all neutral ones and can in principal be deuterated during formation and destruction. Yet, except for ammonia and HNC, the direct destructive route is blocked for an assortment of reasons. First, consider H2CO. As shown by
(), deuteration of formaldehyde leads to the ion H2COD+, with the deuterium on the opposite side of the molecule from the hydrogens. Dissociative recombination then leads just to H2CO + D rather than to HDCO + H, so that no deuteration is accomplished unless there is significant internal rearrangement during recombination, which is assumed not to be the case here. For HCN and HNC, the story is a little more complex. Two protonated ionic forms exist: HCNH+, which is linear, and H2NC+, which is Y-shaped (Talbi & Herbst 1998). Protonation of HCN leads to the linear ion HCNH+ while protonation of HNC leads both to this ion and to the Y-shaped structure H2NC+. Deuteration of HCN leads to the linear ion DNCH+, which, upon dissociative recombination with electrons, can produce HCN + D, DNC + H, and CN + H + D, but not DCN. On the other hand, deuteration of HNC leads to the ion DCNH+ and the non-linear ion DHNC+. Dissociative recombination of DCNH+ can then lead to DCN + H, whereas dissociative recombination of DHNC+ can lead to DNC + H. Thus deuteration of HCN leads to DNC only whereas deuteration of HNC leads to both DCN and DNC. At low temperatures, where the HNC/HCN abundance ratio is near unity, deuteration of HCN through HNC is important. We assume, however, that the reaction of HNC with atomic oxygen yields CO in an exothermic channel with a small barrier (Pineau des Forêts et al. 1990; Schilke et al. 1992). Then, as the temperature rises, the abundance of HNC decreases due to the neutral-neutral reaction with atomic oxygen, and so deuteration of HCN through HNC becomes unimportant.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6531fig3.eps}
\end{figure}](/articles/aa/full/2007/10/aa6531-06/Timg28.gif) |
Figure 3:
Deuterium fractionation ratios. Left: warm-core conditions, right: low-metal conditions. |
| Open with DEXTER |
The abundance ratio DCN/HCN is shown in the top panels of Fig. 3 for warm-core and low-metal elemental abundances, respectively. At low temperatures, the deuteration proceeds through HNC as discussed above. The dependence on temperature decreases monotonically from 20 K upwards. By 50 K, however, the ratio is still equal to or greater than 0.01 at the highest densities considered, which far exceeds the H2D+/H3+ value and so derives mainly from CH2D+/CH3+. What exactly are the formation routes of DCN and DNC at these higher temperatures?
One route comes directly from CH2D+:
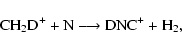 |
(11) |
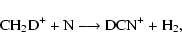 |
(12) |
where the two channels are assumed to have equal rate coefficients. It should be noted that the lower energy isomer of the ionized form of HCN is HNC+ and not HCN+ (Hansel et al. 1998). The separate forms DNC+ and DCN+ show different behavior in the chemical chain of reactions:
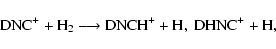 |
(13) |
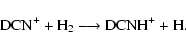 |
(14) |
The subsequent dissociative recombination reactions proceed as:
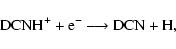 |
(15) |
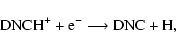 |
(16) |
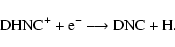 |
(17) |
The other channels
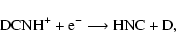 |
(18) |
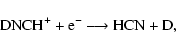 |
(19) |
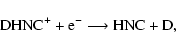 |
(20) |
are assumed to take place with an efficiency smaller by a factor of 2 than the channel leading to deuteration (Roueff 2005), following some experimental results on deuterated molecular ions.
We have not yet explained the strong density dependence of the DCN/HCN abundance ratio, which exceeds that of the primary ion ratio CH2D+/CH3+, especially for the low-metal elemental abundances. Two main factors contribute to this enhancement. As density increases, not only the abundance of the CH5+ ion is enhanced but also those of CH4D+ and CH3D2+ because these species are produced via radiative association of the primary ions with H2, HD and D2. The CH4D+/CH5+ ratio is always larger than the CH2D+/CH3+ with the present chemistry. Dissociative recombination of CH4D+ and CH3D2+ leads to radicals such as CHD and CD2 that react with atomic nitrogen to produce DCN. In addition, the main destruction routes of DCN are the reactions with the abundant ions HCO+ and H3O+ that give DCNH+, which subsequently returns to DCN via dissociative recombination. A further destruction route is the reaction of DCN + H leading to HCN + D, the importance of which decreases with density.
Unlike DCN/HCN, the DNC/HNC abundance ratio is thought to be not relevant at high temperatures, since destruction of both species via reaction with atomic oxygen means that neither can be detected. For completeness, however, the ratio is shown in the bottom panels of Fig. 3.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6531fig4.eps}
\end{figure}](/articles/aa/full/2007/10/aa6531-06/Timg39.gif) |
Figure 4:
Deuterium fractionation ratios. Left: warm-core conditions, right: low-metal conditions. |
| Open with DEXTER |
Let us now consider the often observed abundance ratios involving singly and doubly deuterated isotopologues of formaldehyde, both of which are shown in Fig. 4. The former case is strongly related to the CH2D+/CH3+ ratio since these ions eventually lead to their neutral counterparts, which react with O atoms to form formaldehyde and its isotopologue. And, the temperature profiles are generally in accord with this simple picture. As with the DCN/HCN ratio, however, the density dependence of HDCO/H2CO is stronger than one might expect based on our simple picture, and may also involve a significant role for CH4D+/CH5+. Doubly deuterated formaldehyde presumably derives from CHD2+ and CH3D2+.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6531fig5.eps}
\end{figure}](/articles/aa/full/2007/10/aa6531-06/Timg40.gif) |
Figure 5:
Deuterium fractionation ratios. Left: warm-core conditions, right: low-metal conditions. |
| Open with DEXTER |
We display in Fig. 5 both NH2D/NH3 and HDO/H2O, since water and ammonia can be abundant in interstellar clouds. Much of the deuteration occurs during the destruction phase for these two species, and the abundance ratio HDO/H2O generally follows that of H2D+/H3+ especially for low-metal abundances. Still, there appears to be another mechanism allowing the abundance ratio NH2D/NH3 to exceed H2D+/H3+, often by a considerable amount. A detailed analysis of the formation and destruction reactions shows that NH3D+, the precursor to NH2D, is not formed primarily from the deuteration of NH3 so that the dominant process leading to NH2D occurs during its formation. Since the formation of ammonia and its deuterated isotpologue is a complex affair, it is not facile to find the specific cause of the enhancement in the NH2D/NH3 abundance ratio. According to Turner (2001), NH2D at low temperatures is formed primarily from the radical NH2 via deuteration to form NH2D+, which then reacts with H2 to form NH3D+ + H.
Dissociative recombination of this ion then leads to NH2D. We found some indication that, even at 50 K, NH2D+ is an important precursor to NH2D.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6531fig6.eps}
\end{figure}](/articles/aa/full/2007/10/aa6531-06/Timg41.gif) |
Figure 6:
Deuterium fractionation ratios. Left: warm-core conditions, right: low-metal conditions. |
| Open with DEXTER |
Finally, we consider the case of the abundance ratio C2D/C2H, which is closely related to C2HD+/C2H2+. Figure 6 contains plots of both ratios for warm-core and low-metal elemental abundances. Although the temperature dependence of C2D/C2H presents no surprises, the density dependence with warm-core elemental abundances is an example of a maximum at intermediate densities. It is clear that at densities above
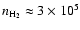 cm-3, the ratio begins to decrease. At these same densities, the abundance ratio of the primary ion precursors still increases but by a small amount. The explanation is as follows: as the density increases the fractional abundances of the C2H2+ ion and its deuterated isotopologue are gradually reduced compared with the fractional abundances of the secondary ion C2H3+ and its deuterated isotopologue. Since the abundance ratio C2H2D+/C2H3+ is less than the abundance ratio C2HD+/C2H2+, the production of C2D and C2H via the more saturated ions leads to a lower abundance ratio. The case of the low-metal elemental abundances is different because the increase in the ratio C2HD+/C2H2+ with increasing density is much less (note the difference in the y-scales of the panels for the two sets of elemental abundances), so that the decrease in the C2D/C2H ratio sets in earlier.
cm-3, the ratio begins to decrease. At these same densities, the abundance ratio of the primary ion precursors still increases but by a small amount. The explanation is as follows: as the density increases the fractional abundances of the C2H2+ ion and its deuterated isotopologue are gradually reduced compared with the fractional abundances of the secondary ion C2H3+ and its deuterated isotopologue. Since the abundance ratio C2H2D+/C2H3+ is less than the abundance ratio C2HD+/C2H2+, the production of C2D and C2H via the more saturated ions leads to a lower abundance ratio. The case of the low-metal elemental abundances is different because the increase in the ratio C2HD+/C2H2+ with increasing density is much less (note the difference in the y-scales of the panels for the two sets of elemental abundances), so that the decrease in the C2D/C2H ratio sets in earlier.
Table 2 shows the predicted ratios for species discussed above at molecular hydrogen densities of 105, 106, and 107 cm-3 and at temperatures of 50, 60, and 70 K for both warm-core (WC) and low-metal (LM) elemental abundances, while Table 3 shows the calculated fractional abundances of the normal isotopologues with respect to molecular hydrogen under the same conditions. Other values are available from the authors.
Table 2:
Calculated abundance ratios between selected singly deuterated and normal isotopologues.
Table 3:
Calculated fractional abundances relative to molecular hydrogen for normal isotopologues.
In order to understand the result of Leurini et al. (2006) that the DCN/HCN abundance ratio is nearly 0.01 in warm (50-75 K) dense (
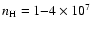 cm-3) clumps in the Orion Bar, we have used a gas-phase steady-state model to calculate the extent of deuterium fractionation at temperatures up to 70 K over a wide range of densities. The calculations are based on two different sets of elemental abundances: one labeled "warm-core'' abundances, in which higher values of heavy elements are used to account for partial evaporation of grain mantles, and the other, the more standard "low-metal'' abundances. We have attempted to interpret the results of the calculations in terms of primary abundance ratios between ions that undergo deuterium exchange reactions although the effects on secondary species are often overlapping. Nevertheless, at the higher temperatures studied, the higher abundance ratios obtained between singly deuterated and normal isotopologues tend to derive from the ions CH2D+ and CH3+ (and to a lesser extent from C2HD+ and C2H2+ ), as realized by
Leurini et al. (2006) since the primary ionic ratio H2D+/H3+ is too small.
cm-3) clumps in the Orion Bar, we have used a gas-phase steady-state model to calculate the extent of deuterium fractionation at temperatures up to 70 K over a wide range of densities. The calculations are based on two different sets of elemental abundances: one labeled "warm-core'' abundances, in which higher values of heavy elements are used to account for partial evaporation of grain mantles, and the other, the more standard "low-metal'' abundances. We have attempted to interpret the results of the calculations in terms of primary abundance ratios between ions that undergo deuterium exchange reactions although the effects on secondary species are often overlapping. Nevertheless, at the higher temperatures studied, the higher abundance ratios obtained between singly deuterated and normal isotopologues tend to derive from the ions CH2D+ and CH3+ (and to a lesser extent from C2HD+ and C2H2+ ), as realized by
Leurini et al. (2006) since the primary ionic ratio H2D+/H3+ is too small.
With both sets of elemental abundances, we obtain that the DCN/HCN ratio is a strong direct function of density. For the warm-core case, we calculate that at a temperature of 50 K, we can explain the measured DCN/HCN value of
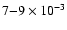 at gas densities that exceed 106 cm-3, whereas for the low-metal case, a similar result is obtained at the higher temperature of 60 K. Although we do not expect a steady-state calculation to be as accurate for fractional abundances of organic species, we do obtain a fractional abundance for HCN of
at gas densities that exceed 106 cm-3, whereas for the low-metal case, a similar result is obtained at the higher temperature of 60 K. Although we do not expect a steady-state calculation to be as accurate for fractional abundances of organic species, we do obtain a fractional abundance for HCN of
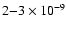 at a molecular hydrogen density of 106 cm-3 in the warm-core conditions, almost independently of the temperature range between 50 and 70 K. This value is surprisingly close to the observed derived fractional density in the Orion Bar by Leurini et al. (2006) of
at a molecular hydrogen density of 106 cm-3 in the warm-core conditions, almost independently of the temperature range between 50 and 70 K. This value is surprisingly close to the observed derived fractional density in the Orion Bar by Leurini et al. (2006) of 
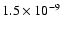 ,
assuming LTE, an H13CN/HCN ratio of 1/70 and a total column density for H2 of
,
assuming LTE, an H13CN/HCN ratio of 1/70 and a total column density for H2 of
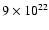 cm-2. At lower densities and higher temperatures, which pertain to the inter-clump medium (150 K,
cm-2. At lower densities and higher temperatures, which pertain to the inter-clump medium (150 K,
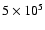 cm-3), we would expect to see little deuteration, mainly because of the high kinetic temperature. The inter-clump material is perhaps best mapped out by formaldehyde. If a limited amount of formaldehyde is to be found in the warm clumps, and our model results show this to be the case at a level of about 10
-9-10-11 depending on the depletions and physical conditions, then HDCO might also be profitably searched for in these regions, since our calculations also show that deuterium fractionation is high for formaldehyde at temperatures through 70 K. Indeed, at 60 K, we obtain that HDCO/H2CO is close to
cm-3), we would expect to see little deuteration, mainly because of the high kinetic temperature. The inter-clump material is perhaps best mapped out by formaldehyde. If a limited amount of formaldehyde is to be found in the warm clumps, and our model results show this to be the case at a level of about 10
-9-10-11 depending on the depletions and physical conditions, then HDCO might also be profitably searched for in these regions, since our calculations also show that deuterium fractionation is high for formaldehyde at temperatures through 70 K. Indeed, at 60 K, we obtain that HDCO/H2CO is close to 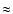 0.01 even at the lowest densities for both sets of elemental abundances.
0.01 even at the lowest densities for both sets of elemental abundances.
It would be desirable to both expand the limited frequency range studied by the APEX survey to search more completely for other molecules and their deuterated isotopologues and to report some upper limits for species not detected. As an example, we find a high fractional abundance of ammonia, so that even with our calculated lower abundance ratios of 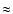 10-3 between the deuterated and normal isotopologues, it might still be possible to detect NH2D, which has two relatively low-lying transitions at 282 GHz and 305.7 GHz (respectively para and ortho). Likewise, it would be interesting to see if HNC, which possesses no transitions within the observed frequency range, cannot be detected from these warm clumps, since our prediction that it has a low fractional abundance is based on the destruction reaction with atomic oxygen, which has not been studied in the laboratory, to the best of our knowledge. Finally, we predict a sufficiently high abundance of C2D at a density of
10-3 between the deuterated and normal isotopologues, it might still be possible to detect NH2D, which has two relatively low-lying transitions at 282 GHz and 305.7 GHz (respectively para and ortho). Likewise, it would be interesting to see if HNC, which possesses no transitions within the observed frequency range, cannot be detected from these warm clumps, since our prediction that it has a low fractional abundance is based on the destruction reaction with atomic oxygen, which has not been studied in the laboratory, to the best of our knowledge. Finally, we predict a sufficiently high abundance of C2D at a density of 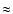 105 cm-3 that it may well be detectable.
105 cm-3 that it may well be detectable.
Acknowledgements
E.H. thanks the National Science Foundation for its support of his research program in astrochemistry and thanks the Observatoire de Paris for providing funds to enable him to travel to Meudon, where much of the work was accomplished. B.P. is grateful to the Alexander von Humboldt Foundation for a research fellowship. The authors thank the referee, Paola Caselli, for her thoughtful comments.
- Aikawa, Y.,
Herbst, E., Roberts, H., & Caselli, P. 2005, ApJ, 620, 330 [NASA ADS] [CrossRef] (In the text)
- Asvany, O., Schlemmer,
S., & Gerlich, D. 2004, ApJ, 617, 685 [NASA ADS] [CrossRef] (In the text)
- Charnley,
S. B., Tielens, A. G. G. M., & Rodgers, S. D.
1997, ApJ, 482, L203 [NASA ADS] [CrossRef]
- Gerin, M., Lis,
D. C., Philipp, S., et al. 2006, A&A, 454, L63 [NASA ADS] [CrossRef] [EDP Sciences]
- Gerlich, D., &
Schlemmer, S. 2002, Planet. Space Sci., 50, 1287 [NASA ADS] [CrossRef] (In the text)
- Gerlich, D., Herbst,
E., & Roueff, E. 2002, Planet. Space Sci., 50,
1275 [NASA ADS] [CrossRef] (In the text)
- Grevesse, N., Noels,
A., & Sauval, A. J. 1996, in ASP Conf. Ser., ed.
S. S. Holt, & G. Sonneborn (San Francisco: ASP), 90,
117
(In the text)
- Hansel, A.,
Glantschnig, M., Scheiring, C., Lindinger, W., & Ferguson,
E. E. 1998, J. Chem. Phys., 109, 1743 [NASA ADS] [CrossRef] (In the text)
- Herbst, E., Adams,
N. G., Smith, D., & Defrees, D. J. 1987, ApJ, 312,
351 [NASA ADS] [CrossRef]
- Le Bourlot, J., Pineau
des Forêts, G., Roueff, E., & Flower, D. R. 1995,
A&A, 302, 870 [NASA ADS] (In the text)
- Leurini, S., Rolffs,
R., Thorwirth, S., et al. 2006, A&A, 454, L47 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lis, D. C., &
Schilke, P. 2003, ApJ, 597, L145 [NASA ADS] [CrossRef] (In the text)
- Millar, T. J.
2002, Planet. Space Sci., 50, 1189 [NASA ADS] [CrossRef]
- Millar, T. J.,
Bennett, A., & Herbst, E. 1989, ApJ, 340, 906 [NASA ADS] [CrossRef]
- Moustefaoui, T.,
Rebrion-Rowe, C., Le Garrec, J.-L., Rower, B. R., &
Mitchell, J. B. A. 1998, Faraday Discussions, 109, 71 [CrossRef] (In the text)
- Nagaoka, A., Watanabe,
N., & Kouchi, A. 2005, ApJ, 624, L29 [NASA ADS] [CrossRef]
- Osamura, Y., Roberts,
H., & Herbst, E. 2004, A&A, 421, 1101 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Osamura, Y., Roberts,
H., & Herbst, E. 2005, ApJ, 621, 348 [NASA ADS] [CrossRef]
- Parise, B., Castets,
A., Herbst, E., et al. 2004, A&A, 416, 159 [NASA ADS] [CrossRef] [EDP Sciences]
- Parise, B.,
Ceccarelli, C., Tielens, A. G. G. M., et al.
2002, A&A, 393, L49 [NASA ADS] [CrossRef] [EDP Sciences]
- Parise, B.,
Ceccarelli, C., Tielens, A. G. G. M., et al.
2006, A&A, 453, 949 [NASA ADS] [CrossRef] [EDP Sciences]
- Pineau des
Forêts, G., Roueff, E., & Flower, D. R. 1990, MNRAS,
244, 668 [NASA ADS]
- Roberts, H., &
Millar, T. J. 2000, A&A, 364, 780 [NASA ADS]
- Roberts, H.,
Herbst, E., & Millar, T. J. 2002, MNRAS, 336, 283 [NASA ADS] (In the text)
- Roberts,
H., Herbst, E., & Millar, T. J. 2003, ApJ, 591, L41 [NASA ADS] [CrossRef]
- Roberts,
H., Herbst, E., & Millar, T. J. 2004, A&A, 424,
905 [NASA ADS] [CrossRef] [EDP Sciences]
- Roueff, E. 2005, J.
Phys. Conf. Ser., 4, 1 [NASA ADS] [CrossRef] (In the text)
- Roueff, E., Lis,
D. C., van der Tak, F. F. S., Gerin, M., &
Goldsmith, P. F. 2005, A&A, 438, 585 [NASA ADS] [CrossRef] [EDP Sciences]
- Schilke, P.,
Walmsley, C. M., Pineau Des Forêts, G., et al. 1992,
A&A, 256, 595 [NASA ADS]
- Smith, D., Adams,
N. G., & Alge, E. 1982, ApJ, 263, 123 [NASA ADS] [CrossRef] (In the text)
-
Stantcheva, T., & Herbst, E. 2003, MNRAS, 340, 983 [NASA ADS]
- Talbi, D., &
Herbst, E. 1998, A&A, 333, 1007 [NASA ADS] (In the text)
- Tielens,
A. G. G. M. 1983, A&A, 119, 177 [NASA ADS] (In the text)
- Turner, B. E.
2001, ApJS, 136, 579 [NASA ADS] [CrossRef]
- Vastel, C., Phillips,
T. G., & Yoshida, H. 2004, ApJ, 606, L127 [NASA ADS] [CrossRef] (In the text)
- Wakelam, V., Herbst,
E., & Selsis, F. 2006, A&A, 451, 551 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Walmsley, C. M.,
Flower, D. R., & Pineau des Forêts, G. 2004, A&A,
418, 1035 [NASA ADS] [CrossRef] [EDP Sciences]
Copyright ESO 2007
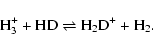
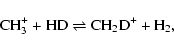
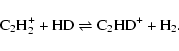
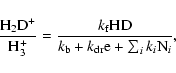
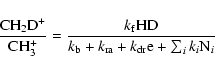
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6531fig1.eps}
\end{figure}](/articles/aa/full/2007/10/aa6531-06/Timg20.gif)
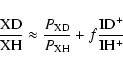
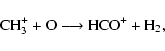
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6531fig2.eps}
\end{figure}](/articles/aa/full/2007/10/aa6531-06/Timg27.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6531fig3.eps}
\end{figure}](/articles/aa/full/2007/10/aa6531-06/Timg28.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6531fig4.eps}
\end{figure}](/articles/aa/full/2007/10/aa6531-06/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6531fig5.eps}
\end{figure}](/articles/aa/full/2007/10/aa6531-06/Timg40.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6531fig6.eps}
\end{figure}](/articles/aa/full/2007/10/aa6531-06/Timg41.gif)