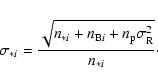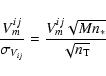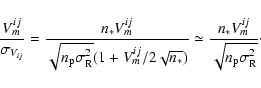A&A 464, 1-12 (2007)
DOI: 10.1051/0004-6361:20066496
AMBER: Instrument description and first astrophysical results
AMBER, the near-infrared spectro-interferometric
three-telescope VLTI instrument
R. G. Petrov1
- F. Malbet2 - G. Weigelt3
- P. Antonelli4
- U. Beckmann3
- Y. Bresson4
- A. Chelli2
- M. Dugué4
- G. Duvert2
- S. Gennari5
- L. Glück2
- P. Kern2
- S. Lagarde4
- E. Le Coarer2
- F. Lisi5
- F. Millour1,2
- K. Perraut2
- P. Puget2
- F. Rantakyrö6 - S. Robbe-Dubois1
- A. Roussel4 - P. Salinari5
- E. Tatulli2,5
- G. Zins2
- M. Accardo5
- B. Acke2,13
- K. Agabi1
- E. Altariba2
- B. Arezki2
- E. Aristidi1
- C. Baffa5
- J. Behrend3
- T. Blöcker3
- S. Bonhomme4
- S. Busoni5
- F. Cassaing7
- J.-M. Clausse4
- J. Colin4
- C. Connot3
- A. Delboulbé2
- A. Domiciano de Souza1,4
- T. Driebe3
- P. Feautrier2
- D. Ferruzzi5
- T. Forveille2
- E. Fossat1
- R. Foy8
- D. Fraix-Burnet2
- A. Gallardo2
- E. Giani5
- C. Gil2,14
- A. Glentzlin4
- M. Heiden3
- M. Heininger3
- O. Hernandez Utrera2
- K.-H. Hofmann3
- D. Kamm4
- M. Kiekebusch6
- S. Kraus3
- D. Le Contel4
- J.-M. Le Contel4
- T. Lesourd9 - B. Lopez4
- M. Lopez9 - Y. Magnard2
- A. Marconi5
- G. Mars4
- G. Martinot-Lagarde9,4
- P. Mathias4
- P. Mège2
- J.-L. Monin2
- D. Mouillet2,15
- D. Mourard4
- E. Nussbaum3
- K. Ohnaka3
- J. Pacheco4
- C. Perrier2
- Y. Rabbia4
- S. Rebattu4
- F. Reynaud10
- A. Richichi11
- A. Robini1 - M. Sacchettini2
- D. Schertl3
- M. Schöller6 - W. Solscheid3
- A. Spang4
- P. Stee4
- P. Stefanini5
- M. Tallon8
- I. Tallon-Bosc8
- D. Tasso4
- L. Testi5
- F. Vakili1 - O. von der Lühe12
- J.-C. Valtier4 - M. Vannier1,6,16
- N. Ventura2
1 - Laboratoire Universitaire d'Astrophysique de Nice, UMR 6525 Université de Nice, Sophia Antipolis/CNRS, Parc Valrose, 06108 Nice Cedex 2, France,
2 - Laboratoire d'Astrophysique de Grenoble, UMR 5571 Université Joseph
Fourier/CNRS, BP 53, 38041 Grenoble Cedex 9, France
3 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
4 - Laboratoire Gemini, UMR 6203 Observatoire de la Côte d'Azur/CNRS, BP 4229, 06304 Nice Cedex 4, France
5 - INAF-Osservatorio Astrofisico di Arcetri, Istituto Nazionale di Astrofisica, Largo E. Fermi 5, 50125 Firenze, Italy
6 - European Southern Observatory, Casilla 19001, Santiago 19, Chile
7 - ONERA/DOTA, 29 av de la Division Leclerc, BP 72, 92322 Chatillon Cedex, France
8 - Centre de Recherche Astronomique de Lyon, UMR 5574 Université Claude Bernard/CNRS, 9 avenue Charles André, 69561 Saint Genis
Laval Cedex, France
9 - Division Technique INSU/CNRS UPS 855, 1 place Aristide
Briand, 92195 Meudon Cedex, France
10 - IRCOM, UMR 6615 Université de Limoges/CNRS, 123 avenue Albert Thomas, 87060 Limoges Cedex, France
11 - European Southern Observatory, Karl Schwarzschild Strasse 2, 85748 Garching, Germany
12 - Kiepenheuer Institut für Sonnenphysik, Schöneckstr. 6,
79104 Freiburg, Germany
13 - Instituut voor Sterrenkunde, KU-Leuven, Celestijnenlaan 200D,
3001 Leuven, Belgium
14 - Centro de Astrofísica da Universidade do Porto, Rua
das Estrelas - 4150-762 Porto, Portugal
15 - Laboratoire Astrophysique de Toulouse, UMR 5572 Université Paul Sabatier/CNRS, BP 826, 65008 Tarbes Cedex, France
16 - Departamento de Astronomia, Universidad de Chile, Chile
Received 3 October 2006 / Accepted 6 December 2006
Abstract
Context. Optical long-baseline interferometry is moving a crucial step forward with the advent of general-user scientific instruments that equip large aperture and hectometric baseline facilities, such as the Very Large Telescope Interferometer (VLTI).
Aims. AMBER is one of the VLTI instruments that combines up to three beams with low, moderate and high spectral resolutions in order to provide milli-arcsecond spatial resolution for compact astrophysical sources in the near-infrared wavelength domain. Its main specifications are based on three key programs on young stellar objects, active galactic nuclei central regions, masses, and spectra of hot extra-solar planets.
Methods. These key science goals led to scientific specifications, which were used to propose and then validate the instrument concept. AMBER uses single-mode fibers to filter the entrance signal and to reach highly accurate, multiaxial three-beam combination, yielding three baselines and a closure phase, three spectral dispersive elements, and specific self-calibration procedures.
Results. The AMBER measurements yield spectrally dispersed calibrated visibilities, color-differential complex visibilities, and a closure phase allows astronomers to contemplate rudimentary imaging and highly accurate visibility and phase differential measurements. AMBER was installed in 2004 at the Paranal Observatory. We describe here the present implementation of the instrument in the configuration with which the astronomical community can access it.
Conclusions. After two years of commissioning tests and preliminary observations, AMBER has produced its first refereed publications, allowing assessment of its scientific potential.
Key words: instrumentation: high angular resolution - techniques:
interferometric - techniques: spectroscopic
1 Introduction
Long-baseline interferometry using optical telescopes has reached an
important stage in its development at the beginning of the 21st
century by combining the light of astrophysical sources collected by
large apertures with the Very Large Telescope Interferometer
(VLTI; Glindemann et al. 2001b,a) and the
Keck Interferometer (KI; Colavita et al. 2003). This
achievement allows the observers to obtain unprecedented spatial
resolution, together with an enhanced flux sensitivity compared to
earlier interferometers. This was first demonstrated by the
extragalactic observations with the KI (Swain et al. 2003) and
VLTI (Jaffe et al. 2004; Wittkowski et al. 2004).
![\begin{figure}
\par\includegraphics[width=17.3cm,clip]{6496fig1.eps}\end{figure}](/articles/aa/full/2007/10/aa6496-06/Timg11.gif) |
Figure 1:
Composite photograph of the AMBER instrument in the integration room of the Laboratoire d'Astrophysique de Grenoble in 2003. The instrument was complete but for its enclosure and for
the beam commutation device. Some integration and test tools are also still present on the table. The beams (white lines) arrive in the bottom left of the picture and travel from the left to the
right. They are split spectrally by dichroïcs in K, H, and J bands (respectively red, green, and blue from left to right) before being fed into single-mode optical fibers that
filter each beam spatially. After the spatial filters, the bands are merged together by a symmetrical set of dichroïcs, then travel right to left through cylindrical optics and a periscope, and is finally focused on the entrance slit of the cryogenic spectrograph in the upper left corner. The 1600 Kg AMBER table is 4.2 by 1.5 m and supports about 300 Kg of optical and
mechanical equipment. |
| Open with DEXTER |
The VLTI (Glindemann et al. 2004) is the infrastructure located on
the summit of Cerro Paranal in Chile that is necessary for performing
optical interferometry. It includes large 8-m telescopes
called Unit Telescopes (UTs) and 2-m telescopes called
Auxiliary Telescopes (ATs), but also the optical train that
allows the light beam collected by the apertures to be conveyed to the
combining instrument. Each beam is partially corrected for
atmospheric wave front perturbation thanks to adaptive optics (AO)
modules on UTs or to tip-tilt correctors for ATs. The beams are
transported to the interferometric laboratory through the telescope
Coudé trains feeding delay lines (DLs) installed in a thermally
stable interferometric tunnel. As a first step, the optical path
difference (OPD) between two beams is set to zero with errors smaller
than
 thanks to the good global metrology of the instrument.
A fringe sensor (Gai et al. 2004) is being implemented in
the OPD control loop to stabilize the fringes within a small fraction
of wavelength. For each beam, the pupils and the images delivered in
the focal laboratory are stabilized. Eventually, a field separator
to be implemented at each telescope (Delplancke et al. 2004) will allow
AO correction and fringe tracking on an off axis reference star up to
1 arc minute away from the scientific source. The ultimate feature of the
VLTI will be a metrology system combined with differential delay lines
allowing us to perform imaging through phase referencing between an
off-axis reference star and the scientific source, as well as highly
accurate differential astrometry (Paresce et al. 2003a). The
implementation of the VLTI is progressive. It started with two
telescopes without fringe tracking and will eventually reach the full
picture described above.
thanks to the good global metrology of the instrument.
A fringe sensor (Gai et al. 2004) is being implemented in
the OPD control loop to stabilize the fringes within a small fraction
of wavelength. For each beam, the pupils and the images delivered in
the focal laboratory are stabilized. Eventually, a field separator
to be implemented at each telescope (Delplancke et al. 2004) will allow
AO correction and fringe tracking on an off axis reference star up to
1 arc minute away from the scientific source. The ultimate feature of the
VLTI will be a metrology system combined with differential delay lines
allowing us to perform imaging through phase referencing between an
off-axis reference star and the scientific source, as well as highly
accurate differential astrometry (Paresce et al. 2003a). The
implementation of the VLTI is progressive. It started with two
telescopes without fringe tracking and will eventually reach the full
picture described above.
The VLTI is completed with focal instruments that clean or calibrate
some perturbations in each beam, combine two or more beams, and record
and analyze the interference fringes in one or several spectral
channels. VINCI (Kervella et al. 2003), a two-way beam combiner
working in the broad K-band with a fiber coupler, has been used for
commissioning the first stages of the VLTI and has produced a wealth
of science (Paresce et al. 2003b) but is no longer proposed to
the community. MIDI (Leinert 2004; Leinert et al. 2003) is
a two-way beam combiner for the mid-infrared N-band featuring
moderate spectral resolution.
AMBER![[*]](/icons/foot_motif.gif) is the
first-generation general-user near-infrared focal instrument of VLTI.
After about two years of preliminary studies and lobbying, actual
development started in 1998 after the European Southern
Observatory (ESO) decided to revive the development of interferometry at the VLT (Paresce et al. 1996). The instrument was installed and obtained its first fringes in March 2004. Subsequent work has focused on technical investigations, commissioning and preliminary scientific observations. Figure 1 is a photograph of the instrument. AMBER builds on experience gained with several optical interferometers: GI2T (Mourard et al. 2003) for the principle of dispersed fringes, FLUOR (Coudé Du Foresto et al. 1998; Coudé du Foresto et al. 2003) for high accuracy with single-mode fibers, and PTI (Colavita et al. 1999; Colavita 1999) for the data reduction scheme.
is the
first-generation general-user near-infrared focal instrument of VLTI.
After about two years of preliminary studies and lobbying, actual
development started in 1998 after the European Southern
Observatory (ESO) decided to revive the development of interferometry at the VLT (Paresce et al. 1996). The instrument was installed and obtained its first fringes in March 2004. Subsequent work has focused on technical investigations, commissioning and preliminary scientific observations. Figure 1 is a photograph of the instrument. AMBER builds on experience gained with several optical interferometers: GI2T (Mourard et al. 2003) for the principle of dispersed fringes, FLUOR (Coudé Du Foresto et al. 1998; Coudé du Foresto et al. 2003) for high accuracy with single-mode fibers, and PTI (Colavita et al. 1999; Colavita 1999) for the data reduction scheme.
Section 2 reviews the main scientific drivers of AMBER,
which allowed us to define the instrumental specifications. The
instrument concept is described in Sect. 3, together
with its different parts. Section 4 discusses the
expected performances of AMBER in relation with what has been measured
currently. Section 5 presents the various operating
modes of AMBER and discusses the calibration procedures.
Table 1:
Summary of the initial scientific requirements and top level specifications for AMBER.
2 Science drivers and specifications
The specifications of AMBER have been defined as giving the highest
priority to three key astrophysical programs: young stellar objects
(YSOs), active galactic nuclei (AGN), and hot giant extra-solar
planets (ESPs). The first one was considered as the minimum objective
and the third one as an ambitious goal at the very edge of what could
be achieved with the technology and VLTI infrastructure expected when
AMBER was to be installed. We used the experience gained with IOTA,
PTI, GI2T, and single-aperture speckle interferometry on
high-angular-resolution instrumentation to define a certain number of
strategic choices:
- operation in the near-infrared domain [1-2.5
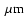 ];
];
- spectrally dispersed observations;
- spatial filtering for high-accuracy absolute visibility;
- very high-accuracy differential visibility and phase;
- imaging information from closure phase.
Table 1 lists the intersection between these strategic choices (columns) and the needs set by the scientific objectives (lines), as summarized below. Framed specifications cooresponds to the most demanding ones.
The study of YSOs is critical to understanding stellar and planetary
formation. Seeing-limited spectrophotometry that observes down to
about 100 AU and, more recently, millimeter wave interferometry,
bispectrum speckle interferometry, and adaptive optics, typically
observing down to 10 AU, gave the outlines of YSO physics, but many
detailed mechanism issues remain open. Long-baseline optical
interferometry, with its milliarcsecond (mas) resolution typically
corresponding to 0.1 AU at 100 pc, is therefore essential for
unravelling the physics of the early stages of star and planet
formation (see reviews by Malbet 2003; Millan-Gabet et al. 2007).
The small-aperture optical interferometers can access the limited
number of YSO brighter than K=7. Since the VLTI should easily reach
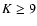 ,
AMBER should give access to hundreds of YSO candidates and
allow a major breakthrough in the field. Simulations of the signatures
of various wind and disk geometries have demonstrated that the
accuracy needed for absolute visibility is about 0.01. In addition
to many broad band programs, moderate spectral resolution observations
within emission lines like Bracket
,
AMBER should give access to hundreds of YSO candidates and
allow a major breakthrough in the field. Simulations of the signatures
of various wind and disk geometries have demonstrated that the
accuracy needed for absolute visibility is about 0.01. In addition
to many broad band programs, moderate spectral resolution observations
within emission lines like Bracket 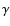 at
at
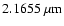 would, for example, allow astronomers to characterize the stellar
wind-launching regions, and to find out if it comes from the star or
from the disk. Given the complexity of the immediate surroundings of
young stars, even rough imaging would be welcome.
would, for example, allow astronomers to characterize the stellar
wind-launching regions, and to find out if it comes from the star or
from the disk. Given the complexity of the immediate surroundings of
young stars, even rough imaging would be welcome.
Observing galactic nuclei allows study of the physics in extreme
conditions at the limits of our physical world set by the horizon of
the massive black hole that they might be hosting. Accretion on such a
black hole is proposed to explain the extreme energetic phenomena
observed in AGN. The nearest AGN are important candidates for testing
the unification schemes (Antonucci & Miller 1985) between the two
main observational categories of AGN. The main unification feature is
a geometrically and optically thick torus able to obscure the central
continuum source if the angle between the torus axis and the
observer's viewing direction is large enough. It is believed that type
1 AGN are seen almost pole-on, whereas type 2 AGN are observed almost edge-on.
The specific requirement for observing AGN is instrument sensitivity.
A coherent magnitude 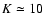 will allow the very brightest
candidates to be observed. With
will allow the very brightest
candidates to be observed. With 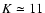 ,
several tens of AGN are
within reach, so that this is the limiting magnitude specification for
AMBER. AGN visibility observation would allow for constraining dust
torus models, but a full demonstration of the unified AGN model would
require model-independent detection of the torus, which is an image in
the near infrared permitted by the AMBER closure phase.
,
several tens of AGN are
within reach, so that this is the limiting magnitude specification for
AMBER. AGN visibility observation would allow for constraining dust
torus models, but a full demonstration of the unified AGN model would
require model-independent detection of the torus, which is an image in
the near infrared permitted by the AMBER closure phase.
Medium spectral-resolution observations in emission lines yields the
structure of the base of the jet in the NLR. Measuring the
differential phase through the line wings yields the size and
kinematics of the BLR, and thereby confirming the presence of a black
hole and evaluating its mass (Marconi et al. 2003). Combining
this angular size with the linear one given by reverberation mapping
gives direct distance measurements on a new scale. This requires a
fringe tracker able to reach the same 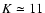 limit.
limit.
The search for and study of extrasolar planets (ESP) is currently one
of the major goals in astronomy, because it is a key ingredient in a
cultural investigation of the place of life, conscience, and mankind
in the Universe. We are living in a fascinating period when these
philosophical questions start being answered by actual physical
measurements. The surprisingly large number of giant hot planets
orbiting very close to their star raises new astrophysical problems
but also opens new observational opportunities. A key issue is
understanding the migration mechanism, its regulation, and
consequences. In particular, are hot giant planets compatible with
planets at more classical locations?
![\begin{figure}
\par\includegraphics[width=15.7cm,clip]{6496fig2.eps}\par\end{figure}](/articles/aa/full/2007/10/aa6496-06/Timg25.gif) |
Figure 2:
The basic concept of AMBER. First, each beam is spatially filtered by a single-mode optical fiber. After each fiber, the beams are collimated so that the spacing between the output pupils
is non redundant. The multiaxial recombination consists in a common optics that merges the three output beams in a common Airy disk containing Young's fringes. Thanks to a cylindrical optics
anamorphoser, this fringed Airy disk is fed into the input slit of a spectrograph. In the focal plane of the spectrograph, each column (in the figure, but in the reality each line) of the
detector contains a monochromatic image of the slit with 3 photometric (P1, P2, P3) zones and one interferogram (IF). In this figure, the detector image contains a view rotated of
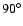 of the AMBER real-time display showing three telescope fringes, in medium-resolution between 2090 and of the AMBER real-time display showing three telescope fringes, in medium-resolution between 2090 and
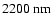 ,
on the bright Be star ,
on the bright Be star  Arae. The three superimposed fringe
patterns form a clear Moiré figure because, in that particular case, the three OPDs were substantially different from zero during the recording. Note that the vertical brighter line indicating the Br
Arae. The three superimposed fringe
patterns form a clear Moiré figure because, in that particular case, the three OPDs were substantially different from zero during the recording. Note that the vertical brighter line indicating the Br emission line.
emission line. |
| Open with DEXTER |
Measuring the variation in the differential phase and visibility with
wavelength at different orbital phases yields the planet orbit and
therefore mass, the planet/star flux ratio, and the planet's
low-resolution (say 30 to 50) spectrum (Vannier et al. 2006).
The latest yields the planet's effective temperature. Combined with
the flux ratio, it allows the radius to be computed and the
mass-radius relationship to be constrained. The shape of the spectrum
constrains the composition of the atmosphere but also its dustiness
(Barman et al. 2001).
The expected signal is very weak (
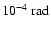 ), but the UTs
collect enough photons to theoretically permit this level of accuracy
in a few hours, if the instrument is extremely stable and all
atmospheric effects are filtered and calibrated extremely well. A
major difficulty is the variable chromatic OPD of dry air and of water
vapor above the telescopes and in the tunnels
(Akeson et al. 2000). A first approach is to instantaneously
fit the differential thickness of water vapor and dry air with the
other parameters. This leads to the initial requirement of
simultaneous J+H+K band observations
), but the UTs
collect enough photons to theoretically permit this level of accuracy
in a few hours, if the instrument is extremely stable and all
atmospheric effects are filtered and calibrated extremely well. A
major difficulty is the variable chromatic OPD of dry air and of water
vapor above the telescopes and in the tunnels
(Akeson et al. 2000). A first approach is to instantaneously
fit the differential thickness of water vapor and dry air with the
other parameters. This leads to the initial requirement of
simultaneous J+H+K band observations![[*]](/icons/foot_motif.gif) . A complementary approach
(Ségransan et al. 2000) is to use the closure phase permitted by
AMBER with three UTs, because it cancels all OPD effects. The closure
phase remains affected by non-OPD effects, such as detector variations
and data processing biases that should vary slowly enough to be
eliminated by an internal modulation of the instrumental closure phase,
as explained in Sect. 5.5.
. A complementary approach
(Ségransan et al. 2000) is to use the closure phase permitted by
AMBER with three UTs, because it cancels all OPD effects. The closure
phase remains affected by non-OPD effects, such as detector variations
and data processing biases that should vary slowly enough to be
eliminated by an internal modulation of the instrumental closure phase,
as explained in Sect. 5.5.
With the specifications and goals set from the three key programs,
AMBER can also be used for constraining fundamental stellar parameters
such as mass, radius, and age, and for stellar activity studies, such
as of star spots and non radial pulsations. A broader program
includes:
- Late stages of stellar evolution. The late stages of
stellar evolution play a crucial role in understanding the chemical
evolution of our Galaxy, since the peeling of stellar surfaces by
strong stellar winds leads to the chemical enrichment of the
interstellar medium. The specific needs of these programs are very
high angular resolution (for example by using the AT telescopes on
the longest possible baselines), and high spectral resolution (10000 or more) to be able to spectrally select active features like spots
or supergranules;
- Environment of hot stars. Be or B[e] stars exhibit
strong emission in the hydrogen lines and are believed to be
surrounded by a large circumstellar rotating and/or an expanding
envelope. Differential visibility and phase constrain the size,
shape, and kinematics of the envelope and help to find the balance
between envelope rotation and latitude-dependent radiation pressure.
The closure phases yield independent constraints on the envelope
asymmetries and will eventually allow reconstructions of the images
able to test differential interferometry deductions;
- Massive stars. Their complex structure is affected by
dramatic events over relatively short periods of time. In the first
stages of their evolution, their powerful stellar radiation ionizes
their close environment in H
 region and feeds the
interstellar medium with high-velocity material. AMBER will resolve
the close multiple systems that were not identified with
observations at lower spatial resolution. The spectral resolution
of AMBER will disentangle the complex kinematics of the close
surroundings of luminous blue variables (LBVs) like the typical
Eta Carinae system.
region and feeds the
interstellar medium with high-velocity material. AMBER will resolve
the close multiple systems that were not identified with
observations at lower spatial resolution. The spectral resolution
of AMBER will disentangle the complex kinematics of the close
surroundings of luminous blue variables (LBVs) like the typical
Eta Carinae system.
The high spectral-resolution mode will be accessible only on a small
number of bright targets, except if an external fringe tracker allows
us to stabilize the fringes and to observe with long (a few seconds)
frame times with AMBER. The VLTI plans include a three telescopes
fringe tracker, called FINITO![[*]](/icons/foot_motif.gif) , operating in the H band, and leaving all the flux in J and K and a fraction of the flux in H for AMBER.
, operating in the H band, and leaving all the flux in J and K and a fraction of the flux in H for AMBER.
3 The AMBER concept
This section is intended to provide the reader (and hopefully the future user of AMBER) with an overview of the key conceptual characteristics of AMBER. The optical principle (Sect. 3.1) and the data reduction (Sect. 3.2) are described in much greater details in other papers in this volume (Robbe-Dubois et al. 2007; Tatulli et al. 2007b). Here, the reader should find a summary and a brief justification of the fundamental choices made in the design of AMBER and its data processing. The selection of the concept is the result of an iteration between scientific specifications, performance,
and complexity estimates in the context of some preferences set by previous experience with interferometric instruments. Section 3.3 insists on the AMBER observables and on the type of source constraints that can be expected from them.
3.1 Optical principle
Figure 2 summarizes the key elements of the AMBER concept. It was designed following a multiaxial beam combination, namely an optical configuration similar to the Young's slits
experiment, which overlaps images of the sources from different telescopes. A set of collimated and mutually parallel beams are focused by a common optical element in a common Airy pattern that
contains fringes. The output baselines are in a non redundant set up, i.e. the spacing between the beams is selected for the Fourier transform of the fringe pattern to show separated fringe peaks at all wavelengths. The Airy disk needs to be sampled by many pixels in the
baseline direction (an average of 4 pixels in the narrowest fringe,
i.e. at least 12 pixels in the output baseline direction), while in
the other direction a single pixel is sufficient. To minimize detector
noise, each spectral channel is concentrated in a single column of
pixels by cylindrical optics. This multiaxial beam combiner has been
selected because it allows an easy and modular evolution from two to
three, or even 4, telescopes and because it simplifies the design of
the interface to the spectrograph and of the spectrograph itself. This
is obtained without loss of potential SNR compared to a coaxial scheme like FLUOR (Coudé Du Foresto et al. 1998).
The fringes are dispersed by a standard long-slit spectrograph on a two-dimensional detector. To work in the K band with resolutions up to 10 000, the spectrograph must be cooled down to about
-60  C with a cold slit in the image plane and a cold pupil stop. In practice, it is simpler to cool it down to the temperature of liquid nitrogen.
C with a cold slit in the image plane and a cold pupil stop. In practice, it is simpler to cool it down to the temperature of liquid nitrogen.
To produce highly accurate measurements, it is necessary to spatially filter the incoming beam's wavefronts to force each one of them to contain only a single coherent mode. To ensure the most accurate visibility measurements, the spatial filter must transmit at least 103 more light in the main guided mode than in all the secondary modes. For the kind of imperfect AO correction (Strehl ratios often below 50%) available for the VLTI, the only way to achieve this
filtering quality with decent light transmission is to use single-mode
optical fibers. The wavefront corrugations are translated in time-dependent intensity fluctuations and a global chromatic "piston''. The word "piston'' designates the average of the wavefront OPD on each telescope aperture. The flux transmitted by each fiber must be monitored in real time for each spectral channel. A fraction of each beam is extracted before the beam combiner and sent directly to the detector through a dispersive element. The instrument must also perform some other individual beam processing before entering the spatial filter, such as correcting for the differential atmospheric refraction in the H and J bands or, in some cases, eliminating one
polarization.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6496fig3.eps}\end{figure}](/articles/aa/full/2007/10/aa6496-06/Timg30.gif) |
Figure 3:
Raw detector image from amber obtained in the three-telescope low-resolution mode on the star  Bootis in April 2006. The stellar signal is spectrally dispersed in the vertical direction and each (pair of) detector line contains a spectral channel. The rows of K band and H band occupy respectively the upper and the lower half of the screen. From left to right, the first, second, and fourth columns represent the photometric beams for the each one of the free telescopes, while the third column contains the interferometric signal, with three superimposed fringe systems.
Bootis in April 2006. The stellar signal is spectrally dispersed in the vertical direction and each (pair of) detector line contains a spectral channel. The rows of K band and H band occupy respectively the upper and the lower half of the screen. From left to right, the first, second, and fourth columns represent the photometric beams for the each one of the free telescopes, while the third column contains the interferometric signal, with three superimposed fringe systems. |
| Open with DEXTER |
Figure 3 displays the raw image that is recorded by the amber detector (see caption for details) in low-resolution mode where the spectrum from 1.4 to
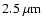 is present. In
medium and high resolution mode only a part of one NIR band is recorded.
is present. In
medium and high resolution mode only a part of one NIR band is recorded.
The description above applies to one spatial filter. Since single-mode
fibers are not fully efficient from 1 to 2.5 microns and the sampling
on the detector depends linearly with the wavelength, AMBER has been
designed to have 3 working spatial filters in J, H, and K. The
parameters have been optimized for each band: numerical aperture of
the single mode fiber, size of the output pupils, and separation
between the different apertures. Dichroics separate the incoming beams
in 3 beams, which are processed separately (from left for K to right
for J in Fig. 2). Output dichroics merges the beams
again at the output of the fibers. The global sizes and spacings of
the output pupils in J, H, and K are set proportionally to the central
wavelength of each filter, so that the Airy disk and inter fringe at
1.25, 1.65, and
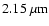 are the same on the detector.
are the same on the detector.
An important additional device, which is not represented in Fig. 2, is the calibration and alignment unit (CAU) used to feed AMBER with the well-characterized artificial fringes needed for the interferometric P2VM calibration described below.
A polarization maintaining single-mode fiber introduces a random OPD between the two polarizations. In the absence of a compensator, this effect can destroy the instrumental contrast. To avoid this, AMBER rejects one of the polarizations of the incoming beams. This results in the loss of 50% of the photons. It is important to note that this polarization direction is fixed according to the interferometric table and is therefore variable when projected on the sky. When model-fitting polarized objects, one should take this effect into account.
The subsystems of AMBER, their specifications, designs, and tests are described in detail in Robbe-Dubois et al. (2007).
3.2 Basic AMBER measures
The VLTI gives access to the complex visibility function of the source at a limited number of spatial frequencies
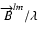 ,
where
,
where
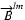 is
the baseline that joins telescopes l and m projected on the sky. If
is
the baseline that joins telescopes l and m projected on the sky. If
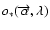 is the source brightness distribution at the angular position
is the source brightness distribution at the angular position
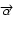 and the wavelength
and the wavelength 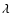 ,
the source complex visibility function is defined by the Fourier transform:
,
the source complex visibility function is defined by the Fourier transform:
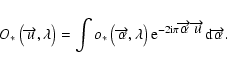 |
(1) |
At the spatial frequency
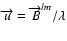 ,
this is
,
this is
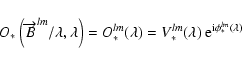 |
(2) |
where
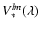 and
and
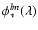 are the amplitude and phase of the complex visibility
are the amplitude and phase of the complex visibility
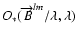 .
When the word "visibility'' is used alone, it refers to the amplitude
.
When the word "visibility'' is used alone, it refers to the amplitude
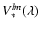 .
.
The wavelength dependence of the spatial frequency transforms the AMBER large spectral coverage from 1.05 to
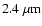 in an important increase in spatial coverage as illustrated by
Fig. 4, which has to be considered when preparing AMBER observations.
in an important increase in spatial coverage as illustrated by
Fig. 4, which has to be considered when preparing AMBER observations.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{6496fig4.eps}\end{figure}](/articles/aa/full/2007/10/aa6496-06/Timg45.gif) |
Figure 4:
Exploration of the u-v plane using spectral coverage. The
two figures represent the typical fringed visibility function as a
function of u and v, as produced by a binary. On the left we have
the u-v tracks obtained with a single spectral channel and 10 hours of observations with UT1-UT3-UT4. On the right, we represent the u-v coverage obtained from 1.05 to 2.4 microns with only one snapshot observation with the same telescopes. As demonstrated by (Millour et al. 2007), the constraints on the binary angular separation are similar for the left and right u-v
coverages, but in the spectrally resolved case we obtain the spectra of the components in addition. |
| Open with DEXTER |
For each elementary frame and in each AMBER spectral channel, i.e. in
each line of the detector, we have an interferometric and three
photometric signals that have been processed by the same optics and
the same dispersive elements (as shown in Figs. 2 and 3). For a single-mode instrument, the Fourier interferogram (Fourier transform of the fringe pattern in the
interferometric channel) is
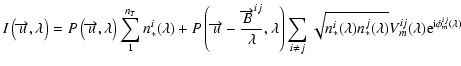 |
|
|
(3) |
where
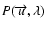 is the single-telescope transfer
function at the spatial frequency
is the single-telescope transfer
function at the spatial frequency
 and wavelength
and wavelength
 ,
,
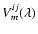 and
and
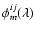 are the
measured visibility and phase and
are the
measured visibility and phase and
 is the total
contribution of beam i to the source flux collected in the
interferometric channel. In the following we note n*i,
Vmij and
is the total
contribution of beam i to the source flux collected in the
interferometric channel. In the following we note n*i,
Vmij and
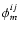 for
for
 ,
,
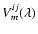 and
and
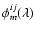 respectively,
except when the wavelength dependence is explicitly used.
respectively,
except when the wavelength dependence is explicitly used.
The first term in Eq. (3) is the low-frequency peak
affected only by a fixed instrumental term
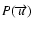 and
scaled by the total number of photons
and
scaled by the total number of photons
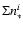 collected in
all beams. The second term is the fringe peak, with a phase
collected in
all beams. The second term is the fringe peak, with a phase
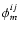 and an amplitude equal to the measured coherence flux
and an amplitude equal to the measured coherence flux
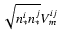 at frequency
at frequency
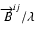 .
The number of photons n*idetected in each frame are deduced from the photometric channels. In
an ideal interferogram where the fringe peaks are fully separated, the
measured visibility is obtained by dividing the Fourier interferogram
at frequency
.
The number of photons n*idetected in each frame are deduced from the photometric channels. In
an ideal interferogram where the fringe peaks are fully separated, the
measured visibility is obtained by dividing the Fourier interferogram
at frequency
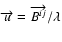 by
its value at frequency 0 and correcting by the known
photometry:
by
its value at frequency 0 and correcting by the known
photometry:
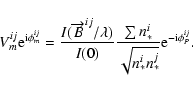 |
(4) |
The e
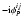 corresponds to a correction of the effect of the differential piston between beams i and j. The measured visibility is
corresponds to a correction of the effect of the differential piston between beams i and j. The measured visibility is
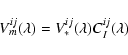 |
(5) |
where
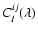 contains internal AMBER instrumental terms
contains internal AMBER instrumental terms
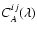 ,
which are removed by the calibration procedure below. It is also affected by the "piston jitter'', i.e. the variation of the piston during acquisition of the frame. If
,
which are removed by the calibration procedure below. It is also affected by the "piston jitter'', i.e. the variation of the piston during acquisition of the frame. If
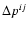 is
this jitter, supposed to be smaller than the total piston excursion (because we use short frame times), we can consider that fringes were drifting almost linearly during the frame and the contrast loss is then given by
is
this jitter, supposed to be smaller than the total piston excursion (because we use short frame times), we can consider that fringes were drifting almost linearly during the frame and the contrast loss is then given by
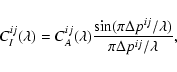 |
(6) |
which can be corrected if the piston jitter within one frame can be deduced from the piston variations between two consecutive frames.
A single-mode fiber collects light within an "antenna'' lobe
 describing the relative contribution of a
point on the sky at an angular distance
describing the relative contribution of a
point on the sky at an angular distance
 of
the pointing direction. The source observed by AMBER is integrated and
weighted by this "antenna lobe'' The instantaneous antenna function
depends on the geometry of the fiber, and does so for each aperture
PSF partially corrected by adaptive optics. The exact measured
visibility also depends on the degree of coherence between the antenna
functions of each individual aperture. Single-mode interferometers
give access only to the "modal'' visibility defined by relatively
complex relations to be found in Mège et al. (2003). It is
important to note that:
of
the pointing direction. The source observed by AMBER is integrated and
weighted by this "antenna lobe'' The instantaneous antenna function
depends on the geometry of the fiber, and does so for each aperture
PSF partially corrected by adaptive optics. The exact measured
visibility also depends on the degree of coherence between the antenna
functions of each individual aperture. Single-mode interferometers
give access only to the "modal'' visibility defined by relatively
complex relations to be found in Mège et al. (2003). It is
important to note that:
- For sources smaller than the Airy disk of individual apertures,
the modal visibility is equal to the source visibility;
- For extended sources, there is no simple way to separate the
contributions of the source and of the individual aperture PSF.
What has been done so far (van Boekel et al. 2003) is to
consider the object as the sum of a small source, for which the
above applies, and of a source substantially larger than the Airy
disk, which produces a completely incoherent contribution. When
this is wrong, one should use the modal visibility in the
model-fitting procedure, which assumes a model of the average
adaptive-optics corrected PSF. Some simplifications can be found
for particular objects, such as double stars.
A full discussion of this topic is beyond the scope of this paper. To
our last present knowledge, the problem has not yet been resolved for
a general source. We now say that AMBER (and other VLTI or KeckI
single-mode instruments) perform well when the source is smaller than
the individual aperture Airy disks (which is a severe restriction for
interferometers with small baseline/diameters ratios). In the
following we do not distinguish between the modal and the true complex
visibility so use
 for both.
for both.
Fully separating the fringe peaks in a multi-axial beam combiner
implies a large separation between output pupils (i.e. many fringes
per Airy disk) and a window that is much larger than the Airy disk and
would thus imply reading a very large number of pixels, which is not
acceptable when one is limited by detector read-out noise. To overcome
the problem of partially overlapping fringe peaks, a generalization of
the ABCD algorithm used in the PTI interferometer
(Colavita 1999) has been developed to establish a linear
relation between the values measured in each pixel and the complex
coherence for each baseline (for details
see Tatulli et al. 2007b). Fundamentally, the technique consists in
finding the modulus and phase for each baseline, which allows the
calibrated fringe shapes (the carrying waves) to be fitted in the
data. This fit is linear and is based on the visibility-to-pixel
matrix, computed from a set of calibration measurements using the
artificial coherent source unit (CAU) of the instrument. These
measurements are the photometry and interferometry from each beam
alone and the interferograms for each pair of beams at 0 and close
to 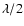 OPD. This matrix is then inverted to get the
pixel to visibility matrix (P2VM) used to obtain the complex
visibility in each frame from the intensities measured in each pixel.
This P2VM matrix takes all stable instrumental effects into account,
such as the detector gain table, the shape and the overlap of the
output fiber beams, and the instrument's chromatic OPD.
OPD. This matrix is then inverted to get the
pixel to visibility matrix (P2VM) used to obtain the complex
visibility in each frame from the intensities measured in each pixel.
This P2VM matrix takes all stable instrumental effects into account,
such as the detector gain table, the shape and the overlap of the
output fiber beams, and the instrument's chromatic OPD.
Analytical computations and numerical simulations show that this P2VM approach can be implemented without any SNR cost (Tatulli & LeBouquin 2006), at least when the SNR per frame is larger than 1.
3.3 AMBER observables
During the observation, we record NEXP exposures of NDIT frames, each exposed during the detector integration time, DIT. Typically a calibrated point is made of NEXP = 5 exposures of NDIT = 1000
frames of DIT = 20 to 100 ms. For each baseline lm, and in each spectral channel, we obtain a measure of the intensity and of the visibility amplitude
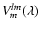 and phase
and phase
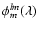 ,
used to derive the various AMBER observables.
,
used to derive the various AMBER observables.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6496fig5.eps} \end{figure}](/articles/aa/full/2007/10/aa6496-06/Timg71.gif) |
Figure 5:
Data used for spectral calibration. Top: source spectrum (
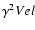 ); Middle: the calibrator star flat spectrum (shifted by -0.5); Bottom: the reference Gemini spectrum (shifted by -1). Note the atmospheric water-vapor doublets at 2.01 and ); Middle: the calibrator star flat spectrum (shifted by -0.5); Bottom: the reference Gemini spectrum (shifted by -1). Note the atmospheric water-vapor doublets at 2.01 and
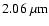 used for calibration in K-band medium-resolution observations.
used for calibration in K-band medium-resolution observations. |
| Open with DEXTER |
Each one of the photometric beams yields a spectrum of the source
within the chosen spectral window. The raw AMBER spectrum must be
calibrated in intensity and in wavelength, which in medium and high
resolution modes requires acquiring a spectral calibrator with a known
continuum shape and spectral features as illustrated by
Fig. 5. The spectrum is a crucial element of AMBER
model fitting. Simultaneous observations of high-resolution infrared
spectra, for example with the ISAAC instrument, have often been found
to be very useful (Malbet et al. 2007; Meilland et al. 2007b).
The absolute visibility in each spectral channel is the direct result
of the P2VM data processing. As discussed above, the measured absolute
visibility is affected by the piston jitter within one frame. This
jitter should be frozen by VLTI fringe tracking or measured when the
flux per frame is high enough. Currently this correction is impossible
because the vibrations in the Unit Telescope produce a piston
variation that is almost always larger than 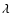 between
consecutive frames. A partial correction of the effect is obtained
using a calibrator star:
between
consecutive frames. A partial correction of the effect is obtained
using a calibrator star:
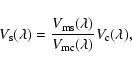 |
(7) |
where
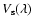 is the calibrated visibility of the target,
is the calibrated visibility of the target,
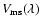 and
and
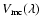 are the visibilities measured
on the target and on the calibrator, and
are the visibilities measured
on the target and on the calibrator, and
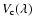 is the known
visibility of the calibrator. This correction is poor (0.03 to 0.07
visibility accuracy), if we cannot apply a frame-by-frame piston
jitter correction. Then, it is particularly important to have a
frame-selection criterion, independent of flux and tending to select
an equivalent set of frames for the science and the calibration
source. Currently the best solution is to select calibrators with
magnitudes comparable to the science source and to select the same
percentage of best contrasts in both cases. Even with an excellent
jitter correction, using a calibrator will always be necessary for
good accuracy measurements to compensate for slow instrumental
variations modifying the value of all the second-order instrumental
defects. For example, a small change in the position of the CAU beams
will change the contrast of the CAU source and therefore the corrected
instrumental contrast.
is the known
visibility of the calibrator. This correction is poor (0.03 to 0.07
visibility accuracy), if we cannot apply a frame-by-frame piston
jitter correction. Then, it is particularly important to have a
frame-selection criterion, independent of flux and tending to select
an equivalent set of frames for the science and the calibration
source. Currently the best solution is to select calibrators with
magnitudes comparable to the science source and to select the same
percentage of best contrasts in both cases. Even with an excellent
jitter correction, using a calibrator will always be necessary for
good accuracy measurements to compensate for slow instrumental
variations modifying the value of all the second-order instrumental
defects. For example, a small change in the position of the CAU beams
will change the contrast of the CAU source and therefore the corrected
instrumental contrast.
The absolute visibility mainly depends on the equivalent size of the
source in the direction of the baseline. A fit of absolute visibility
as a function of baseline length allows us to estimate the equivalent
radial intensity profile, such as the limb darkening. This has been
illustrated by AMBER observations of 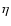 Carinae that permitted
Weigelt et al. (2007) to obtain a remarkable fit of the
central-wind limb-darkening by Hillier & Lanz (2001) model. A fit
of visibility as a function of position angle of the projected
baseline yields the source anisotropy, which can be related to
flattened inclined disks (Malbet et al. 2007), sometimes
combined with a very strong polar flow (Meilland et al. 2007b) or
an optical wind enhanced in the polar direction of a fast rotator
(Weigelt et al. 2007; Domiciano de Souza et al. 2005) or a combination of
all these factors. Distinguishing between these possibilities requires
prior knowledge of the source. Visibility alone does not allow
axisymmetric and non axisymmetric solutions to be disentangled between
(except with a very good u-v coverage) and will be of little use if
the structure of the objet is completely unknown.
Carinae that permitted
Weigelt et al. (2007) to obtain a remarkable fit of the
central-wind limb-darkening by Hillier & Lanz (2001) model. A fit
of visibility as a function of position angle of the projected
baseline yields the source anisotropy, which can be related to
flattened inclined disks (Malbet et al. 2007), sometimes
combined with a very strong polar flow (Meilland et al. 2007b) or
an optical wind enhanced in the polar direction of a fast rotator
(Weigelt et al. 2007; Domiciano de Souza et al. 2005) or a combination of
all these factors. Distinguishing between these possibilities requires
prior knowledge of the source. Visibility alone does not allow
axisymmetric and non axisymmetric solutions to be disentangled between
(except with a very good u-v coverage) and will be of little use if
the structure of the objet is completely unknown.
The differential (or relative) visibility
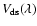 is the source visibility in the spectral channel
is the source visibility in the spectral channel 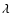 ,
often called work channel, calibrated by the average
visibility of a reference channel:
,
often called work channel, calibrated by the average
visibility of a reference channel:
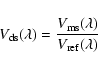 |
(8) |
where
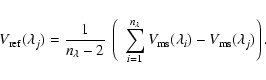 |
(9) |
This is the standard way to build the reference channel in AMBER data processing. The users can choose many other definitions of the reference channel, such as using selected continuum channels. The ideal is, of course, to use channels where the source is known or particularly well-constrained, but in any case, the exact definition of the reference channel, which depends of the source and of data processing constraints, must be injected in the model fitting. The important feature is that the differential visibility is independent of most of the systematic effects affecting the absolute visibility, and it does not need the use of a calibrator star. In particular, the differential visibility will be insensitive to the piston jitter over a limited wavelength range.
The relative visibility basically yields the same physical information as the spectrally-resolved absolute visibility, but it is much better calibrated, at the cost of losing information on the reference channel.
In optical, as well as in radio astronomy, source phase information
refers to the phase of its complex visibility. In a single-mode
interferogram, the phase is related to the position of the fringes,
and in the absence of nanometer accuracy metrology, the measured phase
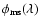 is affected by an unknown instrumental term
linked to the VLTI+AMBER differential piston
is affected by an unknown instrumental term
linked to the VLTI+AMBER differential piston
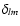 and to the
instantaneous atmospheric piston plm between beams l and m:
and to the
instantaneous atmospheric piston plm between beams l and m:
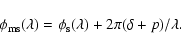 |
(10) |
Introducing a development of the source phase
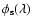 ,
as a function of the wave number
,
as a function of the wave number
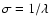 :
:
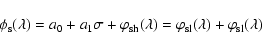 |
(11) |
where
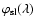 stands for the straight line that can be
fitted through the measured phase and that contains the piston
residual, as well as the equivalent piston of the source phase
averaged over the reference channel. The higher terms of the phase
polynomial development
stands for the straight line that can be
fitted through the measured phase and that contains the piston
residual, as well as the equivalent piston of the source phase
averaged over the reference channel. The higher terms of the phase
polynomial development
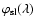 are the source
information, which can be extracted from differential phase
measurements. We first fit the measured phase
are the source
information, which can be extracted from differential phase
measurements. We first fit the measured phase
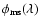 phase with a linear function of
phase with a linear function of 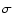 .
Then we correct the coherent
flux
.
Then we correct the coherent
flux
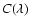 for this linear phase phasor, and we integrate it in
a reference channel:
for this linear phase phasor, and we integrate it in
a reference channel:
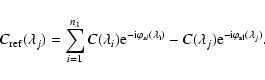 |
(12) |
The differential phase is defined by:
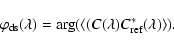 |
(13) |
If the reference channel has been defined in channels where the source phase is equal to 0, for example in the spectral continuum channel of a point-like or a symmetrical source,
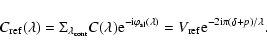 |
(14) |
This yields the higher-order term
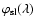 .
We obtain phase information on the source, but we have lost the equivalent piston of the reference channel.
.
We obtain phase information on the source, but we have lost the equivalent piston of the reference channel.
As for the differential visibility, there are many ways to define the reference channel, which must be injected in the source model-fitting process. Equation (14) gives the definition of the reference channel used in AMBER data processing.
A remarkable feature of the differential phase is that, for non
resolved (i.e. smaller than 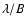 )
sources, it is proportional
to the variation of the photocenter of the source
(Petrov 1989). Given a sufficient SNR, the photocenter
variation with
)
sources, it is proportional
to the variation of the photocenter of the source
(Petrov 1989). Given a sufficient SNR, the photocenter
variation with 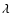 can be measured on very unresolved sources
with many very rich astrophysical applications. This includes
unresolved circumstellar disks and imaging of unresolved spotted stars
(Petrov 1988) or of non radial oscillation modes
(Jankov et al. 2002). One of the most promising applications is
the resolution and the kinematics of QSO BLR. With a fringe tracking
up to
can be measured on very unresolved sources
with many very rich astrophysical applications. This includes
unresolved circumstellar disks and imaging of unresolved spotted stars
(Petrov 1988) or of non radial oscillation modes
(Jankov et al. 2002). One of the most promising applications is
the resolution and the kinematics of QSO BLR. With a fringe tracking
up to 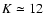 ,
one should be able to measure photocenter
variations and therefore direct distances for some Cepheids of the
Magellan Cloud.
,
one should be able to measure photocenter
variations and therefore direct distances for some Cepheids of the
Magellan Cloud.
The closure phase between baselines B_12, B_23 and B_31 is the phase of the average "bispectral product'' of the coherent fluxes
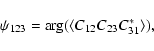 |
(15) |
and it is a very classical property of long-baseline interferometry that this closure phase is independent of any OPD terms affecting individually each beam. This includes the achromatic piston, as well as the chromatic OPD:
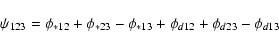 |
(16) |
where
 are error terms linked to the baseline ij, due
for example to a change in the detector gain table since the
calibration of the P2VM. Usually, these terms are very small so it can
be considered that for many applications the closure phase is only a
function of the source. Unlike the differential phase, the closure
phase is independent of any assumption on a reference channel. A
sufficient number of closure phases, combined with accurate visibility
measurements, allows reconstruction of relatively complex images, as
demonstrated by the 2006 "image reconstruction beauty contest''
(Lawson et al. 2006), which was based on "realistic'',
low-contrast, AMBER 3AT data, obtained over three simulated nights of
observations. The best three image reconstructions were quite good,
demonstrating a real imaging capability with a three-telescope optical
interferometer.
are error terms linked to the baseline ij, due
for example to a change in the detector gain table since the
calibration of the P2VM. Usually, these terms are very small so it can
be considered that for many applications the closure phase is only a
function of the source. Unlike the differential phase, the closure
phase is independent of any assumption on a reference channel. A
sufficient number of closure phases, combined with accurate visibility
measurements, allows reconstruction of relatively complex images, as
demonstrated by the 2006 "image reconstruction beauty contest''
(Lawson et al. 2006), which was based on "realistic'',
low-contrast, AMBER 3AT data, obtained over three simulated nights of
observations. The best three image reconstructions were quite good,
demonstrating a real imaging capability with a three-telescope optical
interferometer.
For any triplet of baselines, the closure phase is zero for any
axisymmetric object. For non-axisymmetric candidates, the closure
phase decreases with the third power of the object angular size when
it is getting unresolved. Then, a non zero closure phase is a strong
indication of a source with an interferometrically resolved
non-axisymmetric feature, like the binary system
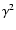 Velorum
(Millour et al. 2007) or the
Velorum
(Millour et al. 2007) or the 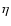 Carinae wind in the blue
part of the Br
Carinae wind in the blue
part of the Br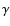 line (Weigelt et al. 2007).
line (Weigelt et al. 2007).
4 AMBER current and potential performances
In this section we first present the expected performances of AMBER on
the VLTI and then briefly discuss their current status with some
indications of the cause and the predictable evolution of limitations.
The AMBER measures are affected first by the photon
noise of the source and of the background and by the detector read-out
noise, called the fundamental noises. In the following we give the
errors on the visibility and the phases using the standard Fourier
formalism (among many others, see for example Petrov et al. 1986), which has been shown to be sufficient for SNR estimations during AMBER commissioning, when we compared
Fourier SNR estimation and statistics on the measures and found them
in good agreement well within a factor 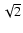 .
From the
interferometric Eq. (3) and the complex
visibility estimator 4 it is possible to derive the
error on the visibility estimator (with the approximation that all
noises and pixels are statistically independent):
.
From the
interferometric Eq. (3) and the complex
visibility estimator 4 it is possible to derive the
error on the visibility estimator (with the approximation that all
noises and pixels are statistically independent):
![$\displaystyle \sigma_{V_{ij}} = \frac{1}{\sqrt{n_{i}n_{j}}}
\Bigg[\sqrt{\sum_{i...
...ac{\sigma_{*i}}{2\sqrt{n_{*i}}}+\frac{\sigma_{*j}}{2\sqrt{n_{*j}}}\right)\Bigg]$](/articles/aa/full/2007/10/aa6496-06/img100.gif) |
|
|
(17) |
where n*i and
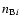 are the number of source and background
photons per frame in one spectral channel,
are the number of source and background
photons per frame in one spectral channel, 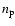 is the number of pixels used to record one spectral channel, and
is the number of pixels used to record one spectral channel, and
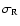 is the detector read out noise per pixel. The first term of this equation results from the contribution of fundamental noises to the error on the coherent flux and the second term results from the photometric correction applied to obtain the visibility from the coherent flux (Tatulli et al. 2007b). The value of
is the detector read out noise per pixel. The first term of this equation results from the contribution of fundamental noises to the error on the coherent flux and the second term results from the photometric correction applied to obtain the visibility from the coherent flux (Tatulli et al. 2007b). The value of
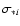 is the relative error on the measure of the contribution of beam i to the flux in the interferometric channel:
is the relative error on the measure of the contribution of beam i to the flux in the interferometric channel:
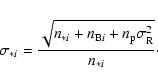 |
(18) |
In AMBER, the contribution of the thermal background is smaller than
the read-out noise for all the usual short exposure times (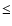
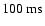 )
except after
)
except after
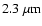 .
Then two cases must be considered. At high flux, when
.
Then two cases must be considered. At high flux, when
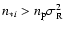 ,
the relative error on the visibility is given by
,
the relative error on the visibility is given by
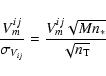 |
(19) |
where M is the number of frames and n* is the average number of
photons per channel, per frame, and per telescope, which are supposed
equal for all telescopes. The performance of AMBER, defined here as,
for example, the time needed to achieve a given SNR, is proportional
to
n*V2. Then, the coherent magnitude is given by the flux
n*V2. This applies for relatively bright and low-contrast
sources. At lower flux, when
 ,
,
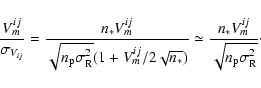 |
(20) |
The performance of AMBER is proportional to
(n*V)2 and the coherent magnitude is given by the flux n*V. This case represents faint sources with whatever contrasts.
The limiting magnitude of AMBER is set by
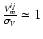 for the average spectral
channel. The actual data processing shows that frames not complying
with this criteria yield absurd estimated complex visibility that
destroy ensemble averages. In practice, such frames are eliminated in
the data processing. During the first commissioning of AMBER, frame
times between
for the average spectral
channel. The actual data processing shows that frames not complying
with this criteria yield absurd estimated complex visibility that
destroy ensemble averages. In practice, such frames are eliminated in
the data processing. During the first commissioning of AMBER, frame
times between
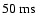 and
and
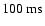 gave contrasts
between
0.15<V<0.2 on an unresolved calibrator. Knowing that the
average measured AMBER instrumental contrast is V=0.8 in medium
resolution (MR) and V=0.7 in low resolution (LR), this yields an
actual VLTI+atmosphere contrast of
gave contrasts
between
0.15<V<0.2 on an unresolved calibrator. Knowing that the
average measured AMBER instrumental contrast is V=0.8 in medium
resolution (MR) and V=0.7 in low resolution (LR), this yields an
actual VLTI+atmosphere contrast of
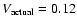 in low resolution
and
in low resolution
and
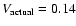 in medium resolution. If the VLTI was only
limited by the atmospheric piston jitter and by vibrations "within the
specifications'' (i.e. 10% of contrast loss due to VLTI non
atmospheric effects), these contrasts would be
in medium resolution. If the VLTI was only
limited by the atmospheric piston jitter and by vibrations "within the
specifications'' (i.e. 10% of contrast loss due to VLTI non
atmospheric effects), these contrasts would be
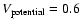 in
medium resolution and
in
medium resolution and
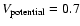 in low resolution. The
commissioning with AT indeed confirmed these VLTI+atmosphere contrast
values. Putting these actual and potential contrast values in Eq. (20) yields the number of photons per channel and per frame needed to achieve the condition
in low resolution. The
commissioning with AT indeed confirmed these VLTI+atmosphere contrast
values. Putting these actual and potential contrast values in Eq. (20) yields the number of photons per channel and per frame needed to achieve the condition
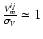 .
These values are given in Table 2.
.
These values are given in Table 2.
Table 2:
Number of photons per frame and per channel needed for the
frame to contribute to the ensemble averages, as a function of the
observing mode and considering the measured and the potential
(vibration-free) atmosphere+VLTI+AMBER visibility.
Table 3 gives the number of photons per frame and per spectral channel collected during the first commissioning of the instrument, before the implementation of the IRIS focal laboratory "infrared image sensor''.
Table 3:
Number of photons collected per 50 ms frame and per spectral channel in the K band in different observation modes.
Combining the collected flux given in Table 3 and
the minimum needed flux in Table 2 yields the current
and potential limiting magnitudes of AMBER displayed in Table
4.
Table 4:
Current, potential, and achieved limiting magnitudes of AMBER in the K band, for
 frames.
frames.
The "current'' value corresponds to the currently measured fluxes and
atmosphere+VLTI+AMBER instrumental visibility. The "achieved'' value
gives the magnitude of calibrators on which actual fringes have been
recorded. This value is available only for average conditions because
of the limited number of attempts. In LR mode there is a gap between
the "current'' and the "achieved'' values. The most likely explanation
was the fast fringe drift due to the poor quality of early delay-line
models. It is worth noting that the current values should allow a
successful observation of NGC1068 and maybe of a couple of other AGN
(if the MACAO adaptive optics behave correctly on these faint and
extended sources in the visible).
The "potential'' value corresponds to the currently measured
transmissions combined with a VLTI+atmosphere contrast with reduced
vibrations allowing the UT to approach the AT vibration levels and the
initial VLTI specifications. The limiting magnitude in LR should then
be 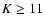 ,
therefore compliant with AMBER specifications for an
ambitious AGN program. This limit should be extended to all modes as
soon as fringe tracking is operational. The final limit will be set by
the quality of the vibration correction. These limiting magnitudes
correspond to an
,
therefore compliant with AMBER specifications for an
ambitious AGN program. This limit should be extended to all modes as
soon as fringe tracking is operational. The final limit will be set by
the quality of the vibration correction. These limiting magnitudes
correspond to an
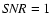 per spectral channel and per frame. Achieving
an accuracy on
per spectral channel and per frame. Achieving
an accuracy on
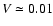 requires averaging 104 50 ms frames, which requires between 500 and 1500 seconds of actual observations.
requires averaging 104 50 ms frames, which requires between 500 and 1500 seconds of actual observations.
By analogy with the visibility error computation, the phase uncertainty is written as
 |
(21) |
Usually the reference channel is set much larger than the individual
spectral channel, and it contributes little to the error on the
differential phase, which allows the above estimation to be used for
the differential phase. Typically a visibility fundamental SNR of 100 therefore corresponds to a differential phase error of 0.007 radians.
However, the differential phase is not affected by the same
calibration problems. Currently we approach 10-3 rad on very
bright sources for which we should have smaller errors. We are
currently limited by data-processing problems (problem of the optimum
correction of the frame-by-frame piston) and by the difficulty of
fitting variable chromatic OPD, mainly due to variations in the
thickness of water vapor in the tunnels.
In theory, the accuracy on the closure phase should be about
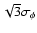 .
However, with the UT, the number of frames
where the three baselines simultaneously show good fringes is
extremely small. In practice, the limit is about
.
However, with the UT, the number of frames
where the three baselines simultaneously show good fringes is
extremely small. In practice, the limit is about
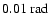 ,
even for
very bright sources. The situation is supposed to be very different
with three AT. The current impossibility of having very accurate
closure phases with 3 UT is a serious drawback for the ESP program.
,
even for
very bright sources. The situation is supposed to be very different
with three AT. The current impossibility of having very accurate
closure phases with 3 UT is a serious drawback for the ESP program.
5 Operating AMBER
AMBER is working within the standard Science Operations framework in
use for the VLT instruments. The VLTI Science Operations is described
in Rantakyrö et al. (2004), so here we highlight only those issues
relevant to the AMBER general user, who can concentrate on the
scientific objectives of the run rather than on details of the
telescopes, VLTI, and AMBER operations. In this framework, the user's
main, if not single, concern is to make certain that the proper
calibration procedures are used.
The first calibration is to measure the P2VM specific to the observing
mode. The P2VM can be modified by any change in the spectrograph setup,
and the operating procedure will force the observer to measure a new
P2VM for any new set up, prior to science observations. The observer
must choose between a standard-accuracy P2VM, to be within the
specifications of AMBER, and a high-accuracy one, to try to approach
the goals of highest accuracy.
- Standard-accuracy P2VM: to achieve 0.01 absolute visibility
accuracy, a P2VM is computed with about 105 photons recorded in
each line of each interferogram. With the maximum flux allowed
without saturating the detector, a full calibration takes about 7 min, i.e. about the time for the VLTI to acquire the source and
put it through all its subsystems. The errors introduced by the
standard P2VM are substantially decreased for differential phase
(0.001 radians) or visibility (0.001);
- High-accuracy P2VM: In practice, extremely high accuracy
(
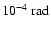 )
is expected only with differential measures and a
107-photon P2VM should be sufficient. This needs three hours
before the beginning or after the end of the night, so it implies
restrictions on the scheduling of setup changes. It still has to be
investigated whether the stability of the P2VM over a few hours is
good enough to allow the use of such a long calibration.
)
is expected only with differential measures and a
107-photon P2VM should be sufficient. This needs three hours
before the beginning or after the end of the night, so it implies
restrictions on the scheduling of setup changes. It still has to be
investigated whether the stability of the P2VM over a few hours is
good enough to allow the use of such a long calibration.
Any set of observations includes observing dark images (warm shutters closed) and sky images (telescopes offset) that are later used in the data reduction. The observer chooses the number of dark and sky exposures. The standard value is currently one dark and one sky for five source exposures. The observers also define the offset of the telescopes, to make sure that the "sky'' direction is actually source free.
All interferometric observables, including the differential and the
closure phases, are affected by systematic effects that can be removed
or reduced using a calibrator star with known complex visibility. An
important task for the observer is to choose good calibrators. Ideally
a calibrator is a point source; however, finding strictly non resolved
and bright-enough stars is a real problem. A good calibrator is then a
single, non variable star, which can be considered as a uniform disk
with a known diameter. Then the visibility of the calibrator is known
and its differential and closure phases are zero. "Primary''
calibrators, found in databases of measured diameters for bright stars
(Richichi et al. 2004), are used when they are close enough to
the science target in magnitude, visibility and angular coordinates.
The same databases of measured diameters have been used to validate
tools for selecting and qualifying much more numerous "secondary''
calibrators from the color indices found in astronomical catalogues
(Bonneau et al. 2006).
A spectral calibrator is required for medium and high
spectral-resolution modes. Usually, it is a star with a clean and
well-known continuum allowing calibration of the relative intensities
recorded by AMBER and use of the telluric lines for accurate
wavelength-table calibration. It is also strongly advised to
systematically obtain a calibrated high-resolution spectrum of the
source during or close to the interferometric run, from ISAAC
(Moorwood et al. 1999) or other spectrographs.
5.5 Beam commutation for closure and differential phase calibration
To have accurate differential and closure phases, the observer can use
the "differential'' observing mode, in which a beam commutation device
(BCD) is used to exchange beams 1 and 2 at the entrance of AMBER at
the end of each exposure. This inverts the source differential phase
for B12 and the source closure phase without changing the
instrumental terms. Then, computing the differences between exposures
with and without beam commutation (BCD "in'' and "out'') yields
differential and closure phase with strongly reduced instrumental
effects (Vannier et al. 2006; Petrov et al. 2003). The
commutation takes less than 5 s and can therefore be performed
much more often than a science-calibrator exchange.
Observing is performed through the VLT control system using the
standard tool (P2PP: Phase 2 Preparation Package) to create blocks of
observations. These blocks contain several procedures, called
templates, to set up the instrument, to point the interferometer, to
optimize the beam injection into AMBER, to search for fringes, and to
acquire observation data. P2PP allows changing some of the parameters
for these procedures, like the wavelength range, the spectral
dispersion, or the detector integration time.
The observation block is executed through the breaker of observing
blocks (BOB), which ensures that all steps are carried out
successfully. Some of the templates are executed in parallel, such as
the injection of light into the AMBER fibers for each telescope. The
night astronomer has control over BOB and can abort or redo part of
the procedures. The system also asks the night astronomer to make
critical choices such as whether to continue or abort a so far
unsuccessful fringe search.
As for other VLT instruments, AMBER has a standard real-time display
that shows the raw data. It also has a quick-look monitor that
displays visibilities and phases reduced online in almost real time.
The data is automatically archived and passed to the data reduction
pipeline that analyses the data almost immediately after acquisition
so that the night astronomer and/or the visiting astronomer can check
the quality of the data.
6 Conclusion
With its coherent combination of three unit telescopes, AMBER
currently makes the VLTI the world's largest optical telescope with a
total surface >
 and a maximum baseline
>
and a maximum baseline
>
 corresponding to a spatial resolution than
corresponding to a spatial resolution than
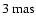 in the K band.
in the K band.
The capacity to measure closure phases gives AMBER an
image-reconstruction capability with different configurations of three
VLTI telescopes. The measurement of individual closure phases already
yields decisive constraints on the source geometry. AMBER includes a
high-performance infrared-cooled spectrograph allowing the structure
and the physics of the source to be constrained by comparing the
measures at different wavelengths. Differential interferometry based
on simultaneous interferometric measures in different spectral
channels yields a gain in accuracy of at least a factor 10. Analyzing
spectral channels simultaneously boosts the uniqueness and robustness
of measured parameters and images, particularly with spectral
regularization functions. At low spectral resolution, the spectral
coverage massively increases the instantaneous spatial coverage. AMBER made its first fringes in Paranal in the second quarter of 2004.
For the general user, the first 3-UT period started in October 2005
and 3-AT open time is starting in April 2007. Currently it is possible
to observe in low, medium, and high resolution in the H and K bands.
The full potential in the medium and high spectral resolution depends
on the availability of the three-telescope fringe tracker FINITO,
which has already been successfully tested with AT and will very
likely be available with ATs in October 2007. With the UTs, this
depends on the quality of the correction of the vibrations that
currently affect the UT Coudé trains.
The first astrophysical observations in 2004 and 2005 has led to a set
of refereed papers that can be found in this volume. They all
illustrate the power of the spectral dimension of interferometric
measures in situations of very poor u-v coverage. On young Herbig
stars with high mass (MWC 297; Malbet et al. 2007) and
intermediate mass (HD 104237; Tatulli et al. 2007a), the
variation of visibility through Br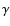 allowed them to discuss the
connection between dust envelope and wind-driven gas and their
relative geometry. On the Be star
allowed them to discuss the
connection between dust envelope and wind-driven gas and their
relative geometry. On the Be star 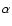 Arae
(Meilland et al. 2007b), observations in the continuum and in the
Br
Arae
(Meilland et al. 2007b), observations in the continuum and in the
Br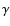 line allowed severe constraints on a wind found to be
axisymmetric with a thin equatorial disk in Keplerian rotation and a
very strong polar flow. Another Be star,
line allowed severe constraints on a wind found to be
axisymmetric with a thin equatorial disk in Keplerian rotation and a
very strong polar flow. Another Be star, 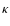 CMa
(Meilland et al. 2007a), showed a very different, small, non
axisymmetric, and probably non-Keplerian envelope. The dusty B[e] star
CPD-
CMa
(Meilland et al. 2007a), showed a very different, small, non
axisymmetric, and probably non-Keplerian envelope. The dusty B[e] star
CPD-
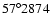 (Domiciano de Souza et al. 2007), observed with AMBER
and MIDI, has non-spherical dust and gas envelopes with different
global geometries, perhaps again due to polar gas outflows. For the
Wolf Rayet + O binary system
(Domiciano de Souza et al. 2007), observed with AMBER
and MIDI, has non-spherical dust and gas envelopes with different
global geometries, perhaps again due to polar gas outflows. For the
Wolf Rayet + O binary system
 Velorum
(Millour et al. 2007), measures including a strong closure
phase in the continuum and in various carbon and helium emission
lines, allowed the separation of the components spectra, the measure
of the angular separation implying a revision of the Hipparcos
distance, and the detection of material outside the immediate vicinity
of the components that might be the signature of the wind-wind
collision. Measurements in medium and high spectral resolution of the
most luminous and massive luminous blue variable
Velorum
(Millour et al. 2007), measures including a strong closure
phase in the continuum and in various carbon and helium emission
lines, allowed the separation of the components spectra, the measure
of the angular separation implying a revision of the Hipparcos
distance, and the detection of material outside the immediate vicinity
of the components that might be the signature of the wind-wind
collision. Measurements in medium and high spectral resolution of the
most luminous and massive luminous blue variable 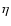 Carinae
(Weigelt et al. 2007), allowed reconstruction of a central,
optically-thick, wind structure elongated in the direction of the axis
of the Homonculus nebulae and well-modeled in the continuum and
emission lines with remarkable agreement with the radiative transfer
code of Hillier & Lanz (2001). Last but not least,
Chesneau et al. (2007) reported the early AMBER interferometric
observation of the outburst of RS Oph performed 5.5 days after the
outburst which provided an estimation of the extent of the continuum,
Br
Carinae
(Weigelt et al. 2007), allowed reconstruction of a central,
optically-thick, wind structure elongated in the direction of the axis
of the Homonculus nebulae and well-modeled in the continuum and
emission lines with remarkable agreement with the radiative transfer
code of Hillier & Lanz (2001). Last but not least,
Chesneau et al. (2007) reported the early AMBER interferometric
observation of the outburst of RS Oph performed 5.5 days after the
outburst which provided an estimation of the extent of the continuum,
Br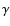 and He I
and He I
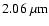 forming regions and some physical
constraints on the ejection process. The global picture that emerges
is a non-spherical fireball at high-velocity expansion.
forming regions and some physical
constraints on the ejection process. The global picture that emerges
is a non-spherical fireball at high-velocity expansion.
The transmission measured on AMBER and the VLTI shows that the current
coherent limiting magnitude is
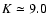 with a VLTI+atmosphere
fringe contrast of 0.12. When the correction of the UT vibration
allow a VLTI+atmosphere fringe contrast of 0.5, the limiting
coherent magnitude of AMBER on the VLTI will reach
with a VLTI+atmosphere
fringe contrast of 0.12. When the correction of the UT vibration
allow a VLTI+atmosphere fringe contrast of 0.5, the limiting
coherent magnitude of AMBER on the VLTI will reach
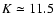 in
the 20% best-seeing conditions. This will allow breakthrough science
on a large number of AGN and QSO. With the ATs, the VLTI+atmosphere
fringe contrast already ranges from 0.5 to 0.9. When FINITO is
operational, all spectral resolution modes will be accessible on the
AT for
in
the 20% best-seeing conditions. This will allow breakthrough science
on a large number of AGN and QSO. With the ATs, the VLTI+atmosphere
fringe contrast already ranges from 0.5 to 0.9. When FINITO is
operational, all spectral resolution modes will be accessible on the
AT for  in average conditions and
in average conditions and  in the 20% best
conditions, with enormous possibilities in stellar physics.
in the 20% best
conditions, with enormous possibilities in stellar physics.
Acknowledgements
The AMBER project![[*]](/icons/foot_motif.gif) was founded by the French
Centre National de la Recherche Scientifique (CNRS), the Max Planck
Institute für Radioastronomie (MPIfR) in Bonn, the Osservatorio
Astrofisico di Arcetri (OAA) in Firenze, the French Region Provence Alpes Côte D'Azur, and the European Southern Observatory (ESO). The CNRS funding has been made through the Institut National des Sciences de l'Univers (INSU) and its Programmes Nationaux (ASHRA, PNPS, PNP).
was founded by the French
Centre National de la Recherche Scientifique (CNRS), the Max Planck
Institute für Radioastronomie (MPIfR) in Bonn, the Osservatorio
Astrofisico di Arcetri (OAA) in Firenze, the French Region Provence Alpes Côte D'Azur, and the European Southern Observatory (ESO). The CNRS funding has been made through the Institut National des Sciences de l'Univers (INSU) and its Programmes Nationaux (ASHRA, PNPS, PNP).
The OAA co-authors acknowledge partial support from MIUR grants to
the Arcetri Observatory (A LBT interferometric arm, and
analysis of VLTI interferometric data and From Stars to
Planets: accretion, disk evolution and planet formation) and from
INAF grants to the Arcetri Observatory (Stellar and
Extragalactic Astrophysics with Optical Interferometry). C. Gil's
work was supported in part by the Fundação para a Ciência e
a Tecnologia through project POCTI/CTE-AST/55691/2004 from POCTI,
with funds from the European program FEDER.
The preparation and interpretation of AMBER observations benefit
from the tools developed by the Jean-Marie Mariotti Center for
optical interferometry JMMC![[*]](/icons/foot_motif.gif) and from the databases
of the Centre de Données Stellaires (CDS), and of the
Smithsonian/NASA Astrophysics Data System (ADS).
and from the databases
of the Centre de Données Stellaires (CDS), and of the
Smithsonian/NASA Astrophysics Data System (ADS).
We would like to thank the successive directors of INSU/CNRS,
G. Debouzy, F. Casoli, and A.-M. Lagrange, along with the ASHRA
president P. Léna and the VLT program manager M. Tarenghi of ESO
for their crucial help in setting up and supporting the Consortium.
We also thank S. Bensammar, V. Coudé du Foresto, and G. Perrin for
their advice in defining the AMBER concept and Consortium.
We are very grateful to the ESO staff in Garching and Paranal for
their help in the design and commissioning of AMBER.
The key mechanical design and manufacturing have been provided by
the Division Technique de l'INSU and by the mechanical workshops of
the Observatoire de Bordeaux, Observatoire de la Côte d'Azur,
and Université de Nice.
- Akeson, R. L.,
Swain, M. R., & Colavita, M. M. 2000, in
Interferometry in Optical Astronomy, ed. P. J. Léna &
A. Quirrenbach, Proc. SPIE, 4006, 321
(In the text)
- Antonucci,
R. R. J. & Miller, J. S. 1985, ApJ, 297,
621 [NASA ADS] [CrossRef] (In the text)
- Barman, T. S.,
Hauschildt, P. H., & Allard, F. 2001, ApJ, 556, 885 [NASA ADS] [CrossRef] (In the text)
- Bonneau, D., Clausse,
J.-M., Delfosse, X., et al. 2006, A&A, 456, 789 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chesneau, O.,
Nardetto, N., Millour, F., et al. 2007, A&A, 464, 119 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Colavita, M. M.
1999, PASP, 111, 111 [NASA ADS] [CrossRef]
- Colavita, M., Akeson,
R., Wizinowich, P., et al. 2003, ApJ, 592, L83 [NASA ADS] [CrossRef] (In the text)
- Colavita, M. M.,
Wallace, J. K., Hines, B. E., et al. 1999, ApJ, 510,
505 [NASA ADS] [CrossRef]
- Coudé Du Foresto,
V., Perrin, G., Ruilier, C., et al. 1998, in Astronomical
Interferometry, ed. R. D. Reasenberg, Proc. SPIE V, 3350,
856
- Coudé du Foresto,
V., Bordé, P. J., Mérand, A., et al. 2003, in
Interferometry for Optical Astronomy II, ed. W. A. Traub,
Proc. SPIE, 4838, 280
- Delplancke, F.,
Nijenhuis, J., de Man, H., et al. 2004, in New Frontiers in
Stellar Interferometry, ed. W. A. Traub, Proc. SPIE, 5491,
1528
(In the text)
- Domiciano de Souza,
A., Kervella, P., Jankov, S., et al. 2005, A&A, 442,
567 [NASA ADS] [CrossRef] [EDP Sciences]
- Domiciano de Souza,
A., Driebe, T., Chesneau, O., et al. 2007, A&A, 464,
81 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gai, M., Menardi, S.,
Cesare, S., et al. 2004, in New Frontiers in Stellar
Interferometry, ed. W. A. Traub, Proc. SPIE 5491, 528
(In the text)
- Glindemann, A.,
Albertsen, M., Andolfato, L., et al. 2004, in New Frontiers in
Stellar Interferometry, ed. W. A. Traub, Proc. SPIE, 5491,
447
(In the text)
- Glindemann, A.,
Ballester, P., Bauvir, B., et al. 2001a, The Messenger, 106,
1 [NASA ADS]
- Glindemann, A.,
Bauvir, B., Delplancke, F., et al. 2001b, The Messenger, 104,
2 [NASA ADS]
- Hillier, D. J.
& Lanz, T. 2001, in Spectroscopic Challenges of Photoionized
Plasmas, ed. G. Ferland & D. W. Savin, ASP Conf.
Ser., 247, 343
(In the text)
- Jaffe, W.,
Meisenheimer, K., Röttgering, H. J. A., et al.
2004, Nature, 429, 47 [NASA ADS] [CrossRef]
- Jankov, S., Vakili,
F., Domiciano de Souza, Jr., A., & Janot-Pacheco, E. 2002, in
IAU Coll. 185: Radial and Nonradial Pulsationsn as Probes of
Stellar Physics, ed. C. Aerts, T. R. Bedding, &
J. Christensen-Dalsgaard, ASP Conf. Ser., 259, 172
(In the text)
- Kervella, P., Gitton,
P. B., Ségransan, D., et al. 2003, in Interferometry
for Optical Astronomy II, ed. W. A. Traub, Proc SPIE, 4838,
858
(In the text)
- Lawson, P. R.,
Cotton, W. D., Hummel, C. A., et al. 2006, in
Advances in Stellar Interferometry, ed. J. Monnier,
M. Schöller, & W. C. Danchi, Proc. SPIE,
6268
(In the text)
- Leinert, C. 2004, in
New Frontiers in Stellar Interferometry, ed. W. A. Traub, Proc
SPIE, 5491, 19
- Leinert, C., Graser,
U., Przygodda, F., et al. 2003, Ap&SS, 286, 73 [NASA ADS]
- Malbet, F. 2003,
Ap&SS, 286, 131 [NASA ADS]
- Malbet, F., Benisty,
M., De Wit, W. J., et al. 2007, A&A, 464, 43 [NASA ADS] [CrossRef] [EDP Sciences]
- Marconi, A.,
Maiolino, R., & Petrov, R. G. 2003, Ap&SS, 286,
245 [NASA ADS] (In the text)
- Mège, P., Malbet,
F., & Chelli, A. 2003, in Interferometry for Optical Astronomy
II, ed. W. A. Traub, 329, Proc. SPIE, 4838,
(In the text)
- Meilland, A.,
Millour, F., Stee, P., et al. 2007a, A&A, 464, 73 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Meilland, A., Stee,
P., Vannier, M., et al. 2007b, A&A, 464, 59 [NASA ADS] [CrossRef] [EDP Sciences]
- Millan-Gabet, R.,
Malbet, F., Akeson, R., et al. 2007, Protostars and Planets V,
539
- Millour, S., Petrov,
R., Chesneau, O., et al. 2007, A&A, 464, 107 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Moorwood, A., Cuby,
J.-G., Ballester, P., et al. 1999, The Messenger, 95, 1 [NASA ADS] (In the text)
- Mourard, D., Abe, L.,
Domiciano, A., et al. 2003, in Interferometry for Optical
Astronomy II, ed. W. A. Traub, Proc. SPIE, 4838, 9
(In the text)
- Paresce, F.,
Delplancke, F., Derie, F., et al. 2003a, in Interferometry for
Optical Astronomy II, ed. W. A. Traub, Proc. SPIE, 4838,
486
(In the text)
- Paresce, F., Mourard,
D., Bedding, T., et al. 1996, The Messenger, 83, 14 [NASA ADS] (In the text)
- Paresce, F., Van
Boekel, R., Correia, S., et al. 2003b, in Interferometry for
Optical Astronomy II, ed. W. A. Traub, Proc SPIE, 4838,
235
(In the text)
- Petrov, R., Roddier,
F., & Aime, C. 1986, Opt. Soc. Am. J. A: Optics and Image
Science 3, 634
(In the text)
- Petrov, R. G.
1988, in NOAO-ESO Conference on High-Resolution Imaging by
Interferometry: Ground-Based Interferometry at Visible and Infrared
Wavelengths, ed. F. Merkle, 235
(In the text)
- Petrov, R. G.
1989, in Diffraction-Limited Imaging with Very Large Telescopes,
ed. D. M. Alloin & J.-M. Mariotti, NATO ASIC Proc., 274,
249
(In the text)
- Petrov, R. G.,
Vannier, M., Lopez, B., et al. 2003, in EAS Publ. Series, ed.
C. Aime & R. Soummer, 297
- Rantakyrö,
F. T., Galliano, E., Hummel, C. A., et al. 2004, in
New Frontiers in Stellar Interferometry, ed. W. A. Traub,
Proc. SPIE, 5491, 1690
(In the text)
- Richichi, A.,
Percheron, I., & Khristoforova, M. 2004, VizieR Online Data
Catalog, 343, 10773 [NASA ADS] (In the text)
- Robbe-Dubois, S.,
Lagarde, S., Antonelli, P., et al. 2007, A&A, 464, 13 [NASA ADS] [CrossRef] [EDP Sciences]
- Ségransan, D.,
Beuzit, J.-L., Delfosse, X., et al. 2000, in Interferometry in
Optical Astronomy, ed. P. J. Léna &
A. Quirrenbach, Proc. SPIE, 4006, 269
(In the text)
- Swain, M., Vasisht,
G., Akeson, R., et al. 2003, ApJ, 596, L163 [NASA ADS] [CrossRef] (In the text)
- Tatulli, E. &
LeBouquin, J.-B. 2006, MNRAS, 368, 1159 [NASA ADS] (In the text)
- Tatulli, E., Isella,
A., Natta, A., et al. 2007a, A&A, 464, 55 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Tatulli, E., Millour,
F., Chelli, A., et al. 2007b, A&A, 464, 29 [CrossRef] [EDP Sciences]
- van Boekel, R.,
Kervella, P., Schöller, M., et al. 2003, A&A, 410,
L37 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Vannier, M., Petrov,
R. G., Lopez, B., & Millour, F. 2006, MNRAS, 367, 825 [NASA ADS] (In the text)
- Weigelt, G., Kraus,
S., Driebe, T., et al. 2007, A&A, 464, 87 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Wittkowski, M.,
Kervella, P., Arsenault, R., et al. 2004, A&A, 418,
L39 [NASA ADS] [CrossRef] [EDP Sciences]
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=17.3cm,clip]{6496fig1.eps}\end{figure}](/articles/aa/full/2007/10/aa6496-06/Timg11.gif)
![\begin{figure}
\par\includegraphics[width=15.7cm,clip]{6496fig2.eps}\par\end{figure}](/articles/aa/full/2007/10/aa6496-06/Timg25.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6496fig3.eps}\end{figure}](/articles/aa/full/2007/10/aa6496-06/Timg30.gif)
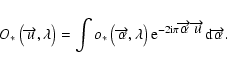
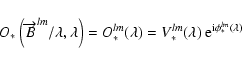
![\begin{figure}
\par\includegraphics[width=12cm,clip]{6496fig4.eps}\end{figure}](/articles/aa/full/2007/10/aa6496-06/Timg45.gif)
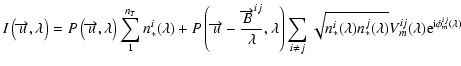
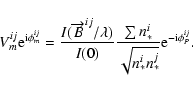
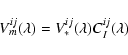
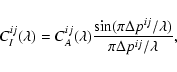
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6496fig5.eps} \end{figure}](/articles/aa/full/2007/10/aa6496-06/Timg71.gif)
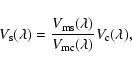
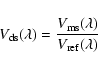
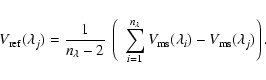
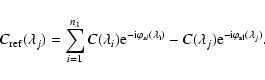
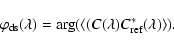
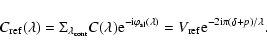
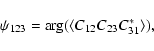
![$\displaystyle \sigma_{V_{ij}} = \frac{1}{\sqrt{n_{i}n_{j}}}
\Bigg[\sqrt{\sum_{i...
...ac{\sigma_{*i}}{2\sqrt{n_{*i}}}+\frac{\sigma_{*j}}{2\sqrt{n_{*j}}}\right)\Bigg]$](/articles/aa/full/2007/10/aa6496-06/img100.gif)