A&A 464, 399-404 (2007)
DOI: 10.1051/0004-6361:20066170
J. Hartlap - P. Simon - P. Schneider
Argelander-Institut![]() für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received 3 August 2006 / Accepted 24 November 2006
Abstract
Aims. The maximum-likelihood method is the standard approach to obtain model fits to observational data and the corresponding confidence regions. We investigate possible sources of bias in the log-likelihood function and its subsequent analysis, focusing on estimators of the inverse covariance matrix. Furthermore, we study under which circumstances the estimated covariance matrix is invertible.
Methods. We perform Monte-Carlo simulations to investigate the behaviour of estimators for the inverse covariance matrix, depending on the number of independent data sets and the number of variables of the data vectors.
Results. We find that the inverse of the maximum-likelihood estimator of the covariance is biased, the amount of bias depending on the ratio of the number of bins (data vector variables), p, to the number of data sets, n. This bias inevitably leads to an - in extreme cases catastrophic - underestimation of the size of confidence regions. We report on a method to remove this bias for the idealised case of Gaussian noise and statistically independent data vectors. Moreover, we demonstrate that marginalisation over parameters introduces a bias into the marginalised log-likelihood function. Measures of the sizes of confidence regions suffer from the same problem. Furthermore, we give an analytic proof for the fact that the estimated covariance matrix is singular if p>n.
Key words: methods: analytical - methods: data analysis - gravitational lensing
For the evaluation of the log-likelihood the population covariance matrix
![]() and its inverse
and its inverse
![]() or estimates thereof are needed. In most cases, no exact analytical expression for
or estimates thereof are needed. In most cases, no exact analytical expression for
![]() can be given, although numerous authors make use of analytical approximations. An example from the field of weak gravitational lensing is Semboloni et al. (2006), who use the Gaussian approximation to the covariance matrix of the shear correlation functions given by Schneider et al. (2002). Other possibilities are to estimate
can be given, although numerous authors make use of analytical approximations. An example from the field of weak gravitational lensing is Semboloni et al. (2006), who use the Gaussian approximation to the covariance matrix of the shear correlation functions given by Schneider et al. (2002). Other possibilities are to estimate
![]() from the data themselves (e.g. Budavári et al. 2003; Hetterscheidt et al. 2006) or to obtain it from a simulated data set whose properties are comparable to the original data (e.g. Pan & Szapudi 2005). In the latter paper, the authors observed that the estimated covariance matrix becomes singular if p, the number of entries of the data vectors, exceeds the number of observations / simulated data vectors. As a remedy, they propose to use the Singular Value Decomposition (SVD, Press et al. 1992) to obtain a pseudo-inverse of the covariance matrix, but do not investigate the properties of the resulting estimate of
from the data themselves (e.g. Budavári et al. 2003; Hetterscheidt et al. 2006) or to obtain it from a simulated data set whose properties are comparable to the original data (e.g. Pan & Szapudi 2005). In the latter paper, the authors observed that the estimated covariance matrix becomes singular if p, the number of entries of the data vectors, exceeds the number of observations / simulated data vectors. As a remedy, they propose to use the Singular Value Decomposition (SVD, Press et al. 1992) to obtain a pseudo-inverse of the covariance matrix, but do not investigate the properties of the resulting estimate of
![]() in detail.
In this paper, we prove analytically that the rank of the standard estimator of the covariance matrix cannot exceed the number of observations. We then point out that, even if this estimator is not singular, simple matrix inversion yields a biased estimator of
in detail.
In this paper, we prove analytically that the rank of the standard estimator of the covariance matrix cannot exceed the number of observations. We then point out that, even if this estimator is not singular, simple matrix inversion yields a biased estimator of
![]() .
This may, if not corrected for, cause a serious underestimate of the size of the confidence regions. This problem has also been noticed by Hirata et al. (2004) and Mandelbaum et al. (2006), who use Monte-Carlo simulations to determine the correct confidence contours in cases where the covariance matrix is noisy.
We report on the existence of a simpler method to remove this bias, which can be derived for Gaussian noise and statistically independent data vectors, and test the validity of this method when these assumptions are violated.
.
This may, if not corrected for, cause a serious underestimate of the size of the confidence regions. This problem has also been noticed by Hirata et al. (2004) and Mandelbaum et al. (2006), who use Monte-Carlo simulations to determine the correct confidence contours in cases where the covariance matrix is noisy.
We report on the existence of a simpler method to remove this bias, which can be derived for Gaussian noise and statistically independent data vectors, and test the validity of this method when these assumptions are violated.
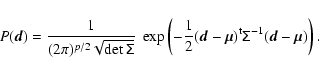 |
(2) |
We now prove our statement for an unknown mean vector ![]() ,
which is estimated from the data using
,
which is estimated from the data using
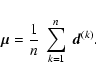 |
(5) |
Another interesting implication of Eq. (9) is that the mean vector and the estimated covariance matrix are distributed independently (again see Anderson 2003), although they are computed from the same data vectors. First, note that
![]() and
and
![]() are statistically independent for
are statistically independent for ![]() .
This can be seen by computing the covariance between the two vectors:
.
This can be seen by computing the covariance between the two vectors:
| |
= | (10) | |
| = | 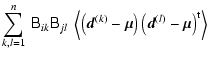 |
(11) | |
| = | 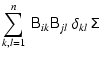 |
(12) | |
| = | (13) |
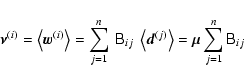 |
(14) |
Since
![]() does not depend on
does not depend on
![]() ,
which in turn is statistically independent of the remaining
,
which in turn is statistically independent of the remaining
![]() ,
this shows the independence of estimated mean and covariance.
,
this shows the independence of estimated mean and covariance.
From (3), an estimator for
![]() can be obtained by matrix inversion:
can be obtained by matrix inversion:
The amount of bias in
![]() thus depends essentially on the ratio of the number of entries p in the data vectors (henceforth referred to as the number of bins) to the number of independent observations n.
It leads to an underestimation of the size of confidence regions by making the log-likelihood function steeper, but it does not change the maximum-likelihood point and thus does not affect the parameter estimates themselves.
thus depends essentially on the ratio of the number of entries p in the data vectors (henceforth referred to as the number of bins) to the number of independent observations n.
It leads to an underestimation of the size of confidence regions by making the log-likelihood function steeper, but it does not change the maximum-likelihood point and thus does not affect the parameter estimates themselves.
From (16) it follows that an unbiased estimator of
![]() is given by
is given by![]()
To illustrate Eq. (17), and also to probe how the pseudo-inverse of the estimated covariance obtained by the Singular Value Decomposition behaves (see below), we perform the following experiment:
first, we choose an analytical form for the population covariance
![]() .
We use three different models:
.
We use three different models:
We then create n data vectors of length p1 according to
![]() ,
where
,
where
![]() is a noise vector drawn from a multivariate Gaussian distribution with mean zero and covariance
is a noise vector drawn from a multivariate Gaussian distribution with mean zero and covariance
![]() .
The choice of the model vector
.
The choice of the model vector ![]() is arbitrary, and in fact for the present purpose it would be sufficient to set
is arbitrary, and in fact for the present purpose it would be sufficient to set
![]() .
For later use, however, we choose the linear model
mi=axi + b, where
.
For later use, however, we choose the linear model
mi=axi + b, where
![]() is the value of the free variable corresponding to the centre of the ith bin.
is the value of the free variable corresponding to the centre of the ith bin.
From this synthetic set of observations we estimate the mean data vector and the covariance matrix, which yields the estimator
![]() .
Next, both
.
Next, both
![]() and
and
![]() are inverted using the Singular Value Decomposition (see below). Finally, we compute the unbiased estimate
are inverted using the Singular Value Decomposition (see below). Finally, we compute the unbiased estimate
![]() of the inverse covariance as given
in (17).
of the inverse covariance as given
in (17).
To probe the dependence of the bias of the estimators for
![]() ,
n new data vectors are created subsequently
with pj=p1/j bins, for all integer
,
n new data vectors are created subsequently
with pj=p1/j bins, for all integer
![]() ,
where the population covariance
,
where the population covariance
![]() for pj bins can be obtained from the original
for pj bins can be obtained from the original
![]() by averaging over
by averaging over
![]() )-sub-blocks of
)-sub-blocks of
![]() .
This strategy of re-binning has the advantage that the true covariance is known exactly for all pj.
.
This strategy of re-binning has the advantage that the true covariance is known exactly for all pj.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6170fig1.ps}
\end{figure}](/articles/aa/full/2007/10/aa6170-06/Timg82.gif) |
Figure 1:
Ratios of the trace of
|
| Open with DEXTER | |
Since the bias in Eq. (16) is just a scalar factor, we record the traces of the estimators
![]() and
and
![]() for each number of bins p. To improve our statistics, we repeat the procedure outlined above 104 times and average over the traces computed in each step.
for each number of bins p. To improve our statistics, we repeat the procedure outlined above 104 times and average over the traces computed in each step.
In Fig. 1, we plot the ratios of the trace of
![]() to the traces of
to the traces of
![]() and
and
![]() ,
respectively. Not using the bias-corrected
,
respectively. Not using the bias-corrected
![]() can have considerable impact on the size of confidence regions of parameter estimates: for p<n-2, the components of
can have considerable impact on the size of confidence regions of parameter estimates: for p<n-2, the components of
![]() will be too large compared to those of the true inverse covariance, and the log-likelihood will decrease too steeply, resulting in confidence contours too small.
will be too large compared to those of the true inverse covariance, and the log-likelihood will decrease too steeply, resulting in confidence contours too small.
We also plot the traces of
![]() for the different covariance models beyond
for the different covariance models beyond ![]() ,
where the estimator
,
where the estimator
![]() is singular. These data points have been obtained using the Singular Value Decomposition to invert the covariance matrix, yielding a decomposition of the form
is singular. These data points have been obtained using the Singular Value Decomposition to invert the covariance matrix, yielding a decomposition of the form
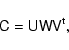 |
(21) |
Having obtained an unbiased estimator of the inverse covariance
matrix, one may still be concerned about a possible bias in the
log-likelihood function, since it consists of the product of
![]() and
and
![]() (Eq. (1)), since
(Eq. (1)), since ![]() and
and
![]() are estimated from the same set of observations. In other words, the question is if it is possible to write
are estimated from the same set of observations. In other words, the question is if it is possible to write
![\begin{displaymath}\mathcal{L}_i(\vec{d}\vert\pi_i) =\log\left\{ \left[ \prod_{j...
...\exp\left[ \mathcal{L(\vec{d}\vert\vec{\pi})}\right]\right\} .
\end{displaymath}](/articles/aa/full/2007/10/aa6170-06/img98.gif) |
(24) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6170fig2.ps}
\end{figure}](/articles/aa/full/2007/10/aa6170-06/Timg104.gif) |
Figure 2:
Triangles, solid lines: ratio of the sum over all
pixels of the marginalised likelihood computed using
|
| Open with DEXTER | |
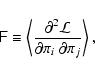 |
(25) |
To demonstrate the bias in
![]() ,
we compute the Fisher matrix for the straight line and power-law fits using (Tegmark et al. 1997)
,
we compute the Fisher matrix for the straight line and power-law fits using (Tegmark et al. 1997)
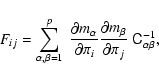 |
(26) |
In Fig. 2, we give the ratio of
![]() ,
computed using the unbiased estimated covariance
,
computed using the unbiased estimated covariance
![]() ,
to the value computed using the true covariance (boxes and dashed lines). One sees that in this case the size of the confidence regions is significantly overestimated, for p/n approaching unity by as much as
,
to the value computed using the true covariance (boxes and dashed lines). One sees that in this case the size of the confidence regions is significantly overestimated, for p/n approaching unity by as much as ![]()
![]() for the straight line case, and by a comparable, albeit slightly smaller factor for the power-law fit.
for the straight line case, and by a comparable, albeit slightly smaller factor for the power-law fit.
The derivation of the unbiased estimator
![]() rests on the assumptions of Gaussian noise and statistically independent data vectors. To test the performance of this estimator in real world situations, where one or both of these assumptions may be violated, we make use of an example from the domain of weak gravitational lensing. For an introduction to this field we refer the reader to Bartelmann & Schneider (2001).
rests on the assumptions of Gaussian noise and statistically independent data vectors. To test the performance of this estimator in real world situations, where one or both of these assumptions may be violated, we make use of an example from the domain of weak gravitational lensing. For an introduction to this field we refer the reader to Bartelmann & Schneider (2001).
We simulate a weak lensing survey consisting of one single field, containing ![]() galaxies, which are assigned a random ellipticity
galaxies, which are assigned a random ellipticity ![]() .
.
![]() is a complex number, which is related to the quadrupole moment of the light distribution of a galaxy (see Bartelmann & Schneider 2001).
The two components of the ellipticity are drawn from a Gaussian distribution with dispersion
is a complex number, which is related to the quadrupole moment of the light distribution of a galaxy (see Bartelmann & Schneider 2001).
The two components of the ellipticity are drawn from a Gaussian distribution with dispersion
![]() .
.
The goal of the survey is to measure the shear correlation function
![]() and to fit a model prediction to it. An estimator for
and to fit a model prediction to it. An estimator for ![]() is given by (Schneider et al. 2002)
is given by (Schneider et al. 2002)
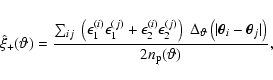 |
(27) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6170fig3.ps}
\end{figure}](/articles/aa/full/2007/10/aa6170-06/Timg123.gif) |
Figure 3:
Ratio of the traces of the unbiased estimator
|
| Open with DEXTER | |
We also need the covariance matrix of
![]() ,
which, since we only have one measurement, is estimated using the bootstrapping algorithm (e.g. Efron & Tibshirani 1993): First, we create a catalogue of all
,
which, since we only have one measurement, is estimated using the bootstrapping algorithm (e.g. Efron & Tibshirani 1993): First, we create a catalogue of all
![]() possible pairs of galaxies in the field. We then create
possible pairs of galaxies in the field. We then create
![]() bootstrap realisations of the survey by repeatedly drawing
bootstrap realisations of the survey by repeatedly drawing ![]() pairs with replacement from the catalogue. From these, we estimate the mean data vector and the covariance matrix of the shear correlation function. As before, we do this for various numbers of bins, where we record the dependence of the traces of
pairs with replacement from the catalogue. From these, we estimate the mean data vector and the covariance matrix of the shear correlation function. As before, we do this for various numbers of bins, where we record the dependence of the traces of
![]() ,
,
![]() and
and
![]() on binning. For the simple case of pure shape noise, the population covariance is diagonal and can be easily computed using (Schneider et al. 2002)
on binning. For the simple case of pure shape noise, the population covariance is diagonal and can be easily computed using (Schneider et al. 2002)
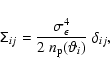 |
(28) |
In principle, both of the assumptions made for the derivation of Eq. (17) are violated: the noise in the shear correlation function is ![]() -distributed, because
-distributed, because
![]() ,
where
,
where ![]() is drawn from a Gaussian. However, the number of degrees of freedom of the
is drawn from a Gaussian. However, the number of degrees of freedom of the ![]() -distribution, which equals the number of pairs, is very large, so that it is very well approximated by a Gaussian (central limit theorem). We therefore do not expect any significant influence on the performance of
-distribution, which equals the number of pairs, is very large, so that it is very well approximated by a Gaussian (central limit theorem). We therefore do not expect any significant influence on the performance of
![]() .
We expect a larger impact by the fact that the data vectors resulting from the bootstrapping procedure are not statistically independent, since different bins necessarily contain the identical galaxy pairs. Strictly speaking, also the requirements for the application of the bootstrap procedure are not met, since the pairs of galaxies which we use to sample the distribution of the shear correlation function are not statistically independent. However, we argue that drawing individual galaxies instead of pairs is not correct, since this would sample the distribution of
.
We expect a larger impact by the fact that the data vectors resulting from the bootstrapping procedure are not statistically independent, since different bins necessarily contain the identical galaxy pairs. Strictly speaking, also the requirements for the application of the bootstrap procedure are not met, since the pairs of galaxies which we use to sample the distribution of the shear correlation function are not statistically independent. However, we argue that drawing individual galaxies instead of pairs is not correct, since this would sample the distribution of ![]() ,
not the one of
,
not the one of ![]() .
.
The outcome of ![]()
![]() realisations of this experiment is given in Fig. 3 (solid line), with
realisations of this experiment is given in Fig. 3 (solid line), with
![]() and
and
![]() .
The figure shows that, in spite of the correlations among the pairs of galaxies and the data vectors,
.
The figure shows that, in spite of the correlations among the pairs of galaxies and the data vectors,
![]() is wrong by only
is wrong by only ![]()
![]() ,
and may well be used in bootstrap applications like this.
,
and may well be used in bootstrap applications like this.
Finally, we explore the impact of non-Gaussian noise. For this
purpose, we perform the same experiment as before, only replacing the
Gaussian noise vectors ones,
![]() ,
with a log-normal
distribution. These are computed using
,
with a log-normal
distribution. These are computed using
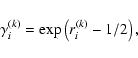 |
(29) |
We have given a proof for the fact that the standard estimator of the covariance matrix (3) is singular for p>n if the mean vector used in (3) is known, and for p>n-1 if the mean is estimated from the same data set as the covariance matrix.
Furthermore, we noted that the inverse of the maximum-likelihood
estimator of the covariance matrix is a biased estimator of the
inverse population covariance matrix. This bias depends basically on
the ratio of the number of bins to the number of independent
observations and can be quite severe as these two numbers become
comparable. If uncorrected for, it will lead to a significant
underestimation of the size of confidence regions derived from
maximum-likelihood fits. The bias can be corrected for p<n-2
by using the estimator (17) instead, which was derived by Anderson (2003) under the assumption of Gaussian errors and statistically independent data vectors.
We stress that there is no contradiction between the foregoing two statements: The singularity of
![]() for p>n-1 derives from linear algebra alone, whereas the fact that
for p>n-1 derives from linear algebra alone, whereas the fact that
![]() is zero for p=n-2 is due to the statistical distribution of the covariance matrix.
Going beyond p=n-1, we find that it is not advisable to use the Singular Value Decomposition to invert the estimated covariance matrix, since the bias of the pseudo-inverse does not seem to be controllable and depends strongly on the population covariance matrix, which is a priori unknown.
is zero for p=n-2 is due to the statistical distribution of the covariance matrix.
Going beyond p=n-1, we find that it is not advisable to use the Singular Value Decomposition to invert the estimated covariance matrix, since the bias of the pseudo-inverse does not seem to be controllable and depends strongly on the population covariance matrix, which is a priori unknown.
Given the unbiased estimator
![]() ,
we argue that also the log-likelihood function is unbiased. However, great care has to be taken if one wishes to perform further analysis of
,
we argue that also the log-likelihood function is unbiased. However, great care has to be taken if one wishes to perform further analysis of
![]() :
since it is a statistical variable, any nonlinear operation on it has the potential to cause a bias. We demonstrate this for the case of marginalisation over certain parameters, where the bias is relatively mild for the examples we chose. The situation is much worse if one tries to quantify the size of the confidence regions. The square root of the determinant of the inverse Fisher matrix shows a significant amount of bias, and therefore should not be used as absolute measures of measurement uncertainty.
:
since it is a statistical variable, any nonlinear operation on it has the potential to cause a bias. We demonstrate this for the case of marginalisation over certain parameters, where the bias is relatively mild for the examples we chose. The situation is much worse if one tries to quantify the size of the confidence regions. The square root of the determinant of the inverse Fisher matrix shows a significant amount of bias, and therefore should not be used as absolute measures of measurement uncertainty.
The upshot of all this is the following: avoid to use more bins for your likelihood fit than you have realisations of your data. If your errors are Gaussian and the data vectors are statistically independent, use the estimator
![]() to obtain an unbiased estimate of the inverse covariance matrix and the log-likelihood function. If one or both of these two requirements are not fulfilled, the estimator is not guaranteed to work satisfactorily; this should be checked from case to case.
to obtain an unbiased estimate of the inverse covariance matrix and the log-likelihood function. If one or both of these two requirements are not fulfilled, the estimator is not guaranteed to work satisfactorily; this should be checked from case to case.
Finally, we note that the estimates of the covariance matrix and its inverse can be quite noisy. If one has prior knowledge about the structure of the covariance matrix, one can develop estimators with a much lower noise level. Since this noise is responsible for most of the problems discussed in this paper, these improved estimators may also be useful in situations where the requirements for the use of
![]() are not fulfilled. We will explore these possibilities in a future paper.
are not fulfilled. We will explore these possibilities in a future paper.
Acknowledgements
We wish to thank Tim Eifler for useful suggestions, Jack Tomsky for pointing us to Anderson's book and Jens Rödiger, Martin Kilbinger, Ismael Tereno and Marco Hetterscheidt for careful reading of the manuscript.