Principle, estimators, and illustration
A&A 464, 29-42 (2007)
DOI: 10.1051/0004-6361:20064799
AMBER: Instrument description and first astrophysical results
E. Tatulli1,2 - F. Millour1,3 - A. Chelli1 - G. Duvert1 - B. Acke1,14 - O. Hernandez Utrera1 - K.-H. Hofmann4 - S. Kraus4 - F. Malbet1 - P. Mège1 - R.G. Petrov3 - M. Vannier3,6,13 - G. Zins1 - P. Antonelli5 - U. Beckmann4 - Y. Bresson5 - M. Dugué5 - S. Gennari2 - L. Glück1 - P. Kern1 - S. Lagarde5 - E. Le Coarer1 - F. Lisi2 - K. Perraut1 - P. Puget1 - F. Rantakyrö6 - S. Robbe-Dubois3 - A. Roussel5 - G. Weigelt4 - M. Accardo2 - K. Agabi3 - E. Altariba1 - B. Arezki1 - E. Aristidi3 - C. Baffa2 - J. Behrend4 - T. Blöcker4 - S. Bonhomme5 - S. Busoni2 - F. Cassaing7 - J.-M. Clausse5 - J. Colin5 - C. Connot4 - A. Delboulbé1 - A. Domiciano de Souza3,5 - T. Driebe4 - P. Feautrier1 - D. Ferruzzi2 - T. Forveille1 - E. Fossat3 - R. Foy8 - D. Fraix-Burnet1 - A. Gallardo1 - E. Giani2 - C. Gil1,15 - A. Glentzlin5 - M. Heiden4 - M. Heininger4 - D. Kamm5 - M. Kiekebusch6 - D. Le Contel5 - J.-M. Le Contel5 - T. Lesourd9 - B. Lopez5 - M. Lopez9 - Y. Magnard1 - A. Marconi2 - G. Mars5 - G. Martinot-Lagarde5,9 - P. Mathias5 - J.-L. Monin1 - D. Mouillet1,16 - D. Mourard5 - E. Nussbaum4 - K. Ohnaka4 - J. Pacheco5 - C. Perrier1 - Y. Rabbia5 - S. Rebattu5 - F. Reynaud10 - A. Richichi11 - A. Robini3 - M. Sacchettini1 - D. Schertl4 - M. Schöller6 - W. Solscheid4 - A. Spang5 - P. Stee5 - P. Stefanini2 - M. Tallon8 - I. Tallon-Bosc8 - D. Tasso5 - L. Testi2 - F. Vakili3 - O. von der Lühe12 - J.-C. Valtier5 - N. Ventura1
1 -
Laboratoire d'Astrophysique de Grenoble, UMR 5571 Université Joseph
Fourier/CNRS, BP 53, 38041 Grenoble Cedex 9, France
2 - INAF-Osservatorio Astrofisico di Arcetri, Istituto Nazionale di
Astrofisica, Largo E. Fermi 5, 50125 Firenze, Italy
3 - Laboratoire Universitaire d'Astrophysique de Nice, UMR 6525
Université de Nice - Sophia Antipolis/CNRS, Parc Valrose, 06108
Nice Cedex 2,
France
4 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69,
53121 Bonn, Germany
5 - Laboratoire Gemini, UMR 6203 Observatoire de la Côte
d'Azur/CNRS, BP 4229, 06304 Nice Cedex 4, France
6 - European Southern Observatory, Casilla 19001, Santiago 19,
Chile
7 - ONERA/DOTA, 29 av de la Division Leclerc, BP 72, 92322
Chatillon Cedex, France
8 - Centre de Recherche Astronomique de Lyon, UMR 5574 Université
Claude Bernard/CNRS, 9 avenue Charles André, 69561 Saint Genis
Laval Cedex, France
9 - Division Technique INSU/CNRS UPS 855, 1 place Aristide
Briand, 92195 Meudon Cedex, France
10 - IRCOM, UMR 6615 Université de Limoges/CNRS, 123 avenue Albert
Thomas, 87060 Limoges Cedex, France
11 - European Southern Observatory, Karl Schwarzschild Strasse 2,
85748 Garching, Germany
12 - Kiepenheuer Institut für Sonnenphysik, Schöneckstr. 6,
79104 Freiburg, Germany
13 - Departamento de Astronomia, Universidad de Chile, Chile
14 - Instituut voor Sterrenkunde, KU-Leuven, Celestijnenlaan 200D,
3001 Leuven, Belgium
15 - Centro de Astrofísica da Universidade do Porto, Rua
das Estrelas, 4150-762 Porto, Portugal
16 - Laboratoire Astrophysique de Toulouse, UMR 5572 Université
Paul Sabatier/CNRS, BP 826, 65008 Tarbes Cedex, France
Received 2 January 2006 / Accepted 1 March 2006
Abstract
Aims. In this paper, we present an innovative data reduction method for single-mode interferometry. It has been specifically developed for the AMBER instrument, the three-beam combiner of the Very Large Telescope Interferometer, but it can be derived for any single-mode interferometer.
Methods. The algorithm is based on a direct modelling of the fringes in the detector plane. As such, it requires a preliminary calibration of the instrument in order to obtain the calibration matrix that builds the linear relationship between the interferogram and the interferometric observable, which is the complex visibility. Once the calibration procedure has been performed, the signal processing appears to be a classical least-square determination of a linear inverse problem. From the estimated complex visibility, we derive the squared visibility, the closure phase, and the spectral differential phase.
Results. The data reduction procedures have been gathered into the so-called amdlib software, now available for the community, and are presented in this paper. Furthermore, each step in this original algorithm is illustrated and discussed from various on-sky observations conducted with the VLTI, with a focus on the control of the data quality and the effective execution of the data reduction procedures. We point out the present limited performances of the instrument due to VLTI instrumental vibrations which are difficult to calibrate.
Key words: technique: interferometric - methods: data analysis - instrumentation: interferometers
AMBER is the first-generation near-infrared three-way beam combiner (Petrov et al. 2007) of the Very Large Telescope Interferometer (VLTI). This instrument simultaneously provides spectrally dispersed visibility for three baselines and a closure phase at three different spectral resolutions. AMBER has been designed to investigate the milli-arcsec surrounding of astrophysical sources like young and evolved stars or active galactic nuclei, and to possibly detect exoplanet signal. The main new feature of this instrument compared to other interferometric instruments is the simultaneous use of modal filters (optical fibers) and a dispersed fringe combiner using spatial coding. The AMBER team has therefore carefully investigated a data processing strategy for this instrument and is providing a new type of data reduction method.
Given the astonishingly quick evolution of ground based optical
interferometers in only two decades, in terms of baseline lengths and
number of recombined telescopes, the interest of using the practical
characteristics of single-mode fibers to carry and recombine the
light, as first proposed by Connes et al. (1987) with his conceptual FLOAT
interferometer, is now well established. Furthermore, in the light of the
FLUOR experiment on the IOTA interferometer, which demonstrated the "on-sky'' feasibility of such interferometers for
the first time,
Coudé Du Foresto et al. (1997) showed that making use of single mode waveguides
could also increase the performances of optical interferometry, thanks
to their remarkable properties of spatial filtering, which change the
phase fluctuations of the atmospheric turbulent wavefront into
intensity fluctuations. Indeed, by monitoring these
fluctuations in real time thanks to dedicated photometric outputs and by performing instantaneous photometric calibration, he experimentally proved that
single-mode interferometry could achieve visibility measurements with
precisions of ![]() or lower. Achievement of such
performance level has since been confirmed with the IONIC integrated optic
beam combiner set up on the same interferometer (LeBouquin et al. 2004).
or lower. Achievement of such
performance level has since been confirmed with the IONIC integrated optic
beam combiner set up on the same interferometer (LeBouquin et al. 2004).
![\begin{figure}
\par\begin{tabular}{cc}
\includegraphics[height=4.8cm]{4799fig1.eps} &
\includegraphics[height=4.8cm]{4799fig2.eps}\end{tabular}
\par\end{figure}](/articles/aa/full/2007/10/aa4799-06/Timg9.gif) |
Figure 1: Left panel: Sketch of the AMBER instrument. The light enters the instrument from the left and is propagating from left to right until the raw data are recorded on the detector. Further details are given in the text. Right panel: AMBER reconstituted image from the raw data recorded during the 3-telescope observation of the calibrator HD135382 in February 2005, in the medium spectral resolution mode. DK corresponds to a dark region, Pk are the vertically dispersed spectra obtained from each telescope, and IF is the spectrally dispersed interferogram. |
| Open with DEXTER | |
Hence, following the path opened by the FLUOR experiment, the AMBER instrument - the three-beam combiner of the VLTI (Petrov et al. 2007) - makes use of the filtering properties of single-mode fibers. However, in contrast to FLUOR, PTI (Colavita 1999a) or VINCI on the VLTI (Kervella et al. 2003), where the fringes are coded temporally with a movable piezzo-electric mirror, the interference pattern is scanned spatially thanks to separated output pupils, the separation fixing the spatial coding frequency of the fringes, as in the case of the GI2T interferometer (Mourard et al. 2000). Thus, if data reduction methods have already been proposed for single-mode interferometers using temporal coding (Colavita 1999b; Kervella et al. 2004), this paper is the first to present a signal-processing algorithm dedicated to single-mode interferometry with spatial beam recombination. Moreover, in the case of AMBER, the configuration of the output pupils, i.e. the spatial coding frequency, imposes a partial overlap of the in the three telescopes case interferometric peaks in the Fourier plane. As a consequence, data reduction based on the classical estimators in the Fourier plane (Mourard et al. 1994; Roddier & Lena 1984) cannot be performed. The AMBER data reduction procedure is based on a direct analysis in the detector plane, a principle that is an optimization of the "ABCD'' estimator as derived in Colavita (1999b). The specificity of the AMBER coding and its subsequent estimation of the observables arises from the desire to characterize and to make use of the linear relationship between the pixels (i.e. the interferograms on the detector) and the observables (i.e. the complex visibilities). In other words, the AMBER data reduction algorithm is based on modelling the interferogram in the detector plane.
In Sect. 2, we present the AMBER experiment from a signal-processing point of view and we introduce the interferometric equation governing this instrument. We develop the specific data reduction processes of AMBER in Sect. 3, and then derive the estimators of the interferometric observables. Successive steps in the data reduction method are given in Sect. 4, as performed by the software provided to the community. Finally, the data-reduction algorithm is validated in Sect. 5 through several "on-sky'' observations with the VLTI (commissioning and science demonstration time (SDT)). Present and future performances of this instrument are discussed.
The process of image formation of AMBER is sketched in
Fig. 1 (left) from a signal-processing point of view. It
consists of three major steps. First, the beams from the three
telescopes are filtered by single-mode fibers to convert phase
fluctuations of the corrugated wavefronts into intensity fluctuations
that are monitored. The fraction of light entering the fiber is
called the coupling coefficient (Shaklan & Roddier 1988) and it depends on the
Strehl ratio (Coudé du Foresto et al. 2000). At this point, a pair of conjugated
cylindrical mirrors compresses, by a factor of about 12, the individual
beams exiting from fibers into one dimensional elongated beams to be
injected in the entrance slit of the spectrograph. For each of the
three beams, beam-splitters placed inside the spectrograph select part
of the light and induce three different tilt angles so that each beam
is imaged at different locations of the detector. These are called
photometric channels and are each one relative to a corresponding
incoming beam. The remaining parts of the light of the three beams
are overlapped on the detector image plane to form fringes. The spatial
coding frequencies of the fringes f are fixed by the separation of
the individual output pupils. They are
![]() ,
where d is the output pupil diameter. Since the
beams hit a spectral dispersing element (a prism glued on a mirror or
one of the two gratings) in the pupil plane, the interferogram
and the photometries are spectrally dispersed perpendicularly to the
spatial coding. The dispersed interferogram arising from the
beam combination, as well as the photometric outputs are recorded on the
infrared detector, which characteristics are given in
Table 1.
,
where d is the output pupil diameter. Since the
beams hit a spectral dispersing element (a prism glued on a mirror or
one of the two gratings) in the pupil plane, the interferogram
and the photometries are spectrally dispersed perpendicularly to the
spatial coding. The dispersed interferogram arising from the
beam combination, as well as the photometric outputs are recorded on the
infrared detector, which characteristics are given in
Table 1.
Table 1: Detector properties.
The detector consists in a
![]() pixel array with the vertical dimension
aligned with the wavelength direction. The first 20 pixels of each scanline
of the detector are masked and never receive any light, allowing us to
estimate the readout noise and bias during an exposure.
The light from the two (resp. 3) telescopes comes in three (resp. 4) beams,
one "interferometric'' beam where the interference fringes are located, and
two (resp. three) "photometric'' beams. These 3 (resp. 4) beams are
dispersed and spread over three (resp. 4) vertical areas on the detector.
The detector is read in subwindows. Horizontally, these subwindows are
centered on the regions where the beams are dispersed, with a typical width
of 32 to 40 pixels. Vertically, the detector can be set up to read up to
three subwindows (covering up to three different wavelength ranges). The
raw data format used by AMBER records individually these subframes. However,
as sketched in the right panel of Fig. 1,
the AMBER raw data can be conceived as the grouping together of these subwindows:
pixel array with the vertical dimension
aligned with the wavelength direction. The first 20 pixels of each scanline
of the detector are masked and never receive any light, allowing us to
estimate the readout noise and bias during an exposure.
The light from the two (resp. 3) telescopes comes in three (resp. 4) beams,
one "interferometric'' beam where the interference fringes are located, and
two (resp. three) "photometric'' beams. These 3 (resp. 4) beams are
dispersed and spread over three (resp. 4) vertical areas on the detector.
The detector is read in subwindows. Horizontally, these subwindows are
centered on the regions where the beams are dispersed, with a typical width
of 32 to 40 pixels. Vertically, the detector can be set up to read up to
three subwindows (covering up to three different wavelength ranges). The
raw data format used by AMBER records individually these subframes. However,
as sketched in the right panel of Fig. 1,
the AMBER raw data can be conceived as the grouping together of these subwindows:
The following demonstration is given considering a generic
![]() telescope interferometer. In the specific case of AMBER,
however,
telescope interferometer. In the specific case of AMBER,
however,
![]() or
or
![]() .
Each line of the detector
being independent of each other, we can focus our
attention on one single spectral channel
.
Each line of the detector
being independent of each other, we can focus our
attention on one single spectral channel![]() , which is assumed to be
monochromatic here. The effect of a spectral bandwidth on the
interferometric equation is treated in Sect. 3.6.1.
, which is assumed to be
monochromatic here. The effect of a spectral bandwidth on the
interferometric equation is treated in Sect. 3.6.1.
Interferometric output: when only the ith beam is
illuminated, the signal recorded in the interferometric channel is the
photometric flux Fi spread on the Airy pattern aik, which is the
diffraction pattern of the ith output pupil weighted by the
single-mode of the fiber, k is the pixel number on the detector, and ![]() is the associated angular variable.
Then, Fi results in the total source photon flux N attenuated by the
total transmission of the ith optical train ti, i.e. the
product of the optical throughput (including atmosphere and optical
train of the VLTI and the instrument) and the coupling coefficient of
the single-mode fiber:
is the associated angular variable.
Then, Fi results in the total source photon flux N attenuated by the
total transmission of the ith optical train ti, i.e. the
product of the optical throughput (including atmosphere and optical
train of the VLTI and the instrument) and the coupling coefficient of
the single-mode fiber:
Such an analysis can be done for each pair of beams arising from the
interferometer.
As a result, the interferogram recorded on the detector can be written
in the general form:
The AMBER data-reduction algorithm is based on the modelling of the interferogram in the detector plane. Such a method requires an accurate calibration of the instrument.
The estimated photometric fluxes Pi are computed from the photometric
channels (see Eq. (4)):
| mk = ckijRij - dkijIij. | (12) |
Table 2: Acquisition sequence of calibration files.
![\begin{figure}
\par\begin{tabular}{ccc}
\includegraphics[height=5.3cm]{4799fig3...
...4.eps} &
\includegraphics[height=5.3cm]{4799fig5.eps}\end{tabular}
\end{figure}](/articles/aa/full/2007/10/aa4799-06/Timg46.gif) |
Figure 2:
Outputs of the calibration procedures. Examples have been chosen for one given wavelength:
|
| Open with DEXTER | |
The calibration procedure is performed thanks to an internal source
located in the Calibration and Alignment Unit (CAU) of AMBER
(Petrov et al. 2007). It consists of acquiring a sequence of high
signal-to-noise ratio calibration files, whose successive
configurations are summarized in Table 2 and explained
below. Since the calibration is done in laboratory, the desired level
of accuracy for the measurements is insured by choosing the appropriate
integration time. As an example, typical integration times in "average accuracy'' mode are (for the full calibration process)
![]() for, respectively, low, medium, and high spectral resolution modes in the K band and 100 times higher for the "high accuracy'' calibration mode.
for, respectively, low, medium, and high spectral resolution modes in the K band and 100 times higher for the "high accuracy'' calibration mode.
The sequence of calibration files has been chosen to accommodate both two and three-telescope operations. For a two-telescope operation, only the 4 first steps are needed. Raw data FITS files produced by the ESO instruments bear no identifiable name and can only be identified as, e.g., files relevant to the calibration of the V2PM matrix, by the presence of dedicated FITS keywords (ESO's pipeline Data PRoduct keys or "DPR keys'') in their header. The DPR keys used are listed in Table 2.
First (steps 1 and 2 - and 5 when in 3-telescope mode), for each
telescope beam, an image is recorded with
only this shutter opened. The fraction of flux
measured between the interferometric channel and the illuminated
photometric channel leads to an accurate estimation of the vki functions. Then, in order to compute the carrying waves ckijand dkij, one needs to have two independent (in terms of
algebra) measurements of the interferogram since there are two
unknowns (per baseline) to compute. The principle is the following:
two shutters are opened simultaneously (steps 3/4, 6/7,
and 8/9) and for each pair of beams, then the interferogram is recorded on
the detector. Such an interferogram corrected for its DC component
and calibrated by the photometry yields the knowledge of the
ckij carrying wave. To obtain its quadratic counterpart, the
previous procedure is repeated by introducing a known phase shift close to 90 degree
![]() using piezoelectric mirrors at the entrance of beams 2 and 3. Computing the
dkij function from the knowledge of ckij and
using piezoelectric mirrors at the entrance of beams 2 and 3. Computing the
dkij function from the knowledge of ckij and ![]() is straightforward.
Note that by construction: (i) the carrying waves are computed with the unknown system phase
is straightforward.
Note that by construction: (i) the carrying waves are computed with the unknown system phase ![]() (possible phase of the internal source, differential optical path difference introduced at the CAU level, etc.), and (ii) since the internal source in the CAU is slightly
resolved by the largest baseline (1-3) of the output pupils, the
carrying waves for this specific baseline are weighted by the
visibility
(possible phase of the internal source, differential optical path difference introduced at the CAU level, etc.), and (ii) since the internal source in the CAU is slightly
resolved by the largest baseline (1-3) of the output pupils, the
carrying waves for this specific baseline are weighted by the
visibility ![]() of the internal source. Hence, at this point, the carrying waves are following expressions that are slightly different from their original definition given by Eqs. (6) and (7):
of the internal source. Hence, at this point, the carrying waves are following expressions that are slightly different from their original definition given by Eqs. (6) and (7):
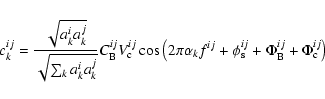 |
(14) |
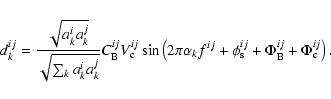 |
(15) |
| |
Figure 3: Contrast loss due to polarization effects and partial resolution of the internal source as a function of the wavelength. The 3-telescope P2VM used is the same as the one presented in Fig. 2. The errors bars are roughly at the level of the contrast loss rms along the wavelength. In other words, the contrast loss is constant over the wavelength range. |
| Open with DEXTER | |
Figure 3 illustrates Eq. (16). For the baselines (1,2) and (2,3), the contrast loss arises from polarization effects, since the internal source is unresolved. We find
![]() and
and
![]() ,
respectively. For the third baseline (1,3), the internal source is partially resolved, which explains an higher contrast loss,
,
respectively. For the third baseline (1,3), the internal source is partially resolved, which explains an higher contrast loss,
![]() .
.
The values
![]() and
and
![]() ,
the bias part of R2 and I2, can be easily computed from the definition of the real and
imaginary part of the coherent fluxes, which are linear combinations
of the DC continuum-corrected interferograms mk. If
,
the bias part of R2 and I2, can be easily computed from the definition of the real and
imaginary part of the coherent fluxes, which are linear combinations
of the DC continuum-corrected interferograms mk. If
![]() and
and
![]() are the coefficients of the P2VM
matrix, Rb and Ib verify the respective following
equations:
are the coefficients of the P2VM
matrix, Rb and Ib verify the respective following
equations:
For each spectral channel, the squared visibility and closure phase (in
the three telescope case) can be estimated from the interferogram.
Taking advantage of the spectral dispersion, the differential phase can be
computed as well. In the following paragraphs, we denote with
![]() the
ensemble average of the different quantities. This average can be
performed either on the frames within an exposure and/or on the wavelengths.
the
ensemble average of the different quantities. This average can be
performed either on the frames within an exposure and/or on the wavelengths.
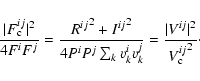 |
(23) |
As a result the visibility - atmospheric issues apart - has still to be calibrated by observing a reference source.
In practice, because data are noisy, we perform an ensemble average on the frames that compose the data cube (see Sect. 2.1) to estimate the expected values of the square coherent flux and the photometric fluxes, respectively. Taking the average of the squared modulus of the
coherent flux, i.e. doing a quadratic estimation, allows us to handle
the problem of the random differential piston
![]() ,
but
introduces a quadratic bias due to the zero-mean photon and detector
noises (Perrin 2003).
The expression of the squared visibility estimator, unbiased by
fundamental noises is therefore:
,
but
introduces a quadratic bias due to the zero-mean photon and detector
noises (Perrin 2003).
The expression of the squared visibility estimator, unbiased by
fundamental noises is therefore:
Using the squared visibility estimator of Eq. (24), the theoretical error bars on the squared visibility can be computed from its second-order Taylor expansion (Kervella et al. 2004; Papoulis 1984):
![\begin{displaymath}\sigma^2(\vert V^{ij}\vert^2) = \frac{1}{M}\left[\frac{\sigma...
...)}{\overline{P^iP^j}^2}\right]\overline{\vert V^{ij}\vert^2}^2
\end{displaymath}](/articles/aa/full/2007/10/aa4799-06/img82.gif) |
(26) |
By definition, the closure phase is the phase of the so-called
bispectrum B123. The bispectrum results in the ensemble average of
the coherent flux triple product and then estimated as
The differential phase is the phase of the so-called cross spectrum W12. For each baseline, the latter is estimated from the
complex coherent flux taken at two different wavelengths ![]() and
and ![]() :
:
Note that, in order to distinguish between the atmospheric piston
![]() and the linear component of the differential phase
and the linear component of the differential phase
![]() ,
the fitting techniques described above can be performed by only using spectral channels corresponding to the continuum of the source (i.e. outside spectral features) where its differential phase of the object is assumed to be zero.
,
the fitting techniques described above can be performed by only using spectral channels corresponding to the continuum of the source (i.e. outside spectral features) where its differential phase of the object is assumed to be zero.
The above derivation of the interferometric equation assumes a
monochromatic spectral channel. In practice, the spectral width of one
spectral channel is non zero and depends on the resolution
![]() of the spectrograph. As a consequence the coherence
length
of the spectrograph. As a consequence the coherence
length
![]() of the interferogram is finite and equals
of the interferogram is finite and equals
![]() ,
where
,
where ![]() is the
reference wavelength in the spectral channel. Assuming a
linear decomposition of the phase of the interferogram and neglecting higher orders, the
interferogram is attenuated by a factor
is the
reference wavelength in the spectral channel. Assuming a
linear decomposition of the phase of the interferogram and neglecting higher orders, the
interferogram is attenuated by a factor ![]() ,
which can be
written
,
which can be
written
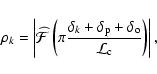 |
(36) |
In the medium and high resolutions (where
![]() and
and
![]() ,
respectively),
however, the OPD
,
respectively),
however, the OPD ![]() due the spatial sampling of AMBER can be neglected. Indeed
this approximation leads to a relative error of the coefficient below 10-3 and 10-5, respectively, which is within the specified
error bars of the visibility. In such a case, the loss of spectral
coherence simply results in biasing the visibility frame to frame by a
factor
due the spatial sampling of AMBER can be neglected. Indeed
this approximation leads to a relative error of the coefficient below 10-3 and 10-5, respectively, which is within the specified
error bars of the visibility. In such a case, the loss of spectral
coherence simply results in biasing the visibility frame to frame by a
factor
![]() .
This bias can be corrected by
knowing the shape of the spectral filter and by estimating the piston
.
This bias can be corrected by
knowing the shape of the spectral filter and by estimating the piston
![]() thanks to Eq. (33).
thanks to Eq. (33).
Although a quadratic estimation of the visibility has been performed
to avoid the differential piston to completely cancel out the fringes,
the high frequency variations of the latter during the integration
time - so called high-pass jitter - nevertheless blur the fringes.
As a result, the coherent flux, thus the visibility, is attenuated. On
average, the attenuation coefficient ![]() of the squared visibility
is given by Colavita (1999b):
of the squared visibility
is given by Colavita (1999b):
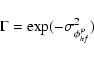 |
(38) |
For the time being, this atmospheric effect is compensated by calibrating the source visibility with a reference source observed shortly before and after the scientific target to insure similar atmospheric conditions. We have also planned in the near future to provide a more accurate calibration of this effect, based on computing the variance of the so-called "first difference phase jitter'', which is the difference of the average piston taken between two successive exposures, as proposed by Colavita (1999b) for the PTI interferometer and successfully applied by Malbet et al. (1998). However, jitter analysis (as illustrated in Sect. 5.2) cannot be tested and validated as long as the extra-sources of vibrations due to VLTI instabilities (delay lines, adaptive optics, etc.), hardly calibratable, are clearly identified and suppressed. Note as well that the use of the accurate fringe tracker FINITO (Gai et al. 2002), soon expected to operate on the VLTI, should drastically reduce the jitter attenuation, hence allowing integration on much longer times than the coherence time of the atmosphere in order to reach fainter stars.
A dedicated software to reduce AMBER observations has been developed by the AMBER consortium. This consists of a library of C functions, called amdlib, plus high-level interface programs. The amdlib functions are used at all stages of AMBER data acquisition and reduction: in the observation software (OS) for wavelength calibration and fringe acquisition, in the (quasi) real time display program used during the observations, in the online data reduction pipeline customary for ESO instruments, and in various offline front end applications, noticeably a Yorick implementation (AmmYorick). The amdlib library is meant to incorporate all the expertise on AMBER data reduction and calibration acquired throughout the life of the instrument, which are bound to evolve with time.
The data obtained with AMBER ("raw data'') consist of an exposure, i.e., a time series of frames read on the infrared camera, plus all relevant information from AMBER sensors, observed object, VLTI setup, etc., stored in FITS TABLE format, according to ESO interface document VLT-ICD-ESO-15000-1826. Saving the raw, uncalibrated data, although more space-consuming, permits us to benefit afterwards, by replaying the calibration sequences and the data reduction anew, from all the improvements that could have been deposited in amdlib in the meantime.
The library contains a set of "software filters'' that refine the raw
data sets to obtain calibrated "science data frames''. This treatment
is performed on all of the raw data frames, irrespective of their future
use (calibration or observation). A second set of functions performs
high-level data extraction on these calibrated frames, either to
compute the V2PM (see Sect. 4.3) from a set of calibration data or to
extract the visibilities from a set of science target observations,
the end product in this case being a reduced set of visibilities per
object, stored in the optical interferometry standard
![]() format (Pauls et al. 2005).
format (Pauls et al. 2005).
First, all frames pixels are tagged valid if not present in the
currently available bad pixel list of the AMBER detector. Then they
are converted to photoevent counts. This step necessitates, for each
frame, precisely modelling of the spatially and temporarily variable
bias added by the electronics. The detector exhibits a pixel-to-pixel (high
frequency) bias whose pattern is constant in time but which
depends on the detector integration time (DIT) and the size and
location of the subwindows read on the detector. Thus, after each
change in the detector setup, a new pixel
bias map (PBM) is measured prior to the observations by averaging
a large number of frames acquired with the detector facing a cold
shutter![]() .
This PBM is then simply removed from all frames prior to any other
treatment.
.
This PBM is then simply removed from all frames prior to any other
treatment.
Once this fixed pattern has been removed, the detector
may still be affected by a time-variable "line'' bias, i.e., a
variable offset for each detector line. This bias is estimated for
each scan line and each frame as the mean value of the corresponding
line of masked pixels ("DK'' column in
Fig. 1) and then
substracted from the rest of the line of pixels.
The detector has an image persistence of ![]()
![]() ;
consequently, all frames are corrected for this effect before
calibration. Pixels are then converted to photoevent counts by
multiplying by the pixel's gain. Currently the map of the pixel gains
used is simply a constant e-/ADU value (see Table 1)
multiplied by a "flat field'' map acquired during laboratory tests.
Finally, the rms of the values in the
masked pixel set, which were calibrated as the rest of the detector, gives
the frame's detector noise.
;
consequently, all frames are corrected for this effect before
calibration. Pixels are then converted to photoevent counts by
multiplying by the pixel's gain. Currently the map of the pixel gains
used is simply a constant e-/ADU value (see Table 1)
multiplied by a "flat field'' map acquired during laboratory tests.
Finally, the rms of the values in the
masked pixel set, which were calibrated as the rest of the detector, gives
the frame's detector noise.
Finally, each frame is converted to the handier "science data'' structure, which contains only the calibrated image of the "interferometric channel'' and (up to) three 1D vectors, the corresponding instantaneous photometry of each beam, corrected for the above-mentioned spectral displacement.
Computation of the V2PM matrix is performed by the
function amdlibComputeP2vm(). This function processes the 4 or 9 files described in Sect. 3.2 applying by each of them the detector
calibration, image alignment, and conversion to "science data''
described above, then computing the vki (Eq. (10))
and the carrying waves ckij and dkij of the V2PM
matrix (Eq. (13)).
The result is stored in a FITS file, improperly called, for historical
reasons, "the P2VM''![]() .
.
The P2VM matrix is the most important set of calibration values needed to retrieve visibilities. The shape of the carrying waves (the cks and dks ) and, in lesser measure, the associated vks are the imprints of all the changes in intensity and phase that the beams suffer between the output of each fiber and detection on the infrared camera. Any change in the AMBER optics situated in this zone, either by moving, e.g., a grating, or just thermal long-term effects, render the P2VM unusable. Thus, the P2VM matrix must be recalibrated each time a new spectral setup is called that involves changing the optical path behind the fibers.
All the instrument observing strategies and operations are governed by the need to avoid unnecessary optical changes, and care is taken at the operating system level to assure a recalibration of the P2VM whenever a "critical'' motor affecting the optical path is set in action. To satisfy these needs, the P2VM computation has been made mandatory prior to science observations and is given an unique ID number. All the science data files produced after the P2VM file inherit this ID, which associates them with their "governing'' calibration matrix. The amdlib library takes the opportunity of the P2VM file being pivotal to the data reduction, and unique, to make it a placeholder for all the other calibration tables needed to reduce the science data, namely the spectral calibration, bad pixels, and flat field tables.
The amdlibExtractVisibilities() function, in sequence is
This section aims to present, step-by-step, the data reduction procedures performed on real interferometric measurements arising from VLTI observations. Results are discussed, focusing on key points in the process.
Assuming the calibration process has been properly performed following Sect. 3.2, the first step in the derivation of the observables is to estimate the real and imaginary parts of the coherent flux. This is done by inverting the calibration matrix and obtaining the P2VM matrix, shown by Eqs. (17) and (18). Figure 4 gives an example of the fringe fitting process for an observation of the calibrator star HD135382 with three telescopes.
However, before going further in the data reduction process, it might be worthwhile for the users to check the validity of the fit and then to detect any potential problems in the data. Such a step can be easily done by computing the residual
![]() between the measurements mk and the model
between the measurements mk and the model
![]() :
:
![\begin{displaymath}[\widetilde{m}_k]= {\rm V2PM} [\widetilde{R}^{ij}, \widetilde{I}^{ij}]
\end{displaymath}](/articles/aa/full/2007/10/aa4799-06/img126.gif) |
(39) |
![\begin{displaymath}\chi^2_{\rm res} = [\widetilde{m}_k - m_k]^{\rm T} \mathcal{C}_{\rm M}^{-1} [\widetilde{m}_k - m_k].
\end{displaymath}](/articles/aa/full/2007/10/aa4799-06/img127.gif) |
(40) |
![\begin{figure}
\par\includegraphics[width=4.5cm,clip]{4799fig7.eps}
\end{figure}](/articles/aa/full/2007/10/aa4799-06/Timg128.gif) |
Figure 4: Example of fringe-fitting by the carrying waves in the 3-telescope case. The DC-corrected interferogram is plotted (dashdot line) with the error bars. The result of the fit is overplotted (solid line). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.3cm,clip]{4799fig8.eps}\hspace*{4mm}
\includegraphics[width=5.3cm,clip]{4799fig9.eps}
\end{figure}](/articles/aa/full/2007/10/aa4799-06/Timg130.gif) |
Figure 5:
Left: sample of 100 successive interferograms as recorded during the observation with two telescopes of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{4799fig10.eps}\hspace*{2mm} ...
....eps}\hspace*{2mm}
\includegraphics[width=5cm,clip]{4799fig12.eps}
\end{figure}](/articles/aa/full/2007/10/aa4799-06/Timg132.gif) |
Figure 6:
Visibility as a function of the fringe SNR criterion. Left: for jitter-free simulated data, using the real photometry observed on
|
| Open with DEXTER | |
For each frame of the set of data, Eq. (20) provides an estimation of the fringe signal-to-noise ratio. As an example, Fig. 5 presents 100 fringes recorded on the detector during the 2-telescope observation of the calibrator
![]() in July 2005, first in the order they appeared during the observation and then after re-ordering them following the fringe criterion.
in July 2005, first in the order they appeared during the observation and then after re-ordering them following the fringe criterion.
The aim of computing this criterion can be twofold: (i) during the observations, as mentioned in Sect. 3.4, it allows us to detect the fringes and therefore to initiate the recording of the data only when it is meaningful; and (ii) calculated a posteriori during the data reduction phase, it enables us to select the best frames (in terms of SNR) before estimating the observables. This second point is especially important where frames are recorded in the presence of strong and variable fringe jitter.
In the ideal and unrealistic case where the fringes are not moving during the integration time, the fringe contrast is not attenuated by vibrations, and the frame-by-frame estimated visibility is constant, no matter what the photometric flux level is in each arm of the interferometer. As a result, the visibility as a function the function of the fringe SNR is constant, with the error bars increasing as the fringe SNR decreases. This is illustrated in Fig. 6 (left). To obtain this set of jitter-free data, we have built interferograms using the carrying waves of the calibration matrix that simulate perfectly stable AMBER fringes. Then, we have added the photometry taken on the
![]() data, which allowed us to keep realistic photometric realizations taking the correct transmissions of the instrument into account. In that case, selecting the best fringes has no other goal than to improve the SNR of the observables by excluding the data with poor flux.
data, which allowed us to keep realistic photometric realizations taking the correct transmissions of the instrument into account. In that case, selecting the best fringes has no other goal than to improve the SNR of the observables by excluding the data with poor flux.
In the presence of atmospheric turbulence and lack of a fringe tracker, the fringes are moving during the integration time, leading to lower the visibility. On average, the squared visibility is attenuated by a factor
![]() ,
where
,
where
![]() is the variance of the atmospheric high pass jitter, as explained in Sect. 3.6.2. The frame-by-frame visibility, though, undergoes a random attenuation around this average loss of contrast. An example of the effect of the atmospheric jitter is given in Fig. 6 (middle), where a previous set of simulated data has been used, adding a frame-by-frame random attenuation taking the
is the variance of the atmospheric high pass jitter, as explained in Sect. 3.6.2. The frame-by-frame visibility, though, undergoes a random attenuation around this average loss of contrast. An example of the effect of the atmospheric jitter is given in Fig. 6 (middle), where a previous set of simulated data has been used, adding a frame-by-frame random attenuation taking the
![]() integration time of the
integration time of the
![]() observation into account. Once again, fringe selection only enables us to increase the SNR of the observables here.
observation into account. Once again, fringe selection only enables us to increase the SNR of the observables here.
However, when we look at the real set of data obtained from the observation of
![]() , we obtain the plot displayed in Fig. 6 (right). The dispersion of the visibility, especially for low fringe SNR is unexpectedly large and can definitively not be explained by pure atmospheric OPD vibrations. As a matter of fact, these variations are due to the present strong vibrations along the VLTI instrumentation (adaptive optics, delay lines, etc.), as this effect was previously revealed by the VINCI recombiner. These vibrations strongly reduce the fringe contrast and subsequently the value of the estimated visibilities, which explains the behavior of the visibilities as a function of the fringe SNR. Indeed, when the visibility tends toward 0, because of severe jitter attenuation, the fringe criterion tends toward 0 as well. In contrast, the visibility plotted as a function of the fringe SNR saturates for high values of the latter.
, we obtain the plot displayed in Fig. 6 (right). The dispersion of the visibility, especially for low fringe SNR is unexpectedly large and can definitively not be explained by pure atmospheric OPD vibrations. As a matter of fact, these variations are due to the present strong vibrations along the VLTI instrumentation (adaptive optics, delay lines, etc.), as this effect was previously revealed by the VINCI recombiner. These vibrations strongly reduce the fringe contrast and subsequently the value of the estimated visibilities, which explains the behavior of the visibilities as a function of the fringe SNR. Indeed, when the visibility tends toward 0, because of severe jitter attenuation, the fringe criterion tends toward 0 as well. In contrast, the visibility plotted as a function of the fringe SNR saturates for high values of the latter.
The major issue is that such an effect is hardly calibratable because potentially non stationary. Hence, one convenient way to overcome the problem, beside increasing the error bars artificially to take this phenomenon into account, is to only select the fringes that are less affected by the vibrations, that is, the fringes with the highest fringe SNR. One can then choose the percentage of selected frames from which the visibility will be estimated. The threshold must be chosen according to the following trade-off: reducing the number of frames considered allows to get rid of most of the jitter attenuation, but, from a certain number when the sample is not large enough to perform statistics, it increases the noise on the visibility. Furthermore, it leads to mis-estimate the quadratic bias (see Eq. (25)), which is by essence a statistical quantity, and consequently drives to introduce a bias in the visibility.
Obviously, such a selection process must be handled with care, and its robustness with regard to the selection level has to be established for any given observation. In other words, for this method to be valid, the expected value for the calibrated visibility must remain the same, with only the error bars changing and eventually reaching a minimum at some specific selection level. In particular, this method seems well adapted, above all, to cases where the calibrator exhibits a magnitude close to the source's one, where the visibility distribution versus the SNR is expected to behave similarly. Going into further details af this point is nevertheless beyond the scope of this paper as it will be deeply developed in Millour et al. (2007). However note that we experimentally found this procedure to be generally robust, and for typical observations performed until now with the VLTI, choosing ![]() of the frames as the final sample appeared to be a good compromise.
of the frames as the final sample appeared to be a good compromise.
Note that, in order to produce the curve of Fig. 6, visibilities were computed frame by frame (i.e. M=1). Thus, the semi-empirical calculation of the error bars given below in Sect. 5.3 does not work, and one has to use a full theoretical expression of the noise. From an analysis in Fourier space, Petrov et al. (2003) show that the theoretical error on the frame-by-frame visibility could be written:
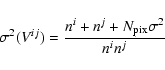 |
(41) |
Finally, despite fringe selection has been performed to deal at best with the uncalibratable VLTI vibrations, the dispersion of the selected visibilities still has to be quadratically added to the error bar arising from the fundamental noises (as computed in Sect. 5.3), in order to account for the reminiscent jitter attenuation, which has been reduced but not totally canceled out.
![\begin{figure}
\par\includegraphics[width=4.8cm,clip]{4799fig13.eps}
\end{figure}](/articles/aa/full/2007/10/aa4799-06/Timg137.gif) |
Figure 7:
Estimation of the raw squared visibility and its error-bars as a function of the wavelength for the observed calibrator
|
| Open with DEXTER | |
In order to validate the computation of the error bars, we used bootstrapping techniques (Efron & Tibshirani 1993). By making sampling with replacement, such a method constructs a large population of N elements (N estimated squared visibility) from the original measurements (M coherent and photometric fluxes). If N is large enough, the statistical parameters, i.e. the mean value and the dispersion of this population are converging toward the expected value and the root mean square of the estimated parameters, respectively. N large enough, these quantities can be calculated by fitting a Gaussian distribution p(V2) to the histogram of the bootstrapped population.
Figure 8 gives an example of the histogram and the resulting Gaussian fit. Using this method with N=500, we find for the same set of data
![]() ,
which is in excellent agreement with previous computation.
,
which is in excellent agreement with previous computation.
![\begin{figure}
\par\includegraphics[width=4.8cm,clip]{4799fig14.eps}
\end{figure}](/articles/aa/full/2007/10/aa4799-06/Timg140.gif) |
Figure 8: Histogram of the bootstrapped population of estimated squared visibilities for a given wavelength. The fit of this histogram by a Gaussian function is superimposed. The mean value and the root mean square of the Gaussian distribution give the statistics of the estimated visibility. |
| Open with DEXTER | |
Note that, although we observed this object in the low resolution mode with reasonably high flux, we find a relative error on the order of ![]() .
Such a large error bar is due to the atmospheric and intrumental jitter that, in the absence of fringe tracking, prevents an integration time from being longer than a few tenth of milliseconds. When this latter device will be available, we expect to lower this error below the
.
Such a large error bar is due to the atmospheric and intrumental jitter that, in the absence of fringe tracking, prevents an integration time from being longer than a few tenth of milliseconds. When this latter device will be available, we expect to lower this error below the ![]() level, down to
level, down to ![]() for the brightest cases (assuming perfect fringe tracking, see Petrov et al. 2007; Malbet et al. 1998). But it is not possible to achieve AMBER's ultimate performances at that time.
for the brightest cases (assuming perfect fringe tracking, see Petrov et al. 2007; Malbet et al. 1998). But it is not possible to achieve AMBER's ultimate performances at that time.
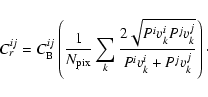 |
(42) |
| |
Figure 9:
Example of differential phases and closure
phase computation on an observed object with a rotating feature in
the
|
| Open with DEXTER | |
In the current situation, closure phases are computed using the estimator of Eq. (28), but a previous frame selection is performed before making the ensemble average of the bispectrum, because in all the data available there was a very low amount of frames that simultaneously presented three fringe patterns. We chose an empirical selection criterion as the product of the three individual fringe SNR criteria (as defined by Eq. (20)). Internal error bars the closure phases are computed statistically, taking the root mean square of all the individual frames divided by the square root of the number of frames (assuming statistical independence of the frames), since the estimations of the tested theoretical error bars do not give satisfactory results up to now.
An example of closure phase and closure phase error bars is given in
Fig. 9. The object is ![]() Arae,
which contains a rotating feature in the
Arae,
which contains a rotating feature in the
![]() emission line (Meilland et al. 2007).
A full description of how the closure phase and closure phase errors
are computed will be part of the second paper on the AMBER data reduction (Millour et al. 2007).
emission line (Meilland et al. 2007).
A full description of how the closure phase and closure phase errors
are computed will be part of the second paper on the AMBER data reduction (Millour et al. 2007).
![\begin{figure}
\par\includegraphics[width=15.4cm,clip]{4799fig16.eps}
\end{figure}](/articles/aa/full/2007/10/aa4799-06/Timg146.gif) |
Figure 10:
Piston estimation from the fringe
pattern. From left to right is (i) the raw fringe pattern, the
corresponding phase; (ii) the estimated linear component of the phase from the least square fit; and (iii) a piston time-sequence over 250 s. Note that the piston rms is around
|
| Open with DEXTER | |
The computation of the linear component of the differential phase; that is, the piston estimation is done on each spectral band separately (J, H, or K), using the least-square method described in Sect. 3.5.4. This algorithm was extensively tested on the sky and validated as a part of the observing software of the AMBER instrument. An example of the fitting process, as well as of the piston estimate is given in Fig. 10.
We have described the data reduction formalism of the AMBER/VLTI instrument, that is, the principles of the algorithm that lead to the computation of the AMBER observables. This innovative signal processing is performed in three main steps: (i) the calibration of the instrument, which provides the calibration matrix that gives the linear relationship between the interferogram and the complex visibility; (ii) the inversion of the calibration matrix to obtain the so-called P2VM matrix and then the complex visibility; and (iii) the estimation of the AMBER observables from the complex visibility, namely the squared visibility, the closure phase, and the differential phase.
Note that this analysis requires the calibration matrix to be both perfectly stable in time and very precise, i.e. recorded with a much higher SNR than the SNR of the interferograms. If the instrument is not stable between the calibration procedures and the observations, the P2VM will drift and, as a result, the estimated observables will be biased. And if the calibration is not precise enough, it will be the limiting factor for the SNR of the observables. For the latter problem, it is thus recommended to set, during the calibration process, an integration time that insures a P2VM accuracy at least a factor of 10 higher than the accuracy expected on the measurements. To check the former problem of stability, it is advised to record one P2VM before and one P2VM directly after the observation. This procedure allows us to quantify the drift of the instrument along the observations and to potentially reject the data if the drift appears to be significant. Note, however, that stability measurements in laboratory have shown the AMBER instrument to be generally stable on the hour scale at least.
Regarding the closure phase and the differential phase, we have produced the theoretical estimators arising from the specific technique of AMBER data reduction, as well as brief illustrations from real observations. A thorough analysis, including practical issues and performances, of these two observables, which deal the phase of the complex visibility, will be given in a forthcoming paper (Millour et al. 2007)
For the squared visibility, we have defined an estimator that is self-calibrated from the instrumental contrast and we have investigated its biases. The quadratic bias, which is an additive quantity and results in the quadratic estimation in the presence of zero-mean value additive noise, can be easily corrected, providing the computation of the error of the fringe measurements. Atmospheric and instrumental biases, which attenuate the visibility through multiplicative attenuation factors, come from (i) the high frequency fringe motion during the integration time - namely the jitter - and (ii) from the loss of spectral coherence when the fringes are not centered at the zero optical path difference - namely the atmospheric differential piston. The latter can be estimated from the differential phase and its consecutive attenuation can be corrected by knowing the shape of the spectral filter and the resolution of the spectrograph. When strictly arising from atmospheric turbulence, The former can be calibrated by a reference source, provided it has been observed shortly before/after the object of interest. When instrumental, hardly calibratable vibrations accumulate in the jitter phenomenon, as presently the case for the VLTI, we propose a method based on sample selection that allows reduction of the attenuation and the associated dispersion on the visibilities.
However at this point, because of the presence of these instrumental vibrations and because of the absence of the FINITO fringe tracker, it is possible neither to develop an optimized tool for identifying and calibrating the biases coming from the atmospheric turbulence nor to present an analysis of the ultimate performances of the AMBER/VLTI instrument. These points will be developed in our next paper on the AMBER data reduction methods, once the problems mentioned above, which are independent of the AMBER instrument, would have been resolved.
Acknowledgements
The AMBER projectwas founded by the French Centre National de la Recherche Scientifique (CNRS), the Max Planck Institute für Radioastronomie (MPIfR) in Bonn, the Osservatorio Astrofisico di Arcetri (OAA) in Firenze, the French Region "Provence Alpes Côte D'Azur'' and the European Southern Observatory (ESO). The CNRS funding has been made through the Institut National des Sciences de l'Univers (INSU) and its Programmes Nationaux (ASHRA, PNPS, PNP).
The OAA co-authors acknowledge partial support from MIUR grants to the Arcetri Observatory: A LBT interferometric arm, and analysis of VLTI interferometric data and From Stars to Planets: accretion, disk evolution and planet formation and from INAF grants to the Arcetri Observatory Stellar and Extragalactic Astrophysics with Optical Interferometry. C. Gil work was supported in part by the Fundação para a Ciência e a Tecnologia through project POCTI/CTE-AST/55691/2004 from POCTI, with funds from the European program FEDER.
The preparation and interpretation of AMBER observations benefit from the tools developed by the Jean-Marie Mariotti Center for optical interferometry JMMC
and from the databases of the Centre de Données Stellaires (CDS) and of the Smithsonian/NASA Astrophysics Data System (ADS).
The data reduction software amdlib is freely available on the AMBER site http://amber.obs.ujf-grenoble.fr. It has been linked to the public domain software Yorick
to provide the user-friendly interface ammyorick.