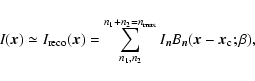 |
(1) |
A&A 463, 1215-1225 (2007)
DOI: 10.1051/0004-6361:20066259
P. Melchior1 - M. Meneghetti1,2 - M. Bartelmann1
1 - Zentrum für Astronomie, ITA, Universität Heidelberg,
Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
2 - INAF-Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
Received 17 August 2006 / Accepted 6 December 2006
Abstract
Aims. We discuss the applicability and reliability of the shapelet technique for scientific image analysis.
Methods. We quantify the effects of non-orthogonality of sampled shapelet basis functions and misestimation of shapelet parameters. We perform the shapelet decomposition on artificial galaxy images with underlying shapelet models and galaxy images from the GOODS survey, comparing the publicly available IDL implementation with our new C++ implementation.
Results. Non-orthogonality of the sampled basis functions and misestimation of the shapelet parameters can cause substantial misinterpretation of the physical properties of the decomposed objects. Additional constraints, image preprocessing and enhanced precision have to be incorporated in order to achieve reliable decomposition results.
Key words: methods: data analysis - techniques: image processing - surveys
Refregier (2003) proposed the "shapelets'' function set, composed of a scalable version of the eigenfunctions of the harmonic oscillator in quantum mechanics. They form an orthonormal basis set of Gauss-Hermite polynomials. Because of their continuity, finite extent and their smooth peaks, they offer themselves for decomposing galaxy images or the like. In particular, they were proposed as an image processing and analysis technique for weak-lensing studies (Chang et al. 2004; Refregier & Bacon 2003; Heymans et al. 2006; Kuijken 2005; Massey et al. 2005,2006; Goldberg & Bacon 2005), morphological classification of galaxies (Kelly & McKay 2004) and Sun spots (Young et al. 2005), and also in the field of medical computer tomography (Weissman et al. 2004).
So far, the shapelet technique has proven to reconstruct the decomposed objects from the set of expansion coefficients in a way which looks visually good; i.e. differences to the originals are marginal (Refregier 2003). Massey & Refregier (2005) defined a goodness-of-fit measure to quantify, what a good reconstruction means: the residuals have to be at noise level. For achieving that, the decomposition has to be optimized with respect to a set of parameters. As the parameter space is highly degenerate, additional constraints are necessary to choose a particular point in this space. But it is yet unknown, if the selection of these constraints or the accuracy with which their fulfillment is verified introduces an uncertainty in or even a bias on the expansion coefficients. In fact, every study of object properties derived from shapelet coefficients might be affected by a yet unclear error contribution.
Another object of concern is the computational complexity. Since the shapelet method is known to be slow compared to other image analysis techniques, it is important to find ways to speed up the execution.
This paper is organized as follows: In Sect. 2, we summarize the basic relations for the shapelet function set and describe the procedure for finding optimal decomposition parameters. In Sect. 3, we discuss potential problems that can arise from the optimized decomposition procedure. In Sect. 4, we show how these problems can be remedied by means of additional constraints and image preprocessing. In Sect. 5, we compare the design choices, the decomposition results (of artificial and observed galaxy images), the errors made by and the computational performance of two shapelet implementations, the publicly available IDL code and our independently developed C++ code. We conclude in Sect. 6.
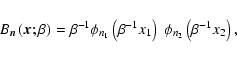 |
(2) |
![\begin{displaymath}\phi_{n}(x) = \left[2^n \pi^{\frac{1}{2}} n!\right]^{-\frac{1}{2}}\ H_n(x) {\rm e}^{-\frac{{x^2}}{2}},
\end{displaymath}](/articles/aa/full/2007/09/aa6259-06/img30.gif) |
(3) |
These definitions imply that the shapelets' operating range is limited by
After the decomposition, one can derive all information that depends on the brightness distribution of an object in the much smaller shapelet space instead of the real space, thus saving memory and
computation time. The equation relating the shapelet coefficients to the flux (or other quantities such as the centroid position) is given
by Refregier (2003),
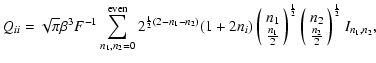 |
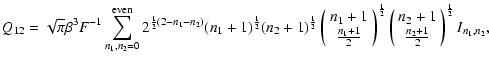 |
(6) |
Equation (1) shows that a shapelet decomposition depends on four external parameters: the scale size ![]() ,
the maximum shapelet order
,
the maximum shapelet order ![]() and the two components
of the centroid position
and the two components
of the centroid position
![]() .
The essential task for achieving a faithful shapelet decomposition is finding optimal values for these parameters, such that the residual between the original image and its reconstruction from shapelet coefficients is minimized.
.
The essential task for achieving a faithful shapelet decomposition is finding optimal values for these parameters, such that the residual between the original image and its reconstruction from shapelet coefficients is minimized.
Massey & Refregier (2005) defined a goodness-of-fit function
The number of coefficients is related to ![]() via Eq. (1):
via Eq. (1):
Since Eq. (8) is linear in the unknown shapelet coefficients
![]() ,
we can solve analytically for their values when
,
we can solve analytically for their values when ![]() is minimal (e.g. Frieden 1983),
is minimal (e.g. Frieden 1983),
Thus, optimizing the decomposition means finding the set of parameters for which ![]() becomes unity. One has to consider, though, that
becomes unity. One has to consider, though, that ![]() is a discrete parameter, which forbids using minimization algorithms for continuous parameters, but in turn restricts the parameter space
severely. In addition, one must investigate whether the parameter set can be determined uniquely.
is a discrete parameter, which forbids using minimization algorithms for continuous parameters, but in turn restricts the parameter space
severely. In addition, one must investigate whether the parameter set can be determined uniquely.
Massey & Refregier (2005) suggested the following procedure: Starting with
![]() ,
the value of
,
the value of ![]() is searched where
is searched where
![]() as defined in Eq. (8) is a slowly varying continuous function for the majority of images (see Fig. 4). This allows an easy and fast decomposition of objects, yielding reconstructions that look visually good and have low
as defined in Eq. (8) is a slowly varying continuous function for the majority of images (see Fig. 4). This allows an easy and fast decomposition of objects, yielding reconstructions that look visually good and have low ![]() .
The
question arises if the decomposition is in all cases able to extract the physical
information correctly. We show two classes of potential problems, where physical properties of the decomposed objects are indeed incorrectly measured. One class is related to the violation of the orthonormality condition of the shapelet basis functions, the other one regards misestimation of the shapelet parameters.
.
The
question arises if the decomposition is in all cases able to extract the physical
information correctly. We show two classes of potential problems, where physical properties of the decomposed objects are indeed incorrectly measured. One class is related to the violation of the orthonormality condition of the shapelet basis functions, the other one regards misestimation of the shapelet parameters.
Adopting the methodology of Berry et al. (2004), we explore the domains of non-orthonormality by inspecting the diagonal and non-diagonal entries of the covariance matrix.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6259_01.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg49.gif) |
Figure 1:
Largest (dashed, blue) and smallest (solid, black) diagonal elements of the covariance matrix MT M as a function of |
| Open with DEXTER | |
To make things worse, undersampling is essentially equivalent to random sampling (Berry et al. 2004). Since oscillations of the basis functions appear on smaller scales than the grid spacing, small shifts of the grid points can lead to arbitrary differences in the function values.
Massey & Refregier (2005) suggested a way of dealing with undersampling: instead of using vectors sampled at certain grid points, the value from integrating the basis functions within each pixel should be used. But this approach also leads to non-orthogonal basis vectors, independent of the scale size (see dotted curve in Fig. 2).
![\begin{figure}
\par\includegraphics[width=8.8cm]{6259_02.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg51.gif) |
Figure 2:
Largest non-diagonal element of the covariance matrix MT M as a function of |
| Open with DEXTER | |
Another problem arises when the scale size is too large for the shapelet basis functions to be contained inside the image. Since the shapelets need infinite support for their
orthonormality, power will be lost due to truncation at the image boundaries, as shown by the lower curve in Fig. 1 at high ![]() .
Again, also the orthogonality is violated in this domain (see. Fig. 2).
.
Again, also the orthogonality is violated in this domain (see. Fig. 2).
Massey & Refregier (2005) mention the possibility of fitting the sky background
brightness by adding a constant function to the set of the shapelet basis functions. As can be seen from the dashed curve in Fig. 2, this again violates orthogonality
globally. This means, it introduces covariances between the coefficients even in such domains of ![]() where the shapelet basis functions themselves remain orthogonal.
where the shapelet basis functions themselves remain orthogonal.
As mentioned in Sect. 2, the set of external shapelet parameters will not be uniquely defined (see the degeneracy region with
![]() in Fig. 4).
We need to specify which set should be chosen. This choice will affect the shapelet coefficients and the quantities derived from them. Quantifying the impact of parameter misestimation on the results of the shapelet decomposition is the aim of this section.
in Fig. 4).
We need to specify which set should be chosen. This choice will affect the shapelet coefficients and the quantities derived from them. Quantifying the impact of parameter misestimation on the results of the shapelet decomposition is the aim of this section.
For this purpose, a visually selected galaxy from the GOODS CDF South (Fig. 3) was decomposed until ![]() was compatible with unity (with minimal
was compatible with unity (with minimal ![]() ). Then,
starting from the optimal values (
). Then,
starting from the optimal values (
![]() fixed from the image; cf. Fig. 4), the decomposition was repeated with varied external parameters. For each decomposition, the flux and the ellipticity (defined by Eq. (7)) were derived from the shapelet coefficients together with the
fixed from the image; cf. Fig. 4), the decomposition was repeated with varied external parameters. For each decomposition, the flux and the ellipticity (defined by Eq. (7)) were derived from the shapelet coefficients together with the ![]() of the fit.
of the fit.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6259_03.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg53.gif) |
Figure 3:
Example galaxy from GOODS CDF South. The image was chosen because of its typical deep field signal-noise-ratio and its significant substructure. The image size is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6259_04.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg55.gif) |
Figure 4:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=0.7\textheight]{6259_05.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg56.gif) |
Figure 5:
Impact of the variation of |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[height=0.7\textheight]{6259_06.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg57.gif) |
Figure 6:
Impact of the variation of |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[height=0.7\textheight]{6259_07.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg58.gif) |
Figure 7:
Impact of the variation of
|
| Open with DEXTER | |
The maximum order ![]() was varied between 0 and 20. In each case, the centroid was fixed, and
was varied between 0 and 20. In each case, the centroid was fixed, and ![]() was chosen to minimize
was chosen to minimize ![]() at the given
at the given ![]() according to Eq. (11). As expected, the fit improves with increasing
according to Eq. (11). As expected, the fit improves with increasing ![]() (top panel of Fig. 5).
(top panel of Fig. 5).
As can be seen in the middle panel of Fig. 5, the flux
will be underestimated for low ![]() due to the lack of substructures represented in the reconstruction. On the other hand, the reconstruction tends to pick up smaller noise features farther away from the center when
due to the lack of substructures represented in the reconstruction. On the other hand, the reconstruction tends to pick up smaller noise features farther away from the center when ![]() exceeds the preferred value
exceeds the preferred value
![]() .
Thus the flux and especially the ellipticity (bottom panel of Fig. 5) become noisy at high
.
Thus the flux and especially the ellipticity (bottom panel of Fig. 5) become noisy at high ![]() .
The correlation of the two components of the ellipticity originates from the orientation of the galaxy along the top-right to bottom-left direction.
.
The correlation of the two components of the ellipticity originates from the orientation of the galaxy along the top-right to bottom-left direction.
Obviously, setting the maximum order to an arbitrary value will cause a misestimation of
the coefficients and the derived quantities if the selected ![]() was too low to represent the entire object or too high to remain unbiased by surrounding noise.
was too low to represent the entire object or too high to remain unbiased by surrounding noise.
From the top panel of Fig. 6, one can conclude that ![]() is not strongly affected by a change in
is not strongly affected by a change in ![]() :
the largest values are
:
the largest values are
![]() .
The shapelet
decomposition is obviously able to cope with a mispredicted scale size and yet provides visually good-looking reconstructions. Minimizing
.
The shapelet
decomposition is obviously able to cope with a mispredicted scale size and yet provides visually good-looking reconstructions. Minimizing ![]() w.r.t.
w.r.t. ![]() is fortunately
simple due to the lack of local minima and the smoothness of the curve, but crucial because of the non-trivial dependence of the other quantities on
is fortunately
simple due to the lack of local minima and the smoothness of the curve, but crucial because of the non-trivial dependence of the other quantities on ![]() .
.
The misestimation of the flux (middle panel of Fig. 6) for
![]() is easily understood: since the central peak is most significant, the peak height is essentially fixed for each reconstruction. If
is easily understood: since the central peak is most significant, the peak height is essentially fixed for each reconstruction. If
![]() ,
the reconstruction peaks sharply, falls off too fast and misses the outer parts of the object, thus the flux is underestimated. If
,
the reconstruction peaks sharply, falls off too fast and misses the outer parts of the object, thus the flux is underestimated. If
![]() ,
the central peak becomes broader and the outer
regions of the reconstructions are too bright, thus the flux is overestimated.
,
the central peak becomes broader and the outer
regions of the reconstructions are too bright, thus the flux is overestimated.
The variation of the ellipticity estimator (bottom panel of Fig. 6) is also problematic. Since increasing ![]() at constant
at constant ![]() increases
increases
![]() (cf. (4)), we see a similar behavior as before in the bottom panel of
Fig. 5, where
(cf. (4)), we see a similar behavior as before in the bottom panel of
Fig. 5, where ![]() was increased: Due to the intrinsic orientation of the galaxy, both components of the ellipticity are correlated. With
was increased: Due to the intrinsic orientation of the galaxy, both components of the ellipticity are correlated. With
![]() ,
the model is more compact and the ellipticity is dominated by the galactic core which has excess flux top-right of the center. With
,
the model is more compact and the ellipticity is dominated by the galactic core which has excess flux top-right of the center. With
![]() ,
the outer parts become more important;
because of excess flux far below the center the
,
the outer parts become more important;
because of excess flux far below the center the
![]() flip
sign but remain correlated.
flip
sign but remain correlated.
In order to clarify if the determination of the centroid can safely be done during the iterations of the optimized decomposition without biasing the outcome, both components
![]() were varied by 5 pixels, thus moving the centroid along a straight line from
were varied by 5 pixels, thus moving the centroid along a straight line from
![]() to
to
![]() .
The other parameters
were kept fixed.
.
The other parameters
were kept fixed.
As the top panel of Fig. 7 shows, the
goodness-of-fit is not
affected very much; largest values are
![]() .
Interestingly,
the
.
Interestingly,
the ![]() minimum is not at the optimal value (determined by calculating the centroid in real space), but rather shifted by roughly one pixel towards the top right corner of
the image. This indicates that the optimized decomposition procedure (suggested by Massey & Refregier (2005) and outlined in Sect. 2) tends to
converge to a slightly different centroid. In this case, the fit improves (lower
minimum is not at the optimal value (determined by calculating the centroid in real space), but rather shifted by roughly one pixel towards the top right corner of
the image. This indicates that the optimized decomposition procedure (suggested by Massey & Refregier (2005) and outlined in Sect. 2) tends to
converge to a slightly different centroid. In this case, the fit improves (lower ![]() ), but it no longer represents the imaged object because the centroid is readjusted under the assumption that the object (without noise) can be perfectly represented by the employed shapelet model. This assumption is not satisfied in general.
), but it no longer represents the imaged object because the centroid is readjusted under the assumption that the object (without noise) can be perfectly represented by the employed shapelet model. This assumption is not satisfied in general.
The underestimation of the flux is ![]() 8% (middle panel of Fig. 7). If the center is misaligned, the flux is underestimated due the loss of regions in the reconstruction far away from the new center. The rise of
8% (middle panel of Fig. 7). If the center is misaligned, the flux is underestimated due the loss of regions in the reconstruction far away from the new center. The rise of
![]() at high
at high
![]() indicates a positive flux region on the top-right side of the galaxy, which can be confirmed by inspecting Fig. 3.
indicates a positive flux region on the top-right side of the galaxy, which can be confirmed by inspecting Fig. 3.
The ellipticity estimator is highly problematic and rather unpredictable (bottom panel of Fig. 7), because its deviation depends on the orientation of the object w.r.t. the image borders.
The first three solutions tackle problems related to the non-orthogonality of the basis functions, the last three show how optimal shapelet parameters can be found and how a realistic error estimate for the shapelet coefficients can be performed.
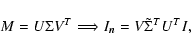 |
(12) |
This approach accounts for the non-orthogonality of the basis set, caused by e.g. severe truncation at the image boundary or inclusion of a non-orthogonal element. The drawback of the SVD approach is its memory consumption: since M is a matrix with dimensions
![]() ,
the matrix U has the dimensions
,
the matrix U has the dimensions
![]() .
For typically sized images this amounts to matrices sized of the order of 100 MB, rendering the implementation inacceptably slow for most purposes.
.
For typically sized images this amounts to matrices sized of the order of 100 MB, rendering the implementation inacceptably slow for most purposes.
Since potentially more than one object is contained in the image, the
overall image has to be segmented in a next step such that each frame
contains only one object. SE XTRACTOR or equivalents
accomplish this by grouping pixels above certain brightness
thresholds. If other objects overlap with this frame, they have to
be masked with noise whose features were determined in the previous step.
Otherwise the locality condition for the shapelet decomposition
- meaning that the decomposed object is centered at
![]() and has
a limited extent - will be violated and the physical information
obtained from this "combined'' object will be corrupted by the
appearance of the other objects.
and has
a limited extent - will be violated and the physical information
obtained from this "combined'' object will be corrupted by the
appearance of the other objects.
Note that no noise-removal step has to (and should) be done by arbitrarily discriminating between the object of interest and the surrounding noise. The great benefit of the shapelet technique is that the optimized decomposition itself will provide this discrimination better than any simple object-finding algorithm, since it reproduces the actual shape of the object instead of e.g. convolving the image with predefined kernels. In fact, procedures similar to the shapelet decomposition (e.g. wavelet decomposition) have been proposed to tackle this problem in a more quantitative way (Bertin 2005).
Very faint and small objects that are decomposed with very low ![]() and
and ![]() must be rejected. Fortunately, these objects carry little physical information.
must be rejected. Fortunately, these objects carry little physical information.
The decomposition of objects with high ![]() must use large
must use large ![]() .
Since the oscillations of the basis functions can then appear on sub-pixel scales, their sampling becomes essentially random. As Massey & Refregier (2005) suggested, one can get rid of this by applying the additional constraint
.
Since the oscillations of the basis functions can then appear on sub-pixel scales, their sampling becomes essentially random. As Massey & Refregier (2005) suggested, one can get rid of this by applying the additional constraint
The opposite case of
![]() becoming large compared to the image dimensions can easily be prevented by placing the object inside a frame that is large enough. This can simply be done during the image segmentation step. The additional border size should be proportional to the object's extent, have a lower bound of the order of 10 pixels and be made such that the frame becomes
square, since the extent of the shapelets is identical along both dimensions. If the object is close to the image boundary such that the frame border cannot be created from the image pixels alone, the missing pixels should be set according to the local noise characteristics.
The inclusion of the additional frame border also helps to remedy the degree-of-freedom singularity:
The form of Eq. (8) demands the additional constraint
becoming large compared to the image dimensions can easily be prevented by placing the object inside a frame that is large enough. This can simply be done during the image segmentation step. The additional border size should be proportional to the object's extent, have a lower bound of the order of 10 pixels and be made such that the frame becomes
square, since the extent of the shapelets is identical along both dimensions. If the object is close to the image boundary such that the frame border cannot be created from the image pixels alone, the missing pixels should be set according to the local noise characteristics.
The inclusion of the additional frame border also helps to remedy the degree-of-freedom singularity:
The form of Eq. (8) demands the additional constraint
Apart from the fact that fixing the centroid does not assume a particular galaxy model, it eases the minimization of ![]() w.r.t.
w.r.t. ![]() because any recentering induces distortions the simplex algorithm has to compensate in order to converge.
because any recentering induces distortions the simplex algorithm has to compensate in order to converge.
We will show in Sect. 5.3 that the error of the centroid determination with our approach and the iterative recentering approach of Massey & Refregier (2005) is ![]() 0.5 pixels (we employed shapelet models for the galaxies there) which is the expected uncertainty due to pixelization of the image.
0.5 pixels (we employed shapelet models for the galaxies there) which is the expected uncertainty due to pixelization of the image.
This can be easily realized by not applying any limit on ![]() .
Unfortunately, the two constraints Eqs. (13) and (14) impose such a limit in special cases, leaving
.
Unfortunately, the two constraints Eqs. (13) and (14) impose such a limit in special cases, leaving
![]() .
The reconstruction can well be visually good, but not all physical information can be extracted or trusted. These objects should therefore be classified as "silver'', in contrast to the "golden'' ones which obey Eq. (15). For a follow-up analysis, one could then decide whether the "silver'' sample should be used or the selection should be restricted to the "gold'' sample.
.
The reconstruction can well be visually good, but not all physical information can be extracted or trusted. These objects should therefore be classified as "silver'', in contrast to the "golden'' ones which obey Eq. (15). For a follow-up analysis, one could then decide whether the "silver'' sample should be used or the selection should be restricted to the "gold'' sample.
Equation (15) also states that ![]() has to be minimal. It is thus insufficient to find a point in parameter space with
has to be minimal. It is thus insufficient to find a point in parameter space with
![]() ,
but one
has to ensure that this parameter set is also the one with the lowest possible
,
but one
has to ensure that this parameter set is also the one with the lowest possible ![]() .
In practice this requires additional iterations at lower
.
In practice this requires additional iterations at lower ![]() .
Condition (15) thus also prefers Eq. (11) to be fulfilled, but this has to be ensured separately.
.
Condition (15) thus also prefers Eq. (11) to be fulfilled, but this has to be ensured separately.
A flattening condition for limiting ![]() when
when ![]() does not improve significantly should not be used because it would lead to an incomplete optimization when
does not improve significantly should not be used because it would lead to an incomplete optimization when ![]() is not strictly monotonically decreasing with
is not strictly monotonically decreasing with ![]() ,
e.g. due to a faint satellite at the object's boundary.
,
e.g. due to a faint satellite at the object's boundary.
Additional - fortunately independent - errors are introduced by the lack of knowledge on the optimal parameter set. If the centroid position is fixed, one can assume its error to vanish
(which is not exactly true, see Sect. 5.3).
The same is true for the error of ![]() when the minimizer converged,
obeying condition Eq. (15). The simplex minimizer for finding
when the minimizer converged,
obeying condition Eq. (15). The simplex minimizer for finding ![]() (fulfilling Eq. (11)) stops when it has localized
(fulfilling Eq. (11)) stops when it has localized ![]() within a previously defined interval. Therefore,
within a previously defined interval. Therefore, ![]() will only be known up to an uncertainty
will only be known up to an uncertainty
![]() that should, of course, be very small, maybe on the order of 1%. Additional uncertainty in
that should, of course, be very small, maybe on the order of 1%. Additional uncertainty in ![]() is introduced by pixel noise and pixelization, so that we expect the actual
is introduced by pixel noise and pixelization, so that we expect the actual
![]() to be somewhat larger.
to be somewhat larger.
The question then arises how
![]() can be translated
into an uncertainty in the shapelet coefficients. The answer to this
question can be obtained by using the rescaling operation, given
in Appendix A of Refregier (2003), which describes the change of the
shapelet coefficients due to a change of the scale size.
Assuming
can be translated
into an uncertainty in the shapelet coefficients. The answer to this
question can be obtained by using the rescaling operation, given
in Appendix A of Refregier (2003), which describes the change of the
shapelet coefficients due to a change of the scale size.
Assuming ![]() will for sure be within a 10% interval
(this assumption will be justified in
Sect. 5.3), one could identify the change
of each individual coefficient by corresponding
rescaling with a 3-
will for sure be within a 10% interval
(this assumption will be justified in
Sect. 5.3), one could identify the change
of each individual coefficient by corresponding
rescaling with a 3-![]() error. In contrast to the error introduced by
uncorrelated pixel noise, the uncertainty in
error. In contrast to the error introduced by
uncorrelated pixel noise, the uncertainty in ![]() will in general affect
coefficients differently. As we will also show in
Sect. 5.3, this error will be the dominant
contribution to the coefficient error.
will in general affect
coefficients differently. As we will also show in
Sect. 5.3, this error will be the dominant
contribution to the coefficient error.
Furthermore, we decided to define our implementation as a C++ library, such that other codes that need the shapelet method can easily link with it. This approach is not possible with IDL because IDL scripts are interpreted and therefore not executables in their own right.
In particular, our implementation performs the following steps to decompose images, employing the solutions pointed out in Sect. 4. For the task of estimating the noise characteristics and segmenting the image into frames, SE XTRACTOR is the standard choice in astronomy. Unfortunately, it is not available as library, only as standalone executable. Since we did not want our library to use system calls, we decided to implement algorithms similar to those in SE XTRACTOR in our library. Thus, the whole image preprocessing (noise estimation and subtraction, image segmentation and removal of overlapping objects) is done internally in our code, before the object's frame is passed to the shapelet decomposition. Also, the centroid of the object is directly computed from the cleaned frame.
For the determination of the shapelet coefficients, we use the ![]() method (see Sect. 2); the SVD method is also implemented, but not used as default. We optimize the parameters
method (see Sect. 2); the SVD method is also implemented, but not used as default. We optimize the parameters ![]() and
and ![]() ,
which have to fulfill the constraints given by
Eqs. (11) and (13)-(15). We
pay particular attention to find the lowest possible
,
which have to fulfill the constraints given by
Eqs. (11) and (13)-(15). We
pay particular attention to find the lowest possible ![]() .
.
![]() remains fixed at the value derived from the cleaned frame. After the convergence of the minimizer, the errors on the
shapelet coefficients are computed from the pixel noise and the uncertainty in
remains fixed at the value derived from the cleaned frame. After the convergence of the minimizer, the errors on the
shapelet coefficients are computed from the pixel noise and the uncertainty in ![]() (see Sect. 4.6). If the decomposition violates condition (15), the object is classified as "silver'' so that it can be excluded from the further analysis. A flattening condition is not employed.
(see Sect. 4.6). If the decomposition violates condition (15), the object is classified as "silver'' so that it can be excluded from the further analysis. A flattening condition is not employed.
In both cases, in order to guarantee the comparability of the implementations, the images were cut to contain the object of interest in a square frame, large enough not to run into the problem of boundary truncation - the IDL code was modified such that it does not further cut the frame. The noise characteristics were estimated using our noise algorithm and then passed to both shapelet codes. We can thus focus on the optimization procedure employed by the different codes.
Kelly & McKay (2004) identified the ten most powerful (i.e. largest on average) shapelet coefficients of galaxy images from SDSS. Using these coefficients and their
variances, we defined a multivariate Gaussian probability distribution. To create more individual galaxy shapes, we included minor coefficients, whose variance was chosen to be smaller than of the major ones; their mean was set to zero. Sampling from this probability distribution, we
generated 1000 flux-normalized galaxy images with
![]() and
and
![]() .
To each of these shapelet models, we applied a moderate level of Gaussian noise with zero mean and constant standard deviation of
.
To each of these shapelet models, we applied a moderate level of Gaussian noise with zero mean and constant standard deviation of
![]() .
.
We then decomposed these images into shapelets using the IDL code and our C++ implementation with
![]() and
and
![]() .
These restrictions are quite loose, but helpful to constrain the parameter space for this comparison.
.
These restrictions are quite loose, but helpful to constrain the parameter space for this comparison.
![\begin{figure}
\par\includegraphics[height=8.8cm]{6259_08.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg96.gif) |
Figure 8:
Comparison of the final decomposition |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=8.6cm]{6259_09.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg98.gif) |
Figure 9:
Comparison of the final decomposition |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=8.6cm]{6259_10.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg99.gif) |
Figure 10:
Comparison of the final decomposition
|
| Open with DEXTER | |
Generally speaking, both implementations are able to decompose the given images with a ![]() near unity as required (see Fig. 8). The IDL version typically needs
higher orders to achieve the same goodness-of-fit: The mean
near unity as required (see Fig. 8). The IDL version typically needs
higher orders to achieve the same goodness-of-fit: The mean ![]() for C++ is 9.79, but 11.97 for IDL (see Fig. 9). Both implementations tend to higher
for C++ is 9.79, but 11.97 for IDL (see Fig. 9). Both implementations tend to higher ![]() than the underlying shapelet model because noise can obscure the smallest features of the model most effectively, requiring higher additional shapelet modes to correct for that.
than the underlying shapelet model because noise can obscure the smallest features of the model most effectively, requiring higher additional shapelet modes to correct for that.
The other optimized shapelet parameter is the scale size ![]() .
In Fig. 10, the scale size of the decomposition results is compared to the one of the underlying shapelet model. For both implementations one can clearly see a correlation, with significantly larger scatter in the IDL case. Interestingly, the images for which the IDL decomposition misestimates the scale size considerably form the group of images with
.
In Fig. 10, the scale size of the decomposition results is compared to the one of the underlying shapelet model. For both implementations one can clearly see a correlation, with significantly larger scatter in the IDL case. Interestingly, the images for which the IDL decomposition misestimates the scale size considerably form the group of images with
![]() ,
the maximum allowed order. This
shows that a misprediction of the scale size is compensated by using higher shapelet orders.
,
the maximum allowed order. This
shows that a misprediction of the scale size is compensated by using higher shapelet orders.
To quantify the overall quality of the decomposition, we computed the mean and the Pearson correlation coefficient for several quantities of the model with the decomposition output (see Table 1). It becomes obvious from these numbers that the decomposition results are more reliable in the C++ than in the IDL implementation, regarding both the value of the external shapelet parameters and the quantities derived from the shapelet coefficients.
Table 1:
Means and Pearson correlation coefficient
![]() of the decomposition order
of the decomposition order ![]() ,
the scale size
,
the scale size ![]() ,
the flux F, the components of the ellipticity
,
the flux F, the components of the ellipticity ![]() ,
and the axis ratio r of the true shapelet model (denoted by 0) and the reconstruction using the two implementations.
,
and the axis ratio r of the true shapelet model (denoted by 0) and the reconstruction using the two implementations.
![]() is the mean distance in shapelet space between the true model and the reconstructions (defined in 16). In the last line the mean centroid shift between the model and the reconstruction is given; consider that the IDL implementation iteratively corrects the centroid, whereas the C++ implementation keeps it fixed.
is the mean distance in shapelet space between the true model and the reconstructions (defined in 16). In the last line the mean centroid shift between the model and the reconstruction is given; consider that the IDL implementation iteratively corrects the centroid, whereas the C++ implementation keeps it fixed.
![\begin{figure}
\par\includegraphics[height=8.6cm]{6259_11.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg110.gif) |
Figure 11:
Comparison of the final decomposition |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=8.6cm]{6259_12.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg111.gif) |
Figure 12:
Comparison of the final decomposition |
| Open with DEXTER | |
We selected 2660 galaxies from GOODS subject to the constraint that the object frame does not contain more than 10 000 pixels. The reason for this selection is twofold: The speed of the code scales at least linearly with the number of pixels, so we wanted to keep the procedure reasonably fast, and the typical objects for shapelet decomposition (e.g. in weak lensing studies) are faint and rather small.
The noise mean and variance were estimated using our noise algorithm. The noise mean was subtracted from the images before decomposition; the noise variance was passed to the shapelet codes.
As can be seen from Fig. 11, both implementations are able to achieve a reconstruction with
![]() .
There is a clear cutoff at
.
There is a clear cutoff at
![]() for the C++ code that is less prominent for the IDL code. This could be due to the use of a flattening condition during the optimization procedure in the IDL code, which allows higher
for the C++ code that is less prominent for the IDL code. This could be due to the use of a flattening condition during the optimization procedure in the IDL code, which allows higher ![]() if the residuals do not reduce significantly when increasing
if the residuals do not reduce significantly when increasing ![]() .
.
The comparison of the maximal orders shows a clear correlation which has to be expected from the two implementations, since it shows that both use low order for small and faint objects and higher order for brighter and bigger objects (see Fig. 12). Again, with IDL there is a larger
fraction of objects at the
![]() limit, but the trend is not as clear as with the simulated images.
limit, but the trend is not as clear as with the simulated images.
![\begin{figure}
\includegraphics[height=8.6cm]{6259_13.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg114.gif) |
Figure 13:
Comparison of the final decomposition
|
| Open with DEXTER | |
The most surprising comparison is the one of the final scale sizes (see Fig. 13). We can see the expected spread, but there is an alignment of data points along constant
![]() .
For some reason, the IDL optimization procedure prefers some values of
.
For some reason, the IDL optimization procedure prefers some values of ![]() ,
although this is a free and continuous parameter. This effect could explain the generally larger scatter of
,
although this is a free and continuous parameter. This effect could explain the generally larger scatter of
![]() for the simulated images, too. As we have discussed in Sect. 3.2, the result of such an inconsistency will affect the whole optimization outcome and therefore the quality and reliability of any follow-up analysis based on shapelet coefficients.
for the simulated images, too. As we have discussed in Sect. 3.2, the result of such an inconsistency will affect the whole optimization outcome and therefore the quality and reliability of any follow-up analysis based on shapelet coefficients.
With the simulated galaxy images and the decomposition results of the two codes at hand (cf. Sect. 5.2.1), we can investigate which effect gives rise to what kind of error.
![\begin{figure}
\par\includegraphics[width=8.8cm]{6259_14.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg115.gif) |
Figure 14:
Distribution of centroid errors for simulated images with underlying shapelet models. The centroid is obtained from the optimized shapelet coefficients. Only decompositions with
|
| Open with DEXTER | |
It seems reasonable to assume that the uncertainty in the shapelet parameters percolates through the decomposition process and creates the scatter in the quantities derived from shapelet coefficients. But the misestimation of the shapelet parameters can also create systematic biases: Figs. 6 and 7 clearly show that it is quite likely to underestimate the flux F if ![]() is underestimated or the centroid
is underestimated or the centroid
![]() is shifted away from its optimal value; exactly this behavior is conspicuous in the IDL results.
is shifted away from its optimal value; exactly this behavior is conspicuous in the IDL results.
When we compare the distribution of centroid determination errors
![]() (see Fig. 14 and last line of Table 1), we can clearly see that both codes are affected by a mean uncertainty of
(see Fig. 14 and last line of Table 1), we can clearly see that both codes are affected by a mean uncertainty of ![]() 0.5 pixels, which is compatible with the expected impact of pixelization. It shows that the procedure of fixing the centroid from the pixel data (as suggested in Sect. 4.4) produces errors which are not significantly larger than when the centroid is an optimized parameter, even when the galaxy model is a shapelet model.
0.5 pixels, which is compatible with the expected impact of pixelization. It shows that the procedure of fixing the centroid from the pixel data (as suggested in Sect. 4.4) produces errors which are not significantly larger than when the centroid is an optimized parameter, even when the galaxy model is a shapelet model.
Thus, the underestimation of F in the IDL results must have different reasons. The distribution of the relative error
![]() in Fig. 15 shows again the larger scatter for
in Fig. 15 shows again the larger scatter for
![]() but also reveals its slight underestimation, e.g. the maximum bin is at
but also reveals its slight underestimation, e.g. the maximum bin is at
![]() ,
which could give rise to an underestimated F.
,
which could give rise to an underestimated F.
The distribution of
![]() in the C++ results has roughly a Gaussian shape in the center but broad wings at both sides. When we set the
in the C++ results has roughly a Gaussian shape in the center but broad wings at both sides. When we set the
![]() intervals such that they
correspond to 68%, 95% and 99% confidence limits, we obtain
intervals such that they
correspond to 68%, 95% and 99% confidence limits, we obtain
![]() and
and
![]() .
.
![]() is the value we employed for the estimation of
is the value we employed for the estimation of
![]() in Sect. 4.6.
in Sect. 4.6.
Since we know the coefficients of the underlying shapelet model I0, we can quantify the error of the obtained shapelet coefficients in shapelet space by the simple Euclidean metric
![\begin{figure}
\par\includegraphics[width=8.8cm]{6259_15.eps}\end{figure}](/articles/aa/full/2007/09/aa6259-06/Timg128.gif) |
Figure 15:
Distribution of relative |
| Open with DEXTER | |
After calibrating the strength of the different machines, it was interesting to see what performance benefit could be gained by the use of C++ (see Table 2).
Although our code tests more strictly whether the set of shapelet parameters used for the decomposition actually obeys Eq. (15) and thus needs more iterations, it outperforms the IDL code significantly, showing speedup factors between 5 and 14. Most of the performance gain is probably due to the fact that, in terms of computation time, IDL is not well suited for moderate to large numerical problems.
Table 2:
Runtime comparison of the implementations: C++ on Pentium
![]() 4 (3 GHz), IDL on Xeon (2.8 GHz). The last column shows a rough estimate of the runtime of the IDL implementation on the slower Pentium
4 (3 GHz), IDL on Xeon (2.8 GHz). The last column shows a rough estimate of the runtime of the IDL implementation on the slower Pentium
![]() machine using the conversion factor 1.15.
machine using the conversion factor 1.15.
However, the trust in the estimators of the physical properties relies on the
assumption that there is a single decomposition result. Since the shapelet decomposition depends on four external parameters (the scale size ![]() ,
the maximum decomposition order
,
the maximum decomposition order ![]() and the
components of the centroid
and the
components of the centroid
![]() ), it is inevitable to choose
appropriate parameters. Unfortunately, it is not sufficient for finding a reliable parameter set that the reconstruction has residuals at noise level, i.e.
), it is inevitable to choose
appropriate parameters. Unfortunately, it is not sufficient for finding a reliable parameter set that the reconstruction has residuals at noise level, i.e.
![]() .
In fact, increasing
.
In fact, increasing ![]() makes it more and more likely to find a continuous and growing range of parameters obeying
makes it more and more likely to find a continuous and growing range of parameters obeying
![]() .
This degeneracy has to be broken by ensuring that
both conditions 11 and 15
are fulfilled. If this is not the case, deviations of the shapelet parameters from the optimal values will introduce arbitrary errors on the shapelet coefficients and therefore on all quantities derived from them, even though
.
This degeneracy has to be broken by ensuring that
both conditions 11 and 15
are fulfilled. If this is not the case, deviations of the shapelet parameters from the optimal values will introduce arbitrary errors on the shapelet coefficients and therefore on all quantities derived from them, even though
![]() .
.
In addition, the sampled shapelet basis vectors have to remain orthonormal to guarantee the correctness of the decomposition results. The orthonormality can be violated by undersampling, boundary truncation and introduction of non-orthogonal elements. There is no way to avoid undersampling, but the use of suitably large frames and the subtraction of noise before the decomposition can remedy the other reasons for non-orthonormality.
We showed that the proposed solutions do indeed result in a faithful representation of the decomposed objects, not only at the visual level but also concerning their physical properties. By comparing the results of our C++ implementation with the publicly available IDL code, we found that our code is both more reliable and has considerable performance benefits.
Acknowledgements
The authors thank Catherine Heymans, Sergey E. Koposov and Marco Barden, the GOODS and COMBO-17 team for providing the GOODS galaxy images used for the presented work.