A&A 463, 1143-1152 (2007)
DOI: 10.1051/0004-6361:20065237
H. Önel1,2 - G. Mann1 - E. Sedlmayr2
1 - Astrophysical Institute Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
2 - University of Technology Berlin, Centre of Astronomy and Astrophysics,
Hardenbergstraße 36, 10623 Berlin, Germany
Received 20 March 2006 / Accepted 26 October 2006
Abstract
Aims. The electron transport is investigated numerically after an electron transport model is deduced.
Methods. This model for electron propagation considers global electric and magnetic fields, as well as local Coulomb collisions. A new way to handle the electron's pitch angle evolution by using a binary dice within the treatment of the Coulomb scattering is introduced. The conditions in the solar plasma are represented by average and commonly used models, such that numerical simulations can be performed easily.
Results. The model for electron propagation finally obtained makes it possible to investigate how the Coulomb collisions act on the pitch angle, while electrons are transported through the solar plasma. Some chosen numerical results for different initial conditions are presented in the paper.
Key words: Sun: particle emission - Sun: flares - Sun: magnetic fields - Sun: atmosphere - X-rays: bursts - Sun: radio radiation
In solar flares a large amount of energy is released in the form
of particles and enhanced emissions of radiation from the radio up to
the ![]() -ray regions.
Energetic electrons accelerated in these events
are of special interest, since they are considered to be responsible for
the observable non-thermal radio and X-ray radiations (Lin 1974).
It is generally accepted that these electrons are accelerated up to high
energies in all directions along the magnetic field in the corona,
triggered by the process of magnetic reconnection.
-ray regions.
Energetic electrons accelerated in these events
are of special interest, since they are considered to be responsible for
the observable non-thermal radio and X-ray radiations (Lin 1974).
It is generally accepted that these electrons are accelerated up to high
energies in all directions along the magnetic field in the corona,
triggered by the process of magnetic reconnection.
After these energetic electrons are generated in the corona at their acceleration site, they travel towards the dense chromosphere, and if they have sufficient energy they can produce X-ray emission via bremsstrahlung (Brown 1972). On the other hand, there are also electrons travelling away from the Sun, namely towards the higher corona, and possibly into the interplanetary space, if they meet open field lines. These electrons may reach the Earth within a few minutes (Lin 1974). There they can be studied by in situ measurements (e.g., by the WIND spacecraft).
![\begin{figure}
\par\includegraphics[width=8cm]{5237xsec.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg10.gif) |
Figure 1: Schematic illustration of propagating energetic electrons towards the Sun's surface and in the interplanetary medium generated at the acceleration site. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm]{5237spec.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg11.gif) |
Figure 2: Dynamical radio spectrum of an event from March 11, 1999 obtained by the Radio Sweep Spectropolarimeter at the Astrophysical Institute Potsdam (AIP) in Germany. The frequency is shown on a reversed axis in dependence on time, whereas the radiation intensities are colour coded. |
| Open with DEXTER | |
Figure 1 shows the energetic electrons leaving the acceleration site in the corona. Fast electrons passing through the solar plasma cause radio signatures via beam-plasma instabilities (see Melrose 1985). The electrons directed outwards excite type III radio emission. It is possible to observe and to study these electrons by radio observations. Figure 2 presents a dynamic radio spectrum from March 11, 1999 (Önel et al. 2006,2005) obtained by the Radio Sweep Spectropolarimeter (Mann et al. 1992). The frequencies are recorded in the range from 110 MHz to 400 MHz and are plotted versus the time period of 8:18:50 UT to 8:19:05 UT. This spectrum contains one type III burst originating at 370 MHz and 8:19:51.5 UT. It also contains a second faint type III burst starting at 320 MHz level at 8:19:55.5 UT, which is superimposed by a type U burst. While the type III bursts are generated by fast electrons drifting outward along open field lines, the type U bursts are assumed to be created by fast drifting electrons in closed magnetic field structures (see Yokoyama et al. 2002). In such a case, the electrons also produce radio continuum radiation in terms of so-called type IV radio bursts (see, e.g., Robinson 1985, as a review).
In 2002, NASA launched RHESSI the Ramaty High Energy Solar Spectroscopic Imager
(Lin et al. 2002), which is designed to observe the
hard X- and ![]() -ray radiation emitted by the Sun with a high
temporal, spatial, and energy resolution. One of RHESSI's main mission objectives is to provide information on the particle acceleration processes during solar flares. Since RHESSI can only observe hard X- and
-ray radiation emitted by the Sun with a high
temporal, spatial, and energy resolution. One of RHESSI's main mission objectives is to provide information on the particle acceleration processes during solar flares. Since RHESSI can only observe hard X- and ![]() -ray
radiation from the Sun, it can only indirectly provide information about the acceleration process itself (Brown 1971). Therefore, a model for particle propagation is needed to acquire
information about the particle acceleration site, which is in general different
from the radiation emission site.
-ray
radiation from the Sun, it can only indirectly provide information about the acceleration process itself (Brown 1971). Therefore, a model for particle propagation is needed to acquire
information about the particle acceleration site, which is in general different
from the radiation emission site.
In this paper, a model for the propagation of a test electron through the solar plasma is studied. The journey of such a test electron through the solar plasma is influenced by the global magnetic and electric fields as well as by local Coulomb collisions. These influences are investigated in a quantitative manner, both separately and jointly. The propagating electrons are also affected by the local plasma waves via wave-particle interaction (e.g., Kunow et al. 1991), which is not taken into account in the present study: In the solar corona the particle number density and the collision frequency are quite high. In addition, the magnetic field diverges much more than the interplanetary field. Therefore the wave particle interactions only have a little influence on the electron propagation in the solar plasma. Whenever needed, the model presented in this paper can easily be applied to proton or ion propagations with minor tuning only.
In Sect. 2 the set of equations regarding the electron motion in the solar plasma is derived. Next, in Sect. 3 the plasma background, i.e., the spatial behaviour of the particle density, the electric field, and magnetic field are introduced under coronal and interplanetary conditions. The results are presented and discussed in Sect. 4, which is then followed by a summary of the main issues in Sect. 5.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5237dens.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg12.gif) |
Figure 3: Total particle density is shown as a function of heliocentric distance. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5237efld.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg13.gif) |
Figure 4: The global model for the electric field based on Eqs. (22) and (25) is shown. |
| Open with DEXTER | |
Initially the effects of Coulomb collisions are neglected to study only the pure influence of the magnetic and electric field on the propagation of a test electron through the coronal and interplanetary plasma. The frictionless motion of a test electron on which a general force ![]() and a magnetic flux density
and a magnetic flux density ![]() acts can be described by the most general equation of motion
acts can be described by the most general equation of motion
Only electrons with initial energies up to 50 keV are regarded in this paper. Thus, Eq. (1) describes the electron motion in a non relativistic manner and the deviation of Eq. (1) due to relativistic effects is only of the order of 12%. Furthermore, the global electric and magnetic fields are considered to be aligned with each other. In addition, the magnetic field is assumed to
have only small spatial variations, i.e., it fulfils the relationship
The 3-dimensional problem described by Eq. (1) can be
treated in a 2-dimensional manner, if Alfvén's gyro centre approximation and Eq. (5) are used. Then the particle propagation can be separated into two different motions, namely into the drift motion (i.e., motion that is parallel to the magnetic field), and into the gyro motion (Larmor motion, i.e., motion that is perpendicular to the magnetic field), as follows:
![\begin{figure}
\par\includegraphics[width=8.9cm,clip]{5237bfld.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg37.gif) |
Figure 5:
The global model for the magnetic flux density according to Eq. (29) is shown in dependence on the heliocentric distance in units of the solar radius. The heliocentric radii
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm]{5237_wri.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg38.gif) |
Figure 6:
Arithmetically averaged outer movement of 1000 test electrons. Top left: the averaged altitude is plotted in dependence on time r[t]. Top right: the averaged electron plasma frequency is plotted in dependence on time f[t]. Bottom left: the averaged pitch angle is plotted in dependence on time
|
| Open with DEXTER | |
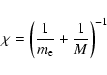 |
(9) |
So far all equations have been deterministic, but this changes if the Coulomb collisions are considered correctly, as it is explained in the following. The mean scattering angle
![]() vanishes due to the symmetry of the scattering process.
That is expected if the test particle is scattered randomly without any preferred direction at each collision. However, the mean squared scattering angle
vanishes due to the symmetry of the scattering process.
That is expected if the test particle is scattered randomly without any preferred direction at each collision. However, the mean squared scattering angle
![]() does not vanish in general. It follows that it is
does not vanish in general. It follows that it is
Even though many equally distributed scattering processes do not affect the pitch angle (
![]() ), each single Coulomb collision does. Each collision deflects the test electron either in one or in the other scattering direction with the same probability, which has to be considered within the general equation of motion when solving iteratively. Hence after one time step
), each single Coulomb collision does. Each collision deflects the test electron either in one or in the other scattering direction with the same probability, which has to be considered within the general equation of motion when solving iteratively. Hence after one time step
![]() ,
the pitch angle changes with respect to Coulomb collisions as
,
the pitch angle changes with respect to Coulomb collisions as
![\begin{figure}
\par\includegraphics[width=16cm]{5237_wra.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg57.gif) |
Figure 7:
Arithmetically averaged outer movement of 1000 test electrons. Top left: the averaged altitude is plotted in dependence on time r[t]. Top right: the averaged electron plasma frequency is plotted in dependence on time f[t]. Bottom left: the averaged pitch angle is plotted in dependence on time
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=9cm]{5237fit1.eps}\hspace*{2mm}
\includegraphics[width=9cm]{5237fit2CMJN.eps} }
\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg58.gif) |
Figure 8:
On the left hand-side the random walk of 1000 electrons is illustrated. All electrons start their motion with the same initial conditions: initial heliocentric radial distance of about
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5237owri.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg61.gif) |
Figure 9:
Influence of the initial pitch angle for the inner transport process. Top: The electron's kinetic energy is illustrated at the point
|
| Open with DEXTER | |
For the total velocity,
In summary, if the initial altitude
r0:=r[t0], the initial velocity
![]() ,
and the initial pitch angle
,
and the initial pitch angle
![]() are known, it is possible to calculate the propagation of an electron away from the acceleration site with the following final equations of motion:
are known, it is possible to calculate the propagation of an electron away from the acceleration site with the following final equations of motion:
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5237oeri.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg86.gif) |
Figure 10:
Influence of the initial energy for the inner transport process. Top: the electron's kinetic energy is illustrated at the point
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5237fo1.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg87.gif) |
Figure 11:
The electrons' heliocentric altitude is plotted as a function of time.
Each line represents the minimum mean square deviation of 1000 calculations
depending on the initial electron energy (for pitch angle of |
| Open with DEXTER | |
Equation (19) can be deduced from the momentum
equation assuming an isothermal and
hydrostatic equilibrium (see, e.g., Mann et al. 1999; Önel 2004).
This density model agrees very well with the white-light observations of the corona by Koutchmy (1994). Please note that Eq. (19) turns into the
![]() -fold Newkirk (1961) model if
-fold Newkirk (1961) model if
![]() is used and the temperature is chosen to be
is used and the temperature is chosen to be
![]() K. In this case
K. In this case ![]() becomes
becomes ![]() .
The quantity
.
The quantity
![]() denotes the full particle number density in the lower corona. The Newkirk parameter
denotes the full particle number density in the lower corona. The Newkirk parameter ![]() is a free parameter. It makes it poissible to adjust the Newkirk (1961) density model to the present conditions on the Sun (Koutchmy 1994):
is a free parameter. It makes it poissible to adjust the Newkirk (1961) density model to the present conditions on the Sun (Koutchmy 1994): ![]() is chosen to be 1 in the case of a quiet Sun (very little magnetic activity at the equatorial regions). It is chosen to be 4 in the case of an active Sun, and 10 in the case of the presence of dense coronal loop structures. A moderate choice of
is chosen to be 1 in the case of a quiet Sun (very little magnetic activity at the equatorial regions). It is chosen to be 4 in the case of an active Sun, and 10 in the case of the presence of dense coronal loop structures. A moderate choice of ![]() for the Newkirk parameter has been made in this paper, since a lot of energetic particles are released in periods of increased solar activity.
for the Newkirk parameter has been made in this paper, since a lot of energetic particles are released in periods of increased solar activity.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5237fo2.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg105.gif) |
Figure 12: Same as in Fig. 11, but with a different scale. |
| Open with DEXTER | |
The lower corona fits the described barometric, static, and isothermal model of Newkirk (1961) quite well. On the other hand, it is well known that a steady flow of plasma continuously takes place due to solar wind. Even though the model of Newkirk (1961) is appropriate to describe the density behaviour in the low corona very well, it fails to describe the observed densities in the high corona. Therefore, a density model for the high corona and the interplanetary medium, which considers the solar wind,is needed.
Such a model can be found in terms of a special solution of the wind equation developed by Parker (1981)
After the density models for the lower and the higher atmosphere
have been introduced separately, both of them shall be united in one
global model for the atmosphere.
This global model obtained from the combination between both previously introduced
models is used in the present paper
for the numerical calculations.
The combination of both models is simply performed by using
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5237fi1.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg125.gif) |
Figure 13: Same as in Fig. 11, but for inward transport. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{5237hist.eps}\end{figure}](/articles/aa/full/2007/09/aa5237-06/Timg133.gif) |
Figure 14:
Histogram showing the number of the electrons, which manage to penetrate down to an altitude of 0.03
|
| Open with DEXTER | |
At this point, the condition stated in Eq. (2) shall be investigated. According to that condition, the magnetic moment will only be an adiabatic constant of motion, if
![]() is fulfilled. To verify this relation,
is fulfilled. To verify this relation,
![]() is used, and the largest
is used, and the largest
![]() possible is estimated.
possible is estimated.![]() For 50 keV electrons with a pitch angle of
For 50 keV electrons with a pitch angle of
![]() the magnetic field of Eq. (29)
fulfils the condition
the magnetic field of Eq. (29)
fulfils the condition
![]() ,
within the whole distance range from
,
within the whole distance range from
![]() to 1 AU. The Larmor radius varies from
to 1 AU. The Larmor radius varies from
![]() m to
m to
![]() m.
m.
Note, that the electric field is considered to be aligned parallelly to the magnetic field. The introduced magnetic model does not take Parker's spiral into account. The direction of the magnetic field line is not of major importance for the electron motion, but the magnetic field strength is, because the electron is guided along the magnetic field, and the direction of the gyromotion does not influence its drift motion (Alfvén's gyro centre approximation, Eqs. (6) and (7)). After introducing the radial behaviour of the density and the temperature as well as the global electric and magnetic field, the conditions of the background plasma are well described for studying the propagation of energetic electrons in the corona and interplanetary space numerically. That is done in the next section.
According to the type III radio burst observations, the acceleration site is assumed to be located near the 300 MHz level (e.g., see Fig. 2).
Thus this electron plasma frequency is chosen in correspondence to the test
electron's initial heliocentric altitude of
![]() ,
with the density model (see Eq. (22)
for
,
with the density model (see Eq. (22)
for ![]() ,
as in Fig. 3) used.
At first a test electron with an initial energy of 20 keV and an initial pitch angle of
,
as in Fig. 3) used.
At first a test electron with an initial energy of 20 keV and an initial pitch angle of ![]() is considered. In the beginning, the motion towards
the Sun is regarded (Fig. 6).
Due to the electron's high initial energy, the effect of the global electric field, which acts
in the form of an acceleration on it, is very weak, since the potential difference between
the height of
is considered. In the beginning, the motion towards
the Sun is regarded (Fig. 6).
Due to the electron's high initial energy, the effect of the global electric field, which acts
in the form of an acceleration on it, is very weak, since the potential difference between
the height of
![]() and the bottom of the corona is about
137 V. On the other hand, the influence of the increasing magnetic field
leads to a the mirror force acting outward, i.e., against the inward motion.
Thus, the drift energy (Fig. 6, bottom right panel) is dramatically transferred into the Larmor energy accompanied with
a monotonic increase of the pitch angle (Fig. 6, bottom left panel). Here, the drift energy and Larmor energy are defined as the kinetic energy with respect to the motion parallel and perpendicular to the magnetic field, respectively. The amount of the total energy (as the sum of the drift and Larmor energy) is weakly decreasing
due to the influence of the Coulomb collisions (Fig. 6).
The action of the Coulomb collisions is also seen in the scatter-like increase of the pitch angle.
After 0.3 s the electron reaches a height of
and the bottom of the corona is about
137 V. On the other hand, the influence of the increasing magnetic field
leads to a the mirror force acting outward, i.e., against the inward motion.
Thus, the drift energy (Fig. 6, bottom right panel) is dramatically transferred into the Larmor energy accompanied with
a monotonic increase of the pitch angle (Fig. 6, bottom left panel). Here, the drift energy and Larmor energy are defined as the kinetic energy with respect to the motion parallel and perpendicular to the magnetic field, respectively. The amount of the total energy (as the sum of the drift and Larmor energy) is weakly decreasing
due to the influence of the Coulomb collisions (Fig. 6).
The action of the Coulomb collisions is also seen in the scatter-like increase of the pitch angle.
After 0.3 s the electron reaches a height of
![]() above the photosphere
(Fig. 6, top left panel).
This height corresponds to an electron plasma frequency
above the photosphere
(Fig. 6, top left panel).
This height corresponds to an electron plasma frequency![]() of 335 MHz (Fig. 6, top left panel).
Thus, the electron would cause a reverse drifting type III radio burst
with a drift rate of 117 MHz s-1, i.e.,
a positive drift rate, which means that the burst drifts towards higher frequencies.
of 335 MHz (Fig. 6, top left panel).
Thus, the electron would cause a reverse drifting type III radio burst
with a drift rate of 117 MHz s-1, i.e.,
a positive drift rate, which means that the burst drifts towards higher frequencies.
As already mentioned, the Coulomb collisions cause a random
motion of the electron. A test electron with an initial energy of 20 keV
and an initial pitch angle of ![]() starts at a height of
starts at a height of
![]() above the photosphere, to illustrate that behaviour. Each repetition of this calculation (1000 times in total) gives a random walk of such a test electron. They are depicted in
Fig. 8 together with the best fit of the 1000 electron trajectories, according to the minimum mean square deviation.
Even if throughout all of these calculations the same initial conditions are used, 1000 different solutions are obtained for each run. It can clearly be seen that there are electron trajectories, which indicate that the test electrons stop at different heights
for each performed calculation. This kind of behaviour follows from the
binary dice, which was introduced in Eq. (11) to treat the Coulomb collisions correctly.
above the photosphere, to illustrate that behaviour. Each repetition of this calculation (1000 times in total) gives a random walk of such a test electron. They are depicted in
Fig. 8 together with the best fit of the 1000 electron trajectories, according to the minimum mean square deviation.
Even if throughout all of these calculations the same initial conditions are used, 1000 different solutions are obtained for each run. It can clearly be seen that there are electron trajectories, which indicate that the test electrons stop at different heights
for each performed calculation. This kind of behaviour follows from the
binary dice, which was introduced in Eq. (11) to treat the Coulomb collisions correctly.
The motion of electrons with different initial energies, but the same initial pitch angles of ![]() are considered in Fig. 13. It can be seen there that the electron with an initial energy of 3 keV already stops after
are considered in Fig. 13. It can be seen there that the electron with an initial energy of 3 keV already stops after
![]() .
Those electrons with initial energies greater than 20 keV are able to penetrate deep into the low corona within
.
Those electrons with initial energies greater than 20 keV are able to penetrate deep into the low corona within
![]() .
.
A similar study but for the outer motion is presented for the corona
in Fig. 11 and for the interplanetary space in Fig. 12.
Here, all electrons have an initial pitch angle of ![]() again. The electron with the initial energy of 10 keV
already stops in the corona after 1 s. Electrons with
an initial energy higher than 20 keV are able to leave the corona
and reach the distance of 1 AU after few 1000 s (Fig. 12).
As expected, the electrons with a higher initial energy
reach 1 AU more quickly than the ones with a low initial energy.
again. The electron with the initial energy of 10 keV
already stops in the corona after 1 s. Electrons with
an initial energy higher than 20 keV are able to leave the corona
and reach the distance of 1 AU after few 1000 s (Fig. 12).
As expected, the electrons with a higher initial energy
reach 1 AU more quickly than the ones with a low initial energy.
Next the outer motion (i.e., toward the interplanetary space) is considered for an electron with an initial energy of 30 keV and an initial pitch
angle of ![]() (Fig. 7). Here, it starts
again at the
(Fig. 7). Here, it starts
again at the
![]() level (
level (
![]() )
and reaches the
)
and reaches the
![]() level
at a height of
level
at a height of
![]() above the photosphere after approximately
above the photosphere after approximately
![]() .
This motion would cause a type III radio burst with a drift rate of
.
This motion would cause a type III radio burst with a drift rate of
![]() ,
which is a reasonable
type III drift rate (Mann & Klassen 2002). Because of the decreasing
global magnetic field, the Larmor energy is dramatically
converted into drift energy (Fig. 7, bottom right panel).
Due to Coulomb collisions the electron loses about
,
which is a reasonable
type III drift rate (Mann & Klassen 2002). Because of the decreasing
global magnetic field, the Larmor energy is dramatically
converted into drift energy (Fig. 7, bottom right panel).
Due to Coulomb collisions the electron loses about ![]() of
its initial energy during its motion (Fig. 7).
Because the electrostatic potential between
of
its initial energy during its motion (Fig. 7).
Because the electrostatic potential between
![]() and 1 AU
is about 1.6 keV and due to the decreasing particle density of the atmosphere and its high drift energy, this electron is able to leave the solar atmosphere, with just a little loss of energy. It reaches the distance of 1 AU from the centre of the Sun after 2000 s (see Fig. 12) with a final energy of
23 keV (Fig. 7, bottom right panel).
and 1 AU
is about 1.6 keV and due to the decreasing particle density of the atmosphere and its high drift energy, this electron is able to leave the solar atmosphere, with just a little loss of energy. It reaches the distance of 1 AU from the centre of the Sun after 2000 s (see Fig. 12) with a final energy of
23 keV (Fig. 7, bottom right panel).
To study the dependence of the penetration depth on the initial
pitch angle of an electron, a test electron with an initial energy of 20 keV
is considered to start at a height of
![]() above the photosphere.
The initial pitch angle varys between
above the photosphere.
The initial pitch angle varys between ![]() and
and ![]() .
As
expected, an electron with a small initial pitch angle can penetrate
deeper into the lower corona than those with higher initial pitch angles
(Fig. 9).
But they lose a large amount of energy due to Coulomb collisions,
as shown in Fig. 9.
For instance, an electron with an initial pitch angle of
.
As
expected, an electron with a small initial pitch angle can penetrate
deeper into the lower corona than those with higher initial pitch angles
(Fig. 9).
But they lose a large amount of energy due to Coulomb collisions,
as shown in Fig. 9.
For instance, an electron with an initial pitch angle of ![]() is able
to penetrate down up to a height of
is able
to penetrate down up to a height of
![]() ,
while it loses energy
from initially 20 keV down to
5 keV at the end (see Fig. 9).
,
while it loses energy
from initially 20 keV down to
5 keV at the end (see Fig. 9).
In addition, the dependence of the penetration depth and the final energy
from the initial one is demonstrated in Fig. 10, where the initial pitch
angle is chosen to be ![]() again, for instance. As expected, electrons
with smaller initial energy lose much more energy due to Coulomb collisions
than those of higher initial energies. On the other hand, electrons with
an initial energy higher than 20 keV are able to
penetrate substantially deep into the low corona,
i.e., down to
again, for instance. As expected, electrons
with smaller initial energy lose much more energy due to Coulomb collisions
than those of higher initial energies. On the other hand, electrons with
an initial energy higher than 20 keV are able to
penetrate substantially deep into the low corona,
i.e., down to
![]() above the
photosphere (Fig. 10).
above the
photosphere (Fig. 10).
In one further attempt, the penetration depth
(inner transport) is calculated for electrons starting with an initial pitch angle
of ![]() at an initial altitude over the photosphere of
at an initial altitude over the photosphere of
![]() ,
where the 300 MHz level is expected. Due to the chosen pitch angle, there is no gyro motion for the electrons in these calculations and the Larmor energy vanishes, while the total kinetic energy is represented by the drift energy only. The initial drift energy has been varied from 3 keV up to 50 keV. This study answered the question of how many electrons have been able to reach
an altitude of
,
where the 300 MHz level is expected. Due to the chosen pitch angle, there is no gyro motion for the electrons in these calculations and the Larmor energy vanishes, while the total kinetic energy is represented by the drift energy only. The initial drift energy has been varied from 3 keV up to 50 keV. This study answered the question of how many electrons have been able to reach
an altitude of
![]() above the photosphere or less.
Its results can be seen in Fig. 14.
The number of those electrons that have been able to penetrate
through the solar corona toward the photosphere increased dramatically
with the increasing energy. But even in those calculations where the
initial energy has been set to 50 keV, 3.8% of 1000 electrons
have not been able to reach a height less than or equal to
above the photosphere or less.
Its results can be seen in Fig. 14.
The number of those electrons that have been able to penetrate
through the solar corona toward the photosphere increased dramatically
with the increasing energy. But even in those calculations where the
initial energy has been set to 50 keV, 3.8% of 1000 electrons
have not been able to reach a height less than or equal to
![]() above the photosphere due to Coulomb collisions.
above the photosphere due to Coulomb collisions.
The major improvement of the deduced model is the new way of treating the effects of the Coulomb scattering process on the pitch angle by introducing a binary dice Eq. (11). We are not aware of any other transport model (e.g., Bai 1982; Leach & Petrosian 1981; Brown 1972; Lu & Petrosian 1988; Estel & Mann 1999; Emslie 1978), that has considered the influence of the Coulomb scattering process on the pitch angle.
The presented transport model allows investigation of the electron energies along their trajectories, and it is based on observations of the electrons traversing the coronal and interplanetary plasma. That makes it poissible to locate the altitude of the acceleration site by means of reverse modelling, when a sufficient number of electrons propagating inwards and outwards is considered (see Sect. 2.3). In the case of the electrons travelling inward, it is sufficient to observe the locations and sources of the chromospheric X-ray radiation, whereas this information for the electrons travelling outwards is measured in situ.
Acknowledgements
The authors want to thank H. Blersch and his team from the computer room of the Physics Department at the University of Technology Berlin, which supported our work with computer power. Furthermore, the authors would like to express their thanks to M. Skender and R. Miteva for their many helpful comments. We also appreciate the anonymous referee, whose skilled remarks helped to improve this paper. Last but not least, we thank our language editor E. Buzay.