A&A 463, 627-634 (2007)
DOI: 10.1051/0004-6361:20066325
On the hydrogen neutral outflowing disks of B[e] supergiants
M. Kraus1 - M. Borges Fernandes2 - F. X. de Araújo3
1 - Astronomical Institute AV CR, Fricova 298, 251 65 Ondrejov, Czech Republic
2 -
Observatório do Valongo (UFRJ), Ladeira do Pedro Antonio 43, Rio de Janeiro 20080-090, Brazil
3 -
Observatório Nacional, Rua General José Cristino 77, 20921-400 São Cristovão, Rio de Janeiro, Brazil
Received 31 August 2006 / Accepted 19 November 2006
Abstract
Context. B[e] supergiants are known to possess geometrically thick dusty disks. Disk-forming wind models in the literature have, however, been found to be insufficient in reproducing the observed dust emission. This problem arises due to the severe assumption that, as for classical Be stars, the near-infrared excess emission originates in the disk. Modeling of the free-free and free-bound emission therefore results in an upper limit for the disk mass loss rate as well as for the disk opacity. Dust condensation in the disk can thus severely be hampered.
Aims. In order to overcome the dust formation problem, and based on our high-resolution optical spectroscopy and model results, we propose a revised scenario for the non-spherical winds of B[e] supergiants: a normal B-type line-driven polar wind and an outflowing disk-forming wind that is neutral in hydrogen at, or very close to the stellar surface.
Methods. We concentrate on the pole-on seen LMC B[e] supergiant R 126 and calculate the line luminosities of the optical [O I] emission lines and their emergent line profiles with an outflowing disk scenario. In addition, we compute the free-free and free-bound emission from a line-driven polar wind and model the spectral energy distribution in the optical and near-infrared.
Results. Good fits to the [O I] line luminosities are achieved for an outflowing disk that is neutral in hydrogen right from the stellar surface. Neutral thereby means that hydrogen is ionized by less than 0.1%. Consequently, the free-free and free-bound emission cannot (dominantly) arise from the disk and cannot limit the disk mass loss rate. The hydrogen neutral outflowing disk scenario therefore provides an ideal environment for efficient dust formation. The spectral energy distribution in the optical and near-infrared range can be well fitted with the stellar continuum plus free-free and free-bound emission from the polar line-driven wind. Our modeling further delivers minimum values for
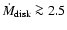
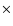
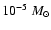 yr-1 and for the density contrast between equatorial and polar wind of
yr-1 and for the density contrast between equatorial and polar wind of 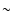 10.
10.
Key words: stars: mass-loss - stars: winds, outflows - supergiants - stars: individual: R 126 - stars: emission-line, Be - stars: early-type
The spectra of B[e] supergiants show the so-called hybrid character which is
defined by the co-existence of a line-driven polar wind and a high density but
low velocity equatorial wind (Zickgraf et al. 1985). The latter is
assumed to form a disk-like structure. This disk is the location of the
low-ionized metals, of the sometimes observed CO and TiO molecular emission
bands (McGregor et al. 1988, 1989; Zickgraf et al.
1989) as well as of the hot dust, pronounced in the mid-IR
excess emission (e.g. Zickgraf 1992).
The disk formation mechanism, as well as the disk structure, are however still
unsolved problems.
Porter (2003) has studied the possible nature of these disks by modeling
their spectral energy distribution (SED). He found that neither an outflowing
disk-forming wind nor a Keplerian viscous disk in their simplest form can
easily account for the observed free-free and dust emission self-consistently.
The optical spectra of B[e] supergiants exhibit strong [O I] emission
(see e.g. Kraus & Borges Fernandes 2005; Kraus et al.
2006; and Fig. 1). Besides other typical features like
strong Balmer emission, Fe II and [Fe II] emission, and mid-IR excess
emission, the [O I] emission lines are one of the main characteristics of
stars with the B[e] phenomenon (Lamers et al. 1998).
The fact that O I and H I have about equal ionization
potentials requests that the [O I] emission region must be neutral in
hydrogen. Its most plausible location is therefore the high-density disk.
Test calculations for an outflowing disk scenario, that were aimed to reproduce
the observed strong [O I] line luminosities, have been performed for some
Magellanic Cloud B[e] supergiants (Kraus & Borges Fernandes 2005;
Kraus et al. 2006). These computations revealed that, in order to
keep the disk mass loss rates at reasonable values, the disk material
must be neutral in hydrogen either at or at least very close to the stellar
surface, resulting in a hydrogen neutral disk.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig1.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg10.gif) |
Figure 1:
The [O I] lines in the FEROS spectrum of R 126. They all show a redshift of about 260 km s-1 caused by the radial velocity of the LMC. |
| Open with DEXTER |
In this paper we present model results for the Large Magellanic Cloud (LMC) B[e] supergiant R 126. We use a simple outflowing disk scenario and request that
the disk is neutral in hydrogen right from the stellar surface.
We show that with such a model we can explain observations like the strong
[O I] line luminosities. In addition, this scenario provides a way out
of the dust formation problem mentioned by Porter (2003).
The paper is structured as follows:
in Sect. 2 we give details on the test star and on our observations.
Section 3 introduces the problem of the nature of the B[e] supergiants disks. We emphasize the need of a revised disk model and propose
the hydrogen neutral disk as a reasonable scenario.
In Sect. 4 we present our hydrogen neutral disk model and
calculate the emerging [O I] line luminosities as well as their line
profiles. In Sect. 5 we fit the SED in the optical and near-IR range
by calculating the free-free and free-bound emission from the polar
wind. In addition, we determine the density ratio between equatorial and polar
wind components and show that our model results in a lower limit. The
validity of our assumptions is discussed in Sect. 6, and
the conclusions are summarized in Sect. 7.
2 The LMC B[e] supergiant R 126
The LMC B[e] supergiant R 126 (HD 37974, LHA 120-S 127) is supposed to have a pole-on seen disk. This orientation has the following advantages (see
Fig. 2): (i) it guarantees that we see all of the [O I] emission and none is hidden by the star or absorbed by the dusty disk
because the [O I] emission originates from regions close to the star where
no dust has yet formed, and (ii) it simplifies the analysis due to the high
degree of symmetry. R 126 has also been studied by Porter (2003) so
that we can directly compare our results. The stellar parameters of this object
have been derived by Zickgraf et al. (1985) who found:
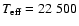 K, L* = 1.2
K, L* = 1.2 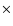
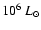 ,
,
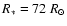 ,
and an interstellar extinction value of
E(B-V) = 0.25.
These values will be used for our calculations throughout the paper.
,
and an interstellar extinction value of
E(B-V) = 0.25.
These values will be used for our calculations throughout the paper.
We obtained high- and low-resolution optical spectra of R 126 at the ESO 1.52-m telescope (agreement ESO/ON-MCT) in La Silla (Chile) using the Fiber-fed
Extended Range Optical Spectrograph (FEROS) and the Boller & Chivens
spectrograph, respectively. FEROS is a bench-mounted Echelle spectrograph with
fibers, that cover a sky area of 2 arcsec, located at the Cassegrain focus with
a wavelength coverage from 3600 Å to 9200 Å and a spectral resolution
of R = 55 000 (in the region around 6000 Å). It has a complete automatic
on-line reduction, which we adopted. The spectra were taken on December 18,
1999, with an exposure time of 4500 s. The S/N ratio in the 5500 Å region is approximately 100.
The low-resolution Boller & Chivens (B&C) spectrum was taken on October 31,
1999, with an exposure time of 900 s and a slit width of 4 arcsec. The
instrumental setup employed provides a resolution of 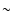 4.6 Å in the
range of 3800-8700 Å. In the 5500 Å continuum region, the S/N ratio is
aproximately 200. The B&C spectrum was reduced using standard IRAF
tasks, such as bias subtraction, flat-field normalization, and wavelength
calibration. We have done absolute flux calibration using spectrophotometric
standards from Hamuy et al. (1994).
4.6 Å in the
range of 3800-8700 Å. In the 5500 Å continuum region, the S/N ratio is
aproximately 200. The B&C spectrum was reduced using standard IRAF
tasks, such as bias subtraction, flat-field normalization, and wavelength
calibration. We have done absolute flux calibration using spectrophotometric
standards from Hamuy et al. (1994).
Equivalent widths and line intensities in both linearized spectra have been
measured using the IRAF task that computes the line area above the adopted
continuum. Uncertainties in our measurements come mainly from the position of
the underlying continuum and we estimate the errors to be about 20%. The
emerging [O I] lines resolved within the FEROS spectrum are shown in
Fig. 1.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig2.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg14.gif) |
Figure 2:
Sketch of the pole-on seen disk around R 126 (not to scale). The disk
(dark grey shaded) is assumed to be neutral in hydrogen right from the stellar
surface, giving raise to [O I] emission. Further out, molecules and dust
will form. The disk material moves outwards with
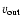 ,
resulting in an observable line-of-sight velocity ( ,
resulting in an observable line-of-sight velocity (
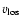 ). Free-free and free-bound
emission is restricted to the (polar) wind (light grey shaded). The system is
axially symmetric (around z-axis) and symmetric with respect to the disk
mid-plane. ). Free-free and free-bound
emission is restricted to the (polar) wind (light grey shaded). The system is
axially symmetric (around z-axis) and symmetric with respect to the disk
mid-plane. |
| Open with DEXTER |
3 On the nature of B[e] supergiant stars' disks
The nature of the B[e] supergiant stars' disks is a long-standing problem.
Recently, Porter (2003) investigated the possibility of dust formation
in the disk of the B[e] supergiant R 126 for two different approaches: an outflowing disk-forming wind, and a Keplerian viscous disk. He found that both
models failed in reproducing the observed dust and free-free emission
self-consistently. And he suggested a way out of this by allowing for
substantial alteration especially of the exponent of the radial density
distribution from
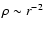 to a considerably flatter one of r-1.7. The advantage of a flatter density profile is that at every
location in the disk a higher density (and hence opacity) is maintained,
allowing for more efficient dust condensation and therefore for an enhanced
dust emission over the disk. Such a modification finally resulted in a good
fit to the SED of R 126 (see Fig. 6 of Porter 2003), but for the
price that the disk density distribution now no longer corresponds to
a constant velocity outflow (which requests
to a considerably flatter one of r-1.7. The advantage of a flatter density profile is that at every
location in the disk a higher density (and hence opacity) is maintained,
allowing for more efficient dust condensation and therefore for an enhanced
dust emission over the disk. Such a modification finally resulted in a good
fit to the SED of R 126 (see Fig. 6 of Porter 2003), but for the
price that the disk density distribution now no longer corresponds to
a constant velocity outflow (which requests
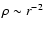 ).
A possible interpretation of
such a flatter density profile might be that the disk slows down with distance,
a scenario that lacks any observational evidence.
).
A possible interpretation of
such a flatter density profile might be that the disk slows down with distance,
a scenario that lacks any observational evidence.
To test Porter's modified outflowing disk scenario, we took the
parameters of his best-fit model and calculated the emerging [O I] line
luminosities. These turned out to be at least a factor of 50 lower than
the values we observed. This means that we need a much higher density within
the [O I] line forming region than can be provided by Porter's disk model.
The most severe limitation in his model calculations was the assumption
that, as in the case of classical Be stars, the free-free emission arises in
the high density disk, while contributions from the polar wind are negligible.
Fitting the near-IR part of the SED with free-free emission from the outflowing
disk therefore determines the disk mass loss rate. Consequently, this value is
an upper limit for the disk density and hence opacity. Dust can only
condensate at distances with reasonable values of temperature and opacity. An upper limit for the disk density, defined by the free-free emission, can
therefore severely hamper efficient dust formation in the disk, which turned
out to be the major reason why Porter (2003) could not fit the observed
dust emission of R 126 with the original outflowing disk scenario.
The detection of strong [O I] line emission in the spectra of e.g. B[e] supergiants requests that there must be a rather high density disk
region which is neutral in hydrogen (
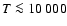 K), but still hot enough
(
K), but still hot enough
(
![$6000\la T~[{\rm K}] \la 8000$](/articles/aa/full/2007/08/aa6325-06/img17.gif) )
for effective excitation of the levels in O I. First test calculations that were aimed to reproduce the [O I] line luminosities with an outflowing disk scenario have been performed by Kraus & Borges Fernandes (2005) and Kraus et al. (2006).
These computations showed that, in order to keep the disk mass loss rates at
reasonable values, the disks must be neutral in hydrogen either at,
or at least very close to the stellar surface.
)
for effective excitation of the levels in O I. First test calculations that were aimed to reproduce the [O I] line luminosities with an outflowing disk scenario have been performed by Kraus & Borges Fernandes (2005) and Kraus et al. (2006).
These computations showed that, in order to keep the disk mass loss rates at
reasonable values, the disks must be neutral in hydrogen either at,
or at least very close to the stellar surface.
The existence of hydrogen neutral disks around B[e] supergiants is additionally
supported by recent ionization structure calculations in non-spherically
symmetric winds. These computations have shown that the wind material in the
equatorial plane can indeed recombine at, or close to the stellar surface if
either the equatorial mass flux is enhanced compared to the polar one
(Kraus & Lamers 2003), or
even decreased in combination with a reduction in surface temperature due to
rapid rotation of the star (Kraus 2006; Kraus & Lamers 2006).
Having a hydrogen neutral disk around a luminous object is therefore not
as unrealistic as it might seem at first glance. In fact, it has several
striking advantages: if the disk is predominantly neutral,
the free-free and free-bound emission can no longer be generated
in the disk, but must (mainly) originate within the polar wind.
The disk mass loss rate is therefore not strictly linked to the
free-free emission causing the near-IR excess.
Hence, the disk mass loss rate might be (much) higher than the upper
limit used by Porter (2003).
A higher disk density is certainly needed to reproduce the observed
[O I] line luminosities. And finally, a higher disk density will increase
the disk opacity and will allow for
more efficient dust condensation in the disk, needed to reproduce the observed
IR excess.
In the following we will investigate and test the suggested model scenario of a hydrogen neutral disk around a luminous object by analysing in detail the
observed [O I] lines from the B[e] supergiant R 126.
4 The (hydrogen) neutral disk
4.1 The disk geometry
The disk is assumed to be wedge-shaped (see sketch in Fig. 2)
and we use the same value of
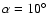 for the constant disk half
opening angle as Porter (2003).
For simplicity we assume that the disk has a constant outflow velocity
within the [O I] emitting region. The influence of a velocity distribution
on the final results is discussed in Sect. 6.
for the constant disk half
opening angle as Porter (2003).
For simplicity we assume that the disk has a constant outflow velocity
within the [O I] emitting region. The influence of a velocity distribution
on the final results is discussed in Sect. 6.
In a disk-forming wind of constant outflow velocity,
the hydrogen particle density distribution at all latitudes
within the disk can be written in the form
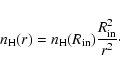 |
(1) |
The parameter
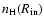 ,
given by
,
given by
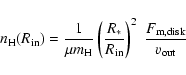 |
(2) |
with the disk mass flux,
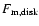 ,
and the (constant) disk
outflow velocity,
,
and the (constant) disk
outflow velocity,
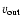 (see Fig. 2),
describes the density at the inner radius,
(see Fig. 2),
describes the density at the inner radius,
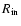 ,
of the
[O I] emitting region. This inner radius corresponds to the hydrogen
recombination distance in the disk and is in principle a free
parameter in our calculations, but here we use
,
of the
[O I] emitting region. This inner radius corresponds to the hydrogen
recombination distance in the disk and is in principle a free
parameter in our calculations, but here we use
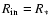 since this
defines a lower limit to the disk density needed to reproduce the [O I] line luminosities. The validity of our assumption that the disk is
neutral in hydrogen right from the stellar surface is discussed in
Sect. 6.
The oxygen and electron density distributions are parameterized in terms
of the hydrogen density, i.e.
since this
defines a lower limit to the disk density needed to reproduce the [O I] line luminosities. The validity of our assumption that the disk is
neutral in hydrogen right from the stellar surface is discussed in
Sect. 6.
The oxygen and electron density distributions are parameterized in terms
of the hydrogen density, i.e.
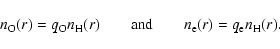 |
(3) |
The parameters 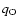 and
and 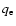 describe the relative abundances of
oxygen and electrons with respect to hydrogen. For
describe the relative abundances of
oxygen and electrons with respect to hydrogen. For 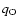 we use a typical
LMC abundance value of 1/3 solar, with a solar oxygen abundance of
we use a typical
LMC abundance value of 1/3 solar, with a solar oxygen abundance of
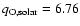
 10-4 (Grevesse & Sauval 1998).
Since we do not know the ionization fraction of the disk a priori, we keep
10-4 (Grevesse & Sauval 1998).
Since we do not know the ionization fraction of the disk a priori, we keep
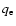 as a free parameter.
as a free parameter.
The forbidden emission lines arise from the five lowest energy levels of the
O I atom that are excited via collisions with free electrons. These levels
are shown schematically in Fig. 3. For simplicity, we labeled them
from 1 to 5 corresponding to their increasing energy. The three lines resolved
in our high-resolution optical spectra are indicated; they belong to the
transitions
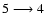 (5577 Å),
(5577 Å),
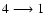 (6300 Å),
and
(6300 Å),
and
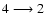 (6363 Å).
(6363 Å).
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{6325fig3.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg32.gif) |
Figure 3:
Sketch of the five lowest energy levels within O I from which the
forbidden lines arise. The transitions of our interest are indicated. |
| Open with DEXTER |
While the lines 6300 Å and 6363 Å arise from the same upper level, which
means that their line ratio is independent of the density and temperature but
is determined purely by atomic parameters, the situation is different for
line ratios with the 5577 Å line. This line arises from the highest energy
level in our 5-level atom (Fig. 3). It is therefore obvious that
the 5577 Å line will only become strong if level 5 is populated efficiently,
either due to a huge number of available free electrons or by electrons with
rather high energy. Line ratios with the 5577 Å line are thus sensitive
tracers for the temperature and ionization fraction in the disk.
In our spectra, the 6300 Å line is the one with highest luminosity. We will
therefore use the 6300 Å/5577 Å line luminosity ratio to investigate
density and temperature in the disk around R 126.
Forbidden lines are optically thin. The emissivity at any location r in the
disk of a transition
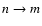 is given by
is given by
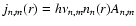 where nn(r) is the level population of
the upper level, n, at this location. The level populations are calculated by
solving the statistical equilibrium equations in our 5-level atom. Collision
parameters are taken from Mendoza (1983) and atomic parameters from
Wiese et al. (1966) and from Kafatos & Lynch (1980).
The line luminosity finally follows from integration of the emissivity over the
emitting disk volume.
where nn(r) is the level population of
the upper level, n, at this location. The level populations are calculated by
solving the statistical equilibrium equations in our 5-level atom. Collision
parameters are taken from Mendoza (1983) and atomic parameters from
Wiese et al. (1966) and from Kafatos & Lynch (1980).
The line luminosity finally follows from integration of the emissivity over the
emitting disk volume.
Due to the nearly equal ionization potentials of O and H, the [O I] emission must arise in those parts of the disk in which hydrogen is
predominantly neutral. This does not mean that hydrogen must be 100% neutral,
since effects like collisional ionization that might take place in the high
density disk could keep the hydrogen material ionized at a (very) low level,
providing free electrons to collisionally excite O I. Further sources
of free electrons in the disk are elements like Mg, Si, Fe, Al, etc. with
ionization potentials (much) lower than 13.6 eV. These metals will remain
ionized at a certain fraction even in a completely hydrogen neutral environment.
The ionization fraction, 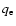 ,
in the disk is therefore the sum of
all free electrons provided by hydrogen and the metals, i.e.
,
in the disk is therefore the sum of
all free electrons provided by hydrogen and the metals, i.e.
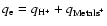 .
.
To get a handle on the possible individual contributions to the total number
of free electrons in the disk, we make a first guess.
If all possible elements with ionization potential lower than 13.6 eV would
be fully singly ionized (including also C with
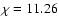 eV
and Cl with
eV
and Cl with
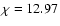 eV), then a maximum number of free electrons
of
eV), then a maximum number of free electrons
of
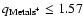
 10-4 would be provided by the
metals in the disk. This number accounts for an LMC metallicity of 1/3 solar.
On the other hand, if only 1% of hydrogen in the disk remains ionized, the
ionization fraction would be
10-4 would be provided by the
metals in the disk. This number accounts for an LMC metallicity of 1/3 solar.
On the other hand, if only 1% of hydrogen in the disk remains ionized, the
ionization fraction would be
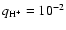 which is at least a factor 100 higher than what can be expected from the metals.
Our assumption of a hydrogen neutral disk around R 126 therefore requests
that the total disk ionization fraction should be
which is at least a factor 100 higher than what can be expected from the metals.
Our assumption of a hydrogen neutral disk around R 126 therefore requests
that the total disk ionization fraction should be
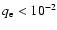 .
.
To derive the ionization fraction in the disk of R 126 we calculated
the line luminosities and the 6300 Å/5577 Å line ratio for a large range
of 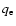 values and for different temperatures. These calculations were
done in several steps: for a given ionization fraction and temperature we first
varied the density parameter,
values and for different temperatures. These calculations were
done in several steps: for a given ionization fraction and temperature we first
varied the density parameter,
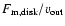 (see
Eq. (2)), in order to reproduce the
observed line luminosity of the 6300 Å line. This
density parameter is plotted as a function of
(see
Eq. (2)), in order to reproduce the
observed line luminosity of the 6300 Å line. This
density parameter is plotted as a function of 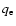 in the lower panel
of Fig. 4. With the proper density parameter, we then calculated
the line luminosities of all [O I] lines and derived the
6300 Å/5577 Å line ratio. This line ratio is plotted as a function of
in the lower panel
of Fig. 4. With the proper density parameter, we then calculated
the line luminosities of all [O I] lines and derived the
6300 Å/5577 Å line ratio. This line ratio is plotted as a function of 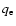 in the upper panel of Fig. 4. In this plot we also included the observed line ratio, shown as the dotted line.
in the upper panel of Fig. 4. In this plot we also included the observed line ratio, shown as the dotted line.
Our calculations cover a temperature range between 7500 K and 9000 K. The
curves in the upper panel of Fig. 4 all show the same trend of a decrease in line ratio with increasing ionization fraction. This effect is
clear, because the number of free electrons determines the collisional
excitation rate of the levels. The more electrons, the higher the probability
for collisional excitation even of the level with highest energy (i.e. level 5)
from which the 5577 Å line arises. The second obvious effect is the decrease
in line ratio with increasing temperature, since the temperature determines the
kinetic energy of the free electrons. For low temperatures, the energy of the
free electrons is not high enough to effectively excite level 5, reducing the
5577 Å line emission and hence increasing the line ratio.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig4.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg42.gif) |
Figure 4:
Upper panel: variation of the line ratio with disk ionization fraction.
The three curves are for the different temperatures as indicated. The dotted
line represents the observed line ratio from R 126. It indicates a disk
temperature in the range 9000 K to about 8000 K with corresponding ionization
fractions of 10-5 and 4  10-4, respectively. Lower panel:
density parameter of the disk found from fitting the observed 6300 Å line
luminosity over a huge range of ionization fractions. For details see text.
10-4, respectively. Lower panel:
density parameter of the disk found from fitting the observed 6300 Å line
luminosity over a huge range of ionization fractions. For details see text. |
| Open with DEXTER |
For the three temperature values used to calculate the theoretical curves in
Fig. 4 we find agreement with the observed line ratio for the
following parameter combinations: for 9000 K we find an ionization fraction of 10-5, and for 8000 K we find an ionization fraction of 4 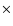 10-4.
For a temperature of 7500 K, we cannot reproduce the observed line ratio.
10-4.
For a temperature of 7500 K, we cannot reproduce the observed line ratio.
Our calculations show that when accounting for the line luminosity and line
ratio observed from R 126, the ionization fraction is rather low for high
temperatures, while an ionization fraction of up to 10% might exist for a temperature as low as 7800 K. This behaviour is only strictly valid for
a given observed line luminosity. In order to restrict the range of valid
or reasonable disk parameters, we take account of the fact that the
ionization fraction can only increase with increasing temperature, since
collisional ionization will act more efficiently. This indicates that for the
disk around R 126 we can exclude high temperatures (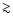 9000 K) as well as
low temperatures (
9000 K) as well as
low temperatures (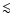 8000 K), and we conclude that the [O I] line
forming region in the disk of R 126 has a temperature range of
8000 K), and we conclude that the [O I] line
forming region in the disk of R 126 has a temperature range of 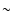
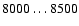 K with a corresponding ionization fraction range of 5
K with a corresponding ionization fraction range of 5 
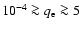
 10-5. This range in ionization fraction
states that less than 0.05% of hydrogen in the disk is ionized. We can
therefore conclude that the disk around R 126 is indeed neutral in hydrogen.
10-5. This range in ionization fraction
states that less than 0.05% of hydrogen in the disk is ionized. We can
therefore conclude that the disk around R 126 is indeed neutral in hydrogen.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig5.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg48.gif) |
Figure 5:
Calculated increase in [O I] line luminosities from the hydrogen
neutral disk around R 126. The observed, extinction corrected values are
indicated with arrows. The observations have been taken with an aperture radius
of 2
 ,
corresponding to an outer edge of the observed wind of about
1.5 ,
corresponding to an outer edge of the observed wind of about
1.5 
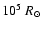 at the distance of the LMC. This value is used
as the extent of the line luminosity integration, but the [O I] line
luminosities clearly saturate already within about 500 R*.
at the distance of the LMC. This value is used
as the extent of the line luminosity integration, but the [O I] line
luminosities clearly saturate already within about 500 R*. |
| Open with DEXTER |
Figure 5 shows the increase in [O I] line luminosities
calculated for a disk of 8000 K and an ionization fraction of 4  10-4. The lines saturate within a few hundred stellar radii. The
observed values are indicated by the arrows to the right.
10-4. The lines saturate within a few hundred stellar radii. The
observed values are indicated by the arrows to the right.
4.3 Disk outflow velocity and mass loss rate
For a temperature of 8000 K as derived in the previous section, we end up with
a density parameter of
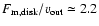
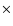 10-11 g cm-3 for the disk of R 126 (see Fig. 4). To compare our results with those of Porter (2003), we need to convert this density parameter into
a mass loss rate. For this, the outflow velocity,
10-11 g cm-3 for the disk of R 126 (see Fig. 4). To compare our results with those of Porter (2003), we need to convert this density parameter into
a mass loss rate. For this, the outflow velocity,
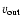 ,
of the disk is needed. For a pole-on seen disk with radially outflowing
material, the maximum observable line-of-sight velocity,
,
of the disk is needed. For a pole-on seen disk with radially outflowing
material, the maximum observable line-of-sight velocity,
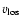 ,
is
linked to the outflow velocity via
,
is
linked to the outflow velocity via
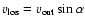 (see
Fig. 2). The range in possible
(see
Fig. 2). The range in possible
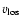 values over the
different disk outflow directions above and below the disk mid-plane leads to
symmetrical doppler shifts of the line center, while thermal and turbulent
velocities as well as the spectral resolution of the instrument result in a Gaussian profile of the line. Thus, optically thin lines formed in a pole-on
seen outflowing disk should be symmetric with respect to their laboratory
wavelength. The observed [O I] lines are indeed symmetric
(Fig. 1) and their profiles show a Gaussian shape with a FWHM of
values over the
different disk outflow directions above and below the disk mid-plane leads to
symmetrical doppler shifts of the line center, while thermal and turbulent
velocities as well as the spectral resolution of the instrument result in a Gaussian profile of the line. Thus, optically thin lines formed in a pole-on
seen outflowing disk should be symmetric with respect to their laboratory
wavelength. The observed [O I] lines are indeed symmetric
(Fig. 1) and their profiles show a Gaussian shape with a FWHM of
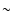 9.2 km s-1.
9.2 km s-1.
To derive a possible outflow contribution from the observed lines,
we first calculate the following test profiles:
(i) a pure Gaussian line profile and (ii) a pure outflowing disk profile.
The results are shown in the left panel of Fig. 6. The calculated
lines are normalized to their maximum value, and
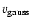 and
and
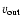 are chosen such that they result in a FWHM value of
9.2 km s-1. The pure outflowing disk (neglecting the influence of FEROS'
spectral resolution) results in a flat-topped profile with steeply rising wings.
The narrow observed [O I] lines show a better agreement with a Gaussian line shape, and the fact that the observed [O I] lines have
widths that are only marginally broader than the velocity resolution of FEROS
indicates that the intrinsic FWHM of the lines can only be on the order of
2-3 km s-1. Such a low intrinsic FWHM can be ascribed to pure
thermal broadening.
are chosen such that they result in a FWHM value of
9.2 km s-1. The pure outflowing disk (neglecting the influence of FEROS'
spectral resolution) results in a flat-topped profile with steeply rising wings.
The narrow observed [O I] lines show a better agreement with a Gaussian line shape, and the fact that the observed [O I] lines have
widths that are only marginally broader than the velocity resolution of FEROS
indicates that the intrinsic FWHM of the lines can only be on the order of
2-3 km s-1. Such a low intrinsic FWHM can be ascribed to pure
thermal broadening.
Since spectra taken with FEROS are not flux-calibrated, the reproduction of
the line profiles can only give qualitative results. We took exemplarily the
line profile of the 6363 Å line obtained with FEROS, corrected it for the LMC radial velocity component of 260 km s-1, and normalized the line to its
maximum intensity. This normalized line profile is what we intend to fit.
We first used a pure Gaussian line profile with FWHM of 9.2 km s-1
(resulting from FEROS' spectral resolution plus thermal broadening of the line)
which results in a good fit (mid panel of Fig. 6).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig6.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg52.gif) |
Figure 6:
Normalized profiles of the [O I] 6363 Å line. Left:
theoretical profiles for either a pure Gaussian or a pure outflowing disk
profile. Middle: fit of a Gaussian profile with FWHM of 9.2 km s-1resulting from FEROS' spectral resolution plus thermal motion of the gas.
Right: fit of the same Gaussian including an outflow component causing
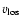 of either 2 km s-1 or 4 km s-1. While the first one still gives a reasonable fit, the latter one clearly results in a too broad line profile.
of either 2 km s-1 or 4 km s-1. While the first one still gives a reasonable fit, the latter one clearly results in a too broad line profile. |
| Open with DEXTER |
Next we combined this Gaussian profile with an outflowing disk profile for
different values of
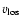 .
This was done to see for which value of
.
This was done to see for which value of
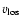 the line profile starts to alter. We found that a possible
the line profile starts to alter. We found that a possible
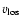 contribution must be smaller than
contribution must be smaller than 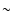 2 km s-1 (right panel of Fig. 6) resulting in an outflow velocity of
2 km s-1 (right panel of Fig. 6) resulting in an outflow velocity of
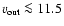 km s-1 for
km s-1 for
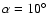 .
The value of
.
The value of 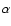 should be taken as an upper limit since the range of possible B[e] supergiant
disk values has been estimated by Zickgraf (1992) to be
should be taken as an upper limit since the range of possible B[e] supergiant
disk values has been estimated by Zickgraf (1992) to be
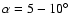 .
A thinner disk will result in a higher outflow velocity for the
same value of
.
A thinner disk will result in a higher outflow velocity for the
same value of
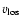 (see Fig. 7). Nevertheless, even
considering a thinner disk, the outflow velocity is considerably smaller than
the values of 60-80 km s-1 usually ascribed to the disks of B[e] supergiants. In the case of R 126, no good estimates for the real disk outflow
velocity exist and only a detailed investigation of the line profiles from
emission lines that might be connected with the disk will help to clarify this point.
(see Fig. 7). Nevertheless, even
considering a thinner disk, the outflow velocity is considerably smaller than
the values of 60-80 km s-1 usually ascribed to the disks of B[e] supergiants. In the case of R 126, no good estimates for the real disk outflow
velocity exist and only a detailed investigation of the line profiles from
emission lines that might be connected with the disk will help to clarify this point.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig7.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg56.gif) |
Figure 7:
Disk outflow velocity as function of disk half opening angle for
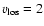 km s-1 as derived from the [O I] line profile fitting. km s-1 as derived from the [O I] line profile fitting. |
| Open with DEXTER |
An outflow velocity of 11.5 km s-1 as derived above together with the
disk density parameter derived from the [O I] line luminosity calculations
and a disk opening angle of 20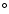 results in a total disk mass loss rate
of
results in a total disk mass loss rate
of
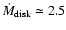
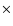
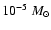 yr-1. This
is about a factor of 10 higher than the value used by Porter
yr-1. This
is about a factor of 10 higher than the value used by Porter![[*]](/icons/foot_motif.gif) (2003), and well in agreement with the postulated need for a higher disk
density in order to account for the observed [O I] line luminosities of R 126.
(2003), and well in agreement with the postulated need for a higher disk
density in order to account for the observed [O I] line luminosities of R 126.
Based on recent observations with the Spitzer Space Telescope Infrared
Spectrograph, Kastner et al. (2006) derived a total dust mass of the
disk around R 126 of 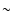 3
3 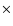
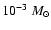 ,
and they claimed
that the dust is contained between 120 AU and 2500 AU.
In order to compare this dust mass with our derived disk mass loss rate, we
assume a gas to dust ratio of about 100 and convert the total mass into a disk
mass loss rate for our outflowing disk model. We end up with a density
parameter of
,
and they claimed
that the dust is contained between 120 AU and 2500 AU.
In order to compare this dust mass with our derived disk mass loss rate, we
assume a gas to dust ratio of about 100 and convert the total mass into a disk
mass loss rate for our outflowing disk model. We end up with a density
parameter of
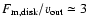
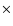 10-10 g cm-3and a disk mass loss rate of
10-10 g cm-3and a disk mass loss rate of
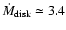
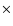
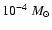 yr-1. This is about 170 times higher than the value
used by Porter (2003) and about 13 times higher than our value,
and confirms that the disk around R 126 must indeed be more massive than
previously thought.
yr-1. This is about 170 times higher than the value
used by Porter (2003) and about 13 times higher than our value,
and confirms that the disk around R 126 must indeed be more massive than
previously thought.
In addition, the inner edge of the dusty disk of 120 AU, which corresponds to
about 360 R*, lies within our [O I] saturation region. This
confirms that our value for the disk mass loss rate is indeed a lower limit.
5 The polar wind
With our assumption of a hydrogen neutral disk right from the stellar surface,
the free-free and free-bound emission is restricted to the ionized wind parts
(see Fig. 2). At all latitudes above and below the equatorial disk
we assume that the star has a normal B-type line-driven wind, which we refer to
as the polar wind. Its radial density distribution, following from the equation
of mass continuity, is
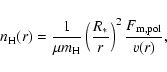 |
(4) |
where
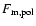 is the mass flux of the polar wind.
The velocity increase in line-driven winds can be approximated with a
is the mass flux of the polar wind.
The velocity increase in line-driven winds can be approximated with a 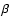 -law with
-law with 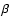 typically in the range of 0.8-1.0 for hot star winds
(see e.g. Lamers & Cassinelli 1999). We assume that the wind
temperature is constant which allows for a simplified treatment of the
intensity calculation. At every point along the impact parameter,
typically in the range of 0.8-1.0 for hot star winds
(see e.g. Lamers & Cassinelli 1999). We assume that the wind
temperature is constant which allows for a simplified treatment of the
intensity calculation. At every point along the impact parameter, 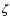 (see
Fig. 2), the intensity is given by
(see
Fig. 2), the intensity is given by
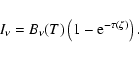 |
(5) |
The optical depth
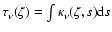 is
defined by the line-of-sight integral (with the line-of-sight perpendicular
to the disk mid-plane) over the absorption coefficient,
is
defined by the line-of-sight integral (with the line-of-sight perpendicular
to the disk mid-plane) over the absorption coefficient,
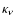 ,
defined by
,
defined by
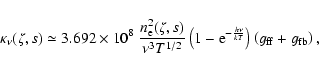 |
(6) |
and integration limits depending on the geometry of the system
(Fig. 2). The parameters
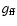 and
and
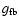 are the
gaunt factors for free-free and free-bound processes, respectively, and have
been calculated (e.g. by Kraus 2000) over a large frequency range and
for different temperatures. Due to the symmetry and the assumed constant wind
temperature, the total observable flux density of the free-free
and free-bound emission is given by
are the
gaunt factors for free-free and free-bound processes, respectively, and have
been calculated (e.g. by Kraus 2000) over a large frequency range and
for different temperatures. Due to the symmetry and the assumed constant wind
temperature, the total observable flux density of the free-free
and free-bound emission is given by
 |
(7) |
where
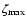 is the outer edge of the ionized wind and d is the
distance to the object. Due to the pole-on view,
the dusty disk around R 126 might cause absorption of the free-free
and free-bound emission from the rear parts of the wind (i.e. below the disk).
However, as stated by Kastner et al. (2006), the dust is expected to
exist only at large distances, i.e. beyond 120 AU. For the wind densities of
our interest, we found that the free-free and free-bound emission is generated
much closer to the star, and any absorbing influence of the dust can be
neglected.
is the outer edge of the ionized wind and d is the
distance to the object. Due to the pole-on view,
the dusty disk around R 126 might cause absorption of the free-free
and free-bound emission from the rear parts of the wind (i.e. below the disk).
However, as stated by Kastner et al. (2006), the dust is expected to
exist only at large distances, i.e. beyond 120 AU. For the wind densities of
our interest, we found that the free-free and free-bound emission is generated
much closer to the star, and any absorbing influence of the dust can be
neglected.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig8.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg80.gif) |
Figure 8:
Calculated SED of R 126 consisting of the stellar continuum and the
free-free and free-bound continuum from the polar wind. The theoretical spectrum
is reddened to the R 126 value. Photometric data are from Zickgraf et al.
(1985, open circles), and from the public databases DENIS (squares),
2MASS (triangles), and MSX (filled circles). Not included here is the modeling
of the dust emission to account for the mid-IR excess. |
| Open with DEXTER |
To calculate the electron density at every point in the wind, we need
to know the polar mass loss rate and terminal velocity. Literature values for
R 126 are still not well constrained and vary over a huge range, depending on
the geometry and the method used by individuals to derive them. As an example
serves the terminal velocity for which Bjorkman (1998) gives
650 km s-1 while Zickgraf et al. (1985) found
1800 km s-1. Due to this uncertainty by almost a factor of 3 we
calculate the free-free and free-bound emission by varying the density
parameter, i.e. the ratio
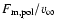 ,
instead of the
individual parameters
,
instead of the
individual parameters
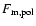 and
and
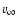 .
The total continuum, including the stellar emission,
is then reddened with the extinction of R 126, and compared with
photometric data from the literature. A good fit to the SED in the optical
and near-IR is achieved for
.
The total continuum, including the stellar emission,
is then reddened with the extinction of R 126, and compared with
photometric data from the literature. A good fit to the SED in the optical
and near-IR is achieved for
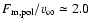
 10-12 g cm-3 and
10-12 g cm-3 and
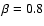 (see Fig. 8).
(see Fig. 8).
Table 1:
Model parameters for the polar and equatorial (i.e. the disk-forming)
winds. Please note that the disk parameters only hold for the [O I] line
forming region.
The density parameters for the equatorial and polar wind as summarized in
Table 1 result in a the density contrast on the order of
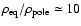 .
This value turns out to be a lower
limit, because all parameters are chosen such that any change
(like (i) a smaller disk opening angle; (ii) the existence of a small
ionized inner disk part; (iii) a vertical density distribution within the disk
due to a latitude dependence of the parameter
.
This value turns out to be a lower
limit, because all parameters are chosen such that any change
(like (i) a smaller disk opening angle; (ii) the existence of a small
ionized inner disk part; (iii) a vertical density distribution within the disk
due to a latitude dependence of the parameter
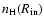 ;
(iv) a cut-off in [O I] line luminosities before saturation is reached) will
immediately request a higher disk density in order to reproduce the observed
[O I] line luminosities.
;
(iv) a cut-off in [O I] line luminosities before saturation is reached) will
immediately request a higher disk density in order to reproduce the observed
[O I] line luminosities.
With a disk density parameter of 10 times the polar one, but a disk ionization
fraction of less than 10-3, the radial electron density distribution
within the disk is at least a factor of 100 lower than the one in the polar
wind. A contribution of the disk to the free-free and free-bound continuum is
therefore indeed negligible, justifying our assumption that the free-free and
free-bound emission is generated purely within the polar wind.
6 Discussion
For our description of the disk model in Sect. 4.1 we made two severe assumptions, namely we requested that
(i) the disk is neutral in hydrogen right from the stellar surface, i.e.
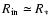 ,
and that
(ii) the disk has a constant outflow velocity. We will now discuss the validity
of these assumptions.
,
and that
(ii) the disk has a constant outflow velocity. We will now discuss the validity
of these assumptions.
A hydrogen neutral disk right from the stellar surface.
We requested that the disk around the rather hot central star is predominantly
neutral in hydrogen right from the stellar surface. Recent ionization structure
calculations by Kraus & Lamers (2003) in non-spherical winds of B[e] supergiants have shown that in the equatorial region hydrogen can indeed
recombine close to the stellar surface, resulting in a geometrically thick
hydrogen neutral disk. To quantify this, we refer to their model C which was
calculated for a star with the same effective temperature as R 126. Further
parameters given in their Table 1 were an electron temperature of 10 000 K,
and an equatorial surface density of 3.3 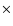 1012 cm-3. With these
parameters, Kraus & Lamers (2003) found that hydrogen recombines in the
equatorial plane at a distance of
1012 cm-3. With these
parameters, Kraus & Lamers (2003) found that hydrogen recombines in the
equatorial plane at a distance of
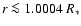 .
.
Our model calculations for the [O I] line luminosities revealed a disk density parameter of about 2.2 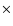 10-11 g cm-3 (see Table 1) which results in an equatorial density on the stellar
surface of
10-11 g cm-3 (see Table 1) which results in an equatorial density on the stellar
surface of
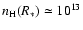 cm-3. This density is about 3 times higher than the one used by Kraus & Lamers (2003). Consequently,
recombination of the disk material will happen even closer to the stellar
surface. It is therefore reasonable to adopt that the disk around the B[e] supergiant R 126 is neutral in hydrogen right from the stellar surface.
cm-3. This density is about 3 times higher than the one used by Kraus & Lamers (2003). Consequently,
recombination of the disk material will happen even closer to the stellar
surface. It is therefore reasonable to adopt that the disk around the B[e] supergiant R 126 is neutral in hydrogen right from the stellar surface.
The constant disk outflow velocity. In order
to describe the disk density distribution with only one free parameter, i.e.
the density parameter
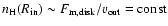 ,
we set the disk outflow velocity constant within the
[O I] line forming region. Figure 5 shows that the line
luminosities of the [O I] lines saturate within about 500 R*; the
5577 Å line saturates even within 50 R*. Let us assume that the
disk-forming wind also has a velocity distribution according to the
,
we set the disk outflow velocity constant within the
[O I] line forming region. Figure 5 shows that the line
luminosities of the [O I] lines saturate within about 500 R*; the
5577 Å line saturates even within 50 R*. Let us assume that the
disk-forming wind also has a velocity distribution according to the
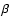 -law. Such a velocity law then mainly influences the formation of the
5577 Å line. This line is created mainly in those wind parts in which
the wind is still accelerating, while the other two [O I] lines are
unaffected from a
-law. Such a velocity law then mainly influences the formation of the
5577 Å line. This line is created mainly in those wind parts in which
the wind is still accelerating, while the other two [O I] lines are
unaffected from a 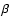 -type velocity law. Their luminosities are produced
at distances at which the velocity has reached already its terminal value.
-type velocity law. Their luminosities are produced
at distances at which the velocity has reached already its terminal value.
According to the equation of mass continuity, Eq. (4), a lower
velocity at a certain distance results in a higher wind density and therefore
in a higher level population. Consequently, the luminosity of the
5577 Å line arising in the accelerated wind region is somewhat enhanced
compared to the luminosity created in an outflow of constant (i.e. terminal)
velocity. A higher line luminosity, however, results in a lower
6300 Å/5577 Å line ratio. Therefore, in order to fit the observations,
a slightly different combination of disk ionization fraction and density
parameter will be necessary.
We calculated the disk ionization fraction and density parameter for an outflowing disk with a temperature of 8000 K and a velocity law with
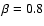 .
From our fitting procedure we found the following results:
.
From our fitting procedure we found the following results:
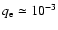 and
and
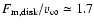
 10-11 g cm-3.
Even though the ionization fraction is a factor of 2.5 higher than in the case
of the constant outflow velocity (see Table 1), the total amount
of ionized hydrogen in the disk is still only 0.1%. In addition, the total
disk mass loss rate found with the
10-11 g cm-3.
Even though the ionization fraction is a factor of 2.5 higher than in the case
of the constant outflow velocity (see Table 1), the total amount
of ionized hydrogen in the disk is still only 0.1%. In addition, the total
disk mass loss rate found with the 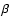 -type disk wind scenario is now
-type disk wind scenario is now
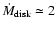
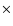
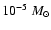 yr-1. This
value is only slightly lower than the value derived with the constant outflow
velocity scenario in Sect. 4.3. Therefore, the conclusion of a hydrogen neutral disk with a density ratio of about a factor of 10 between equatorial and polar wind remains valid.
yr-1. This
value is only slightly lower than the value derived with the constant outflow
velocity scenario in Sect. 4.3. Therefore, the conclusion of a hydrogen neutral disk with a density ratio of about a factor of 10 between equatorial and polar wind remains valid.
We want to emphasize that not much is known about the real velocity
distribution of the outflowing disks around B[e] supergiants. Since a 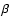 -type velocity law does not drastically alter the results, the
assumption of a constant outflow velocity as a first guess seems therefore
to be a reasonable approach.
-type velocity law does not drastically alter the results, the
assumption of a constant outflow velocity as a first guess seems therefore
to be a reasonable approach.
7 Conclusions
This paper is not aimed to present a detailed analysis of R 126 and to derive
its wind and disk parameters with high accuracy, but to present a somewhat
revised model for the outflowing disk scenario. We suggest that the disks
around B[e] supergiants are neutral in hydrogen at, or close to the stellar
surface. Indications for such a model come from observations as well as
from theory and are here briefly summarized:
- Former investigations of the disks around B[e] supergiants assumed
that the observed near-IR excess is caused by free-free emission from the disk,
as it is the case for classical Be stars. A contribution from the polar wind
was thought to be neglibible. Fitting of the near-IR excess with free-free
emission arising purely in the outflowing disk delivers a disk mass loss
rate that defines an upper limit to the disk (dust) density.
The resulting dust emission was however found to be too low to account
for the observed IR excess (Porter 2003).
- Porter (2003) tried to solve this dust emission problem by
allowing for a flatter disk density distribution. However, his modified disk
model for the B[e] supergiant R 126 is not able to reproduce the observed
[O I] line luminosities, underestimating them by about a factor of 50! To
account for the [O I] line luminosities a (much) higher disk density is
needed.
- Due to the nearly equal ionization potentials of O I and H
I, the existence of strong [O I] emission further requests that in the
line forming region hydrogen must be predominantly neutral.
- Recent ionization structure calculations in non-spherically symmetric
winds of B[e] supergiants have revealed that the wind material indeed
recombines in the equatorial plane already at, or very close to the stellar
surface, resulting in a hydrogen neutral equatorial disk or zone (see e.g.
Kraus & Lamers 2003, 2006; Kraus 2006).
The most important consequence of such a hydrogen neutral disk is the fact
that the disk can no longer be considered as the formation location of the
free-free emission causing the near-IR excess. This emission must then mainly
be produced in the line-driven polar wind. Consequently, the fitting of the
free-free emission does not result in an upper limit to the disk mass loss rate
anymore. Instead, the disk mass loss rate, and hence the disk density, can be
(much) higher, providing an ideal environment for the [O I] line emission
as well as for efficient dust condensation to account for the observed IR excess.
We tested the scenario of a hydrogen neutral disk for the LMC B[e] supergiant R 126 by modeling the line luminosities and line ratios of the
[O I] emission lines resolved in our high-resolution optical spectra.
The parameters derived for the disk and wind of R 126 are the following:
To summarize, based on a detailed investigation of the emerging [O I] emission lines we found that the disk around the B[e] supergiant R 126 is
neutral in hydrogen right from the stellar surface. Since all B[e] supergiants show strong [O I] line emission, we postulate that the hydrogen neutral ouflowing disk scenario might also hold for the other members of the B[e] supergiant class.
Acknowledgements
We thank the anonymous referee for suggestions and critical comments
that helped to improve the paper.
M.K. acknowledges financial support from GA CR 205/04/1267.
M.B.F. is supported by CNPq (Post-doc position - 150170/2004-1).
- Bjorkman, J. E.
1998, in B[e] stars, ed. A. M. Hubert, & C. Jaschek (Kluwer
Academic Publishers), 194
(In the text)
- Grevesse, N., &
Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] (In the text)
- Hamuy, M., Suntzeff, N.
B., Heathcote, S. R., et al. 1994, PASP, 106, 566 [NASA ADS] [CrossRef] (In the text)
- Kafatos, M., &
Lynch, J. P. 1980, ApJS, 42, 611 [NASA ADS] [CrossRef] (In the text)
- Kastner, J. H.,
Buchanan, C. L., Sargent, B., & Forrest, W. J. 2006, ApJ, 638,
L 29
(In the text)
- Kraus, M. 2000, Ph.D. Thesis,
University of Bonn, Germany
(In the text)
- Kraus, M. 2006,
A&A, 456, 151 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kraus, M.,
& Borges Fernandes, M. 2005, in The nature and evolution of
disks around hot stars, ed. R. Ignace, & K. G. Gayley (San
Francisco: ASP), ASP Conf. Ser., 337, 254
(In the text)
- Kraus, M., & Lamers, H.
J. G. L. M. 2003, A&A, 405, 165 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kraus, M., & Lamers, H.
J. G. L. M. 2006, in Stars with the B[e] Phenomenon, ed. M. Kraus,
& A. S. Miroshnichenko (San Francisco: ASP), ASP Conf. Ser.,
355, 57
(In the text)
- Kraus, M., Borges
Fernandes, M., Andrade Pilling, D., & de Araújo, F. X.
2006, in Stars with the B[e] Phenomenon, ed. M. Kraus, & A. S.
Miroshnichenko (San Francisco: ASP), ASP Conf. Ser., 355, 163
(In the text)
- Lamers, H. J. G. L. M.,
& Cassinelli, J. P. 1999, Introduction to stellar winds
(Cambridge University Press)
(In the text)
- Lamers, H. J. G. L.
M., Zickgraf, F.-J., de Winter, D., Houziaux, L., & Zorec, J.
1998, A&A, 340, 117 [NASA ADS] (In the text)
- McGregor, P.
J., Hillier, D. J., & Hyland, A. R. 1988, ApJ, 334, 639 [NASA ADS] [CrossRef] (In the text)
- McGregor, P.
J., Hyland, A. R., & McGinn, M. T. 1989, A&A, 223, 237 [NASA ADS] (In the text)
- Mendoza, C. 1983, IAU
Symp., 103, 143 [NASA ADS] (In the text)
- Porter, J. M. 2003,
A&A, 398, 631 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Wiese, W. L., Smith, M.
W., & Glennon, B. M. 1966, Atomic Transition Probabilities
(National Standard Reference Data System, Washington DC), Vol.
1
(In the text)
- Zickgraf, F.-J. 1992,
in Nonisotropic and Variable Outflows from Stars, ed. L. Drissen,
C. Leitherer, & A. Nota (San Francisco: ASP), ASP Conf. Ser.,
22, 75
(In the text)
- Zickgraf, F.-J.,
Wolf, B., Stahl, & Humphreys, R. M. 1989, A&A, 220,
206 [NASA ADS] (In the text)
- Zickgraf, F.-J.,
Wolf, B., Stahl, O., Leitherer, C., & Klare, G. 1985, A&A,
143, 421 [NASA ADS] (In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig1.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg10.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig2.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg14.gif)
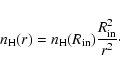
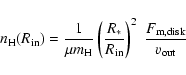
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{6325fig3.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg32.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig4.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig5.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg48.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig6.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg52.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig7.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg56.gif)
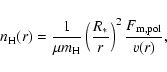
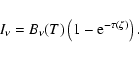
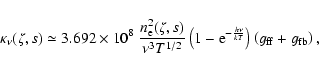

![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6325fig8.eps}\end{figure}](/articles/aa/full/2007/08/aa6325-06/Timg80.gif)