A&A 463, 427-443 (2007)
DOI: 10.1051/0004-6361:20066031
S. Pasetto - C. Chiosi
Department of Astronomy, Padova University, Vicolo dell'Osservatorio 2, 35122, Padova, Italy
Received 13 July 2006 / Accepted 17 November 2006
Abstract
Aims. Basing on the projected distribution of the galaxies in the Local Group, Sawa & Fujimoto found that they all seem to distribute on a rather thin plane containing the two mayor local galaxies of the Local Group, Milky Way and Andromeda, and all their dwarf satellites. As their conclusion could be severely biased by projectional distortion effects, we re-analyse the whole issue using a different approach. In brief, adopting known data on positions and distances, we make use of the analytical geometry and look for the plane that minimizes the distances of all galaxies to it. A planar distribution is indeed found that, however, does not coincide with the plane found by Sawa & Fujimoto. Why? The second part of this study is devoted to answer this question and to find a dynamical justification for the planar distribution.
Methods. To this aim, we apply the Hamilton Method (Minimum Action) to investigate the dynamics of the two major system of the Local Group, Milky Way and Andromeda, under the action of external forces exerted by nearby galaxies or groups external to the Local Group.
Results. We find that the planar distribution is fully compatible with the minimum action and that the external force field is likely parallel to the plane. It pulls the galaxies of the Local Group without altering their planar distribution. Special care is paid to evaluate the robustness of this result.
Conclusions. In this paper we have examined the spatial distribution of galaxies in the Local Group. They are confined to a plane that can be statistically and dynamically understood as the result of the Minimum Action. The planar distribution seems to be stable for a large fraction of the Hubble time. The external force field, that has likely been constant over the same time interval, does not alter the planar distribution as it is nearly parallel to it. Effects due to undetected halos of sole Dark Matter are briefly discussed. They could be a point of uncertainty of the present study.
Key words: stellar dynamics - Local Group - galaxies: dwarf
Recent reviews of the state-of-art of our understanding of the structure, past history, galaxy content, and stellar populations in individual galaxies of the Local Group (LG) are by van den Bergh (1999), Mateo (1998) and Grebel (2001). However, our present knowledge of the proper motions of Andromeda (M 31) and most galaxies of the LG is dramatically insufficient and inadequate to correctly reconstruct the past and present structure of the LG. As a matter of facts, no orbital parameters can be derived with adequate precision to constrain the space of velocities for all known objects. As a consequence of it, the dynamical evolution of the LG galaxies, and the dynamical origin of the dwarf satellites orbiting around and interacting with the two major galaxies, i.e. Milky Way (MW) and M 31, are not clear.
Over the years, many authors addressed these issues both observationally and theoretically, with the aim of understanding the evolution of the LG galaxies. Since the first observations of Barnard (1917), perhaps the most important steps toward understanding the nature of the LG is the determination of the proper motion and tangential motion of M 31, which unfortunately are still poorly known. The first important study dealing with the evolution of the LG, supposedly in isolation, is by Kahn & Woltjer (1959). The authors based their study on the spherical gravitational collapse and expansion approximation. As consequence of it, with the aid of the third Kepler's law they predicted only radial orbits for the MW and M 31 from the origins to the present time. The possibility of a tangential motion for M 31 with respect to the MW was automatically ruled out. Another model of the LG based on pure radial orbits for M 31 and MW has been presented by Lynden-Bell & Lin (1977). The authors made use of the second law of Newton applied to the motion of the two major components of the LG. Yahil et al. (1977) focused on the determination of the circular velocity of our own galaxy using the LG as reference system. They studied the origin of the LG angular momentum and for the first time emphasised how the tidal force exerted by external proto-groups could be the cause of the origin of the LG angular momentum, and how this interpretation should be preferred to the cosmological origin proposed by Hoyle (1951), Peebles (1969) and Thuan & Gott (1977). They supposed that the spin-orbit coupling in the first stages of the Universe could occur, even if the angular moment gained by the spin of Dark Matter halos and then transferred to the orbits could be too small even for the largest eccentricity orbits (Ostriker et al. 1974; Ostriker & Peebles 1973). As these conclusions were not in agreement with previous studies, they spurred the first attempts to measure the proper motions of M 31 (different from zero).
Gott & Thuan (1978) first presented the equations governing
the motion of the LG members. This study, however, still made use
the radial approximation for the relative motion of MW and M 31. In
their picture, thanks to the Thompson scattering before the
recombination time (
![]() ), the matter is coupled with
radiation and it does not present random motions but only the motion
of the Hubble flow. After recombination, the matter decouples from
radiation: therefore galaxies and galaxy clusters can freely form
thanks to the small unstable fluctuations of the density
(Gunn & Gott 1972; Peebles 1974). In this context,
the equations for the motion of MW and M 31 have been written for the
first time. This yielded an upper limit for the redshift at
which the proper motions originated, z<1500. At earlier epochs,
speaking of proper motions was not physically meaningful. These
conclusions are, however, based on the fact that the vorticity of
the CMB as well as that of the initial conditions are null.
Nowadays minor anisotropies of the CMB have been discovered by WMAP
(Bennett et al. 2003; Saha et al. 2006) thus somewhat weakening the above assumptions.
Notwithstanding the new
observational and theoretical developments, the study of
Gott & Thuan (1978) is still a landmark on the origin of
the LG angular momentum.
), the matter is coupled with
radiation and it does not present random motions but only the motion
of the Hubble flow. After recombination, the matter decouples from
radiation: therefore galaxies and galaxy clusters can freely form
thanks to the small unstable fluctuations of the density
(Gunn & Gott 1972; Peebles 1974). In this context,
the equations for the motion of MW and M 31 have been written for the
first time. This yielded an upper limit for the redshift at
which the proper motions originated, z<1500. At earlier epochs,
speaking of proper motions was not physically meaningful. These
conclusions are, however, based on the fact that the vorticity of
the CMB as well as that of the initial conditions are null.
Nowadays minor anisotropies of the CMB have been discovered by WMAP
(Bennett et al. 2003; Saha et al. 2006) thus somewhat weakening the above assumptions.
Notwithstanding the new
observational and theoretical developments, the study of
Gott & Thuan (1978) is still a landmark on the origin of
the LG angular momentum.
Subsequently, Lynden-Bell (1981) presented the equations for a non purely radial motion of M 31. The history of the orbital equations for the LG galaxies became even more complicated with results intermediate to those by Lynden-Bell (1981) and Einasto & Lynden-Bell (1982).
An independent treatment of the equations of motion for the LG members was presented by Mishra (1985).
Using the solutions of the restricted 3-body problem and assuming
the ellipticity of
![]() estimated by
Einasto & Lynden-Bell (1982) and Yahil et al. (1977), it was
argued that M 31 and MW are on a linear orbit and that the minor
galaxies maintain a planar motion throughout at all times.
estimated by
Einasto & Lynden-Bell (1982) and Yahil et al. (1977), it was
argued that M 31 and MW are on a linear orbit and that the minor
galaxies maintain a planar motion throughout at all times.
A milestone along the road of the evolution and formation of the LG was set by the Nearby Galaxies Catalog (hereinafter NBG) of Tully (1988), a sample of 2367 galaxies with systematic velocities less than 3000 km s-1. The spatial location of the NBG galaxies is shown in Fig. 1 to give an idea of structure of the Local Universe. A first systematic investigation of the effect of the external galaxies on the LG has been presented in Raychaudhury & Lynden-Bell (1989). Studying the influence of the gravitational quadrupole interaction by external galaxies on the LG, the authors proved that the LG is not tidally isolated and presented a new set of equations for the motion of its galaxies. Even if the equations and the proper motion of M 31 given by Raychaudhury & Lynden-Bell (1989) are not fully correct (e.g. see Dunn & Laflamme 1993), the fundamental result still remains: the LG is not isolated and the proper motion of M 31 is not null.
In the same years, a flourish of theoretical studies began (Peebles 1994,1995,1989). In Peebles (1989) the equations of motion were revised with the aid of the Hamiltonian Principle and a new method for tracing back the orbits of the LG galaxies was presented and subsequently adapted to the LG problem by Peebles et al. (1989) and Peebles (1994), together with new determinations of the tangential motion of M 31 (Peebles 1995,1990). In the series of studies by Peebles and collaborators, and other independent groups as well, an interesting result was obtained (Goldberg 2001b; Shaya et al. 1995; Sharpe et al. 1999; Peebles et al. 2001; Peebles 1995): the solutions for the local minimum or stationary points of the action are compatible with a tangential motion of M 31 as large as the radial motion.
Following the same methodology, Dunn & Laflamme (1993)
independently derived the value for the proper motion of M 31
![]() mas/yr.
Despite this great improvement in the knowledge of the LG, new
problems arose regarding its cosmological origins as noted by
Governato et al. (1997). They pointed out the strong dependence
of the theoretical models on the cosmological parameters for the
peculiar velocities of galaxies in CDM context. The same
dependence has been suspected for some observational constraints,
e.g. for the distances or the radial velocities
(Byrd et al. 1994; Valtonen et al. 1993). Recently a new
determination of the mass of M 31 has been derived by
Evans & Wilkinson (2000). In contrast with all previous dynamical
estimates, the mass assigned to M 31 is smaller than the mass of MW.
This result can be explained recalling that it stems from the
notion that the velocity vector of M 31 is purely radial and that
the mass is derived from velocity arguments. One may argue that the
lower mass assigned to M 31 could be taken as an hint that the motion
of M 31 is not merely radial.
mas/yr.
Despite this great improvement in the knowledge of the LG, new
problems arose regarding its cosmological origins as noted by
Governato et al. (1997). They pointed out the strong dependence
of the theoretical models on the cosmological parameters for the
peculiar velocities of galaxies in CDM context. The same
dependence has been suspected for some observational constraints,
e.g. for the distances or the radial velocities
(Byrd et al. 1994; Valtonen et al. 1993). Recently a new
determination of the mass of M 31 has been derived by
Evans & Wilkinson (2000). In contrast with all previous dynamical
estimates, the mass assigned to M 31 is smaller than the mass of MW.
This result can be explained recalling that it stems from the
notion that the velocity vector of M 31 is purely radial and that
the mass is derived from velocity arguments. One may argue that the
lower mass assigned to M 31 could be taken as an hint that the motion
of M 31 is not merely radial.
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{6031fig01.eps}\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg6.gif) |
Figure 1: A sketch of the spatial distribution of the NBG galaxies in the Local Universe. The Sculptor-Coma cluster is highlighted and bigger dots are used for M 31, MW and the LG galaxies of 1. From Tully & Fisher (1988). |
| Open with DEXTER | |
Moreover, attempts were made to find the spatial distribution of the
LG galaxies, e.g. Hartwick (2000) suggested that the
galaxies crowd on a highly flattened ellipsoid with axial ratios
![]() which to a good
approximation can be considered as a planar distribution. Another
problem under investigation was the anisotropic distribution of
inner sub-haloes with respect to larger haloes in relation to the
Holmberg effect (Sales & Lambas 2004). General consensus on
this issue has not yet been reached (Knebe et al. 2004). In
particular it is unclear and matter of debate whether
disruption-tidal effects can create the apparent polar alignment of
the dwarf satellites around the mother galaxy or, for the particular
case of the LG, the position of the dwarf galaxies is the
consequence of peculiar directions of pre-existing cosmological
filaments. See for instance Fig. 1 which displays the
spatial distribution of the NBG galaxies. In a recent paper,
Kroupa et al. (2005) suggest a planar distribution of the
satellites of MW, which however could also be explained as a consequence of the distribution of sub-haloes (Zentner et al. 2005) in the early cosmological stages
(Kang et al. 2005). Another important result for
the sub-halo alignment in cosmological simulations was obtained by
Libeskind et al. (2005). The same problem is under
investigation for M 31 (Koch & Grebel 2006). Finally,
Sawa & Fujimoto (2005) have recently proposed a new dynamical
model based on the existence an orbital plane for M 31 and MW.
which to a good
approximation can be considered as a planar distribution. Another
problem under investigation was the anisotropic distribution of
inner sub-haloes with respect to larger haloes in relation to the
Holmberg effect (Sales & Lambas 2004). General consensus on
this issue has not yet been reached (Knebe et al. 2004). In
particular it is unclear and matter of debate whether
disruption-tidal effects can create the apparent polar alignment of
the dwarf satellites around the mother galaxy or, for the particular
case of the LG, the position of the dwarf galaxies is the
consequence of peculiar directions of pre-existing cosmological
filaments. See for instance Fig. 1 which displays the
spatial distribution of the NBG galaxies. In a recent paper,
Kroupa et al. (2005) suggest a planar distribution of the
satellites of MW, which however could also be explained as a consequence of the distribution of sub-haloes (Zentner et al. 2005) in the early cosmological stages
(Kang et al. 2005). Another important result for
the sub-halo alignment in cosmological simulations was obtained by
Libeskind et al. (2005). The same problem is under
investigation for M 31 (Koch & Grebel 2006). Finally,
Sawa & Fujimoto (2005) have recently proposed a new dynamical
model based on the existence an orbital plane for M 31 and MW.
In this paper we address some of the above issues. The plan is as follows. In Sect. 2 we examine the spatial distribution of the LG galaxies: starting from the analysis of Sawa & Fujimoto (2005) and using a different procedure (Principal Component Analysis) we find that a common plane really exists but different from the one found by Sawa & Fujimoto (2005). We then proceed to study the dynamics of the LG. In Sect. 3 we present the Hamilton method of Constrained Minimum Action. In Sect. 4 we present the samples of galaxies in the Local Universe we have adopted to study the dynamics of the LG and the effects on this by nearby galaxies. In Sect. 5 we minimize the Action and present the results. In Sect. 6 we examine in detail the robustness of the procedure we have adopted. In Sect. 7 we evaluate the effect of external galaxies on the dynamics of the LG. The main result is that the orbits of the dominant galaxies of the LG are dynamically consistent with a plane that within the uncertainties coincides with the one derived in Sect. 2 from mere geometrical considerations. This is indeed the plane that minimizes the action. Several important implications of this finding are discussed in the above sections. Finally, in Sect. 8 we draw some concluding remarks.
As already mentioned, from the visual inspection of the sky-projected spatial distribution of the LG galaxies Sawa & Fujimoto (2005) suggest the existence of an orbital plane for MW, M 31 and satellites. However the idea is not new. 2D studies have already been employed to establish planes in the LG. Limiting ourselves to a few examples, Hartwick (2000) suggested a flat ellipsoid which is not too different from a plane; studies of the LG dynamics, see for instance Kahn & Woltjer (1959) and Raychaudhury & Lynden-Bell (1989). Finally Kunkel (1979), () and Fusi Pecci et al. (1995) suggested that the satellite dwarf galaxies of the MW and M 31 lie on planes.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{6031fig02.eps}\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg8.gif) |
Figure 2: Hammer's projection with the amplitude of distortion (in percent) according to the code 1 = no distortion, 100 = extremely high distortion. The heavy dots are the galaxies of Table 1. The arrows indicate the regions of larger concentration of objects that could be interpreted as hints of underlying 3D structures. They, however, occur in regions of large distortion. |
| Open with DEXTER | |
We suspect, however, that the plane found by Sawa & Fujimoto (2005) largely results from distortion effects affecting the visual inspection of spatial structures. Therefore, in this section we reconsider the whole subject and check whether such a plane can be derived from other objective methods.
Our analysis of the galaxies distribution stands on the Mateo (1998) sample of LG galaxies (see the entries of Table 1). Whenever required the radial velocities are taken from Tully & Fisher (1988), however updated to more recent determinations if available (see below). The same sample has been used by Sawa & Fujimoto (2005).
Following Sawa & Fujimoto (2005) we start by looking at the projected
distribution of the LG members on the celestial sphere. It is soon
evident that this way of proceeding is severely biased by the type
of projection in use. To illustrate the point, in
Fig. 2 we show the Hammer projection on which the
contours of projection-induced distortion on the map are superposed.
The distortion is measured by the ratio of the infinitesimal areas
given by the jacobian of the transformation matrix between the
cartesian coordinate system and the projected coordinate system. The
amplitude of distortion is given in percent, i.e. normalised to an un-distorted projection. As a matter of fact the major clustering of objects that could suggest peculiar spatial structures such as filaments, planes etc, actually occurs in regions of the Hammer
plane with distortion amounting to about 50-75 percent. Therefore,
visual inspections of the projected distribution to infer spatial
structures could lead to wrong conclusions. Other kinds of
projection do not make a better job. For instance in
Figs. 3 and 4 we show the Mercator and
Cassini projections, respectively. We have added the Tissot's
circles, which are equal circles on the celestial sphere to better
visualise the effects of projectional distortions. In principle, the
combination of these two projections could improve upon the correct
view of different areas on the celestial sphere. In the Mercator
projection all the lines with the same angles with respect to the
meridians are straight lines, and thus reduce the distortion near
the equatorial plane of the MW (
![]() is conventionally
adopted). Unfortunately, as all dwarf galaxies of the LG have
is conventionally
adopted). Unfortunately, as all dwarf galaxies of the LG have
![]() ,
in the direction
,
in the direction
![]() they are masked by the Galactic Plane, even the
Mercator projection does not help us very much. The Cassini
projection ensures instead a good approximation toward the Galactic
Pole. Once again the few apparent structures that could hint for
real 3D structures are located near regions of large distortion.
Therefore, the main result of this first analysis is that the 3D structure of the LG when projected onto 2D surfaces could mimic planar distributions that may not exist in reality.
they are masked by the Galactic Plane, even the
Mercator projection does not help us very much. The Cassini
projection ensures instead a good approximation toward the Galactic
Pole. Once again the few apparent structures that could hint for
real 3D structures are located near regions of large distortion.
Therefore, the main result of this first analysis is that the 3D structure of the LG when projected onto 2D surfaces could mimic planar distributions that may not exist in reality.
![\begin{figure}
\par\includegraphics[width=5.4cm,clip]{6031fig03.eps}\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg12.gif) |
Figure 3: Mercator's projection with Tissot's circles. The Mercator projection provides a good representation near the equatorial plane and a very poor one towards the poles. The lack of galaxies near the galactic plane is due to Galactic absorption. Clearly the apparent distribution is not uniform. There seem to be several 2D structures that could perhaps hint for real 3D structures. However, the same remark made in Fig. 2 would apply also here. |
| Open with DEXTER | |
| |
Figure 4: Cassini's projection with Tissot's circles. The North and South Galactic Poles are now well represented. Once again a few 2D structures can be noticed. They, however are located in regions of high distortion so that the same remark made in Fig. 2 would apply also here |
| Open with DEXTER | |
Table 1: Parameters of LG galaxies used in this study.
For the above reasons, we decided to approach the problem in a different way, i.e. making use of the analytical geometry to
investigate the idea of Sawa & Fujimoto (2005). We start
by assuming that the Sawa & Fujimoto (2005)
conclusion is true, i.e. LG galaxies crowd on a plane, but
check it. The method we have adopted is ultimately the Principal
Components Analysis (see for instance Jobson 1994). Given
N galaxies (of the LG), with coordinates
![]() we want to find the plane that best
approximates their spatial distribution. In other words, given
N points, which are the principal directions of the plane
best approximating these points?
we want to find the plane that best
approximates their spatial distribution. In other words, given
N points, which are the principal directions of the plane
best approximating these points?
![\begin{figure}
\par\includegraphics[width=12cm,clip]{6031fig05.eps}\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg16.gif) |
Figure 5: Projection onto the coordinate planes (X,Y) and (X,Z) as indicated, and two 3D views ( bottom left and right panels) of the our plane best minimizing the distance (location) of the LG galaxies. The (X,Y) projection ( top left panel) is parallel to the equatorial plane of the MW. The big red filled circles are MW and M 31. The yellow circles are the dwarf satellites on either sides of the plane. Looking at the 3D view in which the plane is seen edge-on ( bottom right), MW and M 31 are very close to it and within the uncertainty can be considered as belonging to it. See the text for details. |
| Open with DEXTER | |
The Hessian normal representation of a plane is suited to our aims
| (1) |
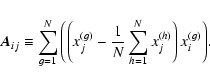 |
(6) |
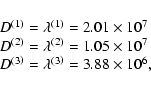
The situation of the plane is shown in Fig. 5
where the top left and right panels show the LG galaxies projected
onto the plane of the MW and perpendicular to it, whereas the bottom
left and right panels show the same galaxies projected face-on and
edge-on onto the plane minimizing D. From the lower right panel
of Fig. 5 we see that the two dominant galaxies (MW
and M 31) do not strictly belong to the plane. However, considering
the uncertainties in the position of each galaxy, we may reasonably
conclude that also the two major galaxies of the system
belong to the plane![]() .
.
Starting from this first result we may also assume that the geometrical plane contains the barycentre of the system. This in not true in general but limited to the LG. It follows that the distribution of the baryonic (and dark) matter is symmetric with respect to this plane. Furthermore, the fact that the two most massive galaxies belong to the plane could perhaps indicate that the effect, if any, of still undetected massive bodies influencing the LG dynamics is small and likely was such in past. On the problem of the mass tracers (White et al. 1988; Davis & Peebles 1983) we will come back in Sect. 3. To conclude we may provisionally assume that
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6031fig06.eps}\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg31.gif) |
Figure 6: The 3D view of the three planes we have found with Eq. (7) together with the plane found by Sawa & Fujimoto (2005) seen edge-on and the galaxies of the LG. The two encircled zones highlight the position of MW and M 31 and their satellites. None of our planes coincides with that of Sawa & Fujimoto (2005). See the text for more details. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6031fig07.eps}\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg32.gif) |
Figure 7:
3D-view of the LG as observed from the same view angle
adopted by Sawa & Fujimoto (2005), i.e.
|
| Open with DEXTER | |
To strengthen our result we extend the above analysis as follows. Let us suppose that all the galaxies of the LG are located on a plane. It goes without saying that this plane contains also the vector joining MW and M 31. Now we may turn the argument around and, fixing the straight line joining MW and M 31, we may consider the manyfold of planes passing through this line. Therefore our previous analysis and result are now translated into finding the plane of the manyfold that minimizes the distances to it of all remaining galaxies. We would like to note here that the degree of freedom to our disposal (rotation of the plane around the MW-M 31 line) is not a mere mathematical problem: it is indeed due to the yet unsolved question of the tangential motion of M 31 with respect to the MW (widely discussed in Sect. 1). Similar, though not identical reasoning was followed by Sawa & Fujimoto (2005) when deriving the orbits of M 31 and MW by means of the projection analysis. Fixing the plane is equivalent to reduce the degree of freedom for the motion of M 31 and to set a constraint on the dynamics of the LG as a whole (Pasetto & Chiosi 2006, in preparation).
If the MW-M 31 vector belongs to the plane in question (reasonable assumption), the motion is mainly central and plane. Small perturbations of the central motion will be investigated in the Sect. 6.3. We are interested here to investigate the possibility that the orbital plane of the two main galaxies might be related to the plane we have just derived from mere geometrical considerations. As this result is not the rule, different determinations of the proper motion of M 31 are possible, see for instance Raychaudhury & Lynden-Bell (1989) and Sawa & Fujimoto (2005), depending on the kind of different physical considerations that guided the authors towards the reconstruction of the dynamical history of the LG.
The target now is to minimize the Eq. (3) imposing
the constraint given by Eq. (4) and the additional one
that the normal to the minimization plane has to be orthogonal to
the MW-M 31 vector
![]() .
The latter constraint is expressed by the relation
.
The latter constraint is expressed by the relation
| (8) |
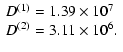 |
(11) |
Clearly the two planes defined by the systems of Eqs. (7) and (10) are not the same. Indeed system (10) is a simplification of system (7). However, the difference between the two planes is small as shown in Fig. 8. This amply justifies the use of the results from system (10) in the analysis below.
To investigate the dynamics of the LG we use the Hamilton's principle of Minimum Action. The method was developed and adapted to cosmological problems in Lagrangian description by Peebles (1989), and its applicability was tested by Peebles (1980) and Bondi (1960). The key ingredients are the boundary conditions applied to the initial and end point of each trajectory.
Each mass point (galaxy) evolves under the gravitational potential
of an expanding Universe constrained by the condition
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6031fig08.eps}\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg41.gif) |
Figure 8: The two planes minimizing the spatial distribution of galaxies in the LG. One is the best plane derived from solving the system of Eq. (5) and given by the eigen-vectors of Eq. (7) that has already been presented, the other is obtained from the system of Eqs. (9) and the eigen-vectors of Eq. (10). This second solution assumes that the vector MW-M 31 lays on the plane. Within the uncertainty the two planes coincide. |
| Open with DEXTER | |
An intrinsic difficulty of the variational principle is that it does not yield the equations of motion when the action (13) is minimum, but more generally when the derivatives are null. So a path that minimizes the action (13) satisfies the equations of motion but the opposite is not true. A path that satisfies the Euler-Lagrange equations could not correspond to a minimum of the action (Whittaker 1989). This leads to the problem of determining the stationary points of the action integral. The issue will be addressed in the next section limited to our specific situation.
Another severe difficulty of the Action Principle concerns the mass tracers to use. The methods requires that the Baryonic Matter can be used as mass tracer and that no lumps of sole Cold Dark Matter are around altering the estimate derived from baryons. The problem has long been debated with controversial results (Natarajan & Springel 2004; Dunn & Laflamme 1995; White et al. 1988; Davis & Peebles 1983).
Despite these points of uncertainty and considering that we are not interested in the direct determination of the cosmological parameters (e.g. Dunn & Laflamme 1995), we adopt the Action method. It allows us to easily test the results for different cosmological models.
In the general case of a cosmologically flat Universe, the curvature
of the Universe is given by
A suitable representation of the orbits to be inserted in the
system (15) has been proposed by
Peebles (1989). They are expressed as a linear
combination of suitable universal functions of time with unknown
coefficients
![]()
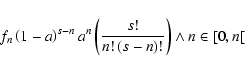 |
(19) |
Another useful expression is the one proposed by
Giavalisco et al. (1993) who assume that the series representing
the quasi-linear solution has to be as close as possible to the
linear solution and to converge to it in the limit of small
perturbations. Therefore the leading term of Eq. (17) is
the linear approximation of Zel'dovich
(e.g. Coles & Lucchin 2002). This approximation holds good
only in the earliest stages of the Universe due to its linear
character. However it has widely been used to describe density
perturbations over large scales, treating galaxy clusters as
particles. This is possible because the strongly non linear motions
inside a cluster (LG as well as other nearby groups) somewhat
balance each other, so that the motion of the barycentre is
influenced only by its closest neighbourhood. Thanks to it we may
adopt the equations
![\begin{displaymath}%
D_0 = D\left( {t_0 } \right) = \left[ {\frac{{\dot a}}{a}\int_0^a
{\frac{{{\rm d}a}}{{\dot a^3 }}} } \right]_{a_0 }.
\end{displaymath}](/articles/aa/full/2007/08/aa6031-06/img56.gif) |
(21) |
As there are many different minima of the action (13) able to reproduce a given set of initial conditions, another version of the least action method has recently been proposed by Goldberg & Spergel (2000) and applied to reconstruct the haloes of MW and M 31 (Goldberg 2001b) considered as isolated systems.
As explained in Sect. 5 we have tried different algorithms to check the results originating from different minima of the action.
To consider the LG as an isolated system, the forces exerted by the
external galaxies or groups must be lower than those developed by
the internal galaxies. Typically an external mass M at a distance ![]() will produce a force for unitary mass
will produce a force for unitary mass ![]()
![]() if it is sufficiently spherical so that
multi-pole contribution can be neglected. The mutual forces that MW
and M 31 exert each other have two main contributions: a mean force
produced by distant bodies (see Table 2) that is is the target of this
study) and a fluctuating force due to the dwarf galaxies inside the
LG (Pasetto & Chiosi 2006, in preparation). To give a rough
idea of the problem, let us consider the LG as made by a number Nof galaxies of mass
if it is sufficiently spherical so that
multi-pole contribution can be neglected. The mutual forces that MW
and M 31 exert each other have two main contributions: a mean force
produced by distant bodies (see Table 2) that is is the target of this
study) and a fluctuating force due to the dwarf galaxies inside the
LG (Pasetto & Chiosi 2006, in preparation). To give a rough
idea of the problem, let us consider the LG as made by a number Nof galaxies of mass ![]() ,
assumed to be uniformly and spherically
distributed. At any distance r from the centre of the LG
the inner total mass
,
assumed to be uniformly and spherically
distributed. At any distance r from the centre of the LG
the inner total mass
![]() is given by
is given by
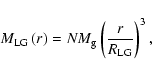 |
(22) |
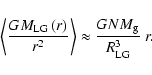 |
(23) |
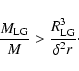 |
(24) |
The major source of data is the NBG together with many subsequent implementations. To mention a few, we recall Peebles (1989), Raychaudhury & Lynden-Bell (1989), Peebles (1990), (), Peebles (1994, 1995), Sharpe et al. (1999), Peebles et al. (2001), and references.
The key data to use here are the distances and the radial velocities. The uncertainty affecting the distances is particularly relevant here because it influences very much the derivation and prediction of a galaxy orbit and its evolution in turn. Thoughtful analyses of the importance of good distances in tracking-back the orbits of the LG galaxies are by Valtonen et al. (1993) and Byrd et al. (1994) to whom the reader should refer for details. Their reconstruction of the orbits of MW and M 31 is based on the distances of Maffei 1 (Buta & McCall 1983) and IC 342 (McCall 1989) (based in turn on recent determinations of the Galaxy extinction). In these studies, the highest uncertainty cames from the distance of Maffei 1. The authors assumed 1.8 Mpc, much shorter than 3.9 Mpc given by Tully & Fisher (1988) and the recent determination of 3.5 Mpc reported by Fingerhut et al. (2003).
Over the years many efforts have been made to cope with the
uncertainty due to distances. Recently Phelps (2002)
showed that a canonical transformation of the action (13)
can be used to work directly with the natural boundary conditions at
redshift z=0 and the angular position
![]() of
a moving observer. Similar attempts have been made either by
changing the orbit functions (Giavalisco et al. 1993) or the
action (Schmoldt & Saha 1998), or using the method of variable
end-points and the "transversality'' condition
(Whiting 2000).
of
a moving observer. Similar attempts have been made either by
changing the orbit functions (Giavalisco et al. 1993) or the
action (Schmoldt & Saha 1998), or using the method of variable
end-points and the "transversality'' condition
(Whiting 2000).
In the following we will select a sample of external galaxy groups for which we will evaluate the dynamical effects on the LG. Fortunately the uncertainty on the distances for this sample are found not to significantly affect our results. In any case we will always keep in mind that distances are the crucial parameter of our analysis and observational astronomy in general, see e.g. Carrasco et al. (2004) and Walker (2003).
Given these premises, we briefly review the main properties of the most massive galaxies or galaxy groups in both the LG itself and the surroundings that could dynamically affect the LG. These are:
Table 2: External galaxy groups gravitationally influencing the LG dynamics.
These are the eight dominant galaxy groups. They contains about 90 per cent of all the light and so, if we assume that the light is a tracer of the mass, as argued in Sect. 3, these are the key objects whose motion has to be investigated in order to derive the force field acting on the LG. The analysis will be made in two steps: (i) first we will consider only the eight objects listed in Table 2; (ii) second, following Peebles et al. (2001), we will increase the sample adding a number of galaxies of smaller mass. The new list is shown in Table 3. This would allow us to estimate the dependence of the results on the number of objects under consideration or in other words to evaluate how small mass objects "perturb'' the orbits of the large mass ones.
Table 3: Complementary sample of low mass galaxies.
The main goal of this section is to provide a physical explanation for the planar distribution of the galaxies in the LG found in Sect. 2. With the least action principle (Sect. 3) we want to estimate the influence of the external galaxy groups (see Table 2) on the LG (see Table 1) and look for a dynamical justification of the planar distribution we have found from the mere geometrical analysis. Knowing the external force field acting on the LG could indeed cast light on whether the planar distribution is a temporary situation holding only at the present time t=t0, whereas the galaxy phase-space could tell a different story for all ages different from t0.
To this aim, using the galaxies of Table 2, we minimize the action for an unconstrained Lagrangian given by Eq. (13)![]() .
.
We adopt the standard cosmological scenario with cosmological
constant and the condition
![]() we have
already shown in Eq. (14). The standard cosmological
model is for H0 = 72 km s-1 Mpc-1,
we have
already shown in Eq. (14). The standard cosmological
model is for H0 = 72 km s-1 Mpc-1,
![]() and
and
![]() .
The orbits of the eight dominant groups
together with the MW and M 31 are followed from redshift
z=60 till now. The orbits resulting from the minimization
procedure are presented in Fig. 9.
.
The orbits of the eight dominant groups
together with the MW and M 31 are followed from redshift
z=60 till now. The orbits resulting from the minimization
procedure are presented in Fig. 9.
To avoid solutions with overlapping orbits that cannot be treated
with the technique of polynomial expansion of the orbits as a function of the Universe expansion parameter, we have introduced a smoothing length ![]() in the gravitational potential. The
acceleration acting on the
in the gravitational potential. The
acceleration acting on the ![]() particle and measured by a comoving observer at rest respect to distant matter is given by
particle and measured by a comoving observer at rest respect to distant matter is given by
![\begin{figure}
\par\includegraphics[width=7.45cm,clip]{6031fig09.eps}\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg93.gif) |
Figure 9:
Orbits of the eight dominant galaxies or groups of galaxies
derived from the minimization of the unconstrained action of Eq. (13). The orbits are shown as in Peebles (1989) for the sake of comparison. The orbits
of MW and M 31 are highlighted. The circle has a radius
|
| Open with DEXTER | |
The smoothing length is the lower limit below
which the analysis cannot be pushed, and hence the maximum
resolution of the plane thickness. This is dynamically extremely
relevant because it allows us to avoid un-physical solutions in the
minimization of the action. Indeed the case of two orbits crossing
each other would inevitably lead to a merger, which cannot be
properly treated by the technique in use here. Fortunately, it has
recently been proved that orbit crossing events are less of a problem as far as the number of solutions able to minimize the
action (13) is concerned (Whiting 2000). In
other words, this means that the dynamics we are going to analyse
is collisionless. It is worth noting that this description
may not hold at the earliest stages of the Universe (redshift
![]() )
when the galaxy sizes were likely comparable to their
mean separation (Dunn & Laflamme 1995). However, the approach
we have adopted can be justified in statistical sense: if we
consider our galaxy groups (and dominant galaxies) as mass point,
each with dimension
)
when the galaxy sizes were likely comparable to their
mean separation (Dunn & Laflamme 1995). However, the approach
we have adopted can be justified in statistical sense: if we
consider our galaxy groups (and dominant galaxies) as mass point,
each with dimension
![]() ,
the smoothing length,
the system of eight point-like galaxy groups can be considered
isolated. This is because the volume occupied by the their orbits,
,
the smoothing length,
the system of eight point-like galaxy groups can be considered
isolated. This is because the volume occupied by the their orbits,
![]()
![]() (see Fig. 9), is greater than
the total volume occupied by the objects,
(see Fig. 9), is greater than
the total volume occupied by the objects, ![]()
![]() .
Two objects of radius
.
Two objects of radius
![]() have an effective radius of
have an effective radius of
![]() and a cross section
and a cross section
![]() .
In the very early stages of the Universe,
assuming uniform distribution and random motion for the N objects
of Table 2, we can define the mean
free path as
.
In the very early stages of the Universe,
assuming uniform distribution and random motion for the N objects
of Table 2, we can define the mean
free path as
![]() ,
where the relative
mean velocity of the LG members is nearly equal to the mean velocity
of the group itself,
,
where the relative
mean velocity of the LG members is nearly equal to the mean velocity
of the group itself,
![]() .
Therefore, the mean free
path of collisions is
.
Therefore, the mean free
path of collisions is
![]() ,
about 15 Mpc for the eight massive objects of
Table 2, i.e. larger than the
dimensions we are interested in. This means that we expect
collisions to rarely affect the motion of the objects in the sample
(but see e.g. Diemand 2005; Diemand et al. 2005).
The same considerations cannot be extended to the total sample given
by Tables 1-3
because of the very large range of masses spanned by the objects.
It is worth recalling here that the constraints given by Eq. (12) refer to the present time, whereas back in the
past (z=60) the positions were random and the velocities null. In
other words, but for the very initial stages, as soon as the
collisionless description can be applied, the results we have
presented are a good description of the real galaxy motions.
,
about 15 Mpc for the eight massive objects of
Table 2, i.e. larger than the
dimensions we are interested in. This means that we expect
collisions to rarely affect the motion of the objects in the sample
(but see e.g. Diemand 2005; Diemand et al. 2005).
The same considerations cannot be extended to the total sample given
by Tables 1-3
because of the very large range of masses spanned by the objects.
It is worth recalling here that the constraints given by Eq. (12) refer to the present time, whereas back in the
past (z=60) the positions were random and the velocities null. In
other words, but for the very initial stages, as soon as the
collisionless description can be applied, the results we have
presented are a good description of the real galaxy motions.
Finally, the motions can be referred to the barycentre of
the system to simply and correctly follow the Universe expansion.
The new positions and velocities are given in Table 4 (and in Fig. 9). For instance, referred to the barycentre of the group
![]() kpc, the velocity vector of M 31 at the
present time is
kpc, the velocity vector of M 31 at the
present time is
![]() km s-1 and the projection of the
velocity vector onto the line joining the barycentre to the M 31
position is
km s-1 and the projection of the
velocity vector onto the line joining the barycentre to the M 31
position is
![]() km s-1. This is one of the many possible velocity
vectors matching this radial projection, however, it is the only
one minimizing the action of Eq. (13).
km s-1. This is one of the many possible velocity
vectors matching this radial projection, however, it is the only
one minimizing the action of Eq. (13).
Table 4: Velocities and positions of the galaxies used in the minimization procedure.
This kind of analysis based on the same sample of Table 2 has already been made by Dunn & Laflamme (1993) to derive the proper motion of M 31.
At this stage, an interesting question can be posed. Is there any correlation between the plane found in Sect. 2 and the action minimization? In other words how would the action minimum change if the plane is added as constraint to the whole procedure?
Using the representation of the plane given by Eq. (10), we impose that the positions of M 31 and MW are
those given by the observations, the same for the radial velocity of
M 31, and that the present-day velocity vectors of the two galaxies
belong to the plane. From a dynamical point of view, the latter
hypothesis is not equivalent to that adopted by
Sawa & Fujimoto (2005). They assumed a central &
plane motion for the LG galaxies and derived the dynamical history
of the LG. Here no assumption is made neither on
the angular momentum or torsion of the LG, nor the
quadrupole-quadrupole interaction, nor the inertia tensor of our
main galaxies (see Eq. (25) and
Dunn & Laflamme (1993) for similar considerations). Finally,
owing to the expected minimum thickness of the theoretical plane
caused by the smoothing length, we allow for the possibility that
the velocity vector cannot to exactly belong to the plane,
although very close to it. From a mathematical point of view, this
means that a anholonomic constraint has to be chosen instead of the
pure holonomic one used in Sect. 2. Therefore the
holonomic constraint evaluated only at the time t=t0 and
expressed by
The solution for the minimization is shown in Fig. 10 and the companion Table 5. In general the velocities remain the same as before but for M 31 and MW for which they significantly change. This simply reflects the constraint that at t=t0 the two galaxies in the phase space belong to the manifold expressed by the conditions (12) and (27). The most interesting and important result is that now the action is significantly lower than in the previous case. We suspect that profound implications are hidden in this result. We may provisionally conclude that the orbits of MW and M 31 lie on a plane and that this likely coincides with that derived from the geometrical analysis.
Table 5: Velocities derived from the Constrained Minimum Action.
Before proceeding further, there are a number of considerations to be made here:
![\begin{figure}
\par\includegraphics[width=13cm,clip]{6031fig10.eps}\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg118.gif) |
Figure 10: Orbits of the galaxy groups and the two dominant galaxies derived from the constrained minimization of the action. The constraints are given by relations (27) and (28). The dots and circles along each orbit have the same meaning as in Fig. 9. The circles correspond to the present age. |
| Open with DEXTER | |
We proceed now to test the solution we have obtained as far as three points of weakness are concerned.
In this subsection we test the possible dependence of the results
from the minimization method. In literature there are several
algorithms of optimization in multidimensional spaces. In
general, a great advantage is possible if the gradient in the
action (13) can be calculated
Finally as we were more interested in the physical meaning of the result, we preferred not to look for the absolute minimum for the action. Instead, following Efron & Tibshirani (1986) we considered the mean minimum value of the action resulting from a statistical interpretation of the results. As far as the orbits are concerned we performed many numerical experiments in which a fraction of galaxies of our sample has been randomly dropped from the configuration space and their distances randomly varied within the uncertainties, and finally the minimization has been recomputed. The final adopted values are for the statistical interpretation of the orbits. The results are presented in Table 6. A few simulations have been also calculated using the largest set of galaxies of Table 3. All results are fully compatible with those of Table 6. To fully and properly perform a statistical analysis one should also vary the velocities within their uncertainties. The estimated time cost of such analysis is very large. Fortunately, the small mass for most of galaxies in Table 3 ensures us that the final result would not significantly differ from the the present one.
As in the real space the tangent to the solution for the orbits
given by Eq. (17) is expected to strongly depend on the
number of terms in the polynomial expansion of the solution, we
have extended it up to the ninth term (N=9)
Finally, we would like to remark that the analytical representation of the orbits and the minimization procedure do not affect the plane position which is only revealed by the Principal Direction analysis. Small errors in the plane determination could result from the approximation made in Eq. (28). Therefore, they are only due to the velocity section of the tangent bundle of the configuration space where our smooth Lagrangian function (13) is defined.
Table 6: Mean value of the velocities derived from the analysis explained in the text.
Table 7: Local minimum velocity vectors for the solutions given by Eq. (32).
Finally, we evaluate the effect of changing the number of galaxies used to determine the force field acting on the LG. The analytical representation of the orbits is the one of Eq. (17) and the total galaxy sample is the sum of Tables 2 and 3. The new velocity vectors are found to be very similar to those of Table 6. This check is very time consuming and more subjected to the errors in the distance values of Table 3. Recalling that the number of interactions scales as Np2, the computational time is greatly increased. The little change in the velocity vectors that is found with the enlarged sample of galaxies is particularly interesting because it implies that the forces acting on the LG galaxies are primarily of internal origin. This is best illustrated by the shape of the equal gravitational potential surfaces and the field lines around each galaxy or galaxy group of the large sample (Tables 2 and 3) that are shown in Fig. 11. The gravitational potential around each object is nearly spherical and the field lines are nearly radial (see also Fig. 12 below). With these external gravitational fields, no significant effect can be produced on the LG galaxies even if the distance errors in some of the galaxies of 3 could be relevant.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6031fig11.eps}\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg173.gif) |
Figure 11: Surfaces of constant gravitational potential for the galaxies and groups of galaxies given in Tables 3 and 2. The colour code makes it evident how the spherical symmetry dominates. The position of the LG is indicated. |
| Open with DEXTER | |
In this section we examine in more detail the spatial shape of the gravitational potential (and associate field lines) shown in Fig. 11 in order to better understand the effect of the external force field on the planar distribution of the LG galaxies discovered in Sect. 2. To this aim we limit ourselves to consider only the subgroup strictly belonging to the LG neighbourhood (see Table 2). As pointed out by Dunn & Laflamme (1993) it is plausible that in the past dynamics and angular momentum (that ultimately depend on the quadrupole moment of the external gravitational potential, see Eq. (25)) of the LG have been strongly influenced not only by the two most massive spiral galaxies, M 31 and MW, but also by the nearest external galaxies. At the present time the dominant feature of the force field is the two-body interaction between the two dominant spirals. The present-day situation is illustrated in Fig. 12 where we see the typical dipolar structure of the field line generated by MW and M 31. This ensures that only the central forces are governing the dynamics of the two major galaxies.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{6031fig12.eps}\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg174.gif) |
Figure 12: The force field showing the radial behaviour of the streamlines of the MW and M 31 projected on the geometrical plane that minimizes the distances of the LG galaxies. |
| Open with DEXTER | |
The plane corresponding to the central motion of MW and M 31 not necessarily has to coincide with the plane derived from geometrical arguments. Indeed the dynamics of the dwarf galaxies satellites of MW and M 31 could be fully incompatible with the planar distribution indicated by the geometry. The latter indeed could be a transient situation with no correlation with the orbital plane revealed by the minimum action. In Fig. 12 we plot the dipole force field at the present time (t=t0) over the geometrical plane. The dipole force field is the one derived from the minimum action (Sect. 5) whereas the geometrical plane is the one derived from Eq. (10). On the geometrical plane the present-day dipole structure of the force field is still evident.
To cast light on the dynamical significance of the geometrical plane, instead of investigating the dynamics due to the central force between the two major galaxies, we must clarify the influence of the external galaxies on both the geometrical plane and the central force plane.
Following Raychaudhury & Lynden-Bell (1989), the force field minimizing
the action can be expressed as
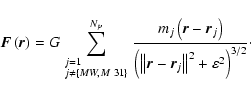 |
(33) |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{6031fig13.eps}
{\hspace*{2mm}\includegraphics[width=5.6cm,clip]{6031fig14.eps}\hspace*{2mm}}
\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg176.gif) |
Figure 13: Top panel: face-on view of the plane minimizing the action and the geometrical distances of the LG galaxies together with the field line of the gravitational interaction exerted by the external galaxies on the LG. Bottom panel: the same but viewed edge-on. Note how the field lines are nearly parallel to the plane. See the text for more details. |
| Open with DEXTER | |
The force field of the external galaxies that minimize the action is clearly parallel to the plane. This means that the force perturbing the central dynamical forces of the LG is dragging the plane toward the direction orthogonal to the normal direction, in other words the force field is pulling the plane along it. The geometrical and central force planes coincide within the uncertainty of the procedure we adopted to bring all this into evidence. As we have not made any special assumption for the angular momentum of the LG this finding is very interesting. Indeed the solution with velocity vectors belonging to the geometrical plane does not give any hint about the inclination of the central force plane. An infinite set of different possibilities is compatible with the assumption that the velocity vectors of M 31 and MW belong to the geometrical plane, but the solution that minimize the action show that the orbits should be parallel to the geometrical plane, at least from z=2. Interestingly enough, the coincidence between the geometrical and central force planes stems from the minimum action. The external field might have been significantly different at epochs earlier than z=2 (Dunn & Laflamme 1993) but ever since it did not change too much. The orbits derived from the minimum action (Sect. 5) belong to the geometrical plane. The two planes have been coincident for a large fraction of the Hubble time (nearly all).
This makes it possible to constrain the proper motions of the dwarf
galaxies external to the LG (Sawa & Fujimoto 2005), or more
realistically to constrain the dwarf galaxies (mostly irregulars) of
the LG that are preferentially located at large distances from the
two major galaxies and are subjected to a lower degree of spherical
symmetry in the force field due to the dark matter halo of the two massive spirals, see
(Pasetto et al. 2003). The force field lines shown
in Fig. 13 are likely to describe,
with no significant variations with time, the direction and
intensity of the force since very early epochs, say ![]() .
.
In this paper we have investigated the spatial distribution of the galaxies in the LG. They seem to share a common plane. The plane has been first geometrically singled out and then dynamically interpreted.
The geometrical discovery has been made using the Principal Component Analysis for an un-weighed sample. The plane we find does not coincide with those recently suggested by Sawa & Fujimoto (2005), on the base of the sky-projected distribution, and Kunkel (1979) and Grebel et al. (1999) from dynamical studies limited to the MW and M 31 sub-systems.
Major uncertainty of our analysis is the issue of the mass
tracers. Indeed the luminous objects have been used to derive from
merely geometrical arguments the plane minimizing their distances to
this. We have reasonably supposed that pure Dark Matter haloes do not
likely exist in the LG at least for redshifts ![]() .
However,
the presence of such pure Dark Matter haloes, while not affecting
the determination of the geometrical plane, could affect on the
orbital motions and the planar distribution of galaxies that we have
derived from the dynamical analysis.
.
However,
the presence of such pure Dark Matter haloes, while not affecting
the determination of the geometrical plane, could affect on the
orbital motions and the planar distribution of galaxies that we have
derived from the dynamical analysis.
The second part of the article is devoted to investigate the dynamics of the two dominant galaxies of the LG, MW and M 31, under the action of external forces exerted by nearby galaxies or galaxy groups external to the LG. The aim is to prove whether the planar distribution we have found is stable in time or it is a mere coincidence that will disappear in the future. We have demonstrated that the force field acting on the dynamics of the LG as a whole is compatible with the geometrical plane, in other words with a planar distribution that remain stable for very long periods of time. The result is that there is no external force field able to destroy the planar distribution. Once again the possible presence of undetected pure Dark Matter haloes may be a drawback of the present study.
Putting together the information from the geometrical and dynamical analysis the real thickness of the plane is estimated to be about 200 kpc.
Furthermore, despite the uncertainties, there is a strong
hint that the motion of the galaxies inside the LG is due to a central force field. The long membership of the two spiral galaxies
to the plane, for about 10 Gyr, provides some information on the
virialization state of the LG and the proper motions. However,
despite the extensive use by Sawa & Fujimoto (2005), the
presence of a plane should be adopted only to determine of proper
motions of the dwarf galaxies in the outskirts of the LG, as close
to the dominant spirals the gravitational potential and the
fly-by encounters are far from being collisionless and
scatter phenomena can complicate the description (see Pasetto &
Chiosi 2006, in preparation). We would like to remark that from the
results of Table 6 we can derive the proper
motions expected for M 31. Following Vallenari et al. (2006)
(their Eq. (4)) and assuming that the Sun is at rest in the Local
Standard of Rest system, the velocity system (U,V,W) of Eq. (4)
in Vallenari et al. (2006) is aligned with our velocity system.
Therefore the peculiar velocity of M 31 is simply the velocity given
in Table 6 once translated into the velocity
system centered on the MW. We obtain
![]() ,
fully compatible with
Dunn & Laflamme (1993).
As expected the proper motions turn out to be small due to the
nearly parallel motion of M 31 with respect to the MW. This result
also indirectly confirms that the numerical errors in our analysis
are quite small as we derive a radial velocity of M 31 equal to
,
fully compatible with
Dunn & Laflamme (1993).
As expected the proper motions turn out to be small due to the
nearly parallel motion of M 31 with respect to the MW. This result
also indirectly confirms that the numerical errors in our analysis
are quite small as we derive a radial velocity of M 31 equal to
![]() which is virtually identical to the one
we have initially imposed, i.e. the observational value
which is virtually identical to the one
we have initially imposed, i.e. the observational value
![]() .
.
Finally in Fig. 14 we plot and compare with ours the planes found by Kroupa et al. (2005) around the MW and by Koch & Grebel (2006) around M 31. First of all, the planes found by Kroupa et al. (2005) and Koch & Grebel (2006) differ from each other (have different normals). While the normal to the plane around MW seems to be aligned with the direction toward M 31 this is not the case for the plane around M 31 whose normal does not align with the direction towards the MW. Second, both planes do not coincide with our plane. The problem is rather complicated and in part mirrors the different methods that have been adopted in the three studies to address the subject and to determine the planes. They stem indeed from different dynamical considerations. In brief, the gravitational interaction among galaxies can be studied in two regimes. On long distances it can be investigated as a collisionless process best described by a statistical method. This is the approach of the present study as well as of many others in literature. Basing on this, we have derived the spatial structure and evolution of the MW and M 31 complexes together with their satellites. On short distances, the gravitational interaction is best modelled by collisional dynamics. This is the typical case of studies on the orbits of satellites of big mother galaxies and the effect of these latter on the spatial distribution of their nearby dwarf galaxies. In this context Koch & Grebel (2006) suggested for the M 31 group a tidal break up of a pre-existing dominant galaxy. This fact could partially explain the lack of collinearity between the planes for the M 31 and MW complexes. However, it is likely that also the progenitor of M 31 has been influenced by the external force field we have analysed in the present study. Furthermore, the seemingly parallel pull of the external field minimizing the action could have influenced, roughly in the same manner, both the proto-M 31 and the proto-MW (if any). As a final consideration on this issue, it may well be that on a local scale, i.e. when studying the dynamical behaviour of the satellite galaxies belonging to the MW and M 31 complexes, they seem to lie on planes with different inclination, but the generalisation of this result to the whole LG may not be correct. On the grand scale of the whole LG all galaxies seem to belong to a rather thin slab with its own (different) inclination which is dot destroyed by external actions. A study of the LG including both the collisional effects among interacting dwarf galaxies and the tidal effects by the external field on the orbits of the dwarf galaxies is underway (Pasetto & Chiosi 2006, in preparation).
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{6031fig15.eps}\end{figure}](/articles/aa/full/2007/08/aa6031-06/Timg182.gif) |
Figure 14: The planes for the dwarf galaxies around the MW (Kroupa et al. 2005) and M 31 (Koch & Grebel 2006) compared to our plane. Unfortunately, we cannot show the plane of Sawa & Fujimoto (2005) as no equation for it has been given explicitly by the authors. |
| Open with DEXTER | |
In this paper we tried to set the ground for future analysis in which the two regimes for the gravitational interaction can be taken into account. Specifically, we tried to impose constraints to the tangent bundle space of a smooth collisionless Lagrangian function generated by a group of galaxy clusters, using equations that stem from a local analysis and the probable existence of a plane revealed by merely geometrical considerations. The Lagrangian is constrained only at the time-boundaries of its region by means of the velocity space over there. In other words, the action minimization is constrained at the two temporal extremes: at the origin of the Universe by means of the Hamilton Principle (in the Peebles interpretation) and at the present time by means of the observational velocities and positions. Therefore, the action minimization here is one of the first order, i.e. a free, unconstrained minimization but for the temporal extremes with no other constraint along the minimization path. The next step forward would be to include the collisional regime. Unfortunately, in this case the dynamical interactions easily loose memory of the initial conditions. Therefore the dynamics of the LG must be investigated by imposing additional new and suitable constraints on the tangent bundle space of the Lagrangian. Precious hints come from the stellar content of the mother and dwarf galaxies of the LG Koch & Grebel (2006). In other words, the dynamical history of individual galaxies is recorded not only in their space-time geodesics or their past orbits (that anyhow are still poorly determined despite the many efforts in literature) but also in their past history of star formation and chemical enrichment on which we know lots more, see e.g. the reconstruction of this information made over the past two decades deciphering the colour-magnitude diagrams of their stellar populations (see Gallart et al. 2005, for a recent review of the subject and references therein). The target is ambitious but feasible.
Acknowledgements
This study was financed by the University of Padua by means of a post-doc fellowship to S. Pasetto and the Department of Astronomy by providing indirect logistic support (computers, infrastructure, etc). No financial resource has been allocated to the project by the Italian Ministry of Education, University and Research (MIUR).
Here we describe the simple method used to minimize the
distance expressed by Eq. (3) subjected to
the constraint given in Eq. (4) and the constraint that
the plane we are looking for must be orthogonal the vector joining
M 31 and MW, i.e.
![]() .
This
additional holonomic constraint can be written as
.
This
additional holonomic constraint can be written as
![]() .
The problem can be further simplified assuming as
origin of the coordinate system of reference one of the two major
galaxies. This means that the constant c of Eq. (2)
can be set to zero c=0. Therefore
.
The problem can be further simplified assuming as
origin of the coordinate system of reference one of the two major
galaxies. This means that the constant c of Eq. (2)
can be set to zero c=0. Therefore
![]() and
and
![]() are the system of
independent constraints. The distance defined by Eq. (3) in the Euclidean space E3 will present a stationary point
are the system of
independent constraints. The distance defined by Eq. (3) in the Euclidean space E3 will present a stationary point ![]() if the gradients of the constraints
in
if the gradients of the constraints
in ![]() are able to express
are able to express ![]() as a linear
combination of them, i.e are a basis for
as a linear
combination of them, i.e are a basis for
![]() ,
the
space orthogonal to the manifold of
,
the
space orthogonal to the manifold of ![]() .
This leads to
.
This leads to
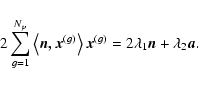 |
(A.1) |
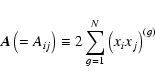 |
(A.2) |
| (A.4) |
| (A.5) |
However, as we are more interested in the components of the
ortho-normal vector ![]() more than in the Lagrange's
multipliers
more than in the Lagrange's
multipliers
![]() and
and
![]() ,
we can work directly on
the system (A.3). Taking the scalar product of both members
of (A.3) we obtain
,
we can work directly on
the system (A.3). Taking the scalar product of both members
of (A.3) we obtain
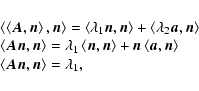 |
(A.6) |
![\begin{displaymath}%
\begin{array}{l}
n_j \left[ {\sum\limits_{g = 1}^N {\left(...
...\right] = \lambda _1, \\
\end{array} \right. \\
\end{array}\end{displaymath}](/articles/aa/full/2007/08/aa6031-06/img201.gif) |
(A.7) |
![\begin{eqnarray*}\left\{ \begin{array}{l}
n_1 \left[ {\sum\limits_{g = 1}^N {\l...
... 1}^3 {n_i x_i^g } } \right)} } \right].\\
\end{array} \right.
\end{eqnarray*}](/articles/aa/full/2007/08/aa6031-06/img202.gif)