A&A 463, 261-264 (2007)
DOI: 10.1051/0004-6361:20065689
Screening effect on electron capture in presupernova stars
M. Q. Liu
- J. Zhang
- Z. Q. Luo
Institute of Theoretical Physics, China West Normal
University, Nanchong 637002, PR China
Received 25 May 2006 / Accepted 12 October 2006
Abstract
Aims. With the new electron capture results from the improved GT resonance distribution, we analyzed the electron screening effect on electron capture at the presupernova stage.
Methods. The relativistically degenerate electron liquid screening potential derived from the linear response theory are adopted. The calculation of the electron capture rates is based on the shell-model. Both the change of electron energy and the shift in the threshold for electron capture in screening are taken into account.
Results. The results indicate that the influence of electron screening on the electron capture is prominent in high-density matter. As the improved electron capture rate is considered, screening effect on the electron capture rate increases by about 1 percent at
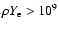 g/cm3.
g/cm3.
Conclusions. The influence of screening on the electron capture reaction is about 10 percent for 56Co at
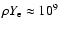 g/cm3. Screening may affect the structure and evolution of presupernova and should be included in any precise simulation.
g/cm3. Screening may affect the structure and evolution of presupernova and should be included in any precise simulation.
Key words: supernovae: general - nuclear reactions, nucleosynthesis, abundances
- methods: numerical
The electron capture process plays a large role in astrophysics
because it is a key process in the evolution of presupernova star
and the explosion of supernova (SN, Woosley et al.
2002). In this process, the electron number density
decreases, and the electron degenerate pressure decreases
accordingly. One of the products in the capture process, the
neutrinos, escape and take plenty of energy away from the star when
the density is below the trapped density of the neutrino. Both the
decrease in degenerate pressure and the loss of energy accelerate
the collapse (Bethe et al. 1979, 1990) of
the star.
The weak interaction processes, including the electron capture and
 decay, in dense matter have been investigated extensively in
last decades. Based on the simple shell model, Fuller et al. (1982, hereafter FFN) accomplished pioneering work,
in which they discussed the location and the strength of the
Gamow-Teller (GT) resonance transition and made detailed calculations
of 226 nuclei with mass number A ranging from 21 to 60. Auferheide
et al. (1994) pointe out that the nuclei with A>60 should
also be taken into account in the theoretical analysis because the core
region of presupernova is mainly composed of neutron-rich nuclei.
They extended FFN's work to some nuclei with A>60 and provided the
weak interaction rates of the 150 most abundant isotopes with some
key temperatures and densities at the presupernova stage. In recent
years, the large-scale shell-model calculations and the shell-model
Mont Carlo calculations (SMMC) of the GT strength distribution were
done by Langanke & Martinez-Pinedo
(1997, 2000, hereafter LMP). Their results indicate
that the improved electron capture rates are significantly lower
than usually adopted in core collapse calculation.
decay, in dense matter have been investigated extensively in
last decades. Based on the simple shell model, Fuller et al. (1982, hereafter FFN) accomplished pioneering work,
in which they discussed the location and the strength of the
Gamow-Teller (GT) resonance transition and made detailed calculations
of 226 nuclei with mass number A ranging from 21 to 60. Auferheide
et al. (1994) pointe out that the nuclei with A>60 should
also be taken into account in the theoretical analysis because the core
region of presupernova is mainly composed of neutron-rich nuclei.
They extended FFN's work to some nuclei with A>60 and provided the
weak interaction rates of the 150 most abundant isotopes with some
key temperatures and densities at the presupernova stage. In recent
years, the large-scale shell-model calculations and the shell-model
Mont Carlo calculations (SMMC) of the GT strength distribution were
done by Langanke & Martinez-Pinedo
(1997, 2000, hereafter LMP). Their results indicate
that the improved electron capture rates are significantly lower
than usually adopted in core collapse calculation.
People have also addressed the effect of the electron screening in a
weak interaction. In the 1950s, Reitz (1950) analyzed the
effect of screening on  decay by solving the Dirac equation
and concluded that the screening slightly decreases the
decay by solving the Dirac equation
and concluded that the screening slightly decreases the 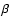 decay rate. After that, the screening effect on Fermi function and
Coulomb correction in
decay rate. After that, the screening effect on Fermi function and
Coulomb correction in 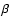 decay were considered (Chen et al. 1966; Matese et al. 1966). Gutierrez
(1996) suggested that the decrease in electron Fermi energy is equal
to the shift in the chemical potential of nuclei before and after
the capture reaction. Luo et al. (1996, 2001) argue
that the screening also affects the phase space distribution of the
electron besides the Fermi energy. The calculation showed that the
screening can reduce the rate of change of electron fraction by
decay were considered (Chen et al. 1966; Matese et al. 1966). Gutierrez
(1996) suggested that the decrease in electron Fermi energy is equal
to the shift in the chemical potential of nuclei before and after
the capture reaction. Luo et al. (1996, 2001) argue
that the screening also affects the phase space distribution of the
electron besides the Fermi energy. The calculation showed that the
screening can reduce the rate of change of electron fraction by 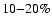 .
With the same method as Gutierrez, Bravo (1999) solved
the nuclear statistical equation and found that the neutronization
rate is higher than
.
With the same method as Gutierrez, Bravo (1999) solved
the nuclear statistical equation and found that the neutronization
rate is higher than 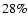 at some temperatures and densities.
at some temperatures and densities.
Numerical simulations show that the SN explosion depends on the
persupernova structure and the evolution mode, which is especially
sensitive to the physical parameters' input. The parameters are
closely related to the electron fraction and the weak interaction
rates at the presupernova stage (Heger et al. 2001).
Therefore, it is imperative to calculate the electron capture rates
with high precision. In this paper, the screening effects on the
electron capture rates for the improved results from Langanke et al.
(1999) are evaluated.
For the convenience of explaining the results, it is necessary to
briefly introduce the formulae of our calculations. The capture rate
for the kth nucleus (Z, A) in thermal equilibrium at
temperature T is given by a sum over the initial parent states i and the final daughter states f (Pruet et al. 2003),
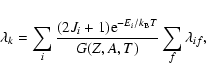 |
(1) |
where Ji and Ei are the spin and excitation energy of the
parent states, 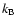 the Boltzmann factor, G(Z,A,T) the nuclear
partition function,
the Boltzmann factor, G(Z,A,T) the nuclear
partition function,
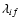 the electron capture rate from
one of the initial states to all possible final states,
the electron capture rate from
one of the initial states to all possible final states,
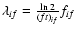 with the relation
with the relation
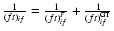 .
The ft-values and the corresponding GT or Fermi transition
matrix elements are related to the following equations,
.
The ft-values and the corresponding GT or Fermi transition
matrix elements are related to the following equations,
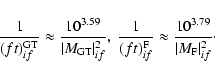 |
(2) |
The phase space integral fif is defined as
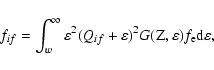 |
(3) |
where
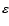 is the electron energy (the energy is in unit of
is the electron energy (the energy is in unit of
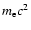 in this paper except when explicitly written with the unit MeV),
in this paper except when explicitly written with the unit MeV), 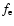 is the Fermi-Dirac distribution function of the
electrons, and
is the Fermi-Dirac distribution function of the
electrons, and
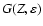 is the Coulomb correction factor.
The nuclear energy difference between the parent and daughter nuclei
is the Coulomb correction factor.
The nuclear energy difference between the parent and daughter nuclei
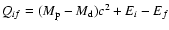 ,
where
,
where 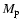 and
and 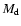 are the mass of
the parent and daughter nucleus, respectively, and Ef is the
excitation energy of daughter state. Without considering the
screening, the threshold energy w equals the static energy of
an electron if the energy difference Qif is less than the
static energy of an electron; otherwise it is equal to |Qif|.
are the mass of
the parent and daughter nucleus, respectively, and Ef is the
excitation energy of daughter state. Without considering the
screening, the threshold energy w equals the static energy of
an electron if the energy difference Qif is less than the
static energy of an electron; otherwise it is equal to |Qif|.
The screening mainly affects the electron capture in three facets.
(1) The screening changes the Coulomb in-wave function of the
electron, which, however, can be neglected because the screening
potential D is much less than the average energy of the electrons.
(2) The screening decreases the electron energy
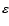 in
the capture reaction to
in
the capture reaction to
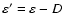 .
(3) The
screening relatively decreases the number of the high energy
electrons whose energy is more than the threshold energy of electron
capture. Thus, the threshold energy will increase from w to
.
(3) The
screening relatively decreases the number of the high energy
electrons whose energy is more than the threshold energy of electron
capture. Thus, the threshold energy will increase from w to
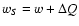 ,
where
,
where 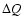 represents the change in binding
energy of the final and initial nuclei due to the presence of the
electron gas. In the plasma, a nucleus has its binding energy
increased due to interactions with the dense electron gas. In the
Wigner-Seitz approximation, the extra binding of an atom can be
written as
represents the change in binding
energy of the final and initial nuclei due to the presence of the
electron gas. In the plasma, a nucleus has its binding energy
increased due to interactions with the dense electron gas. In the
Wigner-Seitz approximation, the extra binding of an atom can be
written as
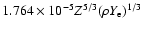 MeV (Salpeter et al. 1969). Because of the charge
dependence of this binding, the effective nuclear Q-value changes
at high density. In general, the average Q-value for each electron
will increase by (FFN 1982)
MeV (Salpeter et al. 1969). Because of the charge
dependence of this binding, the effective nuclear Q-value changes
at high density. In general, the average Q-value for each electron
will increase by (FFN 1982)
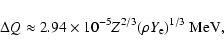 |
(4) |
where Z is the charge of nucleus, 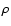 the mass density and
the mass density and 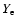 the electron fraction. Thus the phase space integral with
screening is written as
the electron fraction. Thus the phase space integral with
screening is written as
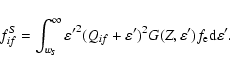 |
(5) |
Then, the key point in the calculation that includes the screening
is to calculate the screening potential D. Recently, Itoh et al. (2002) used the linear response
theory to calculate the screening potential caused by
relativistically degenerate electron. This theory is widely used in the field of solid-state
physics and liquid physics. Their results provide a more precise
screening potential,
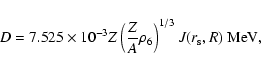 |
(6) |
where 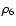 is the density in unit of 106 g/cm3,
is the density in unit of 106 g/cm3,
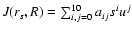 ,
,
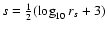 ,
,
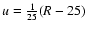 ,
,
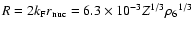 ,
and
,
and
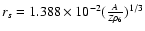 .
One can find the
factor aij in Itoh et al. (2002), and
.
One can find the
factor aij in Itoh et al. (2002), and
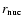 is the
nuclear radius and
is the
nuclear radius and 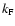 the electron Fermi wave number,
the electron Fermi wave number,
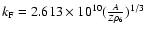 .
Formula (6) is valid for
.
Formula (6) is valid for
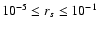 and
and
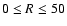 ,
which are usually fulfilled in the presupernova
environment.
,
which are usually fulfilled in the presupernova
environment.
Table 1:
The effect of electron screening on 56Co
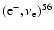 Fe. (
Fe. (
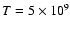 K,
K,
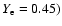 ,
C1 denotes the screening factor in the fiducial GT resonance distribution, C2 denotes the screening factor with the improved GT resonance distribution.
,
C1 denotes the screening factor in the fiducial GT resonance distribution, C2 denotes the screening factor with the improved GT resonance distribution.
Table 2:
The effect of electron screening on 56Co
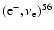 Fe, where the left panel is the results of
Fe, where the left panel is the results of
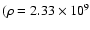 g/cm3,
g/cm3,
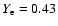 ,
D=0.095 MeV,
,
D=0.095 MeV,
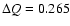 MeV and the right panel
is the results of
MeV and the right panel
is the results of
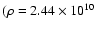 g/cm3,
g/cm3,
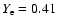 ,
D=0.208 MeV,
,
D=0.208 MeV,
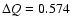 MeV). The other notes are the same as that in Table 1.
MeV). The other notes are the same as that in Table 1.
Figure 1 shows the variation in D and 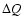 for
for
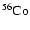 with
with
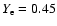 .
From Fig. 1, one
can see that both corrections increase with density, and the
correction of threshold energy
.
From Fig. 1, one
can see that both corrections increase with density, and the
correction of threshold energy 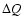 is more obvious than Dat high density. Therefore, the electron capture rate with a low
threshold energy will be easier to change in the high density
environment of presupernova.
is more obvious than Dat high density. Therefore, the electron capture rate with a low
threshold energy will be easier to change in the high density
environment of presupernova.
Provided the excited state distribution of nucleus is known, the
electron capture rates can be obtained with high precision.
Unfortunately, the nuclei in the presupernova environment are
usually unstable, and the distribution of the high excited states
are almost continuous (particularly for the heavier nuclei), so it is
difficult to get an explicit distribution for each nucleus.
Following the technique of Auderheide et al. (1994), we employed the
so-called Brink hypothesis and assumed that the distribution of the
parent excited states is similar to that of the ground state and
that the location of the GT resonance moves upward in the daughter
nucleus by the same amount.
People can split the sum of final states of daughter nuclei into two
parts for convenience. One is the contribution 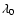 from the
low-energy region near the ground state and the other is the
contribution
from the
low-energy region near the ground state and the other is the
contribution
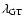 from the resonance region dominated by
the GT resonance transition. The GT strength distribution is similar
to a Gaussian distribution (Kar et al. 1994) and the GT
resonance energy
from the resonance region dominated by
the GT resonance transition. The GT strength distribution is similar
to a Gaussian distribution (Kar et al. 1994) and the GT
resonance energy
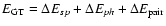 ,
where
,
where
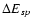 is the energy difference between
the new occupied neutron orbital and the ground state;
is the energy difference between
the new occupied neutron orbital and the ground state;
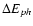 is the repulsion energy that should be supplied to pull the
neutron out of the daughter ground state;
is the repulsion energy that should be supplied to pull the
neutron out of the daughter ground state;
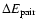 is the
cost of breaking a neutron pair in daughter nucleus with an even
number of neutrons. The resonance transition matrix element
is the
cost of breaking a neutron pair in daughter nucleus with an even
number of neutrons. The resonance transition matrix element
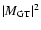 can be derived from the model calculation, such as the
simple shell-model calculation (FFN 1982). With Auderheide's
method, we take
can be derived from the model calculation, such as the
simple shell-model calculation (FFN 1982). With Auderheide's
method, we take
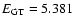 MeV,
MeV,
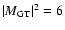 (quenching factor
is 0.5) for 56Co in this paper.
(quenching factor
is 0.5) for 56Co in this paper.
LMP adopted the shell-model diagonalization in the pf shell
with modified KB3 interaction to calculate the electron capture
rates of six important odd-odd nuclei in LMP (1999). They
find that the GT centroids
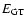 is typically 2 MeV higher and the
resonance transition matrix element decreases more than the previous
estimation. These changes make the electron capture rates 1 order
of magnitude too low compared to the fiducial results (Aufderheide
et al. 1994; FFN 1982) except for 58Mn. More
detailed large-scale shell-model calculations by LMP show that the
electron capture rates are significantly lower for nuclei with the
mass number ranging from 45 to 65 in the presupernova environment.
For example, the electron capture rate of 56Co is
is typically 2 MeV higher and the
resonance transition matrix element decreases more than the previous
estimation. These changes make the electron capture rates 1 order
of magnitude too low compared to the fiducial results (Aufderheide
et al. 1994; FFN 1982) except for 58Mn. More
detailed large-scale shell-model calculations by LMP show that the
electron capture rates are significantly lower for nuclei with the
mass number ranging from 45 to 65 in the presupernova environment.
For example, the electron capture rate of 56Co is
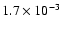 s-1 by FFN and is
s-1 by FFN and is
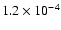 s-1 by
LMP at temperature T=109 K and density
s-1 by
LMP at temperature T=109 K and density
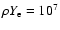 g/cm3 (FFN 1982b; LMP
2000). However, the effect of screening on the electron
capture is ignored in these calculations.
g/cm3 (FFN 1982b; LMP
2000). However, the effect of screening on the electron
capture is ignored in these calculations.
We here calculate the electron capture rates with screening for
capture reaction of 56Co, which is one of the most important
electron capturing nuclei in presupernova. We take
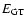 as 8.2 MeV and
as 8.2 MeV and
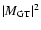 as 7.7 in the improved method derived by LMP (1999). In addition, the quenching factor changes from 0.5 to 0.55. For a comparison,we define a screening factor, a ratio C between the electron capture rates with (
as 7.7 in the improved method derived by LMP (1999). In addition, the quenching factor changes from 0.5 to 0.55. For a comparison,we define a screening factor, a ratio C between the electron capture rates with (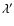 )
and
without (
)
and
without (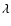 )
screening,
)
screening,
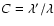 .
.
We show the influence of electron screening on the reaction
56Co
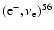 Fe at different temperatures,
densities, and electron fraction in Tables 1 and 2, where
Fe at different temperatures,
densities, and electron fraction in Tables 1 and 2, where
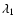 is the electron capture rate in the
fiducial GT resonance distribution and
is the electron capture rate in the
fiducial GT resonance distribution and 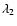 the electron
capture rate with the improved GT resonance distribution. Although
the modified rates obviously decrease, they are not as low as LMP's
results. The reason is that LMP handle the ground state (J=4) and
the first excited states (J=3, 5 and 1) of parent nucleus,
respectively. Their calculation adopts 33 Lanczos iterations and
each state (
the electron
capture rate with the improved GT resonance distribution. Although
the modified rates obviously decrease, they are not as low as LMP's
results. The reason is that LMP handle the ground state (J=4) and
the first excited states (J=3, 5 and 1) of parent nucleus,
respectively. Their calculation adopts 33 Lanczos iterations and
each state (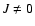 )
in the parent nucleus is connected to 99
states in the daughter nucleus. Such treatment is more precise and
complicated. But we found the electron capture rate by adopting
LMP's GT resonance transition location and strength is close to
their detailed results, so here we can estimate the effect of
screening by the Brink hypothesis.
)
in the parent nucleus is connected to 99
states in the daughter nucleus. Such treatment is more precise and
complicated. But we found the electron capture rate by adopting
LMP's GT resonance transition location and strength is close to
their detailed results, so here we can estimate the effect of
screening by the Brink hypothesis.
From the results of 56Co
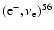 Fe, we can from
Table 1 find that the screening factors decrease with
density when
Fe, we can from
Table 1 find that the screening factors decrease with
density when 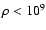 g/cm3. At
g/cm3. At
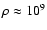 g/cm3, the
screening factor reaches its minimum for 56Co, which indicates
that the screening effect is at the maximum in this case. Comparing
to Aufderheide's results, the screening effect on the improved
electron capture rates is decreased at low density (
C2>C1 )
and enhanced at higher density (109 g/cm
g/cm3, the
screening factor reaches its minimum for 56Co, which indicates
that the screening effect is at the maximum in this case. Comparing
to Aufderheide's results, the screening effect on the improved
electron capture rates is decreased at low density (
C2>C1 )
and enhanced at higher density (109 g/cm
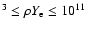 g/cm3). The GT resonance transition mainly occur at high
density. Larger
g/cm3). The GT resonance transition mainly occur at high
density. Larger
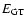 makes the GT transition rates decrease and
then it makes the screening more important so that the screening
factor decrease about 1 percent. The electron capture is a decisive
factor in inducing core collapse in the high-density region
makes the GT transition rates decrease and
then it makes the screening more important so that the screening
factor decrease about 1 percent. The electron capture is a decisive
factor in inducing core collapse in the high-density region
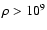 g/cm3, which means the screening effect should be
included at the collapse stage of presupernova. Table 2
shows the screening factors in densities
g/cm3, which means the screening effect should be
included at the collapse stage of presupernova. Table 2
shows the screening factors in densities
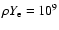 g/cm3 and
g/cm3 and
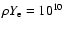 g/cm3. It shows that the higher the temperature,
the closer to 1 the screening factor is (i.e. the effect of
screening is closer to zero). The reason is that when the
temperature is higher, the average electron energy is higher than
the screening potential. It can also be found that the influence of
temperature is low because the Fermi energy of the electron is
decided by density. Screening factors stay about 0.9 when
g/cm3. It shows that the higher the temperature,
the closer to 1 the screening factor is (i.e. the effect of
screening is closer to zero). The reason is that when the
temperature is higher, the average electron energy is higher than
the screening potential. It can also be found that the influence of
temperature is low because the Fermi energy of the electron is
decided by density. Screening factors stay about 0.9 when
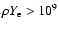 g/cm3 for 56Co (i.e. the influence of screening is
about 10 percent). We expect the other nuclei have similar results
to 56Co since their corrections to the GT transition are
similar (LMP 2000, 1999). Presupernova structure and
the subsequent evolution of collapse process may be modified due to
the screening effect on electron capture. Theoretically, screening
will decrease the collapse velocity, prolong the collapse timescale,
increase the loss of neutrino energy, and so on. But there are many
feedback effects in the numerical simulations, so these effects need
to be confirmed by detailed numerical simulations.
g/cm3 for 56Co (i.e. the influence of screening is
about 10 percent). We expect the other nuclei have similar results
to 56Co since their corrections to the GT transition are
similar (LMP 2000, 1999). Presupernova structure and
the subsequent evolution of collapse process may be modified due to
the screening effect on electron capture. Theoretically, screening
will decrease the collapse velocity, prolong the collapse timescale,
increase the loss of neutrino energy, and so on. But there are many
feedback effects in the numerical simulations, so these effects need
to be confirmed by detailed numerical simulations.
Acknowledgements
This work was supported by the National Natural Science Foundation
of China under Grant No. 10347008. One of the authors (Menquan Liu)
would like to thank Bin Wang at Peking University for useful discussions
and help with preparing this paper.
- Aufderheide, M. B.,
Fushiki, I., Woosley, S. E., et al. 1994, ApJS, 91, 389 [NASA ADS] [CrossRef] (In the text)
- Bethe, H. A. 1990,
Rev. Mod. Phys., 62, 801 [NASA ADS] [CrossRef] (In the text)
- Bethe, H. A., Brown, G.
E., Applegate, J., et al. 1979, Nucl. Phys. A, 324, 487 [NASA ADS] [CrossRef] (In the text)
- Bravo, E., &
Garcia-Senz, D. 1999, MNRAS, 307, 984 [NASA ADS] [CrossRef]
- Chen, F. S., Durand,
L., & McGee, I. J. 1966, Phys. Rev., 146, 638 [NASA ADS] [CrossRef] (In the text)
- Fuller, G. M., Fowler, W.
A., & Newman, M. J. 1982, ApJ, 252, 715 [NASA ADS] [CrossRef] (In the text)
- Fuller, G. M., Fowler,
W. A., & Newman, M. J. 1982, ApJS, 48, 279 [NASA ADS] [CrossRef] (In the text)
- Gutierrez, J.,
Garcia-Berro, E., Iben, I., & Isern, J. 1996, ApJ, 459,
701 [NASA ADS] [CrossRef]
- Heger, A., Woosley,
S. E., Martinez-Pinedo, G., et al. 2001, ApJ, 560, 325 [NASA ADS] [CrossRef] (In the text)
- Itoh, N., Tomizawa, N.,
Tamamura, M., et al. 2002, ApJ, 579, 380 [NASA ADS] [CrossRef] (In the text)
- Kar, K., Ray, A., &
Sarkar, S. 1994, ApJ, 434, 662 [NASA ADS] [CrossRef] (In the text)
- Koonin, S. E., Dean, D.
J., & Langanke, K. 1997, Phys. Rep., 278, 1 [NASA ADS] [CrossRef] (In the text)
- Langanke, K., &
Martinez-Pinedo, G. 1999, Phys. Lett. B, 453, 187 [NASA ADS] (In the text)
- Langanke, K., &
Martinez-Pinedo, G. 2000, Nucl. Phys. A, 673, 481 [NASA ADS] [CrossRef] (In the text)
- Luo, Z. Q., & Peng,
Q. H. 1996, Science in China (Series A), 39, 776 (In the text)
- Luo, Z. Q., & Peng,
Q. H. 2001, ChAA, 25, 1 (In the text)
- Matese, J. J., &
John, W. R. 1966, Phys. Rev., 150, 846 [NASA ADS] [CrossRef] (In the text)
- Pruet, J., &
Fuller, G. M. 2003, ApJS, 149, 189 [NASA ADS] [CrossRef] (In the text)
- Reitz, J. R. 1950,
Phys. Rev., 77, 10 [NASA ADS] [CrossRef] (In the text)
- Salpeter, E. E., &
Van Horn, H. M. 1969, ApJ, 155, 183 [NASA ADS] [CrossRef] (In the text)
- Woosley, S. E.,
Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2007
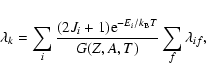
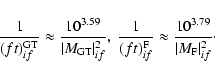
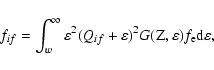
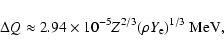
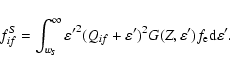
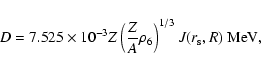
![\begin{figure}
\par\includegraphics[width=9cm,clip]{5689fig1.eps}
\end{figure}](/articles/aa/full/2007/07/aa5689-06/Timg50.gif)