A&A 463, 399-404 (2007)
DOI: 10.1051/0004-6361:20065589
K. M. Aggarwal - F. P. Keenan
Astrophysics Research Centre, School of Mathematics and Physics, Queen's University, Belfast BT7 1NN, Northern Ireland, UK
Received 11 May 2006 / Accepted 16 November 2006
Abstract
Aims. In this paper we report calculations for energy levels and radiative rates for transitions in Fe XVI.
Methods. The General purpose Relativistic Atomic Structure Package ( GRASP) has been adopted for the calculations of energy levels and radiative rates.
Results. Energies for the lowest 134 levels among the (1s22s2) 2p63![]() ,
2p53s2, 2p53s3p, 2p53s3d, 2p53p3d, and 2p53p2 configurations of Fe XVI are reported. Additionally, radiative rates, oscillator strengths, and line strengths are reported for all electric dipole (E1), magnetic dipole (M1), electric quadrupole (E2), magnetic quadrupole (M2), and electric octupole (E3) transitions among these levels. Comparisons are made with the available results in the literature, and the accuracy of the present results is assessed. Finally, lifetimes for all excited levels are also listed, although no measurements are presently available with which to compare these.
,
2p53s2, 2p53s3p, 2p53s3d, 2p53p3d, and 2p53p2 configurations of Fe XVI are reported. Additionally, radiative rates, oscillator strengths, and line strengths are reported for all electric dipole (E1), magnetic dipole (M1), electric quadrupole (E2), magnetic quadrupole (M2), and electric octupole (E3) transitions among these levels. Comparisons are made with the available results in the literature, and the accuracy of the present results is assessed. Finally, lifetimes for all excited levels are also listed, although no measurements are presently available with which to compare these.
Key words: atomic data - atomic processes
In a recent paper (Aggarwal & Keenan 2006) we reported energy levels, radiative rates, collision strengths, and excitation rate coefficients for transitions among 39
levels of the (1s22s22p6) nl; ![]() 7,
7, ![]() 4 configurations of Fe XVI. However, many lines of Fe XVI in the 15-17
4 configurations of Fe XVI. However, many lines of Fe XVI in the 15-17 ![]() X-ray range are
frequently observed in astrophysical and laboratory plasmas, and some of these arise from the inner (L) shell excitation of Fe XVI, such as: 2p63s + e-
X-ray range are
frequently observed in astrophysical and laboratory plasmas, and some of these arise from the inner (L) shell excitation of Fe XVI, such as: 2p63s + e-
![]() 2p53
2p53![]() 3
3
![]() (see, for example, Dere et al. 2001). These emission lines particularly arise at comparatively higher temperatures, and hence
atomic data for such transitions are also useful in fusion plasmas. Therefore, in this paper we focus on the inner shell electron impact excitation of Fe XVI.
(see, for example, Dere et al. 2001). These emission lines particularly arise at comparatively higher temperatures, and hence
atomic data for such transitions are also useful in fusion plasmas. Therefore, in this paper we focus on the inner shell electron impact excitation of Fe XVI.
Earlier calculations for this ion have been performed by Cornille et al. (1994) and Bautista (2000). Cornille et al. adopted the SuperStructure (SS) code of
Eissner et al. (1974) for the generation of wavefunctions, and the distorted-wave (DW) code of Eissner & Seaton (1972) for the computations of collision
strengths (![]() ). They included 44 levels of the 2p63s, 2p53s2, 2p53s3p and 2p53s3d configurations in their calculations, and reported values of
). They included 44 levels of the 2p63s, 2p53s2, 2p53s3p and 2p53s3d configurations in their calculations, and reported values of ![]() at a
single energy of 60 Ryd. The main deficiency of their work is that they neither considered the variation of
at a
single energy of 60 Ryd. The main deficiency of their work is that they neither considered the variation of ![]() with energy, nor included the contribution of resonances in
the determination of excitation rates. Both of these deficiencies were removed in the subsequent work of Bautista, who adopted a semi-relativistic R-matrix approach
(Berrington et al. 1995). In his calculations, he included 59 LS terms of the 2p63
with energy, nor included the contribution of resonances in
the determination of excitation rates. Both of these deficiencies were removed in the subsequent work of Bautista, who adopted a semi-relativistic R-matrix approach
(Berrington et al. 1995). In his calculations, he included 59 LS terms of the 2p63![]() ,
2p53s2, 2p53s3p, 2p53s3d, 2p53p3d, and 2p53p2configurations, and obtained results for fine-structure transitions through an algebraic transformation. In this process, he also included the relativistic effects through
term coupling coefficients (TCC). Since Fe XVI is a moderately heavy ion (Z = 26), both configuration interaction (CI) and relativistic effects are supposed to be
important in the determination of wavefunctions, and subsequently of
,
2p53s2, 2p53s3p, 2p53s3d, 2p53p3d, and 2p53p2configurations, and obtained results for fine-structure transitions through an algebraic transformation. In this process, he also included the relativistic effects through
term coupling coefficients (TCC). Since Fe XVI is a moderately heavy ion (Z = 26), both configuration interaction (CI) and relativistic effects are supposed to be
important in the determination of wavefunctions, and subsequently of ![]() .
He observed that the contribution of resonances has enhanced the effective collision
strengths (
.
He observed that the contribution of resonances has enhanced the effective collision
strengths (![]() )
by up to three orders of magnitude, depending on the temperature, and the relativistic effects have enhanced these by several orders of magnitude, for
some of the transitions. Since both of these observed enhancements are unusually high, one of our aims is to assess the accuracy of his reported results, apart from making
other improvements.
)
by up to three orders of magnitude, depending on the temperature, and the relativistic effects have enhanced these by several orders of magnitude, for
some of the transitions. Since both of these observed enhancements are unusually high, one of our aims is to assess the accuracy of his reported results, apart from making
other improvements.
Table 1: Energy levels (in Ryd) and mixing coefficients of Fe XVI.
In the present work, we include 134 levels among the (1s22s2) 2p63![]() ,
2p53s2, 2p53s3p, 2p53s3d, 2p53p3d, and 2p53p2 configurations of Fe
XVI. Additionally, our approach is fully relativistic, as we employ the GRASP (General purpose Relativistic Atomic Structure Package) code of Dyall et al. (1989) for the
generation of wavefunctions, and the Dirac Atomic R-matrix Code (DARC) of Norrington & Grant (2007) for computations of
,
2p53s2, 2p53s3p, 2p53s3d, 2p53p3d, and 2p53p2 configurations of Fe
XVI. Additionally, our approach is fully relativistic, as we employ the GRASP (General purpose Relativistic Atomic Structure Package) code of Dyall et al. (1989) for the
generation of wavefunctions, and the Dirac Atomic R-matrix Code (DARC) of Norrington & Grant (2007) for computations of ![]() ,
and subsequently of
,
and subsequently of ![]() .
However, it may be noted that the 2p53d2 configuration has been deliberately excluded from the calculations, because it generates 45 levels and all of which lie above the lowest 134 already included. The same argument applies to other higher configurations, such as 2p53
.
However, it may be noted that the 2p53d2 configuration has been deliberately excluded from the calculations, because it generates 45 levels and all of which lie above the lowest 134 already included. The same argument applies to other higher configurations, such as 2p53![]() 4
4![]() and 2p54
and 2p54![]() .
Since all of these
configurations give rise to energy levels above the 134 levels included presently, their inclusion in a calculation will not significantly affect the results for energy
levels and/or the radiative rates among the lowest 134 levels. For example, a calculation performed with the additional inclusion of the 2p53d2, 2p53
.
Since all of these
configurations give rise to energy levels above the 134 levels included presently, their inclusion in a calculation will not significantly affect the results for energy
levels and/or the radiative rates among the lowest 134 levels. For example, a calculation performed with the additional inclusion of the 2p53d2, 2p53![]() 4
4![]() and
2p54
and
2p54![]() configurations, resulting in a total of 1201 levels, yields energy levels within 1 eV (or equivalently within 0.1%) with those listed in Table 1. Therefore,
their specific inclusion in a calculation may affect the results of effective collision strengths (at higher electron temperatures), due to the inclusion of resonances arising
from the higher levels, but will not affect the reported results of energy levels and/or the radiative rates. Furthermore, the calculations for
configurations, resulting in a total of 1201 levels, yields energy levels within 1 eV (or equivalently within 0.1%) with those listed in Table 1. Therefore,
their specific inclusion in a calculation may affect the results of effective collision strengths (at higher electron temperatures), due to the inclusion of resonances arising
from the higher levels, but will not affect the reported results of energy levels and/or the radiative rates. Furthermore, the calculations for ![]() (and subsequently for
(and subsequently for
![]() )
are computationally demanding, as the size of the Hamiltonian matrix is large (13 330), and hence will take a considerably long time to conclude. Therefore, in this
paper we report our results for energy levels and radiative rates (A-values) for five types of transitions, namely electric dipole (E1), electric quadrupole (E2), magnetic
dipole (M1), magnetic quadrupole (M2) and electric octupole (E3), as all of these are required in the modelling of plasmas. Additionally, we report lifetimes for all excited
levels, although no measurements are presently available with which to compare these results.
)
are computationally demanding, as the size of the Hamiltonian matrix is large (13 330), and hence will take a considerably long time to conclude. Therefore, in this
paper we report our results for energy levels and radiative rates (A-values) for five types of transitions, namely electric dipole (E1), electric quadrupole (E2), magnetic
dipole (M1), magnetic quadrupole (M2) and electric octupole (E3), as all of these are required in the modelling of plasmas. Additionally, we report lifetimes for all excited
levels, although no measurements are presently available with which to compare these results.
The 2p63![]() ,
2p53s2, 2p53s3p, 2p53s3d, 2p53p3d, and 2p53p2 configurations of Fe XVI give rise to 134 fine-structure levels, listed in Table 1.
Our calculated energies obtained from the GRASP code, with and without including Breit and QED effects, are given in this table along with those from the
experimental compilations of NIST (http://physics.nist.gov/PhysRefData). For our calculations, we have used the option of extended average level (EAL), in which a
weighted (proportional to 2j+1) trace of the Hamiltonian matrix is minimized. This produces a compromise set of orbitals describing closely lying states with moderate
accuracy. The inclusion of Breit and QED effects lowers the energies up to a maximum of 0.08 Ryd (
,
2p53s2, 2p53s3p, 2p53s3d, 2p53p3d, and 2p53p2 configurations of Fe XVI give rise to 134 fine-structure levels, listed in Table 1.
Our calculated energies obtained from the GRASP code, with and without including Breit and QED effects, are given in this table along with those from the
experimental compilations of NIST (http://physics.nist.gov/PhysRefData). For our calculations, we have used the option of extended average level (EAL), in which a
weighted (proportional to 2j+1) trace of the Hamiltonian matrix is minimized. This produces a compromise set of orbitals describing closely lying states with moderate
accuracy. The inclusion of Breit and QED effects lowers the energies up to a maximum of 0.08 Ryd (![]() 0.2%) - see for example, levels 61, 101 and 131. In general, the
theoretical energies agree well in magnitude with the experimental ones, but differences are up to 0.4 Ryd (
0.2%) - see for example, levels 61, 101 and 131. In general, the
theoretical energies agree well in magnitude with the experimental ones, but differences are up to 0.4 Ryd (![]() 0.7%) for some levels, such as: 11, 57 and 70. Additionally,
our energies without the Breit and QED corrections are comparatively in better agreement with the corresponding experimental results, although the latter are available for only
a few levels.
0.7%) for some levels, such as: 11, 57 and 70. Additionally,
our energies without the Breit and QED corrections are comparatively in better agreement with the corresponding experimental results, although the latter are available for only
a few levels.
However, the level orderings in theory and experiment are slightly different in a few instances, such as for levels: 11/12 and 61/62. Most of these levels have energies very
close to each other, and differing amount of configuration interaction (CI) may result in slightly different level orderings. However, a more serious problem is of level
indentification. Some of the levels of a configuration with the same J value are highly mixed, such as levels 11/17 (2p53s3p 2D3/2, 4D3/2), 26/30
(2p53p2 4P
![]() ,
2P
,
2P
![]() )
and 66/76 (2p53s3d 2D
)
and 66/76 (2p53s3d 2D
![]() ,
2P
,
2P
![]() ). For these (and other similar) levels the identification of a particular
level is not unique, and is not based on the strength of the dominant eigenvector alone. This is a common problem in all atomic structure calculations, especially when the
levels of a configuration are highly mixed, and the addition of more CI complicates the identifications further rather than making the task easier. Therefore, the configuration
and the J values given in Table 1 are definite, but the corresponding LSJ designation provided for a level is only for guidance, and is liable to interchange. This is the
main reason that some of the experimental levels, such as 2p53s(1P)3p 2D3/2 and 2p53s(3P)3p 2D3/2, i.e. levels 11 and 24, appear to be listed at
the wrong places.
). For these (and other similar) levels the identification of a particular
level is not unique, and is not based on the strength of the dominant eigenvector alone. This is a common problem in all atomic structure calculations, especially when the
levels of a configuration are highly mixed, and the addition of more CI complicates the identifications further rather than making the task easier. Therefore, the configuration
and the J values given in Table 1 are definite, but the corresponding LSJ designation provided for a level is only for guidance, and is liable to interchange. This is the
main reason that some of the experimental levels, such as 2p53s(1P)3p 2D3/2 and 2p53s(3P)3p 2D3/2, i.e. levels 11 and 24, appear to be listed at
the wrong places.
We have taken all precautions to label the levels in Table 1, although some ambiguity in their designations cannot be avoided as discussed above. Furthermore, in the absence of any other theoretical or experimental energies to compare with, we have performed another calculation from the Flexible Atomic Code (FAC) of Gu (2003), which is easily available from the website http://kipac-tree.stanford.edu/fac. Energy levels obtained from this code are also listed in Table 1, and the excellent agreement (within 0.1 Ryd) between the GRASP and FAC energy levels gives confidence in our results. The level orderings are also (nearly) the same in both calculations, although some closely spaced levels, such as 41/42, 69/70 and 102/103, have switched positions. Finally, in the last column of Table 1 we have included the mixing coefficients (largest three where appropriate), which may be helpful for further comparisons and redesignations of the levels.
The absorption oscillator strength (fij) and radiative rate Aji (in s-1) for a transition ![]() are related by the following expression:
are related by the following expression:
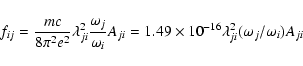 |
(1) |
Table 4:
Transition wavelengths (
![]() in
in ![]() ), radiative rates (Aji in s-1), and oscillator strengths (fij, dimensionless)
for some (
), radiative rates (Aji in s-1), and oscillator strengths (fij, dimensionless)
for some (![]() 10-8) magnetic dipole (M2) and electric octupole (E3) transitions of Fe XVI. (
10-8) magnetic dipole (M2) and electric octupole (E3) transitions of Fe XVI. (
![]() 10
10![]() ).
).
for the electric dipole (E1) transitions:
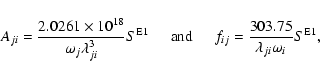 |
(2) |
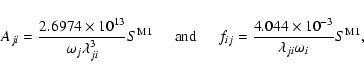 |
(3) |
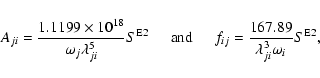 |
(4) |
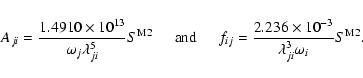 |
(5) |
In the absence of other similar A-values being available in the literature with which to compare, it is difficult to assess the accuracy of our present results. A general criterion to assess the accuracy is to compare the length and velocity forms of the f- or A-values. Before we discuss these we would like to remind readers that such comparisons are only desirable, but are not a fully sufficient test to assess accuracy, as different calculations (or combinations of configurations) may give comparable f-values in the two forms, but entirely different results in magnitude - see Aggarwal et al. (2007) for further details and comparisons.
Since the electric dipole (E1) transitions are comparatively more important, we focus on the accuracy assessments of their A-values alone. Among the stronger transitions
(i.e.
![]() ), the length and velocity forms differ by over 20% for 267 (10%) transitions, whereas only 49 (2%) transitions have differing A-values of over 50%.
Among these, four transitions, namely 25-66, 57-118, 65-115 and 66-128, have the ratio
), the length and velocity forms differ by over 20% for 267 (10%) transitions, whereas only 49 (2%) transitions have differing A-values of over 50%.
Among these, four transitions, namely 25-66, 57-118, 65-115 and 66-128, have the ratio
![]() with values of up to 10. Therefore,
based on a satisfactory agreement between the two forms, we may state that the accuracy of our listed A-values is better than 20% for a majority of the strong transitions.
Differences between the two forms for weaker transitions (f < 0.01) can sometimes be several orders of magnitude. Particularly noteworthy are 5 transitions, namely 27-155 (
with values of up to 10. Therefore,
based on a satisfactory agreement between the two forms, we may state that the accuracy of our listed A-values is better than 20% for a majority of the strong transitions.
Differences between the two forms for weaker transitions (f < 0.01) can sometimes be several orders of magnitude. Particularly noteworthy are 5 transitions, namely 27-155 (
![]() ), 38-81 (
), 38-81 (
![]() ), 65-99 (
), 65-99 (
![]() ), 69-70 (
), 69-70 (
![]() ), and 76-120 (
), and 76-120 (
![]() ), for which the ratio
), for which the ratio
![]() is very large. However, all such transitions are very weak, and hence sensitive to mixing coefficients, but do not affect the overall accuracy of the calculations. Before
concluding we make one more comparison with our calculations from FAC.
is very large. However, all such transitions are very weak, and hence sensitive to mixing coefficients, but do not affect the overall accuracy of the calculations. Before
concluding we make one more comparison with our calculations from FAC.
A comparison made between the A-values from GRASP and FAC (not listed in Table 2) indicates excellent agreement for a majority of the strong transitions. However, 143 (5%) of the transitions have f-values differing by over 20%, whereas only 42 (1.6%) transitions differ by over 50%. Among these, only three transitions, namely 34-88, 35-88 and 41-88, have the f-values differing by an order of magnitude. Considering that the calculations have been performed for a large number of transitions, such differences for a few transitions do not affect the overall accuracy of our results, and we may state with confidence that our listed A-values are probably accurate to better than 20% for a majority of the strong transitions.
The lifetime ![]() for a level j is defined as follows:
for a level j is defined as follows:
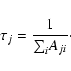 |
(6) |
In the present work, results for energy levels, radiative rates, oscillator strengths, and line strengths for all transitions among the lowest 134 levels of Fe XVI have been presented. Additionally, results for radiative rates have been presented for five types of transitions, namely E1, E2, E3, M1 and M2. A complete set of results are likely to be useful for the modelling of a variety of plasmas.
Based on the comparison made between the length and velocity forms of the oscillator strengths, as well as the comparison between the GRASP and FAC calculations, we assess that our radiative rates are accurate to better than 20% for a majority of strong transitions. Similarly, based on the comparison between the GRASP and FAC calculations, as well as with the available compiled experimental results, our energy levels are assessed to be accurate to better than 1%. However, the level designations are likely to fluctuate for a few of them, for which further work is recommended.
Lifetimes for all excited levels of Fe XVI are listed, but no comparisons could be possible due to the paucity of other theoretical or experimental results.
Our calculations for collision strengths, and subsequently for excitation rates, are in progress. These calculations, being highly computationally demanding, will take a considerably long time to conclude. We hope to present our results for these highly desired and important parameters in future.
Acknowledgements
This work has been financed by the Engineering and Physical Sciences and Particle Physics and Astronomy Research Councils of the United Kingdom, and FPK is grateful to AWE Aldermaston for the award of a William Penney Fellowship. Finally, we thank an anonymous referee for a critical reading of the earlier version of the paper, and for providing some constructive comments.