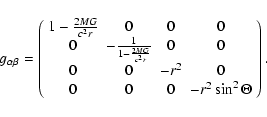 |
(1) |
A&A 463, 315-320 (2007)
DOI: 10.1051/0004-6361:20065521
S. Knop1,2 - P. H. Hauschildt1 - E. Baron2
1 - Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg, Germany
2 -
University of Oklahoma, 440 West Brooks, Rm 100, Norman, OK 73019-2061, USA
Received 28 April 2006 / Accepted 10 November 2006
Abstract
Aims. We present a general method to calculate radiative transfer including scattering in the continuum as well as in lines in spherically symmetric systems that are influenced by the effects of general relativity (GR). We utilize a comoving wavelength ansatz that allows to resolve spectral lines throughout the atmosphere.
Methods. The used numerical solution is an operator splitting (OS) technique that uses a characteristic formal solution. The bending of photon paths and the wavelength shifts due to the effects of GR are fully taken into account, as is the treatment of image generation in a curved spacetime.
Results. We describe the algorithm we use and demonstrate the effects of GR on the radiative transport of a two level atom line in a neutron star like atmosphere for various combinations of continuous and line scattering coefficients. In addition, we present grey continuum models and discuss the effects of different scattering albedos on the emergent spectra and the determination of effective temperatures and radii of neutron star atmospheres.
Key words: radiative transfer - relativity - scattering
In the last few decades much effort has been put into the modeling of radiative transfer in relativistically moving atmospheres such as novae and supernovae. One of the state of the art techniques to solve this problem is the operator splitting (OS) method. This method has been successfully used to solve radiative transfer problems with scattering and complete treatment of non-local thermodynamic equilibrium (NLTE) effects.
However, these sophisticated methods for treating radiative transfer have not been used in a general relativistic environment, although the form of the GR equation of transfer does, basically, not differ from the special relativistic version and the OS method can be applied to such problems.
There have been several successful attempts to model the emergent spectra of general relativistic systems such as neutron stars. These models also account for magnetic fields or different surface temperatures. However, the radiative transfer in these cases generally solves classical plane parallel problems. See Zavlin & Pavlov (2002) for a review.
Here we present an OS method of solving GR radiative transfer problems in spherical (Schwarzschild) geometry. Other authors have solved the radiative transfer problem in GR. For instance Schinder & Bludman (1989) solve the moment equations of radiative transfer with a variable Eddington factor method. The advantage of OS is not only that it does not depend on closure conditions but can also solve magneto-optical transfer, what could prove to be important as far as neutron stars are concerned.
Zane et al. (1996) developed a characteristics method to solve general relativistic radiative transport problems. They utilize the constants of motion for the description of photon orbits that arise due to the Killing vectors of the spherically symmetric spacetime and use the analytical connection of an affine parameter with the radial coordinate as well as choosing the momentum variables along the characteristics to be constant to formulate the radiative transport equation. Although this simplifies the equation in the case of flows such as accretion onto black holes and neutron stars, the lack of a comoving wavelength description forces the use of a large number of characteristics to resolve the (in this case) angular dependent absorption coefficients and a huge number of wavelength points to resolve the shift of spectral lines through the atmosphere. The latter is necessary even in the case of static general relativistic atmospheres, e.g., in neutron stars.
We avoid these problems by using a comoving wavelength coordinate which explicitly accounts for the coupling of different wavelengths. This ansatz is the important core part of this work. Since in order to calculate detailed spectra you need to resolve spectral lines throughout the atmosphere and you cannot afford to use a wavelength description that depends on the layer of the atmosphere that you are at. Since in order to perform NLTE calculations you would have to add a significant number of wavelengths to your computation to resolve the spectral line at hand in every layer with the desired quality.
In the following we present calculations of general relativistic radiative line and continuum transfer with a complete treatment of scattering. In order to demonstrate the functionality of the method, we chose a simple test case similar to a neutron star atmosphere.
Lindquist found the equation for radiative transfer for a comoving metric (Lindquist 1966). He used the photon distribution function as variable to describe the radiation field. The works of Schinder & Bludman (1989) and Zane et al. (1996) follow this ansatz.
However, we want to utilize a description of the radiation via the specific intensity that is suitable for our method of solution.
Rather than using the general metric used by Lindquist,
we neglect the effects of the atmosphere on the metric and use
the Schwarzschild solution:
The equation of radiative transfer in the Schwarzschild metric is then found in its characteristic form:
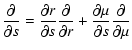 |
(3) | ||
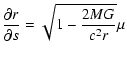 |
(4) | ||
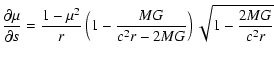 |
(5) | ||
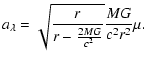 |
(6) |
However, there is a fundamental difference from the special relativistic equation
of transfer. The coefficient ![]() does not change sign in
monotonic flows that describe, e.g., supernova and nova
atmospheres. In the GR case, this coefficient is linear in
does not change sign in
monotonic flows that describe, e.g., supernova and nova
atmospheres. In the GR case, this coefficient is linear in ![]() and
hence the sign of
and
hence the sign of ![]() will be different for ingoing (
will be different for ingoing (![]() )
and outgoing (
)
and outgoing (![]() )
photons.
)
photons. ![]() couples different
wavelengths and determines how the spectral features shift due to the
flow or the gravitational field. In the case of a supernova atmosphere
the different parts of the atmosphere all move away from each other so
that the direction of the wavelength shift along a ray is always the
same, hence
couples different
wavelengths and determines how the spectral features shift due to the
flow or the gravitational field. In the case of a supernova atmosphere
the different parts of the atmosphere all move away from each other so
that the direction of the wavelength shift along a ray is always the
same, hence ![]() has the same sign along the ray. In a gravitational field, ingoing photons will be blueshifted and outgoing
photons will be redshifted and hence, the sign of
has the same sign along the ray. In a gravitational field, ingoing photons will be blueshifted and outgoing
photons will be redshifted and hence, the sign of ![]() changes. This presents a difficulty as the direction of flow of
information in the wavelength space is reversed along a ray and the
transfer equation is no longer an initial value problem in wavelength
space, but a 2-point boundary value problem.
changes. This presents a difficulty as the direction of flow of
information in the wavelength space is reversed along a ray and the
transfer equation is no longer an initial value problem in wavelength
space, but a 2-point boundary value problem.
Mihalas already realized this in Mihalas (1980) and
outlined a simple ray by ray formal solution
to this problem. However, this solution is of little use for the construction
of an approximate ![]() -operator for an ALI-iteration.
To solve this problem we use the OS method
described in detail in Baron & Hauschildt (2004).
-operator for an ALI-iteration.
To solve this problem we use the OS method
described in detail in Baron & Hauschildt (2004).
The treatment of arbitrarily flows of information in the wavelengthspace means
that every spatial point at all wavelengths can influence the intensity
at a given spatial point at a given wavelength. This forces you to use a matrix notation for the formal solution where you have to implement proper
boundary conditions gouverned by ![]() at every spatial point for all
wavelengths to ensure a locally stable upwind scheme for the wavelength discretization.
at every spatial point for all
wavelengths to ensure a locally stable upwind scheme for the wavelength discretization.
The GR case is a rather simple application to this method since the flow of information in the wavelengthspace just changes once on a ray, namely at the point of tangency or in the case of core intersecting rays at the innermost layer.
To make this method work with the GR case you have to calculate ![]() for every
wavelength on all points of a given characteristic and determine the appropriate discretization
of the derivative at this point. Furthermore you have to know the pathlength between two neighboring points on a ray to be able to calculate the change of optical
depth along the ray for all wavelengths. In addition to that you must determine the angles
of intersection with a given layer for all characteristics in order to perform angular integrations.
for every
wavelength on all points of a given characteristic and determine the appropriate discretization
of the derivative at this point. Furthermore you have to know the pathlength between two neighboring points on a ray to be able to calculate the change of optical
depth along the ray for all wavelengths. In addition to that you must determine the angles
of intersection with a given layer for all characteristics in order to perform angular integrations.
A photon in a gravitational field not only experiences a wavelength shift but also is deflected since it moves on a null-geodesic for the given spacetime. Since we are employing a characteristics based solution we can fully account for this effect. The spatial derivatives in Eq. (2) describe the geometry of our characteristics. They are still geodesics and can be described by an affine parameter.
In order to obtain the rays, the
![]() part of Eq. (2) has to be integrated. For the Schwarzschild metric it is
possible to analytically describe the photon orbits in terms of constants of
the motion. In addition, we have to relate the affine parameter to the distance
along the characteristics. In the one dimensional case, the integration is
simple and fast. Since the spacetime just outside the atmosphere will, in
general, not be flat, we extend our calculation of the characteristics into a regime of spacetime that can be considered flat - in our test calculations
discussed below, we chose a boundary of ten Schwarzschild-radii - to make sure
that we calculate the spectrum from a correct set of angles that represent the
imaging of the source in curved spacetime.
part of Eq. (2) has to be integrated. For the Schwarzschild metric it is
possible to analytically describe the photon orbits in terms of constants of
the motion. In addition, we have to relate the affine parameter to the distance
along the characteristics. In the one dimensional case, the integration is
simple and fast. Since the spacetime just outside the atmosphere will, in
general, not be flat, we extend our calculation of the characteristics into a regime of spacetime that can be considered flat - in our test calculations
discussed below, we chose a boundary of ten Schwarzschild-radii - to make sure
that we calculate the spectrum from a correct set of angles that represent the
imaging of the source in curved spacetime.
We assume vacuum conditions outside the atmosphere and, therefore, the intensities will not change along the characteristic outside the atmosphere, of course except for being redshifted due to the gravitational field what is trivial to account for.
We solve the test radiative transfer problems in a spherical model
configuration with 50 radial points (layers). We assume an exponential density
structure
For a given optical depth (![]() )
grid we integrate the radial grid via
)
grid we integrate the radial grid via
| |
Figure 1: Radius is plotted over optical depth. The optical depth was calculated from the wavelength independent continuous opacity. The atmosphere is about 60 m thick, but the layers with an optical depth around one lie just centimeters below the outermost layer. |
| Open with DEXTER | |
In Fig. 1 we plot the radial structure of the test atmosphere versus
the optical depth grid that we used for the calculations in Sect. 4. The method of Baron & Hauschildt (2004) makes it necessary to
provide a spatial boundary condition for the characteristics which is done via
the diffusion approximation. We generate a simple grey temperature structure
with the Hopf-function (Chandrasekhar 1950). To describe the single
spectral line of the two-level-atom, we define a wavelength
![]() as the center of the line and use a Gaussian profile centered on this wavelength:
as the center of the line and use a Gaussian profile centered on this wavelength:
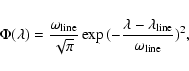 |
(9) |
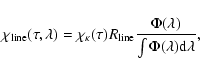 |
(10) |
It should be noted that the Gaussian width of the line is only 0.01 Å. This is very small and does not represent a line width one would expect in neutron star atmosphere due to the large temperatures and pressures present in such an atmosphere. The small width was chosen to highlight the effects of GR on radiative transfer. Since the atmosphere of a neutron star is only a few centimeters thick, the intrinsic wavelength shifts within the atmosphere are very small and the GR effects can be tested best with very narrow lines.
A detailed treatment of radiative transfer especially in the general relativistic environment of a neutron star atmosphere is desirable, since constraints on the mass-radius relation are needed for the understanding of neutron star interiors and its equation of state. The constraint should be as strict as possible and, therefore, the radiative transfer should be as sophisticated as possible.
Realistic models will need a multidimensional description and have characteristics in the atmosphere that extend over larger portions of spacetime and hence have a larger intrinsic wavelength shift. Furthermore there may be configurations of blended lines that create a rapidly changing opacity as seen, e.g., in the UV spectra of classical novae (Hauschildt et al. 1995).
Furthermore, in realistic models of accretion columns on neutron stars the atmosphere extends over larger regions of spacetime and the intrinsic line shifts will be much larger. Therefore, there are physical systems where you expect, that detailed general relativistic radiative transfer is important. Besides this method is not limited to static atmospheres but can also be applied to gamma-ray-bursts, accretion scenarios, or neutrino transport in early phases of core collapse supernovae.
Since we treat the radiative transfer problem with scattering, we need
to specify the quantities
![]() and
and
![]() to
define the scattering albedo.
The true absorption and the scattering part of the continuum opacity can now
be expressed through:
to
define the scattering albedo.
The true absorption and the scattering part of the continuum opacity can now
be expressed through:
| (11) | ||
| (12) |
| (13) | |||
| (14) |
| (15) |
| (16) |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5521_02.eps}\end{figure}](/articles/aa/full/2007/07/aa5521-06/Timg47.gif) |
Figure 2: Results for non-scattering model line and continuum. |
| Open with DEXTER | |
We calculate the emerging spectra of the model line for various
combinations of scattering parameters for the continuum and for the line - hence providing a NLTE treatment of the line transfer.
In Figs. 2 to 6 we always show
two cases with different gravitational masses - one with M = 0 and the other with
![]() .
The wavelength scale at the bottom corresponds
to the massless case and the upper scale to the one solar mass
case. The emerging line profiles are plotted over each other in order to be easily compared.
All calculated spectra include the full treatment of scattering unless it is
indicated that a scattering parameter was set to one.
.
The wavelength scale at the bottom corresponds
to the massless case and the upper scale to the one solar mass
case. The emerging line profiles are plotted over each other in order to be easily compared.
All calculated spectra include the full treatment of scattering unless it is
indicated that a scattering parameter was set to one.
We include the massless case in order to verify the code by comparing the results to the thoroughly tested special relativistic code and obtained the same results with both methods. In addition, all other tests such as omitting the line and recovering a flat continuum for constant thermal sources, sudden changes in the wavelength resolution, and wavelength dependent boundary conditions produced correct results.
In Fig. 2 the continuum as well as the line are purely
thermal. In the massless case this results in a symmetric absorption
line while in the general relativistic case for one solar mass the
line profile deforms and becomes asymmetric with an extended wing to
the red, although the effect is very small. The line profiles are
normalized to the continuum and the equivalent widths of the two lines
are different. Although the radial structure and the run of the
opacities is exactly the same in both cases, the effective opacity is
different. due to the factor
![]() in Eq. (2).
in Eq. (2).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5521_03.eps}\end{figure}](/articles/aa/full/2007/07/aa5521-06/Timg50.gif) |
Figure 3:
The model line and the continuum are scattering with
|
| Open with DEXTER | |
In Fig. 3 the line and the continuum are scattering with
![]() and
and
![]() .
In the massless case this results in a symmetric absorption profile
with line wings
slightly in emission, while in the general relativistic case the
line profile is very asymmetric with an emission feature on the blue
side and an extended red absorption wing.
.
In the massless case this results in a symmetric absorption profile
with line wings
slightly in emission, while in the general relativistic case the
line profile is very asymmetric with an emission feature on the blue
side and an extended red absorption wing.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5521_04.eps}\end{figure}](/articles/aa/full/2007/07/aa5521-06/Timg51.gif) |
Figure 4:
The model line scatters with
|
| Open with DEXTER | |
The model parameters used to generate Fig. 4 resemble those
of Fig. 3. The only difference is a stronger scattering in the continuum
![]()
![]() 10-6. The strength and shape of the blue
emission depends on the scattering in the continuum. For a strong scattering
continuum even in the massless case an emission feature appears in both wings
of the line. It can be explained with the Schuster-mechanism (Mihalas 1978).
In the relativistic case this mechanism appears to be amplified and strongly
distorted in the red wing. To rule out any effect of line scattering, we have
calculated a model line with pure scattering (
10-6. The strength and shape of the blue
emission depends on the scattering in the continuum. For a strong scattering
continuum even in the massless case an emission feature appears in both wings
of the line. It can be explained with the Schuster-mechanism (Mihalas 1978).
In the relativistic case this mechanism appears to be amplified and strongly
distorted in the red wing. To rule out any effect of line scattering, we have
calculated a model line with pure scattering (
![]() )
in the
continuum and no scattering in the line. The result is shown in Fig. 5. The massless case shows the expected absorption profile with the wings
in emission. In the relativistic case, the shape of the blue emission feature
does not change compared to the cases with less scattering. However, its slope
extends way farther into the blue, while on the red side of the line a very
broad emission feature extends much farther to the red, although the
peak is not as high as the blue peak. In addition, we have calculated a purely scattering
(
)
in the
continuum and no scattering in the line. The result is shown in Fig. 5. The massless case shows the expected absorption profile with the wings
in emission. In the relativistic case, the shape of the blue emission feature
does not change compared to the cases with less scattering. However, its slope
extends way farther into the blue, while on the red side of the line a very
broad emission feature extends much farther to the red, although the
peak is not as high as the blue peak. In addition, we have calculated a purely scattering
(
![]() )
model line
combined with a purely absorptive continuum. This decouples the model line
from the thermal pool. The results are shown in Fig. 6. Due to the scattering, the line is very strong, but the
deformation of the lines wings is essentially the same as in Fig. 2,
where the line did not scatter.
)
model line
combined with a purely absorptive continuum. This decouples the model line
from the thermal pool. The results are shown in Fig. 6. Due to the scattering, the line is very strong, but the
deformation of the lines wings is essentially the same as in Fig. 2,
where the line did not scatter.
The effects of GR for the given atmosphere are most obvious for a scattering continuum. The resulting lineshape is strongly asymmetric. Scattering in the line has no discernible effect on the shape of the line. The actual deformation due to GR effects is also very small for pure linescattering.
The emergent lineshapes are related in principle to P-Cygni profiles, since there is also a constant wavelength shift - the dopplershift - throughout the atmosphere. However there is a fundamental difference between the two cases, since in an expanding atmosphere where P-Cygni profiles are observed there is a point of last contact of a photon with the atmosphere, hence the information of the dopplershift at the point of emission in respect to the observer is conserved. In the gravitational field the wavelength of the photon gets shifted even without any interaction with the atmosphere.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5521_05.eps}\end{figure}](/articles/aa/full/2007/07/aa5521-06/Timg52.gif) |
Figure 5:
The model line is nonscattering with a completely scattering -
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5521_06.eps}\end{figure}](/articles/aa/full/2007/07/aa5521-06/Timg53.gif) |
Figure 6:
The model line is completely scattering -
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{5521_07.eps}\end{figure}](/articles/aa/full/2007/07/aa5521-06/Timg54.gif) |
Figure 7:
The spectrum was corrected for the gravitational redshift and fitted
with a blackbody with the known effective temperature of the model -
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{5521_08.eps}\end{figure}](/articles/aa/full/2007/07/aa5521-06/Timg55.gif) |
Figure 8:
The spectrum was corrected for the gravitational redshift and fitted
with a blackbody with the known effective temperature of the model -
|
| Open with DEXTER | |
As another application to general relativistic transfer we calculated grey
continuum models. To do so we changed our wavelength resolution and omitted the
model line from our calculations (
![]() ). In the following we
present the emerging continuous spectra for varying values of
). In the following we
present the emerging continuous spectra for varying values of
![]() .
.
The temperature structure of the model is grey with an effective temperature of 104 K (the absolute value of the effective temperature is not important for the testing). The emergent spectra are nearly blackbody spectra with only a slightly distorted overall shape as they are a little bit broader than the blackbody.
To determine the effective temperature
from an observation one would have to correct for the gravitational redshift
and then try to fit a blackbody to the spectrum. This procedure will only
deliver physically relevant results if the scattering conditions in the
atmosphere are known. As long as all photons are absorbed and none scattered -
![]() - (see Fig. 7) the emergent spectrum
(corrected for gravitational redshift) is fitted with a blackbody with a temperature that is the same as the effective temperature of the model. For
models with non-zero scattering -
- (see Fig. 7) the emergent spectrum
(corrected for gravitational redshift) is fitted with a blackbody with a temperature that is the same as the effective temperature of the model. For
models with non-zero scattering -
![]() in Fig. 8
and
in Fig. 8
and
![]() in Fig. 10 - the emerging spectra are
much bluer than the blackbody fit with the model effective temperature. In
Figs. 9 and 11 we corrected the temperatures of the
blackbody fits to match the emerging spectra. The apparent temperatures are
much higher than the effective temperature of the model.
in Fig. 10 - the emerging spectra are
much bluer than the blackbody fit with the model effective temperature. In
Figs. 9 and 11 we corrected the temperatures of the
blackbody fits to match the emerging spectra. The apparent temperatures are
much higher than the effective temperature of the model.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{5521_09.eps}\end{figure}](/articles/aa/full/2007/07/aa5521-06/Timg57.gif) |
Figure 9: The model spectrum is the same as in Fig. 8, but this time the temperature of the blackbody was chosen to fit the spectrum. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{5521_10.eps}\end{figure}](/articles/aa/full/2007/07/aa5521-06/Timg58.gif) |
Figure 10:
The spectrum was corrected for the gravitational redshift and fitted
with a blackbody with the known effective temperature of the model -
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{5521_11.eps}\end{figure}](/articles/aa/full/2007/07/aa5521-06/Timg59.gif) |
Figure 11: The model spectrum is the same as in Fig. 10, but this time the temperature of the blackbody was chosen to fit the spectrum. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{5521_12.eps}\end{figure}](/articles/aa/full/2007/07/aa5521-06/Timg60.gif) |
Figure 12: Thermalisation depth is plotted over optical depth. Since the radial structure is only known on a discrete grid the value of the thermalisation depth for a given temperature was determined via linear interpolation. |
| Open with DEXTER | |
To prove the consistency of our results, we plot the thermalisation depth
![]() - the optical depth where the
- the optical depth where the
![]() - over the scattering parameter
- over the scattering parameter
![]() .
Since the emergent spectrum is Planckian,
.
Since the emergent spectrum is Planckian,
![]() is the optical depth where the temperature of the atmosphere equals the temperature of the blackbody fit. The results are plotted
in Fig. 12.
is the optical depth where the temperature of the atmosphere equals the temperature of the blackbody fit. The results are plotted
in Fig. 12.
The results are consistent with the simple model
![]() .
Hence, in the GR case the determination of
effective temperatures via blackbody fits or simple radiative transfer models
that neglect scattering will be inconsistent and result in systematic errors of
the effective temperatures.
Therefore, it is desirable to solve the scattering
problem in a GR environment selfconsistently in a full blown atmospheric code with the method of solution that we present in this paper.
.
Hence, in the GR case the determination of
effective temperatures via blackbody fits or simple radiative transfer models
that neglect scattering will be inconsistent and result in systematic errors of
the effective temperatures.
Therefore, it is desirable to solve the scattering
problem in a GR environment selfconsistently in a full blown atmospheric code with the method of solution that we present in this paper.
We have developed a method to solve continuum and line radiative
transfer problems in spherically symmetric spacetimes that fully
accounts for general relativistic effects and can account
for scattering in the continuum and the lines. It uses a comoving
frame wavelength formalism that allows resolution of spectral lines
throughout the atmosphere without significantly increasing the number
of wavelength
points. The method was developed and tested in static neutron
star-like atmospheres, but is generally applicable to general
relativistic
systems. Only the photon orbits and the wavelength coupling term ![]() would be different in other GR systems. The test models provide an illustration of possible results for realistic model
atmospheres for neutron stars. The results show that the emergent
line profiles in general relativistic atmospheres cannot be described
in detail with non-relativistic radiative transfer. The influence of
the continuous scattering opacity on the shape of the lines is large.
would be different in other GR systems. The test models provide an illustration of possible results for realistic model
atmospheres for neutron stars. The results show that the emergent
line profiles in general relativistic atmospheres cannot be described
in detail with non-relativistic radiative transfer. The influence of
the continuous scattering opacity on the shape of the lines is large.
The apparent effective temperature of continuous spectra also depends strongly on the strength of the scattering. Therefore, it is necessary to include the treatment of scattering in the radiative transfer solution in order to obtain a consistent physical model of a neutron star atmosphere and similar cases. The method that we have presented here is a first step to develop a thorough treatment of general relativistic atmosphere models in 3D. It can be directly applied to multi-level NLTE calculations of relativistic neutron star atmospheres, which we will present in a subsequent paper.