A&A 462, 1165-1170 (2007)
DOI: 10.1051/0004-6361:20066284
Trojan planets in HD 108874?
(Research Note)
R. Schwarz2 - R. Dvorak1 - E. Pilat Lohinger1 - Á. Süli2 - B. Érdi2
1 - Institute for Astronomy, University of Vienna, Türkenschanzstr. 17, 1180 Wien, Austria
2 -
Eötvös Loránd University, Departement of Astronomy, Pázmány Péter
sétány 1/A, Budapest 1518, Hungary
Received 22 August 2006 / Accepted 16 October 2006
Abstract
Aims. It turned out recently that, in addition to a large planet with a semimajor axis 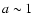 AU and a low eccentricity (
AU and a low eccentricity (
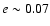 ), the extrasolar planetary system HD 108874 harbors another massive planet with
), the extrasolar planetary system HD 108874 harbors another massive planet with
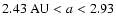 AU. The inner planet is orbiting the G5 host star in the habitable zone (=HZ); so that we could established stable regions for Earth-like Trojan planets.
AU. The inner planet is orbiting the G5 host star in the habitable zone (=HZ); so that we could established stable regions for Earth-like Trojan planets.
Methods. We integrated some 105 orbits of fictitious Trojans around the Lagrangian points for up to 107 years and checked the stability of the orbital elements and their chaoticity with the aid of the Fast Lyapunov Indicator.
Results. It turns out that this multiplanetary system is the first one where - with the uncertainties in eccentricity and semimajor axes of the outer planet - the existence of Trojan terrestrial planets in stable orbits in the HZ is possible for some combinations of the orbital parameters.
Key words: celestial mechanics - chaos - stars: planetary systems
Today there are about 209 confirmed planets in 169 extrasolar planetary systems (=EPS). We only have observational evidence for planets from 6 earth masses (Gliese 876 d) up to
several Jupiter masses. To ensure that an orbit of a planet with a mass comparable to
the Earth is stable in the
so-called habitable zone (=HZ)![[*]](/icons/foot_motif.gif) around its host star in
planetary systems with Jupiter-like planets, there are different possible
configurations:
around its host star in
planetary systems with Jupiter-like planets, there are different possible
configurations:
- a hot Jupiter moves very close to the central star;
- a large planet orbits far enough outside the HZ that it does not significantly perturb the
motion of a terrestrial planet inside the HZ;
- if Jupiter itself moves inside the HZ, a terrestrial planet may be
in the so-called coorbital motion like a satellite
or a Trojan
![[*]](/icons/foot_motif.gif) .
.
A lot of work has already been devoted to the existence of terrestrial planets in
EPS during the past ten years. We mention the very interesting work of Menou
& Tabachnik (2003), Laughlin & Chambers (2002), Pilat-Lohinger & Dvorak
(2002), Pilat Lohinger et al. (2003), and Jones & Sleep (2002). Additional studies concern specific systems
e.g. Pál & Sándor (2003), Dvorak et al. (2003a,b), and Asghari et al. (2004).
In this new work we concentrate on one specific system with two planets and on how
terrestrial planets may survive in the 1:1 resonance (Nauenberg 2002).
According to Laughlin & Chambers (2002), a possible formation of
two planets in a 1:1 mean motion resonance could be the result of an interaction of the forming planets with the
protoplanetary disc.
The chances for a single planetary system having a terrestrial planet moving
in the HZ is a lot greater than for multiplanetary systems.
When we check Table 1, it is evident that some of these systems could in
fact have such Earth-like satellites and/or Earth-like Trojans (=ET; see e.g. Dvorak et al. 2004;
Érdi & Sándor 2005; Schwarz et al. 2005). Note that in Table 1 (also Table 2) the location and the size of the HZ depends on the
spectral type of the the host stars. Main parameters:
1st column: name, 2nd column: spectral type,
3rd column: mass of the star, 4th column: the minimum mass of the giant planet,
5th column: distance (semimajor axis a [AU]) from the central star,
6th column: initial eccentricity of the extrasolar planet,
7th column: extension of the HZ [AU], and
8th column: partly inside the HZ in [%].
Table 1:
List of all EPSs with only one giant planet moving in the HZ of their
host stars.
Table 2:
As in Table 1 for multiplanetary systems.
In this study we are interested in a multiple system where one giant planet is moving in the
HZ and another large planet disturbs the motion of the first planet and thus
reduces the largeness of stable regions for ETs.
Unfortunately, up to now no stable region around the Lagrangian points for any
of the multiple planetary systems has been confirmed by theoretical
studies (Table 2). Using the results of recent observations,
we have one very good candidate, HD 108874 (Vogt et al. 2002).
This sunlike star was known to have only one massive planet with
approximately Jupitermass and an orbit with low eccentricity in the
HZ. But recently a second planet was observed outside the orbit
of the already known one (Vogt et al. 2005), which we present in Table 3.
We checked orbits of fictitious bodies in the regions
around the Lagrangian points L4 and L5 via numerical
simulations for a wide range of orbital parameters of the second perturbing planet.
Our research concentrated on investigations of orbits around L4,
because test computations showed no significant differences in the
stable regions around both equilibrium points.
The dynamical model was a restricted n-body problem, where we took the central star,
the two large planets, and fictitious Trojans into account. The
Trojan planets were thought to have low masses compared to the large planets
and were therefore set to m4=0. This assumption is reasonable as the results
of former computations have shown (Schwarz 2005; Schwarz et al. 2005).
To take the possible observational errors into account, especially of the
semimajor axis and the eccentricity of
the perturbing outer giant, we computed orbits of fictitious Trojan planets in 9 different models. We took the nominal values (Extrasolar Planets
Catalogue maintained by J. Schneider![[*]](/icons/foot_motif.gif) ), but also lower and
upper bounds for both parameters, i.e. eccentricity e and
semimajor axis a according to the given error bars (see Table 3):
), but also lower and
upper bounds for both parameters, i.e. eccentricity e and
semimajor axis a according to the given error bars (see Table 3):
- Models M1x, namely M11, M12, and M13 with a=2.43 AU and three values for the eccentricity
e=0.18, 0.25, 0.32.
- Models M2x, namely M21, M22, and M23 with a=2.68 AU and again
e=0.18, 0.25, 0.32.
- Models M3x, namely M31, M32, and M33 with a=2.93 AU and
e=0.18, 0.25, 0.32.
For a multiplanetary system it is necessary to integrate long enough to
see how the secular resonances between the two large planets (like in the Jupiter
- Saturn system) act on the orbit of a Trojan planet. We thus have undertaken
two different runs for each model:
- 1.
- a complete survey of the region around the Lagrange point with a grid in
the argument of perihelion
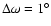 and
and
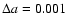 AU for 106 years within
the borders
AU for 106 years within
the borders
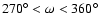 and 1.01 AU
< a < 1.09 AU;
and 1.01 AU
< a < 1.09 AU;
- 2.
- two cuts within this region where we fixed, on the one hand, the semimajor
axis a (exactly the one of the Lagrange point) and varied the angle
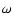 ;
on the other hand, we fixed the angle
;
on the other hand, we fixed the angle 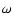 and varied the semimajor axes a;
the integration time was set to 107 years.
and varied the semimajor axes a;
the integration time was set to 107 years.
Our stability criterion was based on the maximum eccentricity achieved during the
integration time; when
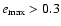 ,
it turned out - according to numerical
results - that the fictitious body has left the region around the
Lagrangian equilibrium point L4.
,
it turned out - according to numerical
results - that the fictitious body has left the region around the
Lagrangian equilibrium point L4.
Table 3:
Orbital elements of the EPS HD 108874.
The importance of long-term integrations is evident when we
compare the results for different time scales of integration
up to 107 years (Fig. 7). The stability regions
shrink significantly and, for the long integration time, there is only a small
stable region around the equilibrium point.
Finally we mention that the integration method was the Lie-integration![[*]](/icons/foot_motif.gif) already used extensively in
many of our applications (e.g. Hanslmeier & Dvorak 1984; Lichtenegger 1984;
Dvorak et al. 2004). We also used a different
method to ensure the numerical results of the computations, namely the
fast Lyapunov indicator (FLI, Froeschlé et al. 1997). This is a fast method of qualitatively distinguishing
between regular and chaotic motion in
a dynamical system. This indicator is defined as the norm of the largest
tangent vector (see Froeschlé et al. 1997).
already used extensively in
many of our applications (e.g. Hanslmeier & Dvorak 1984; Lichtenegger 1984;
Dvorak et al. 2004). We also used a different
method to ensure the numerical results of the computations, namely the
fast Lyapunov indicator (FLI, Froeschlé et al. 1997). This is a fast method of qualitatively distinguishing
between regular and chaotic motion in
a dynamical system. This indicator is defined as the norm of the largest
tangent vector (see Froeschlé et al. 1997).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6284f1.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg19.gif) |
Figure 1:
Stability of the Lagrange point L4 taking the outer planet's
perturbations into account. On the x-axis we plotted the initial semimajor axes, on the y-axis the
initial eccentricity of the second planet; light grey indicates unstable motions, and dark
grey indicates motion of a stable Trojan, where we used
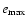 during
the whole integration as a check.
during
the whole integration as a check. |
| Open with DEXTER |
First of all, we checked the numerical stability of the point L4 itself. In the simple
elliptic restricted problem, ignoring the outer planet, this equilibrium point is well
inside the stable region for all given values of the eccentricity of the
planet and the mass ratio of
the primary bodies is well below the value
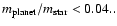 .
This is also true in the full three-body problem
when the Trojan planet has a mass comparable to the
Earth (Marchal 1990; Schwarz et al. 2005).
When we take the second planet into account in our model then the dynamics changes significantly.
In Fig. 1 we ploted the maximum eccentricity on the a, e plane, where we show the results for integrations of orbits of objects initially
started exactly in L4 of the inner giant planet for an
integration time of 107 years.
We varied the initial semimajor axis of the outer planet
with
.
This is also true in the full three-body problem
when the Trojan planet has a mass comparable to the
Earth (Marchal 1990; Schwarz et al. 2005).
When we take the second planet into account in our model then the dynamics changes significantly.
In Fig. 1 we ploted the maximum eccentricity on the a, e plane, where we show the results for integrations of orbits of objects initially
started exactly in L4 of the inner giant planet for an
integration time of 107 years.
We varied the initial semimajor axis of the outer planet
with
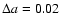 AU and the initial eccentricity with
AU and the initial eccentricity with
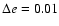 in the
borders covering the uncertainties well in the determined orbital elements
of the second planet.
in the
borders covering the uncertainties well in the determined orbital elements
of the second planet.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6284f2.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg23.gif) |
Figure 2:
Captions similar to Fig.1 but with results from the computations of the
FLIs. GG2 stands for the outer Gasgiant. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6284f3.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg24.gif) |
Figure 3:
FLI for different initial conditions of the outer planet in
a (x-axis) and e (y-axis). In the upper left corner the two giant planets are in a weak
chaotic zone, and the large region in dark grey corresponds to regular orbits of both planets. |
| Open with DEXTER |
In the respective plot (Fig. 1) we also marked the positions of the
mean motion resonances (=MMR) between the two
large planets. From this plot we can see that the model M1x is quite close to the
7:2 resonance, that the model M2x is far from dangerous 4:1 MMR, and that the
model M3x is far from the 5:1 MMR.
The results of the computations of the FLIs are shown in Fig. 2 and are very
similar to the ones of Fig. 1. The vertical stripes of chaotic orbits correspond to MMRs.
We also made computations in the framework of the 3-body problem (the host star and two
planets) for different a and e of the outer planet to check the stability
of the planets by using the FLIs. It turns out (Fig. 3) that for some of the orbital parameters
the two planets are moving in weakly chaotic orbits (but stable up to 108 years).
In Fig. 4 we show such an orbit with irregular jumps in eccentricity.
![\begin{figure}
\par\includegraphics[angle=270,width=6.9cm,clip]{6284f4.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg25.gif) |
Figure 4:
The chaotic orbits of both planets of HD 108874 with the initial
conditions M13 for 108 years. |
| Open with DEXTER |
It turns out that the model M1x for all three different eccentricities
do not have any stable orbits for Trojans around L4. For M12 and M13, this
is due to the chaoticity of the orbits of the two planets themselves, and
M23 is also in such a chaotic domain.
The orbits of the fictitious Trojans, for the largest initial eccentricity (e=0.32) in models
M23 and M33, are also unstable and the Trojan planets do not remain in the vicinity
of L4 for time scales longer than 1 Myr; this is already visible from
Figs. 1 and 2. The stable region for the Trojan planets is shown in Fig. 5 (upper graph)
for M21, where we can see that this region around the
equilibrium point L4 (located at a=1.051 and
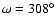 )
extends
from
)
extends
from
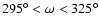 and
and
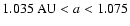 AU.
For M22 (Fig. 5, lower graph) we see only some spots of stable orbits,
which we suspected would disappear for a longer integration. In fact the cuts (see next chapter)
confirm this behavior that there are not many orbits that are left to be
stable ETs.
In Fig. 6 (upper graph) for M31 we again observe a slightly larger
stable region around the equilibrium point, which extends
from
AU.
For M22 (Fig. 5, lower graph) we see only some spots of stable orbits,
which we suspected would disappear for a longer integration. In fact the cuts (see next chapter)
confirm this behavior that there are not many orbits that are left to be
stable ETs.
In Fig. 6 (upper graph) for M31 we again observe a slightly larger
stable region around the equilibrium point, which extends
from
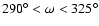 and
and
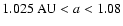 AU.
It can be understood that in this model the
perturbing planet is farther away from the inner planet and - which is maybe
more important - also far away from any low order MMR.
We show the extension in semimajor axes and
AU.
It can be understood that in this model the
perturbing planet is farther away from the inner planet and - which is maybe
more important - also far away from any low order MMR.
We show the extension in semimajor axes and 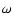 in Table 4 for different models.
The stable region in model M32 almost disappears for a higher eccentricity of the outer
planet. M21* and M31* show the results for more massive planets
in Table 4 for different models.
The stable region in model M32 almost disappears for a higher eccentricity of the outer
planet. M21* and M31* show the results for more massive planets![[*]](/icons/foot_motif.gif) .
.
![\begin{figure}
\par\includegraphics[angle=270,width=7.4cm,clip]{6284f5.ps}\par\vspace*{1.2cm}
\includegraphics[angle=270,width=7.4cm,clip]{6284f6.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg31.gif) |
Figure 5:
Stability regions around L4 in Models M21 and M22. The
initial semimajor axis (y-axis) is plotted versus the initial angular
distance from the equilibrium point L4. The dark regions around the point
L4 (a=1.051 AU,
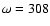 )
show that the maximum eccentricity during the integration time was always )
show that the maximum eccentricity during the integration time was always
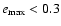 with such initial conditions.
with such initial conditions. |
| Open with DEXTER |
As already mentioned in a system with two planets, we need to take into account
the secular resonances between the two planets and how they act on the orbit of a
Trojan. The effect was recently explained fully by Robutel et al. (2005) for
the Jupiter Trojans. Therefore, to define the stability regions with greater
accuracy, we need to integrate long enough to
include the effects of secular resonances. In Fig. 7 we
show how the largeness with respect to the angular distance to L4 shrinks with a longer
integration-time.
Table 4:
Extensions of stable regions for different models with respect to the
semimajor axes and the angular distance to the Langange point L4.
![\begin{figure}
\par\includegraphics[angle=270,width=6.7cm,clip]{6284f9.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg36.gif) |
Figure 7:
Cuts with a fixed semimajor axis with changing angular distance to
the Lagrange point L4, which is located at
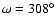 .
The different curves show how the
extension of the stable region shrinks with the integration time; full line
results after 107 years, dotted line after 106 years, hatched region
after 105 years. .
The different curves show how the
extension of the stable region shrinks with the integration time; full line
results after 107 years, dotted line after 106 years, hatched region
after 105 years. |
| Open with DEXTER |
We decided to extend the integration time
to 107 years for two cuts through L4. In one direction we fixed
 and varied a, and vice versa in the other direction, we fixed the aand varied
and varied a, and vice versa in the other direction, we fixed the aand varied 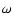
![[*]](/icons/foot_motif.gif) . These computations were only undertaken for the former stable regions found in models
M21, M22, M31, and M32.
In Fig. 8 we can see the cuts of M21 and M22 that determine the stable regions in the
direction of the larger semimajor axis a and with respect to the angular
distance to the Lagrange point L4. The valley of stable orbits can
be approximated by an ellipse around the Langrange point, where initial conditions inside lead to stable orbits.
. These computations were only undertaken for the former stable regions found in models
M21, M22, M31, and M32.
In Fig. 8 we can see the cuts of M21 and M22 that determine the stable regions in the
direction of the larger semimajor axis a and with respect to the angular
distance to the Lagrange point L4. The valley of stable orbits can
be approximated by an ellipse around the Langrange point, where initial conditions inside lead to stable orbits.
![\begin{figure}
\par\includegraphics[angle=270,width=7.4cm,clip]{6284f10.ps}\par\vspace*{0.8cm}
\includegraphics[angle=270,width=7.4cm,clip]{6284f11.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg39.gif) |
Figure 8:
Cut with a fixed semimajor axis and cut with a fixed pericenter;
upper graph for model M21, lower graph for model M22.
The crossing of the two lines is the Lagrange point L4; the z-axis is the maximum
eccentricity for the integration time of 107 years. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=7.9cm,clip]{6284f12.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg40.gif) |
Figure 9:
Cut with a fixed semimajor axis and cut with a fixed pericenter
for the model M31*. This model presents the results for more massive
planets (50 percent larger) to take into account the influence
of the inclination of the orbits with respect to the line of sight of the
observations. The crossing of the two lines is the Lagrange point L4; the z-axis
is the maximum eccentricity. |
| Open with DEXTER |
Out of the different possibilities for stable orbits of ETs in
the HZ of EPSs, we have investigated in this paper the system HD 108874 that
has two large planets: one moving in the HZ with a small eccentric orbit and
another one outside with a larger eccentricity. Taking the uncertainties of the orbital
parameters into account - the semimajor axis of the outer planet and its eccentricity -
we made numerical simulations of orbits of the fictitious ETs of the inner
planet.
It turned out that the stability region for the ETs
is quite small and that it disappears for most (5 out of 9 models) of the estimated orbital
parameters. The results agree partly with former computations by Érdi & Sándor
(2005), who in their study used a different, i.e. smaller, eccentricity of
the outer planet. In addition they showed how the region shrinks with the assumption
of a second planet.
In our study we found stable regions for ETs with
orbital parameters of the two giant planets which lie well inside the error
bars from the observations. Since the masses given by the observers are minimum masses for the planets involved,
we checked the stability regions for higher masses, namely twice the given
ones. In this case, all the Trojan orbits turn out to be unstable. With lower masses, stable regions for the
model (just 50 percent heavier than the minimum masses) M21 and M31 still persist, but the extensions are somewhat
smaller (see Table 4 and Fig. 9)![[*]](/icons/foot_motif.gif) .
We did not take the inclinations of these fictitious planets into account; but from studies of the Jupiter
Trojans we know that for small eccentricities these region may be slightly larger than estimated in our study (Robutel et al. 2005).
To detect a terrestrial Trojan planet in HD 108874 via observations will be
rather difficult but not impossible (Schneider 2006).
.
We did not take the inclinations of these fictitious planets into account; but from studies of the Jupiter
Trojans we know that for small eccentricities these region may be slightly larger than estimated in our study (Robutel et al. 2005).
To detect a terrestrial Trojan planet in HD 108874 via observations will be
rather difficult but not impossible (Schneider 2006).
Acknowledgements
For the realization of
this study we need to thank the Austrian Science Foundation (=FWF, project
P16024-N05) and the ISSI Institute in Bern, which supported us in the framework
of the ISSI team "Evolution of habitable planets''. R.S.
did this work in the framework of a Schrödinger grant of the FWF
(J2619-N16); E.P.-L. wishes to acknowledge the support by the FWF
Herta Firnberg grant (T122). Thanks also go to the "Wissenschaftlich-Technische Zusammenarbeit Österreich-Ungarn'' project
A12-2004: Dynamics of extrasolar planetary Systems.
- Asghari, N.,
Broeg, C., Carone, L., et al. 2004, A&A, 426, 353 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dvorak, R.,
Pilat-Lohinger, E., Funk, B., & Freistetter, F. 2003a, A&A,
398, L1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Dvorak, R.,
Pilat-Lohinger, E., Funk, B., & Freistetter, F. 2003b, A&A,
410, L13 [NASA ADS] [CrossRef] [EDP Sciences]
- Dvorak, R.,
Pilat-Lohinger, E., Schwarz, R., & Freistetter, F. 2004,
A&A, 426, 37 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Érdi, B., &
Sándor, Zs. 2005, CMDA, 92, 113 [NASA ADS] (In the text)
- Froeschlé,
C., Lega, E., & Gonczi, R. 1997, CMDA, 67, 41 [NASA ADS] (In the text)
- Hanslmeier,
A., & Dvorak, R. 1984, A&A, 132, 203 [NASA ADS] (In the text)
- Jones, B. W., &
Sleep, P. N. 2002, A&A, 393, 1015 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kasting, J. F.,
Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef]
- Lammer, H.,
Kulikov, Yu., Penz, T., et al. 2005, in A Comparison of the
Dynamical Evolution of Planetary Systems, ed. R. Dvorak, & S.
Ferraz-Mello (Springer), 273
- Laughlin, G.,
& Chambers, J. E. 2002, AJ, 124, 592 [NASA ADS] [CrossRef] (In the text)
-
Lichtenegger, H. 1984, CMDA, 34, 357 (In the text)
- Marchal, C. 1990,
The Three-Body Problem (Elsevier), 49
(In the text)
- Menou, K., &
Tabachnik, S. 2003, AJ, 583, 473 [NASA ADS] [CrossRef] (In the text)
- Nauenberg, M.
2002, AJ, 124, 2332 [NASA ADS] [CrossRef] (In the text)
- Pál, A., &
Sándor, Zs. 2003, Proceedings of the 3rd Austrian-Hungarion
Workshop on Trojans and related topics, ed. F. Freistetter, R.
Dvorak, & B. Érdi, 25
(In the text)
- Pilat-Lohinger, E.,
& Dvorak, R. 2002, CMDA, 82, 143 [NASA ADS]
- Pilat-Lohinger, E.,
Funk, B., & Dvorak, R. 2003, A&A, 400, 1085 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Robutel, P.,
Gabern, F., & Jorba, A. 2005, Celest. Mech. Dyn. Astron., 92,
53 [NASA ADS] [CrossRef] (In the text)
- Schneider, J.
2006, private communication
(In the text)
- Schwarz, R.,
Pilat-Lohinger, E., Dvorak, R., Érdi, B., & Sándor,
Zs. 2005, Astrobiol. J., 5, 579 [NASA ADS] (In the text)
- Schwarz, R.
2005b, Ph.D. Thesis, University of Vienna, online database:
http://media.obvsg.at/dissd
(In the text)
- Vogt, S. S., Butler, P.
R., Marcy, W. G., et al. 2002, AJ, 568, 352 [NASA ADS] [CrossRef] (In the text)
- Vogt, S. S., Butler, P.
R., Marcy, W. G., et al. 2005, AJ, 632, 638 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{6284f1.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg19.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6284f2.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6284f3.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg24.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=6.9cm,clip]{6284f4.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg25.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.4cm,clip]{6284f5.ps}\par\vspace*{1.2cm}
\includegraphics[angle=270,width=7.4cm,clip]{6284f6.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg31.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.4cm,clip]{6284f7.ps}\par\vspace*{1.2cm}
\includegraphics[angle=270,width=7.4cm,clip]{6284f8.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg32.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=6.7cm,clip]{6284f9.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg36.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.4cm,clip]{6284f10.ps}\par\vspace*{0.8cm}
\includegraphics[angle=270,width=7.4cm,clip]{6284f11.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg39.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.9cm,clip]{6284f12.ps}\end{figure}](/articles/aa/full/2007/06/aa6284-06/Timg40.gif)