A&A 462, 875-887 (2007)
DOI: 10.1051/0004-6361:20065955
M. Schirmer1 - T. Erben2 - M. Hetterscheidt2 - P. Schneider2
1 - Isaac Newton Group of Telescopes, Calle Alvarez Abreu 70,
38700 Santa Cruz de La Palma, Spain
2 - Argelander-Institut für Astronomie (AIfA),
Universität Bonn, Auf dem Hügel 71,
53121 Bonn, Germany
Received 3 July 2006 / Accepted 6 November 2006
Abstract
Aims. The aim of the present work is the construction of a mass-selected galaxy cluster sample based on weak gravitational lensing methods. This sample will be subject to spectroscopic follow-up observations.
Methods. We apply the mass aperture statistics (S-statistics) and a new derivative of it (the P-statistics) to 19 square degrees of high quality, single colour wide field imaging data obtained with the WFI@MPG/ESO 2.2 m telescope. For the statistics a family of filter functions is used that approximates the expected tangential radial shear profile and thus allows for the efficient detection of mass concentrations. The exact performance of the P-statistics still needs to be evaluated by means of simulations.
Results. We find that the two samples of mass concentrations found with the P- and S-statistics have very similar properties. The overlap between them increases with the S/N of the detections made. In total, we present a combined list of 158 possible mass concentrations, which is the first time that such a large and blindly selected sample is published. 72 of the detections are associated with concentrations of bright galaxies. For about 22 of those we found spectra in the literature, indicating or proving that the galaxies seen are indeed spatially concentrated. 16 of those were previously known to be clusters or have meanwhile been secured as such. We currently follow-up a larger number of them spectroscopically to obtain deeper insight into their physical properties. The remaining 55% of the possible mass concentrations found are not associated with any optical light. We show that those "dark'' detections are mostly due to noise, and appear preferentially in shallow data.
Key words: cosmology: dark matter - galaxies: clusters: general - gravitational lensing
The selection of mass concentrations using the shear caused by their weak gravitational lensing effect suffers from a number of disadvantages. The most important one is the high amount of noise contributed by the intrinsic ellipticities of lensed galaxies. This largely blurs the view of the cosmic density distribution, letting peaks disappear, and fakes peaks where there actually is no overdensity. It can only be beaten down to some degree by deep observations in good seeing. The other disadvantage is that any mass along the line of sight will contribute to the signal, giving rise to false peaks. Such projection effects or cosmic shear can only be eliminated or at least recognised if redshift information of either the lensed galaxies, or the matter distribution in the field is available. Cosmic shear can act as a source of noise (see for example Maturi et al. 2005), but it has recently been shown by Maturi et al. (2006) that this can partly be filtered out.
![\begin{figure}
\includegraphics[width=15.8cm,clip]{5955fg01.eps}
\end{figure}](/articles/aa/full/2007/06/aa5955-06/Timg32.gif) |
Figure 1:
Left: sky distribution of the GaBoDS fields. The
size of the symbols indicates the covered sky area (not to scale), with
one WFI shot covering 0.32 square degrees. All fields are at high galactic
latitude. Right: image seeing of the 58 coadded WFI@2.2 mosaics used for
the lensing analysis. The average seeing is 0
|
| Open with DEXTER | |
In the present work we use the aperture mass statistics (
![]() )
(Schneider 1996, hereafter S96) and a derivative of it for the
shear-selection of density peaks, based on 19 square degrees of sky coverage.
The purpose of the work is to establish a suitable filter function for
)
(Schneider 1996, hereafter S96) and a derivative of it for the
shear-selection of density peaks, based on 19 square degrees of sky coverage.
The purpose of the work is to establish a suitable filter function for
![]() ,
and then apply it to an (inhomogeneous) set of data. The sample
returned is currently the largest sample of shear-selected cluster candidates,
yet is dwarfed by the total number of galaxy clusters known.
,
and then apply it to an (inhomogeneous) set of data. The sample
returned is currently the largest sample of shear-selected cluster candidates,
yet is dwarfed by the total number of galaxy clusters known.
The outline of this paper is as follows. In Sect. 2 we give an overview of
the data used, concentrating on its quality and showing the usefulness for
this analysis. Section 3 contains a discussion of our implemented version of
![]() ,
particularly with regard to the chosen spatial filter functions. We
also introduce a new statistics, deduced from
,
particularly with regard to the chosen spatial filter functions. We
also introduce a new statistics, deduced from
![]() .
In Sect. 4 we present
and discuss our detections, and we conclude in Sect. 5.
.
In Sect. 4 we present
and discuss our detections, and we conclude in Sect. 5.
Throughout the rest of this paper we use common weak lensing notations, and refer the reader to Bartelmann & Schneider (2001) and Schneider et al. (2006) for more details and technical coverage.
The only difference between the current version of THELI and the one we used for the reduction of the survey data over the last years, is that for the image coaddition EISdrizzle was used, which is meanwhile replaced by Swarp. The latter method leads to a 4% smaller PSF in the final image in case of superb intrinsic image seeing as in our survey. The PSF anisotropy patterns themselves are indistinguishable between the two coaddition methods. Since the natural seeing variations (Fig. 1) in our images are much larger than those 4%, our analysis remains unaffected.
![\begin{figure}
\includegraphics[width=17cm,clip]{5955fg02.ps}
\end{figure}](/articles/aa/full/2007/06/aa5955-06/Timg36.gif) |
Figure 2:
Left: the average
|
| Open with DEXTER | |
PSF anisotropies are rather small and usually well-behaved with WFI@2.2, which
we have demonstrated several times (Schirmer et al. 2004; Erben et al. 2005; Schirmer et al. 2003, for example).
With a well-focussed telescope, 1% of anisotropy in sub-arcsecond seeing
conditions can be achieved, with a long-term statistical mode of around 2%
(see Fig. 3). Discontinuities in the PSF are largely absent across
chip borders. Slightly defocused exposures exhibit anisotropies of ![]() .
We
rejected individual exposures from the coaddition if one or more CCDs had an
anisotropy larger than 6% in either of the ellipticity components
.
We
rejected individual exposures from the coaddition if one or more CCDs had an
anisotropy larger than 6% in either of the ellipticity components
![]() or
or
![]() .
These anisotropies arise from astigmatism, and they flip by 90 degrees if one passes from an intrafocal to an extrafocal exposure
(see Schirmer et al. 2003, for an example of this, and Fig. B.2 for a typical
PSF anisotropy pattern in our data).
.
These anisotropies arise from astigmatism, and they flip by 90 degrees if one passes from an intrafocal to an extrafocal exposure
(see Schirmer et al. 2003, for an example of this, and Fig. B.2 for a typical
PSF anisotropy pattern in our data).
Since such intra- and extrafocal exposures are roughly equally numbered for a
larger set of exposures, anisotropies due to defocusing average out in the
coadded images. Those have on average an anisotropy of ![]() with a similar
amount in the rms (variation of the PSF across the field). This is illustrated
in Fig. 2, where we show the combined PSF anisotropy properties
for all coadded mosaic images. The left panel shows the uncorrected mean
ellipticity components, having
with a similar
amount in the rms (variation of the PSF across the field). This is illustrated
in Fig. 2, where we show the combined PSF anisotropy properties
for all coadded mosaic images. The left panel shows the uncorrected mean
ellipticity components, having
![]() and
and
![]() .
These anisotropies are small and become
.
These anisotropies are small and become
![]() after PSF correction for all mosaics.
after PSF correction for all mosaics.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5955fg03.ps}
\end{figure}](/articles/aa/full/2007/06/aa5955-06/Timg41.gif) |
Figure 3:
Characteristic PSF anisotropies
|
| Open with DEXTER | |
The middle plot of Fig. 2 shows the uncorrected rms values for
![]() ,
i.e. the deviations of the PSF from a constant
anisotropy across the field. The rms of both components peaks around 1% and
is reduced by a factor of 2 after PSF correction (right panel). The tail of
the distribution seen in the middle plot essentially vanishes.
,
i.e. the deviations of the PSF from a constant
anisotropy across the field. The rms of both components peaks around 1% and
is reduced by a factor of 2 after PSF correction (right panel). The tail of
the distribution seen in the middle plot essentially vanishes.
To evaluate the remaining residuals from PSF correction more quantitatively,
we calculated the correlation function between stellar ellipticity and shear
before and after PSF correction (Fig. 4), separately
for the various survey data sources and over all galaxy positions,
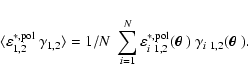 |
(1) |
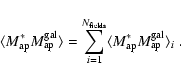 |
(2) |
To summarise, our PSF correction effectively takes out mimicked coherent shear
patterns from the data, yet small residuals remain, which are much smaller
than the coherent shear signal (a few percent) we expect from a typical
cluster at intermediate redshift range (
![]() ).
).
![\begin{figure}
\par\includegraphics[width=7.3cm]{5955fg04.ps}
\end{figure}](/articles/aa/full/2007/06/aa5955-06/Timg48.gif) |
Figure 4: Shown is the correlation between stellar ellipticity and measured shear before ( left panel) and after ( right panel) PSF correction for the 58 survey fields. The median improvement is a factor of 3, but residuals are still present. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5955fg05.ps}
\end{figure}](/articles/aa/full/2007/06/aa5955-06/Timg49.gif) |
Figure 5:
|
| Open with DEXTER | |
For the detection process we use SExtractor (Bertin & Arnouts 1996) to create a
primary source catalogue. The weight map created during the coaddition
(see Erben et al. 2005) is used in this first step, guaranteeing that the highly
varying noise properties in the mosaic images are correctly taken into
account. This leads to a very clean source catalogue that is free from
spurious detections. The number of connected pixels (DETECT_MINAREA) used in
this work for the object detection was 5, and we set the detection threshold
(DETECT_THRESH) to 2.5.
These thresholds are rather generous. ![]() of the objects detected
are rejected again in the later filtering process since they were too small
or too faint for a realiable shear measurement, or other problems appeared
during the measurement of their shapes or positions.
of the objects detected
are rejected again in the later filtering process since they were too small
or too faint for a realiable shear measurement, or other problems appeared
during the measurement of their shapes or positions.
In the second step we calculate the basic lensing quantities using
KSB (Kaiser et al. 1995). This includes PSF anisotropy correction, and the
recalculation of the objects' first brightness moments since
SExtractor yielded positions with insufficient accuracy![]() for the
purpose of our analysis. Details of our implementation of
KSB are given in Erben et al. (2001), and a mathematical description of the
PSF anisotropy correction process itself can be found in Bartelmann & Schneider (2001).
for the
purpose of our analysis. Details of our implementation of
KSB are given in Erben et al. (2001), and a mathematical description of the
PSF anisotropy correction process itself can be found in Bartelmann & Schneider (2001).
On the KSB level we filter such that only galaxies for which no
problems in the determination of centroids occurred remain in the catalogue.
Galaxies with
half-light radii (![]() )
smaller than 0.1-0.2 pixels than the left
ridge of the stellar branch in an
)
smaller than 0.1-0.2 pixels than the left
ridge of the stellar branch in an ![]() -mag-diagramme are
rejected from the lensing catalogue, as are those with exceedingly bright
magnitudes or a low detection significance (
-mag-diagramme are
rejected from the lensing catalogue, as are those with exceedingly bright
magnitudes or a low detection significance (
![]() ). See the left
panel of Fig. 6 for an illustration of these cuts. From the same
panel it can be seen that a significant number of galaxies have half-light
radii comparable to or a bit smaller than the PSF, which makes their shape
measurement noisier. Yet their number is large enough so that the shear
selection of galaxy clusters profit significantly when these objects are
included in the calculation. By including these objects, we gain
). See the left
panel of Fig. 6 for an illustration of these cuts. From the same
panel it can be seen that a significant number of galaxies have half-light
radii comparable to or a bit smaller than the PSF, which makes their shape
measurement noisier. Yet their number is large enough so that the shear
selection of galaxy clusters profit significantly when these objects are
included in the calculation. By including these objects, we gain ![]() in
terms of the number density of galaxies, and
in
terms of the number density of galaxies, and ![]() in terms of
signal-to-noise of the detections.
in terms of
signal-to-noise of the detections.
Furthermore, all galaxies with a PSF corrected modulus of the ellipticity
larger than 1.5 are removed from the catalogue (the ellipticity can become
larger than 1 due to the PSF correction factors, but is then downweighted), as
are those for which the
correction factor
![]() (see Erben et al. 2001). The
fraction of rejected galaxies due to the cut-off in
(see Erben et al. 2001). The
fraction of rejected galaxies due to the cut-off in ![]() is relatively
small, as can be seen from the right panel in Fig. 6.
is relatively
small, as can be seen from the right panel in Fig. 6.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{5955fg06.eps}
\end{figure}](/articles/aa/full/2007/06/aa5955-06/Timg54.gif) |
Figure 6:
Left panel: stars appear as a vertical branch
in a
|
| Open with DEXTER | |
An overall impression of the remaining objects in the final catalogues is
given in Fig. B.1. In total, typically 10-25% of the objects are
rejected from the initial catalogue due to the KSB filtering steps.
The remaining average number density of galaxies per field is
![]() (min: 6, max: 28), not corrected for the
SExtractor-masked areas (as described at the beginning of this
section; on the order of 5% per field). For the width of the ellipticity
distribution we
measure
(min: 6, max: 28), not corrected for the
SExtractor-masked areas (as described at the beginning of this
section; on the order of 5% per field). For the width of the ellipticity
distribution we
measure
![]() for each of the two ellipticity components,
averaged over all survey fields. Both n and
for each of the two ellipticity components,
averaged over all survey fields. Both n and
![]() determine
the signal-to-noise of the various mass concentrations detected.
determine
the signal-to-noise of the various mass concentrations detected.
The variance of
![]() for the unlensed case, respectively the weak lensing
regime, is given by
for the unlensed case, respectively the weak lensing
regime, is given by
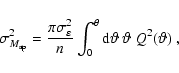 |
(4) |
We then define the S-statistics, or the S/N for
![]() respectively the measured amount of tangential shear, as
respectively the measured amount of tangential shear, as
The filter function Q that maximizes S for a given density (or shear)
profile of the lens can be derived using either a variational principle
(Schirmer 2004), or the Cauchy-Schwarz inequality (S96, Weinberg & Kamionkowski 2002). It is
obtained for
The noise of
![]() can be estimated from
can be estimated from
![]() itself as was shown by
Kruse & Schneider (1999) and S96. In the weak lensing case its variance evaluates as
itself as was shown by
Kruse & Schneider (1999) and S96. In the weak lensing case its variance evaluates as
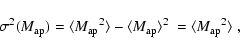 |
(9) |
| |
= | 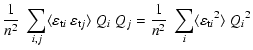 |
|
| = | (10) |
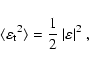 |
(11) |
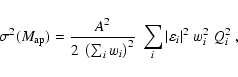 |
(12) |
If
![]() is evaluated close to the border of an image or on a data field with
swiss-cheese topology due to the masking of bright stars, then the aperture
covers an "incomplete'' data field. Therefore, the returned value of
is evaluated close to the border of an image or on a data field with
swiss-cheese topology due to the masking of bright stars, then the aperture
covers an "incomplete'' data field. Therefore, the returned value of
![]() does no longer give a result in the sense of its original definition in S96,
which was a measure related to the filtered surface mass density inside the
aperture. Yet it is still a valid measure of the tangential shear inside the
aperture, including the S/N-estimate in Eq. (13), and
can thus be used for the detection of mass concentrations.
does no longer give a result in the sense of its original definition in S96,
which was a measure related to the filtered surface mass density inside the
aperture. Yet it is still a valid measure of the tangential shear inside the
aperture, including the S/N-estimate in Eq. (13), and
can thus be used for the detection of mass concentrations.
Since the number density of background galaxies inside an aperture is not a constant over the field due to the masking of brighter stars (and the presence of the field border), we have to check for possible unwanted effects. As long as the holes in the galaxy distribution are small compared to the aperture size, and as long as their number density is small enough so that no significant overlapping of holes takes place, the effects on the S-statistics are negligible (see Fig. B.4). In fact, the decreased number density just leads to a lowered significance of the peaks detected in such areas, without introducing systematic effects.
If the size of the holes becomes comparable to the aperture, spurious peaks
appear in the S-map at the position of the holes. This is because the
underlying galaxy population changes significantly when the aperture is moved
to a neighbouring grid point. When such affected areas were present in our
data, then we excluded them from the statistics and masked them in the
S-maps, even though these spurious peaks are typically not very significant
(
![]() ). Our threshold for not evaluating the S-statistics at a
given grid point is reached if the effective number density of the galaxies in
the aperture affected is reduced by more than 50% due to the presence of
holes (or the image border). Spurious peaks become very noticeable if the
holes cover about 80% of the aperture. This is rarely the case for our data
unless the aperture size is rather small (2'), or a particular
star is very bright. We conclude that our final statistics is free from any
such effects.
). Our threshold for not evaluating the S-statistics at a
given grid point is reached if the effective number density of the galaxies in
the aperture affected is reduced by more than 50% due to the presence of
holes (or the image border). Spurious peaks become very noticeable if the
holes cover about 80% of the aperture. This is rarely the case for our data
unless the aperture size is rather small (2'), or a particular
star is very bright. We conclude that our final statistics is free from any
such effects.
Wright & Brainerd (2000) and Bartelmann (1996) derived an expression for the tangential shear
of the universal NFW profile. Based on their finding we can construct a new
filter function
![]() over the interval
over the interval
![]() ,
having the shape
,
having the shape
| |
Figure 7:
Left panel:
|
| Open with DEXTER | |
Due to the mathematical complexity of
![]() ,
the calculation of the
S-statistics is rather time consuming for a field with
,
the calculation of the
S-statistics is rather time consuming for a field with
![]() galaxies. We introduce an approximating filter function with simpler
mathematical form that produces similarly good results as
galaxies. We introduce an approximating filter function with simpler
mathematical form that produces similarly good results as
![]() .
It is
given by
.
It is
given by
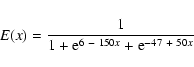 |
(16) |
We thus have a filter function based upon the two-dimensional parameter space
![]() .
The differences between
.
The differences between
![]() and
and
![]() are indistinguishable in the noise once applied to real data,
so that we do not consider
are indistinguishable in the noise once applied to real data,
so that we do not consider
![]() henceforth.
henceforth.
It is not the first time that
![]() filters following the tangential shear
profile are proposed or used. We have already utilised the filter in Eq. (15) to confirm a series of luminosity-selected galaxy clusters
(Schirmer et al. 2004). Before that, Padmanabhan et al. (2003) approximated
filters following the tangential shear
profile are proposed or used. We have already utilised the filter in Eq. (15) to confirm a series of luminosity-selected galaxy clusters
(Schirmer et al. 2004). Before that, Padmanabhan et al. (2003) approximated
![]() with
with
Differences in the efficiency of such "tangential'' filters are thus expected
to arise for very deep surveys only, and/or in case of high redshift clusters
(z=0.6 and more, for which our survey is not sensitive). In all other cases
they are hardly distinguishable from each other since the noise in the images
and the deviations from the assumed radial symmetry of the shear field and the
NFW profile are dominant. Thus we consider the
![]() filter to be
optimally suited for our survey. For a comparison with other filters that do
not follow the tangential profile, see the example shown in Fig. B.3.
filter to be
optimally suited for our survey. For a comparison with other filters that do
not follow the tangential profile, see the example shown in Fig. B.3.
![\begin{figure}
\center{\includegraphics[width=7.5cm,clip]{5955fg08.ps} }
\end{figure}](/articles/aa/full/2007/06/aa5955-06/Timg101.gif) |
Figure 8:
Expected optimal S/N-ratios for NFW dark
matter haloes
for four different cluster masses (M200) and two different image
depths. The mathematical derivation of the S/N for a particular cluster at
a given redshift is given in Appendix A. Note that the
filter scale is not constant along each of the curves since the shear fields
get smaller in angular size with increasing lens redshift. Note also that we
used a lower integration limit of
|
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=16.5cm,clip]{5955fg09.eps}
\end{figure}](/articles/aa/full/2007/06/aa5955-06/Timg103.gif) |
Figure 9:
Left panel: the normalised PDF for the peaks based
on the entire survey area, averaged over all scales and |
| Open with DEXTER | |
As a result, our S-statistics is insensitive for structures of mass equal or
less
than
![]()
![]() for all redshifts. In data of average
depth (
for all redshifts. In data of average
depth (
![]() )
we can detect mass concentractions of
)
we can detect mass concentractions of
![]()
![]() out to
z=0.10, 0.22 and 0.32,
respectively. The same objects would still be seen at
z=0.22, 0.34 and 0.46
in the deeper exposures with twice the number density of usable background
galaxies.
out to
z=0.10, 0.22 and 0.32,
respectively. The same objects would still be seen at
z=0.22, 0.34 and 0.46
in the deeper exposures with twice the number density of usable background
galaxies.
The main idea behind the P-statistics is that a real peak has an extended
shear field, i.e. it will be picked up by
![]() in a larger number of
different
filter scales. In other words, as the aperture size changes, different samples
of galaxies are used and all of them will yield a signal above the detection
threshold (provided a sufficient lensing strength). On the contrary, a
spurious peak mimicked by the noise of the intrinsic galaxy ellipticity is not
expected to show such a behaviour, thus the P-statistics will prefer a true
peak over a false peak. In order to distinguish between individual S/Nmeasurements made with the P- and S-statistics, we will use the terms
in a larger number of
different
filter scales. In other words, as the aperture size changes, different samples
of galaxies are used and all of them will yield a signal above the detection
threshold (provided a sufficient lensing strength). On the contrary, a
spurious peak mimicked by the noise of the intrinsic galaxy ellipticity is not
expected to show such a behaviour, thus the P-statistics will prefer a true
peak over a false peak. In order to distinguish between individual S/Nmeasurements made with the P- and S-statistics, we will use the terms
![]() and
and
![]() henceforth.
henceforth.
We calculate the P-statistics as follows:
There is some arbitrariness in the way we implemented the P-statistics
for this work. A further optimisation can be performed based on future
simulations. For example, the lower threshold of ![]() for the peaks
considered can be decreased or increased. The former would make the
P-statistics smoother since more peaks
are included, but does not yield any further advantage since it picks up too
much noise. Increasing the threshold beyond 3.5 reduces the number of peaks
entering the statistics significantly. This makes the determination of the
noise level unstable, and one starts losing less significant peaks.
Instead of choosing a constant cut at 2.5
for the peaks
considered can be decreased or increased. The former would make the
P-statistics smoother since more peaks
are included, but does not yield any further advantage since it picks up too
much noise. Increasing the threshold beyond 3.5 reduces the number of peaks
entering the statistics significantly. This makes the determination of the
noise level unstable, and one starts losing less significant peaks.
Instead of choosing a constant cut at 2.5![]() ,
a dynamic threshold
as a function of filter scale would be more appropriate. This is motivated
by the fact that the contamination of the S-statistics with noise depends
on the aperture size chosen. Maturi et al. (2006) have implemented such a dynamic
threshold for their analysis.
,
a dynamic threshold
as a function of filter scale would be more appropriate. This is motivated
by the fact that the contamination of the S-statistics with noise depends
on the aperture size chosen. Maturi et al. (2006) have implemented such a dynamic
threshold for their analysis.
Further improvements could be gained by not feeding the P-statistics from
the entire
![]() parameter space. Concentrating on a smaller
set of filter scales could yield a more discriminative power. In addition, the
chosen smoothing length of 40
parameter space. Concentrating on a smaller
set of filter scales could yield a more discriminative power. In addition, the
chosen smoothing length of 40
![]() yields the best compromise between
smoothing out position variations in the lensing detections while maintaining
the spatial resolving power of the P-statistics. This value appears optimal
for our survey, but may well be different for other data sets.
yields the best compromise between
smoothing out position variations in the lensing detections while maintaining
the spatial resolving power of the P-statistics. This value appears optimal
for our survey, but may well be different for other data sets.
To this end we created 10 copies of our entire survey catalogue with
randomised galaxy orientations, destroying any lensing signal, but keeping the
galaxy positions and thus all other data characteristics fixed. We then
calculated the PDFs for all local maxima (overdense regions) and
minima (underdense regions) of the
observations and the randomisations, accumulating the detections from the
entire parameter space probed. The middle and right panel of Fig.
9 show the difference between the PDFs of the observed and the
randomised data sets. Both PDFs, for the S- and the P-statistics, are
significantly skewed, showing an excess of peaks and voids above thresholds
of about
![]() and
and
![]() .
.
We show below that the samples obtained with both statistics have very similar properties, and that the two methods complement each other for peaks with low S/N. Hence, hereafter we do not distinguish between the samples drawn from the two statistics unless significant differences occur.
The detections made with both statistics are combined and summarised in Tables
B.2 to B.4. Those peaks seen with the
S-statistics have the best matching filter scale reported, i.e. the one
yielding the highest S/N. Column 1 contains numeric labels for the
detections, followed by a string indicating with which statistics it was
made. The third and fourth column contain the detection significances
![]() and
and
![]() (if applicaple). Columns five, six and seven carry a classification
parameter (see
below), a richness estimate of a possible optical counterpart if present, and
the distance of the peak from the latter. This is followed by the filter scale
and the
(if applicaple). Columns five, six and seven carry a classification
parameter (see
below), a richness estimate of a possible optical counterpart if present, and
the distance of the peak from the latter. This is followed by the filter scale
and the
![]() parameter (if applicable), and then the name of the
survey field in which the detection was made. Finally, we report the redshift
of an optical counterpart if known.
parameter (if applicable), and then the name of the
survey field in which the detection was made. Finally, we report the redshift
of an optical counterpart if known.
The classes are defined as follows and are based on galaxies taken from the
range
![]() .
Thus these glaxies are not members of the catalogue of
lensed background galaxies (see also the left panel of Fig. 6).
.
Thus these glaxies are not members of the catalogue of
lensed background galaxies (see also the left panel of Fig. 6).
We consider classes 1 to 4 to be reliable optical counterparts, and refer to them as bright peaks henceforth. Classes 5 are rather dubious, and go as dark peaks together with those lines of sight classified as 6. See Fig. B.5 for an illustration of bright peaks of classes 1-4.
The boundaries between the classes are permeable. For example, if we find
an overdensity of 12 galaxies, and 4 or 5 of them stand out from the rest
by their brightness and are of elliptical type, the class 5 object would
become a class 4. Similarly, if we find 20 galaxies of similar brightness,
but they show a significantly higher concentration than the rest of the
sample, it becomes class 3. On the other hand, if the distance between
the mass peak and the centre of the optical peak exceeds 100 arcseconds,
we decrease the class by one step. The same holds if the galaxies seen appear
to be at redshift higher than ![]() 0.3 or more, then we lower the rank
by 1 since our selection method becomes less sensitive with increasing
redshift. About 20% of our sample were up- or downgraded in this way.
0.3 or more, then we lower the rank
by 1 since our selection method becomes less sensitive with increasing
redshift. About 20% of our sample were up- or downgraded in this way.
Whenever spectra were available, they confirmed our assumption of spatial concentrations in all cases. In order to secure the 50 most promising candidates, we recently started a large spectroscopic survey aiming at between 20 and 50 galaxies per target. This will not only pin down the redshifts of the possible clusters, but also allow us to identify further projection effects and in some cases possible physical connections with nearby peaks (e.g. #029, 056, 074, 084, 092, 128, 136, 141, 158). We will report these results in future papers.
The ![]() redshift range of the peaks confirmed so far is
redshift range of the peaks confirmed so far is
![]() .
We therefore predominantly probe the lower redshift range
of clusters, which is consistent with the theoretically expected sensitivity
of our survey (see Kruse & Schneider 1999, and Fig. 8).
.
We therefore predominantly probe the lower redshift range
of clusters, which is consistent with the theoretically expected sensitivity
of our survey (see Kruse & Schneider 1999, and Fig. 8).
We also checked for possible X-ray emission at the position of the peaks, creating statistical stacks from the images of the Rosat All Sky Survey (Voges et al. 1999) for classes (1, 2), and (3, 4) and (5, 6). Only for the stack made of classes 1 and 2 do we see a signal, coming exclusively from #039 (Abell 901) and #082 (Abell 1364) which form the most prominent clusters in our sample. The other two stacks show no enhanced flux at the combined target positions.
Table 1: Average angular offsets between the peak and the optical counterpart.
Most obvious is the small overlap of barely ![]() between the two
samples, as can be seen from the second column in Tables B.2 to B.4. Since the P-statistics
looks at a broader
range of filter scales instead of one single scale, it overcomes the
instability of the S-statistics against changes in the aperture size
between the two
samples, as can be seen from the second column in Tables B.2 to B.4. Since the P-statistics
looks at a broader
range of filter scales instead of one single scale, it overcomes the
instability of the S-statistics against changes in the aperture size
![]() and the scaling parameter
and the scaling parameter
![]() .
Hence it is capable of
giving significance to a peak that otherwise goes unnoticed by the
S-statistics. Since we have a minimum detection threshold of
.
Hence it is capable of
giving significance to a peak that otherwise goes unnoticed by the
S-statistics. Since we have a minimum detection threshold of ![]() for the peaks entering the calculation of the P-statistics, we expect
peaks that are not seen by the S-statistics since they never reach the
for the peaks entering the calculation of the P-statistics, we expect
peaks that are not seen by the S-statistics since they never reach the
![]() selection threshold.
selection threshold.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5955fg10.ps}
\end{figure}](/articles/aa/full/2007/06/aa5955-06/Timg137.gif) |
Figure 10: Shown is the spatial distribution of the 158 detected peaks for the WFI field of view. Open symbols indicate the bright peaks with classes 1-4, the filled ones peaks with classes 5 and 6. The symbol size represents the detection significance. The pattern is indistinguishable from a random distribution, and we also do not see differences for peaks obtained with either the S- or the P-statistics (not shown). |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=7.5cm]{5955fg11.ps}
\end{figure}](/articles/aa/full/2007/06/aa5955-06/Timg138.gif) |
Figure 11: Shows the fraction of detections made in either the S- or the P-statistics, or in both. |
| Open with DEXTER | |
| |
Figure 12:
Left: shows the peaks detected either with
the S-statistics, or those detected with both methods, normalised to the
previous and as a function of
|
| Open with DEXTER | |
However, there is a drawback to the increased stability gained in this
way. Peaks associated to small or low shear fields will appear only for a
few neighbouring filter scales over the ![]() level. Hence they
will not be selected with the P-statistics, since we calculate the latter
from the full
level. Hence they
will not be selected with the P-statistics, since we calculate the latter
from the full
![]() parameter space, which dilutes such a
signal. Those peaks can be picked up by the S-statistics, though.
parameter space, which dilutes such a
signal. Those peaks can be picked up by the S-statistics, though.
Figure 12 shows that the small overlap between the two
samples is mainly due to peaks with a low S/N of either
![]() or
or
![]() .
For peaks with
.
For peaks with
![]() the sample overlap roughly doubles
(
the sample overlap roughly doubles
(![]() 60%), and becomes 100% for
60%), and becomes 100% for
![]()
![]() ). The small
overlap observed for the entire samples therefore likely arises from the
fact that both methods do not work efficiently in finding all lensing
signals close to the detection threshold. This is expected and has been
shown on N-body simulations for the S-statistics e.g. by Reblinsky et al. (1999)
(see also Hennawi & Spergel 2005; Hamana et al. 2004, and Sect. 4.8). The
P-statistics has not yet been characterised in this context, but given the
great similarities of the S-and the P-sample we expect that the
P-statistics has a comparable efficiency.
). The small
overlap observed for the entire samples therefore likely arises from the
fact that both methods do not work efficiently in finding all lensing
signals close to the detection threshold. This is expected and has been
shown on N-body simulations for the S-statistics e.g. by Reblinsky et al. (1999)
(see also Hennawi & Spergel 2005; Hamana et al. 2004, and Sect. 4.8). The
P-statistics has not yet been characterised in this context, but given the
great similarities of the S-and the P-sample we expect that the
P-statistics has a comparable efficiency.
Upon counting the bright and dark peaks in the five main data sources of our
survey (see Sect. 2.1), we find differences in the ratio
between bright and dark peaks (Table B.5). Namely, the
ASTROVIRTEL and EIS data, and our own observations, show an excess of
![]() in terms of dark peaks as compared to the bright peaks, and are
about comparable to each other. The EDisCS
survey has a factor 2.1 more dark peaks, but is also that part of our survey
with the most shallow exposures. Contrary, the COMBO-17 data has twice as
many bright as darks peaks, but this comes not as a surprise since the S11
and A901 fields are centred on known galaxy clusters with significant
sub-structure. If we subtract the known clusters and all detections likely
associated with them, we still have an "excess'' of 40% for the bright peaks
in COMBO-17. Again, this is not unplausible since the COMBO-17 fields form by
far the deepest part of our survey, which let us detect more mass
concentrations. But the latter holds for both bright and dark peaks,
as the number of detections per square degree shows (Table B.5).
in terms of dark peaks as compared to the bright peaks, and are
about comparable to each other. The EDisCS
survey has a factor 2.1 more dark peaks, but is also that part of our survey
with the most shallow exposures. Contrary, the COMBO-17 data has twice as
many bright as darks peaks, but this comes not as a surprise since the S11
and A901 fields are centred on known galaxy clusters with significant
sub-structure. If we subtract the known clusters and all detections likely
associated with them, we still have an "excess'' of 40% for the bright peaks
in COMBO-17. Again, this is not unplausible since the COMBO-17 fields form by
far the deepest part of our survey, which let us detect more mass
concentrations. But the latter holds for both bright and dark peaks,
as the number of detections per square degree shows (Table B.5).
| |
Figure 13: Shown is the number of bright peaks (solid line) and dark peaks (dashed line) as a function of exposure time ( left) and galaxy number density ( right). Shallow exposures with low number density have more dark peaks than deeper exposures. |
| Open with DEXTER | |
| |
Figure 14: Left: histogram of the exposure times. The peak at 57 ks represents the Chandra Deep Field South (CDF-S). Right: number density of galaxies in the 58 fields after all filtering steps, leaving a total number of about 710 000 usable galaxies. The distribution reflects the distribution of exposure times shown in the left panel. |
| Open with DEXTER | |
In order to check if the dark peaks might arise due to imperfect PSF
correction, we compare their occurrence with the remaining PSF residuals
in our lensing catalogues (Figs. 4 and 5).
Therein we do not find evidence that the imperfect PSF correction
gives rise to dark peaks. However,
Fig. 13 indicates that small exposure times
(less than 10-12 ks) and/or a low number density (less than
![]() )
of galaxies foster the occurrence of dark peaks. Yet this
has to be seen with some caution, in particular because we have only a small
number of deep fields (mainly COMBO-17) as compared to the shallow ones, and
the deep fields are partially concentrated on known structures. If we take the
known
structures into account and remove them from the statistics, we are still left
with a smaller fraction of dark peaks in the deep exposures, but the question
remains in how far the particular pointings of those fields introduce a bias.
To answer this question empirically, we would need about 10 empty fields of 20 ks exposure time each.
)
of galaxies foster the occurrence of dark peaks. Yet this
has to be seen with some caution, in particular because we have only a small
number of deep fields (mainly COMBO-17) as compared to the shallow ones, and
the deep fields are partially concentrated on known structures. If we take the
known
structures into account and remove them from the statistics, we are still left
with a smaller fraction of dark peaks in the deep exposures, but the question
remains in how far the particular pointings of those fields introduce a bias.
To answer this question empirically, we would need about 10 empty fields of 20 ks exposure time each.
Due to the
![]() filter we use, and to the large inhomogeneity of our survey,
we cannot directly compare the occurrence of dark peaks in our data to
existing numerical simulations. Also, these simulations usually make
significantly more optimistic assumptions in terms of usable number
density of galaxies and field of view than we could realise with GaBoDS
(see Reblinsky & Bartelmann 1999; Hennawi & Spergel 2005; Jain & van Waerbeke 2000, for example). In particular Hamana et al. (2004)
have shown that in their simulations (n=30) they expect to detect 43
real peaks (efficiency of
filter we use, and to the large inhomogeneity of our survey,
we cannot directly compare the occurrence of dark peaks in our data to
existing numerical simulations. Also, these simulations usually make
significantly more optimistic assumptions in terms of usable number
density of galaxies and field of view than we could realise with GaBoDS
(see Reblinsky & Bartelmann 1999; Hennawi & Spergel 2005; Jain & van Waerbeke 2000, for example). In particular Hamana et al. (2004)
have shown that in their simulations (n=30) they expect to detect 43
real peaks (efficiency of ![]() 60%), scaled to the same area as GaBoDS and
drawn with S/N>4 from mass reconstruction maps. A similar number of false
peaks appear as well, being either pure noise peaks, or peaks with an
expected S/N<4 being pushed over this detection limit. The latter
would be labelled as bright peaks in our case. Our absolute numbers
are different (72 bright and 86 dark peaks) since we use a very different
selection method. Yet, if we interpret our dark peaks as noise peaks,
the ratio between our bright and dark peaks is comparable to the ratio between
their true and false peaks.
60%), scaled to the same area as GaBoDS and
drawn with S/N>4 from mass reconstruction maps. A similar number of false
peaks appear as well, being either pure noise peaks, or peaks with an
expected S/N<4 being pushed over this detection limit. The latter
would be labelled as bright peaks in our case. Our absolute numbers
are different (72 bright and 86 dark peaks) since we use a very different
selection method. Yet, if we interpret our dark peaks as noise peaks,
the ratio between our bright and dark peaks is comparable to the ratio between
their true and false peaks.
This interpretation, i.e. dark peaks are mostly noise peaks, is strengthened by the fact that with increasing peak S/N the fraction of dark peaks is decreasing (see Table B.6), for both the S- and the P-statistics. However, our observational data base (sky coverage) is too small to tell if this trend, i.e. the dark peaks dying out, continues for higher values of the S/N.
We defined the secondary P-statistics, which is calculated from the
S-statistics. Does the latter find several peaks in different filter
scales at the same position, then the P-statistics makes a detection.
The samples obtained with the P- and
the S-statistics appear very similar, in particular in terms of the
fractions of bright and dark peaks. The overlap of both samples is small
for mass peaks with low S/N (
![]() ), and increases
to 100% for more reliable peaks (
), and increases
to 100% for more reliable peaks (
![]() ). This reflects the low detection
efficiency for both statistics for less significant peaks, but also shows
that they complement each other for low S/N. The performance and
efficiency of the P-statistics has yet to be better investigated by means
of simulations, which will also lead to an optimised choice of parameters
from which it is calculated.
). This reflects the low detection
efficiency for both statistics for less significant peaks, but also shows
that they complement each other for low S/N. The performance and
efficiency of the P-statistics has yet to be better investigated by means
of simulations, which will also lead to an optimised choice of parameters
from which it is calculated.
The global PDFs for both the S- and P-statistics show clear excess peaks for higher values of S/N as compared to randomised copies of our data set. Thus the presence of lensing mass concentrations in our survey data is confirmed.
We introduced a classification scheme in order to associate the hypothetical mass peaks detected with possible luminous matter. From the 158 detections we made with the combined S- and P-statistics, 72 (46%) appear to have an optical counterpart. For 22 of those we found spectra in the literature, confirming the above mentioned redshift range, and that indeed a mass concentration exists along those particular lines of sight. We matched all detections made with the ROSAT All Sky Survey, finding that only the two most prominent clusters show X-ray emission. Statistically stacking the other fields did not reveal any excess X-ray flux for the remaining mass concentrations.
For a smaller number of the peaks we have spectroscopic evidence that they are due to projection effects. We expect that in our currently conducted spectroscopic follow-up survey more such projection cases will be uncovered, together with a confirmation of a very significant fraction of the remaining bright peaks. In a future paper we will also compare this shear-selected sample with an optically selected sample using matched filter techniques.
We gained some insight into the subject of dark peaks, which are not preferred
by the S- or the P-statistics. They appear preferentially in shallow data
with a small number density of galaxies, indicating that a large fraction of
those could be due to noise (i.e. instrinsic galaxy ellipticies), or they are
statistical flukes (see e.g. von der Linden et al. 2006). Nevertheless, in our deep fields
we also observe a significant fraction of dark peaks, but our statistics can
not be unambiguously interpreted since those fields are biased towards
clusters with significant sub-structure, and we have only a very small number
of them. Real physical objects such as very underluminous clusters or
protoclusters are expected to contribute to shear-selected cluster samples
(see e.g. Weinberg & Kamionkowski 2002), albeit we estimate that their fraction is small.
Lastly, at least on the mass scale of galaxies, the last year has seen
astonishing examples of objects having several
![]() of neutral
hydrogen, yet they appear entirely dark in the optical as if no star formation
had ever taken place in them (see the Arecibo Galaxy
Environments Survey, and therein e.g. Auld et al. 2006; Minchin et al. 2006,2005).
Whether similar objects can still exist on the cluster mass scale and thus
give rise to dark peaks in shear-selected cluster samples is currently
unclear.
of neutral
hydrogen, yet they appear entirely dark in the optical as if no star formation
had ever taken place in them (see the Arecibo Galaxy
Environments Survey, and therein e.g. Auld et al. 2006; Minchin et al. 2006,2005).
Whether similar objects can still exist on the cluster mass scale and thus
give rise to dark peaks in shear-selected cluster samples is currently
unclear.
Finally, we would like to repeat that the Garching-Bonn Deep Survey has been
made with a 2 m telescope. Most numerical simulations done so far are much more
optimistic in terms of the number density reached (
![]() )
and
correspond to surveys that are currently conducted (or will be in the near
future) with 4m- and 8m-class telescopes, such as SUPRIME33 (Miyazaki et al. 2005) or
the CFHTLS
)
and
correspond to surveys that are currently conducted (or will be in the near
future) with 4m- and 8m-class telescopes, such as SUPRIME33 (Miyazaki et al. 2005) or
the CFHTLS![]() . One noteworthy
exception will be the
KIDS
. One noteworthy
exception will be the
KIDS![]() (Kilo Degree Survey) obtained with OmegaCAM@VST, covering 1500 square
degrees starting in 2007.
(Kilo Degree Survey) obtained with OmegaCAM@VST, covering 1500 square
degrees starting in 2007.
Acknowledgements
This work was supported by the BMBF through the DLR under the project 50 OR 0106, by the BMBF through DESY under the project 05AE2PDA/8, and by the DFG under the projects SCHN 342/3-1 and ER 327/2-1. Furthermore we appreciate the support given by ASTROVIRTEL, a project funded by the European Commission under FP5 Contract No. HPRI-CT-1999-00081. The authors thank Ludovic van Waerbeke (UBC), and Nevin Weinberg and Marc Kamionkowski (both CalTec) for fruitful discussions, and the anonymous referee for his (her) very useful comments which significantly improved this paper.
According to S96, the S/N for
![]() for a cluster at the
origin of the coordinate system evaluates as
for a cluster at the
origin of the coordinate system evaluates as
The tangential shear for a radially symmetric NFW profile was given by
Wright & Brainerd (2000) as
| g(x) | = | ![$\displaystyle \left\{\begin{array}{ll}
g_<(x) & \;\;(x < 1) \\ [0.3cm]
\frac{1...
...{\rm {ln}}~2 & \;\;(x = 1) \\ [0.15cm]
g_>(x) & \;\;(x > 1)
\end{array}\right.$](/articles/aa/full/2007/06/aa5955-06/img158.gif) |
(A.3) |
| x | = | (A.4) | |
| = | (A.5) | ||
| = | 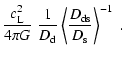 |
(A.6) |
![\begin{displaymath}D(z_1,z_2) = \frac{c_{\rm L}}{H_0}\;\frac{1}{1+z_2}
\int_{a_...
... d}a \left[a\;\Omega_0 + a^4\;\Omega_\Lambda\right]^{-1/2}}\;,
\end{displaymath}](/articles/aa/full/2007/06/aa5955-06/img170.gif) |
(A.7) |
The functional expression for g(x) is identical to the one already given
in Eq. (14), and contains the shape of the shear profile.
Finally, fixing the remaining numerical parameters provides us with all
information to calculate the S/N. From our data we have
![]() ,
and we assume two different image depths which we base on empirical
findings. One is shallow with
,
and we assume two different image depths which we base on empirical
findings. One is shallow with
![]() and z0=0.4, and the deeper one
given by
and z0=0.4, and the deeper one
given by
![]() and z0=0.5.
and z0=0.5.
The S/N then evaluates as
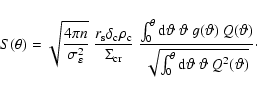 |
(A.9) |
Table B.1: The 58 fields used for this work.
![\begin{figure}
\includegraphics[width=18cm]{5955fg17.eps}
\end{figure}](/articles/aa/full/2007/06/aa5955-06/Timg183.gif) |
Figure B.3:
Tangential shear and S-profile for the two
largest clusters in the survey data. In the upper row the tangential shear
is shown, with the TANH filter that yielded the highest S/N overlaid as a
solid line. For better comparison the amplitude of TANH was scaled so
that it best fits the tangential shear. All data points are mutually
independent. The lower row shows the S-profile of the two clusters for
different filters Q. The NFW filter is plotted for 10 different values of
Note: Although the tangential shear is smaller for A901 than for S11, the S/N is higher due to the larger number density of galaxies with measured shapes (n=15 arcmin-2 for S11, and n=24 arcmin-2 for A901). |
Table B.2: Shear-selected mass concentrations (part 1). The first column contains a label for the peak, and the second one indicates if the detection was made with either the S- or the P-statistics (or both). The next two columns contain the corresponding significances. The classification shows if along the line of sight an overdensity of galaxies is found, with class 1 meaning a very obvious overdensity, and class 6 no overdensity. The richness indicates how many galaxies were found as compared to the average density in this field, and we give the distance between the peak and the optical counterpart. Finally, we have the name of the survey field in which the detection was made, and possibly a redshift for the counterpart. An asterisk behind the redshifts indicates that it is based on the measurement of less than three galaxies.
Table B.3: Shear-selected mass concentrations (part 2).
Table B.4: Shear-selected mass concentrations (part 3).
Table B.5: Bright (classes 1 to 4) and dark (5-6) peaks for the various survey data sources. The columns contain the data source, the number of bright and dark peaks, the ratio between dark and bright peaks, the average exposure times and image seeing, the area covered, plus the number of bright and dark peaks per unit area. For the COMBO-17 field we give in parenthesis the corresponding values when the known structures are subtracted.
Table B.6: Number of bright (classes 1-4) and dark (5-6) peaks and their ratios for the S- and the P-statistics.
![\begin{figure}
\includegraphics[width=18cm]{5955fg19.eps}
\end{figure}](/articles/aa/full/2007/06/aa5955-06/Timg195.gif) |
Figure B.5:
Illustrates the typical appearance of bright clusters
of various classes, as defined in Sect. 4.2. Note that the
resolution is in general not high enough to distinguish smaller member
galaxies from stars. The field of view is 4
|