A&A 462, 459-471 (2007)
DOI: 10.1051/0004-6361:20065677

Weak lensing survey of galaxy clusters in the CFHTLS Deep[*]

R. Gavazzi - G. Soucail

Laboratoire d'Astrophysique de Toulouse-Tarbes, Observatoire Midi-Pyrénées, UMR5572 CNRS & Université Paul Sabatier, 14 Avenue Edouard Belin, 31400 Toulouse, France

Received 23 May 2006 / Accepted 30 October 2006

Abstract
Aims. We present a weak lensing search of galaxy clusters in the 4 deg2 of the CFHT Legacy Survey Deep. This work aims at building a mass-selected sample of clusters with well controlled selection effects. This present survey is a preliminary step toward a full implementation in the forthcoming 170 deg2 of the CFHTLS Wide survey.
Methods. We use the deep i' band images observed under subarcsecond seeing conditions to perform weak lensing mass reconstructions and to identify high convergence peaks. Thanks to the availability of deep u*g'r'i'z' exposures, sources are selected from their photometric redshifts in the weak lensing analysis. We also use lensing tomography to derive an estimate of the lens redshift. After considering the raw statistics of peaks we check whether they can be associated to a clear optical counterpart or to published X-ray selected clusters.
Results. Among the 14 peaks found above a signal-to-noise detection threshold $\nu=3.5$, nine are secure detections with estimated redshift $0.1\la z_{\rm l}\la0.7$ and a velocity dispersion $450\la\sigma_v\la 700 ~ {\rm km~ s}^{-1}$. This low mass range is accessible thanks to the high density of background sources. Considering the intersection between the shear-selected clusters and XMM-LSS X-ray clusters in the D1 field, we observe that the ICM gas in these low-mass clusters ( $T_{\rm X}\sim1{-}2$ keV) is not hotter than the temperature inferred from shear, this trend being different for published massive clusters. A more extended weak lensing survey, with higher statistics of mass structures will be a promising way to bypass several of the problems related to standard detection methods based on the complex physics of baryons.

Key words: gravitational lensing - galaxies: clusters: general - cosmology: large-scale structure

  
1 Introduction

In the context of hierarchical structure formation within the Lambda Cold Dark Matter paradigm ($\Lambda$CDM), clusters of galaxies are the very latest structures to assemble. They are also the most extended gravitationally bound systems in the Universe and constitute a key laboratory for cosmology. The time evolution of clusters as well as their abundance and spatial clustering properties are essentially driven by gravity sourced by the CDM mass content (e.g.  Haiman et al. 2001; Borgani & Guzzo 2001; Eke et al. 1996).

Therefore the main physical parameter for a cluster of galaxies is its total mass. However most of observations only have an indirect access to cluster masses and rather measure quantities like the SZ decrement, X-ray or optical/NIR luminosities, the line-of-sight velocity dispersion of the cluster-member galaxies or the temperature of the hot gas in the intra-cluster medium (ICM) from X-ray (e.g.  Bahcall & Bode 2003; Olsen et al. 1999; Bahcall et al. 1995; Carlstrom et al. 2002; Romer et al. 2001; Gladders & Yee 2000; Carlberg et al. 1996). Hence difficulties arise because one needs well calibrated proxies to convert observables into theoretically relevant quantities like mass and because the process of detecting clusters of galaxies with such indirect methods might suffer various kinds of selection effects. Therefore any attempt to use clusters of galaxies as efficient cosmological probes cannot afford making extensive assessments of the assumed calibration of the scaling laws in the local Universe and at high redshift (e.g.  Arnaud et al. 2005; da Silva et al. 2004; Arnaud & Evrard 1999).

Gravitational lensing is among the best ways to test biases in the above techniques. The bending of light by intervening matter along the line of sight from distant sources to the observer only depends on the mass properties of structures without regards of its nature (baryonic or not, luminous or dark) or dynamical state (relaxed or not, hydrostatic equilibrium...). Since the early 90's several groups have reported the detection of a weak lensing signal around massive clusters of galaxies. However the broad range of observational configurations (field of view, depth, seeing, ground- or space-based images, etc) makes difficult a direct comparison of published results. For reviews see Mellier (1999) and Bartelmann & Schneider (2001). Progresses have been made in this direction with weak lensing studies of sizable samples of optically or X-ray selected clusters (Bardeau et al. 2006; Cypriano et al. 2004; Dahle et al. 2002; Clowe et al. 2006). Different mass estimates globally agree although outliers perturb a simple relation between X-ray (or dynamical) and lensing mass estimates (e.g.  Wu 2000; Allen 1998; Arabadjis et al. 2004). This suggests that dynamical activity is still important for massive halos and that asphericity and projection effects may complicate both weak lensing and other mass estimates (Metzler et al. 2001; De Filippis et al. 2005; de Putter & White 2005; Gavazzi 2005; Hoekstra 2003; Clowe et al. 2004).

In parallel, the idea of direct detection of galaxy clusters by their weak lensing signal starts to emerge. By measuring the coherent stretching of distant galaxies by intervening structures, one is able to infer the projected density field (i.e. the so-called convergence). Hence high convergence peaks may be identified as massive clusters of galaxies. This is the idea of a direct weak lensing cluster survey (hereafter WLCS), aimed at building a mass-selected cluster sample directly comparable to CDM theory (through N-body cosmological simulations). On the theoretical side, pioneering analytical predictions based on the mass function of halos have been proposed (Schneider 1996; Kruse & Schneider 1999), but they were not able to properly account for projection effects (Reblinsky & Bartelmann 1999). In addition Bartelmann et al. (2001) showed that WLCSs are very sensitive to the details of the clusters density profile. More recently, ray-tracing into N-body cosmological simulations have been used to properly address the critical issue of projections and clusters' asphericity (Tang & Fan 2005; White et al. 2002; Padmanabhan et al. 2003; Hamana et al. 2004) and the way to reduce the effect of noise on cluster detections through an optimised data filtering procedure (Starck et al. 2006; Maturi et al. 2005; Hennawi & Spergel 2005). A step forward will also probably be made with simplified analytical models of the convergence one-point PDF (Das & Ostriker 2006; Taruya et al. 2002). Under standard observational conditions, these works predict that at $z\sim0.2$ clusters more massive than $M\sim5\times 10^{13}~{M}_{\odot}$ can be recovered with a signal-to-noise ratio $\nu=3$. This limit drops to $M\sim2\times 10^{14}~{M}_{\odot}$ at $z\sim0.7$. Therefore the main targets of WLCSs are massive clusters of galaxies.

From the point of view of observations, we can mention a few serendipitous detections of galaxies clusters via weak gravitational lensing (e.g.  Schirmer et al. 2004; Dahle et al. 2003; Schirmer et al. 2003). A few examples have also been found to show up through weak lensing techniques without any clear optical counterpart and gave support for the existence for the so-called "dark clumps'' (Miralles et al. 2002; Umetsu & Futamase 2000). The practical implementation of a systematic WLCS is however very new. Miyazaki et al. (2002) studied an area of 2.1 deg2 with Suprime-Cam on Subaru telescope under excellent seeing conditions. They report an excess of $4.9\pm2.3$ convergence peaks with signal-to-noise $\nu>5$. Hetterscheidt et al. (2005) report the detection of $\sim $5 cluster candidates over a set of 50 disconnected VLT/FORS deep images covering an effective area of 0.64 deg2 while Wittman et al. (2006) present preliminary results for the first 8.6 deg2 of the Deep Lens Survey (eight detections). Haiman et al. (2004) also make interesting predictions for future WLCS applications in the LSST survey.

In this paper we present a weak lensing analysis of the Deep CFHT Legacy Survey[*] covering $4 \times 1$ deg2 in five optical bands ( u*g'r'i'z') under subarcsec seeing condition as a pilot analysis for the ongoing Wide Survey which will cover 170 deg2. The present work proposes to carry out weak lensing mass reconstructions in the Deep fields and focus on high convergence peaks in order to shed light on WLCS capabilities. The relatively high sample variance of the Deep images prevents any cosmological application of WLCSs but the great depth and amount of photometry make us with an excellent laboratory for a future application to the Wide data.

The paper is organised as follows. In Sect. 2 we briefly review the basics of weak gravitational lensing. In Sect. 3 we present the data at hand, the specific treatment required for weak lensing signal extraction and photometric redshifts. We show mass reconstructions (i.e. convergence maps) in Sect. 4 inferred from the coherent shear field imprinted on distant background sources. We also measure the statistics of high convergence peaks whereas we focus on their properties in Sect. 5 by studying the associated optical and X-ray counterparts (when available). We discuss our main achievements and conclude in Sect. 6.

In the following we assume the "concordance model'' cosmological background with $H_0 = 70~~ {\rm km~ s}^{-1}~ {\rm Mpc}^{-1}$, $\Omega_{\rm m}=0.3$ and $\Omega_\Lambda=0.7$. All magnitudes are expressed in the AB photometric system.

  
2 Basic lensing equations

In this section we briefly summarise the necessary background of gravitational lensing and especially the weak lensing regime which concerns the present analysis. We refer the reader to the reviews of Mellier (1999) and Bartelmann & Schneider (2001) for more detailed accounts.

The fundamental quantity for gravitational lensing is the lens Newtonian potential $\psi(\vec{\theta})$ at angular position $\vec{\theta}$ which is related to the surface mass density $\Sigma(\vec{\theta})$ projected onto the lens plane through

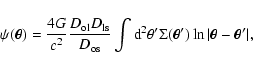\begin{displaymath}\psi(\vec{\theta}) = \frac{4 G}{c^2} \frac{D_{\rm ol}D_{\rm l... ...igma(\vec{\theta}') \ln\vert \vec{\theta}-\vec{\theta}'\vert , \end{displaymath} (1)

where $D_{\rm ol}$, $D_{\rm os}$ and $D_{\rm ls}$ are angular distances to the lens, to the source and between the lens and the source respectively. The deflection angle $\vec{\alpha}=\vec{\nabla}\psi$ relates a point in the source plane $\vec{\beta}$ to its image(s) in the image plane $\vec{\theta}$ through the lens equation $\vec{\beta}=\vec{\theta}-\vec{\alpha}(\vec{\theta})$. The local relation between $\vec{\beta}$ and $\vec{\theta}$is the Jacobian matrix $a_{ij}=\partial \beta_i/\partial \theta_j$

 \begin{displaymath} a_{ij} = \delta_{ij} - \psi_{,ij} = \left(\begin{array}{cc}... ...mma_2 \\ -\gamma_2 & 1-\kappa+\gamma_1 \end{array}\right) . \end{displaymath} (2)

The convergence $\kappa(\vec{\theta})=\Sigma(\vec{\theta})/\Sigma_{\rm crit}$ is directly related to the surface mass density via the critical density

 \begin{displaymath} \Sigma_{\rm crit}= \frac{c^2}{4 \pi G}\frac{D_{\rm os}}{D_{\rm ol}D_{\rm ls}} , \end{displaymath} (3)

and satisfies the Poisson equation

 \begin{displaymath} \Delta \psi = \psi_{,11}+\psi_{,22} = 2 \kappa. \end{displaymath} (4)

The 2-component shear is $\gamma=\gamma_1+{\rm i} \gamma_2 = \frac{1}{2}(\psi_{,11}-\psi_{,22})+{\rm i}\psi_{,12}$in complex notation. An elliptical object in the image plane is characterised by its complex ellipticity e defined from the second moments tensor Qij of the surface brightness distribution as

 \begin{displaymath} e = \frac{Q_{11} - Q_{22} + 2{\rm i} Q_{12}}{Q_{11} + Q_{22} + 2 \ \left(Q_{11}Q_{22} - Q_{12}^2\right)^{1/2}}\cdot \end{displaymath} (5)

This observed ellipticity can be related to the intrinsic ellipticity of the source $e_{\rm s}$ by:

 \begin{displaymath} e = \left\{\begin{array}{cc} \displaystyle \frac{e_{\rm ... ...}^* + g^*} & {\rm , for}~~\vert g\vert > 1 \end{array}\right. \end{displaymath} (6)

where $g=\gamma/(1-\kappa)$ is the so-called reduced shear and *denotes complex conjugation (Geiger & Schneider 1998; Seitz & Schneider 1997). In the weak lensing regime ( $g\sim\gamma \ll 1$), Eq. (6) reduces to $e=e_{\rm s}+\gamma$. Provided the random orientation of sources reduces the averaged source ellipticity to zero, e provides an unbiased estimate for the shear $\gamma $. The noise associated to this estimator is due to the scatter in the intrinsic ellipticity of sources with a typical value $\sigma_{\rm e}\sim0.3$ per component.

In the equations above we can isolate a geometric term which linearly scales the lensing quantities $\kappa $, $\psi$, and $\gamma $ and only depends on the distance ratio  $D_{\rm ls}/D_{\rm os}$. We thus can write $\gamma=w(z_{\rm l},z_{\rm s}) \gamma_\infty$ (and so forth for $\kappa $ and $\psi$) with $w(z_{\rm l},z_{\rm s})=D_{\rm ls}/D_{\rm os}\Theta(z_{\rm s}-z_{\rm l})$ and $\Theta(x)$ is the Heavyside step function. If sources are not confined in a thin plane, we account for the distribution in redshift by defining an ensemble average distance factor  $W(z_{\rm l})$ such that:

 \begin{displaymath} W(z_{\rm l})=\langle w(z_{\rm l},z_{\rm s})\rangle_{z_{\rm ... ...displaystyle\int_0^\infty {\rm d}z_{\rm s}~ n(z_{\rm s})}\cdot \end{displaymath} (7)

If we now consider a broad distribution of mass intervening between sources and the observer, we can use the Born approximation for the propagation of light in a clumpy Universe to infer the effective convergence experienced by light bundles:
 
                           $\displaystyle \kappa_{\rm eff}(\vec{\theta})$ = $\displaystyle \int_0^{l_{\rm H}}\frac{\rho(l,\vec{\theta}) - \overline{\rho}(l)}{\Sigma_{\rm crit}(l)} ~ {\rm d}l$  
  = $\displaystyle \frac{3}{2} \Omega_{\rm m} \left(\frac{H_0}{c}\right)^2 \int_0^{\... ...d}\chi~ W(\chi) f_k(\chi) \frac{\delta( f_k(\chi)\vec{\theta},\chi)}{a(\chi)} ,$ (8)

with l (resp. $\chi$) the proper (resp. comoving) distance, a the scale factor and $\delta(\vec{r})$ the density contrast. At this level we clearly see the projection nature of weak lensing signal. This means that a given $\kappa $-peak can be the result of a single $\delta$-peak (e.g. a cluster of galaxies) or the sum of two or more less pronounced $\delta$-peaks (e.g. groups or filaments aligned along the line of sight...).

  
3 The data

  
3.1 Imaging and photometry

The CFHTLS Deep survey is intimately linked to the Supernovae Legacy Survey (SNLS, Astier et al. 2006) as they share the same data. In practice, for each observed field data are taken sequentially every 3-4 nights, 6 months per year and in 4 observing bands ( g', r', i', z'). Additional u*data are included but they are not part of the SNLS and do not require time sampling. Most of the data have a seeing requirement limited to 0.9 $^{\prime\prime}$. Data acquisition is still under progress at CFHT so the depth of the Deep fields is still improving. Data processing (astrometry, photometric calibration, final stacking and production of catalogues) is performed at Terapix[*] for the CFHTLS community. The final data are released regularly by the CADC[*]. The present analysis is based on 2 sets of data released subsequently (the details of the release contents can be found on the Terapix Web site). For the weak lensing signal extraction we used the T0002 data while the deeper images and catalogues from the T0003 release were included for the photometric redshift production. The shear analysis (see below) was already performed on the T0002 data release at the time of T0003 data release. Since the i' band images did not gain much depth between T0002 and T0003, the weak lensing analysis, which is based on shape measurements of galaxies and is not sensitive to magnitude completeness, remained almost unchanged. Conversely the gain in exposure time and limiting magnitudes for other filters was extremely useful for photometric redshifts (see Sect. 3.3).

The Deep survey is made of four independent patches called D1, D2, D3 and D4. For each field and filter, Table 1 summarises the main observational properties of the T0002/T0003 release data in terms of coordinates, seeing, exposure time and depth. Because of the presence of bright stars, fields boundaries, defects in the CCDs and gaps between them with low signal-to-noise ratios, a substantial part of the images cannot be used for weak lensing analysis. Hence, the masked regions generally result in a loss of 20% of the field area. In Fig. 1, holes in the distribution of stars reveal the masked regions. The effective usable area is given in Table 1. The total working area for the weak lensing analysis is 3.61 deg2.

Table 1: Summary of CFHTLS Deep data, release T0003 (T0002/T0003 for i' band). The limiting magnitudes correspond to 50% completeness and are expressed in AB system. Seeing is measured in T0002 release i' images.


  \begin{figure} \par\includegraphics[width=16cm]{5677fig1.eps} \includegraphics[width=16.2cm]{5677fig2.eps} \end{figure} Figure 1: Stellar ellipticities in the CFHTLS Deep fields for D1... D4 from left to right. Upper row: polarisation field before and after PSF anisotropy correction (respectively red upper and lower black panels.). Lower row: projection of the stellar ellipticities in the (e1,e2) plane before and after PSF anisotropy correction (black crosses and red dots respectively).
Open with DEXTER

  
3.2 Shear measurement

The coherent stretching of background sources produced by the weak lensing effect is measured using i' band images. From one field to another the depth of the catalogues is slightly varying but for better coherence between the fields, we define a common magnitude cut for the selection of background sources 22<i'<26. In addition, close galaxy pairs with angular separations less than 3 $^{\prime\prime}$ are discarded to avoid blended systems with biased ellipticity measurements. Small galaxies with a half flux radius $r_{\rm h}$ smaller than that of stars are also rejected.

The reliability of shear measurements is expected to be comparable to the current cosmic shear survey analyses like the one already performed by Semboloni et al. (2006) and Hoekstra et al. (2006) who found similar results with independent pipelines in the same fields. Throughout this paper, we report results of shear analysis performed in the i' band which presents the best balance between depth and seeing. However we checked that we can extract a similar signal in the other noisier g', r' and z' bands. This has also been assessed by Semboloni et al. (2006) who report a similar cosmic shear signal in the deep fields using both r' and i' bands.

Blurring and distortion of stars and galaxies produced by instrument defects, optical aberration, telescope guiding, atmospheric seeing and differential refraction are corrected using the Point Spread Function (PSF) of stars over the whole field. Several correction techniques and control of systematic errors have been proposed over the past 10 years (see e.g.  Bartelmann & Schneider 2001; Mellier 1999). In the following we use the most popular KSB method initially proposed by Kaiser et al. (1995). Several teams have already demonstrated that this technique can correct systematics down to a lower value than the very weak cosmic shear signal (van Waerbeke et al. 2005; Heymans et al. 2006). It is therefore well suited for this analysis too. The KSB implementation used here is identical to that of Gavazzi et al. (2004).

The observed ellipticity components $ e^{\rm obs}_{\alpha=1,2}$ are made of the intrinsic ellipticity components $e^{\rm src}_\alpha$, and linear distortion terms that express the instrument and atmospheric contaminations and the contribution of gravitational shear to the galaxy ellipticity. Each ellipticity component is transformed as:

  
    $\displaystyle e^{\rm obs}_\alpha = e^{\rm src}_\alpha + P^\gamma_{\alpha\beta} g_\beta + P^{\rm sm}_{\alpha\beta}q^*_\beta,$ (9a)
    $\displaystyle {\rm with\ \ } P^\gamma_{\alpha\beta} = P^{\rm sh}_{\alpha\beta} ... ...sm}_{\alpha\gamma} \left(\frac{P^{\rm sh}}{P^{\rm sm}}\right)_ {\gamma\beta}^*,$ (9b)

where g is the reduced gravitational shear, $P^{\rm sm}$ is the smear polarisability, $P^{\rm sh}$ the shear polarisability and $P^\gamma$ the isotropic circularisation contribution to the final smearing. Sources are detected with SExtractor (Bertin & Arnouts 1996) but shape parameters are calculated with Imcat[*]. Because the noise present in these measured quantities is important, all these tensors are simplified to half their trace (see e.g.  Erben et al. 2001).

$\left(\frac{P^{\rm sh}}{P^{\rm sm}}\right)^*$ and q* are measured from field stars. Their spatial variation across the field is fitted by a second order polynomial, applied individually to each one of the 36 CCDs composing the MegaCam focal plane. Stars are selected in the magnitude-$r_{\rm h}$ plane, as usual. q* is the anisotropic part of the PSF, which is subtracted from observed ellipticities. The residuals for stars are shown in Fig. 1 . After correction, these latter are consistent with a $\sigma_\gamma\simeq0.004$ rms featureless white noise. In Sect. 4.1, we present mass reconstructions inferred from the shear field measured on distant source galaxies. If we perform the same reconstructions on stars, we only get white noise as expected from a correct PSF smearing correction. Its rms is $\sigma_\kappa\sim0.001$ when smoothed with a Gaussian kernel of width 1 arcmin, which is much below the signal we are interested in (typically $0.01\la \kappa\la 0.5$, see below).

The smearing part of the PSF contained in the $P^\gamma$ term depends on the magnitude of the object and on its size as compared to the seeing disk. To optimally extract $P^\gamma$, we derived it from an averaged value over its 40 nearest neighbours in the magnitude $-r_{\rm h}$ plane. The variance of ellipticities inside this neighbourhood is then used as a weighting scheme for the shear analysis. The weight assigned to each galaxy is:

 \begin{displaymath} w_{i} = \frac{1}{\sigma_{{\rm e},i}^2} = \frac{P^{\gamma~2}} {P^{\gamma~2}\sigma_0^2 + \sigma_{i}^2}, \end{displaymath} (10)

where $\sigma_0$ prevents from over-weighting some objects. It is set to the 1D intrinsic dispersion in galaxy ellipticities $\sigma_{\rm e}=0.23$ and $\sigma_i$ is the observed dispersion of ellipticities over the 40 nearest neighbours in the magnitude-$r_{\rm h}$ plane.

At this level, we have 132 000 (resp. 104 000, 162 000 and 114 000) galaxies with reliable shape parameters in the D1 (resp. D2, D3 and D4) field leading to a source surface number density of $n_{\rm bg}=38.0$(resp. 30.6, 35.4, 34.5) arcmin-2. These values are much higher than the usual ones in weak lensing studies, which turn around 15-20 galaxies arcmin-2. The magnitude cut i'<26explains these high densities although it makes difficult an accurate determination of the redshift distribution of such faint objects. In the following we shall refer to this source catalogue as CA. Because several galaxies have large uncertainties on their shape parameters, one should correct this density by considering the effective density which would have been achieved if all uncertainties were limited by the intrinsic dispersion in source ellipticity. More precisely, if we define $ N_{\rm eff}=\sum_i (\sigma_{\rm e}/\sigma_{{\rm e},i})^2$, the effective source number density would then be $n_{\rm bg}^{\rm eff} = 25.3$(resp. 20.7, 21.6, 21.0) arcmin-2. This quantity represents what could be achieved under deep space-based observing conditions.

Figure 2 illustrates the effect of our weighting scheme (Eq. (10)) in the magnitude distribution of sources. The weighting scheme efficiently down-weights objects fainter than $i'\sim 24$ and most of the signal is carried by galaxies brighter than $i'\sim25$. Actually i'= 24 is the magnitude above which shape measurement errors start to increase above the intrinsic scatter of source ellipticities.


  \begin{figure} \par\includegraphics[width=8.8cm]{5677fig3.eps} \end{figure} Figure 2: i' band magnitude distribution of background sources. For clarity we represent the whole magnitude distribution although the CA catalogue only contains galaxies in the range 22<i'<26. The dashed red line illustrates the effective change in magnitude distribution of lensed sources when accounting for the weighting scheme of Eq. (10). The weights are normalised so as to conserve the total number of objects.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm]{5677fig4.eps} \end{figure} Figure 3: Redshift distribution of sources brighter than i'=26. Thin solid black: (resp. thick solid red) the weighting scheme in Eq. (10) which reduces the contribution of faint-distant sources is (resp. not) taken into account. For comparison the unweighted redshift distribution of i'<24 sources is shown (dashed blue). This latter distribution is renormalised to the same total number of objects as the $i'\protect \la26$ sample.
Open with DEXTER

  
3.3 Photometric redshifts

The number of filters available in the CFHTLS Deep images allows a direct estimate of the redshift of each source according to its Spectral Energy Distribution (SED) from u*g'r'i'z' bands. We used the publicly available catalogue of photometric redshifts recently carried out by Ilbert et al. (2006) for which the accuracy has been extensively assessed against spectroscopic data[*]. In some cases Ilbert et al. used additional non-CFHTLS data in other photometric bands to improve the precision of their photometric redshifts. We refer the reader to this work for further accounts. Here we briefly mention that photometric redshifts have been checked to be reliable enough for our purpose down to $i'\sim25$. The authors mention that the accuracy is reduced at redshift $z_{\rm phot}>1.5$.

In the following we use Ilbert et al. (2006) photometric redshifts in three distinct ways, each of them requiring different precision on $z_{\rm phot}$.

  
4 Mass reconstructions

  
4.1 Convergence maps from observed shear

From the source catalogue CA defined in Sect. 3, we can infer the shear field $\gamma(\vec{\theta})$ and deduce the associated convergence field $\kappa(\vec{\theta})$. They are related by:

 \begin{displaymath} \kappa(\vec{\theta}) = \int_{\mathbb{R} ^2} K(\vec{\theta}-... ...theta})^* \gamma(\vec{\vartheta}) {\rm d}^2 \vec{\vartheta}, \end{displaymath} (11)

where $K(\vec{\theta})=\frac{1}{\pi}\frac{-1}{(\theta_1-{\rm i} \theta_2)^2}$is a complex convolution kernel (Kaiser & Squires 1993, hereafter KS93). The shear field is smoothed with a Gaussian filter $G(\theta)\propto\exp(-\frac{\theta^2}{2\theta_{\rm s}^2})$ with $\theta_{\rm s}=1$ arcmin. The convergence field is consequently smoothed by the same filter. The resulting convergence maps present correlated noise properties (van Waerbeke 2000).

 \begin{displaymath} \langle \kappa_n(\vec{\vartheta}) \kappa_n(\vec{\vartheta}+... ...xp\left(-\frac{ \vec{\theta}^2}{4\theta_{\rm s}^2}\right)\cdot \end{displaymath} (12)

$\sigma_{\rm e} (4\pi n_{\rm bg}\theta_{\rm s}^2)^{-1/2}$ characterises the noise level. We measured a value 0.0196, 0.0225, 0.0202 and 0.0221 for D1, D2, D3 and D4, respectively.


  \begin{figure} \par\includegraphics[width=8.5cm]{5677fig5.eps} \includegraphics[width=8.5cm]{5677fig6.eps} \end{figure} Figure 4: Convergence maps inferred from the ellipticity field of background sources for D1 ( top) and D2 ( bottom). The shear field is estimated by smoothing the ellipticity field of sources galaxies selected in catalogue CA. Then, Eq. (11) is used the convert $\gamma $ into the $\kappa $ field. The largest masked regions are visible as fuzzy $\kappa \sim 0$ regions. Contours levels start at 3$\sigma $ with a $0.5\sigma $ arithmetic increase. The Gaussian filtering scale is 1 arcmin. The 14 peaks with $\nu >3.5$ are labeled.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.5cm]{5677fig7.eps} \includegraphics[width=8.5cm]{5677fig8.eps} \end{figure} Figure 5: Same a Fig. 4 for fields D3 ( top) and D4 ( bottom).
Open with DEXTER

In principle, the convergence computed from Eq. (11) must be real and its imaginary component should only be due to noise and possible residual systematics. We checked this assumption by rotating the shear field by 45$^\circ$ and found the reconstructed maps to be consistent with noise as described by Eq. (12).

The KS93 inversion in Eq. (11) is done by a direct summation over all sources without pixelling, smoothing and Fourier transforming the data. This reduces boundary and mask effects on mass reconstructions. Several techniques have been proposed so far since the original KS93 method. Most of them are useful in high shear regions (where $g\la 1$) and for small fields of view. However the wide MegaCam images and the complex field geometry imposed by the masks make difficult, time consuming and unnecessary the implementation of more complex techniques. In addition, van Waerbeke (2000) has shown that noise properties of KS93 method are well controlled and consistent with Eq. (12).

Figures 4 and 5 show the convergence maps for D1, D2, D3 and D4 deduced from the catalogue CA. Contours in units of the signal-to-noise ratio (SNR or $\nu$) are overlaid, with $\nu$ defined as

 \begin{displaymath} \nu = {\rm SNR} = \frac{\kappa}{\sigma_{\rm e}} \sqrt{4~ \pi~ n_{\rm bg}~\theta_{\rm s}^2}. \end{displaymath} (13)

In the present data we detect $\sim $46 positive peaks with $\nu>3$ and 5 peaks with $\nu>4$. In order to avoid too much contamination by noise peaks but to detect as much true peaks as possible, we therefore fix the threshold at $\nu=3.5$. The 14 peaks detected within this limit will constitute our working sample in the rest of the paper. We discuss in more detail the statistics of these peaks in Sect. 4.2 and their possible association to galaxy clusters in Sect. 5.

  
4.2 Statistics of peaks

Several authors investigated the possibility to use convergence peaks as clusters of galaxies candidates. Simplified analytical calculations based on the Halo Mass Function (as inferred from the Press-Schechter formalism for instance) provided the first predictions for wide field imaging surveys (Schneider 1996; Kruse & Schneider 1999). Then, thanks to the development of numerical simulations, quantitative estimates of projection effects and cluster selection functions (in terms of mass and redshift) became available (Tang & Fan 2005; Jain & van Waerbeke 2000; White et al. 2002; Hamana et al. 2004; Reblinsky & Bartelmann 1999; Padmanabhan et al. 2003; Hennawi & Spergel 2005).

The practical implementation of a Weak Lensing Cluster Survey (WLCS) requires the control of noise present in observations, either due to the intrinsic ellipticity of sources or to the intervening large scale structures (LSS) along the line of sight. Although the "compensated aperture mass filter'' has early been proposed as an efficient filter for peak statistics (Schirmer et al. 2004; Hetterscheidt et al. 2005; Schirmer et al. 2006; Schneider 1996; Kruse & Schneider 1999; Schirmer et al. 2003), it has been shown that such a filter may not be as efficient as an optimised filter which would account for the contribution of LSS to the noise budget and the shape of the dark matter halos we aim at detecting (Maturi et al. 2005; Hennawi & Spergel 2005). It turns out that a simple Gaussian filter of width $\theta_{\rm s}\sim1{-}2$ arcmin is close to the optimal linear filter and has been extensively studied in simulations (Tang & Fan 2005; White et al. 2002; Hamana et al. 2004). In addition a promising multiscale wavelets technique has also been proposed recently (Starck et al. 2006) but has not been applied to real data yet. Therefore we shall use a simple Gaussian filter with scale $\theta_{\rm s}=1$ arcmin as already applied onto the mass reconstructions of Sect. 4.1.

Figure 6 shows the cumulative number of maxima peaks $N({>}\nu )$ as well as the symmetric number of minima peaks for the four Deep fields. The latter curve is flipped ( $\nu\rightarrow-\nu$) for an easier comparison. The net excess of maxima with $\nu \ga 4$ as compared to minima at the corresponding negative threshold is visible, thus showing the non-Gaussian nature of the convergence field (see also Miyazaki et al. 2002). The statistical significance of this excess is still low due to the large cosmic variance in such a small sky coverage. In addition it should be kept in mind that CFHTLS Deep fields of view were chosen to be free of any known massive nearby cluster.

The theoretical analysis of Hamana et al. (2004) is well suited for a direct comparison with our results since the survey area, the smoothing scale, and the noise properties are the same. We found a satisfying agreement when considering their Fig. 7 although the sample variance is large.


  \begin{figure} \par\includegraphics[width=8.8cm]{5677fig9.eps} \end{figure} Figure 6: Cumulative counts of $N({>}\nu )$ maxima peaks (solid black) and corresponding counts of $N({<}\!\!-\nu)$ minima peaks (dashed blue) curve per square degree in the Deep survey. The surrounding dotted lines represent $1\sigma $ Poisson errors. The excess of positive maxima is marginally seen as compared to negative minima, thus showing the non-Gaussianity of the convergence field.
Open with DEXTER

An extensive study of $\kappa $-peaks statistics in the Wide CFHTLS survey would provide valuable cosmological information for cosmic shear studies and would help breaking some degeneracies (mainly between $\Omega_{\rm m}$and $\sigma_8$) present in the shear 2-point correlation function. Such an analysis is beyond the scope of the present work but the full implementation of the $\kappa $-peaks statistics in the presently released CFHTLS-Wide data is in progress. It is noteworthy that in order to extract the associated cosmological signal, there is no need to measure the mass or the redshift of each peak, neither to identify them with clusters (or projected groups, etc.). However, instead of a blind counting exercise of convergence peaks, we propose in the following to characterise the structures responsible for the highest convergence maxima peaks.


  \begin{figure} \par\mbox{\includegraphics[width=8.9cm,height=5.5cm]{5677fig10.ep... ...3mm} \includegraphics[width=8.9cm,height=5.5cm]{5677fig11.eps} } \end{figure} Figure 7: Increase of shear signal strength (i.e. equivalent Einstein radius) as a function of source redshift around peak Cl-02. The source catalogue is split into 10 quantiles. Contours show 1, 2 and 3$\sigma $ CL regions around the best fit $\theta _{\rm E}$ and $z_{\rm l}$. Peak Cl-02 exhibits the expected profile for a cluster with velocity dispersion $\sigma_v=760\pm110~ {\rm km~ s}^{-1}$ and redshift $z_{\rm l}=0.52^{\rm +0.14}_{-0.11}$ with $\chi ^2/{\rm d.o.f.}=0.6$ (thick line). The upper panel uses photometric redshifts of sources down to i'=26 whereas the lower panel is limited by $i'\protect \la 24.5$, showing that including faint sources does not affect our analysis in a statistically significant way.
Open with DEXTER

   
5 Properties of $\nu >3.5$ peaks

In this section we attempt to estimate the redshift, mass and luminosity of structure(s) responsible of the 14 $\kappa $-peaks with $\nu\ge3.5$. This significance threshold is rather low so we expect a substantial amount of contamination by noise fluctuations. We focus on the physical properties of the detected peaks and test whether they can be associated to galaxies over-densities. The first step in this peak identification is to estimate a redshift, taking advantage of photometric redshifts. Two methods are explored, one which is directly related to the shear signal dependency on lens redshift and which does not require an explicit identification of the peak with galaxies, and the other which is related to the identification of a localised over-density in the photometric redshift distribution of galaxies. Results from the two approaches are summarised in Table 2.

  
5.1 Lens tomography

The basics of lens tomography are the following: in the case of a real deflector at redshift $z_{\rm l}$, the shear signal must increase in a characteristic way as a function of the source redshift according to the $w(z_{\rm l},z_{\rm s})=D_{\rm ls}/D_{\rm os}$ term. Early applications can be found in Wittman et al. (2003,2001) and Hennawi & Spergel (2005). The shape of the shear increase versus the source redshift allows to derive the lens redshift. In the following, we apply this technique to estimate the lens redshift of each peak and check whether the shear behaviour around peaks is consistent with the lensing hypothesis or is rather a noise fluctuation.

Table 2: Catalogue of convergence peaks / galaxy clusters in CFHTLS Deep fields.

We measure the shear profile around each peak between 1 and 5 arcmin from the centre, using sources having $i'\la 26$ and their individual photometric redshifts. Assuming that the lens mass distribution at redshift $z_{\rm l}$ follows a Singular Isothermal Sphere (SIS) profile, the shear is simply

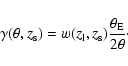\begin{displaymath}\gamma(\theta,z_{\rm s}) = w(z_{\rm l},z_{\rm s}) \frac{\theta_{\rm E}}{2 \theta}\cdot \end{displaymath} (14)

The Einstein radius $\theta _{\rm E}$ is related to the characteristic cluster velocity dispersion by $\sigma_v= 186.2~ {\rm km~ s}^{-1}~ (\theta_{\rm E}/1 \hbox{$^{\prime\prime}$ })^{1/2}$. We fit the shear function for the unknown lens redshift $z_{\rm l}$ and Einstein radius $\theta _{\rm E}$ by minimising a $\chi^2(z_{\rm l},\theta_{\rm E})$ of the form

 \begin{displaymath} \chi^2(z_{\rm l},\theta_{\rm E}) = \sum_i \frac{\left( e_{{... ...\theta_{\rm E}}{2\theta_{i}}\right)^2}{\sigma_{{\rm e},i}^2} \end{displaymath} (15)

where $w_{i}=w(z_{\rm l},z_{{\rm s},i})$, $\sigma_{{\rm e},i}$ is given by Eq. (10) and $e_{{\rm t},i}$ is the tangential component of ellipticity. The dependency of $\chi^2$ with $\theta _{\rm E}$ can be easily removed by considering that $\frac{\partial \chi^2}{\partial \theta_{\rm E}}=0$ for any $z_{\rm l}$ if $\theta _{\rm E}$ satisfies

 \begin{displaymath} \widehat{\theta_{\rm E}} = \frac{ 2\sum_i \frac{e_{{\rm t},... ...\sum_i \frac{ w_{i}^2}{\theta_{i}^2\sigma_{{\rm e},i}^2}}\cdot \end{displaymath} (16)

It can be inserted into Eq. (15) to give

 \begin{displaymath} \chi^2(z_{\rm l}) = \sum_i \frac{e_{{\rm t},i}^2}{\sigma_{{... ...{\sum_i \frac{w_{i}^2}{\theta_{i}^2\sigma_{{\rm e},i}^2}}\cdot \end{displaymath} (17)

In order to illustrate the method we plot on the upper panel of Fig. 7 the value of the Einstein radius measured in the 10 $z_{\rm s}$ quantiles of sources between 1 and 5 arcmin from the centre of the peak Cl-02, detected with $\nu=5.5$. The increase of $\theta _{\rm E}$ with redshift $z_{\rm s}$is clear and allows an unambiguous identification of the lens redshift. Error bars come from the scatter in observed (measurement+intrinsic) ellipticities as determined by Eq. (10). Contours show the 68.3%, 95.4% and 99.3% CL regions for $z_{\rm l}$ and $\theta _{\rm E}$. The thick curve represents the function $\theta_{\rm E}\times w(z_{\rm l},z_{\rm s})$for the best fit values $z_{\rm l}=0.52^{\rm +0.14}_{-0.11}$ and $\theta_{\rm E}=17^{\rm +5.5}_{-4.5}\hbox{$^{\prime\prime}$ }$ leading to a velocity dispersion $\sigma_v=760\pm110~ {\rm km~ s}^{-1}$. Because of the rather large statistical uncertainties, the detailed radial shape of the shear profile introduced in the $\chi^2$ fit is not much important. For significant peaks in the reconstructed mass maps a redshift estimate directly evaluated from the lensing properties of the peaks is a viable method. It could in particular be applied to any putative "dark clump'' where no bright galaxies can be associated with the mass peaks.

The lower panel of Fig. 7 shows that limiting the analysis to brighter sources (including i'<24.5 photometric redshifts) does not make significant changes. We checked that this is also true for other peaks. This suggests that, even if photometric redshift of i'>24.5 galaxies may suffer larger uncertainties, the effect on lens tomography, and lensing in general, is negligible. This is due to the saturation of the curve $D_{\rm ls}/D_{\rm os}$ at high $z_{\rm s}$ and to the weighting scheme (Eq. (10)), as already mentioned in Sect. 3.3. Table 2 presents the constraints on $\sigma_v$ and $z_{\rm l}$ given by tomography for the 14 peaks. Most of them have fitted velocity dispersion values limited to $\sigma_v\la 700~ {\rm km~ s}^{-1}$. There is no massive cluster with $\sigma_v>800 ~ {\rm km~ s}^{-1}$ below redshift $\sim $0.7 in the Deep survey. This is not a surprise as the Deep fields were initially selected for their lack of well identified Abell clusters for example. In addition we observed that if the signal-to-noise ratio is too low or tomography provides a bad $\chi^2/{\rm d.o.f.}>2$, then the inferred lens redshift is systematically $z_{\rm l}=0$. Two peaks (Cl-04 and Cl-12) are such that tomography fails in constraining lens redshift and velocity dispersion. However this is may also be attributed to the fact that these two peaks are noise fluctuations rather than being produced by real galaxy clusters.


  \begin{figure} \par\includegraphics[width=8.8cm,height=8.5cm]{5677fig12.eps} \end{figure} Figure 8: Photometric redshift distribution of galaxies around convergence peaks with a candidate optical counterpart. The green dashed curve is the lens redshift as constrained by tomography (Sect. 5.1), showing a remarquable agreement with $z_{\rm phot}$ excesses for the most significant peaks. The total number of galaxies in the peaks should not be seen as richness since we did not correct for the presence of masks and the increasing incompleteness as z increases.
Open with DEXTER

  
5.2 Optical counterparts

Here again we use photometric redshifts to check whether an optical counterpart can be assigned to our 14 high convergence peaks with $\nu >3.5$.

We first examine galaxies in a circular aperture of 2 arcmin around each peak. This radius corresponds to a linear physical scale of 400 to 860 kpc for a lens redshift ranging from 0.2 to 0.7 respectively. Therefore this is the radius within which the highest density of bright galaxies is expected, most of them being early-type galaxies. In addition, most of these galaxies are localised in a narrow range of photometric redshifts once the background $z_{\rm phot}$-distribution is subtracted. The background is defined in the region beyond 6 arcmin of all peaks. In this preliminary step we only consider galaxies brighter than i'=23 and with a best fit SED template type T of type earlier than the spectral type T=44[*].

9 peaks out of 14 meet this criterion whereas there is no clear optical associable counterpart for the remaining 5 peaks (rows filled with dashes in Table 2). For each of the former 9 $\kappa $-peaks, we define the cluster redshift as the location of the most prominent $z_{\rm phot}$ excess peak. We iteratively apply a 4$\sigma $ clipping to remove outliers and get a reliable redshift and its corresponding statistical uncertainty. Distributions can be seen in Fig. 8. The tomographic $z_{\rm l}$ probability distribution function of Sect. 5.1 (marginalised over velocity dispersion) is overlayed for comparison. We see a remarquable agreement for the most significant peaks.

The peculiar case of Cl-14 deserves a special attention. Cl-14 clearly exhibits a bimodal distribution that lens tomography is unable to reveal, probably because of the low detection level. The first excess is at $z\simeq0.15$, and is $d=75\hbox{$^{\prime\prime}$ }$ away from the convergence peak location. It is consistent with an XMM-LSS detection at a similar redshift (see Sect. 5.4). However the second peak, at redshift $z\simeq0.57$, is much closer to the convergence peaks ( $d=14\hbox{$^{\prime\prime}$ }$) although it does not match an XMM-LSS peak. It is likely that both components may contribute to the overall convergence. This is a clear example of the projection effects already mentioned at the end of Sect. 2. In the following we will consider separately these two components, labeled Cl-14a for the $z\simeq0.15$ peak and Cl-14b for the furthest one.

We also define the luminosity-weighted optical centre using the bright galaxies (i'<23) in the $z_{\rm phot}$ excess range. Optical centres are less than one arcmin away from the convergence peak location, as expected from the spatial resolution of the mass maps. The observed offsets are reported in column $\Delta(\alpha,\delta)$ of Table 2. From the new defined centre and the present cluster photometric redshift, we re-estimate the lensing velocity dispersion (central part of Table 2). The velocity dispersions of Cl-14a and b are fitted simultaneously. Although they are slightly correlated, we can deblend the system and put constraints on both components. In any case, Cl-14b is the dominant contribution to the convergence peak.

In order to relate lensing velocity dispersion and the excess of foreground galaxies we measure the number $\Lambda$ of Mr<M0 galaxies in a fiducial physical radius $R_0=1.43 ~ {\rm Mpc}$ and a slice $\delta z_{\rm phot}=\pm0.10$, with M0=-20 in the rest-frame r' band. The most distant of our peaks being at $z\sim0.74$, the sample of photometric redshifts that will be close to complete at M0 corresponds to $i'\sim23.5$, which is a conservative limit for accurate photometric redshifts. Their contribution to the L>L* luminosity function is very low anyway. Assuming a luminosity function with slope $\alpha$, the total luminosity in the aperture is

 \begin{displaymath} L_{\rm aper} = L_* \Lambda \frac{\Gamma(2+\alpha,0)}{\Gamma(1+\alpha,q)}\simeq 1.24 \Lambda L_* , \end{displaymath} (18)

with q=100.4(M*-M0) and assuming $\alpha=-1.09$, M*=-21.21(Blanton et al. 2003). This procedure limits the impact of bad photometric redshifts as compared to a simple summation of galaxies luminosities. Because photometric redshifts are imperfect, we need to subtract a background contribution which is evaluated using galaxies outside 1.5R0 of all peaks in the corresponding redshift slice. We also compensate for the aperture area lost in masked regions. Cl-14a and Cl-14b are considered independently.

The correlation between lensing velocity dispersion and richness is shown in Fig. 9 for the eight systems Cl-01, Cl-02, Cl-03, Cl-05, Cl-06, Cl-07, Cl-08, Cl-12 and the Cl-14 which is split into its two componants. We also add a peak with snr $\nu=3.4$ as it is part of the XMM-LSS cluster sample (see Sect. 5.4). The range of richness and velocity dispersion probed by our sample is quite narrow so it is difficult to put tight constraints on the scaling relation between these quantities. A linear regression yields: $\sigma_v \sim 251 ~ {\rm km~ s}^{-1}\Lambda^{0.21}$. The slope is however poorly constrained.

For our assumed isothermal mass profile, the projected mass enclosed in radius R0 is:

 \begin{displaymath} M(<R_0) = \pi \sigma_v^2 R_0 / G . \end{displaymath} (19)

From the data we find $\sigma=96\pm7 ~ {\rm km~ s}^{-1}\Lambda^{1/2}$ (solid green line of Fig. 9). Combining Eqs. (18) and (19), this translates into a r' band mass-to-light ratio $M/L_r=168\pm24 ~h_{\rm 70}~(M/L)_\odot$ inside the aperture R0. The z=0.74 peak Cl-08 slightly departs from this relation but this could partly be due evolution of galaxies luminosities. In addition, weak lensing mass estimates for such high redshift clusters are particularly sensitive to the high redshift sources. Since the accuracy of photometric redshifts is more hazardous at $z_{\rm s}> 1.5$ the lensing-inferred velocity dispersion of this cluster is more uncertain. Otherwise our M/L ratio is consistent with recent estimates (see e.g.  Yee & Ellingson 2003; Bardeau et al. 2005; Popesso et al. 2006).


  \begin{figure} \par\includegraphics[width=8.8cm]{5677fig13.eps} \end{figure} Figure 9: Correlation between richness and lensing velocity dispersion for Cl-01, Cl-03, Cl-05, Cl-06, Cl-07, Cl-08, Cl-12, Cl-14a-b and XLSSC44. The dotted red line is a raw linear fit leading to the scaling $\sigma_v \sim 251 ~ {\rm km~ s}^{-1}\Lambda^{0.21}$. If we assume a constant mass-to-light ratio, we find $\sigma_v = (95\pm 7) \Lambda^{1/2} ~ {\rm km~ s}^{-1}$ i.e.   $M/L_r=168\pm24 ~h_{\rm 70}~(M/L)_\odot$ ( solid green line).
Open with DEXTER

  
5.3 Merits of lens tomography

It is instructive to compare the redshift arising from lens tomography ( $z_{\rm tomo}$) and the redshift $z_{\rm phot}$ given by an excess of foreground galaxies (i.e. cluster members identified by their photometric redshift). It is not a surprise that most WLCSs detections peak at $\langle z_{\rm tomo}\rangle \simeq \langle z_{\rm phot} \rangle\simeq 0.25$because is corresponds to the redshift range in which gravitational lensing is most efficient for the source population we are considering.

In Fig. 10 we plot the comparison between these two redshift estimates for the 8 clusters having a well identified optical counterpart (namely clusters Cl-01, Cl-02, Cl-03, Cl-05, Cl-06 Cl-07, Cl-08, Cl-12). Cl-14 was discarded due to its apparent complexity. Although the statistic is quite small and errors on $z_{\rm tomo}$ are large, there is a remarquable agreement between both redshifts for the high signal-to-noise systems, which is very encouraging. In addition, we already pointed out that Cl-04, for which tomography fails in giving a lens redshift, has no optical (nor X-ray) counterpart and is likely a false detection. Tomography helps eliminating such cases.

In order to improve this correlation, it will be important to improve the quality of photometric redshifts, especially for the faintest background sources. It is not clear how much the catastrophic redshifts in the source catalogue perturb lens tomography, but certainly for accurate tomographic redshift estimates it will be important to increase the number of filters for photometric redshifts, especially in infrared bands (Bolzonella et al. 2000). In addition, it is noteworthy that our sample is made of low mass clusters ( $\sigma_v\sim400{-}600 ~ {\rm km~ s}^{-1}$). For more massive clusters, like those expected in the CFHTLS-Wide survey, the method will greatly gain in accuracy and reliability (Hennawi & Spergel 2005).


  \begin{figure} \par\includegraphics[width=8.8cm]{5677fig14.eps} \end{figure} Figure 10: Comparison between lens tomography and direct photometric redshift methods to estimate the redshift of the $\nu >3.5$ $\kappa $-peaks. Only those peaks with a clear optical counterpart are included in the figure. Red diamonds represent the 4 most significant $\nu \ge 4$ peaks whereas blue squares code for the remaining 4 lower snr peaks. Due to its complexity Cl-14 is not included in this figure.
Open with DEXTER

  
5.4 Comparison to X-ray data

The CFHTLS-Deep D1 field is part of the XMM-LSS survey[*]. We therefore took advantage of the publicly available X-ray database to cross-correlate our sample of $\kappa $-peaks/clusters with those X-ray detections published in Valtchanov et al. (2004), Willis et al. (2005), and Pierre et al. (2006).

The matching is very good. Over the seven $\nu >3.5$ peaks detected in D1, four are XMM-LSS clusters with luminosity $1.5\times 10^{43}\la L_{\rm X,bol}\la6.5\times 10^{43}$ erg/s and temperature $1\la T_{\rm X}\la 2$ keV. However the most pronounced $\nu=5.5$ D1 peak, namely Cl-02, is not part of the XMM-LSS sample because it falls in a region lost by the X-ray survey (pointing G12, Pierre et al. 2006). Peaks Cl-04 and Cl-10 do not exhibit any optical counterpart and are not detected in X-ray either. This confirms that Cl-04 and Cl-10 are likely false detections due to noise fluctuations.

There are 9 publicly available XMM-LSS clusters in the D1 field of view in the classes C1-C2[*]. 4 of them are part of our weak lensing cluster sample although we note that a $\nu=3.4$ peak at $\alpha=02^{\rm h}24^{\rm m}31.7^{\rm s}$ and $\delta=-04^{\rm o}13{\rm '}55{\rm ''}$ is also part of the XMM-LSS sample (XLSSC44 at z=0.26, $T_{\rm X}=1.37^{\rm +0.28}_{-0.16}$ keV). This cluster has been missed by the weak lensing survey because it does not meet the $\nu >3.5$ detection threshold. Its lensing velocity dispersion is $\sigma_{v,{\rm } \rm lens}=466^{\rm +105}_{-143}~ {\rm km~ s}^{-1}$. The remaining 4 XMM-LSS clusters which are not part of our sample: XLSSC38 (z=0.58, $T_{\rm X}$unknown), XLSSC11 (z=0.05, $T_{\rm X}=0.64^{\rm +0.11}_{-0.07}$ keV), XLSSC29 (z=1.05, $T_{\rm X}=4.07^{\rm +1.72}_{-0.99}$ keV) and XLSSC5 (z=1.05, $T_{\rm X}=3.67^{\rm +3.50}_{-1.33}$ keV) are either very low or very high redshift clusters for which lensing efficiency is low. Therefore it is not surprising that they are missing in our weak lensing sample.

Note also that the peak Cl-01, located in D4 and which is the strongest peak matches an X-ray detected ROSAT cluster at redshift z=0.13and luminosity $L_{{\rm X},[0.5{-}2.0]}=14.5\pm2.5\times10^{43}$ erg s-1(de Grandi et al. 1999).


  \begin{figure} \par\includegraphics[width=8.8cm]{5677fig15.eps} \end{figure} Figure 11: Correlation between X-ray and lensing-inferred temperature $k_{\rm B} T_{\rm lens}= \mu m_{\rm H} \sigma _v^2$ (black diamonds) for Cl-03, Cl-05, Cl-07, Cl-14 and XLSSC44. The results of Cypriano et al. (2004) on massive clusters are reported for comparison (red stars) as well as those of Bardeau et al. (2006) (green crosses). The bisectrix line (dotted) represents energy equipartition between hot ICM gas and dark matter + galaxies collisionless fluid.
Open with DEXTER

We now compare lensing velocity dispersion and X-ray temperature for the five D1 XMM-LSS clusters Cl-03, Cl-05, Cl-07, Cl-14 and XLSSC44. More precisely and following Cypriano et al. (2004), we compare the lensing velocity dispersion inferred temperature $k_{\rm B} T_{\rm lens}= \mu m_{\rm H} \sigma _v^2$of dark matter particles to the X-ray temperature of hot ICM gas particles. $\mu m_{\rm H}$ is the mean particule weight per free electron. It is set to the same value $\mu=0.61$ as Cypriano et al. (2004). We also include in the comparison data from the study of Bardeau et al. (2006) of 11 X-ray luminous clusters at z=0.2. Under the assumption of energy equipartition these temperatures would be equal. If non gravitational sources of gas heating/cooling are at work we expect some departure from this relation $T_{\rm X} \ne T_{\rm lens}$. Conversely the mass (and thus $\sigma_v$ and $T_{\rm lens}$) of shear-selected clusters may be increased by projections of unrelated material along the line of sight.

Although the statistics is rather poor, Fig. 11 suggests that shear-selected clusters are well aligned onto the bisectrix $T_{\rm X} = T_{\rm lens}$. Gas and collisionless particles share the same amount of energy. This behaviour seems to be less true for massive clusters. For example Cypriano et al. (2004) found that for $T_{\rm X} \ga 8$ keV, the gas is hotter than expected by pure gravitational effects. This supports the presence of off-equilibrium physical processes (unrelaxed clusters, merging).

The low redshift component of Cl-14 (Cl-14a) has been used for Fig. 11 although it should be considered with caution. Both lensing and X-ray properties of this cluster may be contaminated by projection effects: Cl-14b seems to dominate the lensing signal whereas the nearby Cl-14a dominates the X-rays signal.

  
6 Discussion and conclusion

In this work we attempted to analyse the weak lensing signal in the 4 deg2 images of the CFHTLS Deep fields. For a proper signal extraction we payed special attention to the removal of residual systematics and got a large sample of distant lensed sources, thanks to the exceptional depth of the images. We then used standard KS93 inversion technique to infer the projected surface mass density (i.e. the convergence field) and focused on maxima peaks with a signal-to-noise ratio $\nu >3.5$. We found 14 such peaks and discussed the possibility to use the statistics of maxima peaks as a test for the non-Gaussianity of the convergence field. The lack of massive clusters is not surprising since the Deep field of view is only 4 deg2 and the 4 MegaCam fields were selected a priori as free from already known rich clusters. It turns out that half of the $\nu >3.5$ convergence peaks (either with or without an optical counterpart) are in D1 and at redshift $z\sim0.28$, i.e. in the redshift range with best lensing efficiency. How much of this excess is due to the 10% lower noise level in D1 relative to D2, D3, D4 or is pure sample variance (enhanced by the strong spatial clustering of galaxy clusters)? The latter is our favoured explanation since a 10% change in SNR for D1 peaks would not significantly change the ranking of peaks in Table 2. At $z\sim0.28$, $1\deg$ scale corresponds to 15  h70-1 Mpc and the cosmic variance of the cluster-cluster correlation function is still high.

Looking for excesses of galaxies around convergence peaks we found that $\sim $35% of our $\nu >3.5$ candidates turn out to be false or inconclusive detections. Our cluster candidates are not very massive systems but look more like small clusters/large groups having $400\la\sigma_v \la 600 ~ {\rm km~ s}^{-1}$. Most of them lie at redshift $\sim $0.3 although we found a clear detection at z=0.74. All the D1 XMM-LSS clusters that lie in the lensing relevant redshift range $0.1\la z \la 0.6$ are detected with a SNR $\nu \ga 3.4$. The completeness of WLCSs is however lower than X-ray techniques for clusters detections. If one aims at reducing the amount of false detections (higher efficiency), the sample completeness of WLCSs turns out to be very low. This has already been pointed out in simulations (e.g.  White et al. 2002; Hennawi & Spergel 2005; Hamana et al. 2004).

Projections effects were observed in at least one of our detections (Cl-14). The other systems turn out to have lensing-inferred mass (or velocity dispersion) properties consistent with their optical ( $M/L_r\sim170~h_{\rm 70}~(M/L)_\odot$) and X-rays ( $\sigma_v^2\propto T_{\rm lens}\simeq T_{\rm X}$) counterparts.

We used lens tomography around $\kappa $-peaks to estimate the deflector redshift as well as its velocity dispersion. To this end we made an extensive use of photometric redshifts in the sample of background sources. With accurate photometric redshifts, tomography can improve weak lensing cluster surveys capabilities since it helps distinguishing real clusters and noise fluctuations. The agreement between tomographic redshifts and photometric redshifts of cluster members is remarquable for the most significant peaks.

Although the field area of the CFHTLS Deep survey is not wide enough for cosmological application, we have demonstrated that CFHTLS image quality is well suited for WLCSs as it is the case for cosmic shear signal extraction (Semboloni et al. 2006). The full implementation of this technique to the CFHTLS Wide survey is on-going and will provide us with a few hundred shear-selected clusters. The large sky coverage will balance the lower density of background sources as compared to the Deep fields and will clearly favour the detection of higher mass systems with velocity dispersion in the range $700{-}1200~ {\rm km~ s}^{-1}$. Given our findings for the Deep fields, we can forecast that a detection threshold as high as $\nu \ga 4.5$ will be required for a robust WLCS in the shallower Wide survey. This will be done at the expense of finding intermediate mass structures with $\sigma_v \sim 400{-}700 ~ {\rm km~ s}^{-1}$.

In addition half of this survey (the W1 region) will also be covered by the XMM-LSS survey. This will give the necessary calibration of scaling relations between mass and direct observables for clusters of galaxies to be used as efficient cosmological probes. A more detailed comparison with the performances of ongoing other clusters survey techniques (optical, SZ with Planck) will also become possible. The low completeness of WLCSs is balanced by their well controlled selection function since one needs cosmological simulations with relatively low resolution and essentially no gas physics.

The opposite approach is also possible. We mentioned in Sect. 4.2 that it would be more interesting to use the statistics of $\kappa $-peaks as a test of the non Gaussianity of the convergence field. This contains complementary information on cosmological parameters relative to the cosmic shear 2-point correlation function. Like e.g. the skewness it helps breaking the observed degeneracy between $\Omega_{\rm m}$ and $\sigma_8$ with shear correlation functions. In this respect it is not necessary to check whether individual peaks are real or false detections nor to assign a redshift and mass with expensive follow-up for each convergence peak.

Both WLCSs (with cluster identifications) and raw $\kappa $-peaks statistics are complementary applications of weak gravitational lensing. They both will soon provide new insightful constraints on the evolution of large-scale structure driven by Dark Matter and perhaps giving important clues on the behaviour of Dark Energy as a function of redshift.

Acknowledgements
We are thankful to R. Pelló and F. Ienna for making photometric redshifts available and for useful comments on their handling. The comments of the anonymous referee greatly helped improving the quality of this work. We acknowledge fruitful discussions with C. Benoist, A. Blanchard, C. Marmo, Y. Mellier and L. Olsen. R.G. is supported at LATT by a postdoctoral contract #1019 from the CNRS. We thank the Programme National de Cosmologie of the CNRS for financial support.

References

 
Copyright ESO 2007