A&A 462, 495-506 (2007)
DOI: 10.1051/0004-6361:20065468
Relations between Interstellar medium tracers in galaxies
G. Galletta1 - V. Casasola1,3 - L. Piovan1,4 - E. Merlin1 - D. Bettoni2
1 - Dipartimento di Astronomia, Università di Padova, Vicolo
dell'Osservatorio 2, 35122 Padova, Italy
2 - INAF - Osservatorio Astronomico di Padova, Vicolo dell
'Osservatorio 5, 35122 Padova, Italy
3 -
Observatoire de Paris-LERMA, 61 Av. de l'Observatoire, 75014 Paris, France
4 -
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, Garching bei München,
Germany
Received 20 April 2006 / Accepted 20 September 2006
Abstract
Aims. We study the relations existing between fluxes emitted at the CO(1-0) line, 60 and 100 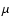 m wavelengths, and the B and soft X-ray wavebands for galaxies of all morphological types. The large set of data that we created allowed us to revisit some of the already known relations between the different tracers of the interstellar medium (ISM): the link between the FIR flux and the CO line emission, the relation between X-ray emission in non-active galaxies and the blue or FIR luminosity.
m wavelengths, and the B and soft X-ray wavebands for galaxies of all morphological types. The large set of data that we created allowed us to revisit some of the already known relations between the different tracers of the interstellar medium (ISM): the link between the FIR flux and the CO line emission, the relation between X-ray emission in non-active galaxies and the blue or FIR luminosity.
Methods. Using both catalogues of galaxies and works in the literature, we collected fluxes in the FIR, 21 cm, and CO(1-0) lines and in the soft X-ray for two samples, consisting of normal and interacting galaxies, respectively. By joining these samples, we have data for a total of 2953 galaxies, not all observed in these four wavebands.
Results. All the relations found are discussed in the frame of the star formation activity that is the link for most of them. We note that when an active star formation is present, it may link the galaxy fluxes at almost all wavelengths, from X to microwaves. In contrast, in early-type galaxies where the current star formation rate has faded, the X-FIR fluxes link disappears. This result for early-type galaxies is discussed and explained in detail in the frame of a suitable theoretical model, obtained by coupling chemo-dynamical N-body simulations with a dusty spectrophotometric code of population synthesis.
Key words: galaxies: ISM - galaxies: fundamental parameters -
infrared: ISM - radio lines: ISM - X-rays: ISM
The observations of galaxies at various wavelengths, going from
radio to X-ray, allow the study of the relationships between
the various phases of the interstellar gas and between gas, dust,
and stars. Some of these relations have already been known for many
years, such as the one between CO and far-infrared (FIR)
luminosities (Sanders & Mirabel 1985; Solomon & Sage 1988; Sanders et al. 1986; Devereux & Young 1991). Others,
connected with X-ray emission, have been studied more recently
(Ranalli et al. 2003; Griffiths & Padovani 1990; David et al. 1992).
![\begin{figure}
\par\includegraphics[width=15cm,clip]{5468fig1.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg13.gif) |
Figure 1:
The relation between the flux from the CO(1-0) line and
at 100 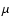 m, plotted as a full line, with the representative
points of the single galaxies plotted with different symbols. The
crosses at the upper left of the figures represent the mean errors
for the fluxes in the whole sample. For comparison, the relation
found by Bregman et al. (1992) for a sample of early-type galaxies is
shown as a dotted line. The early-type galaxies and early spirals
from E to Sb are plotted in the left panel, while the late spirals
are plotted in the right panel. m, plotted as a full line, with the representative
points of the single galaxies plotted with different symbols. The
crosses at the upper left of the figures represent the mean errors
for the fluxes in the whole sample. For comparison, the relation
found by Bregman et al. (1992) for a sample of early-type galaxies is
shown as a dotted line. The early-type galaxies and early spirals
from E to Sb are plotted in the left panel, while the late spirals
are plotted in the right panel. |
| Open with DEXTER |
At present, different tracers of the gas are known, such as
millimetric lines for the cold molecular gas, the 21 cm line for
atomic hydrogen at 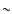 100 K, IR bands for molecules at thousands
of degrees, UV lines, and X-ray emission for hotter gas. The dust
distribution is also traced by FIR emission at 60 and 100
100 K, IR bands for molecules at thousands
of degrees, UV lines, and X-ray emission for hotter gas. The dust
distribution is also traced by FIR emission at 60 and 100 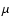 m, if
the grains are warm (Bregman et al. 1992), or at 170
m, if
the grains are warm (Bregman et al. 1992), or at 170 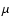 m, if they are
colder (Popescu et al. 2002). The diffusion of large archives of
observations at the above wavelengths (except for molecular lines) has
allowed the compilation of catalogues in the past years containing
a huge number of galaxies. Using these catalogues and the works
presented in the literature, we collected fluxes in FIR, 21 cm,
CO(0-1) line, and soft X-ray for two broad samples of normal
(Bettoni et al. 2003a) and interacting (Casasola et al. 2004a) galaxies. By joining
these samples, we have amassed data for a total of 2953 galaxies,
not all observed in these four wavebands. The fluxes measured
with the different tracers now allow a study of the
link between dust, gas, and stars based on hundreds of
galaxies.
m, if they are
colder (Popescu et al. 2002). The diffusion of large archives of
observations at the above wavelengths (except for molecular lines) has
allowed the compilation of catalogues in the past years containing
a huge number of galaxies. Using these catalogues and the works
presented in the literature, we collected fluxes in FIR, 21 cm,
CO(0-1) line, and soft X-ray for two broad samples of normal
(Bettoni et al. 2003a) and interacting (Casasola et al. 2004a) galaxies. By joining
these samples, we have amassed data for a total of 2953 galaxies,
not all observed in these four wavebands. The fluxes measured
with the different tracers now allow a study of the
link between dust, gas, and stars based on hundreds of
galaxies.
It is known that the fluxes emitted by a galaxy at very different
wavelengths may be linked by means of the star formation
mechanism (see Ranalli et al. 2003; David et al. 1992).
For instance, the formation of massive stars generates
heating of the dust clouds they are embedded in, by absorption
of their UV radiation, and produces a re-emission of this energy in
the FIR. This process links the current star formation rate
to the IR emission at 60 and 100 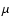 m (Thronson & Telesco 1986). The
ionizing radiation of stars may also produce evaporation of the
molecular clouds. Inside these clouds, where the particle density is
high enough to produce a significant number of collisions between H2 and CO molecules, these are excited and produce
photons, but in optically thick regions. The warming by the UV
stellar light makes these regions less dense, thereby making visible the CO lines at their edge. Because of this mechanism, these lines are
considered tracers of the cold molecular hydrogen that does not emit
observable lines. The newly formed stars are also responsible for the
X-ray emission produced by very massive stars, by core-collapse SN,
and by high-mass X-ray binaries. According to the mechanisms
described above, we expect that galaxies with active star formation will
have a FIR emission, but also CO and X-ray emissions induced by the
more massive stars, linked by different kinds of relations.
m (Thronson & Telesco 1986). The
ionizing radiation of stars may also produce evaporation of the
molecular clouds. Inside these clouds, where the particle density is
high enough to produce a significant number of collisions between H2 and CO molecules, these are excited and produce
photons, but in optically thick regions. The warming by the UV
stellar light makes these regions less dense, thereby making visible the CO lines at their edge. Because of this mechanism, these lines are
considered tracers of the cold molecular hydrogen that does not emit
observable lines. The newly formed stars are also responsible for the
X-ray emission produced by very massive stars, by core-collapse SN,
and by high-mass X-ray binaries. According to the mechanisms
described above, we expect that galaxies with active star formation will
have a FIR emission, but also CO and X-ray emissions induced by the
more massive stars, linked by different kinds of relations.
When the star formation decreases or vanishes, the FIR emission decreases
as well, but it may be fed by the stellar light absorbed and re-emitted
in the infrared by dust (cirrus), while low-mass X-ray binaries and type I SN
contribute to the high energy galaxy spectrum. In addition, AGB stars,
surrounded by dust, and the cooling flows of the interstellar medium
ejected by supernovae may together produce additional IR and X emission.
To study the activity of the galaxies at different wavebands, we
collected data on galaxies starting from the original data on fluxes
in the 60, 100 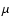 m, CO(1-0) lines, and in the soft X-ray used to compile
our catalogues (Bettoni et al. 2003b; Casasola et al. 2004b). The merging of these two
catalogues produces 1764 known values of
FIR fluxes (1837 have 100
m, CO(1-0) lines, and in the soft X-ray used to compile
our catalogues (Bettoni et al. 2003b; Casasola et al. 2004b). The merging of these two
catalogues produces 1764 known values of
FIR fluxes (1837 have 100 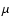 m flux), 391 soft X-ray fluxes, and 434 values for the CO(1-0) line luminosity. We extracted the values of the distance moduli,
blue absolute magnitudes, and morphological classification for all of them
from the LEDA catalogue (Paturel et al. 1997).
m flux), 391 soft X-ray fluxes, and 434 values for the CO(1-0) line luminosity. We extracted the values of the distance moduli,
blue absolute magnitudes, and morphological classification for all of them
from the LEDA catalogue (Paturel et al. 1997).
These are 1038 galaxies with evident signs of interactions or disturbed morphologies according
to the catalogues of Arp (1966), Arp & Madore (1987), and Vorontsov-Velyaminov (1959). We shall refer to them as "perturbed
galaxies''. The remaining 1915 galaxies that appear neither morphologically
nor dynamically perturbed are called "normal galaxies''.
In our sample, we have 253 galaxies that have a spectral classification for the
nucleus, and 231 of these appear to host an AGN (Seyfert 1, 2 or transition type,
Seyfert 3 or Liners) according to the classifications of Ho et al. (1997) and
Véron-Cetty & Véron (2003). Most of the remaining 2722 galaxies lack information
about nuclear spectrum or have spectra of HII regions (22 starburst spectra).
They are not included in any AGN catalogue and, for this reason, we refer to them
in the following discussion as "non active galaxies'' and to the others as "active
galaxies''. With all these data, we crossed the various tracers to understand
and revisit the main relations existing between X, FIR, CO, and B luminosities.
![\begin{figure}
\par\includegraphics[width=15.4cm,clip]{5468fig2.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg15.gif) |
Figure 2:
Left: the X-ray luminosity plotted vs. blue luminosity, in
solar units, for late-type, non-active galaxies. The relation corresponding
to emission caused by discrete sources, indicated in Eq. (4)
is plotted as a dotted line.
Right: X-ray luminosity vs. FIR luminosity, in solar units
for the late-type, non-active galaxies. The linear relation indicated in Eq. (7) is plotted as a dashed line. |
| Open with DEXTER |
The relations existing between different cold components of the ISM, such as
the molecular gas and the dust, have been studied for many years
(Sanders & Mirabel 1985; Solomon & Sage 1988; Bregman et al. 1992). They find that the global galaxy luminosity
derived from CO(1-0) line is directly related with the flux at 100 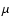 m.
With our large sample we tested these relations using galaxies
of different morphological types and activity or interaction.
m.
With our large sample we tested these relations using galaxies
of different morphological types and activity or interaction.
In Fig. 1 we plotted the logarithm of the flux measured from CO(1-0)
line vs. the logarithm of the IRAS flux at 100 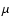 m. In our plots, we have
193 galaxies with classification from E to Sb and 178 from Sbc to Sm. The
relation found by Bregman et al. (1992) for a sample of early-type galaxies,
m. In our plots, we have
193 galaxies with classification from E to Sb and 178 from Sbc to Sm. The
relation found by Bregman et al. (1992) for a sample of early-type galaxies,
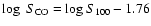 ,
is also
plotted as comparison.
,
is also
plotted as comparison.
The relations are evident with this wider sample of galaxies.
In these diagrams, active and non-active galaxies appear mixed together
without clear differences and have been plotted together. The same behaviour
appears for interacting and non interacting galaxies, which are not distinguished
in our plots.
For all the galaxy types, we find:
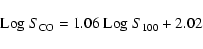 |
(1) |
with a correlation coefficient of 0.74 and an r.m.s. of 0.37. In the above
formula, S100 is in mJy and
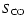 is in Jy km s-1.
Similar relations exist between the CO fluxes and the FIR magnitudes, defined as:
is in Jy km s-1.
Similar relations exist between the CO fluxes and the FIR magnitudes, defined as:
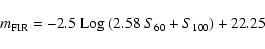 |
(2) |
where S60 and S100 the fluxes at 60 and 100 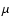 m respectively,
are in mJy. We find for all the galaxy types
m respectively,
are in mJy. We find for all the galaxy types
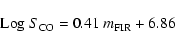 |
(3) |
with a correlation coefficient of 0.69 and rms of 0.40.
The results are based on 179 early types and 170 late-type galaxies.
These relations are not plotted in this paper due to their similarity
with Fig. 1.
We note that irregular galaxies are not fitted by these relations but
are widespread. In our sample there are just 10 galaxies and their
representative points have not been plotted in Fig. 1.
We are interested in understanding what relations exist between  ,
the X-ray
luminosity, and the other global galaxy properties. From the literature, it is
known that a proportionality exists between
,
the X-ray
luminosity, and the other global galaxy properties. From the literature, it is
known that a proportionality exists between  produced by
discrete sources and LB, the blue luminosity of the whole galaxy.
This relation has been studied by Ciotti et al. (1991) and compared by Beuing et al. (1999)
with soft X-ray fluxes measured by the ROSAT satellite. It appears that late-type
galaxies have a global X-ray luminosity directly proportional to LB, while
early-type systems are dominated by emission produced by hot diffuse gas, and
their
produced by
discrete sources and LB, the blue luminosity of the whole galaxy.
This relation has been studied by Ciotti et al. (1991) and compared by Beuing et al. (1999)
with soft X-ray fluxes measured by the ROSAT satellite. It appears that late-type
galaxies have a global X-ray luminosity directly proportional to LB, while
early-type systems are dominated by emission produced by hot diffuse gas, and
their  is proportional to the square power of the blue luminosity, as
discussed by Beuing et al. (1999). For this reason, the early and late-type
galaxies are discussed separately.
is proportional to the square power of the blue luminosity, as
discussed by Beuing et al. (1999). For this reason, the early and late-type
galaxies are discussed separately.
With our data, the X-ray luminosity of galaxies with a morphological type later
than Sb can be fitted by a linear relation as a function of
LB (in Fig. 2, left panel). The direct proportionality is expressed by the
equation:
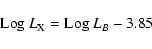 |
(4) |
with an rms from observed data of
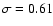 based on 63 galaxies. In this
formula and in the following, all the luminosities are expressed in solar units.
based on 63 galaxies. In this
formula and in the following, all the luminosities are expressed in solar units.
If, instead of the blue luminosity, we use the galaxy area
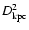 ,
calculated
from the apparent diameter measured at the 25 mag arcsec2 isophote and
converted in kpc2, we
discover that the relation is still present, but with a wider spread. It becomes
,
calculated
from the apparent diameter measured at the 25 mag arcsec2 isophote and
converted in kpc2, we
discover that the relation is still present, but with a wider spread. It becomes
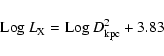 |
(5) |
(
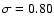 )
for a sample of 64 galaxies.
)
for a sample of 64 galaxies.
A relation similar to that of Ciotti et al. (1991) has been found by some authors
(Ranalli et al. 2003; Griffiths & Padovani 1990; David et al. 1992), but using 60 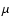 m fluxes or FIR
luminosities. The values of
m fluxes or FIR
luminosities. The values of
 are calculated using the formula
are calculated using the formula
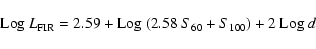 |
(6) |
where
 is in solar luminosities, fluxes are in mJy, and the galaxy
distance d is in Mpc.
is in solar luminosities, fluxes are in mJy, and the galaxy
distance d is in Mpc.
From our data it is possible to find a relation between  and
and
 that fits the values of late-type galaxies. We found
that fits the values of late-type galaxies. We found
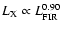 ,
similar to the
,
similar to the
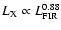 found by
Ranalli et al. (2003) for fluxes between 0.5 and 2 keV and to the
found by
Ranalli et al. (2003) for fluxes between 0.5 and 2 keV and to the
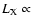
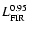 found by David et al. (1992) using fluxes between 0.5
and 4.5 keV. Forcing the relation to a linear proportionality between
found by David et al. (1992) using fluxes between 0.5
and 4.5 keV. Forcing the relation to a linear proportionality between
 and
and
 we find:
we find:
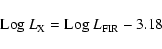 |
(7) |
with a 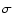 of 0.47, based on 147 galaxies.
This relation is plotted in the right panels of Figs. 2 to 4.
of 0.47, based on 147 galaxies.
This relation is plotted in the right panels of Figs. 2 to 4.
![\begin{figure}
\par\includegraphics[width=15.4cm,clip]{5468fig3.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg33.gif) |
Figure 3:
Left: the X-ray luminosity plotted vs. blue luminosity,
for early-type, non-active galaxies. The relation corresponding to emission
caused by diffuse gas, valid for early-type galaxies and indicated in Eq.
(10) is plotted as a full line.
Right: X-ray luminosity vs. FIR luminosity for the early-type galaxies.
The linear relation for late-type, non-active galaxies indicated in Eq. (7)
is plotted as a dashed line. |
| Open with DEXTER |
We note that the B and FIR luminosities are also connected in late-type
galaxies by means of a linear relation fitted by:
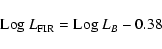 |
(8) |
with rms = 0.5. This equation, inserted into the relation (4)
gives
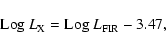 |
(9) |
similar to the result of Eq. (7) and to that found by
Ranalli et al. (2003). This is an independent way to confirm our results
and to verify the existence of a global link between
 ,
B light, and X-ray emission. The connection between B luminosity
or galaxy area and X or FIR luminosities will be discussed in
Sect. 5.
,
B light, and X-ray emission. The connection between B luminosity
or galaxy area and X or FIR luminosities will be discussed in
Sect. 5.
![\begin{figure}
\par\includegraphics[width=15.4cm,clip]{5468fig4.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg36.gif) |
Figure 4:
Left: the X-ray luminosity plotted vs. blue luminosity
for active galaxies, separated according to the type of activity. The relation corresponding to
emission caused by diffuse gas, valid for early-type galaxies and indicated in Eq.
(10) is plotted as a full line. Right: X-ray luminosity vs. FIR luminosity
for the active galaxies. The linear relation for late-type galaxies indicated in Eq. (7) is plotted as a dashed line. |
| Open with DEXTER |
When the early-type galaxies are considered in the relations
involving X-ray emission, the correlations become less evident. Considering
soft X-ray and B luminosities, we find a relation
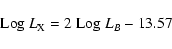 |
(10) |
(
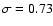 )
based on 224 galaxies and plotted in the left panel
of Fig. 3.
The above formula agrees with the expected relation for X-ray
emission coming from hot diffuse gas, as discussed by Beuing et al. (1999).
)
based on 224 galaxies and plotted in the left panel
of Fig. 3.
The above formula agrees with the expected relation for X-ray
emission coming from hot diffuse gas, as discussed by Beuing et al. (1999).
The relation still holds if
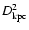 (kpc2) is used. It becomes
(kpc2) is used. It becomes
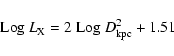 |
(11) |
(
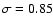 )
for 226 early-type galaxies from E to Sb.
)
for 226 early-type galaxies from E to Sb.
Many galaxies with high blue luminosity, indication of high masses and of a
recent star formation, lie quite far from the mean line, with different behaviour
than late-type galaxies.
If the X-ray fluxes are compared with FIR luminosity, the disagreement with
the behaviour found in late-type galaxies is more evident. The plot  vs.
vs.
 for early-type galaxies shows the representative points of the
galaxies above the relation (7) for late-type galaxies
(Fig. 3, right panel). To understand this apparent disagreement, we
should use a theoretical analysis of the FIR emission, as explained
in Sect. 4.
for early-type galaxies shows the representative points of the
galaxies above the relation (7) for late-type galaxies
(Fig. 3, right panel). To understand this apparent disagreement, we
should use a theoretical analysis of the FIR emission, as explained
in Sect. 4.
Active galaxies (Seyfert 1, Seyfert 2, and Liners) have X-ray, B, and FIR fluxes
that are not linked. This happens because, to the emission mechanisms
stimulating the light emission at the different wavebands described for non
active galaxies, an X-ray emission comes from nucleus. In fact, the points
representative of these active galaxies are spread in the plot over the discrete
source line and around the diffuse gas line (see Fig. 4, left side).
In the  -
-
 diagram (Fig. 4, right side) the spread is similar
to that of early-type galaxies plotted in Fig. 3, but we separately plotted
the active galaxies because of the particular nature of their X-ray emission,
due to the nuclear contribution.
diagram (Fig. 4, right side) the spread is similar
to that of early-type galaxies plotted in Fig. 3, but we separately plotted
the active galaxies because of the particular nature of their X-ray emission,
due to the nuclear contribution.
4 Modelling
 ,
L
,
L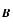 ,
and
L
,
and
L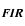 of early-type galaxies
of early-type galaxies
To cast light on the nature of the relations observed
between  ,
LB, and
,
LB, and
 for early-type
galaxies, one has to consider the various
components of a galaxy (stars, gas, and dust) and to understand
their mutual interactions as far as the spectral energy
distribution (SED) is concerned. There are two basic schemes for
modelling the formation and evolution of early type galaxies: (1) the
semi-analytical models on which a great deal of our understanding of
the chemo-spectro-photometric properties is derived; and (2) the
N-Body Tree-SPH simulations that, in contrast, have been used only
occasionally to study spectro-photometric properties of
early type galaxies. In the following part of this section
we proceed as follows. First, we analyse the drawbacks of
semi-analytical models, in particular dealing with the calculation
of the infrared emission of early-type galaxies. Second, we discuss
how dynamical simulations and a dusty
spectrophotometric code, when mixed together, allow us to move forward
a step in the calculations of the SEDs properties. Third, we show
in detail how our model has been built and the coupling between
dynamics and dusty population synthesis was done.
for early-type
galaxies, one has to consider the various
components of a galaxy (stars, gas, and dust) and to understand
their mutual interactions as far as the spectral energy
distribution (SED) is concerned. There are two basic schemes for
modelling the formation and evolution of early type galaxies: (1) the
semi-analytical models on which a great deal of our understanding of
the chemo-spectro-photometric properties is derived; and (2) the
N-Body Tree-SPH simulations that, in contrast, have been used only
occasionally to study spectro-photometric properties of
early type galaxies. In the following part of this section
we proceed as follows. First, we analyse the drawbacks of
semi-analytical models, in particular dealing with the calculation
of the infrared emission of early-type galaxies. Second, we discuss
how dynamical simulations and a dusty
spectrophotometric code, when mixed together, allow us to move forward
a step in the calculations of the SEDs properties. Third, we show
in detail how our model has been built and the coupling between
dynamics and dusty population synthesis was done.
The semi-analytical models approximate a galaxy to a point-mass
system in which gas is turned into stars by means of suitable
recipes for star formation, and heavy elements are produced by
stellar nucleosynthesis and stellar winds/explosions. The
standard evolutionary population synthesis technique (EPS) is
usually applied to derive the SED of the galaxy, with models
able to explain many global features of early type galaxies,
as amply described by many authors (Arimoto & Yoshii 1989; Gibson 1997; Tantalo et al. 1998; Bressan et al. 1994; Tantalo et al. 1996; Arimoto & Yoshii 1987). There are three important and
problematic issues of these models to be discussed for our purposes.
First, to determine the age at which the galactic wind
sets (Larson 1974; Larson & Dinersten 1975), we need some hypothesis about dark
and baryonic matter with their relative distributions and about the
heating and cooling efficiency of the various mechanisms to
properly evaluate the total gravitational potential well and to
describe the thermal history of the gas. In this scheme it turns
out that the galactic wind occurs typically for ages
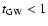 Gyr,
later in a massive early-type galaxy and much earlier in galaxies of lower mass
(Arimoto & Yoshii 1989; Gibson 1997; Tantalo et al. 1998,1996; Bressan et al. 1994; Arimoto & Yoshii 1987; Chiosi et al. 1998).
The maximum duration of star-forming activity therefore follows
the trend
Gyr,
later in a massive early-type galaxy and much earlier in galaxies of lower mass
(Arimoto & Yoshii 1989; Gibson 1997; Tantalo et al. 1998,1996; Bressan et al. 1994; Arimoto & Yoshii 1987; Chiosi et al. 1998).
The maximum duration of star-forming activity therefore follows
the trend
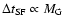 in these models.
This trend of the SFH is, however, contrary to what is required by the
observed trend forward the
in these models.
This trend of the SFH is, however, contrary to what is required by the
observed trend forward the 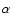 -enhancement for early type galaxies,
which implies that the maximum duration of the star forming activity
should decrease when the galaxy mass increases
-enhancement for early type galaxies,
which implies that the maximum duration of the star forming activity
should decrease when the galaxy mass increases
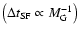 (see Tantalo & Chiosi 2004; Kuntschner 2000; Trager et al. 2000b; Thomas et al. 2005; Bressan et al. 1996; Trager et al. 2000a, for more details on the
enhancement in
(see Tantalo & Chiosi 2004; Kuntschner 2000; Trager et al. 2000b; Thomas et al. 2005; Bressan et al. 1996; Trager et al. 2000a, for more details on the
enhancement in 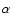 -elements and the SFH of early-type
galaxies).
-elements and the SFH of early-type
galaxies).
Second, after the galactic wind phase, star formation no longer
occurs and the evolution is merely passive. However, AGB and RGB
stars continue to lose gas in amounts that are comparable
to those before the galactic wind (Chiosi 2000). What is
the fate of this gas? One may imagine that the large amount of gas
lost by stars will expand into the dark matter halo and heat up to
an energy and overwhelm the gravitational potential, and will escape
the galaxy. Most likely a sort of dynamical equilibrium is reached
in which gas is continuously ejected by stars and lost by the
galaxy. It may happen therefore that some amount of gas is always
present in the galaxy. The question is not obvious because, if an
early type galaxy is free of gas and contains only stars, the SED is
expected to drop off long ward of about
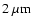 ,
and no IR emission
should be detected. However, as already pointed out long ago
by Guhathakurta et al. (1986) and Knapp et al. (1989) (see also Fig. 3), many
early-type galaxies of the local universe emit in the IR. The origin
of this flux in the MIR/FIR is most likely due to the dust present
in a diffuse ISM that, once emits at those wavelengths
heated up by the galactic radiation field.
Therefore to match the IR emission, one
has to allow for some amount of diffuse ISM. An interesting
question is therefore how much gas can be present today in
an elliptical galaxy and how it is distributed across the galaxy.
Even if we can correctly estimate the amount of gas ejected by
stars, the fate of this gas goes beyond the possibilities of
classical semi-analytical models.
,
and no IR emission
should be detected. However, as already pointed out long ago
by Guhathakurta et al. (1986) and Knapp et al. (1989) (see also Fig. 3), many
early-type galaxies of the local universe emit in the IR. The origin
of this flux in the MIR/FIR is most likely due to the dust present
in a diffuse ISM that, once emits at those wavelengths
heated up by the galactic radiation field.
Therefore to match the IR emission, one
has to allow for some amount of diffuse ISM. An interesting
question is therefore how much gas can be present today in
an elliptical galaxy and how it is distributed across the galaxy.
Even if we can correctly estimate the amount of gas ejected by
stars, the fate of this gas goes beyond the possibilities of
classical semi-analytical models.
As a third point, note that, when we fold many
SSPs to calculate a galaxy SED using the classical EPS technique, we
simply convolve their fluxes with the SFH of the galaxy. Many
classical spectrophotometric semi-analytical models of galaxies are
built in this way: there is no dust at the level of SSPs and again
no dust at the level of the galaxy model (see
e.g. Buzzoni 2002; Tantalo et al. 1998; Arimoto & Tarrab 1990; Kodama & Arimoto 1997; Tantalo et al. 1996; Arimoto & Yoshii 1987; Buzzoni 2005; Bruzual & Charlot 1993).
To calculate the emission by dust, a higher level
of sophistication is required for the model. Indeed, one has to
develop a model in which the sources of radiation and the
emitting/absorbing medium are distributed, so as to face and solve the
problem of the radiative transfer simulating the
interactions in a realistic way among the various physical components of a galaxy.
Among recent models of this kind are those by
Silva et al. (1998), Devriendt et al. (1999), and Takagi et al. (2003).
Two drawbacks of the semi-analytical models therefore concern (1)
the description of galactic wind, which is supposed
to occur within a finite time interval; and (2) the star formation
history that is reversed, allowing longer SFH for more massive
galaxies. These two problems, combined with a lack of geometrical
information about the distribution of gas and dust, make
semi-analytical models unsuitable properly for calculating the IR
emission of early type galaxies. To improve upon them we need to use
the results from dynamical simulations. They have been shown to
be able to properly model the ejection of gas by the galaxy as a
sort of continuous process, taking place whenever a gas particle
heated up by various mechanism has acquired a higher velocity than
the escape velocity (see
e.g. Springel 2001; Chiosi & Carraro 2002; Carraro et al. 1998; Kawata 2001). They are able to
reproduce the SF history of early-type galaxies both in the context
of the monolithic collapse scenario (Chiosi & Carraro 2002; Kawata 2001) and
recently in the context of hierarchical scenario (De Lucia et al. 2006).
Finally, the galaxy is no longer a mass point, but a fully
three-dimensional structure of the galaxy is available with spatial
distribution of stars and gas.
With the aid of N-Body Tree-SPH
simulations based on quasi-cosmological initial conditions in the
standard-cold dark matter scenario (S-CDM), Merlin & Chiosi (2006) modelled the formation
and evolution of two early-type galaxies of different total mass
(dark + baryonic matter in the cosmological proportions 9:1). The
total masses under considerations are
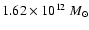 (Model A) and
(Model A) and
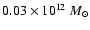 (Model B). The galaxies
have been followed from their separation from the global expansion
of the universe to their collapse to virialized structures, the
formation of stars, and subsequent nearly passive evolution. They are
followed for a long period of time, i.e. 13 Gyr (Model A) and 5 Gyr
(Model B), or at least well beyond the stages of active star
formation that occurs within the first 3 to 4 Gyr (see below). The
models take into account radiative cooling by several processes,
heating by energy feed back from supernova explosions (both types I
and II), and chemical enrichment. All the models conform to the
so-called revised monolithic scheme, because mergers of
substructures have occurred very early in the life of the galaxy. Some
parameters and results of the two models are summarised in Table 1. Note that the shape of the resulting galaxies is
nearly spherical both in dark matter and stars.
(Model B). The galaxies
have been followed from their separation from the global expansion
of the universe to their collapse to virialized structures, the
formation of stars, and subsequent nearly passive evolution. They are
followed for a long period of time, i.e. 13 Gyr (Model A) and 5 Gyr
(Model B), or at least well beyond the stages of active star
formation that occurs within the first 3 to 4 Gyr (see below). The
models take into account radiative cooling by several processes,
heating by energy feed back from supernova explosions (both types I
and II), and chemical enrichment. All the models conform to the
so-called revised monolithic scheme, because mergers of
substructures have occurred very early in the life of the galaxy. Some
parameters and results of the two models are summarised in Table 1. Note that the shape of the resulting galaxies is
nearly spherical both in dark matter and stars.
Table 1:
Initial parameters for the dynamical simulations of
Merlin & Chiosi (2006) in the Standard CMD scenario, where masses are in units
of
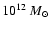 ,
radii are in kpc, and ages are in Gyr.
,
radii are in kpc, and ages are in Gyr.
The third drawback of the classical semi-analytical model was the lack
of a description of the dusty component, which for our purposes
needs to be included. The semi-analytical chemo-spectro-photometric
model developed by Piovan et al. (2006b) allows us to overcome this
issue. It takes into account not only the geometrical structure of
galaxies of different morphological types, but also the effect of dust
in converting the UV and optical light in FIR radiation. In brief,
the Piovan et al. (2006b) model follows the infall scheme, allows for
the onset of galactic winds, and contains three main components: (i)
the diffuse interstellar medium composed of gas and dust whose
emission and extinction properties have been studied in detail by
Piovan et al. (2006a); (ii) the large complexes of molecular clouds in
which new stars are formed; and (iii) the stars of any age and
chemical composition. The total gas and star mass provided by the
chemical model are distributed over the whole volume by means of
suitable density profiles, one for each component and depending on
the galaxy type (spheroidal, disk, and disk plus bulge). The galaxy
is then split into suitable volume elements to each of which the
appropriate amounts of stars, molecular clouds and interstellar
medium are assigned.
Each elemental volume absorbs radiation from all other volumes
and from the interstellar medium in between. The elemental volume also
emits the absorbed light again and produces radiation by the stars that
it contains.
On the other hand, the star formation, the initial mass function, and the
chemical enrichment of the Piovan et al. (2006b) model are very similar to those
by Bressan et al. (1994), Tantalo et al. (1996),
Tantalo et al. (1998), and Portinari et al. (1998).
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{5468fig5.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg56.gif) |
Figure 5:
Top panel: the masses of stars (continuous line) and
gas (dashed line) for the dynamical model of
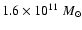 baryonic mass as a function of the number of virial radii.
The virial radius for this model is about 300 kpc. Bottom
panel: the same as the upper panel, but for the dynamical model of
baryonic mass
baryonic mass as a function of the number of virial radii.
The virial radius for this model is about 300 kpc. Bottom
panel: the same as the upper panel, but for the dynamical model of
baryonic mass
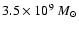 .
For this model the
virial radius is about 42 kpc. .
For this model the
virial radius is about 42 kpc. |
| Open with DEXTER |
The description of an early-type galaxy as far as predicting
its spectro-photometric infrared properties can therefore be
realised with a suitable combination of dynamical and
spectro-photometric approaches. Coupling the dynamical models with
spectro-photometric synthesis requires a number of steps that
deserve some remarks.
Figure 5 shows the
cumulative distribution of gas and stars as a function of the radial
galactocentric distance normalized to the virial radius for model A
(top panel) and model B (bottom panel). The gas is generally
distributed in the external regions of the galaxy and steeply
decreases inward. In contrast, the stars are more concentrated toward
the centre. The gradients in the spherically averaged star- and gas-
content provided by the dynamical models are the primary information
to load into the spectro-photometric code of Piovan et al. (2006b). They
allow us to infer the amount of gas contained within a given radius
or within a given aperture. We fix the total dimension of the portion of
the average model that produces the IR flux at a diameter
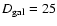 kpc, consistent with the mean galaxy size of the observed sample.
kpc, consistent with the mean galaxy size of the observed sample.
As the spectro-photometric code of Piovan et al. (2006b) suited to
describing early-type galaxies is written in spherical symmetry, we
have to derive suitable spherical distributions for the density of
stars and gas to be used into the model. The task is facilitated by
the nearly spherical shape of the dynamical models. To this aim, we
consider the sphere of radius
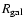 centred at the centre of
mass of the stellar component. The sphere is then divided into a
number of thin spherical shells whose derived average density of
stars and gas is shown in Fig. 6. Even if the
centre of mass of the star and gas distributions may not be exactly
coincident, this is not relevant here, so the same coordinate centre
can be used for both components.
centred at the centre of
mass of the stellar component. The sphere is then divided into a
number of thin spherical shells whose derived average density of
stars and gas is shown in Fig. 6. Even if the
centre of mass of the star and gas distributions may not be exactly
coincident, this is not relevant here, so the same coordinate centre
can be used for both components.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5468fig6.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg59.gif) |
Figure 6:
The averaged density profiles of gas and stars for the model of
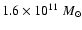 baryonic mass at the age of 13 Gyr. The
continuous lines are the best fit obtained.
baryonic mass at the age of 13 Gyr. The
continuous lines are the best fit obtained. |
| Open with DEXTER |
In order to secure a smooth behaviour at the galaxy radius
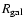 ,
the star and gas density profiles are represented by the law:
,
the star and gas density profiles are represented by the law:
![\begin{displaymath}\rho _{i}=\rho _{0i}\left[ 1+\left( \frac{r}{r_{\rm c}^{i}}\right)
^{2}\right] ^{-\gamma _{i}}
\end{displaymath}](/articles/aa/full/2007/05/aa5468-06/img60.gif) |
(12) |
where "i'' stands for "stars'' or "gas'', and
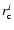 are the corresponding core radii. The above
representation is suited more to our aims than is the classical King
law. The fits are shown in Fig. 6. They
are normalized in such a way that the integral over the galaxy
volume corresponds to the amount of gas contained inside
are the corresponding core radii. The above
representation is suited more to our aims than is the classical King
law. The fits are shown in Fig. 6. They
are normalized in such a way that the integral over the galaxy
volume corresponds to the amount of gas contained inside
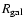 .
.
In the dynamical models, the period of
intense star formation, during which most of the star mass is built
up, is confined within the first 3 to 4 Gyr. In Model A this is
followed by a long tail of minimal stellar activity that continues
forever. If this activity was real, we would expect a background of
young stars giving rise to a significant emission in the UV-optical
region up to the present, which is not compatible with the observed
spectra of typical early-type galaxies. As already pointed out by
Merlin & Chiosi (2006) this minimal stellar activity is an artefact of the
poor mass-resolution for the baryonic component, in other words, the
low number of particles considered in the numerical simulations. To
cope with this, we simply set the star formation rate to zero when
only one or two star particles are involved. This is equivalent to
cutting the star formation rate for ages older than about 5 Gyr. The
problem does not occur with model B simply because the last computed
model is at 6 Gyr.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{5468fig7.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg62.gif) |
Figure 7:
Basic quantities of the chemical models for a prototype
early-type galaxy of
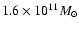 baryonic mass as a
function of the age. Top-left panel: the star formation rate
obtained from the chemo-dynamical model of
baryonic mass as a
function of the age. Top-left panel: the star formation rate
obtained from the chemo-dynamical model of
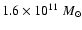 baryonic mass (SFR). Top-right panel: the evolution
of the metallicity Z. Bottom-left panel: the masses for both
the classical and the chemo-dynamical model of baryonic matter
(thick and thin dashed lines), stars (thick and thin continuous
lines), and gas (thick and thin dotted lines) are shown. The mass of gas and
stars inside 25 kpc are also shown (open circles) for the age of
13 Gyr. Bottom-right panel: the fractional masses for both
the models of stars (thick and thin continuous lines) and gas (thick
and thin dotted lines) are shown.
baryonic mass (SFR). Top-right panel: the evolution
of the metallicity Z. Bottom-left panel: the masses for both
the classical and the chemo-dynamical model of baryonic matter
(thick and thin dashed lines), stars (thick and thin continuous
lines), and gas (thick and thin dotted lines) are shown. The mass of gas and
stars inside 25 kpc are also shown (open circles) for the age of
13 Gyr. Bottom-right panel: the fractional masses for both
the models of stars (thick and thin continuous lines) and gas (thick
and thin dotted lines) are shown. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5468fig8.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg63.gif) |
Figure 8:
The same as in Fig. 7, but for the model with
total baryonic mass of
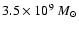 . . |
| Open with DEXTER |
To this aim we plugged the star formation history (SFH) of
dynamical models into the chemical code of Portinari et al. (1998), and
the closed-box approximation was adopted. The total
baryonic mass of the chemical models is the same as in the dynamical
ones, and equally so for the initial mass function of the stars composing
each star particle: Kroupa (1998) in our case. In Fig. 7 we show the results obtained by inserting the SFH of
Model A into a classical chemical model with total baryonic mass where
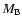 equal to
equal to
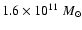 .
The top panels display
the adopted SFH (left) and the gas metallicity of the chemical
model, respectively. The bottom left panel shows the temporal
variation in the star mass
.
The top panels display
the adopted SFH (left) and the gas metallicity of the chemical
model, respectively. The bottom left panel shows the temporal
variation in the star mass
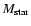 and gas mass
and gas mass
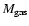 ,
whereas the bottom right panel shows the ratios
,
whereas the bottom right panel shows the ratios
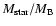 and
and
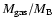 for both the dynamical and chemical
model. The agreement is very good, thus confirming the
internal consistency between the descriptions of the same object. We
also show the amount of gas at 13 Gyr contained in the whole
galaxy for both the dynamical and the classical
chemical models and the amount of gas contained
inside
for both the dynamical and chemical
model. The agreement is very good, thus confirming the
internal consistency between the descriptions of the same object. We
also show the amount of gas at 13 Gyr contained in the whole
galaxy for both the dynamical and the classical
chemical models and the amount of gas contained
inside
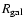 (open squares). Indeed there is little gas left
over inside the 25 kpc radius region. Similarly in Fig. 8, we show the results obtained inserting the SFH of
Model B into a classical chemical model with total baryonic mass of
(open squares). Indeed there is little gas left
over inside the 25 kpc radius region. Similarly in Fig. 8, we show the results obtained inserting the SFH of
Model B into a classical chemical model with total baryonic mass of
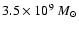 .
The only difference is that the
maximum age of the dynamical model is 5 Gyr. This cross-checking
of the models is particularly significant because: first,
it ensures that the results of the analytical models fairly
reproduce those of the dynamical simulations as far as some
important features are concerned; second, it ensures that we can
safely use the result of chemical models to prolong the evolutionary
history of Model B up to the present; third, we can safely
apply the population synthesis technique of Piovan et al. (2006b).
.
The only difference is that the
maximum age of the dynamical model is 5 Gyr. This cross-checking
of the models is particularly significant because: first,
it ensures that the results of the analytical models fairly
reproduce those of the dynamical simulations as far as some
important features are concerned; second, it ensures that we can
safely use the result of chemical models to prolong the evolutionary
history of Model B up to the present; third, we can safely
apply the population synthesis technique of Piovan et al. (2006b).
Knowing the amount of gas, we need to specify the fraction of it in the
form of dust to finally be able to derive the whole SED from X to
FIR and look for relationships between the luminosity in the X, B,
and FIR pass-bands we want to interpret. Our models, both
semi-analytical and chemo-dynamical, are not suitable to describing
the evolution of the compositions and abundances of both
gas and dust phases.
The relative proportions of the various
components of the dust would require detailed study of the
evolution of the dusty environment and complete information on
the dust yields, as in the models of Dwek (1998,2005).
This
would lead to a better and more physically sounded correlation
between the composition of dust and the star formation and chemical
enrichment history of the galaxy itself, although at the price of
increasing the complexity and the uncertainty of the problem.
The key parameter in calculating the amount of dust is the dust-to-gas
ratio, defined as
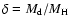 ,
where
,
where 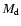 and
and 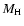 are the total dust and hydrogen mass, respectively. For the Milky
Way and the galaxies of the Local Group,
are the total dust and hydrogen mass, respectively. For the Milky
Way and the galaxies of the Local Group, 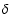 is estimated to
vary from about 1/100 to 1/500 and typical values
is estimated to
vary from about 1/100 to 1/500 and typical values
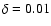 ,
,
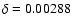 ,
and
,
and
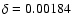 are used for the
Milky Way (MW) and the Large and Small Magellanic Clouds (LMC and
SMC). These dust-to-gas mass ratios describe a decreasing sequence,
going from the MW to the LMC and SMC. Since these galaxies also
describe a sequence of decreasing metallicity, a simple assumption
is to hypothesize
are used for the
Milky Way (MW) and the Large and Small Magellanic Clouds (LMC and
SMC). These dust-to-gas mass ratios describe a decreasing sequence,
going from the MW to the LMC and SMC. Since these galaxies also
describe a sequence of decreasing metallicity, a simple assumption
is to hypothesize
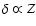 in such a way as to match the
approximate results for MW, LMC, and SMC:
in such a way as to match the
approximate results for MW, LMC, and SMC:
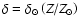 .
This relation
simply implies that the higher the metal content of a galaxy, the
higher the abundance of grains per H atom. However, the
metallicity difference not only implies a difference in the
absolute abundance of heavy elements in the dust, but also a
difference in the composition pattern as a function of the
star formation history (Dwek 1998,2005). Despite these
uncertainties (Devriendt et al. 1999), the relation
.
This relation
simply implies that the higher the metal content of a galaxy, the
higher the abundance of grains per H atom. However, the
metallicity difference not only implies a difference in the
absolute abundance of heavy elements in the dust, but also a
difference in the composition pattern as a function of the
star formation history (Dwek 1998,2005). Despite these
uncertainties (Devriendt et al. 1999), the relation
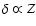 is often adopted to evaluate the amount of dust in galaxy models
(e.g. Silva et al. 1998) by simply scaling the dust content adopted
for the ISM of the MW to the metallicity under consideration.
is often adopted to evaluate the amount of dust in galaxy models
(e.g. Silva et al. 1998) by simply scaling the dust content adopted
for the ISM of the MW to the metallicity under consideration.
The
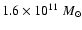 and
and
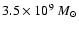 galaxy models reach an average metallicity of solar and
slightly more than twice solar, respectively. To describe them, we
adopted the description of Piovan et al. (2006b,a) where a
model of dusty ISM is built by taking different metallicities into account.
The problem, however, remained unsettled for metallicities
higher than the solar one, where relative proportions holding good
for the MW average diffuse ISM model were adopted and the
amount of dust scaled with
galaxy models reach an average metallicity of solar and
slightly more than twice solar, respectively. To describe them, we
adopted the description of Piovan et al. (2006b,a) where a
model of dusty ISM is built by taking different metallicities into account.
The problem, however, remained unsettled for metallicities
higher than the solar one, where relative proportions holding good
for the MW average diffuse ISM model were adopted and the
amount of dust scaled with
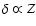 .
Therefore, for the
.
Therefore, for the
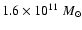 galaxy with solar metallicity, the MW
diffuse-ISM model was adopted
galaxy with solar metallicity, the MW
diffuse-ISM model was adopted
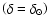 ,
while for the
,
while for the
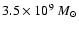 model we
followed the
model we
followed the
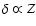 relation, using the MW average
pattern of dust composition.
relation, using the MW average
pattern of dust composition.
The connection between the results of this model and the observed
diagrams are discussed in the next section.
5 Discussion
Our data confirm and extend the previous relations between
various tracers of the ISM in galaxies of different morphological
types. In the literature the relation found by Bregman et al. (1992) between
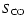 and S100 indicates a direct proportionality (slope = 1)
between the two fluxes and differs from that of Solomon & Sage (1988),
which exhibits a steeper gradient. Our relation (1)
agrees quite well with the proportionality found by Bregman et al. (1992),
the slope we found being equal to 1.06. The similarity between the
two curves in Fig. 1 is evident. As
described in the introduction, this link derives from the excitation of gas clouds by
the currently forming stars and by the warming of the dust in the galaxy.
and S100 indicates a direct proportionality (slope = 1)
between the two fluxes and differs from that of Solomon & Sage (1988),
which exhibits a steeper gradient. Our relation (1)
agrees quite well with the proportionality found by Bregman et al. (1992),
the slope we found being equal to 1.06. The similarity between the
two curves in Fig. 1 is evident. As
described in the introduction, this link derives from the excitation of gas clouds by
the currently forming stars and by the warming of the dust in the galaxy.
In late-type galaxies 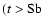 )
our data show the existence of a
linear relation between soft X-ray fluxes and other indicators of
recent and current star formation, such as the B and FIR luminosity,
respectively (Eqs. (4) and (7)). This has been known
since the first X-ray observations of large samples
Fabbiano et al. (1992), and this connection between B and X-ray luminosity
in late type galaxies has been interpreted as due to the
contribution of discrete X-ray sources, whose number is proportional
to the quantity of already formed stars (Beuing et al. 1999; Ciotti et al. 1991). The
recent work of Kim & Fabbiano (2004), which is able to resolve the single
X-ray binaries in 14 galaxies, indicates that the X-ray luminosity
produced by discrete sources is related to B luminosity by a similar
relation, with an intercept value of -3.63, similar to our -3.85 of
Eq. (4).
)
our data show the existence of a
linear relation between soft X-ray fluxes and other indicators of
recent and current star formation, such as the B and FIR luminosity,
respectively (Eqs. (4) and (7)). This has been known
since the first X-ray observations of large samples
Fabbiano et al. (1992), and this connection between B and X-ray luminosity
in late type galaxies has been interpreted as due to the
contribution of discrete X-ray sources, whose number is proportional
to the quantity of already formed stars (Beuing et al. 1999; Ciotti et al. 1991). The
recent work of Kim & Fabbiano (2004), which is able to resolve the single
X-ray binaries in 14 galaxies, indicates that the X-ray luminosity
produced by discrete sources is related to B luminosity by a similar
relation, with an intercept value of -3.63, similar to our -3.85 of
Eq. (4).
In addition to the interstellar radiation, which is proportional to
the number of already formed stars, the X-ray emission is also produced
by HII regions, where there is an ongoing vigorous star
formation (David et al. 1992). This latter contribution appears more
evident in FIR light and may explain the existence of a similar
linear relation between  and
and
 .
.
In early type galaxies the behaviour of these relations is
quite different. For most of these galaxies, the star
formation is exhausted and it may be present in a few of them,
eventually fed by gas accretion phenomena. Different mechanisms have
been suggested to explain the X-ray emission in this kind of
galaxies. In particular the main ones are the thermal emission due
to hot ISM and the emission generated by a relatively old population
of end objects of stellar evolution, composed of type I supernovae
remnants and low-mass X-ray binaries that have not yet evolved. In particular,
the X-ray emission for the fainter galaxies is compatible with
discrete sources and seems to be dominated by compact accreting
systems, while for the brighter objects the emission from hot
diffuse gas still present in the galactic-potential well is present
as an additional component (Beuing et al. 1999). The number size of this
population of relatively old objects is well represented by the
total blue luminosity of the galaxy. For this reason the X-ray
fluxes are still linked in early type galaxies to the total blue
luminosity, representing the more recent part of the history of star
formation in the galaxy.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5468fig9.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg80.gif) |
Figure 9:
 vs.
vs.  diagram as in Fig. 3, right panel,
but with the values deduced for the two template models of the
early-type galaxy (filled circles). The diamonds represent the
E-S0 galaxies, the triangles the S0a-Sb galaxies. The
masses of the two theoretical models are also indicated.
diagram as in Fig. 3, right panel,
but with the values deduced for the two template models of the
early-type galaxy (filled circles). The diamonds represent the
E-S0 galaxies, the triangles the S0a-Sb galaxies. The
masses of the two theoretical models are also indicated. |
| Open with DEXTER |
In the FIR, however, mechanisms different from the
emission from warm dust heated by the newly born stars predominate,
since the star formation in most of these systems is almost exhausted.
The FIR emission comes from circumstellar dusty shells around AGB
stars and from an interstellar medium due to the outflow of dusty
gas from AGB and RGB stars, as described in Sect. 4.
The key point for interpreting the observed trends is that we are
dealing with an emission coming from a more or less small amount of
dust distributed over the whole galaxy and heated by an average
interstellar radiation field due to all the stars of any age. The
situation is quite different from what happens, for instance, in
starburst galaxies where high optical depth dusty regions reprocess
the light coming from newly born stars embedded in the parental
environment. We can therefore conclude that in most of our
early-type galaxies, the mechanism of IR emission is not strictly
related to the star formation, and the link between the younger
generations of stars and dust emission is lost. For these reasons
one may expect that the soft X-ray luminosity in early type galaxies
is traced by the total blue luminosity but not by the FIR
luminosity. With the end of the star formation, the FIR
emission of these galaxies has faded out and an early type galaxy
with the same  of a late type will have a lower
of a late type will have a lower
 .
This
could explain the location of the points in Fig. 3 (right
panel), on the left side of the linear relation.
.
This
could explain the location of the points in Fig. 3 (right
panel), on the left side of the linear relation.
To check if this interpretation is correct we try to apply the
detailed chemo-dynamical spectrophotometric model described in the
previous section, in such a way as to estimate the luminosities
produced by the stars in connection with the various phenomena
present inside the galaxy, taking the contribution by
dust into account as well. Since the theoretical model cannot derive the  luminosity, we proceed in the following way.
luminosity, we proceed in the following way.
The luminosities LB and
 are directly derived
from the model. Then, we assume that the X-ray production of these
galaxies is proportional to LB according to our relation (10). In this way we may estimate the expected X-ray flux
and define a representative point in the
are directly derived
from the model. Then, we assume that the X-ray production of these
galaxies is proportional to LB according to our relation (10). In this way we may estimate the expected X-ray flux
and define a representative point in the
 vs.
vs.  plot.
plot.
We start considering two template models in which all the
parameters are fixed using the clues coming from the dynamical
simulations of Merlin & Chiosi (2006), as described in Sect. 4. The King profiles represented in Fig. 6
are similar for all the components, with
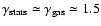 and
and
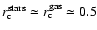 kpc, while the dimension of the galaxy is an average one
corresponding to most of the galaxies available in the catalogue.
The SFH is exactly the one obtained by the dynamical simulations.
The two values of
kpc, while the dimension of the galaxy is an average one
corresponding to most of the galaxies available in the catalogue.
The SFH is exactly the one obtained by the dynamical simulations.
The two values of
 and
and  obtained for the
obtained for the
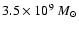 and
and
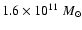 baryonic mass
models are plotted in Fig. 9. The more massive galaxy
fits well into the region defined by the actually observed galaxies.
The calculated levels of emission
baryonic mass
models are plotted in Fig. 9. The more massive galaxy
fits well into the region defined by the actually observed galaxies.
The calculated levels of emission
 and
and
 of this galaxy are very low, and for this
reason they belong to a region where we do not have enough
observations. Its weak
of this galaxy are very low, and for this
reason they belong to a region where we do not have enough
observations. Its weak
 emission can be
explained by the dynamical evolution in which almost all the gas is
consumed to form stars so the galactic winds are very efficient
(see Chiosi & Carraro 2002, for more details about galactic winds in low-mass
galaxies). Therefore, even if the trend of this galaxy is
the expected one for early-type galaxies (the model stays above the
linear relation), nothing can be said with more certainty, because we lack
observed data in that region of the diagram.
emission can be
explained by the dynamical evolution in which almost all the gas is
consumed to form stars so the galactic winds are very efficient
(see Chiosi & Carraro 2002, for more details about galactic winds in low-mass
galaxies). Therefore, even if the trend of this galaxy is
the expected one for early-type galaxies (the model stays above the
linear relation), nothing can be said with more certainty, because we lack
observed data in that region of the diagram.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5468fg10.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg83.gif) |
Figure 10:
Models
of the
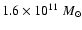 baryonic mass galaxy in the
baryonic mass galaxy in the
 vs.
vs.  diagram with the variation of the galactic radius (filled
circles), the mass of stars (filled diamonds), and finally, the mass
of gas (empty circles). We represented: E galaxies (empty
diamonds), E/S0 galaxies (pluses), S0 galaxies (crosses), S0sgalaxies (empty squares), Sa-Sb (empty triangles).
diagram with the variation of the galactic radius (filled
circles), the mass of stars (filled diamonds), and finally, the mass
of gas (empty circles). We represented: E galaxies (empty
diamonds), E/S0 galaxies (pluses), S0 galaxies (crosses), S0sgalaxies (empty squares), Sa-Sb (empty triangles). |
| Open with DEXTER |
Much more interesting is the model of higher mass.
The calculated
luminosities of the model, with its exhaustion of its star
formation, seem to agree well with the observations of early-type
galaxies.
However, the model needs to be checked against other
possibilities, in order to understand how the
various parameters of the model influence the spreading of
early-type galaxies into the observational data. First of all we
have to check the effects of the geometrical parameters and of the
masses of stars/gas.
In Fig. 10 we show the model of
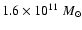 baryonic mass when varying the galactic radius, keeping the
galactic centre in the centre of mass of the stellar component. The
radii taken into account range from 6 kpc to 50 kpc. All the
other parameters are fixed. Four models are represented
and connected by a continuous line. For larger radii we observe
an increase in both
baryonic mass when varying the galactic radius, keeping the
galactic centre in the centre of mass of the stellar component. The
radii taken into account range from 6 kpc to 50 kpc. All the
other parameters are fixed. Four models are represented
and connected by a continuous line. For larger radii we observe
an increase in both
 and
and  ,
with a more emphasized
increase in
,
with a more emphasized
increase in  .
Since the density profile is unchanged, both
the increases in luminosity are simply due to the bigger amount of
material considered, taking larger radii in the
dynamical simulation into account. The stronger increase in
.
Since the density profile is unchanged, both
the increases in luminosity are simply due to the bigger amount of
material considered, taking larger radii in the
dynamical simulation into account. The stronger increase in  than
than
 can be explained simply:
can be explained simply:  is linearly related to LB, which is directly connected to the stellar luminosity. The
stellar component is more massive and more concentrated toward the
centre than the gaseous one (Fig. 5, upper panel).
It follows that at increasing radius we introduce more stars and more gas
into the models, but the added amount of stars is bigger
than the gaseous one, shifting LB (and then the linearly
related
is linearly related to LB, which is directly connected to the stellar luminosity. The
stellar component is more massive and more concentrated toward the
centre than the gaseous one (Fig. 5, upper panel).
It follows that at increasing radius we introduce more stars and more gas
into the models, but the added amount of stars is bigger
than the gaseous one, shifting LB (and then the linearly
related  )
more than
)
more than
 .
Finally, we observe how, even if
taking the smallest radius of 6 kpc into account, it is not
possible to move the theoretical point near the linear relation
holding for spirals.
.
Finally, we observe how, even if
taking the smallest radius of 6 kpc into account, it is not
possible to move the theoretical point near the linear relation
holding for spirals.
We also investigated in Fig. 10 what happens if we forget
about the clues coming from dynamical simulations on the masses of
stars and gas, and we arbitrarily start varying the amounts of stars
or gas, keeping everything fixed. The shift of
the model of lowest radius if we are changing the mass of stars
inside
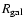 ,
going in fractions from f*=0.2 to f*=1.0of the total amount of stars in the dynamical model.
The effect is simply to move the point along a line about parallel
to the linear relation. A smaller amount of stars implies a
lower luminosity LB (and therefore a lower
,
going in fractions from f*=0.2 to f*=1.0of the total amount of stars in the dynamical model.
The effect is simply to move the point along a line about parallel
to the linear relation. A smaller amount of stars implies a
lower luminosity LB (and therefore a lower  ), but also a
lower
), but also a
lower
 ,
because the weaker radiation field makes dust
cooler and shifts the peak of dust emission to wavelengths longer
than
,
because the weaker radiation field makes dust
cooler and shifts the peak of dust emission to wavelengths longer
than
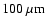 ,
resulting in smaller
,
resulting in smaller
 .
Finally,
we show five models in Fig. 10 by obtained
fixing the amount of stars and varying the mass of gas (and
therefore of dust) from
.
Finally,
we show five models in Fig. 10 by obtained
fixing the amount of stars and varying the mass of gas (and
therefore of dust) from
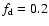 to
to
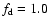 ,
of
the total amount of gas in the dynamical model.
,
of
the total amount of gas in the dynamical model.
The effect of this huge increase in the mass of diffuse gas and dust (in
the original model at
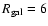 kpc only
kpc only 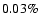 of the gas is
inside
of the gas is
inside
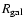 )
is to shift the models straight toward the linear
relation. It can be explained in the following way. Increasing the
amount of diffuse gas/dust (with all the parameters fixed and the
star formation exhausted) implies more absorption of the stellar
radiation and therefore a lower LB (and
)
is to shift the models straight toward the linear
relation. It can be explained in the following way. Increasing the
amount of diffuse gas/dust (with all the parameters fixed and the
star formation exhausted) implies more absorption of the stellar
radiation and therefore a lower LB (and  ). On the
other hand,
). On the
other hand,
 remains almost unchanged or becomes lower.
The reason is that the strongly increased mass of dust makes the
average stellar radiation field weaker, therefore the increased
emission of dust (due to the bigger mass) peaks at wavelengths
longer than
remains almost unchanged or becomes lower.
The reason is that the strongly increased mass of dust makes the
average stellar radiation field weaker, therefore the increased
emission of dust (due to the bigger mass) peaks at wavelengths
longer than
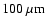 ,
leaving
,
leaving
 almost unchanged. Even if
in this way we can shift the model toward the linear relation, the
situation is physically unrealistic, requiring a huge amount of
gas/dust concentrated in the centre of an early-type galaxy with
exhausted star formation, which is not commonly observed and also
not predicted by dynamical models.
almost unchanged. Even if
in this way we can shift the model toward the linear relation, the
situation is physically unrealistic, requiring a huge amount of
gas/dust concentrated in the centre of an early-type galaxy with
exhausted star formation, which is not commonly observed and also
not predicted by dynamical models.
Other geometrical parameters that must be examined are the
scale radii
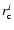 of the King's laws - Eq. (12) - that describe the distribution of the stellar
and gaseous components. The averaged profiles shown in Fig. 6 and used for the models of Figs. 9 and 10 are both characterised by
of the King's laws - Eq. (12) - that describe the distribution of the stellar
and gaseous components. The averaged profiles shown in Fig. 6 and used for the models of Figs. 9 and 10 are both characterised by
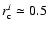 ,
allowing for a concentrated amount of stars and gas in the inner
regions. Keeping all the other parameters fixed, we investigated
what happens if we allow for a uniform distribution of one or both of
the physical components. Three cases have been considered: a uniform
distribution of gas keeping the stellar one fixed
,
allowing for a concentrated amount of stars and gas in the inner
regions. Keeping all the other parameters fixed, we investigated
what happens if we allow for a uniform distribution of one or both of
the physical components. Three cases have been considered: a uniform
distribution of gas keeping the stellar one fixed
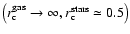 ,
a uniform
distribution of stars keeping fixed the gaseous one
,
a uniform
distribution of stars keeping fixed the gaseous one
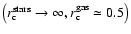 and, finally, a uniform distribution of both the components
and, finally, a uniform distribution of both the components
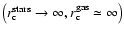 .
The results are shown in Fig. 11 for two radii
of the galaxy model,
.
The results are shown in Fig. 11 for two radii
of the galaxy model,
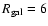 kpc and
kpc and
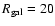 kpc,
respectively. The three different distributions give a similar
result: a lower
kpc,
respectively. The three different distributions give a similar
result: a lower
 ,
shifting the point to the left, and a
slightly higher
,
shifting the point to the left, and a
slightly higher  .
.
This can be explained in the following way: for
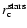 and
and
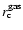 both
both 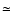 0.5 and the diffuse ISM
and the stars are both concentrated in the inner region of the
galaxy with a density of stars/gas of many orders of magnitude higher
than the outer regions. This is the condition for producing high
0.5 and the diffuse ISM
and the stars are both concentrated in the inner region of the
galaxy with a density of stars/gas of many orders of magnitude higher
than the outer regions. This is the condition for producing high
 ,
because we find that the regions of higher density of
dust are the same in which there is also the higher average
radiation field heating dust. The spatial distribution of the ISM
favours the interaction with the stellar radiation. When we destroy
this coupling between stellar emission and density of gas, as we do
allowing for a uniform distribution of gas or stars or both, the
emission in the
,
because we find that the regions of higher density of
dust are the same in which there is also the higher average
radiation field heating dust. The spatial distribution of the ISM
favours the interaction with the stellar radiation. When we destroy
this coupling between stellar emission and density of gas, as we do
allowing for a uniform distribution of gas or stars or both, the
emission in the
 becomes weaker. The weakening of the dusty
emission is stronger for the bigger radius of 20 kpc because in
all three cases one or both the components are distributed over
a huge galactic volume and we then have a low density of gas, eventually
coupled with weak radiation field. For the 6 kpc model, even if
the coupling in the central regions is destroyed, the galaxy is
small enough to keep a acceptable level of
becomes weaker. The weakening of the dusty
emission is stronger for the bigger radius of 20 kpc because in
all three cases one or both the components are distributed over
a huge galactic volume and we then have a low density of gas, eventually
coupled with weak radiation field. For the 6 kpc model, even if
the coupling in the central regions is destroyed, the galaxy is
small enough to keep a acceptable level of
 ,
even when the matter
is equally distributed across all the galaxy volume.
,
even when the matter
is equally distributed across all the galaxy volume.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5468fg11.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg95.gif) |
Figure 11:
Models
of the more massive galaxy of
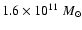 baryonic
mass in the
baryonic
mass in the
 vs.
vs.  diagram for various core radii
diagram for various core radii
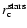 and
and
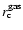 ,
plotted as filled circles. The
thin arrows indicate the original model, while the thick arrows
indicate the shift of the model for various core radii. We
represented: E galaxies (empty diamonds), E/S0 galaxies
(pluses), S0 galaxies (crosses), S0s galaxies (empty squares),
Sa-Sb (empty triangles). ,
plotted as filled circles. The
thin arrows indicate the original model, while the thick arrows
indicate the shift of the model for various core radii. We
represented: E galaxies (empty diamonds), E/S0 galaxies
(pluses), S0 galaxies (crosses), S0s galaxies (empty squares),
Sa-Sb (empty triangles). |
| Open with DEXTER |
The last and main point to be examined is how varying the star
formation history affects the position of the galaxies on the
 vs.
vs.  plot. In Figs. 10 and 11,
the galaxies of different morphological types form a sequence that,
going from systems in which the star formation was exhausted long ago to
systems in which star formation is still active, moves toward the
linear relation and thereby suggesting the key role played by star
formation. First of all we calculate the
plot. In Figs. 10 and 11,
the galaxies of different morphological types form a sequence that,
going from systems in which the star formation was exhausted long ago to
systems in which star formation is still active, moves toward the
linear relation and thereby suggesting the key role played by star
formation. First of all we calculate the
 and
and  obtained by the SEDs and the models by Piovan et al. (2006b) of real
galaxies of the local universe: three
spiral galaxies
obtained by the SEDs and the models by Piovan et al. (2006b) of real
galaxies of the local universe: three
spiral galaxies
 and
and
 and two starburst
galaxies
and two starburst
galaxies
 and
and  .
The key point is that the SFHs of
these galaxies allow us to cover an acceptable
number of different star
formation histories. All these SFHs, unlike the ones of the ellipticals
obtained by dynamical simulations, never end; in the case of the
two starbursters, a strong burst of star formation is added in the
last millions of years. A huge amount of
.
The key point is that the SFHs of
these galaxies allow us to cover an acceptable
number of different star
formation histories. All these SFHs, unlike the ones of the ellipticals
obtained by dynamical simulations, never end; in the case of the
two starbursters, a strong burst of star formation is added in the
last millions of years. A huge amount of
 therefore comes
from the young and deeply obscured region of star formation and not
only from the diffuse component.
therefore comes
from the young and deeply obscured region of star formation and not
only from the diffuse component.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5468fg12.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg100.gif) |
Figure 12:
 vs.
vs.  for galaxy models of spirals and
starbursters. Five theoretical models, taken from Piovan et al. (2006b),
are represented: three spirals (M 100, M 51 and NGC 6946) and two
starbursters (Arp 220 and M 82). Different morphological types are
plotted as in Fig. 11.
for galaxy models of spirals and
starbursters. Five theoretical models, taken from Piovan et al. (2006b),
are represented: three spirals (M 100, M 51 and NGC 6946) and two
starbursters (Arp 220 and M 82). Different morphological types are
plotted as in Fig. 11. |
| Open with DEXTER |
The results, presented in Fig. 12, show that
the three models of spirals stay near the linear relation, while the
two starbursters stay below the line, with the model of
 ,
powered by a huge burst of star formation falling well below the
linear relation. The stronger the emission coming from the
regions of star formation, the bigger the shift toward higher
,
powered by a huge burst of star formation falling well below the
linear relation. The stronger the emission coming from the
regions of star formation, the bigger the shift toward higher
 and lower
and lower  (due to the lower LB). The results
from these models are quite similar to the observational data:
for
(due to the lower LB). The results
from these models are quite similar to the observational data:
for  we get
we get
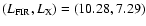 with the observations giving
(10.37,7.01), for
with the observations giving
(10.37,7.01), for
 we have
we have
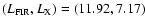 compared with
(11.99,7.60), and for M 82 we get
compared with
(11.99,7.60), and for M 82 we get
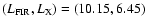 against
(9.79,6.31).
However, these galaxy models, even if they represent
real galaxies well, differ in many parameters from the early-type galaxy
model of
against
(9.79,6.31).
However, these galaxy models, even if they represent
real galaxies well, differ in many parameters from the early-type galaxy
model of
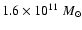 ,
like geometry and mass.
These parameters, together with the SFH, obviously concur to
determine the position of the models on the
,
like geometry and mass.
These parameters, together with the SFH, obviously concur to
determine the position of the models on the
 vs.
vs.  plot. To isolate the effect of the SFH, we first re-calculated the SFHs
of the five theoretical models above, rescaled to
the mass of
plot. To isolate the effect of the SFH, we first re-calculated the SFHs
of the five theoretical models above, rescaled to
the mass of
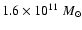 of the early-type galaxy
model. In Fig. 13 we can see four of the five SFH obtained.
Second, we fixed all the geometrical parameters to the same
values as for the average model of the
of the early-type galaxy
model. In Fig. 13 we can see four of the five SFH obtained.
Second, we fixed all the geometrical parameters to the same
values as for the average model of the
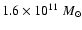 early type galaxy. The additional parameters, i.e. the escape
time of young stars from parental molecular clouds, the library of
SEDs of young dusty regions and the mass of gas in the diffuse and
molecular component, are fixed to the values used in
Piovan et al. (2006b) for spirals and starbursters, as appropriate.
early type galaxy. The additional parameters, i.e. the escape
time of young stars from parental molecular clouds, the library of
SEDs of young dusty regions and the mass of gas in the diffuse and
molecular component, are fixed to the values used in
Piovan et al. (2006b) for spirals and starbursters, as appropriate.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5468fg13.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg106.gif) |
Figure 13:
Different adopted star formation histories for the model of
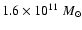 baryonic mass. The SFHs of Piovan et al. (2006b) have been
re-calculated for the same mass of the dynamical model.
The upper panels represent two spiral-like SFHs, while lower panels show two
starburst-like SFHs that peaked in the last million years.
baryonic mass. The SFHs of Piovan et al. (2006b) have been
re-calculated for the same mass of the dynamical model.
The upper panels represent two spiral-like SFHs, while lower panels show two
starburst-like SFHs that peaked in the last million years. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5468fg14.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg108.gif) |
Figure 14:
 vs.
vs.  for galaxy models of fixed
for galaxy models of fixed
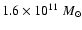 baryonic mass for various SFHs (large circles and
squares) or at fixed SFH for various masses from
baryonic mass for various SFHs (large circles and
squares) or at fixed SFH for various masses from
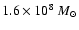 to
to
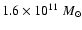 (large filled diamonds).
Large circles and squares represent, respectively, models with
spiral-like SFH and starburst-like SFH. Large filled circles and
squares are obtained using Eq. (4), while large open
circles and squares depend on Eq. (10). Different
morphological types are plotted as in Fig. 11.
(large filled diamonds).
Large circles and squares represent, respectively, models with
spiral-like SFH and starburst-like SFH. Large filled circles and
squares are obtained using Eq. (4), while large open
circles and squares depend on Eq. (10). Different
morphological types are plotted as in Fig. 11. |
| Open with DEXTER |
In Fig. 14 we finally show the results
obtained as a function of the SFH for the galaxy of
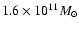 ,
keeping all the other parameters fixed. It is
interesting to observe that, since now the star formation never ends
and the galactic wind is not included, the classical semi-analytical
chemical evolution can be much more safely coupled to the
spectro-photometric code. The effect of varying the SFH at fixed
mass is to enhance the
,
keeping all the other parameters fixed. It is
interesting to observe that, since now the star formation never ends
and the galactic wind is not included, the classical semi-analytical
chemical evolution can be much more safely coupled to the
spectro-photometric code. The effect of varying the SFH at fixed
mass is to enhance the
 ,
keeping the
,
keeping the  almost fixed
and shifting the points toward the linear relation at higher
infrared luminosities. This is ultimately due to the strong and
efficient reprocessing of the light coming from very young stars,
occurring in the dusty star-forming regions. As a consequence of
this, models with starburst-like SFHs shift, as expected, toward
higher
almost fixed
and shifting the points toward the linear relation at higher
infrared luminosities. This is ultimately due to the strong and
efficient reprocessing of the light coming from very young stars,
occurring in the dusty star-forming regions. As a consequence of
this, models with starburst-like SFHs shift, as expected, toward
higher
 luminosity than do models with spiral-like SFH,
because of the stronger star formation and, therefore, emission
from young dusty regions. This can be also understood if we look in
detail at the relative contribution to
luminosity than do models with spiral-like SFH,
because of the stronger star formation and, therefore, emission
from young dusty regions. This can be also understood if we look in
detail at the relative contribution to
 coming from the
regions of star formation (let us define it
coming from the
regions of star formation (let us define it
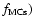 and represent
it as usual in
and represent
it as usual in
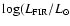 )
and from the diffuse interstellar
medium
)
and from the diffuse interstellar
medium
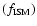 .
We get the values (
.
We get the values (
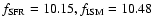 ), (
), (
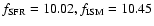 ), (
), (
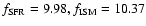 )
for the three models with spiral-like SFHs, while we
have (
)
for the three models with spiral-like SFHs, while we
have (
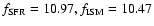 )
and (
)
and (
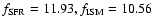 )
for the models with starburst-like SFHs. The stronger
the contribution from star forming regions, the higher is
)
for the models with starburst-like SFHs. The stronger
the contribution from star forming regions, the higher is
 when keeping LB (and
when keeping LB (and  )
almost unchanged. Models
slightly dominated by the ISM contribution, but with a significant
contribution coming from obscured newly born stars are more suitable
to the linear relation of spirals.
)
almost unchanged. Models
slightly dominated by the ISM contribution, but with a significant
contribution coming from obscured newly born stars are more suitable
to the linear relation of spirals.
It is worth noticing that in Fig. 14 we show both the
results obtained by applying the early-type linear relation between
 and LB - Eq. (10) - and the late-type one -
Eq. (4). Since, however, the SFHs used (see Fig. 13) are typical of late type galaxies (or starbursters), it is
physically much sounder to apply Eq. (4) to obtain the
and LB - Eq. (10) - and the late-type one -
Eq. (4). Since, however, the SFHs used (see Fig. 13) are typical of late type galaxies (or starbursters), it is
physically much sounder to apply Eq. (4) to obtain the
 luminosity. As a last point, we also calculated a sequence of
models in which one of the SFHs of the spirals has been chosen
(namely the one of NGC 6946) with all the parameters fixed and only
the mass varied. As we see from Fig. 14, the effect
of varying the mass is to shift the object diagonal by almost along
the relation. This is explained simply by the smaller amounts of
stars/gas emitting radiation.
luminosity. As a last point, we also calculated a sequence of
models in which one of the SFHs of the spirals has been chosen
(namely the one of NGC 6946) with all the parameters fixed and only
the mass varied. As we see from Fig. 14, the effect
of varying the mass is to shift the object diagonal by almost along
the relation. This is explained simply by the smaller amounts of
stars/gas emitting radiation.
We have been able to describe the relations existing in a galaxy
between the various tracers of the ISM and to fix the coefficients
of the relations existing between FIR, B, and X-ray luminosity, both
for early- and late-type galaxies.
The large set of data we used allowed us to more clearly redefine the
relationship between the CO and the 100 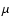 m fluxes. We found
that the relation, first obtained by Bregman et al. (1992) for early type
galaxies, is also valid for late type galaxies. In these galaxies, the
X-ray flux also appears linked to B and FIR emissions.
m fluxes. We found
that the relation, first obtained by Bregman et al. (1992) for early type
galaxies, is also valid for late type galaxies. In these galaxies, the
X-ray flux also appears linked to B and FIR emissions.
The only relation lacking from observations, i.e. the one
between  and
and
 ,
was studied by the use of the most
recent chemo-dynamical models coupled with dusty evolutionary
population synthesis.
,
was studied by the use of the most
recent chemo-dynamical models coupled with dusty evolutionary
population synthesis.
The calculated luminosities of the models seem to confirm our
hypothesis about a connection between the exhaustion of the star
formation and the "migration'' of the early type galaxies above the
linear relation in the  vs.
vs.
 plot. In the frame of our
assumptions, we may therefore conclude that the prediction of our
dusty chemo-dynamical models of galaxy evolution is consistent with
the observed lack of a direct relation between
plot. In the frame of our
assumptions, we may therefore conclude that the prediction of our
dusty chemo-dynamical models of galaxy evolution is consistent with
the observed lack of a direct relation between  and
and
 for early type galaxies and is due to the different mechanisms for
producing FIR light in galaxies where the active star formation
is no longer active. In most of our early-type galaxies, the
mechanism of IR emission is no longer strictly related to the ongoing
star formation and to the reprocessing of the radiation in the dense
regions where new stars are born. The FIR emission therefore comes
most likely from circumstellar dusty shells around AGB stars and
from an interstellar diffuse medium due to the outflow of dusty gas
from AGB and RGB stars.
for early type galaxies and is due to the different mechanisms for
producing FIR light in galaxies where the active star formation
is no longer active. In most of our early-type galaxies, the
mechanism of IR emission is no longer strictly related to the ongoing
star formation and to the reprocessing of the radiation in the dense
regions where new stars are born. The FIR emission therefore comes
most likely from circumstellar dusty shells around AGB stars and
from an interstellar diffuse medium due to the outflow of dusty gas
from AGB and RGB stars.
Finally, we can summarize that: (i) the SFH
of the galaxies seems to have the stronger effect on the
position of early-type galaxies in the  vs.
vs.
 plot; (ii)
other parameters, like the radius of the galaxy and the scale radii
of stars and gas, play a secondary role, even if they can
significantly contribute to the scatter of the models in the region
above the linear relation; (iii) the mass is the main parameter in
explaining the scatter of the points along the linear relation.
plot; (ii)
other parameters, like the radius of the galaxy and the scale radii
of stars and gas, play a secondary role, even if they can
significantly contribute to the scatter of the models in the region
above the linear relation; (iii) the mass is the main parameter in
explaining the scatter of the points along the linear relation.
Acknowledgements
This research was partially funded by the University of Padua
with Funds ex 60% 2005. We acknowledge Prof. C. Chiosi for
useful discussions of the theoretical subjects of this paper. L. Piovan is pleased
to acknowledge the hospitality and stimulating environment provided by the
Max-Planck-Institut für Astrophysik in Garching where part of the
work was done during his visit as an EARA
fellow on leave from the Department of Astronomy of the Padua
University. We also thank the referee for the detailed and useful comments
about this topic.
- Arimoto, N.,
& Yoshii, Y. 1987, A&A, 173, 23 [NASA ADS]
- Arimoto, N.,
& Yoshii, Y. 1989, A&A, 224, 361 [NASA ADS]
- Arimoto, N.,
& Tarrab, I. 1990, A&A, 228, 6 [NASA ADS]
- Arp, H. 1966, Atlas of
Peculiar Galaxies Publisher: California Institute of Technology,
Pasaadena, CA
(In the text)
- Arp, H. C., & Madore,
B. F. 1987, A Catalog of Southern Peculiar Galaxies and
Associations (Cambridge University Press)
(In the text)
- Bettoni, D., Galletta,
G., & García-Burillo, S. 2003a, A&A, 405, 5 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bettoni, D.,
Galletta, G., & Garcia-Burillo, S. 2003b, VizieR Online Data
Catalog, 340, 50005 [NASA ADS]
- Beuing, J.,
Döbereiner, S., Böhringer, H., & Bender, R. 1999,
MNRAS, 302, 209 [NASA ADS] [CrossRef] (In the text)
- Bregman, J. N., Hogg,
D. E., & Roberts, M. S. 1992, ApJ, 387, 484 [NASA ADS] [CrossRef] (In the text)
- Bressan, A.,
Chiosi, C., & Fagotto, F. 1994, ApJS, 94, 63 [NASA ADS] [CrossRef]
- Bressan, A.,
Chiosi, C., & Tantalo, R. 1996, A&A, 311, 425 [NASA ADS]
- Bruzual, G, &
Charlot, S. 1993, ApJ, 405, 538 [NASA ADS] [CrossRef]
- Buzzoni, A. 2002,
AJ, 123, 1188 [NASA ADS] [CrossRef]
- Buzzoni, A. 2005,
MNRAS, 361, 725 [NASA ADS] [CrossRef]
- Casasola, V.,
Bettoni, D., & Galletta, G. 2004a, A&A, 422, 941 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Casasola, V.,
Bettoni, D., & Galletta, G. 2004b, VizieR Online Data Catalog,
342, 20941 [NASA ADS]
- Carraro, G., Lia,
C, & Chiosi, C., 1998, MNRAS, 297, 1021 [NASA ADS] [CrossRef]
- Chiosi, C. 1980,
A&A, 83, 206 [NASA ADS]
- Chiosi, C.,
Bressan, A., Portinari, L., & Tantalo, R. 1998, A&A, 339,
355 [NASA ADS]
- Chiosi, C. 2000,
A&A, 364, 423 [NASA ADS] (In the text)
- Chiosi, C., &
Carraro, G. 2002, MNRAS, 335, 335 [NASA ADS] [CrossRef]
- Ciotti, L., Pellegrini,
S., Renzini, A., & D'Ercole, A. 1991, ApJ, 376, 380 [NASA ADS] [CrossRef] (In the text)
- David, L. P., Jones,
C., & Forman, W. 1992, ApJ, 388, 82 [NASA ADS] [CrossRef]
- De Lucia, G.,
Springel, V., White, S. D. M., & Kauffmann, G. 2006,
MNRAS, 366, 499 [NASA ADS] [CrossRef] (In the text)
- de Vaucouleurs, G., de
Vaucouleurs, A., Corwin, H. G., et al. 1991, Third Reference
Catalogue of Bright Galaxies (RC3) (New York: Springer-Verlag)
- Devereux,
N. A., & Young, J. S. 1991, ApJ, 371, 515 [NASA ADS] [CrossRef]
- Devriendt,
J. E. G., Guiderdoni, B., & Sadat, R. 1999, A&A,
350, 381 [NASA ADS] (In the text)
- Dwek, E. 1998, ApJ,
501, 643 [NASA ADS] [CrossRef]
- Dwek, E. 2005, The
Spectral Energy Distributions of Gas-Rich Galaxies: Confronting
Models with Data, ed. C. C. Popescu, & R. J. Tuffs,
AIP Conf., Proc., 761, 103
- Fabbiano, G.,
Kim, D.-W., & Trinchieri, G. 1992, ApJS, 80, 531 [NASA ADS] [CrossRef] (In the text)
- Gibson, B. K.,
& Matteucci, F. 1997a, ApJ, 475, 47 [NASA ADS] [CrossRef]
- Gibson, B. K.
1997b, MNRAS, 290, 471 [NASA ADS]
- Griffiths,
R. E., & Padovani, P. 1990, ApJ, 360, 483 [NASA ADS] [CrossRef]
-
Guhathakurta, P., Knapp, G. R., Kim, D. W., & Jura,
M. 1986, Baas, 18, 926 [NASA ADS] (In the text)
- Ho, L. C., Filippenko,
A. V., & Sargent, W. L. W. 1997, ApJS, 112,
315 [NASA ADS] [CrossRef] (In the text)
- Kawata, D. 2001,
ApJ, 558, 598 [NASA ADS] [CrossRef]
- Kim, D.-W., &
Fabbiano, G. 2004, ApJ, 611, 846 [NASA ADS] [CrossRef] (In the text)
- Kodama, T., &
Arimoto, N. 1997, A&A, 320, 41 [NASA ADS]
- Knapp, G. R.,
Guhathakurta, P., Kim, D.-W., & Jura, M. A. 1989, ApJS,
70, 329 [NASA ADS] [CrossRef] (In the text)
- Kuntschner,
H. 2000, MNRAS, 315, 184 [NASA ADS] [CrossRef]
- Kroupa, P. 1998,
MNRAS, 298, 231 [NASA ADS] [CrossRef] (In the text)
- Larson, R. B.
1974, MNRAS, 169, 229 [NASA ADS]
- Larson, R. B.,
& Dinerstein, H. L. 1975, PASP, 87, 911 [NASA ADS] [CrossRef]
- Merlin, E., &
Chiosi, C. 2006, MNRAS, in press
[arXiv:astro-ph/0605052]
(In the text)
- Paturel, G., Andernach, H.,
Bottinelli, L., et al. 1997, A&AS, 124, 109 [NASA ADS] (In the text)
- Piovan, L.,
Tantalo, R., & Chiosi, C. 2006a, MNRAS, 366, 923 [NASA ADS] (In the text)
- Piovan, L.,
Tantalo, R., & Chiosi, C., 2006b, MNRAS, in press
[arXiv:astro-ph/0605541]
(In the text)
- Popescu, C. C.,
Tuffs, R. J., Völk, H. J., Pierini, D., &
Madore, B. F. 2002, ApJ, 567, 221 [NASA ADS] [CrossRef] (In the text)
- Portinari,
L., Chiosi, C., & Bressan, A. 1998, A&A, 334, 505 [NASA ADS] (In the text)
- Ranalli, P.,
Comastri, A., & Setti, G. 2003, A&A, 399, 39 [NASA ADS] [CrossRef] [EDP Sciences]
- Sanders, D. B.,
& Mirabel, I. F. 1985, ApJ, 298, L31 [NASA ADS] [CrossRef]
- Sanders, D. B.,
Scoville, N. Z., Young, J. S., et al. 1986, ApJL,
305, L45 [NASA ADS] [CrossRef]
- Silva, L., Granato,
G. L., Bressan, A., & Danese, L. 1998, ApJ, 509, 103 [NASA ADS] [CrossRef] (In the text)
- Solomon, P. M.,
& Sage, L. J. 1988, ApJ, 334, 613 [NASA ADS] [CrossRef]
- Springel, V.,
Yoshida, N., & White, S. D. M. 2001, New Astron., 6,
79 [NASA ADS]
- Tagaki, T.,
Vansevicius, V., & Arimoto, N. 2003, Publ. Astron. Soc. Jpn.,
55, 385 [NASA ADS] (In the text)
- Tantalo, R.,
Chiosi, C., & Bressan, A. 1996, A&A, 311, 361 [NASA ADS]
- Tantalo, R.,
Chiosi, C., Bressan, A., Marigo, P., & Portinari, L. 1998,
A&A, 335, 823 [NASA ADS]
- Tantalo, R.,
& Chiosi, C. 2004, MNRAS, 353, 405 [NASA ADS] [CrossRef]
- Thomas, D.,
Maraston, C., Bender, R., & de Oliveira, C. M., 2005, ApJ,
621, 673 [NASA ADS] [CrossRef]
- Thronson,
H. A., & Telesco, C. M. 1986, ApJ, 311, 98 [NASA ADS] [CrossRef] (In the text)
- Trager,
S. C., Faber, S. M., Worthey, G., & González,
J. J. 2000a, AJ, 119, 164 [NASA ADS] [CrossRef]
- Trager,
S. C., Faber, S. M., Worthey, G., & González,
J. J. 2000b, AJ, 120, 165 [NASA ADS] [CrossRef]
- Véron-Cetty, M.-P.,
& Véron, P. 2003, A&A, 412, 399 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Vorontsov-Velyaminov,
B. A. 1959, Atlas and catalog of interacting galaxies
(In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=15cm,clip]{5468fig1.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg13.gif)
![\begin{figure}
\par\includegraphics[width=15.4cm,clip]{5468fig2.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg15.gif)
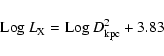
![\begin{figure}
\par\includegraphics[width=15.4cm,clip]{5468fig3.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg33.gif)
![\begin{figure}
\par\includegraphics[width=15.4cm,clip]{5468fig4.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg36.gif)
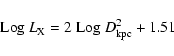
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{5468fig5.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5468fig6.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg59.gif)
![\begin{displaymath}\rho _{i}=\rho _{0i}\left[ 1+\left( \frac{r}{r_{\rm c}^{i}}\right)
^{2}\right] ^{-\gamma _{i}}
\end{displaymath}](/articles/aa/full/2007/05/aa5468-06/img60.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{5468fig7.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg62.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5468fig8.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg63.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5468fig9.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg80.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5468fg10.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg83.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5468fg11.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg95.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5468fg12.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5468fg13.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg106.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5468fg14.eps}
\end{figure}](/articles/aa/full/2007/05/aa5468-06/Timg108.gif)