A&A 462, 7-20 (2007)
DOI: 10.1051/0004-6361:20065649
R. S. Koehler1,2 - P. Schuecker2 - K. Gebhardt3
1 - Universitätssternwarte München, Ludwig-Maximilians-Universität,
Scheinerstrasse 1, 81579 München, Germany
2 -
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstraße 1, 85748 Garching, Germany
3 -
University of Texas, Astronomy Department,
1 University Station, C1 400, Austin, TX 78712, USA
Received 22 May 2006 / Accepted 1 September 2006
Abstract
Context. The phases and amplitudes of baryonic acoustic oscillations in the galaxy power spectrum can be used as cosmological probes to constrain different cosmological models and especially the equation of state parameter w of dark energy.
Aims. It will be shown that the phases as well as the amplitudes of baryonic acoustic oscillations can be extracted out of a galaxy power spectrum, including various observational effects like growth suppression, redshift space distortions, and galaxy biasing. The phases of baryonic acoustic oscillations are used as a standard ruler for a cosmological test to constrain w over a large redshift range with a minimum of assumptions.
Methods. A non-oscillating phenomenological fitting function is used to extract the oscillatory part of the galaxy power spectrum and to disentangle phase information from amplitude information. The method is tested with simulated data of the Hubble Volume Simulation to include redshift space effects, non-linear structure growth, and biasing. A cosmological test is introduced, which compares the extracted oscillations to a theoretical model template to derive constraints on the w parameter.
Results. The phenomenological fitting function is found to model the various distortions of the galaxy power spectrum to the sub-percent level. The various distortions only boost the amplitude of the oscillations. The theoretical template is accurate enough to test for small deviations in the phases of the oscillations, resulting from different w values. A cosmological test, using the baryonic acoustic oscillations as a standard ruler, is able to constrain w in a robust way. These constraints are based solely on the phase of these oscillations, assuming no errors of the value at the end of the Compton drag epoch, as the standard ruler. The w constraints are expected to further improve when the full two dimensional redshift space effects and the amplitudes of the baryonic acoustic oscillations are taken into account.
Key words: cosmological parameters - large-scale structure of Universe
Acoustic oscillations as observed in the temperature anisotropies of
the cosmic microwave background radiation (CMB) are traditionally used
to constrain the values of certain cosmological parameters. The
intrinsic amplitudes and locations of the oscillations are determined
by the densities and pressures of the various energy components in the
very early and hot Universe. The oscillations are furthermore modified
by their subsequent geometric projection onto the present hypersphere,
where they are observed. It turns out that both intrinsic CMB
oscillations and their geometric projection are mainly shaped by the
physical properties at high redshifts. Excluding the very large scales
where cosmic variance makes analysis quite difficult, the observed
oscillations in the CMB are highly degenerate regarding certain changes of the
energy density
![]() and the equation of state parameter,
and the equation of state parameter,
![]() ,
of the dark energy, dominating at low
redshifts (see also Caldwell et al. 1998).
,
of the dark energy, dominating at low
redshifts (see also Caldwell et al. 1998).
However, related so-called baryonic acoustic oscillations (BAOs) are expected to be observable at lower redshifts in the matter power spectrum. Therefore, the phases of the BAOs can be used as cosmic rulers in a similar manner as the CMB oscillations, but now at much smaller redshifts (Eisenstein et al. 1998). Here, the observed phases are affected by the late-time geometry and thus by the value of w, the prime cosmological parameter of the present investigation.
The BAOs are classical Doppler peaks in the density distribution of matter (e.g., Hu & Sugiyama 1996). They are triggered in the hot Universe by oscillatory velocity patterns of the baryons. These velocity oscillations are generated, in the same environment as the CMB density oscillations, by sound waves on scales where radiation pressure could stabilize the fluid against gravitational collapse. At later times, this oscillatory velocity pattern of the baryon field kinematically produces a new field of matter density fluctuations in the form of quasi-regular matter oscillations. The amplitudes of these BAOs are determined by the ratio of baryonic matter to the overall matter density. The BAOs thus constitute a quasi-regular pattern of oscillating substructures superposed with small amplitudes onto a general density field that fluctuates irregularly with amplitudes that are several hundreds of times higher.
The imprints of the BAOs on galaxy and clusters distributions, gravitational shear maps, etc. can provide a clean cosmic ruler for precise tests of the w parameter, at least in principle. The characteristic scale, s, of these imprints is the comoving distance, sound waves can travel during the epoch where baryons and photons are strongly coupled through Compton and Thomson scattering (Compton drag). Cosmological tests based on the resulting sound horizon, s, as a metric ruler are expected to have only very small systematic errors because the phases of the BAOs located at scales that are small compared to s are solely determined by well-understood physical processes. A practical problem is, however, how to separate the oscillatory BAO modes from the irregular fluctuation field with sufficient accuracy.
One might object that the small amplitudes of the BAOs can easily be washed out especially by structure growth that can mix perturbation modes with adjacent wavenumbers k. This is certainly true for oscillations in the non-linear regime (Meiksin et al. 1999). On larger scales, however, recent observations of 2dF galaxies at redshifts z<0.3 clearly show several BAOs in the galaxy power spectrum (Cole et al. 2005). In addition, the sequence of BAOs in k-space is projected into a single wiggle in the space domain. The corresponding excess galaxy correlation was in fact observed in the two-point spatial correlation function of the luminous red SDSS galaxies at z<0.5 (Eisenstein et al. 2005). In addition to these observational indications, results from recent numerical simulations suggest that within certain redshift and scale ranges, stable BAOs could exist as useful probes for cosmological investigations (e.g., Seo & Eisenstein 2005; Springel et al. 2005; Jeong & Komatsu 2006). However, several critical issues like the exact behavior of baryons during structure growth on BAO-scales can only be discussed with much larger simulations and a better understanding of galaxy formation.
Applications of BAOs for cosmological tests of w are confronted with
the following situation. Present observational constraints of wusing different combinations of CMB, galaxy clusters, galaxies, and
gravitational lensing data are all found to be consistent with w=-1,
i.e., the value for the cosmological constant. The ![]() error
of the w values, derived from partially dependent observations,
is around 10-20%
(for a recent review see, e.g., Schuecker 2005). To improve current
estimates, we thus have to extract the BAOs and to measure their
phases quite accurately in the presence of non-linear and
scale-dependent effects. Therefore, even tiny systematic errors in the
analysis on percent levels can have severe consequences for the
observational accuracy of w.
error
of the w values, derived from partially dependent observations,
is around 10-20%
(for a recent review see, e.g., Schuecker 2005). To improve current
estimates, we thus have to extract the BAOs and to measure their
phases quite accurately in the presence of non-linear and
scale-dependent effects. Therefore, even tiny systematic errors in the
analysis on percent levels can have severe consequences for the
observational accuracy of w.
The basic aim of the present paper is to describe a new, simple, and robust method to extract BAOs from (non)linear, scale, and redshift-dependent biased, redshift-space galaxy power spectra under realistic light cone survey conditions. For brevity, we call the method "fit and extract'' (FITEX). The method has the potential to reduce many of the abovementioned sources of systematic errors. Our starting point is to use as few assumptions as possible for the extraction of the BAOs from a complex power spectrum. For reasons that will become clear later, we do the separation by fitting a flexible non-oscillating function to an observable which is directly related to the transfer function and not to the power spectrum itself. The crucial point is to show that BAOs extracted in this simple manner are still governed by simple physical processes, and that FITEX stays robust even under complex survey conditions. We believe that such model-independent approaches are quite important, especially in light of the fact that at least in the near future we cannot expect to model the abovementioned non-linear and scale-dependent effects with accuracies on the sub-percent level.
Our computations are, in several cases, optimized to galaxy surveys
typically covering several 100 square degrees on the sky in the
redshift range between z=2-4. This choice is motivated by the Hobby
Eberly Dark Energy Experiment (HETDEX), which is planned to measure
the w parameter with several million Ly-![]() emitting galaxies
at these redshifts (Hill & McQueen 2004; Gebhardt et al., in prep.). We see
the results of the present paper as a useful contribution to a realistic error forecast for this important project.
emitting galaxies
at these redshifts (Hill & McQueen 2004; Gebhardt et al., in prep.). We see
the results of the present paper as a useful contribution to a realistic error forecast for this important project.
We organized the paper as follows. In Sect. 2 we indicate the basic idea of the FITEX algorithm. In the following sections we test its performance to separate BAOs from a complex power spectrum under linear conditions (Sect. 3), under quasi-non-linear conditions (Sect. 4), in redshift space (Sect. 5), and from biased samples (Sect. 6). Finally, we illustrate the performance of FITEX including all effects and use a cosmological test of was a benchmark to investigate the quality of the BAO extraction together with the theoretical template (Sect. 7). Our results are mainly based on a deep data wedge extracted by the Virgo Consortium from the Hubble Volume Simulation. The paper thus presents for the first time constraints on the application of BAOs for cosmological tests under realistic light cone survey conditions.
If not mentioned explicitly, we assume a spatially flat
Friedmann-Lemaître Robertson-Walker world model with the Hubble
constant in units of
![]() ,
the present values of the total matter density
,
the present values of the total matter density
![]() and baryon density
and baryon density
![]() ,
the density of
relativistic matter (e.g., neutrinos)
,
the density of
relativistic matter (e.g., neutrinos)
![]() ,
and the
mean CMB temperature
,
and the
mean CMB temperature
![]() (concordance cosmology).
(concordance cosmology).
In this section, we discuss the "theoretical wiggle function'', that is, a reference function (see Eq. (1) below) we use in our cosmological tests of w to match the BAOs extracted in a certain manner from the complex galaxy power spectrum. The power spectrum may be written in the form P(k,z) = A(k,z,b) kn T2(k). The amplitude A(k,z,b) includes the primordial amplitude, redshift, and scale-dependent effects of redshift space distortions, linear and non-linear structure growth, and galaxy biasing, which will be discussed in the course of the paper. The exponent n is the slope of the primordial power spectrum, and T(k) the transfer function. Our further treatment of the formation of BAOs is based on Hu & Sugiyama (1996), where a detailed description of the relevant physical processes can be found, and on the fitting equations derived by Eisenstein & Hu (1998).
Between the epoch of matter-radiation equality at
redshift
![]() (concordance cosmology) and the end
of the Compton drag epoch at
(concordance cosmology) and the end
of the Compton drag epoch at
![]() ,
the baryons follow a regular velocity
pattern that can generate new density fluctuations kinematically. On
small scales and at
,
the baryons follow a regular velocity
pattern that can generate new density fluctuations kinematically. On
small scales and at ![]() ,
this effect (velocity overshoot)
overrides the intrinsic density fluctuations of the baryons. As
adiabatic modes dominate the isocurvature modes, the baryon density
oscillates as
,
this effect (velocity overshoot)
overrides the intrinsic density fluctuations of the baryons. As
adiabatic modes dominate the isocurvature modes, the baryon density
oscillates as ![]() .
The phase of the BAOs is frozen out at
.
The phase of the BAOs is frozen out at ![]() at the value ks, with
at the value ks, with
![]() being the comoving sound horizon at
being the comoving sound horizon at ![]() and k the comoving wavenumber of the oscillation. The BAOs are thus
and k the comoving wavenumber of the oscillation. The BAOs are thus ![]() out of phase with the
corresponding CMB fluctuations. The sound horizon s at
out of phase with the
corresponding CMB fluctuations. The sound horizon s at ![]() is the standard ruler we are looking for. Its value
calibrates the phases of the theoretical wiggle function and can be
measured quite easily with CMB experiments on the sub-percent
level. This includes the contribution of unknown relativistic
energy components (Eisenstein & White 2004).
For consistency with the Hubble Volume Simulations
(see Sect. 4) we use
is the standard ruler we are looking for. Its value
calibrates the phases of the theoretical wiggle function and can be
measured quite easily with CMB experiments on the sub-percent
level. This includes the contribution of unknown relativistic
energy components (Eisenstein & White 2004).
For consistency with the Hubble Volume Simulations
(see Sect. 4) we use
![]() .
.
The sinusoidal fluctuations in the baryon density are dampened by
expansion drag, gravitational forcing, and Silk damping. In addition,
cosmic expansion forces the velocity contributions to fall off at
large scales and amplitudes to decline when dark matter dominates the
energy density. While these effects only reduce the amplitude of the
fluctuations and do not affect the phase, the damping may be summarized by the
pseudo transfer function
![]() ,
with j0 the
spherical Bessel function of order zero, the exponent
,
with j0 the
spherical Bessel function of order zero, the exponent
![]() ,
which is basically independent from cosmology,
,
which is basically independent from cosmology,
![]() ,
and
,
and
![]() with
with
![]() .
However, velocity overshoot
dominates only on scales that are small compared to s. On larger scales, the
original sound horizon, s, appears to be reduced by
.
However, velocity overshoot
dominates only on scales that are small compared to s. On larger scales, the
original sound horizon, s, appears to be reduced by
![]() ,
with
,
with
![]() .
This correction of s is about 0.2% at
.
This correction of s is about 0.2% at
![]() and 1.3% at
and 1.3% at
![]() .
Though relatively small, the corrections are important as they
change the length of the standard ruler s depending on k. Collecting all scale-dependent terms we get the oscillatory solution (theoretical wiggle function)
.
Though relatively small, the corrections are important as they
change the length of the standard ruler s depending on k. Collecting all scale-dependent terms we get the oscillatory solution (theoretical wiggle function)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5649f1a.ps}\vspace*{5mm}
\includegraphics[width=8cm,clip]{5649f1b.ps}\end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg55.gif) |
Figure 1:
Comparison of different terms
of the transfer function computed with
|
| Open with DEXTER | |
The different terms of the transfer function are shown in
Fig. 1. The upper panel shows the components that
determine the global shape of the transfer function. Note that an additional oscillating component, the first term in Eq. (3),
is necessary to describe the transition from large to small scales
with sufficient accuracy. This is a direct consequence of the fact
that the main effect of the baryons on the transfer function is a damping of the overall growth of dark matter between
![]() and
and ![]() ,
which significantly reduces the fluctuation power at scales smaller than s. The resulting break is the imprint of
the baryons on the power spectrum, which is easiest to observe. The term
,
which significantly reduces the fluctuation power at scales smaller than s. The resulting break is the imprint of
the baryons on the power spectrum, which is easiest to observe. The term
![]() thus contributes mainly to the shape as it is rapidly
declining on scales smaller than s to model the damping effect of the baryons.
thus contributes mainly to the shape as it is rapidly
declining on scales smaller than s to model the damping effect of the baryons.
In the lower panel of Fig. 1, the two parts of the
baryon transfer function are shown. One can clearly see the first to
fifth oscillations. Note that
![]() declines very fast and is
almost zero after the second oscillation. It is compared to the second
term of the baryonic transfer function, Tw(k), and a reference
function,
declines very fast and is
almost zero after the second oscillation. It is compared to the second
term of the baryonic transfer function, Tw(k), and a reference
function,
![]() ,
which is formally constructed to contain
all oscillations. Thus, the reference function includes both
the small-scale oscillations from Tw(k) and the large-scale
oscillations from
,
which is formally constructed to contain
all oscillations. Thus, the reference function includes both
the small-scale oscillations from Tw(k) and the large-scale
oscillations from
![]() .
The latter is, however, also
determined by the dark matter function
T0(k,1,1) (see
Eq. (3) below). Therefore, excluding or including knowledge of the
shape of the dark matter function for the extraction of BAOs
corresponds to working either with Tw(k) or with
.
The latter is, however, also
determined by the dark matter function
T0(k,1,1) (see
Eq. (3) below). Therefore, excluding or including knowledge of the
shape of the dark matter function for the extraction of BAOs
corresponds to working either with Tw(k) or with
![]() .
Both Tw(k) and
.
Both Tw(k) and
![]() agree
reasonably well beyond
agree
reasonably well beyond
![]() ,
especially when one keeps in mind that only the phases of the
oscillations are relevant as the amplitudes are subject to distortions
anyway (see below).
,
especially when one keeps in mind that only the phases of the
oscillations are relevant as the amplitudes are subject to distortions
anyway (see below).
The good agreement between the phases of Tw(k) and
![]() means
that quite simple physics as described by Tw (mainly velocity
overshoot and Silk damping) dominate the oscillations expected to be
seen in the overall power spectrum. However, on larger scales, the physics get
more complex due to the growing influence of CDM and the backreaction
of the baryons on structure growth. Thus Tw and
means
that quite simple physics as described by Tw (mainly velocity
overshoot and Silk damping) dominate the oscillations expected to be
seen in the overall power spectrum. However, on larger scales, the physics get
more complex due to the growing influence of CDM and the backreaction
of the baryons on structure growth. Thus Tw and
![]() differ accordingly. Nevertheless, on small
scales, Tw is a good theoretical wiggle function for BAOs phases that can
be used as a standard ruler for cosmological tests, with a minimum of
theoretical assumptions.
differ accordingly. Nevertheless, on small
scales, Tw is a good theoretical wiggle function for BAOs phases that can
be used as a standard ruler for cosmological tests, with a minimum of
theoretical assumptions.
The main advantages of constraining cosmological parameters with BAOs are its small systematic errors, the ability to discriminate between geometrical effects (homogeneous universe) and structure growth effects (inhomogeneous universe) of cosmological parameters, and the potential to constrain dark energy without assuming a certain dark matter model. The observed phase of the BAOs is only affected by the geometry of the universe, while the observed amplitude of the oscillations is mainly affected by structure growth and other amplitude effects (see Sects. 4 to 6). It is thus very important to extract the BAOs from the power spectrum in a way that does not mix these two benchmarks. As suggested by the previous discussion, BAOs, described by simple physical processes, should be extracted by subtracting the shape of the non-oscillatory part of the transfer function. This method is able to disentangle phase effects from amplitude effects in an effective manner.
In contrast to this method, previous studies (Blake & Glazebrook 2003; Angulo et al. 2005; Hütsi 2005; Seo & Eisenstein 2005; White 2005) used the CDM-based theoretical non-oscillatory
power spectrum,
![]() ,
given in Eisenstein & Hu (1998) to analyze the BAOs. This is done by dividing the measured power spectrum,
,
given in Eisenstein & Hu (1998) to analyze the BAOs. This is done by dividing the measured power spectrum,
![]() ,
by this
reference power spectrum. Assuming that the transfer function
can be split into a shape part,
,
by this
reference power spectrum. Assuming that the transfer function
can be split into a shape part,
![]() ,
and an oscillatory
part,
,
and an oscillatory
part,
![]() ,
where
,
where
![]() (Sect. 2), the result of such a division is
(Sect. 2), the result of such a division is
In addition, the use of a theoretical non-oscillatoy reference power spectrum,
![]() ,
or the related theoretical "boosted'' transfer function,
,
or the related theoretical "boosted'' transfer function,
![]() ,
has a number of drawbacks: (1) the shape of the transfer function and thus the power spectrum vary with the cosmological
parameters. To compute a reference power spectrum one has to
know the exact values of several cosmological parameters. Furthermore
one has to assume a CDM model as a prior. (2) The reference power spectrum
has to be flexible to compensate for various distortions: structure
growth, redshift space distortions, biasing, etc. distort the transfer
function and thus its shape. Most of the effects vary with redshift as
well as with k. (3) The reference power spectrum has to be exact on the
sub-percent level. The BAOs make up only
,
has a number of drawbacks: (1) the shape of the transfer function and thus the power spectrum vary with the cosmological
parameters. To compute a reference power spectrum one has to
know the exact values of several cosmological parameters. Furthermore
one has to assume a CDM model as a prior. (2) The reference power spectrum
has to be flexible to compensate for various distortions: structure
growth, redshift space distortions, biasing, etc. distort the transfer
function and thus its shape. Most of the effects vary with redshift as
well as with k. (3) The reference power spectrum has to be exact on the
sub-percent level. The BAOs make up only ![]()
![]() of the transfer
function depending on the ratio
of the transfer
function depending on the ratio
![]() .
An analytical function has to be more accurate to extract the oscillations from the transfer function.
(4) It is non-trivial to provide an assumption-free template for the
resulting power ratio to perform a cosmological test. Instead, very accurate
knowledge of the cosmology as well as amplitude effects is needed.
.
An analytical function has to be more accurate to extract the oscillations from the transfer function.
(4) It is non-trivial to provide an assumption-free template for the
resulting power ratio to perform a cosmological test. Instead, very accurate
knowledge of the cosmology as well as amplitude effects is needed.
Most of these issues are well-known and useful corrections are already available from the simulations. However, these calibrations have certainly not reached the sub-percent accuracy level that is necessary for the cosmological tests, and one can doubt whether this is achievable at all. Furthermore, one of the main advantages of the BAO method, the ability not to assume a certain dark matter model, is negated.
Equations (1)-(3) instead suggest that
the computation of the difference of transfer functions to extract BAOs is the
most direct approach. Therefore, FITEX does not divide the observed power spectrum by
a theoretical non-oscillating reference power spectrum, but subtracts a phenomenological
non-oscillating fitting function from the observed boosted transfer function, to extract
the BAOs. Formally FITDEX can be described as follows:
To test FITEX, i.e., the combination of both the fitting function F(k) and the wiggle function Tw(k) under linear conditions, we
first computed normalized transfer functions with CMBfast with the parameter values w=-1 (the transfer functions are affected by w only on scales above several Gpc (Ma et al. 1999)),
![]() ,
,
![]() ,
h=0.70, the primordial slope n=1, the average CMB temperature
,
h=0.70, the primordial slope n=1, the average CMB temperature
![]() K, the He mass fraction after primordial nucleosynthesis
K, the He mass fraction after primordial nucleosynthesis
![]() ,
and the number of neutrino families
,
and the number of neutrino families
![]() .
In the
second step, the phenomenological continuum function (Eq. (6)) was fitted to the multi-component transfer functions in the
range
.
In the
second step, the phenomenological continuum function (Eq. (6)) was fitted to the multi-component transfer functions in the
range
![]() .
The results were subtracted
from the original transfer functions to extract the BAOs. One example
with
.
The results were subtracted
from the original transfer functions to extract the BAOs. One example
with
![]() is shown in Fig. 2. In
the first panel, the multi-component transfer function is
plotted (solid line) as well as the phenomenological fitting
function (dashed line). In the second and third panels, the
differences between the transfer function and the continuum fit are
plotted (solid lines), together with the theoretical wiggle functions (dashed lines)
computed with Eq. (1).
is shown in Fig. 2. In
the first panel, the multi-component transfer function is
plotted (solid line) as well as the phenomenological fitting
function (dashed line). In the second and third panels, the
differences between the transfer function and the continuum fit are
plotted (solid lines), together with the theoretical wiggle functions (dashed lines)
computed with Eq. (1).
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{5649f2a.ps}\vspace*{3mm}
\includegraphics[width=7.4cm,clip]{5649f2b.ps}\end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg80.gif) |
Figure 2: Performance of the phenomenological fitting function under linear conditions. The upper panel shows the CMB fast transfer function (solid line) and the best non-oscillating fit (dashed line). In the lower panels, the residuals of the subtraction are plotted (solid line), as well as the theoretical transfer function (dashed line). The original model gives the performance of the original theoretical function (Eq. (1)), while the corrected model uses the modified function (Eq. (7)). |
| Open with DEXTER | |
With typical baryon fractions,
![]() ,
baryonic oscillations
are hardly visible as they make up only
,
baryonic oscillations
are hardly visible as they make up only ![]()
![]() of the
multi-component transfer function. This illustrates the main
observational challenge in using wiggles as a metric ruler for
cosmological investigations. On small scales,
of the
multi-component transfer function. This illustrates the main
observational challenge in using wiggles as a metric ruler for
cosmological investigations. On small scales,
![]() ,
Fig. 2 shows that the
theoretical wiggle function describes the baryonic oscillations to a satisfactory degree. This is expected, as the transfer function is
dominated by the effects of velocity overshoot and Silk damping on
these scales and the wiggle function was designed to model these
effects. On large scales,
,
Fig. 2 shows that the
theoretical wiggle function describes the baryonic oscillations to a satisfactory degree. This is expected, as the transfer function is
dominated by the effects of velocity overshoot and Silk damping on
these scales and the wiggle function was designed to model these
effects. On large scales,
![]() ,
the BAOs have
to cope with competing CDM effects that dominate in these
k-ranges. As the influence of CDM increases, the transfer function
can not be described by baryonic physics alone, and further corrections
and assumptions have to be applied. Two related effects are:
,
the BAOs have
to cope with competing CDM effects that dominate in these
k-ranges. As the influence of CDM increases, the transfer function
can not be described by baryonic physics alone, and further corrections
and assumptions have to be applied. Two related effects are:
(1) Turnover-effect: the turnover in the matter power spectrum occurs
on the scale
![]() of the particle horizon at
of the particle horizon at
![]() ,
which coincides with the approximate location of the first wiggle. No
observation has hitherto clearly revealed this turnover in spectral
power. The main problem in identifying the turnover is mostly due to
the fact that it is located at large scales where precise
measurements of spectral power are difficult: the surveys cover too
small volumes with slice-like shapes leading to strong smoothing (up
to factors of two for the 2dF survey, Percival et al. 2001) and significant leakage in the
derived power spectra. Under such conditions it appears quite
difficult if not impossible to discriminate the first wiggle from the
turnover when even the position of the turnover could not yet been
determined to some accuracy. To do this, an excellent signal-to-noise
ratio would be needed, as well as precise knowledge of the underlying
linear theory matter power spectrum. This includes information of
distortions of the power spectrum to the sub-percent level. As a consequence, a model-independent approach like separating the BAOs
from the multi-component transfer function with a phenomenological
fitting function will only be able to detect the first wiggle when the
baryon fraction is about as high as 40 percent or more, as we found
with CMBfast simulations. However, we will show that our cosmological
test is most sensitive to changes of w on scales around
,
which coincides with the approximate location of the first wiggle. No
observation has hitherto clearly revealed this turnover in spectral
power. The main problem in identifying the turnover is mostly due to
the fact that it is located at large scales where precise
measurements of spectral power are difficult: the surveys cover too
small volumes with slice-like shapes leading to strong smoothing (up
to factors of two for the 2dF survey, Percival et al. 2001) and significant leakage in the
derived power spectra. Under such conditions it appears quite
difficult if not impossible to discriminate the first wiggle from the
turnover when even the position of the turnover could not yet been
determined to some accuracy. To do this, an excellent signal-to-noise
ratio would be needed, as well as precise knowledge of the underlying
linear theory matter power spectrum. This includes information of
distortions of the power spectrum to the sub-percent level. As a consequence, a model-independent approach like separating the BAOs
from the multi-component transfer function with a phenomenological
fitting function will only be able to detect the first wiggle when the
baryon fraction is about as high as 40 percent or more, as we found
with CMBfast simulations. However, we will show that our cosmological
test is most sensitive to changes of w on scales around
![]() .
Therefore, the inability of a model-independent approach to detect the first BAO does not matter much as this first wiggle barely contributes any information to the
cosmological test, even more as the amplitude of the first wiggle is
comparatively low as it is dampened by CDM effects (see Sect. 7).
.
Therefore, the inability of a model-independent approach to detect the first BAO does not matter much as this first wiggle barely contributes any information to the
cosmological test, even more as the amplitude of the first wiggle is
comparatively low as it is dampened by CDM effects (see Sect. 7).
(2) Phase-shift effects: as mentioned in Sect. 2, the
increasing effect of dark matter on large scales introduces a k-dependent phase-shift of the BAOs. The theoretical wiggle function
(Eq. (1)) already includes a phenomenological correction
for this effect (replacing s by ![]() ). A similar effect on
the phases, but in the opposite direction, is introduced by the
damping of baryons on structure growth. In fact, the main effect of
baryons on the multi-component power spectrum is, assuming a standard
cosmology, a sharp break in power starting on scales smaller than the
turnover. Formally, this break is caused by the rapid decay of the
). A similar effect on
the phases, but in the opposite direction, is introduced by the
damping of baryons on structure growth. In fact, the main effect of
baryons on the multi-component power spectrum is, assuming a standard
cosmology, a sharp break in power starting on scales smaller than the
turnover. Formally, this break is caused by the rapid decay of the
![]() component of the transfer function (see Fig. 1). As the break occurs right after the turnover, it is very
hard to distinguish shape components from oscillations. For the
extraction of BAOs in that scale range, we have found that this
spectral break must be modeled in detail (with an accuracy on the
sub-percent level) or artificial phase-shifts with sizes of the order
of interesting w effects are introduced when naive fitting functions
ignoring this baryonic backreaction are subtracted from the
multi-component power spectrum. Thus the model independent fitting
function presented in this work (Eq. (6)), but also
traditional wiggle-free dark matter transfer functions with a slightly
different functional approach like those given in Bardeen et al. (1986) or Efstathiou et al. (1992), introduce artificial phase-shifts of the generic form
component of the transfer function (see Fig. 1). As the break occurs right after the turnover, it is very
hard to distinguish shape components from oscillations. For the
extraction of BAOs in that scale range, we have found that this
spectral break must be modeled in detail (with an accuracy on the
sub-percent level) or artificial phase-shifts with sizes of the order
of interesting w effects are introduced when naive fitting functions
ignoring this baryonic backreaction are subtracted from the
multi-component power spectrum. Thus the model independent fitting
function presented in this work (Eq. (6)), but also
traditional wiggle-free dark matter transfer functions with a slightly
different functional approach like those given in Bardeen et al. (1986) or Efstathiou et al. (1992), introduce artificial phase-shifts of the generic form
The simulated data used to test FITEX for BAO extraction under more
realistic conditions are provided by the
![]() version of
the Hubble Volume Simulations conducted by the Virgo Consortium
(Evrard et al. 2002). One billion dark matter particles were simulated
with h=0.7,
version of
the Hubble Volume Simulations conducted by the Virgo Consortium
(Evrard et al. 2002). One billion dark matter particles were simulated
with h=0.7,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
and the normalization of the matter power spectrum,
,
and the normalization of the matter power spectrum,
![]() ,
in a cube with a comoving length of
,
in a cube with a comoving length of
![]() and a mass of 2.25
and a mass of 2.25 ![]()
![]() per
particle. The simulations were started with a "glass-like''
load (see, e.g., Baugh et al. 1995). During the simulation itself, long range gravitational forces were computed on a 10243 grid yielding a Nyquist critical frequency
of
per
particle. The simulations were started with a "glass-like''
load (see, e.g., Baugh et al. 1995). During the simulation itself, long range gravitational forces were computed on a 10243 grid yielding a Nyquist critical frequency
of
![]() .
The short range gravitational
forces were computed via direct summation and softened on a scale of
.
The short range gravitational
forces were computed via direct summation and softened on a scale of
![]() .
We used the 10
.
We used the 10 ![]()
![]() fraction of the XW extended deep wedge, which uses periodic boundary
conditions from a redshift of z=4.4 to provide a survey light cone up to the redshift
fraction of the XW extended deep wedge, which uses periodic boundary
conditions from a redshift of z=4.4 to provide a survey light cone up to the redshift
![]() .
The light cone output comprises data that includes cluster
evolution and thus mimics real life observations. Larger distance from the observer correspond to higher redshifts where structures are less pronounced due to linear and non-linear growth.
.
The light cone output comprises data that includes cluster
evolution and thus mimics real life observations. Larger distance from the observer correspond to higher redshifts where structures are less pronounced due to linear and non-linear growth.
Table 1: Parameters of the cubes for the power spectrum estimation. Column 1: cube number; Col. 2: comoving length of the cube (concordance cosmology); Col. 3: redshift range covered by the cube; Col. 4: fundamental mode of the discrete Fourier transformation, which corresponds to the sample bin size of the power spectrum in k space; Col. 5: nyquist critical wavenumber of the fast Fourier transformation.
Power spectra,
![]() ,
were estimated at different
redshifts and for different galaxy biasing schemes b (see below)
with the fast Fourier transform using the variance-optimized method of
Feldman et al. (1994) for cubes along the line-of-sight
(LOS) of the XW wedge. All the cubes were selected to fully fit into the light cone so as to not introduce a non-trivial window function. The parameters of the cubes are given in
Table 1. Note that the spectroscopic SDSS survey of
normal galaxies covers an effective volume that is comparable to
cubes with
,
were estimated at different
redshifts and for different galaxy biasing schemes b (see below)
with the fast Fourier transform using the variance-optimized method of
Feldman et al. (1994) for cubes along the line-of-sight
(LOS) of the XW wedge. All the cubes were selected to fully fit into the light cone so as to not introduce a non-trivial window function. The parameters of the cubes are given in
Table 1. Note that the spectroscopic SDSS survey of
normal galaxies covers an effective volume that is comparable to
cubes with
![]() .
The errors of the power
spectral densities at wavenumber k were estimated with standard mode
counting arguments by
.
The errors of the power
spectral densities at wavenumber k were estimated with standard mode
counting arguments by
![]() to provide a first estimate.
Here,
to provide a first estimate.
Here, ![]() is the mean comoving particle number density in the box, and L the
length of the box. We found that the initial glass load reduces the
shot noise level significantly below the standard Poisson case at
redshifts z>2 (see Smith et al. 2003). Instead of correcting our
spectral estimator for this artifact (see, e.g., Smith et al. 2003), we could in the end neglect its impact on the cosmological
test because our phenomenological fitting function was flexible
enough to compensate for the small residuals of this artifact seen in
our standard scale range
is the mean comoving particle number density in the box, and L the
length of the box. We found that the initial glass load reduces the
shot noise level significantly below the standard Poisson case at
redshifts z>2 (see Smith et al. 2003). Instead of correcting our
spectral estimator for this artifact (see, e.g., Smith et al. 2003), we could in the end neglect its impact on the cosmological
test because our phenomenological fitting function was flexible
enough to compensate for the small residuals of this artifact seen in
our standard scale range
![]() .
.
To extract the BAOs from the power spectra
![]() ,
we computed the corresponding boosted transfer
functions first,
,
we computed the corresponding boosted transfer
functions first,
![]() ,
assuming a primordial spectrum with n = 1 (see
below). Figure 3 shows the estimated power
spectra and the corresponding boosted transfer functions for an unbiased dark matter particle distribution in configuration
space. Error bars include shot noise and sample variance. In most
spectra the 2nd and 3rd BAOs are clearly visible. For
,
assuming a primordial spectrum with n = 1 (see
below). Figure 3 shows the estimated power
spectra and the corresponding boosted transfer functions for an unbiased dark matter particle distribution in configuration
space. Error bars include shot noise and sample variance. In most
spectra the 2nd and 3rd BAOs are clearly visible. For
![]() ,
the phenomenological fitting function
(Eq. (6)) can be computed very accurately as it is
constrained by a large number of spectral data with relatively small
errors, which can be traced reasonably well by a power law. Sample
variance is negligible, as in this k-range, each spectral point
represents the average over a large number of modes. For
,
the phenomenological fitting function
(Eq. (6)) can be computed very accurately as it is
constrained by a large number of spectral data with relatively small
errors, which can be traced reasonably well by a power law. Sample
variance is negligible, as in this k-range, each spectral point
represents the average over a large number of modes. For
![]() ,
only a very small number of spectral
densities, each estimated with a small number of independent modes,
exists and the phenomenological function has to fit a wiggle that
coincides with the turnover. Therefore, the results in the range
,
only a very small number of spectral
densities, each estimated with a small number of independent modes,
exists and the phenomenological function has to fit a wiggle that
coincides with the turnover. Therefore, the results in the range
![]() vary quite a bit. However, we already
excluded this range from the cosmological test (see vertical dashed
lines in Fig. 3 and the discussion at the end
of Sect. 3).
vary quite a bit. However, we already
excluded this range from the cosmological test (see vertical dashed
lines in Fig. 3 and the discussion at the end
of Sect. 3).
The extracted BAOs for the four cubes 7-10 of the XW deep wedge
simulation corresponding to the redshifts z= 1.8-3.7 are shown in
Fig. 4. Spectral densities in the range
![]() ,
which is relevant for unbiased
cosmological tests, are plotted together with the theoretical
wiggle function (Eqs. (1) and (7)) multiplied
by an appropriate amplitude
,
which is relevant for unbiased
cosmological tests, are plotted together with the theoretical
wiggle function (Eqs. (1) and (7)) multiplied
by an appropriate amplitude ![]() .
We see that even
for very large galaxy samples filling a box-like survey volume with a length of
.
We see that even
for very large galaxy samples filling a box-like survey volume with a length of
![]() ,
error bars are mainly determined
by sample variance and are of the same order as the amplitudes of the
BAOs. Therefore, only surveys with significantly larger survey volumes
can show the BAOs with higher significance.
,
error bars are mainly determined
by sample variance and are of the same order as the amplitudes of the
BAOs. Therefore, only surveys with significantly larger survey volumes
can show the BAOs with higher significance.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{5649f3a.ps}\vspace*{5mm}
\includegraphics[width=6.9cm,clip]{5649f3b.ps}\end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg116.gif) |
Figure 3:
Upper panel: power spectra of the matter distribution from the
cubes 7 (upper spectrum) to 10 (lower spectrum) of the XW deep
wedge N-body simulation with superposed linear theory
predictions. The linear matter power spectrum was taken from
Eisenstein & Hu (1998). Amplitude corrections for linear
structure growth were implemented in the standard manner. For
better illustration, the 2nd, 3rd, and 4th spectra are shifted
downwards by the factors
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{5649f4a.ps}\hspace*{4mm}
\i...
...9f4c.ps}\hspace*{4mm}
\includegraphics[width=4cm,clip]{5649f4d.ps} \end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg117.gif) |
Figure 4: Extracted baryonic oscillations of dark matter particles (dots) with error bars including shot noise and sample variance at different redshifts ranging from z = 1.8 ( upper left panel) to z = 3.8 ( lower right panel). Superimposed is the theoretical wiggle function (Eq. (1)) with an appropriate amplitude. |
| Open with DEXTER | |
We further see that the amplitudes of the wiggle functions in
Fig. 4 decrease with increasing redshift, due to
growth suppression (we verified the amplitude change with zaccording to standard linear structure growth). This is a direct
consequence of the fact that distortions of the power spectrum are
directly translated into the boosted transfer function and thus into
distortions of the amplitude of the BAOs. To see how this works and how deviations from
the assumed primordial spectrum with n=1 affect the wiggle function,
we rewrite the primordial spectrum in the form
![]() with
with
![]() small compared to unity. For the assumed power spectrum,
P(k,z,b)=A(k,z,b)knT2(k), this choice gives
small compared to unity. For the assumed power spectrum,
P(k,z,b)=A(k,z,b)knT2(k), this choice gives
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{5649f5.ps} \end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg123.gif) |
Figure 5:
Wiggle extraction from power spectra with different primordial k dependencies.
The resulting oscillations using FITDEX on primordial models with a spectral index n=1
(solid line) are compared to a model with different spectral index n=0.9 (long dashed line)
and a running spectral index with
|
| Open with DEXTER | |
Only the amplitudes of the wiggle functions are
modulated by possibly scale-dependent factors. Although a lot of
interesting information about galaxy formation and cosmology is
contained in the amplitude factors of the wiggle function, we skip
this detail here and perform an amplitude rescaling,
![]() ,
with A(k,z,b) being a basically arbitrary function after
rescaling, summarizing distortions like structure growth, galaxy
biasing, redshift space effects, deviations from the
Harrison-Zel'dovich case, etc. Thus, with FITEX we are not deriving a pure undistorted wiggle function, but a spectrum that is subject to
all the distortions that work on the power spectrum.
,
with A(k,z,b) being a basically arbitrary function after
rescaling, summarizing distortions like structure growth, galaxy
biasing, redshift space effects, deviations from the
Harrison-Zel'dovich case, etc. Thus, with FITEX we are not deriving a pure undistorted wiggle function, but a spectrum that is subject to
all the distortions that work on the power spectrum.
While the oscillations extracted from the Hubble Volume Simulations are consistent with the theoretical template, the error bars prevent a precise evaluation of the accuracy of FITEX
(all 4 cubes will be combined later, see Fig. 15).
To get a better estimate of non-linearities that might wash out wiggles at higher k values,
we use a non-linear analytic form of the power spectrum. This was computed by Jeong & Komatsu (2006) using
3rd-order perturbation theory, which is able to model non-linear N-body matter power spectra to better than 1% at z>2 and
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{5649f6.ps}\end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg125.gif) |
Figure 6: BAO extracted from an analytic power spectrum of Jeong & Komatsu (2006) that includes non-linear growth at z=2.3 (dots). The continuous line is the theoretical wiggle function derived in Sect. 2, multiplied by an appropriate amplitude. See the text for a more detailed discussion of the treatment of the amplitudes of the wiggle function and the analytic power spectrum. |
| Open with DEXTER | |
Figure 6 shows the results of the FITEX extraction applied to the analytic non-linear power spectrum using Hubble Volume parameters. As expected, the amplitude deviates from the theoretical prediction at small k-values, where the shape contribution of the baryons dominates (see Fig. 1), but the phase of the oscillations in the analytical non-linear function is recovered to better than 1% accuracy. This clearly shows, that, at least in theory, FITEX is able to model non-linear effects and recover the oscillations with high accuracy.
As an additional test, the power spectrum of the Hubble Volume Simulation (OCTANT data), a wedge covering one eighth of the sky from
z = 0-1.3 including redshift-space effects, was computed with about 60 million particles in a fast Fourier box with a length of
![]() and the FITDEX algorithm used to extract the oscillations (Fig. 7). The oscillations can be seen, although non-linear growth is heavily washing out the wiggles at
and the FITDEX algorithm used to extract the oscillations (Fig. 7). The oscillations can be seen, although non-linear growth is heavily washing out the wiggles at
![]() .
.
Furthermore, we see a very good correspondence between a FITEX-extracted wiggle function obtained from N-body simulations as well as the analytic non-linear power spectrum and the theoretical wiggle function of FITEX (Eq. (1)) in the HETDEX redshift range. Both linear and non-linear structure growth change the power spectrum and thus the BAOs, but FITEX still gives quite stable and easy to analyze results for the 2nd to 5th BAO. The presence of the BAOs is consistent with the results of recent simulations of, e.g., Springel et al. (2005) and Seo & Eisenstein (2005). However, no specific method to extract the BAOs was applied and their simulations did not include light cone effects. In the following we concentrate on the effects of redshift space and scale-dependent galaxy biasing on the results obtained with FITEX.
The main problem in relating redshift space coordinates with comoving coordinates is the differentiation between red-shifting due to the expansion of the Universe and red-shifting due to peculiar velocities of the measured particles. Two effects might be important.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{5649f7.ps} \end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg128.gif) |
Figure 7: Extracted BAOs using the Hubble Volume Simulation covering one eighth of the sky from redshift 0 to 1.3. Error bars include sample variance and shot noise, but do not cover the washing out effects introduced by the correlation of modes through non-linear growth and distant observer approximation. |
| Open with DEXTER | |
(1) In the linear regime and in combination with the distant observer
approximation, peculiar velocities introduce a boosting factor ![]() along the LOS. Only the k-modes parallel to the LOS,
along the LOS. Only the k-modes parallel to the LOS,
![]() ,
are boosted by the square of the factor
,
are boosted by the square of the factor
![]() with
with
![]() ,
D(z) the linear structure growth, and b(k,z) the biasing parameter (Kaiser
1987).
,
D(z) the linear structure growth, and b(k,z) the biasing parameter (Kaiser
1987).
(2) In the non-linear regime, velocity dispersion of galaxies in
(partially) virialized structures cause the well-known "fingers of
God'' effect in redshift space. We assume that the effect is mainly
restricted to small scales and is describable by a simple exponential
damping of the power spectrum by the factor
![]() .
Here, the redshift-dependent parameter
.
Here, the redshift-dependent parameter ![]() gives a measure of the average pairwise velocity dispersion in the given redshift shell.
gives a measure of the average pairwise velocity dispersion in the given redshift shell.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{5649f8a.ps}\vspace*{3mm}
\includegraphics[width=7.1cm,clip]{5649f8b.ps} \end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg134.gif) |
Figure 8: Redshift space spectra divided by their corresponding real space spectra at different redshifts (filled areas). Overplotted lines represent the best fit of the kernel of Eq. (10). |
| Open with DEXTER | |
The combination of (1) and (2) constitute one version of the standard
dispersion model of peculiar velocities, which relate the
one-dimensional redshift and real space power spectra by
Figure 8 illustrates the combined effect in more
detail. Two redshift space power spectra, as obtained from the Hubble
Volume Simulation, were divided by their corresponding real space
spectra at different redshifts and plotted as filled areas. The kernel
of Eq. (10) was fitted to this ratio and the best-fit
results superposed. We found that the model is
accurate on the 5%-level over the complete redshift range. For
z>2, the parameter ![]() is virtually zero because no
virialization had time to take place on the scales shown. As redshift
decreases, galaxy clusters start to form and virialize and the
is virtually zero because no
virialization had time to take place on the scales shown. As redshift
decreases, galaxy clusters start to form and virialize and the
![]() parameter starts to distort not the amplitude in the
two dimensional power spectrum depending on the angular component, like
parameter starts to distort not the amplitude in the
two dimensional power spectrum depending on the angular component, like ![]() does,
but changes the amplitude depending on the modulus of the k vector.
This means that the shape of the wiggles could be
influenced by this effect as the amplitude of the power spectrum and
thus the amplitude of the wiggles is dampened at high k-values.
does,
but changes the amplitude depending on the modulus of the k vector.
This means that the shape of the wiggles could be
influenced by this effect as the amplitude of the power spectrum and
thus the amplitude of the wiggles is dampened at high k-values.
Fortunately, this anisotropy only gradually changes the amplitude of each consecutive mode in a k-shell, from perpendicular to parallel, which is then averaged. This is illustrated in Fig. 9 where the ratios of boosted transfer functions are plotted. A rough idea about the relation between redshift space effects and the amplitudes of BAOs is provided by the ratio between BAO and the transfer function plotted in the upper part of Fig. 9.
Two examples of wiggle functions boosted by redshift-space effects and extracted with FITEX are plotted in Fig. 10. The result of the anisotropic redshift space is that modes with a more parallel component get more weight than those with a more perpendicular component, which are not boosted. Whereas the overall shape of the wiggle function appears to be slightly changed, the phases of the wiggles are not distorted at all. Instead, the whole wiggle function receives a boost of the monopole component of the Kaiser factor.
The fitting function is obviously able to model the redshift space distortions on the sub-percent level and oscillations can be derived. If the wiggles were not extracted with FITEX-like methods, but by dividing the observed power spectrum by a standard non-oscillatory linear theory power spectrum, as was done by in Springel et al. (2005, Fig. 10) and Cole et al. (2005, Fig. 13), the baseline of the oscillations would start to depart from zero at smaller scales. Such an oscillation spectrum could not easily be used in a cosmological test as it fit only nontrivial theoretical model spectra.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5649f9.ps}\end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg141.gif) |
Figure 9: Ratios of boosted redshift and real-space transfer functions for different redshifts. As expected, the redshift space effects increase with decreasing redshift in a smooth manner. Increasing ratios at high redshifts are an artifact caused by the glass-like initial load of the N-body simulations. To illustrate the relation between redshift space effects and amplitudes of BAOs, the ratio between BAOs and the transfer function is plotted in the upper panel. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{5649f10a.ps}\vspace*{5mm}
\includegraphics[width=7.2cm,clip]{5649f10b.ps}\end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg143.gif) |
Figure 10:
Comparison of wiggle functions at z=1.2 ( upper panel) and z=2.3 ( lower
panel) obtained from real space (filled circles and continuous lines)
and redshift space (open circles and dashed lines). Note the overall
boost of the wiggle functions by redshift space effects, which,
however, leaves the phases of the BAOs invariant.
The non-linear growth effects start to wash out the wiggles
at
|
| Open with DEXTER | |
In the Hubble Volume, CDM particles are simulated. What is
actually observed are galaxies made out of dark matter and baryonic
matter, especially in the case of the proposed HETDEX survey, where
Lyman-![]() emitting galaxies are used as tracers of the underlying
matter distribution. Because of the different properties of dark
matter and baryonic matter (Benson et al. 2000; Le Delliou et al. 2006), both need not necessarily follow exactly the same density distribution.
emitting galaxies are used as tracers of the underlying
matter distribution. Because of the different properties of dark
matter and baryonic matter (Benson et al. 2000; Le Delliou et al. 2006), both need not necessarily follow exactly the same density distribution.
To test the stability of FITEX under such conditions, we introduce some
sort of biasing into the N-body simulations. Formally, biasing is described
by the mean biasing function (Dekel & Lahav 1999),
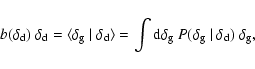 |
(11) |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{5649f11.ps}\end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg158.gif) |
Figure 11: Ratios of biased and unbiased boosted transfer functions for two samples with different scale-dependent biasing at z=2.3. A factor of 2 was subtracted from the strong bias (dashed line) for enhanced visibility, while the weak biasing (solid line) remains unchanged. The theoretical wiggle function is plotted on top of the figure to illustrate the scale of the biasing effects. |
| Open with DEXTER | |
We use the simple stochastic and slightly
non-linear Eulerian biasing scheme (e.g., Cole et al. 1998; Yoshida et al. 2001). First, local overdensities for each dark matter particle are computed
by smoothing the distribution with a Gaussian,
![]() and
and
![]() .
The
overdensities
.
The
overdensities
![]() are then transformed into normalized
overdensities,
are then transformed into normalized
overdensities,
![]() ,
with
,
with
![]() being the root
mean square of the
being the root
mean square of the
![]() -values. Finally, a function is
introduced that describes the probability of a dark matter particle
with overdensity
-values. Finally, a function is
introduced that describes the probability of a dark matter particle
with overdensity
![]() to be tagged as a "galaxy'',
to be tagged as a "galaxy'',
![]() ,
with
,
with
![]() being a threshold at
which the probability is set to zero. This simulates the lower
probability of galaxies forming in low density regions like voids. The
parameter
being a threshold at
which the probability is set to zero. This simulates the lower
probability of galaxies forming in low density regions like voids. The
parameter ![]() controls the stochastic spread of the biasing
function as well as its non-linearity. A value of
controls the stochastic spread of the biasing
function as well as its non-linearity. A value of
![]() is
a good compromise between reasonable non-linearity and a comparably
tight spread. Two samples with
is
a good compromise between reasonable non-linearity and a comparably
tight spread. Two samples with
![]() and 0.6 were
generated. Both parameters,
and 0.6 were
generated. Both parameters, ![]() and
and
![]() ,
were adjusted to
model the biasing parameters and number densities found by
observation. SUBARU data (Hamana et al. 2004) suggests a comoving LAE density of
,
were adjusted to
model the biasing parameters and number densities found by
observation. SUBARU data (Hamana et al. 2004) suggests a comoving LAE density of
![]()
![]()
![]() and a biasing parameter of
and a biasing parameter of ![]() 4-5 at a redshift z = 5,
which should decrease slightly with redshift. As discussed in
Sect. 4 the biasing function
4-5 at a redshift z = 5,
which should decrease slightly with redshift. As discussed in
Sect. 4 the biasing function
![]() should
translate into a boost of the power spectrum b2(k,z). Because the
average slope of the biasing function is
should
translate into a boost of the power spectrum b2(k,z). Because the
average slope of the biasing function is ![]() ,
to first order
we expect
,
to first order
we expect
![]() .
.
The two prescriptions lead to a biasing that either decreases
or increases with k (see
Fig. 11). Both values are consistent with the
calculated ![]() parameter. The comparatively strong scale dependence
of the biasing becomes evident when the ratios of
the boosted transfer functions are compared with the ratio of the
wiggle amplitude to the transfer function plotted on top of
Fig. 11.
parameter. The comparatively strong scale dependence
of the biasing becomes evident when the ratios of
the boosted transfer functions are compared with the ratio of the
wiggle amplitude to the transfer function plotted on top of
Fig. 11.
Figure 12 illustrates that FITEX
extracts BAOs even from biased galaxy distributions. The
wiggle functions of the less strongly biased sample,
the more strongly biased sample, and the unbiased
sample, at z = 2.3, are plotted. The unbiased and biased oscillations vary
because of shot noise, as the biased samples have a 2 and 10 times
lower point density, respectively.
Superimposed are the theoretical wiggle
functions (Eq. (1)), normalized to the unbiased wiggle
function and multiplied by the first moment of the
biasing, ![]() .
The boost of the power spectrum
obviously translates into an amplitude boost of the BAOs. As in
redshift space, only the phenomenological fitting function as used in
FITEX extracts the BAOs with a zero baseline, unlike when using a linear theory power spectrum.
.
The boost of the power spectrum
obviously translates into an amplitude boost of the BAOs. As in
redshift space, only the phenomenological fitting function as used in
FITEX extracts the BAOs with a zero baseline, unlike when using a linear theory power spectrum.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5649f12.ps}\end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg173.gif) |
Figure 12:
Boosted wiggle functions extracted with FITEX and theoretical wiggle
functions for the unbiased sample (filled circles and continuous
line), for the strongly biased sample (triangles and shot-dashed line),
and for the less biased sample (open circles and long-dashed
line). The theoretical wiggle functions are multiplied by the
|
| Open with DEXTER | |
However, not only the overall boost of the power spectrum, but also
the k-dependency of the biasing function should directly affect the
amplitude of the BAOs. We tried to verify this by fitting the Tw(k) function supplemented by a "linear biasing model'' to describe the
extracted wiggle function
![]() .
We
notice that both parameters a0 and a1 are highly degenerate,
mainly due to the fact that only data points at the extrema of the
wiggle function significantly contribute to the fit. Data points at or
near the nodes of the wiggle function are very insensitive to changes
of the amplitude. Due to the degeneracy, any amplitude a0 can easily be compensated by an appropriate value of the
parameter a1. Though the full fits had the expected
slopes, the effects were very small and of no significance for the
cosmological test. We may thus conclude that in a cosmological test,
which is mostly about detecting phase-shifts, it seems to be enough to
fit the theoretical wiggle function with only
an amplitude parameter, when the k-dependent biasing is as weak as
simulated here. However, more realistic simulations are needed to
analyze higher order effects.
.
We
notice that both parameters a0 and a1 are highly degenerate,
mainly due to the fact that only data points at the extrema of the
wiggle function significantly contribute to the fit. Data points at or
near the nodes of the wiggle function are very insensitive to changes
of the amplitude. Due to the degeneracy, any amplitude a0 can easily be compensated by an appropriate value of the
parameter a1. Though the full fits had the expected
slopes, the effects were very small and of no significance for the
cosmological test. We may thus conclude that in a cosmological test,
which is mostly about detecting phase-shifts, it seems to be enough to
fit the theoretical wiggle function with only
an amplitude parameter, when the k-dependent biasing is as weak as
simulated here. However, more realistic simulations are needed to
analyze higher order effects.
The cosmological test compares the phases of the extracted BAOs with the theoretical wiggle function projected onto the hypersphere of the observer. As the theoretical template does not model the amplitude of the oscillations with high accuracy, we are not able to include amplitude effects in the cosmological test and marginalize over the wiggle amplitude. Future tests should include this parameter, which is sensitive to wby, e.g., structure growth.
A general feature of the test is that one first has to assume a certain reference cosmology to get the metric scale of the wiggle function from the data, and to perform the comparison of the metric scale of the theoretical wiggle function relative to the chosen reference cosmology in a second step (Glazebrook & Blake 2005). In the present paper, we are interested in the performance of the BAOs extracted with FITEX in constraining the redshift-independent part of the w parameter of the dark energy. The amplitude of the theoretical function is also fitted, but later marginalized. The remaining cosmological parameters are fixed to their values given at the end of Sect. 1.
As metric scales, comoving distances of the BAOs parallel and
perpendicular to the LOS are used. Recall that in the plane-parallel
or distant observer approximation, comoving distances between two points with the same angular positions, but different redshifts, are
![]() ,
where
H(z)=H0E(z) is the Hubble parameter at redshift z and E(z) the
w-dependent transformation of the Hubble constant, H0, from
redshift zero to z (e.g., Peebles 1993). To compute not distances
between two points in space with different redshifts, but parallel
scaling factors between the two sets of cosmologies denoted by primed
and unprimed symbols, one has to take the limit
,
where
H(z)=H0E(z) is the Hubble parameter at redshift z and E(z) the
w-dependent transformation of the Hubble constant, H0, from
redshift zero to z (e.g., Peebles 1993). To compute not distances
between two points in space with different redshifts, but parallel
scaling factors between the two sets of cosmologies denoted by primed
and unprimed symbols, one has to take the limit
![]() ,
which yields
,
which yields
| |
Figure 13: Transformation of perpendicular (solid) and parallel (dashed) distances in comparison to the concordance model with w0 = -0.7 ( upper part) and w0 = -1.3 ( lower part). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5649f14.ps} \end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg182.gif) |
Figure 14: Scaled wiggle functions at z = 2.5 for w0=-0.7 (dashed line) compared to the w0 = -1 cosmology (solid line, top panel). The normalized modulus of the difference between the reference cosmology and the scaled cosmology is shown in the bottom panel. The dashed vertical lines mark the region relevant for the cosmological test. |
| Open with DEXTER | |
Figure 14 shows the scaled wiggle function at redshift z=2.5 for w0=-0.7. The reference and the distorted wiggle function are plotted. Note that an elongation of the coordinates in real space leads to a compression of the coordinates in k-space and vice versa. In the upper panel, it can be seen that the wiggle function gets more and more out of phase as k increases. Thus the sensitivity of a cosmological test should increase at high values of k. However, the amplitudes of the oscillations decrease exponentially with k(e.g., Silk damping). This can be seen in the lower panel of Fig. 14 where the scaled wiggle function is subtracted from the reference (w0=-1) wiggle function: though the difference in phase is increasing, the amplitude decreases so fast that the difference between the projected oscillations increases at small values of k and decreases at high values of k.
The present version of the cosmological test comprises the following
steps: (1) angular and redshift coordinates of the "observed''
(simulated) data are transformed into comoving coordinates using a concordance model as the reference cosmology. (2) The comoving data
sample is Fourier-transformed to estimate the boosted transfer
functions. (3) BAOs are extracted with FITEX. (4) The theoretical
wiggle function is computed for the corresponding cosmological
model. (5) The parallel and perpendicular scaling factors between the
test cosmology and the reference cosmology are computed at the
redshift of the data sample. (6) The theoretical wiggle function is
scaled by constructing a three-dimensional wiggle function, scaling
each mode and collapsing it to one dimension. (7) The observed wiggle
function is compared to the re-scaled theoretical wiggle function
assuming Gaussian statistical errors (![]() test). Only the steps (4-7) have to be repeated to test a different cosmology, allowing a fast test of various parameters.
test). Only the steps (4-7) have to be repeated to test a different cosmology, allowing a fast test of various parameters.
![\begin{figure}
\par\includegraphics[width=4cm,clip]{5649f15a.ps}\hspace*{4mm}
\...
...15c.ps}\hspace*{4mm}
\includegraphics[width=4cm,clip]{5649f15d.ps} \end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg183.gif) |
Figure 15: Combined wiggle functions from the four Hubble Volume cubes. The upper left panel shows the combined data point (dots) with self-consistent error bars for the 100 square degree field. The upper right panel shows expected error bars for 200 square degrees and the lower row with error bars for 300 and 600 square degrees, respectively. The continuous lines are the theoretical wiggle functions for the reference (concordance) cosmology. |
| Open with DEXTER | |
Note that the three-dimensional wiggle function is only constructed to simulate the effects of different parallel and perpendicular scaling factors. It does not address the anisotropy introduced by redshift space effects because we found that this only boosts the various modes, but does not change the phases of the theoretical wiggle function (see Sect. 5). The boost effect of the redshift space distortions, along with other boosting effects like biasing and growth suppression, will force us to add an additional parameter to the cosmological test.
Figure 15 shows the combined wiggle function of the four XW wedge cubes of the Hubble Volume Simulation in the upper left panel. The combination is performed by averaging over k-bins of discrete size. The errors represent the standard deviation of all wiggle points in the corresponding k-bins. After averaging, the 2nd to 5th BAOs are now clearly visible. We thus conclude that a volume at least 4 times larger than SDSS has to be sampled to see the BAOs with FITEX with high significance. One has to keep in mind, though, that our cubes are located at much higher redshifts, where the smoothing effect of non-linear structure growth is obviously much smaller. We also neglected the fact that larger sky coverages reduce the sizes of the fundamental modes, leading to higher (better) sampling rates of BAOs.
With the 100 square degree sample, the possibility of data points appearing at positions that severely inhibit the accuracy of the cosmological test is relatively high, due to the high sample variance. Especially as only a few data points, which are far away from positions where theoretical wiggle functions of different cosmological models intersect, have great statistical weight in the cosmological test. This fact is shown in Fig. 14, where the modulus of the difference between the theoretical transfer functions for two models depending on the position in k-space is plotted.
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{5649f16.ps} \end{figure}](/articles/aa/full/2007/04/aa5649-06/Timg184.gif) |
Figure 16:
|
| Open with DEXTER | |
Figure 16 shows the results of the cosmological test
obtained with BAOs extracted with FITEX under different survey
conditions. For surveys covering 100 square degrees we would expect errors of
![]() .
The asymmetry of the error distributions directly reflects
the increased sensitivity of metric scales on w for w0>-1 compared
to w0<-1. At these w0 values, the theoretical wiggle function gets
quite compressed, so that at large k values the amplitude decreases
rapidly due to Silk damping. When
.
The asymmetry of the error distributions directly reflects
the increased sensitivity of metric scales on w for w0>-1 compared
to w0<-1. At these w0 values, the theoretical wiggle function gets
quite compressed, so that at large k values the amplitude decreases
rapidly due to Silk damping. When
![]() ,
the
theoretical wiggle function formally mimics the case of zero amplitude, so that low values of w0 are excluded with about the same significance as the "no-wiggle'' case of zero amplitude. The minima of all error distributions plotted in Fig. 16 are slightly
off-set from the input w0=-1 value, but well within all formal
,
the
theoretical wiggle function formally mimics the case of zero amplitude, so that low values of w0 are excluded with about the same significance as the "no-wiggle'' case of zero amplitude. The minima of all error distributions plotted in Fig. 16 are slightly
off-set from the input w0=-1 value, but well within all formal
![]() ranges.
ranges.
Note that the constraints given above are based solely on the phases of the oscillations in the one-dimensional power spectrum, assuming perfect knowledge of the sound horizon at drag epoch. The w-constraints are expected to further improve when the full two dimensional redshift space effects as well as the amplitudes of the BAOs are used.
Perhaps the most important result of the present investigation is the
comparatively small decrease of only 8% of
![]() when comparing the
w test with unbiased matter distributions in configuration
space, (dashed line in Fig. 16) i.e., the simplest survey
condition, with the test that includes all aforementioned effects (solid line).
The robustness of the
FITEX method to extract BAOs from boosted transfer functions with
phenomenological fitting functions is mainly related to the fact that
only the amplitudes of the wiggle functions are boosted by
redshift-space and biasing effects, but the phases are not affected.
when comparing the
w test with unbiased matter distributions in configuration
space, (dashed line in Fig. 16) i.e., the simplest survey
condition, with the test that includes all aforementioned effects (solid line).
The robustness of the
FITEX method to extract BAOs from boosted transfer functions with
phenomenological fitting functions is mainly related to the fact that
only the amplitudes of the wiggle functions are boosted by
redshift-space and biasing effects, but the phases are not affected.
To give an idea of the performance of FITEX based on surveys of larger size, we extrapolated the results from the 100 square degree data. The upper right panel of Fig. 15 shows wiggle functions extracted from the 100 square degree data, but with error bars expected for 200-600 square degrees. The error bars were extrapolated by scaling them according to the expected number of additional k-modes. The different survey fields are thus assumed to be not adjacent.
Figure 15 shows that increasing the survey volume to 200 square degrees does not reduce the error bars significantly, still allowing for crucial data points at peaks of the oscillating wiggle function to be reduced to zero amplitude. Error bars are still of the same order of magnitude as the oscillations. Only at 300 square degrees (lower left panel), the probability for smoothing out the oscillations due to statistical errors gets considerably low. Following our extrapolations, for a survey of 600 square degrees, the errors are expected to get much smaller than the amplitude of the oscillations, and the chance of statistical deviations from the predicted function is of an order of magnitude that allows for very accurate cosmological probing.
The accuracies of the w0 parameter (Fig. 16) range
from
![]() for 100 sq. deg, which corresponds to 3 SDSS volumes,
to
for 100 sq. deg, which corresponds to 3 SDSS volumes,
to
![]() for 600 sq. deg, corresponding to 21 SDSS volumes. These results are obtained
for biased samples in redshift space, i.e., the most complex survey
condition. The improvement is directly related to the larger number of
independent k-modes in larger survey volumes and is consistent with results
obtained with Monte-Carlo simulations (Blake & Glazebrook 2003, their Fig. 8).
Future studies should also investigate the various parameters of the cosmological test to get
constraints under less strong priors.
for 600 sq. deg, corresponding to 21 SDSS volumes. These results are obtained
for biased samples in redshift space, i.e., the most complex survey
condition. The improvement is directly related to the larger number of
independent k-modes in larger survey volumes and is consistent with results
obtained with Monte-Carlo simulations (Blake & Glazebrook 2003, their Fig. 8).
Future studies should also investigate the various parameters of the cosmological test to get
constraints under less strong priors.
We have seen that it is critical for the extraction of BAOs to either fit a phenomenological function to the continuum of the boosted transfer function (FITEX), or to calculate the shape of the boosted transfer function, including all distortions down to the sub-percent level. The latter approach has been carried out recently. Glazebrook & Blake (2005), Hütsi (2005), and Springel et al. (2005) used a linear theory power spectrum and divided the "observed'' data by this reference. Almost the same approach, but with the addition of linearizing the observational data before the division to correct for non-linear structure growth was used in Angulo et al. (2005). There are two drawbacks of this method:
First, the ratio of a complex power spectrum and a reference power spectrum does not resemble a wiggle function as defined in the text, but something more complicated (see Eq. (4)). The simple form of the theoretical wiggle function (Eq. (1)) is strongly deformed by both the chosen transfer function of the reference spectrum and the distortions introduced by redshift space and galaxy biasing. These distortions make the comparison with theoretically expected model spectra unnecessarily complicated. FITEX transforms the observed power spectrum into a boosted transfer function where the subtraction of a non-oscillating phenomenological continuum function is directly related to Tw(k), multiplied by an amplitude factor.
The second drawback is the linear theory power spectrum itself. By
computing a correct shape of the power spectrum, one has to rely
strongly on assumptions about the nature of the dark matter and
various other physical processes. The method is no more the "assumption
free'' approach that was intended. Furthermore, the calculation of the
amplitude factor that includes all the distortions ranging from linear
structure growth, non-linear structure growth to redshift space
distortions and biasing is a problem. This calculation has to be
accurate to the sub-percent level, as the oscillations themselves make
up only ![]()
![]() of the transfer function.
of the transfer function.
A more phenomenological approach was conducted by White (2005). He assumed that redshift space distortions as well as linear and non-linear structure growth could be calculated with reasonable accuracy. Leaving only the ratio between dark matter power spectra and "galaxy'' power spectra, he found that one can fit this ratio with about 2% accuracy using a cubic polynomial. This adds further evidence that a phenomenological approach can model power spectrum distortions without assuming much about the physics of the distortions themselves.
With the FITEX method, we have shown that one is able to extract the BAOs without any strong priors on the nature of dark matter or the shape of the power spectrum from the complex multi-component transfer function. All the aforementioned effects are modeled by the continuum function and need not be known very accurately, as long as the phases of the oscillations are not distorted or washed out. This extraction is accurate on the sub-percent level within k-ranges relevant for the cosmological test. Furthermore, FITDEX is able to disentangle phase information from amplitude information which could in the future be used to test the geometry of the Universe on the one hand and the growth history on the other hand. This type of cosmological test could be used to discriminate dark energy from modified gravity theories.
Acknowledgements
We thank Ralf Bender for initiating this work on baryonic acoustic oscillations, the HETDEX team, the Virgo Consortium for the provision of the data of the Hubble Volume Simulation, Urs Seljak and Mathias Zaldarriga for the CMBfast software, and Daniel Eisenstein and Wayne Hu for the software to compute transfer functions for high baryon fractions.