A&A 461, 793-811 (2007)
DOI: 10.1051/0004-6361:20066130
R. Meijerink1 - M. Spaans2 - F. P. Israel1
1 - Sterrewacht Leiden, PO Box 9513, 2300 RA, Leiden,
The Netherlands
2 - Kapteyn Astronomical Institute, PO Box 800, 9700 AV Groningen,
The Netherlands
Received 28 July 2006 / Accepted 6 October 2006
Abstract
Aims. The nuclei of active galaxies harbor massive young stars, an accreting central black hole, or both. In order to determine the physical conditions that pertain to molecular gas close to the sources of radiation, numerical models are constructed.
Methods. These models iteratively determine the thermal and chemical balance of molecular gas that is exposed to X-rays (1-100 keV) and far-ultraviolet radiation (6-13.6 eV), as a function of depth.
Results. We present a grid of XDR and PDR models that span ranges in density (
102-106.5 cm-3), irradiation (
100.5-105 G0 and
![]() erg cm-2 s-1) and column density (
erg cm-2 s-1) and column density (
![]() cm-2). Predictions are made for the most important atomic fine-structure lines, e.g., [CII], [OI], [CI], [SiII], and for molecular species like HCO+, HCN, HNC, CS and SiO up to J=4, CO and 13CO up to J=16, and column densities for CN, CH, CH+, HCO, HOC+, NO and N2H+. We find that surface temperatures are higher (lower) in PDRs compared to XDRs for densities >104 (<104) cm-3. For the atomic lines, we find that, largely due to the different XDR ionization balance, the fine-structure line ratios of [SiII] 35
cm-2). Predictions are made for the most important atomic fine-structure lines, e.g., [CII], [OI], [CI], [SiII], and for molecular species like HCO+, HCN, HNC, CS and SiO up to J=4, CO and 13CO up to J=16, and column densities for CN, CH, CH+, HCO, HOC+, NO and N2H+. We find that surface temperatures are higher (lower) in PDRs compared to XDRs for densities >104 (<104) cm-3. For the atomic lines, we find that, largely due to the different XDR ionization balance, the fine-structure line ratios of [SiII] 35 ![]() m/[CII] 158
m/[CII] 158 ![]() m, [OI] 63
m, [OI] 63 ![]() m/[CII] 158
m/[CII] 158 ![]() m, [FeII] 26
m, [FeII] 26 ![]() m/[CII] 158
m/[CII] 158 ![]() m and [CI] 369
m and [CI] 369 ![]() m/[CI] 609
m/[CI] 609 ![]() m are larger in XDRs than in PDRs, for a given density, column and irradiation strength. Similarly, for the molecular lines, we find that the line ratios HCN/HCO+ and HNC/HCN, as well as the column density ratio CN/HCN, discriminate between PDRs and XDRs. In particular, the HCN/HCO+ 1-0 ratio is <1 (>1) for XDRs (PDRs) if the density exceeds 105 cm-3 and if the column density is larger than 1023 cm-2. For columns less than 1022.5 cm-2 the XDR HCN/HCO+ 1-0 ratio becomes larger than one, although the individual HCN 1-0 and HCO+ 1-0 line intensities are weaker. For modest densities,
n=104-105 cm-3, and strong radiation fields (>100 erg s-1 cm-2), HCN/HCO+ ratios can become larger in XDRs than PDRs as well. Also, the HCN/CO 1-0 ratio is typically smaller in XDRs, and the HCN emission in XDRs is boosted with respect to CO only for high (column) density gas, with columns in excess of 1023 cm-2 and densities larger than 104 cm-3. Furthermore, CO is typically warmer in XDRs than in PDRs, for the same total energy input. This leads to higher CO J=N+1-N/CO 1-0,
m are larger in XDRs than in PDRs, for a given density, column and irradiation strength. Similarly, for the molecular lines, we find that the line ratios HCN/HCO+ and HNC/HCN, as well as the column density ratio CN/HCN, discriminate between PDRs and XDRs. In particular, the HCN/HCO+ 1-0 ratio is <1 (>1) for XDRs (PDRs) if the density exceeds 105 cm-3 and if the column density is larger than 1023 cm-2. For columns less than 1022.5 cm-2 the XDR HCN/HCO+ 1-0 ratio becomes larger than one, although the individual HCN 1-0 and HCO+ 1-0 line intensities are weaker. For modest densities,
n=104-105 cm-3, and strong radiation fields (>100 erg s-1 cm-2), HCN/HCO+ ratios can become larger in XDRs than PDRs as well. Also, the HCN/CO 1-0 ratio is typically smaller in XDRs, and the HCN emission in XDRs is boosted with respect to CO only for high (column) density gas, with columns in excess of 1023 cm-2 and densities larger than 104 cm-3. Furthermore, CO is typically warmer in XDRs than in PDRs, for the same total energy input. This leads to higher CO J=N+1-N/CO 1-0, ![]() ,
line ratios in XDRs. In particular, lines with
,
line ratios in XDRs. In particular, lines with ![]() ,
like CO(16-15) and CO(10-9) observable with HIFI/Herschel, discriminate very well between XDRs and PDRs. This is crucial since the XDR/AGN contribution will typically be of a much smaller (possibly beam diluted) angular scale and a 10-25
,
like CO(16-15) and CO(10-9) observable with HIFI/Herschel, discriminate very well between XDRs and PDRs. This is crucial since the XDR/AGN contribution will typically be of a much smaller (possibly beam diluted) angular scale and a 10-25![]() PDR contribution can already suppress XDR distinguishing features involving HCN/HCO+ and HNC/HCN. For possible future observations, column density ratios indicate that CH, CH+, NO, HOC+ and HCO are good PDR/XDR discriminators.
PDR contribution can already suppress XDR distinguishing features involving HCN/HCO+ and HNC/HCN. For possible future observations, column density ratios indicate that CH, CH+, NO, HOC+ and HCO are good PDR/XDR discriminators.
Key words: galaxies: ISM - galaxies: active, X-rays: ISM - X-rays: galaxies
The radiation that emanates from galaxy nuclei, such as those of NGC 253 and NGC 1068 or even more extreme (ultra-)luminous infrared galaxies, is believed to originate from regions with active star formation, an accretion disk around a central super-massive black hole or both (e.g. Silk 2005; Maloney 1999; Sanders & Mirabel 1996). The unambiguous identification of the central energy source, or the relative contributions from stars and an active galaxy nucleus (AGN), remains a major challenge in the study of active galaxy centers. The general aim of this paper is to determine how the properties of the irradiated interstellar medium (ISM) may further our understanding.
Table 1: "Standard'' clouds.
Unlike emission at optical wavelengths, atomic, molecular and dust emission in the far-infrared and (sub-)mm range allow one to probe deeply into the large column densities of gas and dust that occupy the centers of active galaxies. Observational studies of the ISM in galaxy centers have been presented by various authors (cf. Aalto 2005; Baan 2005; Ott et al. 2005; Israel 2005; Spoon et al. 2003,2005,2001; Klöckner et al. 2003; Israel & Baas 2002; Garrett et al. 2001; Hüttemeister & Aalto 2001; Curran et al. 2000). Theoretical models show that the spectral energy distribution of the radiation representing star formation (peaking in the ultraviolet) and AGN (peaking in the X-ray regime) activity respectively influences the thermal and chemical balance of the ambient ISM in fundamentally different ways (Meijerink & Spaans 2005; Maloney et al. 1996; Lepp & Dalgarno 1996). The specific aim of this paper is thus to study the extent to which emission from commonly observed molecular and atomic line transitions may be used as a diagnostic tool in the study of external galaxy centers to determine the ambient conditions in general, and the type of irradiation in particular.
To this effect, we have extended the chemical calculations described
by Meijerink & Spaans (2005; hereafter Paper I) for ultraviolet and
X-ray irradiated gas to a much larger parameter space of ambient
conditions and we have performed detailed radiative transfer
calculations to compute the line intensities of many atomic and
molecular transitions. We refer the interested reader to Paper I for a
detailed description of the combined photon-dominated region
(PDR)/X-ray dominated region (XDR) code that we have used to compute
the impact of ultraviolet (PDR) and X-ray (XDR) photons on nearby ISM.
The results described here will be applied to observations of external
galaxy centers in a subsequent paper (Meijerink et al., in
preparation). Stäuber et al. (2005) also developed PDR and XDR codes,
for applications to Young Stellar Objects. The main difference is that
this code has a time dependent chemistry and that it includes ice
evaporation at t=0. This affects the chemistry compared with
traditional steady-state models of pure gas-phase PDRs (e.g.,
CN/HCN). This is not relevant for our cloud models. However,
freeze-out and evaporation start to become important for clouds with
density
![]() cm-3.
cm-3.
The current spatial resolution of sub-millimeter telescopes, such as the James Clerk Maxwell Telescope (JCMT), the Institute de Radio Astronomie Millimétrique (IRAM) telescope and even the Combined Array for Research in Submillimeter Astronomy (CARMA) or the Submillimeter Array (SMA), is insufficient to resolve individual clouds in extragalactic sources. By using these telescopes, each resolution element thus measures the combined emission from a large ensemble of molecular clouds. As a consequence, it is frequently impossible to use a single model cloud solution to describe the observed molecular lines. Instead, more complicated solutions involving two or more model clouds, with differing densities and incident radiation fields, are needed. This contrasts with the study of Galactic objects, where usually a single model cloud solution is sufficient to fit the measurements of single resolution elements.
In this paper, we calculate a grid of "standard'' clouds sampling the different physical conditions believed to be relevant for the centers of active galaxy nuclei. In order to sample both the hierarchical size and (column) density properties of the ISM, we have chosen to construct models for a number of fixed sizes as well as densities. Note that the column densities are not the same for each model, since we use fixed cloud sizes. In these clouds, we investigate the detailed column density dependence for the line ratios HCN/CO, HNC/HCN, HCO+/HCN, SiO/CO and CS/HCN, which include line ratios observed in several galaxies. From our computational grid, one or more, properly weighted, models can be chosen to reproduce observed atomic and molecular lines.
We distinguish three different "standard'' clouds, each with their own
characteristic combinations of size and volume density range, hence
also column density (cf. Table 1), for which we
calculate a set of models for different incident radiation fields, and
where a distinction between irradiation by far-ultraviolet (FUV) and
X-ray photons is made. The X-ray radiation field is a power-law
distribution
![]() integrated between 1 and 100 keV, where
integrated between 1 and 100 keV, where
![]() .
A low energy cut-off of 1 keV is
chosen, since most of the emitted radiation below 1 keV is absorbed in
the hot, highly ionized medium close to the black hole. This power
law spectrum is generally believed to be representative for accreting
black holes. Please note that this differs from Paper I, where we used
a thermal distribution at 106 K instead. The ultraviolet radiation
field (6-13.6 eV) is expressed in multiples of the Habing flux, where
G0=1 corresponds to
.
A low energy cut-off of 1 keV is
chosen, since most of the emitted radiation below 1 keV is absorbed in
the hot, highly ionized medium close to the black hole. This power
law spectrum is generally believed to be representative for accreting
black holes. Please note that this differs from Paper I, where we used
a thermal distribution at 106 K instead. The ultraviolet radiation
field (6-13.6 eV) is expressed in multiples of the Habing flux, where
G0=1 corresponds to
![]() erg cm-2 s-1,
which is the local Galactic interstellar radiation field. We express
the X-ray flux in erg s-1 cm-2. An accreting black hole with
an X-ray luminosity of 1044 erg s-1, produces an X-ray flux
of 100 erg-1 cm-2 at a distance of 100 pc, when there is
not extinction. We use a line width
erg cm-2 s-1,
which is the local Galactic interstellar radiation field. We express
the X-ray flux in erg s-1 cm-2. An accreting black hole with
an X-ray luminosity of 1044 erg s-1, produces an X-ray flux
of 100 erg-1 cm-2 at a distance of 100 pc, when there is
not extinction. We use a line width
![]() km s-1. Cloud
type A represents compact, high-density environments such as molecular
cloud cores, and clouds very close to active nuclei; cloud type B
corresponds to more traditional molecular cloud environments, and
cloud type C is representative of the more diffuse extended
(molecular) medium in which clouds of type B are usually embedded.
km s-1. Cloud
type A represents compact, high-density environments such as molecular
cloud cores, and clouds very close to active nuclei; cloud type B
corresponds to more traditional molecular cloud environments, and
cloud type C is representative of the more diffuse extended
(molecular) medium in which clouds of type B are usually embedded.
Late-type galaxies frequently have radial metallicity gradients, with the highest metallicity in the center (Vila-Costas & Edmunds 1992; Zaritsky et al. 1994). For this reason, we have adjusted the metallicity used in Table 2 of Paper I. The published metallicity gradients and suggestions of a gradient flattening in the very center have led us to adopt a twice Solar metallicity as a reasonable value. Since [C]/[O] abundance ratios decrease at higher metallicities, we have taken the carbon abundance equal to the oxygen abundance (see, for instance, Garnett et al. 1999; Kobulnicky & Skillman 1998). Note that the [C]/[O] ratio affects the abundances of O2 and H2O. See for example Spaans & van Dishoeck (2001) and especially Fig. 2 in Bergin et al. (2000).
From the models, we have calculated the intensities of the molecular rotational lines of HCN, HNC, HCO+, CS and SiO (upto J=4), [CI], [CII], [OI], [SiII] and other fine-structure lines. For CO and 13CO we calculated the intensities of the rotational lines up to J=16, in order to make predictions for future observing facilities such as the ESO Herschel/HIFI space mission. We use the Leiden Atomic and Molecular Database (LAMDA) as described in Schöier et al. (2005) to retrieve the collisional data needed for the calculations. Where no collisional data are available for commonly observed molecules such as CN, CH, CH+, HCO, HOC+, NO and N2H+, we only give column densities.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics*[angle=0]{6130fi1a.ps}}\par\resizebox{8.8cm}{!}{\includegraphics*[angle=0]{6130fi1b.ps}}
\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg20.gif) |
Figure 1: Surface temperatures for PDR ( top) and XDR ( bottom) models. |
| Open with DEXTER | |
To illustrate the coupling differences of FUV and X-ray photons to the gas, we first discuss the surface temperatures of the low, mid, and high density models respectively over the parameter space given for the PDR and XDR models in Table 1. We calculated a larger range of radiation fields for the PDR models than for the XDR models, for reasons related to the heating efficiency which are discussed below. The resulting surface temperatures as a function of gas density and incident radiation intensity for both PDR and XDR models are shown in Fig. 1.
The most important heating mechanism at the edge of a PDR is
photo-electric heating. FUV photons are absorbed by dust grains, which
release electrons that lose their surplus kinetic energy to the gas by
Coulomb interactions. The efficiency of this process increases, when
the grains are more negatively charged, which is determined by a
complex interplay of the impinging radiation field G0, electron
density ![]() and gas temperature T. The absolute efficiency is very
low, since about 0.5-3 percent of the photon energy goes into gas
heating. This sharply contrasts with direct X-ray heating, important
at the edge of XDRs. Direct ionization of an atom yields a kinetic
electron with an energy higher than 1 keV. This electron heats,
ionizes and excites the gas. Depending on the H, H2, He and
electron abundances, the heating efficiency can be up to 70 percent,
much higher than for photo-electric heating. However, there is an
opposing effect, namely the much lower absorption cross section for
X-rays. Since the cross sections scale roughly as E-3, there are
many fewer X-ray photons absorbed than FUV photons.
and gas temperature T. The absolute efficiency is very
low, since about 0.5-3 percent of the photon energy goes into gas
heating. This sharply contrasts with direct X-ray heating, important
at the edge of XDRs. Direct ionization of an atom yields a kinetic
electron with an energy higher than 1 keV. This electron heats,
ionizes and excites the gas. Depending on the H, H2, He and
electron abundances, the heating efficiency can be up to 70 percent,
much higher than for photo-electric heating. However, there is an
opposing effect, namely the much lower absorption cross section for
X-rays. Since the cross sections scale roughly as E-3, there are
many fewer X-ray photons absorbed than FUV photons.
We find that at high densities (n > 104 cm-3) PDR models
produce higher surface temperatures than the XDR models. At low
densities, however, we find the opposite, especially in the case of
high radiation fields. This is explained by the drop in the efficiency
of photo-electric heating due to grain charging at densities n <
105 cm-3 when the same impinging radiation field is
considered. This is nicely illustrated in Fig. 6 of
Kaufman et al. (1999), where the ratios of the intensity of the
[CII] 158 ![]() m and [OI] 63
m and [OI] 63 ![]() m lines to the total far-infrared
intensity emitted from the surface of the clouds are plotted as a
function of density and radiation field. This ratio is a measure of
the heating efficiency, since [CII] 158
m lines to the total far-infrared
intensity emitted from the surface of the clouds are plotted as a
function of density and radiation field. This ratio is a measure of
the heating efficiency, since [CII] 158 ![]() m and [OI] 63
m and [OI] 63 ![]() m are
the most important coolants in PDRs.
m are
the most important coolants in PDRs.
In the regime discussed here, the surface temperatures of the XDR
models are quite well correlated with
![]() ,
where
,
where ![]() is the
energy deposition per particle and n the total hydrogen density.
This means that the highest surface temperatures are found at the
lowest densities and highest impinging radiation fields.
Consequently, the contours of equal surface temperature are almost
straight lines in the XDR plot of Fig. 1. In
the PDR models their behavior is more complicated, as already
discussed by Kaufman et al. (1999), since grains are involved in heating
the gas. At the edge of the cloud, the cooling is dominated by [CII]
158
is the
energy deposition per particle and n the total hydrogen density.
This means that the highest surface temperatures are found at the
lowest densities and highest impinging radiation fields.
Consequently, the contours of equal surface temperature are almost
straight lines in the XDR plot of Fig. 1. In
the PDR models their behavior is more complicated, as already
discussed by Kaufman et al. (1999), since grains are involved in heating
the gas. At the edge of the cloud, the cooling is dominated by [CII]
158 ![]() m and [OI] 63
m and [OI] 63 ![]() m, which have critical densities of
m, which have critical densities of
![]() cm-3 and
cm-3 and
![]() cm-3 for collisions with atomic and
molecular hydrogen. The cooling rate in this regime is more or less
proportional to n2. The heating rate is at least proportional to n, because the grain density is proportional to n. It can be
larger, because grains become less positively charged at increasing
electron densities making it easier for electrons to escape the
grains, so that the heating efficiency increases. Nevertheless, the
density dependence of heating remains less steep than n2, i.e.,
less than that of cooling, which causes a drop in the temperature at
n < 104 cm-3 and for fixed G0 with increasing density.
Between
cm-3 for collisions with atomic and
molecular hydrogen. The cooling rate in this regime is more or less
proportional to n2. The heating rate is at least proportional to n, because the grain density is proportional to n. It can be
larger, because grains become less positively charged at increasing
electron densities making it easier for electrons to escape the
grains, so that the heating efficiency increases. Nevertheless, the
density dependence of heating remains less steep than n2, i.e.,
less than that of cooling, which causes a drop in the temperature at
n < 104 cm-3 and for fixed G0 with increasing density.
Between
![]() cm-3 where the [CII] 158
cm-3 where the [CII] 158 ![]() m
line thermalizes, the drop in temperature stagnates. For densities
between
n=104-105 cm-3 and
G0 < 104, we also find that
the surface temperature drops with increasing n. The [OI] 63
m
line thermalizes, the drop in temperature stagnates. For densities
between
n=104-105 cm-3 and
G0 < 104, we also find that
the surface temperature drops with increasing n. The [OI] 63![]() m
line thermalizes at higher densities
n=105-106 cm-3 and,
therefore, cooling will be proportional to n. Heating increases
faster with density, which results in a higher surface temperature.
For G0>104, we find that the surface temperature rises up to
m
line thermalizes at higher densities
n=105-106 cm-3 and,
therefore, cooling will be proportional to n. Heating increases
faster with density, which results in a higher surface temperature.
For G0>104, we find that the surface temperature rises up to
![]() cm-3 due to the increase in the heating
efficiency with density at fixed G0. Above this density and at
these high temperatures, coolants with high critical densities and
excitation energies such as the [OI] 6300 Å line become important,
causing the surface temperature to drop again.
cm-3 due to the increase in the heating
efficiency with density at fixed G0. Above this density and at
these high temperatures, coolants with high critical densities and
excitation energies such as the [OI] 6300 Å line become important,
causing the surface temperature to drop again.
When we compare the surface temperatures with those derived by
Kaufman et al. (1999), we find that our model surface temperatures are
higher. A possible explanation for this has been discussed recently by
Röllig et al. (2006), who present scaling relations for heating and
cooling as a function of metallicity Z. They state that the
photo-electric heating rate is ![]() Z for n<103 cm-3increasing to Z2 when n>106 cm-3. The cooling rate is
always proportional to Z, and, therefore, higher metallicities
result in higher surface temperatures. Note however that the
temperature differences found are very likely not only because of a
change in metallicity. In the PDR comparison test
(Röllig et al. 2006), we found significant scatter between different
PDR codes in the thermal balance. Therefore, one should not take the
absolute values of line intensities too literally in the
interpretation of data.
Z for n<103 cm-3increasing to Z2 when n>106 cm-3. The cooling rate is
always proportional to Z, and, therefore, higher metallicities
result in higher surface temperatures. Note however that the
temperature differences found are very likely not only because of a
change in metallicity. In the PDR comparison test
(Röllig et al. 2006), we found significant scatter between different
PDR codes in the thermal balance. Therefore, one should not take the
absolute values of line intensities too literally in the
interpretation of data.
In principle, we can use combinations of fine-structure line intensities to constrain densities and incident radiation fields. Here we discuss how such line ratios depend on gas density, ambient radiation field strength, and cloud column density, and compare the results for the PDR and XDR models. In previous studies only results for PDRs were shown. Wolfire et al. (1990) were the first to show [CII]/[SiII] contour plots for PDRs. Recently, Kaufman et al. (2006) showed updated plots for [SiII] and [FeII] for PDR gas. The fine-structure lines are selfconsistently calculated in the PDR and XDR codes, and we take line-trapping into account for ALL lines.
In Fig. A.1, we show the [SiII] 34.8 ![]() m/[CII] 158
m/[CII] 158 ![]() m fine-structure line ratio for both the PDR and the
XDR models. The [SiII] 34.8
m fine-structure line ratio for both the PDR and the
XDR models. The [SiII] 34.8 ![]() m line has an energy of E/k=414 K
and a critical density of
m line has an energy of E/k=414 K
and a critical density of
![]() cm-3, while this
is E/k=92 K and
cm-3, while this
is E/k=92 K and
![]() cm-3 for the [CII]
158
cm-3 for the [CII]
158 ![]() m. Very high radiation fields produce gas temperatures in the
PDR models that are sufficiently high to excite the [SiII] and [CII]
upper states and the ratio depends mostly on density. With lower
radiation fields, the surface temperature drops. The upper level
energy of [SiII] 34.8
m. Very high radiation fields produce gas temperatures in the
PDR models that are sufficiently high to excite the [SiII] and [CII]
upper states and the ratio depends mostly on density. With lower
radiation fields, the surface temperature drops. The upper level
energy of [SiII] 34.8 ![]() m is reached first and the [SiII]/[CII]
line ratio drops. As the density increases at a given FUV radiation
field, the ratios limit to roughly constant values that are set by the
corresponding surface temperatures.
m is reached first and the [SiII]/[CII]
line ratio drops. As the density increases at a given FUV radiation
field, the ratios limit to roughly constant values that are set by the
corresponding surface temperatures.
In the XDR models, the ratio is not only determined by the temperature
and density, but also by the fractional abundances and column
densities. In PDRs clearly defined layers occur, in which carbon and
silicon are both almost fully ionized, but throughout XDRs neutral and
ionized species co-exist. Despite the fact that surface temperatures
in the XDR models are lower, we find much higher [SiII]/[CII] ratios,
since silicon is much easier to ionize than carbon. The dominant
source for ionization is not the direct absorption of an X-ray photon
(primary ionization), but the produced kinetic electron. This electron
can ionize a species either directly by collisions (secondary
ionizations) or indirectly by first exciting H and H2 and producing
Lyman ![]() and Lyman-Werner photons, which then may ionize species
in turn. The cross section of Si for secondary ionization is about
twice that of C. This does not, however, fully explain the order of
magnitude difference between the calculated PDR and XDR ratios. This
difference also reflects the fact that ionization of C can only be
done by Lyman-Werner photons, whereas both Lyman
and Lyman-Werner photons, which then may ionize species
in turn. The cross section of Si for secondary ionization is about
twice that of C. This does not, however, fully explain the order of
magnitude difference between the calculated PDR and XDR ratios. This
difference also reflects the fact that ionization of C can only be
done by Lyman-Werner photons, whereas both Lyman ![]() and
Lyman-Werner photons are capable of ionizing Si. It is thus harder to
ionize C than Si in regions where the gas is mostly atomic, which
results in a large increase of the ratio for all densities at a given
irradiation strength.
and
Lyman-Werner photons are capable of ionizing Si. It is thus harder to
ionize C than Si in regions where the gas is mostly atomic, which
results in a large increase of the ratio for all densities at a given
irradiation strength.
This also explains the fairly constant ratio below
![]() erg s-1 cm-2 for
erg s-1 cm-2 for
![]() cm-3, which results from an interplay between various
effects. With ambient radiation fields constant, we find that the
surface temperatures drop with increasing density in the XDR. At lower
temperatures and higher densities, H2 is more easily formed. Both
the temperature drop itself and the enhanced H2 (leading to more
carbon ionizations) thus suppresses the [SiII]/[CII] ratio, but this
is compensated by the relatively high critical density of the [SiII]
34.8
cm-3, which results from an interplay between various
effects. With ambient radiation fields constant, we find that the
surface temperatures drop with increasing density in the XDR. At lower
temperatures and higher densities, H2 is more easily formed. Both
the temperature drop itself and the enhanced H2 (leading to more
carbon ionizations) thus suppresses the [SiII]/[CII] ratio, but this
is compensated by the relatively high critical density of the [SiII]
34.8 ![]() m line.
m line.
For the highest, >16 erg s-1 cm-2, radiation fields, where carbon is highly ionized, we find the same trend as seen for the PDR, i.e., the ratio is mostly dependent on density for the highest radiation fields, and then there is a decrease in the ratio when the temperature drops below the upper-state energy of [SiII].
At the lowest densities and highest X-ray radiation fields, we find
that the effect of column density become important as well. Since we
fixed cloud sizes, in each cloud type the lowest density models imply
also the lowest column densities. In the high irradiation models,
carbon is almost fully ionized at the XDR edge. The fractional
abundance of ionized carbon drops toward the H/H2 transition and
then increases again for the reasons discussed earlier. In the lowest
(column) density models, we only produce the highly ionized part,
suppressing the ratio even more. This is best seen in the diagram for
the high density XDR models, at densities n=104 cm-3. The
ratio increases from
![]() to 30 erg s-1 cm-2 and then
drops again. Hence, if we increase the column densities of these
models by a factor of
to 30 erg s-1 cm-2 and then
drops again. Hence, if we increase the column densities of these
models by a factor of ![]() 30, the ratios only depend on radiation
field strength and not on density.
30, the ratios only depend on radiation
field strength and not on density.
![\begin{figure}
{\includegraphics[height=160mm,clip=]{6130fig2.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg36.gif) |
Figure 2:
[OI] 63 |
| Open with DEXTER | |
![\begin{figure}
{\includegraphics[height=160mm,clip=]{6130fig3.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg37.gif) |
Figure 3:
[CI] 369 |
| Open with DEXTER | |
In Fig. 2, we show the [OI] 63 ![]() m/[CII]
158
m/[CII]
158 ![]() m ratio. The critical density is
m ratio. The critical density is
![]() cm-3 and the upper-state energy is
E/k=228 K for [OI] 63
cm-3 and the upper-state energy is
E/k=228 K for [OI] 63 ![]() m. In the PDR models and at very high
incident radiation fields, this ratio depends mostly on density as in
the case for the [SiII]/[CII] ratio, since once again temperatures are
sufficiently high to excite both upper-state levels. When the surface
temperature drops for lower radiation fields, the upper-state energy
of [OI] is reached first. The [OI]/[CII] ratio then drops, with a flat
density dependence for n<104 cm-3 and G0<103. The decrease
in this line ratio is, however, less pronounced than that in the
[SiII]/[CII] ratio, because the upper-state energy of [OI] is lower
than that of [SiII]. When G0<103 and
n>105.5 cm-3, the
ratio is roughly constant at the same density for all values of G0.
Here, the more difficult excitation of [OI] at lower temperatures is
counteracted by the C+ layer becoming thinner at lower radiation
fields.
m. In the PDR models and at very high
incident radiation fields, this ratio depends mostly on density as in
the case for the [SiII]/[CII] ratio, since once again temperatures are
sufficiently high to excite both upper-state levels. When the surface
temperature drops for lower radiation fields, the upper-state energy
of [OI] is reached first. The [OI]/[CII] ratio then drops, with a flat
density dependence for n<104 cm-3 and G0<103. The decrease
in this line ratio is, however, less pronounced than that in the
[SiII]/[CII] ratio, because the upper-state energy of [OI] is lower
than that of [SiII]. When G0<103 and
n>105.5 cm-3, the
ratio is roughly constant at the same density for all values of G0.
Here, the more difficult excitation of [OI] at lower temperatures is
counteracted by the C+ layer becoming thinner at lower radiation
fields.
In the XDR, the [OI]/[CII] ratio is again more complex due to its
dependence on density, radiation field, ionized carbon fraction and
total column density. The ratios are overall much higher than in the
PDR models, since carbon does not become fully ionized. At the largest
![]() ,
temperatures are high enough to create a dependence on
density only. At lower radiation fields, the [OI]/[CII] ratio drops as
temperatures approach the upper-state energy of the [OI] 63
,
temperatures are high enough to create a dependence on
density only. At lower radiation fields, the [OI]/[CII] ratio drops as
temperatures approach the upper-state energy of the [OI] 63 ![]() m
line. When we decrease the radiation field even more, we find that the
C+ fraction is rapidly reduced at high (>105 cm-3)
densities and the ratio increases again. At high
(>16 erg s-1 cm-2) radiation field strength and low
densities, a large
m
line. When we decrease the radiation field even more, we find that the
C+ fraction is rapidly reduced at high (>105 cm-3)
densities and the ratio increases again. At high
(>16 erg s-1 cm-2) radiation field strength and low
densities, a large
![]() is maintained throughout the whole cloud,
since the relevant type A cloud size is only one parsec. For that
reason, we find here the same effect as already seen in the
[SiII]/[CII] ratio, since column densities increase toward higher
densities. At the highest radiation fields and lowest densities, the
ratio is suppressed since carbon remains partially ionized over the
full extent of the clouds considered here. We do not find the highest
ratio at the highest radiation field in the lower density models.
is maintained throughout the whole cloud,
since the relevant type A cloud size is only one parsec. For that
reason, we find here the same effect as already seen in the
[SiII]/[CII] ratio, since column densities increase toward higher
densities. At the highest radiation fields and lowest densities, the
ratio is suppressed since carbon remains partially ionized over the
full extent of the clouds considered here. We do not find the highest
ratio at the highest radiation field in the lower density models.
In Fig. A.2, we show the [FeII] 26 ![]() m/[CII] 158
m/[CII] 158 ![]() m intensity ratio. [FeII] 26
m intensity ratio. [FeII] 26 ![]() m is very difficult
to excite due to its high critical density
m is very difficult
to excite due to its high critical density
![]() cm-3 and upper-state energy E/k=554 K.
Thus, the change in ratio with increasing density at high incident
radiation fields is much larger than that seen for the [SiII]
34.8
cm-3 and upper-state energy E/k=554 K.
Thus, the change in ratio with increasing density at high incident
radiation fields is much larger than that seen for the [SiII]
34.8 ![]() m/[CII] 158
m/[CII] 158 ![]() m ratio. In the PDR models and at high
incident radiation fields, the ratio mostly depends on the density. At
lower radiation field strengths, approaching the upper-state energy of
[FeII], the ratio drops.
m ratio. In the PDR models and at high
incident radiation fields, the ratio mostly depends on the density. At
lower radiation field strengths, approaching the upper-state energy of
[FeII], the ratio drops.
The same trends are seen at high radiation fields in the XDR models,
but again, we find much higher ratios than in the PDR models. It is
possible to ionize iron with Lyman ![]() photons, but not
carbon. At moderate radiation fields, we again find ratios to be more
or less independent of density, for the reason that we have already
discussed in the [SiII]/[CII] case. At the lowest densities and
highest radiation fields in each cloud type, we find that the ratios
are similarly suppressed as was the case for [SiII] 35
photons, but not
carbon. At moderate radiation fields, we again find ratios to be more
or less independent of density, for the reason that we have already
discussed in the [SiII]/[CII] case. At the lowest densities and
highest radiation fields in each cloud type, we find that the ratios
are similarly suppressed as was the case for [SiII] 35 ![]() m/[CII]
158
m/[CII]
158 ![]() m and [OI] 63
m and [OI] 63 ![]() m/[CII] 158
m/[CII] 158 ![]() m.
m.
In Fig. 3, we show the [CI] 369 ![]() m/[CI]
609
m/[CI]
609 ![]() m intensity ratio. The critical densities of these lines are
m intensity ratio. The critical densities of these lines are
![]() cm-2 for [CI] 609
cm-2 for [CI] 609 ![]() m and
m and
![]() cm-2 for [CI] 369
cm-2 for [CI] 369 ![]() m, typically lower
than the densities we are considering here. The upper-state energies
are E/k=24 and 63 K for [CI] 609
m, typically lower
than the densities we are considering here. The upper-state energies
are E/k=24 and 63 K for [CI] 609![]() m and [CI] 369
m and [CI] 369 ![]() m,
respectively. In the PDR models, the [CI] lines originate from the
C+/C/CO transition layer. The temperatures in this layer slightly
rise with increasing incident radiation field strengths and range
between
T=20-100 K (comparable to the upper-state energies). This
explains the small increase in the ratio for larger G0 at the same
density. The ratio does not change much as a function of density,
since we are above the critical density. The change we do see,
however, has a temperature dependence. When densities are lowered,
recombination rates are lower as well. By consequence, at higher
densities, the transition layer is closer to the edge of the cloud and
at higher temperatures, which raises the ratio.
m,
respectively. In the PDR models, the [CI] lines originate from the
C+/C/CO transition layer. The temperatures in this layer slightly
rise with increasing incident radiation field strengths and range
between
T=20-100 K (comparable to the upper-state energies). This
explains the small increase in the ratio for larger G0 at the same
density. The ratio does not change much as a function of density,
since we are above the critical density. The change we do see,
however, has a temperature dependence. When densities are lowered,
recombination rates are lower as well. By consequence, at higher
densities, the transition layer is closer to the edge of the cloud and
at higher temperatures, which raises the ratio.
In the XDR, neutral carbon occurs throughout the cloud, and is also
abundant at relatively high temperatures. The spread in temperatures
is large, which was already seen in Sect. 3, and this determines for
a large part differences in the ratios. The temperature of a cloud is
determined by
![]() ,
resulting in the highest ratios for low n and
high
,
resulting in the highest ratios for low n and
high ![]() ,
opposite to the situation in the PDR models. The three
cloud types, with their different low, mid and high density ranges
nevertheless show very similar spreads in ratios. This is caused by
the difference in column densities, which also has a very important
effect. The low, mid, and high density models have their own fixed
cloud size, and in each standard cloud type, column densities increase
toward higher densities in the same density range. The higher density
models contain larger regions of low temperature, which suppresses the
ratio at these densities even more. This can also be understood by
considering the ratio at n=104 cm-3 in the mid (type B) and
high (type C) density range. The high density model at
n=104 cm-3 has a smaller cloud size and therefore a higher
line ratio.
,
opposite to the situation in the PDR models. The three
cloud types, with their different low, mid and high density ranges
nevertheless show very similar spreads in ratios. This is caused by
the difference in column densities, which also has a very important
effect. The low, mid, and high density models have their own fixed
cloud size, and in each standard cloud type, column densities increase
toward higher densities in the same density range. The higher density
models contain larger regions of low temperature, which suppresses the
ratio at these densities even more. This can also be understood by
considering the ratio at n=104 cm-3 in the mid (type B) and
high (type C) density range. The high density model at
n=104 cm-3 has a smaller cloud size and therefore a higher
line ratio.
Molecular rotational lines are also characteristic for the physical
condition of ISM gas and may also be used to constrain gas densities
and incident radiation fields. In the following, we discuss a number
of ratios, involving the molecular species 12CO, 13CO, HCN,
HNC, HCO+, SiO and CS. Although we reproduce in this Paper only a
limited number of the diagrams showing the calculated line intensity
ratios, all model data are available on-line![]() . Hence, the reader
can determine all line ratios and integrate over all possible lines of
sight as interest dictates. Here we concentrate on molecular lines
that we consider particularly useful to distinguish between PDRs and
XDRs. We have calculated the line intensities by using a
one-dimensional version of the radiation transfer code described in
Poelman & Spaans (2006,2005).
. Hence, the reader
can determine all line ratios and integrate over all possible lines of
sight as interest dictates. Here we concentrate on molecular lines
that we consider particularly useful to distinguish between PDRs and
XDRs. We have calculated the line intensities by using a
one-dimensional version of the radiation transfer code described in
Poelman & Spaans (2006,2005).
![\begin{figure}
{\includegraphics[height=150mm,clip=]{6130fig4.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg42.gif) |
Figure 4: CO(2-1)/CO(1-0) ratio for PDR ( left) and XDR ( right) models. |
| Open with DEXTER | |
![\begin{figure}
{\includegraphics[height=145mm,clip=]{6130fig5.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg43.gif) |
Figure 5: CO(4-3)/CO(1-0) ratio for PDR ( left) and XDR ( right) models. |
| Open with DEXTER | |
In Fig. A.3, we show the CO(1-0) line intensity for
cloud types A (high-density), B (mid-density) and C (low-density) for
both the PDR and XDR model cases (cf. Table 1). All
three cloud types are relevant for CO (and 13CO) since these
molecules are present ubiquitously on all galactic scales. The CO(1-0)
line has an upper state energy E/k=5.53 K and a critical density
![]() cm-3. In the low density PDR models
(
n=102-103 cm-3), we find that the intensity increases with
density only. In the mid (
n=103-104 cm-3) and high
(
n=104-106.5 cm-3) density range, we also find a small line
intensity increase at higher incident radiation fields. The emission
of the CO(1-0) line is optically thick and the emitted line intensity
mostly depends on the gas temperature near the
cm-3. In the low density PDR models
(
n=102-103 cm-3), we find that the intensity increases with
density only. In the mid (
n=103-104 cm-3) and high
(
n=104-106.5 cm-3) density range, we also find a small line
intensity increase at higher incident radiation fields. The emission
of the CO(1-0) line is optically thick and the emitted line intensity
mostly depends on the gas temperature near the ![]() surface. Although the upper-state energy is below the gas temperature,
we find a significant increase in the line intensity. At higher
densities, gas-grain interactions may significantly increase gas
temperatures in the highly attenuated part of the cloud. Since the
escape probability
surface. Although the upper-state energy is below the gas temperature,
we find a significant increase in the line intensity. At higher
densities, gas-grain interactions may significantly increase gas
temperatures in the highly attenuated part of the cloud. Since the
escape probability
![]() when
when ![]() ,
these
parts also add a small contribution to the line intensity, which is
proportional to
,
these
parts also add a small contribution to the line intensity, which is
proportional to ![]()
![]() .
For an elaborate discussion of the
CO(1-0) line intensity dependence on G0 and n see
Wolfire et al. (1989). In general, the line intensities do not vary much
in the PDR models, as opposed to what is seen in the XDR models. In
all PDR models, the CO(1-0) lines are optically thick. In the XDR
models for type C clouds (
n=102-103 cm-3), the line
intensities vary over two orders of magnitude. Because of the fixed
cloud size, models at higher densities have larger column densities.
Even at the point farthest from the cloud edge, the low density gas in
type C clouds causes relatively little radiation attenuation, and with
high incident radiation it is at very high temperature and in a highly
ionized state throughout. Under these conditions warm CO gas present,
but only in very small amounts. Therefore, at such points in parameter
only very weak line emission is produced and the lines are optically
thin. In the high density range (
n=104-106.5 cm-3) of type
A clouds, on the other hand, the spread in intensity is much
reduced. Although at densities of n=104 cm-3 most of the cloud
is still at a high temperature and in a highly ionized state, there is
sufficient column density to have CO abundances large enough to
produce significant line emission. At even higher densities
(n=106 cm-3), the column densities are high enough to
attenuate the radiation field in such a way that a large CO fraction
is produced (
.
For an elaborate discussion of the
CO(1-0) line intensity dependence on G0 and n see
Wolfire et al. (1989). In general, the line intensities do not vary much
in the PDR models, as opposed to what is seen in the XDR models. In
all PDR models, the CO(1-0) lines are optically thick. In the XDR
models for type C clouds (
n=102-103 cm-3), the line
intensities vary over two orders of magnitude. Because of the fixed
cloud size, models at higher densities have larger column densities.
Even at the point farthest from the cloud edge, the low density gas in
type C clouds causes relatively little radiation attenuation, and with
high incident radiation it is at very high temperature and in a highly
ionized state throughout. Under these conditions warm CO gas present,
but only in very small amounts. Therefore, at such points in parameter
only very weak line emission is produced and the lines are optically
thin. In the high density range (
n=104-106.5 cm-3) of type
A clouds, on the other hand, the spread in intensity is much
reduced. Although at densities of n=104 cm-3 most of the cloud
is still at a high temperature and in a highly ionized state, there is
sufficient column density to have CO abundances large enough to
produce significant line emission. At even higher densities
(n=106 cm-3), the column densities are high enough to
attenuate the radiation field in such a way that a large CO fraction
is produced (![]() 10-4), but still at a temperature of
10-4), but still at a temperature of
![]() K. Here, the CO(1-0) line emission produced in XDRs can be
two to four times stronger than that in PDRs.
K. Here, the CO(1-0) line emission produced in XDRs can be
two to four times stronger than that in PDRs.
For the CO(2-1) line, the upper state energy is E/k=16.60 K and the
critical density is
![]() cm-3. Although not
shown, the line intensities exhibit a behavior as a function of
density and radiation field very similar that that of the CO(1-0)
line. Because of the higher upper state energy, we find a somewhat
stronger dependence on radiation field in the PDR models. The effect
of the larger critical density is hard to see, due to the large
optical depths, but do show up when we consider the CO(2-1)/CO(1-0)
ratio. This ratio is shown in Fig. 4. In the PDR
models, the ratio does not differ more than a factor of two over the
full density range considered here. In the XDR models, very large line
intensity ratios of 30 or more are found, especially at high incident
radiation fields. It is, however, very questionable whether we will
actually observe these high ratios, since the intensity of the emitted
emission is low. The CO(2-1)/CO(1-0) ratio dependence on density and
radiation field is in general weak, especially in PDRs, since the
upper state energies are not very high and the difference in critical
density is small.
cm-3. Although not
shown, the line intensities exhibit a behavior as a function of
density and radiation field very similar that that of the CO(1-0)
line. Because of the higher upper state energy, we find a somewhat
stronger dependence on radiation field in the PDR models. The effect
of the larger critical density is hard to see, due to the large
optical depths, but do show up when we consider the CO(2-1)/CO(1-0)
ratio. This ratio is shown in Fig. 4. In the PDR
models, the ratio does not differ more than a factor of two over the
full density range considered here. In the XDR models, very large line
intensity ratios of 30 or more are found, especially at high incident
radiation fields. It is, however, very questionable whether we will
actually observe these high ratios, since the intensity of the emitted
emission is low. The CO(2-1)/CO(1-0) ratio dependence on density and
radiation field is in general weak, especially in PDRs, since the
upper state energies are not very high and the difference in critical
density is small.
The CO(4-3) line (see Fig. A.4) has an upper state
energy E/k=55.32 K and critical density
![]() cm-3. As expected, the emitted intensity
shows more variation with density and radiation field. In
Fig. 5, we show the CO(4-3)/CO(1-0) line intensity
ratio. In the low density range (cloud type C), PDR models still
produce a line ratio increase only as function of density, but the
variation in the ratio has grown to more than a factor of two, as
opposed to only 20 percent in the corresponding CO(2-1)/CO(1-0)
ratio. The XDRs for this cloud type show a complex behavior with
density and radiation field and the ratios cover a much larger range
from about 2 to 40. At low radiation fields, only a density dependence
is seen. At high radiation field strengths, the effect of the column
density comes into play. In the mid density (type B) PDRs, the highest
line ratios are seen for the highest densities and radiation
fields. The XDRs in this range show only a dependence on radiation
field. The effect of the higher density is compensated by the fact
that at lower densities relatively more gas is at high
temperatures. The gas temperature plays a large role in the density
range applicable to this cloud type. CO is present at much higher
temperatures in the XDRs. Therefore, the XDR line ratios for the same
density and incident radiation field can be more than ten times larger
than in the PDR. This difference slowly disappears when the critical
density of the CO(4-3) line is reached and the CO(4-3) line also
thermalizes, which is seen in the high density range (cloud type A) at
densities n > 105 cm-3.
cm-3. As expected, the emitted intensity
shows more variation with density and radiation field. In
Fig. 5, we show the CO(4-3)/CO(1-0) line intensity
ratio. In the low density range (cloud type C), PDR models still
produce a line ratio increase only as function of density, but the
variation in the ratio has grown to more than a factor of two, as
opposed to only 20 percent in the corresponding CO(2-1)/CO(1-0)
ratio. The XDRs for this cloud type show a complex behavior with
density and radiation field and the ratios cover a much larger range
from about 2 to 40. At low radiation fields, only a density dependence
is seen. At high radiation field strengths, the effect of the column
density comes into play. In the mid density (type B) PDRs, the highest
line ratios are seen for the highest densities and radiation
fields. The XDRs in this range show only a dependence on radiation
field. The effect of the higher density is compensated by the fact
that at lower densities relatively more gas is at high
temperatures. The gas temperature plays a large role in the density
range applicable to this cloud type. CO is present at much higher
temperatures in the XDRs. Therefore, the XDR line ratios for the same
density and incident radiation field can be more than ten times larger
than in the PDR. This difference slowly disappears when the critical
density of the CO(4-3) line is reached and the CO(4-3) line also
thermalizes, which is seen in the high density range (cloud type A) at
densities n > 105 cm-3.
![\begin{figure}
{\includegraphics[height=48mm,clip=]{6130fi6a.ps} }
{\includegrap...
...6130fi6c.ps} }
{\includegraphics[height=48mm,clip=]{6130fi6d.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg52.gif) |
Figure 6: CO(16-15)/CO(1-0), CO(16-15)/CO(10-9), CO(10-9)/CO(7-6) and CO(7-6)/CO(3-2) ratio for PDR ( left) and XDR ( right) models. |
| Open with DEXTER | |
In cloud type A XDRs (
n=104-106.5 cm-3), CO is present
throughout the cloud, even when energy deposition rates
![]() are
large and temperatures are high (
are
large and temperatures are high (![]() K). This warm CO gas
produces emission originating from high rotational transitions even
when densities are not high (e.g., n=104 cm-3). Contrary to
the situation in XDRs, most CO in PDRs is produced beyond the H/H2transition and it has on average much lower temperatures
(
K). This warm CO gas
produces emission originating from high rotational transitions even
when densities are not high (e.g., n=104 cm-3). Contrary to
the situation in XDRs, most CO in PDRs is produced beyond the H/H2transition and it has on average much lower temperatures
(
![]() K), causing lower intensities and line
ratios. Therefore, it is very likely, that future missions such as
Herschel/HIFI will be able to distinguish between PDRs and XDRs, by
observing high rotational transitions such as CO(16-15), CO(10-9), and
CO(7-6).
K), causing lower intensities and line
ratios. Therefore, it is very likely, that future missions such as
Herschel/HIFI will be able to distinguish between PDRs and XDRs, by
observing high rotational transitions such as CO(16-15), CO(10-9), and
CO(7-6).
In Fig. A.5, we show the PDR and XDR intensities of
the CO(7-6), CO(10-9) and CO(16-15) lines for the high density range
(cloud type A). We find that for both PDRs and XDRs, the spread in
intensities increases for higher rotational lines, since the critical
densities of these transitions are higher. However, this spread is
much larger for PDRs than for XDRs. The CO(16-15) line intensity
ranges from ![]() 10-10 (n=104 cm-3 and G0=102) to
10-10 (n=104 cm-3 and G0=102) to
![]() 10-3 erg s-1 cm-2 sr-1(
n=106.5 cm-3 and G0=105) for the PDR models, while this
is
10-3 erg s-1 cm-2 sr-1(
n=106.5 cm-3 and G0=105) for the PDR models, while this
is ![]() 10-4 (n=104 cm-3) to
10-4 (n=104 cm-3) to
![]() 10-2 erg s-1 cm-2 sr-1(
n=106.5 cm-3) for the XDR models. PDRs show only
significant CO(16-15) emission at very high densities and radiation
fields (
10-2 erg s-1 cm-2 sr-1(
n=106.5 cm-3) for the XDR models. PDRs show only
significant CO(16-15) emission at very high densities and radiation
fields (![]() cm-3 and
cm-3 and
![]() ). This very dense
and strongly irradiated gas, however, has a very small filling factor
on large (galaxy) scales, and, the probability of observing a PDR with
a very high CO(16-15) intensity is low.
). This very dense
and strongly irradiated gas, however, has a very small filling factor
on large (galaxy) scales, and, the probability of observing a PDR with
a very high CO(16-15) intensity is low.
The difference between the PDR and XDR models is seen even better by considering the intensity ratios of these high rotational transitions (see Fig. 6). A good example is the CO(16-15)/CO(1-0) ratio, which ranges from 10-3 to 103 for PDRs, and from 10 to >104 for XDRs. Especially for densities between 104-105 cm-3, it is very easy to distinguish PDRs from XDRs.
![\begin{figure}
{\includegraphics[height=145mm,clip=]{6130fig7.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg57.gif) |
Figure 7: 13CO(2-1)/13CO(1-0) ratio for PDR ( left) and XDR ( right) models. |
| Open with DEXTER | |
![\begin{figure}
{\includegraphics[height=145mm,clip=]{6130fig8.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg58.gif) |
Figure 8: 13CO(3-2)/13CO(1-0) ratio for PDR ( left) and XDR ( right) models. |
| Open with DEXTER | |
The 13CO lines have critical densities and upper state energies for the rotational transitions almost identical to those of 12CO. As we have adopted an abundance ratio 12C/13C = 40 in our models, 13CO abundances are relatively low and the lines are much less optically thick.
The 13CO(1-0) line intensities (Fig. A.6), show the same trends with density and radiation field as the CO(1-0) line, but there is a larger spread in intensity. For example, the difference in the CO(1-0) line emission in the low density PDRs (cloud type C) is a factor of two and more than a factor of 3 for the 13CO line. This effect is even larger for the XDRs. We find similar results for both the 13CO(2-1) (not shown) and 13CO(3-2) line intensities as is evident from the corresponding 13CO line ratios (see Fig. 7 and 8). A nice illustration of the CO and 13CO behavior is supplied by the the CO(4-3)/CO(1-0) versus the 13CO(3-2)/13CO(1-0) intensity ratio for the low density PDRs (cloud type C). The CO(4-3) line is pumped due to the fact that the lower rotational lines become optically thick. The CO(4-3)/CO(1-0) ratio changes only a factor of two, which is a factor two and a half for the 13CO(3-2)/13CO(1-0) ratio, despite the lower critical density of 13CO(3-2).
![\begin{figure}
{\includegraphics[height=150mm,clip=]{6130fig9.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg59.gif) |
Figure 9: 13CO(1-0)/CO(1-0) ratio for PDR ( left) and XDR ( right) models. |
| Open with DEXTER | |
In Figs. 9 and A.8, the important isotopical intensity ratios of 13CO(1-0)/CO(1-0) and 13CO(3-2)/CO(3-2) are shown. Although for all cloud types (density regimes) the line intensities are larger in the XDR, the PDR isotopical ratios exceed those of XDRs, which means that the opacities of the XDR lines are larger as well.
Figure 10 shows the [CI] 609 ![]() m/13CO(2-1)
ratios. For the same gas density and incident radiation field, PDRs
have much lower ratios than XDRs. In the PDRs, the spread in the ratio
is generally not very large. At low densities, ratios rapidly decrease
from 72 (n=102 cm-3) to 18 (n=103) and then slowly fall off
from 14.5 (n=104 cm-3) to 2 (n=106 cm-3). While the
PDR ratios show a more or less steady decrease with density, a rather
different picture is seen in XDRs. In each density range (cloud type),
the ratio changes by several orders of magnitude. For the lowest
density in each cloud type, the column density is too low to attenuate
the incident radiation field sufficiently to allow large amounts of CO
to be present. On the other hand, neutral carbon occurs throughout the
cloud, and, therefore, a large increase in the ratios are seen toward
high
m/13CO(2-1)
ratios. For the same gas density and incident radiation field, PDRs
have much lower ratios than XDRs. In the PDRs, the spread in the ratio
is generally not very large. At low densities, ratios rapidly decrease
from 72 (n=102 cm-3) to 18 (n=103) and then slowly fall off
from 14.5 (n=104 cm-3) to 2 (n=106 cm-3). While the
PDR ratios show a more or less steady decrease with density, a rather
different picture is seen in XDRs. In each density range (cloud type),
the ratio changes by several orders of magnitude. For the lowest
density in each cloud type, the column density is too low to attenuate
the incident radiation field sufficiently to allow large amounts of CO
to be present. On the other hand, neutral carbon occurs throughout the
cloud, and, therefore, a large increase in the ratios are seen toward
high
![]() .
.
![\begin{figure}
{\includegraphics[height=154mm,clip=]{6130fi10.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg60.gif) |
Figure 10:
CI 609 |
| Open with DEXTER | |
In Fig. A.9, we show the HCN(1-0) and HCN(4-3) line
intensities for high density (cloud A type) PDR and XDR models only.
Where the CO(4-3) line has a critical density of
![]() cm-3, the HCN(1-0) line has a critical
density of
cm-3, the HCN(1-0) line has a critical
density of
![]() cm-3. Higher rotational
transitions such as HCN(2-1),
cm-3. Higher rotational
transitions such as HCN(2-1),
![]() cm-3, and
HCN(4-3),
cm-3, and
HCN(4-3),
![]() cm-3, have even higher critical
densities. The HCN rotational lines specifically trace the dense gas
component in galaxies, and the line intensities from low and medium
density gas are low. The HCN(1-0) line intensities range from
cm-3, have even higher critical
densities. The HCN rotational lines specifically trace the dense gas
component in galaxies, and the line intensities from low and medium
density gas are low. The HCN(1-0) line intensities range from
![]() to
to
![]() erg s-1 cm-2 sr-1for the low and mid density (type C en B) PDR models, and even less
for the corresponding XDR models. Because of their poor observational
prospects, we have limited ourselves to only showing the model results
in the high density range (cloud type A). Typically, the HCN(1-0)
emission is stronger in PDRs by a factor of about two for densities
larger than 105 cm-3. The HCN(4-3) diagrams show behavior
very similar to that of HCN(1-0), but the PDR and XDR line strengths
are now somewhat closer.
erg s-1 cm-2 sr-1for the low and mid density (type C en B) PDR models, and even less
for the corresponding XDR models. Because of their poor observational
prospects, we have limited ourselves to only showing the model results
in the high density range (cloud type A). Typically, the HCN(1-0)
emission is stronger in PDRs by a factor of about two for densities
larger than 105 cm-3. The HCN(4-3) diagrams show behavior
very similar to that of HCN(1-0), but the PDR and XDR line strengths
are now somewhat closer.
Typically, the HCN(1-0) emission is stronger in PDRs by a factor of about two for densities larger than 105 cm-3. Our results are consistent with the chemical calculations of Lepp & Dalgarno (1996) for different ionization rates, as follows. Our depth dependent models cause the HCN line emissivities to be the result of a line-of-sight integral over the HCN abundance pattern that results from a varying (attenuated) X-ray flux. Lepp & Dalgarno (1996, their Fig. 3) find a rather narrow range of ionization rates for which the HCN abundance is high and consequently the XDR HCN line emissivities have difficulty competing with the PDR ones. The HCN(4-3) contour plots show about the same features as seen for the HCN(1-0). However, the PDR and XDR line strengths are now somewhat closer.
![\begin{figure}
\par\mbox{\resizebox{7cm}{!}{\includegraphics*[angle=0]{6130f11a.ps}}\resizebox{7cm}{!}{\includegraphics*[angle=0]{6130f11b.ps}} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg66.gif) |
Figure 11: Cumulative HCN(1-0)/CO(1-0) line intensity ratios for PDR ( left) and XDR ( right). |
| Open with DEXTER | |
![\begin{figure}
{\includegraphics[height=53mm,clip=]{6130f12a.ps} }
{\includegraphics[height=53mm,clip=]{6130f12b.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg67.gif) |
Figure 12: HCN(1-0)/CO(1-0) and HCN(4-3)/CO(4-3) ratios for PDR ( left) and XDR ( right) models. |
| Open with DEXTER | |
Intensity ratios of lines from the same species, such as the
CO(4-3)/CO(1-0) ratio, vary with column density, due to the
temperature gradient throughout the cloud, optical depth effects,
varying abundance etc. Intensity ratios of lines from different
species, in addition vary because of abundance ratio differences,
complicating the interpretation of such line intensity ratios. In
this section we turn our attention to the HCN/CO ratio, and start by
showing in Figs. 11 and A.10 the cumulative line intensity ratios for a set of PDRs and XDRs at densities ranging from
n=104-106 cm-3and incident fluxes between
G0=103-105(
![]() erg s-1 cm-2). The cumulative line intensity
is the emergent intensity arising from the edge of the cloud to column
density
erg s-1 cm-2). The cumulative line intensity
is the emergent intensity arising from the edge of the cloud to column
density
![]() :
:
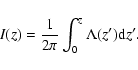 |
(1) |
When
![]() is low in the XDR model, the gas is molecular, and the
HCN/CO abundance ratio is more or less constant. A slow rise in the
ratio is seen, as the CO line becomes optically thick. When the outer
part of the cloud is atomic (for high
is low in the XDR model, the gas is molecular, and the
HCN/CO abundance ratio is more or less constant. A slow rise in the
ratio is seen, as the CO line becomes optically thick. When the outer
part of the cloud is atomic (for high
![]() ), HCN shows a maximum,
before the H/H2 transition. This also produces a maximum in the
HCN(1-0)/CO(1-0) ratio. In the PDR, the variation is not that large
for column densities
), HCN shows a maximum,
before the H/H2 transition. This also produces a maximum in the
HCN(1-0)/CO(1-0) ratio. In the PDR, the variation is not that large
for column densities
![]() cm-2. In the XDRs, however,
the variation between
cm-2. In the XDRs, however,
the variation between
![]() and 1023 cm-2 can be
rather large.
and 1023 cm-2 can be
rather large.
In Fig. 12, we show the HCN(1-0)/CO(1-0) and HCN(4-3)/ CO(4-3) line ratios for a fixed cloud size of one parsec (cloud type A). The variation in the ratios is relatively large, due to the high critical densities of the HCN transitions. The PDR models produce the highest HCN(1-0)/CO(1-0) ratios, which are attained at large densities (n>106 cm-3) and may exceed unity. The corresponding XDRs have ratios are only 0.1-0.2. The interpretation of the low J transitions is very difficult due to high opacities, especially in the PDRs. For this reason, we also show the HCN(4-3)/CO(4-3) ratio, which shows similar trends with density and radiation field, but with somewhat lower absolute ratios.
In Fig. A.11, we show the HCO+(1-0) and
HCO+(4-3) line intensities, with critical densities
![]() and
and
![]() cm-3,
respectively. These critical densities are significantly lower than
for HCN, causing a smaller spread in line intensities. Typically, the
HCO+ lines are stronger in XDRs than in PDRs by a factor of at
least three. This is a direct consequence of the higher ionization
degree in XDRs (Meijerink & Spaans 2005), leading to an enhanced
HCO+ formation rate.
cm-3,
respectively. These critical densities are significantly lower than
for HCN, causing a smaller spread in line intensities. Typically, the
HCO+ lines are stronger in XDRs than in PDRs by a factor of at
least three. This is a direct consequence of the higher ionization
degree in XDRs (Meijerink & Spaans 2005), leading to an enhanced
HCO+ formation rate.
Note in this that Lepp & Dalgarno (1996, their Fig. 2) find a rather wide range of ionization rates for which the HCO+ abundance is large. As for the HCN discussed above, this is consistent with our results since we integrate the depth dependent HCO+ abundance profile that results from the attenuation of the impinging X-ray flux. The HCO+ line-of-sight integral thus picks up a large contribution and competes favorably with the PDR line emissivities.
![\begin{figure}
\par\mbox{
\resizebox{7cm}{!}{\includegraphics*[angle=0]{6130f13a.ps}}\resizebox{7cm}{!}{\includegraphics*[angle=0]{6130f13b.ps}} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg75.gif) |
Figure 13: Cumulative HCN(1-0)/HCO+(1-0) line intensity ratios for PDR ( left) and XDR ( right). |
| Open with DEXTER | |
![\begin{figure}
{\includegraphics[height=47mm,clip=]{6130f14a.ps} }
{\includegraphics[height=47mm,clip=]{6130f14b.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg76.gif) |
Figure 14: HCN(1-0)/HCO+(1-0) and HCN(4-3)/HCO+(4-3) ratios for PDR ( left) and XDR ( right) models. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{
\resizebox{7.4cm}{!}{\includegraphics*[angle=0]{6130f1...
...s}}\resizebox{7.4cm}{!}{\includegraphics*[angle=0]{6130f15b.ps}} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg77.gif) |
Figure 15: Cumulative HNC(1-0)/HCN(1-0) line intensity ratios for PDR ( left) and XDR ( right). |
| Open with DEXTER | |
In Figs. 13 and A.12, we show the cumulative HCN(1-0)/ HCO+(1-0) and HCN(4-3)/HCO+(4-3) line intensity ratios, for the same PDR and XDR models as in Sect. 5.5. Depending on the incident radiation field, HCN or HCO+ is more abundant at the PDR edge of the cloud. Around the H/H2 transition a minimum in the HCO+ abundance is seen in the PDR. Deeper into the cloud, the HCO+ abundance increases again, and is then constant. This is also the case for HCN, and the HCN/HCO+ abundance ratio is larger than unity. Therefore, at sufficiently large columns and densities, the HCN(1-0)/HCO+(1-0) line intensity ratio becomes larger than one.
In the XDR models, HCO+ is chemically less abundant than HCN for
very large
![]() (Meijerink & Spaans 2005). For larger columns
HCO+ becomes more abundant, however, and eventually the cumulative
column density of HCO+ becomes larger than HCN (see specifically
Fig. 10 in Paper I). This follows directly from the fact that the
HCO+ abundance is high over a much wider range of ionization rates
than HCN (Lepp & Dalgarno 1996, their Figs. 2 and 3).
(Meijerink & Spaans 2005). For larger columns
HCO+ becomes more abundant, however, and eventually the cumulative
column density of HCO+ becomes larger than HCN (see specifically
Fig. 10 in Paper I). This follows directly from the fact that the
HCO+ abundance is high over a much wider range of ionization rates
than HCN (Lepp & Dalgarno 1996, their Figs. 2 and 3).
Figure 14 clearly shows that the HCN/HCO+ ratio discriminates between PDRs and XDRs in the density range between n=105 and 106.5 cm-3 (cloud type A). The HCN(1-0)/ HCO+(1-0) and HCN(4-3)/HCO+(4-3) line ratios are both much larger in the PDR models than XDR models, for columns of 1023 cm-2 and larger (Paper I). The difference ranges between a factor of 4-10, depending on the density. The XDR HCN(1-0)/ HCO+(1-0) ratio becomes larger than unity for more modest columns of 1022.5 cm-2 and less.
![\begin{figure}
{\includegraphics[height=50mm,clip=]{6130f16a.ps} }
{\includegraphics[height=50mm,clip=]{6130f16b.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg78.gif) |
Figure 16: HNC(1-0)/HCN and HNC(4-3)/HCN(4-3) ratios for PDR ( left) and XDR ( right) models. |
| Open with DEXTER | |
The critical densities of HCN and HNC are almost identical, so that
the only differences in line ratio should be due to differences in the
abundances. In PDRs, HCN is more abundant in the radical region, but
deeper in the cloud the abundance ratio approaches unity. In XDRs, HCN
is more abundant in the highly ionized part of the cloud. However, HNC
is equally or even more abundant than HCN deep into the cloud. As a
result, the HNC(1-0)/HCN(1-0) line intensity ratio is around one for
the PDRs if the column density is larger than 1022 cm-2,
while the HNC(1-0)/HCN(1-0) ratio is less than unity for
![]() cm-2. The XDR models, however, show low ratios for the low,
cm-2. The XDR models, however, show low ratios for the low, ![]() 104 cm-3, densities and strong, >10 erg s-1 cm-2,
radiation fields. The ratios increase for lower incident radiation
fields, and at highest densities (
n=106.5 cm-3) the line
ratios are always larger than one, irrespective of irradiation.
104 cm-3, densities and strong, >10 erg s-1 cm-2,
radiation fields. The ratios increase for lower incident radiation
fields, and at highest densities (
n=106.5 cm-3) the line
ratios are always larger than one, irrespective of irradiation.
In the PDRs, the HNC(4-3)/HCN(4-3) ratio quickly drops below unity at densities below n=105 cm-3. This density is far below the critical densities of the lines, and therefore high temperatures are needed to excite them. Such high temperatures are indeed found in the radical regions of the PDRs, but there the HNC abundance is much lower than the HCN abundance, which explains the drop in the ratio. In the XDRs, the HNC(4-3)/HCN(4-3) ratios are quite similar to the HNC(1-0)/HCN(1-0) ratios, except for densities n>106 cm-3, where they are even high than these.
![\begin{figure}
{\includegraphics[height=54mm,clip=]{6130f17a.ps} }
{\includegraphics[height=54mm,clip=]{6130f17b.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg80.gif) |
Figure 17: CS(1-0)/HCN and CS(4-3)/HCN(4-3) ratios for PDR ( left) and XDR ( right) models. |
| Open with DEXTER | |
![\begin{figure}
{\includegraphics[height=45mm,clip=]{6130fi18.ps} }\end{figure}](/articles/aa/full/2007/03/aa6130-06/Timg81.gif) |
Figure 18: CN/HCN column density ratios for PDR ( left) and XDR ( right) models. |
| Open with DEXTER | |
| |
Figure 19: Cumulative CN/HCN column density ratios for PDR ( left) and XDR ( right) models. |
| Open with DEXTER | |
Although SiO is usually considered to be a good tracer of shocks, we do find that the SiO(1-0)/CO(1-0) ratio is typically larger in XDRs than in PDRs by a factor of 2-3, for densities around 105.5 cm-3. For the higher excitation J=4-3 lines, the effect disappears because CO is generally warmer in XDRs compared to PDRs.
The CS(1-0)/HCN(1-0) ratio is a factor of two larger (smaller) in XDRs for densities above (below) 105 cm-3. Interestingly, the corresponding 4-3 ratio continues this trend but changes in the ratio from 104 to 106 cm-3 are now as large as a factor of 10.
Unfortunately, for many molecular species of interest no reliable collisional cross sections are available. For these species we are unable to accurately predict line intensities, but we can still calculate the column density ratios. In this section, we discuss column density ratios for a number of species that are of potential interest in attempts to discriminate between PDRs and XDRs.
In Fig. 18, we show the CN/HCN column density
ratios. There is an enormous difference between the ratios for PDRs
and XDRs. In the PDRs, the cloud type A ratios range from 0.5
(![]() cm-3) to 2.0 (
cm-3) to 2.0 (![]() cm-3), while in the
XDR models the same ratio varies from 40 (
cm-3), while in the
XDR models the same ratio varies from 40 (![]() cm-3) to
over a 1000 (
cm-3) to
over a 1000 (![]() cm-3). We find higher CN/HCN ratios at
lower densities, where the chemical rates are lower, making it more
difficult to form large molecules. The PDR ratios are only dependent
on density, which is explained by the fact that most CN and HCN
molecules are formed beyond the H/H2 transition. This part of the
cloud is shielded from FUV photons and the chemistry is dominated by
the cosmic ray ionization rate, which is the same in every model. In
the XDR models, there is much less variation in the CN and HCN
abundance throughout the cloud. The variations do not exceed more than
two to three orders of magnitude, while this is over ten orders of
magnitude in the PDR models. All parts of the cloud contribute almost
equally to the column density ratio, including the region with very
high
cm-3). We find higher CN/HCN ratios at
lower densities, where the chemical rates are lower, making it more
difficult to form large molecules. The PDR ratios are only dependent
on density, which is explained by the fact that most CN and HCN
molecules are formed beyond the H/H2 transition. This part of the
cloud is shielded from FUV photons and the chemistry is dominated by
the cosmic ray ionization rate, which is the same in every model. In
the XDR models, there is much less variation in the CN and HCN
abundance throughout the cloud. The variations do not exceed more than
two to three orders of magnitude, while this is over ten orders of
magnitude in the PDR models. All parts of the cloud contribute almost
equally to the column density ratio, including the region with very
high
![]() .
.
![]() is a major factor in the resulting ratio, and
therefore the XDRs also show a large dependence on incident radiation
field.
is a major factor in the resulting ratio, and
therefore the XDRs also show a large dependence on incident radiation
field.
In Fig. 19, we show the PDR and XDR cumulative CN/HCN ratios for a few specific densities and radiation fields. The variation in the cumulative column density ratio is much less in the XDR models than in the PDR models. At PDR edges, the gas is highly ionized (as in the XDRs), and here we find ratios resembling those of XDRs. Abundances, however, are very low here because of the high photo-dissociation rate.
In Fig. A.17, we show the CH/HCN column density
ratio. The differences between the ratios in PDRs and XDRs are even
larger than in the case of CN/HCN. While the PDR ratios increase from 0.2 (![]() cm-3)
to 0.9 (
cm-3)
to 0.9 (![]() cm-3), the XDR
ratios range from 20 to more than 10 000. The PDR ratio does not depend
on density only. At relatively low densities
(
cm-3), the XDR
ratios range from 20 to more than 10 000. The PDR ratio does not depend
on density only. At relatively low densities
(
![]() cm-3), we find a dependency on incident
radiation field as well. CH reaches its maximum abundance at greater
depths than HCN, which means that the cumulative ratio is still
increasing at large column densities. Our model cloud sizes are not
large enough to allow the ratio to converge to a constant ratio (see
Fig. A.18). For the XDR models, we can
roughly state that the ratio increases toward higher
cm-3), we find a dependency on incident
radiation field as well. CH reaches its maximum abundance at greater
depths than HCN, which means that the cumulative ratio is still
increasing at large column densities. Our model cloud sizes are not
large enough to allow the ratio to converge to a constant ratio (see
Fig. A.18). For the XDR models, we can
roughly state that the ratio increases toward higher
![]() .
However,
at
.
However,
at ![]() cm-3 the lowest ratio is not found at the lowest
incident radiation field strength. At such densities, the limited
cloud sizes are comparable to the depth of the H/H2 transition.
This transition is included in models with the lowest radiation field
strengths, but not in those with the highest radiation field
strengths.
cm-3 the lowest ratio is not found at the lowest
incident radiation field strength. At such densities, the limited
cloud sizes are comparable to the depth of the H/H2 transition.
This transition is included in models with the lowest radiation field
strengths, but not in those with the highest radiation field
strengths.
In Fig. A.19, we show the CH+/HCN ratios for
both PDR and XDR models. They range from 10-6(![]() cm-3) to
cm-3) to
![]() (
(![]() cm-3) in
the PDRs, and from 10-3 (
cm-3) in
the PDRs, and from 10-3 (![]() cm-3) to over 1000
(
cm-3) to over 1000
(![]() cm-3) in the XDRs. In the PDR models, the highest
CH+ abundance is seen close to the edge of the cloud but it
decreases very quickly beyond the H/H2 transition. HCN, on the
contrary, reaches its highest abundance beyond this transition. This
explains the decrease of the PDR cumulative column density ratios with
increasing depth (Fig. A.20). The PDR
models show a dependence on both density and incident radiation field
for this ratio. The decrease in the ratio with increasing density is
caused by the fact that on the one hand CH+ is more easily
destroyed (due to higher recombination rates) and on the other hand
HCN more easily formed when densities are higher. The ratios do not
converge to a constant value deep into the cloud. At identical
densities, the ratio increases with increasing radiation field, since
the HCN column densities become smaller while the CH+ column
densities become larger for the cloud-size considered here. In the XDR
models, the largest ratios are seen for the highest
cm-3) in the XDRs. In the PDR models, the highest
CH+ abundance is seen close to the edge of the cloud but it
decreases very quickly beyond the H/H2 transition. HCN, on the
contrary, reaches its highest abundance beyond this transition. This
explains the decrease of the PDR cumulative column density ratios with
increasing depth (Fig. A.20). The PDR
models show a dependence on both density and incident radiation field
for this ratio. The decrease in the ratio with increasing density is
caused by the fact that on the one hand CH+ is more easily
destroyed (due to higher recombination rates) and on the other hand
HCN more easily formed when densities are higher. The ratios do not
converge to a constant value deep into the cloud. At identical
densities, the ratio increases with increasing radiation field, since
the HCN column densities become smaller while the CH+ column
densities become larger for the cloud-size considered here. In the XDR
models, the largest ratios are seen for the highest
![]() (low
density and high incident radiation field). The fluctuations in the
CH+ and HCN abundances are more gradual. The HCN abundance
increases and the CH+ abundance decreases when the X-ray photons
are gradually absorbed. Therefore, the XDR cumulative column densities
ratios show less variation than the PDR ratios (see
Fig. A.20).
(low
density and high incident radiation field). The fluctuations in the
CH+ and HCN abundances are more gradual. The HCN abundance
increases and the CH+ abundance decreases when the X-ray photons
are gradually absorbed. Therefore, the XDR cumulative column densities
ratios show less variation than the PDR ratios (see
Fig. A.20).
Figure A.21 shows the HCO/HCO+ column density
ratios. For the PDRs, we find much larger ratios than for the XDRs.
The PDRs show ratios between 0.1 (![]() cm-3) and 10.0
(
cm-3) and 10.0
(![]() cm-3), while the ratios in the XDR range from
10-5 (
cm-3), while the ratios in the XDR range from
10-5 (![]() cm-3) to 10-3(
cm-3) to 10-3(![]() cm-3). In the PDRs, the ratios depend only on
density for radiation fields G0<104. With larger incident
radiation fields, the ratio becomes dependent on the radiation field
strength as well. The HCO abundance reaches its maximum and more or
less constant abundance somewhat deeper into the cloud than HCO+.
As column density increases, the HCO/HCO+ ratio slowly converges to
a constant value (see Fig. A.22). For
large radiation fields (G0>104), the cloud size considered here is
too small to allow column densities to converge to a constant ratio.
In the XDR models, the ratio depends on both density and radiation
field in all regimes. The lowest ratios are seen for high
cm-3). In the PDRs, the ratios depend only on
density for radiation fields G0<104. With larger incident
radiation fields, the ratio becomes dependent on the radiation field
strength as well. The HCO abundance reaches its maximum and more or
less constant abundance somewhat deeper into the cloud than HCO+.
As column density increases, the HCO/HCO+ ratio slowly converges to
a constant value (see Fig. A.22). For
large radiation fields (G0>104), the cloud size considered here is
too small to allow column densities to converge to a constant ratio.
In the XDR models, the ratio depends on both density and radiation
field in all regimes. The lowest ratios are seen for high
![]() (n=104 cm-3 and
(n=104 cm-3 and
![]() ).
).
In Fig. A.23, we show the HOC+/HCO+column density ratios. The XDRs show larger ratios, ranging from
10-4 (![]() cm-3) to 0.6 (
cm-3) to 0.6 (![]() cm-3), than
PDRs, where the ratios range from 10-7 to 10-5. The XDR
ratios increase for larger
cm-3), than
PDRs, where the ratios range from 10-7 to 10-5. The XDR
ratios increase for larger
![]() (with maximum at
(with maximum at
![]() cm-3 and
cm-3 and
![]() ). The behavior is more complex for
the PDR models. The ratios depend on density only for G0>104, but
below this value there is also a dependency on radiation field
strength. This is explained by the fact that ratios drop very fast,
when the gas becomes molecular
(Fig. A.24), but abundances are still
significant. A large fraction of the gas at the edge of the cloud is
molecular for densities
n>105.5 cm-3 and radiation fields
G0<104. Here we find a fast decrease in the ratio for lower
radiation fields.
). The behavior is more complex for
the PDR models. The ratios depend on density only for G0>104, but
below this value there is also a dependency on radiation field
strength. This is explained by the fact that ratios drop very fast,
when the gas becomes molecular
(Fig. A.24), but abundances are still
significant. A large fraction of the gas at the edge of the cloud is
molecular for densities
n>105.5 cm-3 and radiation fields
G0<104. Here we find a fast decrease in the ratio for lower
radiation fields.
In Fig A.25, we show the NO/CO column density
ratios. The ratios in XDRs are much larger, 10-4(![]() cm-3) to 10-3 (
cm-3) to 10-3 (![]() cm-3), than for
PDRs (
10-6-10-5). In the PDR the ratios are largely determined
in the molecular part of the cloud and depend more or less on density
only. The ratios in the XDR depend mostly on
cm-3), than for
PDRs (
10-6-10-5). In the PDR the ratios are largely determined
in the molecular part of the cloud and depend more or less on density
only. The ratios in the XDR depend mostly on
![]() .
The largest
ratios are seen for the largest
.
The largest
ratios are seen for the largest
![]() (
(![]() cm-3 and
cm-3 and
![]() ).
).
CO(1-0) lines have optical depths of
![]() .
Therefore, it could be possible to observe NO(1-0)/CO(1-0) line
intensity ratios as large as 0.1, while the maximum column density
ratios are only 10-3.
.
Therefore, it could be possible to observe NO(1-0)/CO(1-0) line
intensity ratios as large as 0.1, while the maximum column density
ratios are only 10-3.
In Fig. A.27, we show the N2H+/CO column
density ratio. In both PDRs and XDRs the model ratios are rather low.
They decrease with density in the PDR (
10-7-10-9), which is
opposite to the behavior in XDRs. In the XDRs, we find a decrease
with increasing
![]() .
There are collisional data available for
N2H+, but since the abundances are so low, the line intensities
are too small to be observable.
.
There are collisional data available for
N2H+, but since the abundances are so low, the line intensities
are too small to be observable.
We have presented a large set of PDR and XDR models that can be used
to determine the physical conditions that pertain to irradiated gas
clouds. This grid spans a large range in densities (
![]() cm-3), irradiation (
G0=100.5-105 and
cm-3), irradiation (
G0=100.5-105 and
![]() erg cm-2 s-1) and column
densities (
erg cm-2 s-1) and column
densities (
![]() cm-2). We
have used the results to make predictions for the intensities and
ratios of the most important atomic fine-structure lines, e.g., [CII],
[OI], [CI], [SiII], and [FeII], rotational lines for molecular species
such as HCO+, HCN, HNC, CS and SiO (up to J=4), CO and 13CO
up to J=16, and for column densities for CN, CH, CH+, HCO,
HOC+, NO, and N2H+. It is not possible to to present
all the results, but they are available on-line at the following URL:
http://www.strw.leidenuniv.nl/~meijerin/grid/ Here
we summarize the most important conclusions:
cm-2). We
have used the results to make predictions for the intensities and
ratios of the most important atomic fine-structure lines, e.g., [CII],
[OI], [CI], [SiII], and [FeII], rotational lines for molecular species
such as HCO+, HCN, HNC, CS and SiO (up to J=4), CO and 13CO
up to J=16, and for column densities for CN, CH, CH+, HCO,
HOC+, NO, and N2H+. It is not possible to to present
all the results, but they are available on-line at the following URL:
http://www.strw.leidenuniv.nl/~meijerin/grid/ Here
we summarize the most important conclusions:
We conclude that both atomic fine-structure and molecular rotational lines have significant diagnostic value to allow us to distinguish between clouds irradiated by star-bursts (FUV) and by active galactic nuclei (X-ray) in the centers of galaxies. Note, however, that the line intensities (and ratios) presented in this work do not take the, likely complex, kinematics of nuclear gas into account. For example, gas rotating in an accretion disk around an AGN will cause the line widths of, say, HCN, HNC and HCO+ transitions to differ, depending on where their chemical abundances peak with depth.
The XDR/AGN contribution will typically be of a much smaller (possibly beam diluted) angular scale than that of a PDR/Starburst. A 10-25% PDR contribution may already suppress our ability to recognize XDR excitation from HCN/HCO+ and HNC/HCN line ratios. A solution to this can be found in thevery high J CO lines (e.g., CO(16-15)), that are excellent indicators of an XDR contribution. These very high rotational lines will be observable with the ESA Herschel (HIFI) space observatory scheduled for launch in the near future; they can be seen in absorption in the near-infrared with Subaru. Currently available (sub)millimeter facilities lack the spatial resolution to separate the PDR/stellar and XDR/AGN contributions in distant active galaxies. Up to now, these components can only be spatially resolved in the Milky Way. However, the resolving power of ALMA will bring this possibility within reach for external galaxy centers as well.
Acknowledgements
We thank Dieter Poelman for making his radiation transfer code beta3D available to us.