A&A 461, 999-1012 (2007)
DOI: 10.1051/0004-6361:20065855
H. Jakob1 - C. Kramer1 - R. Simon1 - N. Schneider4,2,1 - V. Ossenkopf1,3 - S. Bontemps2 - U. U. Graf1 - J. Stutzki1
1 - KOSMA, I. Physikalisches Institut,
Universität zu Köln,
Zülpicher Straße 77,
50937 Köln, Germany
2 -
Observatoire de Bordeaux,
Université de Bordeaux 1,
BP 89, 33270 Floirac, France
3 -
SRON, National Institute for Space Research,
PO Box 800, 9700 AV Groningen, The Netherlands
4 -
SAp/CEA Saclay, 91191 Gif-sur-Yvette, France
Received 19 June 2006 / Accepted 11 September 2006
Abstract
Aims. We present an overview of a high-mass star formation region through the major (sub-)mm, and far-infrared cooling lines to gain insight into the physical conditions and the energy budget of the molecular cloud.
Methods. We used the KOSMA 3 m telescope to map the core (
![]() )
of the Galactic star-forming region DR21/DR21 (OH) in the Cygnus X region in the two fine structure lines of atomic carbon (C I
)
of the Galactic star-forming region DR21/DR21 (OH) in the Cygnus X region in the two fine structure lines of atomic carbon (C I
![]() and
and
![]() ), in four mid-J transitions of CO and 13CO, and in CS J=7-6. These observations were combined with FCRAO J=1-0 observations of 13CO and C18O. Five positions, including DR21, DR21 (OH), and DR21 FIR1, were observed with the ISO/LWS grating spectrometer in the [O I] 63 and 145
), in four mid-J transitions of CO and 13CO, and in CS J=7-6. These observations were combined with FCRAO J=1-0 observations of 13CO and C18O. Five positions, including DR21, DR21 (OH), and DR21 FIR1, were observed with the ISO/LWS grating spectrometer in the [O I] 63 and 145 ![]() m lines, the [C II] 158
m lines, the [C II] 158 ![]() m line, and four high-J CO lines. We discuss the intensities and line ratios at these positions and apply the local thermal equilibrium (LTE) and non-LTE analysis methods in order to derive physical parameters such as mass, density and temperature. The CO line emission was modeled up to J=20.
m line, and four high-J CO lines. We discuss the intensities and line ratios at these positions and apply the local thermal equilibrium (LTE) and non-LTE analysis methods in order to derive physical parameters such as mass, density and temperature. The CO line emission was modeled up to J=20.
Results. From non-LTE modeling of the low- to high-J CO lines, we identify two gas components, a cold one at temperatures of
![]() K and one with
K and one with
![]() K at a local clump density of about n(H2)
K at a local clump density of about n(H2) ![]() 104-106 cm-3. While the cold quiescent component is massive, typically containing more than 94% of the mass, the warm, dense, and turbulent gas is dominated by mid- and high-J CO line emission and its large line widths. The medium must be clumpy with a volume-filling of a few percent. The CO lines are found to be important in cooling the cold molecular gas, e.g. at DR21 (OH). Near the outflow of the UV-heated source DR21, the gas cooling is dominated by line emission of atomic oxygen and of CO. Atomic and ionised carbon play a minor role.
104-106 cm-3. While the cold quiescent component is massive, typically containing more than 94% of the mass, the warm, dense, and turbulent gas is dominated by mid- and high-J CO line emission and its large line widths. The medium must be clumpy with a volume-filling of a few percent. The CO lines are found to be important in cooling the cold molecular gas, e.g. at DR21 (OH). Near the outflow of the UV-heated source DR21, the gas cooling is dominated by line emission of atomic oxygen and of CO. Atomic and ionised carbon play a minor role.
Key words: ISM: clouds - ISM: abundances - radio lines: ISM - line: profiles - stars: formation - ISM: individual objects: DR21 - ISM: individual objects: DR21 (OH)
Emission lines of C II, C I, and CO in molecular clouds are among the most important diagnostic probes of star formation and are particularly important for studying the influence of massive stars and their UV radiation on the environment. Obtaining the physical parameters of such regions is often done with simplified radiative transfer assumptions. Local thermal equilibrium (LTE) and the large velocity gradient (LVG) analysis have been proven to yield good results for the bulk of the cold gas (see, e.g., Black 2000). However, the assumption of a homogeneous medium does not represent the typical physical conditions of a high-mass star-formation region. Instead, the observing beam will contain several gas components with different excitation conditions and with unknown filling factors. The observed line transitions are sensitive to gas at different densities, temperatures, and opacities, corresponding to different regions. By selecting designated lines as tracers of the different parts of the gas, one can obtain a rather complete coverage of excitation conditions accounting for different physical and also chemical conditions within the beam. A more differenciated analysis using non-LTE radiative-transfer algorithms (see van Zadelhoff et al. 2002, for an overview) is needed for this purpose. It can provide a more detailed description of the structure of the cloud including clumpiness and temperature or density gradients (e.g., Ossenkopf et al. 2001; Williams et al. 2004).
Using the results of this analysis, we can try to retrieve a self-consistent picture including all major processes driving and being driven by high-mass star-formation (e.g., with respect to turbulence or chemistry), thereby obtaining a detailed view of the photon-dominated regions (PDRs) in the environment of young stars. These PDRs are transition regions from ionised and atomic to dense molecular gas in which the physics and chemistry of the gas are dominated by the UV radiation from young massive stars. Processes heating and cooling the clouds are qualitatively well-understood on a theoretical level (e.g., Sternberg & Dalgarno 1989; Tielens & Hollenbach 1985), and in general we find a reasonable agreement between the theoretical predictions and observations of the brightest cooling lines. Still, there is an ongoing debate about the details of the energy input contributing to the heating. We find a combination of mechanisms, such as stellar far-ultraviolet radiation (FUV), dynamical energy through shocks or supernovae, or an enhanced cosmic-ray rate. There are also many open questions with respect to the chemical composition of these regions. The role of nonequilibrium chemistry is still not understood well. For instance, polycyclic aromatic hydrocarbons (PAHs) as a reservoir of fresh gas-phase carbon (e.g., Habart et al. 2005; Oka et al. 2004) may change the overall picture.
Emission from warm carbon in the form of atoms or ions or of carbonated molecules (mainly CO) provides a significant fraction of the gas cooling at sub-millimeter and far-infrared (FIR) wavelengths (e.g., Giannini et al. 2001; Bradford et al. 2003,2005; Kramer et al. 2004; Schneider et al. 2003; Giannini et al. 2000). Finding the prevailing cooling channels among these and other species (e.g., [O I], H2O, OH) may provide significant insight into the details of the chemical composition and the energy balance of PDRs. Since systematic observations of sub-mm and FIR cooling lines with good spatial resolution are still sparse, data to test the model predictions are still largely missing, and many questions concerning the details of the chemistry and energy balance remain unanswered. By studying a well-known, massive Galactic star-forming region, we aim at gaining new insight into these problems.
The DR21 H II-region/molecular cloud is part of the Cygnus X complex of molecular clouds.
Cygnus X is known to host a large number of H II-regions
(Wendker 1984; Downes & Rinehart 1966) associated with molecular clouds
seen, as in the CfA 12CO 1-0 survey (Leung & Thaddeus 1992).
An extended (11 square degrees) map of the Cygnus X region in the
13CO 2-1 line and smaller maps in the CO and 13CO 3-2 lines were obtained with the KOSMA telescope and are presented
in Schneider et al. (2006) (from now on SBS2006).
The distance to DR21 was sometimes estimated to be ![]() kpc,
based on visual interstellar extinction and radial velocity (e.g., Campbell et al. 1982).
For this paper, we follow the argumentation in SBS2006 based on a morphological comparison of the molecular line
data with mid-IR emission and the OB associations, and favour a value of
1.7 kpc as the distance toward DR21 and DR21 (OH). However, for easier comparison with the literature, we explicitly
give all relevant physical properties as a function of distance.
kpc,
based on visual interstellar extinction and radial velocity (e.g., Campbell et al. 1982).
For this paper, we follow the argumentation in SBS2006 based on a morphological comparison of the molecular line
data with mid-IR emission and the OB associations, and favour a value of
1.7 kpc as the distance toward DR21 and DR21 (OH). However, for easier comparison with the literature, we explicitly
give all relevant physical properties as a function of distance.
The DR21 region has been subject to numerous studies at different wavelengths.
Several active star-formation sites and cometary-shaped H II-regions were identified
in maps of radio continuum emission (e.g., Cyganowski et al. 2003; Dickel et al. 1983).
Ammonia observations by Mauersberger et al. (1985) were interpreted
as evidence of high densities (![]() 105.5
105.5
![]() )
paired with a high degree of clumpiness.
The H2O masers (Genzel & Downes 1977) and a
recently obtained map of 1.3-mm continuum emission (Motte et al. 2005)
show that DR21 belongs to a north-south orientated
chain of massive star-forming complexes.
An additional indication of active star formation is also given by observations of vibrationally
excited H2, tracing the hot, shocked gas in the vicinity of DR21 and DR21 (OH)
(e.g., Garden et al. 1986;
and more recent results by Davis et al. 2006).
The H2 images reveal an extended (5'=2.5 pc(D/1.7 kpc)) northeast
to southwest orientated outflow centred on DR21.
To the west, the outflow is highly collimated, whereas toward the eastern side, gas is expanding in a blister style (Lane et al. 1990).
Jaffe et al. (1989) found very intense CO 7-6 emission peaking on the H II-region and following the H2-emission.
)
paired with a high degree of clumpiness.
The H2O masers (Genzel & Downes 1977) and a
recently obtained map of 1.3-mm continuum emission (Motte et al. 2005)
show that DR21 belongs to a north-south orientated
chain of massive star-forming complexes.
An additional indication of active star formation is also given by observations of vibrationally
excited H2, tracing the hot, shocked gas in the vicinity of DR21 and DR21 (OH)
(e.g., Garden et al. 1986;
and more recent results by Davis et al. 2006).
The H2 images reveal an extended (5'=2.5 pc(D/1.7 kpc)) northeast
to southwest orientated outflow centred on DR21.
To the west, the outflow is highly collimated, whereas toward the eastern side, gas is expanding in a blister style (Lane et al. 1990).
Jaffe et al. (1989) found very intense CO 7-6 emission peaking on the H II-region and following the H2-emission.
Table 1: List of observational parameters for KOSMA.
In this paper, we present the results of sub-mm mapping observations with KOSMA and discuss far-IR line intensities observed with ISO. This comprehensive data set allowed us to study the spatial and, partly also, the kinematic structure of all major cooling lines of the ISM in the vicinity of DR21 and DR21(OH). In Sect. 3, we analyse the line emission and continuum data toward five positions, by comparing the spatial distribution, line profiles, and the physical properties through selected line ratios and the far-IR dust continuum. In Sect. 4, we model the integrated line intensity ratios and absolute intensities with radiative transfer models. The impact of the line emission on the total cloud cooling is dicussed in Sect. 5, and a summary is given in Sect. 6.
We used the KOSMA-3 m submm-telescope to map the DR21/DR21 (OH) region in seven rotational mid-J transitions of CO, 13CO, and CS and in the two fine-structure transitions of C I. These data were combined with ISO/LWS FIR line observations toward single positions of [O I], [C II], and CO. The dataset is complemented with 13CO and C18O 1-0 FCRAO observations.
The region centred on DR21/DR21 (OH)
was mapped in the two atomic
carbon fine-structure transitions at 492 GHz (609 ![]() m,
3P1-3P0; hereafter 1-0) and 809 GHz (370
m,
3P1-3P0; hereafter 1-0) and 809 GHz (370 ![]() m,
3P2-3P1; hereafter 2-1) and the mid-J rotational
transitions of CO (J=3-2, J=4-3, J=6-5, and J=7-6),
13CO (J=3-2, and J=6-5)
using the dual channel 345 and 230/660 GHz SIS receiver, and the
SubMillimeter Array Receiver for Two frequencies (SMART) at the KOSMA telescope.
SMART is a dual-frequency, eight-pixel SIS-heterodyne receiver that
simultaneously observes in the 650 and 350
m,
3P2-3P1; hereafter 2-1) and the mid-J rotational
transitions of CO (J=3-2, J=4-3, J=6-5, and J=7-6),
13CO (J=3-2, and J=6-5)
using the dual channel 345 and 230/660 GHz SIS receiver, and the
SubMillimeter Array Receiver for Two frequencies (SMART) at the KOSMA telescope.
SMART is a dual-frequency, eight-pixel SIS-heterodyne receiver that
simultaneously observes in the 650 and 350 ![]() m atmospheric
windows (Graf et al. 2002).
All observations were taken in the period between 2003 and 2006.
m atmospheric
windows (Graf et al. 2002).
All observations were taken in the period between 2003 and 2006.
An area of
![]() was mapped in the two [C I] lines and the CO 7-6 line on a
was mapped in the two [C I] lines and the CO 7-6 line on a
![]() grid with a total integration time of 160 s per position.
The observations before 2005 were performed in DBS, with a secondary mirror chop throw of 6' fixed in azimuth.
Due to the extent of the DR21 cloud complex, self-chopping is present in some of the DBS-mode observations.
In Appendix B, we describe how we processed these data in order to reduce the impact of the self-chopping.
The CO and 13CO 3-2, and CO 4-3 were observed in an OTF mapping mode on a fully-sampled grid.
A zeroth-order baseline was subtracted from the calibrated spectra.
In addition to CO 3-2, we simultaneously obtained the CS 7-6 line in the image sideband of the 345 GHz channel.
Pointing was frequently checked on
Jupiter,
the sun, and then confirmed on DR21 itself.
The resulting accuracy was better than
grid with a total integration time of 160 s per position.
The observations before 2005 were performed in DBS, with a secondary mirror chop throw of 6' fixed in azimuth.
Due to the extent of the DR21 cloud complex, self-chopping is present in some of the DBS-mode observations.
In Appendix B, we describe how we processed these data in order to reduce the impact of the self-chopping.
The CO and 13CO 3-2, and CO 4-3 were observed in an OTF mapping mode on a fully-sampled grid.
A zeroth-order baseline was subtracted from the calibrated spectra.
In addition to CO 3-2, we simultaneously obtained the CS 7-6 line in the image sideband of the 345 GHz channel.
Pointing was frequently checked on
Jupiter,
the sun, and then confirmed on DR21 itself.
The resulting accuracy was better than ![]() .
Larger 13CO 3-2 and 2-1 maps are presented in SBS2006.
Due to their lower spatial resolution, we did not consider the J = 2-1 data here.
.
Larger 13CO 3-2 and 2-1 maps are presented in SBS2006.
Due to their lower spatial resolution, we did not consider the J = 2-1 data here.
The 12CO and 13CO 6-5 observations were
presented in Köster (1998).
The typical DSB receiver temperatures in the high-frequency channel was between 160-220 K.
The 13CO 6-5 observations cover a region of
![]() centred on DR21, while the 12CO observations extend farther to the
north covering a region of
centred on DR21, while the 12CO observations extend farther to the
north covering a region of
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=14.cm,clip]{5855fig1.eps}
\end{figure}](/articles/aa/full/2007/03/aa5855-06/Timg64.gif) |
Figure 1:
View of the DR21/DR21 (OH) high-mass star-forming region.
Left: overlay of the KOSMA 13CO 3-2 map (cf. Schneider et al. 2006/SBS2006) in contours
on a Spitzer IRAC 8 |
| Open with DEXTER | |
Atmospheric calibration was done by measuring the atmospheric emission
at the reference position to derive the opacity.
Sideband imbalances were corrected using standard atmospheric models (Cernicharo 1985)
and assuming a receiver sideband gain of 0.5.
Spectra taken simultaneously in the two frequency bands near 492 and 810 GHz
were calibrated with an averaged water-vapor value.
The [C I] 2-1 and CO 7-6 lines, observed simultaneously in two
sidebands, were also corrected for sideband imbalance.
Their pointing is identical, and the relative calibration error
between these two transitions is very small.
We scaled the antenna temperature data
to the
![]() scale
using main beam efficiencies
scale
using main beam efficiencies
![]() as listed in Table 1.
The HPBWs (40'' to 80'') and
as listed in Table 1.
The HPBWs (40'' to 80'') and
![]() were determined using continuum scans on Jupiter.
From observations of standard calibration sources, we estimate that the absolute calibration
is accurate to within
were determined using continuum scans on Jupiter.
From observations of standard calibration sources, we estimate that the absolute calibration
is accurate to within
![]() .
Most spectra were taken under
excellent weather conditions with typical values of the atmospheric opacity along the line-of-sight
better than 1.0 at 350 and 600
.
Most spectra were taken under
excellent weather conditions with typical values of the atmospheric opacity along the line-of-sight
better than 1.0 at 350 and 600 ![]() m, and better than 0.5 above 870
m, and better than 0.5 above 870 ![]() m.
m.
Table 2: Positions of ISO observations in absolute coordinates.
The ISO long wavelength spectrometer (LWS, Clegg et al. 1996) 43-197 ![]() m grating
scans (AOT L01) were obtained for 5 positions in the DR21 region from the ISO Data Archive (IDA)
(see Table 2 and Fig. 7).
We removed duplicate scans, overlapping positions, or data with a very poor spectral resolution from the sample.
m grating
scans (AOT L01) were obtained for 5 positions in the DR21 region from the ISO Data Archive (IDA)
(see Table 2 and Fig. 7).
We removed duplicate scans, overlapping positions, or data with a very poor spectral resolution from the sample.
The grating scans contain the FIR continuum, the atomic fine structure lines of
[O I] at 63 and 145 ![]() m, ionised atomic lines of [C II] at 158
m, ionised atomic lines of [C II] at 158 ![]() m,
[O III] at 52 and 88
m,
[O III] at 52 and 88 ![]() m, [N II] at 122
m, [N II] at 122 ![]() m,
and the high-J CO molecular lines J = 14-13 through J = 17-16.
All spectra were processed with the ISO Spectral Analysis Package (ISAP, v. 2.1).
In ISAP, the data were deglitched by hand, defringed (detectors 4-9), and corrected for flux clipping (the
extended source correction). Some artefacts
remain after the processing
(see Fig. 7) and were not corrected.
Line strengths were measured within ISAP. See Table 4 for further details.
m,
and the high-J CO molecular lines J = 14-13 through J = 17-16.
All spectra were processed with the ISO Spectral Analysis Package (ISAP, v. 2.1).
In ISAP, the data were deglitched by hand, defringed (detectors 4-9), and corrected for flux clipping (the
extended source correction). Some artefacts
remain after the processing
(see Fig. 7) and were not corrected.
Line strengths were measured within ISAP. See Table 4 for further details.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{5855fig2.eps}\hspace*{6mm}
\includegraphics[angle=-90,width=7.7cm,clip]{5855fig3.eps}
\end{figure}](/articles/aa/full/2007/03/aa5855-06/Timg79.gif) |
Figure 2:
Integrated intensity map of CO 4-3 ( left) and CO 7-6 ( right) of DR21 and DR21 (OH).
The integration interval is -20 to 30
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{5855fig4.eps}\hspace*{6mm}
\includegraphics[angle=-90,width=7.7cm,clip]{5855fig5.eps}
\end{figure}](/articles/aa/full/2007/03/aa5855-06/Timg80.gif) |
Figure 3:
Integrated intensity map of [C I] 1-0 ( left) and of [C I] 2-1 ( right).
The integration interval is -10 to 20
|
| Open with DEXTER | |
We used 13CO and C18O 1-0 data from a large-scale mapping
project of the whole Cygnus X region
using the FCRAO 14 m
telescope. These data were obtained between December 2003 and
January 2006 and will be presented in more detail in upcoming
papers (Simon et al., in prep.).
The data were observed using the 32 pixel array SEQUOIA in an OTF mapping mode
(at an angular resolution of ![]() 50'').
In this paper, we use smoothed data to have the same angular resolution of
80'' as the KOSMA data.
50'').
In this paper, we use smoothed data to have the same angular resolution of
80'' as the KOSMA data.
Figure 1 gives an overview centred on DR21 (OH) (designated as W75 S by some authors).
The Spitzer 8 ![]() m and 4.5
m and 4.5 ![]() m data by Marston et al. (2004) show the small-scale structure of this region at
angular resolutions between 1.3''-3''.
Several bright IR objects, in particular near DR21 C
m data by Marston et al. (2004) show the small-scale structure of this region at
angular resolutions between 1.3''-3''.
Several bright IR objects, in particular near DR21 C![]() ,
delineate the dense ridge of gas and dust in both wavelength bands.
The map of 8
,
delineate the dense ridge of gas and dust in both wavelength bands.
The map of 8 ![]() m emission is dominated by many streamers of emission, which appear to connect to the ridge, and diffuse emission.
This is mainly emission from polycyclic aromatic hydrocarbons (PAHs), which are the prime absorbers of far-ultraviolet (FUV) radiation from the surrounding and
embedded massive stars. Bright 8
m emission is dominated by many streamers of emission, which appear to connect to the ridge, and diffuse emission.
This is mainly emission from polycyclic aromatic hydrocarbons (PAHs), which are the prime absorbers of far-ultraviolet (FUV) radiation from the surrounding and
embedded massive stars. Bright 8 ![]() m emission therefore highlights the photon-dominated surface regions
of molecular clouds (PDRs).
The molecular outflow along DR21 E, C, and W is traced well by 4.5
m emission therefore highlights the photon-dominated surface regions
of molecular clouds (PDRs).
The molecular outflow along DR21 E, C, and W is traced well by 4.5 ![]() m emission, mainly due to
strong lines of shock-excited or UV-pumped H2
m emission, mainly due to
strong lines of shock-excited or UV-pumped H2 ![]() = 0-0 S(9).
No ro-vibrational lines of CO
= 0-0 S(9).
No ro-vibrational lines of CO ![]() = 1-0 and only weak Br
= 1-0 and only weak Br![]() have been found in this band (Smith et al. 2006).
have been found in this band (Smith et al. 2006).
Figure 1 (contours on right panel) and Fig. 2
show the KOSMA maps of integrated emission of the rotational transitions CO 3-2,
4-3, and 7-6, which preferentially trace the warm and dense molecular gas around DR21 and along the north-south orientated molecular ridge.
Apart from the ridge, the most obvious feature in the maps is the line emission
along the outflow axis oriented NE-SW.
The main axis of the strong 3-2, 4-3, and 7-6 emission (FWHM ![]() 230
230
![]() ,
resp.
,
resp. ![]() 1.9 pc (D/1.7 kpc)) is tilted by 20
1.9 pc (D/1.7 kpc)) is tilted by 20![]() with respect to
the right ascension axis and correlates nicely with extended H2 emission lobes (Garden et al. 1986).
The red-shifted CO line-wing emission is stronger toward the west side, whereas the blue-shifted emission is more pronounced to the east indicating
that this side is closer to the observer.
with respect to
the right ascension axis and correlates nicely with extended H2 emission lobes (Garden et al. 1986).
The red-shifted CO line-wing emission is stronger toward the west side, whereas the blue-shifted emission is more pronounced to the east indicating
that this side is closer to the observer.
Morphologically, the CO 3-2 map shows a very similar shape in comparison to the CO 4-3 data.
Detailed differences can be seen better if the maps are smoothed to the same resolution.
In Fig. 6, we present two cuts along the outflow and along the main ridge from these data.
At DR21, all CO line integrated intensities are very similar.
Toward position DR21 E, the emission of CO 3-2 and 4-3 stays at a high level, while the 7-6 emission drops.
Toward the west, all three line intensities decline in a similar fashion.
Away from DR21, along the N-S cut, the CO 3-2 emission is dominant, whereas
CO 4-3 and CO 7-6 are sequentially weaker.
Strong CO 7-6 emission is limited to the DR21 core.
DR21 (OH) is located 180
![]() north of DR21 and clearly separated from the DR21 region by a gap in the ridge.
DR21 (OH) is bright in the lower J transitions, but appears weaker in the J = 7-6 transition.
north of DR21 and clearly separated from the DR21 region by a gap in the ridge.
DR21 (OH) is bright in the lower J transitions, but appears weaker in the J = 7-6 transition.
13CO 3-2 (contours on left panel of Fig. 1) was selected to map the column density in the region.
This transition traces the molecular ridge showing two maxima of emission at DR21 C and
DR21 (OH).
The total mass of the ridge is ![]() 104
104 ![]() (D/1.7 kpc)2 (SBS2006).
13CO
weakly follows the outflow from DR21 E to W.
Following the molecular ridge farther to the north, an elongated emission band roughly
coincides in position with three far-infrared sources.
The southernmost source, DR21 FIR1, was observed by ISO/LWS.
Marston et al. (2004) find an extremly red object (ERO 3) here, illuminating a shell-like halo in the 4.5
(D/1.7 kpc)2 (SBS2006).
13CO
weakly follows the outflow from DR21 E to W.
Following the molecular ridge farther to the north, an elongated emission band roughly
coincides in position with three far-infrared sources.
The southernmost source, DR21 FIR1, was observed by ISO/LWS.
Marston et al. (2004) find an extremly red object (ERO 3) here, illuminating a shell-like halo in the 4.5 ![]() m band.
The other two, FIR2 and FIR3,
coincide with MSX point sources.
Like the FIR sources, this northern region is slightly tilted to the east, indicating flux contribution to mainly low-J CO emission
from all three embedded far-IR sources.
13CO reaches up to FIR3, which marks the edge of the dense ridge to the north.
m band.
The other two, FIR2 and FIR3,
coincide with MSX point sources.
Like the FIR sources, this northern region is slightly tilted to the east, indicating flux contribution to mainly low-J CO emission
from all three embedded far-IR sources.
13CO reaches up to FIR3, which marks the edge of the dense ridge to the north.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{5855fig6.eps}
\end{figure}](/articles/aa/full/2007/03/aa5855-06/Timg86.gif) |
Figure 4:
Integrated intensity map of CS 7-6.
The integration interval is -10 to 4
|
| Open with DEXTER | |
C I 1-0 and 2-1 appear in good agreement with the shape of the molecular ridge as traced by 13CO.
Even though the emission around DR21 in [C I] (see Fig. 3) appears more centrally peaked than in the CO maps, the main axis between positions E and W is clearly visible.
The molecular ridge is seen to extend from the southeast through DR21 and through DR21 (OH)
3' northwards.
DR21 (OH) is visible as an elongated, less compact region linking-up to the far-infrared sources farther north.
The DR21 (OH) region appears to harbour multiple sources, as there is no central emission peak.
The [C I] 1-0 map reveals a southern peak and extended weaker emission in the north.
This substructure may not be significant because the variation is only about ![]() .
Chandler et al. (1993) identified five compact sources in the DR21 (OH) region (indicated in Fig. 1) using 1.3-mm thermal dust emission at 11'' resolution.
The C I 2-1 is, compared to 1-0, relatively weak toward DR21 (OH) and suggests a lower temperature
than for DR21 C
(see below).
North of DR21 (OH), the carbon emission stretches over the three far-IR spots FIR1, FIR2, and FIR3.
Here, the upper atomic carbon line is in good agreement with the overall shape of optically thin low-J CO isotopomers,
i.e., the C18O 2-1 map by Wilson & Mauersberger (1990), and to some extent with our 13CO 3-2 map.
A more distinct morphology analysis is not possible due to the remaining noise and some self-chopping residuals.
.
Chandler et al. (1993) identified five compact sources in the DR21 (OH) region (indicated in Fig. 1) using 1.3-mm thermal dust emission at 11'' resolution.
The C I 2-1 is, compared to 1-0, relatively weak toward DR21 (OH) and suggests a lower temperature
than for DR21 C
(see below).
North of DR21 (OH), the carbon emission stretches over the three far-IR spots FIR1, FIR2, and FIR3.
Here, the upper atomic carbon line is in good agreement with the overall shape of optically thin low-J CO isotopomers,
i.e., the C18O 2-1 map by Wilson & Mauersberger (1990), and to some extent with our 13CO 3-2 map.
A more distinct morphology analysis is not possible due to the remaining noise and some self-chopping residuals.
![\begin{figure}
\par\includegraphics[angle=-90,width=3.75cm,clip]{5855fig7.eps}\h...
...e*{0.3mm}
\includegraphics[angle=-90,width=3.2cm,clip]{5855figb.eps}\end{figure}](/articles/aa/full/2007/03/aa5855-06/Timg89.gif) |
Figure 5:
Spectra of all observed species at the five ISO positions. Grey
filled spectra outlined in black: observed lines;
thin grey lines: line profiles modeled with the radiative transfer code S IML INE (see Sect. 4.2).
All spectra are shown at a common spatial resolution of 80'' and on a
|
| Open with DEXTER | |
The map in Fig. 4 reveals two condensations at DR21 and around DR21 (OH).
The southern peak is centred on the H II-region and follows the direction of the outflow to the west.
The FWHM is 133
![]()
![]() 102
102
![]() .
The northern complex (FWHM 108
.
The northern complex (FWHM 108
![]()
![]() 156
156
![]() )
is extended and may contain several unresolved cores (see above).
The emission extends up to the FIR1 position, but does not cover all three FIR spots.
The lines of CS 7-6 and C18O 1-0are the only lines in our sample that show brighter
emission toward DR21 (OH) than toward the southern molecular cloud/H II-region DR21.
For CS, this has also been observed by Shirley et al. (2003).
)
is extended and may contain several unresolved cores (see above).
The emission extends up to the FIR1 position, but does not cover all three FIR spots.
The lines of CS 7-6 and C18O 1-0are the only lines in our sample that show brighter
emission toward DR21 (OH) than toward the southern molecular cloud/H II-region DR21.
For CS, this has also been observed by Shirley et al. (2003).
In the following, we concentrate on the 5 ISO/LWS positions (as indicated in Fig. 1).
In Fig. 5, we present spectra of 12CO, 13CO, and C18O towards these positions, together with spectra of C I, and of CS 7-6 between -30 to
![]() .
We present all observations at a common resolution of
.
We present all observations at a common resolution of
![]() .
In Table 3, we give the corresponding line fluxes.
.
In Table 3, we give the corresponding line fluxes.
The 12CO emission from the DR21/H II-region shows broad wing emission due to the outflowing molecular gas
(with line widths of more than
![]() and peak temperatures well above 20 K).
A self-absorption dip at the velocity of
and peak temperatures well above 20 K).
A self-absorption dip at the velocity of
![]() is most pronounced in mid-J CO lines at DR21 C where the peak intensity drops by a factor of two at the line centre.
Toward DR21 (OH), CO shows blue-skewed, double-peaked lines with self-absorption.
In both cases, the velocity of the line reversal nicely matches the corresponding emission in 13CO and C I and is very likely
caused by the same cold material in the dust lane.
is most pronounced in mid-J CO lines at DR21 C where the peak intensity drops by a factor of two at the line centre.
Toward DR21 (OH), CO shows blue-skewed, double-peaked lines with self-absorption.
In both cases, the velocity of the line reversal nicely matches the corresponding emission in 13CO and C I and is very likely
caused by the same cold material in the dust lane.
With widths of 4 to
![]() ,
the line shapes of 13CO are similar to the [C I] profiles.
The 13CO 6-5 emission (
,
the line shapes of 13CO are similar to the [C I] profiles.
The 13CO 6-5 emission (
![]() K) at all five positions indicates the presence of warm and dense gas.
At DR21 C, 13CO 6-5 shows broad symmetric wing emission that is underlying a narrow component.
The velocity extent of the wings is similar to that in mid-J CO lines.
A better signal-to-noise ratio would allow a more accurate estimate.
Only weak line wings are visible in the lower 13CO 3-2 line since it
primarily traces the quiescent gas.
K) at all five positions indicates the presence of warm and dense gas.
At DR21 C, 13CO 6-5 shows broad symmetric wing emission that is underlying a narrow component.
The velocity extent of the wings is similar to that in mid-J CO lines.
A better signal-to-noise ratio would allow a more accurate estimate.
Only weak line wings are visible in the lower 13CO 3-2 line since it
primarily traces the quiescent gas.
DR21 is associated with molecular gas centred at a velocity of
![]() .
In addition to this, weaker emission between
.
In addition to this, weaker emission between ![]() and
and
![]() is associated with the W75 N complex
approximately 11 pc (D/1.7 kpc) to the northwest.
Some authors (e.g., Dickel et al. 1978) conclude that both clouds are actually interacting. SBS2006 shows channel maps revealing a link between both clouds.
Diffuse emission in the 13CO J=1-0 and both [C I] transitions and
absorption in the red wing of the low-J CO lines (up to J=4-3) suggest that this material is located in front of the DR21 complex.
We do not discuss this contribution further here but instead refer the reader to SBS2006.
is associated with the W75 N complex
approximately 11 pc (D/1.7 kpc) to the northwest.
Some authors (e.g., Dickel et al. 1978) conclude that both clouds are actually interacting. SBS2006 shows channel maps revealing a link between both clouds.
Diffuse emission in the 13CO J=1-0 and both [C I] transitions and
absorption in the red wing of the low-J CO lines (up to J=4-3) suggest that this material is located in front of the DR21 complex.
We do not discuss this contribution further here but instead refer the reader to SBS2006.
Table 3:
Line-integrated intensities in [
![]() ]
(upper table) and in [10-7 erg s-1 cm-2 sr-1] (lower table) of the low- and mid-J
CO isotopomeric lines and of the CS 7-6 line observed at KOSMA and FCRAO.
In order to prevent the
]
(upper table) and in [10-7 erg s-1 cm-2 sr-1] (lower table) of the low- and mid-J
CO isotopomeric lines and of the CS 7-6 line observed at KOSMA and FCRAO.
In order to prevent the
![]() velocity component from adding to the integrated intensity,
the listed intensities were integrated only over the
velocity component from adding to the integrated intensity,
the listed intensities were integrated only over the
![]() component.
As the 12CO lines merge with the second velocity component, these spectra were fitted using a 2-component Gaussian
with the
component.
As the 12CO lines merge with the second velocity component, these spectra were fitted using a 2-component Gaussian
with the
![]() velocity component masked out.
All line intensities are reported for 80'' angular resolution (higher angular resolution data have been smoothed).
velocity component masked out.
All line intensities are reported for 80'' angular resolution (higher angular resolution data have been smoothed).
Figure 7 shows the ISO/LWS continuum fluxes, together with spectrally unresolved lines of [C II], [O I], [O III], [N II], and rotational high-J CO transitons. The following sections discuss the dust and line emission at the individual positions.
In all five cases, the far-infrared dust-continuum flux - with strong emission lines masked out - was ![]() -fitted with a single isothermal grey-body model
-fitted with a single isothermal grey-body model
![]() with
a fixed solid angle (
with
a fixed solid angle (
![]() sr, assuming that the emission fills the 80'' aperture)
and a dust opacity
sr, assuming that the emission fills the 80'' aperture)
and a dust opacity
![]() with
with ![]() .
Spectral indices are typically found between 1.0 and 2.0 (see Goldsmith et al. 1997, for a discussion of observations and grain models).
Although the spectral index is known to vary with the cloud type and optical depth, we assumed a fixed
.
Spectral indices are typically found between 1.0 and 2.0 (see Goldsmith et al. 1997, for a discussion of observations and grain models).
Although the spectral index is known to vary with the cloud type and optical depth, we assumed a fixed ![]() for all 5 positions (but see discussion in Sect. 4.2.3).
A fixed
for all 5 positions (but see discussion in Sect. 4.2.3).
A fixed ![]() of 1.5 is compatible with the grain models of Preibisch et al. (1993), Pollack et al. (1994), and observations,
e.g., by Walker et al. (1990).
The total infrared dust continuum flux and bolometric luminosity per position was derived by integrating the fit-model
of 1.5 is compatible with the grain models of Preibisch et al. (1993), Pollack et al. (1994), and observations,
e.g., by Walker et al. (1990).
The total infrared dust continuum flux and bolometric luminosity per position was derived by integrating the fit-model ![]() .
The integration interval (1-1000
.
The integration interval (1-1000 ![]() m) covers the expected intensity maxima between 50-80
m) covers the expected intensity maxima between 50-80 ![]() m and corresponds to the range used,
e.g., by Calzetti et al. (2000).
Errors in the fit parameters were estimated as described in the following.
We assumed
(i) the optical depths
m and corresponds to the range used,
e.g., by Calzetti et al. (2000).
Errors in the fit parameters were estimated as described in the following.
We assumed
(i) the optical depths
![]() and total fluxes are accurate to about
and total fluxes are accurate to about ![]() %, mainly due to the remaining calibration artefacts within the LW1-5 bands;
(ii) the temperature fit error is less than 2%, but the absolute error also depends on the quality of SW1 detector data (leftmost data points in Fig. 7).
%, mainly due to the remaining calibration artefacts within the LW1-5 bands;
(ii) the temperature fit error is less than 2%, but the absolute error also depends on the quality of SW1 detector data (leftmost data points in Fig. 7).
We found extinctions between
![]() and temperatures between 31-43 K (cf. Table 5).
In contrast to the extinction, the variation in dust temperature is small.
Considering that we used a single-temperature model, these temperatures were probably biased by the warmer dust.
Evidence of cold dust peaking above 100
and temperatures between 31-43 K (cf. Table 5).
In contrast to the extinction, the variation in dust temperature is small.
Considering that we used a single-temperature model, these temperatures were probably biased by the warmer dust.
Evidence of cold dust peaking above 100 ![]() m is visible at DR21 W, E, (OH) and FIR1 in Fig. 7; but
disentangling this component would require longer wavelength data,
and the contribution to the integrated grey-body flux is relatively small.
The cold dust is studied in detail by, e.g., Chandler et al. (1993) and Motte et al. (2005).
We derived the molecular hydrogen column density from the conversion N(H2)/
m is visible at DR21 W, E, (OH) and FIR1 in Fig. 7; but
disentangling this component would require longer wavelength data,
and the contribution to the integrated grey-body flux is relatively small.
The cold dust is studied in detail by, e.g., Chandler et al. (1993) and Motte et al. (2005).
We derived the molecular hydrogen column density from the conversion N(H2)/
![]() cm-2 mag-1 (Bohlin et al. 1978, cf. Table 5),
and if placed at the distance of 1.7 kpc, the molecular gas masses vary between
150-1800
cm-2 mag-1 (Bohlin et al. 1978, cf. Table 5),
and if placed at the distance of 1.7 kpc, the molecular gas masses vary between
150-1800 ![]() .
.
The peak of the beam-averaged dust temperature is ![]() 43 K at DR21 C.
With
43 K at DR21 C.
With
![]() ,
the strongest continuum sources are DR21 C and DR21 (OH).
Due to the high temperature towards DR21 C, the flux density is higher at short wavelengths,
but drops below the flux density of DR21 (OH) above
,
the strongest continuum sources are DR21 C and DR21 (OH).
Due to the high temperature towards DR21 C, the flux density is higher at short wavelengths,
but drops below the flux density of DR21 (OH) above ![]() 200
200 ![]() m.
For DR21 (OH), we estimated a higher mass than for the DR21 E-W complex (1814, resp. 1257
m.
For DR21 (OH), we estimated a higher mass than for the DR21 E-W complex (1814, resp. 1257 ![]() ).
Chandler et al. (1993) assumed temperatures between 25 K and 40 K and
derived a slightly lower total mass of 1650
).
Chandler et al. (1993) assumed temperatures between 25 K and 40 K and
derived a slightly lower total mass of 1650 ![]()
![]() for the sources at DR21 (OH).
for the sources at DR21 (OH).
Table 4:
The ISO/LWS high-J CO and atomic FIR lines at 80'' resolution.
The transformation between flux densities and surface brightnesses was made using the
beam sizes given in Table 5.10 of the ISO-LWS Handbook v. 2.1.
The beam solid angle varies between
![]() sr and
sr and
![]() sr.
Because the lines are unresolved, the line widths were held to the instrumental line width: 0.29 or 0.60
sr.
Because the lines are unresolved, the line widths were held to the instrumental line width: 0.29 or 0.60 ![]() m
for detectors 0-4 and 5-9, respectively.
Correction factors between 0.37 to 0.85 for extended sources have been applied.
We assume a 30% absolute photometry uncertainty for LWS.
m
for detectors 0-4 and 5-9, respectively.
Correction factors between 0.37 to 0.85 for extended sources have been applied.
We assume a 30% absolute photometry uncertainty for LWS.
Table 5:
Results of dust continuum single-component fit,
with ![]() fixed at 1.5, and
fixed at 1.5, and ![]() is
is
![]() sr.
sr.
The LWS-band covers many important far-IR cooling lines and
tracers of the photon-dominated regime of molecular clouds.
Table 4 gives the integrated line intensities of [C II] (158 ![]() m), high-J CO, and [O I] (63 and 145
m), high-J CO, and [O I] (63 and 145 ![]() m)
derived from the ISO observations quoted above.
In this paragraph, we focus on the carbon-bearing species
needed for Sect. 4 and postpone the discussion of the other lines to the end of Sect. 4.
m)
derived from the ISO observations quoted above.
In this paragraph, we focus on the carbon-bearing species
needed for Sect. 4 and postpone the discussion of the other lines to the end of Sect. 4.
At DR21, highly-excited CO emission is visible at all three positions, but most prominently around the H II-region at DR21 C.
The centre position with more than
![]() erg s-1 cm-2 sr-1 in mid- and high-J CO
is also the brightest continuum source in the mapped region.
The emission stems from large columns of warm quiescent gas that are heated by an embedded object.
Toward the East and West positions, where vibrationally excited H2 outlines the molecular outflow (Garden et al. 1986),
the FIR continuum is somewhat weaker and more important, the continuum flux does not correlate with the unusually
strong FIR line emission.
This gas is visible in the line wings of mid-J CO lines (Fig. 5) and in the bright H2 line emission
at 4.5
erg s-1 cm-2 sr-1 in mid- and high-J CO
is also the brightest continuum source in the mapped region.
The emission stems from large columns of warm quiescent gas that are heated by an embedded object.
Toward the East and West positions, where vibrationally excited H2 outlines the molecular outflow (Garden et al. 1986),
the FIR continuum is somewhat weaker and more important, the continuum flux does not correlate with the unusually
strong FIR line emission.
This gas is visible in the line wings of mid-J CO lines (Fig. 5) and in the bright H2 line emission
at 4.5 ![]() m in the IRAC map (Fig. 1).
Lane et al. (1990) conclude that neither a single C- nor a single J-shock can account for the observed far-IR line emission alone and
additional heating through FUV radiation is required.
Although DR21 (OH) has the second strongest continuum, the sources associated with this position are surprisingly inactive in far-IR line emission.
We find four high-J CO line detections, but due to a lower scanning resolution, the values given
in Table 4 have a higher uncertainty.
The far-IR source FIR1 is the faintest with respect to the line fluxes, although the continuum is stronger than towards DR21 W.
High-J CO was not detected at FIR1, so we give upper limits in the table.
m in the IRAC map (Fig. 1).
Lane et al. (1990) conclude that neither a single C- nor a single J-shock can account for the observed far-IR line emission alone and
additional heating through FUV radiation is required.
Although DR21 (OH) has the second strongest continuum, the sources associated with this position are surprisingly inactive in far-IR line emission.
We find four high-J CO line detections, but due to a lower scanning resolution, the values given
in Table 4 have a higher uncertainty.
The far-IR source FIR1 is the faintest with respect to the line fluxes, although the continuum is stronger than towards DR21 W.
High-J CO was not detected at FIR1, so we give upper limits in the table.
The [C II] emission is detected at all five positions and
peaks at DR21 E. Toward the West, the flux decreases by almost 50%.
The low [C II] flux of
![]() erg s-1 cm-2 sr-1at DR21 (OH) may indicate a lack of ionised carbon or
that the temperature is too low for excitation in the upper energy level
(
erg s-1 cm-2 sr-1at DR21 (OH) may indicate a lack of ionised carbon or
that the temperature is too low for excitation in the upper energy level
(
![]() K above ground).
At DR21 FIR1, [C II] is again slightly enhanced compared to DR21 (OH).
K above ground).
At DR21 FIR1, [C II] is again slightly enhanced compared to DR21 (OH).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{5855figc.eps}\end{figure}](/articles/aa/full/2007/03/aa5855-06/Timg136.gif) |
Figure 6:
Cut along the DR21 outflow axis (top)
and along the ridge (bottom) centred on DR21 C in the CO 3-2, 4-3, and 7-6 integrated emission.
The 80
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{5855figd.eps}\par\...
...e*{7.6mm}\includegraphics[angle=-90,width=7.25cm,clip]{5855fige.eps}\end{figure}](/articles/aa/full/2007/03/aa5855-06/Timg137.gif) |
Figure 7: ISO/LWS Spectral Energy Distribution (SED) of the DR21 region (upper panel), and the DR21 (OH) and DR21 FIR1 region (lower panel). Curves indicate the best greybody fit corresponding to the values given in Table 5. |
| Open with DEXTER | |
Table 6:
C I and 13CO line ratio R (in
![]() ;
values taken from Table 3),
excitation temperature (with lower and upper
;
values taken from Table 3),
excitation temperature (with lower and upper ![]() limits), and C I, 13CO (with relative upper and lower errors),
and C18O column densities (bracketed by
limits), and C I, 13CO (with relative upper and lower errors),
and C18O column densities (bracketed by
![]() of 13CO).
All abundances X are relative to the H2 column densities (first row; taken from Col. 4 of Table 5).
of 13CO).
All abundances X are relative to the H2 column densities (first row; taken from Col. 4 of Table 5).
In this section we analyse the line properties of the observed carbon species from ISO/LWS data and combine these results with the KOSMA observations. We start with an LTE approach and then model the line emission with full radiative transfer.
We estimated the composition of the molecular gas with respect to the carbon abundance in the main gas-phase species CO, C, and C+. This was done by assuming LTE and optically thin line emission. We therefore used the less abundant isotopomeres 13CO and C18O. We list the results for excitation temperature, column density, and abundance in Table 6.
The column density of
![]() is determined in two ways again assuming optically thin emission.
First, by adopting
is determined in two ways again assuming optically thin emission.
First, by adopting
![]() (Eq. (C.9)) with the 13CO 6-5 to 3-2 integrated intensity
line ratio
(Eq. (C.9)) with the 13CO 6-5 to 3-2 integrated intensity
line ratio
![]() ,
and using Eq. (C.10).
This ratio is a sensitive temperature measure from
,
and using Eq. (C.10).
This ratio is a sensitive temperature measure from ![]() 20 K up to a few 100 K.
The excitation temperatures vary between 30 and 46 K and represent upper limits
because of possible self-absorption due to a high optical thickness in the lower transition.
The temperatures agree with values from Wilson & Mauersberger (1990), who find 20-65 K from NH3 emission,
and are always below the C I temperatures from above, indicating an origin from different gas.
The 13CO column density,
20 K up to a few 100 K.
The excitation temperatures vary between 30 and 46 K and represent upper limits
because of possible self-absorption due to a high optical thickness in the lower transition.
The temperatures agree with values from Wilson & Mauersberger (1990), who find 20-65 K from NH3 emission,
and are always below the C I temperatures from above, indicating an origin from different gas.
The 13CO column density,
![]()
![]() ,
varies by a factor of 2 as the C I column density.
,
varies by a factor of 2 as the C I column density.
The same scatter is found if we estimate the column density,
in an alternative approach,
from 13CO 1-0 rather than 13CO 6-5 (Eq. (C.11))
and derive temperatures with Eq. (C.8).
Those column densities tend to be higher, between
![]()
![]() ,
indicating that a larger amount of the gas traced by 13CO is cold.
,
indicating that a larger amount of the gas traced by 13CO is cold.
Table 7:
The physical parameters for the observed ISO/LWS positions.
The radii listed in Col. 2 give the inner and outer edge of each shell.
Columns 3 to 7 lists the temperature, clump-averaged number density of H2, volume filling, column density
of H2, and the gas mass.
For these columns, the first entry is the mass-averaged value for the whole cloud, values in parentheses show averages within each shell.
The last column lists the reduced ![]() fit result for 11 lines (6 KOSMA, 2 FCRAO and 3 ISO).
fit result for 11 lines (6 KOSMA, 2 FCRAO and 3 ISO).
Considering the optically thin emission of C18O,
we estimated the total molecular gas column density from Eq. (C.12)
using both 13CO
![]() estimates as limits.
We found high C18O column densities of about
estimates as limits.
We found high C18O column densities of about
![]() cm-2 along the ridge
and
cm-2 along the ridge
and
![]() cm-2 toward E and W.
cm-2 toward E and W.
In order to get a rough estimate of the C+ column density from the ISO data, we
assumed
![]() [cm-2] (erg s-1 cm-2 sr
-1)-1(Crawford et al. 1985), which is a good approximation for
an excitation temperature of >91 K and a density
[cm-2] (erg s-1 cm-2 sr
-1)-1(Crawford et al. 1985), which is a good approximation for
an excitation temperature of >91 K and a density
![]()
![]() .
The peak column density derived this way,
.
The peak column density derived this way,
![]()
![]() ,
is observed towards DR21 C and E, while
only about 28% of the peak value is found towards DR21 (OH).
,
is observed towards DR21 C and E, while
only about 28% of the peak value is found towards DR21 (OH).
The comparison between the C18O and 13CO column density (for the lower
![]() limit
in Table 6) shows that the abundance ratio
limit
in Table 6) shows that the abundance ratio
![]() is typically near the canonical local abundance ratio
[490]:[65]=7.5 (Langer & Penzias 1990).
is typically near the canonical local abundance ratio
[490]:[65]=7.5 (Langer & Penzias 1990).
The atomic carbon abundances [C I]/[H2] fall in the range of
![]() .
The high values are only observed at the E and W positions.
In the cooler northern positions, the abundance is reduced by a factor up to 10.
This contrasts with the values of
.
The high values are only observed at the E and W positions.
In the cooler northern positions, the abundance is reduced by a factor up to 10.
This contrasts with the values of
![]() found in cold dark clouds
by Keene et al. (1997).
found in cold dark clouds
by Keene et al. (1997).
Except for DR21 FIR1, there is a good correlation between X(C I) and X(C18O).
Toward DR21 (OH),
the C18O and [C I] abundances are systematically lower than toward DR21 by factors 2-3,
although the position with the lowest [C I] abundance
(10-6), FIR1, has the highest C18O abundance
(up to
![]() ).
).
Mookerjea et al. (2006) present a compilation of the C/CO abundance ratios versus H2 column densities for Galactic star-forming regions and diffuse clouds.
The ratio at the positions DR21 E, W, and FIR1, 0.07-0.17, agrees well with the relation
![]() given there for Cepheus B.
DR21 and DR21 (OH) deviate from this relation but are still within the observed scatter.
We therefore
underline their conclusion that C I is no straightforward tracer of total H2 column densities and total masses.
given there for Cepheus B.
DR21 and DR21 (OH) deviate from this relation but are still within the observed scatter.
We therefore
underline their conclusion that C I is no straightforward tracer of total H2 column densities and total masses.
The amount of carbon in the carbon bearing species C+, C0, and CO
can be compared - by using their relative abundances (last row of Table 6).
The neutral atomic carbon relative abundance is rather homogeneous at about 9-16% of the total carbon gas content at all five positions.
The rest is shared between CO and C II.
Ionised carbon has the highest abundance
toward DR21 E (26%).
Here, the gas is very likely exposed to a high UV radiation field and carbon species are photodissociated to C I and ionised further to C II.
High fractional CO abundances (>85%), such as for DR21 (OH) and FIR1, were also reported for S 106 (>86%, Schneider et al. 2003) and W3 Main (>60%, Kramer et al. 2004).
The ratios in other sources are, e.g., 37:07:56 for IC 63 (Jansen et al. 1996),
NGC2024 with 40:10:50 (Jaffe & Plume 1995), or
![]() Carina with 68:15:16 (Brooks et al. 2003).
Carina with 68:15:16 (Brooks et al. 2003).
In a self-consistent approach, the temperature, column and number density, total molecular mass, volume filling, and mass composition were determined using a 1D radiative transfer code (S IML INE, Ossenkopf et al. 2001). In order to describe these physical conditions, we created heterogeneous models with internal clumping and turbulence in a spherically symmetric geometry for each of the 5 observed regions. The physical parameters of a shell are defined by their values at the inner radius, and the radial dependence is described by a power-law.
A model with two nested shells provided reasonable results in most cases:
(i) a hot and dense molecular interface zone wrapped around a central H II-region;
(ii) a massive cold cloud, the envelope region, enclosing the interface region.
While in the inner component primarily the mid- and high-J CO emission lines are excited,
this envelope is responsible for self-absorption and the low lying lines of 13CO and C18O.
We set the abundance of species with respect to molecular hydrogen to standard values (see Table 7).
The source size is a crucial parameter that is not well-confined by the line profiles or
the map we obtained.
A small cloud model can easily produce similar results to those for a bigger cloud with a lower volume filling.
We therefore approximated the radii using high-resolution line and continuum observations
(Wilson & Mauersberger 1990; Jaffe et al. 1989; Chandler et al. 1993; Vallée & Fiege 2006; Lane et al. 1990).
The inner cut-off was assumed to be 0.04 pc (<104 AU), except for
DR21 C where we estimated ![]() 0.12 pc from the 14.7 GHz continuum (Roelfsema et al. 1989).
The H II-region is considered to be free of molecular gas, so we neglected the continuum contribution by ionised gas.
Gradients within the shells in any of the parameters were initially set to zero
and were adjusted during the fit if required.
0.12 pc from the 14.7 GHz continuum (Roelfsema et al. 1989).
The H II-region is considered to be free of molecular gas, so we neglected the continuum contribution by ionised gas.
Gradients within the shells in any of the parameters were initially set to zero
and were adjusted during the fit if required.
We used the following recipe to find appropriate model parameters.
(i) The linewidth is approximated by adjusting the turbulent velocity field until both the low-J and mid-J line wings match the observed profile.
As line emission from the inner warm gas is shielded by the colder envelope gas closer to the surface,
the width of the CO absorption dip in the line centre constrains the turbulent velocity dispersion of this envelope component;
(ii) the H2-density is defined locally as a clump-density parameter, and was varied independently between 104 and 107
![]() for both shells.
The high densities are a pre-requisite for high-J CO excitation;
(iii)
in the optically thin line wings we see material from the inner shell predominantly where the
simulated macroturbulent motion leads to the higher line width
which is only partly shielded by the outer shell.
This allows us to fit the temperatures of both the inner and the outer shells from the line shape;
(iv) the model allows us to differentiate between radial and turbulent gas motion.
Where lines of high opacity toward the line centre showed a blue-skewed profile,
we introduced radial infall as a plausible explanation.
If possible, we tried to keep the radial component close to zero.
for both shells.
The high densities are a pre-requisite for high-J CO excitation;
(iii)
in the optically thin line wings we see material from the inner shell predominantly where the
simulated macroturbulent motion leads to the higher line width
which is only partly shielded by the outer shell.
This allows us to fit the temperatures of both the inner and the outer shells from the line shape;
(iv) the model allows us to differentiate between radial and turbulent gas motion.
Where lines of high opacity toward the line centre showed a blue-skewed profile,
we introduced radial infall as a plausible explanation.
If possible, we tried to keep the radial component close to zero.
The full line profiles of CO, 13CO, and C18O from KOSMA and FCRAO were taken into account in a
reduced ![]() fit in
fit in ![]() 1900 degrees of freedom with 20-28 free parameters.
The second velocity component is masked out by a window centred on
1900 degrees of freedom with 20-28 free parameters.
The second velocity component is masked out by a window centred on
![]() .
For the ISO lines, we fit the integrated flux of three lines.
CO 14-13 is not considered because no consistent fit was possible in conjunction with the other CO lines.
In total, we included 11 lines weighted by the
.
For the ISO lines, we fit the integrated flux of three lines.
CO 14-13 is not considered because no consistent fit was possible in conjunction with the other CO lines.
In total, we included 11 lines weighted by the ![]() determined
from a baseline region not including any lines.
The spectra do not contain any obvious baseline ripples above the system noise.
determined
from a baseline region not including any lines.
The spectra do not contain any obvious baseline ripples above the system noise.
We independently optimized the model parameters for each position.
Figure 5 shows the derived line profiles.
At all five positions, we obtained solutions of better than
![]() ,
which we
consider - given the number of fitted lines - a very good result and definitely
are much better than for a single-component model.
,
which we
consider - given the number of fitted lines - a very good result and definitely
are much better than for a single-component model.
Within the interface-zone,
a temperature range from 80 K (at DR21 FIR1) to 148 K (at DR21 C) for gas masses of 15-60 ![]() is found.
This temperature is much higher than the typical LTE excitation temperature of the mid-J CO line peak.
The fit converges toward solutions with a high density of about 106
is found.
This temperature is much higher than the typical LTE excitation temperature of the mid-J CO line peak.
The fit converges toward solutions with a high density of about 106
![]() and
with a volume filling of a few percent, indicating a non-homogeneous distribution.
The warm gas dominates the emission in the line wings and therefore is explained by
the steep turbulent velocity gradient with velocities up to
and
with a volume filling of a few percent, indicating a non-homogeneous distribution.
The warm gas dominates the emission in the line wings and therefore is explained by
the steep turbulent velocity gradient with velocities up to
![]() .
Because the envelope is much colder and more massive (cf. Sect. 4.2.3),
the average temperature in the regions
DR21 C with 36 K and DR21 (OH) with 31 K is rather low compared to the E, W, and
FIR1 position. There, the gas temperature rises up to 60 K, but the gas masses are only a few hundred
solar masses.
Besides the mass fraction,
the steepness of the gradient in excitation condition and line width
between inner and outer components determines whether we
see a distinct self-absorption (e.g., DR21 C) or a flat-top (e.g., DR21 W) line profile.
Table 7 compiles a list of the derived physical parameters.
A detailed discussion of the individual positions is given in Appendix A.
.
Because the envelope is much colder and more massive (cf. Sect. 4.2.3),
the average temperature in the regions
DR21 C with 36 K and DR21 (OH) with 31 K is rather low compared to the E, W, and
FIR1 position. There, the gas temperature rises up to 60 K, but the gas masses are only a few hundred
solar masses.
Besides the mass fraction,
the steepness of the gradient in excitation condition and line width
between inner and outer components determines whether we
see a distinct self-absorption (e.g., DR21 C) or a flat-top (e.g., DR21 W) line profile.
Table 7 compiles a list of the derived physical parameters.
A detailed discussion of the individual positions is given in Appendix A.
As a consistency check, we computed the CS and C I profiles using the same model parameters as derived from CO. This implies a homogeneous distribution of CS and C I with CO, which is only affected by the abundances of the species.
For both species we also obtained excellent fit results.
The resulting line profiles are shown in Fig. 5.
CS 7-6 is only excited where the H2 density and temperatures are sufficiently high;
hence, we only find CS emission in the dense regions DR21 C and (OH).
The models fit best to the observations for an abundance of X(CS) =
![]() (Hatchell et al. 1998),
whereas the range
(Hatchell et al. 1998),
whereas the range
![]() to
to
![]() given by Shirley et al. (2003) is clearly too low for this region.
given by Shirley et al. (2003) is clearly too low for this region.
Instead of a carbon abundance variation across the positions (as found in Sect. 4.1),
an abundance X(C I) of
![]() fits our [C I] observations nicely.
The C I excitation temperatures, as derived in Sect. 4.1.1,
fall in the range covered by the two-component radiative transfer model.
fits our [C I] observations nicely.
The C I excitation temperatures, as derived in Sect. 4.1.1,
fall in the range covered by the two-component radiative transfer model.
| |
Figure 8: Cooling curves of the best-fit model line fluxes (marked by open symbols) of CO, 13CO, and C18O. Observed line intensities are indicated as filled symbols (see Table 3). At position DR21 C, we included two observations by Boreiko & Betz (1991) of CO and 13CO J=9-8. Since the 13CO 6-5 map does not cover the postitions DR21 (OH) and DR21 FIR1 on a fully sampled grid, we expect a larger error. The high-J CO emission at DR21 FIR1 are upper limits. |
| Open with DEXTER | |
The volume filling,
![]() ,
is a model parameter capable of increasing the clump density
without increasing the overall mass as well.
The determined
,
is a model parameter capable of increasing the clump density
without increasing the overall mass as well.
The determined
![]() is usually low between 1% to 8% (Col. 5 in Table 7).
At DR21 C, this is confirmed by our observations of the CS 7-6 transition,
which is sensitive to densities of several 106
is usually low between 1% to 8% (Col. 5 in Table 7).
At DR21 C, this is confirmed by our observations of the CS 7-6 transition,
which is sensitive to densities of several 106
![]() :
Given the high H2 column density (up to
:
Given the high H2 column density (up to
![]() cm-2),
this translates to a column-to-volume density ratio of about 0.006 pc.
If we assume that the visible extent of the DR21 source (
cm-2),
this translates to a column-to-volume density ratio of about 0.006 pc.
If we assume that the visible extent of the DR21 source (![]() 0.69 pc in CS, after deconvolving the beam) is similar
to the size along the line-of-sight, a volume filling of
0.69 pc in CS, after deconvolving the beam) is similar
to the size along the line-of-sight, a volume filling of ![]() 0.01 is derived.
A high degree of small-scale spatial and velocity structure is also needed to explain the hyper-fine-structure
anomalies observed in ammonia data toward DR21 (Stutzki 1985).
Shirley et al. (2003), who studied CS 5-4 in a sample of high-mass star-forming regions,
derived a volume filling with a median of 0.14.
This is one order of magnitude higher than our results for the dense regions DR21 and DR21 (OH).
0.01 is derived.
A high degree of small-scale spatial and velocity structure is also needed to explain the hyper-fine-structure
anomalies observed in ammonia data toward DR21 (Stutzki 1985).
Shirley et al. (2003), who studied CS 5-4 in a sample of high-mass star-forming regions,
derived a volume filling with a median of 0.14.
This is one order of magnitude higher than our results for the dense regions DR21 and DR21 (OH).
The total mass for all 5 positions is
![]()
![]() ,
which is mostly shared between DR21 C and DR21 (OH) with
,
which is mostly shared between DR21 C and DR21 (OH) with ![]()
![]()
![]() each.
In direct comparison to the masses derived from dust observation in Sect. 3.3.1, we find that our model
gives higher masses
(
each.
In direct comparison to the masses derived from dust observation in Sect. 3.3.1, we find that our model
gives higher masses
(
![]() ), except for the DR21 (OH) model mass.
To compare our mass estimate with masss from the literature, often derived
for a different distance, we scaled the mass in Table 7 with the square of the distance, basically
assuming that the column density, computed from the observed lines, is
independent of the distance. This approach is consistent with a
local radiative transfer treatment, such as LTE or escape probability
analyses, where the molecular excitation does not depend on the total
gas mass. For the self-consistent radiative transfer code, this
assumption is, however, not completely justified, but deviations
from this simple scaling relation are to be expected. When comparing
the values from Table 7 to results obtained for
much larger distances, our quadratically scaled mass estimates are
therefore always expected to be too high; and when comparing them
to results for lower distances, they should be systematically lower.
Shirley et al.
estimated virial masses of 561
), except for the DR21 (OH) model mass.
To compare our mass estimate with masss from the literature, often derived
for a different distance, we scaled the mass in Table 7 with the square of the distance, basically
assuming that the column density, computed from the observed lines, is
independent of the distance. This approach is consistent with a
local radiative transfer treatment, such as LTE or escape probability
analyses, where the molecular excitation does not depend on the total
gas mass. For the self-consistent radiative transfer code, this
assumption is, however, not completely justified, but deviations
from this simple scaling relation are to be expected. When comparing
the values from Table 7 to results obtained for
much larger distances, our quadratically scaled mass estimates are
therefore always expected to be too high; and when comparing them
to results for lower distances, they should be systematically lower.
Shirley et al.
estimated virial masses of 561 ![]() (D/1.7 kpc) for DR21 (resp. 714
(D/1.7 kpc) for DR21 (resp. 714 ![]() (D/1.7 kpc) for DR21 (OH)).
These estimates are lower than our masses
but were calculated over a much smaller radius of 0.17 pc(D/1.7 kpc), while our region covers up to 0.7 pc.
Ossenkopf et al. (2001) estimated the DR21 mass using a radiative transfer analysis of CS data.
They estimated 578
(D/1.7 kpc) for DR21 (OH)).
These estimates are lower than our masses
but were calculated over a much smaller radius of 0.17 pc(D/1.7 kpc), while our region covers up to 0.7 pc.
Ossenkopf et al. (2001) estimated the DR21 mass using a radiative transfer analysis of CS data.
They estimated 578 ![]() (D/1.7 kpc)2 at a (cloud-averaged) density of
(D/1.7 kpc)2 at a (cloud-averaged) density of
![]()
![]() .
Their lower density is partly explained by the larger outer radius,
which was chosen to be 1.0 pc(D/1.7 kpc).
It is also probably due to the larger physical cloud size at the
assumed distance of D=3 kpc, which prevents the simple quadratic
distance scaling of the mass in a self-consistent radiative-transfer
treatment.
.
Their lower density is partly explained by the larger outer radius,
which was chosen to be 1.0 pc(D/1.7 kpc).
It is also probably due to the larger physical cloud size at the
assumed distance of D=3 kpc, which prevents the simple quadratic
distance scaling of the mass in a self-consistent radiative-transfer
treatment.
The total mass of DR21 (OH)
corresponds to a cloud-averaged column density of ![]()
![]() cm-2.
The value of
cm-2.
The value of
![]() cm-2 reported by Richardson et al. from 1100
cm-2 reported by Richardson et al. from 1100 ![]() m data
and our value given in Table 5 based on the far-IR dust-emission are higher by a factor of 5-10.
A flatter spectral index
m data
and our value given in Table 5 based on the far-IR dust-emission are higher by a factor of 5-10.
A flatter spectral index ![]() may explain why dust and line-observation analyses result in different conclusions.
Values between 1.0 (Vallée & Fiege 2006) and 2.0 (Chandler et al. 1993) were discussed for DR21 (OH) in the literature.
If
may explain why dust and line-observation analyses result in different conclusions.
Values between 1.0 (Vallée & Fiege 2006) and 2.0 (Chandler et al. 1993) were discussed for DR21 (OH) in the literature.
If ![]() is lower than the assumed 1.5, this will have a significant effect on the derived
is lower than the assumed 1.5, this will have a significant effect on the derived ![]() .
For instance, with
.
For instance, with
![]() ,
the column density is reduced to about one fourth of our value at
,
the column density is reduced to about one fourth of our value at ![]() ,
so is then consistent with the CO-model results.
,
so is then consistent with the CO-model results.
An alternative explanation of the discrepancy could be depletion
as a result of a freeze-out of CO onto grains.
Some authors (e.g., Vallée & Fiege 2006, and references therein) use a depletion factor of 10 or more (X(CO) =
![]() at DR21 (OH))
as appropriate for star-forming clouds.
In Jørgensen et al. (2004), the abundance is reduced by a factor of 10 for the conditions T<30 K and
at DR21 (OH))
as appropriate for star-forming clouds.
In Jørgensen et al. (2004), the abundance is reduced by a factor of 10 for the conditions T<30 K and
![]() cm-2.
The DR21 (OH) envelope and the resulting column density would comply with these conditions.
However, the CO line data analysis does not allow us to draw conclusions toward depletion.
cm-2.
The DR21 (OH) envelope and the resulting column density would comply with these conditions.
However, the CO line data analysis does not allow us to draw conclusions toward depletion.
As noted before, a precise determination of the outer radii of the model clouds, hence their mass, is quite uncertain, and a small increase may already more than double the mass. In the models of DR21 C and DR21 (OH), we found no reasonable solutions for radii much smaller than 0.6 pc matching the 13CO and C18O 1-0 observations. As a possible indication of a systematic error in the column density, we typically see that the observed peak temperature of the C18O 1-0 line is weaker than predicted by the models (see Fig. 5) while the 13CO 1-0 line is reproduced well. This can either be a result of an inaccurate modeling of density and temperature conditions, or our assumption about the fixed abundances for CO, 13CO, or C18O is incorrect.
The models overestimate the 13CO 3-2 peak temperature.
Except for DR21 E, this transition is optically thick (![]() )
and reflects the kinetic temperature of the envelope gas.
As the CO 3-2 to 7-6 lines also become optically thick in the envelope,
the brightness temperature at the self-absorbing line centre of these mid-J lines is governed by
the same material.
The very deep (
)
and reflects the kinetic temperature of the envelope gas.
As the CO 3-2 to 7-6 lines also become optically thick in the envelope,
the brightness temperature at the self-absorbing line centre of these mid-J lines is governed by
the same material.
The very deep (![]() 5 K) absorption dip in CO 7-6 observed by Jaffe et al. (1989) indicates very cold foreground gas (<20 K),
which we cannot reproduce with only one component for the outer shell.
A better match of the observed intensities may be possible by adding a third colder layer outside of the envelope.
5 K) absorption dip in CO 7-6 observed by Jaffe et al. (1989) indicates very cold foreground gas (<20 K),
which we cannot reproduce with only one component for the outer shell.
A better match of the observed intensities may be possible by adding a third colder layer outside of the envelope.
Since the cold and warm components certainly are intermixed to some extent rather than separated into two nested shells, the focus during the modeling was put on a qualitative description of the different components and should not be seen as a geometric representation of the real cloud structure. We demonstrated, however, that the simplified assumption of a spherical cloud is adequate for estimating physical properties, such as mass, density, filling factors, and temperature.
Table 8:
Total cooling intensities of CO, [C I], [C II], and [O I].
The values in parentheses show the relative
contribution to the sum
![]() .
The total cooling efficiency
.
The total cooling efficiency
![]() is defined by
is defined by
![]() .
For comparison, we also list the
.
For comparison, we also list the ![]() defined by
defined by
![]() .
.
In addition to the high-J CO lines (see Sect. 3.3.2), ISO provided the integrated line intensities of
[O I] (63 and 145 ![]() m) (Table 4).
Their relative strength and cooling efficiency depends on the temperature and density regime:
At low temperatures, rotational mm- and submm-lines of CO dominate the cooling of the molecular and neutral gas.
At temperatures above
m) (Table 4).
Their relative strength and cooling efficiency depends on the temperature and density regime:
At low temperatures, rotational mm- and submm-lines of CO dominate the cooling of the molecular and neutral gas.
At temperatures above ![]() K, pure rotational transitions of OH, H2O, H2, and the 63
K, pure rotational transitions of OH, H2O, H2, and the 63 ![]() m [O I] line become more important.
The [O I] at 63
m [O I] line become more important.
The [O I] at 63 ![]() m and the atomic and ionic fine-structure lines of [C II] and [C I] are
diagnostic lines for PDRs.
Due to the nearby H II-regions, the ionic lines [O III] and [N II] are also expected to be strong emitters and may serve as diagnostics
to distinguish the fraction of [C II] emission coming from the neutral and ionised gas.
For completeness, we included the [O III] (52 and 88
m and the atomic and ionic fine-structure lines of [C II] and [C I] are
diagnostic lines for PDRs.
Due to the nearby H II-regions, the ionic lines [O III] and [N II] are also expected to be strong emitters and may serve as diagnostics
to distinguish the fraction of [C II] emission coming from the neutral and ionised gas.
For completeness, we included the [O III] (52 and 88 ![]() m) and [N II] (122
m) and [N II] (122 ![]() m) lines in the table.
m) lines in the table.
Since DR21 E, C and W are lined up along the outflow axis, we compared the emission in the outflow
lobes with the central position.
The strong [O I] emission at 63 ![]() m decreases rapidly toward the west (cf., Lane et al. 1990).
This line easily becomes optically thick and Poglitsch et al. (1996) indeed found a deeply absorbed line toward DR21.
The 63
m decreases rapidly toward the west (cf., Lane et al. 1990).
This line easily becomes optically thick and Poglitsch et al. (1996) indeed found a deeply absorbed line toward DR21.
The 63 ![]() m emission extends toward the E position at almost the same strength as toward the centre.
As the
m emission extends toward the E position at almost the same strength as toward the centre.
As the ![]() at the same time drops down, the gas traced by O I must be a separate, necessarily warm component.
The [O I] line at 145
at the same time drops down, the gas traced by O I must be a separate, necessarily warm component.
The [O I] line at 145 ![]() m is peaked at DR21 C, showing only a slight east-west asymmetry.
m is peaked at DR21 C, showing only a slight east-west asymmetry.
If we assume thermalized optically thin [O I] emission, we can derive the excitation temperature from
![]() (Eq. (C.13)), where
(Eq. (C.13)), where
![]() is the ratio of [O I] 145/63
is the ratio of [O I] 145/63 ![]() m emission (cf. Table 4).
The ratios of observed intensities, 0.06-0.12, result in temperatures between 170 to 370 K and are to be seen
as strict upper limits, since
m emission (cf. Table 4).
The ratios of observed intensities, 0.06-0.12, result in temperatures between 170 to 370 K and are to be seen
as strict upper limits, since
![]() decreases for optically thick [O I] 63
decreases for optically thick [O I] 63 ![]() m
line emission.
The [O I] line ratio at DR21 (OH) of
m
line emission.
The [O I] line ratio at DR21 (OH) of
![]() = 0.29 requires a temperature just below 100 K.
We detect the weakest emission of [O I] at DR21 FIR1.
Errors in
= 0.29 requires a temperature just below 100 K.
We detect the weakest emission of [O I] at DR21 FIR1.
Errors in
![]() become too large to estimate
a temperature here.
become too large to estimate
a temperature here.
As expected for the position of the H II-region,
both ionised [O III] lines are strong at DR21 C and decrease toward the sides.
Furthermore, the [O III] 88/52 ![]() m line ratio is a good tracer of the
electron density in the range
102-105
m line ratio is a good tracer of the
electron density in the range
102-105
![]() ,
while being insensitive to abundance and temperature variations (Rubin et al. 1994).
At DR21 C, a ratio of about 0.4 indicates an electron density of
,
while being insensitive to abundance and temperature variations (Rubin et al. 1994).
At DR21 C, a ratio of about 0.4 indicates an electron density of
![]()
![]() .
In the east, the ratio rises to 0.8 indicating an extension of the H II-region to this side.
To the west, the ratio is above 1.4.
An electron density below 102
.
In the east, the ratio rises to 0.8 indicating an extension of the H II-region to this side.
To the west, the ratio is above 1.4.
An electron density below 102
![]() ,
consistent with the observed [O III] line ratio at DR21 (OH),
indicates a low degree of ionisation.
No H II-region has been identified in this area, e.g., in the VLA 6-cm continuum
(Palmer et al. 2004). Thus, the finding of [O III] emission is a bit surprising.
The [O III] ratio
,
consistent with the observed [O III] line ratio at DR21 (OH),
indicates a low degree of ionisation.
No H II-region has been identified in this area, e.g., in the VLA 6-cm continuum
(Palmer et al. 2004). Thus, the finding of [O III] emission is a bit surprising.
The [O III] ratio
![]() found at DR21 FIR1 is not covered by the Rubin et al. model but corresponds to a very low
found at DR21 FIR1 is not covered by the Rubin et al. model but corresponds to a very low
![]() .
.
The [N II] 122 ![]() m line was only detected at the E and W positions, while the
m line was only detected at the E and W positions, while the ![]() noise limit
at the position of the H II-region DR21 C still permits centrally-peaked emission.
The fraction of [C II] stemming from the H II-region can be estimated from the intensity ratio of [C II] to [N II].
The Galactic abundance ratio C/N in dense H II-regions
leads to an expected ratio of [C II]/[N II] = 1.1 (Kramer et al. 2005, and references therein).
With the observed [C II]/[N II] ratio between 11-19 for DR21, less than 10% of the [C II] emission is estimated to come from the ionised gas.
noise limit
at the position of the H II-region DR21 C still permits centrally-peaked emission.
The fraction of [C II] stemming from the H II-region can be estimated from the intensity ratio of [C II] to [N II].
The Galactic abundance ratio C/N in dense H II-regions
leads to an expected ratio of [C II]/[N II] = 1.1 (Kramer et al. 2005, and references therein).
With the observed [C II]/[N II] ratio between 11-19 for DR21, less than 10% of the [C II] emission is estimated to come from the ionised gas.
A determination of the O I and C II abundances may be difficult.
If we assume that their abundance is closely connected to the dense molecular gas,
we can calculate and fit the emission of these two species
by adjusting the abundance of the two-shell radiative transfer models (Sect. 4.2).
At DR21 C, we find abundances of
![]() for O I and
for O I and
![]() for C II.
For both C II and the O I 63
for C II.
For both C II and the O I 63 ![]() m line, the opacity toward the line centre is about 9, and the line profile is deeply self-absorbed.
The high energy above the ground level of O I leads to almost complete absorption of the centre emission leaving signatures of warm gas only in the wings.
The 145
m line, the opacity toward the line centre is about 9, and the line profile is deeply self-absorbed.
The high energy above the ground level of O I leads to almost complete absorption of the centre emission leaving signatures of warm gas only in the wings.
The 145 ![]() m transition (
m transition (
![]() )
is unaffected and is a better measure of the abundance.
As C II has only one transition and also shows some absorption in the model profiles,
the abundance may be less accurate.
At DR21 (OH), the abundance of O I is
)
is unaffected and is a better measure of the abundance.
As C II has only one transition and also shows some absorption in the model profiles,
the abundance may be less accurate.
At DR21 (OH), the abundance of O I is ![]()
![]() and
and
![]() for C II.
The abundances at all five observed positions vary between
for C II.
The abundances at all five observed positions vary between
![]() for O I and
for O I and
![]() for C II.
for C II.
Compared to our LTE estimate in Sect. 4.1, the C II amount derived here is higher by factors of 13-160. Because of recombination reactions, it is rather unlikely to have a large amount of C II hidden in the cold gas, so this can be considered as an upper limit.
The relative importance of the various line tracers among each other and with respect to the FIR continuum provides a detailed signature of the heating and cooling processes in the DR21 molecular cloud. Table 8 lists the cooling intensities at the five selected ISO positions E, C, W, OH, and FIR1.
The total line cooling intensity,
![]() ,
derived by summing
the contributions of CO, C I, C II, and O I, peaks at position C,
dropping to less than 15% of this peak value at FIR1.
,
derived by summing
the contributions of CO, C I, C II, and O I, peaks at position C,
dropping to less than 15% of this peak value at FIR1.
The relative contributions to
![]() vary strongly at the 5
positions. [O I] is the strongest coolant at positions E and C,
while CO is strongest at W, (OH), and FIR1, tying up more than
50% of the total cooling. The relative contribution of CO to
vary strongly at the 5
positions. [O I] is the strongest coolant at positions E and C,
while CO is strongest at W, (OH), and FIR1, tying up more than
50% of the total cooling. The relative contribution of CO to
![]() varies between 26% at E and 76% at (OH), while
the relative contribution of [C II] is less, varying between 7% at
C and 21% at FIR1. The two [C I] fine-structure lines contribute
generally less than 2%. The ratio of CO cooling relative to [C I]
cooling peaks at C at 114 and drops to less than 50 at FIR1.
varies between 26% at E and 76% at (OH), while
the relative contribution of [C II] is less, varying between 7% at
C and 21% at FIR1. The two [C I] fine-structure lines contribute
generally less than 2%. The ratio of CO cooling relative to [C I]
cooling peaks at C at 114 and drops to less than 50 at FIR1.
We also compared
![]() with the FIR continuum to derive the
gas cooling efficiency
with the FIR continuum to derive the
gas cooling efficiency
![]() as a measure of the fraction of
FUV photon energy which goes into gas heating.
The value of
as a measure of the fraction of
FUV photon energy which goes into gas heating.
The value of
![]() varies by one order of magnitude,
between 0.2% at (OH) and 1.5-2% at the two outflow positions
E and W.
varies by one order of magnitude,
between 0.2% at (OH) and 1.5-2% at the two outflow positions
E and W.
Table 8 also lists the cooling efficiency
![]() only taking the 158
only taking the 158 ![]() m [C II] and the
63
m [C II] and the
63 ![]() m [O I] lines into account, ignoring CO and other species,
as is often done in the literature.
Then,
m [O I] lines into account, ignoring CO and other species,
as is often done in the literature.
Then, ![]() varies between 0.04% at (OH) and 1% at E.
varies between 0.04% at (OH) and 1% at E.
Several studies in the literature have determined the gas heating
efficiency ![]() in Galactic star-forming regions and in
external galaxies. Vastel et al. (2001) find values typically of
0.2-0.4% in Galactic star-forming regions, 1.1% at the Orion
Bar, and less than 0.035% toward W49N. For W3 Main/IRS5,
Kramer et al. (2004) report
in Galactic star-forming regions and in
external galaxies. Vastel et al. (2001) find values typically of
0.2-0.4% in Galactic star-forming regions, 1.1% at the Orion
Bar, and less than 0.035% toward W49N. For W3 Main/IRS5,
Kramer et al. (2004) report ![]() of
of
![]() % similar to
the value found in DR21 C. Malhotra et al. (2001) find efficiencies
between 0.05 and 0.3% in 60 unresolved normal galaxies.
Kramer et al. (2005) find efficiencies between 0.21 and 0.36% in the
centres and spiral-arm positions of M 83 and M 51.
% similar to
the value found in DR21 C. Malhotra et al. (2001) find efficiencies
between 0.05 and 0.3% in 60 unresolved normal galaxies.
Kramer et al. (2005) find efficiencies between 0.21 and 0.36% in the
centres and spiral-arm positions of M 83 and M 51.
The PDR models, e.g., by Kaufman et al. (1999), predict the heating
efficiency ![]() of a cloud illuminated from all sides between
0.01% to 1.5%, and our values are within these theoretical limits.
of a cloud illuminated from all sides between
0.01% to 1.5%, and our values are within these theoretical limits.
A remarkable point is that only a few percent of the mass (up to 20% at DR21 E) is efficiently heated.
Considering only the cold envelope component of our radiative transfer models, i.e., removing the warm interface zone,
shows that the heated gas accounts for most of the CO emission
(80% to 94%, summing over
![]() )
in terms of radiated energy.
)
in terms of radiated energy.
Since the total line power of all lines that we consider,
![]() ,
does not include the contributions from other cooling lines
(e.g., of H2, H2O, OH, and PAHs), we may miss some of the cooling energy.
,
does not include the contributions from other cooling lines
(e.g., of H2, H2O, OH, and PAHs), we may miss some of the cooling energy.
We have presented the first comprehensive mapping of sub-mm lines in the whole DR21/DR21 (OH) region.
The line emission of [C I] at 492 GHz and 809 GHz, CO 3-2, 4-3, 6-5, and 7-6, 13CO 3-2and 6-5, and of CS 7-6reveals contributions from different gas components:
(i) a very wide-winged emission in mid-J CO transitions having a line width of more than
![]() and self-absorption; and
(ii) narrow (4 to
and self-absorption; and
(ii) narrow (4 to
![]() )
emission in the other lines.
Based on these lines, and supported by mm- and FIR-lines from FCRAO and ISO, we confined temperature, density, masses, and volume filling
for five positions toward DR21, DR21 (OH), and DR21 FIR1 using a radiative transfer code by modeling the
spectral line profiles.
)
emission in the other lines.
Based on these lines, and supported by mm- and FIR-lines from FCRAO and ISO, we confined temperature, density, masses, and volume filling
for five positions toward DR21, DR21 (OH), and DR21 FIR1 using a radiative transfer code by modeling the
spectral line profiles.
Acknowledgements
The KOSMA 3 m submillimeter telescope at the Gornergrat-Süd is operated by the University of Cologne in collaboration with the Radio Astronomy Department of the Argelander-Institute for Astronomy (Bonn) and supported by special funding from the Land NRW. The observatory is administrated by the International Foundation Gornergrat & Jungfraujoch.
Table 7 lists the derived physical parameters (shell- and model-averaged) for temperature, H2 number density, volume filling factors, H2 column density, and molecular gas mass. The resulting spectral profiles are compared with the observed lines in Fig. 5. The plots in Fig. 8 show the fit of the integrated emission for CO, 13CO, and C18O up to J=20 in comparison to the observed lines. In the following, we discuss details of the individual positions.
This position covers the DR21 H II-region. Its surrounding molecular cloud (within a radius of ![]() 0.6 pc) forms the southern part of the molecular ridge.
Our best-fit model indicates that the envelope at a temperature of 40 K
comprises roughly 94% of the total mass, leaving 6% for the warm (about 150 K) and dynamically active gas
(
0.6 pc) forms the southern part of the molecular ridge.
Our best-fit model indicates that the envelope at a temperature of 40 K
comprises roughly 94% of the total mass, leaving 6% for the warm (about 150 K) and dynamically active gas
(
![]() between 4.5 and 29
between 4.5 and 29
![]() )
subject to shocks and UV-heating.
Jaffe et al. already found indications in 1989 of a warm component with a mass of 55
)
subject to shocks and UV-heating.
Jaffe et al. already found indications in 1989 of a warm component with a mass of 55 ![]() (D/1.7 kpc)2, which is fully consistent with our result from Table 7.
The by far more massive, colder gas component was only indirectly traced by the CO J = 7-6 line reversal in their study.
In our model, the properties of this gas component in the envelope shell are much better constrained
by the C18O and 13CO J=1-0 transitions, which are close to optically thin (
(D/1.7 kpc)2, which is fully consistent with our result from Table 7.
The by far more massive, colder gas component was only indirectly traced by the CO J = 7-6 line reversal in their study.
In our model, the properties of this gas component in the envelope shell are much better constrained
by the C18O and 13CO J=1-0 transitions, which are close to optically thin (
![]() resp. 0.8).
The turnover at
resp. 0.8).
The turnover at
![]() (cf. Fig. 8) results from the
increasing critical density
leading to sub-thermal excitation of the
high-J transitions
at the clump density of about
(cf. Fig. 8) results from the
increasing critical density
leading to sub-thermal excitation of the
high-J transitions
at the clump density of about
![]()
![]() .
Boreiko & Betz (1991) observed CO and 13CO 9-8 at comparable resolution onboard the Kuiper Airborne Observatory (KAO).
We indicate their integrated fluxes in Fig. 8 for DR21 C.
There is good agreement with 13CO, but CO J=9-8 is weaker than the J=7-6 line presented here.
This may indicate a stronger flattening of the CO rotation curve that
could only be explained by a discontinuous density or temperature structure.
.
Boreiko & Betz (1991) observed CO and 13CO 9-8 at comparable resolution onboard the Kuiper Airborne Observatory (KAO).
We indicate their integrated fluxes in Fig. 8 for DR21 C.
There is good agreement with 13CO, but CO J=9-8 is weaker than the J=7-6 line presented here.
This may indicate a stronger flattening of the CO rotation curve that
could only be explained by a discontinuous density or temperature structure.
In support of a shock driven excitation, Lane et al. (1990) gives an upper limit to CO J = 22-21 of
![]() erg s-1 cm-2 sr-1 in a
erg s-1 cm-2 sr-1 in a
![]() beam.
Considering beam dilution, this limit is still high compared to the intensity of CO 17-16, the highest rotational line considered here.
Our prediction with the radiative transfer model of
beam.
Considering beam dilution, this limit is still high compared to the intensity of CO 17-16, the highest rotational line considered here.
Our prediction with the radiative transfer model of
![]() erg s-1 cm-2 sr-1can explain why this detection attempt failed, although
we cannot fully exclude the presence of >200 K warm gas.
erg s-1 cm-2 sr-1can explain why this detection attempt failed, although
we cannot fully exclude the presence of >200 K warm gas.
The east side of the DR21 H II-region is not located on the molecular ridge, but is enriched with
gas ejected from the ridge.
The lack of cold gas gives rise to an average temperature of 62 K for a gas mass of ![]() 240
240 ![]() .
It appears from the Spitzer/IRAC image that a fraction of gas in the east is undergoing a blister phase.
Unlike the western outflow side, it is not stopped by a dense cloud and expands unhampered.
We find that 20% of the gas is heated to about 90 K and accelerated to velocities up to
.
It appears from the Spitzer/IRAC image that a fraction of gas in the east is undergoing a blister phase.
Unlike the western outflow side, it is not stopped by a dense cloud and expands unhampered.
We find that 20% of the gas is heated to about 90 K and accelerated to velocities up to
![]() .
As the radiative transfer code is not designed for outflow geometries,
we applied a turbulent velocity gradient from 32 to
.
As the radiative transfer code is not designed for outflow geometries,
we applied a turbulent velocity gradient from 32 to
![]() to simulate the outflow.
For the envelope gas, the asymmetry of the CO profiles indicates a motion away from the core at
to simulate the outflow.
For the envelope gas, the asymmetry of the CO profiles indicates a motion away from the core at
![]() .
Because of the steep drop in high-J CO emission, the local clump density was fitted
below
.
Because of the steep drop in high-J CO emission, the local clump density was fitted
below
![]()
![]() .
.
Molecular line emission and radiative transfer models of DR21 W are similar to position DR21 E:
the gas is warmer than in the ridge (>50 K) but not at densities above 105
![]() .
The warm (
.
The warm (
![]() K) gas contributes with a small fraction of about 3.5% to the total derived mass of
K) gas contributes with a small fraction of about 3.5% to the total derived mass of
![]()
![]() .
A turbulent velocity gradient between 30 and
.
A turbulent velocity gradient between 30 and
![]() is responsible for line wing emission.
The CO lines show only weak self-absorption although the opacity is high at the line centre.
This is plausible because the cloud surface is illuminated by the cluster at DR21 C, so
we had to implement a positive temperature gradient from 44 K to 55 K across the cloud envelope.
is responsible for line wing emission.
The CO lines show only weak self-absorption although the opacity is high at the line centre.
This is plausible because the cloud surface is illuminated by the cluster at DR21 C, so
we had to implement a positive temperature gradient from 44 K to 55 K across the cloud envelope.
The position of DR21 (OH) is dominated by cold gas from the ridge at a temperature below 30 K over a size of up to 0.7 pc.
For the modeling, we simplified the scenario of several embedded cores, as reported by, e.g., Mangum et al. (1992) (at possibly different systemic velocities),
to a single clumpy core defined by the warm interface region with an outer radius of 0.2 pc.
The significant mid- and high-J CO emission is a clear indication of warm and dense gas.
We find that only 2%, or 34 ![]() of the gas is heated to
of the gas is heated to ![]() 100 K and at densities of 106
100 K and at densities of 106
![]() or more.
There is no evolved outflow associated with this position, but Garden et al. (1986) and Richardson et al. (1994) see indications
of a very young outflow associated with high temperatures and shocks.
In our model, half of the warm gas mass is at relative velocities
or more.
There is no evolved outflow associated with this position, but Garden et al. (1986) and Richardson et al. (1994) see indications
of a very young outflow associated with high temperatures and shocks.
In our model, half of the warm gas mass is at relative velocities
![]() ,
creating the line wing emission.
The observed blue-skewed CO line profiles are compatible with radial infall motion of the envelope gas of
,
creating the line wing emission.
The observed blue-skewed CO line profiles are compatible with radial infall motion of the envelope gas of
![]() .
.
The northern FIR-region contains at least three sub-sources.
Besides FIR1, the 80
![]() beam partly covers the second source FIR2, so we have to consider this as contamination.
The modeled outer radius overlaps slightly with the neighbouring source, but is well within the beam.
Because high-J CO is not detected at DR21 FIR1, we can constrain the temperature to
beam partly covers the second source FIR2, so we have to consider this as contamination.
The modeled outer radius overlaps slightly with the neighbouring source, but is well within the beam.
Because high-J CO is not detected at DR21 FIR1, we can constrain the temperature to ![]() 82 K.
Given the CO 7-6 flux at this position, the lower limit of the temperature in the inner region is T>50 K.
The relatively weak self-absorption of the low-J lines is probably due to the presence of moderately warm gas (up to 40 K) in the outer surface layers,
supporting the flat density profile used in the model.
82 K.
Given the CO 7-6 flux at this position, the lower limit of the temperature in the inner region is T>50 K.
The relatively weak self-absorption of the low-J lines is probably due to the presence of moderately warm gas (up to 40 K) in the outer surface layers,
supporting the flat density profile used in the model.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{5855figk.eps}
\end{figure}](/articles/aa/full/2007/03/aa5855-06/Timg276.gif) |
Figure B.1:
OTF map of the 13CO 2-1 emission (SBS2006).
An emission-free position is indicated by the triangle on the right and was used as OFF position
for the OTF observations.
The box indicates the map size of the DBS-mode observations in Figs. 2 and 3.
The circle in the top left corner indicates the 120'' beam size.
The smaller circles labeled ON1&ON2, OFF1, and OFF2 show an examplary DBS measurement (cf. Fig. B.2)
with a field rotation angle
|
Before the implementation of an on-the-fly-mode (OTF), dual-beam-switch (DBS) was the only efficient observing mode to use SMART at KOSMA.
Therefore, observations in 2003 and 2004 of CO 7-6 and [C I] had to be performed in DBS-mode.
In this mode,
a chopping secondary mirror is used for fast periodic switching between an ON and an OFF position (signal- and reference phase).
After some time, usually 20 s, determined by the stability of the system,
the telescope is moved so that the reference phase is now the ON, and the new OFF
position falls exactly on the opposite side. In the data reduction, each OFF position is weighted equally.
Slight differences in the optical path lengths usually lead to strong
standing waves in the spectra when using a simple BS-mode. The period of these waves
corresponds to the optical distance to the subreflector. These standing waves are very efficiently suppressed in DBS-mode.
However, mapping the extended sources is rather difficult if the chopper throw (between 5'-6') is small compared to the size of the source
and the chopper movement is fixed to one direction (azimuth for KOSMA).
Under those conditions, mapping needs careful planning to prevent self-chopping within the source.
The observing time is thus not only constrained by source visibility but also by sky rotation.
For an hour angle of ![]() ,
the secondary throw is only in right ascension, while for other angles there is a component in declination.
The 13CO 3-2 position-switched OTF-map in Fig. B.1 shows that
the DR21 ridge is N-S orientated and that the field rotation angles
,
the secondary throw is only in right ascension, while for other angles there is a component in declination.
The 13CO 3-2 position-switched OTF-map in Fig. B.1 shows that
the DR21 ridge is N-S orientated and that the field rotation angles ![]() of less than
of less than
![]() are preferred in order to prevent chopping into the ridge of emission with both OFF beams.
are preferred in order to prevent chopping into the ridge of emission with both OFF beams.
To reduce the impact of artefacts remaining after the standard DBS reduction pipeline,
all DBS data were corrected in the following way (see Fig. B.2 for an example):
(i)
regardless of whether the DBS-spectra (Fig. B.2a) show self-chopping or not,
the emission in the difference (Fig. B.2b) of the two OFF positions is analysed.
Any significant signal here is considered as pollution. This assumption
holds as long as at least one of the two OFF positions is free of emission and no absorption against the continuum is present.
In the example (Figs. B.2c and d) only the OFF-position of Beam 1 (OFF1) is contaminated;
(ii) if a signal in the difference is detected above the noise level, the algorithm tries to reconstruct the emission signal (Fig. B.2d)
by removing Beam 1 from the final spectrum (Fig. B.2e), i.e. we use only ON2-OFF2 here.
This scheme works well for situations where standing waves are negligible.
In cases where standing-wave patterns are persistent, we transform the spectra to Fourier-space, mask-out the standing wave frequencies,
and transform the data back to user-space.
Due to the shorter integration time, this procedure increases the noise level by a factor of ![]() .
In case of DR21, this method successfully recovered the emission, because one OFF position was
always nearly free of emission. If, however, the source extends over more than twice the chop throw
in all directions, this method does not work.
.
In case of DR21, this method successfully recovered the emission, because one OFF position was
always nearly free of emission. If, however, the source extends over more than twice the chop throw
in all directions, this method does not work.
A simple determination of the excitation temperature and the column density of C I can be made
if we assume the emission is optically thin and the level popolation is given by thermal excitation.
The column density of a material in an excited state u is given by:
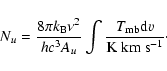 |
(C.1) |
To estimate the excitation temperature from the two transitions 13CO J = 3-2 and J = 1-0,
we use Eq. (C.4) which then translates into
The 13CO and C18O column density can then be approximated by these equations: