A&A 461, 1057-1063 (2007)
DOI: 10.1051/0004-6361:20065776
Tides in asynchronous binary systems
O. Toledano1 - E. Moreno2 - G. Koenigsberger1 - R. Detmers3 - N. Langer3
1 - Instituto de Ciencias Físicas, Universidad Nacional Autonoma de México, Apdo. Postal 48-3, Cuernavaca, Mor. 62251, Mexico
2 -
Instituto de Astronomía, Universidad Nacional Autonoma de México, Apdo. Postal 70-264, D.F. 04510, Mexico
3 -
Sterrenkundig Instituut, Universiteit Utrecht, Postbus 80.000, Utrecht, The Netherlands
Received 8 June 2006 / Accepted 8 October 2006
Abstract
Context. Stellar oscillations are excited in non-synchronously rotating stars in binary systems due to the tidal forces. Tangential components of the tides can drive a shear flow which behaves as a differentially forced rotating structure in a stratified outer medium.
Aims. The aims of this paper are to show that our single-layer approximation for the calculation of the forced oscillations yields results that are consistent with the predictions for the synchronization timescales in circular orbits,

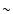 a6, thus providing a simplified means of computing the energy dissipation rates,
a6, thus providing a simplified means of computing the energy dissipation rates, 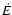 .
Furthermore, by calibrating our model results to fit the relationship between synchronization timescales and orbital separation, we are able to constrain the value of the kinematical viscosity parameter,
.
Furthermore, by calibrating our model results to fit the relationship between synchronization timescales and orbital separation, we are able to constrain the value of the kinematical viscosity parameter,  .
.
Methods. We compute the values of 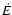 for a set of 5
for a set of 5
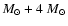 model binary systems with different orbital separations, a, and use these to estimate the synchronization timescales.
model binary systems with different orbital separations, a, and use these to estimate the synchronization timescales.
Results. The resulting
 vs. a relation is comparable to that of Zahn (1977, A&A, 57, 383) for convective envelopes, providing a calibration method for the values of
vs. a relation is comparable to that of Zahn (1977, A&A, 57, 383) for convective envelopes, providing a calibration method for the values of  .
For the
.
For the
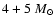 binary modeled in this paper,
binary modeled in this paper,  is in the range 0.0015-0.0043
is in the range 0.0015-0.0043
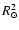 /day for orbital periods in the range 2.5-25 d. In addition,
/day for orbital periods in the range 2.5-25 d. In addition, 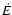 is found to decrease by
is found to decrease by 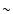 2 orders of magnitude as synchronization is approached, implying that binary systems may approach synchronization relatively quickly but that it takes a much longer timescale to actually attain this condition.
2 orders of magnitude as synchronization is approached, implying that binary systems may approach synchronization relatively quickly but that it takes a much longer timescale to actually attain this condition.
Conclusions. The relevance of these results is threefold: 1) our model allows an estimate for the numerical value of  under arbitrary conditions in the binary system; 2) it can be used to calculate the energy dissipation rates throughout the orbital cycle for any value of eccentricity and stellar rotational velocity; and 3) it provides values of the tangential component of the velocity perturbation at any time throughout the orbit and predicts the location on the stellar surface where the largest shear instabilities may be occurring. We suggest that one of the possible implication of the asymmetric distribution of
under arbitrary conditions in the binary system; 2) it can be used to calculate the energy dissipation rates throughout the orbital cycle for any value of eccentricity and stellar rotational velocity; and 3) it provides values of the tangential component of the velocity perturbation at any time throughout the orbit and predicts the location on the stellar surface where the largest shear instabilities may be occurring. We suggest that one of the possible implication of the asymmetric distribution of 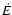 over the stellar surface is the generation of localized regions of enhanced surface activity.
over the stellar surface is the generation of localized regions of enhanced surface activity.
Key words: stars: oscillations - stars: rotation - stars: binaries: general
A binary system is said to be in equilibrium when the orbit is circular, the stellar rotation period and the orbital period are synchronized and the spin axes of both stars are aligned and perpendicular to the orbital plane. In any other case, oscillations are excited and the tidal deformations which
are time-dependent become inevitably dissipative. We will focus on the situation in which the stellar rotation period differs from the orbital period, that is, a non-synchronously rotating system. To describe the degree of non-synchronicity, we define
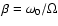 ,
where
,
where 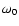 and
and 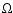 are the rotational and orbital angular velocities, respectively.
are the rotational and orbital angular velocities, respectively.
As in the case of the terrestrial tides, the resulting asymmetrical shape of the star is due
to a second order gravitational effect, the differential force. Thus, the rising tidal bulges,
opposite to each other and comparable in size, are associated with the so called,
equilibrium tide. Additionally, a set of surface oscillations commonly
known as the dynamical tide, characterized by a wide variety of harmonic frequencies, is established.
This oscillatory response of the star depends on 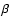 and on the stellar and orbital parameters. In addition, it depends on the capability of the stellar material to transfer angular momentum
and energy between its different layers, which is represented by the viscosity,
and on the stellar and orbital parameters. In addition, it depends on the capability of the stellar material to transfer angular momentum
and energy between its different layers, which is represented by the viscosity,  .
.
The tidally induced oscillations have both radial and azimuthal components. If we focus on the
azimuthal component and keep in mind that the tidal forces decrease as r3, with r the
distance between a mass element and the center of the perturbing star, it is evident
that since an external layer of a perturbed star is subjected to a larger tidal force than a layer below it, a differentially rotating structure will be produced in any 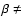 1 binary system.
If
1 binary system.
If 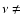 0, the interaction between the different layers takes the form of a shearing flow,
thereby leading to energy dissipation. The viscosity and the azimuthal velocity are
the crucial parameters defining the amount of energy that is dissipated,
0, the interaction between the different layers takes the form of a shearing flow,
thereby leading to energy dissipation. The viscosity and the azimuthal velocity are
the crucial parameters defining the amount of energy that is dissipated, 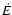 .
.
The long term trend of the angular momentum transfer and dissipative effects in binary systems
is one in which the rotation frequency becomes synchronous with the orbital frequency.
The theoretical framework for the calculation of tidal synchronization was developed
by Zahn (1966, 1977, 1989), who invoked the tidal friction as a physical mechanism asociated with
tidally excited oscillations which contribute to the angular momentum transfer. In stars with
convective envelopes, redistribution of angular momentum occurs through dissipation processes like
turbulent viscosity, retarding the equilibrium tide. In stars with radiative envelopes, the
mechanism found by Zahn (1975, 1977) is the action of radiative damping taking place on the dynamical tide. Zahn (1977, 1989) found
the characteristic timescale for synchronization as a function of a, the major semi-axis
of the orbit;

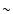 a6 for stars with convective envelopes and
a6 for stars with convective envelopes and

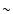 a8.5 for stars with radiative envelopes.
a8.5 for stars with radiative envelopes.
On orbital timescales, the tidal oscillations can produce observable photometric and absorption
line-profile variability (see, for example, Smith 1977; Gies & Kullavanijaya 1988; Willems & Aerts 2002).
Moreno & Koenigsberger (1999) presented a simplified model for the calculation of the
surface oscillations of a star driven by the tidal interaction in a binary system. The
calculation is performed for a thin surface layer of small surface elements distributed
along the equatorial belt of the star. The solution of the equations of motion for these
surface elements provides the velocity perturbations in the radial and azimuthal directions
as a function of time within the orbital cycle of the binary. In the non-inertial
reference frame used to solve the equations of motion the model includes the gravitational forces
of both stars, gas pressure, centrifugal, coriolis, and viscous forces. In the model we
compute only the motion of the center of mass of each surface element, thus ignoring the
details of the inner motions within these elements. In this approximation, the buoyancy
force is not taken into account.
Finally, we note that the results in this paper are obtained using a polytropic
index n=1.5, corresponding to a rigorous convective envelope, instead of n=1 as was used
previously (Moreno et al. 2005; Koenigsberger et al. 2006), although the difference between the results obtained for these two values of n is not significant.
Moreno et al. (2005) extended the model to include the computation of the photospheric absorption
lines that would be produced by the perturbed stellar surface. This ab initio calculation
of the line profile variability due to the forced tidal oscillations was applied to the case of
 Per, showing that from a qualitative standpoint, the predicted line profile
variability is comparable to the observations.
More recently, the model was used to analyze the
peculiar line-profile variability in the optical counterpart of the X-ray binary 2S0114+650
(Koenigsberger et al. 2006), leading to the conclusion that the tidal perturbations could be
the "trigger'' for the periodic ejection of wind material at densities that are higher than
the average wind density. They hypothesize that these effects result from the combined action
of the shear energy dissipation, the radial oscillations and the radiation pressure. The
significance of this result is that, in addition to providing a tool for studying line profile
variability in binary systems, the model provides a means of constraining the value of the viscosity, which is the parameter involved in the energy dissipation mechanisms. Thus, although the model is designed to study the variability in binary systems on orbital timescales, it is of interest to explore whether it yields results that are consistent with the long-term behavior,
specifically, the tidal evolutionary theories. That is, using the value of viscosity and the
angular velocity perturbations obtained from the calculation, an estimate of the rate of dissipated mechanical energy,
Per, showing that from a qualitative standpoint, the predicted line profile
variability is comparable to the observations.
More recently, the model was used to analyze the
peculiar line-profile variability in the optical counterpart of the X-ray binary 2S0114+650
(Koenigsberger et al. 2006), leading to the conclusion that the tidal perturbations could be
the "trigger'' for the periodic ejection of wind material at densities that are higher than
the average wind density. They hypothesize that these effects result from the combined action
of the shear energy dissipation, the radial oscillations and the radiation pressure. The
significance of this result is that, in addition to providing a tool for studying line profile
variability in binary systems, the model provides a means of constraining the value of the viscosity, which is the parameter involved in the energy dissipation mechanisms. Thus, although the model is designed to study the variability in binary systems on orbital timescales, it is of interest to explore whether it yields results that are consistent with the long-term behavior,
specifically, the tidal evolutionary theories. That is, using the value of viscosity and the
angular velocity perturbations obtained from the calculation, an estimate of the rate of dissipated mechanical energy, 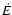 ,
can be derived. The timescale over which
,
can be derived. The timescale over which 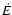 becomes negligible is a measure of the synchronization timescale of the binary system.
Thus, the results of this one-layer calculation of the tidal oscillations may be compared with
the predictions of tidal synchronization theory such as those of Zahn (1977, 1989) yielding,
on the one hand, a test of the Moreno et al. (2005) model and, on the other, a constraint on the numerical values of the viscosity. These are two of the objectives of this paper.
becomes negligible is a measure of the synchronization timescale of the binary system.
Thus, the results of this one-layer calculation of the tidal oscillations may be compared with
the predictions of tidal synchronization theory such as those of Zahn (1977, 1989) yielding,
on the one hand, a test of the Moreno et al. (2005) model and, on the other, a constraint on the numerical values of the viscosity. These are two of the objectives of this paper.
The expression for the calculation of the viscous energy dissipation rate is derived in
Sects. 2 and 3; in Sect. 4 we present the results of our model calculations for a 5
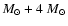 binary system at different orbital separations and compare our predictions
with the synchronization timescales of Zahn; and in Sect. 5 we discuss the implications of
this result and present the conclusions.
binary system at different orbital separations and compare our predictions
with the synchronization timescales of Zahn; and in Sect. 5 we discuss the implications of
this result and present the conclusions.
The approximate treatment of angular momentum transfer between the equatorial surface layer and the
rigidly-rotating inner region of the star is made assuming that the equatorial external layer behaves as
a shearing thin disk, in analogy with the dissipation mechanisms described for accretion disks
(see for example, Frank et al. 1985; Lynden-Bell & Pringle 1974). In the assumed differentially rotating medium, tangential stresses between adjacent layers are assumed to be the mechanism of transport of angular momentum. Included in these is the angular momentum transport due to magnetic
torques, which has been shown to be the dominant mechanism in recent stellar model
calculations (Petrovic et al. 2005) where the formulation of Spruit (2002) is used to treat the magnetic field. In our calculations, the mechanisms by which transfer of angular momentum in the shear flow occurs are englobed in the viscosity.
We adopt the approach for the transport of angular momentum that
consists of imagining an idealized situation in which parts of a ring-shaped outer layer
slide over a rigidly-rotating inner region. If friction between adjacent layers is assumed
to exist and if the angular velocity increases or decreases outwards, a net torque will be
exerted by the outer ring on the inner region. The resulting torques will work towards synchronizing the outer and inner region, dissipating energy in the process.
For this mechanism to be active, the particles in the external ring have to be able to interact
with those in the inner rotating region. However, contrary to the case of many accretion disk
models where the particle velocity is Keplerian, the velocity of different layers on a stellar
surface is determined by the stellar rotation, the tidal forcing and the viscosity
of the material.
Let us assume that the viscosity in the gaseous shearing medium is a turbulent one. Gas elements
with small random motions at a typical turbulent velocity
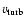 ,
travel a distance
,
travel a distance
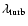 (the characteristic length and velocity scales of the turbulence), in all directions
before mixing with the surroundings. There exists a typical turbulent viscosity,
(the characteristic length and velocity scales of the turbulence), in all directions
before mixing with the surroundings. There exists a typical turbulent viscosity,
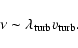 |
(1) |
However, both
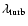 and
and
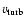 are unknown parameters. A clever solution to this problem was proposed in the early 1970' s by Shakura & Sunyaev (1973), consisting of a simple parametrization of
the two turbulence scales. For the length scale, they assumed isotropy
and characterized it by the typical size of the largest turbulent eddies which cannot exceed the
thickness H of the assumed ring
are unknown parameters. A clever solution to this problem was proposed in the early 1970' s by Shakura & Sunyaev (1973), consisting of a simple parametrization of
the two turbulence scales. For the length scale, they assumed isotropy
and characterized it by the typical size of the largest turbulent eddies which cannot exceed the
thickness H of the assumed ring
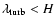 .
For the velocity scale, a more straightforward
scaling could be made. That is, if the turbulent velocity were supersonic, emerging shock waves would dissipate the energy and reduce the velocity to that of, or below, the sound speed. This leads to the choice of a
.
For the velocity scale, a more straightforward
scaling could be made. That is, if the turbulent velocity were supersonic, emerging shock waves would dissipate the energy and reduce the velocity to that of, or below, the sound speed. This leads to the choice of a
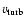 that is subsonic, thus
that is subsonic, thus
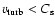 ,
and the viscosity can be written;
,
and the viscosity can be written;
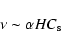 |
(2) |
with
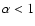 .
This is the well-known
.
This is the well-known 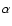 -prescription of
Shakura & Sunyaev (1973).
-prescription of
Shakura & Sunyaev (1973).
The physical idea of the viscous torque g is to assume that, if the gas flow is turbulent to
some extent, gas particles of adjacent layers will be exchanged in the radial direction (Frank 1985). Since the two different radial flows of material originating in both layers will have different specific angular momenta, this will cause a net transfer of angular momentum between them.
We can then calculate the magnitude of the viscous torque on the equatorial stellar region
in terms of a kinematic turbulent viscosity  ,
which can be expressed as
,
which can be expressed as
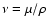 .
Here
.
Here 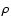 is the local density of the gas and
is the local density of the gas and 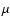 is the coefficient of shear viscosity
which is related to the component
is the coefficient of shear viscosity
which is related to the component
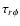 of the viscous stress tensor in cylindrical
coordinates (r,
of the viscous stress tensor in cylindrical
coordinates (r, 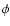 ,
z) by (Landau & Lifshitz 1984):
,
z) by (Landau & Lifshitz 1984):
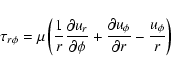 |
(3) |
where ur, 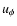 are the radial and azimuthal components of the velocity field.
Now, inserting
are the radial and azimuthal components of the velocity field.
Now, inserting
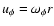 with
with
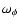 as the rotational angular
velocity of the tidal shear flow,
as the rotational angular
velocity of the tidal shear flow,
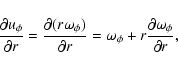 |
(4) |
and neglecting the shear effects in the radial direction, the viscous stress tensor becomes,
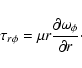 |
(5) |
This is a tangential force per unit area, and multiplying
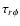 by the lever arm r,
gives the viscous torque per unit area exerted by the sliding ring-shaped outer layer on the
rigidly-rotating inner region. Integrating over the area of interaction (
by the lever arm r,
gives the viscous torque per unit area exerted by the sliding ring-shaped outer layer on the
rigidly-rotating inner region. Integrating over the area of interaction (
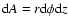 ),
),
where we have used that the density per unit area on the equatorial plane of the
equatorial stellar region is
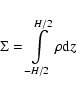 |
(9) |
with H the width of the equatorial stellar region. With
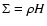 ,
the torque can also be expressed as
,
the torque can also be expressed as
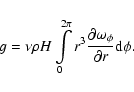 |
(10) |
According to this model, no net angular momentum is transported unless there is shearing differential rotation; that is, the condition for net angular momentum transport is,
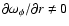 .
.
A natural consequence of the shearing differential rotation is the dissipation
of energy, 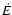 .
Let us consider the energy dissipation caused by the viscous torque
acting on the stellar equatorial external layer between r and r +
.
Let us consider the energy dissipation caused by the viscous torque
acting on the stellar equatorial external layer between r and r + 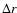 .
The net differential viscous torque on this layer is
.
The net differential viscous torque on this layer is
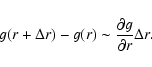 |
(11) |
Since the torque is acting in the direction of the angular velocity
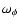 ,
the rate of work exerted onto the external layer is;
,
the rate of work exerted onto the external layer is;
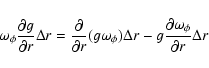 |
(12) |
where the first term of the right-hand side represents the rate of transported mechanical
energy through the gas by the torque, and the term
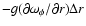 ,
the corresponding local rate of loss of mechanical energy converted into heat in the gas. We are
interested in the dissipation caused by the viscous torques within the gas at a rate
,
the corresponding local rate of loss of mechanical energy converted into heat in the gas. We are
interested in the dissipation caused by the viscous torques within the gas at a rate
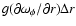 on the external layer of width
on the external layer of width 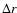 .
.
The local dissipation rate on an equatorial surface element with an azimuthal width
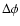 is
is
Since we require an estimate of the dissipation rate on the entire surface of the star, the previous description must be extended to include the dissipation produced at polar angles (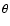 ).
An approximate generalization can be performed considering that the same dissipation mecanisms
apply to a series of rings of thickness
).
An approximate generalization can be performed considering that the same dissipation mecanisms
apply to a series of rings of thickness
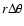 ,
situated across the star from the north
pole to the south pole, and the elements in these rings with an azimuthal angle
,
situated across the star from the north
pole to the south pole, and the elements in these rings with an azimuthal angle 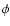 have the same angular velocity as that of the equatorial element with the same azimuth
have the same angular velocity as that of the equatorial element with the same azimuth 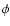 .
This approximation was used by Moreno et al. (2005) for the line-profile calculation.
.
This approximation was used by Moreno et al. (2005) for the line-profile calculation.
From Eq. (14), the local dissipation rate on any surface element is
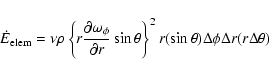 |
(15) |
with
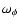 the angular velocity of the equatorial
surface element in the meridian of the element. Integrating in polar
angle, we obtain the dissipation rate on a meridional shell,
the angular velocity of the equatorial
surface element in the meridian of the element. Integrating in polar
angle, we obtain the dissipation rate on a meridional shell,
To obtain the total dissipation rate 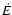 ,
this equation must be integrated over the azimuthal coordinate
,
this equation must be integrated over the azimuthal coordinate 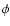 .
We use the following approximation:
.
We use the following approximation:
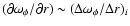 ,
where
,
where
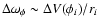 ,
with ri the radial position of
the ith equatorial surface element, and
,
with ri the radial position of
the ith equatorial surface element, and
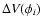 the difference of
azimuthal velocity of the element and the inner stellar region.
Then, with
the difference of
azimuthal velocity of the element and the inner stellar region.
Then, with
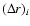 the radial thickness of the element,
the total energy dissipation can be obtained as a sum over the n equatorial surface elements,
the radial thickness of the element,
the total energy dissipation can be obtained as a sum over the n equatorial surface elements,
where additionally,
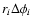 is simplified by the factor li, which
represents the azimuthal length of the element.
is simplified by the factor li, which
represents the azimuthal length of the element.
For a super-synchronously rotating star, the transfer of angular momentum tends to brake the outer stellar layers, causing the total energy of
the system to gradually decline. This, in turn, drives the system towards synchronization and,
therefore,
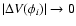 .
.
Zahn (1977, 1989) found two different relations between the synchronization timescale and the
orbital separation in binary systems, depending on whether the star's outer envelope is radiative,
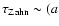 /R1)8.5, or convective,
/R1)8.5, or convective,
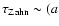 /R1)6. He proposed that for
stars with convective envelopes, the most efficient synchronizing mechanism is due to turbulent viscosity.
In what follows, we will concentrate on this formulation, a choice that is motivated
a posteriori by the results we derive and by the possibility that,
even in stars with radiative envelopes, turbulence is induced by the differential rotation.
/R1)6. He proposed that for
stars with convective envelopes, the most efficient synchronizing mechanism is due to turbulent viscosity.
In what follows, we will concentrate on this formulation, a choice that is motivated
a posteriori by the results we derive and by the possibility that,
even in stars with radiative envelopes, turbulence is induced by the differential rotation.
Zahn (1977) gives in his Eq. (6.1) an approximate characteristic synchronization
timescale
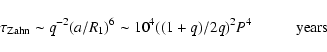 |
(20) |
where
q=M2/M1 is the mass ratio of the secondary to the primary star and ais the orbital separation in solar units, R1 is the equilibrium radius of the star in solar
units and P is the orbital period in days.
Adopting our one-layer model for calculating the tidal oscillations, and assuming that
all of the energy dissipation associated with the shearing forces occurs on this surface layer,
we can estimate the timescale required for the rotation period of the star to be
synchronized with the orbital period of its companion as follows.
If
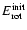 and
and
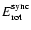 are the present and synchronization stellar rotational energies,
computed with the moment of inertia of a rigid sphere and the azimuthal velocity at the stellar equator,
are the present and synchronization stellar rotational energies,
computed with the moment of inertia of a rigid sphere and the azimuthal velocity at the stellar equator,
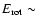 (1/2)I(
(1/2)I(
 (1/5)M1
(1/5)M1
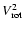 ,
then a rough estimate of the timescale needed to synchronize the system is
,
then a rough estimate of the timescale needed to synchronize the system is
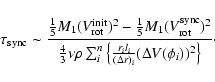 |
(21) |
In order to compare the above synchronization rates with those that are
inferred from Zahn's (a/R1)6 prediction, our code was used to compute
values of
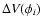 and ri for a set of binary models with
different orbital periods.
and ri for a set of binary models with
different orbital periods.
The test binary system that was selected consists of a Main Sequence intermediate-mass
system with M1= 5 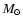 ,
M2= 4
,
M2= 4 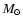 and R1= 3.2
and R1= 3.2 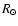 in a circular orbit. Observational evidence (Tassoul 2000; Pan 1997; Mathews & Mathieu 1992;
Witte & Savonije 1999) provides constraints for the circularization timescales of such systems, and
in a circular orbit. Observational evidence (Tassoul 2000; Pan 1997; Mathews & Mathieu 1992;
Witte & Savonije 1999) provides constraints for the circularization timescales of such systems, and
 is found to be shorter than
is found to be shorter than
 (Claret & Cunha 1997; Zahn 1977; Hut 1981).
(Claret & Cunha 1997; Zahn 1977; Hut 1981).
We chose to fix the value of
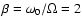 ,
which means that for decreasing
orbital separations, the rotational angular velocity,
,
which means that for decreasing
orbital separations, the rotational angular velocity,
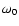 ,
increases proportionately with
the increasing orbital angular velocity
,
increases proportionately with
the increasing orbital angular velocity 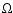 .
Although this might seem like a somewhat arbitrary choice, it is important to note that it is
.
Although this might seem like a somewhat arbitrary choice, it is important to note that it is 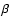 rather than
rather than
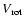 that plays a fundamental role in defining the frequencies and amplitudes of the oscillations. An intuitive way this can be understood
is to consider two binary systems with different
that plays a fundamental role in defining the frequencies and amplitudes of the oscillations. An intuitive way this can be understood
is to consider two binary systems with different 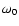 ,
but both with
,
but both with 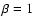 .
Because
.
Because
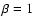 corresponds to the equilibrium condition, no oscillations are present, regardless of
how much larger one of the values of
corresponds to the equilibrium condition, no oscillations are present, regardless of
how much larger one of the values of 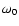 may be with respect to the other one.
may be with respect to the other one.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5776fig1.ps}\end{figure}](/articles/aa/full/2007/03/aa5776-06/Timg89.gif) |
Figure 1:
Top: the difference of azimuthal velocity of each surface element and the rigidly
rotating inner stellar body, 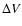 ( (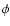 )
along the equatorial region for
a )
along the equatorial region for
a
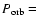 5 d binary system. The angle
5 d binary system. The angle 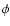 is measured with respect to the line
connecting the two stars. Bottom: the component of the velocity in the radial direction
of each surface element along the equatorial belt for the same model. The star is rotating
at twice the orbital frequency.
is measured with respect to the line
connecting the two stars. Bottom: the component of the velocity in the radial direction
of each surface element along the equatorial belt for the same model. The star is rotating
at twice the orbital frequency. |
| Open with DEXTER |
Figure 1 illustrates the example of 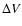 (
(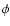 )
and Vralong the equatorial belt for the
)
and Vralong the equatorial belt for the
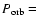 5 day binary system. The abscissa
corresponds to the location of the surface element along the equator with respect to the line
connecting the two stars. The largest differences between the surface azimuthal velocity
and the inner rigid-body rotating region are in general associated with the tidal bulges
(
5 day binary system. The abscissa
corresponds to the location of the surface element along the equator with respect to the line
connecting the two stars. The largest differences between the surface azimuthal velocity
and the inner rigid-body rotating region are in general associated with the tidal bulges
(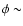 0 and 180
0 and 180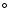 )
and the locations perpendicular to the axis of the orbit,
and it is at these locations where the largest energy dissipation occurs. Note that the
tangential component is
)
and the locations perpendicular to the axis of the orbit,
and it is at these locations where the largest energy dissipation occurs. Note that the
tangential component is 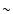 2 orders of magnitude larger than the radial component, making
it the dominant source of energy dissipation
2 orders of magnitude larger than the radial component, making
it the dominant source of energy dissipation![[*]](/icons/foot_motif.gif) .
When the orbital separation
decreases, the azimuthal variation is no longer smooth, with shorter scale oscillations appearing,
as illustrated in Fig. 2 where we plot
.
When the orbital separation
decreases, the azimuthal variation is no longer smooth, with shorter scale oscillations appearing,
as illustrated in Fig. 2 where we plot 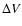 (
(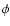 )
for the
)
for the
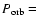 2.5 day binary system.
Because we are considering circular orbits,
2.5 day binary system.
Because we are considering circular orbits, 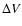 (
(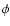 )
shown in Figs. 1 and 2 do not change significantly as a function of orbital phase and it is possible to assign a single
)
shown in Figs. 1 and 2 do not change significantly as a function of orbital phase and it is possible to assign a single 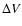 (
(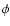 ) curve to each of the models. This would not be the case if the orbit were eccentric, where strong changes occur between periastron and apastron phases.
) curve to each of the models. This would not be the case if the orbit were eccentric, where strong changes occur between periastron and apastron phases.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5776fig2.ps}\end{figure}](/articles/aa/full/2007/03/aa5776-06/Timg92.gif) |
Figure 2:
The azimuthal velocity 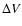 ( (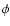 )
along the equatorial region of surface
elements with angle )
along the equatorial region of surface
elements with angle 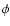 at a given time, for the
at a given time, for the
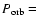 2.5 day binary system and with
2.5 day binary system and with
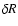 = 0.01 R1 and = 0.01 R1 and 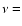 0.0043
0.0043 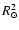 d-1. d-1. |
| Open with DEXTER |
The value of the external oscillating layer's density, 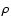 ,
was obtained by computing
stellar structure models using the code described in Yoon & Langer (2005). The value
,
was obtained by computing
stellar structure models using the code described in Yoon & Langer (2005). The value
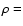 10-7 g cm-3 that we adopted corresponds to
the average density in the external 73 layers of the theoretical 5
10-7 g cm-3 that we adopted corresponds to
the average density in the external 73 layers of the theoretical 5 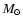 star. These
73 layers comprise approximately
star. These
73 layers comprise approximately
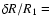 0.01, which is the thickness of the outer
layer that we adopted for the oscillations calculation.
0.01, which is the thickness of the outer
layer that we adopted for the oscillations calculation.
The remaining input parameter that needs to be defined for the oscillations code as
well as for computing the synchronization times using Eq. (21) is the viscosity,  .
Our practice (see Moreno et al. 2005) has been to use the smallest value of
.
Our practice (see Moreno et al. 2005) has been to use the smallest value of  allowed by the code. That is, when the oscillation amplitudes are very large, the
surface elements may either overlap with or become detached from their neighboring elements,
at which time the computation can no longer proceed. This is prevented by assigning
a sufficiently large value to the viscosity parameter. Our initial set of calculations
were performed with
allowed by the code. That is, when the oscillation amplitudes are very large, the
surface elements may either overlap with or become detached from their neighboring elements,
at which time the computation can no longer proceed. This is prevented by assigning
a sufficiently large value to the viscosity parameter. Our initial set of calculations
were performed with 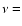 0.005
0.005
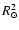 day-1, which is slightly larger than
the minimum
day-1, which is slightly larger than
the minimum  allowed for the
allowed for the
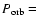 2.5 day binary system. The results yielded
a least-means-square fit with
2.5 day binary system. The results yielded
a least-means-square fit with

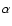 (a/R1)5.7, which is similar
to that of
(a/R1)5.7, which is similar
to that of

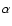 (a/R1)6, but displaced vertically on the
log
(a/R1)6, but displaced vertically on the
log
 vs. a plane. Thus, the next step consisted in adjusting
the values of
vs. a plane. Thus, the next step consisted in adjusting
the values of  to make
to make
 coincide with
coincide with
 .
The resulting values of
.
The resulting values of  and energy dissipation rates are listed in the last two columns of Table 1, and the
synchronization timescales are plotted in Fig. 3. Note that the 0.0015-0.0043
and energy dissipation rates are listed in the last two columns of Table 1, and the
synchronization timescales are plotted in Fig. 3. Note that the 0.0015-0.0043 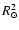 /d range in
/d range in  suggests that part of the turbulent viscosity is itself produced through the
tidal perturbations processes, since the closest binaries require the largest values of
suggests that part of the turbulent viscosity is itself produced through the
tidal perturbations processes, since the closest binaries require the largest values of  .
.
Table 1:
Binary system models for the
 vs. a calculation.
vs. a calculation.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5776fig3.ps}\end{figure}](/articles/aa/full/2007/03/aa5776-06/Timg99.gif) |
Figure 3:
Synchronization timescales (squares) calculated from our tidal oscillation model
for a fixed 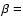 2, and
2, and 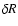 = 0.01 R1, and for values of = 0.01 R1, and for values of  as listed in Table 1 compared with Zahn's (1977) relation for stars with convective envelopes (continuous line).
as listed in Table 1 compared with Zahn's (1977) relation for stars with convective envelopes (continuous line). |
| Open with DEXTER |
We thus find that the shear energy dissipation due to the tangential velocity components
of the surface layer used in our approximate treatment of the tidal interaction leads to
synchronization timescales that are consistent with those predicted by Zahn's
treatment of the star's entire structure for the case in which the outer envelope is
convective.
The viscosity and the thickness of the oscillating layer are free parameters that
are not a priori constrained. We find that for a given orbital separation,
the energy dissipation rates may span a range of up to 2 orders of magnitude,
depending on the combination of  and
and
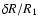 .
In Fig. 4 we illustrate
the dependence of the energy dissipation rate on viscosity (left panels) and on the
thickness of the layer (right panels). For
.
In Fig. 4 we illustrate
the dependence of the energy dissipation rate on viscosity (left panels) and on the
thickness of the layer (right panels). For
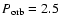 days, the energy dissipation rates
decrease with increasing viscosity. Since the explicit dependence of
days, the energy dissipation rates
decrease with increasing viscosity. Since the explicit dependence of 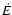 on the
viscosity is linear, (see Eq. (17)) the energy dissipation would be expected to increase
for increasing viscosity. On the other hand, because there is also a strong dependence of
the dissipation rates on the amplitudes of the oscillations, and larger viscosities tend to reduce
the amplitude of oscillation, the net result is a decrease in dissipation rates for
larger viscosities. We thus see that for the closest binary systems, it is this decrease
in oscillation amplitudes with increasing viscosities that dominates the behavior of
on the
viscosity is linear, (see Eq. (17)) the energy dissipation would be expected to increase
for increasing viscosity. On the other hand, because there is also a strong dependence of
the dissipation rates on the amplitudes of the oscillations, and larger viscosities tend to reduce
the amplitude of oscillation, the net result is a decrease in dissipation rates for
larger viscosities. We thus see that for the closest binary systems, it is this decrease
in oscillation amplitudes with increasing viscosities that dominates the behavior of 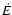 .
.
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{5776fig4.eps}\end{figure}](/articles/aa/full/2007/03/aa5776-06/Timg102.gif) |
Figure 4:
Energy dissipation rates calculated for different viscosities  with a fixed layer thickness with a fixed layer thickness  = 0.01 R1 ( left column) and for a changing layer thickness with a fixed viscosity = 0.01 R1 ( left column) and for a changing layer thickness with a fixed viscosity 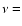 0.025
0.025 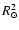 d-1 ( right column).
Three binary systems with different orbital periods are illustrated, from top to bottom: d-1 ( right column).
Three binary systems with different orbital periods are illustrated, from top to bottom:
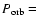 2.5, 10 and 25 d.
2.5, 10 and 25 d. |
| Open with DEXTER |
For the longer orbital periods (
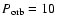 days), the interplay between the
effect of increasing viscosity and decreasing oscillation amplitudes becomes
more clear. In the middle panel of Fig. 4 we see how
days), the interplay between the
effect of increasing viscosity and decreasing oscillation amplitudes becomes
more clear. In the middle panel of Fig. 4 we see how 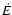 first increases
with increasing
first increases
with increasing  and then decreases as the oscillation amplitudes rapidly
decline, due to the continued increase in
and then decreases as the oscillation amplitudes rapidly
decline, due to the continued increase in  .
.
The thickness of the layer also has a strong influence on the value
of 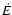 .
In the binary with the shortest orbital period,
.
In the binary with the shortest orbital period, 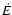 increases
systematically by up to 2 orders of magnitude when increasing
increases
systematically by up to 2 orders of magnitude when increasing 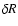 from R1/200 to R1/50. For longer period binaries, however (middle and
bottom panels, right), there is a critical point at which
from R1/200 to R1/50. For longer period binaries, however (middle and
bottom panels, right), there is a critical point at which 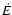 reaches a maximum value and then starts to decrease with increasing
reaches a maximum value and then starts to decrease with increasing
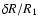 .
For the
.
For the
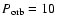 days system this
critical value is
days system this
critical value is
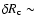 1/75 R1 while for the
1/75 R1 while for the
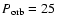 days case the turn around point appears at
days case the turn around point appears at
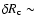 1/100 R1.
Hence, the dependence of dissipation on the thickness of the layer
is approximately linear up to the thickness
1/100 R1.
Hence, the dependence of dissipation on the thickness of the layer
is approximately linear up to the thickness
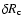 /R1, with
/R1, with 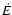 increasing monotonically. However, once the layer is thicker than
increasing monotonically. However, once the layer is thicker than
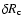 /R1,
the surface layer has more inertia and its azimuthal velocity amplitudes become
smaller and, once again, it is this effect that dominates the trend in
/R1,
the surface layer has more inertia and its azimuthal velocity amplitudes become
smaller and, once again, it is this effect that dominates the trend in 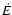 .
.
The energy dissipation rates computed from the results of the one-layer stellar oscillation
model for binary systems lead to the possibility of constraining the value of the viscosity  .
This can be performed by comparing the value of the synchronization timescale for a given
binary system as obtained from our model
.
This can be performed by comparing the value of the synchronization timescale for a given
binary system as obtained from our model
 ,
with the synchronization timescale curve predicted by Zahn's relation for the same system,
,
with the synchronization timescale curve predicted by Zahn's relation for the same system,
 .
The difference between
.
The difference between
 and
and
 ,
if attributed to viscosity alone, allows its value to be determined. For the system parameters listed in Table 1 we derive
,
if attributed to viscosity alone, allows its value to be determined. For the system parameters listed in Table 1 we derive  in the range 0.0015-0.0043
in the range 0.0015-0.0043 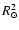 d-1 = 0.84-2.41
d-1 = 0.84-2.41 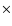 1014 cm2 s-1. If we apply the analogy with accretion disk studies where the viscosity is incorporated in the
1014 cm2 s-1. If we apply the analogy with accretion disk studies where the viscosity is incorporated in the
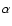 -parameter, an approximate relationship between kinematical viscosity and the
Shakura & Sunyaev
-parameter, an approximate relationship between kinematical viscosity and the
Shakura & Sunyaev 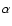 value is
value is
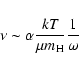 |
(22) |
from where
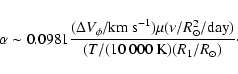 |
(23) |
Adopting the results illustrated in Fig. 2 for the maximum azimutal velocity,
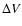 (
(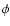 ), assuming a mean molecular weight for a fully ionized gas,
), assuming a mean molecular weight for a fully ionized gas, 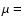 0.62,
0.62,
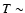 10 000 K, and using
10 000 K, and using 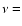 0.005
0.005 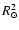 d-1, the above equation yields
values of
d-1, the above equation yields
values of 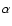
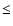 0.002.
0.002.
It is interesting also to compare this result with the values of the corresponding sum of
diffusion coefficients for rotational mixing that are computed by the
Binary Evolutionary Code (BEC; Petrovic et al. 2005, and references therein).
In order to make this comparison, BEC was run for a
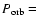 5 d binary system with
masses 5+4
5 d binary system with
masses 5+4 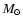 .
The computation was stopped after an evolutionary time of
.
The computation was stopped after an evolutionary time of
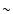 106 years in order to examine the values of these coefficients. The
106 years in order to examine the values of these coefficients. The 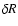 = 0.01 R1 layer that we adopted for the oscillations calculations is equivalent to 73 layers of the
BEC computation, and the sum of the values of the combined diffusion coefficients for rotational
mixing
= 0.01 R1 layer that we adopted for the oscillations calculations is equivalent to 73 layers of the
BEC computation, and the sum of the values of the combined diffusion coefficients for rotational
mixing![[*]](/icons/foot_motif.gif) from these layers is 1.65
from these layers is 1.65 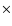 1014 cm2 s-1 (=0.0030
1014 cm2 s-1 (=0.0030 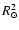 /d). It is not, however, clear how the values obtained for these 73 layers should be combined in order
to compare the result with the
/d). It is not, however, clear how the values obtained for these 73 layers should be combined in order
to compare the result with the  parameter that is used in the one-layer calculation, and the
sum is most likely an overestimate. On the other hand, this value does not include the effects
due to a magnetic field, which would tend to increase the value of the diffusion coefficient for
each layer.
parameter that is used in the one-layer calculation, and the
sum is most likely an overestimate. On the other hand, this value does not include the effects
due to a magnetic field, which would tend to increase the value of the diffusion coefficient for
each layer.
The energy dissipation rate, which is extracted from
the rotational energy
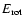 of the star through the action of de-spinning, is calculated from the difference between its initial rotational energy and the energy at the time of synchronization
divided by the synchronization timescale. Thus, this represents an average
of the energy dissipation rate over the time it takes the star to reach synchronization. However,
the rate of dissipation is expected to be a function of time, gradually vanishing
as the system approaches synchronization. Indeed, Fig. 5 illustrates the dependence on
of the star through the action of de-spinning, is calculated from the difference between its initial rotational energy and the energy at the time of synchronization
divided by the synchronization timescale. Thus, this represents an average
of the energy dissipation rate over the time it takes the star to reach synchronization. However,
the rate of dissipation is expected to be a function of time, gradually vanishing
as the system approaches synchronization. Indeed, Fig. 5 illustrates the dependence on 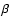 of the energy dissipation rate due to azimuthal motions, showing that as
of the energy dissipation rate due to azimuthal motions, showing that as
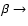 1,
1,
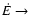 0. Figure 5 corresponds to the model binary system with
0. Figure 5 corresponds to the model binary system with
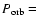 5 days,
5 days, 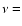 0.005
0.005 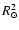 day-1, and other parameters as used for Table 1.
day-1, and other parameters as used for Table 1.
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{5776fig5CMJN.eps}\end{figure}](/articles/aa/full/2007/03/aa5776-06/Timg115.gif) |
Figure 5:
Energy dissipation rates for different values of 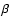 ,
for a binary system with
M1= 5 ,
for a binary system with
M1= 5 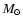 ,
M2= 4 ,
M2= 4 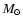 ,
R1= 3.2 ,
R1= 3.2 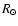 , ,
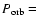 5 d,
5 d, 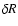 = 0.01 R1 and = 0.01 R1 and 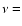 0.005
0.005 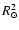 d-1. d-1. |
| Open with DEXTER |
Though we have not addressed the case of excentric binary systems in this paper, it is important to
note that due to the dependence of angular velocity with orbital separation,
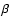 is a function of orbital phase. This effect, combined with the variation in orbital
separation, leads to strongly varying energy dissipation rates over the orbital cycle.
An exhaustive study of the available parameter space is beyond the scope of the
present paper, but will be the objective of a forthcoming investigation.
It is, however, worth noting that within the framework of Zahn's (1977) theory,
the synchronization timescales are several orders of magnitude smaller than the
circularization timescales. Hence, all binary systems should evolve to pseudo-synchronization
(i.e., average orbital angular velocity = rotational angular velocity) long
before the orbit is circularized. Thus, large numbers of asynchronous binary systems
in circular orbits are not expected to exist for stars on the Main Sequence.
is a function of orbital phase. This effect, combined with the variation in orbital
separation, leads to strongly varying energy dissipation rates over the orbital cycle.
An exhaustive study of the available parameter space is beyond the scope of the
present paper, but will be the objective of a forthcoming investigation.
It is, however, worth noting that within the framework of Zahn's (1977) theory,
the synchronization timescales are several orders of magnitude smaller than the
circularization timescales. Hence, all binary systems should evolve to pseudo-synchronization
(i.e., average orbital angular velocity = rotational angular velocity) long
before the orbit is circularized. Thus, large numbers of asynchronous binary systems
in circular orbits are not expected to exist for stars on the Main Sequence.
An interesting consequence suggested by Fig. 5 is that non-synchonous binary systems will
tend rapidly towards values of 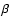 near unity, but will live for a relatively longer time
near the equilibrium value, but without having achieved it. Given the very large uncertainties
in the observable parameters, primarily
near unity, but will live for a relatively longer time
near the equilibrium value, but without having achieved it. Given the very large uncertainties
in the observable parameters, primarily
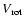 sin i and R1, it is not easy to
establish whether a particular binary system has actually achieved equilibrium. Thus,
there may be a large number of non-synchronously rotating binary systems in which observable
effects due to the tidal oscillations may be present. In particular, the peculiar X-ray emission
that is observed in a small number of B-star binary systems in which there is evidence
for non-synchronous rotation (Haro et al. 2003) may be a manifestation of tidally-induced
activity. Although the detailed mechanism for converting tidal energy into X-ray emission
is not known, we have previously speculated (Moreno et al. 2005; Koenigsberger et al. 2006)
that the shear produced by the relative azimuthal motions of the outer stellar layers
may lead to magnetic field generation near the stellar surface as well as mass ejection
episodes. Thus, the X-ray emission could be associated with these processes.
The possible connection between surface activity and tidal interactions has already
been investigated in connection with the distribution of star spots in RS CVn-type
binary systems (Holtzwarth & Schüssler 2002).
sin i and R1, it is not easy to
establish whether a particular binary system has actually achieved equilibrium. Thus,
there may be a large number of non-synchronously rotating binary systems in which observable
effects due to the tidal oscillations may be present. In particular, the peculiar X-ray emission
that is observed in a small number of B-star binary systems in which there is evidence
for non-synchronous rotation (Haro et al. 2003) may be a manifestation of tidally-induced
activity. Although the detailed mechanism for converting tidal energy into X-ray emission
is not known, we have previously speculated (Moreno et al. 2005; Koenigsberger et al. 2006)
that the shear produced by the relative azimuthal motions of the outer stellar layers
may lead to magnetic field generation near the stellar surface as well as mass ejection
episodes. Thus, the X-ray emission could be associated with these processes.
The possible connection between surface activity and tidal interactions has already
been investigated in connection with the distribution of star spots in RS CVn-type
binary systems (Holtzwarth & Schüssler 2002).
Other observational manifestations of this activity may be "turbulence'' above the expected
value for the effective temperature of the star, and photometric and line profile variability.
For example, the theoretical absorption line profiles that were computed for the optical
counterpart of the X-ray binary system 2S0114+650 required a "macroturbulence''
parameter of 37.5 km s-1 to match the observations (Koenigsberger et al. 2006),
significantly larger than the thermal speeds expected in a B1-supergiant star. However,
the problem of excessively large "macroturbulent'' velocities is widely encountered
among massive stars and, to our knowledge, there has been no systematic study made to
determine whether the problem is more severe in binary stars than in single stars.
We have shown that a single-layer approximation for the calculation of tidal oscillations
yields results that are consistent with the predictions of Zahn's (1966, 1977, 1989) theory
for the synchronization timescales in circular orbits,
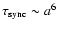 ,
thus providing a simplified means of computing the energy dissipation rates,
,
thus providing a simplified means of computing the energy dissipation rates, 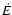 in binary systems. Furthermore, by calibrating our model results to fit Zahn's relationship,
we are able to constrain the value of the kinematical viscosity parameter,
in binary systems. Furthermore, by calibrating our model results to fit Zahn's relationship,
we are able to constrain the value of the kinematical viscosity parameter,  .
For the binary
system models considered in this investigation,
.
For the binary
system models considered in this investigation, 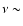 0.0015-0.0043
0.0015-0.0043
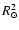 /day. This is
significantly larger than values typically obtained from detailed computations of the interior
structure of stellar convective layers, in the absence of magnetic fields.
/day. This is
significantly larger than values typically obtained from detailed computations of the interior
structure of stellar convective layers, in the absence of magnetic fields.
Our code makes no assumption regarding the energy dissipation mechanism except that
the dissipation processes can be described through the parameter  .
We
show in this paper that if we assume that the energy dissipation mechanism is related to
turbulent viscosity, we arrive at Eq. (19), which allows us to compute energy
dissipation rates using the output of the code, and we show that the derived energy dissipation
rates are consistent with those predicted by theoretical models of stars with convective envelopes.
However, the code includes no a priori assumptions regarding the energy transport mechanism.
In order to compare the results of the code with the theory for stars having outer radiative
envelopes, the effects due to radiative damping need to be incorporated in the derivation
of the synchronization timescale, which goes beyond the scope of the present investigation.
.
We
show in this paper that if we assume that the energy dissipation mechanism is related to
turbulent viscosity, we arrive at Eq. (19), which allows us to compute energy
dissipation rates using the output of the code, and we show that the derived energy dissipation
rates are consistent with those predicted by theoretical models of stars with convective envelopes.
However, the code includes no a priori assumptions regarding the energy transport mechanism.
In order to compare the results of the code with the theory for stars having outer radiative
envelopes, the effects due to radiative damping need to be incorporated in the derivation
of the synchronization timescale, which goes beyond the scope of the present investigation.
In summary, however, we have shown that the Moreno et al. (2005) one-layer model yields
results that are consistent with other theoretical calculations of the tidal interactions
in binary systems. It has the advantage that it can be used to compute the tidal oscillations
for arbitrary stellar rotational velocities and orbital excentricities, allowing an estimate
for the numerical value of  under general conditions in binary systems.
In addition, the code provides values of the radial and tangential components of the
oscillation velocities at any time throughout the orbit, as well as the location on the
stellar surface where the largest shear instabilities may be occurring. This allows
a comparison with observational quantities, such as absorption line profiles and diagnostics
of surface activity and should allow a methodical exploration of the impact that tidal
oscillations may have on the surface properties of stars in non-synchronously rotating
binary systems.
under general conditions in binary systems.
In addition, the code provides values of the radial and tangential components of the
oscillation velocities at any time throughout the orbit, as well as the location on the
stellar surface where the largest shear instabilities may be occurring. This allows
a comparison with observational quantities, such as absorption line profiles and diagnostics
of surface activity and should allow a methodical exploration of the impact that tidal
oscillations may have on the surface properties of stars in non-synchronously rotating
binary systems.
Acknowledgements
GK thanks S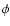 ren Meibom, Luis Mochan and Daniel Proga for helpful discussions. Support from
CONACYT grant 36569 and UNAM/PAPIIT IN119205 are acknowledged.
ren Meibom, Luis Mochan and Daniel Proga for helpful discussions. Support from
CONACYT grant 36569 and UNAM/PAPIIT IN119205 are acknowledged.
- Claret, A., &
Cunha, N. C. S. 1997, A&A, 318, 187 [NASA ADS] (In the text)
- Frank, J., King, A. R.,
& Raine, D. J. 1985, Accretion Power in Astrophysics (Cambridge
University Press), 65
(In the text)
- Gies, D. R., &
Kullavanijaya, A. 1988, ApJ, 326, 813 [NASA ADS] [CrossRef] (In the text)
- Haro, S., Juárez,
J. J., & Koenigsberger, G. 2004, in IAU Symp. 215, Stellar
Rotation, ASPCS, ed. A. Maeder, & P. Eenens, 163
- Heger, A. 1998, Ph.D.
Dissertation, Technische Universität, München,
Fakultät für Physik, MPA 1120
- Holzwarth, V., &
Schüssler, M. 2002, AN, 323, 399 [NASA ADS]
- Hut, P. 1981, A&A,
99, 126 [NASA ADS] (In the text)
- Koenigsberger, G.,
Georgiev, L., Moreno, E., et al. 2006, A&A, 458, 513 [NASA ADS] [CrossRef] [EDP Sciences]
- Landau, L. D., &
Lifshitz, E. M. 1984, Fluid Mechanics (Pergamon Press)
(In the text)
- Lynden-Bell, &
Pringle 1974, MNRAS, 168, 803 [NASA ADS] (In the text)
- Mathews, L. D., &
Mathieu, R. D. 1992, ASP Conf. Ser., 32, 244 [NASA ADS] ed. H. McAlister,
& W. I. Hartkopf
(In the text)
- Moreno, E., &
Koenigsberger, G. 1999, RMA&A, 35, 157 (In the text)
- Moreno, E.,
Koenigsberger, G., & Toledano, O. 2005, A&A, 437, 641 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pan, K. 1997, A&A,
321, 597 (In the text)
- Petrovic, J., Langer,
N., Yoon, S.-C., & Heger, A. 2005, A&A, 435, 247 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Shakura, N. I., &
Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] (In the text)
- Smith, M. A. 1977, ApJ,
215, 574 [NASA ADS] [CrossRef] (In the text)
- Spruit, H. C. 2002,
A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Tassoul, J.-L. 2000,
Stellar Rotation (Cambridge University Press), ISBN 0521772184
(In the text)
- Willems, B., &
Aerts, C. 2002, A&A, 384, 441 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Witte, M. G., &
Savonije, G. J. 1999, A&A, 350, 129 [NASA ADS] (In the text)
- Yoon, & Langer, N.
2005, A&A, 443, 643 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Zahn, J. P. 1966,
Annales d'Astrophysique, 29(4)
(In the text)
- Zahn, J. P. 1975,
A&A, 41, 329 [NASA ADS] (In the text)
- Zahn, J. P. 1977,
A&A, 57, 383 [NASA ADS] (In the text)
- Zahn, J. P. 1989,
A&A, 220, 112 [NASA ADS] (In the text)
Copyright ESO 2007
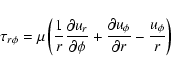
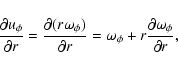
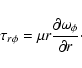
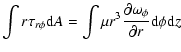
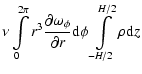
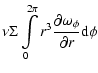
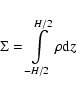
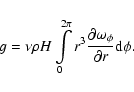
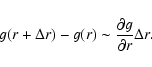
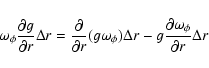
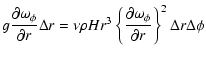
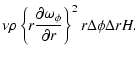
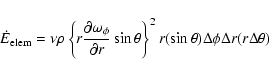
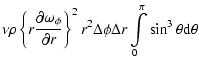
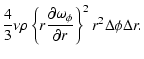
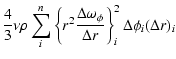
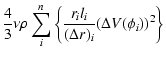
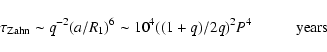
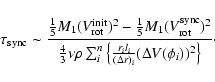
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5776fig1.ps}\end{figure}](/articles/aa/full/2007/03/aa5776-06/Timg89.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5776fig2.ps}\end{figure}](/articles/aa/full/2007/03/aa5776-06/Timg92.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5776fig3.ps}\end{figure}](/articles/aa/full/2007/03/aa5776-06/Timg99.gif)
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{5776fig4.eps}\end{figure}](/articles/aa/full/2007/03/aa5776-06/Timg102.gif)
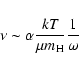
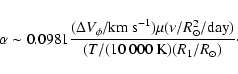
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{5776fig5CMJN.eps}\end{figure}](/articles/aa/full/2007/03/aa5776-06/Timg115.gif)