A&A 461, 1037-1047 (2007)
DOI: 10.1051/0004-6361:20065473
Structure and dynamics of the class I young stellar object L1489 IRS
C. Brinch1
- A. Crapsi1
- M. R. Hogerheijde1
- J. K. Jørgensen2
1 - Leiden Observatory, Leiden University, PO Box 9513, 2300 RA
Leiden, The Netherlands
2 - Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Mail
Stop 42, Cambridge, MA 02138, USA
Received 21 April 2006 / Accepted 11 October 2006
Abstract
Context. During protostellar collapse, conservation of angular momentum leads to the formation of an accretion disc. Little is known observationally about how and when the velocity field around the protostar shifts from infall-dominated to rotation-dominated.
Aims. We investigate this transition in the low-mass protostar L1489 IRS, which is known to be embedded in a flattened, disc-like structure that shows both infall and rotation. We aim to accurately characterise the structure and composition of the envelope and its velocity field, and find clues to its nature.
Methods. We construct a model for L1489 IRS consisting of an flattened envelope and a velocity field that can vary from pure infall to pure rotation. We obtain best-fit parameters by comparison to 24 molecular transitions from the literature, and using a molecular excitation code and a Voronoi optimisation algorithm. We test the model against existing millimeter interferometric observations, near-infrared scattered light imaging, and 12CO ro-vibrational lines.
Results. We find that L1489 IRS is well described by a central stellar mass of 1.3 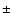 0.4
0.4 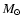 surrounded by a 0.10
surrounded by a 0.10 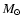 flattened envelope with approximate scale height
flattened envelope with approximate scale height
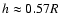 ,
inclined at
,
inclined at
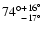 .
The velocity field is strongly dominated by rotation, with the velocity vector making an angle of
.
The velocity field is strongly dominated by rotation, with the velocity vector making an angle of 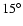
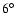 with the azimuthal direction. Reproducing low-excitation transitions requires that the emission and absorption by the starless core 1' (8400 AU) east of L1489 IRS is included properly, implying that L1489 IRS is located partially behind this core.
with the azimuthal direction. Reproducing low-excitation transitions requires that the emission and absorption by the starless core 1' (8400 AU) east of L1489 IRS is included properly, implying that L1489 IRS is located partially behind this core.
Conclusions. We speculate that L1489 IRS was originally formed closer to the center of this core, but has migrated to its current position over the past few times 105 yr, consistent with their radial velocity difference of 0.4 km s-1. This suggests that L1489 IRS' unusual appearance may be result of its migration, and that it would appear as a "normal'' embedded protostar if it were still surrounded by an extended cloud core. Conversely, we hypothesize that the inner envelopes of embedded protostars resemble the rotating structure seen around L1489 IRS.
Key words: ISM: kinematics and dynamics - ISM: molecules - ISM:
individual objects: L1489 IRS - radio lines: ISM - stars: formation
1 Introduction
The last three decades has provided a detailed understanding of the process of
low-mass star formation through theoretical work and advancements in the
observational facilities (see for example the review by André et al. 2000; or several reviews in Reipurth et al. 2006). These achievements
have given us a detailed view on infant stars through their various stages of
formation. Low-mass stars form out of dark molecular clouds when dense regions
can collapse under the influence of their own gravity. When sufficient density
is reached, a protostellar object is formed, still deeply embedded in a surrounding envelope. Conservation of angular momentum leads to the formation
of a disc around the protostar onto which the surrounding dust and gas is
accreted, although little details are known of how exactly discs grow. As the
stellar wind starts to clear out the envelope, the star and the disc becomes
visible in the optical and infrared and the object enters the classical T Tauri
stage which then later evolves into a main sequence star
(Shu 1977; Adams et al. 1988; Lizano & Shu 1989). Most observed Young Stellar Objects
(YSOs) are usually classified based on the shape of their spectral energy
distribution (SED) as either a Class I, II, or III (Lada & Wilking 1984). Class I
objects are deeply embedded in dense cores, while Class II objects are
surrounded by actively accreting discs. Class III objects have little material
left in a disc, but are still descending to the Main Sequence. Sometimes,
however, a YSO does not clearly fit into one of these categories. Those objects
are most likely the ones that can shed light on some of the missing pieces of
the picture. In this paper we study one such transitional object, L1489 IRS,
and investigate the structure, dynamics, and composition of its circumstellar
material.
L1489 IRS (IRAS 04016+2610) is classified as a Class I object based on its SED
and visibility at near-infrared wavelengths (Myers et al. 1987). Like many
embedded YSOs, line profiles of dense gas tracers like HCO+ J = 3-2 and
4-3 show red-shifted absorption dips usually interpreted as indications of
inward motions in the envelopes (Mardones et al. 1997; Gregersen & Evans 2000). However,
Hogerheijde (2001) shows that the spatially resolved HCO+ J = 1-0
emission exhibits a flattened, 2000 AU radius structure dominated by Keplerian
rotation. In this aspect, L1489 IRS more closely resembles a T Tauri star with
a circumstellar disc (Guilloteau & Dutrey 1998; Simon et al. 2000; Koerner & Sargent 1995). T Tauri
discs, however, are in general much smaller than the disc structure seen in
L1489 IRS with radii of several hundreds of AU. Scattered light imaging by
Padgett et al. (1999) shows the central stellar object and the presence of a slightly flaring dark lane, consistent with the disc-like configuration
inferred from the HCO+ 1-0 observations. Careful analysis if the
circumstellar velocity field by Hogerheijde (2001) revealed that infalling
motions are present at 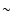 10% of the Keplerian velocities.
Hogerheijde hypothesized that L1489 IRS is in a short-lived
transitional stage between a collapsing envelope (Class I) and a viscously
supported, Keplerian disc (Class II). Observations of ro-vibrational CO absorption lines at 4.7
10% of the Keplerian velocities.
Hogerheijde hypothesized that L1489 IRS is in a short-lived
transitional stage between a collapsing envelope (Class I) and a viscously
supported, Keplerian disc (Class II). Observations of ro-vibrational CO absorption lines at 4.7 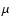 m showed that the inward motions continue to within
1 AU from the central star (Boogert et al. 2002).
m showed that the inward motions continue to within
1 AU from the central star (Boogert et al. 2002).
In this paper we address a number of questions about L1489 IRS. We construct a model for the circumstellar structure that accommodates all
observations, ranging from an extensive set of single-dish molecular line
measurements to the interferometric observations, the scattered light imaging,
and the CO ro-vibrational absorption lines. Hogerheijde (2001)
adopted a flared disc model with a fixed scale height for the structure
inspired by the interferometric imaging. In this Paper we choose a description
for the circumstellar structure that can be smoothly varied from spherical to
highly flattened, and investigate if the full data set requires a disc-like
configuration. We also adopt a velocity field that can range from purely
Keplerian to completely free-fall, or any combination of the two. By
considering the full data set, stronger constraints can be set on the velocity
field and the dynamical state of L1489 IRS than possible before. We perform a rigorous optimisation of the model for L1489 IRS using all available
single-dish line data, and test the model by comparing the interferometric
observations, the scattered light imaging, and the CO ro-vibrational absorption
lines to predictions from the model. Once we have established a satisfactory
model, also taking into account the immediate cloud environment, we explore the
nature of L1489 IRS. Does it represent a transitional state between Class I and II? Do all YSOs go through this stage? Or is L1489 IRS is some way special?
The layout of this Paper is as follows. Section 2 present our data
set and a detailed overview of the model and fit optimisation procedure.
Section 3 describes our best fit model and its reliability,
including comparison with observations of interferometric observations,
scattered light imaging, and CO ro-vibrational absorption lines.
Section 4 discusses our results in the light of the nature and
evolutionary state of L489 IRS and explores the wider implications for our
understanding of star formation. Section 5 concludes the Paper with a brief summary.
2 Observations and model description
The primary data set on L1489 IRS used in this paper was published by
Hogerheijde et al. (1997) and Jørgensen et al. (2004), and consists of 24 transitions among 12 molecular species. Figure 1 shows all 24 spectra. Table 1 lists the transitions, integrated line strengths,
line widths, and relevant beam sizes of the single-dish telescopes. In all
cases, line intensities are on the main-beam antenna temperature scale, using
the appropriate beam efficiencies. The integrated intensities are obtained by
fitting a Gaussian to the line. In some cases, no lines are visible above the
noise level, and 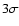 upper limits are given. The signal-to-noise ratio of
the HNC 4-3 and H2CO 515-414 spectra was insufficient for a proper Gaussian fit; instead the spectra are simply integrated from -4 to +4 km s-1 with respect to the systemic velocity of +7.2 km s-1. In addition to these molecular line data, we also use the total mass derived from the 850
upper limits are given. The signal-to-noise ratio of
the HNC 4-3 and H2CO 515-414 spectra was insufficient for a proper Gaussian fit; instead the spectra are simply integrated from -4 to +4 km s-1 with respect to the systemic velocity of +7.2 km s-1. In addition to these molecular line data, we also use the total mass derived from the 850 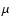 m continuum observations by JCMT/SCUBA
(Hogerheijde & Sandell 2000).
m continuum observations by JCMT/SCUBA
(Hogerheijde & Sandell 2000).
![\begin{figure}
\par\includegraphics[width=16.15cm,clip]{5473f01.ps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg11.gif) |
Figure 1:
The 24 single-dish molecular line spectra used for the model optimisation (histograms). The solid lines show the best-fit results for the model of L1489 IRS (see also Fig. 5). |
| Open with DEXTER |
Apart from the single dish data which we use in the model optimisation, we
compare predictions by the model to other previously published observations: a HCO+ J = 1-0 interferometer map from the BIMA and OVRO arrays
(Hogerheijde et al. 1998), CO ro-vibrational absorption spectra from the Keck
Telescope (Boogert et al. 2002), and the near-infrared scattered light imaging
from HST/NICMOS (Padgett et al. 1999).
Previous studies of L1489 IRS clearly indicate that an axi-symmetric
description of its circumstellar structure is required. In the following
subsections we construct a description of the density
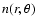 ,
gas
temperature
,
gas
temperature
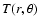 ,
and velocity field
,
and velocity field
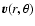 =
=
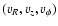 .
Throughout we attempt to keep the number
of free parameters at a minimum. In the end we arrive at four free parameters,
in addition to the eight molecular abundances which we fit but assume constant
throughout the source, and seven parameters that we hold fixed
(Table 2).
.
Throughout we attempt to keep the number
of free parameters at a minimum. In the end we arrive at four free parameters,
in addition to the eight molecular abundances which we fit but assume constant
throughout the source, and seven parameters that we hold fixed
(Table 2).
We adopt an axi-symmetric description of the gas density n(R,z) consistent
with the spherical model from (Jørgensen et al. 2002). These authors deduce a total mass of 0.097 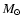 and a density following a radial power Law with
slope -1.8 between radii of 7.8 and 9360 AU. We truncate this model at the
observed outer radius of L1489 IRS of 2000 AU, but keep the power-law slope and
mass conserved. Instead of a simple radial power law,
and a density following a radial power Law with
slope -1.8 between radii of 7.8 and 9360 AU. We truncate this model at the
observed outer radius of L1489 IRS of 2000 AU, but keep the power-law slope and
mass conserved. Instead of a simple radial power law,
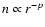 with
p=1.8, we adopt a Plummer-like profile,
with
p=1.8, we adopt a Plummer-like profile,
![$n\propto [1+(r/r_0)^2]^{-p/2}$](/articles/aa/full/2007/03/aa5473-06/img17.gif) with
r0 = 4.0 AU. This description keeps the density finite at all radii, but since r0 is much smaller than the scales of interest here, the resulting density
distribution is identical to that used by Jørgensen et al. (2002).
with
r0 = 4.0 AU. This description keeps the density finite at all radii, but since r0 is much smaller than the scales of interest here, the resulting density
distribution is identical to that used by Jørgensen et al. (2002).
From this spherically symmetric density distribution we construct an axi-symmetric, flattened configuration by multiplying by a factor
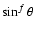 ,
where f can take any value
,
where f can take any value 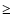 0 (see Stamatellos et al. 2004, where this approach was used for modelling starless cores). The adopted density distribution now becomes,
0 (see Stamatellos et al. 2004, where this approach was used for modelling starless cores). The adopted density distribution now becomes,
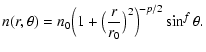 |
|
|
(1) |
For f=0 this reduces to a spherically symmetric structure, while for f>10
the resulting profiles becomes largely indistinguishable as they approach a step function (Fig. 2). The mass contained in the structure is
kept constant at 0.097 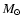 by adjusting n0 as f is varied. The only
free parameter in the density description is the flattening parameter f.
by adjusting n0 as f is varied. The only
free parameter in the density description is the flattening parameter f.
Table 1:
Single-dish molecular line data set.
![\begin{figure}
\par\includegraphics[width=8.05cm,clip]{5473f02.ps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg23.gif) |
Figure 2:
Progression of flattening of the adopted density structure as f is increased from 0 (purely spherical) to 10 in Eq. (1). |
| Open with DEXTER |
The temperature of the gas and the dust (which we assume to be identical)
in the circumstellar structure of L1489 IRS depends on the stellar luminosity
which is 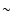
 (Kenyon et al. 1993a) and the infrared radiative
transfer through the structure. Since most of the circumstellar material is
optically thin to far-infrared radiation, the deviations introduced by the
flattening on the temperature structure are minor. Furthermore, the line
excitation does not depend strongly on small temperature differences. A spherically symmetric description of the temperature therefore suffices. Using
the continuum radiation transfer code DUSTY (Nenkova et al. 1999) and the density
structure of Eq. (1) with p=1.8 and f=0, we find that the
temperature is well described by,
(Kenyon et al. 1993a) and the infrared radiative
transfer through the structure. Since most of the circumstellar material is
optically thin to far-infrared radiation, the deviations introduced by the
flattening on the temperature structure are minor. Furthermore, the line
excitation does not depend strongly on small temperature differences. A spherically symmetric description of the temperature therefore suffices. Using
the continuum radiation transfer code DUSTY (Nenkova et al. 1999) and the density
structure of Eq. (1) with p=1.8 and f=0, we find that the
temperature is well described by,
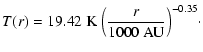 |
|
|
(2) |
There are no free parameters in this description of the temperature.
The velocity field is parameterized by a central, stellar mass 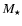 and an angle
and an angle 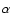 in such a way that,
in such a way that,
| |
|
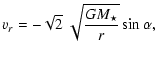 |
(3) |
| |
|
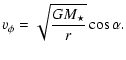 |
(4) |
For 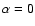 this reduces to pure Keplerian rotation around a mass
this reduces to pure Keplerian rotation around a mass 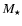 without any inward motions; for
without any inward motions; for
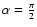 the velocity field is
that of free fall to a mass
the velocity field is
that of free fall to a mass 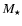 .
Intermediate values of
.
Intermediate values of 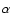 produce
a velocity field where material spirals inward. The implicit assumption in this
description is that both components of the velocity field vary inversely
proportional with
produce
a velocity field where material spirals inward. The implicit assumption in this
description is that both components of the velocity field vary inversely
proportional with 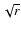 .
Note that
.
Note that 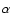 should not be
confused with the geometric angle determining the direction of the flow lines.
should not be
confused with the geometric angle determining the direction of the flow lines.
In this description there are two free parameters, the stellar mass 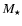 and the angle
and the angle 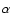 which is kept constant with radius. In addition to this
ordered velocity field, we add a turbulent velocity field with FWHM
0.2 km s-1.
which is kept constant with radius. In addition to this
ordered velocity field, we add a turbulent velocity field with FWHM
0.2 km s-1.
The excitation of the molecules and the line radiative transfer is calculated
using the Accelerated Monte Carlo code RATRAN (Hogerheijde & van der Tak 2000).
Collisional excitation rates are taken from the Leiden Atomic and Molecular
Database LAMDA (Schöier et al. 2005). We lay out the model onto three nested
8  6 grids (Fig. 3). The innermost grid cell is subdivided
four times, so that the innermost cell is resolved down to 4 AU. All
properties are calculated as cell averages, by numerically integration over the
cell and divide by its volume. To reduce
computing time, cells with H2 densities below 103 cm-3 are dropped.
Such cells do not contribute significantly to the line emission or absorption.
Dust continuum emission is included through a standard gas-to-dust ratio of 100:1 and dust emissivity from Ossenkopf & Henning (1994) for thin ice mantles which
has been accreted and coagulated for about 105 years.
6 grids (Fig. 3). The innermost grid cell is subdivided
four times, so that the innermost cell is resolved down to 4 AU. All
properties are calculated as cell averages, by numerically integration over the
cell and divide by its volume. To reduce
computing time, cells with H2 densities below 103 cm-3 are dropped.
Such cells do not contribute significantly to the line emission or absorption.
Dust continuum emission is included through a standard gas-to-dust ratio of 100:1 and dust emissivity from Ossenkopf & Henning (1994) for thin ice mantles which
has been accreted and coagulated for about 105 years.
Synthetic observations are created from the molecular excitation by performing
ray-tracing after placing the object at a distance of 140 pc and an inclination i (a free parameter). The resulting spectra are convolved with the
appropriate Gaussian beams. Figure 1 shows the best-fit model
spectra (the best fit is discussed in Sect. 3).
During the optimisation of the fit (Sect. 2.5) it became obvious that several
lines, and especially those of lower-lying rotational transitions taken in
large beams, were contaminated by emission with small line width. This emission
component is especially clear in the C18O 1-0 and 2-1 lines, the CS 2-1 line, the HCN 1-0 line, and, to some extent, the HCO+ 1-0 line
(Fig. 1). The emission has a
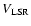 of 6.8 km s-1,
slightly lower than that of L1489 IRS of 7.2 km s-1. Cold fore- or
background gas with small turbulent velocity is the likely cause for this
component. The 850
of 6.8 km s-1,
slightly lower than that of L1489 IRS of 7.2 km s-1. Cold fore- or
background gas with small turbulent velocity is the likely cause for this
component. The 850 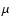 m SCUBA map from Hogerheijde & Sandell (2000) reveals that
L1489 IRS sits at the edge of an extended, probably starless, cloud core with a radius of 60'' (8400 AU). Cold gas in this core therefore contributes to the
low-J emission lines, and especially in spectra taken with large beams.
m SCUBA map from Hogerheijde & Sandell (2000) reveals that
L1489 IRS sits at the edge of an extended, probably starless, cloud core with a radius of 60'' (8400 AU). Cold gas in this core therefore contributes to the
low-J emission lines, and especially in spectra taken with large beams.
We construct a simple description for the neighbouring core, so that we can
take its emission into account in our optimisation of the model for L1489 IRS,
as well as its absorption if this source is located behind the core. We
approximate the core as spherical with a radius of 60'', which is roughly the
distance of L1489 IRS to its centre. We assume that it is isothermal at 10 K
and that it has abundances typical for starless cores (Jørgensen et al. 2004).
For the species which does not show any cloud core emission, the abundances are
unconstrained and we just set the abundances sufficiently low. In the case of
CO we use an abundance of 5 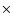 10-5. The CS abundance is set to
2
10-5. The CS abundance is set to
2 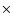 10-9, and the HCO+ and HCN abundances are 27
10-9, and the HCO+ and HCN abundances are 27 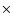 10-9 and
4
10-9 and
4 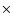 10-9 respectively. We derive its density distribution by fitting
the 850
10-9 respectively. We derive its density distribution by fitting
the 850 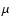 m emission from Hogerheijde & Sandell (2000). We find an adequate fit
for a radial power-law with slope -2 and a density of
4
m emission from Hogerheijde & Sandell (2000). We find an adequate fit
for a radial power-law with slope -2 and a density of
4 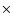 106 cm-3 at r=1000 AU resulting in a cloud mass of
2.9
106 cm-3 at r=1000 AU resulting in a cloud mass of
2.9 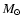 .
This is consistent with the drop off in density found in many
starless cores on scales (r > 1000 AU) that are relevant to us
(André et al. 1996). Because it falls outside even our largest beam on L1489 IRS
we do not investigate if the density in the neighbouring core levels off at the
center, as is seen for many starless cores. The relative smoothness of the
850
.
This is consistent with the drop off in density found in many
starless cores on scales (r > 1000 AU) that are relevant to us
(André et al. 1996). Because it falls outside even our largest beam on L1489 IRS
we do not investigate if the density in the neighbouring core levels off at the
center, as is seen for many starless cores. The relative smoothness of the
850 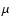 m emission suggest that this is the case, however.
m emission suggest that this is the case, however.
Using RATRAN we calculate the expected emission and the optical depth of each of
the observed transitions. In our model optimisation procedure (see below), the
emission from L1489 IRS and the neighbouring core are added on a channel-by-channel basis, with the appropriate spatial offset for the core. We
find that we can only make a fit that is reasonable if L1489 IRS is located
behind the core; we need both the emission and the opacity of the cloud. This
is taken into account by first attenuating the emission from L1489 IRS by the
core's opacity, again on a channel-by-channel basis, and subsequently
adding the core's emission in each channel, followed by beam convolution.
In this section we derived only an approximate model for the neighbouring core.
Its effects are taken into account in the model spectra, but the description of
the core is not accurate enough to include in the model optimisation. This
would require a much more detailed analysis than possible here. In the
procedure outlined in the next section, we therefore mask out those regions in
the spectra strongly affected by the emission and absorption of the core.
2.5 Optimising the fit
Our model has four free parameters: the inclination i, the flatness parameter f, the stellar mass 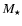 ,
and the angle of the velocity field
,
and the angle of the velocity field 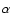 .
In addition, the abundances of the molecules are unknown. All other parameters
are held fixed. Table 2 lists the parameters.
.
In addition, the abundances of the molecules are unknown. All other parameters
are held fixed. Table 2 lists the parameters.
Considering the size of the parameter space and the time it takes to calculate
a single spectrum![[*]](/icons/foot_motif.gif) the task of finding the parameter vector resulting in the best fit is
non-trivial. This is further complicated by the degeneracy of the model results
to different parameters. For example, increasing the abundance can have the
same effect on the line intensity as increasing the inclination or the
flatness, but these will have very different effects on the line profile shape.
the task of finding the parameter vector resulting in the best fit is
non-trivial. This is further complicated by the degeneracy of the model results
to different parameters. For example, increasing the abundance can have the
same effect on the line intensity as increasing the inclination or the
flatness, but these will have very different effects on the line profile shape.
Instead of calculating all possible models in the allowed parameter space, we
use Voronoi tessellation of the parameter
cube (see e.g. Kiang 1966, for details on Voronoi tessellation). A random
set of n points pn in the parameter cube is picked and model spectra are
calculated for each of these. Then the parameter cube is divided into Voronoi
cells, defined as the volume around a point pi in the parameter cube
containing all points q closer to pi than to any other of the points pn
(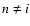 ). The parameter cube is scaled in arbitrary units, so that the
allowed parameter ranges falls between 0 and 1. On this dimensionless unit cube
a simple metric in d dimensions is used to define the cells,
). The parameter cube is scaled in arbitrary units, so that the
allowed parameter ranges falls between 0 and 1. On this dimensionless unit cube
a simple metric in d dimensions is used to define the cells,
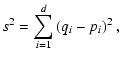 |
|
|
(5) |
assuming that the solution depend linearly on all parameters. This assumption
is not true especially for large values of s, but because we have no
knowledge of the geometry of the parameter space, we use the simplest possible
measure. In order to minimise the effect this has on our final solution we can
increase the initial sample rate so that the average distance between the
points becomes smaller. After one or two iterations, the volume of each cell is
small enough so that the assumption of linear dependence is good. By scaling
the parameters to the same range we make sure that each parameter is weighted
equally in the distance measure.
The cell which contains the point pi resulting in the best fit is chosen,
and a new set of random points are picked within this cell, and the procedure
is iterated until sufficient convergence has been achieved. This method is only
guaranteed to reach the true best fit if only one global minimum exist and if
there are no (or few) local minima. To check whether we find the true optimum,
we make several runs, with different randomly distribution initial points. We
find that we always reach the same minimum, and conclude that local minima are
few and not very deep.
For every calculated model spectrum, the fitness is evaluated by regriding the
model spectrum to the channel width of the corresponding observed spectrum,
centering it on the LSR velocity of 7.2 km s-1, and calculating the 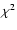 between the model and the observed spectrum,
between the model and the observed spectrum,
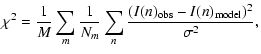 |
|
|
(6) |
where M is the number of spectra and N is the number of velocity channels
in the mth spectrum. This way we give an equal weight to all spectra even
though the number of channels vary in each spectrum. Those channels affected by
the neighbouring core are not included in the 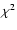 measure. Every spectra
has a fixed passband of 14 km s-1 so that an equal amount of baseline is
included for each spectrum.
measure. Every spectra
has a fixed passband of 14 km s-1 so that an equal amount of baseline is
included for each spectrum.
Using this method, with a set of 24 random points per iteration, we converge on
an optimal solution after four to five iterations, corresponding to 10 to 12 days of CPU time. For practical reasons we initially chose only to consider the
most structured lines (CO, HCO+ and CS), lowering the computational time to
about a single day and getting a quick but rough handle on the initial
parameter cube. We then included the other lines to obtain the overall best
solution.
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{5473f04.ps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg39.gif) |
Figure 4:
The histograms show the 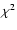 distributions of models around the
best fit position where only one parameter is varied at each time.
A Gaussian, centered on the best fit in each panel, is fitted to the
distributions. The dispersion of the Gaussians is given in each panel.
distributions of models around the
best fit position where only one parameter is varied at each time.
A Gaussian, centered on the best fit in each panel, is fitted to the
distributions. The dispersion of the Gaussians is given in each panel. |
| Open with DEXTER |
Getting a handle on the uncertainties in the obtained parameter values is a difficult matter due to the size and complexity of the parameter space. As
mentioned above, we have no knowledge of the overall geometry of the parameter
space and given the long computation time of the optimisation algorithm, we
cannot make a correlation analysis of each pair of parameter and neither can we
make 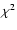 surfaces. Still, it is very important to get an estimate on the
stability and reliability of our solution.
surfaces. Still, it is very important to get an estimate on the
stability and reliability of our solution.
A simple error analysis is done for the four model dependent parameters, the
flatness, the velocity angle, the stellar mass, and the inclination, by fixing
three of the parameters at their best fit values, and calculating models in
which the fourth parameter is gradually increased from its lower boundary to
the upper boundary. Histograms of the resulting (inverse) 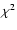 values is
shown in Fig. 4. The
values is
shown in Fig. 4. The 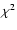 values are approximately normally
distributed, with the main discrepancy in the high values of the inclination,
velocity field, and the flatness. This relates to the non-linear nature of the
trigonometric functions associated with these three parameters.
values are approximately normally
distributed, with the main discrepancy in the high values of the inclination,
velocity field, and the flatness. This relates to the non-linear nature of the
trigonometric functions associated with these three parameters.
A Gaussian has been fitted to each of the histograms in Fig. 4. The
centre of the Gaussian is fixed on the best fit value and the hight is fixed by
the 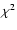 value of the best fit so that only the variance,
value of the best fit so that only the variance, 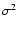 ,
is
free. Reasonable fits are achieved for each parameter with the
,
is
free. Reasonable fits are achieved for each parameter with the  value
given in each panel. These values are taken to be a rough estimate of the
magnitude of the error in each of the four parameters. For the inclination and
flatness, where the error is greater than the allowed parameter range, the
error is of course determined by the physical constrains on the parameter value
(e.g., the inclination cannot be greater than
value
given in each panel. These values are taken to be a rough estimate of the
magnitude of the error in each of the four parameters. For the inclination and
flatness, where the error is greater than the allowed parameter range, the
error is of course determined by the physical constrains on the parameter value
(e.g., the inclination cannot be greater than 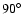 ). Note that the error
bars are typically smaller than the explored range in each parameter by a factor of 2-10.
). Note that the error
bars are typically smaller than the explored range in each parameter by a factor of 2-10.
With this kind of one dimensional error analysis we do not take into account
the fact that the parameters are likely to be highly correlated. A few
exploratory calculations, where one parameter was held fixed at its best fit
value while the other three where randomly pertubed around their best fit
values, indicated that there indeed exist a strong correlation between the
parameters. Indeed, a degeneracy exists between the central mass and the
inclination, which again is degenerate with the flattening. Only a full
parameter space study can fully disentangle this and is beyond the scope of
this paper.
Because the abundance parameter mainly serves to scale the intensity in every
channel of the spectrum, and does not change the shape of the profile much,
this kind of error analysis is of little use. For any combination of the four free parameters that reproduces the observations, a corresponding abundance is
found from the optically thin isotopic lines. These abundances are relatively
insensitive to the exact geometry because of their optically thin nature.
Therefore we assume that the error in the abundance values obtained here is
entirely dominated by the 20% calibration error of the observed spectra.
Throughout this work we have assumed constant abundance for all the molecular
species. In reality, abundances will depend on the chemistry and molecules will
freeze out below a certain temperature. This gives rise to a drop in the
abundances at a certain radius and it will affect, to some extent, the shape of
the profiles but more prominently, the line ratios. Specifically, by removing
low temperature material from the gas phase, low excitation lines become
relatively weaker. Our model does not suffer from the problem of over-producing
the low J lines, except for the case of HCO+; a more complex abundance
model would likely provide a better fit to the J= 1-0 and 3-2 lines.
However, this would require a careful chemical analysis which is beyond the
scope of this paper. A few tests showed that letting CO freeze out at 20 K does
not change the best fit parameters significantly, except for the abundance
which will then have to be re-optimised.
3 Results
Figure 1 compares the data to the synthetic spectra based on the
best fit model obtained with the optimisation procedure described above. The
results for the combined emission of L1489 IRS and the neighbour core is shown
in Fig. 5. Because the emission from the core only contributes to the
low J lines, this figure only shows the species in which the combined
spectrum show any difference from the L1489 IRS spectrum alone. For all species
not shown in Fig. 5, the combined spectra is indistinguishable from
the one shown in Fig. 1.
Table 2 lists the parameters of the best fit.
![\begin{figure}
\par\includegraphics[width=16.35cm,clip]{5473f05.ps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg42.gif) |
Figure 5:
The combined emission from the L1489 IRS model and the neighbour
cloud core. Only spectra which are affected significantly by the
cloud core emission are shown here. |
| Open with DEXTER |
The inclination angle of 74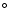 falls within the range of 60
falls within the range of 60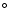 to 90
to 90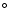 which is inferred from the scattered light image of
Padgett et al. (1999) and the modelling of the infrared spectral energy
distribution Kenyon et al. (1993b). Section 3.2.2 shows that this inclination
and the flattening parameter f=3.8 reproduce the scattered light image,
including the detectability of the central star. The resulting density
distribution can be well approximated by a disk with a vertical density
distribution
which is inferred from the scattered light image of
Padgett et al. (1999) and the modelling of the infrared spectral energy
distribution Kenyon et al. (1993b). Section 3.2.2 shows that this inclination
and the flattening parameter f=3.8 reproduce the scattered light image,
including the detectability of the central star. The resulting density
distribution can be well approximated by a disk with a vertical density
distribution 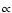
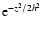 and a scale height of
and a scale height of
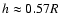 .
The maximum deviation of this approximation is only 4%, up to an angle of 60
.
The maximum deviation of this approximation is only 4%, up to an angle of 60 above the midplane. Hogerheijde (2001) described L1489 IRS with flared disc with an adopted
density scale height of h = 0.5 R, so our best fit model shows that the
structure might in fact be flatter than previously assumed. However,
Hogerheijde (2001) used an inclination of
above the midplane. Hogerheijde (2001) described L1489 IRS with flared disc with an adopted
density scale height of h = 0.5 R, so our best fit model shows that the
structure might in fact be flatter than previously assumed. However,
Hogerheijde (2001) used an inclination of 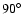 for the flared disc
(a flat disc at
for the flared disc
(a flat disc at
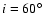 was also tried), so the projected column density
distribution are quite similar in both cases.
was also tried), so the projected column density
distribution are quite similar in both cases.
The best fitting velocity vector makes an angle of only 15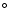 with respect
to the azimuthal direction, consistent with Hogerheijde (2001) who shows
that rotation is the primary component in the velocity field. However, our
central stellar mass of 1.35
with respect
to the azimuthal direction, consistent with Hogerheijde (2001) who shows
that rotation is the primary component in the velocity field. However, our
central stellar mass of 1.35 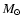 is considerably higher than the
0.65
is considerably higher than the
0.65 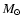 derived by Hogerheijde. Part of this is due to
different definitions of the velocity field. Hogerheijde
reports a mass expected for Keplerian motion based on the azimuthal component
of the velocity field alone, while the mass derived here results in
derived by Hogerheijde. Part of this is due to
different definitions of the velocity field. Hogerheijde
reports a mass expected for Keplerian motion based on the azimuthal component
of the velocity field alone, while the mass derived here results in
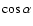 times the Keplerian velocity (Eq. (4)). In addition, a different inclination is found. These two factors together would give a mass of
1.2
times the Keplerian velocity (Eq. (4)). In addition, a different inclination is found. These two factors together would give a mass of
1.2 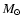 for our model. This mass is still 80% higher than that from
Hogerheijde but our best fit has a
for our model. This mass is still 80% higher than that from
Hogerheijde but our best fit has a 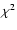 value of 1.69.
That is nearly half that of the best model of Hogerheijde of
value of 1.69.
That is nearly half that of the best model of Hogerheijde of
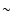 3. We ascribe this difference to a more thorough search of the parameter
space.
3. We ascribe this difference to a more thorough search of the parameter
space.
Table 2:
Best fit parameters.
The best fitting abundances are consistent with the abundances obtained for
L1489 IRS in (Jørgensen et al. 2004) to within a factor of 2-3 although the
values obtained here are all higher. This may be due to higher line opacities
in our model as a result of the different adopted velocity fields;
Jørgensen et al. do not include a systematic velocity field and only
a single turbulent line width. Consistent with this previous work, we find no
evidence for depletion of CO, in accord with the relatively high temperatures
exceeding the 20 K evaporation temperature of CO throughout most of the disc.
Another interesting finding is the CN/HCN abundance ratio of 1.0, which is more
reminiscent of dark clouds than of circumstellar discs, suggesting that
chemically, L1489 IRS is close to its original cloud core and that
photo-dissociation does not play a major role yet (Thi et al. 2004).
The overall correspondence of our model to the data is good and most of the
spectra are well reproduced. The line widths of C18O and C17O are
well reproduced, and the C17O 2-1 and 3-2 lines are found to exclusively
trace L1489 IRS and be uncontaminated by the neighbouring core. All three C18O and the C17O 1-0 line have narrow line peaks that originate in
the neighbour core; some C18O J= 1-0 emission that is not reproduced can
either be caused by additional material along the line of sight, or be due to
the approximate nature of our description of the core.
The sulfur bearing lines are not very intense and show little structure. Again
we see a narrow peak in the CS J= 2-1 almost entirely accounted for by the
neighbouring core and perhaps also in the SO line. The non-detection of
C34S 2-1 places an upper limit on the CS abundance in the neighbouring
cloud of 2 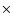 10-9. The CS 7-6 line is poorly fit, but the observed
spectrum has low signal-to-noise.
10-9. The CS 7-6 line is poorly fit, but the observed
spectrum has low signal-to-noise.
The HCO+ lines are the strongest among our sample and show most structure in
their profiles. It was important to be able to reproduce the double peak in the
HCO+ J= 4-3 line because this feature is a very clear tracer of the
velocity structure in L1489 IRS. Our model is able to reproduce this feature.
However, we do not observe the double peak in the HCO+ J= 3-2 line but
only a slight asymmetry. This provided a major constraint on the velocity
field. The neighbour core does not contribute in the 4-3 line but it makes up
for almost all of the excess emission seen in the 1-0 and 3-2 lines of HCO+.
Of the nitrogen bearing species, HCN J= 1-0 with its three hyperfine
components shows very narrow lines, which is well reproduced by the neighbour
core model which dominates the emission. The HCN J= 4-3 line is much broader
and uncontaminated by the neighbouring core. A narrow peak in the spectrum at
8 km s-1 cannot be due to the neighbour core and we assume it is noise.
The HNC 4-3 line has a rather low signal to noise ratio and can only provide a reliable estimate within a factor of a few. CN J= 1-0 also has a low signal
to noise ratio, but in the case of CN, the abundance is well constrained by the
J= 3-2 line.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{5473f06.eps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg55.gif) |
Figure 6:
a) Best possible fit with a spherical model to the HCO+ J= 4-3 line. b) The best fit to the same line where the flattening f and
the inclination i are kept as free parameters. Below, the residuals
are shown with the mean and two standard deviations indicated. |
| Open with DEXTER |
All spectra discussed above have been obtained with single-dish telescopes that
do not resolve the 2000 AU radius source. One can wonder if it is justifiable
to use a non-spherical model when the single-dish observations does not contain
any spatial information. Although the scattered-light and interferometer images
show that the structure is non-spherical, one could argue that introducing the
flattening is simply a way to improve the fit by adding a free parameter.
However, this is not the case. Figure 6 shows the best fit to the
HCO+ J = 4-3 line, with a spherical model (f=0) and a model where the
flattening and inclination are free parameters. The flattened model provides a considerably better fit with lower 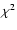 value. And, more importantly, the
spherical model shows too much self absorption. Our optimisation algorithm
returns the model which minimises the difference between data and model for
each velocity channel. In a spherical model the column simply becomes too high.
By flattening the model and adjusting the inclination, we can exactly reproduce
the right amount of self absorption seen in the data while keeping the total
column density high enough to produce the right line strength. The degeneracy
between these two parameters are resolved by the velocity field, and thus it
turns out that it is actually possible to retrieve spatial information from
single dish observations.
value. And, more importantly, the
spherical model shows too much self absorption. Our optimisation algorithm
returns the model which minimises the difference between data and model for
each velocity channel. In a spherical model the column simply becomes too high.
By flattening the model and adjusting the inclination, we can exactly reproduce
the right amount of self absorption seen in the data while keeping the total
column density high enough to produce the right line strength. The degeneracy
between these two parameters are resolved by the velocity field, and thus it
turns out that it is actually possible to retrieve spatial information from
single dish observations.
Ward-Thompson & Buckley (2001) have argued that the amount of self-absorption can
also be regulated by adjusting the turbulent velocity dispersion. We can indeed
change the quality of the spherical fit by changing the amount of turbulence.
We cannot, however, do that without also changing the velocity distance between
the two peaks. Thus in order to fit the line width we must decrease the mass
and thereby the magnitude of the velocity field, which no longer reproduces the
observed infall asymmetry. We therefore find that varying the turbulent
velocity width in a spherical model does not reproduce the observations.
With the fit parameters derived above, we can now test our model by comparison
to other observations of L1489 IRS not used in the fit. The neighbouring cloud
is not considered in the following.
![\begin{figure}
\par\includegraphics[height=7.1cm,width=7.4cm,clip]{5473f07.eps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg56.gif) |
Figure 7:
a) Interferometer map in HCO+ J= 1-0; b) the corresponding
synthesised map based on our best model; c) and d) models with f=1
and f=8 respectively. The white contour lines show the integrated
intensity, starting at 0.25 Jy bm-1 and increasing in steps of
0.5 Jy bm-1. The colour scale shows the velocity centroid in
units of km s-1. |
| Open with DEXTER |
We have used our model to produce a synthetic interferometer map of the HCO+ J = 1-0 emission which can be directly compared to the data presented by
Hogerheijde (2001). Figure 7 compares the model predictions of
the integrated intensity and velocity centroid maps to the observations
reproduced from Hogerheijde (2001). We also show a model with f=1 and on
with f=8 for comparison. The model images were made by taking the unconvolved
image cubes from RATRAN and then, using the (u,v) settings from the original
data set, making synthetic visibilities with the "uvmodel'' task from the MIRIAD
software package. This is what we would get if the interferometer observed our
model object. Then we applied the usual deconvolution with the invert, clean,
and restore routines in order to reconstruct an image from the visibilities.
The resulting synthetic image of our best fit model resembles the observations
closely within the uncertainty of the abundance which sensitively affects the
apparent size, when it is taken into account that the observations also
partially recover the neighbouring core that is ignored in the model
(Fig. 7, panel b). However, the f=8 model in panel d) is also in
good agreement with the data which partially can be explained by the fact that,
due to the non-linearity of the sine function, the difference between an f=3
and f=10 model is much less than the difference between an f=1 and f=3 model. This is also reflected in Fig. 2. In any case, panel c) is
obviously in poor agreement with the data, which shows that in order to fit the
interferometer data, a flattened structure is needed.
This kind of analysis is very useful to investigate the spatial distribution of
the emission which is lacking in the single dish data. Importantly, we see that
the flattening which we introduced and the amount of which we determined from
the line profile results in a projected shape that is very close to what we see
in the data image. Also, because the cuts are the same in both panels, the
extent of the emission and therefore the physical size scale of the model is
consistent.
3.2.2 Near-infrared image
We subsequently test our best-fit model through a comparison with the
near-infrared scattered light image of Padgett et al. (1999). A reproduction of
this image is shown in the top left panel of Fig. 8. Using the
density structure and inclination found in Sect. 3 and the
properties of the central star as described in the introduction as input, we
calculated the scattering light emission with RADMC, a two-dimensional
radiation transfer code (Dullemond & Dominik 2004). Then, using the ray-tracing code
RADICAL (Dullemond & Turolla 2000), we extract the fluxes over the full spectral
range of 1 to 850 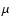 m and image our model in the F110W, F160W, F210W
NICMOS bands.
m and image our model in the F110W, F160W, F210W
NICMOS bands.
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{5473f08.eps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg57.gif) |
Figure 8:
The top left panel shows the false colour NICMOS image of L1489 IRS
from Padgett et al. (1999). In the three remaining panels are shown
synthetic three-colour composite images based on our model. |
| Open with DEXTER |
Our best fit model of Sect. 3 automatically provides a good fit
to the sub-millimetre part of the spectral energy distribution, confirming that
our model is consistent with the results of Jørgensen et al. (2002). The
near-infrared observations are more difficult to match. The column density in
the inner part is too high to provide the clear view of the central star that
shows prominently in NICMOS images. However, if we reduce the scale height in
the inner 250 AU to h=0.15R, the column density is reduced and the central
star becomes detectable in the near-infrared. This adaptation does not affect
the sub-millimetre emission or the molecular line intensities viewed in the
much larger single-dish beams. Recently obtained high-resolution data from the
Submillimeter Array (SMA) in Hawaii may be able to test this assumption of the
geometry in the inner 2
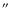 = 280 AU (Brinch et al., in prep.).
= 280 AU (Brinch et al., in prep.).
The resulting three-colour composite images of our best fit model as well as a f=1 and f=8 model, is shown in Fig. 8. Although this can only be a qualitative comparison, our model is able to reproduce most of the striking
features evidenced by the observations. The opening angle of the dust cavity is
found to be somewhat dependent on the flattening parameter f in our model.
Although it is difficult to judge the agreement, this result seems to favour a relatively low value of f as opposed to what we found above for the
interferometric map. The non-monotonic behaviour along the axis in the f=1 model is a combination of the finite gridding of the density structure and the
effect of scattering. It has a very narrow cavity and so the base of the
scattering nebula is actually absorbed by the high density material in the
inner part. In the other models the cavity is large enough to allow all the
scattered photons to escape.
We also reproduce the near-infrared colours, confirming our adopted density
distribution between 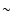 100 AU and
100 AU and 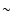 2000 AU. Each of the NICMOS fluxes
are reproduces to within about 40%. Although a detailed modelling of L1489 IRS
on these scales where most of the near-infrared emission is coming from was
beyond the scope of this paper, we present this prediction to demonstrate that
it is possible to combine the information contained in near-infrared images and
sub-millimetre single dish measurements to obtain a self-consistent model on
scales ranging from within a few AU up to several thousand AU.
2000 AU. Each of the NICMOS fluxes
are reproduces to within about 40%. Although a detailed modelling of L1489 IRS
on these scales where most of the near-infrared emission is coming from was
beyond the scope of this paper, we present this prediction to demonstrate that
it is possible to combine the information contained in near-infrared images and
sub-millimetre single dish measurements to obtain a self-consistent model on
scales ranging from within a few AU up to several thousand AU.
The cavity seen in the NICMOS image is likely associated with a molecular
outflow. However, Hogerheijde et al. (1998) show that L1489 IRS only drives a modest 12CO outflow, and little or no impact on the line profiles is
expected. Therefore, an outflow has not been incorporated into the model
described in this paper.
Finally we apply our model to fit the CO ro-vibrational absorption bands, again
by using RATRAN. Here we assume that initially all CO molecules are in the
vibrational ground state (v=0) but can be excited to a v=1 state by
absorption of a photon from the central star, producing the absorption lines in
the P and R branches corresponding to
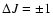 transitions.
Observations of these bands from the Keck/NIRSPEC instrument has been presented
by Boogert et al. (2002). The spectrally resolved absorption lines revealed
inward motions up to 100 km s-1. Using the same method as
Boogert et al. we calculated the ro-vibrational absorption lines in
our model, and plot the average of the P(6)-P(15) lines in Fig. 9.
transitions.
Observations of these bands from the Keck/NIRSPEC instrument has been presented
by Boogert et al. (2002). The spectrally resolved absorption lines revealed
inward motions up to 100 km s-1. Using the same method as
Boogert et al. we calculated the ro-vibrational absorption lines in
our model, and plot the average of the P(6)-P(15) lines in Fig. 9.
We find that our model fits the data as well as the results from
Boogert et al., who use a contracting flared disc with power laws for
the temperature, density, and infall velocity. This means that the amount of
inward velocity that we obtained from the fit to the single dish lines together
with the adopted density profile can explain the observed infall, even at radii
much smaller than probed with the single dish lines. In Fig. 9 we
see that absorption is present all the way up to at least 100 km s-1. In
our model, this velocity translates into a radius of 0.02 AU. Material
absorbing at 50 and 20 km s-1 is located at 0.06 and 0.4 AU respectively.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5473f09.ps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg60.gif) |
Figure 9:
An average of the observed 12CO P(6)-P(15) lines with a similarly
averaged model result over plotted. |
| Open with DEXTER |
4 Discussion
In this paper we derive an accurate model for the circumstellar material of
L1489 IRS. We find that it is well described by a flattened structure with a radius of 2000 AU, in sub-Keplerian motion around a 1.35 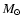 central
star. While the structure resembles discs found around T Tauri stars
(e.g. Simon et al. 2000), its 2000 AU radius is much larger than T Tauri discs
(typically several hundred AU). Also, discs around T Tauri stars are often well
described by pure Keplerian motions except for a few cases, e.g. AB Aur, in
which outwards non-Keplerian motions are measured (Lin et al. 2006; Piétu et al. 2005).
In this section we discuss the evolutionary state of L1489 IRS, and
particularly whether it represents a unique case or if other forming stars may
go through a similar stage. We start by deriving the life span of the current
configuration. We then explore the relation of L1489 IRS to its neighbouring
core. Finally, we discuss a number of open questions that only new observations
can answer.
central
star. While the structure resembles discs found around T Tauri stars
(e.g. Simon et al. 2000), its 2000 AU radius is much larger than T Tauri discs
(typically several hundred AU). Also, discs around T Tauri stars are often well
described by pure Keplerian motions except for a few cases, e.g. AB Aur, in
which outwards non-Keplerian motions are measured (Lin et al. 2006; Piétu et al. 2005).
In this section we discuss the evolutionary state of L1489 IRS, and
particularly whether it represents a unique case or if other forming stars may
go through a similar stage. We start by deriving the life span of the current
configuration. We then explore the relation of L1489 IRS to its neighbouring
core. Finally, we discuss a number of open questions that only new observations
can answer.
By integrating the trajectory of a particle at 2000 AU we find the infall time
scale to be 2.3 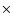 104 years. Dividing the 0.097
104 years. Dividing the 0.097 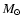 of the
circumstellar material yields a mass accretion rate of 4.3
of the
circumstellar material yields a mass accretion rate of 4.3 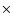
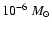 yr-1. Estimating the radius of the central star from the
mass-radius relation (Stahler 1988) to be 4
yr-1. Estimating the radius of the central star from the
mass-radius relation (Stahler 1988) to be 4 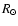 results on an accretion luminosity of
results on an accretion luminosity of
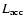 = G
= G
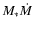 /
/
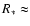 46
46 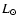 corresponding to about ten times the observed bolometric luminosity from the
YSO Kenyon et al. (1993a). This suggest that not all inspiraling material falls
directly onto the star. The result is somewhat higher than the one found
by Hogerheijde (2001), although the modelling approach used in that paper
was completely different.
corresponding to about ten times the observed bolometric luminosity from the
YSO Kenyon et al. (1993a). This suggest that not all inspiraling material falls
directly onto the star. The result is somewhat higher than the one found
by Hogerheijde (2001), although the modelling approach used in that paper
was completely different.
In our model we also assume a constant angle 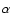 for the direction of the
velocity vector. In reality, this direction could vary with radius as the
angular momentum distribution changes. For example, at smaller radii,
for the direction of the
velocity vector. In reality, this direction could vary with radius as the
angular momentum distribution changes. For example, at smaller radii, 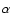 could be smaller as the velocity field more closely resembles pure Keplerian
rotation. The inspiral time, and mass accretion rate, can therefore be very
different. Only higher resolution observations can investigate this further.
could be smaller as the velocity field more closely resembles pure Keplerian
rotation. The inspiral time, and mass accretion rate, can therefore be very
different. Only higher resolution observations can investigate this further.
Is L1489 IRS in any way special? No objects like it are reported in the
literature. Since its life time is of the order of a few 104 yr, roughly
5-10% of the embedded phase, more objects like it would be expected. It is
possible that L1489 IRS was formed out of a core with unusually large angular
momentum, which led to the formation of an untypically large disc. We cannot
exclude that possibility, but hydrodynamical simulations are required to
investigate how much angular momentum would be required, and if turbulent cloud
cores can contain such amounts of rotation.
An intriguing possibility is that the proximity of the neighbouring core is in
some way related to L1489 IRS' special nature. The core is 60'' (8400 AU)
away in projection, and located in front of L1489 IRS, likely by a distance of
comparable magnitude. Its systemic velocity is 0.4 km s-1 lower than that
of L1489 IRS itself, indicating that L1489 IRS and the core currently are
moving away from one another, at least in the direction along the line of
sight. Could the neighbouring core be feeding material onto the disc of
l1489 IRS? The velocity gradient is such that it merges smoothly with the
velocities in the core (see Fig. 7). This suggest that a physical
link between the core and the disc may exist. If the core feeds material onto
the disc, this could be significant source of angular momentum, thus keeping
the disc large. It is, however, not easy to understand why gas in the core
would be gravitationally bound to the L1489 IRS star, because of the
significant mass reservoir in the core itself of 2.9 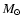 .
.
Another hypothesis is that L1489 IRS actually originated inside the core, but
has since migrated away. Its current velocity offset of 0.4 km s-1 is
sufficient to move it to its current location 60'' away in a few times
105 yr, the typical life time of an embedded YSO. We of course do not know
how far its offset along the line of sight is, or what its three-dimensional
velocity vector is like. Its line-of-sight velocity of 0.4 km s-1 is not
very different from the velocity dispersion of T Tauri stars and the turbulent
motions in cloud complexes. One could propose that L1489 IRS' natal core was a turbulent, transient structure, and that, once formed, the YSO migrated with
its gravitationally bound disc-like environment to a location outside the
surrounding cloud core, in effect "stripping'' the Class I object from most of
its envelope. In this scenario we would now be seeing the inner, rotating
Class I envelope around L1489 IRS unobscured by the outer envelope. This might
account for the different appearance of L1489 IRS.
This hypothesis can be tested in two ways. First, "normal'' Class I objects can
be studied at high spatial resolution and in dense gas tracers to explore if
the inner envelope is dominated by rotation on 1000 AU scales. Second,
hydrodynamical calculations can be used to explore on what time scales newly
formed YSOs can migrate away from their nascent cloud core. Searching for other
objects like L1489 IRS would also be very useful. Potential targets would
appear compact in sub-millimetre continuum images, but show strong emission
lines in dense gas tracers. L1489 IRS shows HCO+ lines with intensities of
several K, while a few tenths of K is more typical for T Tauri discs
(Thi et al. 2004).
5 Summary
We have made a two-dimensional axi-symmetric disc-like model of the Young
Stellar Object L1489 IRS. Line radiation transfer calculations produce
synthetic spectra which can be directly compared to observations. We show that
a flattened model gives a better description than a spherical one. Our model
also reproduces millimeter interferometric imaging, near-infrared scattered
light images, and CO ro-vibrational absorption spectroscopy.
We conclude further that the central star has a mass of 1.35 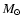 .
The
velocity vectors make an angle of 15
.
The
velocity vectors make an angle of 15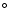 with the azimuthal direction. The
velocity field is dominated by rotation, while small but significant amount of
infall are present.
with the azimuthal direction. The
velocity field is dominated by rotation, while small but significant amount of
infall are present.
A neighouring cloud core is present next to L1489 IRS. This cloud is well
modelled by generic dark cloud parameters and we argue that it is likely
situated in front of L1489 IRS. We speculate that this core could be feeding
high angular-momentum material onto the L1489 IRS disc, explaining the unusual
size of this object. Another explanation could be that L1489 IRS is an ordinary
Class I object which has migrated away from its parental core, leaving it
surrounded by only its gravitationally bound inner envelope. If this is true,
L1489 IRS may provide valuable insight on the formation of protoplanetary
discs.
This paper shows that it is possible to construct a global model of a Young
Stellar Object that is able to fit observations on a wide range of spatial
scales. Single dish line observations provide enough information to make highly
detailed models of circumstellar structures, even on scales that are
unresolved. However, on scales as small as 100 AU, the description may no
longer be accurate, as evidenced by the near-infrared scattered light which
suggest additional flattening of the disc-like structure. Recently obtained
interferometer imaging with the Submillimeter Array may provide more insight on
the inner several hundred AU around L1489 IRS (Brinch et al., in prep.).
Acknowledgements
This research was supported by the European Research Training Network "The
Origin of Planetary Systems'' (PLANETS, contract number HPRN-CT-2002-00308). C.B.
is supported by the European Commission through the FP6 - Marie Curie Early
Stage Researcher Training programme. The research of MRH is supported by a VIDI
grant from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek. The
research of J.K.J. is supported by NASA Origins Grant NAG5-13050
- Adams,
F. C., Shu, F. H., & Lada, C. J. 1988, ApJ, 326,
865 [NASA ADS] [CrossRef]
- André, P.,
Ward-Thompson, D., & Motte, F. 1996, A&A, 314, 625 [NASA ADS] (In the text)
- André, P.,
Ward-Thompson, D., & Barsony, M. 2000, Protostars and
Planets IV, 59
(In the text)
- Boogert,
A. C. A., Hogerheijde, M. R., & Blake,
G. A. 2002, ApJ, 568, 761 [NASA ADS] [CrossRef] (In the text)
-
Dullemond, C. P., & Dominik, C. 2004, A&A, 417,
159 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Dullemond, C. P., & Turolla, R. 2000, A&A, 360,
1187 [NASA ADS] (In the text)
-
Gregersen, E. M., & Evans, N. J. 2000, ApJ, 538,
260 [NASA ADS] [CrossRef]
-
Guilloteau, S., & Dutrey, A. 1998, A&A, 339, 467 [NASA ADS]
-
Hogerheijde, M. R. 2001, ApJ, 553, 618 [NASA ADS] [CrossRef] (In the text)
-
Hogerheijde, M. R., & Sandell, G. 2000, ApJ, 534, 880 [NASA ADS] [CrossRef] (In the text)
-
Hogerheijde, M. R., & van der Tak, F. F. S.
2000, A&A, 362, 697 [NASA ADS] (In the text)
-
Hogerheijde, M. R., van Dishoeck, E. F., Blake,
G. A., & van Langevelde, H. J. 1997, ApJ, 489,
293 [NASA ADS] [CrossRef] (In the text)
-
Hogerheijde, M. R., van Dishoeck, E. F., Blake,
G. A., & van Langevelde, H. J. 1998, ApJ, 502,
315 [NASA ADS] [CrossRef] (In the text)
-
Jørgensen, J. K., Schöier, F. L., &
van Dishoeck, E. F. 2002, A&A, 389, 908 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Jørgensen, J. K., Schöier, F. L., &
van Dishoeck, E. F. 2004, A&A, 416, 603 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kenyon,
S. J., Calvet, N., & Hartmann, L. 1993a, ApJ, 414,
676 [NASA ADS] [CrossRef] (In the text)
- Kenyon,
S. J., Whitney, B. A., Gomez, M., & Hartmann, L.
1993b, ApJ, 414, 773 [NASA ADS] [CrossRef] (In the text)
- Kiang, T. 1966,
Z. Astrophys., 64, 433 [NASA ADS] (In the text)
- Koerner,
D. W., & Sargent, A. I. 1995, AJ, 109, 2138 [NASA ADS] [CrossRef]
- Lada, C. J.,
& Wilking, B. A. 1984, ApJ, 287, 610 [NASA ADS] [CrossRef] (In the text)
- Lin, S.-Y., Ohashi,
N., Lim, J., et al. 2006, ApJ, 645, 1297 [NASA ADS] [CrossRef]
- Lizano, S.,
& Shu, F. H. 1989, ApJ, 342, 834 [NASA ADS] [CrossRef]
- Mardones,
D., Myers, P. C., Tafalla, M., et al. 1997, ApJ, 489,
719 [NASA ADS] [CrossRef]
- Myers,
P. C., Fuller, G. A., Mathieu, R. D., et al.
1987, ApJ, 319, 340 [NASA ADS] [CrossRef] (In the text)
- Nenkova, M.,
Ivezic, Z., & Elitzur, M. 1999, LPI Contributions, 969, 20 [NASA ADS] (In the text)
-
Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] (In the text)
- Padgett,
D. L., Brandner, W., Stapelfeldt, K. R., et al.
1999, AJ, 117, 1490 [NASA ADS] [CrossRef] (In the text)
- Piétu, V.,
Guilloteau, S., & Dutrey, A. 2005, A&A, 443, 945 [NASA ADS] [CrossRef] [EDP Sciences]
- Reipurth,
B., Jewitt, D., & Keil, K., ed. 2006, in press, Protostars
and Planets V (University of Arizona Press)
(In the text)
- Schöier,
F. L., van der Tak, F. F. S., van Dishoeck,
E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Shu, F. H. 1977,
ApJ, 214, 488 [NASA ADS] [CrossRef]
- Simon, M.,
Dutrey, A., & Guilloteau, S. 2000, ApJ, 545, 1034 [NASA ADS] [CrossRef]
- Stahler,
S. W. 1988, ApJ, 332, 804 [NASA ADS] [CrossRef] (In the text)
-
Stamatellos, D., Whitworth, A. P., André, P., &
Ward-Thompson, D. 2004, A&A, 420, 1009 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Thi, W.-F., van
Zadelhoff, G.-J., & van Dishoeck, E. F. 2004,
A&A, 425, 955 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Ward-Thompson, D., & Buckley, H. D. 2001, MNRAS, 327,
955 [NASA ADS] [CrossRef] (In the text)
- Wilson,
T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS]
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=16.15cm,clip]{5473f01.ps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg11.gif)
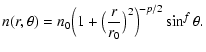
![\begin{figure}
\par\includegraphics[width=8.05cm,clip]{5473f02.ps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg23.gif)
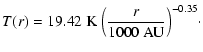
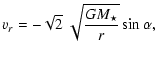
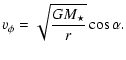
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{5473f03.eps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg34.gif)
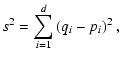
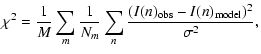
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{5473f04.ps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=16.35cm,clip]{5473f05.ps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg42.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{5473f06.eps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg55.gif)
![\begin{figure}
\par\includegraphics[height=7.1cm,width=7.4cm,clip]{5473f07.eps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{5473f08.eps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg57.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5473f09.ps}\end{figure}](/articles/aa/full/2007/03/aa5473-06/Timg60.gif)