A&A 461, 1121-1125 (2007)
DOI: 10.1051/0004-6361:20064920
A study of CME and type II shock kinematics based on coronal density measurement
K.-S. Cho1,2 - J. Lee2 - Y.-J. Moon1 - M. Dryer3,4 - S.-C. Bong1 - Y.-H. Kim1 -
Y. D. Park1
1 - Korea Astronomy and Space Science Institute,
Hwaamdong, Yuseong-Gu, Daejeon, 305-348, Korea
2 - Center for
Solar-Terrestrial Research, New Jersey Institute of Technology,
Newark, NJ 07102, USA
3 -
NOAA Space Environment Center, 325 Broadway,
Boulder, CO 80303, USA
4 - Exploration Physics
International, Inc., Huntsville, AL 35806, USA
Received 27 January 2006 / Accepted 5 September 2006
Abstract
Aims. The aim of this paper is to determine location and speed of a coronal shock from a type II burst spectrum without relying on any coronal density model, and to use the result to discuss the relationship between the type II burst and Coronal Mass Ejection (CME).
Methods. This study is made for the 2004 August 18 solar eruption observed by Green Bank Solar Radio Burst Spectrometer (GBSRBS) and a limb CME/streamer simultaneously detected by Mauna Loa Solar Observatory (MLSO) MK4 coronameter. We determine the background density distribution over the area of interest by inverting the MLSO MK4 polarization map taken just before the CME onset. Using the two-dimensional density distribution and the type II emission frequencies, we calculate the type II shock heights along several radial directions selected to encompass the entire position angles of the CME. We then compare these emission heights with those of the CME to determine at which position angle the type II burst propagated. Along the most plausible position angle, we finally determine the height and speed of the shock as functions of time.
Results. It turns out that the type II emission height calculated along a southern streamer best agrees to the observed height of the CME flank. Along this region, both the shock and CME moved at a speed ranging from 800 to 600 km
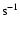 .
We also found that the streamer boundary already had enhanced density compared to other parts before the CME and formed a low Alfvénic region.
.
We also found that the streamer boundary already had enhanced density compared to other parts before the CME and formed a low Alfvénic region.
Conclusions. We therefore conclude that the type II burst was generated at the interface of the CME flank and the streamer, as favorable for the shock formation.
Key words: shock waves - Sun: coronal mass ejections (CMEs) - Sun: radio radiation - Sun: corona - polarization - methods: observational
Type II radio bursts usually appear in a form of two frequency bands
drifting with time, which correspond to the local plasma frequency
and its harmonic, and are an important tracer for shock waves
propagating away from the sun (Wild & McCready 1950). From a
typical density distribution we can infer that metric type II bursts
are generated in the low corona, 1.2-2.5 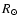 ,
and
deca-hecto-kilometric type II bursts, in the interplanetary space.
It is now agreed that decametric and longer wavelength type II
bursts are due to Coronal Mass Ejections (CMEs), but the association
of the metric type II bursts with CMEs remains as controversial
(Gopalswamy et al. 1998; Cliver et al. 1999). Classen &
Aurass (2002) suggested that type II emission can be generated not
only by CME shocks but also by the flare-produced shocks. In
occasional radio imaging observations, type II sources usually
appear broadly along the outer edge of the CMEs (e.g., Maia et al.
2000), but in some cases, type II bursts were found near the CME flank (e.g., Gary et al. 1984; Gopalswamy et al. 1997). It was also
proposed that the association between metric type II bursts and CMEs
depends on the local Alfvén speed as well as on CME energetics (Gopalswamy et al. 2001a, 2005).
,
and
deca-hecto-kilometric type II bursts, in the interplanetary space.
It is now agreed that decametric and longer wavelength type II
bursts are due to Coronal Mass Ejections (CMEs), but the association
of the metric type II bursts with CMEs remains as controversial
(Gopalswamy et al. 1998; Cliver et al. 1999). Classen &
Aurass (2002) suggested that type II emission can be generated not
only by CME shocks but also by the flare-produced shocks. In
occasional radio imaging observations, type II sources usually
appear broadly along the outer edge of the CMEs (e.g., Maia et al.
2000), but in some cases, type II bursts were found near the CME flank (e.g., Gary et al. 1984; Gopalswamy et al. 1997). It was also
proposed that the association between metric type II bursts and CMEs
depends on the local Alfvén speed as well as on CME energetics (Gopalswamy et al. 2001a, 2005).
In this paper, we present an analysis of an event that is designed
to trace the type II burst from its generation in the low corona.
Study of this single event would not entirely resolve the
long-standing debate over the origin of all type II bursts. We
however believe that the present dataset and our new strategy have
several advantages to offer an unusual insight into the origin of
type II bursts. The advantages are as follows.
First, recent studies of CME dynamics have mostly used SOHO/LASCO C2
and C3 data, which provides excellent white light images in 2-32 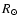 .
However type II shocks are believed to form in the
lower corona, 1.2-2.5
.
However type II shocks are believed to form in the
lower corona, 1.2-2.5 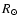 ,
and one has to extrapolate the
CME dynamics measured by LASCO observations back into the low corona
typically assuming constant speed (e.g., Cho et al. 2003; Lara et al. 2003; Shanmugaraju et al. 2003). Such extrapolation is not
desirable not only because it introduces additional uncertainty but
because the bow shock surrounding a CME is not well represented by a
single height at any given instant. We also note that CME leading
edge is found at 2.2
,
and one has to extrapolate the
CME dynamics measured by LASCO observations back into the low corona
typically assuming constant speed (e.g., Cho et al. 2003; Lara et al. 2003; Shanmugaraju et al. 2003). Such extrapolation is not
desirable not only because it introduces additional uncertainty but
because the bow shock surrounding a CME is not well represented by a
single height at any given instant. We also note that CME leading
edge is found at 2.2 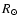 on average at the time of type II
onset, which is just at the inner edge of the LASCO FOV (see
Gopalswamy et al. 2005). To avoid these problems, we use the MK4
coronameter of Mauna Loa Solar Observatory (MLSO) to directly see
the CME's kinematics in the type II formation region (<
on average at the time of type II
onset, which is just at the inner edge of the LASCO FOV (see
Gopalswamy et al. 2005). To avoid these problems, we use the MK4
coronameter of Mauna Loa Solar Observatory (MLSO) to directly see
the CME's kinematics in the type II formation region (<
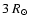 ). The coronameter also has a high time cadence (3 min) and thus is expected to provide us with near-simultaneous
data of CME kinematics corresponding to the type II emission.
). The coronameter also has a high time cadence (3 min) and thus is expected to provide us with near-simultaneous
data of CME kinematics corresponding to the type II emission.
Second, most studies have used coronal density models in order to
convert the frequencies of type II spectra to the height of the
shock (Robinson & Stewart 1985; Thompson et al.
1995). Use of a specific density model, however, leaves ambiguity,
not because the density model is inaccurate, but because the real
density distribution can vary with time and location (Bemporad et al. 2003; Guhathakurta & Fisher 1998; Parenti et al. 2000). In the
present study, we will estimate the coronal density using the
polarization brightness data of MLSO MK4 coronameter to avoid the
ambiguity introduced by using a fixed density model. A previous
attempt to directly measure the density was made by Mancuso et al.
(2003) who used SOHO Ultra Violet Coronagraph Spectrometer (UVCS)
observations of the O VI doublet line to estimate type II shock
speeds in the range from 1.5 to 2.3 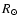 .
.
Third, we argue that the coincidence of type II bursts with CMEs in
terms of their onset times or speeds is insufficient evidence for
identifying the origin of type II bursts. As an extreme case, we
consider it possible that the flare, CME, and type II burst can
occur almost simultaneously but at different places within the
active region. As another, the CME may expand maintaining its shape
so that the speed at the CME front may not be much different from
the speed at the flank. In both cases we cannot locate the type II
bursts with the timing or speed measurement alone. To resolve this
ambiguity, the density distribution should be known, at least, in
two-dimensional space so that we can distinguish between the flare
site, CME front, and CME flank. In this regard, neither a density
model-based result (usually given as a function of solar radius) nor
a spectrometer-based result (usually one dimensional density
distribution not in a radial direction) would help. Use of a
two-dimensional polarization map is our advantage compared with
other works.
In summary, we expect that the present dataset will allow to locate
the type II burst source on the two dimensional plane without
relying on the extrapolation of CME dynamics and density models, and
that such result will help to resolve the ambiguity about the origin
of the type II burst. Plan of this paper is as follows: in Sect. 2, we describe the radio and white-light observations. In Sect. 3,
we present the result of the density measurement, location of the
CME and the type II shock, and speed measurement. Finally, a
conclusion is given in Sect. 4.
We study a CME event and the associated type II burst that occurred
on 2004 August 18 mainly using the MLSO coronameter and Green Bank
Solar Radio Burst Spectrometer (GBSRBS). The associated flare
occurred at S14W90 and was classified as a GOES class X1.8 flare.
The flare started at 17:30 UT and peaked at 17:40 UT with a duration
time of 25 min.
The MK4 coronameter produces white-light brightness and
polarization maps every 3 min in the wavelength range from 700
to 950 nm with a field of view from 1.08 to 2.85 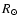 (Elmore
et al. 2003). We use the enhanced images available through the
MLSO's
website
(Elmore
et al. 2003). We use the enhanced images available through the
MLSO's
website![[*]](/icons/foot_motif.gif) that are produced by applying an artificial vignetting function to
the polarization brightness data. The angular and pixel resolutions
of the MK4 coronameter are about 20'' and 5.93'', respectively.
that are produced by applying an artificial vignetting function to
the polarization brightness data. The angular and pixel resolutions
of the MK4 coronameter are about 20'' and 5.93'', respectively.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4920fig1.eps}
\end{figure}](/articles/aa/full/2007/03/aa4920-06/Timg8.gif) |
Figure 1:
Vignetted MK4 negative images of
the CME on 2004 August 18. The MK4 field of view is from 1.08 to 2.85 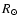 .
Arrows indicate the CME heights measured along two
dotted lines of the CME nose ( .
Arrows indicate the CME heights measured along two
dotted lines of the CME nose (
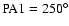 )
and CME flank
( )
and CME flank
(
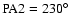 )
near the helmet streamer, respectively. )
near the helmet streamer, respectively. |
| Open with DEXTER |
Figure 1 shows the vignetted MK4 CME images taken at 17:44 UT (left
panel) and 17:50 UT (right panel), respectively. We set two dotted
guide lines, PA1 and PA2, to indicate the CME nose and flank,
respectively, marking the heights of the CME front along each
position angle with arrows. It is obvious to our eyes that the CME
nose moved out along the position angle PA1. The height of the nose
was about 2.0 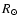 at 17:44 UT and
at 17:44 UT and 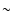 2.3
2.3 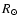 at 17:50 UT. It was a little bit subtle to locate the CME flank at PA2,
because the half width of the whole CME is about 30
at 17:50 UT. It was a little bit subtle to locate the CME flank at PA2,
because the half width of the whole CME is about 30 and PA2
is only 20
and PA2
is only 20 away from PA1. It is however clear from a movie1 that this CME was interacting with the southern streamer
at the angle PA2. We consider that the part of CME away from its
nose and interacting with the nearby streamer should correspond to
the CME flank. This is why we believe that PA2 should correspond to
the southern flank of the CME. Since there was a data gap between 17:32 UT and 17:44 UT in MLSO/MK4 observation, the CME was first
seen only at 17:44 UT in the MK4 field of view.
away from PA1. It is however clear from a movie1 that this CME was interacting with the southern streamer
at the angle PA2. We consider that the part of CME away from its
nose and interacting with the nearby streamer should correspond to
the CME flank. This is why we believe that PA2 should correspond to
the southern flank of the CME. Since there was a data gap between 17:32 UT and 17:44 UT in MLSO/MK4 observation, the CME was first
seen only at 17:44 UT in the MK4 field of view.
Table 1:
Kinematics of CME and type II shock.
The GBSRBS is located in a radio quiet zone at NRAO's Green Bank
site, and produces high quality radio dynamic spectra with low noise
interferences in the range from 18 MHz to 70 MHz with 565 frequency
channels with 1 s time resolution (White et al. 2005). The low noise is an
advantage for our purpose of estimating the type II burst
frequencies. We use the background subtracted dynamic spectrum,
which is available at the
website![[*]](/icons/foot_motif.gif) of Green Bank
observatory.
of Green Bank
observatory.
Figure 2 shows the GBSRBS dynamic spectrum together with lightcurves
of GOES 0.5-4 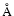 flux (dashed line) and total radio flux
integrated from 18 MHz to 70 MHz (solid line). The type II burst
started at 17:44 UT, just at the first appearance time of the CME in
the MK4 coronameter. While the harmonic band of the type II burst
started at 17:46 UT and lasted for about 40 min from above 70 MHz to 20 MHz, the fundamental band has a frequency drifting from
about 60 MHz at 17:44 UT to 18 MHz at 17:58 UT.
flux (dashed line) and total radio flux
integrated from 18 MHz to 70 MHz (solid line). The type II burst
started at 17:44 UT, just at the first appearance time of the CME in
the MK4 coronameter. While the harmonic band of the type II burst
started at 17:46 UT and lasted for about 40 min from above 70 MHz to 20 MHz, the fundamental band has a frequency drifting from
about 60 MHz at 17:44 UT to 18 MHz at 17:58 UT.
The CME first appears on the MLSO images at 17:44 UT. The onset time
of the CME (i.e. the onset time of the eruption leading to the CME)
is estimated to be 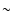 17:32 UT if we extrapolate the height-time
plot to the solar surface using the height 2.06
17:32 UT if we extrapolate the height-time
plot to the solar surface using the height 2.06 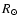 and the
speed 878 km
and the
speed 878 km
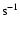 of the CME at 17:46 UT (see Table 1).
This well agrees to the onset time of the eruptive prominence (17:32-17:34 UT) as we found in BBSO H
of the CME at 17:46 UT (see Table 1).
This well agrees to the onset time of the eruptive prominence (17:32-17:34 UT) as we found in BBSO H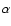 and TRACE EUV (1600 Å)
images. On the other hand, the starting time of type II burst rather
coincides with the first appearance of the CME in MK4 field of view.
and TRACE EUV (1600 Å)
images. On the other hand, the starting time of type II burst rather
coincides with the first appearance of the CME in MK4 field of view.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4920fig2.eps} \end{figure}](/articles/aa/full/2007/03/aa4920-06/Timg17.gif) |
Figure 2:
Dynamic spectrum of the type II burst observed by the GBSRBS on 2004 August 18.
Dotted white line in the upper panel indicates the frequency drift
of the fundamental emission band of the burst. The dashed and solid
lines in lower panel denote the GOES X-ray flux and total radio flux
curve, respectively. |
| Open with DEXTER |
We derive the coronal density distribution by inversion of polarized
brightness measurement (van de Hulst 1950) using the LASCO IDL
routine (pb_inverter.pro) in the SolarSoft
package![[*]](/icons/foot_motif.gif) . Detailed
description of the routine can be found in Hayes et al. (2001). The left panel of Fig. 3 shows the selected MLSO
coronal polarization brightness image. This data was taken at 17:06 UT, before the CME onset time (17:32-17:34 UT), and thus
represents the background coronal density. The lines denoted with a to h are the selected position angles ranging from 219
. Detailed
description of the routine can be found in Hayes et al. (2001). The left panel of Fig. 3 shows the selected MLSO
coronal polarization brightness image. This data was taken at 17:06 UT, before the CME onset time (17:32-17:34 UT), and thus
represents the background coronal density. The lines denoted with a to h are the selected position angles ranging from 219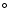 to 288
to 288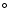 that encompass the entire area later
swept by the CME. Shown in the right panel is a difference image
between two MLSO images at 17:06 UT and 17:03 UT. Since the
difference image exhibits no noticeable plasma motion, we assume
that our density measurement will not be contaminated by any mass
motion.
that encompass the entire area later
swept by the CME. Shown in the right panel is a difference image
between two MLSO images at 17:06 UT and 17:03 UT. Since the
difference image exhibits no noticeable plasma motion, we assume
that our density measurement will not be contaminated by any mass
motion.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4920fig3.eps} \end{figure}](/articles/aa/full/2007/03/aa4920-06/Timg18.gif) |
Figure 3:
MLSO coronal polarization brightness data ( left) just before the CME event and its difference image ( right).
Coronal density was measured along the dotted lines at 9 position angles (a = 219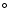 ,
b = 225 ,
b = 225 ,
c = 231 ,
c = 231 (PA2),
d = 237 (PA2),
d = 237 ,
e = 250 ,
e = 250 (PA1), f = 270 (PA1), f = 270 ,
g = 276 ,
g = 276 ,
g' = 282 ,
g' = 282 ,
and h = 288 ,
and h = 288 ,
respectively). ,
respectively). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4920fig4.eps}
\end{figure}](/articles/aa/full/2007/03/aa4920-06/Timg19.gif) |
Figure 4:
Measured coronal density
distributions along the position angles denoted in Fig. 3. The
distributions at the northern flank of the CME at 276 (g)
and 282 (g)
and 282 (g') are similar to each other. Dotted lines
denoted as NK1 and NK2 represent the one- and two-fold Newkirk
density models, respectively. (g') are similar to each other. Dotted lines
denoted as NK1 and NK2 represent the one- and two-fold Newkirk
density models, respectively. |
| Open with DEXTER |
Figure 4 shows the measured density distributions along the selected
position angles (defined in Fig. 3) by using an averaged
polarization data taken at 17:06 UT, which is usually acquired once
a day from 5 sequential images. As comparison, we also plot density
distributions from a popular model, the one and two-fold Newkirk
models (Newkirk 1961) denoted as NK1 and NK2, respectively. As
shown in the figure, the derived electron densities near southern
helmet streamer (b, c, d) are most enhanced, lying between one-fold
(NK1) and two-fold (NK2) Newkirk models at some heights (1.6-2.2 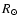 ). The density found along the position angle (e),
that is swept by CME nose is less than NK1 at height above 1.8
). The density found along the position angle (e),
that is swept by CME nose is less than NK1 at height above 1.8 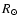 .
The northern streamer region (f, g, h) shows the
least amount of density in the high corona.
.
The northern streamer region (f, g, h) shows the
least amount of density in the high corona.
We note that another small CME had occurred before the CME under
current investigation. According to LASCO data it first appeared at
17:30 UT at a height of 2.36 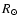 near the southern streamer,
and later (>18:05 UT) was cannibalized by our CME, similar to the
CME interaction case described by Gopalswamy et al. (2001b, 2004).
Depending on how significantly the preceding CME had modified the
background density at 17:06 UT, the density derived above may or may
not correctly represent the background density at the type II shock
forming time (17:44 UT). We thus carefully re-examined all MLSO MK4
difference images between 17:06 and 17:32 UT to find any CME
signature near the active region (S14W90). However, we detected no
obvious feature of the preceding CME in all difference images.
Perhaps the intensity of the preceding CME was too low to be
detected by the MLSO MK4 coronameter. Note that MK4 is considerably
less sensitive to CMEs than LASCO because MK4 measures polarization
brightness of photosphere radiation scattered by free electrons in
the corona, while LASCO measures coronal radiation in total
intensity. While the CME itself was not detected in MLSO images, the
density variation caused by that CME could have affected the MLSO
images. We thus determine the density distribution at the
CME-streamer interface (PA2 in Fig. 3) by using all available images
between 17:06 and 17:32 UT and then compare to the density profile
that is estimated by using the averaged polarization data taken at
17:06 UT. We found about 20% density enhancement after 17:15 UT in
the range between 1.4 and 2.2
near the southern streamer,
and later (>18:05 UT) was cannibalized by our CME, similar to the
CME interaction case described by Gopalswamy et al. (2001b, 2004).
Depending on how significantly the preceding CME had modified the
background density at 17:06 UT, the density derived above may or may
not correctly represent the background density at the type II shock
forming time (17:44 UT). We thus carefully re-examined all MLSO MK4
difference images between 17:06 and 17:32 UT to find any CME
signature near the active region (S14W90). However, we detected no
obvious feature of the preceding CME in all difference images.
Perhaps the intensity of the preceding CME was too low to be
detected by the MLSO MK4 coronameter. Note that MK4 is considerably
less sensitive to CMEs than LASCO because MK4 measures polarization
brightness of photosphere radiation scattered by free electrons in
the corona, while LASCO measures coronal radiation in total
intensity. While the CME itself was not detected in MLSO images, the
density variation caused by that CME could have affected the MLSO
images. We thus determine the density distribution at the
CME-streamer interface (PA2 in Fig. 3) by using all available images
between 17:06 and 17:32 UT and then compare to the density profile
that is estimated by using the averaged polarization data taken at
17:06 UT. We found about 20% density enhancement after 17:15 UT in
the range between 1.4 and 2.2 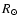 due to the preceding CME.
This time-dependent density is taken into account in the next
section.
due to the preceding CME.
This time-dependent density is taken into account in the next
section.
We use the measured density distributions (Fig. 4) in converting the
observed type II frequencies to the shock heights. We first measure
the emission frequencies in the fundamental band (the white dotted
line in dynamic spectrum of Fig. 2), and estimate the corresponding
electron densities under the assumption that the radio emission is
generated at plasma frequency (
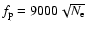 [Hz]) due
to the disturbed electrons by the type II shock. The emission
heights are deduced from the density function determined from a
polynomial fitting of the measured density profiles (Fig. 4). We
measure the CME heights using the vignetted white-light images from
MLSO, at its nose and flank (i.e., along the dotted lines in Fig. 1
from 17:44 UT to 17:53 UT). The measurement error for the CME height, as deduced from 10 trial measurements of a CME position in
the MK4 vignetted image, is about 0.01
[Hz]) due
to the disturbed electrons by the type II shock. The emission
heights are deduced from the density function determined from a
polynomial fitting of the measured density profiles (Fig. 4). We
measure the CME heights using the vignetted white-light images from
MLSO, at its nose and flank (i.e., along the dotted lines in Fig. 1
from 17:44 UT to 17:53 UT). The measurement error for the CME height, as deduced from 10 trial measurements of a CME position in
the MK4 vignetted image, is about 0.01 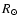 (about 2-pixel)
and that of speed is about 95 km
(about 2-pixel)
and that of speed is about 95 km
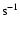 ,
respectively.
,
respectively.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{4920fig5CMJN.eps}
\end{figure}](/articles/aa/full/2007/03/aa4920-06/Timg21.gif) |
Figure 5:
Height-time plot of CME
front (triangles) and CME flank (filled circles). Each line denotes
the coronal shock height estimated from the radio data and the
measured coronal density distribution along the position angles.
Dotted line represents the shock height estimated by assuming 20%
density enhancement along PA2 during the period between 17:15 and 17:32 UT. |
| Open with DEXTER |
Figure 5 shows the type II shock heights calculated along the
selected position angles (solid lines) in comparison with the CME
heights (symbols). Triangles and filled circles correspond to the
CME front and the CME flank, respectively. The lines e and c
correspond to the shock heights estimated along the CME front (PA1
in Fig. 3) and the southern helmet streamer (PA2 in Fig. 3),
respectively. For the first  10 min, the CME front
propagated from 1.9 to 2.5
10 min, the CME front
propagated from 1.9 to 2.5 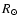 and the flank followed it by
a nearly constant distance (about 0.3
and the flank followed it by
a nearly constant distance (about 0.3 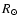 ). It appears that
the type II shock heights, estimated from the density profile
measured near the southern helmet streamer (c, b, d) contacting with
the CME, are consistent with the heights of the southern CME flank
(filled circles). All the others show a large deviation from both
CME front (triangles) and CME flank (filled circles). We thus regard
that type II burst was generated at the place where the CME
interacts with the streamer at the southern flank.
). It appears that
the type II shock heights, estimated from the density profile
measured near the southern helmet streamer (c, b, d) contacting with
the CME, are consistent with the heights of the southern CME flank
(filled circles). All the others show a large deviation from both
CME front (triangles) and CME flank (filled circles). We thus regard
that type II burst was generated at the place where the CME
interacts with the streamer at the southern flank.
The dotted line in Fig. 5 represents the shock height when we take
into account the time dependent density enhancement. In this case
the type II shock heights better agree with those of the southern
CME flank. This suggests that there could indeed be additional
density enhancement (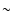 20%) along the CME flank due to the
passage of the preceding CME along the streamer.
20%) along the CME flank due to the
passage of the preceding CME along the streamer.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{4920fig6.eps}
\end{figure}](/articles/aa/full/2007/03/aa4920-06/Timg22.gif) |
Figure 6:
Speed comparison among
coronal shock (solid line) estimated density profile (c) along
southern CME flank, CME front (triangles), southern CME flank (filled
circles). The error bars indicates the uncertainty (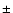 95 km 95 km
 )
of CME speed due to measurement errors (2-pixels) in
MK 4 image. )
of CME speed due to measurement errors (2-pixels) in
MK 4 image. |
| Open with DEXTER |
As we mentioned in Sect. 1, imaging comparison is the best way to
inspect the relationship between type II bursts and CMEs, but in its
absence, one has to use density measurements. In Fig. 6 we compare
the speed of the type II burst with that of the CME. Since the
heights of the type II source and CME flank coincide, their speeds
also agree to each other within the error range. Note however that
the CME front also has similar speed, because the CME flank followed
the front by a nearly constant distance behind. It is thus our view,
based on this single event, that the speed and timing alone cannot
tell at which part of the CME the type II emission is generated, and
that locating ability (such as in Fig. 5) is necessary to address
the origin of type II bursts.
Another noteworthy thing in this figure is that the type II speed
tends to be nearly constant (or slowly decreasing) with time. This
behavior is inconsistent with that of the flare waves associated
with type II bursts, e.g., Moreton waves. Usually the Moreton waves
show a strong deceleration at about -1500 m
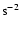 ,
which
is thought as they are generated by initially strong shocks by
flares (e.g., blast waves) and then decay to fast mode waves with
strong deceleration (Warmuth et al. 2004a,b). The nearly constant
shock speed shown in Fig. 6 is rather consistent with the behavior
of a piston driven shock by a CME (Leblanc et al. 2001).
,
which
is thought as they are generated by initially strong shocks by
flares (e.g., blast waves) and then decay to fast mode waves with
strong deceleration (Warmuth et al. 2004a,b). The nearly constant
shock speed shown in Fig. 6 is rather consistent with the behavior
of a piston driven shock by a CME (Leblanc et al. 2001).
Table 1 summarizes the kinematics of the CME and type II shock. As
mentioned, the speeds of the CME flank and type II shock are
comparable to each other within the MK4 CME measurement error (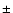 95 km
95 km
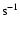 ). A mean speed of type II shock is about 650 km
). A mean speed of type II shock is about 650 km
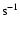 that is similar to those of CME flank (720 km
that is similar to those of CME flank (720 km
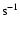 )
and CME front (740 km
)
and CME front (740 km
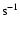 ). Both the type II shock speed and the CME flank speed show a similar tendency of
weak deceleration. The local Alfvén speeds are calculated
by adopting the active region magnetic field model (Dulk & Mclean
1978), which was first used by the Gopalswamy et al. (2001a) to
estimate Alfvén speed profile, together with the measured
MK4 density distributions along the CME front and the CME flank,
respectively (Fig. 4). It appears that the Alfvénic Mach
number is 1.2 at the CME front and 2.0 at the CME flank, suggesting
that the latter is more favorable for generating the shock.
). Both the type II shock speed and the CME flank speed show a similar tendency of
weak deceleration. The local Alfvén speeds are calculated
by adopting the active region magnetic field model (Dulk & Mclean
1978), which was first used by the Gopalswamy et al. (2001a) to
estimate Alfvén speed profile, together with the measured
MK4 density distributions along the CME front and the CME flank,
respectively (Fig. 4). It appears that the Alfvénic Mach
number is 1.2 at the CME front and 2.0 at the CME flank, suggesting
that the latter is more favorable for generating the shock.
In this paper, we analyzed an event of metric type II burst and a
CME that occurred on 2004 August 18 to understand their
relationship. We excluded from the beginning the possibility of
flare produced type II shock because of the inconsistent timing
between the type II burst and the flare impulsive phase. It is later
found through the analysis that the shock speed is nearly constant,
which is also against the behavior of shock speed found for the
flare associated events (Warmuth et al. 2004a,b).
Our analysis was focused on not only whether the type II bursts is
related to the CME, but at which part of the CME the type II burst
was generated. Our technique used for this purpose is to compare,
for agreement, the densities inferred from the GBSRBS type II
spectrum with those calculated from the two-dimensional polarization
map of MLSO/MK4 coronameter. It turns out that this technique based
on 2D density measurement is sensitive enough to locate the type II
emission source within the width of the CME 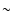 30
30 .
Of
course, this locating capability of our technique is not only
limited by the pixel resolution of the MLSO coronameter, but depends
on the density inhomogeneity in the region of interest. If the
electrons were distributed in the corona with real radial symmetry,
our technique would make little difference from other works based on
one-dimensional density models. In this event, the presence of a
streamer caused a nonradial density contrast by a sufficient amount,
and we were able to distinguish whether the type II burst is
generated at the CME nose or at its flank (
.
Of
course, this locating capability of our technique is not only
limited by the pixel resolution of the MLSO coronameter, but depends
on the density inhomogeneity in the region of interest. If the
electrons were distributed in the corona with real radial symmetry,
our technique would make little difference from other works based on
one-dimensional density models. In this event, the presence of a
streamer caused a nonradial density contrast by a sufficient amount,
and we were able to distinguish whether the type II burst is
generated at the CME nose or at its flank (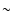 20
20 away
from the nose).
away
from the nose).
Our result that the type II burst was generated along the flank of
the CME interacting with the adjacent streamer agrees to the earlier
speculations presented by Classen & Aurass (2002), Reiner et al.
(2003), Mancuso & Raymond (2004), and Cho et al. (2005). A
difference between the latter studies and ours is that we here
attempt to locate the shock within a partial area of the CME,
whereas in other studies the idea was inferred from inconsistent
locations of the CME front and the type II source based on a
one-dimensional density model. Not only the location but also the
nearly constant speed of the type II emission source found in this
study supports the existing idea that the type II shock could be
bow/piston driven by the top or the flanks of CMEs when they
interact with the high density structure of the corona.
We also found that the electron density along the southern streamer
was already more enhanced than other neighboring regions before
being swept by the CME. To be more specific, the density
distribution along the streamer is comparable to that of the
one-fold Newkirk model in the type II formation regions
(1.6 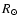 and 2.3
and 2.3 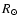 ), whereas at the other region
including northern streamer the density falls below the Newkirk
model. Such density contrast can lead to different
Alfvénic Mach numbers along the CME, although the speed of
the CME flank is comparable to that of the CME front (800 to 600 km
), whereas at the other region
including northern streamer the density falls below the Newkirk
model. Such density contrast can lead to different
Alfvénic Mach numbers along the CME, although the speed of
the CME flank is comparable to that of the CME front (800 to 600 km
 ). This CME speed is consistent with the average speed
of metric type II associated CMEs (Gopalswamy et al. 2005).
). This CME speed is consistent with the average speed
of metric type II associated CMEs (Gopalswamy et al. 2005).
We used an active region magnetic field model (Dulk & McClean 1978)
to estimate the Alfvénic Mach number of 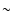 1.2 at the
CME nose and
1.2 at the
CME nose and 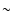 2 in the CME flank. This may account for
our result in that the CME flank's mass motion moves with a speed
that exceeds the local Alfvénic values and, thus, is
favorable for generating the type II shocks.
2 in the CME flank. This may account for
our result in that the CME flank's mass motion moves with a speed
that exceeds the local Alfvénic values and, thus, is
favorable for generating the type II shocks.
While the present result for a single event strongly supports the
scenario of the type II shock generation at the CME flank
interacting with the nearby streamer, a more extended study will be
required in order to draw a more definite conclusion on the
association between type II and CME.
Acknowledgements
The authors are very grateful to N. Gopalswamy for his valuable
comments and suggestions that help to improve the manuscript. We
thank Joan T. Burkepile and S. White for providing the MLSO/MK4 data
and GBSRBS data, respectively. K.S.C. gratefully acknowledges the help
of R. A. Howard in estimation of coronal density using MLSO pB data.
This work has been supported by the MOST funds (M1-0104-00-0059 and
M1-0407-00-0001) of the Korean Government. J.L. has been supported by
NSF under grant AST-0307670 to New Jersey Institute of Technology.
Y.J.M. and Y.D.P. were supported by the Korea Research Foundation
(KRF-2005-070-C00059) of the Korean Government. M.D. appreciates the
hospitality of the NOAA Space Environment Center during his emeritus
tenure.
- Bemporad,
A., Poletto, G., Suess, S. T., et al. 2003, ApJ, 593, 1146 [NASA ADS] [CrossRef] (In the text)
- Cho, K.-S., Moon,
Y.-J., Dryer, M., et al. 2003, J. Geophys. Res., 108(A12), SSH
8-1
(In the text)
- Cho, K.-S., Moon,
Y.-J., Dryer, M., et al. 2005, J. Geophys. Res., 110(A12),
A12101
(In the text)
- Classen, A.,
& Aurass, H. 2002, A&A, 384, 1098 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cliver, E. W.,
Webb, D. F., & Howard, R. A. 1999, Sol. Phys., 187, 89 [NASA ADS] [CrossRef] (In the text)
- Dulk, G. A., &
McLean, D. J. 1978, Sol. Phys., 57, 279 [NASA ADS] [CrossRef] (In the text)
- Elmore, D. F.,
Burkepile, J. T., Darnell, J. A., Lecinski, A. R., & Stanger,
A. L. 2003, Proc. SPIE, 4843
(In the text)
- Gary, D. E., Dulk,
G. A., House, L., et al. 1984, A&A, 134, 222 [NASA ADS] (In the text)
-
Gopalswamy, N., Kundu, M. R., Manoharan, P. K., et al. 1997, ApJ,
486, 1036 [NASA ADS] [CrossRef] (In the text)
-
Gopalswamy, N., Kaiser, M. L., Lepping, R. P., et al. 1998, J.
Geophys. Res., 103, 307 [NASA ADS] [CrossRef] (In the text)
-
Gopalswamy, N., Lara, A., Kaiser, M. L., & Bougeret, J.-L.
2001a, J. Geophys. Res., 106, 25261 [NASA ADS] [CrossRef] (In the text)
-
Gopalswamy, N., Yashiro, S., Kaiser, M. L., Howard, R. A., &
Bougeret, J.-L. 2001b, ApJ, 548, L91 [NASA ADS] [CrossRef] (In the text)
-
Gopalswamy, N., Yashiro, S., Krucker, S., Stenborg, G., &
Howard, R. A. 2004, J. Geophys. Res., 109, A12105 [CrossRef] (In the text)
-
Gopalswamy, N., Aguilar-Rodriguez, E., Yashiro, S., et al. 2005, J.
Geophys. Res., 110, A12 (In the text)
-
Guhathakurta, M., & Fisher, R. 1998, ApJ, 499, L215 [NASA ADS] [CrossRef] (In the text)
- Hayes, A. P.,
Vourlidas, A., & Howard, R. A. 2001, ApJ, 548, 1081 [NASA ADS] [CrossRef] (In the text)
- Lara, A.,
Gopalswamy, N., Nunes, S., Munoz, G., & Yashiro, S. 2003,
Geophys. Res. Lett., 30(12), 8016
(In the text)
- Leblanc, Y.,
Dulk, G. A., Vourlidas, A., & Bougeret, J.-L. 2001, J. Geophys.
Res., 160, 25, 301
(In the text)
- Maia, D., Pick, M.,
Vourlidas, A., & Howard, R. 2000, ApJ, 528, L49 [NASA ADS] [CrossRef] (In the text)
- Mancuso, S.,
& Raymond, J. C. 2004, A&A, 413, 363 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mancuso, S.,
Raymond, J. C., Kohl, J., Ko, Y.-K., & Wu, R. 2003, A&A,
400, 347 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Newkirk, G.
Jr. 1961, ApJ, 133, 983 [NASA ADS] [CrossRef] (In the text)
- Parenti, S.,
Bromage, B. J. I., Poletto, G., et al. 2000, A&A, 363, 800 [NASA ADS] (In the text)
- Reiner, M. J.,
Vourlidas, A., Cyr, O. C. St., et al. 2003, ApJ, 590, 533 [NASA ADS] [CrossRef] (In the text)
- Robinson,
R. D., & Stewart, R. T. 1985, Sol. Phys., 97, 145 [NASA ADS] [CrossRef] (In the text)
-
Shanmugaraju, A., Moon, Y.-J., Dryer, M., & Umapathy, S. 2003,
Sol. Phys., 215, 164 [NASA ADS] (In the text)
- Thompson,
R. J., Kennewell, J. A., & Prestage, N. P. 1995, Sol. Phys.,
166, 371 [NASA ADS] [CrossRef].
(In the text)
- van de Hulst, H.
C. 1950, Bull. Astron. Inst. Netherlands, 11 (410), 135
(In the text)
- Warmuth,
A., Vrsnak, B., Magdalenic, J. Hanslmeier, A., & Otruba, W.
2004a, A&A, 418, 1101 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Warmuth,
A., Vrsnak, B., Magdalenic, J., Hanslmeier, A., & Otruba, W.
2004b, A&A, 418, 1117 [NASA ADS] [CrossRef] [EDP Sciences]
- White, S. M.,
Bastian, T. S., Bradley, R., Parashare, C., & Wye, L. 2005, in
From Clark Lake to the Long Wavelength Array: Bill Erickson's Radio
Science, ed. N. E. Kassim, M. R. Perez, W. Junor, & P. A.
Henning, ASP Conf. Ser., 345, 176
- Wild, J. P., &
McCready, L. L. 1950, Austral. J. Sci. Res., A3, 387 [NASA ADS] (In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4920fig2.eps} \end{figure}](/articles/aa/full/2007/03/aa4920-06/Timg17.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4920fig4.eps}
\end{figure}](/articles/aa/full/2007/03/aa4920-06/Timg19.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{4920fig5CMJN.eps}
\end{figure}](/articles/aa/full/2007/03/aa4920-06/Timg21.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{4920fig6.eps}
\end{figure}](/articles/aa/full/2007/03/aa4920-06/Timg22.gif)