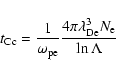A&A 461, 1127-1132 (2007)
DOI: 10.1051/0004-6361:20053736
Excitation of electrostatic fluctuations by jets in a flaring plasma
R. Miteva - G. Mann - C. Vocks - H. Aurass
Astrophysikalisches Institut Potsdam,
An der Sternwarte 16, 14482 Potsdam, Germany
Received 30 June 2005 / Accepted 6 September 2006
Abstract
Context. During magnetic reconnection as the proposed basic process of solar flares, hot high speed plasma streams (jets) are ejected from the reconnection site. Jets are sometimes associated with type III radio bursts as signatures of electron beams in the solar corona.
Aims. The interaction of such a jet with the surrounding coronal plasma is investigated concerning the generation of electrostatic fluctuations.
Methods. The conditions of excitations of such waves are studied in detail under coronal conditions by solving the linearized Vlasov-Maxwell equations.
Results. The interaction of a jet with the background plasma leads to an instability for a small range of jet speeds exciting electrostatic waves in the sense of the ion-acoustic mode. Electrons can be energized by their interaction with these electrostatic fluctuations. Such energetic electrons can be the source of type III radio bursts and/or non-thermal X-ray radiation as observed during solar flares.
Key words: waves - instabilities - acceleration of particles - Sun: flares - Sun: radio radiation
During solar flares stored magnetic field energy is suddenly
released and transferred into plasma heating, mass motions (e.g., jets and/or coronal mass ejections), energetic particles (e.g., electrons, protons, and heavy ions), and radiation
across the whole electromagnetic spectrum, i.e., from
radio waves up to 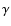 -rays (Heyvaerts
1981). It is commonly accepted that the process of magnetic
reconnection is responsible for this happening. If two
magnetic field lines with opposite directions approach
each other due to their photospheric footpoint motion, a current
sheet is established between them (see Fig. 1). If the electric
current exceeds a certain critical value, the anomalous resistivity is
suddenly increased by exciting plasma waves owing to various plasma
instabilities (see, e.g., Treumann & Baumjohann 1997). That
leads to the onset of magnetic reconnection. Due to the strong
curvature of the magnetic field lines after their reconnection, the
plasma is shooting away from the reconnection site leading to the
establishment of (sometimes oppositely directed) jets of hot
plasma (see Fig. 1). As already discussed by Yokoyama & Shibata
(1994, 1995), magnetic reconnection is the most probable mechanism
leading to the generation of the solar jets. For instance,
such jets are really seen in soft X-ray images from Yohkoh
(Shibata et al. 1992, 1994; Strong et al. 1992).
-rays (Heyvaerts
1981). It is commonly accepted that the process of magnetic
reconnection is responsible for this happening. If two
magnetic field lines with opposite directions approach
each other due to their photospheric footpoint motion, a current
sheet is established between them (see Fig. 1). If the electric
current exceeds a certain critical value, the anomalous resistivity is
suddenly increased by exciting plasma waves owing to various plasma
instabilities (see, e.g., Treumann & Baumjohann 1997). That
leads to the onset of magnetic reconnection. Due to the strong
curvature of the magnetic field lines after their reconnection, the
plasma is shooting away from the reconnection site leading to the
establishment of (sometimes oppositely directed) jets of hot
plasma (see Fig. 1). As already discussed by Yokoyama & Shibata
(1994, 1995), magnetic reconnection is the most probable mechanism
leading to the generation of the solar jets. For instance,
such jets are really seen in soft X-ray images from Yohkoh
(Shibata et al. 1992, 1994; Strong et al. 1992).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3736fig1.eps}
\end{figure}](/articles/aa/full/2007/03/aa3736-05/Timg8.gif) |
Figure 1:
Sketch of the magnetic field configuration possibly leading
to reconnection and, subsequently, to the establishment of
jets in the solar corona. The insert on the left-hand side
shows an enlargement of the magnetic field lines at the
reconnection site. |
| Open with DEXTER |
Aurass et al. (1994) reported on the first detection of
correlated type III radio bursts and plasma jets in the corona by
a comprehensive analysis of radio and soft X-ray data. Solar
type III radio bursts are usually regarded as the signature of
beams of supra-thermal electrons (Nelson & Melrose 1985). These
electron beams excite high frequency plasma (e.g., Langmuir) waves,
which convert into escaping radio waves by scattering at ion
density fluctuations and/or by coalescence with other plasma
waves. Thus, the radio emission takes place near the local
electron plasma frequency
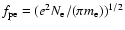 (e, elementary charge;
(e, elementary charge; 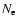 ,
electron number density;
,
electron number density;
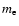 ,
electron mass) and/or its harmonics (Melrose 1985). Since
the electron plasma frequency depends on the electron number
density, the higher/lower frequencies are emitted in the lower/higher
corona, respectively, due to the gravitational stratification of the
solar atmosphere.
,
electron mass) and/or its harmonics (Melrose 1985). Since
the electron plasma frequency depends on the electron number
density, the higher/lower frequencies are emitted in the lower/higher
corona, respectively, due to the gravitational stratification of the
solar atmosphere.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{3736fig2.eps}
\end{figure}](/articles/aa/full/2007/03/aa3736-05/Timg12.gif) |
Figure 2:
Dynamic radio spectrum recorded by the radio spectralpolarimeter
(Mann et al. 1992) of the Astrophysical Institute Potsdam
in the frequency range 110-400 MHz. It shows an example
of a solar type III and U radio bursts. Further explanations
are given in Sect. 1. |
| Open with DEXTER |
An example of a solar type III radio burst
is presented in Fig. 2. It shows a dynamic radio spectrum in the
range 110-400 MHz. At first, a stripe of enhanced radio
emission starts near 350 MHz at 08:18:51 UT and rapidly drifts
towards lower frequencies down to 110 MHz. That is a typical
type III radio burst, which is considered to be an electron beam
traveling along open magnetic field lines outwards in the corona.
Another feature started near 300 MHz at 08:18:53 UT reached
230 MHz at 08:18:57 UT and turned back towards higher
frequencies. It reached 400 MHz at 08:19:00 UT. Such a feature
is called a type U radio burst. According our interpretation, it
should be considered as an electron beam traveling along closed
magnetic field lines in the corona. The dynamic radio spectrogram
indicates that both electron beams are generated near the same
place and time in the corona.
Pick et al. (1994) presented a joint observation from the soft
X-ray telescope (SXT) aboard Yohkoh and Nançay
multi-frequency radioheliograph. A type III/U radio burst has
been used as a tracer of a coronal structure and its subsequent
development. Kundu et al. (1994, 1995) looked for non-thermal
radio emission at metric wavelengths from flaring solar X-ray
bright points (XBPs) identified in Yohkoh/SXT data. Several
type IIIs were clearly associated (temporal and spatial) with
isolated flaring XBPs. The authors also noted a jet-like feature,
which is well directed along the path of the electron beams
responsible for the type III radio burst.
The association between metric type III bursts and soft X-ray jets
has been summarized by Raulin et al. (1996). In this work,
further evidence is presented for the production of non-thermal
electrons associated with soft X-ray jets. The most important
result is the finding that the centroids of the type III bursts at
different frequencies are aligned in the direction of the soft
X-ray jets. The authors conclude that the soft X-ray jets are
probably the dense coronal structures along which the type III
electron beams propagate.
The interaction of a hot neutral plasma stream (jet) with the
surrounding plasma is studied in terms of a kinetic approach
in the present paper. This interaction gives rise to the
excitation of electrostatic fluctuations at which electrons can be
energized. The dispersion relation of electrostatic waves is
derived in a kinetic manner, i.e., from the Vlasov-Maxwell equations,
in Sect. 2. The interaction of a hot jet with the coronal background
plasma is studied in Sect. 3. In Sect. 4, the conditions of
excitation of electrostatic fluctuations are discussed for the
circumstances of the interaction of a jet with the surrounding
background plasma. The movement of an electron in an oscillatory
electrostatic field is investigated in Sect. 5. The results of
the paper are summarized in Sect. 6.
A collisionless plasma can be described by the well-known Vlasov-Maxwell
equations (see, e.g., Krall & Trivelpiece 1986; and Baumjohann
& Treumann 1997).
It is intended to study the interaction of a hot neutral plasma stream
(jet) with the surrounding background plasma with the aim searching
for plasma wave excitation. That is usually done by a linear
treatment of the Vlasov-Maxwell equations leading to a
homogeneous system of equations
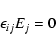 |
(1) |
with the dielectric tensor
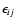 .
The determinant of the
tensor
.
The determinant of the
tensor
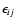 provides the dispersion relation of the different
waves. Here,
provides the dispersion relation of the different
waves. Here, 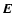 denotes the vector of the electric field accompanied
by these plasma waves.
The jet and the waves are assumed to propagate along the ambient
magnetic field. That is chosen to be the z-direction. Since it is
intended to look for the excitation of electrostatic waves, the system of
Eq. (1) can be reduced to
denotes the vector of the electric field accompanied
by these plasma waves.
The jet and the waves are assumed to propagate along the ambient
magnetic field. That is chosen to be the z-direction. Since it is
intended to look for the excitation of electrostatic waves, the system of
Eq. (1) can be reduced to
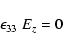 |
(2) |
with
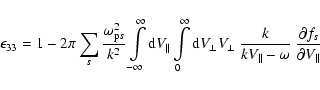 |
(3) |
with the wave number k and the frequency 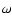 (Baumjohann & Treumann 1997).
Here, each kind of particle s with the charge qs, the mass ms, the
temperature Ts, and the velocity distribution function fs
interacts with each other by electromagnetic forces. Ns and
(Baumjohann & Treumann 1997).
Here, each kind of particle s with the charge qs, the mass ms, the
temperature Ts, and the velocity distribution function fs
interacts with each other by electromagnetic forces. Ns and
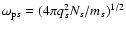 denote
the number density of each kind of particles and its corresponding
plasma frequency, respectively.
denote
the number density of each kind of particles and its corresponding
plasma frequency, respectively.
Since a magnetized plasma is
considered, the velocity distribution function fs basically depends on
the particle velocities parallel (
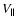 )
and perpendicular
(
)
and perpendicular
(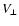 )
to the ambient magnetic field, i.e.,
)
to the ambient magnetic field, i.e.,
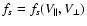 .
For the presented study, a drifting Maxwellian distribution is assumed
for the velocity distribution function
.
For the presented study, a drifting Maxwellian distribution is assumed
for the velocity distribution function
![\begin{displaymath}f_{s} = \frac{1}{(2\pi v_{{\rm th},s}^{2})^{3/2}} ~
{\rm e}...
...V_{\parallel}-V_{0,s})^{2}+V_{\perp}^{2}]/2v_{{\rm th},s}^{2}}
\end{displaymath}](/articles/aa/full/2007/03/aa3736-05/img22.gif) |
(4) |
with
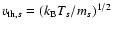 as the thermal velocity
of the particle species s, since the jet is regarded as propagating
along the magnetic field lines. V0,s denotes the drift velocity
of the species s. Inserting the velocity distribution function (4)
into Eq. (3) and performing the integrals, one gets the expression
for the dispersion relation of electrostatic waves
as the thermal velocity
of the particle species s, since the jet is regarded as propagating
along the magnetic field lines. V0,s denotes the drift velocity
of the species s. Inserting the velocity distribution function (4)
into Eq. (3) and performing the integrals, one gets the expression
for the dispersion relation of electrostatic waves
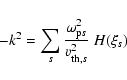 |
(5) |
with
 .
.
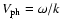 is the phase velocity. The function H(x) is given by
is the phase velocity. The function H(x) is given by
with the well-defined plasma dispersion function
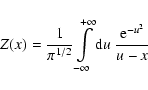 |
(7) |
(Baumjohann & Treumann 1997). Figure 3 shows the numerical behavior of the
H(x)-function.
The H-function changes its sign at x = 1.3, takes a global
minimum of -0.2875 at x = 2.1, and finally tends to zero
for
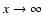 .
.
Now, the interaction of a hot plasma jet with the coronal
background plasma is studied. Both, the background plasma and the jet
are neutral. In the case of the background plasma the electrons
and protons have the temperature T0, and their drift velocity is zero.
Then, its parameters can be fixed to be
The jet is drifting with the velocity V0 with respect to the
background plasma. The electrons of the jet are considered to be hot,
i.e., their temperature is
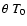 (with
(with
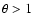 ), whereas the protons
of the jet have the same temperature as the protons of the background
plasma. The number density of the jet electrons is
), whereas the protons
of the jet have the same temperature as the protons of the background
plasma. The number density of the jet electrons is 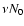 ,
i.e., N0 gives the total number density of all electrons in the
combined jet-background plasma system.
The same is valid for the protons since neutral plasma is considered.
Finally, the parameters of the jet are given by
,
i.e., N0 gives the total number density of all electrons in the
combined jet-background plasma system.
The same is valid for the protons since neutral plasma is considered.
Finally, the parameters of the jet are given by
Here, the indices e, p, b, and j are abbreviations for the electrons, the protons,
the background plasma, and the jet, respectively.
Thus, the considered plasma represents
a four component plasma. Then, the dispersion relation of Eq. (5)
reduces to
-q2 = 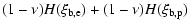 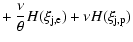 |
(8) |
with
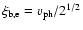 ,
,
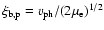 ,
,
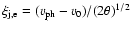 ,
and
,
and
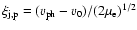 (
(
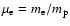 ;
;
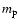 ,
proton mass).
Here, the frequency
,
proton mass).
Here, the frequency 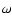 ,
the wave number k, the phase velocity
,
the wave number k, the phase velocity
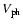 ,
and the drift velocity V0 are normalized to the plasma frequency
,
and the drift velocity V0 are normalized to the plasma frequency
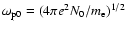 ,
the Debye length
,
the Debye length
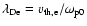 ,
and the thermal electron speed
,
and the thermal electron speed
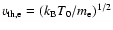 ,
respectively,
(
,
respectively,
(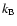 ,
Boltzmann's constant).
Here the quantities
,
Boltzmann's constant).
Here the quantities
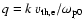 ,
,
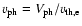 and
and
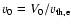 are already normalized ones.
are already normalized ones.
![\begin{figure}
\includegraphics[width=8.5cm,clip]{3736fig4.eps}\par
\end{figure}](/articles/aa/full/2007/03/aa3736-05/Timg61.gif) |
Figure 4:
Results of the numerical evaluation of Eq. (8) for choosing
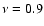 and
and
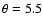 .
The growth
rate .
The growth
rate 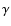 is presented in its dependence on the wave
frequency
is presented in its dependence on the wave
frequency 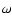 and jet speed
and jet speed
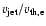 . . |
| Open with DEXTER |
To discuss under which conditions a wave-like solution of Eq. (8), i.e., q2 > 0,
is obtained, the conditions under which
the right hand becomes negative must be evaluated. Since the jet speeds
are in the range 10-1000 km s-1 (Shimojo et al. 1996) and
the thermal electron velocity is 4600 km s-1 for a coronal temperature
of
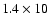 6 K,
6 K,
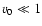 .
Therefore, the waves excited
by the jet plasma interaction have phase speeds with
.
Therefore, the waves excited
by the jet plasma interaction have phase speeds with
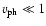 .
That leads to
.
That leads to
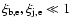 and, consequently, to
and, consequently, to
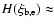 1 and
1 and
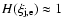 .
The H-function
(see Eq. (6)) has a global minimum of -0.2875 (see Fig. 3) at x = 2.1.
If the jet speed is adjusted in such a way that the H-function takes
its minimum, a wave-like solution of Eq. (8), i.e., q2 > 0, appears
necessary, if
.
The H-function
(see Eq. (6)) has a global minimum of -0.2875 (see Fig. 3) at x = 2.1.
If the jet speed is adjusted in such a way that the H-function takes
its minimum, a wave-like solution of Eq. (8), i.e., q2 > 0, appears
necessary, if
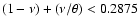 and hence
and hence
![$\nu > 0.7125/[1-1/\theta]$](/articles/aa/full/2007/03/aa3736-05/img69.gif) .
This condition should be fulfilled in the sense of a rough estimate,
i.e., at least
.
This condition should be fulfilled in the sense of a rough estimate,
i.e., at least
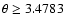 (for
(for
 ). From observations (see Shimojo 1999; Shimojo & Shibata 2000), one could estimate the upper temperature limit of the jet, i.e.,
). From observations (see Shimojo 1999; Shimojo & Shibata 2000), one could estimate the upper temperature limit of the jet, i.e.,
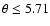 (which leads to
(which leads to
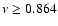 ). In conclusion, only a jet with hot electrons is able to provide a wave-like solution of Eq. (8).
). In conclusion, only a jet with hot electrons is able to provide a wave-like solution of Eq. (8).
For discussing the jet plasma interaction,
the jet parameters observed during the solar event on December 28, 1993
(Shimojo 1999, p. 66) are adopted for a careful numerical evaluation of Eq. (8).
At this event the jet had a speed of 532 km s-1 (=0.12
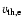 with
with
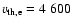 km s-1 for a coronal temperature of
km s-1 for a coronal temperature of
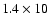 6 K)
and a temperature of 7.4-
6 K)
and a temperature of 7.4-
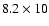 6 K (i.e.,
6 K (i.e.,
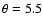 ).
Choosing
).
Choosing 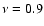 and
and
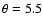 for the parameters, the numerical evaluation
of Eq. (8) provides an instability for jet speeds in the interval
0.09 < v0 < 0.15, i.e., in the range 415-690 km s-1 (Fig. 4),
leading to an excitation of electrostatic waves up to frequencies
of 0.01
for the parameters, the numerical evaluation
of Eq. (8) provides an instability for jet speeds in the interval
0.09 < v0 < 0.15, i.e., in the range 415-690 km s-1 (Fig. 4),
leading to an excitation of electrostatic waves up to frequencies
of 0.01
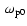 .
These waves are of the ion-acoustic mode
(Baumjohann & Treumann 1997). The maximum of the growth rate
.
These waves are of the ion-acoustic mode
(Baumjohann & Treumann 1997). The maximum of the growth rate
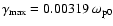 appears at a frequency
appears at a frequency
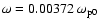 (Fig. 4). In summary, the interaction of the jet with the background plasma leads
to an instability for a small range of jet speeds, i.e., 415-690 km s-1,
exciting electrostatic waves in the sense of the ion-acoustic mode.
The appearance of the instability requires hot electrons in the jet.
(Fig. 4). In summary, the interaction of the jet with the background plasma leads
to an instability for a small range of jet speeds, i.e., 415-690 km s-1,
exciting electrostatic waves in the sense of the ion-acoustic mode.
The appearance of the instability requires hot electrons in the jet.
The equation of motion of an electron considered to be a test particle in an
electrostatic field is usually given by
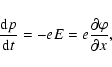 |
(9) |
with the electrostatic potential 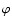 ,
the momentum
,
the momentum
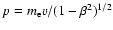 ,
and particle velocity v(
,
and particle velocity v(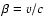 ;
c, velocity of light).
Introducing dimensionless quantities, the equation of motion
is transformed into the normalized one:
;
c, velocity of light).
Introducing dimensionless quantities, the equation of motion
is transformed into the normalized one:
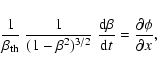 |
(10) |
with
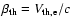 .
In Eq. (9), the time t, the spatial coordinate x, and the electrostatic potential
.
In Eq. (9), the time t, the spatial coordinate x, and the electrostatic potential
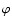 are normalized to
the inverse of the electron plasma frequency
are normalized to
the inverse of the electron plasma frequency
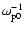 ,
the Debye-length
,
the Debye-length
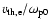 ,
and
,
and
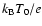 ,
i.e.,
,
i.e.,
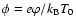 ,
respectively.
Additionally, the definition of the velocity
,
respectively.
Additionally, the definition of the velocity
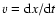 ,
i.e.,
,
i.e.,
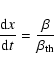 |
(11) |
in normalized quantities, must be introduced to the system of equations for describing
the test particle motion.
The ansatz
![\begin{displaymath}\phi = \phi_0 ~ {\rm e}^{\gamma ~ t} ~ {\rm {cos}}~[q ~ x(t) - \omega ~ t]
\end{displaymath}](/articles/aa/full/2007/03/aa3736-05/img92.gif) |
(12) |
is adopted for the spatial-temporal behavior of the electrostatic potential.
Here, the same normalization has been employed.
The electrostatic fluctuations are generated by the instability appearing due to
the jet plasma interaction (see Sect. 3).
Since the conditions of maximum growth rate should be used,
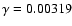 ,
,
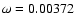 ,
and q = 0.05 are chosen.
At the thermal, i.e., undisturbed level, the amplitude of the electrostatic (ion-acoustic)
fluctuations can be assumed to be about
,
and q = 0.05 are chosen.
At the thermal, i.e., undisturbed level, the amplitude of the electrostatic (ion-acoustic)
fluctuations can be assumed to be about
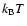 ,
i.e.,
,
i.e.,
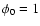 .
The normalized equations of motion (Eqs. (10) and (11)) have
been numerically solved with the choice of these parameters. Since the electron
is regarded as a test particle, it must be collisionless with respect
to Coulomb collisions. To be sure concerning this subject, the
initial velocity of the electron is chosen to be 4 times the thermal one, i.e.,
.
The normalized equations of motion (Eqs. (10) and (11)) have
been numerically solved with the choice of these parameters. Since the electron
is regarded as a test particle, it must be collisionless with respect
to Coulomb collisions. To be sure concerning this subject, the
initial velocity of the electron is chosen to be 4 times the thermal one, i.e.,
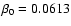 with a thermal electron velocity of 4600 km s-1.
It corresponds to a kinetic energy of about 1 keV. In summary, the initial conditions
are
x(t=0) = 0 and
with a thermal electron velocity of 4600 km s-1.
It corresponds to a kinetic energy of about 1 keV. In summary, the initial conditions
are
x(t=0) = 0 and
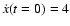 in the sense of normalized quantities.
The resulted movement in the x-t plane is presented in Fig. 5.
in the sense of normalized quantities.
The resulted movement in the x-t plane is presented in Fig. 5.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3736fig5.eps}
\end{figure}](/articles/aa/full/2007/03/aa3736-05/Timg97.gif) |
Figure 5:
Spatial movement of the test electron in the x-t plane
for q=0.05,
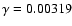 ,
and ,
and
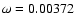 . . |
| Open with DEXTER |
As seen in Fig. 5, the electron is initially moving with a nearly
constant velocity until
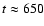 in the initial phase.
Then, its motion is dramatically changed into a much more slower one
superimposed by an oscillatory motion with a frequency increasing
with time. That can be explained in the following manner:
initially, the amplitude of the electrostatic wave (see Eq. (12))
wave is small, so that its influence on the electron motion
can be neglected. Then, the electron homogeneously propagates
with a constant velocity of
in the initial phase.
Then, its motion is dramatically changed into a much more slower one
superimposed by an oscillatory motion with a frequency increasing
with time. That can be explained in the following manner:
initially, the amplitude of the electrostatic wave (see Eq. (12))
wave is small, so that its influence on the electron motion
can be neglected. Then, the electron homogeneously propagates
with a constant velocity of 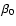 .
Since the amplitude of the electrostatic field is increasing with time t,
its influence on the particle motion will become essential, if
the potential energy of the particle in the electrostatic wave
is comparable with the kinetic energy of the particle, i.e.,
.
Since the amplitude of the electrostatic field is increasing with time t,
its influence on the particle motion will become essential, if
the potential energy of the particle in the electrostatic wave
is comparable with the kinetic energy of the particle, i.e.,
![\begin{displaymath}\frac{W}{k_{\rm B}T_{0}} = \frac{1}{\beta^{2}_{\rm th}} \left...
...\sqrt{1-\beta^{2}}}-1 \right] = \phi_{0} ~ {\rm e}^{\gamma t}.
\end{displaymath}](/articles/aa/full/2007/03/aa3736-05/img100.gif) |
(13) |
That state is reached after the time
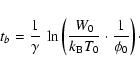 |
(14) |
One gets tb = 652 for
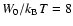 corresponding to
corresponding to
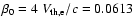 (
(
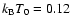 keV for
keV for
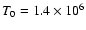 K),
as can be seen in Fig. 5.
After this time the electrostatic field dramatically changes the particle
movement. Namely, the particle co-moves with the electrostatic wave,
i.e., its averaged velocity is the phase speed of the wave, as depicted
in Fig. 5. An oscillatory motion with temporally increasing frequency
is superimposed upon this slow co-motion with the wave.
That can be demonstrated in the following way: Inserting the ansatz (12)
into Eq. (10) one gets
K),
as can be seen in Fig. 5.
After this time the electrostatic field dramatically changes the particle
movement. Namely, the particle co-moves with the electrostatic wave,
i.e., its averaged velocity is the phase speed of the wave, as depicted
in Fig. 5. An oscillatory motion with temporally increasing frequency
is superimposed upon this slow co-motion with the wave.
That can be demonstrated in the following way: Inserting the ansatz (12)
into Eq. (10) one gets
![\begin{displaymath}\frac{1}{\beta_{\rm th}} ~
\frac{{\textrm d}\beta}{{\textrm...
...
-q ~ \phi_{0} ~ {\rm e}^{\gamma t} ~ \sin~[q~x(t)-\omega t]
\end{displaymath}](/articles/aa/full/2007/03/aa3736-05/img106.gif) |
(15) |
in the non-relativistic approach (i.e., 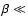 1).
In the case of the co-motion with the wave, the function x(t)can be expressed by
1).
In the case of the co-motion with the wave, the function x(t)can be expressed by
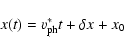 |
(16) |
with
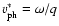 as the phase velocity of the wave,
Here,
as the phase velocity of the wave,
Here,  represents the oscillatory motion superimposed
on the slowly translatory motion. Inserting the expression (16) into Eq. (15)
and using Eq. (11) one obtains
represents the oscillatory motion superimposed
on the slowly translatory motion. Inserting the expression (16) into Eq. (15)
and using Eq. (11) one obtains
![\begin{displaymath}\frac{{\rm d}^{2} \delta x}{{\rm d}t^{2}} = -q \phi_{0} ~ {\rm e}^{\gamma t}
~ \sin~[q~ \delta x + q~x_{0}].
\end{displaymath}](/articles/aa/full/2007/03/aa3736-05/img111.gif) |
(17) |
Since the oscillatory motion has small amplitudes,
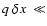 1 should
be assumed. Then, Eq. (17) reduces to
1 should
be assumed. Then, Eq. (17) reduces to
![\begin{displaymath}\frac{{\rm d}^{2} \delta x}{{\rm d}t^{2}} + \varpi^{2} \delta x =
-q ~ \phi_{0} ~ {\rm e}^{\gamma t} ~ \sin~[qx_{0}]
\end{displaymath}](/articles/aa/full/2007/03/aa3736-05/img113.gif) |
(18) |
with
![$\varpi^{2} = q^{2} \phi_{0} \exp(\gamma t) \cos[qx_{0}]$](/articles/aa/full/2007/03/aa3736-05/img114.gif) .
Equation (18) actually represents an equation of an oscillatory motion
with the frequency
.
Equation (18) actually represents an equation of an oscillatory motion
with the frequency 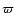 ,
which increases with time.
That can be really observed in Fig. 5.
(For instance, x0 can be adjusted in such a way that
,
which increases with time.
That can be really observed in Fig. 5.
(For instance, x0 can be adjusted in such a way that
![$\sin~[qx_{0}] =0$](/articles/aa/full/2007/03/aa3736-05/img116.gif) .) Adopting the parameters
used in the numerical solution of the Eqs. (10) and (11),
one finds a period of
.) Adopting the parameters
used in the numerical solution of the Eqs. (10) and (11),
one finds a period of
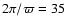 at t = 800 for the
oscillatory motion. This value is similar to that deduced
from the numerical calculations as depicted in Fig. 5.
It should be emphasized that a total agreement between the analytical
approach and the numerical solution should not be
expected since the numerical result (Fig. 5) is the exact one,
whereas the analytical treatment presented above is only
an approximative approach. It, however, demonstrates
the appearance of an oscillatory motion with a temporally
increasing frequency during the co-motion with the wave.
at t = 800 for the
oscillatory motion. This value is similar to that deduced
from the numerical calculations as depicted in Fig. 5.
It should be emphasized that a total agreement between the analytical
approach and the numerical solution should not be
expected since the numerical result (Fig. 5) is the exact one,
whereas the analytical treatment presented above is only
an approximative approach. It, however, demonstrates
the appearance of an oscillatory motion with a temporally
increasing frequency during the co-motion with the wave.
While co-moving with the wave, the electron gets
energy from the electrostatic wave (Fig. 6).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{3736fig6.eps}
\end{figure}](/articles/aa/full/2007/03/aa3736-05/Timg118.gif) |
Figure 6:
Energy gain of the test electron with the time during the movement
for q=0.05,
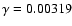 ,
and ,
and
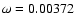 . . |
| Open with DEXTER |
Figure 6 shows that the particle gets an energy of 80
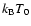 within
a period of
within
a period of 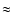
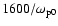 ,
i.e., the electron obtains an energy of 10 keV within 0.85
,
i.e., the electron obtains an energy of 10 keV within 0.85 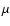 s
for
s
for
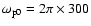 MHz, for instance.
The value of 300 MHz has been chosen for this example, since type III
radio bursts associated with jets usually appear at this frequency level
(see, e.g., Fig. 1).
MHz, for instance.
The value of 300 MHz has been chosen for this example, since type III
radio bursts associated with jets usually appear at this frequency level
(see, e.g., Fig. 1).
During magnetic reconnection, which is the basic process of solar flares,
jets of hot plasma are ejected from the reconnection site into the
surrounding coronal plasma. The interaction of such jets with
background plasma leads to the excitation of electrostatic waves
due to an instability if the jet speed is in the range 415-690 km s-1.
Such values are typical ones for jets as observed in the soft X-ray images by Yohkoh
(Shimojo et al. 1996; Shimojo & Shibata 2000).
If the jet penetrates into the surrounding coronal plasma, it
is decelerated due to Coulomb collisions within a period of the
order of the Coulomb collision time
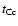 ,
which is given by
,
which is given by
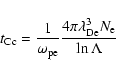 |
(19) |
with
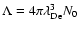 (Estel & Mann 1999). At the 300 MHz level and a
coronal temperature of
(Estel & Mann 1999). At the 300 MHz level and a
coronal temperature of
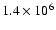 K, one gets
K, one gets
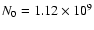 cm-3 and
cm-3 and
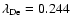 cm
resulting in
cm
resulting in
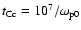 .
In comparison, the growing time
.
In comparison, the growing time
 for the excitation of
electrostatic waves is given by
for the excitation of
electrostatic waves is given by
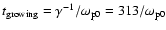 for
for
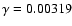 .
Thus, the instability acts much faster than the
deceleration of the jet due to Coulomb collisions.
.
Thus, the instability acts much faster than the
deceleration of the jet due to Coulomb collisions.
As discussed in this paper, the plasma stream ejected from the reconnection
site passes through the surrounding coronal plasma leading to
the excitation of electrostatic fluctuations in terms of the
ion-acoustic mode. If these fluctuations act on supra-thermal
electrons, these electrons co-move with the wave (Fig. 5) and gain
energy (Fig. 6). That process represents a collisionless
energizing and/or heating of the electrons during flares. It is
well-known that electrons are rapidly heated in a collisionless
manner during flares. That is impressively seen in the hard X-ray
emission of the flaring plasma as observed by the spacecraft RHESSI, for instance.
Since the instability only appears in a small range of the jet
speed (Fig. 4), the enhanced level of electrostatic fluctuations
is localized in a small spatial region in the corona. Consequently, if
the energized electrons leave the region of instability, some of
them can run away with a high velocity along a magnetic field
line. That leads to either solar type III or type U radio bursts
during their propagation along open and closed magnetic field
lines (see Fig. 1 for example), respectively.
The observations show that there are generally three kinds of events
(Aurass et al. 1994; Pick et al. 1994; Raulin et al. 1996):
- i.
- jets that are not accompanied by type III bursts;
- ii.
- jets with a simultaneous appearance of type III bursts;
- iii.
- jets accompanied with type III bursts, but with a temporal delay concerning the
jet onset time.
They can be explained
in the framework of our approach. Since the instability only occurs
in a small range of the jet speed around V0, jets with a speed
smaller than V0 do not give rise to an electrostatic instability
and, hence, to type III bursts (case i). On the other hand, if the jet
speed is greater than V0, it is initially not able to excite electrostatic
fluctuations. However, the jet is decelerating due to its interaction
with the surrounding plasma, e.g., due to Coulomb collisions.
Then, it needs time until the jet speed
slows down to V0 leading to the onset of the electrostatic
instability and, consequently, to the occurrence of type III radio bursts
(case iii). That could be the reason of the observed delay between the onset of the
jet and that of the type III burst (Aurass et al. 1994).
Only in the special case, at which the jet speed is very close to V0,
can the type III radio bursts simultaneously appear with the jet (case ii).
In summary, the interaction of a solar jet ejected from the reconnection
site with the surrounding plasma leads to both the collisionless
energizing and/or heating of electrons (as seen in the hard X-ray
emission) and to type III bursts (as observed in the solar radio
emission during flares). Here, the kinetic energy of the jet is
partly transfered into energy of electrostatic fluctuations
and, subsequently, into the energy of the electrons.
Acknowledgements
The authors thank to
Germar Rausche and Hakan Önel for helpful and stimulating
discussions. RM was financially supported by Deutscher Akademisher
Austauschdienst (DAAD) grant Ref. 324 A/03/10336.
- Aurass, H., Klein,
K.-L., & Martens, P. C. H. 1994, Sol. Phys., 155, 203 [NASA ADS] [CrossRef] (In the text)
- Baumjohann,
W., & Treumann R. A. 1997, Basic Space Plasma Physics (London:
Imperial College Press)
(In the text)
- Estel, C., &
Mann, G. 1999, A&A, 345, 276 [NASA ADS] (In the text)
- Heyvaerts, J.
1981, in Solar Flare Magnetohydrodynamics, ed. E. R. Priest (Gordon
and Breach Science Publishers), Ch. 8
(In the text)
- Krall, N. A., &
Trivelpiece, A. W. 1986, Principles of Plasma Physics (San
Francisco Press)
(In the text)
- Kundu, M. R., Strong,
K. T., Pick, M., et al. 1994, in Proc. Kofu Symposium, ed. S.
Enome, & T. Hirayama, NRO Rep., 360, 343
(In the text)
- Kundu, M. R., Raulin,
J. P., Nitta, N., et al. 1995, ApJ, 447, L135 [NASA ADS] [CrossRef] (In the text)
- Mann G., Aurass, H.,
Voigt, W., & Paschke, J. 1992, in Proc. First SOHO Workshop,
ESA SP-446, 447
(In the text)
- Melrose, D. B.
1985, in Solar Radiophysics, ed. D. J. McLean, & N. R. Labrum
(Cambridge: Cambridge University Press), Chs. 8, 9
(In the text)
- Nelson, G. J., &
Melrose, D. B. 1985, in Solar Radiophysics, ed. D. J. McLean, &
N. R. Labrum (Cambridge: Cambridge University Press), Ch. 13
- Pick, M., Raoult, A.,
Trottet, G., et al. 1994, in Proc. Kofu Symposium, ed. S. Enome,
& T. Hirayama, NRO Rep., 360, 263
(In the text)
- Raulin, J. P.,
Kundu, M. R., Hudson, H. S., Nitta, N., & Raoult, A. 1996,
A&A, 306, 299 [NASA ADS] (In the text)
- Shibata, K.,
Ishido, Y., Acton, L. W., et al. 1992, PASJ, 44, L173 [NASA ADS] (In the text)
- Shibata, K.,
Yokoyama, T., & Shimojo, M. 1994, in Proc. Kofu Symposium, ed.
S. Enome, & T. Hirayama, NRO Rep., 360, 75
(In the text)
- Shimojo, M. 1999,
Studies of Solar Coronal X-ray Jets, Ph.D. Thesis, Graduate
University for Advance Studies, Japan
(In the text)
- Shimojo, M.,
& Shibata, K. 2000, ApJ, 542, 1100 [NASA ADS] [CrossRef] (In the text)
- Shimojo, M.,
Hashimoto, S., Shibata, K., et al. 1996, PASJ, 48, 123 [NASA ADS] (In the text)
- Strong, K. T.,
Harvey, K, Hirayama, T., et al. 1992, PASJ, 44, L161 [NASA ADS] (In the text)
- Treumann R. A.,
& Baumjohann, W. 1997, Advanced Space Plasma Physics (London:
Imperial College Press)
(In the text)
- Yokoyama, T.,
& Shibata, K. 1994, in Proc. Kofu Symposium, ed. S. Enome,
& T. Hirayama, NRO Rep., 360, 367
(In the text)
- Yokoyama, T.,
& Shibata, K. 1995, Nature, 375, 42 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2007
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3736fig1.eps}
\end{figure}](/articles/aa/full/2007/03/aa3736-05/Timg8.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{3736fig2.eps}
\end{figure}](/articles/aa/full/2007/03/aa3736-05/Timg12.gif)
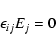
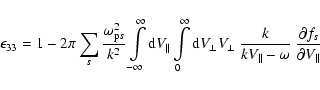
![\begin{displaymath}f_{s} = \frac{1}{(2\pi v_{{\rm th},s}^{2})^{3/2}} ~
{\rm e}...
...V_{\parallel}-V_{0,s})^{2}+V_{\perp}^{2}]/2v_{{\rm th},s}^{2}}
\end{displaymath}](/articles/aa/full/2007/03/aa3736-05/img22.gif)
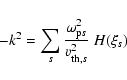
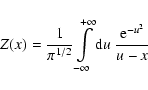
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{3736fig3.eps}
\end{figure}](/articles/aa/full/2007/03/aa3736-05/Timg28.gif)
![\begin{figure}
\includegraphics[width=8.5cm,clip]{3736fig4.eps}\par
\end{figure}](/articles/aa/full/2007/03/aa3736-05/Timg61.gif)
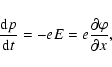
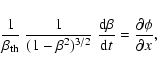
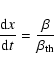
![\begin{displaymath}\phi = \phi_0 ~ {\rm e}^{\gamma ~ t} ~ {\rm {cos}}~[q ~ x(t) - \omega ~ t]
\end{displaymath}](/articles/aa/full/2007/03/aa3736-05/img92.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3736fig5.eps}
\end{figure}](/articles/aa/full/2007/03/aa3736-05/Timg97.gif)
![\begin{displaymath}\frac{W}{k_{\rm B}T_{0}} = \frac{1}{\beta^{2}_{\rm th}} \left...
...\sqrt{1-\beta^{2}}}-1 \right] = \phi_{0} ~ {\rm e}^{\gamma t}.
\end{displaymath}](/articles/aa/full/2007/03/aa3736-05/img100.gif)
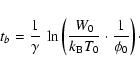
![\begin{displaymath}\frac{1}{\beta_{\rm th}} ~
\frac{{\textrm d}\beta}{{\textrm...
...
-q ~ \phi_{0} ~ {\rm e}^{\gamma t} ~ \sin~[q~x(t)-\omega t]
\end{displaymath}](/articles/aa/full/2007/03/aa3736-05/img106.gif)
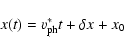
![\begin{displaymath}\frac{{\rm d}^{2} \delta x}{{\rm d}t^{2}} = -q \phi_{0} ~ {\rm e}^{\gamma t}
~ \sin~[q~ \delta x + q~x_{0}].
\end{displaymath}](/articles/aa/full/2007/03/aa3736-05/img111.gif)
![\begin{displaymath}\frac{{\rm d}^{2} \delta x}{{\rm d}t^{2}} + \varpi^{2} \delta x =
-q ~ \phi_{0} ~ {\rm e}^{\gamma t} ~ \sin~[qx_{0}]
\end{displaymath}](/articles/aa/full/2007/03/aa3736-05/img113.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{3736fig6.eps}
\end{figure}](/articles/aa/full/2007/03/aa3736-05/Timg118.gif)