A&A 461, 381-384 (2007)
DOI: 10.1051/0004-6361:20066245
New electron-proton Bremsstrahlung rates for a hot plasma where the electron
temperature is much smaller than the proton temperature
M. Mayer
Institute of Astronomy, Madingley Road,
Cambridge CB3 0HA, UK
Received 14 August 2006 / Accepted 21 September 2006
Abstract
Context. Observations of X-Ray sources harbouring a black hole and an accretion disc show the presence of at least two spectral components. One component is black-body radiation from an optically thick standard accretion disc. The other is produced in a optically thin corona and usually shows a powerlaw behaviour. Electron-proton (ep) bremsstrahlung is one of the contributing radiation mechanisms in the corona. Soft photons from the optically thick disc can Compton cool the electrons in the corona and therefore lead to a two-temperature plasma, where electrons and ions have different temperatures.
Aims. We qualitatively discuss effects on ep-bremsstrahlung in the presence of such a two-temperature plasma.
Methods. We use the classical dipole approximation allowing for non-relativistic electrons and protons and apply quantum corrections through high-precision Gaunt factors.
Results. In the two-temperature case (
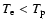 )
the protons cause a significant fraction of the ep-bremsstrahlung if their speed is high compared to the electrons. We give accurate values for ep-bremsstrahlung including quantum-mechanical corrections in the non-relativistic limit and give some approximations in the relativistic limit.
)
the protons cause a significant fraction of the ep-bremsstrahlung if their speed is high compared to the electrons. We give accurate values for ep-bremsstrahlung including quantum-mechanical corrections in the non-relativistic limit and give some approximations in the relativistic limit.
Conclusions. The formulae presented in this paper can be used in models of black hole accretion discs where an optically thin corona can comprise a two-temperature plasma. This work could be extended to include the fully relativistic case if required.
Key words: radiation mechanisms: general - X-rays: general
Models of black hole accretion discs are widely used to explain
spectral characteristics of X-Ray observations of such objects.
These models usually consist of an optically thin and hot corona and
a cool, optically thick standard accretion disc. The
optically thin corona consists of a two-temperature plasma. Electrons
cool by bremsstrahlung, mainly by electron-proton bremsstrahlung.
The electron-proton system has got a dipole moment while the
electron-electron and proton-proton system can only emit
radiation through the (much weaker) quadrupole moment.
Eardley et al. (1975) presented a model for Cyg
X-1 incorporating a two-temperature plasma in the inner parts of the
accretion flow. This kind of model has been subsequently developed
(e.g. Shapiro et al. 1976; Zycki et al. 1995) and applied to
different objects (Haardt & Maraschi 1991,1993) and
different geometries (Wandel & Liang 1991).
The calculation of the rate of bremsstrahlung coming from a hot gas
has received much attention over a long period
of time
(e.g. Blumenthal & Gould 1970; Brussaard & van de Hulst 1962; Gould 1980,1981).
Today the bremsstrahlung rate is known with a very high accuracy.
All these calculations however assume electron and proton temperature to be
equal.
In the following we limit ourselves to a purely classical and
non-relativistic treatment of electron-proton bremsstrahlung. We do
this in order to highlight the elementary physical processes
involved. Since we apply Gaunt factors to account for quantum
mechanical effects, our results are strictly accurate only in the
non-relativistic case. An expansion to the fully relativistic case
is feasible but beyond the scope of this paper.
In this contribution we first highlight the physical mechanism in
Sect. 2 and then present a recalculation of the
electron-proton Bremsstrahlung rate for a
two-temperature plasma in the non-relativistic limit in
Sect. 3. While we limit ourselves to a electron-proton
plasma, the formulae can easily be modified to consider mixtures of
ions with different mass and charge. We give a discussion of the results and our conclusions in Sect. 4.
2 The mechanism
Electron-proton Bremsstrahlung in the standard picture is created through the acceleration of electrons in the
field of a proton. This acceleration leads to the emission of
electromagnetic radiation resulting in the loss of kinetic electron energy. We show this situation in Fig. 1.
Consider a electron and a proton travelling at a speed
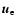 and
and
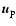 ,
respectively, have an encounter at a minimal distance
d and at a relative speed of
,
respectively, have an encounter at a minimal distance
d and at a relative speed of
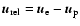 .
The Coulomb field leads to a mutual attraction with the
corresponding Coulomb force
.
The Coulomb field leads to a mutual attraction with the
corresponding Coulomb force
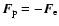 with
with
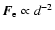 and subsequently to
an acceleration
and subsequently to
an acceleration
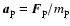 and
and
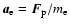 .
This interaction happens on a characteristic timescale
.
This interaction happens on a characteristic timescale
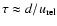 and the change in the speed of the particles
is small compared to their velocity (small-angle scattering).
and the change in the speed of the particles
is small compared to their velocity (small-angle scattering).
After the interaction, the speed of the electron is
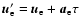 and that of the proton is
and that of the proton is
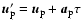 .
The change in kinetic energy for the electron and proton can
be written as
.
The change in kinetic energy for the electron and proton can
be written as
where we have made use of the fact that
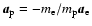 and the change in speed
and the change in speed
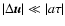 .
Thus we can
neglect terms of the order
.
Thus we can
neglect terms of the order 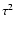 .
Both the
electrons and the proton lose kinetic energy (
.
Both the
electrons and the proton lose kinetic energy (
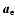 and
and
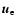 form an angle larger than
form an angle larger than 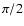 and thus their scalar product
is negative).
and thus their scalar product
is negative).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6245fig1.eps}
\end{figure}](/articles/aa/full/2007/02/aa6245-06/Timg29.gif) |
Figure 1:
Trajectory of an electron (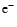 )
at speed )
at speed
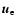 .
For
simplicity the proton (p) is assumed to be at rest. At the closest
approach, the acceleration .
For
simplicity the proton (p) is assumed to be at rest. At the closest
approach, the acceleration
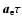 moves the electron
closer to the proton and the electron loses kinetic energy.
moves the electron
closer to the proton and the electron loses kinetic energy. |
| Open with DEXTER |
It is evident from Eqs. (1) and (2)
that for a one-temperature plasma, where the mean speed of the
electron is faster by a factor of
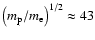 than the speed of the
protons, most of the energy of the electron-proton
bremsstrahlung arises from the kinetic energy change of the electrons.
than the speed of the
protons, most of the energy of the electron-proton
bremsstrahlung arises from the kinetic energy change of the electrons.
However for a two-temperature plasma the ratio for the mean speed of
protons and electrons is given by
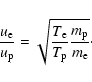 |
(3) |
For
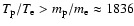 the mean speed of the protons
exceeds the mean speed of the electrons and then the change in kinetic
energy is greater for the protons. In this case it is the protons
which are responsible for providing the energy to create a photon leading to
electron-proton bremsstrahlung.
the mean speed of the protons
exceeds the mean speed of the electrons and then the change in kinetic
energy is greater for the protons. In this case it is the protons
which are responsible for providing the energy to create a photon leading to
electron-proton bremsstrahlung.
We now explore this mechanism in a classical and non-relativistic
treatment of electron-proton bremsstrahlung in the dipole-approximation.
3 Non-relativistic electron-proton Bremsstrahlung
The emission per unit time t, volume V and photon energy
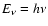 for
a single proton can be expressed as (e.g. Rybicki & Lightman 1979)
for
a single proton can be expressed as (e.g. Rybicki & Lightman 1979)
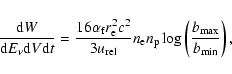 |
(4) |
where
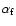 is the fine-structure constant,
is the fine-structure constant,
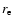 is the classical electron radius, c the speed of light,
is the classical electron radius, c the speed of light,
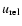 the relative
velocity of the ion with respect to the electron, and
the relative
velocity of the ion with respect to the electron, and 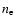 and
and 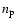 are
the electron and ion number densities, respectively.
are
the electron and ion number densities, respectively.
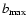 and
and
 are the maximum and
minimum value of the impact parameter. Through the definition of the Gaunt factor
are the maximum and
minimum value of the impact parameter. Through the definition of the Gaunt factor
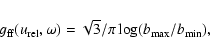 |
(5) |
where
 and
and 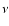 is the frequency of the
bremsstrahlung photon, and subsequent use of quantum mechanical calculations of
is the frequency of the
bremsstrahlung photon, and subsequent use of quantum mechanical calculations of
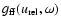 we do not need to specify the
maximum and minimum impact parameters here and instead can use Gaunt
factors from the literature which already account for quantum mechanical
effects.
we do not need to specify the
maximum and minimum impact parameters here and instead can use Gaunt
factors from the literature which already account for quantum mechanical
effects.
Substituting the Gaunt factor into (4), we get
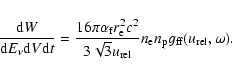 |
(6) |
For a one temperature plasma, the electrons are much faster (a
factor of
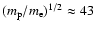 ). Thus the protons can be
considered to be at rest and the relative velocity is dominated by the
speed of the electron. To get the electron-proton bremsstrahlung rate for this type of
plasma, it is sufficient to average the single proton emission rate over
the (assumed Maxwellian) velocity distribution of the electrons. Then
the energy of the photon is extracted from the kinetic energy of the
electron which slows, i.e. cools down.
). Thus the protons can be
considered to be at rest and the relative velocity is dominated by the
speed of the electron. To get the electron-proton bremsstrahlung rate for this type of
plasma, it is sufficient to average the single proton emission rate over
the (assumed Maxwellian) velocity distribution of the electrons. Then
the energy of the photon is extracted from the kinetic energy of the
electron which slows, i.e. cools down.
For a two-temperature plasma, however, the proton speed can become
comparable or even exceed the electron speed. Hence we need to
consider that and write the relative speed as
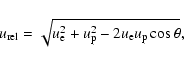 |
(7) |
where 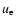 and
and 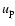 are the electron and proton speed, respectively,
and
are the electron and proton speed, respectively,
and 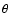 the angle between the two speed vectors.
the angle between the two speed vectors.
For an isotropic Maxwellian distribution for the electrons and protons we
have the probability d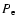 for an electron to have a speed
between
for an electron to have a speed
between 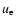 and
and
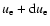
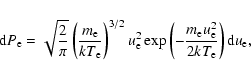 |
(8) |
and the corresponding probability
d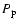 for a proton to have a speed between
for a proton to have a speed between 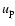 and
and
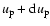
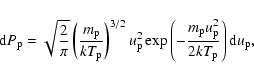 |
(9) |
where k is the Boltzmann constant.
Note that
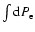 and
and
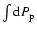 are normalised to unity.
are normalised to unity.
For the total emissivity of the electron-proton bremsstrahlung we have to
average over d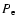 and d
and d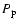 ,
respectively. We have to calculate,
using Eqs. (6)-(9)
,
respectively. We have to calculate,
using Eqs. (6)-(9)
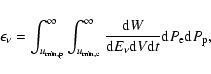 |
(10) |
where
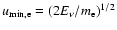 and
and
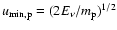 accounts for the photon
discreteness effect.
The result then still depends on the angle
accounts for the photon
discreteness effect.
The result then still depends on the angle 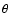 to lie between the velocities
to lie between the velocities 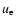 and
and 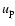 .
We then need to integrate over the probability for an
angle
.
We then need to integrate over the probability for an
angle 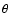 to occur. For an assumed isotropic distribution of angles, the probability for an angle between
to occur. For an assumed isotropic distribution of angles, the probability for an angle between 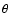 and
and
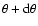 is
is
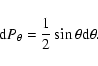 |
(11) |
The angle averaged integral can be written in the form
| |
|
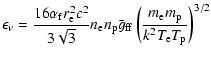 |
(12) |
| |
|
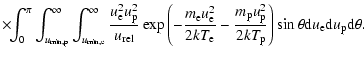 |
(13) |
This finally has to be integrated over the photon energy to get the
bremsstrahlung rate. For the energy and temperature dependent Gaunt
factor,
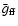 ,
we use
Sutherland (1998). Thus we do not longer need to justify our
choice for the maximum and minimum impact parameter. Higher precision
values are now hidden in the tabulated values of
,
we use
Sutherland (1998). Thus we do not longer need to justify our
choice for the maximum and minimum impact parameter. Higher precision
values are now hidden in the tabulated values of
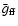 ,
taken from Sutherland (1998).
,
taken from Sutherland (1998).
The integral over the electron and proton velocities has to be taken
carefully. As long as
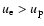 ,
the electron-proton bremsstrahlung is
mainly caused by the kinetic energy change of the
electron. For
,
the electron-proton bremsstrahlung is
mainly caused by the kinetic energy change of the
electron. For
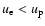 ,
the electron-proton bremsstrahlung is caused
by the kinetic energy change of the proton,
as then the electrons do not have much energy to put in the bremsstrahlung.
The electron-proton bremsstrahlung rate, however, is then reduced by a factor
,
the electron-proton bremsstrahlung is caused
by the kinetic energy change of the proton,
as then the electrons do not have much energy to put in the bremsstrahlung.
The electron-proton bremsstrahlung rate, however, is then reduced by a factor
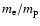 ,
correcting for centre of mass effects.
,
correcting for centre of mass effects.
In our calculations, we divided the velocity integrals accordingly and
get the contributions of protons and electrons to the electron-proton bremsstrahlung rate.
We give the corresponding analytic results for two limiting cases,
and
where the first result includes a one-temperature plasma, where
the protons are virtually at rest and the second corresponds to a two-temperature
plasma, where only the protons contribute to the electron-proton
bremsstrahlung and the electrons are virtually at rest.
Energy integrated this leads to
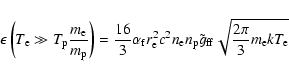 |
(14) |
and
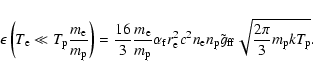 |
(15) |
Here,
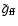 is the frequency, i.e. photon energy, averaged Gaunt factor
(approximately
is the frequency, i.e. photon energy, averaged Gaunt factor
(approximately
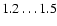 )
)
The results for the one-temperature plasma reproduces the well known
result from the literature (e.g. Rybicki & Lightman 1979). For
the two-temperature plasma the electron-proton bremsstrahlung rate
depends on the temperature of the protons, accordingly. In either case the formulae only
depend on the temperature of the species which mainly cause
bremsstrahlung. The general dependence on the temperature is the same
in both limiting cases (proportional to
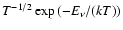 in the energy-dependent and T1/2 in the
energy integrated case).
in the energy-dependent and T1/2 in the
energy integrated case).
We show sample electron-proton bremsstrahlung spectra for a gas at different electron
and proton temperatures in Fig. 2. Note that the electron
component of the electron-proton bremsstrahlung shows a high-energy cut-off at lower energies
than the proton component. Although the magnitude of electron-proton
bremsstrahlung caused by the kinetic energy of protons is always lower
than that of bremsstrahlung created by the kinetic energy of electrons
for the cases considered here, the total, energy integrated
bremsstrahlung contribution of protons can be dominant due to the higher high
energy cut-off. This effect is shown in Fig. 3 where
we plot the energy integrated electron-proton
bremsstrahlung rate for protons and electron as a function of electron
temperature. We also plot the corresponding electron-electron
bremsstrahlung rate, taken from Svensson (1982).
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{6245fig2.eps}
\end{figure}](/articles/aa/full/2007/02/aa6245-06/Timg78.gif) |
Figure 2:
Electron-proton Bremsstrahlung emissivity
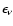 of a optically
thin gas for different combinations of electron and proton
temperatures. The total emissivity is plotted as a solid line, the
contribution of electrons as a dotted line and the proton
contribution as a dash-dotted line. Note the different relative contributions of proton
and electron bremsstrahlung for the same proton temperature, but
different electron temperature.
of a optically
thin gas for different combinations of electron and proton
temperatures. The total emissivity is plotted as a solid line, the
contribution of electrons as a dotted line and the proton
contribution as a dash-dotted line. Note the different relative contributions of proton
and electron bremsstrahlung for the same proton temperature, but
different electron temperature. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{6245fig3.eps}
\end{figure}](/articles/aa/full/2007/02/aa6245-06/Timg79.gif) |
Figure 3:
Electron-proton Bremsstrahlung emissivity of a optically
thin gas for different electron temperatures at a proton
temperature of
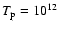 K. For electron temperatures lower than K. For electron temperatures lower than
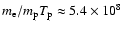 K the contributions of the
protons dominate (then the electron-proton bremsstrahlung rate is
essentially independent of the electron temperature),
while for larger electron temperatures the
classical result is reproduced. The long-dashed lines indicate the
limiting cases calculated in Eqs. (14) and (15), respectively, while the short-dashed line gives
the electron-electron Bremsstrahlung rate of
Svensson (1982). Note that for electron temperatures
in excess of approx. K the contributions of the
protons dominate (then the electron-proton bremsstrahlung rate is
essentially independent of the electron temperature),
while for larger electron temperatures the
classical result is reproduced. The long-dashed lines indicate the
limiting cases calculated in Eqs. (14) and (15), respectively, while the short-dashed line gives
the electron-electron Bremsstrahlung rate of
Svensson (1982). Note that for electron temperatures
in excess of approx.
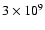 K the electrons are
relativistic and the plotted bremsstrahlung rate may be a very
crude approximation in this regime. K the electrons are
relativistic and the plotted bremsstrahlung rate may be a very
crude approximation in this regime. |
| Open with DEXTER |
The results for the electron-proton bremsstrahlung are only valid for non-relativistic protons and
electrons. However a first-order estimate of the relativistic correction can
be made by multiplying the energy integrated bremsstrahlung rate
with
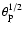 and
and
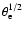 in the relativistic
case (
in the relativistic
case (
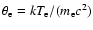 and
and
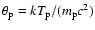 ). This leads to a steepening of
the temperature dependence from T1/2 in the non-relativistic to
T in the relativistic energy integrated
case as indicated by Svensson (1982) for
). This leads to a steepening of
the temperature dependence from T1/2 in the non-relativistic to
T in the relativistic energy integrated
case as indicated by Svensson (1982) for
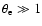 .
Gould (1980,1981) finds a
first-order correction factor of
.
Gould (1980,1981) finds a
first-order correction factor of
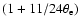 for
for
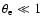 .
.
Figure 3 shows that for electron
temperatures in excess of 109 K electron-electron bremsstrahlung is
the dominant emission process. Hence a relativistic treatment of
electron-proton bremsstrahlung may not be
necessary. Haug (1975) however shows that although
electron-electron bremsstrahlung dominates the emission the electron-proton
bremsstrahlung still contributes half of the electron-electron
bremsstrahlung rate.
4 Conclusions
We have recalculated electron-proton bremsstrahlung for a
two-temperature plasma. Owing to the increasing importance of the
proton speed relative to the electron speed for
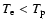 ,
the protons
can contribute significantly to the electron-proton bremsstrahlung. They dominate
the electron-proton Bremsstrahlung losses for electron temperatures lower than
,
the protons
can contribute significantly to the electron-proton bremsstrahlung. They dominate
the electron-proton Bremsstrahlung losses for electron temperatures lower than
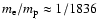 times the proton temperature.
times the proton temperature.
While our results are strictly valid only in the
non-relativistic regime, we give a crude extrapolation for the
relativistic case. The work presented here should only be considered
as exploratory work to outline the influence of a two-temperature
plasma on the electron-proton bremsstrahlung. If calculated for both the non-relativistic and
relativistic regime, one needs to account for the relativistic
kinematics and consider the Bethe & Heitler (1934) cross section,
adjusted for the effect presented here. While it is certainly needed
and desirable, such a treatment is beyond the scope of this paper. The
apparent dominance of electron-electron bremsstrahlung for electron
temperatures in excess of 109 K, however, does not make it that necessary.
The mechanism presented here, seen in the context of Coulomb
collisions between electrons and protons, is already well known in plasma physics. The NRL Plasma
Formulary (Huba 2006), a standard reference in plasma
physics for more than 25 years, gives
a formula for the Coulomb collision rate which depends only on the
electron temperature for
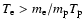 .
This is the classical
Spitzer (1962) result. For higher proton temperatures,
the electron temperature dependence weakens and the collision rate
only depends on the proton temperature owing to their larger speed
compared to the electrons. This effect is seen as wellin the work by
Stepney (1983) who derives the Coulomb collision rate in
a fully relativistic framework. Similar to our extrapolation
for the electron-proton bremsstrahlung rate,
they find a change in the exponent of the temperature dependence of +1/2, i.e. from T-3/2 to T-1.
.
This is the classical
Spitzer (1962) result. For higher proton temperatures,
the electron temperature dependence weakens and the collision rate
only depends on the proton temperature owing to their larger speed
compared to the electrons. This effect is seen as wellin the work by
Stepney (1983) who derives the Coulomb collision rate in
a fully relativistic framework. Similar to our extrapolation
for the electron-proton bremsstrahlung rate,
they find a change in the exponent of the temperature dependence of +1/2, i.e. from T-3/2 to T-1.
The importance of the effect presented in this paper needs to be
examined by comparing the characteristic timescales for Coulomb
collisions to equilibrate electron and proton temperature and the
Bremsstrahlung timescale. While it may not be of that strong influence
for the energetics of the two-temperature plasma, it could have an
observable signature due to the higher high-energy cut-off for the
Bremsstrahlung created by the kinetic energy of the protons, if it is
not hidden behind some more important emission mechanisms at these
energies.
Acknowledgements
M.M. thanks J.E. Pringle for encouraging this work and helpful
discussions. M.M. acknowledges
support from PPARC and useful suggestions by the anonymous referee.
- Bethe,
H. A., & Heitler, W. 1934, Proc. R. Soc. London A, 146,
83 [NASA ADS] (In the text)
- Blumenthal,
G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42,
237 [NASA ADS] [CrossRef]
- Brussaard, P. J.,
& van de Hulst, H. C. 1962, Rev. Mod. Phys., 34, 507 [NASA ADS] [CrossRef]
- Eardley, D. M.,
Lightman, A. P., & Shapiro, S. L. 1975, ApJ, 199,
L153 [NASA ADS] [CrossRef] (In the text)
- Gould, R. J.
1980, ApJ, 238, 1026 [NASA ADS] [CrossRef]
- Gould, R. J.
1981, ApJ, 243, 677 [NASA ADS] [CrossRef]
- Haardt, F., &
Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef]
- Haardt, F., &
Maraschi, L. 1993, ApJ, 413, 507 [NASA ADS] [CrossRef]
- Haug, E. 1975, Z.
Naturforsch. A, 30, 1546 (In the text)
-
Huba, J. D. 2006, NRL Plasma Formulary, Naval Research
Laboratory, 2006 revised version
(In the text)
- Rybicki, G. B.,
& Lightman, A. P. 1979, Radiative processes in
astrophysics (New York, Wiley-Interscience), 393
(In the text)
- Shapiro, S. L.,
Lightman, A. P., & Eardley, D. M. 1976, ApJ, 204,
187 [NASA ADS] [CrossRef]
- Spitzer, L. 1962,
Physics of Fully Ionized Gases (Physics of Fully Ionized Gases (New
York: Interscience), 2nd edition
(In the text)
- Stepney, S. 1983,
MNRAS, 202, 467 [NASA ADS] (In the text)
- Sutherland, R. S.
1998, MNRAS, 300, 321 [NASA ADS] [CrossRef] (In the text)
- Svensson, R. 1982,
ApJ, 258, 335 [NASA ADS] [CrossRef] (In the text)
- Wandel, A., &
Liang, E. P. 1991, ApJ, 380, 84 [NASA ADS] [CrossRef] (In the text)
- Zycki, P. T.,
Collin-Souffrin, S., & Czerny, B. 1995, MNRAS, 277, 70 [NASA ADS]
Copyright ESO 2006
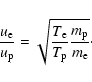
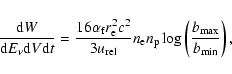
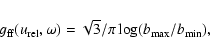
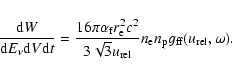
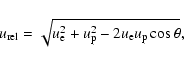
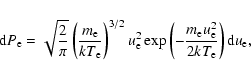
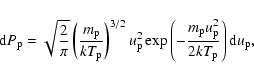
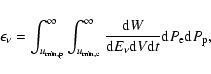
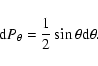
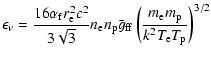
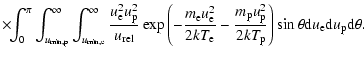
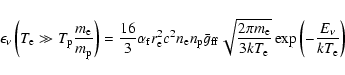
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{6245fig2.eps}
\end{figure}](/articles/aa/full/2007/02/aa6245-06/Timg78.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{6245fig3.eps}
\end{figure}](/articles/aa/full/2007/02/aa6245-06/Timg79.gif)