A&A 461, 509-522 (2007)
DOI: 10.1051/0004-6361:20065756
I. Platais1 - C. Melo2,3 - J.-C. Mermilliod4 - V. Kozhurina-Platais5 - J. P. Fulbright1 - R. A. Méndez2 - M. Altmann2 - J. Sperauskas6
1 -
Department of Physics and Astronomy, Johns Hopkins University,
3400 North Charles Street, Baltimore, MD 21218, USA
2 -
Departamento de Astronomía, Universidad de Chile, Casilla 36-D, Santiago, Chile
3 -
European Southern Observatory, Casilla 19001, Santiago 19, Chile
4 -
Laboratoire d'Astrophysique de l'École polytechnique fédérale de Lausanne, 1290 Chavannes-des-Bois, Switzerland
5 -
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore,
MD 21218, USA
6 -
Vilnius University Observatory, Ciurlionio 29, Vilnius 2009, Lithuania
Received 2 June 2006 / Accepted 21 August 2006
Abstract
Context. Young open clusters provide important clues to the interface between the main sequence and pre-main-sequence phases of stellar evolution. The young and nearby open cluster IC 2391 is well-suited to studies of these two evolutionary phases.
Aims. We establish a bona fide set of cluster members and then analyze this set in terms of binary frequency, projected rotational velocities, [Fe/H], and lithium abundance. In the wake of the Hipparcos distance controversy for the Pleiades, we compare the main-sequence fitting distance modulus to the Hipparcos mean parallax for IC 2391.
Methods. We have obtained new proper motions for 6991 stars down to
![]() -16 over a
-16 over a ![]() 9-deg2 area of the sky comprising IC 2391. The precision of proper motions,
9-deg2 area of the sky comprising IC 2391. The precision of proper motions,
![]() mas yr-1, allowed us to calculate reliable membership probabilities. We also obtained precise radial velocity and
mas yr-1, allowed us to calculate reliable membership probabilities. We also obtained precise radial velocity and ![]() measurements with CORAVEL and FEROS for 76 probable cluster members. The cluster's mean radial velocity is
measurements with CORAVEL and FEROS for 76 probable cluster members. The cluster's mean radial velocity is
![]() km s-1. The FEROS high-resolution spectra were used to determine both the [Fe/H] abundance in the four main sequence dwarfs of IC 2391 and the Li abundance in 47 stars. In addition, new BV CCD photometry was obtained for the majority of probable cluster members.
km s-1. The FEROS high-resolution spectra were used to determine both the [Fe/H] abundance in the four main sequence dwarfs of IC 2391 and the Li abundance in 47 stars. In addition, new BV CCD photometry was obtained for the majority of probable cluster members.
Results. The proper-motion survey covers a 6 times larger sky area than the prior targeted searches for cluster members in IC 2391. A total of 66 stars are considered bona fide cluster members down to a mass equivalent to 0.5 ![]() .
A quarter of them have been newly identified with many in the F2-K5 spectral range, which is crucial for a main-sequence fit. We find a mean [Fe/H] value of
.
A quarter of them have been newly identified with many in the F2-K5 spectral range, which is crucial for a main-sequence fit. We find a mean [Fe/H] value of
![]() ,
when a solar abundance of
,
when a solar abundance of
![]() (Fe) = 7.45 is adopted. The main sequence fitting yields a distance modulus that is 0.19 mag larger than that derived from Hipparcos parallaxes; thus this offset nearly has the size of a similar offset found for the Pleiades. The Li abundance pattern is similar to the earlier findings and is typical for a 40 Myr old open cluster.
(Fe) = 7.45 is adopted. The main sequence fitting yields a distance modulus that is 0.19 mag larger than that derived from Hipparcos parallaxes; thus this offset nearly has the size of a similar offset found for the Pleiades. The Li abundance pattern is similar to the earlier findings and is typical for a 40 Myr old open cluster.
Conclusions. A variety of new data on the probable members of IC 2391 improve essentially all observational parameters of this young open cluster.
Key words: open clusters and associations: individual: IC 2391 - astrometry - stars: kinematics - stars: abundances
IC 2391 is a young (![]() 35 Myr) and nearby (
35 Myr) and nearby (![]() pc) open cluster
located in Vela (
pc) open cluster
located in Vela (
![]() ,
,
![]() ). Its proximity
is very appealing for any detailed studies of intrinsically faint
low-mass stars and brown dwarfs (Barrado y Navascués et al. 2004).
The significance of IC 2391 is clearly demonstrated by a large number
of literature references over the last decade in the SIMBAD Astronomical
Database:
). Its proximity
is very appealing for any detailed studies of intrinsically faint
low-mass stars and brown dwarfs (Barrado y Navascués et al. 2004).
The significance of IC 2391 is clearly demonstrated by a large number
of literature references over the last decade in the SIMBAD Astronomical
Database: ![]() 200 publications where the cluster has been mentioned
or studied. One problem facing the researchers of IC 2391
is the scarcity of confirmed
cluster members. For a long time, the known cluster membership was confined to
merely
200 publications where the cluster has been mentioned
or studied. One problem facing the researchers of IC 2391
is the scarcity of confirmed
cluster members. For a long time, the known cluster membership was confined to
merely ![]() 20 stars, all brighter than
20 stars, all brighter than ![]() (Hogg 1960).
Then, Stauffer et al. (1989) reported on the proper-motion study of
883 stars over a
(Hogg 1960).
Then, Stauffer et al. (1989) reported on the proper-motion study of
883 stars over a
![]() area. Proper motions,
area. Proper motions,
![]() photometry, and high-resolution spectroscopy together
yielded a list of ten additional probable cluster members down
to V=14. This list was substantially extended by using the ROSAT
imaging data (Patten & Simon 1993,1996; Simon & Patten 1998) to take
advantage of the known strong X-ray activity among the young
G-K-M spectral type stars. In the follow-up spectroscopic study,
Stauffer et al. (1997) confirmed the cluster membership of 23 X-ray selected stars down to
photometry, and high-resolution spectroscopy together
yielded a list of ten additional probable cluster members down
to V=14. This list was substantially extended by using the ROSAT
imaging data (Patten & Simon 1993,1996; Simon & Patten 1998) to take
advantage of the known strong X-ray activity among the young
G-K-M spectral type stars. In the follow-up spectroscopic study,
Stauffer et al. (1997) confirmed the cluster membership of 23 X-ray selected stars down to ![]() ,
using the radial velocity,
Li line, and H
,
using the radial velocity,
Li line, and H![]() appearance as membership criteria.
Dodd (2004) attempted to identify more cluster members by
mining USNO-B and 2MASS catalogs. From 185 astrometrically selected
possible cluster members, a total of 35 stars are brighter than
R=15. However, a disturbingly small fraction of these stars
(
appearance as membership criteria.
Dodd (2004) attempted to identify more cluster members by
mining USNO-B and 2MASS catalogs. From 185 astrometrically selected
possible cluster members, a total of 35 stars are brighter than
R=15. However, a disturbingly small fraction of these stars
(![]() 20%) are common with the Patten & Simon (1993) list in
the same magnitude range and spatial coverage. The latest search
for cluster members in the central
20%) are common with the Patten & Simon (1993) list in
the same magnitude range and spatial coverage. The latest search
for cluster members in the central
![]() region
of IC 2391 by the XMM-Newton X-ray observatory resulted in nine
relatively faint possible new members (Marino et al. 2005).
region
of IC 2391 by the XMM-Newton X-ray observatory resulted in nine
relatively faint possible new members (Marino et al. 2005).
As indicated above, proper motions have been used as a kinematic
membership discriminator for IC 2391. However,
only the study by King (1979) provides precise relative proper
motions (
![]() mas yr-1) down to
mas yr-1) down to ![]() over a
over a
![]() area.
In this study, from a total of 232 stars about 40 have proper motions consistent with membership in IC 2391.
No formal membership probabilities are calculated, apparently owing
to the sparseness of the cluster.
Another way to ascertain the membership status, independent of
any assumptions on the astrophysical properties of probable
cluster members, is to use radial velocities.
There is a rich literature on this subject for IC 2391, e.g.,
Feinstein (1961), Buscombe (1965), Perry & Bond (1969), van Hoof (1972),
Levato et al. (1988), Stauffer et al. (1997), Barrado y Navascués et al. (1999).
Nearly 100 stars have had their
radial velocities measured, many of them several times.
In many cases, however, the precision of the radial velocities was
low, especially for the early and very late type stars, thereby largely
precluding assignment of a reliable membership status to them.
area.
In this study, from a total of 232 stars about 40 have proper motions consistent with membership in IC 2391.
No formal membership probabilities are calculated, apparently owing
to the sparseness of the cluster.
Another way to ascertain the membership status, independent of
any assumptions on the astrophysical properties of probable
cluster members, is to use radial velocities.
There is a rich literature on this subject for IC 2391, e.g.,
Feinstein (1961), Buscombe (1965), Perry & Bond (1969), van Hoof (1972),
Levato et al. (1988), Stauffer et al. (1997), Barrado y Navascués et al. (1999).
Nearly 100 stars have had their
radial velocities measured, many of them several times.
In many cases, however, the precision of the radial velocities was
low, especially for the early and very late type stars, thereby largely
precluding assignment of a reliable membership status to them.
Often IC 2391 is considered along with IC 2602, because both have very
similar properties and are separated spatially only by ![]() 50 pc, thus
suggesting a common origin. Their absolute proper motions, however,
differ significantly. The projected total velocity in the
tangential plane for IC 2391 is 33.8 mas yr-1, whereas
for IC 2602 it is only 20.5 mas yr-1 (Robichon et al. 1999).
A much larger tangential velocity of IC 2391 considerably
increases the reliability of membership probabilities drawn from
proper motions, since a smaller fraction of field stars are
expected to share the motion of the cluster. This and the limited
precision of our proper motions are one of the main reasons
for selecting IC 2391 as the subject of this study.
50 pc, thus
suggesting a common origin. Their absolute proper motions, however,
differ significantly. The projected total velocity in the
tangential plane for IC 2391 is 33.8 mas yr-1, whereas
for IC 2602 it is only 20.5 mas yr-1 (Robichon et al. 1999).
A much larger tangential velocity of IC 2391 considerably
increases the reliability of membership probabilities drawn from
proper motions, since a smaller fraction of field stars are
expected to share the motion of the cluster. This and the limited
precision of our proper motions are one of the main reasons
for selecting IC 2391 as the subject of this study.
Randich et al. (2001) spectroscopically analyzed ![]() 50 X-ray selected
candidate members in IC 2391 and IC 2602. From the analysis of 8
Fe I lines in four stars, the mean metallicity of IC 2391 was derived
to be [Fe/H] =
50 X-ray selected
candidate members in IC 2391 and IC 2602. From the analysis of 8
Fe I lines in four stars, the mean metallicity of IC 2391 was derived
to be [Fe/H] =
![]() .
In this study, Li abundance was
obtained for 32 possible members of IC 2391, covering a wide
range of
.
In this study, Li abundance was
obtained for 32 possible members of IC 2391, covering a wide
range of
![]() - from 3500 to 6600 K. It was found that stars
warmer than
- from 3500 to 6600 K. It was found that stars
warmer than ![]() 5800 K or more massive than
5800 K or more massive than ![]() 1
1 ![]() show no
significant signs of Li depletion. For cooler late-G to
early-K stars, the pattern of Li abundances in IC 2391 and the
Pleiades is similar, although hinting that in this
show no
significant signs of Li depletion. For cooler late-G to
early-K stars, the pattern of Li abundances in IC 2391 and the
Pleiades is similar, although hinting that in this
![]() range
Li is less depleted in IC 2391, as one would expect from the age
difference. A more detailed analysis of Li abundance in IC 2391 is
hindered by the small number of stars in the Randich et al. (2001) sample.
range
Li is less depleted in IC 2391, as one would expect from the age
difference. A more detailed analysis of Li abundance in IC 2391 is
hindered by the small number of stars in the Randich et al. (2001) sample.
Young open clusters appear to have stars with a broad range of rotational
rates (Herbst & Mundt 2005). That is also confirmed by the observed
rotational rates for late-type stars (Patten & Simon 1996)
and the ![]() distribution in IC 2391 (Stauffer et al. 1997).
From the standpoint of Li abundances, X-ray luminosities, and
stellar evolution, it is vital to identify fast rotators in
the enlarged sample of cluster stars.
distribution in IC 2391 (Stauffer et al. 1997).
From the standpoint of Li abundances, X-ray luminosities, and
stellar evolution, it is vital to identify fast rotators in
the enlarged sample of cluster stars.
In some aspects, the level of our understanding of the open cluster IC 2391 is
similar to NGC 2451A, which was recently studied by Platais et al. (2001) as one of
the WIYN Open Cluster Study (WOCS) targets.
The lack of comprehensive astrometric cluster membership prompted
us to include IC 2391 among the WOCS clusters. Following the WOCS
strategy (Mathieu 2000), we derived new proper motions and
calculated the cluster membership probabilities. For many probable
cluster members, high-resolution spectroscopy served to measure the
radial velocities, projected rotational velocities ![]() ,
Li abundance, and equivalent width of H
,
Li abundance, and equivalent width of H![]() .
A few carefully
selected cluster stars are used to obtain metallicity [Fe/H].
New CCD photometry is used to construct reliable color-magnitude diagram
and perform the isochrone fit.
.
A few carefully
selected cluster stars are used to obtain metallicity [Fe/H].
New CCD photometry is used to construct reliable color-magnitude diagram
and perform the isochrone fit.
A total of four ![]() inch photographic
plates (
inch photographic
plates (
![]() mm-1), taken
with the 51 cm double astrograph of Cesco Observatory in El Leoncito,
Argentina, were used for astrometry. Two of these
visual-bandpass plates (103a-G emulsion and OG-515 filter) were
obtained in 1967.29, the other two in 1996.14. An
objective wire-grating was used to produce diffraction images for
all stars brighter than
mm-1), taken
with the 51 cm double astrograph of Cesco Observatory in El Leoncito,
Argentina, were used for astrometry. Two of these
visual-bandpass plates (103a-G emulsion and OG-515 filter) were
obtained in 1967.29, the other two in 1996.14. An
objective wire-grating was used to produce diffraction images for
all stars brighter than ![]() .
Each first-epoch plate contains
two exposures: a 30 min and an offset 1 min exposure.
.
Each first-epoch plate contains
two exposures: a 30 min and an offset 1 min exposure.
Our target stars were drawn from the COSMOS/UKST Object Catalog
(Yentis et al. 1992). In this catalog the object brightness is
given in ![]() magnitudes as derived in the natural photographic system
(IIa-J emulsion and GG-395 filter) of the UK 1.2 m Schmidt Telescope
at Siding Spring, Australia (Blair & Gilmore 1982).
Due to the scan-time limitations set by the
measuring machine, the sample selection required an optimization. All stars
down to
magnitudes as derived in the natural photographic system
(IIa-J emulsion and GG-395 filter) of the UK 1.2 m Schmidt Telescope
at Siding Spring, Australia (Blair & Gilmore 1982).
Due to the scan-time limitations set by the
measuring machine, the sample selection required an optimization. All stars
down to
![]() were chosen in a
were chosen in a
![]() rectangle centered on
rectangle centered on
![]() and
and
![]() (equinox J2000.0). A sub-sample
of fainter stars at
(equinox J2000.0). A sub-sample
of fainter stars at
![]() in the same area served as
anonymous astrometric reference stars. Then, within this rectangle
all additional stars down to
in the same area served as
anonymous astrometric reference stars. Then, within this rectangle
all additional stars down to
![]() were selected in a circle
with the radius of
were selected in a circle
with the radius of
![]() centered on
centered on
![]() and
and
![]() .
.
Altogether, our initial sample included over 7000 stars. All measurable images of these stars were digitized with the Yale 2020G PDS microdensitometer in a fine-raster, object-by-object mode. The image positions were determined using the Yale Image Centering routine (Lee & van Altena 1983), which includes a two-dimensional Gaussian fit.
The positions and proper motions were calculated using the standard
SPM (Southern Proper Motion program) astrometric reductions,
described in detail by Girard et al. (1998) and Platais et al. (1998).
Owing to the relatively small 9-deg2 field, only linear and
quadratic plate-tilt terms were used in the proper-motion plate model. The
standard error of proper motions was estimated to range from 1.4 to 2.1 mas yr-1, depending on the star's magnitude and hence
on the number of available grating images. The calculated relative
proper motions are free of apparent systematic errors. The
distribution of proper motions or a vector-point diagram (VPD)
is shown in Fig. 1. A visible clumping of proper motions at
![]() ,
,
![]() mas yr-1 indicates the presence of
IC 2391 members.
mas yr-1 indicates the presence of
IC 2391 members.
The local sample method (Kozhurina-Platais et al. 1995) was used to
calculate the cluster membership. In this method, for each target
star a representative sub-sample (a bin) of other stars is formed that
shares the properties of the target, such as the brightness.
We used a wide 10-mag sliding brightness bin, which for the
brightest and faintest stars narrows down to 5 mag.
No spatial window was used for this sample of proper motions.
Similar to the case of NGC 2451A (Platais et al. 2001), a flat
distribution of field stars in VPD was adopted in the vicinity
of the cluster centroid. The resulting membership probability,
![]() ,
is defined as
,
is defined as
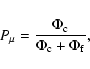 |
(1) |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{5756fg1.eps}
\end{figure}](/articles/aa/full/2007/02/aa5756-06/Timg51.gif) |
Figure 1:
Proper-motion vector point diagram in the area of IC 2391.
A clump of proper motions at
|
| Open with DEXTER | |
Finally, precise equatorial coordinates were calculated for all stars,
choosing UCAC2 stars (Zacharias et al. 2004) as a reference frame.
The coordinate transformation required a quadratic plate model
supplemented with two main cubic distortion terms. The standard
error of that transformation via the least-squares formalism
is ![]() 60 mas. At the epoch and equinox of J2000, the estimated
average accuracy of the catalog
60 mas. At the epoch and equinox of J2000, the estimated
average accuracy of the catalog![]() positions is about 30 mas. We note
that this study provides precise coordinates for many X-ray selected
cluster members, which so far have had only approximate coordinates from
Patten & Simon (1996) and Marino et al. (2005).
positions is about 30 mas. We note
that this study provides precise coordinates for many X-ray selected
cluster members, which so far have had only approximate coordinates from
Patten & Simon (1996) and Marino et al. (2005).
A few sources providing ![]() photometry cover mainly the inner area
of IC 2391, e.g., Hogg (1960), Lyngå (1960), Perry & Hill (1969).
In January 1997 we obtained new CCD BV photometry for the
majority of the possible proper-motion members. The observations were
made at the Cerro Tololo Inter-American Observatory (CTIO) 0.9 m
telescope with the Tektronics
photometry cover mainly the inner area
of IC 2391, e.g., Hogg (1960), Lyngå (1960), Perry & Hill (1969).
In January 1997 we obtained new CCD BV photometry for the
majority of the possible proper-motion members. The observations were
made at the Cerro Tololo Inter-American Observatory (CTIO) 0.9 m
telescope with the Tektronics
![]() CCD chip, which covers
CCD chip, which covers
![]() on the sky.
on the sky.
As in the case of NGC 2451A (Platais et al. 2001), each probable cluster
member or else a group of members with mutual separations less than
![]() 10
10
![]() was observed individually. Only a small fraction
of these stars could be identified on more than one CCD frame in each filter.
In total, 114 CCD frames
were obtained in B and V filters with exposure time varied from 1 to
150 s, depending on the star's magnitude. A set of Landolt (1992) standards
was taken three times a night over 22-24 January, 1997 - spanning our
observations of IC 2391. The twilight sky frames were used to correct
the pixel-to-pixel sensitivity variations.
was observed individually. Only a small fraction
of these stars could be identified on more than one CCD frame in each filter.
In total, 114 CCD frames
were obtained in B and V filters with exposure time varied from 1 to
150 s, depending on the star's magnitude. A set of Landolt (1992) standards
was taken three times a night over 22-24 January, 1997 - spanning our
observations of IC 2391. The twilight sky frames were used to correct
the pixel-to-pixel sensitivity variations.
All CCD frames were reduced using the IRAF DAOPHOTX photometry package. The aperture photometry routine PHOT was applied because the target stars were optimally exposed and well-isolated. The details of transformation of the instrumental magnitudes into the standard BV system for this observing run are given in Platais et al. (2001). The final BV magnitudes are believed to be on the standard system to within 0.02 mag and have a standard error of 0.03 mag in V and 0.02 in B-V. It should be noted that the reddest stars may have a slightly less accurate photometry since the reddest standard star has only B-V=1.18.
Table 2 shows the comparison of our CCD BV photometry with seven
other sources of BV photometry, mainly photoelectric. This table
contains the literature reference, the number of common stars (n),
mean ![]() and
and
![]() in the sense of our CCD
photometry minus the published one. The errors are standard
deviations from the mean calculated difference in magnitude or color.
All the sources of photometry
are consistent, though on average our CCD V-magnitudes
appear to be fainter by
in the sense of our CCD
photometry minus the published one. The errors are standard
deviations from the mean calculated difference in magnitude or color.
All the sources of photometry
are consistent, though on average our CCD V-magnitudes
appear to be fainter by ![]() 0.03 than those from the other sources.
0.03 than those from the other sources.
Table 2: Comparison of BV photometry ``CCD-Source''.
The radial-velocity observations were made with the photoelectric spectrometer
CORAVEL (Mayor 1985; Baranne et al. 1979) on the Danish 1.54 m telescope at
ESO, La Silla, Chile. They were obtained starting in
March 1984 through April 1996 (when the CORAVEL was retired)
during the course of regular
ESO and Danish time runs allocated to the open cluster studies.
In the CORAVEL-type instruments, the spectrum of a star is
electro-mechanically correlated, i.e., scanned with an appropriate
spectral mask in the focal plane. The output correlation profile
can be described with a Gaussian (position, depth, width)
plus a continuum level, readily providing an estimate of radial
velocity and ![]() .
The latter is computed following the
techniques described by Benz & Mayor (1981,1984).
The radial velocities are on the system defined by Udry et al. (1999), calibrated
with high-precision data from the ELODIE spectrograph
(Baranne et al. 1996).
.
The latter is computed following the
techniques described by Benz & Mayor (1981,1984).
The radial velocities are on the system defined by Udry et al. (1999), calibrated
with high-precision data from the ELODIE spectrograph
(Baranne et al. 1996).
The initial sample consisted of only 8 stars, all brighter than B=11.6and already thought to be possible members in 1983.
Three of them (3664 = SHJM 7, 3722, 5382) were found to be SB1
spectroscopic binaries and two were found to be SB2 (389, 4413).
It should be noted that CORAVEL can detect a secondary if the
magnitude difference is smaller than ![]() 1.5-1.8 mag.
1.5-1.8 mag.
The list of candidate cluster members was greatly enlarged by the ROSAT X-ray detections in the area of IC 2391 (Patten & Simon 1996,1993). A total of 17 such stars (B<13.8) were observed once or twice in February 1995 and/or January-April 1996. Among them, two additional likely spectroscopic binaries (5768, 5859) were detected.
Two presumably constant stars are common to the CORAVEL and FEROS
(see Sect. 5) samples. The radial velocity difference, in the sense
CORAVEL-FEROS, for star 4362 is +0.09 km s-1 and for
star 4809 is -0.10 km s-1. This indicates very good agreement
between the two systems.
There are 13 stars in common with the radial-velocity data obtained in
1995 at CTIO by Stauffer et al. (1997). One of them, 5859 = VXR 67a, appears to be
a spectroscopic binary judging from two CORAVEL observations
(Table 3).
The spectroscopic binary, suspected by Stauffer et al. (1997), 4549 = VXR 30, is
a definite SB1 from the CORAVEL data.
For the remaining 11 stars, the radial velocity difference
"CORAVEL-CTIO'' is
![]() km s-1, which is in good
agreement with the listed internal and external errors by Stauffer et al. (1997).
km s-1, which is in good
agreement with the listed internal and external errors by Stauffer et al. (1997).
Table 3 contains all CORAVEL heliocentric radial velocities and their estimated standard errors. The last four entries were obtained with the Lithuanian CORAVEL-type spectrometer (Upgren et al. 2002) at the CASLEO 2.2 m telescope in El Leoncito, Argentina, in February 2002.
Table 4 lists the mean radial velocities,
![]() ,
the associated
errors and other parameters. For a star, depending on the structure
of the correlation profile, up to three sets of parameters
(for components A and B, and a blend) can be given.
The estimated formal standard deviation of the mean radial velocity
is denoted by
,
the associated
errors and other parameters. For a star, depending on the structure
of the correlation profile, up to three sets of parameters
(for components A and B, and a blend) can be given.
The estimated formal standard deviation of the mean radial velocity
is denoted by ![]() .
The estimated mean internal uncertainty
of a radial velocity measurement is denoted by
.
The estimated mean internal uncertainty
of a radial velocity measurement is denoted by
![]()
![]() ,
where n is
the number of measurements. The internal error of an individual observation
consists of three components as described by Baranne et al. (1979) and Mermilliod & Mayor (1989).
We note that the uncertainty,
,
where n is
the number of measurements. The internal error of an individual observation
consists of three components as described by Baranne et al. (1979) and Mermilliod & Mayor (1989).
We note that the uncertainty, ![]() ,
is progressively underestimated at
increasing
,
is progressively underestimated at
increasing ![]() values (Nordstroem et al. 1996).
The ratio, standard deviation
values (Nordstroem et al. 1996).
The ratio, standard deviation ![]() vs. the mean internal uncertainty of
individual measurements, denoted by the E/I, is used to calculate the
probability
vs. the mean internal uncertainty of
individual measurements, denoted by the E/I, is used to calculate the
probability ![]() that the scatter is due to random noise.
A star is considered a spectroscopic binary, if
that the scatter is due to random noise.
A star is considered a spectroscopic binary, if
![]() .
In the case of a single measurement, the
.
In the case of a single measurement, the ![]() is meaningless and
marked by 9.999. Additional Cols. 6-9 contain the
number of measurements, n, the time span in days covered by the observations,
is meaningless and
marked by 9.999. Additional Cols. 6-9 contain the
number of measurements, n, the time span in days covered by the observations,
![]() ,
measured
,
measured ![]() and its standard error. Binarity status
and the component are indicated in last column.
and its standard error. Binarity status
and the component are indicated in last column.
Finally, we note that the systems of ![]() from CORAVEL, FEROS, and
Randich et al. (2001) are all in excellent agreement for
from CORAVEL, FEROS, and
Randich et al. (2001) are all in excellent agreement for
![]() km s-1to within
km s-1to within ![]() 1 km s-1, but can differ by up to
1 km s-1, but can differ by up to ![]() 10 km s-1for large
10 km s-1for large ![]() and/or in some cases of spectroscopic binaries.
and/or in some cases of spectroscopic binaries.
The spectroscopic observations were carried out in two observing runs
in February 2004 and February 2005 using the high-resolution, two-fiber
(![]() 000) FEROS echelle spectrograph (Kaufer et al. 1999) at the ESO
2.2 m telescope in La Silla, Chile. This spectrograph provides
a wavelength range from 360 to 920 nm, covered by 39 echelle orders.
Such a wide wavelength range is essential in the chemical abundance
studies allowing one to select appropriate unblended metal lines.
The observations were taken in the Object-Sky mode
in which the target is centered onto the Object fiber, whereas the Sky fiber
collects the light from the sky background. The reductions of spectra
were performed using the standard FEROS pipeline, which includes flat-fielding,
sky-background subtraction, removal of cosmic rays, wavelength calibration,
and barycentric velocity correction. The pipeline yields a 1D re-binned
spectrum evenly sampled at 0.03 Å steps.
000) FEROS echelle spectrograph (Kaufer et al. 1999) at the ESO
2.2 m telescope in La Silla, Chile. This spectrograph provides
a wavelength range from 360 to 920 nm, covered by 39 echelle orders.
Such a wide wavelength range is essential in the chemical abundance
studies allowing one to select appropriate unblended metal lines.
The observations were taken in the Object-Sky mode
in which the target is centered onto the Object fiber, whereas the Sky fiber
collects the light from the sky background. The reductions of spectra
were performed using the standard FEROS pipeline, which includes flat-fielding,
sky-background subtraction, removal of cosmic rays, wavelength calibration,
and barycentric velocity correction. The pipeline yields a 1D re-binned
spectrum evenly sampled at 0.03 Å steps.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{5756fg2.eps}
\end{figure}](/articles/aa/full/2007/02/aa5756-06/Timg82.gif) |
Figure 2: Drift correction for the night of February 27, 2004. Standard stars are shown as open squares and the mean drift as filled circles. The dashed line is the adopted drift as a function of time. |
| Open with DEXTER | |
Radial velocities are derived by cross-correlation techniques
using a K0 III spectral type digital binary mask as the template
(Baranne et al. 1979; Queloz 1995).
The resulting cross-correlation function (CCF) can in most cases be
approximated by a Gaussian function whose center readily gives the
radial velocity and the width (Gaussian ![]() )
related to
broadening mechanisms such as turbulent motion, gravity pressure, and rotation.
)
related to
broadening mechanisms such as turbulent motion, gravity pressure, and rotation.
Owing to a relatively high
S/N, normally higher than 50 (see Table 5),
the photon noise errors in our radial velocity measurements
typically range between 5-15 m s-1. The final uncertainties in
derived radial velocities are a combination of the photon noise
errors and the overnight spectrograph
drift due to the changes in the index of air refractivity and
atmospheric pressure. Usually, these shifts are on the order of a few
hundred m s-1 per night. One way to correct for this
drift is to have the calibration lamp
illuminate a second fiber while the first fiber receives the
stellar light. Although the FEROS two-fiber configuration allows
for this option (Setiawan et al. 2000), the subsequent data reduction and
analysis is complicated and not warranted for young stars where
the radial-velocity jitter exceeds the internal precision
of measurement by a lot. For example, for very active and young T Tauri
type stars, this jitter is not lower than ![]() 0.6 km s-1 and can be
as high as
0.6 km s-1 and can be
as high as ![]() 2 km s-1 (Melo 2003). With age these
effects gradually abate, though the rotational modulation of stellar
active regions can generate a radial velocity scatter up to
50 m s-1 even at the age of Hyades at
2 km s-1 (Melo 2003). With age these
effects gradually abate, though the rotational modulation of stellar
active regions can generate a radial velocity scatter up to
50 m s-1 even at the age of Hyades at ![]() 600 Myr (Paulson et al. 2004).
We therefore opted for a simpler approach, as described below.
600 Myr (Paulson et al. 2004).
We therefore opted for a simpler approach, as described below.
In order to correct for this drift, 1-3 radial velocity standards from
the CORALIE extra-solar planet survey were observed a few times
during the night. For each standard star, the velocity drift
was computed as the difference between the CORALIE radial velocity and
the observed radial velocity. In the case of more than one standard star,
the mean drift was calculated. The radial-velocity corrections for
the program stars were computed using a linear interpolation between
each two drift points. A typical drift correction is shown in
Fig. 2. Over two observing runs, the rms
of the differences between the corrected radial velocities of standard stars
and the CORALIE radial velocities is below 20 m s-1, indicating
that the procedure works well. One should keep in mind, however, that
the final uncertainty of radial velocities could be higher, since
at some level a linear interpolation might not approximate the actual
pattern of a drift accurately. We note that the rms scatter of the
drift correction between the FEROS and CORALIE radial velocities is
![]() 150 m s-1, similar to the value found by Melo et al. (2001) using
150 m s-1, similar to the value found by Melo et al. (2001) using ![]() Cet as a standard.
Cet as a standard.
A few double-lined spectroscopic binaries were found among our target stars (Table 5, Fig. 5). Their cluster membership status is briefly discussed in Sect. 6.4.
The width, ![]() ,
of the cross-correlation function (CCF) is a product
of several broadening mechanisms related to gravity, turbulence,
magnetic fields, effective temperature, metallicity, and rotation. In addition,
the instrumental profile also contributes to the broadening of spectral
lines and, therefore, to the CCF. Thus, in order to correctly measure the
contribution of rotation to the width of the CCF, we should model all
sources of broadening, except what is due to rotation.
The width of FEROS CCF was calibrated as described in Melo et al. (2001).
For fast rotators (
,
of the cross-correlation function (CCF) is a product
of several broadening mechanisms related to gravity, turbulence,
magnetic fields, effective temperature, metallicity, and rotation. In addition,
the instrumental profile also contributes to the broadening of spectral
lines and, therefore, to the CCF. Thus, in order to correctly measure the
contribution of rotation to the width of the CCF, we should model all
sources of broadening, except what is due to rotation.
The width of FEROS CCF was calibrated as described in Melo et al. (2001).
For fast rotators (
![]() km s-1), the final
km s-1), the final ![]() was derived as follows. The CCF is fitted by a family of functions
was derived as follows. The CCF is fitted by a family of functions
![]() which is a convolution
of the CCF of a non-rotating star, g0, in turn approximated by a Gaussian
and the Gray (1992) rotational profile
computed for a set of discrete rotational velocities,
which is a convolution
of the CCF of a non-rotating star, g0, in turn approximated by a Gaussian
and the Gray (1992) rotational profile
computed for a set of discrete rotational velocities,
![]() .
For each
function
.
For each
function
![]() ,
we can find the radial velocity
,
we can find the radial velocity ![]() ,
the depth D, and the continuum C by minimizing the quantity
,
the depth D, and the continuum C by minimizing the quantity
![]() .
Figure 1 in Melo (2003) illustrates this method.
The uncertainty of the
.
Figure 1 in Melo (2003) illustrates this method.
The uncertainty of the ![]() measurement is
measurement is ![]() 1.5 km s-1 for
1.5 km s-1 for
![]() km s-1 and
km s-1 and ![]() 10% of the
10% of the ![]() value
for
value
for
![]() km s-1. The FEROS measurements of
km s-1. The FEROS measurements of ![]() are listed in Table 5. The averaged
are listed in Table 5. The averaged ![]() values
are given in Table 8. In the case of SB2 spectroscopic
binaries, an average
values
are given in Table 8. In the case of SB2 spectroscopic
binaries, an average ![]() is given only for the A-component.
is given only for the A-component.
The FEROS high-resolution spectra are used to determine the [Fe/H] abundance of IC 2391. However, other abundance studies of relatively young open clusters, such as the Hyades, Pleiades, and the Ursa Major moving group (Paulson et al. 2003; Schuler et al. 2006; Yong et al. 2004), have found that the atmospheres of the G- and K-dwarfs show deviations from the simple, plane-parallel atmosphere models used in most abundance studies. High excitation lines and lines of ionized species are stronger than predicted by simple model atmospheres, even though the same models perform adequately for older G- and K- dwarfs like the Sun. Schuler et al. (2006) suggest that photospheric spots and faculae in young dwarfs can possibly produce such deviations.
Until the solution to this problem is found, we only perform a
simple abundance analysis on a few stars in IC 2391. The atmosphere's
problem is minimized in warmer G-dwarfs, hence we chose
four slowly-rotating G-dwarfs with
![]() values ranging
between 5200 K and 5900 K in the sample.
values ranging
between 5200 K and 5900 K in the sample.
We adopted the list of iron lines from Fulbright et al. (2006). The lines in this
list were selected to be those least affected by blending for use in the
study of metal-rich bulge giants, where the differential analysis was
done relative to Arcturus.
For this study, we used the Sun as the differential standard
and adopt a solar iron abundance of
![]() (Fe) = 7.45. The lines were measured manually
using the IRAF splot package, and the measured equivalent widths are given
in Table 6. We measured the solar line equivalent widths from
the Solar Atlas
by Kurucz et al. (1984) and a high S/N (>200) FEROS sky spectrum.
We did not use lines stronger than
(Fe) = 7.45. The lines were measured manually
using the IRAF splot package, and the measured equivalent widths are given
in Table 6. We measured the solar line equivalent widths from
the Solar Atlas
by Kurucz et al. (1984) and a high S/N (>200) FEROS sky spectrum.
We did not use lines stronger than ![]() 120 mÅ.
120 mÅ.
There is good agreement between the results from the Solar Atlas and the
FEROS solar spectrum. If the gf-values of the Fe lines are adjusted to
yield a solar Fe abundance of
![]() (Fe) = 7.45 for the equivalent
widths measured in the Solar Atlas, the FEROS sky spectrum yields
an Fe I abundance of
(Fe) = 7.45 for the equivalent
widths measured in the Solar Atlas, the FEROS sky spectrum yields
an Fe I abundance of
![]() (97 lines) and an Fe II abundance
of
(97 lines) and an Fe II abundance
of
![]() (5 lines). Therefore, we believe that the instrumental
effects in our differential analysis method are negligible.
(5 lines). Therefore, we believe that the instrumental
effects in our differential analysis method are negligible.
Due to the aforementioned potential problems with the atmospheres,
we did not use
spectroscopic indicators to set the stellar parameters, with the exception
of setting the model atmosphere [m/H] value to match the derived [Fe/H]
value. We used a grid of solar-abundance ratio atmospheres by Fiorella
Castelli![]() that include
updated opacity distribution functions and the 2002 version
of the MOOG spectrum synthesis program (Sneden 1973).
that include
updated opacity distribution functions and the 2002 version
of the MOOG spectrum synthesis program (Sneden 1973).
We set the
![]() values as an average from three
color-to-
values as an average from three
color-to-
![]() calibrations for dwarf stars (Ramírez & Meléndez 2005),
adopting the initial [Fe/H] = 0, very close to the estimate
by Randich et al. (2001). We used B-V,
V-J, and V-Ks color indices to obtain
calibrations for dwarf stars (Ramírez & Meléndez 2005),
adopting the initial [Fe/H] = 0, very close to the estimate
by Randich et al. (2001). We used B-V,
V-J, and V-Ks color indices to obtain
![]() ,
where J and Ks are the 2MASS magnitudes (Skrutskie et al. 2006). In the temperature
range 4400-5700 K, the common stars between our study and
Randich et al. (2001) indicate a nearly perfect match of temperature
scales. If all nine common stars are considered, the rms scatter of
differences approaches 140 K. It should not be overlooked, however,
that such photometrically-calibrated effective temperatures may be
biased (e.g., cooler), if a star is a binary and/or still on the
pre-main-sequence evolutionary tracks. The Ramírez & Meléndez (2005) calibrations do not
consider such effects though their presence in IC 2391 is
undeniable (see Sect. 6.5).
We derived the surface gravities
,
where J and Ks are the 2MASS magnitudes (Skrutskie et al. 2006). In the temperature
range 4400-5700 K, the common stars between our study and
Randich et al. (2001) indicate a nearly perfect match of temperature
scales. If all nine common stars are considered, the rms scatter of
differences approaches 140 K. It should not be overlooked, however,
that such photometrically-calibrated effective temperatures may be
biased (e.g., cooler), if a star is a binary and/or still on the
pre-main-sequence evolutionary tracks. The Ramírez & Meléndez (2005) calibrations do not
consider such effects though their presence in IC 2391 is
undeniable (see Sect. 6.5).
We derived the surface gravities ![]() by
interpolation of the 35-Myr, solar-metallicity isochrone by
Girardi et al. (2002). Finally, we used the relationship provided by
Allende Prieto et al. (2004) to set the microturbulence parameter
by
interpolation of the 35-Myr, solar-metallicity isochrone by
Girardi et al. (2002). Finally, we used the relationship provided by
Allende Prieto et al. (2004) to set the microturbulence parameter ![]() .
.
Table 7: Derived stellar atmosphere parameters and Fe abundance.
The derived atmosphere parameters and Fe abundances are given in
Table 7. The line-by-line abundances show
slight trends with respect to excitation potential and line strength,
but we did not adjust the stellar parameters or remove any high-excitation
lines from the analysis. We point out an especially large difference
(mean of
![]() dex)
between the abundances derived from Fe I and Fe II lines, noting that
by definition these same lines give the same abundance for both species
in the Sun. This is similar to what was seen in studies of other
young open clusters, so we only used the results for the
Fe I lines to derive the mean cluster abundance.
dex)
between the abundances derived from Fe I and Fe II lines, noting that
by definition these same lines give the same abundance for both species
in the Sun. This is similar to what was seen in studies of other
young open clusters, so we only used the results for the
Fe I lines to derive the mean cluster abundance.
The weighted mean [Fe I/H]
value for the four IC 2391 stars is
![]() (s.d.). When adopting the
solar abundance of
(s.d.). When adopting the
solar abundance of
![]() (Fe) = 7.45, the mean [Fe/H] reported
by Randich et al. (2001) translates into
[Fe/H] =
(Fe) = 7.45, the mean [Fe/H] reported
by Randich et al. (2001) translates into
[Fe/H] =
![]() ,
a metallicity estimate nearly identical to
our value. Recently, in the framework of UVES Paranal Observatory Project,
Stütz et al. (2006) obtained elemental abundances for five early-type stars
in IC 2391. The weighted mean [Fe/H] value for the two bona fide cluster
members (HD 74275 = 4522 and SHJM 2 = 3722) from this study is
,
a metallicity estimate nearly identical to
our value. Recently, in the framework of UVES Paranal Observatory Project,
Stütz et al. (2006) obtained elemental abundances for five early-type stars
in IC 2391. The weighted mean [Fe/H] value for the two bona fide cluster
members (HD 74275 = 4522 and SHJM 2 = 3722) from this study is
![]() ,
again in good agreement with our value of [Fe/H]. A third bona fide
member HD 74044 = 7027 was also included in the Stütz et al. (2006) analysis;
however, it shows signs of being chemically peculiar and, hence, is not
suitable for deriving average elemental abundances in cluster stars.
,
again in good agreement with our value of [Fe/H]. A third bona fide
member HD 74044 = 7027 was also included in the Stütz et al. (2006) analysis;
however, it shows signs of being chemically peculiar and, hence, is not
suitable for deriving average elemental abundances in cluster stars.
Abundances derived from Fe I lines are sensitive to the adopted
![]() values: a +100 K increase in
values: a +100 K increase in
![]() will raise
the [Fe/H] value by about +0.10 dex. Our temperature scale comes only
from photometric colors, so it is sensitive to errors in the photometry,
to color shifts due to unresolved binaries, and to the intrinsic
uncertainties of the fitting functions used to derive the
will raise
the [Fe/H] value by about +0.10 dex. Our temperature scale comes only
from photometric colors, so it is sensitive to errors in the photometry,
to color shifts due to unresolved binaries, and to the intrinsic
uncertainties of the fitting functions used to derive the
![]() scales (the
scales (the
![]() values the T(B-V), T(V-J), and T(V-K)calibrations are 88 K, 62 K, and 50 K, respectively). For example,
we note that star 3359 is slightly above the isochrone fitting the main
sequence in two out of the three color-magnitude diagrams (see Sect. 6.5).
If this is due to the problem in photometry,
and we have adopted a
values the T(B-V), T(V-J), and T(V-K)calibrations are 88 K, 62 K, and 50 K, respectively). For example,
we note that star 3359 is slightly above the isochrone fitting the main
sequence in two out of the three color-magnitude diagrams (see Sect. 6.5).
If this is due to the problem in photometry,
and we have adopted a
![]() value that could be lower than
true
value that could be lower than
true
![]() by
by ![]() 50 K, then our final [Fe/H] value for
star 3359 is too low by
50 K, then our final [Fe/H] value for
star 3359 is too low by ![]() 0.05 dex.
0.05 dex.
The equivalent width of Li 6708 Å is known to be a good youth indicator for cool stars (late G to mid-M type stars) whose interiors are fully convective during the pre-main sequence phase (e.g., Martin 1997). For hotter stars (F to mid-G corresponding to B-V=0.4-0.7), the development of a radiative core in the pre-main-sequence phase prevents a rapid Li depletion in these stars. Thus, for hotter stars, the changes in Li abundance are insignificant between a few Myr and the Pleiades age (e.g., Soderblom et al. 1993).
The equivalent width of Li 6708 Å and H![]() was measured
manually using
the IRAF splot task. Because in fast rotating stars this Li feature is
blended with an Fe I line at 6707.441 Å, we applied an empirical
correction (Sect. 2.2 Soderblom et al. 1993) to the equivalent width of the Li
feature for all stars with
was measured
manually using
the IRAF splot task. Because in fast rotating stars this Li feature is
blended with an Fe I line at 6707.441 Å, we applied an empirical
correction (Sect. 2.2 Soderblom et al. 1993) to the equivalent width of the Li
feature for all stars with
![]() km s-1. Then, the equivalent
width was converted into Li abundance,
km s-1. Then, the equivalent
width was converted into Li abundance, ![]() N(Li), via the grid of
curves of growth tabulated by Soderblom et al. (1993). Effective temperatures
were derived as described in Sect. 5.2. The initial analysis of the
N(Li), via the grid of
curves of growth tabulated by Soderblom et al. (1993). Effective temperatures
were derived as described in Sect. 5.2. The initial analysis of the
![]() N(Li) distribution as a function of
N(Li) distribution as a function of
![]() showed
a number of stars with abnormally high Li abundance,
exceeding
showed
a number of stars with abnormally high Li abundance,
exceeding ![]() N(Li) = 3.5 dex. In our FEROS spectra these stars
have
N(Li) = 3.5 dex. In our FEROS spectra these stars
have
![]() km s-1 and a poorly-defined continuum around
the Li feature. For such stars, it was decided to adopt the smoothed
adjacent spectrum just outside the expected width of a Li feature
for a continuum.
The measured equivalent widths, EW(Li), are listed in Table 8.
Ambiguous lithium non-detections due to the high rotational
velocity or binarity are marked by -99.
For stars with
km s-1 and a poorly-defined continuum around
the Li feature. For such stars, it was decided to adopt the smoothed
adjacent spectrum just outside the expected width of a Li feature
for a continuum.
The measured equivalent widths, EW(Li), are listed in Table 8.
Ambiguous lithium non-detections due to the high rotational
velocity or binarity are marked by -99.
For stars with
![]() km s-1, the rms scatter of measured EWs
from two independent measurements is estimated to be
km s-1, the rms scatter of measured EWs
from two independent measurements is estimated to be ![]() 6 mÅ.
In this range of
6 mÅ.
In this range of ![]() ,
there are only three stars, 4362, 4413, and 5859, in common with Randich et al. (2001).
The measurements of EW in both studies agree to within
,
there are only three stars, 4362, 4413, and 5859, in common with Randich et al. (2001).
The measurements of EW in both studies agree to within ![]() of the
errors quoted by Randich et al. (2001). For bona fide cluster members of IC 2391,
the distribution of lithium abundance as a function of
of the
errors quoted by Randich et al. (2001). For bona fide cluster members of IC 2391,
the distribution of lithium abundance as a function of
![]() is
shown in Fig. 3.
is
shown in Fig. 3.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{5756fg3.ps}
\end{figure}](/articles/aa/full/2007/02/aa5756-06/Timg106.gif) |
Figure 3:
Lithium abundance as a function of
|
| Open with DEXTER | |
From the FEROS spectra we also estimated an equivalent width of H![]() .
Eight relatively cool stars in Table 8 show H
.
Eight relatively cool stars in Table 8 show H![]() in emission and therefore have negative EW values.
in emission and therefore have negative EW values.
One of the goals of this paper is to assemble a list of bona fide members
of IC 2391 and their basic properties down to ![]() .
Such a list is expected
to be useful for subsequent future studies of this sparse open cluster.
.
Such a list is expected
to be useful for subsequent future studies of this sparse open cluster.
We used the following criteria to decide whether or not to assign the status of bona fide member to a probable cluster member:
A list of bona fide cluster members was used to find the cluster center,
previously not very well known for IC 2391. We assumed a Gaussian profile
to model marginal distributions in right ascension and declination
of the observed star spatial density.
A fit to these distributions yields a cluster center, equal to
![]() and
and
![]() (J2000.0). Due to a highly asymmetric distribution of cluster members,
the uncertainty in the cluster center is about
(J2000.0). Due to a highly asymmetric distribution of cluster members,
the uncertainty in the cluster center is about
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{5756fg4.ps}
\end{figure}](/articles/aa/full/2007/02/aa5756-06/Timg112.gif) |
Figure 4: Histogram of mean radial velocities for bona fide cluster members of IC 2391. The dashed line shows a Gaussian fit that peaks at +14.80 km s-1. |
| Open with DEXTER | |
The sample of bona fide cluster members allowed us to re-examine the
distribution of radial velocities drawn nearly exclusively from this
study only, i.e., the merged list of CORAVEL and
FEROS radial velocities.
We selected 42 stars showing no apparent signs of duplicity.
The distribution of radial velocities was binned in 0.4 km s-1increments and then fitted with a Gaussian (Fig. 4). The best fit yields a mean
radial velocity of
![]() km s-1 (s.d.). This is
very close to the mean radial velocity of
14.6 km s-1 estimated from the Stauffer et al. (1997) data.
The distribution of radial velocities appears to be slightly skewed.
We believe that small number statistics is a primary source of this
skewness, although stars with
km s-1 (s.d.). This is
very close to the mean radial velocity of
14.6 km s-1 estimated from the Stauffer et al. (1997) data.
The distribution of radial velocities appears to be slightly skewed.
We believe that small number statistics is a primary source of this
skewness, although stars with
![]() km -1
may also contribute to this effect by having their radial velocity slightly
increased.
km -1
may also contribute to this effect by having their radial velocity slightly
increased.
A few stars in Tables 4 and 8 that have their
radial velocities very close to the cluster's mean velocity fail one or two
additional criteria. Two of them, 2717 and 5314, are
located below the main sequence but otherwise would qualify for
cluster membership and probably deserve further scrutiny. The third
star, 5376, is almost a perfect cluster member, notwithstanding the
noted absence of lithium. The available spectrum is rather noisy;
therefore, we cannot be confident about the lack of Li feature, so
additional checks are required. According to Randich et al. (2001), the
cluster member 4636 = SHJM 9, only by ![]() 100 K hotter than star 5376, has
a fairly prominent Li 6708 feature with EW(Li) = 100 mÅ. Hence,
there is no reason to assume that Li would be depleted below detection
in star 5376, if it were a cluster member.
100 K hotter than star 5376, has
a fairly prominent Li 6708 feature with EW(Li) = 100 mÅ. Hence,
there is no reason to assume that Li would be depleted below detection
in star 5376, if it were a cluster member.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.2cm,clip]{5756fg5a.eps}\hs...
...e*{3mm}
\includegraphics[angle=-90,width=7.2cm,clip]{5756fg5d.eps}
\end{figure}](/articles/aa/full/2007/02/aa5756-06/Timg115.gif) |
Figure 5: Examples of cross-correlation function for double-lined spectroscopic binaries found among the FEROS target stars. |
| Open with DEXTER | |
Many of the recent advances in the understanding of IC 2391 rest on the X-ray
source list from ROSAT observations (Patten & Simon 1996,1993). A total of
80 sources have been identified from these observations. Owing to a rather
low spatial resolution (![]() 5-30
5-30
![]() FWHM) for ROSAT detectors,
identification of optical counterparts in many cases is uncertain.
To ensure that none of the possible counterparts with V<19 is missing,
Patten & Simon (1996) provide a total of 184 possible identifications
and then try to narrow down the list using available proper motions,
photometry, and spectroscopy. In essence, the papers by Stauffer et al. (1997),
analyzing 26 counterparts, and Randich et al. (2001), re-analyzing a
subsample from the Stauffer et al. paper, is a continuation of this
effort. We have astrometric data for 49 optical counterparts,
all brighter than
FWHM) for ROSAT detectors,
identification of optical counterparts in many cases is uncertain.
To ensure that none of the possible counterparts with V<19 is missing,
Patten & Simon (1996) provide a total of 184 possible identifications
and then try to narrow down the list using available proper motions,
photometry, and spectroscopy. In essence, the papers by Stauffer et al. (1997),
analyzing 26 counterparts, and Randich et al. (2001), re-analyzing a
subsample from the Stauffer et al. paper, is a continuation of this
effort. We have astrometric data for 49 optical counterparts,
all brighter than ![]() (see cross-identifications in Table 9). Among these stars, 12
are field stars with the membership probability,
(see cross-identifications in Table 9). Among these stars, 12
are field stars with the membership probability, ![]() .
A formal sum of probabilities indicates that the expected number of
cluster members is
.
A formal sum of probabilities indicates that the expected number of
cluster members is ![]() 25. This estimate is lower
than the actual number of members because we could not incorporate
radial distribution in the membership calculation (see Sect. 2).
Indeed, there are 34 bona fide cluster members among
the likely optical counterparts of X-ray sources. We conclude that,
while proven successful in finding many low-mass cluster members,
the X-ray activity alone is not a decisive and comprehensive
membership criterion.
25. This estimate is lower
than the actual number of members because we could not incorporate
radial distribution in the membership calculation (see Sect. 2).
Indeed, there are 34 bona fide cluster members among
the likely optical counterparts of X-ray sources. We conclude that,
while proven successful in finding many low-mass cluster members,
the X-ray activity alone is not a decisive and comprehensive
membership criterion.
To illustrate how deceptive corroborative evidence can sometimes
be, consider star 6576 = WXR 50a. It is listed as a "suspected
cluster member based on photometry and/or spectroscopy'' by Patten & Simon (1996).
Its radial velocity from our study is +15.13 km s-1 and
+17 km s-1 (Stauffer et al. 1997), both very close to the cluster's
mean radial velocity. For this star, the Li abundance is 2.7 (our study)
and 2.6 according to Randich et al. (2001), tightly following the
![]() (Li) vs.
(Li) vs.
![]() trend for IC 2391 (Fig. 3).
A closer inspection of color-magnitude diagrams
V,(V-I) and J,(J-K) shows that a star is located
trend for IC 2391 (Fig. 3).
A closer inspection of color-magnitude diagrams
V,(V-I) and J,(J-K) shows that a star is located
![]() 0.5 mag below the main sequence. However, it is
the proper motion of 6576 (
0.5 mag below the main sequence. However, it is
the proper motion of 6576 (
![]() and
and
![]() mas yr-1)
that, at
mas yr-1)
that, at
![]() apart from the cluster's mean motion,
rules out the cluster membership.
apart from the cluster's mean motion,
rules out the cluster membership.
One star, 4658 = VXR 45a, warrants a special statement. While it is not
listed by us as a bona fide member because it is located relatively far
above the main sequence in the color-magnitude diagram,
its high proper-motion membership probability of
![]() strongly suggests the cluster membership.
This G9 spectral type star, also a BY Dra
type variable V370 Vel, stands out by its huge rotational velocity
of
strongly suggests the cluster membership.
This G9 spectral type star, also a BY Dra
type variable V370 Vel, stands out by its huge rotational velocity
of
![]() km s-1 (Marsden et al. 2004), by far exceeding
any other
km s-1 (Marsden et al. 2004), by far exceeding
any other ![]() measurement in IC 2391
(Stauffer et al. 1997, see also Tables 4 and 8). The short photometric rotational period equal to
measurement in IC 2391
(Stauffer et al. 1997, see also Tables 4 and 8). The short photometric rotational period equal to
![]() days (Patten & Simon 1996) is also clearly visible in the X-ray
time series observations (Marino et al. 2003). If this is a genuine cluster
member, then the question is what mechanism spun it up or prevented the
dissipation of its primordial angular momentum, while most cluster
members similar to star 4658 are slow rotators (
days (Patten & Simon 1996) is also clearly visible in the X-ray
time series observations (Marino et al. 2003). If this is a genuine cluster
member, then the question is what mechanism spun it up or prevented the
dissipation of its primordial angular momentum, while most cluster
members similar to star 4658 are slow rotators (
![]() km s-1).
It should be noted that such ultrafast rotators can be found in
other young open clusters, e.g., in the Pleiades (van Leeuwen et al. 1987),
km s-1).
It should be noted that such ultrafast rotators can be found in
other young open clusters, e.g., in the Pleiades (van Leeuwen et al. 1987),
![]() Per (Prosser 1992), IC 2602 (Stauffer et al. 1997). One possible
explanation of this phenomenon is offered by Barnes & Sofia (1996),
invoking a paradigm of the angular momentum loss saturation.
Per (Prosser 1992), IC 2602 (Stauffer et al. 1997). One possible
explanation of this phenomenon is offered by Barnes & Sofia (1996),
invoking a paradigm of the angular momentum loss saturation.
There is another fast rotator VXR 80a with
![]() km s-1
(Stauffer et al. 1997) among the suspected
cluster members by Patten & Simon (1996). Since we have not measured this
star, the only source of proper motion for VXR 80a = King 391 is
a study by King (1979). In this paper the cluster's proper motion centroid is
at
km s-1
(Stauffer et al. 1997) among the suspected
cluster members by Patten & Simon (1996). Since we have not measured this
star, the only source of proper motion for VXR 80a = King 391 is
a study by King (1979). In this paper the cluster's proper motion centroid is
at
![]() and
and
![]() mas yr-1, derived by using
the counterparts of our bona fide cluster members in King (1979).
If we adopt the standard error of proper
motions
mas yr-1, derived by using
the counterparts of our bona fide cluster members in King (1979).
If we adopt the standard error of proper
motions
![]() mas yr-1, then the proper motion of King 391 is
more than 6
mas yr-1, then the proper motion of King 391 is
more than 6![]() apart from the cluster's mean motion which
rules out the cluster membership.
apart from the cluster's mean motion which
rules out the cluster membership.
The star SHJM 5 also shows
![]() km s-1 (Stauffer et al. 1989).
This star is a member of a visual binary (our star 4757) for which we
have the membership probability
km s-1 (Stauffer et al. 1989).
This star is a member of a visual binary (our star 4757) for which we
have the membership probability
![]() ,
consistent with cluster
membership. Finally, star 2457 with
,
consistent with cluster
membership. Finally, star 2457 with
![]() km s-1 is
another possible cluster member despite its measured radial velocity at
-7.25 km s-1, since its astrometric membership probability is
km s-1 is
another possible cluster member despite its measured radial velocity at
-7.25 km s-1, since its astrometric membership probability is
![]() and it is located just slightly above the main sequence in
both BV and JK color-magnitude diagrams.
and it is located just slightly above the main sequence in
both BV and JK color-magnitude diagrams.
Prior to ROSAT measurements, the so-called SHJM list of 10 relatively
faint cluster members was published by Stauffer et al. (1989).
Cross-identifications of SHJM stars are provided by Patten & Simon (1996).
Based on our astrometry and criteria listed in Sect. 6.1, stars
SHJM 1, 2, 6, 9, 10 appear to be bona fide cluster members, while
SHJM 8 was not measured but SHJM 7 = 3664 has a membership probability of zero.
The membership for SHJM 3 = 1820 and (SHJM 4 + SHJM 5) = 4757 is not
definitely constrained by our data. For SHJM 3 this is because
its radial velocity from our data is +12.76 km s-1, while
Stauffer et al. (1989) provide +19.5 km s-1, thus
indicating a possible spectroscopic binary.
Its astrometric membership probability is only 9%, which is more
a characteristic of a field star.
Our conservative lower limit of equivalent width for the Li feature
for SHJM 3 is 2.5 times larger than the measurement by Stauffer et al. (1989), thus
implying unusually high abundance of Li at
![]() K
in the context of the overall
K
in the context of the overall ![]() (Li) vs.
(Li) vs.
![]() curve for IC 2391
(see Fig. 3).
curve for IC 2391
(see Fig. 3).
3518 = HIP 42504: a 5th magnitude star whose Hipparcos astrometry
is consistent with cluster membership. Its redward position from
the main sequence in the BV and JK CMDs (see Sect. 6.5) indicates
duplicity, which is confirmed by radial velocity measurements (Levato et al. 1988; Feinstein 1961). The
star is an SB1 spectroscopic binary with P = 3.2d, eccentricity
e=0.05, and ![]() -velocity = 14.5 km s-1.
-velocity = 14.5 km s-1.
3658 = HD 74438: this star is ![]() 0.9 magnitudes above the main sequence
in the color-magnitude diagram, indicating a potential triple system.
Its proper-motion membership probability
0.9 magnitudes above the main sequence
in the color-magnitude diagram, indicating a potential triple system.
Its proper-motion membership probability
![]() % is high
and reliable. Feinstein (1961) lists two measurements of radial velocity:
+7.5 and +17.5 km s-1, whereas Buscombe (1965) derives
+21: km s-1 from five spectrograms. Thus, the scatter of radial
velocities is indicative of a non-single status of the star.
A formal mean velocity matches the cluster's radial velocity. We note
that at the XMM-Newton observatory Marino et al. (2005) were able to obtain
only the upper limit of X-ray luminosity for this star, which is typical
of A spectral type stars. On the grounds of the available data, we
consider star 3658 a bona fide cluster member, albeit one requiring
more spectroscopic studies.
% is high
and reliable. Feinstein (1961) lists two measurements of radial velocity:
+7.5 and +17.5 km s-1, whereas Buscombe (1965) derives
+21: km s-1 from five spectrograms. Thus, the scatter of radial
velocities is indicative of a non-single status of the star.
A formal mean velocity matches the cluster's radial velocity. We note
that at the XMM-Newton observatory Marino et al. (2005) were able to obtain
only the upper limit of X-ray luminosity for this star, which is typical
of A spectral type stars. On the grounds of the available data, we
consider star 3658 a bona fide cluster member, albeit one requiring
more spectroscopic studies.
4484 = HIP 42536 = o Velorum:
the brightest star in IC 2391, also a ![]() CMa
type variable. Its Hipparcos parallax
CMa
type variable. Its Hipparcos parallax
![]() mas is very close
to the mean parallax of IC 2391 equal to
mas is very close
to the mean parallax of IC 2391 equal to
![]() (Robichon et al. 1999);
however, Hipparcos proper motion in declination
(Robichon et al. 1999);
however, Hipparcos proper motion in declination
![]() mas yr-1 is 20
mas yr-1 is 20![]() (!) apart from
the cluster's mean proper motion
(!) apart from
the cluster's mean proper motion
![]() (Robichon et al. 1999).
Gontcharov et al. (2001) report a significantly lower absolute proper motion
(Robichon et al. 1999).
Gontcharov et al. (2001) report a significantly lower absolute proper motion
![]() consistent with Robichon et al. (1999). Our
membership probability,
consistent with Robichon et al. (1999). Our
membership probability,
![]() %, and the mean radial velocity of
+15.2 km s-1 by van Hoof (1972) together indicate that the star
is a bona fide cluster member. The discrepant Hipparcos proper
motion can be explained as the effect of unresolved binarity (Wielen et al. 1999).
%, and the mean radial velocity of
+15.2 km s-1 by van Hoof (1972) together indicate that the star
is a bona fide cluster member. The discrepant Hipparcos proper
motion can be explained as the effect of unresolved binarity (Wielen et al. 1999).
5459 = HD 74009: a star with lower membership probability (
![]() )
than the other relatively bright stars. However, the mean radial velocity
of +14 km s-1 by Levato et al. (1988) strongly supports cluster
membership. Apparent variability of the observed
radial velocity (Levato et al. 1988) indicates a possible spectroscopic binary.
)
than the other relatively bright stars. However, the mean radial velocity
of +14 km s-1 by Levato et al. (1988) strongly supports cluster
membership. Apparent variability of the observed
radial velocity (Levato et al. 1988) indicates a possible spectroscopic binary.
7847 = HIP 42823: another bright star in IC 2391 first considered to
be a member by Eggen (1991). Its Hipparcos parallax is only ![]() apart from the mean parallax of IC 2391, while Hipparcos proper motion
deviates from the mean by
apart from the mean parallax of IC 2391, while Hipparcos proper motion
deviates from the mean by ![]() 3 mas yr-1 in both
coordinates. Our membership probability of 78% supports the
association of star 7847 with IC 2391, however, the lack of radial velocity
measurements prevents us from assigning it the status of a definite cluster
member.
3 mas yr-1 in both
coordinates. Our membership probability of 78% supports the
association of star 7847 with IC 2391, however, the lack of radial velocity
measurements prevents us from assigning it the status of a definite cluster
member.
Identifying spectroscopic binaries in star clusters has a dual purpose. First, the evolutionary paths of stars are reasonably well-understood only for single stars; therefore, it is critical that we can identify these stars in the color-magnitude diagram with high confidence. Radial velocities from high-resolution spectroscopy is a powerful tool for detecting close binaries in a wide range of mass ratios. Second, the binaries themselves are very important to astronomy, especially those in the star clusters that provide a coeval sample of stars in a wide range of masses, all having the same initial composition.
The early spectroscopic work in IC 2391 was focussed on bright, early type stars (Levato et al. 1988; Feinstein 1961; van Hoof 1972; Perry & Bond 1969; Buscombe 1965). In Table 1 - last column - we list only double-lined spectroscopic binaries (SB2), single-lined spectroscopic binaries (SB1 or SB as listed in the source), and suspected spectroscopic binaries (SB:), if a star shows a variable radial velocity or the mean radial velocity in different studies is significantly variant. The binaries with orbital solutions are marked with a letter "o''. Since the internal mean error in these studies can reach up to 3-5 km s-1, not all cases of suspected SB may be real.
Table 10: Orbital elements of 4413 = VXR 5.
Among the IC 2391 F-K type main sequence stars, the long-term CORAVEL
observations have revealed two SB2 and four SB1 spectroscopic binaries
(see Tables 3 and 4). An SB2 spectroscopic binary
4413 has a sufficient number of observations
to calculate the orbital elements listed in Table 10. This binary
system (Fig. 6) consists of two nearly equal-mass components
on a fairly eccentric orbit (![]() ). Its
). Its ![]() -velocity of
14.35 km s-1 clearly supports the cluster membership.
-velocity of
14.35 km s-1 clearly supports the cluster membership.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{5756fg6.eps}
\end{figure}](/articles/aa/full/2007/02/aa5756-06/Timg151.gif) |
Figure 6: Radial-velocity curve for spectroscopic binary star 4413 convolved with the orbital period of P = 90.617 days. The filled squares denote component A; open squares - component B. |
| Open with DEXTER | |
According to its proper motion,
![]() and
and
![]() mas yr-1,
the SB2
spectroscopic binary 389 is a field star. As indicated by CORAVEL
observations in Table 3, this binary was not
resolved over four epochs, and these observations yield an estimate
of the
mas yr-1,
the SB2
spectroscopic binary 389 is a field star. As indicated by CORAVEL
observations in Table 3, this binary was not
resolved over four epochs, and these observations yield an estimate
of the ![]() -velocity at 9.27 km s-1 (Table 4).
The Wilson (1941) method allows us to determine the
-velocity at 9.27 km s-1 (Table 4).
The Wilson (1941) method allows us to determine the ![]() -velocity more
precisely and to obtain the mass ratio in this binary system. Thus,
the refined
-velocity more
precisely and to obtain the mass ratio in this binary system. Thus,
the refined ![]() -velocity is +10.24 km s-1
(K
1=19.36 and K
2=21.75 km s-1) and the mass ratio
Ma/Mb=0.89. Clearly, the
-velocity is +10.24 km s-1
(K
1=19.36 and K
2=21.75 km s-1) and the mass ratio
Ma/Mb=0.89. Clearly, the ![]() -velocity of star 389 also rules out
cluster membership.
-velocity of star 389 also rules out
cluster membership.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5756fg7.ps}
\end{figure}](/articles/aa/full/2007/02/aa5756-06/Timg154.gif) |
Figure 7: Color-magnitude diagram for the bona fide members of IC 2391. The bold dots denote single stars or the stars with unknown multiplity status. The open circles indicate spectroscopic binaries. Zero-age main sequence is overplotted using the distance modulus equal to 5.95 mag and zero reddening, E(B-V)=0.0. |
| Open with DEXTER | |
Finally, the FEROS high-resolution spectra obtained in one or two epochs (Table 5) indicate five SB2 binaries, four of them (819, 2540, 3497, 7372) are bona fide cluster members. For a set of four FEROS double-lined spectroscopic binaries, the observed cross-correlation functions are shown in Fig. 5. One of them (star 7711) has a barycentric velocity clearly incompatible with the mean radial velocity of the cluster.
Altogether, among 66 bona fide members, there are seven SB2, six SB1, and
nine suspected spectroscopic binaries. If all spectroscopic binary
categories are considered, then the binary frequency in IC 2391 is
at least ![]() 30%. The location of all 22 spectroscopic binaries in BV
color-magnitude diagram is shown in Fig. 7.
30%. The location of all 22 spectroscopic binaries in BV
color-magnitude diagram is shown in Fig. 7.
There are two sources of complete photometry for the bona fide cluster
members: our CCD BV and 2MASS
![]() (Skrutskie et al. 2006) photometry.
In the case of a missing CCD BV photometry value, we used
photoelectric BV photometry from the literature. Such values in
Table 1 are recognizeable by having only two decimal digits.
The best previous CMD in
(Skrutskie et al. 2006) photometry.
In the case of a missing CCD BV photometry value, we used
photoelectric BV photometry from the literature. Such values in
Table 1 are recognizeable by having only two decimal digits.
The best previous CMD in ![]() is presented
by Perry & Hill (1969). These authors conclude that IC 2391 is unreddened, i.e,
E(B-V)=0.00. It was later confirmed by measurements in the
Vilnius seven-color photometric system (Forbes et al. 1998) and is also adopted
in the present paper. The true reddening probably is not exactly zero;
however, the limited precision of existing
is presented
by Perry & Hill (1969). These authors conclude that IC 2391 is unreddened, i.e,
E(B-V)=0.00. It was later confirmed by measurements in the
Vilnius seven-color photometric system (Forbes et al. 1998) and is also adopted
in the present paper. The true reddening probably is not exactly zero;
however, the limited precision of existing ![]() photometry and still unclear
binarity status of some early spectral type cluster members preclude us
from deriving a better reddening estimate.
The following fits to the CMD, however, do not support
the high value of
E(B-V)=0.06 reported by Barrado y Navascués et al. (2004).
The studies by Stauffer et al. (1997,1989) and Patten & Simon (1996)
mainly employ
photometry and still unclear
binarity status of some early spectral type cluster members preclude us
from deriving a better reddening estimate.
The following fits to the CMD, however, do not support
the high value of
E(B-V)=0.06 reported by Barrado y Navascués et al. (2004).
The studies by Stauffer et al. (1997,1989) and Patten & Simon (1996)
mainly employ ![]() photometry in constructing the CMD of IC 2391,
assuming a distance modulus (m-M) = 6.05.
We note that the latter is 0.23 mag larger than the distance
modulus from Hipparcos parallaxes (Robichon et al. 1999). The color-magnitude
diagrams in these studies indicate that the stars at
photometry in constructing the CMD of IC 2391,
assuming a distance modulus (m-M) = 6.05.
We note that the latter is 0.23 mag larger than the distance
modulus from Hipparcos parallaxes (Robichon et al. 1999). The color-magnitude
diagrams in these studies indicate that the stars at ![]() are
located above the main sequence, presumably still being on the
pre-main-sequence tracks. Our list of bona fide cluster members
allows us to explore the properties of the BV CMD (Fig. 7)
in more detail.
are
located above the main sequence, presumably still being on the
pre-main-sequence tracks. Our list of bona fide cluster members
allows us to explore the properties of the BV CMD (Fig. 7)
in more detail.
We made a trial fit of ZAMS (Aller et al. 1982)
to the BV CMD, assuming zero reddening,
E(B-V)=0.0, and a distance
modulus of
V0-MV=5.95. It appears that bright stars are essentially
unevolved, with the exception of the brightest member,
star 4484 = o Velorum, whose color is suspect due to possible
duplicity (see Sect. 6.3). The lower main sequence seems to end at
![]() giving rise to pre-main sequence stars at fainter
magnitudes. An exact interpretation of the BV color-magnitude
diagram for young open cluster clusters is complicated by the fact
that K dwarfs in the Pleiades are either subluminous and/or have
abnormally blue B-V color (Stauffer et al. 2003), hence falling below
the ZAMS. These authors suggest that all young K dwarfs may
show a similar anomaly, thereby limiting the ability to obtain
an estimate of the so-called PMS isochrone age. We examine this effect
in the following section.
giving rise to pre-main sequence stars at fainter
magnitudes. An exact interpretation of the BV color-magnitude
diagram for young open cluster clusters is complicated by the fact
that K dwarfs in the Pleiades are either subluminous and/or have
abnormally blue B-V color (Stauffer et al. 2003), hence falling below
the ZAMS. These authors suggest that all young K dwarfs may
show a similar anomaly, thereby limiting the ability to obtain
an estimate of the so-called PMS isochrone age. We examine this effect
in the following section.
One of the goals of this study is to obtain a reliable photometric distance from the main sequence fitting. The empirical ZAMS used in Fig. 7 is not adequate for at least two reasons. First, the ZAMS from Aller et al. (1982) is based on the Hyades distance modulus of m-M=3.28 mag , while Hipparcos parallaxes for the Hyades members yield 3.33 mag. Second, at the time of compiling this ZAMS, the metallicities of open clusters were poorly known. The uncertainty in [Fe/H] is directly related to the uncertainty of the amount of the metal-line blanketing effect on colors and magnitudes - a major source of systematic errors in photometric distances.
Recently, Pinsonneault et al. (2003,2004) and An et al. (2006) derived new isochrones
specifically targeted to measuring the distances to open clusters and
other parameters
from the main-sequence fitting. They used the Yale Rotating Evolution
Code (YREC) to construct stellar evolution tracks for masses
![]() and metallicities
and metallicities
![]() .
The tracks were interpolated to provide theoretical isochrones
for stellar ages from 20 Myr to 4 Gyr, with the pre-main sequence phase
included where appropriate. Then, the authors used
the empirical
.
The tracks were interpolated to provide theoretical isochrones
for stellar ages from 20 Myr to 4 Gyr, with the pre-main sequence phase
included where appropriate. Then, the authors used
the empirical
![]() -color transformations from Lejeune et al. (1998) and
applied small additional corrections to isochrones in order to match
the photometry for the Hyades, adopting its metallicity at [Fe/H] = +0.13 dex.
-color transformations from Lejeune et al. (1998) and
applied small additional corrections to isochrones in order to match
the photometry for the Hyades, adopting its metallicity at [Fe/H] = +0.13 dex.
We used these isochrones to derive a precise distance modulus and to
probe the range of possible cluster ages. The key parameter for assuring
reliability of main-sequence fitting is metallicity. Our new
spectroscopic estimate of [Fe/H] for IC 2391 has an accuracy similar to
the metallicities used by An et al. (2006) in their analysis of four
open clusters. In previous studies the isochrone age of IC 2391 is
estimated to be ![]() 30-35 Myr (Mermilliod 1981; Stauffer et al. 1997), while the
location of the lithium-depletion boundary indicates an age of
30-35 Myr (Mermilliod 1981; Stauffer et al. 1997), while the
location of the lithium-depletion boundary indicates an age of
![]() Myr (Barrado y Navascués et al. 2004). We chose 30, 40, and 55 Myr isochrones
from An et al. (2006) and interpolated them to match the cluster's
metallicity of [Fe/H] = +0.06 dex. These isochrones were fitted
to the BV CMD (Fig. 8) by adjusting them to the lower envelope
of main sequence in the color range of
0.2<B-V<0.7 and by assuming
zero reddening,
E(B-V)=0.00 mag. The resulting distance modulus
is
V0-MV=6.01 mag, which is larger by 0.19 mag or
Myr (Barrado y Navascués et al. 2004). We chose 30, 40, and 55 Myr isochrones
from An et al. (2006) and interpolated them to match the cluster's
metallicity of [Fe/H] = +0.06 dex. These isochrones were fitted
to the BV CMD (Fig. 8) by adjusting them to the lower envelope
of main sequence in the color range of
0.2<B-V<0.7 and by assuming
zero reddening,
E(B-V)=0.00 mag. The resulting distance modulus
is
V0-MV=6.01 mag, which is larger by 0.19 mag or ![]() than the distance modulus inferred from the mean parallax via
the Hipparcos combined abscissae solution by Robichon et al. (1999) and van Leeuwen (1999).
Following the argumentation by Pinsonneault et al. (1998) and the study
of NGC 2451A (Platais et al. 2001), we adopted the uncertainty in our
distance modulus to be 0.05 mag.
than the distance modulus inferred from the mean parallax via
the Hipparcos combined abscissae solution by Robichon et al. (1999) and van Leeuwen (1999).
Following the argumentation by Pinsonneault et al. (1998) and the study
of NGC 2451A (Platais et al. 2001), we adopted the uncertainty in our
distance modulus to be 0.05 mag.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5756fg8.ps}
\end{figure}](/articles/aa/full/2007/02/aa5756-06/Timg163.gif) |
Figure 8: Color-magnitude diagram for the bona fide members of IC 2391. See Fig. 7 for the meaning of bold dots and open circles. The fit of 30, 40 (dark curve), and 55 Myr isochrones to CMD assuming zero reddening ( E(B-V)=0.0) yields the distance modulus of V0-MV=6.01 mag. Our estimate of age is 40 Myr. The location of stars below the 40 Myr isochrone at V>11.5 can be explained by anomalous spectral energy distributions in young K dwarfs. |
| Open with DEXTER | |
This result should be considered in the context of a trigonometric
distance to the Pleiades from Hipparcos measurements vs. the Pleiades
distance estimate from the main-sequence fitting.
The Hipparcos measurements yielded a significantly smaller
distance modulus for the Pleiades (i.e.,
![]() mag,
equivalent to
mag,
equivalent to
![]() pc in van Leeuwen 1999) than the distance
modulus from the main-sequence fitting, e.g.,
pc in van Leeuwen 1999) than the distance
modulus from the main-sequence fitting, e.g.,
![]() (Pinsonneault et al. 1998).
(Pinsonneault et al. 1998).
It is distressing to find another open cluster whose Hipparcos
parallax distance is significantly shorter than the photometric
distance. We point out that among the eleven IC 2391 members used by
Robichon et al. (1999)
to derive the mean cluster parallax, only one star (7027 = HIP 42450)
has a smaller Hipparcos parallax than our photometric
parallax. Incidently, this star is the second faintest in the sample.
What kind of systematic errors could possibly bias our
photometric distance? The first is a small uncertainty in the reddening
of IC 2391. If the true reddening is as high as
E(B-V)=0.01 mag,
that alone would reduce the distance modulus by 0.03 mag.
Second, if the true metallicity is solar, i.e., [Fe/H] = 0.0 dex,
it would also reduce the distance modulus by an additional ![]() 0.08 mag.
However, it is unlikely (although not imposssible) that either
parameter is off by this much. Also, a major change in the stellar parameters
would be required to lower the [Fe/H] value enough to account for the
0.19 mag discrepancy in the distance modulus.
0.08 mag.
However, it is unlikely (although not imposssible) that either
parameter is off by this much. Also, a major change in the stellar parameters
would be required to lower the [Fe/H] value enough to account for the
0.19 mag discrepancy in the distance modulus.
In the light of another looming Hipparcos distance problem, it
is instructive to have a look of how it is resolved for the Pleiades open
cluster. The following diverse and independent studies
actually all support the long distance to the Pleiades. Thus, Gatewood et al. (2000)
measured trigonometric parallaxes of seven members of the Pleiades
clusters and obtained an equivalent to the distance modulus
![]() mag. Using the Hubble Space Telescope's Fine
Guidance Sensor, Soderblom et al. (2005) obtained absolute trigonometric parallaxes
for three Pleiades members leading to the distance modulus
mag. Using the Hubble Space Telescope's Fine
Guidance Sensor, Soderblom et al. (2005) obtained absolute trigonometric parallaxes
for three Pleiades members leading to the distance modulus
![]() mag.
When Pan et al. (2004) applied Kepler's third law and the mass-luminosity
relation to their interfermetric measurements, they found that the Pleiades
visual binary star Atlas has
mag.
When Pan et al. (2004) applied Kepler's third law and the mass-luminosity
relation to their interfermetric measurements, they found that the Pleiades
visual binary star Atlas has
![]() mag.
A different set of interferometric observations
for Atlas, combined with the measurements of radial velocities,
produced better-constrained orbital elements and, consequently,
a purely geometric distance or
mag.
A different set of interferometric observations
for Atlas, combined with the measurements of radial velocities,
produced better-constrained orbital elements and, consequently,
a purely geometric distance or
![]() mag
(Zwahlen et al. 2004). More strong evidence comes from the combined
orbital solution of the eclipsing binary HD 23642, yielding the
distance modulus
mag
(Zwahlen et al. 2004). More strong evidence comes from the combined
orbital solution of the eclipsing binary HD 23642, yielding the
distance modulus
![]() mag (Munari et al. 2004). Finally,
the frequency observations in six
mag (Munari et al. 2004). Finally,
the frequency observations in six ![]() Scuti stars in the
Pleiades match the eigenfrequencies of rotating
stellar models best, when assuming
m-M=5.60-5.70 (Fox Machado et al. 2006) and using
the other generally adopted parameters of the Pleiades.
Scuti stars in the
Pleiades match the eigenfrequencies of rotating
stellar models best, when assuming
m-M=5.60-5.70 (Fox Machado et al. 2006) and using
the other generally adopted parameters of the Pleiades.
Regarding Hipparcos parallaxes,
van Leeuwen (2005) indicates that correlations in the abscissa residuals
for bright stars and weight disparities between each two fields-of-view
in the attitude reconstruction process can be attributed to the problematic
parallaxes for some open clusters, particularly the Pleiades.
Makarov (2002) has shown that by accounting for the average residuals
around the so-called reference circle helps to reduce the Pleiades
Hipparcos parallax to an equivalent of
![]() .
This,
however, is not the final word since the raw Hipparcos data are
under complete re-reduction (van Leeuwen & Fantino 2005).
.
This,
however, is not the final word since the raw Hipparcos data are
under complete re-reduction (van Leeuwen & Fantino 2005).
Our BV color-magnitude diagram (Fig. 8)
conclusively shows that the main
sequence extends as deep as ![]() or Mv=+6 and appears to
populate the pre-main-sequence tracks at fainter magnitudes.
If we adopt an age of IC 2391 equal to 40 Myr, our 40-Myr-old
pre-main sequence isochrone (see Fig. 8)
is located above the bulk of presumably pre-main-sequence stars.
That could be explained by the observed "blueshift'' of K dwarfs
in the BV CMD of Pleiades (Stauffer et al. 2003), noting that this effect
in IC 2391 starts at
or Mv=+6 and appears to
populate the pre-main-sequence tracks at fainter magnitudes.
If we adopt an age of IC 2391 equal to 40 Myr, our 40-Myr-old
pre-main sequence isochrone (see Fig. 8)
is located above the bulk of presumably pre-main-sequence stars.
That could be explained by the observed "blueshift'' of K dwarfs
in the BV CMD of Pleiades (Stauffer et al. 2003), noting that this effect
in IC 2391 starts at
![]() or at a spectral type G5.
A 55-Myr old isochrone significantly mitigates this effect but,
on the other hand, it does not fit the upper main sequence well,
suggesting that the isochrone (nuclear) age is less than 55 Myr.
In fact, the age estimate is constrained
just by the single brightest cluster member 4484 = o Velorum.
Because of its suspected duplicity
(see Sect. 6.3) and a
or at a spectral type G5.
A 55-Myr old isochrone significantly mitigates this effect but,
on the other hand, it does not fit the upper main sequence well,
suggesting that the isochrone (nuclear) age is less than 55 Myr.
In fact, the age estimate is constrained
just by the single brightest cluster member 4484 = o Velorum.
Because of its suspected duplicity
(see Sect. 6.3) and a ![]() CMa type variability (van Hoof 1972),
this star is not a typical B3 spectral type subgiant - its color
B-V=-0.18 could be biased and, subsequently, affect the isochrone age.
Summarizing, the age estimate from the BV CMD could be anywhere between 30 and 50 Myr.
CMa type variability (van Hoof 1972),
this star is not a typical B3 spectral type subgiant - its color
B-V=-0.18 could be biased and, subsequently, affect the isochrone age.
Summarizing, the age estimate from the BV CMD could be anywhere between 30 and 50 Myr.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5756fg9.ps}
\end{figure}](/articles/aa/full/2007/02/aa5756-06/Timg176.gif) |
Figure 9:
Color-magnitude diagram for bona fide members of IC 2391 using
2MASS |
| Open with DEXTER | |
Recently Dodd (2004) attempted to use the 2MASS photometry to construct
a CMD of IC 2391. One lesson learned from this exercise is that
the accuracy of 2MASS photometry is inadequate at H>14 (J>15).
Our bona fide cluster members are not fainter than J=11.5, so they
can serve as building blocks in constructing an empirical ZAMS from the
2MASS data. The JK color-magnitude diagram of IC 2391
(Fig. 9) has a considerably larger scatter across
the main sequence than does the BV CMD (Fig. 8),
possibly due to the higher sensitivity to a binary presence.
It is quite possible that several undetected spectroscopic binaries
are still hidden in our sample of bona fide cluster members.
Some other reasons for this scatter may include
source confusion and different photometric measurement reductions
for stars brighter and fainter than ![]() (Cutri et al. 2003).
(Cutri et al. 2003).
In the ![]() CMD (Fig. 9), we overplotted 40 and 100 Myr solar metallicity isochrones from
Bonatto et al. (2004) using the same distance modulus as for the initial ZAMS
fit in Fig. 7, i.e.,
V0-MV=5.95. Only a handful of stars are located right on
the 40 Myr isochrone, which itself poorly fits the upper main sequence.
The best fit with a 100 Myr isochrone is
most likely compromised by some bias in the 2MASS photometry at bright
magnitudes and/or by using a
CMD (Fig. 9), we overplotted 40 and 100 Myr solar metallicity isochrones from
Bonatto et al. (2004) using the same distance modulus as for the initial ZAMS
fit in Fig. 7, i.e.,
V0-MV=5.95. Only a handful of stars are located right on
the 40 Myr isochrone, which itself poorly fits the upper main sequence.
The best fit with a 100 Myr isochrone is
most likely compromised by some bias in the 2MASS photometry at bright
magnitudes and/or by using a
![]() -color transformation that is
somewhat uncertain in this magnitude range.
Thus, choosing a 100 Myr isochrone helps to eliminate the mismatch at
the bright end of main sequence; however, it is very unlikely that IC 2391
is indeed that old.
-color transformation that is
somewhat uncertain in this magnitude range.
Thus, choosing a 100 Myr isochrone helps to eliminate the mismatch at
the bright end of main sequence; however, it is very unlikely that IC 2391
is indeed that old.
Following the referee's suggestion we investigated the ![]() color-magnitude diagram. In these colors it is expected that the K dwarf
"blueshift'' in the CMD would disappear (Stauffer et al. 2003). Our
color-magnitude diagram. In these colors it is expected that the K dwarf
"blueshift'' in the CMD would disappear (Stauffer et al. 2003). Our ![]() CMD
for bona fide cluster members is given in Fig. 10.
We attempted to fit this CMD with 30,35,40,45,50,55-Myr isochrones; however,
a relatively poor match to the essential part of main sequence
comprising F-G spectral type stars (
CMD
for bona fide cluster members is given in Fig. 10.
We attempted to fit this CMD with 30,35,40,45,50,55-Myr isochrones; however,
a relatively poor match to the essential part of main sequence
comprising F-G spectral type stars (
![]() )
prevented
us from improving the distance modulus over a similar fit of the BV CMD.
Hence, we adopted the distance modulus of
V0-MV=6.01 obtained
from the BV CMD. It is difficult to judge what causes
the scatter across the main sequence and the offset of its upper
portion. Possibly, the 2MASS photometry contributes to these
effects, but we also cannot entirely rule out small isochrone calibration
problems for the V-Ks color index. On the other hand, the lower part
of color-magnitude diagram is indeed well-defined and allows us to confirm the
best estimate of isochrone age for IC 2391 at 40 Myr.
)
prevented
us from improving the distance modulus over a similar fit of the BV CMD.
Hence, we adopted the distance modulus of
V0-MV=6.01 obtained
from the BV CMD. It is difficult to judge what causes
the scatter across the main sequence and the offset of its upper
portion. Possibly, the 2MASS photometry contributes to these
effects, but we also cannot entirely rule out small isochrone calibration
problems for the V-Ks color index. On the other hand, the lower part
of color-magnitude diagram is indeed well-defined and allows us to confirm the
best estimate of isochrone age for IC 2391 at 40 Myr.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5756fg10.ps}
\end{figure}](/articles/aa/full/2007/02/aa5756-06/Timg182.gif) |
Figure 10:
|
| Open with DEXTER | |
The so-called lithium-depletion boundary (LDB)
age method yields a higher age for IC 2391
at 50-53 Myr (Barrado y Navascués et al. 2004; Barrado y Navascués et al. 1999) and 50 Myr by Jeffries & Oliveira (2005) using
five different models. It should be noted that this is in line with similarly
higher ages by this method for the ![]() Per cluster (Stauffer et al. 1999) and
the Pleiades (Stauffer et al. 1998). Since our data on IC 2391 do not reach the
lithium-depletion boundary, we are not in a position to resolve
the age differences.
Per cluster (Stauffer et al. 1999) and
the Pleiades (Stauffer et al. 1998). Since our data on IC 2391 do not reach the
lithium-depletion boundary, we are not in a position to resolve
the age differences.
The distribution of ![]() for cluster members ranges from
for cluster members ranges from ![]() 2
to 240 km s-1 (Fig. 11). Such a spread has already
been observed by Stauffer et al. (1997) for the IC 2391+IC 2602 members and can be
interpreted as a result of the early angular momentum
evolution of low-mass stars, which appears to be regulated by the
disk-locking mechanism (e.g., Edwards et al. 1993).
According to this scenario, a gradual dissipation of the disk weakens
the magnetic coupling between the star and its circumstellar disk, thereby
releasing the star to spin up as it contracts during its pre-main-sequence
phase.
2
to 240 km s-1 (Fig. 11). Such a spread has already
been observed by Stauffer et al. (1997) for the IC 2391+IC 2602 members and can be
interpreted as a result of the early angular momentum
evolution of low-mass stars, which appears to be regulated by the
disk-locking mechanism (e.g., Edwards et al. 1993).
According to this scenario, a gradual dissipation of the disk weakens
the magnetic coupling between the star and its circumstellar disk, thereby
releasing the star to spin up as it contracts during its pre-main-sequence
phase.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{5756fg11.ps}
\end{figure}](/articles/aa/full/2007/02/aa5756-06/Timg183.gif) |
Figure 11:
Distribution of |
| Open with DEXTER | |
Herbst & Mundt (2005) analyzed a large data set of rotational periods for
500 low-mass stars in five nearby young open clusters (Orion nebula cluster,
NGC 2264, ![]() Per, IC 2602, and the Pleiades). They show that 50-60%
of the stars still on the convective tracks, i.e., the vertical part
of the pre-main-sequence tracks,
appear to be released from the locking mechanism early
and thus account for the fast rotators.
Conversely, the remaining stars lose a considerable amount of their
angular momentum in the first few million years and enter onto the ZAMS
as slow rotators.
The distribution of
Per, IC 2602, and the Pleiades). They show that 50-60%
of the stars still on the convective tracks, i.e., the vertical part
of the pre-main-sequence tracks,
appear to be released from the locking mechanism early
and thus account for the fast rotators.
Conversely, the remaining stars lose a considerable amount of their
angular momentum in the first few million years and enter onto the ZAMS
as slow rotators.
The distribution of ![]() in IC 2391 (Fig. 11) seemingly
follows this pattern. However, a relatively short empirical
life-time of circumstellar disks of
in IC 2391 (Fig. 11) seemingly
follows this pattern. However, a relatively short empirical
life-time of circumstellar disks of ![]() 6 Myr (Haisch et al. 2001) makes
IC 2391, at its age of 40 Myr, an improper environment for testing the
disk-locking mechanism. Recently, Barnes (2003) put forward
a new interpretation of the observed pattern of rotational velocities
(periods) in star clusters like IC 2391 and older. In this interpretive
paradigm, the observed rotational morphology in G, K, and M stars
along the so-called I and C sequences is driven by dynamos of two
types that evolve in synchrony with the extent of the convective zone in stars.
For IC 2391 the only source of rotational periods for 16 stars is
the study by Patten & Simon (1996). We hope that the much larger sample of
6 Myr (Haisch et al. 2001) makes
IC 2391, at its age of 40 Myr, an improper environment for testing the
disk-locking mechanism. Recently, Barnes (2003) put forward
a new interpretation of the observed pattern of rotational velocities
(periods) in star clusters like IC 2391 and older. In this interpretive
paradigm, the observed rotational morphology in G, K, and M stars
along the so-called I and C sequences is driven by dynamos of two
types that evolve in synchrony with the extent of the convective zone in stars.
For IC 2391 the only source of rotational periods for 16 stars is
the study by Patten & Simon (1996). We hope that the much larger sample of ![]() obtained in this study will help to advance the understanding of
rotational evolution.
obtained in this study will help to advance the understanding of
rotational evolution.
In this study we have significantly advanced the knowledge of IC 2391
in the range
-2<Mv<+8.5 or down to ![]() 0.5
0.5 ![]() .
This is
a first extensive proper-motion study in the region of IC 2391 providing
membership probabilities over a 9 deg2 area, in effect assuring
a high-degree of completeness in the chosen ranges of magnitudes,
as explained in Sect. 2. We have measured the radial velocity for most
of them. The new kinematic members
mainly fill in the F2-K5 spectral region. The CORAVEL
measurements of 31 stars considerably strengthen the membership
status for most of them. Several spectroscopic binaries were detected;
among them seven are double-lined SB2, with one yielding an orbital
solution. The FEROS high-dispersion spectra served to measure
radial velocities and projected rotational velocities and to
estimate Li and Fe abundance. The latter is found to be
.
This is
a first extensive proper-motion study in the region of IC 2391 providing
membership probabilities over a 9 deg2 area, in effect assuring
a high-degree of completeness in the chosen ranges of magnitudes,
as explained in Sect. 2. We have measured the radial velocity for most
of them. The new kinematic members
mainly fill in the F2-K5 spectral region. The CORAVEL
measurements of 31 stars considerably strengthen the membership
status for most of them. Several spectroscopic binaries were detected;
among them seven are double-lined SB2, with one yielding an orbital
solution. The FEROS high-dispersion spectra served to measure
radial velocities and projected rotational velocities and to
estimate Li and Fe abundance. The latter is found to be
![]() on the scale of solar abundance
on the scale of solar abundance
![]() (Fe) = 7.45 dex.
(Fe) = 7.45 dex.
A total of 66 bona fide cluster
members are selected by combining kinematic, spectroscopic, and
photometric membership criteria. The BV, ![]() ,
and
,
and ![]() color-magnitude diagrams were constructed using the bona fide
cluster members. The main sequence
fit yields a distance modulus of
V0-MV=6.01 mag or 159.2 pc
that is significantly larger than the distance modulus and distance
(5.82 mag and 146 pc) from the Hipparcos mean parallax for IC 2391.
color-magnitude diagrams were constructed using the bona fide
cluster members. The main sequence
fit yields a distance modulus of
V0-MV=6.01 mag or 159.2 pc
that is significantly larger than the distance modulus and distance
(5.82 mag and 146 pc) from the Hipparcos mean parallax for IC 2391.
The problem with Hipparcos mean cluster parallaxes could be quite
complicated.
For example, another nearby open cluster NGC 2451A, which is located only
![]() away from IC 2391, does not show any discrepancy between
the Hipparcos parallax and the distance modulus derived from the main sequence
fitting (Platais et al. 2001), while the number of measured stars and their
properties in both clusters are nearly identical. Both clusters are
located near the ecliptic latitude of
away from IC 2391, does not show any discrepancy between
the Hipparcos parallax and the distance modulus derived from the main sequence
fitting (Platais et al. 2001), while the number of measured stars and their
properties in both clusters are nearly identical. Both clusters are
located near the ecliptic latitude of
![]() and
had been observed by Hipparcos relatively frequently and close in
time. Comparative studies of these two open clusters may reveal clues
to the cause of a
and
had been observed by Hipparcos relatively frequently and close in
time. Comparative studies of these two open clusters may reveal clues
to the cause of a ![]() 0.5 mas offset in the Hipparcos mean
parallax for IC 2391.
0.5 mas offset in the Hipparcos mean
parallax for IC 2391.
Among the most important tasks to advance the knowledge about IC 2391 are 1) extending reliable kinematic membership to fainter magnitudes and 2) accumulating high-resolution spectroscopy for all possible cluster members, especially for known or suspected spectroscopic binaries. The cluster population should be cleanly separated into single and binaries stars prior to extensive studies of individual stars and establishing a reliable distance to IC 2391 by other means.
Acknowledgements
We thank Hugo Levato for organizing the observing run at the CASLEO 2.2 m telescope. We appreciate helpful comments by Heiner Schwan and Peter De Cat about the properties of o Velorum. We also thank Jeremy King and Simon Schuler for stimulating discussions on elemental abundances. We thank the referee, John Stauffer, for detailed and thoughtful comments that greatly helped to improve the interpretation of the results. We also thank Deokkeun An, Don Terndrup, and Marc Pinsonneault for their help with the new YREC isochrones generated at Ohio State University. This research made use of the SIMBAD database operated at the CDS, Strasbourg, France. This publication made use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. I. Platais gratefully acknowledges support from the National Science Foundation through grant AST 04-06689 to Johns Hopkins University. J. Fulbright acknowledges support through grants from the W.M. Keck Foundation and the Gordon and Betty Moore Foundation, to establish a program of data-intensive science at to the Johns Hopkins University. M. Altmann and R. Mendez acknowledge the support by the Chilean Centro de Astrofísica FONDAP (15010003). The travel by J. Sperauskas to El Leoncito, Argentina was in part supported by NSF supplemental funding AST 01-39797. We heartily thank Lois J. Evans for meticulous editing of this paper.
Table 4: Mean radial velocities and vsini from Coravel observations.
Table 8: Mean data from FEROS spectroscopy.
Table 9: Cross-identifications with Patten & Simon (1996).