A&A 461, 585-591 (2007)
DOI: 10.1051/0004-6361:20065119
PG 1657+416: a new fast pulsating sdB star
Photometric observations and theoretical model comparison
R. Oreiro1,2 - F. Pérez Hernández1,2 - R. Østensen3 - J. E. Solheim4 - J. MacDonald5 - A. Ulla6
1 - Instituto de Astrofísica de Canarias, 38200 La Laguna,
Spain
2 -
Dpto. de Astrofísica, Universidad de La Laguna, 38200 Tenerife,
Spain
3 -
Isaac Newton Group, Aptdo. correos 321, 38700 Santa Cruz de la
Palma, Spain
4 -
Institute of Theoretical Astrophysics, University of Oslo, PO Box
1029, Oslo, Norway
5 -
Department of Physics and Astronomy, University of Delaware, DE
19716, USA
6 -
Dpto. Física Aplicada, Universidade Vigo, 36310 Vigo, Spain
Received 1 March 2006 / Accepted 15 August 2006
Abstract
Context. Since the discovery in 1997 of stellar oscillations in some B-type hot subdwarfs (sdBs), much effort is being made both observationally and theoretically to characterize this new group of pulsating objects.
Aims. To increase the number of members of such pulsators and to perform a theoretical analysis of new pulsating stars.
Methods. The Nordic Optical Telescope was used to measure the brightness as function of time for a list of selected sdBs. Pulsator candidates were selected by deriving the effective temperatures and gravities of sdB stars from various spectroscopic surveys, and picking targets in the instability region. Pulsational properties were investigated by Fourier analysis. For the theoretical analysis, the predicted frequencies of sdB structural models in the
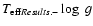 region of interest were computed.
region of interest were computed.
Conclusions. From our list of candidates we detected one, PG 1657+416, as a new oscillating star. Follow-up photometry revealed at least four frequencies in the range 6.9-7.9 mHz, whose amplitudes vary from one data set to another. The theoretical comparison indicates that the observed periods are well reproduced by structural models whose physical parameters are in good agreement with the effective temperature and gravity estimates from a spectral energy distribution fit, which also shows that the sdB has a G5 main sequence companion with
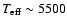 K.
K.
Key words: stars: early-type - stars: subdwarfs - stars: oscillations -
stars: individual: PG 1657+416
We report the discovery of another member of the class of rapidly
pulsating B-type hot subdwarfs (sdBs) named V361 Hya, or EC 14026 stars,
after the prototype.
SdBs are believed to be the field counterparts of the Extreme
Horizontal Branch stars in globular clusters and have a canonical mass of
0.5 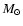 ,
even though there is still some debate concerning their mass
distribution and their prior evolution, especially including binary
formation (Han et al. 2002, 2003).
,
even though there is still some debate concerning their mass
distribution and their prior evolution, especially including binary
formation (Han et al. 2002, 2003).
In 1997, pulsations in sdBs were predicted (Charpinet et al.
1996), and detected observationally (Kilkenny et al. 1997). The
presence of stellar oscillations in sdBs opened up the possibility of
employing asteroseismological techniques for this group of evolved objects (Charpinet et al.
2005a,b; Oreiro et al. 2005; Silvotti et al. 2002; Brassard et al. 2001). V361 Hya stars have
pulsations with frequencies in the range 2-10 mHz that are explained by
p-modes, both radial and non radial, of low degree and low order.
The 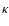 mechanism associated with an opacity bump due to an enhanced
iron abundance in their envelopes, the result of the interplay between gravitational settling and radiative levitation, is responsible for the excitation of stellar oscillations in these stars (Charpinet et al. 1997). The
mechanism associated with an opacity bump due to an enhanced
iron abundance in their envelopes, the result of the interplay between gravitational settling and radiative levitation, is responsible for the excitation of stellar oscillations in these stars (Charpinet et al. 1997). The
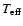 and
and 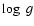 of V361 Hya stars, between 28 400-35 700 K and 5.25-6.11 dex, place
them in an area of the HR diagram where they coexist with non-variable sdBs.
A possible explanation for this co-existence comes from mass loss, which is
thought to play an important role in emptying the iron reserve (Chayer et al. 2004).
of V361 Hya stars, between 28 400-35 700 K and 5.25-6.11 dex, place
them in an area of the HR diagram where they coexist with non-variable sdBs.
A possible explanation for this co-existence comes from mass loss, which is
thought to play an important role in emptying the iron reserve (Chayer et al. 2004).
The star PG 1657+416 was selected from a catalogue of identified hot
subdwarfs (Østensen 2004), whose source in this particular case was the
SDSS First Data Release. The target's high infrared excess (see
Table 1) clearly identifies it as a hot subdwarf plus main sequence
binary system (see eg. Stark & Wade 2003).
PG 1657+416 was included in our sample only after preliminary
temperature and gravity estimates were obtained from fits to Sloan archive
spectroscopy. Although the presence of a companion makes a direct
spectroscopic fit unreliable, our first estimate of its
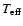 is
33 900 K, which would place the star within the hot end of the instability
region of the rapidly pulsating EC 14026 stars. We used the Nordic Optical
Telescope (NOT) located on La Palma (Canary Islands, Spain) to observe the
object during a three-night campaign devoted to search for such
oscillators.
is
33 900 K, which would place the star within the hot end of the instability
region of the rapidly pulsating EC 14026 stars. We used the Nordic Optical
Telescope (NOT) located on La Palma (Canary Islands, Spain) to observe the
object during a three-night campaign devoted to search for such
oscillators.
As it was observed during the last night of the campaign (May 25th, 2004,
see Table 2 for details), and almost at sunrise, its pulsating
behaviour was only marginally detected, as shown in the upper panel of
Fig. 1. For this reason the object was re-observed in a subsequent
photometric campaign in which the presence of periodic modulations in its
light curve was confirmed.
Table 1:
Photometric information available on the target.
The same telescope (NOT) and instrument (ALFOSC in fast photometry
mode)
were used for the second campaign. PG 1657+416 was observed for 55 min
on
June 6th, 2004 (see Table 2 for details), and the amplitude spectrum
displayed in the lower panel of Fig. 1 was obtained. Some signal
can
be easily seen in the region of 7-8 mHz, thus confirming the oscillatory
nature of the object. The noise levels shown in the
figures are computed as the mean amplitude of the spectra before prewhitening.
The frequency analysis of the discovery and confirmation runs leads to the
frequencies listed in Table 3. Bearing in mind their low
resolution (as indicated by the FWHM in the table), two peaks (f1=6.8,
f2=7.8 mHz) with equal amplitude (2.5 mma![[*]](/icons/foot_motif.gif) ) were suggested in the
discovery
run, while during the confirmation run (see also Table 3),
f1 had a lower amplitude (1.8 mma) while the dominant peak, with
amplitude 3.7 mma, was at f3=7.5 mHz.
) were suggested in the
discovery
run, while during the confirmation run (see also Table 3),
f1 had a lower amplitude (1.8 mma) while the dominant peak, with
amplitude 3.7 mma, was at f3=7.5 mHz.
Table 2:
Date, UT of the first exposure of each run, its corresponding
length, telescope and observers for all the photometric campaigns:
discovery, confirmation, IAC80 and NOT2005.
In spite of the relative faintness of the star (B=15.87, Green et al. 1986), we used one week of observing
time at the 80 cm IAC80 telescope located on Tenerife. The use of no
filter, together with a high cycle time (40 s) and a fast readout obtained
by observing in window mode, which allowed exposure times as long as 37 s,
were needed in order to optimize the quality of the data obtained with a
telescope of this limited size. Information about the observations is given
in Table 2. The data were reduced with the Real Time
Photometry (RTP) software (Østensen 2000): bias correction, sky
subtraction, division by a comparison star and extinction correction were
applied. The useful data after this process gave the light curve shown in
the upper panel of Fig. 2.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5119f1.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg24.gif) |
Figure 1:
Amplitude spectrum of PG 1657+416 obtained with the NOT in May,
2004
(discovery run, upper panel) and that obtained with the NOT in June, 2004
(confirmation run, lower panel). The continuous horizontal lines indicate 3.7 times the noise level (in amplitude), the dashed lines indicate 3 times the noise level. |
| Open with DEXTER |
Table 3:
Frequency, period, amplitude, phase and signal-to-noise ratio of the
pulsations detected in the amplitude spectrum of PG 1657+416 in the
different
runs. Phase is relative to the first data point of each light curve. The
S/N values are after prewhitening.
At the top of Fig. 3 the spectral window that corresponds to the
time series of the IAC80 data is shown. It displays a FWHM of 3 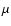 Hz,
which is adopted as the frequency resolution. A closer view of the spectral
window is enclosed in the top-right corner, although within the main panel
the same frequency scale as that used in the panels below is employed. From
the second to the last panel of Fig. 3 the amplitude spectrum and
the subsequent spectra of its prewhitening process are shown. The continuous
horizontal lines indicate 3.7 times the noise level, while the dashed
horizontal ones mark 3 times this value. The vertical dashed lines
correspond to the frequencies that are successively subtracted from the
signal. The results of a non-linear least squares fit are included in
Table 3, where amplitudes, phases and signal-to-noise ratio
are given for four frequencies.
Hz,
which is adopted as the frequency resolution. A closer view of the spectral
window is enclosed in the top-right corner, although within the main panel
the same frequency scale as that used in the panels below is employed. From
the second to the last panel of Fig. 3 the amplitude spectrum and
the subsequent spectra of its prewhitening process are shown. The continuous
horizontal lines indicate 3.7 times the noise level, while the dashed
horizontal ones mark 3 times this value. The vertical dashed lines
correspond to the frequencies that are successively subtracted from the
signal. The results of a non-linear least squares fit are included in
Table 3, where amplitudes, phases and signal-to-noise ratio
are given for four frequencies.
Comparing the amplitudes in the spectrum from the NOT (Fig. 1) and
that from the IAC80 (Fig. 3) some differences are evident. The
latter shows a much lower amplitude, suggesting that beating effects may be
occurring. The light curve from the IAC80 recovers f1 as the dominant
peak, followed in amplitude by f4=7.7 mHz, while f3 (dominant in the
confirmation run) is only 3.16 times above the noise level. Also, a new
frequency (f5=7.1 mHz) with a slightly higher signal-to-noise ratio
(3.68) is found. A marginal peak with a similar signal to noise ratio as that of f3 is still seen at 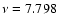 mHz in the residual amplitude spectrum. Contrary to f3, however, this marginal peak was not recovered in the subsequent photometric campaign, detailed below, and thus this frequency is not considered further.
mHz in the residual amplitude spectrum. Contrary to f3, however, this marginal peak was not recovered in the subsequent photometric campaign, detailed below, and thus this frequency is not considered further.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5119f2.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg27.gif) |
Figure 2:
Upper: light curve of PG 1657+416 obtained with the IAC80 telescope
in May, 2005; Middle: light curve obtained with the NOT in May, 2005;
Bottom: detail of the light curve obtained with the NOT and the fit to a
synthetic light curve (in red), computed from the frequencies derived from these data, and listed in Table 3. |
| Open with DEXTER |
Three weeks later, about one and a half hours on each of three nights
were employed to observe PG 1657+416, see Table 2 for details.
Reduced in the same way as previously, the derived light curve is shown in
the middle panel of Fig. 2. The bottom panel displays a detail of
this light curve, where a synthetic light curve has been overplotted as a
red line. The synthetic light curve was computed using the frequencies derived from the frequency analysis, which are included in Table 3.
The light curve of the star obtained during the run NOT-2005 resulted in the
amplitude spectrum shown in Fig. 4, whose spectral window
(shown in the upper panel) displays a
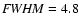
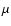 Hz. The frequency
analysis now leads to f3 having the highest amplitude (as in the
confirmation run), and the signal around 7.8 mHz splits into two peaks
(f2, f4) with amplitudes both above 3.7 times the noise level. However,
f1 is not detected in these data. The frequency list from the
run
NOT-2005 is given in Table 3.
Hz. The frequency
analysis now leads to f3 having the highest amplitude (as in the
confirmation run), and the signal around 7.8 mHz splits into two peaks
(f2, f4) with amplitudes both above 3.7 times the noise level. However,
f1 is not detected in these data. The frequency list from the
run
NOT-2005 is given in Table 3.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{5119f3.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg29.gif) |
Figure 3:
Run: IAC80 May, 2005. From top to bottom: spectral window,
amplitude spectrum, and those after successively subtracting peaks from the
signal. The continuous horizontal line indicates 3.7 times the noise level,
whereas the dashed one corresponds to 3 times this level. The vertical
dashed lines mark the frequencies that are removed during the prewhitening
process. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{5119f4.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg30.gif) |
Figure 4:
Run: NOT May, 2005. From top to bottom: spectral window, amplitude
spectrum, and those after successively subtracting peaks from the signal.
The continuous horizontal line indicates 3.7 times the noise level, whereas
the dashed one corresponds to 3 times this level. The vertical dashed lines
mark the frequencies that are removed during the prewhitening process. |
| Open with DEXTER |
Although 22 nights separate the last run taken at the IAC80 from the first
at the NOT, we attempted to combine the data to improve the frequency
resolution and also to avoid possible mistakes coming from the high
side-bands of the spectral window obtained at the NOT. Figure 5
summarizes the results from the analysis, showing the spectral window, the
amplitude spectrum and the prewhitening process. The derived frequencies are
listed in Table 3.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{5119f5.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg31.gif) |
Figure 5:
Run: IAC80+NOT 2005. From top to bottom: spectral window, amplitude
spectrum, and those after successively subtracting peaks from the signal.
The continuous horizontal line indicates 3.7 times the noise level,
the dashed one corresponds to 3 times the noise. The vertical dashed lines
mark the frequencies that are removed during the prewhitening process. |
| Open with DEXTER |
The amplitudes of the detected peaks differ from one data set to
another, from no detection to being the dominant peak. This would
imply that either the detected frequencies suffer from beating effects due
to unresolved peaks, or that the detected frequencies undergo intrinsic
amplitude variations. The data presented here do not allow a deeper analysis
in terms of signal to noise ratio or time coverage to distinguish between the
two options. However, all the detected
frequencies should have an unresolved close frequency if we favour the
beating solution. On the other hand, the suggestion of amplitude variations
is not new for pulsating sdB stars, as this is the case for
PG 1219+534 (Harms et al. 2005) or HS 1824+5745 (Reed et al. 2006), for
example. Further photometric campaigns are needed to better
understand the amplitude spectrum of PG 1657+416.
Despite the amplitude variations, the frequencies f2, f3 and f4 are
above 3.7 times the noise level in the NOT-2005 run. Besides being the
dominant peak in the discovery run, f1 is above 3.7 times the noise level
in the confirmatory observations, and is again the frequency with the highest
amplitude in the IAC80 campaign. On the other hand, f5 is only detected
in the latter campaign, in which its significance is close to the confidence
limit. For these reasons, we will only consider f1, f2, f3 and f4 for the theoretical analysis in next section.
Knowing the 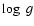 and
and
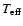 of the target is
desirable to compare the observed and theoretical
frequencies. However, as mentioned before, PG 1657+416 has a companion star
that influences both the photometric magnitudes and the observed spectrum of
the star. For this reason, an accurate fit to the Balmer lines is not easily
achieved, although a first estimate of the sdB effective temperature gives
of the target is
desirable to compare the observed and theoretical
frequencies. However, as mentioned before, PG 1657+416 has a companion star
that influences both the photometric magnitudes and the observed spectrum of
the star. For this reason, an accurate fit to the Balmer lines is not easily
achieved, although a first estimate of the sdB effective temperature gives
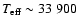 K.
K.
An alternative method to compute the sdB parameters is that described in
Koen et al. (1997), in which the observed flux of the composite system,
coming from spectroscopy or from photometry, is fitted to a sum of two
spectra following the relation:
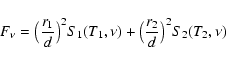 |
(1) |
where d is the distance to the system, and ri, Ti and Si are the radius, temperature and flux emission of each object.
Prior to any fit, both the infrared magnitudes, converted to fluxes using
the factors in Heber et al. (2002), and the flux from the spectrum
were corrected for reddening effects following:
where
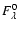 and
and
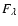 are the corrected and
uncorrected fluxes,
AV=3.1 E(B-V), the color excess obtained
from the maps of Schlegel et al. (1998), and
are the corrected and
uncorrected fluxes,
AV=3.1 E(B-V), the color excess obtained
from the maps of Schlegel et al. (1998), and
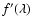 taken
from
Whitford (1958), which can be approximated in the whole spectral range with
an
accuracy better than
taken
from
Whitford (1958), which can be approximated in the whole spectral range with
an
accuracy better than 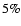 by
by
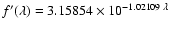 .
.
A least squares fit was performed to the corrected observed fluxes
(spectrum from SDSS with a 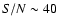 and magnitudes from 2MASS). As a
first
step, Kurucz model atmospheres were used as Si functions, keeping the sdB temperature fixed to the line fitting estimate (
and magnitudes from 2MASS). As a
first
step, Kurucz model atmospheres were used as Si functions, keeping the sdB temperature fixed to the line fitting estimate (
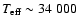 K)
and varying the companion temperature from 3500 to 7500 K, in steps of 250 K. Model atmospheres with
K)
and varying the companion temperature from 3500 to 7500 K, in steps of 250 K. Model atmospheres with 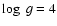 and 4.5 were used for the red
star,
while a model with
and 4.5 were used for the red
star,
while a model with 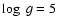 was employed to represent the hot subdwarf.
was employed to represent the hot subdwarf.
The best fit to the continuum, in the sense of a minimum 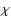 -square
error, is obtained when an atmosphere with
-square
error, is obtained when an atmosphere with
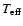 between 5250 and 5750 K is used for the companion. In Fig. 6 the observed
spectrum and magnitudes, together with the best fit for the
(
between 5250 and 5750 K is used for the companion. In Fig. 6 the observed
spectrum and magnitudes, together with the best fit for the
(
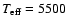 ,
,
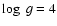 ), (
), (
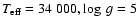 )
combination is shown.
)
combination is shown.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5119f6.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg49.gif) |
Figure 6:
Observed spectrum, 2MASS magnitudes converted to fluxes (asterisks)
and the best fit to a sum of two Kurucz model atmospheres obtained by adding
a spectrum with
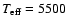 and
and 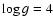 to a sdB model with
to a sdB model with
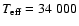 and
and 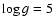 . . |
| Open with DEXTER |
If the red star is assumed to be on the main sequence, then its effective
temperature gives an estimate of its radius. According to main sequence
structural models from the ZAMS to the near end of the H-core burning
(Claret 1995), a star with
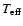 in the range 5250-5750 K
has a radius in the range 0.822-1.4
in the range 5250-5750 K
has a radius in the range 0.822-1.4 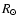 .
As the coefficients of the
flux fit give the r1/r2 ratio, the sdB radius is thus expected to be in
the range 0.124-0.242
.
As the coefficients of the
flux fit give the r1/r2 ratio, the sdB radius is thus expected to be in
the range 0.124-0.242 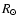 and, by assuming that the sdB mass is 0.47
and, by assuming that the sdB mass is 0.47 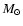 ,
the resultting
,
the resultting 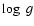 for the hot subdwarf lies in the
range 5.33-5.92 dex, which are typical values for sdB stars.
for the hot subdwarf lies in the
range 5.33-5.92 dex, which are typical values for sdB stars.
Having obtained a good estimate of the effective
temperature for the companion, which we adopt to be
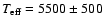 K, a new least squares fit to the observed fluxes was
made. Higher resolution spectra (Munari et al. 2005) were used in order to have a better treatment of the lines. A
K, a new least squares fit to the observed fluxes was
made. Higher resolution spectra (Munari et al. 2005) were used in order to have a better treatment of the lines. A
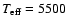 K,
K, 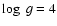 model and a
model and a
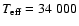 K,
K, 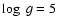 one, with
one, with
![$\rm [Fe/H]=-2.5$](/articles/aa/full/2007/02/aa5119-06/img52.gif) ,
were used as Si functions in this case in order
to compute the coefficients of Eq. (1), and to enable removal
of the companion star contribution to the observed flux.
,
were used as Si functions in this case in order
to compute the coefficients of Eq. (1), and to enable removal
of the companion star contribution to the observed flux.
The last step consists of performing a line profile fit to the residual
spectrum, after subtracting the red star contribution to the observed
spectrum. The line blanketed LTE spectral synthesis model atmospheres of
Heber et al. (2000) were used in the 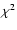 procedure of Bergeron et al.
(1992) as updated by Saffer et al. (1994). The resulting best fit, shown in
Fig. 7, gives
procedure of Bergeron et al.
(1992) as updated by Saffer et al. (1994). The resulting best fit, shown in
Fig. 7, gives
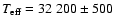 K,
K,
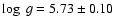 dex,
dex,
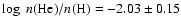 for the sdB.
for the sdB.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5119f7.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg57.gif) |
Figure 7:
Best line fit to the observed flux after subtracting a main
sequence
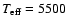 K model atmosphere. K model atmosphere. |
| Open with DEXTER |
Given the number of assumptions made to calculate the parameters just
derived, it is difficult to estimate the relevance of the quoted errors.
If for the main sequence star, model atmospheres
with
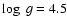 are used instead of those with
are used instead of those with 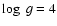 ,
all the parameters remain within the error bars indicated. As
these gravities can be
considered as extreme cases for a main sequence star with
,
all the parameters remain within the error bars indicated. As
these gravities can be
considered as extreme cases for a main sequence star with
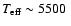 K, we conclude that the choice of an accurate
K, we conclude that the choice of an accurate 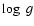 value does not have a significant effect on the results. On the other hand, in the
two firsts steps we used
value does not have a significant effect on the results. On the other hand, in the
two firsts steps we used 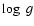 values
smaller than those typical for sdB stars, but this is not expected
to influence the final result, since they are only employed to obtain the
relative fluxes according to
Eq. (1) (mainly a fit to the continuum).
values
smaller than those typical for sdB stars, but this is not expected
to influence the final result, since they are only employed to obtain the
relative fluxes according to
Eq. (1) (mainly a fit to the continuum).
Given the difficulty in estimating the uncertainties in the stellar
parameters derived in the previous section, for the seismic analysis we will make
use of sdB structural models in a wider range of
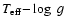 values.
values.
In Fig. 8 three sdB evolutionary sequences (A, B and C) are
plotted, in which ages (in 108 years) are given. These tracks were
produced by evolving a 1.0 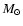 model star from the main sequence
through the helium core flash and on to the white dwarf cooling track using
the stellar evolution code of Jiménez & MacDonald (1996).
Only part of the complete tracks are shown in Fig. 8. Mass loss on
the RGB with Reimer's parameter (Reimers 1975)
model star from the main sequence
through the helium core flash and on to the white dwarf cooling track using
the stellar evolution code of Jiménez & MacDonald (1996).
Only part of the complete tracks are shown in Fig. 8. Mass loss on
the RGB with Reimer's parameter (Reimers 1975) 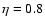 ,
0.7 and 0.695 result in tracks A, B and C respectively, whose physical parameters at the
beginning of the He-core burning phase are given in Table 4. A
dashed error box representing the atmospheric parameters of PG 1657+416 derived in the
previous subsection is also shown in Fig. 8.
,
0.7 and 0.695 result in tracks A, B and C respectively, whose physical parameters at the
beginning of the He-core burning phase are given in Table 4. A
dashed error box representing the atmospheric parameters of PG 1657+416 derived in the
previous subsection is also shown in Fig. 8.
Table 4:
Total mass (M), hydrogen envelope mass (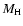 ),
),
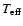 and
and 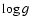 of the structural models at the beginning of the
sdB
time evolution of sequences A, B, C and D.
of the structural models at the beginning of the
sdB
time evolution of sequences A, B, C and D.
The location of a particular sequence in the
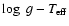 plane
depends mainly on the total mass (M) and on the mass of the H envelope (
plane
depends mainly on the total mass (M) and on the mass of the H envelope (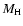 ). A thinner H envelope, which could be due to a higher mass loss
rate, shifts the whole evolutionary sequence towards higher temperatures and
gravities. This is the case for sequences A, B, C, which have almost the
same total mass but an increasing envelope mass. A single star
formation channel for sdBs of this type produces very similar core masses,
independently of the initial conditions because the core mass at helium
ignition depends only weakly on initial mass and heavy element abundance,
whereas the H envelope mass can vary depending on the mass loss efficiency
during the RGB phase. On the other hand, by increasing the total mass, a
sequence with a particular
). A thinner H envelope, which could be due to a higher mass loss
rate, shifts the whole evolutionary sequence towards higher temperatures and
gravities. This is the case for sequences A, B, C, which have almost the
same total mass but an increasing envelope mass. A single star
formation channel for sdBs of this type produces very similar core masses,
independently of the initial conditions because the core mass at helium
ignition depends only weakly on initial mass and heavy element abundance,
whereas the H envelope mass can vary depending on the mass loss efficiency
during the RGB phase. On the other hand, by increasing the total mass, a
sequence with a particular 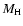 would be shifted towards higher
temperatures. To account for this case, an ad hoc sequence (D) was generated
with a higher total mass so that it crosses the star's location at an
earlier evolutionary stage. Sequence D is indicated in Fig. 8 with a
dashed-dotted line.
would be shifted towards higher
temperatures. To account for this case, an ad hoc sequence (D) was generated
with a higher total mass so that it crosses the star's location at an
earlier evolutionary stage. Sequence D is indicated in Fig. 8 with a
dashed-dotted line.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5119f8.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg71.gif) |
Figure 8:
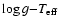 diagram in which three sdB evolutionary
sequences (A, B, C) produced by a complete evolution from a main sequence
star
are displayed. Sequence D was artificially generated so that it has a higher
total mass and crosses the star's location at an earlier evolutionary stage. Some
ages (in 108 years) are given at the points indicated with asterisks. The
values of
diagram in which three sdB evolutionary
sequences (A, B, C) produced by a complete evolution from a main sequence
star
are displayed. Sequence D was artificially generated so that it has a higher
total mass and crosses the star's location at an earlier evolutionary stage. Some
ages (in 108 years) are given at the points indicated with asterisks. The
values of
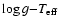 obtained in the previous section for
PG 1657+416 are indicated with a dashed error box.
obtained in the previous section for
PG 1657+416 are indicated with a dashed error box. |
| Open with DEXTER |
Although in the rest of the section we assume that the observed peaks
correspond to modes of a non-rotating star, a rotational origin cannot completely be rejected. For
p-modes the rotational splitting is given by
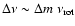 ,
where
,
where
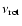 is the average rotation rate
of the star and a difference of
is the average rotation rate
of the star and a difference of
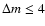 must be considered for
modes with
must be considered for
modes with
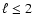 .
Choosing a radius of
.
Choosing a radius of
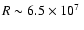 m,
corresponding to the minimum of the structural models shown in Fig. 8,
the smallest separation between the observed frequencies,
f2-f4=0.101 mHz, can be explained as a rotational
splitting if the star is rotating with a velocity greater than about 10 km s-1.
m,
corresponding to the minimum of the structural models shown in Fig. 8,
the smallest separation between the observed frequencies,
f2-f4=0.101 mHz, can be explained as a rotational
splitting if the star is rotating with a velocity greater than about 10 km s-1.
As a first step, we make a crude comparison between the observed frequencies
(f1 to f4) and the non-rotating theoretical ones predicted for
several structural models belonging to the four sequences. In
Fig. 9 we have plotted the theoretical frequencies of those models
within a suitable time interval, according to the star's
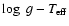 values. The y-axis indicates the age of the models from the beginning
of He-core burning, while the vertical broken lines point out the observed
frequencies.
values. The y-axis indicates the age of the models from the beginning
of He-core burning, while the vertical broken lines point out the observed
frequencies.
The fundamental mode (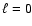 ,
n=1) for sequence A is within
5.36-6.84 mHz, while for sequence B the fundamental mode varies from 4.28
to 5.6 mHz and for sequences C and D from 3.33-3.85 and 3.79-4.82. The observed frequencies would
correspond to modes with radial order n=0,1,2 according to models on
sequence A, models on sequence B indicate the frequencies have a radial
order n=2,3,4, and models on sequences C and D indicate that the
frequencies have radial orders n=4,5,6 and n=2,3,4 respectively.
,
n=1) for sequence A is within
5.36-6.84 mHz, while for sequence B the fundamental mode varies from 4.28
to 5.6 mHz and for sequences C and D from 3.33-3.85 and 3.79-4.82. The observed frequencies would
correspond to modes with radial order n=0,1,2 according to models on
sequence A, models on sequence B indicate the frequencies have a radial
order n=2,3,4, and models on sequences C and D indicate that the
frequencies have radial orders n=4,5,6 and n=2,3,4 respectively.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5119f9.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg77.gif) |
Figure 9:
Theoretical frequencies for structural models of sequences A, B, C
and D. The y-axis indicates the age of the models, while the vertical broken
lines point out the observed frequencies. Crosses: modes with 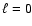 ;
asterisks: models with ;
asterisks: models with 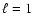 ;
rhombus: ;
rhombus: 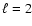 ;
triangles: ;
triangles: 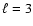 . . |
| Open with DEXTER |
As can be seen in Fig. 9, matching the observed frequency density
formed by f2, f3 and f4 gives a strong constraint on which
model best reproduces the observations. In particular, it appears that models
of sequence A do not produce a dense enough spectrum in the frequency range
of interest, as can be seen in Fig. 9, while models of sequences B
and C show more closely spaced modes.
This fact is better shown in Fig. 10, where the small frequency
separation for models along the four sequences are plotted. The frequency
separation between 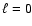 and
and 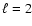 (
(
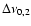 )
is indicated
with crosses, and
)
is indicated
with crosses, and
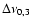 and
and
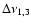 are shown
with
triangles and asterisks, respectively. The values of
f2-f4=0.101 mHz
and
f4-f3=0.163 mHz are overplotted as horizontal broken lines for
comparison.
are shown
with
triangles and asterisks, respectively. The values of
f2-f4=0.101 mHz
and
f4-f3=0.163 mHz are overplotted as horizontal broken lines for
comparison.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5119f10.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg80.gif) |
Figure 10:
The frequency separation
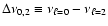 (crosses),
(crosses),
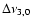 (triangles) and (triangles) and
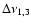 (asterisks) for structural models from sequence
A, B, C and D. The values of
f2-f4=0.101 mHz and
f4-f3=0.163 mHz are overplotted as horizontal broken lines for
comparison.
(asterisks) for structural models from sequence
A, B, C and D. The values of
f2-f4=0.101 mHz and
f4-f3=0.163 mHz are overplotted as horizontal broken lines for
comparison. |
| Open with DEXTER |
It is easily seen in Fig. 10, as suggested in Fig. 9,
that the overall small separation between modes for structural models along
sequence A is greater than that for models on other sequences, especially
those along sequence C. The observed frequency separations are better
reproduced by models of sequences B, C or D, which is in agreement with the
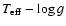 spectroscopic determination.
spectroscopic determination.
Besides the separation within the group formed by f2 to f4, another
constraint for theoretical matching is the frequency separation between this
group and f1. As we are considering four frequencies lying in a close
frequency range (6.9-7.9 mHz), two of them must be of the same degree 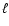 and consecutive radial order n, except if
and consecutive radial order n, except if
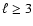 modes are
taken into
account.
modes are
taken into
account.
In order to test the hypothesis of modes of consecutive n and the same
degree 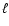 ,
the maximum separation of the observed frequencies
(
f2-f1=0.94 mHz) can be compared with the theoretical frequency
distance between consecutive n values of the same
,
the maximum separation of the observed frequencies
(
f2-f1=0.94 mHz) can be compared with the theoretical frequency
distance between consecutive n values of the same 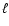 .
In
Fig. 11 the frequency separation of consecutive order for
.
In
Fig. 11 the frequency separation of consecutive order for
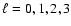 is plotted as a function of time for the four sequences
considered here.
is plotted as a function of time for the four sequences
considered here.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5119f11.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg85.gif) |
Figure 11:
Frequency separation between modes of consecutive radial order for
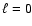 (crosses), 1 (asterisks), 2 (rhombus) and 3 (triangles)
as a
function of time for the four sequences. The observed frequency
separation
f2-f1=0.94 mHz is overplotted as an horizontal broken line for
comparison.
(crosses), 1 (asterisks), 2 (rhombus) and 3 (triangles)
as a
function of time for the four sequences. The observed frequency
separation
f2-f1=0.94 mHz is overplotted as an horizontal broken line for
comparison. |
| Open with DEXTER |
The frequency distance between consecutive n values for models of sequence
A
never reach 1 mHz at any evolutionary state nor 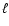 degree
(Fig. 11). However, this frequency separation is considerably lower
for
other sequences. Slightly evolved models of sequence B, and sequence C at
any
evolutionary stage are able to explain f2-f1 as modes of the same degree
and consecutive radial order.
Sequence D seems to be less realistic, as only
degree
(Fig. 11). However, this frequency separation is considerably lower
for
other sequences. Slightly evolved models of sequence B, and sequence C at
any
evolutionary stage are able to explain f2-f1 as modes of the same degree
and consecutive radial order.
Sequence D seems to be less realistic, as only 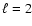 modes
reach the observed separation. Since the theoretical frequency separation
between
modes
reach the observed separation. Since the theoretical frequency separation
between 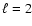 and
and 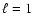 modes (see Fig. 9) is considerably
greater than the small separations shown in Fig. 10, f2 cannot
be
an
modes (see Fig. 9) is considerably
greater than the small separations shown in Fig. 10, f2 cannot
be
an 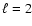 mode in order to explain its close frequencies f3 and f4.
mode in order to explain its close frequencies f3 and f4.
A new member of the rapid EC 14026 (or V361 Hya) pulsator class has
been discovered. The observed electromagnetic spectrum and the photometric
magnitudes are well reproduced by a sdB+G5 system, with the companion star
having
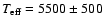 K and the hot subdwarf
K and the hot subdwarf
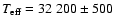 K and
K and
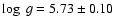 dex.
dex.
The frequency range of the detected pulsations seems to be in good agreement
with those of other stars with similar temperature, for example
PG 1219+534 (
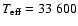 K,
K,
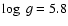 dex), whose main
detected modes lie in the range 6.7-7.8 mHz, or PG 1618+563B (
dex), whose main
detected modes lie in the range 6.7-7.8 mHz, or PG 1618+563B (
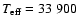 K,
K,
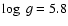 dex), with two detected frequencies at 6.9
and 7.1 mHz. The number as well as the amplitude of the observed modes also
seem to be consistent with other EC 14026 stars of similar parameters.
Amplitude variations are detected, implying that either non resolved peaks
are present or that real amplitude variations occur in PG 1657+416.
For any of these reasons, the possibility of finding additional
excited modes in further observations cannot be discarded.
dex), with two detected frequencies at 6.9
and 7.1 mHz. The number as well as the amplitude of the observed modes also
seem to be consistent with other EC 14026 stars of similar parameters.
Amplitude variations are detected, implying that either non resolved peaks
are present or that real amplitude variations occur in PG 1657+416.
For any of these reasons, the possibility of finding additional
excited modes in further observations cannot be discarded.
We compared observed and predicted
frequencies using structural sdB models along different
evolutionary
sequences. The separation between the
observed frequencies seems to be well reproduced by low order (n=2-6)
p-modes of structural models with physical parameters around those determined
spectroscopically. Although we find that sequences produced by a single
evolutionary channel with a total mass around
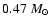 are prefered
to
models with higher masses located in the same region of the
are prefered
to
models with higher masses located in the same region of the
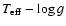 diagram, the limited number of models considered and
frequencies detected are not sufficient to discount any of the proposed
scenarios.
diagram, the limited number of models considered and
frequencies detected are not sufficient to discount any of the proposed
scenarios.
Acknowledgements
R.O. acknowledges Gobierno de Canarias for its financial support and Ángel
R. López-Sánchez for his redden lights. A.U. acknowledges financial
support from the Spanish MEC under research contract AYA2003-09499. This
work has received financial support from the Spanish Plan Nacional del
Espacio under project ESP2004-03855-C03-03. We thank Prof. Uli Heber for
kindly providing the LTE spectral grids, and the anonymous referee for valuable suggestions that greatly improved the manuscript.
The IAC80 is operated on the island
of Tenerife by the Instituto de Astrofísica de Canarias in the Spanish
Observatorio del Teide. Based on observations made with the Nordic Optical
Telescope, operated on the island of La Palma jointly by Denmark, Findland,
Iceland, Norway and Sweden, in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias.
- Bergeron,
P., Saffer, R. A., & Liebert, J. 1992, ApJ, 394, 228 [NASA ADS] [CrossRef] (In the text)
- Brassard,
P., Fontaine, G., Billères, M., et al. 2001, ApJ, 563,
1013 [NASA ADS] [CrossRef] (In the text)
-
Charpinet, S., Fontaine, G., Brassard, P., & Dorman, B. 1996,
ApJ, 471, L103 [NASA ADS] [CrossRef] (In the text)
-
Charpinet, S., Fontaine, G., Brassard, P., et al. 1997, ApJ, 483,
L123 [NASA ADS] [CrossRef] (In the text)
-
Charpinet, S., Fontaine, G., Brassard, P., et al. 2005a, A&A,
443, 251 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Charpinet, S., Fontaine, G., Brassard, P., Green, E. M., &
Chayer, P. 2005b, A&A, 437, 575 [NASA ADS] [CrossRef] [EDP Sciences]
- Chayer, P.,
Fontaine, G., Fontaine, M., et al. 2004, in Extreme Horizontal
Branch Stars and Related Objects, ed. P. Maxted, Ap&SS, 291,
359
(In the text)
- Claret, A.
1995, A&AS, 109, 441 [NASA ADS] (In the text)
- Green, R. F.,
Schmidt, F., & Liebert, J. 1986, ApJS, 61, 305 [NASA ADS] [CrossRef] (In the text)
- Han, Z.,
Podsiadlowski, Ph., Maxted, P. F. L., Marsh, T. R., & Ivanova,
N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] (In the text)
- Han, Z.,
Podsiadlowski, Ph., Maxted, P. F. L., & Marsh, T. R. 2003,
MNRAS, 341, 669 [NASA ADS] [CrossRef] (In the text)
- Harms, S. L.,
Reed, M., & O'Toole, S. 2005, in Second Meeting on Hot
Subdwarfs and Related Objects, ed. R. Østensen, Balt.A., 15,
252
(In the text)
- Heber, U., Reid,
I. N., & Werner, K. 2000, A&A, 363, 198 [NASA ADS] (In the text)
- Heber, U.,
Moehler, S., Napiwotzki, R., Thejll, P., & Green, M. 2002, 383,
938
(In the text)
- Jiménez, R.,
& MacDonald, J. 1996, MNRAS, 283, 271 [NASA ADS] (In the text)
- Kilkenny,
D., Koen, C., O'Donoghue, D., & Stobie, R. S. 1997, MNRAS, 285,
640 [NASA ADS] (In the text)
- Koen, C., Kilkenny,
D., O'Donoghue, D., Van Wick, F., & Stobie, R. S. 1997, MNRAS,
285, 645 [NASA ADS] (In the text)
- Maxted, P. F.
L., Marsh, T. R., Heber, U., et al. 2002, MNRAS, 333, 231 [NASA ADS] [CrossRef]
- Munari, R.,
Sordo, R., Castelli, F., & Zwitter, T. 2005, A&A, 442,
1127 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Oreiro, R.,
Pérez Hernández, F., Ulla, A., et al. 2005, A&A, 438,
257 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Østensen, R. 2000, Time Resolved CCD Photometry, Ph.D. Thesis,
University of Tromsø, Norway
(In the text)
-
Østensen, R. 2004, in Extreme Horizontal Branch Stars and
Related Objects, ed. P. Maxted, Ap&SS, 291, 263
(In the text)
- Reed, M., Eggen, J.
R., Zhou, A.-Y., et al. 2006, MNRAS, in press
(In the text)
- Reimers, D.
1975, Mem. Soc. Roy. Sci. Liege, 8, 369 [NASA ADS] (In the text)
- Saffer, R.,
Bergeron, P., Koester, D., & Liebert, J. 1994, ApJ, 432,
351 [NASA ADS] [CrossRef] (In the text)
- Schlegel,
D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] (In the text)
- Silvotti,
R., Janulis, R., Schuh, S. L., et al. 2002, A&A, 389, 180 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Stark, M., &
Wade, R. 2003, AJ, 126, 1455 [NASA ADS] [CrossRef] (In the text)
- Whitford,
A. E. 1958, AJ, 63, 201 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5119f1.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg24.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5119f2.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg27.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{5119f3.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg29.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{5119f4.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{5119f5.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg31.gif)
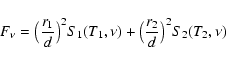
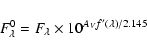
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5119f6.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg49.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5119f7.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg57.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5119f8.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5119f9.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg77.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5119f10.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg80.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5119f11.ps}
\end{figure}](/articles/aa/full/2007/02/aa5119-06/Timg85.gif)