A&A 461, 433-443 (2007)
DOI: 10.1051/0004-6361:20054092
V. A. Dogiel1,2 - S. Colafrancesco3 - C. M. Ko1 - P. H. Kuo1 - C. Y. Hwang1 - W. H. Ip1 - M. Birkinshaw4 - D. A. Prokhorov5
1 - Institute of Astronomy, National Central University, Chung-Li 32054,
Taiwan
2 -
I. E. Tamm Theoretical Physics Division, P. N. Lebedev Physical Institute, 117924
Moscow, Russia
3 - INAF - Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monteporzio,
Italy
4 -
Department of Physics, University of Bristol, Tyndall Avenue, Bristol BS8 1TL, UK
5 -
Moscow Institute of Physics and Technology, Institutskii lane, 141700 Moscow Region,
Dolgoprudnii, Russia
Received 23 August 2005 / Accepted 19 September 2006
Abstract
Aims. The stochastic acceleration of subrelativistic electrons from a background plasma is studied in order to find a possible explanation of the hard X-ray emission detected from the Coma cluster.
Methods. We calculate the necessary energy supply as a function of the plasma temperature and of the electron energy, and we show that, for the same value of the hard X-ray flux, the energy supply changes gradually from its high value for the case when emitting particle are non-thermal to lower values when the electrons are thermal. The kinetic equations we use include terms describing particle thermalization as well as momentum diffusion due to the Fermi II acceleration.
Results. We show that the temporal evolution of the particle distribution function has, at its final stationary stage, a rather specific form. This distribution function cannot be described by simple exponential or power-law expressions. A broad transfer region is formed by Coulomb collisions at energies between the Maxwellian and power-law parts of the distribution functions. In this region the radiative lifetime of a single quasi-thermal electron differs greatly from the lifetime of the distribution function as a whole. For a plasma temperature of 8 keV, the particles emitting bremsstrahlung at 20-80 keV lie in this quasi-thermal regime. We show that the energy supply required by quasi-thermal electrons to produce the observed hard X-ray flux from Coma is one or two orders of magnitude smaller than the value derived from the assumption of a nonthermal origin of the emitting particles. This result may solve the problem of rapid cluster overheating by nonthermal electrons raised by Petrosian (2001): while Petrosian's estimates are correct for nonthermal particles, they are inapplicable in the quasi-thermal range. We finally analyze the change in Coma's Sunyaev-Zeldovich effect caused by the implied distortions of the Maxwellian spectrum of electrons, and we show that evidence for the acceleration of subrelativistic electrons can, in principle, be derived from detailed spectral measurements.
Key words: galaxies: clusters: general - acceleration of particles
An excess of hard X-ray (hereafter HXR) emission above the thermal spectrum has
been found in the energy range 20-80 keV from the Coma cluster of galaxies
(Fusco-Femiano et al. 2004,1999; Rephaeli & Gruber 2002). The validity of this excess is, however, still
unclear because Rossetti & Molendi (2004) re-analyzed the Coma data and found no evidence
for such hard X-ray excess. Further re-analysis of the same data (Fusco-Femiano et al. 2004)
seem to confirm the presence of the HXR excess at the level observed by
Fusco-Femiano et al. (1999) and Rephaeli & Gruber (2002). The recent INTEGRAL observation of Coma
(Renaud et al. 2006) analyzed the morphology of the cluster in the range 18-30 keV and found that the hard X-ray emission comes from an extended source with
a radius ![]() 30 arcmin. The spatial distribution is similar to the thermal
one as obtained with XMM (in the range 0.3-2 keV). The INTEGRAL data indicate
that the upper limit in 30-50 keV range is a factor
30 arcmin. The spatial distribution is similar to the thermal
one as obtained with XMM (in the range 0.3-2 keV). The INTEGRAL data indicate
that the upper limit in 30-50 keV range is a factor ![]() 1.5 above the
mean RXTE spectrum and the non-thermal mechanisms are expected to contribute
1.5 above the
mean RXTE spectrum and the non-thermal mechanisms are expected to contribute
![]()
![]() of the total flux in this region.
of the total flux in this region.
The hard X-ray excess has been interpreted as being due either to inverse Compton (IC) scattering of relic CMB photons by relativistic electrons (see, e.g., Brunetti et al. 2001; Sarazin & Lieu 1998; Fusco-Femiano et al. 1999) or to bremsstrahlung of nonthermal subrelativistic electrons (Kempner & Sarazin 2000; Enßlin et al. 1999). Yet further interpretations have been proposed - X-ray emission by secondary electrons (Blasi & Colafrancesco 1999), or bremsstrahlung emission by subrelativistic protons (Dogiel 2001).
Each of these models has serious problems. In the framework of the IC model
the magnetic field strength can be estimated from the ratio of X-ray to radio
fluxes because both radiations are produced by the same relativistic electrons.
A weak (uniform) value of the magnetic field of order 0.1-0.2 ![]() G is derived
from the IC model. On the other hand, estimates of the magnetic field strength
in the intracluster medium determined from Faraday rotation yield much higher
value of the order of
G is derived
from the IC model. On the other hand, estimates of the magnetic field strength
in the intracluster medium determined from Faraday rotation yield much higher
value of the order of ![]()
![]() in the cluster center
(see, e.g., Clarke et al. 2001; Govoni & Feretti 2004). However, modifications of the IC model such as
the complex electron spectrum model (Schlickeiser et al. 1987) or the model with
anisotropic pitch angle distribution of emitting particles (Petrosian 2001) may
modify the estimates of the IC model quoted above.
in the cluster center
(see, e.g., Clarke et al. 2001; Govoni & Feretti 2004). However, modifications of the IC model such as
the complex electron spectrum model (Schlickeiser et al. 1987) or the model with
anisotropic pitch angle distribution of emitting particles (Petrosian 2001) may
modify the estimates of the IC model quoted above.
Models where the X-rays are generated by nonthermal electron and proton bremsstrahlung are associated with an unacceptably large energy output of emitting particles (Dogiel 2001; Petrosian 2001).
However, the bremsstrahlung model has not been completely explored because emission can also be produced by the quasi-thermal electron component which arises naturally when particles are accelerated from the background thermal plasma. In this case a part of the spectrum is formed under the influence of both Coulomb collisions and a run-away flux of accelerated particles (Gurevich 1960). This class of models was developed by Dogiel (2000) and Liang et al. (2002), who assumed that the hard X-ray flux from a galaxy cluster is generated in regions of electron in-situ acceleration from the thermal pool. In such models the electron distribution function develops an extended transition populated by quasi-thermal electrons. In this region, which lies between the thermal and nonthermal parts of the spectrum, the distribution function differs strongly from the Maxwellian form because it is not an equilibrium distribution (and in this sense it is not thermal), but is formed entirely by the Coulomb collisions (and therefore we cannot define it as nonthermal).
The bremsstrahlung output from the emitting particles is proportional to the lifetime of their distribution function. For electrons with totally nonthermal energies, this lifetime is about the timescale on which a single non-thermal electron suffers ionization losses. In this regime Petrosian's (2001) estimates of the energy output required to reproduce the hard X-ray excess of Coma is completely correct. However, for a given energy in the regime where the spectrum is formed by Coulomb collisions, the lifetimes of the distribution function and that of a single electron may differ dramatically. In fact, the lifetime of, e.g., an equilibrium spectrum is much larger than the characteristic lifetime of a single particle of this spectrum. Therefore, if the hard X-ray Coma flux is emitted by electrons from the quasi-thermal transfer region, a specific and more detailed analysis is necessary for such a situation.
As it was shown by Dogiel (2000) and Liang et al. (2002), if the plasma temperature is of order of several keV, then hard X-rays in the energy range 20-80 keV are produced by this quasi-thermal component of the electron flux. For a fixed radiated luminosity, such as that of the hard X-ray flux from Coma, the rate of energy input into the electrons can be lower than that required in nonthermal bremsstrahlung models. We shall discuss below this energetic problem in more detail. We will show, in addition, that this acceleration process can be tested by looking at the spectral changes in the associated Sunyaev-Zeldovich (SZ) effect from the intracluster medium.
The problem here described will be analyzed in the present paper under the following assumptions:
In the second part of the paper we derive the characteristics of in-situ acceleration from the observed spectrum of X-ray emission and we calculate the distortions of the equilibrium Maxwellian spectrum due to this acceleration. We finally explore whether a signal of acceleration in the Coma halo can be indicated by the associated Sunyaev-Zeldovich effect. In order to compare our results directly with those of Petrosian (2001), we use here the same cosmological model with H0= 60 km s-1 Mpc-1.
Shock acceleration is usually considered as a candidate for particle production in the intracluster medium (see, e.g., Kuo et al. 2003), and for some clusters, the available observations suggest that there are shocks (see, e.g., Fabian et al. 2006; Markevitch et al. 2005) and electrons which might be accelerated by shocks (see, e.g. Miniati et al. 2001; Brunetti et al. 2001; Miniati et al. 2003). However, extended radio and (perhaps) X-ray emission cannot be associated with strong shocks since accelerated electrons are unable to travel large distances from their sources without loosing much of their energy.
Plasma turbulence is hence considered as a viable model for particle (re)acceleration in cluster halos. Numerical calculations show that strong turbulence can be excited in halos (see, e.g., Ricker & Sarazin 2001). If this turbulence generates plasma waves, then a slow stochastic process can accelerate particles through their resonant interactions with the waves. This process can be described as momentum diffusion. We note that particles can also be accelerated directly by hydrodynamic turbulent or quasi-periodic flows in a manner similar to stochastic acceleration by plasma waves (see, e.g., Webb et al. 2003).
The evolution of the distribution function of particles which are scattered by
electromagnetic fluctuations is described by the Fokker-Planck equation which
can be transformed to the diffusion type equation by integration over particle
pitch-angles, if scattering is very effective and the distribution function is
quasi-isotropic. For the mechanism of the in-situ acceleration from background
plasma, the equation can be written in the form
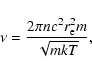 |
(3) |
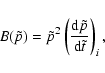 |
(4) |
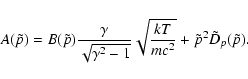 |
(5) |
![$\displaystyle %
\left({{{\rm d}\tilde{p}}\over{{\rm d}\tilde{t}}}\right)_i={1\o...
...t[{{Emc^2(\gamma^2-1)}\over{h^2\omega_{\rm p}^2\gamma^2}}\right]
+0.43\right\},$](/articles/aa/full/2007/02/aa4092-05/img27.gif) |
(6) |
![\begin{displaymath}%
G(\tilde{p})={{\int\limits_{\tilde{p}}^\infty[{\rm d}v/A(v)...
...}v/A(v)]\exp\left(\int\limits_0^v[B(t)/A(t)]{\rm d}t\right)}},
\end{displaymath}](/articles/aa/full/2007/02/aa4092-05/img31.gif) |
(8) |
Detailed information on the conditions necessary to derive a reliable momentum
diffusion coefficient D(p) are not well determined yet. First of all, its
value is determined by a spectrum of electromagnetic fluctuations W(k)(where k is the wave-number of fluctuations) which is basically unknown,
though new theoretical treatments of plasma turbulence (Verma 1999) or X-ray
observations of clusters (see Schuecker et al. 2004) indicate a Kolmogorov-Oboukhoh type spectrum of turbulence in the large scale range,
between 20 kpc and 2.8 Mpc. Secondly, we do not know in details the ratio
between the energy density of the intracluster plasma,
![]() eV cm-3, and that of the magnetic field, UH. This ratio is, moreover,
totally unknown in the regions of particle acceleration. For the magnetic field
strength observed in clusters (whose estimates ranges from
eV cm-3, and that of the magnetic field, UH. This ratio is, moreover,
totally unknown in the regions of particle acceleration. For the magnetic field
strength observed in clusters (whose estimates ranges from ![]() 0.1 to
0.1 to ![]() 10
10 ![]() G, (see e.g. Carilli & Taylor 2002, for a review), the ratio
G, (see e.g. Carilli & Taylor 2002, for a review), the ratio
![]() is in the range
is in the range ![]() 0.4 (low
0.4 (low ![]() plasma) up to
plasma) up to ![]() 1000 (high
1000 (high ![]() plasma). Additional theoretical uncertainties come from the lack of knowledge of the
mechanism through which turbulence is formed in regions of particle
acceleration, whether it is developed by cascade processes (as it is in the new
model of turbulence developed by Goldreich & Sridhar 1997), by intermediate turbulence
model (see, also Cho & Lazarian 2004) or if it is due to the flux instability when a flux of particles escaping from acceleration regions excites there MHD fluctuations due to resonant interaction, as it may occur in the Galactic halo
(see Dogiel et al. 1994) or near shock fronts (Ptuskin & Zirakashvili 2005). Given all these
uncertainties, we are unable to choose reliable parameters of the kinetic
equations, and we have to resort to a quite general description whose overall
features can be, nonetheless, tested against the available data.
plasma). Additional theoretical uncertainties come from the lack of knowledge of the
mechanism through which turbulence is formed in regions of particle
acceleration, whether it is developed by cascade processes (as it is in the new
model of turbulence developed by Goldreich & Sridhar 1997), by intermediate turbulence
model (see, also Cho & Lazarian 2004) or if it is due to the flux instability when a flux of particles escaping from acceleration regions excites there MHD fluctuations due to resonant interaction, as it may occur in the Galactic halo
(see Dogiel et al. 1994) or near shock fronts (Ptuskin & Zirakashvili 2005). Given all these
uncertainties, we are unable to choose reliable parameters of the kinetic
equations, and we have to resort to a quite general description whose overall
features can be, nonetheless, tested against the available data.
In the simplest case of charge particle scattering, the momentum diffusion
coefficient has the form
For the case of low-![]() plasma the momentum diffusion coefficient was derived by
Miller & Steinacker (1992); Schlickeiser & Miller (1998); Steinacker & Miller (1992); Miller et al. (1996) for resonant particle-wave acceleration in solar corona
and in the interstellar medium of the Galaxy. Its analytical form taken from
Schlickeiser & Miller (1998) is
plasma the momentum diffusion coefficient was derived by
Miller & Steinacker (1992); Schlickeiser & Miller (1998); Steinacker & Miller (1992); Miller et al. (1996) for resonant particle-wave acceleration in solar corona
and in the interstellar medium of the Galaxy. Its analytical form taken from
Schlickeiser & Miller (1998) is
The momentum diffusion coefficient in a high-![]() plasma is determined by the spectrum
of magnetic turbulence excited by stochastic plasma motion. In the approximation of
strong turbulence, corresponding to high-
plasma is determined by the spectrum
of magnetic turbulence excited by stochastic plasma motion. In the approximation of
strong turbulence, corresponding to high-![]() plasma, its value depends on whether the
accelerated particles are magnetized or unmagnetized in a random magnetic field.
The coefficients of kinetic equations are determined by pair-correlations of
random velocity and random magnetic fluctuations. Note that there is no
resonant interaction in this case. Below we present general equations for the
momentum diffusion coefficient derived by Dogiel et al. (1987). For magnetized
particles the coefficient of momentum diffusion is given by
plasma, its value depends on whether the
accelerated particles are magnetized or unmagnetized in a random magnetic field.
The coefficients of kinetic equations are determined by pair-correlations of
random velocity and random magnetic fluctuations. Note that there is no
resonant interaction in this case. Below we present general equations for the
momentum diffusion coefficient derived by Dogiel et al. (1987). For magnetized
particles the coefficient of momentum diffusion is given by
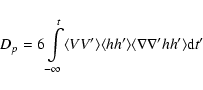 |
(11) |
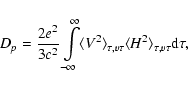 |
(12) |
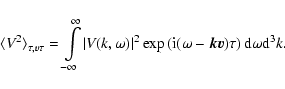 |
(13) |
At the present stage of our knowledge, we cannot prove or disprove the validity of any form of the diffusion coefficient; however, we notice that Clarke et al. (2001) found from ROSAT and radio observations that the total magnetic energy content in clusters is comparable to the total thermal energy content in the same cluster volume.
To circumvent this problem, we derive here the general characteristics of the
acceleration mechanism - i.e., the characteristic time of acceleration (the
dimensionless parameter ![]() ,
see below) necessary to produce the X-ray
excess above the thermal distribution - from the observed flux of hard X-rays
from Coma, a procedure which is independent of the details of the acceleration
process.
,
see below) necessary to produce the X-ray
excess above the thermal distribution - from the observed flux of hard X-rays
from Coma, a procedure which is independent of the details of the acceleration
process.
In the following, the spectrum of turbulence is assumed to be a power-law,
![]() ,
with
,
with ![]() ,
i.e. a spectrum that is close to that
derived by Schuecker et al. (2004). For this fluctuation spectrum the momentum
diffusion coefficient
,
i.e. a spectrum that is close to that
derived by Schuecker et al. (2004). For this fluctuation spectrum the momentum
diffusion coefficient
![]() is also a power-law function of
is also a power-law function of ![]() in a confined range of momenta as follows from Miller & Steinacker (1992); Steinacker & Miller (1992, see Fig. 5).
in a confined range of momenta as follows from Miller & Steinacker (1992); Steinacker & Miller (1992, see Fig. 5).
The energy of accelerated particles
We set the cut-off momentum ![]() at an energy
at an energy
![]() keV, above the range of observations, so that it does not affect the
calculated bremsstrahlung spectrum
keV, above the range of observations, so that it does not affect the
calculated bremsstrahlung spectrum![]() .
In our calculations we take the minimum acceptable value of the cut-off energy to be
.
In our calculations we take the minimum acceptable value of the cut-off energy to be
![]() keV. In the case of resonant interaction this energy corresponds to the
minimum wave-number
keV. In the case of resonant interaction this energy corresponds to the
minimum wave-number
![]()
![]() 10-9 cm-1 in the spectrum of magnetic
fluctuations W(k). Therefore, the energy density of resonant waves is
10-9 cm-1 in the spectrum of magnetic
fluctuations W(k). Therefore, the energy density of resonant waves is
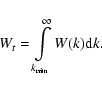 |
(16) |
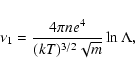 |
(19) |
The dimensionless parameter ![]() for Coma can be derived from observational
data. Thus, Dogiel (2000) analyzed electron acceleration in the central part of
Coma with the density
for Coma can be derived from observational
data. Thus, Dogiel (2000) analyzed electron acceleration in the central part of
Coma with the density
![]() cm-3 while Liang et al. (2002) derived
parameters of acceleration for the average gas density in the Coma halo,
cm-3 while Liang et al. (2002) derived
parameters of acceleration for the average gas density in the Coma halo,
![]() cm-3. It is rather difficult to compare results of these
investigations because different forms of momentum diffusion were used in these
publications.
cm-3. It is rather difficult to compare results of these
investigations because different forms of momentum diffusion were used in these
publications.
We notice that the solution (18) provides an illustrative oversimplification of the solution of Eqs. (7) which is useful in order to get rough quantitative estimates. We present in the following numerical calculations of Eq. (17) which show the time variation of the distribution function f under the influence of stochastic acceleration and Coulomb collisions.
We solve Eq. (17) numerically in order to understand the time evolution of the
distribution function f for a diffusion coefficient
![]() with
with
![]() and q=1. As
discussed earlier,
and q=1. As
discussed earlier,
![]() must have a cutoff for large enough momentum.
For simplicity, we choose the cutoff momentum to be larger than the maximum momentum we
used in our numerical calculations. In fact, the position of the cutoff momentum does not
significantly affect the evolution of the distribution function at small momenta.
must have a cutoff for large enough momentum.
For simplicity, we choose the cutoff momentum to be larger than the maximum momentum we
used in our numerical calculations. In fact, the position of the cutoff momentum does not
significantly affect the evolution of the distribution function at small momenta.
We considered two initial cases: i) transformation of the Maxwellian distribution under the influence of stochastic acceleration. In this case we can estimate the characteristic time for the formation of the particle excess above the thermal distribution; ii) transformation of the resulting nonequilibrium spectrum under the influence of Coulomb collisions only.
These calculations allow us to estimate the power of the electron source necessary to compensate collisional dissipation and to keep the particle excess above the thermal distribution at the level necessary for the production of the observed hard X-ray emission in Coma.
In both cases, we calculate the evolution of the electron spectrum up to the
dimensionless time
![]() (which is equal to 1.85 Gyr for Coma, where
(which is equal to 1.85 Gyr for Coma, where
![]()
![]() 10-14 s-1). As for the boundary conditions,
we use a free boundary condition at the high-momentum boundary of our
calculations, while at the low momentum boundary we used zero-flux boundary
conditions.
10-14 s-1). As for the boundary conditions,
we use a free boundary condition at the high-momentum boundary of our
calculations, while at the low momentum boundary we used zero-flux boundary
conditions.
Figure 1 shows the temporal evolution of the distribution function f formed
by the combined effects of stochastic acceleration and thermalization due to
the Coulomb collisions.
The distribution function is normalized to the value at the low momentum boundary. The
dashed curve shown in this figure is the original Maxwellian distribution, and the dotted
curve is the steady state solution (with a cutoff at large momentum). The five solid
curves represent the distribution function at increasing times
![]() ,
and 4000. The figure shows that the distribution function rapidly
approaches the steady state solution for the relatively low momenta of the quasi-thermal
particle regime (
,
and 4000. The figure shows that the distribution function rapidly
approaches the steady state solution for the relatively low momenta of the quasi-thermal
particle regime (
![]() ). However, for nonthermal relativistic particles the
stationary state is reached on timescales longer than a cluster lifetime. Therefore, in
the framework of this model it is difficult to expect that subrelativistic electrons
emitting hard X-rays and relativistic electrons emitting radio emission are produced by a single mechanism of particle acceleration. Therefore, this analysis cannot be extended to
relativistic energies. Our assumption that the maximum energy of the accelerated
electrons is 110 keV is hence justifiable on the basis of the previous results.
Moreover, as shown by Wolfe & Melia (2006) based on a covariant kinetic theory of
electron plasmas, a power-law tail obtainable from direct or stochastic
acceleration of relativistic particles cannot survive for times longer than
). However, for nonthermal relativistic particles the
stationary state is reached on timescales longer than a cluster lifetime. Therefore, in
the framework of this model it is difficult to expect that subrelativistic electrons
emitting hard X-rays and relativistic electrons emitting radio emission are produced by a single mechanism of particle acceleration. Therefore, this analysis cannot be extended to
relativistic energies. Our assumption that the maximum energy of the accelerated
electrons is 110 keV is hence justifiable on the basis of the previous results.
Moreover, as shown by Wolfe & Melia (2006) based on a covariant kinetic theory of
electron plasmas, a power-law tail obtainable from direct or stochastic
acceleration of relativistic particles cannot survive for times longer than
![]() 20 Myr because the equilibration time scale for relativistic electrons
is quite short for the case of clusters and hence a thermal distribution is
soon established.
20 Myr because the equilibration time scale for relativistic electrons
is quite short for the case of clusters and hence a thermal distribution is
soon established.
![\begin{figure}
\par\includegraphics[height=6.9cm,width=7.65cm,clip]{aa4092fig1.ps} \end{figure}](/articles/aa/full/2007/02/aa4092-05/Timg77.gif) |
Figure 1:
Temporal evolution of the distribution function up to
|
Now let us assume that the acceleration mechanism is interrupted but the
initial distribution function is described by the nonequilibrium form of
Eq. (18). In this case, the dimensionless equation for the distribution
function f is
We show in Fig. 2 that the dissipation time scale is larger than the single
electron ionization loss time scale near the thermal particle region, because
the distribution function there is of almost equilibrium form, and it increases
in the region of nonthermal momenta, where the lifetime of particles increases
as
![]() .
.
![\begin{figure}
\par\includegraphics[height=6.9cm,width=7.65cm,clip]{aa4092fig2.ps} \end{figure}](/articles/aa/full/2007/02/aa4092-05/Timg82.gif) |
Figure 2:
Temporal evolution of the distribution function up to
|
We now return to the problem of the energetics of the emitting electrons.
First, we recall Petrosian's criticism of the bremsstrahlung model
(see Petrosian 2001). He estimated the yield of bremsstrahlung photons as
![]()
![]() 10-6 in the energy range 20-80 keV, where
10-6 in the energy range 20-80 keV, where
![]() is the ratio of ionization to
bremsstrahlung losses. Then for the hard X-ray flux from Coma in this energy
range,
is the ratio of ionization to
bremsstrahlung losses. Then for the hard X-ray flux from Coma in this energy
range,
![]()
![]() 1043 erg s-1, a large amount of energy,
1043 erg s-1, a large amount of energy,
![]() erg s-1 is transferred from the accelerated
electrons to the background plasma by ionization losses. As a result, the
intracluster plasma temperature should rise to a temperature >108 K on a quite short time scale
erg s-1 is transferred from the accelerated
electrons to the background plasma by ionization losses. As a result, the
intracluster plasma temperature should rise to a temperature >108 K on a quite short time scale ![]() 3
3 ![]() 107 yr. We stress here that these conclusions were obtained under the assumption that
the lifetime of a single electron equals the lifetime of the particle
distribution function. These estimates are correct only in the case that the
electrons are nonthermal, and therefore collisionless. However, the previous
energetic arguments cannot be used in energy ranges where the spectrum is
formed by Coulomb collisions because, as we have shown in
Sect. 3, the lifetime of particles differs strongly from the
lifetime of the distribution function (see Fig. 3).
For instance, let us consider the lifetime of thermal electrons at an energy of
about 8 keV. Their individual lifetime is about
107 yr. We stress here that these conclusions were obtained under the assumption that
the lifetime of a single electron equals the lifetime of the particle
distribution function. These estimates are correct only in the case that the
electrons are nonthermal, and therefore collisionless. However, the previous
energetic arguments cannot be used in energy ranges where the spectrum is
formed by Coulomb collisions because, as we have shown in
Sect. 3, the lifetime of particles differs strongly from the
lifetime of the distribution function (see Fig. 3).
For instance, let us consider the lifetime of thermal electrons at an energy of
about 8 keV. Their individual lifetime is about ![]() 106 yr, but the
lifetime of the distribution function at these energies is much longer (almost
infinite) because the distribution function for these energies is almost in
equilibrium. Therefore, the energy supply necessary for the bremsstrahlung
radiation can only be estimated from the corresponding kinetic equations. It
follows that estimates of the energetics based on the lifetime of single
electrons are not appropriate here, and lead to wrong conclusions.
Figure 3 shows, in fact, the variation of the lifetime of the distribution
function in Eq. (18), as derived from Eq. (20). From this
figure we see that the lifetimes of the distribution function and of the
particles are equal to each other only for high (nonthermal) electron
energies.
106 yr, but the
lifetime of the distribution function at these energies is much longer (almost
infinite) because the distribution function for these energies is almost in
equilibrium. Therefore, the energy supply necessary for the bremsstrahlung
radiation can only be estimated from the corresponding kinetic equations. It
follows that estimates of the energetics based on the lifetime of single
electrons are not appropriate here, and lead to wrong conclusions.
Figure 3 shows, in fact, the variation of the lifetime of the distribution
function in Eq. (18), as derived from Eq. (20). From this
figure we see that the lifetimes of the distribution function and of the
particles are equal to each other only for high (nonthermal) electron
energies.
![\begin{figure}
\par\includegraphics[height=7.6cm,width=8.45cm,clip]{aa4092fig3.eps} \end{figure}](/articles/aa/full/2007/02/aa4092-05/Timg87.gif) |
Figure 3:
The lifetime of the electron spectrum (18) derived from
Eq. (17) is shown by the solid curve. The lifetime of a single
electron determined by ionization loss is shown by the dashed-dotted curve.
Here the dimension frequency of Coulomb collisions of thermal particles
|
In order to estimate the energy supply necessary to support the non-equilibrium
distribution (Eq. (18)) we use the following kinetic equations in which we include
bremsstrahlung losses
In the case of nonthermal electrons whose spectrum is, e.g., a power-law, the
last term exceeds the others on the right-hand side of Eq. (21), and
then
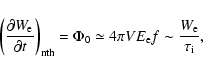 |
(22) |
If the particles are thermal, and their spectrum is described by a Maxwellian, then the
first and the third terms on the right-hand side of Eq. (20) cancel out so that
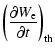 |
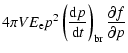 |
||
| (23) |
We can estimate the rate of energy supply to the 50-keV electrons that is required to
generate the observed flux of ![]() 50-keV bremsstrahlung X-ray emission from Coma as a function of different values of the plasma temperature T. For simplicity, we consider
the electron spectrum to be of the form given by Eq. (18). When the temperature T is low, the 50-keV electrons are in the nonthermal particle regime, while for high
plasma temperature these electrons are thermal. From Eqs. (18) and (21)
we obtain the variation of the associated rate of electron heating as a function of the
background temperature T. The required level of heating, normalized to the rate of
heating required for non-thermal particles,
50-keV bremsstrahlung X-ray emission from Coma as a function of different values of the plasma temperature T. For simplicity, we consider
the electron spectrum to be of the form given by Eq. (18). When the temperature T is low, the 50-keV electrons are in the nonthermal particle regime, while for high
plasma temperature these electrons are thermal. From Eqs. (18) and (21)
we obtain the variation of the associated rate of electron heating as a function of the
background temperature T. The required level of heating, normalized to the rate of
heating required for non-thermal particles,
![]() ,
is shown as a function of the temperature in Fig. 4, where the parameters defining the
acceleration of particles are those inferred from the X-ray analysis of the Coma cluster.
We find that when the temperature T is low, the 50-keV electrons are nonthermal and -
as expected - the rate at which they must be heated is independent of the temperature
and is almost equal to
,
is shown as a function of the temperature in Fig. 4, where the parameters defining the
acceleration of particles are those inferred from the X-ray analysis of the Coma cluster.
We find that when the temperature T is low, the 50-keV electrons are nonthermal and -
as expected - the rate at which they must be heated is independent of the temperature
and is almost equal to ![]() .
However, when the plasma temperature T increases, and
the 50-keV electrons shift into the quasi-thermal regime (where the spectrum is formed by
the Coulomb collisions), the required energy supply to maintain the observed hard X-ray
flux from Coma decreases rapidly as the background plasma temperature increases. For a temperature
.
However, when the plasma temperature T increases, and
the 50-keV electrons shift into the quasi-thermal regime (where the spectrum is formed by
the Coulomb collisions), the required energy supply to maintain the observed hard X-ray
flux from Coma decreases rapidly as the background plasma temperature increases. For a temperature ![]() keV, the emitting electrons in Coma are quasi-thermal and the
energy supply they require is one or two orders of magnitude below Petrosian's (2001) result, even by using a simple qualitative estimate. Accurate quantitative calculations may give even higher variations. This result may indeed solve the energetic problem
raised by Petrosian (2001): in fact, the quasi-thermal electrons need much less energy in
order to produce the observed HXR bremsstrahlung radiation with respect to the case of
nonthermal particles.
keV, the emitting electrons in Coma are quasi-thermal and the
energy supply they require is one or two orders of magnitude below Petrosian's (2001) result, even by using a simple qualitative estimate. Accurate quantitative calculations may give even higher variations. This result may indeed solve the energetic problem
raised by Petrosian (2001): in fact, the quasi-thermal electrons need much less energy in
order to produce the observed HXR bremsstrahlung radiation with respect to the case of
nonthermal particles.
![\begin{figure}
\par\includegraphics[height=7.5cm,width=8.5cm,clip]{aa4092fig4.eps}\end{figure}](/articles/aa/full/2007/02/aa4092-05/Timg108.gif) |
Figure 4:
The rate at which energy must be supplied to the 50-keV electrons
generating a fixed bremsstrahlung X-ray flux as a function of
temperature of background gas, normalized to |
As it is clear from our analysis, our model describes the processe of in-situ acceleration reasonably well for relatively long time because of the presence of weak acceleration mechanisms. Therefore, the time variations of both the plasma density and of its temperature are very slow. Attempts to investigate a nonlinear phenomenological model of particle acceleration in Coma were made by Blasi (2000). Such an analysis showed that, due to nonlinear processes, the temperature of plasma increases slowly. However, there are still questions on whether this model can describe correctly the process of thermalization in the cluster atmospheres (see discussion by Wolfe & Melia 2006). The role of non-linear effects certainly needs further analysis which goes beyond the scope of this paper and we will address this issue elsewhere.
We derive here the spectrum of the emitting electrons in Coma from the X-ray data using
the more accurate solution (see Eq. (7)) of the kinetic equation Eq. (2).
We calculate the flux of hard X-ray emission using the equation
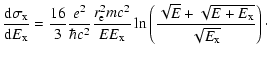 |
(25) |
![\begin{figure}
\par\includegraphics[height=7.2cm,width=8.6cm,clip]{aa4092fig5.eps} \end{figure}](/articles/aa/full/2007/02/aa4092-05/Timg111.gif) |
Figure 5: Bremsstrahlung X-ray flux from the Coma cluster produced by subrelativistic electrons with a cut-off, E=110 keV, T=8.25 keV. The flux measured with Beppo-SAX was taken from Fusco-Femiano et al. (1999). |
The calculated bremsstrahlung spectrum from Coma is shown together with the Beppo-SAX
data in Fig. 5. We consider a the volume of particle acceleration to be
![]()
![]() 1074 cm3 which is smaller than the whole volume of the Coma halo
inferred from radio and soft X-ray data.
In the general case it is convenient using the simplest form of the diffusion
coefficient in Eq. (9). The necessary acceleration time of
1074 cm3 which is smaller than the whole volume of the Coma halo
inferred from radio and soft X-ray data.
In the general case it is convenient using the simplest form of the diffusion
coefficient in Eq. (9). The necessary acceleration time of ![]() keV particles,
keV particles,
![]() ,
is of the order
,
is of the order ![]() 1017 s, independently of the acceleration mechanism. This value is slightly lower than that derived by Dogiel (2000) for the central region of Coma where the
intracluster gas has the highest density.
1017 s, independently of the acceleration mechanism. This value is slightly lower than that derived by Dogiel (2000) for the central region of Coma where the
intracluster gas has the highest density.
For the case of low-![]() plasma we can go a step further and estimate the
necessary density of resonant wave by using the diffusion coefficients for
electrons and protons taken from Steinacker & Miller (1992) and Schlickeiser & Miller (1998). We notice
that the momentum diffusion coefficient derived from these equations
corresponds to the general form (9) in the nonrelativistic energy
range.
plasma we can go a step further and estimate the
necessary density of resonant wave by using the diffusion coefficients for
electrons and protons taken from Steinacker & Miller (1992) and Schlickeiser & Miller (1998). We notice
that the momentum diffusion coefficient derived from these equations
corresponds to the general form (9) in the nonrelativistic energy
range.
Figure 6 shows the momentum diffusion coefficient for electrons for the
low-![]() case.
Only a low energy density in resonant plasma waves,
case.
Only a low energy density in resonant plasma waves,
![]()
![]() 10-13, is required to fit the Coma HXR data. Here
10-13, is required to fit the Coma HXR data. Here ![]() is the energy density of plasma waves and
is the energy density of plasma waves and
![]() is the energy density of the large scale magnetic field.
is the energy density of the large scale magnetic field.
![\begin{figure}
\par\includegraphics[height=7.5cm,width=8.5cm,clip]{aa4092fig6.eps} \end{figure}](/articles/aa/full/2007/02/aa4092-05/Timg117.gif) |
Figure 6:
The dimensionless momentum diffusion coefficient
|
The corresponding electron distribution function is compared with a thermal
spectrum at T = 8.25 keV in Fig. 7. The change in the distribution function
is achieved by ![]()
![]() of the background electrons being quasi-thermal. It
follows that the energy density of thermal electrons is
of the background electrons being quasi-thermal. It
follows that the energy density of thermal electrons is
![]() eV cm-3 and that of the quasi-thermal electrons is
eV cm-3 and that of the quasi-thermal electrons is
![]() eV cm-3, thus yielding the ratio
eV cm-3, thus yielding the ratio
![]() for Coma.
for Coma.
Protons are generally disregarded in the calculation of bremsstrahlung emission because,
having low rates of energy loss, they leave the emitting region before they lose a significant fraction of their energy. On the other hand, if protons escape from a radiating region relatively slowly, they can produce a bremsstrahlung flux whose value is
comparable with that of the electrons. An analysis of the bremsstrahlung radiation
emitted by subrelativistic protons (inverse bremsstrahlung) in the Coma cluster
(Dogiel 2001) showed that protons are able, in fact, to generate the observed hard X-ray
emission. These X-rays are accompanied by the excitation of background nuclei which could
be detectable through the development of prominent carbon and oxygen gamma-ray lines.
Dogiel (2001) estimated the expected flux of these lines. Recently, Iyudin et al. (2004) have
found tracers of this gamma-ray line emission towards the Coma and Virgo clusters at the
expected level. The energy deposition by subrelativistic protons estimated by
Iyudin et al. (2004) is of the order of ![]() 8
8 ![]() 1048 erg s-1, which matches the
required rate if protons produce the observed hard X-ray flux (Dogiel 2001). However,
this process involves subrelativistic protons and so it faces the same problem of
energetics and plasma heating as we discussed in Sect. 4.
1048 erg s-1, which matches the
required rate if protons produce the observed hard X-ray flux (Dogiel 2001). However,
this process involves subrelativistic protons and so it faces the same problem of
energetics and plasma heating as we discussed in Sect. 4.
The theoretical approach we have taken in the present paper allows us to estimate the density of electrons and protons accelerated from the background pool using the kinetic parameters derived from the spectrum of plasma waves, and hence to understand whether protons are important. The momentum diffusion coefficient for protons was taken in the form of Eq. (10). In Fig. 8 the spectrum of protons is shown for the parameters derived in Sect. 5. It can be seen that stochastic acceleration is ineffective for subrelativistic protons (note that a similar conclusion for the Galaxy was also obtained by Schlickeiser & Miller 1998). In order to produce a flux of proton bremsstrahlung comparable with that of electrons, for example at a photon energy 10 keV, the density of 20-MeV protons should be about the same as the density of 10-keV electrons. As shown Fig. 8, this condition is not fulfilled, and so we conclude that the hard-X-ray emission from the Coma cluster cannot be ascribed to proton bremsstrahlung.
![\begin{figure}
\par\includegraphics[height=7.2cm,width=8.5cm,clip]{aa4092fig8.eps} \end{figure}](/articles/aa/full/2007/02/aa4092-05/Timg124.gif) |
Figure 8: The spectrum of subrelativistic electrons (dashed-dotted curve) and protons (solid curve) in the Coma cluster halo are shown as a function of the particle energy. |
In the context of the present study it is important to find observational
resources which can provide independent evidence for the subrelativistic
electron population that we consider to be responsible for the hard X-ray
emission from clusters of galaxies. One possibility is to use a detailed
analysis of the inverse Compton scattering of CMB photons off the population
of sub-relativistic electrons, the SZ effect described by Zeldovich & Sunyaev
(see Zeldovich & Sunyaev 1969). The amplitude and the spectrum of this effect depend on
the distribution function of the electrons in the intracluster medium. As a result of the inverse Compton scattering, the spectrum of the CMB radiation is
shifted to higher frequencies when observed along the line of sight through the
intracluster medium (see for a general review Birkinshaw 1999). The spectral
distortion of the microwave background can be calculated for any electron
distribution function, and not only for the standard Maxwellian spectrum
adopted in most discussions of the Sunyaev-Zeldovich effect: hence, we can
calculate the Sunyaev-Zeldovich effect as due to a nonthermal component of the
electron distribution in the supra-thermal (see, e.g., Blasi et al. 2000; Ensslin & Kaiser 2000)
and relativistic (see Colafrancesco et al. 2003; Shimon & Rephaeli 2002) energy ranges.
To this aim, we use here the electron distribution function derived from the
X-ray data to calculate the Sunyaev-Zeldovich effect using the formalism
presented in Rephaeli (1995) and Birkinshaw (1999). The change in the radiation
temperature
![]() at frequency
at frequency ![]() is given by
is given by
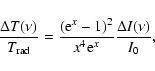 |
(26) |
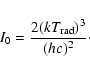 |
(27) |
![$\displaystyle %
\Delta T(\nu)=T_{\rm rad}\tau{{({\rm e}^x-1)^2}\over{{\rm e}^xx...
...
\left({{\exp[-3s)]}\over{\exp[x{\rm e}^{(-s)}]-1}}-{1\over{\exp[x]-1}}\right),$](/articles/aa/full/2007/02/aa4092-05/img131.gif) |
(28) |
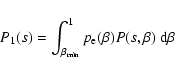 |
(29) |
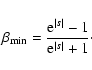 |
(30) |
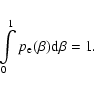 |
(31) |
![\begin{figure}
\par\includegraphics[height=7.6cm,width=6.3cm,clip]{aa4092fig11.eps} \end{figure}](/articles/aa/full/2007/02/aa4092-05/Timg144.gif) |
Figure 11: Difference between the pure thermal and the total (thermal plus quasi-thermal) Sunyaev-Zeldovich effect. |
We can now calculate the Sunyaev-Zeldovich effect from the regions where the acceleration
takes place. Here we should take into account that, as follows from the soft X-ray data,
the volume of the acceleration region,
![]()
![]()
![]() ,
is
comparable with the Beppo-SAX estimate of the emitting volume
,
is
comparable with the Beppo-SAX estimate of the emitting volume
![]()
![]()
![]() .
The total optical depth of the thermal gas in the Coma cluster is
not precisely known. Battistelli et al. (2003) estimated the total optical depth of Coma as
.
The total optical depth of the thermal gas in the Coma cluster is
not precisely known. Battistelli et al. (2003) estimated the total optical depth of Coma as
![]()
![]() 10-3 and De Petris et al. (2002) estimated the depth as
10-3 and De Petris et al. (2002) estimated the depth as
![]()
![]() 10-3. Moreover, some contribution to the optical depth
may be due to an extended halo of cooler gas, with a temperature 0.6-1.3 keV and
density of
10-4-10-3 cm-3 (see Nevalainen et al. 2004).
10-3. Moreover, some contribution to the optical depth
may be due to an extended halo of cooler gas, with a temperature 0.6-1.3 keV and
density of
10-4-10-3 cm-3 (see Nevalainen et al. 2004).
We calculate here the Sunyaev-Zeldovich effects from the thermal volume of the Coma halo
in the absence of particle acceleration (the dashed curve in Fig. 10) and in its presence
(the solid curve in Fig. 10). In these calculations we assumed that the temperature and
the optical depth of the thermal electron population are T=8.25 keV and
![]()
![]() 10-3, as derived from X-ray observations. Such an estimate assumes that the
hot plasma occupies the whole volume of the Coma halo. Assuming that the volume where
particles are accelerated is
10-3, as derived from X-ray observations. Such an estimate assumes that the
hot plasma occupies the whole volume of the Coma halo. Assuming that the volume where
particles are accelerated is
![]()
![]() 1074 cm3, we estimate an optical
depth of the acceleration region (i.e., a part of the total optical depth where the
electron spectrum is distorted by the acceleration) which is
1074 cm3, we estimate an optical
depth of the acceleration region (i.e., a part of the total optical depth where the
electron spectrum is distorted by the acceleration) which is
![]()
![]() 10-4.
10-4.
The difference between the pure thermal and the total (thermal plus quasi-thermal)
Sunyaev-Zeldovich effects is shown in Fig. 11. This figure shows that the presence of
sub-relativistic electrons in Coma produces a further temperature decrement at
![]() GHz and a further temperature increase at higher frequencies. At the same time, the
additional pressure (or energy density) contributed by the sub-relativistic electrons
produce an increase in the frequency of the zero point (i.e., the frequency at which
GHz and a further temperature increase at higher frequencies. At the same time, the
additional pressure (or energy density) contributed by the sub-relativistic electrons
produce an increase in the frequency of the zero point (i.e., the frequency at which
![]() )
of the SZ effect, a value which is uniquely determined by the overall
pressure
)
of the SZ effect, a value which is uniquely determined by the overall
pressure
![]() ,
of the electron population (see Colafrancesco et al. 2003). Also the overall amplitude of the temperature decrement due to the
subrelativistic electrons is proportional to their pressure since
,
of the electron population (see Colafrancesco et al. 2003). Also the overall amplitude of the temperature decrement due to the
subrelativistic electrons is proportional to their pressure since
![]() .
.
The change in the Sunyaev-Zel'dovich effect due to the accelerated electrons produces a temperature decrement
![]() in the frequency range 50-100 GHz.
However, the uncertainty of the available SZ data for Coma does not allow yet to set
definite constraints on the model presented in this paper. Nonetheless, with the new
generation of telescopes for observing the Sunyaev-Zel'dovich effect, such a signal
should be detectable. The major difficulty in seeing this departure from the thermal
Sunyaev-Zel'dovich effect is the presence of background fluctuations in the microwave
background radiation. The expected background anisotropy on degree angular scales of
interest for the Coma cluster is
in the frequency range 50-100 GHz.
However, the uncertainty of the available SZ data for Coma does not allow yet to set
definite constraints on the model presented in this paper. Nonetheless, with the new
generation of telescopes for observing the Sunyaev-Zel'dovich effect, such a signal
should be detectable. The major difficulty in seeing this departure from the thermal
Sunyaev-Zel'dovich effect is the presence of background fluctuations in the microwave
background radiation. The expected background anisotropy on degree angular scales of
interest for the Coma cluster is ![]()
![]() in this frequency range, and has a flat spectrum which is not readily distinguished from the gently-curving spectrum seen in
Figs. 10, 11.
However, the use of multi frequency observations increases the possibility of detection
of the SZ effect associated to sub-relativistic particles since the relative amplitudes
of the thermal and subrelativistic SZ effects change with the frequency over the whole
range (
in this frequency range, and has a flat spectrum which is not readily distinguished from the gently-curving spectrum seen in
Figs. 10, 11.
However, the use of multi frequency observations increases the possibility of detection
of the SZ effect associated to sub-relativistic particles since the relative amplitudes
of the thermal and subrelativistic SZ effects change with the frequency over the whole
range (![]() 30-300 GHz) accessible to SZ experiments.
Some possibility of detecting the distorted spectrum of the Sunyaev-Zel'dovich effect in
the presence of background fluctuations also exists through a detailed spectral
measurement of the cluster over a smaller region to reduce the background fluctuation
signal (although this won't reduce the amplitude of the kinematic Sunyaev-Zel'dovich
effect, which has the same spectrum as the background fluctuations).
Measurements of this type are challenging, but should become possible as the
sensitivity of bolometer arrays in the mm and sub-mm bands increases, provided
that accurate cross-calibration in the different bands is achieved
(Birkinshaw & Lancaster 2005).
30-300 GHz) accessible to SZ experiments.
Some possibility of detecting the distorted spectrum of the Sunyaev-Zel'dovich effect in
the presence of background fluctuations also exists through a detailed spectral
measurement of the cluster over a smaller region to reduce the background fluctuation
signal (although this won't reduce the amplitude of the kinematic Sunyaev-Zel'dovich
effect, which has the same spectrum as the background fluctuations).
Measurements of this type are challenging, but should become possible as the
sensitivity of bolometer arrays in the mm and sub-mm bands increases, provided
that accurate cross-calibration in the different bands is achieved
(Birkinshaw & Lancaster 2005).
The possibility to measure the SZ effect from the population of sub-relativistic or relativistic particles could provide a way to estimate the overall pressure of such particle population and, in turn, to constrain the energy spectrum taken up by such particles in the cluster atmosphere. Even if this demands a large experimental effort, the result will undoubtedly shed additional, and maybe crucial, light on the nature of the acceleration mechanism.
We have analyzed in this paper the process of particle acceleration from a background plasma acting through magnetic fluctuations generated by intracluster turbulence with a specific application to the problem of the origin of hard X-ray emission from the Coma cluster. From the equations describing the influence of Coulomb collisions, we derived the entire electron distribution function from the thermal to the high-energy non-thermal regime. Our analysis allowed us to estimate the energy supply necessary for bremsstrahlung to be responsible for the hard X-ray emission. For nonthermal electrons we confirm that the bremsstrahlung efficiency is low, which makes it almost impossible to regard this electronic component as the source of the hard X-ray excess in Coma. This result is in complete agreement with earlier conclusion (see Petrosian 2001) on the inapplicability of the nonthermal bremsstrahlung interpretation. However, we have also shown here that the bremsstrahlung efficiency increases significantly if the emitting electrons belong to the extended transfer regime between the thermal and nonthermal parts of the electron distribution function. This quasi-thermal regime is formed naturally when emitting particles are accelerated from the background plasma. In the specific case of Coma, we found that the total energy loss rate of the quasi-thermal electrons that emit the HXR radiation in the 20-80 keV range is almost two orders of magnitude lower than for nonthermal particles. This result may solve both the problem of the origin of the HXR emission in Coma and of the excessive heating of the cluster gas in the bremsstrahlung interpretation of the HXR excess.
We have further shown that the distribution function of quasi-thermal electrons that we
derived implies significant distortion of the thermal Sunyaev-Zeldovich effect from the
Coma cluster. Although this additional signal is at the level of ![]()
![]() of the
amplitude of the thermal Sunyaev-Zel'dovich effect and therefore its observation will be
challenging from the experimental side, its definite detection will nonetheless be able
to provide a stringent test of our theoretical model.
of the
amplitude of the thermal Sunyaev-Zel'dovich effect and therefore its observation will be
challenging from the experimental side, its definite detection will nonetheless be able
to provide a stringent test of our theoretical model.
Acknowledgements
The authors thank the Referee whose comments helped us to improve the paper. V.A.D. is grateful to Anisia Tang and Boris Klumov for kind help to perform numerical calculations. C.M.K. is supported in part by the National Science Council of Taiwan grants NSC-92-2112-M-008-046 and NSC-93-2112-M-008-017. P.H.K. is supported in part by the National Science Council of Taiwan grant NSC-93-2112-M-008-006. C.Y.H. is supported in part by the National Science Council of Taiwan grant NSC-93-2112-M-008-016. W.H.I. is supported in part by the National Science Council of Taiwan grants NSC-93-2112-M-008-006 and NSC-93-2752-M-008-001-PAE. V.A.D. and D.A.P. are partly supported by the grant of a President of the Russian Federation "Scientific School of Academician V. L. Ginzburg''.
In the nonrelativistic energy range when ![]() (
(![]() ), the kinetic equation for
), the kinetic equation for
![]() and
and
![]() can be significantly simplified and written in the form
respectively
can be significantly simplified and written in the form
respectively
It was shown by Dogiel (2000) and Liang et al. (2002) that two excesses above the thermal
Maxwellian spectrum are formed in the range
![]() .
When
.
When
![]() ,
the excess is formed by Coulomb collisions (the
collisional regime of quasi-thermal particles), and one can imagine the spectrum
there as a distorted Maxwellian function. For
,
the excess is formed by Coulomb collisions (the
collisional regime of quasi-thermal particles), and one can imagine the spectrum
there as a distorted Maxwellian function. For
![]() the spectrum is formed by
particle interactions with plasma waves (the collisionless regime of nonthermal
particles). For these energies the particle spectrum can be described as power-law over
an extended energy range. We also impose a natural boundary condition for
the spectrum is formed by
particle interactions with plasma waves (the collisionless regime of nonthermal
particles). For these energies the particle spectrum can be described as power-law over
an extended energy range. We also impose a natural boundary condition for
![]() ,
,
| (A.6) |
It is convenient to reduce Eq. (A.2) to the form
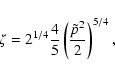 |
(A.8) |
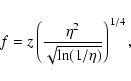 |
(A.9) |
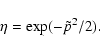 |
(A.10) |
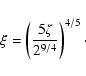 |
(A.11) |
| (A.13) |
The solution of Eq. (A.2) can be presented with the well-known Green
function
![]() for the diffusion equation
for the diffusion equation
![$\displaystyle G(x,x_0~\vert~\tilde{t},\tau)=
{1\over{2\sqrt{\pi}}} {1\over{(\tilde{t}-\tau)^{1/2}}}
\exp\left[-{{(x-x_0)^2}\over{4(\tilde{t}-\tau )}}\right]\cdot$](/articles/aa/full/2007/02/aa4092-05/img190.gif) |
(A.14) |
 |
(A.17) |