A&A 461, 339-349 (2007)
DOI: 10.1051/0004-6361:20066030
Molecular Hanle effect in the Paschen-Back regime
A. I. Shapiro1 - D. M. Fluri1 - S. V. Berdyugina1,2 - J. O. Stenflo1,3
1 - Institute of Astronomy, ETH Zurich, 8092 Zurich, Switzerland
2 - Astronomy Division, PO Box 3000, 90014 University of Oulu, Finland
3 - Faculty of Mathematics & Science, University of Zurich, Germany
Received 13 July 2006 / Accepted 23 September 2006
Abstract
Context. The second solar spectrum resulting from coherent scattering is a main tool for diagnostics of turbulent magnetic fields on the Sun. Scattering on diatomic molecules plays an important role in forming this spectrum and even dominates in some spectral regions.
Aims. In a magnetic field electronic states of a molecule are often perturbed via the Paschen-Back effect. Sometimes this perturbation can completely change the spectrum, not only quantitatively, but even qualitatively. Here we calculate molecular scattering properties taking into account the Paschen-Back effect.
Methods. Starting with the Hund's case (a) wave functions as a basis we obtain with the perturbation theory wave functions of the intermediate Hund's case (a-b) in a magnetic field. Using new, perturbed values of the Landé factors and transition amplitudes we calculate the Mueller matrix for coherent scattering at diatomic molecules in the intermediate Hund's case (a-b) and look for the effects that can be caused by the Paschen-Back effect.
Results. We have found a considerable deviation from the Zeeman regime and discuss here the quantitative and qualitative effects on observed polarization signals for the CN
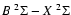 and MgH
and MgH
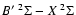 systems as examples.
systems as examples.
Key words: line: formation - magnetic fields - molecular
processes - polarization - radiative transfer - scattering
1 Introduction
The properties of the coherent scattering process are modified in a
magnetic field via the Hanle effect, which provides us with a very
sensitive tool for studying the distribution of weak magnetic fields
on the Sun. The Hanle effect is most sensitive when the magnetic
splitting is comparable to the natural line width. For most atomic
transitions this implies weak magnetic fields, so that the level
splitting can be calculated in the Zeeman effect regime (ZR). For
many molecular transitions even weak magnetic fields can
significantly perturb the internal molecular structure and change
wave functions of molecular levels. Therefore the level splitting
and amplitudes of the transitions should be calculated taking into account the
Paschen-Back effect (PBE) regime (Asensio Ramos & Trujillo Bueno 2006; van Vleck 1926; Berdyugina et al. 2005; Schadee 1978; Hill 1929).
Previously the Hanle effect in the Paschen-Back regime (PBR) was treated
only for atomic transitions by Bommier (1980) and
Landolfi & Landi Degl'Innocenti (1985), who studied the Hanle effect on
level-crossings for the helium D3 and sodium D lines of solar
prominences.
The recent first analysis of molecular scattering polarization (Trujillo Bueno 2003; Bommier et al. 2006; Asensio Ramos & Trujillo Bueno 2005; Landi Degl'Innocenti 2003; Faurobert & Arnaud 2003; Berdyugina et al. 2002) and the first detection of the Hanle effect in molecular lines
on the Sun (Berdyugina & Fluri 2004) revealed the clear
advantages of molecular lines for studying turbulent magnetic
fields by means of the differential Hanle effect, and thus the
necessity to expand the theory of the Hanle effect taking into
account the PBE for the molecular case.
Here, for the first time, we couple the PBE with the Hanle effect
in molecular lines. In Sect. 2 we shortly introduce
the Paschen-Back effect, before we discuss its general influence
on linear polarization. In Sect. 3 we give an
overview of the Hanle effect theory and
present our method of calculation, emphasizing distinctions
between the Zeeman regime (ZR) and Paschen-Back regime (PBR)
calculations. In Sect. 4 we discuss the PBE
influence on scattering profiles. Preliminary results on single line calculations have been previously reported by Shapiro et al. (2006). Here we present more general calculations
for multiplet transitions. Finally in
Sect. 5 we discuss net polarization properties
of scattered radiation and the Hanle effect in the saturated
regime.
We illustrate all our general conclusions with example calculations
for the CN
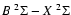 and MgH
and MgH
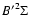 -
-
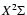 systems, which are strongly
influenced by the PBE even for weak fields.
systems, which are strongly
influenced by the PBE even for weak fields.
2 Paschen-Back effect
The PBE results from the perturbation between different molecular
or atomic states in the presence of a magnetic field. These
interactions change both positions and intensities of lines, which
can completely alter the appearance of the spectrum both
quantitatively and qualitatively.
There are different possibilities for the PBE in molecules. It can
occur, for example, on the fine structure, rotational structure or
between different electronic states. Usually the effect between
different electronic states becomes important only for quite strong
magnetic fields. In our calculations we take into account only the
first two, i.e. on the fine and rotational structures. The relative
importance of these effects and the sequence of their appearance
with increasing magnetic field strength depends on molecular
constants. In the limiting Hund's case (a) (strong spin-orbital
coupling), when the rotational splitting is smaller than the fine
structure splitting, the PBE on the rotational structure first
occurs. On the contrary, in the limiting Hund's case (b) (weak
spin-orbital coupling), the PBE on the fine structure first occurs.
Our calculations of the PBE are based on works of
Kovács (1969), Schadee (1978), Berdyugina et al. (2005)
and can be applied to the intermediate Hund's case (a-b).
In this paper we provide example calculations for
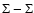 transitions, which are described by Hund's case (b). Because of
the zero orbital momentum of the upper and lower states there is no
PBE on the rotational structure, but there is a quite strong effect
on the fine structure of both states due to small spin-rotational
constants. In this case we therefore calculate the PBE only on the
fine structure.
transitions, which are described by Hund's case (b). Because of
the zero orbital momentum of the upper and lower states there is no
PBE on the rotational structure, but there is a quite strong effect
on the fine structure of both states due to small spin-rotational
constants. In this case we therefore calculate the PBE only on the
fine structure.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6030fig1.eps} \end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg23.gif) |
Figure 1:
The Paschen-Back effect in the doublet level with N=5 for the
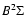 v = 0 state of CN.
v = 0 state of CN. |
| Open with DEXTER |
The level splitting as a function of the magnetic field strength is
shown in Fig. 1 for the doublet with N=5 of the
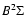 v = 0 state of CN (upper doublet component with
J=5.5, lower with J=4.5). With the increasing magnetic field
strength the electron spin gradually decouples from the rotational
momentum, resulting in modification of the Landé factors. The
PBE becomes apparent in the splitting pattern above about 100 G,
while towards 2 kG the doublet approaches the complete PBE regime,
when the spin is fully decoupled from the rotation. In this case the
sublevels separate in two groups, according to the spin projection
on the magnetic field direction:
v = 0 state of CN (upper doublet component with
J=5.5, lower with J=4.5). With the increasing magnetic field
strength the electron spin gradually decouples from the rotational
momentum, resulting in modification of the Landé factors. The
PBE becomes apparent in the splitting pattern above about 100 G,
while towards 2 kG the doublet approaches the complete PBE regime,
when the spin is fully decoupled from the rotation. In this case the
sublevels separate in two groups, according to the spin projection
on the magnetic field direction:
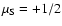 and
and
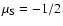 (Herzberg 1950; Berdyugina et al. 2005). Note also that
the levels with magnetic numbers
(Herzberg 1950; Berdyugina et al. 2005). Note also that
the levels with magnetic numbers 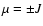 in the upper doublet
state split linearly as in the ZR (because for
them there are no levels to interact with in the fine structure).
in the upper doublet
state split linearly as in the ZR (because for
them there are no levels to interact with in the fine structure).
The PBE also changes the amplitudes of transitions. The dependence
of H
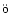 nl-London factors on the magnetic field strength
for the CN (0, 0) band transitions is given in the upper part of
Fig. 2 for main (left panel) and satellite
(right panel) rotational branches. Because of the mixing of states
with different J-values the O and S branches appear, which are
forbidden in the zero-field case. They reach maximum strengths in
the intermediate PBR, and decrease down to zero when approaching the
complete PBR. Note, that in this case (the PBE only on the fine
structure) the sum of the H
nl-London factors on the magnetic field strength
for the CN (0, 0) band transitions is given in the upper part of
Fig. 2 for main (left panel) and satellite
(right panel) rotational branches. Because of the mixing of states
with different J-values the O and S branches appear, which are
forbidden in the zero-field case. They reach maximum strengths in
the intermediate PBR, and decrease down to zero when approaching the
complete PBR. Note, that in this case (the PBE only on the fine
structure) the sum of the H
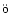 nl-London factors for all
lines of the multiplet is constant and the PBE appears only in the
strength redistribution between different multiplet components.
nl-London factors for all
lines of the multiplet is constant and the PBE appears only in the
strength redistribution between different multiplet components.
The mixing of levels implies that J-values lose their meaning and
become "bad'' quantum numbers. Therefore the definition of
rotational branches strictly holds only in the ZR.
Since magnetic sublevels are grouped according to the spin magnetic
number
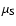 for large magnetic fields (Fig. 1), we
recalculate H
for large magnetic fields (Fig. 1), we
recalculate H
 nl-London factors summing up transitions
according to the value of
nl-London factors summing up transitions
according to the value of
 .
Then, four groups of transitions
with
.
Then, four groups of transitions
with
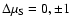 can in principle be distinguished.
They are shown in the lower panels of Fig. 2.
In the complete PBE the transitions with
can in principle be distinguished.
They are shown in the lower panels of Fig. 2.
In the complete PBE the transitions with
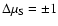 are
forbidden (Herzberg 1950), so their strengths approach zero as
the field increases.
are
forbidden (Herzberg 1950), so their strengths approach zero as
the field increases.
![\begin{figure}
\par\includegraphics[width=14.7cm,clip]{6030fig2.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg31.gif) |
Figure 2:
Dependence of the H
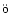 nl-London factors on magnetic field strength for the CN violet
system. Upper panels: calculations for transitions corresponding to the different rotational branches, which are strictly defined only for weak magnetic fields.
Lower panels: the grouping is done for transitions between states with fixed spin projection on
the magnetic field direction, a definition which is representative of the physics in the complete PBR. nl-London factors on magnetic field strength for the CN violet
system. Upper panels: calculations for transitions corresponding to the different rotational branches, which are strictly defined only for weak magnetic fields.
Lower panels: the grouping is done for transitions between states with fixed spin projection on
the magnetic field direction, a definition which is representative of the physics in the complete PBR. |
| Open with DEXTER |
In the cases close to the complete PBE regime these recalculated
H
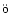 nl-London factors are more representative, because transitions between sublevels
will group according to their
nl-London factors are more representative, because transitions between sublevels
will group according to their
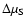 value as well.
value as well.
3 Scattering processes
3.1 General theory of the Hanle effect
To identify the place where the alterations due to the PBE do come
from we give here a short overview of coherent scattering theory,
following the description according to Landi Degl'Innocenti & Landi Degl'Innocenti (1988),
Stenflo (1998,1994,1997) and
Landi Degl'Innocenti & Landolfi (2004).
A radiation field at a fix point of space can be characterized by
the Stokes vector, which generally changes in a scattering process.
To describe the relation between the incident and scattered Stokes
vectors the Mueller matrix 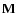 or coherency matrix W
(transformed Mueller matrix:
or coherency matrix W
(transformed Mueller matrix:
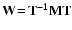 ,
where T is the transformation matrix)
are used.
,
where T is the transformation matrix)
are used.
In the zero field case the Mueller matrix for scattering of one
component of a multiplet can be factorized into a scalar function
depending only on frequency, and the phase matrix
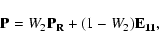 |
(1) |
which describes all the polarization properties. Here 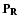 is
the Rayleigh phase matrix, while the
is
the Rayleigh phase matrix, while the
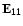 matrix (first
diagonal element is one, the rest zero) represents unpolarized,
isotropic scattering. Therefore the coefficient W2, the so-called
effective scattering polarizability, branches polarized and
unpolarized scattering. It depends only on transition strengths
between magnetic sublevels. There is a well-known expression for W2 (Stenflo 1994):
matrix (first
diagonal element is one, the rest zero) represents unpolarized,
isotropic scattering. Therefore the coefficient W2, the so-called
effective scattering polarizability, branches polarized and
unpolarized scattering. It depends only on transition strengths
between magnetic sublevels. There is a well-known expression for W2 (Stenflo 1994):
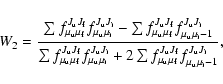 |
(2) |
where all the summations are done under the condition
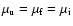 ,
and
,
and
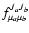 are the
strengths of transitions between
are the
strengths of transitions between
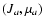 and
and
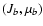 substates. Here i, u and f are initial, intermediate and final
substates, respectively.
substates. Here i, u and f are initial, intermediate and final
substates, respectively.
In a magnetic field the phase matrix 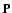 is modified due to the
Hanle effect. To take this into account and to perform the
calculation for the whole multiplet (which is especially important
in case of the PBR) it is necessary to account accurately for all
the scattering levels and interferences between them.
is modified due to the
Hanle effect. To take this into account and to perform the
calculation for the whole multiplet (which is especially important
in case of the PBR) it is necessary to account accurately for all
the scattering levels and interferences between them.
The coherency matrix of a scattering process from the set of initial
substates i via the intermediate substates u to the
final substates f is given by
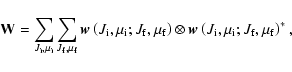 |
(3) |
where the incoherent summation is done over all total momentum and magnetic quantum
numbers of the initial and final states
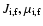 .
Here
.
Here
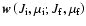 is the Jones matrix for scattering with the fixed quantum numbers of the initial and final
states. Its elements are given by the Kramers-Heisenberg formula
is the Jones matrix for scattering with the fixed quantum numbers of the initial and final
states. Its elements are given by the Kramers-Heisenberg formula
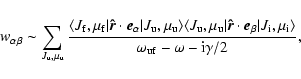 |
(4) |
where the coherent summation is done over all total momentum
and magnetic quantum numbers
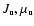 of the intermediate
substate u. In this formula
of the intermediate
substate u. In this formula
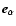 and
and
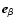 (
(
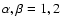 )
are the unit polarization vectors
of emission and absorption, respectively,
)
are the unit polarization vectors
of emission and absorption, respectively, 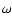 is the frequency
of the scattered radiation,
is the frequency
of the scattered radiation,
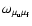 is the frequency
corresponding to the energy difference between the upper and lower
states, and
is the frequency
corresponding to the energy difference between the upper and lower
states, and 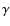 is the damping constant.
is the damping constant.
The Jones matrix elements in Eq. (4) can also be
written in an explicit form:
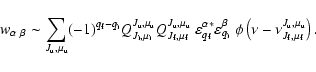 |
(5) |
Here,
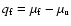 ,
,
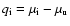 ,
Qab is the
amplitude of the transition between the lower state with quantum numbers
a and the upper state with quantum numbers b,
,
Qab is the
amplitude of the transition between the lower state with quantum numbers
a and the upper state with quantum numbers b,
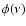 is the
normalized zero-centered Lorentz profile, and
is the
normalized zero-centered Lorentz profile, and
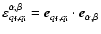 are geometrical factors, where
are geometrical factors, where 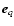 are complex
spherical vectors. It is important that all transition
amplitudes Q in Eq. (5) have the correct sign (cf. Stenflo 1994; Schadee 1978).
are complex
spherical vectors. It is important that all transition
amplitudes Q in Eq. (5) have the correct sign (cf. Stenflo 1994; Schadee 1978).
The basic feature of Eqs. (4) and
(5) is the coherent summation over all quantum
numbers
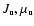 of the intermediate states u, since it is the
source of the interference terms. In contrast,
Eq. (3) only describes blending of lines, arising
from non-interfering transitions with fixed initial and final
quantum numbers.
of the intermediate states u, since it is the
source of the interference terms. In contrast,
Eq. (3) only describes blending of lines, arising
from non-interfering transitions with fixed initial and final
quantum numbers.
Substituting Eq. (5) in
Eq. (3) we obtain
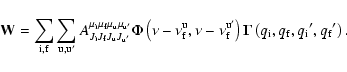 |
(6) |
Here A is a product of
four transition amplitudes (with signs). It depends only on the
quantum numbers of the initial, final and two intermediate states.
The function
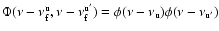 specifies the dependence on frequency of
the scattered photon. The
specifies the dependence on frequency of
the scattered photon. The
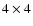 matrix
matrix
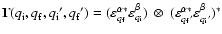 is defined only by the scattering geometry
(directions of the incident and scattered radiation, and of the
magnetic field and polarizations vectors),
is defined only by the scattering geometry
(directions of the incident and scattered radiation, and of the
magnetic field and polarizations vectors),
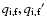 correspond to the interfering upper substates u and u' substates.
correspond to the interfering upper substates u and u' substates.
According to the selection rules, many terms in
Eq. (6) are zero. For example, if we fix
the initial magnetic quantum number
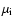 ,
only five different
values for
,
only five different
values for
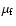 are possible:
are possible:
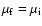 (in this case
there are three interfering magnetic substates with
(in this case
there are three interfering magnetic substates with
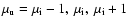 for each component of the fine
structure);
for each component of the fine
structure);
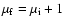 (interfering substates with
(interfering substates with
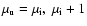 );
);
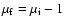 (interfering substates with
(interfering substates with
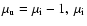 );
);
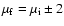 (no interference between excited
substates). Altogether there are 14 different sets of
(no interference between excited
substates). Altogether there are 14 different sets of
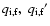 values, and each of them defines one matrix
values, and each of them defines one matrix
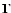 .
.
The representation of the coherency matrix in the form of
Eq. (6) allows us to separate the
dependences on geometry, frequency and transition amplitudes in the
calculations. For example, we need to calculate all
frequency-dependent coefficients A only once, which greatly saves
computing time, especially in the PBR, where transition
amplitude calculations are the most time-consuming. This
representation is also useful for averaging the results over some
distribution of magnetic field directions (for example, for
turbulent fields). In this case we can vary the directions of the
incident and scattered radiation while leaving the magnetic field
direction unchanged in the chosen coordinate system. This is
equivalent to changing the magnetic field direction, but it avoids
redefinitions of the magnetic quantum numbers. Since all the
geometric information is contained in the matrices
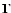 ,
only these 14
,
only these 14
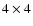 matrices are to be averaged. For a
fixed field direction distribution all matrix coefficients need to
be calculated only once and can then be applied to calculations for
arbitrary magnetic field strengths and quantum numbers. This again
saves the computing time because precise averaging is quite time
consuming.
matrices are to be averaged. For a
fixed field direction distribution all matrix coefficients need to
be calculated only once and can then be applied to calculations for
arbitrary magnetic field strengths and quantum numbers. This again
saves the computing time because precise averaging is quite time
consuming.
The coherency matrix 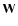 in Eq. (6)
is obtained assuming a Lorentz line profile. In the general case we
have to convolve
in Eq. (6)
is obtained assuming a Lorentz line profile. In the general case we
have to convolve 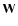 with a Doppler profile. For this
purpose the frequency-dependent function
with a Doppler profile. For this
purpose the frequency-dependent function 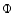 is usually
transformed to the following form (Stenflo 1994):
is usually
transformed to the following form (Stenflo 1994):
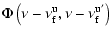 = = 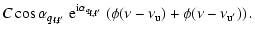 |
(7) |
Here, C is a normalization constant, while the Hanle angle
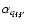 is defined by
is defined by
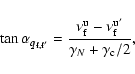 |
(8) |
where 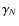 and
and
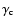 are the radiative and collisional
damping constants.
are the radiative and collisional
damping constants.
Convolving the function
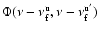 with the
Doppler profile, we obtain from Eq. (7):
with the
Doppler profile, we obtain from Eq. (7):
![$\displaystyle F\left(a, \nu- \nu_{\rm f}^{\rm u}, \nu-\nu_{\rm f}^{\rm u'}\righ...
... u}\right) + \mathcal{H}^{*} \left(a, \nu-{\nu_{\rm f}^{\rm u}}'\right)\right].$](/articles/aa/full/2007/01/aa6030-06/img86.gif) |
|
|
(9) |
Here,
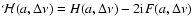 ,
with H being the Voigt function and F the
dispersion function. Therefore, when we taking into account the
Doppler broadening, we just have to replace the function
,
with H being the Voigt function and F the
dispersion function. Therefore, when we taking into account the
Doppler broadening, we just have to replace the function
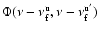 with
with
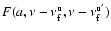 in Eq. (6).
in Eq. (6).
3.2 Interferences
The nature of the Hanle effect is the modification of the
polarization due to interferences between the different
possibilities of the scattering process in dependence of an external
magnetic field. We can rewrite the summation in
Eq. (6) in the following form:
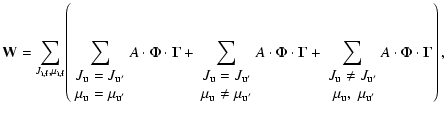 |
|
|
(10) |
where for conciseness all variables of the 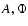 and
and
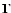 functions have been omitted. In this equation, the first
sum in the brackets contains all diagonal terms, while the two other
sums cover the interferences. For scattering processes through
different intermediate states that are independent of each other,
there will be only diagonal terms. The second sum in
Eq. (10) contains the interference terms
between different magnetic sublevels within one fine structure
component. These terms have their maxima in the zero-field case,
since without magnetic splitting all angles
functions have been omitted. In this equation, the first
sum in the brackets contains all diagonal terms, while the two other
sums cover the interferences. For scattering processes through
different intermediate states that are independent of each other,
there will be only diagonal terms. The second sum in
Eq. (10) contains the interference terms
between different magnetic sublevels within one fine structure
component. These terms have their maxima in the zero-field case,
since without magnetic splitting all angles
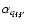 are
zero (see Eq. (8)). In a magnetic field non-zero
angles (due to the magnetic splitting) reduce the interference
terms, which in most cases leads to depolarization of the
scattered radiation. Such modification of the polarization of the
scattered radiation in a magnetic field is the essence of the Hanle
effect. Finally the third sum in Eq. (10)
contains interference terms between different components of the fine
structure. Note that shifts of magnetic sublevels in a magnetic
field also influence these terms. We see now that
Eqs. (6) and (10) in
their general form describe both the Hanle effect and the
interference between different J-states.
are
zero (see Eq. (8)). In a magnetic field non-zero
angles (due to the magnetic splitting) reduce the interference
terms, which in most cases leads to depolarization of the
scattered radiation. Such modification of the polarization of the
scattered radiation in a magnetic field is the essence of the Hanle
effect. Finally the third sum in Eq. (10)
contains interference terms between different components of the fine
structure. Note that shifts of magnetic sublevels in a magnetic
field also influence these terms. We see now that
Eqs. (6) and (10) in
their general form describe both the Hanle effect and the
interference between different J-states.
If different fine or rotational structure components of the
intermediate state are far from each other, we can fix the total
angular momentum of the intermediate substates u in
Eq. (4) and make the summation only over magnetic
quantum numbers
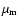 ,
neglecting the third sum in Eq. (10). This allows us to calculate the Hanle
effect for scattering in each component of the multiplet separately.
To account for the whole multiplet we can then sum incoherently the
contributions from all multiplet components. On the other hand, if
different intermediate J-states are close to each
other, we have to coherently add the contributions from all the
multiplet components and make the summation in Eq. (4)
over all involved J-states.
,
neglecting the third sum in Eq. (10). This allows us to calculate the Hanle
effect for scattering in each component of the multiplet separately.
To account for the whole multiplet we can then sum incoherently the
contributions from all multiplet components. On the other hand, if
different intermediate J-states are close to each
other, we have to coherently add the contributions from all the
multiplet components and make the summation in Eq. (4)
over all involved J-states.
3.3 Alterations due to the PBE
The general formulas presented above are valid for both the PBR and
ZR. The PBE perturbs the Jones matrix by changing the amplitudes of
interfering scattering processes
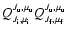 in Eq. (5) and
contributions from them via the alterations of
in Eq. (5) and
contributions from them via the alterations of
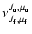 (in comparison with the Zeeman effect), while
leaving all the geometric factors unchanged. Therefore we can
distinguish two possible types of coherency matrix alterations due
to the PBE. Firstly, the PBE modifies the absolute values of the
terms in Eqs. (4) and (5). This
effect alone can dramatically change the spectrum. Secondly, the
different magnetic displacement in the PBE influences the phase of
the terms in Eq. (5). This causes additional
alterations of the interference terms in
Eq. (10) and can even change their signs.
(in comparison with the Zeeman effect), while
leaving all the geometric factors unchanged. Therefore we can
distinguish two possible types of coherency matrix alterations due
to the PBE. Firstly, the PBE modifies the absolute values of the
terms in Eqs. (4) and (5). This
effect alone can dramatically change the spectrum. Secondly, the
different magnetic displacement in the PBE influences the phase of
the terms in Eq. (5). This causes additional
alterations of the interference terms in
Eq. (10) and can even change their signs.
Doppler broadening should be done with care. In the ZR the
numerator of the ratio in Eq. (8) is usually
expressed as
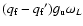 ,
where
,
where 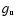 is the
Landé factor of the intermediate state and
is the
Landé factor of the intermediate state and
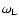 is the
Larmor frequency. In the PBR the magnetic sublevels are not
equidistant, and Landé factors are dependent on the magnetic
field strength and magnetic quantum numbers. Thus we need to use a
more general expression, namely Eq. (8). Moreover,
this equation can also be used for calculations with interferences
between different components of the fine structure. Note that in the
ZR both expressions are equivalent.
is the
Larmor frequency. In the PBR the magnetic sublevels are not
equidistant, and Landé factors are dependent on the magnetic
field strength and magnetic quantum numbers. Thus we need to use a
more general expression, namely Eq. (8). Moreover,
this equation can also be used for calculations with interferences
between different components of the fine structure. Note that in the
ZR both expressions are equivalent.
4 Scattering line profiles in the PBR
In the following we apply the theory developed above to investigate
the influence of the PBE on scattering polarization profiles and
illustrate our results with examples for the CN violet (
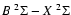 )
system and the
)
system and the
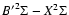 system of MgH. Therefore we will only deal with
the PBE on the fine structure, which is the most interesting case
for the molecular Hanle effect, but some of our conclusions are also
valid for the PBE on the rotational and hyperfine structures. Here we give a more general calculation of a multiplet case compared to
previous results by Shapiro et al. (2006). To
emphasize the difference between the Hanle effect in the PBR and ZR we also carry out calculations neglecting the modifications of the
transition amplitudes and Zeeman shifts due to the PBE. In the
following this is called the ZR calculations.
system of MgH. Therefore we will only deal with
the PBE on the fine structure, which is the most interesting case
for the molecular Hanle effect, but some of our conclusions are also
valid for the PBE on the rotational and hyperfine structures. Here we give a more general calculation of a multiplet case compared to
previous results by Shapiro et al. (2006). To
emphasize the difference between the Hanle effect in the PBR and ZR we also carry out calculations neglecting the modifications of the
transition amplitudes and Zeeman shifts due to the PBE. In the
following this is called the ZR calculations.
For the PBE on the fine structure N is a good quantum number,
while J-states become mixed. Therefore, we calculate the
scattering for the whole multiplet structure, making the summation
over all J-states belonging to the N-multiplet in
Eq. (6). We fix the lower 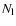 and the
upper
and the
upper 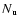 numbers and calculate the scattering profile from the
numbers and calculate the scattering profile from the
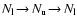 process, neglecting all
transitions between levels with different N numbers. This
calculation contains eight scattering processes, corresponding to
the zero-field definition of the rotational branches (as there are
two ways of choosing J in the zero-field case, for each of the
states - initial, intermediate and final). For example, if
process, neglecting all
transitions between levels with different N numbers. This
calculation contains eight scattering processes, corresponding to
the zero-field definition of the rotational branches (as there are
two ways of choosing J in the zero-field case, for each of the
states - initial, intermediate and final). For example, if
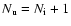 we have to calculate the following transitions: R1 -
R1,
R1 - R S12,
R Q21 - R Q21,
R Q21
- R2, R2 - R2,
R2 - R Q21,
R S12 - R
S12,
R S12 - R1. Three of these branches are forbidden
in the ZR and appear only in the PBR.
we have to calculate the following transitions: R1 -
R1,
R1 - R S12,
R Q21 - R Q21,
R Q21
- R2, R2 - R2,
R2 - R Q21,
R S12 - R
S12,
R S12 - R1. Three of these branches are forbidden
in the ZR and appear only in the PBR.
4.1 Alterations of the wing polarization
The Hanle effect modifies the wing polarization in the PBR, which is
not the case in the ZR. As we see from Eq. (4) the
efficiency of the Hanle effect strongly depends on the magnetic
displacement, which is implicitly contained in the
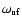 term, and on the transition amplitudes. Both these quantities are
subject to the PBE. However, in the line wings
term, and on the transition amplitudes. Both these quantities are
subject to the PBE. However, in the line wings
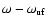 is much larger than the magnetic splitting of the line, which
therefore becomes negligible. Nonetheless, due to the changed
transition amplitudes the PBE influences the scattering
polarization over the whole multiplet and produces modifications of
the polarization in both the line cores and wings. In contrast, the
Zeeman effect only leads to level shifts (without affecting transition
amplitudes) and thus modifies the scattering polarization only in
the line core, leaving the wing linear polarization unchanged for
each component of the fine structure. Therefore, if we neglect the
interference from nearby members of the same multiplet, the linear
polarization in the wing of each multiplet component will in the ZR
not depend on the magnetic field (both direction and strength) and
can be calculated with Eqs. (1) and
(2). In the PBR the situation is different.
is much larger than the magnetic splitting of the line, which
therefore becomes negligible. Nonetheless, due to the changed
transition amplitudes the PBE influences the scattering
polarization over the whole multiplet and produces modifications of
the polarization in both the line cores and wings. In contrast, the
Zeeman effect only leads to level shifts (without affecting transition
amplitudes) and thus modifies the scattering polarization only in
the line core, leaving the wing linear polarization unchanged for
each component of the fine structure. Therefore, if we neglect the
interference from nearby members of the same multiplet, the linear
polarization in the wing of each multiplet component will in the ZR
not depend on the magnetic field (both direction and strength) and
can be calculated with Eqs. (1) and
(2). In the PBR the situation is different.
The observable strengths of the
components depend on magnetic field direction.
The PBE breaks the balance between the 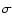 and
and 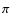 components, whose polarization signals depend on the magnetic field
direction. Therefore, the wing polarization depends on the field
direction as well (in contrast if we in the ZR change the field
direction, the changes of the different components is completely
compensate each other, and the signal remains unchanged). In the PBR
the wing linear polarization for a given multiplet component depends
on the magnetic field and its direction, although the wings are not
influenced by the Hanle effect.
components, whose polarization signals depend on the magnetic field
direction. Therefore, the wing polarization depends on the field
direction as well (in contrast if we in the ZR change the field
direction, the changes of the different components is completely
compensate each other, and the signal remains unchanged). In the PBR
the wing linear polarization for a given multiplet component depends
on the magnetic field and its direction, although the wings are not
influenced by the Hanle effect.
However, far from the multiplet the polarization approaches the
zero-field value in both the PBR and ZR. This can be easily
understood from the principle of spectroscopic stability. Far from
the system of lines we can neglect all quantum numbers that govern
the inner structure of the system. Thus we can consider the system
as a single line with fixed initial and final states, for which
there is neither the PBE nor the Hanle effect. For example, far from
the multiplet resonances the spin can be set to zero, so that the
multiplet will appear as a singlet. Thus, in the wings of the
multiplet we can neglect both the PBE and the Hanle effect, while
within the line system all changes due to the PBE are still
important.
Note that only full inclusion of all rotational branches while taking
into account all possible interferences allows us to obtain the same
signal in the wings of a doublet for the PBR and ZR. This equality
of the wing polarization can be used to test the computational
algorithms.
4.2 Line core depolarization
Calculations for the entire multiplet reveal that even in the zero
field case (thus without Hanle and PBE) there is depolarization in
the line core as compared with the wing polarization. This is
usually not
the case in calculations with one multiplet component.
Indeed, in zero field all coefficients of the phase matrix for
scattering in a single line have the same profiles and the linear
polarization degree Q/I does not depend on frequency.
The reason for the core depolarization is the interferences between
the scattering processes via different fine structure J-levels of
the upper state (the third sum in Eq. (10)),
because we can neglect them in the doublet core but have to take
them into account in the doublet wings. To understand this we
firstly note that the distance between the fine structure levels is
generally much bigger than their natural widths
(Fig. 1). Let us consider one photon scattered in the
doublet core (within several Doppler widths) and choose the
reference system for a molecule at which it was scattered. There are
eight different processes, corresponding to rotational branches (see
above) that can contribute to this scattering. Since the Doppler
width is much larger than the natural width, there is a large
probability that the scattering occurs close to one of these
processes (within several natural widths) but with a different
wavelength mainly due to the Doppler broadening. As the distance
between lines of different branches is much larger than the natural
width, we can neglect all contributions from other scattering
processes. It implies that we can neglect the interferences, despite
the fact that all components are so close in the spectrum, that we
cannot resolve them. This is because the interferences have to be
taken into account before convolving with the Doppler profile, as
only the natural width is important.
Consider now the photon scattered far from the multiplet
resonances. Since the Doppler profile is decreasing much faster then
the Lorentz profile, there is a big probability that this photon was
scattered far from the multiplet because of the uncertainty in the
energy level, rather than because of the Doppler broadening. Thus,
even in the molecular reference system, the photon was scattered far
from the doublet. In this case, however, we cannot isolate the main
component of the scattering process as we did before but we need to
take into account the contributions from all components, which
introduces the interferences terms.
To conclude, the depolarization in the multiplet core is due to the
gradual disappearance of the interference between different fine
structure transitions. It is quite analogous to the Hanle effect,
when decreasing interferences between different magnetic
subcomponents in a magnetic field causes the depolarization in the
line core.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6030fig3.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg108.gif) |
Figure 3:
Scattering profiles for a whole doublet, in the (0, 0) band of the CN violet system. Solid and dashed
curves represent
the PBR and ZR cases respectively. Left panels: P(2),
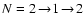 ,
for 200 G field.
Right panels: P(3), ,
for 200 G field.
Right panels: P(3),
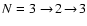 ,
for 0, 1 and 200 G
fields. Note that the PBE and ZE curves for 0 G
and 1 G superimpose, so they are undistinguishable, while the
curves for 200 G can be easily seen separately. The magnetic field is
perpendicular to the line of
sight and is in the plane of the solar surface. The Doppler width ,
for 0, 1 and 200 G
fields. Note that the PBE and ZE curves for 0 G
and 1 G superimpose, so they are undistinguishable, while the
curves for 200 G can be easily seen separately. The magnetic field is
perpendicular to the line of
sight and is in the plane of the solar surface. The Doppler width
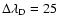 mÅ, the Voigt parameter a=0.0001.
Unpolarized incident radiation field and single scattering at angle mÅ, the Voigt parameter a=0.0001.
Unpolarized incident radiation field and single scattering at angle
 are assumed. Collisional depolarization and continuum
opacity are neglected.
are assumed. Collisional depolarization and continuum
opacity are neglected. |
| Open with DEXTER |
Here we present calculated scattering profiles of CN and MgH transitions for different magnetic fields and Doppler widths. For calculating the lifetimes we use oscillator
strengths from Wallace et al. (1999); Knowles et al. (1988); Kirby et al. (1979). In all
plots we assume an unpolarized incident radiation field and single
scattering at an angle of
 .
Collisional depolarization
and continuum opacity are neglected. As in all plots we choose the
magnetic field direction to be perpendicular to the line of sight,
and the Stokes U and V signals equal to zero. The profiles are
calculated for a realistic Doppler width
.
Collisional depolarization
and continuum opacity are neglected. As in all plots we choose the
magnetic field direction to be perpendicular to the line of sight,
and the Stokes U and V signals equal to zero. The profiles are
calculated for a realistic Doppler width
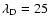 mÅ
which is much larger than the distance between the fine structure
components, or assuming a very narrow width
mÅ
which is much larger than the distance between the fine structure
components, or assuming a very narrow width
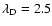 mÅ to
illustrate the profile asymmetries. Note that in all figures we
present the Stokes I profiles only for the 200 G magnetic field.
As we here only deal with ninety degree scattering, the Stokes Iprofiles slightly change due to the Hanle effect. These Hanle
modifications almost completely vanish when taking into account all
scattering angles and modest anisotropy of incident radiation field
for the real Sun.
mÅ to
illustrate the profile asymmetries. Note that in all figures we
present the Stokes I profiles only for the 200 G magnetic field.
As we here only deal with ninety degree scattering, the Stokes Iprofiles slightly change due to the Hanle effect. These Hanle
modifications almost completely vanish when taking into account all
scattering angles and modest anisotropy of incident radiation field
for the real Sun.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6030fig4.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg111.gif) |
Figure 4:
Same as Fig. 3 but for a magnetic field direction perpendicular
to the solar surface and the line of sight. There is no Hanle effect in the usual sense in this case. In
both panels only the curves for 200 G are shown. |
| Open with DEXTER |
In Fig. 3 we present doublet scattering
profiles for P(2) (
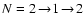 )
and P(3) (
)
and P(3) (
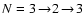 )
transitions in the presence of a horizontal magnetic field. We
assume the spin-rotational constant for the upper state
)
transitions in the presence of a horizontal magnetic field. We
assume the spin-rotational constant for the upper state
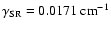 and for lower state
and for lower state
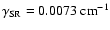 .
The PBE profiles differ significantly
from the ZR case. First of all, the PBE modifies the profile shape.
Furthermore, the integrated line polarization differs in general in
the PBR and ZR cases. In the case of the P(3) transition the main
manifestation of the Hanle effect, i.e. depolarization in the line
core, is easily visible in both the ZR calculations (dashed) and the
full PBE (solid) case. For a magnetic field of 1 G the PBE is too
weak (cf. Figs. 1 and 2) and there
is no difference between the ZR and PBR profiles. For a magnetic
field of 200 G the PBR and ZR polarization differ slightly
across the whole line profile. The biggest difference is near the
line wings. However as the absolute signal there is already quite
small (see corresponding Stokes I profile), such a difference is
not very important and will hardly be observable because of the
continuum polarization. In the case of the P(2) transition the
differences between the PBR and ZR are much bigger. The core
polarization in the PBR is bigger than in the ZR. Near the line
wings the relative contributions from the satellite and forbidden
branches (which are induced by the PBE) become important. As a
result the ZR and PBR polarization levels are completely different.
Note that the P(2) transition is somewhat special: in the ZR the
effective scattering polarizability W2 of the P2 (2) component
is zero and this component does not contribute to the polarization.
In the PBR the situation is changed, and there is quite significant
redistribution of polarization between the doublet components.
.
The PBE profiles differ significantly
from the ZR case. First of all, the PBE modifies the profile shape.
Furthermore, the integrated line polarization differs in general in
the PBR and ZR cases. In the case of the P(3) transition the main
manifestation of the Hanle effect, i.e. depolarization in the line
core, is easily visible in both the ZR calculations (dashed) and the
full PBE (solid) case. For a magnetic field of 1 G the PBE is too
weak (cf. Figs. 1 and 2) and there
is no difference between the ZR and PBR profiles. For a magnetic
field of 200 G the PBR and ZR polarization differ slightly
across the whole line profile. The biggest difference is near the
line wings. However as the absolute signal there is already quite
small (see corresponding Stokes I profile), such a difference is
not very important and will hardly be observable because of the
continuum polarization. In the case of the P(2) transition the
differences between the PBR and ZR are much bigger. The core
polarization in the PBR is bigger than in the ZR. Near the line
wings the relative contributions from the satellite and forbidden
branches (which are induced by the PBE) become important. As a
result the ZR and PBR polarization levels are completely different.
Note that the P(2) transition is somewhat special: in the ZR the
effective scattering polarizability W2 of the P2 (2) component
is zero and this component does not contribute to the polarization.
In the PBR the situation is changed, and there is quite significant
redistribution of polarization between the doublet components.
In Fig. 4 we present scattering profiles for
the same transitions as in Fig. 3, but for a
vertical magnetic field. It is well-known that the Hanle effect is
absent for a vertical field direction (thus in contrast to the
previous case, the polarization for the magnetic fields of 0 and 1 G will be the same). In the case of P(2) the ZR profiles for 200 G are quite close to the 0 G profile in the line core, but
they differ significantly near the blue wing. The PBR polarization
for 200 G is significantly different from both the zero field
polarization and from the 200 G ZR polarization over the whole
profile. Like in the horizontal field case the PBR increases the
line core polarization. For the P(3) transition the changes are
smaller and noticeable only near the line wings.
In Fig. 5 scattering profiles for the
R(1) transition are presented for two values of the Doppler width
in presence of a horizontal field. For a Doppler width of 2.5 mÅ (right panel) it is possible to distinguish different
components of the fine structure (we mark them in the plot with
their zero field wavelengths). We can see that the difference
between the ZR and PBR is mainly due to transition amplitudes
changes for the PBE. If we increase the Doppler width up to 25 mÅ all these differences vanish almost completely. As shown in
the left panel of Fig. 5 only very small
changes of the polarization near the line wings may be noticed.
For larger J values the energy difference between the fine
structure levels increases, so that the efficiency of the PBE
decreases. Therefore the distinction between the PBR and ZR
becomes smaller with increasing J-value. We also find that for
small N numbers the PBE more strongly influences the P-branch
than the R-branch transitions. This is due to the larger effective
scattering polarizability of the satellite branches
P Q12and
P O21, which despite their relative weakness contribute
significantly to the polarization of P-branch transitions.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6030fig5.eps} \end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg116.gif) |
Figure 5:
Scattering profiles for the R(1),
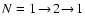 transition.
Left panels: Realistic Doppler width
transition.
Left panels: Realistic Doppler width
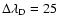 mÅ and a=0.0001, curves for 0, 1, 200 G fields.
Note that like in Fig. 3 the PBE and ZE curves for 0 G
and 1 G superimpose, while the curves for 200 G might be seen
separately (but the difference between them is much smaller than in
Fig. 3). Right panels: very small Doppler width
mÅ and a=0.0001, curves for 0, 1, 200 G fields.
Note that like in Fig. 3 the PBE and ZE curves for 0 G
and 1 G superimpose, while the curves for 200 G might be seen
separately (but the difference between them is much smaller than in
Fig. 3). Right panels: very small Doppler width
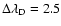 mÅ and a=0.001, curves only for a
field of 200 G.
In the top and right panel the
different components of the doublet are marked: "1'' for
R S12 (0.5), "2'' for R1 (1.5), "3'' for R2 (0.5), "4'' for
R Q21 (1.5). mÅ and a=0.001, curves only for a
field of 200 G.
In the top and right panel the
different components of the doublet are marked: "1'' for
R S12 (0.5), "2'' for R1 (1.5), "3'' for R2 (0.5), "4'' for
R Q21 (1.5). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6030fig6.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg120.gif) |
Figure 6:
Scattering profiles for transitions in the (0, 7) band of the MgH
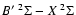 system, assuming
a horizontal field.
Left panel: R(10),
system, assuming
a horizontal field.
Left panel: R(10),
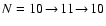 transition.
Right panel: R(25),
transition.
Right panel: R(25),
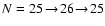 transition.
Solid and dashed lines represent the PBR and ZR calculations, respectively. Doppler width
transition.
Solid and dashed lines represent the PBR and ZR calculations, respectively. Doppler width
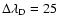 mÅ
field strength 200 G, and spin-rotational constant mÅ
field strength 200 G, and spin-rotational constant
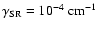 . . |
| Open with DEXTER |
We can expect a bigger change due to the PBE if the separation
between the interacting levels is smaller. The MgH
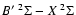 system is an interesting example. The
multiplet splitting in the upper state of this transition has not
been resolved (cf. Balfour & Cartwright 1976), implying that
the spin-rotational constant
system is an interesting example. The
multiplet splitting in the upper state of this transition has not
been resolved (cf. Balfour & Cartwright 1976), implying that
the spin-rotational constant
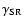 should be quite
small. In Fig. 6 we show an example of
calculations assuming
should be quite
small. In Fig. 6 we show an example of
calculations assuming
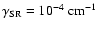 .
The PBR calculations
significantly differ from the ZR, even for quite big N-numbers,
when the doublet structure is well seen (mainly due to the fine
structure splitting of the lower
.
The PBR calculations
significantly differ from the ZR, even for quite big N-numbers,
when the doublet structure is well seen (mainly due to the fine
structure splitting of the lower
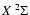 state with
state with
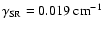 ).
).
The PBR-profiles of the fine structure components of MgH in
Fig. 6 are much narrower than the ZR-profiles.
It has to do with the separation of the magnetic sublevels in the PBE
by spin projection (see Sect. 2). Note also that in the
PBR-calculations different magnetic sublevels cannot intersect each
other. In the ZR-calculations such intersections, implying a strong
increase of the interference terms at certain magnetic field
strengths, are possible. As a result, in the ZR the shapes of the
Q/I signal and the integrated depolarization do not change
monotonously with the field, as it does in the PBR.
For zero magnetic field all contributions to the Jones matrix from
scattering processes via different magnetic substates of one
J state have the same phase (cf. Eq. (5)).
This implies maximum contributions the interference terms (second
sum in Eq. (10)). In a magnetic field, because
of the level splitting, the interference terms in the line core
become smaller and asymptotically disappear when the magnetic
splitting becomes significantly larger than the level's natural
width. The Hanle effect in such fields is called saturated. Note
that in the line wings there is no decrease of the interference
terms in a magnetic field, and the situation is fully identical to
the zero-field case, as we saw before from the principle of
spectroscopic stability.
Depolarization due to the saturated Hanle effect does not depend on
the magnetic field in the ZR calculations. In the present section we
show that in the PBR the situation is different.
In the weak-field approximation (
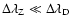 )
we can separate the angular and wavelength
dependent parts of the phase matrix. For a given angular
distribution of the magnetic field vector with the strength B the
depolarization factor due to the Hanle effect (Stenflo 1982)
)
we can separate the angular and wavelength
dependent parts of the phase matrix. For a given angular
distribution of the magnetic field vector with the strength B the
depolarization factor due to the Hanle effect (Stenflo 1982)
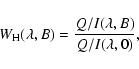 |
(11) |
which depends on the field strength B and wavelength 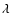 .
It equals to unity in the line wings and is usually smaller than one
in the line core. Also in the PBR
.
It equals to unity in the line wings and is usually smaller than one
in the line core. Also in the PBR
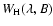 retains
its meaning.
retains
its meaning.
If the fine structure splitting is either much smaller or much
larger than the Doppler width it is possible to neglect the
dependence on wavelength in the line core and characterize the
depolarization for a fixed magnetic field just by
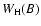 .
Such a quantity was introduced by (Stenflo 1982) and is widely
used in different applications (cf. Berdyugina & Fluri 2004; Faurobert & Arnaud 2003) to explore turbulent fields. This case is
covered by the well-known expression for
.
Such a quantity was introduced by (Stenflo 1982) and is widely
used in different applications (cf. Berdyugina & Fluri 2004; Faurobert & Arnaud 2003) to explore turbulent fields. This case is
covered by the well-known expression for
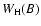 given by
Stenflo (1982) and Landi Degl'Innocenti & Landi Degl'Innocenti (1988).
given by
Stenflo (1982) and Landi Degl'Innocenti & Landi Degl'Innocenti (1988).
In the weak field regime
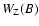 also governs the
integrated depolarization, since most of the radiation comes from
the line core. Since the PBE modifies the shape of
also governs the
integrated depolarization, since most of the radiation comes from
the line core. Since the PBE modifies the shape of
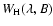 ,
we calculate the integrated depolarization in the
PBE as follows:
,
we calculate the integrated depolarization in the
PBE as follows:
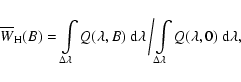 |
(12) |
where the range of the integration covers several Doppler widths.
Note that this quantity does not use the weak field approximation
(although in the weak field approximation it is similar to
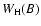 ).
).
In Table 1 we present
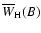 in
the PBR for R2 (0.5) and P1(1.5) lines of the CN (0, 0) band,
assuming a turbulent field, and compare them with
in
the PBR for R2 (0.5) and P1(1.5) lines of the CN (0, 0) band,
assuming a turbulent field, and compare them with
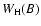 .
The saturated Hanle effect for these lines appears already at a
field strength of
.
The saturated Hanle effect for these lines appears already at a
field strength of
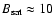 G. We can see
that the PBE introduces additional depolarization in the R and
polarization in the P branch lines. This is because the transition
amplitudes still depend on the magnetic field strength even in the
saturated Hanle regime. Therefore the function
G. We can see
that the PBE introduces additional depolarization in the R and
polarization in the P branch lines. This is because the transition
amplitudes still depend on the magnetic field strength even in the
saturated Hanle regime. Therefore the function
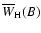 does not reach an asymptotic value but continues to vary
with magnetic field strength.
does not reach an asymptotic value but continues to vary
with magnetic field strength.
Table 1:
Depolarization factors and integrated polarization for the P1(1.5) and R2(0.5) lines of the CN (0, 0) band.
The 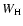 values have been calculated with Eq. (2.12) from Stenflo (1982).
values have been calculated with Eq. (2.12) from Stenflo (1982).
The depolarization in the line core of a doublet is due to two types
of interferences between different magnetic components and between
different components of the fine structure (see
Sect. 4.2). Therefore one can write:
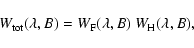 |
(13) |
where
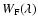 is governs the fine structure
depolarization and
is governs the fine structure
depolarization and
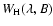 (from Eq. (11))
governs the Hanle depolarization. Note that because of PBE
(from Eq. (11))
governs the Hanle depolarization. Note that because of PBE 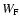 also depends on the magnetic field strength.
also depends on the magnetic field strength.
To study the influence of PBE on the depolarization we introduce
the integrated quantity:
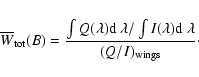 |
(14) |
We can again rewrite this as a product of two depolarization
factors:
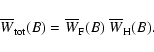 |
(15) |
Because of the interference between different fine structure
components
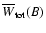 differs from unity even
in the zero field case. In the present section we will use the both
differs from unity even
in the zero field case. In the present section we will use the both
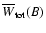 and
and
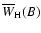 values.
values.
The efficiency of the Hanle effect strongly depends on the Landé
factors of the upper state, which determine the magnetic
displacements of the sublevels and hence the phase shifts. For
molecular lines (and in particular for CN) the Landé factor
usually decreases as the J number increases
(Berdyugina & Solanki 2002). Therefore transitions with small Jare particularly strongly influenced by a magnetic field and
quickly reach the saturated Hanle regime. For all CN transitions
discussed above the saturated Hanle effect occurs already at field
strengths of 10-20 G. Thus for such fields the interference between
different magnetic sublevels in the line core is lost, and as we can
see from Fig. 1 they will never come back again. For
lines with larger J values the saturated Hanle effect requires in
stronger magnetic fields but, due to the increase of the fine
structure splitting with J, the influence of the PBE for such
lines is smaller.
Thus for transitions with small J numbers we have the following
situation. In the line core in case of zero field there is
interference between different magnetic sublevels of each fine
structure component, but there is no interference between the
different fine structure components. In a field of 10-20 G the
saturated Hanle effect occurs, i.e. there is no interference in the
line core at all, but in the line wings both types of interference
are present. For such fields the PBE is very small and we can
completely neglect it. Therefore when the PBE becomes important we
already have reached the saturated Hanle effect, so that we can
calculate the depolarized signal while considering all scattering
processes independently from each other without any interferences,
i.e. neglecting the second and third sums in
Eq. (10).
We can now classify the changes in the Stokes Q profiles caused
by the PBE into two types. Most important is the change of
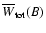 ,
which governs the total line
depolarization. Such changes create well-defined observational
signatures. They can occur only if the transition strengths change
due to magnetic field. This is possible only because of the PBE.
,
which governs the total line
depolarization. Such changes create well-defined observational
signatures. They can occur only if the transition strengths change
due to magnetic field. This is possible only because of the PBE.
The second type of change occurs because the PBE introduces other
displacements, and at the given frequency the contributions from the
various scattering processes are different in the PBR and in the ZR,
the polarization is redistributed over the whole profile. Therefore
the shape of the profile is changed, while the total depolarization
remains the same. Obviously it is much more difficult to identify
this type of change from observational data.
The calculation of the saturated,
integrated Stokes parameters is much easier than dealing with the
general case. It is even possible to give relatively simple
analytical expressions for vertical and horizontal fields. The ratio
will always have the form
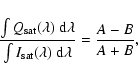 |
(16) |
where for a magnetic field perpendicular
to the solar surface (as in Fig. 4)
For the case when the magnetic field is perpendicular to the line of
sight and lies in the plane of solar surface (Figs. 3 and 5)
Here, in all bilinear products of oscillator strengths the first
factor refers to
absorption (
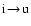 transition), the second to emission
(
transition), the second to emission
(
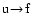 transition). Let us emphasize that these
expressions are valid only in the saturated Hanle regime. They fail
for weaker fields (where we have to account for the all
interferences).
transition). Let us emphasize that these
expressions are valid only in the saturated Hanle regime. They fail
for weaker fields (where we have to account for the all
interferences).
We can make one more simplification, namely assume that the Doppler
width is much larger than the distance between the fine structure
components. In this case we can consider all contribution to the
Jones matrix (see Eqs. (4) and (5))
as having the same frequency profile. Thus all elements of the
coherency matrix in Eq. (6) will also have
the same profile. The profile function will therefore divide out
when forming the fractional polarization, so that the ratio Q/Iwill be a constant.
As we can see from
Figs. 3-5 for the
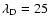 mÅ case this approximation is quite good (for
curves corresponding to a magnetic field of 200 G there is a flat,
almost horizontal part of the profile near the line core).
mÅ case this approximation is quite good (for
curves corresponding to a magnetic field of 200 G there is a flat,
almost horizontal part of the profile near the line core).
With both our approximation (the omission of the interferences and
the single profile approximation) Stokes Q in the line core is
proportional to Stokes I. Because of this we do not need the
integration in Eq. (14) but can write the
saturated
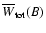 as
as
![\begin{displaymath}\overline{W}_{\rm tot}^{\rm sat} (B) = \frac{{[Q(\lambda_{\rm...
...)/I(\lambda_{\rm core})}]_{\rm sat}}{{(Q/I)}_{\rm wings}}\cdot
\end{displaymath}](/articles/aa/full/2007/01/aa6030-06/img149.gif) |
(19) |
Thus in case of the saturated Hanle effect and large Doppler
broadening,
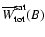 gives us the
ratio between the core and wing polarizations.
gives us the
ratio between the core and wing polarizations.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{6030fig7.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg151.gif) |
Figure 7:
The dependence of saturated depolarization on magnetic field strength. The N numbers of the transitions are indicated in the plot.
The magnetic field is perpendicular to the solar surface. The solid curves represent the PBR case, the dashed lines the ZR case. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{6030fig8.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg152.gif) |
Figure 8:
The same as Fig. 7, but for a magnetic field vector perpendicular to the line of
sight and in the plane of the solar surface. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{6030fig9.eps} \end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg154.gif) |
Figure 9:
Dependence of saturated depolarization on field direction.
Left panel: dependence on declination (angle with the plane which is perpendicular to the solar surface), when the azimuth (angle with the plane that is perpendicular to the
direction on the observer
and contains the normal to
the solar surface) equals zero.
Right panel: dependence on azimuth (when the declination equals zero).
Curves for a P(2),
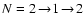 transition in a 200 G field
and for a R(1),
transition in a 200 G field
and for a R(1),
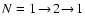 in a 400 G field. We have changed the sign of the depolarization for the
in a 400 G field. We have changed the sign of the depolarization for the
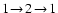 curves to make plots more clear. The solid curves represent the PBR case, the dashed curves the ZR case.
curves to make plots more clear. The solid curves represent the PBR case, the dashed curves the ZR case. |
| Open with DEXTER |
In Figs. 7-9 we present
calculations of
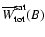 for the CN
transitions, using Eqs. (16)-(18)
to calculate the numerator in the ratio
of Eq. (14). Note that all curves in these
figures are valid only for fields stronger than about 10 G, since
for weaker fields the Hanle effect is not saturated.
for the CN
transitions, using Eqs. (16)-(18)
to calculate the numerator in the ratio
of Eq. (14). Note that all curves in these
figures are valid only for fields stronger than about 10 G, since
for weaker fields the Hanle effect is not saturated.
In Figs. 7 and 8 the dependence of
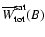 on the magnetic field
strength is shown. The depolarization changes with magnetic field in
the PBR, while in the ZR it remains constant (because in the ZR only
the position of the lines but not their strengths change).
on the magnetic field
strength is shown. The depolarization changes with magnetic field in
the PBR, while in the ZR it remains constant (because in the ZR only
the position of the lines but not their strengths change).
In a vertical field (Fig. 7) the depolarization
for all transitions asymptotically approaches unity with increasing
field strength. The reason is that for a vertical field only
interferences between different components of the doublet are
important. For example, for zero field we only have to take into
account interferences between magnetic sublevels of states with
different J numbers. As these sublevels belong to different Jstates, they will get opposite spin projections on the magnetic
field direction
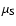 when the field becomes strong (cf.
Fig. 1). The strengths of such transitions will
decrease with field strengths and asymptotically becomes forbidden
in the total PBE (see bottom right panel of
Fig. 2). Thus, the interference between the
different components of a doublet disappears (now, in contrast to
the previous discussion, over the whole profile, including line
wings).
when the field becomes strong (cf.
Fig. 1). The strengths of such transitions will
decrease with field strengths and asymptotically becomes forbidden
in the total PBE (see bottom right panel of
Fig. 2). Thus, the interference between the
different components of a doublet disappears (now, in contrast to
the previous discussion, over the whole profile, including line
wings).
For a horizontal field (Fig. 8) the interference
between the different components of the doublet also goes to zero
for a strong magnetic fields (this property does not depend on field
direction), but the interference between the different magnetic
sublevels of the same doublet component remains significant.
Therefore the asymptotic values of depolarization
are different for the different lines
and do not approach unity as for the vertical field.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6030fig10.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg157.gif) |
Figure 10:
Dependence of depolarization on the magnetic field strength
for the (0, 7) band of the MgH
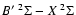 system
for different values of the spin-rotational constant
system
for different values of the spin-rotational constant
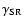 ,
for the transitions R(1), ,
for the transitions R(1),
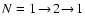 .
Continuous lines represent .
Continuous lines represent
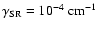 ,
dashed lines ,
dashed lines
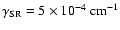 ,
dashed-dotted lines for ,
dashed-dotted lines for
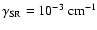 .
Thick curves represent the PBR case, thin the ZR case. .
Thick curves represent the PBR case, thin the ZR case. |
| Open with DEXTER |
The dependence of the saturated depolarization
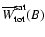 on field direction is presented in
Fig. 9. One can see that the changes due to the
PBE are larger for the above considered above cases - vertical and
horizontal magnetic fields.
on field direction is presented in
Fig. 9. One can see that the changes due to the
PBE are larger for the above considered above cases - vertical and
horizontal magnetic fields.
Significant modifications of the depolarization due to the PBE occurs only in relatively strong magnetic fields 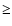 500 G. Only
for
500 G. Only
for
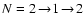 there is a quite
strong effect already for fields of 100-200 G. An absolutely
different situation occurs for the MgH
there is a quite
strong effect already for fields of 100-200 G. An absolutely
different situation occurs for the MgH
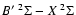 system. Since the spin-rotational constant of the
system. Since the spin-rotational constant of the
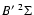 state might be quite small (see
Sect. 4), the PBE becomes important before Hanle
saturation. In this case we cannot neglect the interferences, and
the method described in Sect. 5.2 does not
work. Therefore it is necessary to calculate the full integrals of
Eq. (12), which is quite time consuming. In
Fig. 10 we show the dependence of the
depolarization
state might be quite small (see
Sect. 4), the PBE becomes important before Hanle
saturation. In this case we cannot neglect the interferences, and
the method described in Sect. 5.2 does not
work. Therefore it is necessary to calculate the full integrals of
Eq. (12), which is quite time consuming. In
Fig. 10 we show the dependence of the
depolarization
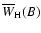 defined by
Eq. (12) on the field strength for several possible
defined by
Eq. (12) on the field strength for several possible
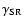 values, assuming the
values, assuming the
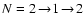 transition. It is obvious that for smaller
transition. It is obvious that for smaller
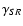 the PBE occurs at weaker fields, and for
the PBE occurs at weaker fields, and for
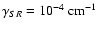 it happens even before the Hanle effect is
saturated. For bigger N values only the scale of the magnetic
field axis is changed, since the Landé factors decrease linearly
with J, while the spin-rotational splitting is proportional to J. Non monotonous shapes of the ZR curves appear due to level
crossings (which lead to increasing interference), while for the
PBR level-crossing is impossible and all curves have monotonous
shapes.
it happens even before the Hanle effect is
saturated. For bigger N values only the scale of the magnetic
field axis is changed, since the Landé factors decrease linearly
with J, while the spin-rotational splitting is proportional to J. Non monotonous shapes of the ZR curves appear due to level
crossings (which lead to increasing interference), while for the
PBR level-crossing is impossible and all curves have monotonous
shapes.
We have presented here for the first time the theory of the
molecular Hanle effect in the PBR and illustrated it with examples
for the CN
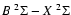 and MgH
and MgH
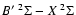 systems. Based on our results we
can draw the following conclusions:
systems. Based on our results we
can draw the following conclusions:
- Since Landé factors of magnetic sublevels and transition
amplitudes are strongly modified by the PBE, the phases and
amplitudes of the Jones matrix elements will be changed.
- The PBE influences the scattering polarization over the whole
system of perturbed transitions. However, far from the multiplet
resonances, the polarization approaches the zero-field value in
agreement with the principle of spectroscopic stability.
- Our calculations for the CN violet system, widely
observable in the second solar spectrum, show that the line profiles
of the individual doublet components significantly change due to the
PBE already for a magnetic field strength of 100 G for levels
with small J values. These changes are however smeared by Doppler
broadening and influence from the second doublet component.
- Detailed calculations of the CN violet system doublets for
different field directions show that the PBE is more important for
P branch transitions than for the R branch.
- The upper state multiplet splitting of the MgH
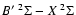 system is still unresolved,
implying a small splitting and thus a strong PBE. Assuming a
spin-rotational constant
system is still unresolved,
implying a small splitting and thus a strong PBE. Assuming a
spin-rotational constant
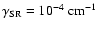 we
find a considerable difference between the PBR and ZR even for
levels with relatively large J values
we
find a considerable difference between the PBR and ZR even for
levels with relatively large J values
- The depolarization of the MgH transitions due to the Hanle
effect is considerably influenced by the PBE already at field
strengths of 10 G.
- We have introduced a simple method for calculations in the saturated
Hanle regime (neglecting the interferences between different
magnetic and fine structure transitions) and have shown that in the
PBR the saturated polarization is magnetic field dependent, in
contrast to the ZR. We discuss its dependence on magnetic field
strength and direction.
Acknowledgements
This work has been supported by SNF grant 20002-103696. S.B.
acknowledges the EURYI Award, from the ESF and SNF, grant
PE002-104552.
-
Asensio Ramos, A., & Trujillo Bueno, J. 2005, ApJ, 635,
L109 [NASA ADS] [CrossRef]
- Asensio Ramos, A., & Trujillo
Bueno, J. 2006, ApJ, 636, 548 [NASA ADS] [CrossRef]
- Balfour, W. J., &
Cartwright, H. M. 1976, A&AS, 26, 389 [NASA ADS] (In the text)
- Berdyugina, S. V., &
Solanki, S. K. 2002, A&A, 385, 701 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Berdyugina, S. V., &
Fluri, D. M. 2004, A&A, 417, 775 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Berdyugina, S. V., Stenflo,
J. O., & Gandorfer, A. 2002, A&A, 388, 1062 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences]
-
Berdyugina, S. V., Braun, P. A., Fluri, D. M., &
Solanki, S. K. 2005, A&A, 444, 947 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences]
- Bommier, V.
1980, A&A, 87, 109 [NASA ADS] (In the text)
- Bommier,
V., Landi Degl'Innocenti, E., & Molodij, G. 2006, in Solar
Polarization, Proc. 4rd SPW, ed. R. Casini, & B. W.
Lites, ASP Conf. Ser., in press
- Faurobert, M., & Arnaud, J.
2003, A&A, 412, 555 [EDP Sciences] [CrossRef] [EDP Sciences]
- Herzberg,
G. 1950, Molecular spectra and molecular structure, Vol. 1, Spectra
of diatomic molecules (New York: Van Nostrand Reinhold) 2nd
edn.
- Hill, E. L.
1929, Phys. Rev., 34, 1507 [NASA ADS] [CrossRef]
- Kirby, K., Saxon,
R. P., & Liu, B. 1979, ApJ, 231, 637 [NASA ADS] [CrossRef]
- Knowles,
P. J., Werner, H.-J., Hay, P. J., & Cartwright,
D. C. 1988, J. Chem. Phys., 89, 7334 [NASA ADS] [CrossRef]
- Kovács, I.
1969, Rotational Structure in the Spectra of Diatomic Molecules
(London: Adam Hilger Ltd.)
(In the text)
- Landi
Degl'Innocenti, E. 2003, in Solar Polarization, Proc. 3rd SPW, ed.
J. Trujillo Bueno, & J. Sánchez Almeida, ASP
Conf. Ser., 307, 164
- Landi
Degl'Innocenti, M., & Landi Degl'Innocenti, E. 1988, A&A,
192, 374 [NASA ADS] (In the text)
-
Landi Degl'Innocenti, E. L., & Landolfi, M. 2004, Physics
of Solids and Liquids
(In the text)
-
Landolfi, M., & Landi Degl'Innocenti, E. 1985, Sol. Phys.,
98, 53 [NASA ADS] [CrossRef] (In the text)
- Schadee, A.
1978, JQRST, 19, 517
-
Shapiro, A. I., Fluri, D. M., Berdyugina, S. V.,
& Stenflo, J. O. 2006, in Solar Polarization, Proc. 4rd
SPW, ed. R. Casini, & B. W. Lites, ASP Conf. Ser., in
press
(In the text)
- Stenflo,
J. O. 1982, Sol. Phys., 80, 209 [NASA ADS] [CrossRef] (In the text)
- Stenflo,
J. O. 1994, Solar Magnetic Fields (Dordrecht: Kluwer)
- Stenflo,
J. O. 1997, A&A, 324, 344 [NASA ADS]
- Stenflo,
J. O. 1998, A&A, 338, 301 [NASA ADS]
- Trujillo
Bueno, J. 2003, in Solar Polarization, Proc. 3rd SPW, ed.
J. Trujillo Bueno, & J. Sánchez Almeida,
ASP Conf. Ser., 307, 407
- van Vleck,
J. H. 1926, Phys. Rev., 28, 980 [NASA ADS] [CrossRef]
- Wallace, L.,
Hinkle, K., Li, G., & Bernath, P. 1999, ApJ, 524, 454 [NASA ADS] [CrossRef]
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6030fig1.eps} \end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=14.7cm,clip]{6030fig2.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg31.gif)
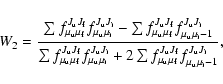
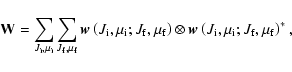
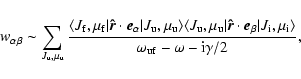
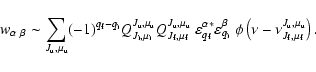
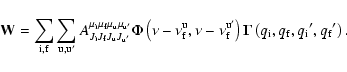
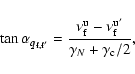
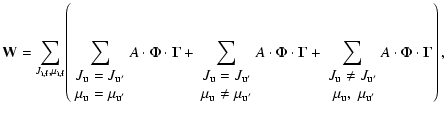
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6030fig3.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg108.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6030fig4.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg111.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6030fig5.eps} \end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg116.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6030fig6.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg120.gif)
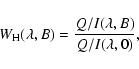
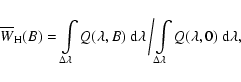
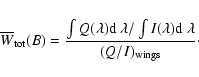
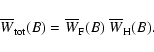
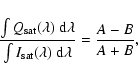
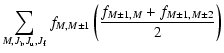
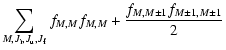
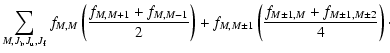
![\begin{displaymath}\overline{W}_{\rm tot}^{\rm sat} (B) = \frac{{[Q(\lambda_{\rm...
...)/I(\lambda_{\rm core})}]_{\rm sat}}{{(Q/I)}_{\rm wings}}\cdot
\end{displaymath}](/articles/aa/full/2007/01/aa6030-06/img149.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{6030fig7.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg151.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{6030fig8.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg152.gif)
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{6030fig9.eps} \end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg154.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{6030fig10.eps}
\end{figure}](/articles/aa/full/2007/01/aa6030-06/Timg157.gif)