A&A 461, 121-134 (2007)
DOI: 10.1051/0004-6361:20065390
X-ray/ultraviolet observing campaign of the Markarian 279 active galactic nucleus outflow:
a close look at the absorbing/emitting gas with Chandra-LETGS
E. Costantini1,2 -
J. S. Kaastra1 -
N. Arav3 -
G. A. Kriss4 -
K. C. Steenbrugge5 -
J. R. Gabel3 -
F. Verbunt2 -
E. Behar6 -
C. M. Gaskell7 -
K. T. Korista8 -
D. Proga9 -
J. Kim Quijano4 -
J. E. Scott10 -
E. S. Klimek7 -
C. H. Hedrick7
1 - SRON National Institute for Space Research,
Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
2 -
Astronomical Institute, Utrecht University,
PO Box 80000, 3508 TA, Utrecht, The Netherlands
3 -
CASA, University of Colorado, 389 UCB, Boulder, CO 80309-0389, USA
4 -
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
5 -
University of Oxford, St John's College Research Centre, Oxford, OX1 3JP, UK
6 -
Department of Physics, Technion, Haifa 32000, Israel
7 -
Department of Physics and Astronomy, University of Nebraska, Lincoln, NE 68588-0111, USA
8 -
Department of Physics, Western Michigan University, Kalamazoo, MI 49008, USA
9 -
Department of Physics, University of Nevada, 4505 South Maryland Parkway, Las Vegas, NV 89154, USA
10 -
Department of Physics, Astronomy, and Geosciences, Towson University, Towson, Maryland 21252, USA
Received 7 April 2006 / Accepted 14 September 2006
Abstract
We present a Chandra-LETGS observation of the Seyfert 1 galaxy Mrk 279. This observation was simultaneous with HST-STIS and FUSE observations,
in the context of a multiwavelength study of this source.
The Chandra pointings were spread over ten days for a total exposure time of  360 ks.
The maximal continuum flux variation is of the order of 30%.
The spectrum of Mrk 279 shows evidence of broad emission features, especially at the wavelength of the O VII triplet. We quantitatively explore the possibility that this emission is produced
in the broad line region (BLR).
We modeled the broad UV emission lines seen in the FUSE and HST-STIS spectra
following the "locally optimally emitting cloud''
approach. This method considers the emission from BLR as arising from "clouds'' with a wide range of densities and distances from the source. We find that the X-ray lines luminosity derived from the best fit BLR model match the observed X-ray features, suggesting that the gas producing the UV lines is sufficient to account for the X-ray emission.
The spectrum is absorbed by ionized gas whose total column density is
360 ks.
The maximal continuum flux variation is of the order of 30%.
The spectrum of Mrk 279 shows evidence of broad emission features, especially at the wavelength of the O VII triplet. We quantitatively explore the possibility that this emission is produced
in the broad line region (BLR).
We modeled the broad UV emission lines seen in the FUSE and HST-STIS spectra
following the "locally optimally emitting cloud''
approach. This method considers the emission from BLR as arising from "clouds'' with a wide range of densities and distances from the source. We find that the X-ray lines luminosity derived from the best fit BLR model match the observed X-ray features, suggesting that the gas producing the UV lines is sufficient to account for the X-ray emission.
The spectrum is absorbed by ionized gas whose total column density is  5
5  1020 cm-2. The absorption spectrum can be modeled by two distinct gas components (log
1020 cm-2. The absorption spectrum can be modeled by two distinct gas components (log
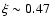 and 2.49, respectively)
both showing a significant outflow velocity. However, the data also allow for the presence of intermediate ionization components.
The distribution of the column densities of such extra components as a function of the ionization parameter is not consistent with a continuous, power-law like, absorber, suggesting a complex structure for the gas outflow for Mrk 279.
and 2.49, respectively)
both showing a significant outflow velocity. However, the data also allow for the presence of intermediate ionization components.
The distribution of the column densities of such extra components as a function of the ionization parameter is not consistent with a continuous, power-law like, absorber, suggesting a complex structure for the gas outflow for Mrk 279.
Key words: galaxies: individual: Mrk 279 - quasars: absorption lines - quasars: emission lines -
quasars: general - X-rays: galaxies
Active galactic nuclei (AGN) are believed to be powered by accretion into a super massive black hole (BH). Through the identification of narrow spectral features in the energy range E< 2 keV,
the basic phenomenology of the absorbing ionized gas out-flowing from the vicinity of the BH
has been established: approximately 60% of the Seyfert 1 galaxies display such an outflow (Crenshaw et al. 1999). Objects with an UV absorber always display an X-ray absorption component (Crenshaw et al. 1999; Kriss 2002). Recent results show that the absorber has multi-ionization components with some of the UV and X-ray outflow probably being part of the same material (Gabel et al. 2005a).
Only in the X-ray band higher ionized components, producing mostly He-like and H-like ions of C, N, O, and up to H-like iron, can be detected. These high ionization components have been reported to have a larger column density (e.g., Netzer et al. 2003; Turner et al. 2005) and sometimes a higher outflow velocity (e.g., Steenbrugge et al. 2005). The physical structure of the absorbing systems related to the BH activity is not understood. Independent measurement of the physical
structure of the out-flowing ionized gas led to incompatible results.
The density structure may be continuous as a function
of the ionization level of the gas (NGC 5548, Kaastra et al. 2002; Steenbrugge et al. 2003). Alternatively,
the absorber is clumped in discrete components, in pressure
equilibrium and surrounded by a hotter and tenuous phase (Krolik & Kriss 1995,2001). The spectrum of
NGC 3783 seems to be well described by this model (Krongold et al. 2003; Netzer et al. 2003).
Finally, there are conflicting results on the spatial extent and
the distance from the ionizing source of such an absorber.
Behar et al. (2003), based on the XMM-Newton observation of NGC 3783,
proposed that the out-flowing X-ray absorber has the same spatial
distribution as the narrow line region (NLR) mapped in UV. This is confirmed by the
UV spectral analysis of this source (Gabel et al. 2005a). This picture would be analogous to the geometry drawn for the
Seyfert 2 galaxies (e.g. NGC 1068, Kinkhabwala et al. 2002; Mrk 3, Sako et al. 2000).
Conversely, a Chandra-LETGS and HETGS study on NGC 5548 suggested that
the outflow is more collimated with a small
opening angle (Steenbrugge et al. 2005). The location of the warm absorbers may be as far as the NLR,
or closer to the source, at
 pc scale, where a molecular torus should exist (see Blustin et al. 2005, and references therein)
or, finally, the ionized gas outflow may be generated by accretion disk instabilities (Proga 2003).
The X-ray line emission spectrum turned out to be an important component in Seyfert 1 galaxies.
Recombination lines, narrow and variable on long time scales
are generally believed to arise in the NLR (e.g. Pounds et al. 2004).
Finally, broad emission features, several Å wide, have recently been detected in the
X-ray spectra of some Seyfert galaxies. Whether
some of them are due to curvatures of the primary continuum hiding absorption (Lee et al. 2001), or are relativistically broadened lines (Ogle et al. 2004; Branduardi-Raymont et al. 2001; Sako et al. 2003), is still unclear.
The modeling of other detected broad excesses as broad lines
or blends of lines, in the soft X-ray spectrum, points to emission from the BLR
(Steenbrugge et al. 2005; Ogle et al. 2004). A deeper understanding of the physics behind such emission features is important for a correct interpretation of the entire X-ray spectrum.
pc scale, where a molecular torus should exist (see Blustin et al. 2005, and references therein)
or, finally, the ionized gas outflow may be generated by accretion disk instabilities (Proga 2003).
The X-ray line emission spectrum turned out to be an important component in Seyfert 1 galaxies.
Recombination lines, narrow and variable on long time scales
are generally believed to arise in the NLR (e.g. Pounds et al. 2004).
Finally, broad emission features, several Å wide, have recently been detected in the
X-ray spectra of some Seyfert galaxies. Whether
some of them are due to curvatures of the primary continuum hiding absorption (Lee et al. 2001), or are relativistically broadened lines (Ogle et al. 2004; Branduardi-Raymont et al. 2001; Sako et al. 2003), is still unclear.
The modeling of other detected broad excesses as broad lines
or blends of lines, in the soft X-ray spectrum, points to emission from the BLR
(Steenbrugge et al. 2005; Ogle et al. 2004). A deeper understanding of the physics behind such emission features is important for a correct interpretation of the entire X-ray spectrum.
Mrk 279 is a Seyfert 1.5 galaxy, located at redshift
z = 0.0305 (Scott et al. 2004).
The source spectrum is affected by a relatively low Galactic absorption
(
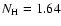
 1020 cm-2, Elvis et al. 1989).
Mrk 279 has been extensively
studied by low resolution instruments (e.g., Weaver et al. 2001,1995)
mainly by virtue of the 6.4 keV iron emission
line, which is characterized by a broad profile and a variable flux.
The first systematic study
on the soft X-ray energy band was carried out in 2002 using Chandra-HETGS, simultaneously with FUSE and HST-STIS (Scott et al. 2004).
At that epoch both UV and X-ray observations show that the source was at
the lower end of its historical flux range (Weaver et al. 2001). The 2-10 keV flux was
1020 cm-2, Elvis et al. 1989).
Mrk 279 has been extensively
studied by low resolution instruments (e.g., Weaver et al. 2001,1995)
mainly by virtue of the 6.4 keV iron emission
line, which is characterized by a broad profile and a variable flux.
The first systematic study
on the soft X-ray energy band was carried out in 2002 using Chandra-HETGS, simultaneously with FUSE and HST-STIS (Scott et al. 2004).
At that epoch both UV and X-ray observations show that the source was at
the lower end of its historical flux range (Weaver et al. 2001). The 2-10 keV flux was
 1.2
1.2 
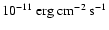 and the 1000 Å flux
was
and the 1000 Å flux
was  0.13
0.13 
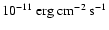 Å-1. While monitored
by FUSE, the source became 7.5 times dimmer from 1999 to 2002 and a similar
behavior was recorded in the
optical (Bachev & Strigachev 2004). In the 2002 multiwavelength observation, a relatively short exposure time combined with a low flux state conspired against the detection of
any significant absorption in the HETGS spectrum.
The ionized absorber in Mrk 279 has indeed quite a low column density
in the X-ray domain (
Å-1. While monitored
by FUSE, the source became 7.5 times dimmer from 1999 to 2002 and a similar
behavior was recorded in the
optical (Bachev & Strigachev 2004). In the 2002 multiwavelength observation, a relatively short exposure time combined with a low flux state conspired against the detection of
any significant absorption in the HETGS spectrum.
The ionized absorber in Mrk 279 has indeed quite a low column density
in the X-ray domain (
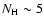

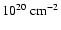 ,
this study), as compared for example to NGC 3783
(
,
this study), as compared for example to NGC 3783
( 3
3  1022 cm-2, Kaspi et al. 2001) or NGC 5548 (
1022 cm-2, Kaspi et al. 2001) or NGC 5548 ( 5
5  1021 cm-2, Kaastra et al. 2002).
1021 cm-2, Kaastra et al. 2002).
A large scale project has more recently focused on Mrk 279.
The observations were carried out using HST-STIS, FUSE and Chandra-LETGS
simultaneously. The methodology and results for the UV absorption is described in Gabel et al. (2005b, hereinafter G05), while Arav et al. (2005)
focus on the modeling of the structure of such an absorber.
For the LETGS data, the theoretical background for the line production from a meta-stable level of O V is described in Kaastra et al. (2004).
In the present paper we present the total modeling of the X-ray spectrum.
The X-ray flux we measure with Chandra-LETGS is  2.18
2.18 
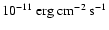 in the 2-10 keV range, while the UV flux
at 1000 Å is almost a factor of ten higher
(
in the 2-10 keV range, while the UV flux
at 1000 Å is almost a factor of ten higher
( 1.23
1.23 
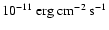 Å-1, G05) than the 2002 UV observation. The flux history in the optical V band, recorded by the 0.9-m University
of Nebraska telescope, shows that the source underwent a large flux rise
during the
Å-1, G05) than the 2002 UV observation. The flux history in the optical V band, recorded by the 0.9-m University
of Nebraska telescope, shows that the source underwent a large flux rise
during the  2 months preceding the present campaign (Gaskell et al., in prep.).
2 months preceding the present campaign (Gaskell et al., in prep.).
The paper is organized as follows. Section 2 is devoted to the analysis of the data and the modeling of the emission and absorption spectral features of Mrk 279. In Sect. 3 we discuss our results and in
Sect. 4 we present our conclusions. The cosmological parameters used are:
H0 = 70 km s-1 Mpc-1,
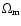 = 0.3, and
= 0.3, and
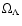 = 0.7.
The quoted errors refer to 84% confidence (
= 0.7.
The quoted errors refer to 84% confidence (
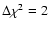 for one interesting parameter), unless otherwise stated.
for one interesting parameter), unless otherwise stated.
Table 1:
Chandra-LETGS observation log of Mrk 279.
![\begin{figure}
\par\includegraphics[angle=90,width=7.9cm,clip]{5390f1.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg21.gif) |
Figure 1:
Upper panel: broad band fluxed spectrum of Mrk 279. The data have been binned by a factor of two. Lower panel: signal to noise ratio for the unbinned spectrum. |
| Open with DEXTER |
2 The data
Mrk 279 was observed seven times spread over ten days for a total duration of 360 ks,
by the Low Energy Transmission Grating Spectrometer (LETGS, Brinkman et al. 2000) coupled to the HRC-S on board of Chandra. The nominal
wavelength range in which LETGS operates is 1.7-150 Å, with an energy resolution of 0.05 Å.
Table 1 lists the observation log for Mrk 279.
The data reduction was carried out using the standard CXC pipeline up to the creation of
the level 1.5 event files. The steps leading to the final event file (level 2)
follow the same line as CXC as for example in the wavelength accuracy
determination and effective area, only make use of an independent procedure, first described in Kaastra et al. (2002).
Higher spectral orders have been taken into account in all spectral fitting. Uniquely
for plotting purposes were the higher orders subtracted,
using a bootstrap method, from the "fluxed'' spectrum (cts s-1 cm-2 Å-1).
The spectrum was differently re-binned, in channel space, depending on the features we wanted to focus on. A large re-binning (factor of 10) was used to model the continuum shape, while a binning of 2 was used for the study of the
spectral features. In Fig. 1 (upper panel) the fluxed broad band spectrum is displayed, while the S/N of the unbinned spectrum is shown in the lower panel.
We have a S/N of at least 5 for all wavelengths between 2-58 Å, except for a small region around the instrumental C I edge near 40 Å. Over most of the 6-48 Å band, S/N is 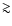 10. This limit of S/N=10 is often seen as a necessary condition for reliable
spectroscopy. The spectral analysis was carried out using the fitting package
SPEX
10. This limit of S/N=10 is often seen as a necessary condition for reliable
spectroscopy. The spectral analysis was carried out using the fitting package
SPEX![[*]](/icons/foot_motif.gif) (ver. 2.0).
(ver. 2.0).
2.1 Time variability
![\begin{figure}
\par\includegraphics[angle=90,width=7.75cm,clip]{5390f2.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg23.gif) |
Figure 2:
LETGS light curve of Mrk 279 in the zeroth spectral order. Bin size: 1000 s.
The individual 7 time segments are labeled at the bottom. The FUSE and HST pointings are also marked. |
| Open with DEXTER |
The light curve of Mrk 279 taken in the zeroth spectral order is shown in
Fig. 2 where we also mark the epochs of the FUSE and HST pointings, during the multi-wavelength campaign.
The count rate c(t) of the X-ray data varies gradually, spanning the range
between 0.49 c/s (during the minimum in observation 4) to 0.82 c/s (at the
maximum of observations 5 and 7). No significant variations on time scales
shorter than 10 ks are observed. Typical time scales
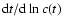 for the more gradual variations are
for the more gradual variations are  120 ks. Details on the X-ray variability will be
discussed elsewhere (Gaskell et al., in prep.).
120 ks. Details on the X-ray variability will be
discussed elsewhere (Gaskell et al., in prep.).
2.2 Continuum spectrum
The continuum shape of the average spectrum is modeled by a power-law (average
photon index
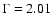
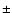 0.01), dominating at shorter wavelengths, and a "modified'' black body emission with an average temperature kT=0.108
0.01), dominating at shorter wavelengths, and a "modified'' black body emission with an average temperature kT=0.108 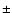
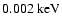 ,
to account for a "soft excess'' at longer wavelengths (18-80 Å, Table 2).
The blackbody model takes into account the modifications by coherent Compton scattering (see Kaastra & Barr 1989). The parameters of this fit are reported in Table 2.
We have also fitted the spectrum of each of the seven observations separately using the same power law plus modified blackbody spectrum as used above for the
combined spectrum. In Fig. 3 these continuum parameters are plotted
in terms of percentage deviation from the value found for the combined spectrum, as a function of the observation number (and therefore of time, Fig. 2).
We see that the power-law parameters agree within
,
to account for a "soft excess'' at longer wavelengths (18-80 Å, Table 2).
The blackbody model takes into account the modifications by coherent Compton scattering (see Kaastra & Barr 1989). The parameters of this fit are reported in Table 2.
We have also fitted the spectrum of each of the seven observations separately using the same power law plus modified blackbody spectrum as used above for the
combined spectrum. In Fig. 3 these continuum parameters are plotted
in terms of percentage deviation from the value found for the combined spectrum, as a function of the observation number (and therefore of time, Fig. 2).
We see that the power-law parameters agree within 
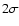 with the average value apart from two outlying points: the value of
with the average value apart from two outlying points: the value of 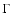 for observation 5 and the 2-10 keV luminosity for observation 4, to which the flux drop in the light curve is ascribed. The modified black body parameters are more stable over time, the maximum deviation being
for observation 5 and the 2-10 keV luminosity for observation 4, to which the flux drop in the light curve is ascribed. The modified black body parameters are more stable over time, the maximum deviation being 
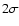 from the mean. The stable shape of the soft thermal component dominates the band where most of the absorption and emission spectral features are, while the power
law dominates at 2-8 Å, where the spectral resolution starts to degrade, making the (few) spectral features at those short wavelength more difficult to study. The largely stable shape of the spectrum supports the assumption that the time-averaged continuum of the combined data can be used
in our modeling of the absorption/emission components.
from the mean. The stable shape of the soft thermal component dominates the band where most of the absorption and emission spectral features are, while the power
law dominates at 2-8 Å, where the spectral resolution starts to degrade, making the (few) spectral features at those short wavelength more difficult to study. The largely stable shape of the spectrum supports the assumption that the time-averaged continuum of the combined data can be used
in our modeling of the absorption/emission components.
Table 2:
Fit parameters of a power-law plus modified blackbody fit
to the total spectrum of Mrk 279. The errors on the parameters are only statistical and
do not include any systematic uncertainty. The fit was restricted to
the 1.9-110 Å range. The spectra were binned by a factor of 10 before
spectral fitting.
![\begin{figure}
\par\includegraphics[angle=90,width=8.1cm,clip]{5390f3.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg32.gif) |
Figure 3:
Percentage deviation from the parameter values of the combined spectrum (Table 2) for: the power-law slope,
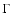 ,
the power-law 2-10 keV luminosity, the temperature ( kT) and the luminosity of the modified black body. The horizontal axis
labels the observation number as defined in Fig. 2. ,
the power-law 2-10 keV luminosity, the temperature ( kT) and the luminosity of the modified black body. The horizontal axis
labels the observation number as defined in Fig. 2. |
| Open with DEXTER |
In the following we will describe first the modeling of the emission spectral features (broad and narrow). We will see how
this is a necessary step in order to further describe the absorbed spectrum.
Residuals to the continuum model show many narrow absorption and emission features and
also some broad excesses, roughly 1 Å wide, especially around the transitions of the most prominent oxygen ions in the X-ray spectrum (O VII and O VIII).
This can be seen, for instance,
in Fig. 4, where the region around the O VII triplet is shown.
We overplot the profile of a broad Gaussian line, only to guide the eye.
Especially in this region, where any absorber is expected to show many (oxygen) features,
the fitting of the absorption lines would
be seriously compromised (e.g. O V and the O II Galactic absorption, Fig. 4) if these broad emission features are ignored. These excesses are present in all seven observations.
![\begin{figure}
\par\includegraphics[angle=90,width=7.65cm,clip]{5390f4.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg33.gif) |
Figure 4:
Residuals, in terms of sigma, to the continuum model in the O VII triplet region. A broad Gaussian (dashed line) has been added only to guide the eye.
The continuum is represented by a power-law plus a modified black body absorbed by galactic absorption. The labels refer to the position of expected absorption/emission narrow lines. |
| Open with DEXTER |
The uncertainty associated with the flux/shape of the broad X-ray lines is such that we are unable to quantify if the broad excesses respond to the average flux variation of  25% experienced by the central source. Therefore, in studying these features we considered the whole data set.
25% experienced by the central source. Therefore, in studying these features we considered the whole data set.
2.3.1 A basic fit for the broad lines
We first attempted a purely phenomenological approach: we included broad Gaussian profiles, at the position of the main H-like and He-like ions of C, N, O
to the continuum described in Sect. 2.2. The intrinsic flux of the lines is of course
intercepted by the absorbers on the line of sight (Sect. 2.4),
which must be consistently taken into account even in this
simple modeling. The resulting unabsorbed profile of the lines is thus expected to be significantly modified with respect to that qualitatively drawn in
Fig. 4. A contribution by narrow emission lines could be included only for O VII and O VIII, as they produce the only measurable narrow
recombination lines (Sect. 2.3.3). For
the O VII triplet we also formally included, beside the measured narrow forbidden line, the recombination and intercombination lines with flux 1/4 of the forbidden line (assuming a purely photoionized gas with density <109 cm-3, Porquet & Dubau 2000).
The centroid of the broad Gaussian lines are kept fixed to the
wavelength of the Ly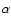 transition for C VI, N VII and O VIII.
For the blended lines, the centroid was at first left
free to vary in the range among the nominal lines' wavelength and later fixed to that value (Table 5). The width of the lines is a difficult parameter to determine. At this stage, we tentatively fixed the FWHM of the individual lines at
transition for C VI, N VII and O VIII.
For the blended lines, the centroid was at first left
free to vary in the range among the nominal lines' wavelength and later fixed to that value (Table 5). The width of the lines is a difficult parameter to determine. At this stage, we tentatively fixed the FWHM of the individual lines at  10 000 km s-1. The width for a triplet is therefore a blend of individual lines. For O VII, the more evident feature in the residuals, we actually fitted the full-width-half-maximum (FWHM) of the blended triplet, keeping it fixed later on to evaluate the errors on the line luminosity.
In Table 3 the result of this fit is listed.
The intrinsic line luminosities listed in Table 3 are derived considering an emission/absorption fit and the relative errors are evaluated from this best fit.
In the last column we list the significance of
each broad excess individually, in terms of
10 000 km s-1. The width for a triplet is therefore a blend of individual lines. For O VII, the more evident feature in the residuals, we actually fitted the full-width-half-maximum (FWHM) of the blended triplet, keeping it fixed later on to evaluate the errors on the line luminosity.
In Table 3 the result of this fit is listed.
The intrinsic line luminosities listed in Table 3 are derived considering an emission/absorption fit and the relative errors are evaluated from this best fit.
In the last column we list the significance of
each broad excess individually, in terms of
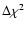 ,
starting from a model with no broad lines.
,
starting from a model with no broad lines. 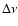 is 1 (where
is 1 (where 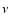 is the number of degrees of freedom) as the width and the centroid of the line are kept fixed. With those constraints,
we determine that the O VII triplet and the O VIII Ly
is the number of degrees of freedom) as the width and the centroid of the line are kept fixed. With those constraints,
we determine that the O VII triplet and the O VIII Ly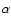 have a significant detection (approximatively 6 and 3
have a significant detection (approximatively 6 and 3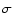 ,
respectively).
Measuring the physical parameters, such as flux and FWHM, from this line-by-line fitting might be a quantitative way to model these excesses.
However, given their relative weakness, this approach leads to severe uncertainties.
First, the absorption lines that are superimposed on
these profiles, the level of the continuum, and possible emission line blending,
contribute to make the flux and width determination of these lines very uncertain.
Second, the weaker lines, whose flux is only a few per cent higher than the continuum, can be easily missed.
,
respectively).
Measuring the physical parameters, such as flux and FWHM, from this line-by-line fitting might be a quantitative way to model these excesses.
However, given their relative weakness, this approach leads to severe uncertainties.
First, the absorption lines that are superimposed on
these profiles, the level of the continuum, and possible emission line blending,
contribute to make the flux and width determination of these lines very uncertain.
Second, the weaker lines, whose flux is only a few per cent higher than the continuum, can be easily missed.
Table 3:
Parameters of the X-ray broad lines from a line-by-line fitting. The line transition, its
centroid (in Å), the FWHM in km s-1 and the rounded correspondent value in Å, the intrinsic line luminosity and the significance are listed (see text for details). Note that for the triplets the FWHM is the result of the blend of the lines.
2.3.2 A synthetic model for the broad lines: the LOC model
We looked for a physical model that would account for all the lines simultaneously.
For instance, in analogy with the UV broad emission lines,
one possibility is that these emission features arise within the BLR.
In order to self consistently test this idea, we first modeled the UV broad lines detected simultaneously by HST-STIS and FUSE.
From the best fit synthetic model we then infer the X-ray line luminosities from the same emission-line gas to be compared with the LETGS data.
In the modeling we considered the luminosity, corrected for the galaxy extinction (
E(B-V)=0.016), of the broad component of the UV line profiles, listed in Table 4
(see also Fig. 1 of G05). The FWHM of the UV lines lie in the range  8500-9500 km s-1.
A full description of the UV data analysis of
the broad lines will be described in Scott et al. (2006, in prep.).
We used Cloudy (Ferland 2004), ver. 95.06, to reproduce the UV emission from the BLR.
The spectral energy distribution (SED) of the incident continuum that we used is shown in Fig. 5. The UV points at 1000 and 1350 Å come from the FUSE and HST-STIS measurements, respectively (G05), while the X-ray ionizing continuum comes from the time averaged LETGS data.
Lacking any information of the high energy spectrum, we artificially cut off the X-ray
power law at
8500-9500 km s-1.
A full description of the UV data analysis of
the broad lines will be described in Scott et al. (2006, in prep.).
We used Cloudy (Ferland 2004), ver. 95.06, to reproduce the UV emission from the BLR.
The spectral energy distribution (SED) of the incident continuum that we used is shown in Fig. 5. The UV points at 1000 and 1350 Å come from the FUSE and HST-STIS measurements, respectively (G05), while the X-ray ionizing continuum comes from the time averaged LETGS data.
Lacking any information of the high energy spectrum, we artificially cut off the X-ray
power law at  150 keV. The low energy part of the SED resembles the shape assumed for the standard photoionizing continuum used in
Cloudy
150 keV. The low energy part of the SED resembles the shape assumed for the standard photoionizing continuum used in
Cloudy![[*]](/icons/foot_motif.gif) .
We kept the luminosity of the ionizing radiation fixed:
.
We kept the luminosity of the ionizing radiation fixed:
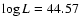 erg s-1, between 1 and 1000 Rydberg, as measured from the SED.
erg s-1, between 1 and 1000 Rydberg, as measured from the SED.
Table 4:
Rest wavelength, along with the observed luminosity and the luminosity predicted by the LOC model of the broad UV lines as measured by FUSE (labeled 1) and HST-STIS (labeled 2). For each observed blended-line, the value of Lum
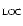 consistently refers to the summed contribution of the lines in the blend.
consistently refers to the summed contribution of the lines in the blend.
![\begin{figure}
\par\includegraphics[angle=90,width=7.4cm,clip]{5390f5.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg42.gif) |
Figure 5:
The spectral energy distribution for Mrk 279. The points at 1000 and
1350 Å are the continuum flux of the simultaneous FUSE and HST-STIS observation, respectively.
The X-ray continuum is taken from the present LETGS data. |
| Open with DEXTER |
In order to reproduce emission from a large range of ionization stages, we followed the
"locally optimally emitting clouds'' prescription (LOC, Baldwin et al. 1995).
For this purpose, we created a grid of values for
the density n and the distance r of the BLR clouds. Once these parameters are set, the
ionization parameter is readily calculated: 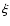 = L/nr2.
We computed the integrated luminosity of the lines,
weighted by a power-law distribution of the density n and the distance r and assuming spherical symmetry (Baldwin et al. 1995):
= L/nr2.
We computed the integrated luminosity of the lines,
weighted by a power-law distribution of the density n and the distance r and assuming spherical symmetry (Baldwin et al. 1995):
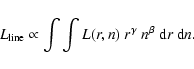 |
(1) |
The 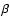 parameter was fixed to -1 (e.g. Korista & Goad 2000),
while the slope of r,
parameter was fixed to -1 (e.g. Korista & Goad 2000),
while the slope of r, 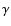 ,
was a free parameter in the fit.
The density n ranged between
,
was a free parameter in the fit.
The density n ranged between  108-12.5 cm-3 with a step of 0.125 in log.
The same step was taken for the radius, which
ranged between 10
14.7-18 cm. Densities lower than n=108 cm-3 are not expected within the BLR, while for densities
n=1013-14 cm-3 the cloud emission would be, in most cases,
continuum rather than lines (Korista et al. 1997). The wide range in distances allows us to completely follow the luminosity
distribution of the main X-ray lines as a function of radius. The gas located at distances
108-12.5 cm-3 with a step of 0.125 in log.
The same step was taken for the radius, which
ranged between 10
14.7-18 cm. Densities lower than n=108 cm-3 are not expected within the BLR, while for densities
n=1013-14 cm-3 the cloud emission would be, in most cases,
continuum rather than lines (Korista et al. 1997). The wide range in distances allows us to completely follow the luminosity
distribution of the main X-ray lines as a function of radius. The gas located at distances
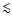 1015.3 cm gives, for all lines, a minor contribution to the integrated luminosity.
The hydrogen column density was fixed to 1023 cm-2, as most of the
emission should occur for
1015.3 cm gives, for all lines, a minor contribution to the integrated luminosity.
The hydrogen column density was fixed to 1023 cm-2, as most of the
emission should occur for
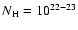 cm-2. Since at all wavelengths
a main reason of uncertainty in the observed line luminosity
is line blending, to bypass this problem the lines predicted by Cloudy for each n and r,
which could be a result of a blend, were summed up (Table 4).
The best fit was reached through a
cm-2. Since at all wavelengths
a main reason of uncertainty in the observed line luminosity
is line blending, to bypass this problem the lines predicted by Cloudy for each n and r,
which could be a result of a blend, were summed up (Table 4).
The best fit was reached through a 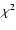 minimization.
minimization.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{5390f6.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg49.gif) |
Figure 6:
Best fit of the intrinsic luminosity of the UV broad emission lines ( upper panel). The model is displayed by a continuous line only to guide the eye. Lower panel: residuals in terms of 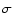 to the best fit.
to the best fit. |
| Open with DEXTER |
Table 5:
Rest wavelengths and intrinsic luminosity (in units of 1041 erg s-1) of the lines in the LETGS (as reported in Table 3) compared with the X-ray line luminosities
as predicted by the LOC model (last column) are listed. Note that the observed X-ray line luminosities were not used in the LOC fitting, which was based on UV data only. Here the triplets location has been identified with the wavelength of the forbidden line.
In Fig. 6 (upper panel), the data and our best fit
are displayed for the FUSE and HST-STIS lines (listed also in Table 4).
The model seems to describe the broad line average emission reasonably well if
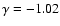
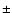 0.14 (this is the 84% confidence level for one interesting
parameter). The value of
0.14 (this is the 84% confidence level for one interesting
parameter). The value of 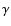 is the only fitted parameter.
The integrated covering factor of the clouds set,
evaluated only on the basis of the fitting of the hydrogen Ly
is the only fitted parameter.
The integrated covering factor of the clouds set,
evaluated only on the basis of the fitting of the hydrogen Ly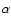 normalization, is 34
normalization, is 34 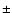 26%.
Another parameter that was not fine-tuned in the fit is the outer radius of the BLR.
The residuals to the best fit model are shown in Fig. 6 (lower panel).
Within
26%.
Another parameter that was not fine-tuned in the fit is the outer radius of the BLR.
The residuals to the best fit model are shown in Fig. 6 (lower panel).
Within 
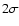 the observed line luminosities agree with the LOC model.
the observed line luminosities agree with the LOC model.
Other complicating factors are likely to contribute to the observed BLR emission line spectrum.
For example, the abundances may be different than solar, the line emitting clouds
may have a wider range of column densities,
or the geometry of the system maybe different than the simple spherical symmetry assumed here.
However here we seek a simple parameterization that explains the bulk of the BLR emission. A detailed model of the UV lines produced by the BLR would be beyond the scope of this paper.
The luminosities of the major X-ray lines, as predicted by the synthetic model are listed in Table 5. In this table, the luminosity of the Gaussian profiles
with which the LETGS spectrum was fitted without using a synthetic
model are listed again, for comparison.
We stress that these lines were not included in the LOC model, which was based instead on the UV data only. This choice was made to minimize possible errors that a fit based on the X-ray data
(complicated by the continuum level and the absorption lines) would have brought to the LOC model fitting. The luminosities predicted by the LOC model are consistent, within the errors, with a crude line by line fitting. In Fig. 7 the best fit radial profile of the intrinsic line
luminosity, integrated along the density (n-1) is displayed for eight interesting ions.
The diamond points locate the luminosity-weighted mean radius (e.g. Bottorff et al. 2002):
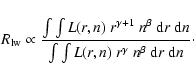 |
(2) |
In the figure, the relevant X-ray ions are included along with O VI, which lies in the FUSE bandpass, and C IV, N V and H Ly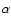 ,
observed by HST-STIS.
Most of the predicted luminosity should arise from clouds located at
,
observed by HST-STIS.
Most of the predicted luminosity should arise from clouds located at
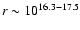 cm.
The UV ions are confined to radii r>1017 cm, while not unexpectedly,
the mean emitting radius for the X-ray lines would lie 10 times further in. Extrapolating the model, we see that in principle the X-ray lines, in contrast to most UV ions, have a non negligible luminosity tail from radii smaller than 1016 cm.
cm.
The UV ions are confined to radii r>1017 cm, while not unexpectedly,
the mean emitting radius for the X-ray lines would lie 10 times further in. Extrapolating the model, we see that in principle the X-ray lines, in contrast to most UV ions, have a non negligible luminosity tail from radii smaller than 1016 cm.
Based on these results, we included in the final X-ray spectral fit six Gaussian profiles with luminosity fixed at the value predicted by the LOC model.
The widths of the individual lines were set to the maximal value found in the UV (FWHM = 9500 km s-1), very similar to the value used in the line-by-line fit (Sect. 2.3.1). For the triplets, the blend of the three lines set
the total FWHM. For O VII, we used instead the same FWHM determined in the phenomenological fit (Table 3).
The wavelengths were left free to adjust in a range of 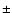 0.2 Å around the centroid of the main line, to take into account the line blending for triplets. The modeled line profiles are
shown in the lower panel of Fig. 8.
The following analysis on the absorption spectrum was performed after the inclusion of the broad emission lines as predicted by the LOC model.
0.2 Å around the centroid of the main line, to take into account the line blending for triplets. The modeled line profiles are
shown in the lower panel of Fig. 8.
The following analysis on the absorption spectrum was performed after the inclusion of the broad emission lines as predicted by the LOC model.
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{5390f7.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg57.gif) |
Figure 7:
Best fit luminosity profiles of eight of the ions considered for the fit. The luminosity was integrated at each radius using the weighting function 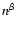 .
For each emission line the diamonds indicate the luminosity-weighted radius. Note that the model underpredicts theobserved luminosity of C IV by .
For each emission line the diamonds indicate the luminosity-weighted radius. Note that the model underpredicts theobserved luminosity of C IV by  40%. 40%. |
| Open with DEXTER |
2.3.3 Narrow emission lines and RRCs
Narrow emission features are not a dominant component of the total spectrum of Mrk 279. The flux
of the O VII forbidden line and the O VIII Ly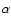 are 1.0
are 1.0 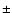 0.6
0.6  10-14 and 7
10-14 and 7 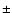 5
5  10-15 erg cm-2 s-1, respectively. Finally, the flux of the O VII He
10-15 erg cm-2 s-1, respectively. Finally, the flux of the O VII He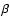 line is 4
line is 4 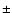 3
3  10-15 erg cm-2 s-1.
Carbon recombination lines are not visible in the combined spectrum.
Radiative recombination continua (RRCs) of C V and C VI (at
10-15 erg cm-2 s-1.
Carbon recombination lines are not visible in the combined spectrum.
Radiative recombination continua (RRCs) of C V and C VI (at
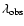 = 32.57 and 26.05 Å, respectively, Fig. 8) are seen.
The temperature of the C V RRC is
= 32.57 and 26.05 Å, respectively, Fig. 8) are seen.
The temperature of the C V RRC is
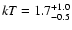 eV, with an emission measure
eV, with an emission measure
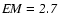
 2
2  1061 cm-3. For the C VI RRC,
1061 cm-3. For the C VI RRC,
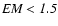
 1061 cm-3, fixing the temperature to the value obtained for C V.
1061 cm-3, fixing the temperature to the value obtained for C V.
![\begin{figure}
\par\includegraphics[height=13.65cm,width=4.7cm,angle=90,clip]{53...
...
\includegraphics[height=13.7cm,width=5cm,angle=90,clip]{5390f8d.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg64.gif) |
Figure 8:
Lower panel: best fit to the LETGS spectrum of Mrk 279 divided per wavelength range.
The broad emission, predicted by the LOC fitting, and the narrow emission features,
shifted up of a factor 2 for plotting purpose, are also overplotted.
Upper panel: absorbing components: Dark dashed and light dot-dashed line: z=0 absorbers. Warm absorber: light solid line (
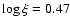 ), dark solid line ( ), dark solid line (
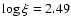 ). ). |
| Open with DEXTER |
Table 6:
Laboratory wavelength, formal EW and outflow velocity for the X-ray absorption lines.
The EW and the column densities predicted by models M1 and M2 assume different covering factors for the absorbing gas and are discussed in the text.
2.4 The absorbed spectrum
The LETGS spectrum shows absorption lines, at the redshift of the source, over the  5-45 Å band, indicating that a gas with a range of ionization stages must be present.
In Table 6 we list these lines, reporting the theoretical wavelength and the measured equivalent width (EW). The H-like and He-like ions of C, N and O are generally well determined. We report also the formal
equivalent widths for several important diagnostic lines that are not
significantly detected. These measurements help to constrain column
densities and the determination of the global properties of the absorber.
The inferred velocity dispersions are affected by large errors for most of the ions considered.
Therefore we took into account only the strongest ions: O VII, O VI,
C VI and C V to calculate a mean velocity dispersion
5-45 Å band, indicating that a gas with a range of ionization stages must be present.
In Table 6 we list these lines, reporting the theoretical wavelength and the measured equivalent width (EW). The H-like and He-like ions of C, N and O are generally well determined. We report also the formal
equivalent widths for several important diagnostic lines that are not
significantly detected. These measurements help to constrain column
densities and the determination of the global properties of the absorber.
The inferred velocity dispersions are affected by large errors for most of the ions considered.
Therefore we took into account only the strongest ions: O VII, O VI,
C VI and C V to calculate a mean velocity dispersion 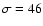
 21 km s-1, using the curve of growth method. This value is in agreement with FUV values as measured by FUSE (G05), namely 50 km s-1. This is the value we adopt in the modeling.
21 km s-1, using the curve of growth method. This value is in agreement with FUV values as measured by FUSE (G05), namely 50 km s-1. This is the value we adopt in the modeling.
![\begin{figure}
\par\includegraphics[angle=90,width=7.5cm,clip]{5390f9.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg72.gif) |
Figure 9:
Detail of the O VIII absorption line, fitted with only one component (
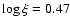 ,
dashed line) and with two components ( ,
dashed line) and with two components (
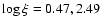 ,
solid line). ,
solid line). |
| Open with DEXTER |
For the lines whose EW is better determined, we fitted also the blueshift with respect to the laboratory wavelength (Table 6).
The uncertainty on the blueshift is proportional to
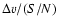 where
where 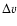 is the velocity resolution at a given wavelength and S/N is the signal-to-noise ratio of the detected feature.
For the lines located at longer wavelength, the shift measurement is in principle more precise.
However, the higher resolution in these regions is compensated by a lower S/N ratio.
Deriving the covering factor of the ionized absorbing gas from the X-ray data is a difficult task, due to insufficient energy resolution. The most simple case is to assume a covering factor of one.
The result of the fit with this assumption is listed in Table 6 (model M1) where the EW and the column density of the most prominent lines are
listed. The fitting was performed using the SLAB model in SPEX, which
calculates the transmission through a thin layer of gas, making
no assumption on the underlying ionization balance (Kaastra et al. 2002). In this model the tunable parameters are: the
individual ionic column densities, the width of the lines, the outflow velocity and the covering factor. However, for this observation of Mrk 279,
additional information is provided by the simultaneous UV data.
In particular, the UV absorber for Mrk 279 shows evidence of two velocity components (indistinguishable with the X-ray resolution) whose covering factor differs from
unity by 10% and 7%, respectively. Here we test this model using the LETGS data.
The model M2 in Table 6
assumes two components (i.e. two SLAB components), as found from the FUSE analysis (G05).
In the first component, the velocity dispersion is
set to
is the velocity resolution at a given wavelength and S/N is the signal-to-noise ratio of the detected feature.
For the lines located at longer wavelength, the shift measurement is in principle more precise.
However, the higher resolution in these regions is compensated by a lower S/N ratio.
Deriving the covering factor of the ionized absorbing gas from the X-ray data is a difficult task, due to insufficient energy resolution. The most simple case is to assume a covering factor of one.
The result of the fit with this assumption is listed in Table 6 (model M1) where the EW and the column density of the most prominent lines are
listed. The fitting was performed using the SLAB model in SPEX, which
calculates the transmission through a thin layer of gas, making
no assumption on the underlying ionization balance (Kaastra et al. 2002). In this model the tunable parameters are: the
individual ionic column densities, the width of the lines, the outflow velocity and the covering factor. However, for this observation of Mrk 279,
additional information is provided by the simultaneous UV data.
In particular, the UV absorber for Mrk 279 shows evidence of two velocity components (indistinguishable with the X-ray resolution) whose covering factor differs from
unity by 10% and 7%, respectively. Here we test this model using the LETGS data.
The model M2 in Table 6
assumes two components (i.e. two SLAB components), as found from the FUSE analysis (G05).
In the first component, the velocity dispersion is
set to 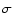 = 50 km s-1 with an assumed covering factor of 0.9. The second
component contains 4% of the column density of the first component,
the velocity dispersion is 28 km s-1 and the covering factor is 0.93.
The predicted EW and the derived column densities for the two models
are compared in the table. With the present LETGS data we are not able to distinguish between the
two approaches (M1 and M2) and the X-ray absorber is consistent
to cover all the line of sight. This is reasonable, as the X-ray
source may be smaller than the UV source such that the ionized gas sees it as point-like.
For simplicity we will assume that the X-ray gas has a covering factor of one.
= 50 km s-1 with an assumed covering factor of 0.9. The second
component contains 4% of the column density of the first component,
the velocity dispersion is 28 km s-1 and the covering factor is 0.93.
The predicted EW and the derived column densities for the two models
are compared in the table. With the present LETGS data we are not able to distinguish between the
two approaches (M1 and M2) and the X-ray absorber is consistent
to cover all the line of sight. This is reasonable, as the X-ray
source may be smaller than the UV source such that the ionized gas sees it as point-like.
For simplicity we will assume that the X-ray gas has a covering factor of one.
In the following, we describe two viable models to physically describe the ionized absorption in Mrk 279: separate gas components differing in ionization parameter, column density and outflow velocity (Sect. 2.4.1) and a continuous column density distribution as a function of the ionization parameter (Sect. 2.4.2).
2.4.1 A two ionization components model
We modeled the data in terms of physical warm absorber components.
For this purpose, we used the XABS model in SPEX.
From an input spectral energy distribution (Fig. 5) for
the ionizing continuum of the source, the model interpolates over a large grid of values for 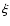 and
and 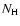 ,
pre-calculated using Cloudy. Abundances are assumed to be solar (Grevesse & Sauval 1998). The data require at least two ionized absorbers located at the redshift of the source. In Table 7 we list the hydrogen column density, the ionization parameters and the outflow velocity of the absorbing gas. The best fit obtained with this model is displayed in the lower panel of Fig. 8. In the upper panel the transmitted spectrum is displayed.
The light solid line refers to the lower ionization absorber while the higher ionization
gas is highlighted with a dark solid line.
The low ionization absorber (component 1 in Table 7) is characterized by a ionization parameter
,
pre-calculated using Cloudy. Abundances are assumed to be solar (Grevesse & Sauval 1998). The data require at least two ionized absorbers located at the redshift of the source. In Table 7 we list the hydrogen column density, the ionization parameters and the outflow velocity of the absorbing gas. The best fit obtained with this model is displayed in the lower panel of Fig. 8. In the upper panel the transmitted spectrum is displayed.
The light solid line refers to the lower ionization absorber while the higher ionization
gas is highlighted with a dark solid line.
The low ionization absorber (component 1 in Table 7) is characterized by a ionization parameter
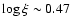 and it is
tightly constrained through fitting the strong absorption lines of C V, C VI,
N VI, O VI and O VII (Fig. 8).
The other component (labeled 2 in Table 7) is slightly faster and more ionized (
and it is
tightly constrained through fitting the strong absorption lines of C V, C VI,
N VI, O VI and O VII (Fig. 8).
The other component (labeled 2 in Table 7) is slightly faster and more ionized (
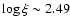 ). The parameters are mostly determined by the O VIII line, but other high ionization absorption lines, detected with a lower significance,
like Fe XVII-Fe XIX, Ne IX, Ne X Mg XI and Si XIII, also contribute.
Adding a second component improves the fit by
). The parameters are mostly determined by the O VIII line, but other high ionization absorption lines, detected with a lower significance,
like Fe XVII-Fe XIX, Ne IX, Ne X Mg XI and Si XIII, also contribute.
Adding a second component improves the fit by
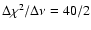 ,
corresponding to a significance >99.5%. Many of the lines of the high ionization
system lie in a region with a lower velocity resolution (
,
corresponding to a significance >99.5%. Many of the lines of the high ionization
system lie in a region with a lower velocity resolution (
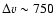 km s-1 at 20 Å)
resulting in larger uncertainties for the physical parameters. However, if only the
km s-1 at 20 Å)
resulting in larger uncertainties for the physical parameters. However, if only the 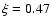 absorber is considered, the O VIII Ly
absorber is considered, the O VIII Ly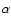 line is poorly fitted (Fig. 9).
Finally, as seen in Table 6, O VIII and O V have
comparable column densities (the ratio is
line is poorly fitted (Fig. 9).
Finally, as seen in Table 6, O VIII and O V have
comparable column densities (the ratio is  2) and
this cannot be reached with a single ionization parameter.
The column density of the two ionization components is
quite low: 1.23 and 3.2
2) and
this cannot be reached with a single ionization parameter.
The column density of the two ionization components is
quite low: 1.23 and 3.2  1020 cm-2 for
1020 cm-2 for
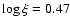 and
and
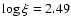 ,
respectively.
,
respectively.
Table 7:
The two absorption components at the redshift of Mrk 279. For each
component we list the value of the ionization parameter 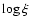 ,
the column density
,
the column density 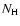 and the outflow velocity
and the outflow velocity
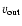 .
.
2.4.2 Continuous distribution model
Alternatively to a discrete-components fit, the absorbed spectra can be modeled also as a continuous distribution of the hydrogen column densities of the ionized medium
as a function of the ionization parameter. This is achieved using the WARM model in SPEX.
The spectrum is fitted by a series of XABS models at intervals of 0.2 in 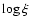 .
At desired values of
.
At desired values of 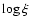 ,
the error on the corresponding hydrogen column density (
,
the error on the corresponding hydrogen column density (
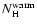 )
is evaluated. We chose a
)
is evaluated. We chose a 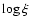 interval
between -1 and 3.2 and we evaluated
interval
between -1 and 3.2 and we evaluated
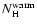 at those 2 points plus 2 equally spaced intermediate points.
These four points (at
at those 2 points plus 2 equally spaced intermediate points.
These four points (at
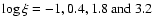 ,
respectively), smoothly connected by the finer grid of
,
respectively), smoothly connected by the finer grid of 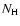 ,
determined by the XABS series, are plotted in Fig. 10
as a solid thick line. Superimposed to that, we plot the derived
hydrogen column density for the more abundant elements: carbon, oxygen, nitrogen and iron. These column densities are inferred from the SLAB model results.
The equivalent hydrogen column densities for each ion are then derived assuming solar abundances.
For this fit we left out the
energies above 6 keV. In that region many K-shell transitions of iron
ions are present, but due to the low effective area and possible calibration uncertainty the column
density of important ions as Fe XXIII-Fe XXIV are highly uncertain.
Moreover, low ionization ions of carbon (C I-C IV) and nitrogen (N I-N V) are not well determined, as their only feature in the X-ray band are their K-edges. At the typical column
density of the warm absorber of Mrk 279, the edge optical
depths of those ions is of the order of
10-(3-4) only.
Therefore, we chose not to include these ions in the SLAB fit.
For the column density of C II, C III, N II and N III, we used the UV determined values reported in Scott et al. (2004). The ionic column density of C IV, N V as well as O VI could be taken from the simultaneous UV data (G05). In Fig. 10, the hydrogen column density derived from
the ionic concentrations for each ion is plotted against the
,
determined by the XABS series, are plotted in Fig. 10
as a solid thick line. Superimposed to that, we plot the derived
hydrogen column density for the more abundant elements: carbon, oxygen, nitrogen and iron. These column densities are inferred from the SLAB model results.
The equivalent hydrogen column densities for each ion are then derived assuming solar abundances.
For this fit we left out the
energies above 6 keV. In that region many K-shell transitions of iron
ions are present, but due to the low effective area and possible calibration uncertainty the column
density of important ions as Fe XXIII-Fe XXIV are highly uncertain.
Moreover, low ionization ions of carbon (C I-C IV) and nitrogen (N I-N V) are not well determined, as their only feature in the X-ray band are their K-edges. At the typical column
density of the warm absorber of Mrk 279, the edge optical
depths of those ions is of the order of
10-(3-4) only.
Therefore, we chose not to include these ions in the SLAB fit.
For the column density of C II, C III, N II and N III, we used the UV determined values reported in Scott et al. (2004). The ionic column density of C IV, N V as well as O VI could be taken from the simultaneous UV data (G05). In Fig. 10, the hydrogen column density derived from
the ionic concentrations for each ion is plotted against the 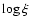 values at which the ion
is most likely formed. In
particular, the
values at which the ion
is most likely formed. In
particular, the 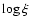 value for each specific ion i is the result of an integration
over large grid of
value for each specific ion i is the result of an integration
over large grid of 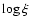 values (
-8.5-6.5) vs. ionic column density (Steenbrugge et al. 2005).
For many ions the column density cannot be determined accurately and as a result there is a large scatter in the values.
At
values (
-8.5-6.5) vs. ionic column density (Steenbrugge et al. 2005).
For many ions the column density cannot be determined accurately and as a result there is a large scatter in the values.
At 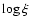 in the range 0-1, the WARM synthetic model is well traced by the single ions of O V-O VI. While the line for
in the range 0-1, the WARM synthetic model is well traced by the single ions of O V-O VI. While the line for 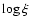 between 2.5 and 3 is determined mainly by the iron ions (Fe XIX-Fe XX) and by the H-like ions of N and C. Carbon ions suffer from a high uncertainty, as some of them lie close to the deep C I instrumental edge.
The differences in the physical models lying behind these two approaches will be discussed in Sect. 3.2.
between 2.5 and 3 is determined mainly by the iron ions (Fe XIX-Fe XX) and by the H-like ions of N and C. Carbon ions suffer from a high uncertainty, as some of them lie close to the deep C I instrumental edge.
The differences in the physical models lying behind these two approaches will be discussed in Sect. 3.2.
![\begin{figure}
\par\includegraphics[angle=90,width=7.45cm,clip]{5390f10.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg89.gif) |
Figure 10:
The hydrogen column density as a function of the
ionization parameter determined for: single ions (individual points) and an 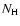 continuous distribution model (solid line). See Sect. 2.4.2 for a full description. continuous distribution model (solid line). See Sect. 2.4.2 for a full description. |
| Open with DEXTER |
So far we have studied the combined spectrum of Mrk 279. A short term
variability in the warm absorber in response to the modest continuum changes
can in principle be detected. However, the analysis of
the imprint of the warm absorber, separately for the seven data sets, did not provide evidence of a statistically significant change. In Fig. 11 we show, as an example, the comparison between the spectra taken during the 4th and 5th time intervals,
when the source underwent a major flux change, on a time scale of 2-3 days (Fig. 2). The 4th spectrum has been normalized by the higher flux unabsorbed continuum of the 5th observation.
In this way any spectral modulation caused by a continuum change in flux and/or shape is canceled out and only the information on the absorbers remain.
In the continuum also broad lines are included, as they are essential components in the evaluation of narrow absorption features. We conclude that
the oxygen complex does not change significantly. The iron UTA region
( 15-18 Å, observed wavelength) is a useful tool to detect a variation of the warm absorber (e.g., Behar et al. 2001; Krongold et al. 2003; Behar et al. 2003) as a small variation of the ionization parameter of the gas would shift the
iron UTA on the wavelength axis. However, no significant shift is detected in the data.
15-18 Å, observed wavelength) is a useful tool to detect a variation of the warm absorber (e.g., Behar et al. 2001; Krongold et al. 2003; Behar et al. 2003) as a small variation of the ionization parameter of the gas would shift the
iron UTA on the wavelength axis. However, no significant shift is detected in the data.
![\begin{figure}
\par\includegraphics[angle=90,width=7.35cm,clip]{5390f11.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg90.gif) |
Figure 11:
Comparison between the 4th and the 5th segment of Mrk 279 observation
(Fig. 2). The 4th spectrum (continuum line with asterisks) is normalized to the unabsorbed continuum of the 5th observation. The 5th spectrum is plotted with the light-solid line. |
| Open with DEXTER |
2.4.4 Absorption at redshift zero
The spectrum of Mrk 279 is also marked by narrow absorption lines which are consistent with
being produced at zero redshift.
Weakly ionized absorption, likely to arise in the ISM of our Galaxy is highlighted by the
O I feature at 23.04 Å and a weaker O II absorption line (Fig. 8).
Such an absorption is well parameterized by a collisionally ionized gas with a very
low temperature (3.1 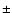 1.2 eV) and a column density of 0.72
1.2 eV) and a column density of 0.72 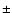 0.08
0.08 
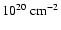 .
Along the line of sight toward this source is a known zero redshift ionized absorber (traced by O VI in the UV band, e.g. Savage et al. 2003). In the
X-ray band we detect ionized material traced by
several absorption lines from O VII, N VI, C V and C VI (Fig. 8).
We modeled this system of lines with a collisionally ionized plasma with a temperature
.
Along the line of sight toward this source is a known zero redshift ionized absorber (traced by O VI in the UV band, e.g. Savage et al. 2003). In the
X-ray band we detect ionized material traced by
several absorption lines from O VII, N VI, C V and C VI (Fig. 8).
We modeled this system of lines with a collisionally ionized plasma with a temperature
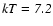
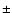 1.7 eV and a column density
1.7 eV and a column density
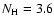
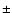 0.3
0.3 
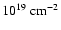 .
.
This absorbing gas may be located in the environment of
the Milky Way (e.g., Sembach et al. 2003; Wang et al. 2005), in the form of high velocity clouds moving and interacting with each other in the
Galactic halo (Collins et al. 2005). Another interpretation locates the absorbing gas at 1-3 Mpc scale, in the local group (Nicastro et al. 2002). A study of the O VI absorption line in the Mrk 279 UV spectrum is presented by Fox et al. (2004). A detailed interpretation of the X-ray absorbing components on the line of sight of Mrk 279 is discussed e.g. in Williams et al. (2006).
3.1 Emission from the broad line region
The broad emission features detected in the LETGS spectrum of Mrk 279 can be modeled in terms of
emission lines from the BLR. Using the LOC model (Baldwin et al. 1995), we found that the UV lines are modeled by emission from clouds whose density and radial
distribution follow a power law. The radial distribution is found to decrease, with a slope
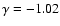
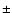 0.14, while the slope for the density distribution was fixed to -1 (Sect. 2.3.2). The integrated covering fraction of
the clouds set, calibrated on the hydrogen Ly
0.14, while the slope for the density distribution was fixed to -1 (Sect. 2.3.2). The integrated covering fraction of
the clouds set, calibrated on the hydrogen Ly fitting, is loosely constrained, being 34
fitting, is loosely constrained, being 34 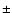 26%. These results are in agreement with the covering fraction of composite quasar spectra (Baldwin 1997). The LOC model was also applied to NGC 5548, another bright Seyfert 1 galaxy (Korista & Goad 2000). In that case, the density and radial distributions slopes,
26%. These results are in agreement with the covering fraction of composite quasar spectra (Baldwin 1997). The LOC model was also applied to NGC 5548, another bright Seyfert 1 galaxy (Korista & Goad 2000). In that case, the density and radial distributions slopes, 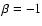 ,
,
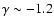 ,
respectively, well explained the HST-STIS data.
In the present paper for the first time the LOC model has been extended to the X-ray band.
The intrinsic luminosity of the X-ray lines have been calculated from this model
and applied in fitting the LETGS data. An independent fit of the X-ray spectrum using Gaussian profiles leads to flux estimates which are consistent, within the errors, with the ones predicted by the LOC model (Table 5), strengthening the validity of this approach.
In the case of Mrk 279, the O VII triplet complex is the most prominent feature (30% above the continuum, Fig. 8), as this oxygen ion is steadily produced in a wide range of physical conditions.
The other broad X-ray lines are weaker (
,
respectively, well explained the HST-STIS data.
In the present paper for the first time the LOC model has been extended to the X-ray band.
The intrinsic luminosity of the X-ray lines have been calculated from this model
and applied in fitting the LETGS data. An independent fit of the X-ray spectrum using Gaussian profiles leads to flux estimates which are consistent, within the errors, with the ones predicted by the LOC model (Table 5), strengthening the validity of this approach.
In the case of Mrk 279, the O VII triplet complex is the most prominent feature (30% above the continuum, Fig. 8), as this oxygen ion is steadily produced in a wide range of physical conditions.
The other broad X-ray lines are weaker ( 10% above the continuum), but
help in modifying the continuum and better constrain the warm absorber parameters. For these lines we cannot draw firm conclusions, as their significance in the data is relatively low.
10% above the continuum), but
help in modifying the continuum and better constrain the warm absorber parameters. For these lines we cannot draw firm conclusions, as their significance in the data is relatively low.
It is feasible that there may be a part of the BLR with a higher ionization and that produces lines only visible in the X-ray band. This may give rise to some additional flux in the lines,
possibly variable in time and thus appearing only in some time
segments.
In principle, measuring the amount of the excess would allow us to quantify
the physical parameters of a highly ionized skin of the BLR.
However this is extremely challenging, firstly because of the relatively low statistical
significance of any additional excess,
secondly because we modeled the BLR using an average source flux that
possibly introduces more scatter in the predicted values of the X-ray lines luminosity.
Being able to study a part of the BLR which only emits in the X-ray band would be indeed
very important in understanding the stratification of the BLR and its
velocity field (e.g., Baldwin 1997; Gonçalves et al. 2001).
Following further the BLR interpretation,
we find that the luminosity-weighted radii (Sect. 2.3.2) map a wide region that extends between 10 and 100 ld from the central source, which produces lines visible
both in UV and X-ray band. The size is smaller ( 67 ld) when only the UV lines are considered.
This estimate is larger than
the BLR size obtained by reverberation mapping studies (<30 ld, Stirpe et al. 1994, and references therein). However, we note that
the ionization conditions within such an extended region are sensitive to the long-term flux history of the source. In particular there is evidence that more than forty days before the present multiwavelength campaign, the V-band flux of Mrk 279 was up to a factor of 8 lower (depending on the host galaxy subtraction, Gaskell et al. 2006, in prep.).
From that epoch, the V band flux, which should be on long time scales correlated also with the
high energy flux, gradually rose to reach the higher state caught by LETGS-FUSE-HST. As the size of the BLR is proportional to the square root of the ionizing luminosity (Peterson 1993), taking the long term flux change into account
would reduce the size estimated here by a factor as large as two or three.
67 ld) when only the UV lines are considered.
This estimate is larger than
the BLR size obtained by reverberation mapping studies (<30 ld, Stirpe et al. 1994, and references therein). However, we note that
the ionization conditions within such an extended region are sensitive to the long-term flux history of the source. In particular there is evidence that more than forty days before the present multiwavelength campaign, the V-band flux of Mrk 279 was up to a factor of 8 lower (depending on the host galaxy subtraction, Gaskell et al. 2006, in prep.).
From that epoch, the V band flux, which should be on long time scales correlated also with the
high energy flux, gradually rose to reach the higher state caught by LETGS-FUSE-HST. As the size of the BLR is proportional to the square root of the ionizing luminosity (Peterson 1993), taking the long term flux change into account
would reduce the size estimated here by a factor as large as two or three.
The luminosity-weighted radius of the higher ionization X-ray ions is located at radii up to ten times smaller than for the UV ions. If the motion of the BLR clouds is purely keplerian, this would imply a velocity broadening up to a factor of three larger. The only broad excess for which we measured the FWHM is the O VII triplet blend
(FWHM = 1.9
+0.7-0.4  104 km s-1, Table 3) which is consistent, within the errors, with such a large broadening. Unfortunately in this data set this possibility cannot be tested on non-blended, higher ionization lines (like for instance C VI).
104 km s-1, Table 3) which is consistent, within the errors, with such a large broadening. Unfortunately in this data set this possibility cannot be tested on non-blended, higher ionization lines (like for instance C VI).
The extrapolation of the BLR model down to small radii shows that the emission of the X-ray BLR has a non-negligible tail that goes down to  0.8 ld from the source, corresponding to
0.8 ld from the source, corresponding to 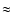 300 Schwarzschild radii, given the BH mass of Mrk 279
(
300 Schwarzschild radii, given the BH mass of Mrk 279
( 3
3 
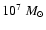 ,
Wandel et al. 1999).
At this specific distance we would
not expect a significant relativistic broadening of the line profile,
but X-ray emission from highly ionized gas that is not efficiently producing UV lines
would be possible (Fig. 7).
,
Wandel et al. 1999).
At this specific distance we would
not expect a significant relativistic broadening of the line profile,
but X-ray emission from highly ionized gas that is not efficiently producing UV lines
would be possible (Fig. 7).
The detection of relativistically broadened line profiles at soft X-ray energy has been claimed for a number of sources
(e.g. Kaastra et al. 2002; Ogle et al. 2004; Branduardi-Raymont et al. 2001). Our LETGS data do not show
significant evidence of an asymmetric profile, especially at the
wavelength of O VIII, N VII and C VI. Moreover, these profiles would be blurred by the wide,
non-relativistic lines produced in the BLR.
Among the H-like lines that we are able to detect in the LETGS band, O VIII lies
in a privileged region, where the effective area is higher and the spectrum is not contaminated by instrumental
features. However, to model a skewed, relativistically broadened, profile for O VIII
is difficult because of the absorption features of the iron UTA at observed wavelength of  17 Å for the warm absorbers intrinsic to Mrk 279, and at
17 Å for the warm absorbers intrinsic to Mrk 279, and at  19 Å for the ionized absorbers in our Galaxy. The structure
of the iron UTA may not be yet completely accounted for in the models and may
cause additional uncertainties.
19 Å for the ionized absorbers in our Galaxy. The structure
of the iron UTA may not be yet completely accounted for in the models and may
cause additional uncertainties.
3.2 The structure of the warm absorber
The spectrum of Mrk 279 is absorbed by at least
two absorption systems (Sect. 2.4.1). They show a significant blueshift with respect to the rest frame of the source and a relatively
high value of the ionization parameter and therefore can be
unmistakably associated with the warm absorber seen in other
Seyfert 1 galaxies (Table 7).
Low ionization metals (e.g. C II, C III, N II) are marginally detected in the UV band, but for completeness included in our analysis (Sect. 2.4.2).
As discussed in Scott et al. (2004),
the association of these ions with the nuclear activity is unlikely.
These lines most probably arise in the Mrk 279 host galaxy because of their low ionization and the lack of any blueshift. The two high ionization components detected in the X-rays may be the only discrete constituents of the warm absorber
(e.g. Krongold et al. 2005) or be only a part of a multi-ionization,
continuous outflow (Steenbrugge et al. 2005). A discrete-components scenario would be supported by finding that the observed components values have the same 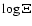 in the curve of thermal stability, which is shown in Fig. 12.
Here we plot the log-log distribution of the pressure ionization parameter (
in the curve of thermal stability, which is shown in Fig. 12.
Here we plot the log-log distribution of the pressure ionization parameter (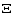 ) vs.
the electronic temperature (T) for Mrk 279.
The value of
) vs.
the electronic temperature (T) for Mrk 279.
The value of  is defined as:
is defined as:
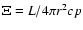 ,
that is the ratio of photon pressure
to gas pressure. This may also be expressed as a function
of
,
that is the ratio of photon pressure
to gas pressure. This may also be expressed as a function
of 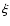 and the electronic temperature T:
and the electronic temperature T:
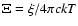 .
The curve
was obtained using Cloudy, calculating
a grid of values of
.
The curve
was obtained using Cloudy, calculating
a grid of values of 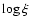 and the relative electronic temperature of a thin
layer of absorbing gas illuminated by an ionizing continuum.
The shape of the curve is sensitive to the SED of the source (Fig. 5).
The filled squares in Fig. 12 correspond to the log
and the relative electronic temperature of a thin
layer of absorbing gas illuminated by an ionizing continuum.
The shape of the curve is sensitive to the SED of the source (Fig. 5).
The filled squares in Fig. 12 correspond to the log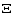 values for the
warm absorbers detected in Mrk 279. Given their position on
the S curve, these component cannot share the same pressure ionization parameter.
This would have ensured a long-lived structure for a discrete-component warm absorber
unless other mechanisms, like magnetic confinement, are playing a role.
If this were case, pressure equilibrium would not be mandatory.
Also a high amplitude variability of the warm absorber in response to a continuum flux variation
could be in favor of a discrete-component model (e.g., Krongold et al. 2005).
Observationally, a small variation of the ionization parameter would cause a detectable shift in the iron M shell UTA complex. In the case of Mrk 279 this possibility cannot be tested, as the variation of the source flux is too small and the warm absorber too shallow to be able to detect a shift in the iron region (Fig. 11).
values for the
warm absorbers detected in Mrk 279. Given their position on
the S curve, these component cannot share the same pressure ionization parameter.
This would have ensured a long-lived structure for a discrete-component warm absorber
unless other mechanisms, like magnetic confinement, are playing a role.
If this were case, pressure equilibrium would not be mandatory.
Also a high amplitude variability of the warm absorber in response to a continuum flux variation
could be in favor of a discrete-component model (e.g., Krongold et al. 2005).
Observationally, a small variation of the ionization parameter would cause a detectable shift in the iron M shell UTA complex. In the case of Mrk 279 this possibility cannot be tested, as the variation of the source flux is too small and the warm absorber too shallow to be able to detect a shift in the iron region (Fig. 11).
On the other hand, also a scenario that considers a continuous distribution over 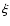 (Sect. 2.4.2) cannot be straightforwardly proven. In Fig. 10 we showed the
results of the WARM model, which mimics a continuous
(Sect. 2.4.2) cannot be straightforwardly proven. In Fig. 10 we showed the
results of the WARM model, which mimics a continuous  distribution (Sect. 2.4.1). We see that the hydrogen column density distribution derived from single ions appears to give a different picture of a power law-like distribution. Indeed, if we take into account
only the higher ionization ions (
distribution (Sect. 2.4.1). We see that the hydrogen column density distribution derived from single ions appears to give a different picture of a power law-like distribution. Indeed, if we take into account
only the higher ionization ions (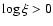 ), removing all the upper limits from the fit,
the data can be modeled by a power-law with index
), removing all the upper limits from the fit,
the data can be modeled by a power-law with index
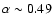 ,
where
,
where
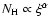 .
This is very similar to what was found for NGC 5548, where Steenbrugge et al. (2005) estimated
.
This is very similar to what was found for NGC 5548, where Steenbrugge et al. (2005) estimated
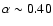 for this
range of ionization parameters (
for this
range of ionization parameters (
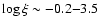 ), despite the fact that the column densities
for the NGC 5548 warm absorber are a factor of
), despite the fact that the column densities
for the NGC 5548 warm absorber are a factor of  10 larger. A similar trend is found for NGC 4051 (
10 larger. A similar trend is found for NGC 4051 (
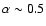 Ogle et al. 2004), with an apparent column density peak at
Ogle et al. 2004), with an apparent column density peak at  at
at
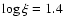 .
We note however
that this result is not completely comparable to Mrk 279 and NGC 5548 as Ogle et al. (2004) compute
.
We note however
that this result is not completely comparable to Mrk 279 and NGC 5548 as Ogle et al. (2004) compute 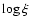 at the peak of the
ionization for each ion. Not taking into account that ions are formed in a range of
at the peak of the
ionization for each ion. Not taking into account that ions are formed in a range of 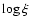 can lead to quite a different distribution.
Finally, in the case of Mrk 279, the extrapolation of the
can lead to quite a different distribution.
Finally, in the case of Mrk 279, the extrapolation of the 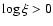 power-law to lower
ionization ions, excludes the lowest ionization ions
from the continuous outflow structure. This is consistent with the idea that those ions are produced in a distant region.
power-law to lower
ionization ions, excludes the lowest ionization ions
from the continuous outflow structure. This is consistent with the idea that those ions are produced in a distant region.
An additional constraint is provided by the WARM model fit (Fig. 10). The
hydrogen column densities from the WARM model have more
robust values, as the SPEX fit synthetically takes
into account all transitions for a given value of the ionization parameter.
The WARM distribution does not suggest a straight power-law fit. However,
the power-law fit to the single ions distribution (
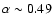 )
nicely adapts to the
)
nicely adapts to the
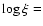 0.4 and 3.2 points at which the
0.4 and 3.2 points at which the 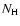 was evaluated in the WARM model (Sect. 2.4.2). If we take this as the signature of a continuous distribution, both the lower ionization end of this distribution (
was evaluated in the WARM model (Sect. 2.4.2). If we take this as the signature of a continuous distribution, both the lower ionization end of this distribution (
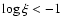 )
and the point evaluated at
)
and the point evaluated at
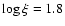 deviate from the power-law distribution (with 4
deviate from the power-law distribution (with 4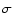 significance). In the framework of the structure of
the ionized outflow, we are most interested in the apparent dip in this continuous distribution at
significance). In the framework of the structure of
the ionized outflow, we are most interested in the apparent dip in this continuous distribution at
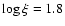 .
We further verified that fitting the data with an additional XABS components
with
.
We further verified that fitting the data with an additional XABS components
with 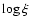 constraint to lie between 0.47 and 2.49 (values from the XABS best fit, see Table 7) does not significantly change the goodness of fit in terms of
constraint to lie between 0.47 and 2.49 (values from the XABS best fit, see Table 7) does not significantly change the goodness of fit in terms of 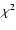 ,
but indeed provides a lower, but significant value for
,
but indeed provides a lower, but significant value for 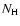 .
Namely we find
.
Namely we find
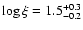 and
and
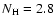
 0.4
0.4  1019 cm-2.
1019 cm-2.
The main conclusion that may be deduced from this exercise is that
the continuous distribution we tried to define is
in fact non-monotonous. We do not find a sharp bimodal distribution with
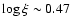 and
and
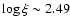 being the only components of the warm absorber (as suggested by the XABS model, Sect. 2.4.1). Intermediate values do exist, but with a column density that is low enough not to be easily detected. This is in contrast with what is predicted by a power-law distribution fit. The statistics does not allow us to detail further these findings. For instance the kinematic
characteristics of this outflow are not precisely determined: the blueshifts of the
two ionization components we find are only marginally different (Table 7).
The kinematic warm absorber structure for Mrk 279 is indeed quite complex. Velocity-resolved spectroscopy of the UV absorption troughs of this source
show that not only partial covering plays a role (Arav et al. 2005, Sect. 2.4),
but that abundances of C, N, and O can differ from solar values (Arav et al. 2006, in prep.).
The N/O and C/O ratio delivered by the X-ray data are affected by large error bars, therefore a direct comparison with the UV results is not conclusive.
being the only components of the warm absorber (as suggested by the XABS model, Sect. 2.4.1). Intermediate values do exist, but with a column density that is low enough not to be easily detected. This is in contrast with what is predicted by a power-law distribution fit. The statistics does not allow us to detail further these findings. For instance the kinematic
characteristics of this outflow are not precisely determined: the blueshifts of the
two ionization components we find are only marginally different (Table 7).
The kinematic warm absorber structure for Mrk 279 is indeed quite complex. Velocity-resolved spectroscopy of the UV absorption troughs of this source
show that not only partial covering plays a role (Arav et al. 2005, Sect. 2.4),
but that abundances of C, N, and O can differ from solar values (Arav et al. 2006, in prep.).
The N/O and C/O ratio delivered by the X-ray data are affected by large error bars, therefore a direct comparison with the UV results is not conclusive.
![\begin{figure}
\par\includegraphics[angle=90,width=7.55cm,clip]{5390f12.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg114.gif) |
Figure 12:
The pressure ionization parameter vs. the electron temperature.
The two components of the warm absorber for Mrk 279 are indicated as squares. |
| Open with DEXTER |
3.3 Density diagnostics
Kaastra et al. (2004) discussed in detail the possibility of the detection of O V absorption lines
from a meta-stable level in Mrk 279. The main
absorption feature (O V )
lies at
)
lies at  22.5 Å in the rest frame of the source (23.18 Å in the observed spectrum, Fig. 8).
This kind of transition of Be-like ions can take place only at particularly high densities.
Therefore, a precise determination of the
physical parameters of such absorption features can serve as an important test for the distance determination of the
warm absorber. Here we try to verify a connection between the parameters deduced from the O V
22.5 Å in the rest frame of the source (23.18 Å in the observed spectrum, Fig. 8).
This kind of transition of Be-like ions can take place only at particularly high densities.
Therefore, a precise determination of the
physical parameters of such absorption features can serve as an important test for the distance determination of the
warm absorber. Here we try to verify a connection between the parameters deduced from the O V line and any of the absorber components in Mrk 279.
line and any of the absorber components in Mrk 279.
The temperatures Kaastra et al. (2004) infer for the gas producing the O V line range between 2-4 eV, corresponding, for the SED of Mrk 279, to
line range between 2-4 eV, corresponding, for the SED of Mrk 279, to
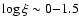 .
This estimate of the ionization parameter, together with the hydrogen column density (
.
This estimate of the ionization parameter, together with the hydrogen column density ( )
that we can derive from the equivalent width of the O V ground state absorption lines
(
)
that we can derive from the equivalent width of the O V ground state absorption lines
(
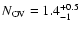

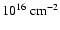 ,
Kaastra et al. 2004),
give already the basic physical quantities of a warm absorber.
In order to ensure that the density value of a gas producing O V
,
Kaastra et al. 2004),
give already the basic physical quantities of a warm absorber.
In order to ensure that the density value of a gas producing O V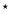 is not unrealistic,
we find that a gas temperature
is not unrealistic,
we find that a gas temperature 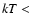 3 eV is needed. For this temperature, the O V/O ratio is
0.02, implying an equivalent hydrogen column density
3 eV is needed. For this temperature, the O V/O ratio is
0.02, implying an equivalent hydrogen column density
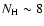

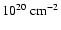 ,
which is still roughly compatible with the column density we find for a continuous-distribution warm absorber model (Fig. 10). The associated
ionization parameter is
,
which is still roughly compatible with the column density we find for a continuous-distribution warm absorber model (Fig. 10). The associated
ionization parameter is
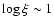 .
The comparison between the temperature of this gas (
.
The comparison between the temperature of this gas ( 3 eV)
and the measured relative population of the
O V meta-stable
levels (0.125-2, Kaastra et al. 2004), provides an estimate for the density (see Fig. 5, Kaastra et al. 2004). We obtain
3 eV)
and the measured relative population of the
O V meta-stable
levels (0.125-2, Kaastra et al. 2004), provides an estimate for the density (see Fig. 5, Kaastra et al. 2004). We obtain
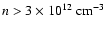 and, as a consequence,
a distance from the ionizing source r0<3
and, as a consequence,
a distance from the ionizing source r0<3 
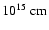 ,
comparable with
the location of a more ionized part of the BLR. This estimate relies uniquely on the tentative
detection of O V
,
comparable with
the location of a more ionized part of the BLR. This estimate relies uniquely on the tentative
detection of O V .
Further observational evidence is needed to support the identification of this line.
.
Further observational evidence is needed to support the identification of this line.
Whether the gas which causes the blueshifted absorption lines is also observed in emission, is a controversial issue. The main reason is that the absorption/emission connection is dependent on unknown parameters, such as the density, the distance, and the overall geometry of the system. The emission counterpart of the X-ray warm absorber may be the
narrow lines produced in the NLR in a form of a bipolar cone with a wide opening
angle (e.g., NGC 3783, Behar et al. 2003).
The observational facts that would support this scenario are: a lack of response of the warm absorber to the central source variability, and the similarity of the absorption and emission lines parameters, such as velocity width, column
density, ionization stage. In the case of Mrk 279, any suggestion of a short-term variation of the absorber parameters as a function of the ionizing flux is unfortunately too weak (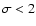 )
to be investigated quantitatively. Narrow emission lines are not affecting the spectrum significantly.
From the study of the possible O V
)
to be investigated quantitatively. Narrow emission lines are not affecting the spectrum significantly.
From the study of the possible O V feature (Sect. 3.3, Kaastra et al. 2004), we inferred an upper limit for the distance of the warm absorber
(r0<3
feature (Sect. 3.3, Kaastra et al. 2004), we inferred an upper limit for the distance of the warm absorber
(r0<3 
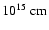 ), at least for an intermediate ionization component. Possibly, the emission counterpart of the X-ray warm absorber would be located at the same distance as the higher ionization BLR lines (i.e. the X-ray lines, Sect. 3.1). Can the BLR cloud themselves produce the warm absorber?
The particular blueshift seen in the absorption feature can be line-of-sight dependent (Elvis 2000), while the broad lines, that can be emitted
over a maximal opening angle of
), at least for an intermediate ionization component. Possibly, the emission counterpart of the X-ray warm absorber would be located at the same distance as the higher ionization BLR lines (i.e. the X-ray lines, Sect. 3.1). Can the BLR cloud themselves produce the warm absorber?
The particular blueshift seen in the absorption feature can be line-of-sight dependent (Elvis 2000), while the broad lines, that can be emitted
over a maximal opening angle of  ,
have a variety of velocity, including extreme blueshifted
components of
,
have a variety of velocity, including extreme blueshifted
components of  -2000 km s-1 (G05).
Moreover the absorbing and emitting gas can have the same structure, as
the BLR "clouds'' can be organized in the form of a wind arising above the accretion disk
(e.g., Bottorff et al. 1997) just like the warm absorber (e.g., Murray et al. 1995; Elvis 2000).
However, one insurmountable discrepancy between the two media is the
measured column density. Indeed, the UV (and X-ray) broad emission lines can be produced for column densities down to
-2000 km s-1 (G05).
Moreover the absorbing and emitting gas can have the same structure, as
the BLR "clouds'' can be organized in the form of a wind arising above the accretion disk
(e.g., Bottorff et al. 1997) just like the warm absorber (e.g., Murray et al. 1995; Elvis 2000).
However, one insurmountable discrepancy between the two media is the
measured column density. Indeed, the UV (and X-ray) broad emission lines can be produced for column densities down to
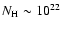 cm-2 (Korista et al. 1997), which is almost two orders of magnitude higher than for the warm absorber of Mrk 279. Furthermore, the evidence of narrow absorption lines (
cm-2 (Korista et al. 1997), which is almost two orders of magnitude higher than for the warm absorber of Mrk 279. Furthermore, the evidence of narrow absorption lines (
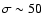 km s-1) point to a stable flow. This would be difficult to maintain in a turbulent medium like the one producing the BLR. The possibility that the broad emission lines are produced by the same gas component as the warm absorber is thus ruled out.
However, in a picture of a windy gas above the accretion disk, our line sight may intercept first a portion of the absorber very close to the central source. Its
transverse thickness must be very small (
km s-1) point to a stable flow. This would be difficult to maintain in a turbulent medium like the one producing the BLR. The possibility that the broad emission lines are produced by the same gas component as the warm absorber is thus ruled out.
However, in a picture of a windy gas above the accretion disk, our line sight may intercept first a portion of the absorber very close to the central source. Its
transverse thickness must be very small (
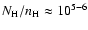 cm).
This sheet of gas may be the outer, low
column density part of the gas structure that produces the broad emission lines.
If the limit on the distance of the absorber is
confirmed (Sect. 3.3), this could be a way to make the
two media coexist at approximately the same distance from the central source.
A correspondence between the distance of the warm absorber and the BLR
was also found in other X-ray sources (e.g. NGC 3516, Netzer et al. 2002).
A physical connection between the BLR and the warm absorber
was proposed for NGC 3783, observed by Chandra-HETGS (Krongold et al. 2003).
cm).
This sheet of gas may be the outer, low
column density part of the gas structure that produces the broad emission lines.
If the limit on the distance of the absorber is
confirmed (Sect. 3.3), this could be a way to make the
two media coexist at approximately the same distance from the central source.
A correspondence between the distance of the warm absorber and the BLR
was also found in other X-ray sources (e.g. NGC 3516, Netzer et al. 2002).
A physical connection between the BLR and the warm absorber
was proposed for NGC 3783, observed by Chandra-HETGS (Krongold et al. 2003).
Finally, the gas temperature inferred from the observed RRCs translates in an ionization parameter
between -1.3 and 0.8, which is certainly consistent with the 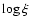 of one of the main absorbing components of the warm absorber in Mrk 279. Therefore, a physical link between the warm absorber and the gas producing the RRCs cannot be ruled out.
of one of the main absorbing components of the warm absorber in Mrk 279. Therefore, a physical link between the warm absorber and the gas producing the RRCs cannot be ruled out.
We have presented the analysis and modeling of the data of Mrk 279, observed for 360 ks by Chandra-LETGS.
For the first time, we have extended to the X-ray band the
"locally optimally cloud'' model, first proposed by Baldwin et al. (1995)
to describe the BLR emission
lines seen in the UV. This has been achieved by fitting first the luminosity of the UV lines, measured simultaneously by FUSE and HST-STIS (G05) and deriving, from the best fit, the X-ray lines luminosity.
In agreement with the LOC model predictions, the distribution of the radial distance of the
BLR "clouds'' follow a power-law with index
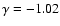
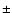 0.14, assuming a density distribution with index
0.14, assuming a density distribution with index  .
We find that the inferred X-ray lines luminosity well describe the X-ray data. If, independently, we fit the X-ray broad emission features with Gaussian profiles, the results are, within the errors,
consistent with the UV modeling. The most evident X-ray broad emission feature, the O VII triplet, which exceeds the continuum by about 30%, is well explained by the LOC model.
The profiles of other important X-ray lines of the H-like and He-like C, N, O ions are less clear in the spectrum and cannot be studied in more detail. It would be important to quantitatively measure the contribution of such ions, as they
may be more sensitive to the physical conditions than O VII, which is steadily produced for a wide range of gas densities and distances from the ionizing source.
There are not significant spectral residuals in excesses after the inclusion of the X-ray broad lines. This suggests first that the gas of the BLR emitting the bulk of the UV emission
is also sufficient to explain the X-ray emission spectrum. Second, that the contribution of
lines arising instead from the innermost region of the accretion disks, and thus have a relativistically broadened profile, is negligible in the case of Mrk 279.
.
We find that the inferred X-ray lines luminosity well describe the X-ray data. If, independently, we fit the X-ray broad emission features with Gaussian profiles, the results are, within the errors,
consistent with the UV modeling. The most evident X-ray broad emission feature, the O VII triplet, which exceeds the continuum by about 30%, is well explained by the LOC model.
The profiles of other important X-ray lines of the H-like and He-like C, N, O ions are less clear in the spectrum and cannot be studied in more detail. It would be important to quantitatively measure the contribution of such ions, as they
may be more sensitive to the physical conditions than O VII, which is steadily produced for a wide range of gas densities and distances from the ionizing source.
There are not significant spectral residuals in excesses after the inclusion of the X-ray broad lines. This suggests first that the gas of the BLR emitting the bulk of the UV emission
is also sufficient to explain the X-ray emission spectrum. Second, that the contribution of
lines arising instead from the innermost region of the accretion disks, and thus have a relativistically broadened profile, is negligible in the case of Mrk 279.
In the radial distribution of the line luminosity, the luminosity-weighted radius for each ion considered defines a wide region of roughly 90 ld for the UV-X-ray BLR (67 ld if only the UV ions are considered). This is larger than predicted by reverberation mapping
studies (Stirpe et al. 1994). However, our estimate could be lowered by a factor up to three noting that the BLR size is sensitive to the long term variations of the continuum flux and that at the epoch
of the present campaign the optical flux was at the higher end of a gradual rise that lasted for nearly two months.
A proper modeling of the broad emission lines in the LETGS spectrum helps in the analysis of the absorbed spectrum. We find the signature of at least two gas components which can be unmistakably associated with a warm absorber. However, there is some evidence that this is only a partial description of the absorption. First, absorption lines do not show any significant variation following the modest changes of the central source flux and, second, the two absorption components cannot be in pressure equilibrium.
This evidence, although not decisive, does not strongly support the hypothesis of a compact absorber (Krongold et al. 2005). We investigated the possibility that the absorbing gas is instead distributed over a wide range of ionization parameters (Steenbrugge et al. 2005). We find that neither of the two models perfectly matches our data. A smooth distribution of the column densities is acceptable, but  does not monotonically increase as a function of
does not monotonically increase as a function of 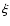 (following for example a power law),
but it is rather significantly bent.
(following for example a power law),
but it is rather significantly bent.
From the exploratory study of the possible O V absorption line to meta-stable level in the Mrk 279 X-ray spectrum, Kaastra et al. (2004)
infer a density for the absorbing gas of the
order of 1014 cm-3. In the context of our analysis, we
find that an intermediate ionization gas component (
 ), with a column density roughly consistent with our
continuous-distribution model, could produce the O V
), with a column density roughly consistent with our
continuous-distribution model, could produce the O V line. This would imply
an upper limit to the distance from the central source of 3
line. This would imply
an upper limit to the distance from the central source of 3  1015 cm for the gas.
Although a distance close to the BL emitting region for the warm
absorber is not new in the literature (e.g., Netzer et al. 2002; Nicastro et al. 1999), in the case of Mrk 279, a global model explaining the coexistence of the complex warm absorber structure and the BLR cannot be easily depicted.
1015 cm for the gas.
Although a distance close to the BL emitting region for the warm
absorber is not new in the literature (e.g., Netzer et al. 2002; Nicastro et al. 1999), in the case of Mrk 279, a global model explaining the coexistence of the complex warm absorber structure and the BLR cannot be easily depicted.
Acknowledgements
The Space Research Organization of the Netherlands is supported
financially by NWO, the Netherlands Organization for Scientific
Research.
- Arav, N., Kaastra, J.,
Kriss, G. A., et al. 2005, ApJ, 620, 665 [NASA ADS] [CrossRef] (In the text)
- Bachev, R., &
Strigachev, A. 2004, Astron. Nachr., 325, 317 [NASA ADS] [CrossRef] (In the text)
- Baldwin,
J. A. 1997, Emission Lines in Active Galaxies: New Methods and
Techniques, IAU Colloq., 159, ASP Conf. Ser., 113, 80
(In the text)
- Baldwin, J.,
Ferland, G., Korista, K., & Verner, D. 1995, ApJ, 455,
L119 [NASA ADS] [CrossRef] (In the text)
- Behar, E., Sako, M.,
& Kahn, S. M. 2001, ApJ, 563, 497 [NASA ADS] [CrossRef]
- Behar, E., Rasmussen,
A. P., Blustin, A. J., et al. 2003, ApJ, 598, 232 [NASA ADS] [CrossRef] (In the text)
- Blustin, A. J.,
Page, M. J., Fuerst, S. V., Branduardi-Raymont, G., &
Ashton, C. E. 2005, A&A, 431, 111 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bottorff, M.,
Korista, K. T., Shlosman, I., & Blandford, R. D.
1997, ApJ, 479, 200 [NASA ADS] [CrossRef] (In the text)
- Bottorff,
M. C., Baldwin, J. A., Ferland, G. J., Ferguson,
J. W., & Korista, K. T. 2002, ApJ, 581, 932 [NASA ADS] [CrossRef] (In the text)
-
Branduardi-Raymont, G., Sako, M., Kahn, S. M., et al.
2001, A&A, 365, L140 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences]
- Brinkman, A. C.,
Gunsing, C. J. T., Kaastra, J. S., et al. 2000, ApJ, 530,
L111 [NASA ADS] [CrossRef] (In the text)
- Collins,
J. A., Shull, J. M., & Giroux, M. L. 2005, ApJ,
623, 196 [NASA ADS] [CrossRef] (In the text)
- Crenshaw,
D. M., Kraemer, S. B., Boggess, A., et al. 1999,
ApJ, 516, 750 [NASA ADS] [CrossRef] (In the text)
- Elvis, M. 2000, ApJ, 545,
63 [NASA ADS] [CrossRef] (In the text)
- Elvis, M., Wilkes,
B. J., & Lockman, F. J. 1989, AJ, 97, 777 [NASA ADS] [CrossRef] (In the text)
- Ferland, G. J., Korista,
K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [NASA ADS] [CrossRef] (In the text)
- Fox, A. J., Savage,
B. D., Wakker, B. P., et al. 2004, ApJ, 602,
738 [NASA ADS] [CrossRef] (In the text)
- Gabel, J. R.,
Kraemer, S. B., Crenshaw, D. M., et al. 2005a, ApJ, 631,
741 [NASA ADS] [CrossRef] (In the text)
- Gabel, J. R.,
Arav, N., Kaastra, J. S., et al. 2005b, ApJ, 623, 85 [NASA ADS] [CrossRef], G05
(In the text)
- Gonçalves,
D. R., Friaça, A. C. S., & Jatenco-Pereira,
V. 2001, MNRAS, 328, 409 [NASA ADS] [CrossRef]
- Grevesse, N.,
& Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] (In the text)
- Kaspi, S., Brandt, W.
N., Netzer, H., et al. 2001, ApJ, 554, 216 [NASA ADS] [CrossRef] (In the text)
- Kaastra,
J. S., & Barr, P. 1989, A&A, 226, 59 [NASA ADS] (In the text)
- Kaastra,
J. S., Steenbrugge, K. C., Raassen, A. J. J.,
et al. 2002, A&A, 386, 427 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences]
- Kaastra, J. S.,
Raassen, A. J. J., Mewe, R., et al. 2004, A&A, 428,
57 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kinkhabwala, A., Sako,
M., Behar, E., et al. 2002, ApJ, 575, 732 [NASA ADS] [CrossRef] (In the text)
- Korista,
K. T., & Goad, M. R. 2000, ApJ, 536, 284 [NASA ADS] [CrossRef] (In the text)
- Korista, K., Baldwin, J.,
Ferland, G., & Verner, D. 1997, ApJS, 108, 401 [NASA ADS] [CrossRef] (In the text)
- Kriss, G. A.
2002, Mass Outflow in Active Galactic Nuclei: New Perspectives, ASP
Conf. Ser., 255, 69
- Krolik, J. H.,
& Kriss, G. A. 1995, ApJ, 447, 512 [NASA ADS] [CrossRef]
- Krolik, J. H.,
& Kriss, G. A. 2001, ApJ, 561, 684 [NASA ADS] [CrossRef]
- Krongold, Y., Nicastro, F.,
Brickhouse, N. S., et al. 2003, ApJ, 597, 832 [NASA ADS] [CrossRef]
- Krongold, Y., Nicastro, F.,
Brickhouse, N. S., Elvis, M., & Mathur, S. 2005, ApJ, 622,
842 [NASA ADS] [CrossRef] (In the text)
- Lee, J. C., Ogle,
P. M., Canizares, C. R., et al. 2001, ApJ, 554,
L13 [NASA ADS] [CrossRef] (In the text)
- Laor, A. 1991, ApJ, 376,
90 [NASA ADS] [CrossRef]
- Murray, N., Chiang, J.,
Grossman, S. A., & Voit, G. M. 1995, ApJ, 451,
498 [NASA ADS] [CrossRef]
- Netzer, H.,
Chelouche, D., George, I. M., et al. 2002, ApJ, 571,
256 [NASA ADS] [CrossRef] (In the text)
- Netzer, H., Kaspi,
S., Behar, E., et al. 2003, ApJ, 599, 933 [NASA ADS] [CrossRef]
- Nicastro, F.,
Fiore, F., & Matt, G. 1999, ApJ, 517, 108 [NASA ADS] [CrossRef]
- Nicastro, F.,
Zezas, A., Drake, J., et al. 2002, ApJ, 573, 157 [NASA ADS] [CrossRef] (In the text)
- Ogle, P. M.,
Mason, K. O., Page, M. J., et al. 2004, ApJ, 606,
151 [NASA ADS] [CrossRef]
- Peterson,
B. M. 1993, PASP, 105, 247 [NASA ADS] [CrossRef] (In the text)
- Porquet, D., &
Dubau, J. 2000, A&AS, 143, 495 [EDP Sciences] [NASA ADS] (In the text)
- Pounds, K. A.,
Reeves, J. N., King, A. R., & Page, K. L. 2004,
MNRAS, 350, 10 [NASA ADS] [CrossRef] (In the text)
- Proga, D. 2003, ApJ, 585,
406 [NASA ADS] [CrossRef] (In the text)
- Sako, M., Kahn,
S. M., Paerels, F., & Liedahl, D. A. 2000, ApJ, 543,
L115 [NASA ADS] [CrossRef] (In the text)
- Sako, M., Kahn, S. M.,
Branduardi-Raymont, G., et al. 2003, ApJ, 596, 114 [NASA ADS] [CrossRef]
- Savage, B. D.,
Sembach, K. R., Wakker, B. P., et al. 2003, ApJS, 146,
125 [NASA ADS] [CrossRef] (In the text)
- Scott, J. E.,
Kriss, G. A., Lee, J. C., et al. 2004, ApJS, 152, 1 [NASA ADS] [CrossRef] (In the text)
- Sembach, K. R.,
Wakker, B. P., Savage, B. D., et al. 2003, ApJS, 146,
165 [NASA ADS] [CrossRef]
- Steenbrugge,
K. C., Kaastra, J. S., de Vries, C. P., &
Edelson, R. 2003, A&A, 402, 477 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences]
- Steenbrugge,
K. C., Kaastra, J. S., Crenshaw, D. M., et al. 2005,
A&A, 434, 569 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Stirpe, G. M.,
Alloin, D., Axon, D. J., et al. 1994, A&A, 285,
857 [NASA ADS] (In the text)
- Turner, T. J.,
Kraemer, S. B., George, I. M., Reeves, J. N., &
Bottorff, M. C. 2005, ApJ, 618, 155 [NASA ADS] [CrossRef]
- Wandel, A., Peterson,
B. M., & Malkan, M. A. 1999, ApJ, 526, 579 [NASA ADS] [CrossRef] (In the text)
- Wang, Q. D., Yao, Y.,
Tripp, T. M., et al. 2005
[arXiv:astro-ph/0508661]
- Weaver, K. A.,
Arnaud, K. A., & Muschotzky, R. F. 1995, ApJ, 447,
121 [NASA ADS] [CrossRef]
- Weaver, K. A.,
Gelbord, J., & Yaqoob, T. 2001, ApJ, 550, 261 [NASA ADS] [CrossRef]
- Williams, R. J.,
Mathur, S., & Nicastro, F. 2006, ApJ, 645, 179 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[angle=90,width=7.9cm,clip]{5390f1.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg21.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=7.75cm,clip]{5390f2.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg23.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=8.1cm,clip]{5390f3.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg32.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=7.65cm,clip]{5390f4.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg33.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=7.4cm,clip]{5390f5.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg42.gif)
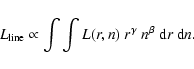
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{5390f6.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg49.gif)
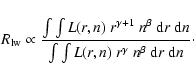
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{5390f7.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg57.gif)
![\begin{figure}
\par\includegraphics[height=13.65cm,width=4.7cm,angle=90,clip]{53...
...
\includegraphics[height=13.7cm,width=5cm,angle=90,clip]{5390f8d.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg64.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=7.5cm,clip]{5390f9.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg72.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=7.45cm,clip]{5390f10.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg89.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=7.35cm,clip]{5390f11.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg90.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=7.55cm,clip]{5390f12.ps}\end{figure}](/articles/aa/full/2007/01/aa5390-06/Timg114.gif)