A&A 461, 373-379 (2007)
DOI: 10.1051/0004-6361:20042505
P. Magain1
- F. Courbin2
- M. Gillon3,1 - S. Sohy1
- G. Letawe1 - V. Chantry1,![]() - Y. Letawe1
- Y. Letawe1
1 - Institut d'Astrophysique et de Géophysique, Université de
Liège, allée du 6 Août 17, 4000 Liège, Belgium
2 -
École Polytechnique Fédérale de Lausanne (EPFL),
Laboratoire d'Astrophysique,
Observatoire,
1290 Sauverny,
Switzerland
3 -
Observatoire de Genève,
51 Chemin des Maillettes,
1290 Sauverny,
Switzerland
Received 8 December 2004 / Accepted 5 September 2006
Abstract
A new method is presented for determining the point
spread function (PSF) of images that lack bright and isolated
stars. It is based on the same principles as the MCS image
deconvolution algorithm. It uses the
information contained in all stellar images to achieve
the double task of reconstructing the PSFs for single or multiple
exposures of the same field and to extract the photometry of
all point sources in the field of view. The use of the full
information available allows us to construct an accurate PSF. The
possibility to simultaneously consider several exposures makes it
well suited to the measurement of the
light curves of blended point sources from data that would be
very difficult or even impossible to analyse with traditional PSF
fitting techniques.
The potential of the method for the
analysis of ground-based and space-based data is tested on
artificial images and illustrated by several examples, including
HST/NICMOS images of a lensed quasar and VLT/ISAAC images of
a faint blended Mira star in the halo of the giant elliptical
galaxy NGC 5128 (Cen A).
Key words: techniques: image processing - techniques: photometric
In recent years, the importance of point source CCD photometry has grown for, among other applications, the determination of colour-magnitude diagrams for stellar clusters, the study of variable stars in clusters or in external galaxies and the search for microlensing events and for planetary transits in light curves, by experiments such as OGLE (e.g. Udalski et al. 2003).
When the stars are sufficiently isolated, aperture photometry may provide quite reliable results. However, this is seldom the case, and techniques based on PSF fitting have to be used when the stellar images overlap. The most popular of these crowded field photometry methods is undoubtedly DAOPHOT (Stetson 1987). In such methods, the PSF is generally determined from the shape of sufficiently isolated point sources.
However, it may happen that the crowding of the field is such that no star is sufficiently isolated to allow a reliable PSF determination. This may severely affect the photometric precision as any error in the PSF will translate in photometric errors for blended stars, which will be accurately separated only if the PSF used in the fitting procedure is the correct one.
In such very crowded fields, it is necessary to use a PSF determination method that is able to give accurate results even in situations where all stars are blended to some degree. This is the aim of the present paper, which combines image deconvolution and PSF determination to reach better performance in both areas and, as a consequence, to provide excellent photometric accuracy.
It has also recently become clear that astronomical image deconvolution is a useful tool for reaching higher spatial resolution and extracting quantitative and precise information from the data. It should not simply be considered as a way to improve low quality images, or as a competitor to other techniques but rather as a complementary method, which better allows us to take full advantage of the existing or future observational techniques.
For example, the Hubble Space Telescope (HST), which has a PSF with a very compact core, still suffers from low frequency blurring due to its extended and complex wings. This is also the case for PSFs obtained with adaptive optics intruments and will be true with the future Extremely Large Telescopes, all using adaptive optics. These extended wings (and in fact also the high frequency signal due to the core of the PSF) can often be efficiently removed by adequate deconvolution methods, at a cost that is negligible compared to the instrument itself.
Similarly to crowded field photometry, the quality of the deconvolution critically depends on the accuracy of the PSF determination. The present paper describes a method that simultaneously allows one to obtain accurate PSFs and to solve the deconvolution problem in fields dominated by point sources, even when the crowding is so severe that all stars are significantly blended.
While deconvolution can be a powerful technique, it is also a
mathematically ill-posed problem. Many algorithms have been proposed
to deconvolve images, but generally with rather modest success. In a
previous paper (Magain et al. 1998; hereafter MCS),
we have shown that one of the main problems with the existing methods
is that they try to recover the light distribution at full resolution,
i.e. as it would be obtained with a perfect instrument (e.g. a space
telescope of infinite size). As the light distribution is not
modelled as a continuous function, but represented on a pixel grid,
with finite pixel size ![]() ,
the sampling theorem implies that
only frequency components up to the Nyquist frequency
,
the sampling theorem implies that
only frequency components up to the Nyquist frequency
![]() can be correctly taken into account. Components of higher
frequency are mixed up with the lower frequency ones by the aliasing
phenomenon and are responsible for some of the artefacts that appear
when using most deconvolution techniques.
can be correctly taken into account. Components of higher
frequency are mixed up with the lower frequency ones by the aliasing
phenomenon and are responsible for some of the artefacts that appear
when using most deconvolution techniques.
In MCS, we have shown that better results can be obtained if one does not attempt to recover the light distribution at infinite resolution, but rather at an improved resolution, which is still compatible with the pixel size chosen to represent the data.
Thus, if
![]() is the total PSF of the observed image
is the total PSF of the observed image
![]() ,
and
,
and
![]() the narrower PSF of the deconvolved
image
the narrower PSF of the deconvolved
image
![]() ,
one should apply a deconvolution kernel
,
one should apply a deconvolution kernel
![]() so
that:
so
that:
| (1) |
In addition, the PSF of the deconvolved image is known, since it is
the function
![]() ,
which is chosen by the user. We thus know
that all point sources will have the same form
,
which is chosen by the user. We thus know
that all point sources will have the same form
![]() ,
and this
prior knowledge may be used to write the solution as:
,
and this
prior knowledge may be used to write the solution as:
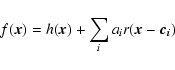 |
(2) |
Moreover, as
![]() itself must satisfy the sampling theorem,
and corresponds to an image obtained with a PSF
itself must satisfy the sampling theorem,
and corresponds to an image obtained with a PSF
![]() ,
MCS
introduce a smoothing term which removes the variations of
,
MCS
introduce a smoothing term which removes the variations of
![]() on a scale length shorter than allowed by
on a scale length shorter than allowed by
![]() .
.
The MCS method has proven able to provide reliable and sometimes quite spectacular results (e.g., Courbin et al. 1997, 1998; Jablonka et al. 2000; Courbin et al. 2000). However, it is obvious that the quality of the deconvolution not only depends on the quality of the algorithm but also on the accuracy of the PSF determination, a point that was not thoroughly addressed in the original MCS paper where the PSF was assumed to be known.
In practice, the PSF is generally determined from the images of point sources (i.e., stars) that are sufficiently isolated. However, in some cases, the fields are so crowded that no isolated point source can be found. We present a method which allows to determine accurate PSFs, especially in critical cases such as crowded fields. Such reliable PSFs are not only essential for meaningful deconvolution, but also for obtaining accurate point source photometry in crowded fields. The algorithm presented here addresses both issues.
In the following, we only consider astronomical images for which the PSF is approximately constant throughout the field of view. This is generally not fully true for real astronomical images but, in most cases, one can restrict the work to small enough areas where the PSF is approximately constant. Note that this is not a problem in crowded stellar fields, where enough stars are available to determine the PSF, even in relatively small subfields.
The usual way to obtain the PSF of an astronomical image is to derive
it from the shape of isolated point sources. The total PSF
![]() corresponds to the shape of such a point source, after recentering and
normalization to a total intensity of 1. This can only be done when
at least one isolated point source of adequate intensity is available
in the field. There exist two classes of images for which this
simple PSF determination is not possible: (1) when no point source is
present and (2) when there are so many point sources than none of them is
sufficiently isolated. We shall deal with the second case (crowded
fields), which is common in a large number of astronomical
observations, such as the galactic plane, dense star clusters or
external galaxies.
corresponds to the shape of such a point source, after recentering and
normalization to a total intensity of 1. This can only be done when
at least one isolated point source of adequate intensity is available
in the field. There exist two classes of images for which this
simple PSF determination is not possible: (1) when no point source is
present and (2) when there are so many point sources than none of them is
sufficiently isolated. We shall deal with the second case (crowded
fields), which is common in a large number of astronomical
observations, such as the galactic plane, dense star clusters or
external galaxies.
Let
![]() be the observed light distribution,
be the observed light distribution,
![]() the
light distribution at a better resolution (as would be observed at
infinite S/N with an instrument of PSF
the
light distribution at a better resolution (as would be observed at
infinite S/N with an instrument of PSF
![]() )
and
)
and
![]() the noise in the observed image. Then:
the noise in the observed image. Then:
| (3) |
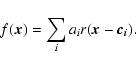 |
(4) |
However, while we know that
![]() may be written in the form (4), we do not know the values of the coefficients ai and
may be written in the form (4), we do not know the values of the coefficients ai and ![]() .
They can thus be considered as free parameters, which will be
determined simultaneously with the PSF
.
They can thus be considered as free parameters, which will be
determined simultaneously with the PSF
![]() .
.
If we consider an image with N pixels, containing M point sources, we are left with the problem of determining N + 3M parameters, i.e. N pixel values of the PSF and 3 parameters for each point source (one intensity and two coordinates). In practice, however, the PSF often has significant values in an area much smaller than the field considered. In such a case, the number of free parameters decreases significantly.
The free parameters are obtained by minimizing the following function:
![\begin{displaymath}{\cal S} = \sum_{j} \frac{1}{\sigma_j^2} (d_j - [s \ast f]_j)^2 + \lambda H(s)
\end{displaymath}](/articles/aa/full/2007/01/aa2505-04/img25.gif) |
(5) |
![\begin{displaymath}H(s) = \sum_{j} (s_j - [g \ast s]_j)
\end{displaymath}](/articles/aa/full/2007/01/aa2505-04/img27.gif) |
(6) |
![\begin{displaymath}\chi^2 = \sum_{j} \frac{1}{\sigma_j^2} (d_j - [s \ast f]_j)^2 \simeq N.
\end{displaymath}](/articles/aa/full/2007/01/aa2505-04/img31.gif) |
(7) |
To illustrate this, let us consider the determination of the PSF from the images of stars in a crowded field and focus on a particular star in that field. The presence of neighbouring peaks in the image may be interpreted as due either to neighbouring stars or to bumps in the PSF. Even if all stars present in the field are considered explicitly in Eq. (4), once the algorithm attemps to minimize (5), it could interpret part of the light in a point source as a bump in the PSF of a neighbouring one. Indeed, the function (5) is likely to have local minima with part of the light in the center of point sources attributed to bumps in the PSF wings.
To avoid such local minima, we proceed in the following way.
First, the PSF is approximated by either an analytic or a known
numerical function (e.g., a sum of Gaussians or a Moffat function).
These functions are fitted to the point sources by least squares
minimization. This first fit provides approximate values for the
intensities ai and the centers ![]() of the point sources, as
well as a very rough estimate of the PSF shape. In construction,
these analytic estimates of the PSF cannot contain bumps in the wings.
of the point sources, as
well as a very rough estimate of the PSF shape. In construction,
these analytic estimates of the PSF cannot contain bumps in the wings.
In a second step, we add a numerical component to that analytic estimate of the PSF. In order to avoid the aforementioned problem of bumps in the wings, we start by adding these numerical residuals in the central region of the PSF and, as the fit proceeds, we gradually extend the region considered. This ensures that the algorithm will attempt to fit the central parts of all stellar images by appropriate intensities in the center pixels of the PSF, and not by bumps in the wings, since the wings are modified only after the center intensities have been correctly fitted. The smoothing constraint (6) is applied to the numerical component only, and not to the first analytic estimate.
In the case of HST images, the fit of an analytic function in the first step is replaced by the fit of a numerical estimate of the PSF, as computed with the Tiny Tim package (Krist & Hook 2004). So, approximate intensities and positions are also obtained for all point sources and, since the PSF shape is fixed at that stage, no unwanted bump can appear in the wings. The second step is the same as for ground-based images: an additional numerical component is added in order to improve the agreement between the PSF and the observed point source images.
The Tiny Tim software computes the total PSF
![]() and not
and not
![]() .
In practice, we found that the results can
be improved by proceeding in two steps. First, the kernel
.
In practice, we found that the results can
be improved by proceeding in two steps. First, the kernel
![]() is
determined from the synthetic image of
is
determined from the synthetic image of
![]() obtained with the
Tiny Tim software. The extremely high S/N of that synthetic image allows
an accurate determination of
obtained with the
Tiny Tim software. The extremely high S/N of that synthetic image allows
an accurate determination of
![]() even if the first approximation
(which we take as the Tiny Tim image itself) is rather far from the
solution, especially in the core. In a second step, this approximate
even if the first approximation
(which we take as the Tiny Tim image itself) is rather far from the
solution, especially in the core. In a second step, this approximate
![]() obtained from a deconvolution of the Tiny Tim image is
used as a first approximation of the PSF to be determined on the
observed images, a first approximation to which a numerical component will
be added.
obtained from a deconvolution of the Tiny Tim image is
used as a first approximation of the PSF to be determined on the
observed images, a first approximation to which a numerical component will
be added.
The number of point sources, as well as the initial guess of their positions and intensities, are determined by using a standard algorithm for detecting point source, such as the DAOFIND task included in DAOPHOT (Stetson 1987). This first guess allows us to obtain a first approximation of the PSF. Then, the image of the residuals is inspected, which allows us to identify areas where the fit is not satisfactory. Additional point sources are added in these areas, until the fit becomes satisfactory. This allows us to improve the accuracy of the PSF which, in turn, allows us to detect fainter blending stars, so that the method simultaneously converges towards higher accuracy in astrometry, photometry and PSF recovery.
In its present form, the program,
running on a standard PC, takes about 1 h to completely process a
![]() image with 25 sources and up to 10 h with 100 sources. It is
thus significantly slower than, e.g., DAOPHOT, which is not surprising since
we put emphasis on the accuracy of the results rather than on the speed.
However, considerable time is saved in the case of a photometric monitoring,
where the sources positions do not need to be recomputed each time (Gillon et al. 2006). Moreover, we are working on the algorithm for finding the
minimum of the function
image with 25 sources and up to 10 h with 100 sources. It is
thus significantly slower than, e.g., DAOPHOT, which is not surprising since
we put emphasis on the accuracy of the results rather than on the speed.
However, considerable time is saved in the case of a photometric monitoring,
where the sources positions do not need to be recomputed each time (Gillon et al. 2006). Moreover, we are working on the algorithm for finding the
minimum of the function ![]() (Eq. (5)), which can also be significantly
improved in terms of computing time.
(Eq. (5)), which can also be significantly
improved in terms of computing time.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{2505fig1.ps}
\end{figure}](/articles/aa/full/2007/01/aa2505-04/Timg33.gif) |
Figure 1: Synthetic images used to check the PSF recovery and photometric accuracy versus crowding. From top left to bottom right: fields containing 3, 6, 12, 25, 50 and 100 stars. Not all stars are visible on the figure because of blending and of the 7.5 mag range. |
| Open with DEXTER | |
We use simulated ground-based observations in order to test the accuracy of the PSF determination and of the photometry (1) as a function of the crowding and (2) as a function of the S/N.
The influence of crowding is tested on six images with the same size, same
PSF and same typical S/N but different numbers of stars in the field, namely 3, 6, 12, 25, 50 and 100. All these images have
![]() pixels, the
PSF has an 8 pixel Full Width at Half Maximum (FWHM) and is constructed as the
sum of two Gaussians, a
first one representing the core and a second one, about two times broader,
accounting for the wings. These two Gaussians have elliptical isopohotes but
their major axes are perpendicular to each other, so that they cannot be well
fitted by a Moffat function. This is not a very favourable case for our
algorithm, since the analytical fit provides a rather poor approximation of
the PSF and the numerical component is thus important.
pixels, the
PSF has an 8 pixel Full Width at Half Maximum (FWHM) and is constructed as the
sum of two Gaussians, a
first one representing the core and a second one, about two times broader,
accounting for the wings. These two Gaussians have elliptical isopohotes but
their major axes are perpendicular to each other, so that they cannot be well
fitted by a Moffat function. This is not a very favourable case for our
algorithm, since the analytical fit provides a rather poor approximation of
the PSF and the numerical component is thus important.
The stars are positioned at random and their intensities are also randomly generated, with a uniform distribution in magnitude and a range of 7.5 mag (i.e. a factor 1000 in intensity). We add a sky background of about 30 e-/pixel. The S/N in the center of the stellar images varies from less than 1 for the faintest stars to about 70 for the brightest ones.
The six simulated images are displayed in Fig. 1, which shows that we go from isolated stars up to such a crowding that all stars are more or less severely blended: in the latter case, the average separation between stars is close to the PSF FWHM.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{2505fig2.ps}\end{figure}](/articles/aa/full/2007/01/aa2505-04/Timg34.gif) |
Figure 2:
Difference between the reconstructed PSF and the exact one, as a
function of crowding. The grey scale goes from |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{2505fig3.ps}
\end{figure}](/articles/aa/full/2007/01/aa2505-04/Timg35.gif) |
Figure 3: Standard deviation of the PSF residuals (in logarithmic scale) versus logarithm of the number of stars in the field. Long dashes: PSF constructed from the image of the brightest star in the field, assumed to be perfectly centered and isolated. Short dashes: PSF constructed from the images of all stars in the field, assumed to be perfectly centered and isolated. Continuous line: our results. |
| Open with DEXTER | |
The differences between the reconstructed PSFs and the exact ones are shown in
Fig. 2, for the six cases considered. The standard
deviation of these residuals is computed in a circular aperture centered on
the PSF and of 32 pixels diameter, i.e. 4 times the PSF FWHM. This is the
area where the PSF intensities may be considered significant (>![]() of the
peak intensity). These standard deviations, in units of the PSF peak
intensity, are plotted in Fig. 3 and compared with the
results which would be obtained in two special cases. First, the PSF that
would be given by the image of the brightest star in the field should it be
completely isolated and, secondly, the PSF that would be deduced from all
stars in the field, should they all be isolated. Figure 3
shows that the recovered PSF is always more accurate than what would
be deduced from the image of the brightest star, the improvement increasing
with the crowding of the field. This means that the advantage provided by the
additional signal more than compensates the handicap due to blending. In the
first four images (number of stars less than 50), our recovered PSF is even
better than the one obtained by summing all the stars in the
field, if they were isolated. Although this might appear unphysical, this is
due to the way we determine the PSF, first by the fit of an analytical
function, then by imposing a smoothing constraint on the numerical residuals.
This results in an efficient correction for the photon noise, which has
Fourier components at significantly higher frequencies than our well sampled
PSF. When the number of stars grows, the relative photon noise decreases and
its reduction by the algorithm no longer can compensate for the effect of
blending, which also becomes more severe.
of the
peak intensity). These standard deviations, in units of the PSF peak
intensity, are plotted in Fig. 3 and compared with the
results which would be obtained in two special cases. First, the PSF that
would be given by the image of the brightest star in the field should it be
completely isolated and, secondly, the PSF that would be deduced from all
stars in the field, should they all be isolated. Figure 3
shows that the recovered PSF is always more accurate than what would
be deduced from the image of the brightest star, the improvement increasing
with the crowding of the field. This means that the advantage provided by the
additional signal more than compensates the handicap due to blending. In the
first four images (number of stars less than 50), our recovered PSF is even
better than the one obtained by summing all the stars in the
field, if they were isolated. Although this might appear unphysical, this is
due to the way we determine the PSF, first by the fit of an analytical
function, then by imposing a smoothing constraint on the numerical residuals.
This results in an efficient correction for the photon noise, which has
Fourier components at significantly higher frequencies than our well sampled
PSF. When the number of stars grows, the relative photon noise decreases and
its reduction by the algorithm no longer can compensate for the effect of
blending, which also becomes more severe.
The accuracy of the photometry is checked in the following way. First, we
compute the error
![]() in the intensity of the source ai, which is
also the total flux in the stellar image since the PSF is normalized. This
error is simply the value returned by the algorithm minus the exact value used
to build the simulated image. Then, we compute a theoretical estimate of the
standard error by assuming that the PSF is fitted by least squares on the
image of a single (eventually blended) star, and that all other stars
have previously been perfectly fitted (i.e. with their exact positions and
intensities). This gives:
in the intensity of the source ai, which is
also the total flux in the stellar image since the PSF is normalized. This
error is simply the value returned by the algorithm minus the exact value used
to build the simulated image. Then, we compute a theoretical estimate of the
standard error by assuming that the PSF is fitted by least squares on the
image of a single (eventually blended) star, and that all other stars
have previously been perfectly fitted (i.e. with their exact positions and
intensities). This gives:
![\begin{displaymath}\frac{\sigma(a)}{a} = \left[ \sum_{j} \left(\frac{a s_j}{\sigma_j}\right)^2 \right]^{-1/2}
\end{displaymath}](/articles/aa/full/2007/01/aa2505-04/img38.gif) |
(8) |
Note that, in the case of a single star and no sky background, this formula
reduces to
![]() ,
i.e. pure Poisson noise, as
expected. The extra noise due to blends is taken into account in
,
i.e. pure Poisson noise, as
expected. The extra noise due to blends is taken into account in ![]() ,
in which the noise corresponding to all stars is included. Thus, all stars
blending the star considered will contribute to an increase of the
uncertainty. However, this formula does not take into account errors in the
photometry due to inaccurate fitting of the neighbouring stars (i.e. it
neglects the covariance terms) and is thus expected to be somewhat optimistic.
,
in which the noise corresponding to all stars is included. Thus, all stars
blending the star considered will contribute to an increase of the
uncertainty. However, this formula does not take into account errors in the
photometry due to inaccurate fitting of the neighbouring stars (i.e. it
neglects the covariance terms) and is thus expected to be somewhat optimistic.
The accuracy of the photometry is quantified by:
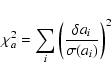 |
(9) |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{2505fig4.ps}
\end{figure}](/articles/aa/full/2007/01/aa2505-04/Timg42.gif) |
Figure 4:
Difference between the reconstructed PSF and the exact one, as a
function of S/N. The grey scale goes from |
| Open with DEXTER | |
The influence of S/N on the PSF accuracy is tested in a similar way. We use
the image with 50 stars discussed in the previous subsection and vary the
exposure level over a large range, i.e. from 30 to 10 000 e-/pixel in
the center of the brightest star. This corresponds to an integrated S/Nvarying from about 20 to 1000 for the brightest star in the field.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2505fig5.eps}\par
\end{figure}](/articles/aa/full/2007/01/aa2505-04/Timg43.gif) |
Figure 5: Standard deviation of the PSF residuals (in logarithmic scale) versus logarithm of peak intensity (see text). Long dashes: PSF constructed from the image of the brightest star in the field, assumed to be perfectly centered and isolated. Short dashes: PSF constructed from the images of all stars in the field, assumed to be perfectly centered and isolated. Continuous line: our results. |
| Open with DEXTER | |
The differences between the reconstructed PSFs and the exact ones are shown in Fig. 4. The standard deviation of these residuals is computed in the same circular aperture as above and compared with the same 2 cases as in the previous subsection. Figure 5 shows that our results are always better than the ones that would be obtained from the brightest star, if it was isolated. At low to moderate S/N (brightest star peak intensity <1000 e-, integrated S/N < 300), our results are also better than what would be obtained from summing all stellar images, assuming they were isolated. Again, this is due to the fact that the smoothing term reduces the effect of the photon noise. At high S/N (400 to 1000), the contribution of the photon noise becomes relatively smaller and its reduction no longer compensates for the degradation due to crowding. Nevertheless, the accuracy of the recovered PSF continuously improves with increasing S/N, as expected.
The accuracy of the photometry as a function of S/N is quantified in the same
way as in the previous subsection. As the S/N increases, the photometry
becomes more accurate, but not as much as Eq. (8) predicts. Indeed,
this equation does not take into account errors coming from inaccuracies in
neighbouring stars (correlated errors). At low S/N, these correlated errors
are much lower than the random ones. However, as the random errors obviously
decrease with increasing S/N, the correlated errors start to play a role, and
the reduced ![]() grows from
grows from ![]() 1 at low S/N to 1.5 at
1 at low S/N to 1.5 at
![]() and 1.9 at
and 1.9 at
![]() (the indicated S/N are the integrated ones for
the brightest star in the field). Thus, even at the highest S/N, the
photometric errors are only about
(the indicated S/N are the integrated ones for
the brightest star in the field). Thus, even at the highest S/N, the
photometric errors are only about ![]() larger than would be
expected in the ideal case (zero correlation). They
can be reduced if the stars'positions can be constrained from many
observations, as is the case in a photometric monitoring.
larger than would be
expected in the ideal case (zero correlation). They
can be reduced if the stars'positions can be constrained from many
observations, as is the case in a photometric monitoring.
One of the main applications of the MCS algorithm, in its original form, was to deconvolve not only an image of a given object, but also a whole set of images of the same object. In such a case the deconvolution process computes a unique sharpened image compatible with all the images of the dataset simultaneously, hence the name simultaneous deconvolution. This specificity of the MCS algorithm has been transposed to the present method. It allows us to determine simultaneously the PSFs for a series of images. If the individual images have been taken at different epochs, the intensities of all point sources in the field are left free during the deconvolution process, leading to the construction of a genuine light curve for all objects.
In such a case, instead of seeking the minimum of a function ![]() which is the sum of a
which is the sum of a ![]() and a smoothing term (Eq. (5)),
one seeks the minimum of a function which is the sum of a
and a smoothing term (Eq. (5)),
one seeks the minimum of a function which is the sum of a ![]() for each of the images considered plus one smoothing term per image.
The PSFs and the source intensities are allowed to vary from image
to image, but the source positions are common to all images. A
translation of the whole image is however allowed to account for
different centerings of the various exposures. All these parameters
(source positions, source intensities, translations and PSF shapes)
are simultaneously determined by the minimization algorithm.
for each of the images considered plus one smoothing term per image.
The PSFs and the source intensities are allowed to vary from image
to image, but the source positions are common to all images. A
translation of the whole image is however allowed to account for
different centerings of the various exposures. All these parameters
(source positions, source intensities, translations and PSF shapes)
are simultaneously determined by the minimization algorithm.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{2505fig6.ps}
\end{figure}](/articles/aa/full/2007/01/aa2505-04/Timg49.gif) |
Figure 6:
Top left: H-band (F160W) HST/NICMOS observation of the
gravitational lens WFI2033-4723. Top right: simultaneous
deconvolution of 4 such images, on a
|
| Open with DEXTER | |
Even if the method presented here assumes that the data only contain point sources, one can adapt the algorithm to allow it to take into account faint diffuse objects.
WFI2033-4723, a quadruply imaged quasar lensed by a distant galaxy, provides a typical case where such a strategy can be applied. The top left panel of Fig. 6 shows a H-band HST/NICMOS observation of that gravitational lens.
A deconvolution of the Tiny Tim PSF (Krist & Hook 2004) is used as
a first approximation of
![]() ,
which is then modified to provide the
best possible deconvolution of the input image, which is first assumed to
contain only four point sources. As the image actually contains a diffuse
background (the lensing galaxy) in addition to the point sources, part of that
background is interpreted as increased PSF wings and another part appears in
the residuals (observed image minus reconvolved model). This latter part may
be subtracted from the original image, which thus allows one to correct for a
part of the diffuse background. That corrected image may then be used to
obtain an improved PSF.
,
which is then modified to provide the
best possible deconvolution of the input image, which is first assumed to
contain only four point sources. As the image actually contains a diffuse
background (the lensing galaxy) in addition to the point sources, part of that
background is interpreted as increased PSF wings and another part appears in
the residuals (observed image minus reconvolved model). This latter part may
be subtracted from the original image, which thus allows one to correct for a
part of the diffuse background. That corrected image may then be used to
obtain an improved PSF.
Applying that procedure iteratively allows us to obtain a PSF which, at each iteration, contains a smaller contamination by the diffuse background. Once that procedure has converged, the PSF is used as input for deconvolution of the original image by the classical MCS algorithm, including a diffuse background.
The result is shown in the top right panel of Fig. 6. The bottom
left panel of Fig. 6 shows the PSF kernel
![]() obtained from deconvolving the PSF computed with the Tiny Tim software while
the bottom right panel shows the numercial component which has to be added to
the former PSF kernel in order to obtain a good deconvolution of the input
image.
obtained from deconvolving the PSF computed with the Tiny Tim software while
the bottom right panel shows the numercial component which has to be added to
the former PSF kernel in order to obtain a good deconvolution of the input
image.
This method has been applied to more complex cases, such as the Cloverleaf gravitational lens H1413+117 (Magain et al. 1988). In that case, it allows us to detect the lensing galaxy as well as part of an Einstein ring, which is completely hidden in the original data (Chantry et al., in preparation).
With the increasing performances of modern telescopes, it becomes
possible to study the stellar populations of objects that were so far
unresolved under standard seeing conditions, around 1
![]() .
One can
even start to resolve (nearby) galaxies into stars and to construct
actual colour-magnitude diagrams. However, while the resolution of the
observations improves, the field of view often decreases, making it
very difficult or even impossible to observe at the same time the
field of interest and the relatively bright, isolated stars
generally required to build the PSF.
.
One can
even start to resolve (nearby) galaxies into stars and to construct
actual colour-magnitude diagrams. However, while the resolution of the
observations improves, the field of view often decreases, making it
very difficult or even impossible to observe at the same time the
field of interest and the relatively bright, isolated stars
generally required to build the PSF.
The search for faint blended variable stars in nearby galaxies is one of the topics directly influenced by the quality of the available PSF. Rejkuba et al. (2003) have found dozens of Mira stars in the halo of the giant elliptical galaxy NGC 5128 (Centaurus A), but also note that strong blends often hamper the accurate measurement of periods. This occurs because the Mira itself can be in a close blend, but also often because the field where it lies is far away from any suitable PSF star. Our method computes the PSF directly from all the stars, blended or not, in the field of view, hence taking advantage of the total S/N of all available point sources. The PSF is also representative of the instrumental/atmospheric blurring at the position of the object of interest in the image.
We have selected one of the Mira candidates found by Rejkuba et al. (2003) using VLT K-band images. The region used for the deconvolution is a subset of the whole image obtained. Figure 7 presents a sample of three images of the same field, taken at different epochs, with very different seeings. The photometry of the Mira star has been carried out on the 21 data frames available and a phase diagram could be constructed, as displayed in the bottom panel of Fig. 8. The photometric uncertainties, estimated from the scatter in the light curve of a constant star of the same magnitude as the Mira, amount to 0.05 mag, as compared to an average of 0.15 mag with the PSF-fitting method. Not only the error bars on the individual photometric points improve by a factor of almost 3 when compared with classical methods (top and middle panels of Fig. 8), but also the period obtained is different. The frequency peaks found in the Fourier analysis of the light curves with the present algorithm are much stronger than with the classical method. The 446 day period is clearly pointed out by the Fourier analysis, while the 246 day period supported by the classical PSF fitting no longer yields a prominent peak.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{2505fig7.ps}
\end{figure}](/articles/aa/full/2007/01/aa2505-04/Timg50.gif) |
Figure 7:
Zoom on a Mira star in the halo of the radio galaxy NGC 5128
(Centaurus A), selected from Rejkuba et al. 2003. Three
VLT K-band images with very different seeing conditions are shown
on the top panels. The exposure time is the same in
all three exposures: 3600 s. The pixel size is 0.144
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2505fig8.ps}
\end{figure}](/articles/aa/full/2007/01/aa2505-04/Timg51.gif) |
Figure 8:
Top panel: light curve (shown here as phase diagram)
of the Mira presented in Fig. 7, as obtained with
standard PSF fitting techniques (DAOPHOT-ALLFRAME). The PSFs are
computed independently in the individual frames from relatively
isolated stars in the field of view, well outside the field
of Fig. 7. The 1 |
| Open with DEXTER | |
The deconvolution-based algorithm presented here has been designed to compute accurate PSFs in fields very crowded with point sources. It not only computes the PSF but also provides the photometry and astrometry of all point sources in the field of view. The algorithm can be applied to single images or to a set of images of a given field. In the latter case, the images are processed simultaneously, in the sense of the MCS deconvolution algorithm: a PSF is computed for each image, by considering all images simultaneously. The photometry of all points sources is obtained for all images in the dataset, i.e., light curves are directly produced.
The method is clearly useful when few or no isolated PSF stars are available in the field of view, in the case of extreme crowding and in the case of strong PSF variation accross the field (in which case the PSF has to be determined from stars very close to the target). It is also very efficient in extracting photometric information from datasets of very heterogeneous quality (e.g., with a broad range of seeing values). In this case, the astrometry of the point sources in the best seeing data effectively constrains the astrometry of the bad seeing data, as long as all the data are processed simultaneously.
Although the present method is not designed to handle images that consist of a mixture of point sources and extended ones, it can treat extended objects that are faint in comparison to the point sources, by running the algorithm in an iterative way.
Acknowledgements
The authors would like to thank Marina Rejkuba for providing the VLT images of the Mira stars presented in Fig. 7, as well as for all the technical details on how they were reduced and calibrated. This work has been supported by ESA and the Belgian Federal Science Policy Office under contracts PRODEX 90195 and Pôle d'Attraction Interuniversitaire P5/36. FC acknowledges financial support from the Swiss National Science Foundation (SNSS).